Optimization Design Method and Experimental Validation of a Solar PVT Cogeneration System Based on Building Energy Demand
Abstract
:1. Introduction
2. PVT Collector Description
3. Building Energy Demand and Solar PVT Cogeneration System Design
3.1. Target Building Overview and Energy Load Calculation
3.1.1. Statistical Calculation of Building Electricity Load
3.1.2. Calculation of the Building Heating Load
3.2. System Optimization Design
3.2.1. Thermal Modeling
- (1)
- The heat capacity of PVT collector has been neglected, and the system is in a quasi-steady state;
- (2)
- The system flow rate is stable, and the Reynolds number for the fluid flowing through the single collector is the same as in the collectors connected in series;
- (3)
- The energy collected by the system can be effectively used;
- (4)
- The correction of the total heat loss coefficient and the effective transmittance of module due to the heat loss of the inlet and outlet pipes have been considered;
- (5)
- The ohmic losses in the solar cell are negligible.
3.2.2. System Optimization Results
- (1)
- The total photovoltaic power generation of the system should be more than or at least equal to the electrical load demand of the building:
- (2)
- The total thermal energy generation of the system should be more than or at least equal to the heat load demand of the building:
- (3)
- The outlet water temperature should be higher than or at least equal to the heat supply temperature (it is set at 45 °C in this study):
- (4)
- The system is made up of the same kind of PVT collectors connected in series and in parallel, so the number M and N should be bigger than or at least equal to 1, as shown in Equation (27):
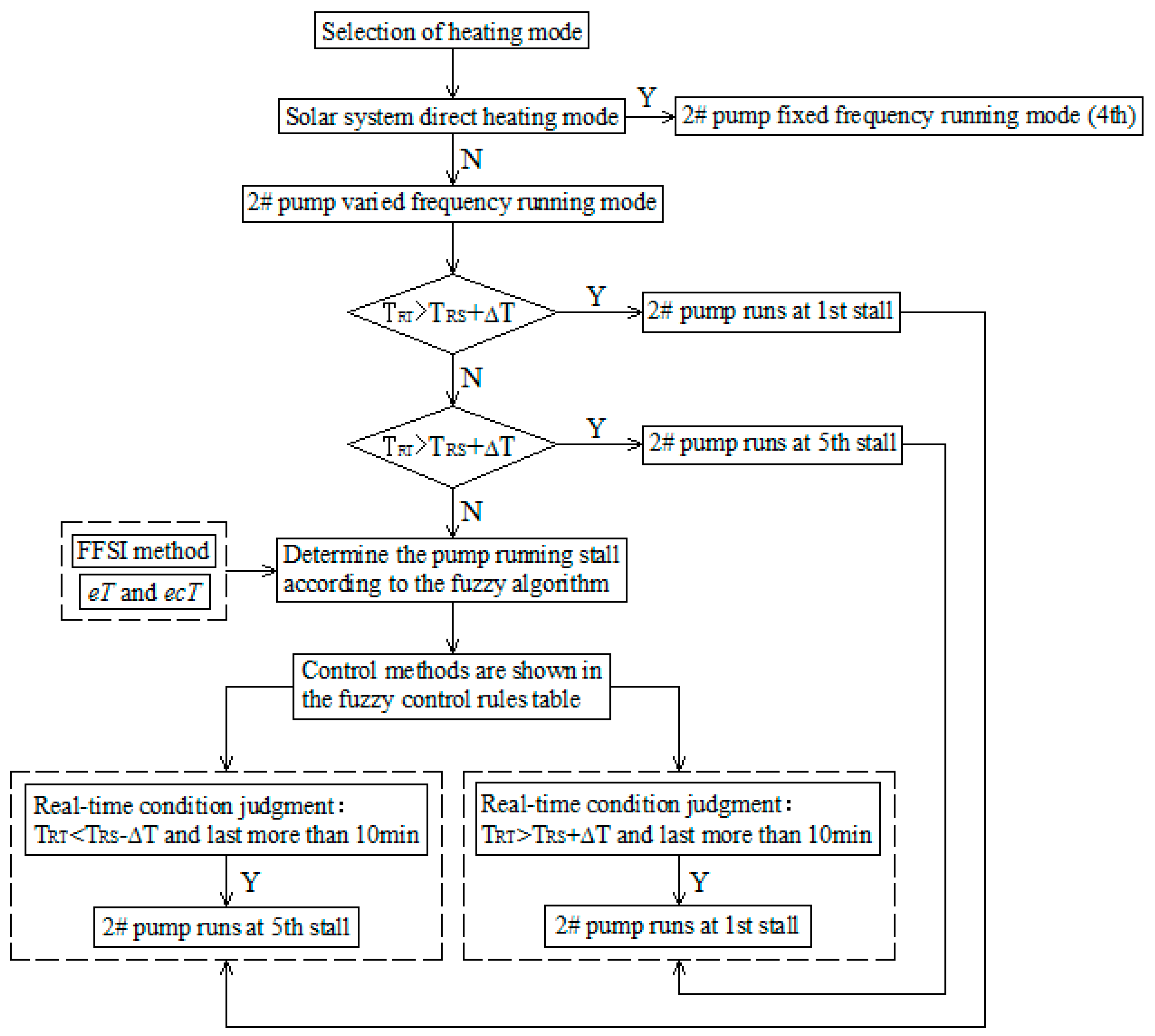
4. Adjustment and Control Method
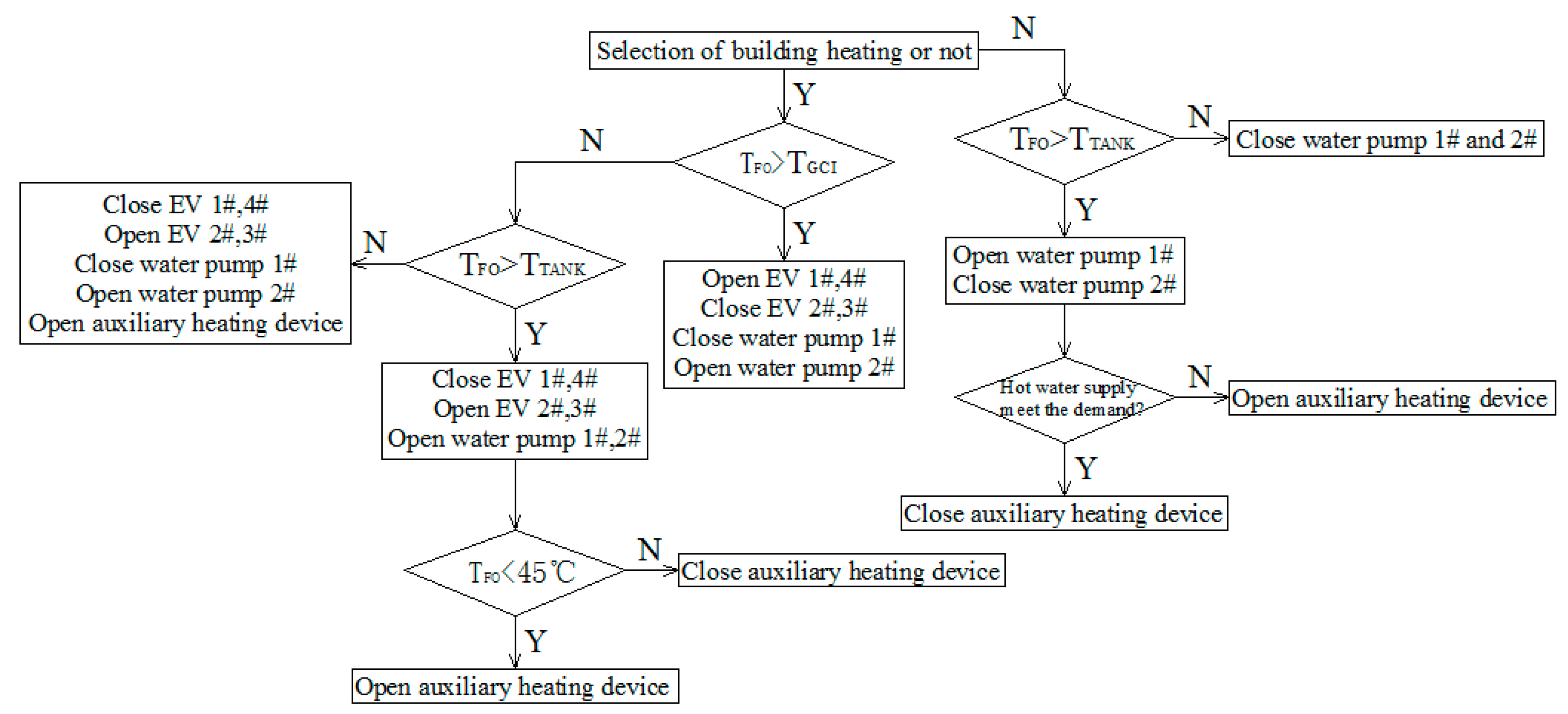
4.1. Pipeline Switching and Auxiliary Heating Device Control Method
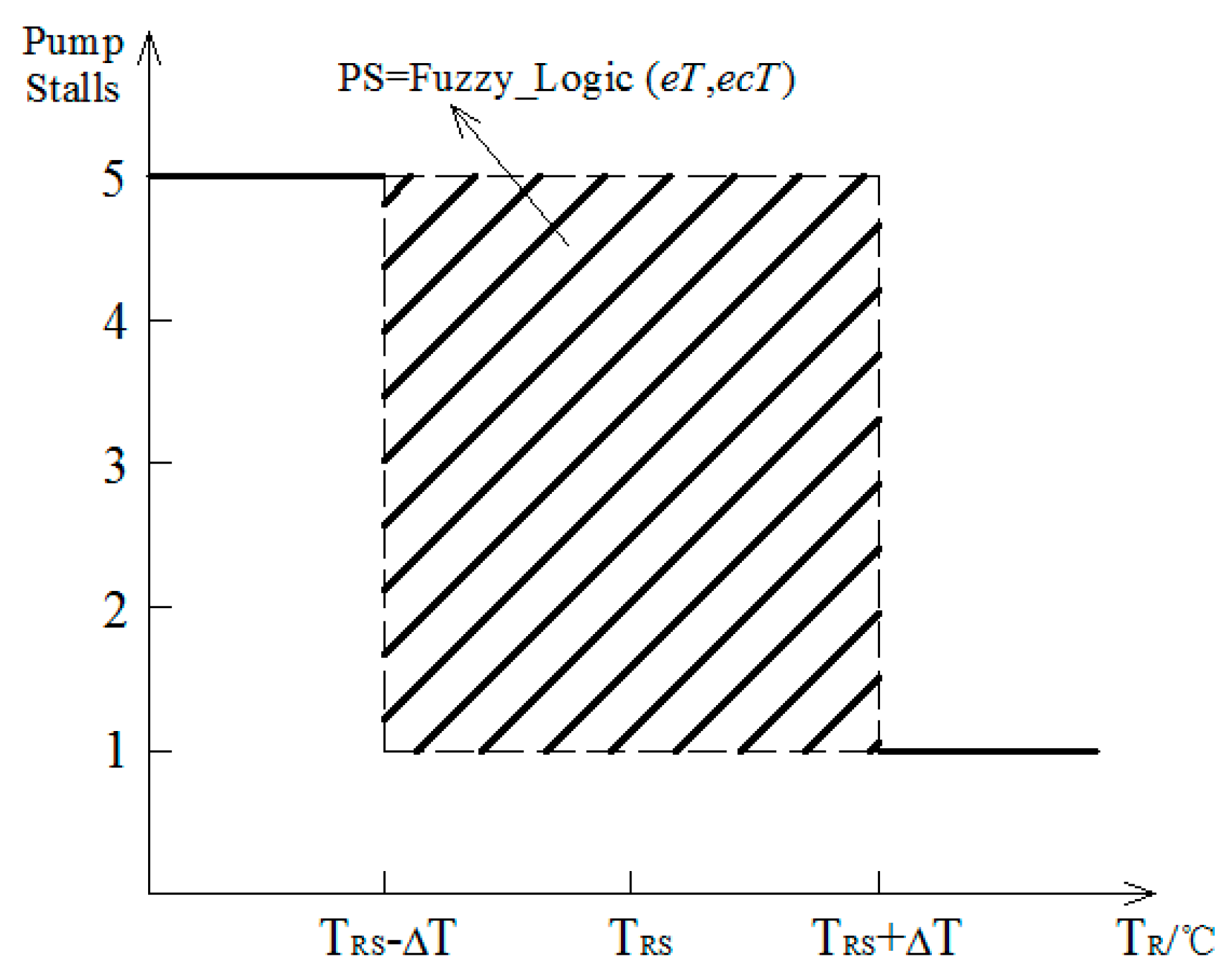
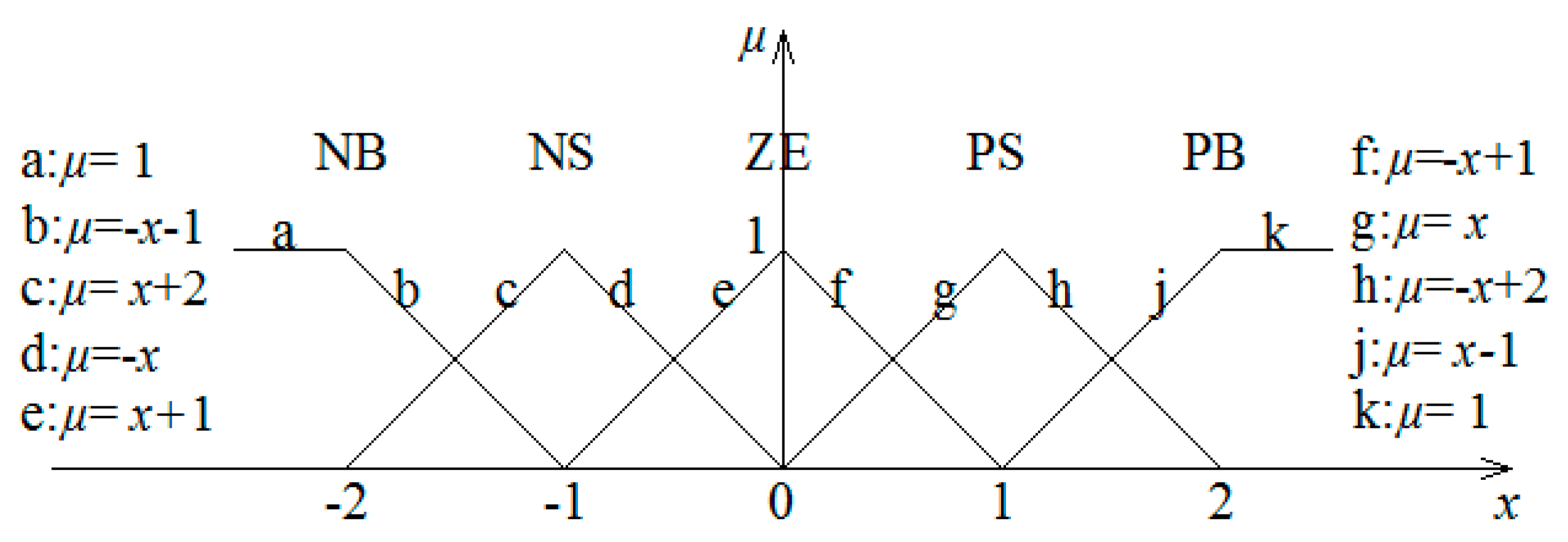
4.2. Circulating Water Pump Frequency Conversion Control Method
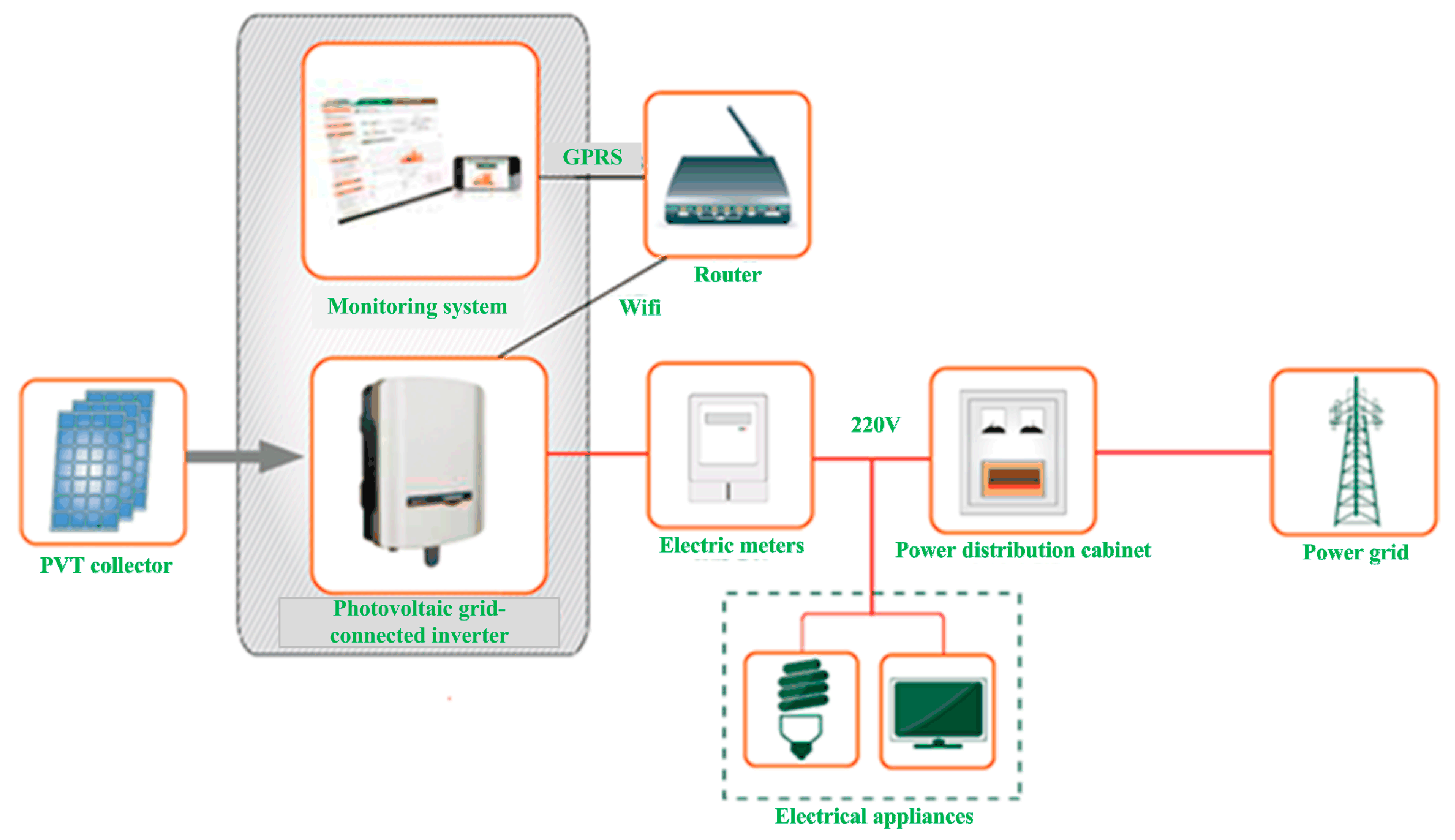
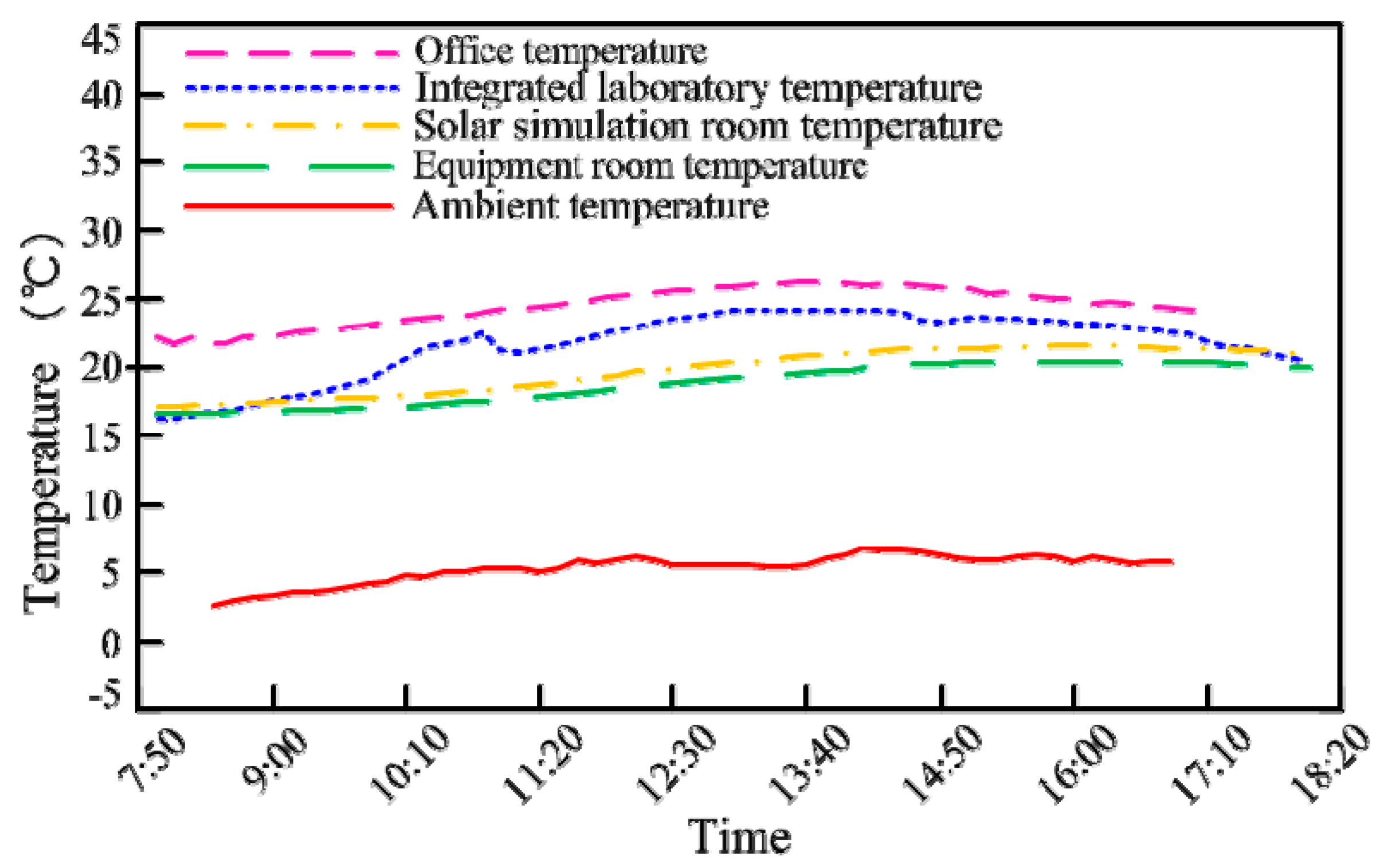
5. Experimental Study and Results Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Qj | the heating load caused by heat transfer of the building envelope, W |
| Ae | the area of the envelope, m2 |
| K | the heat transfer coefficient of the building envelope, W/(m2·°C) |
| Ta,c | the outdoor calculation temperature, °C |
| To,m | the interior set temperature, °C |
| b | the temperature correction coefficient |
| ε1 | the towards correction coefficient |
| ε2 | the outer door correction coefficient |
| ε3 | the height correction coefficient |
| Qi | the cold air penetration heat consumption, W |
| cp | the specific heat capacity of air, kJ/(kg·°C) |
| ρao | the density of air, g/L |
| Qu | the heat gain of PVT collector, W |
| A | the area of PVT collector, m2 |
| Ai | the outer surface area of the inlet water pipe, m2 |
| Ao | the outer surface area of the outlet water pipe, m2 |
| FR | the collector heat transfer factor |
| τ | the transmittance of the PVT collector glass cover |
| α | the absorptivity of solar PV module |
| It | solar radiation intensity, W/m2 |
| UL | overall heat transfer coefficient of the absorber plate, W/(m2·K) |
| Ti | inlet water temperature, °C |
| To | outlet water temperature, °C |
| Ta | ambient temperature, °C |
| N | number of PVT collectors connected in series |
| M | number of PVT collectors connected in parallel |
| the rate of flow of water mass, kg/s | |
| Cp | the specific heat of working fluid, J/(kg·K) |
| ηth,N | the heating efficiency of the system |
| ηCN | the temperature affected photovoltaic power generation efficiency of the Nth PVT collector |
| ηC | the photovoltaic efficiency of the solar cell under standard test conditions |
| TON | the outlet water temperature of the Nth PVT collector connected in series, °C |
| TCN | the temperature of solar cells of the Nth PVT collector, °C |
| TfN | the water temperature of the Nth PVT collector, °C |
| TpN | the temperature of absorber plate of the Nth PVT collector, °C |
| ηmN | the photovoltaic power efficiency of the Nth PVT collector connected in series |
| Quel,N | the total power generation of the system, W |
| Ud | overall heat transfer coefficient of the water pipe, W/(m2·K) |
| β | the packing factor of PVT collector |
| L | the length of PVT collector, m |
| W | the width of PVT collector, m |
| Utc,a | overall heat transfer coefficient from cell to the ambient from top surface, W/(m2·K) |
| Utc,p | overall heat transfer coefficient from cell to the absorber plate, W/(m2·K) |
| Utp,a | overall heat transfer coefficient from the absorber plate to the ambient, W/(m2·K) |
| Tc | temperature of the solar cell, °C |
| Tp | temperature of the absorber plate, °C |
| τg | the transmittance of the solar PV module glass cover |
| αc | the absorptivity of solar cell |
| αp | the absorptivity of the absorber plate |
| F’ | the collector efficiency factor |
| hpf | the heat transfer coefficient from the absorber plate to the water, W/(m2·K) |
| θPV | temperature coefficient of solar PV module, %/K |
| Tref | temperature of standard test conditions, 25 °C in this study |
References
- Florschuetz, L.W. Extension of the Hottel-Whillier model to the analysis of combined photovoltaic/thermal flat plate collectors. Sol. Energy 1979, 22, 361–366. [Google Scholar] [CrossRef]
- Buker, M.S.; Riffat, S.B. Building integrated solar thermal collectors—A review. Renew. Sustain. Energy Rev. 2015, 51, 327–346. [Google Scholar] [CrossRef]
- Bergene, T.; Lovvik, O.M. Model calculation on a flat-plate solar heat collector with integrated solar cells. Sol. Energy 1995, 55, 453–462. [Google Scholar] [CrossRef]
- Garg, H.P.; Agarwal, R.K. Some aspects of a PV/T collector: Forced circulation flat plate solar water heater with solar cells. Energy Convers. Manag. 1995, 36, 87–99. [Google Scholar] [CrossRef]
- Chow, T.T. Performance analysis of photovoltaic-thermal collector by explicit dynamic model. Sol. Energy 2003, 75, 143–152. [Google Scholar] [CrossRef]
- Chow, T.T.; He, W.; Ji, J. Hybrid photovoltaic-thermosiphon water heating system for residential application. Sol. Energy 2006, 80, 298–306. [Google Scholar] [CrossRef]
- He, W.; Chow, T.T.; Ji, J.; Lu, J.; Chan, L. Hybrid photovoltaic and thermal solar-collector designed for natural circulation of water. Appl. Energy 2006, 83, 199–210. [Google Scholar] [CrossRef]
- Hocine, H.B.C.; Touafek, K.; Kerrour, F. Theoretical and experimental studies of a new configuration of photovoltaic–thermal collector. J. Sol. Energy Eng 2017, 139, 021012. [Google Scholar] [CrossRef]
- Dubey, S.; Tiwari, G.N. Thermal modeling of a combined system of photovoltaic thermal (PV/T) solar water heater. Sol. Energy 2008, 82, 602–612. [Google Scholar] [CrossRef]
- Buker, M.S.; Mempouo, B.; Riffat, S.B. Performance evaluation and techno-economic analysis of a novel building integrated PV/T roof collector: An experimental validation. Energy Build. 2014, 76, 164–175. [Google Scholar] [CrossRef]
- Buker, M.S.; Riffat, S.B. Performance analysis of a combined Building Integrated PV/T Collector with a liquid desiccant enhanced dew point cooler. Energy Proced. 2016, 91, 717–727. [Google Scholar] [CrossRef]
- Zondag, H.A.; Vries, D.W.; Helden, W.G.J.; Zolingen, R.J.C.; Steenhoven, A.A. The yield of different combined PV-thermal collector designs. Sol. Energy 2003, 74, 253–269. [Google Scholar] [CrossRef]
- Tse, K.K.; Chow, T.T.; Su, Y. Performance evaluation and economic analysis of a full scale water-based photovoltaic/thermal (PV/T) system in an office building. Energy Build. 2016, 122, 42–52. [Google Scholar] [CrossRef]
- Calise, F.; d’Accadia, M.D.; Vanoli, L. Design and dynamic simulation of a novel solar trigeneration system based on hybrid photovoltaic/thermal collectors (PVT). Energy Convers. Manag. 2012, 60, 214–225. [Google Scholar] [CrossRef]
- Buonomano, A.; Calise, F.; Vicidomini, M. Design, simulation and experimental investigation of a solar system based on PV panels and PVT collectors. Energies 2016, 9, 497. [Google Scholar] [CrossRef]
- Tiwari, A.; Sodha, M.S. Performance evaluation of solar PV/T system: An experimental validation. Sol. Energy 2006, 80, 751–759. [Google Scholar] [CrossRef]
- Rodney, L.; Jones, D.E.; Cole-Appel, B.E. Calculation of performance of N collectors in series from test data on a single collector. Sol. Energy 1979, 23, 535–536. [Google Scholar]
- Dubey, S.; Tiwari, G.N. Analysis of PV/T flat plate water collectors connected in series. Sol. Energy 2009, 83, 1485–1498. [Google Scholar] [CrossRef]
- Shyam; Tiwari, G.N.; Al-Helal, I.M. Analytical expression of temperature dependent electrical efficiency of N-PVT water collectors connected in series. Sol. Energy 2015, 114, 61–76. [Google Scholar]
- Dubey, S.; Tiwari, G.N. Analysis of different configurations of flat plate water collectors connected in series. Int. J. Energy Res. 2008, 32, 1362–1372. [Google Scholar] [CrossRef]
- Shyam; Tiwari, G.N.; Fischer, O.; Mishra, R.K.; Al-Helal, I.M. Performance evaluation of N-photovoltaic thermal (PVT) water collectors partially covered by photovoltaic module connected in series: An experimental study. Sol. Energy 2016, 134, 302–313. [Google Scholar] [CrossRef]
- Raju, V.R.; Narayana, R.L. Effect of flat plate collectors in series on performance of active solar still for Indian coastal climatic condition. J. King Saud Univ. Eng. Sci. 2016. [Google Scholar] [CrossRef]
- Mishra, R.K.; Tiwari, G.N. Energy and exergy analysis of hybrid photovoltaic thermal water collector for constant collection temperature mode. Sol. Energy 2013, 90, 58–67. [Google Scholar] [CrossRef]
- Singh, S.; Agrawal, S. Efficiency maximization and performance evaluation of hybrid dual channel semitransparent photovoltaic thermal module using fuzzyfied genetic algorithm. Energy Convers. Manag. 2016, 122, 449–461. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Zhao, T.; Dai, W. Experimental study on a novel fuzzy control method for staticpressure reset based on the maximum damper position feedback. Energy Build. 2015, 108, 215–222. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, J.; Chen, Y.; Zhan, T.; Liu, H. Fuzzy control model and simulation of supply air system in a test rig of low-temperature hot-water radiator system. Energy Build. 2010, 42, 386–392. [Google Scholar] [CrossRef]
- Tillack, L.; Rishel, J.B. Proper control of HVAC variable speed pumps. ASHRAE J. 1998, 11, 42–47. [Google Scholar]
- Design Standard for Energy Efficiency of Public Buildings; GB 50189-2005; China Building Industry Press: Beijing, China, 2005.
- Code for Design of Heating Ventilation and Air Conditioning; GB 50019-2003; China Planning Press: Beijing, China, 2003.
- Armstrong, P.R. Extension of the Hottel-Whillier-Bliss model to multi-stage collector systems. Int. Telem. Conf. Proc. 1978, 2, 173–176. [Google Scholar]
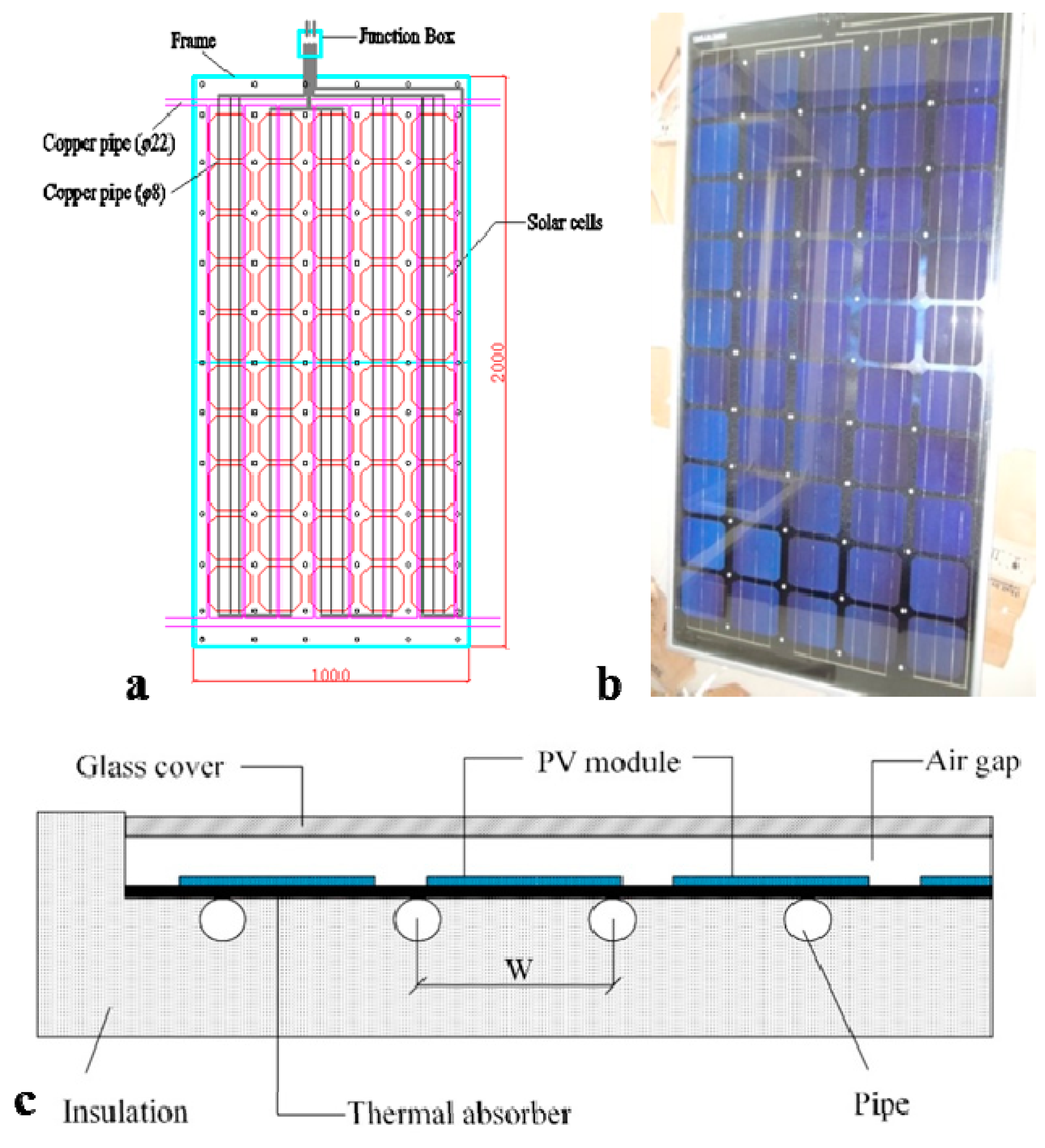
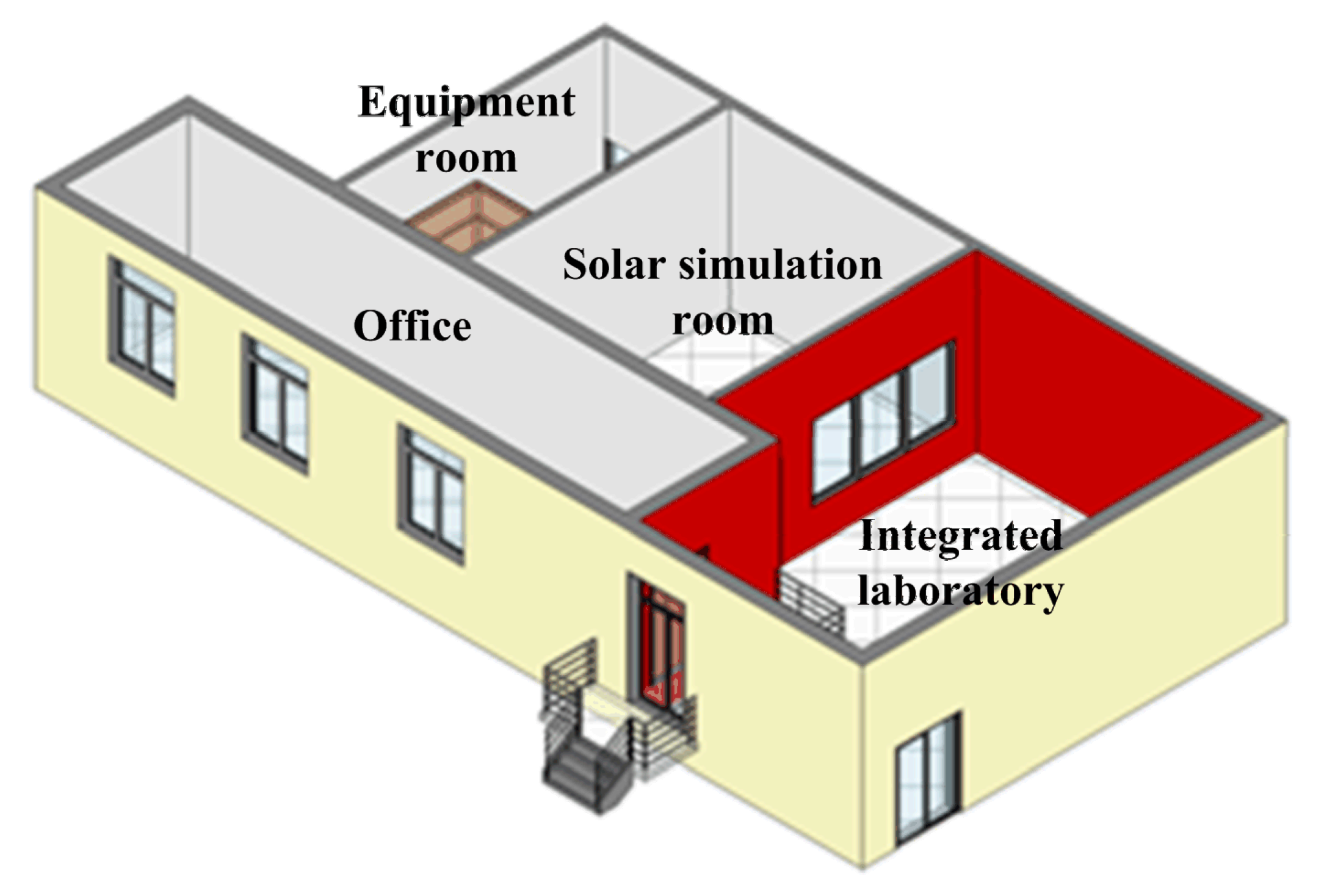
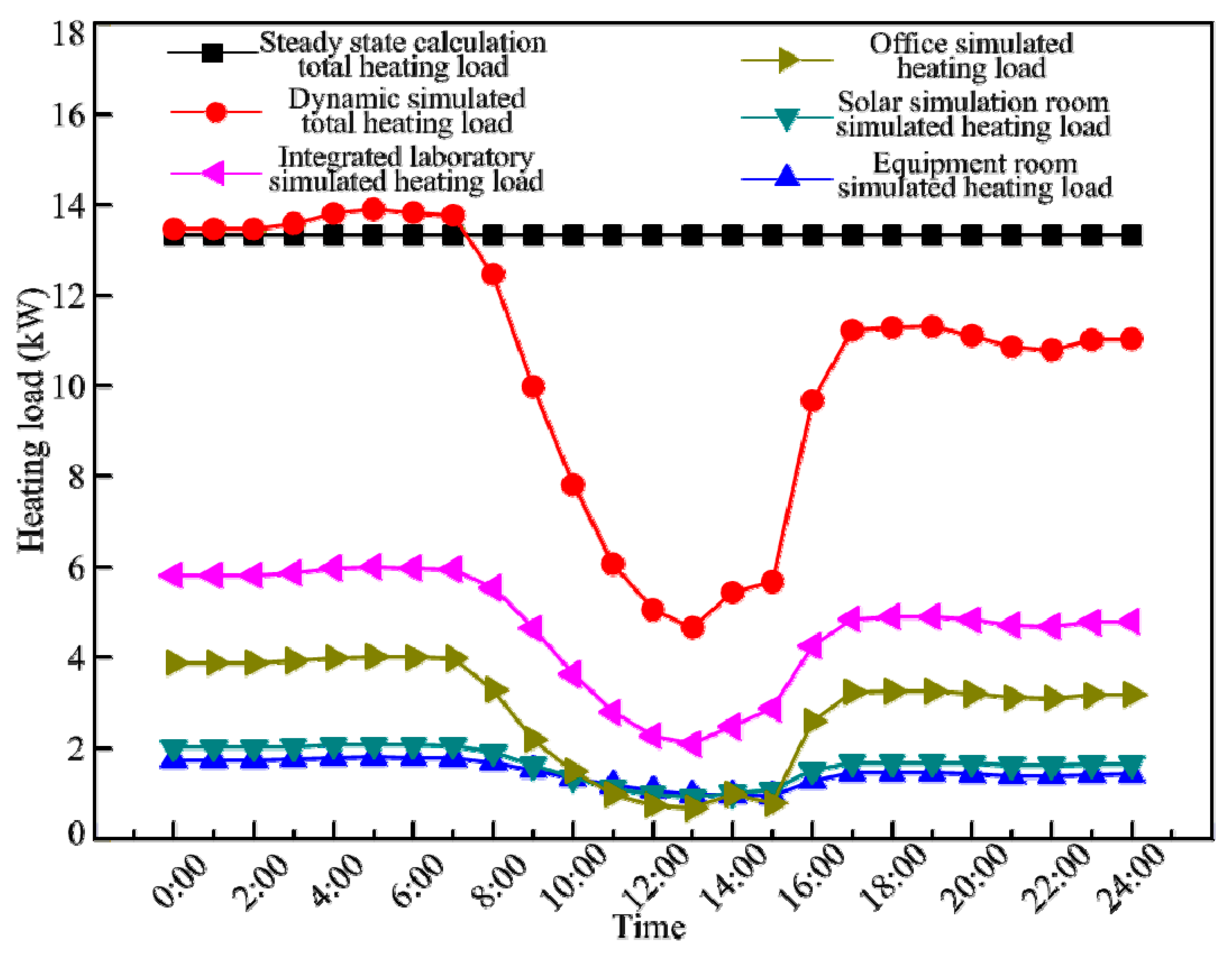
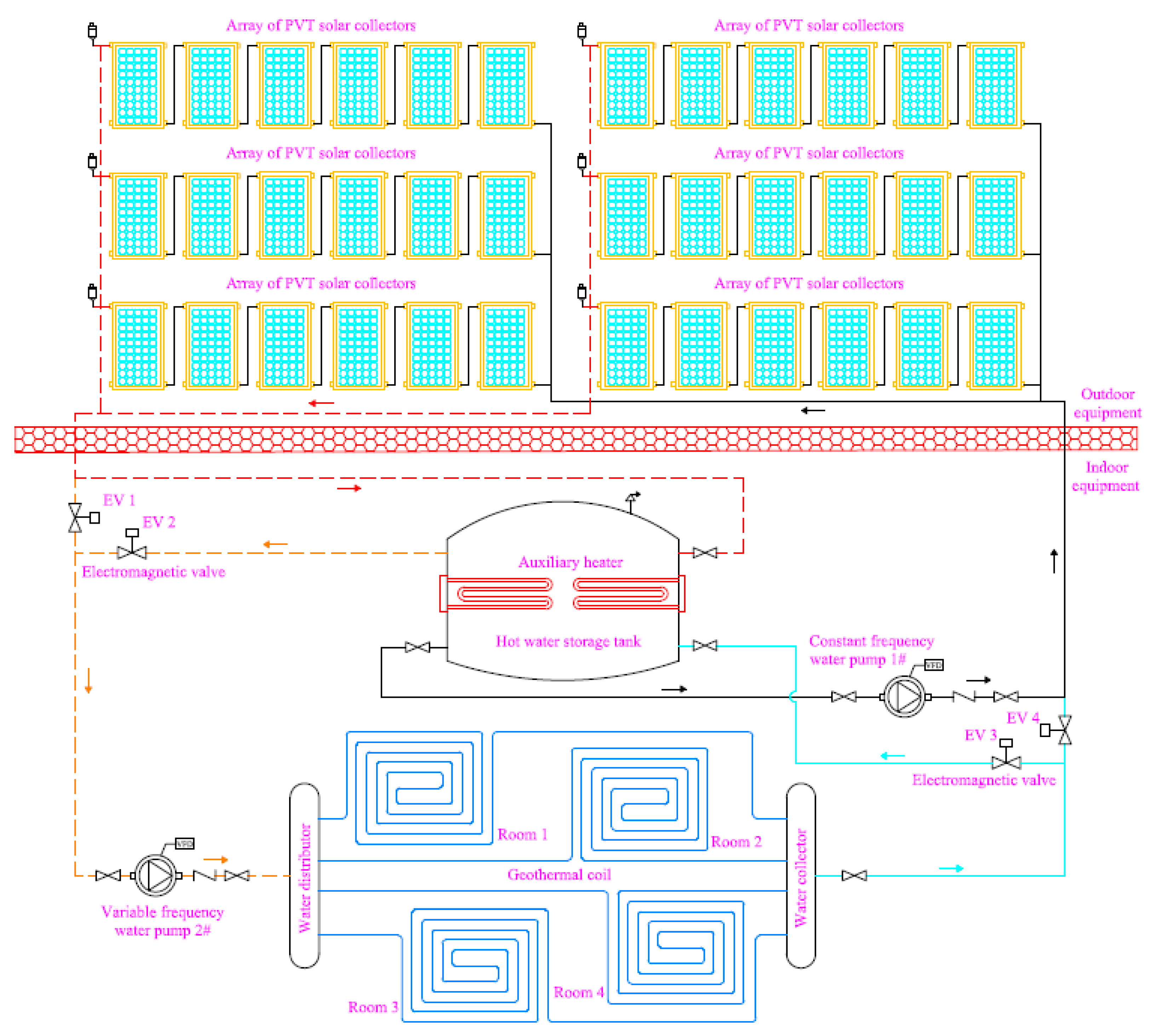


| Material | Thickness (mm) | Density (kg/m3) | Thermal Conductivity (W/m·K) | R Value (m2·K/W) | Heat Capacity (J/kg·K) | Heat Capacitance (J/m2·K) |
|---|---|---|---|---|---|---|
| Glass | 3.2 | 3000 | 1.0 | 3.2 × 10−3 | 500 | 4800 |
| PV | 0.22 | 2330 | 148 | 1.5 × 10−6 | 677 | 355 |
| EVA | 0.5 | 960 | 0.35 | 1.4 × 10−3 | 2090 | 1003 |
| Absorber | 2 | 7280 | 64 | 0.3 × 10−4 | 385 | 5605 |
| EPS | 50 | 80 | 0.04 | 1.2 | 1120 | 4480 |
| Parameters (Unit) | Uoc (V) | Isc (A) | Pemax (W) | Ptmax (W) |
|---|---|---|---|---|
| Value | 33.2 | 6.1 | 195 | 300 |
| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| A1 | 2 | m2 | Utc,a | 9.2 | W/(m2·K) |
| Ai | 10 | m2 | Utc,p | 5.58 | W/(m2·K) |
| Ao | 10 | m2 | αc | 0.9 | |
| FR | 0.6 | τg | 0.95 | ||
| τ | 0.95 | αp | 0.8 | ||
| α | 0.8 | F' | 0.968 | ||
| UL | 8.35 | W/(m2·K) | hpf | 100 | W/(m2·K) |
| cp | 4180 | J/(kg·K) | Utp,a | 4.74 | W/(m2·K) |
| Ud | 1 | W/(m2·K) | θpv | 0.5 | %/K |
| β | 0.67 | Tref | 25 | °C | |
| W | 1 | m | ηref | 0.18 |
| Number of PVT Collectors Connected in Series (N) | Number of PVT Groups Connected in Parallel (M) | Outlet Water Temperature To (°C) | Total Thermal Energy Generation Qu (MJ) | Thermal Efficieny ηth (%) | Total Power Generation Qe (kWh) | Photovoltaic Efficiency ηe (%) |
|---|---|---|---|---|---|---|
| 6 | 6 | 14.59 | 387.15 | 41.45 | 28.78 | 10.9 |
| 3 | 12 | 14.61 | 386.02 | 41.37 | 28.04 | 10.8 |
| 12 | 3 | 14.57 | 382.97 | 41.04 | 27.76 | 10.5 |
| 4 | 9 | 14.60 | 384.99 | 41.26 | 28.03 | 10.7 |
| 9 | 4 | 14.58 | 383.30 | 41.08 | 27.89 | 10.6 |
| 2 | 18 | 14.64 | 387.09 | 41.59 | 28.03 | 10.8 |
| 18 | 2 | 14.57 | 382.63 | 41.00 | 27.44 | 10.3 |
| 1 | 36 | 14.71 | 387.48 | 41.61 | 28.06 | 10.8 |
| 36 | 1 | 14.57 | 382.30 | 40.97 | 26.40 | 10.1 |
| ecT | NB | NS | ZE | PS | PB | |
|---|---|---|---|---|---|---|
| eT | ||||||
| NB | 5 | 5 | 4 | 3 | 3 | |
| NS | 5 | 4 | 3 | 3 | 2 | |
| ZE | 4 | 4 | 3 | 2 | 2 | |
| PS | 4 | 3 | 2 | 2 | 1 | |
| PB | 3 | 3 | 2 | 1 | 1 | |
| Parameters | Uncertainties |
|---|---|
| Ultrasonic flow meter | ±0.5% |
| Pt100 temperature sensor | ±0.1 K |
| Solar radiation intensity | ±5% |
| Ambient temperature sensor | ±0.5 °C |
| Ambient humidity sensor | ±2% |
| Temperature self-recording module | ±0.1 °C |
| Humidity self-recording module | ±1% |
| Parameters | Unit | Values |
|---|---|---|
| Accumulated thermal energy generation in one day | MJ | 288 |
| Average thermal efficiency | % | 23 |
| Average temperature difference between inlet and outlet | °C | 3 |
| Average photovoltaic power | kW | 6.1 |
| Accumulated power generation | kWh | 32 |
| Photovoltaic efficiency | % | 10 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, C.; Liang, R.; Zhang, J. Optimization Design Method and Experimental Validation of a Solar PVT Cogeneration System Based on Building Energy Demand. Energies 2017, 10, 1281. https://doi.org/10.3390/en10091281
Zhou C, Liang R, Zhang J. Optimization Design Method and Experimental Validation of a Solar PVT Cogeneration System Based on Building Energy Demand. Energies. 2017; 10(9):1281. https://doi.org/10.3390/en10091281
Chicago/Turabian StyleZhou, Chao, Ruobing Liang, and Jili Zhang. 2017. "Optimization Design Method and Experimental Validation of a Solar PVT Cogeneration System Based on Building Energy Demand" Energies 10, no. 9: 1281. https://doi.org/10.3390/en10091281
APA StyleZhou, C., Liang, R., & Zhang, J. (2017). Optimization Design Method and Experimental Validation of a Solar PVT Cogeneration System Based on Building Energy Demand. Energies, 10(9), 1281. https://doi.org/10.3390/en10091281





