Wind Energy Potential of Gaza Using Small Wind Turbines: A Feasibility Study
Abstract
1. Introduction
- Solar energy is not enough alone to supply the needed energy, especially during the night and in the short gray days of winter. Moreover, according to local weather statistics, wind speed increases in winter, so that solar energy and wind energy can complement each other.
- Photovoltaic modules are not cheap, roughly 1.2 USD $/Wp, and their manufacturing technology is complicated (Wp denotes peak power and it is used in photovoltaic systems to describe the power rating of installed solar panels. The subscript is to differentiate it from measured power). Small wind turbines, in contrast, have a rather simple manufacturing technology and can be completely manufactured in Gaza. Therefore, wind turbines could have lower costs than solar panels in terms of $/W if manufactured locally. Moreover, manufacturing itself contributes to the local economy.
- Due to the high population density, Gaza city is full of high-rise residential buildings. The majority of the buildings are restricted to five floors as regulated by the local municipality. Therefore, the majority of the city areas will access unobstructed wind at nearly the same height since the land is flat. The height of the buildings of around 50 m and the installation of the turbine on a metal pole allow for wind turbines installed at higher altitudes. All of the roofs in Gaza are flat and, therefore, the installation is possible and technically stable due to the concrete building structure. Although the wind speed is not that high at low altitudes, we expect it will be more efficient at higher altitudes. This issue will be investigated deeply in our research.
- Wind turbines require less land area, which is restricted to the metal pole and, therefore, they fit the small land area of the Gaza Strip.
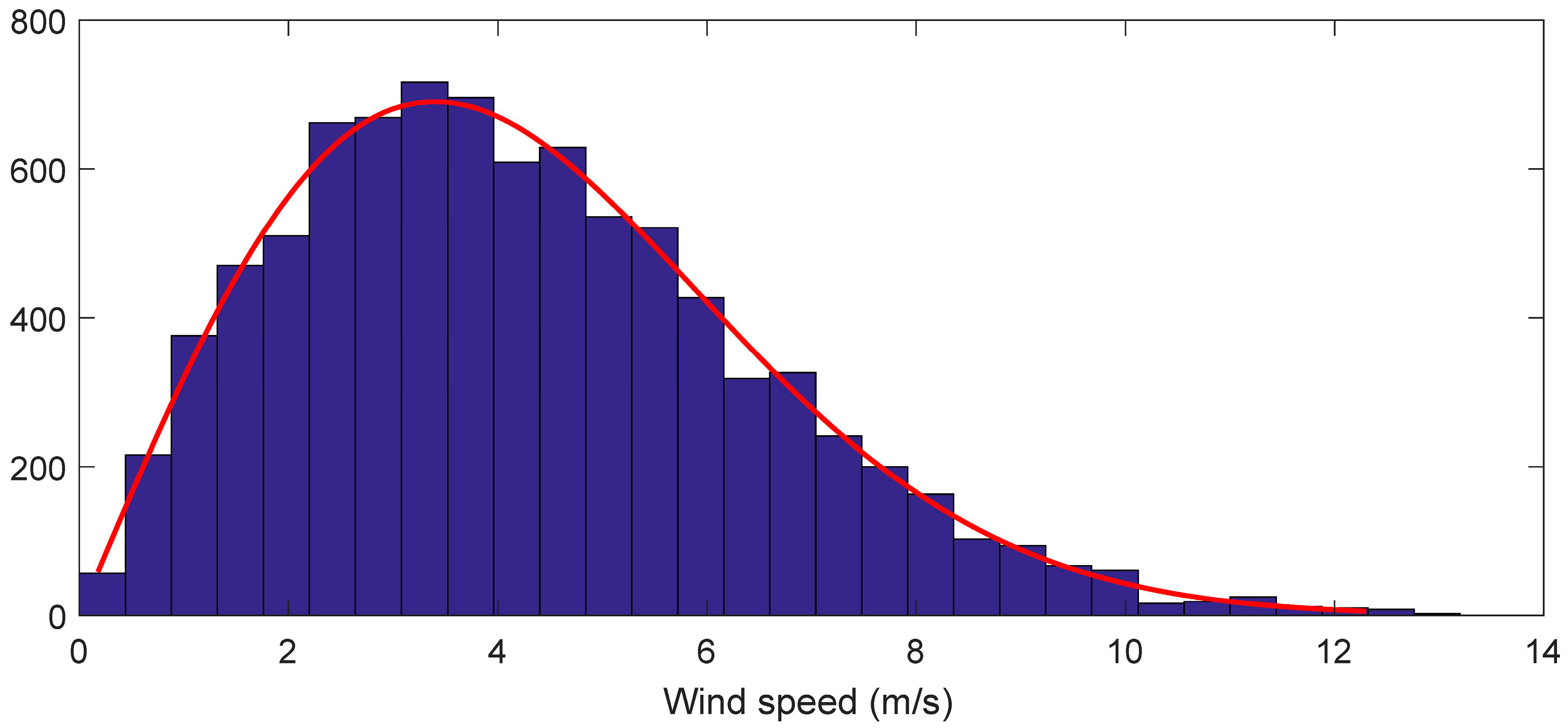
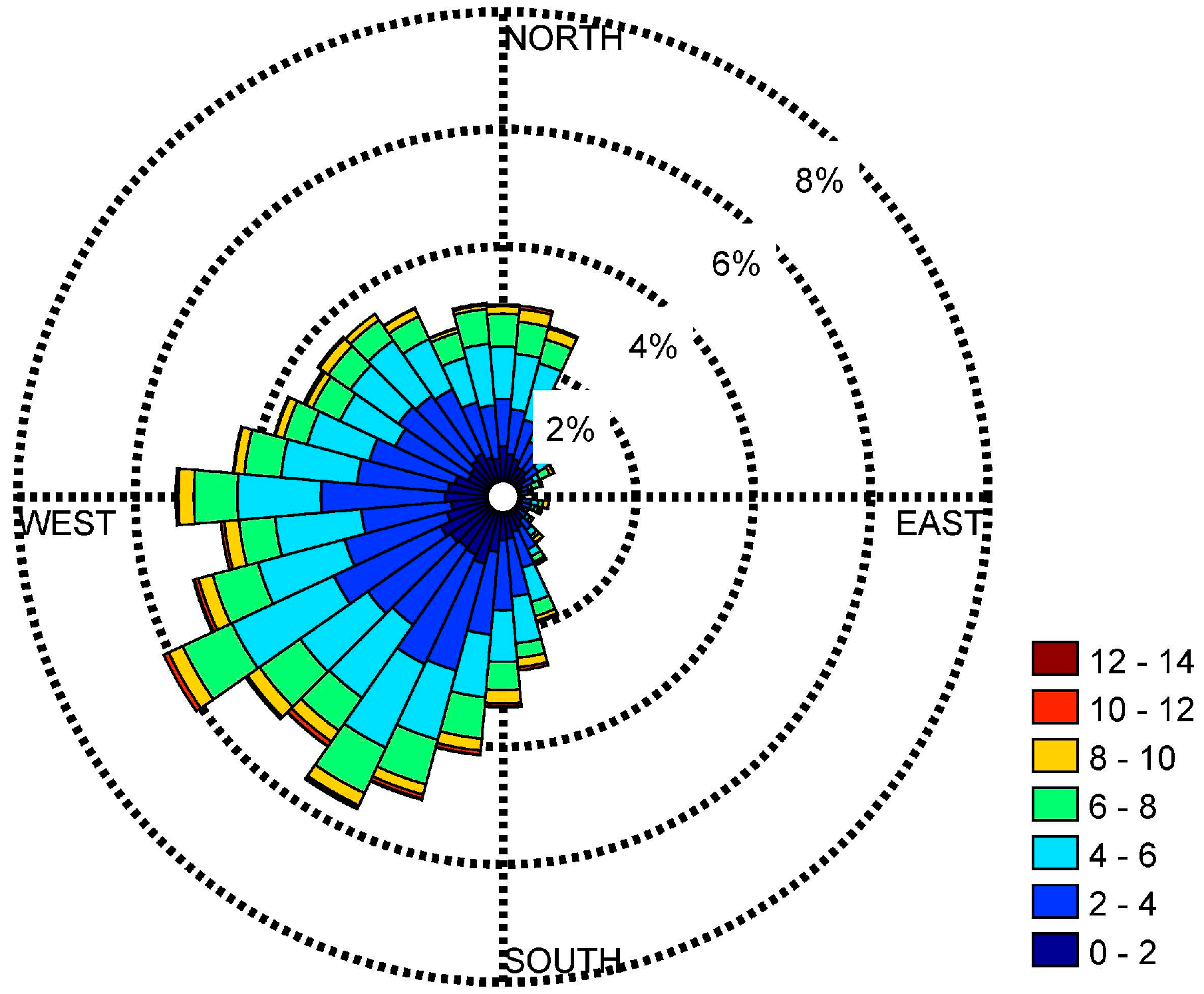
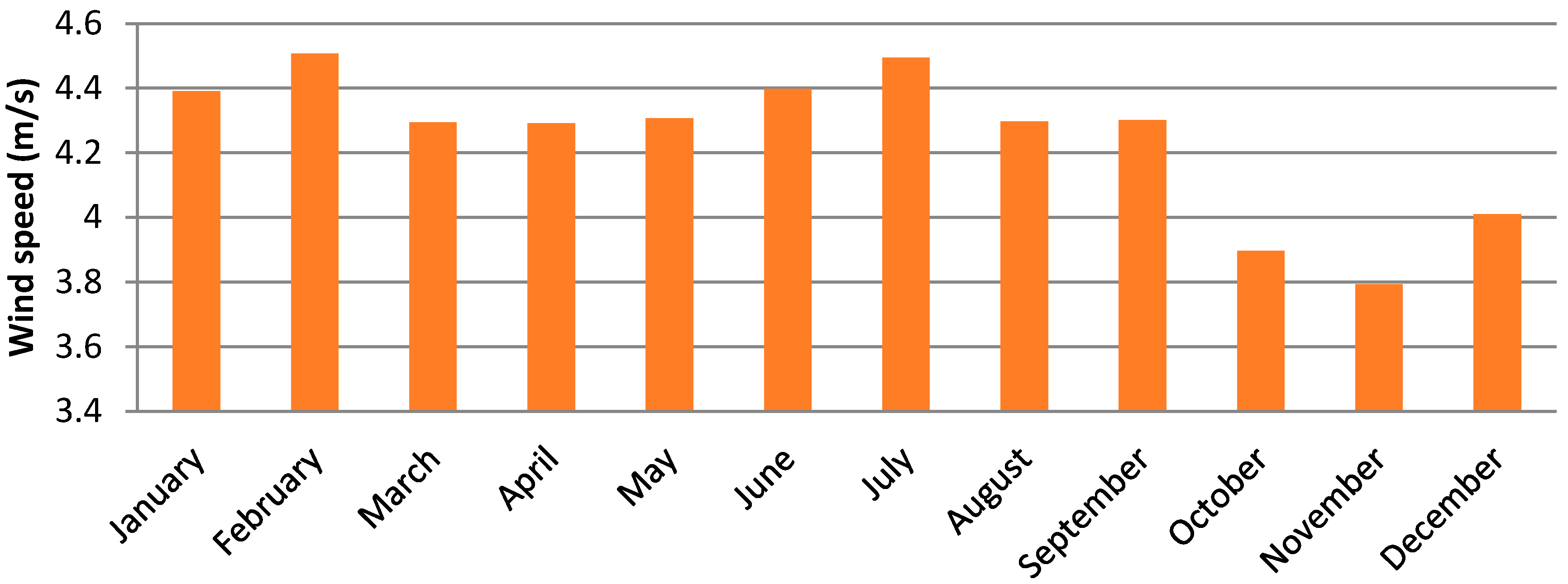
2. Climatic Data
3. Methodology
3.1. Wind Harvesting System Basics
3.2. Theoretical Analysis: Wind Turbine Coefficient and Power
3.3. Wind Turbine Specification
- Output power: It fits home use as the harvested energy is in the range of the average consumption of a household;
- Price (its price is competitive compared with others);
- Operation speed (fits low speed as starts from 2.5 m/s until 15 m/s);
- Efficiency is 30.5% which is relatively good; and
- Weight and size are suitable for home installations.
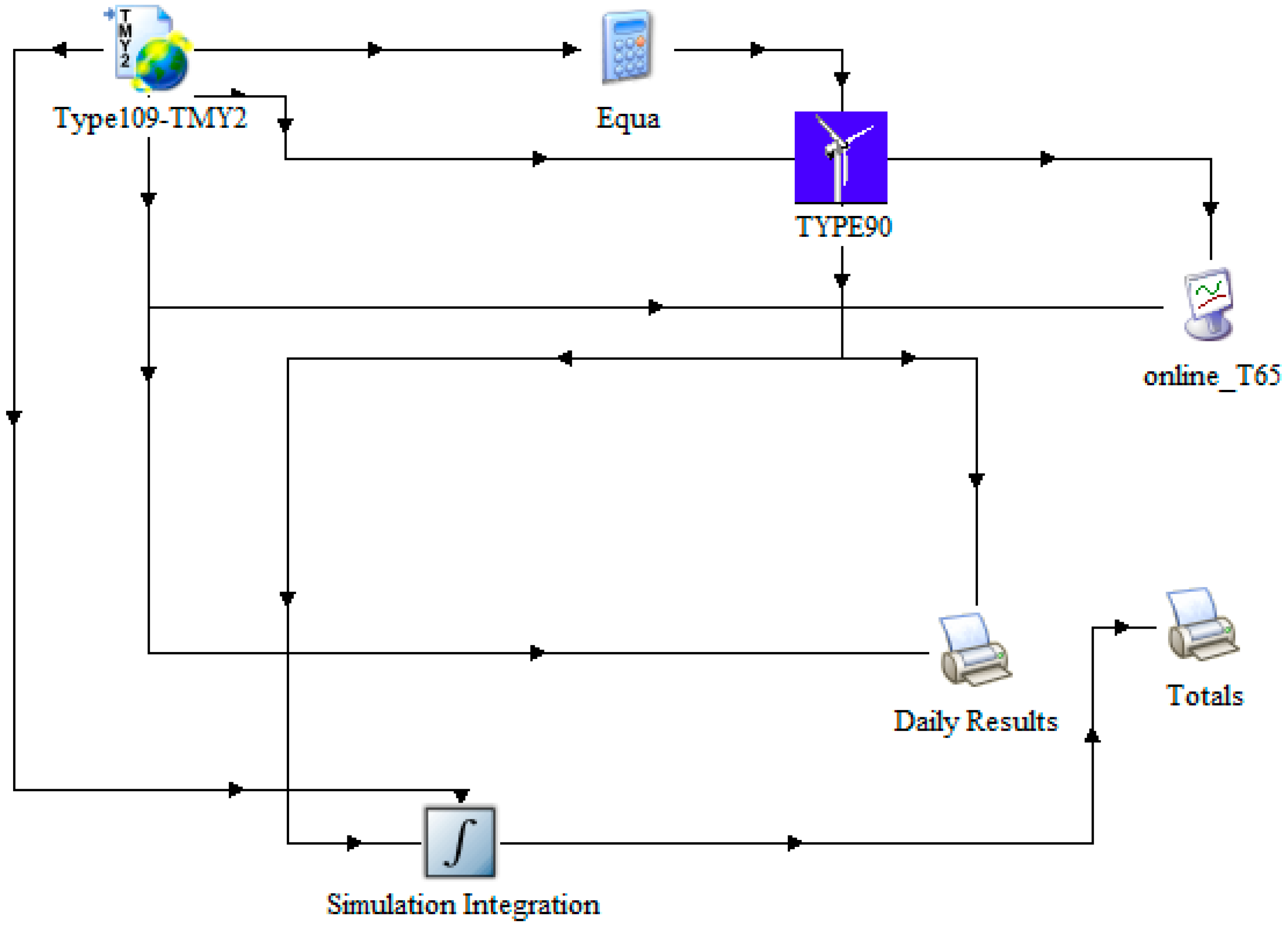
3.4. Simulation Model Using TRNSYS
3.5. Extrapolation of Wind Speed to Different Heights
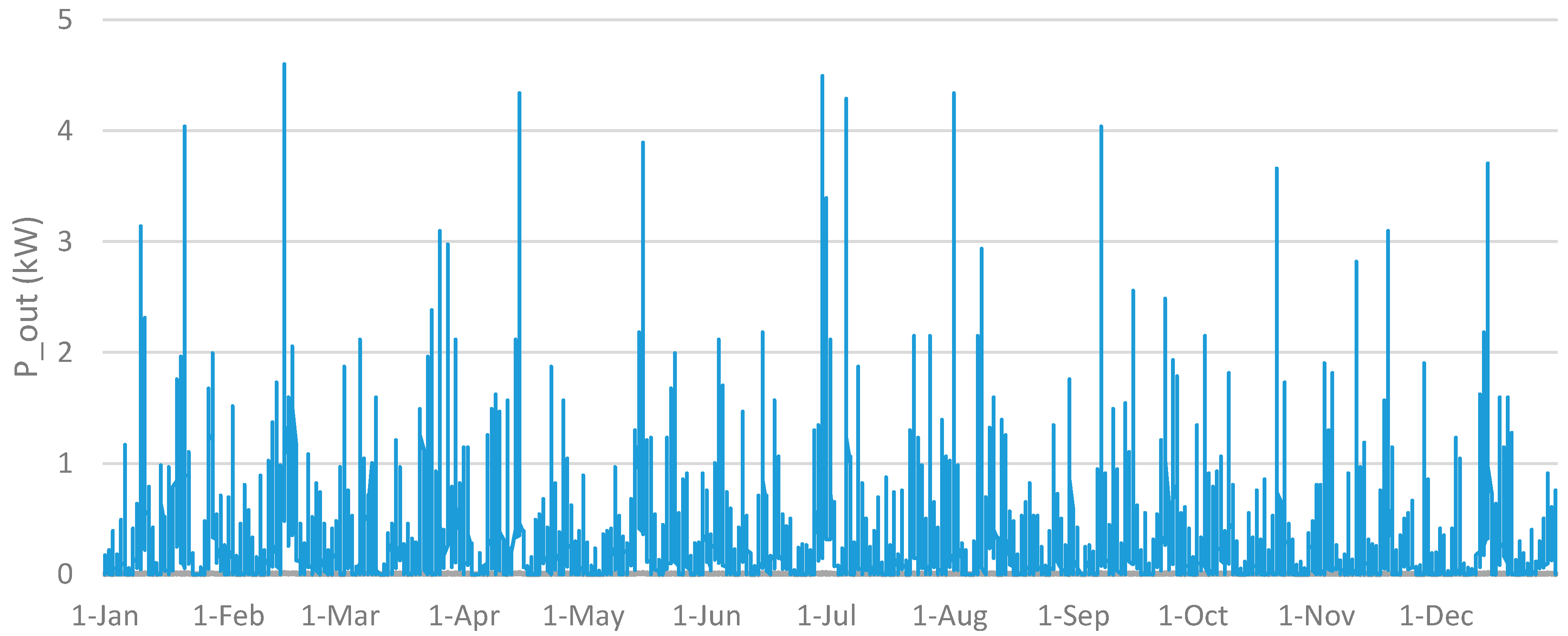
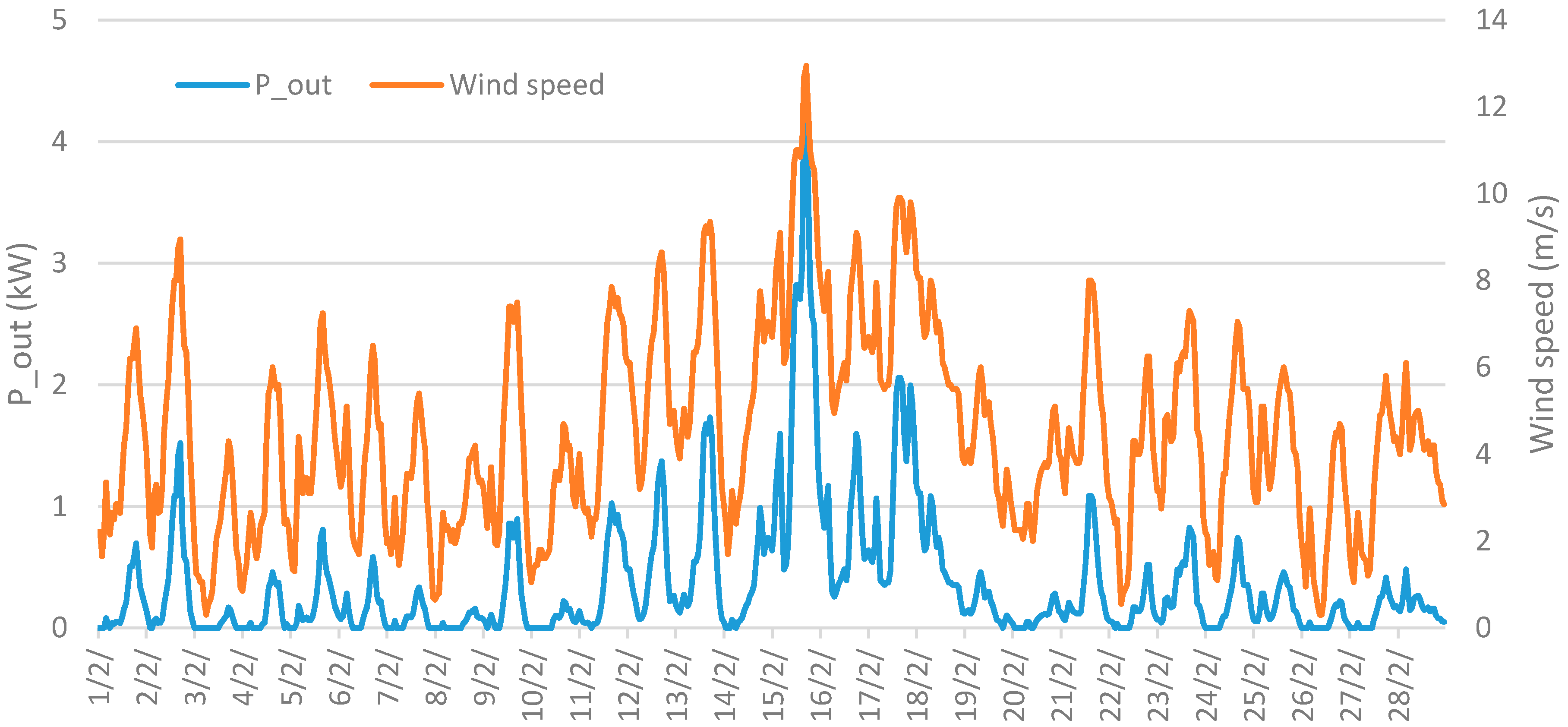
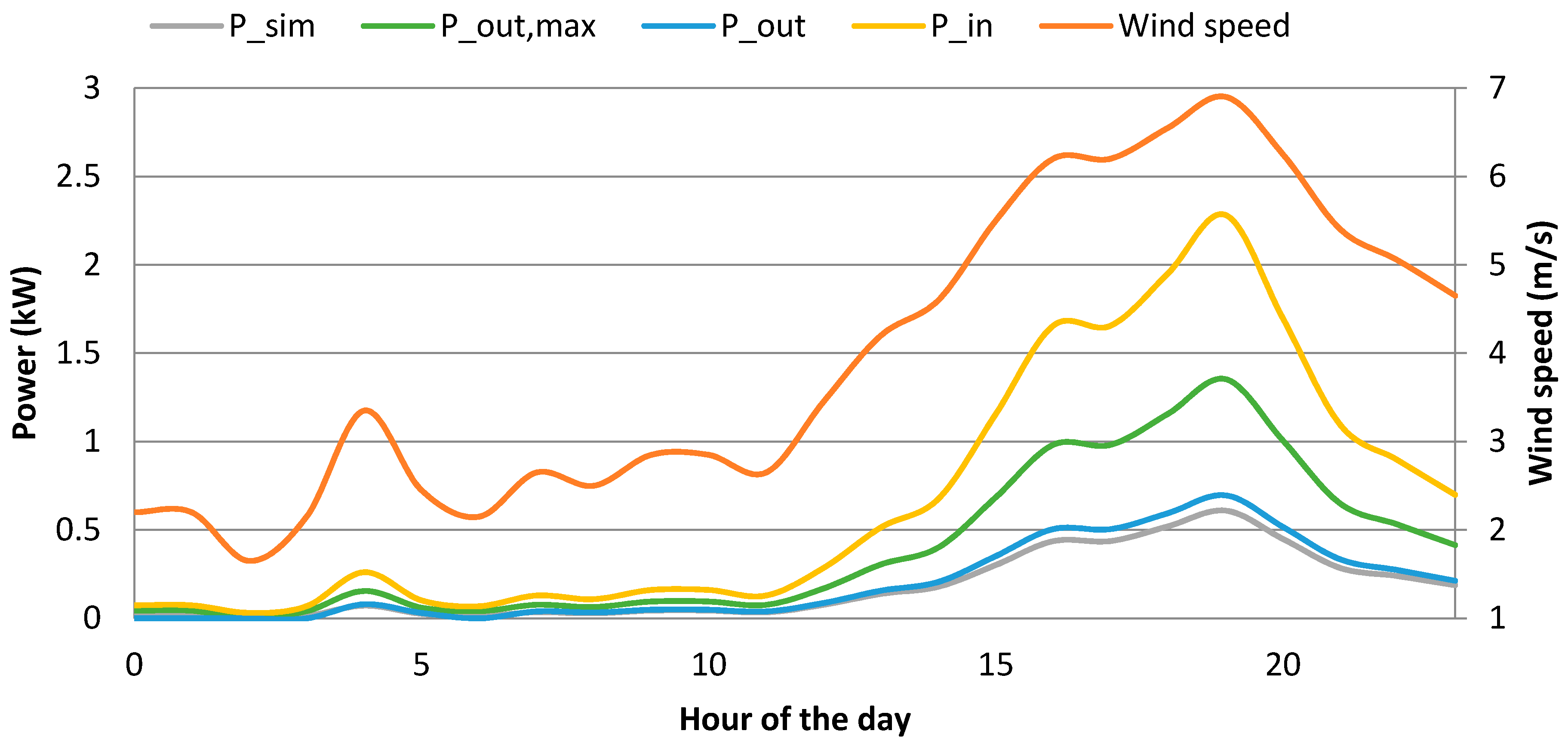
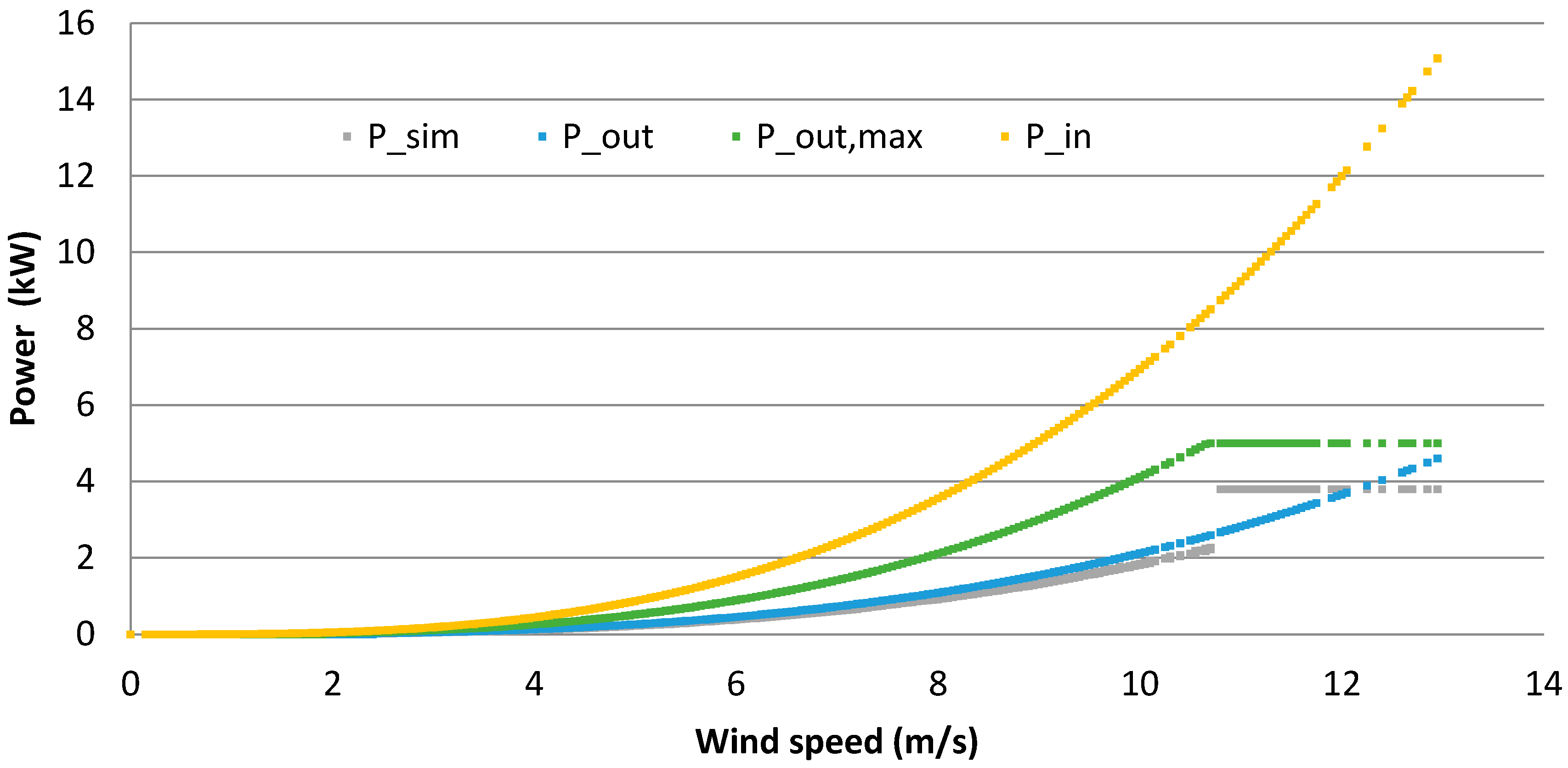
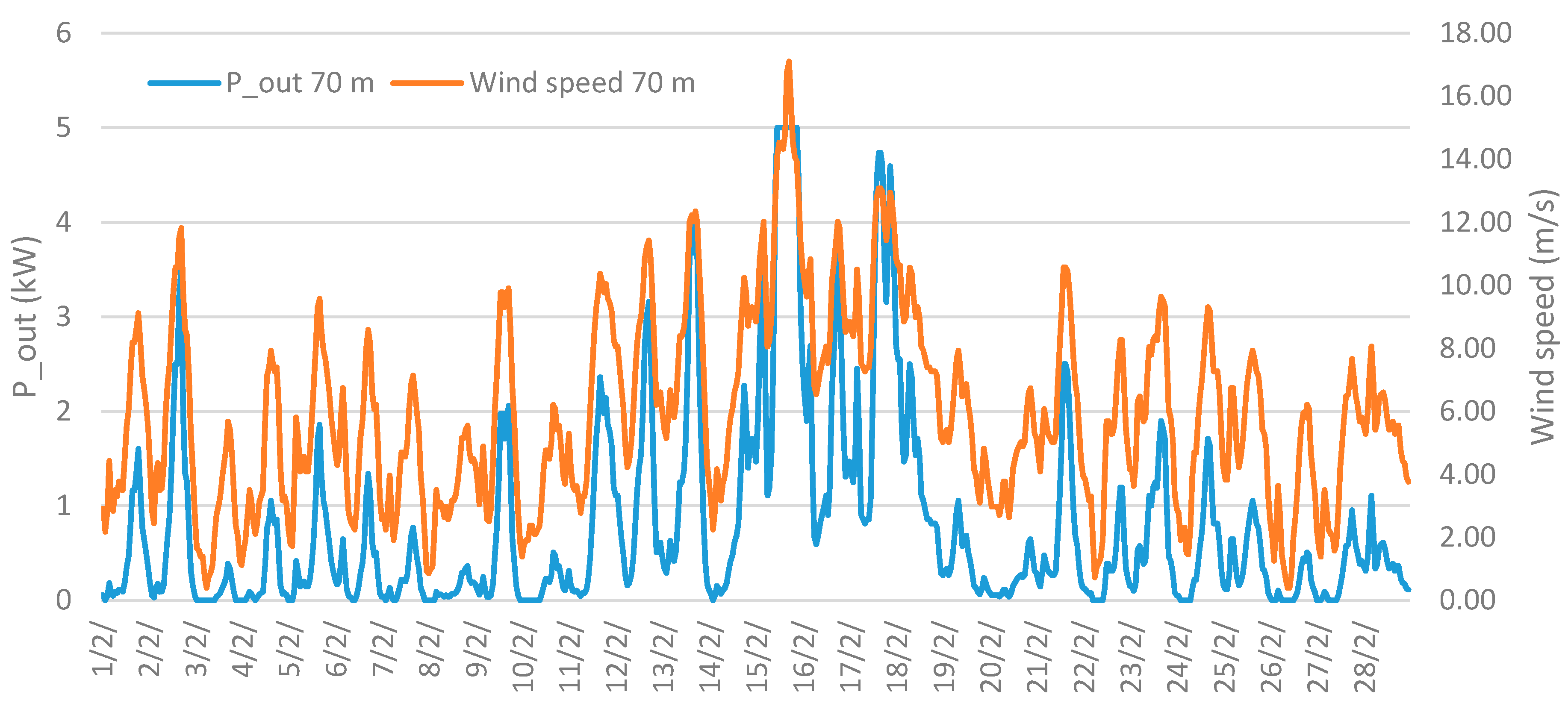
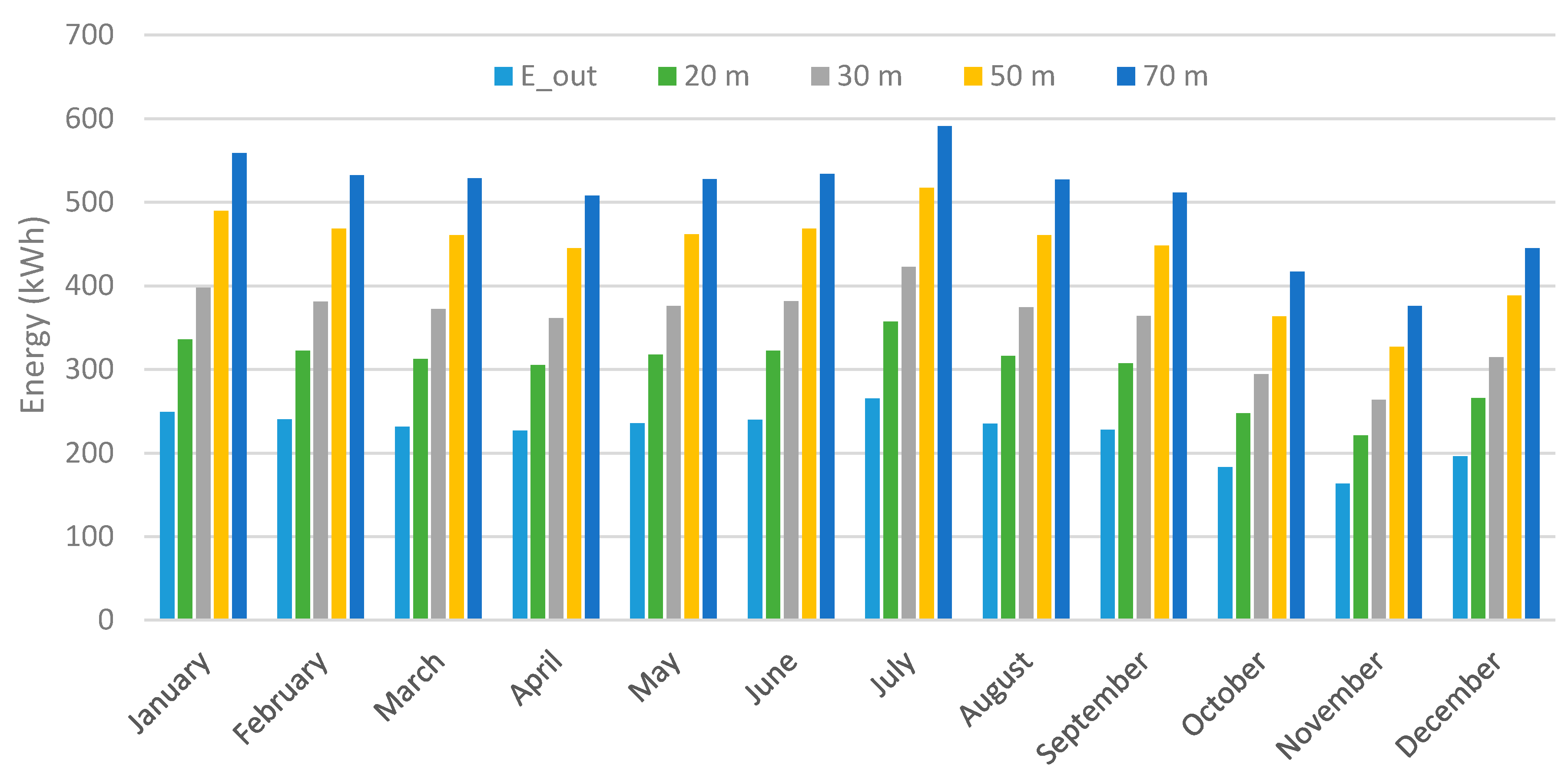
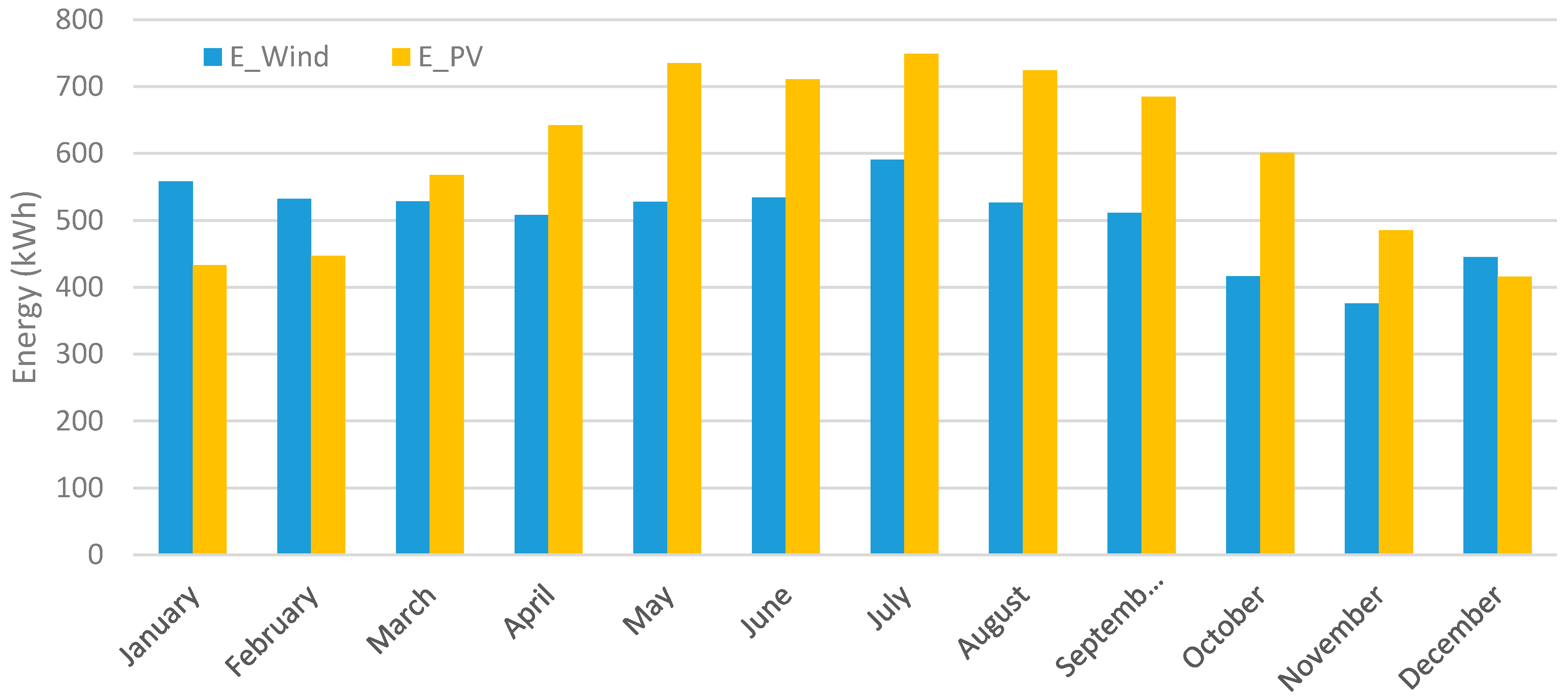
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Renewable Energy Policy Network for the 21st Century; Renewables Global Status Report: Paris, France, 2007.
- Renewable Energy Policy Network for the 21st Century; Renewables Global Status Report: Paris, France, 2017.
- Hamed, T.A.; Flamm, H.; Azraq, M. Renewable energy in the Palestinian Territories: Opportunities and challenges. Renew. Sustain. Energy Rev. 2012, 16, 1082–1088. [Google Scholar] [CrossRef]
- Shabbaneh, R.; Hasan, A. Wind energy potential in Palestine. Renew. Energy 1997, 11, 479–483. [Google Scholar] [CrossRef]
- Weinberger, S. Powerless in Gaza. IEEE Spectr. 2009, 46, 36–41. [Google Scholar] [CrossRef]
- United Nations Country Team in the occupied Palestinian territory. Gaza—Ten years later. Available online: https://unsco.unmissions.org/new-un-report-documents-legacy-10-years-isolation-and-crisis-gaza (accessed on 19 July 2017).
- Alaydi, J.Y. A survey on the assessment of wind energy potential in Gaza Strip. Wind Eng. 2010, 34, 531–541. [Google Scholar] [CrossRef]
- Alaydi, J.Y. A parametric study of solar and wind energy in Gaza strip. Int. J. Sci. Eng. Res. 2013, 4, 140–147. [Google Scholar]
- De Meij, A.; Vinuesa, J.-F.; Maupas, V.; Waddle, J.; Price, I.; Yaseen, B.; Ismail, A. Wind energy resource mapping of Palestine. Renew. Sustain. Energy Rev. 2016, 56, 551–562. [Google Scholar] [CrossRef]
- Abu-Zarifa, A. Design of a Stand-Alone Power Wind Turbine Optimized for Low Wind Speed in Gaza. Int. J. Energy Eng. 2014, 4, 89–93. [Google Scholar]
- Meteonorm. Handbook Part I: Software, version 7.2; Meteotest: Bern, Switzerland, 2017. [Google Scholar]
- NREL. Wind Turbine Components. Available online: http://windeis.anl.gov/guide/basics/turbine.html (accessed on 19 July 2017).
- Watson, D.E. Wind Turbine Power Coefficient (Cp). Available online: http://www.ftexploring.com/wind-energy/wind-power-coefficient.htm (accessed on 19 July 2017).
- Ritter, M.; Shen, Z.W.; López Cabrera, B.; Odening, M.; Deckert, L. Designing an index for assessing wind energy potential. Renew. Energy 2015, 83, 416–424. [Google Scholar] [CrossRef]
- Krusche, N.; Peralta, C.; Chang, C.Y.; Stoevesandt, B. Wind Power Energy in Southern Brazil: Evaluation using a mesoscale meteorological model. Energy Procedia 2015, 76, 164–168. [Google Scholar] [CrossRef]
- Hau, E.; von Renouard, H. Wind Turbines: Fundamentals, Technologies, Application, Economics; Springer: Berlin, Germany, 2003. [Google Scholar]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; Wiley & Sons Ltd.: Chichester, UK, 2012. [Google Scholar]
- Betz, A. Introduction to the Theory of Flow Machines; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Wind Turbine Trade. Datenblatt 09/2015 WTT 5000S (smal) W Windturbine. Available online: http://www.wtt-wind.de/app/download/5796982333/Datenblatt+09-2015+2-3S-3-5S-5+kw.pdf (accessed on 19 July 2017).
- Klein, S. A Transient System Simulation Program (TRNSYS 17) Manual; Thermal Energy System Specialists: Madison, WI, USA, 2010. [Google Scholar]
- Janusevicius, K.; Streckiene, G.; Miseviciute, V. Simulation and analysis of small-scale solar adsorption cooling system for cold climate. Int. J. Environ. Sci. Dev. 2015, 6, 54. [Google Scholar] [CrossRef]
- Crawley, D.B.; Hand, J.W.; Kummert, M.L.; Griffith, B.T. Contrasting the capabilities of building energy performance simulation programs. Build. Environ. 2008, 43, 661–673. [Google Scholar] [CrossRef]
- A TRaNsient System Simulation Program. User’s Manual Solar Energy Laboratory, TRNSYS 16; Solar Energy Laboratory, University of Wisconsin-Madison: Madison, WI, USA, 2004. [Google Scholar]
- Brown, B.G.; Katz, R.W.; Murphy, A.H. Time-Series Models to Simulate and Forecast Wind-Speed and Wind Power. J. Clim. Appl. Meteorol. 1984, 23, 1184–1195. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer Science & Business Media: Berlin, Germany, 1988. [Google Scholar]
- Gunturu, U.B.; Schlosser, C.A. Characterization of wind power resource in the United States. Atmos. Chem. Phys. 2012, 12, 9687–9702. [Google Scholar] [CrossRef]
- Regional Center for Renewable Energy and Energy Efficiency (RCREEE). Latest Electricity Price Schemes in RCREEE Member States. Available online: http://www.rcreee.org/sites/default/files/rs_latest_-electricity_-prices_schemes_in_rcreee_-ms_6-2013_en.pdf (accessed on 19 July 2017).
- Palestinian Central Bureau of Statistics. Household Energy Survey January, 2015: Main Results. Available online: http://www.pcbs.gov.ps/Downloads/book2134.pdf (accessed on 19 July 2017).
- Ritter, M.; Pieralli, S.; Odening, M. Neighborhood Effects in Wind Farm Performance: A Regression Approach. Energies 2017, 10, 365. [Google Scholar] [CrossRef]
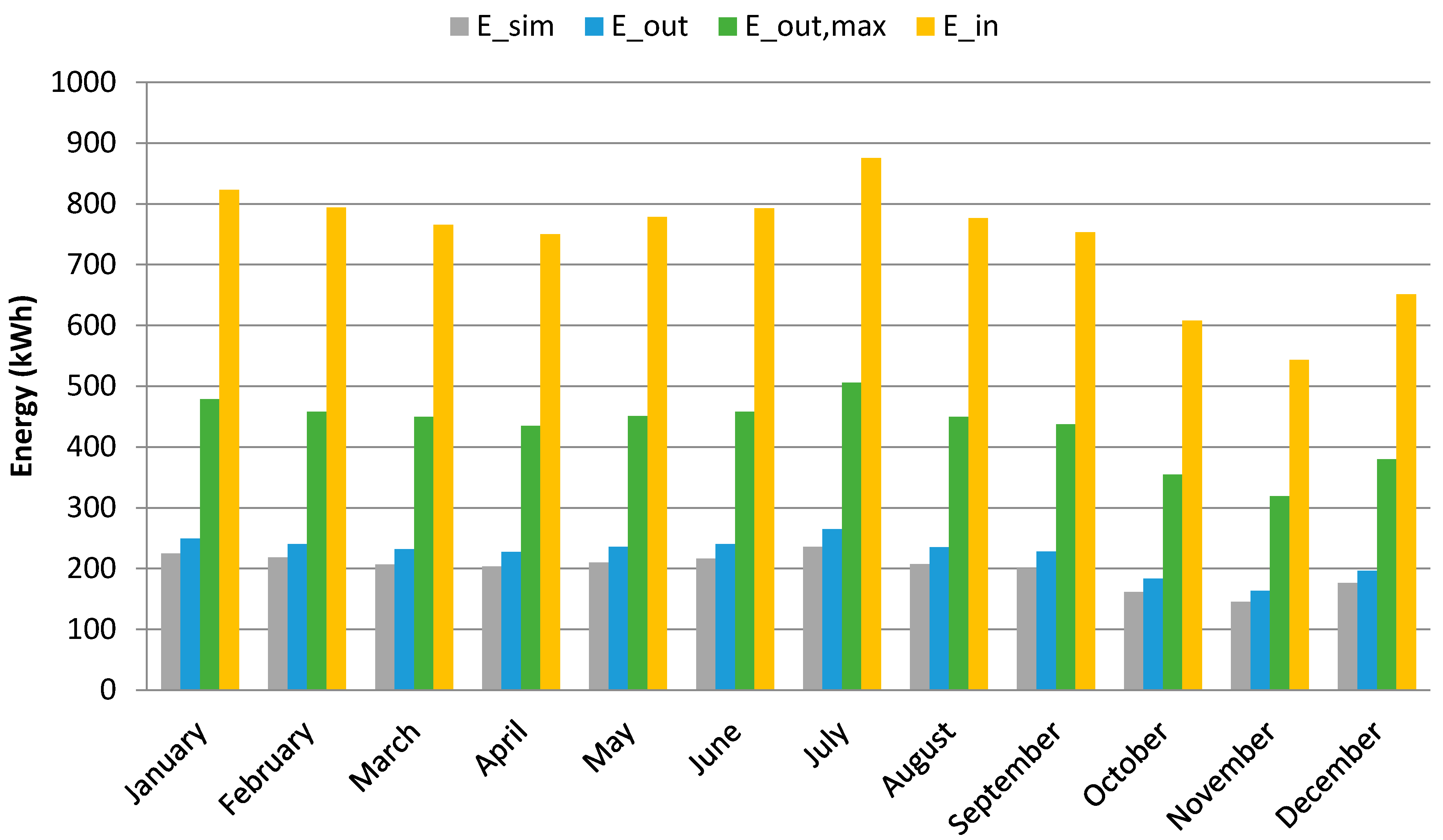
| Wind Turbine Type | WTT 5000S (Small) |
|---|---|
| Blade diameter | 3.8 m |
| Rated speed | 450 rpm |
| Power at 12.5 m/s | 3800 W |
| Power at 15.0 m/s | 5000 W |
| Start wind speed | 2.5 m/s |
| Total efficiency | 30.5% |
| Total weight of the system | approx. 74 kg |
| Name | Component type | Description |
|---|---|---|
| Weather data | Type109-TMY2 | Weather Data Reading and Processing.Typical Meteorological Year (TMY) data |
| Wind turbine | Type90 | Wind Energy Conversion System (WECS). Power versus wind speed data are read in a file. The impact of air density changes and wind speed increase with height are modeled. |
| Online Plotter | online_T65 | Output/Online Plotter/Online Plotter With File. |
| Printer | Type25a and Type25b/Daily and Total results | It can print with a time step that is different from the simulation time step. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elnaggar, M.; Edwan, E.; Ritter, M. Wind Energy Potential of Gaza Using Small Wind Turbines: A Feasibility Study. Energies 2017, 10, 1229. https://doi.org/10.3390/en10081229
Elnaggar M, Edwan E, Ritter M. Wind Energy Potential of Gaza Using Small Wind Turbines: A Feasibility Study. Energies. 2017; 10(8):1229. https://doi.org/10.3390/en10081229
Chicago/Turabian StyleElnaggar, Mohamed, Ezzaldeen Edwan, and Matthias Ritter. 2017. "Wind Energy Potential of Gaza Using Small Wind Turbines: A Feasibility Study" Energies 10, no. 8: 1229. https://doi.org/10.3390/en10081229
APA StyleElnaggar, M., Edwan, E., & Ritter, M. (2017). Wind Energy Potential of Gaza Using Small Wind Turbines: A Feasibility Study. Energies, 10(8), 1229. https://doi.org/10.3390/en10081229






