A Sensitivity Analysis of a Computer Model-Based Leak Detection System for Oil Pipelines
Abstract
:1. Introduction
2. Methodology
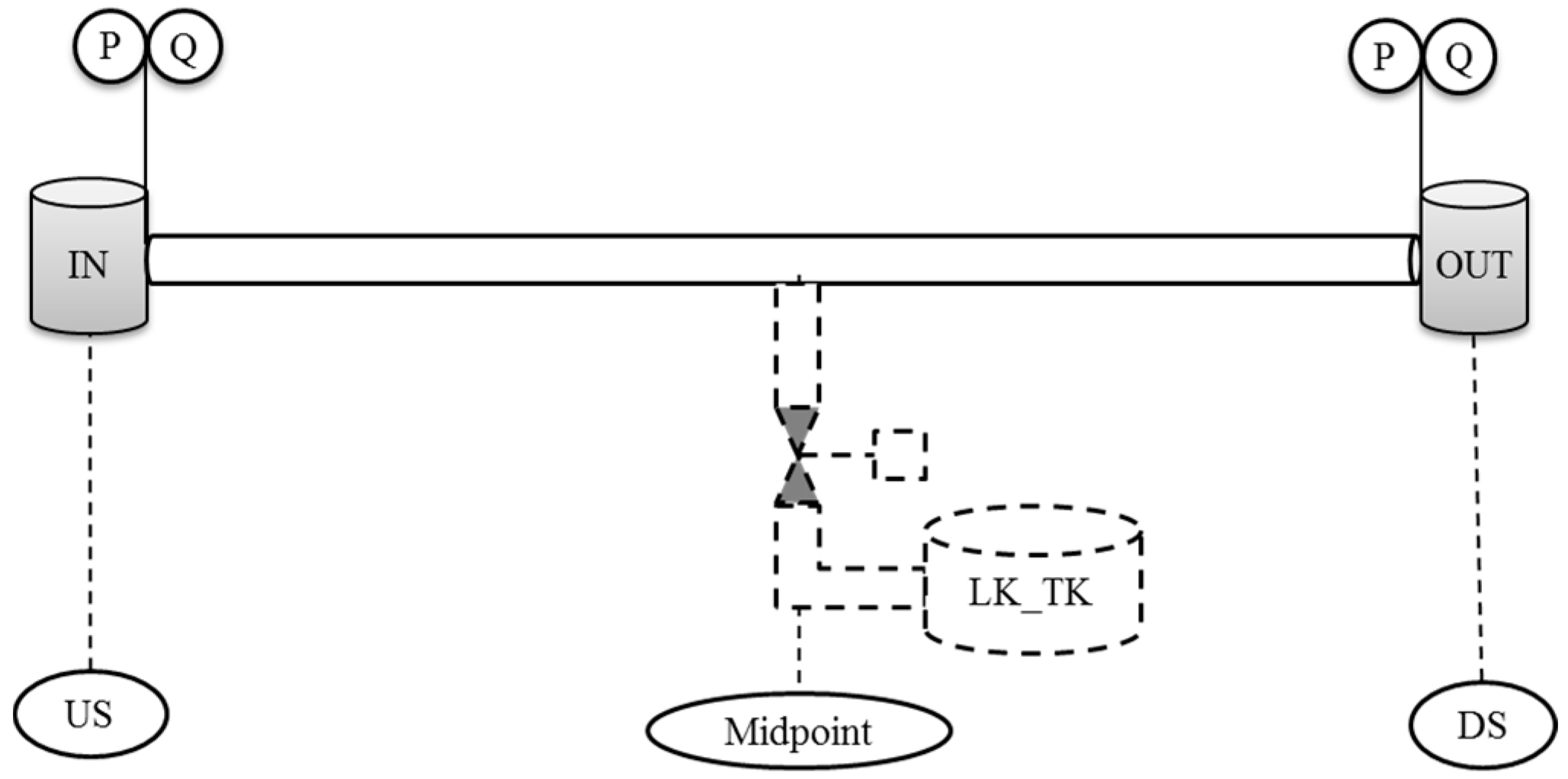
2.1. Leak Detection System
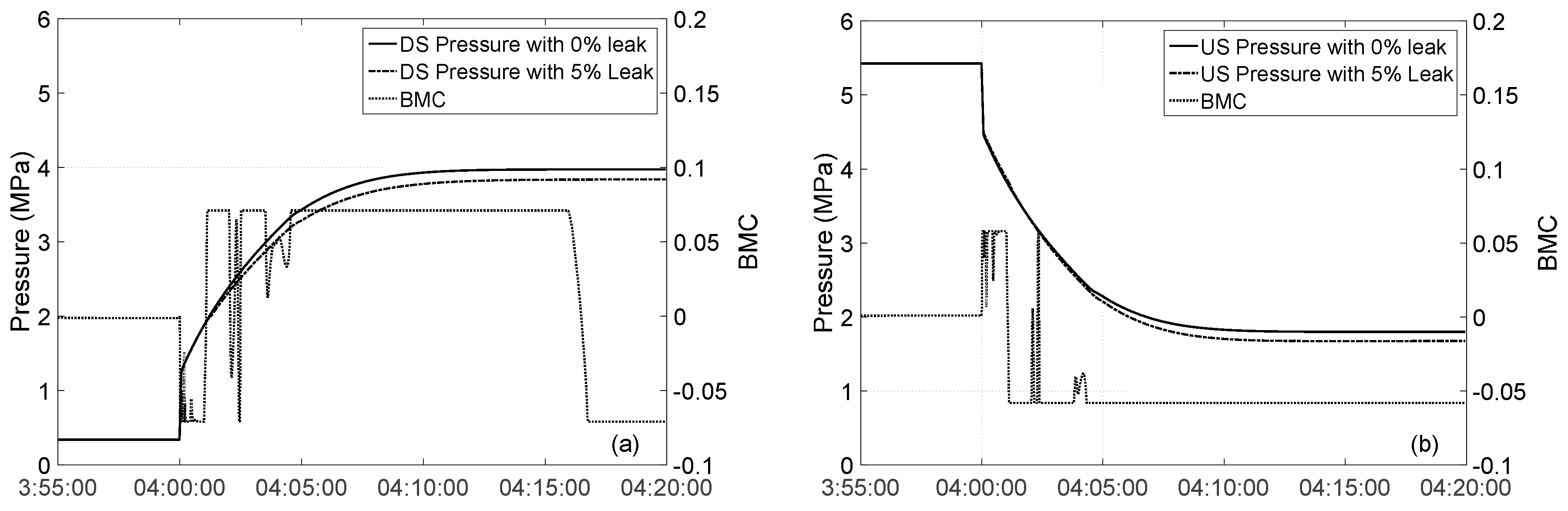
2.2. Simulated Leak Test
2.3. Study Pipeline
2.4. Sources of Uncertainty
3. Results and Discussion
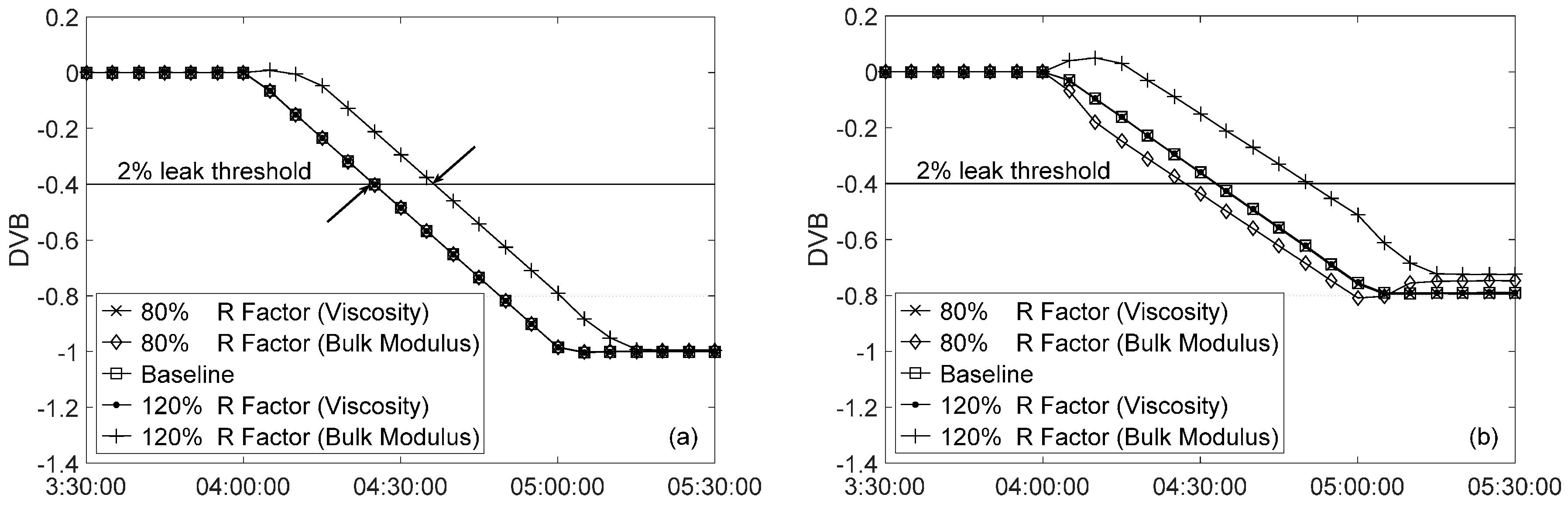
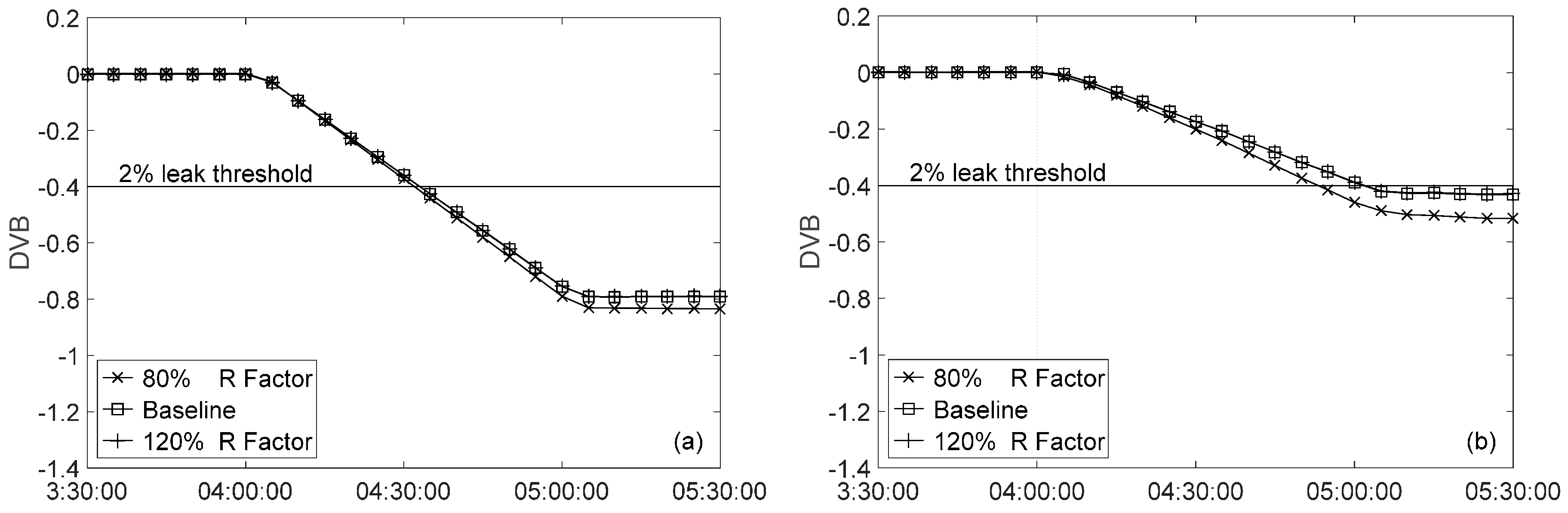
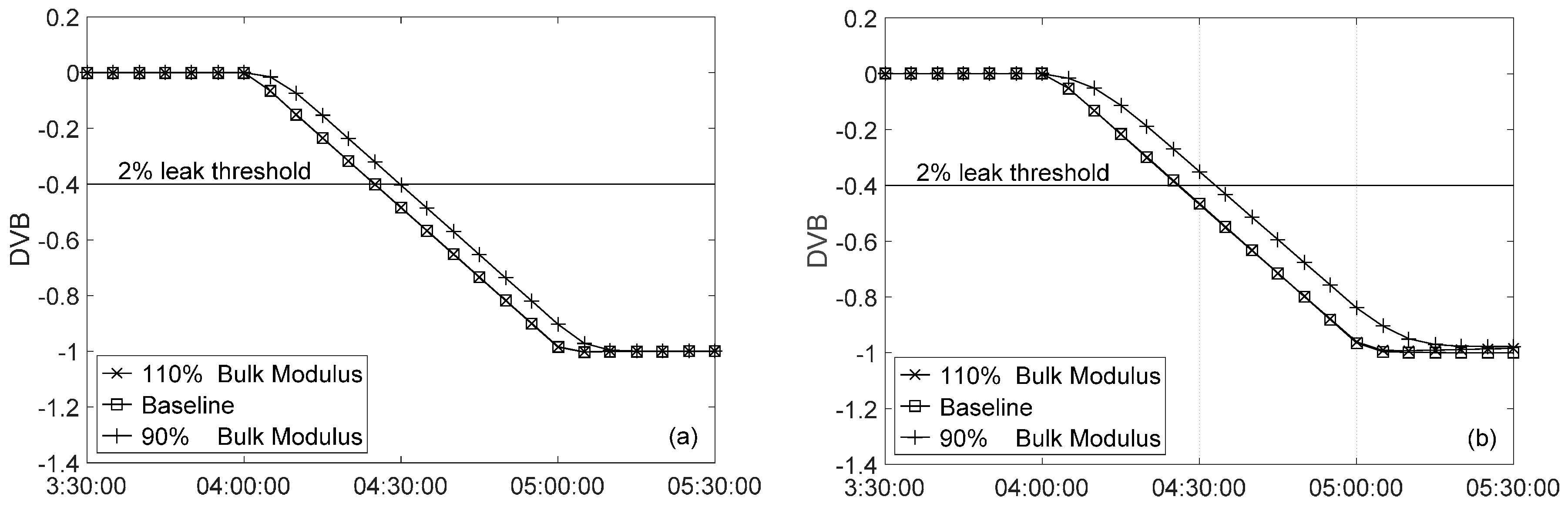
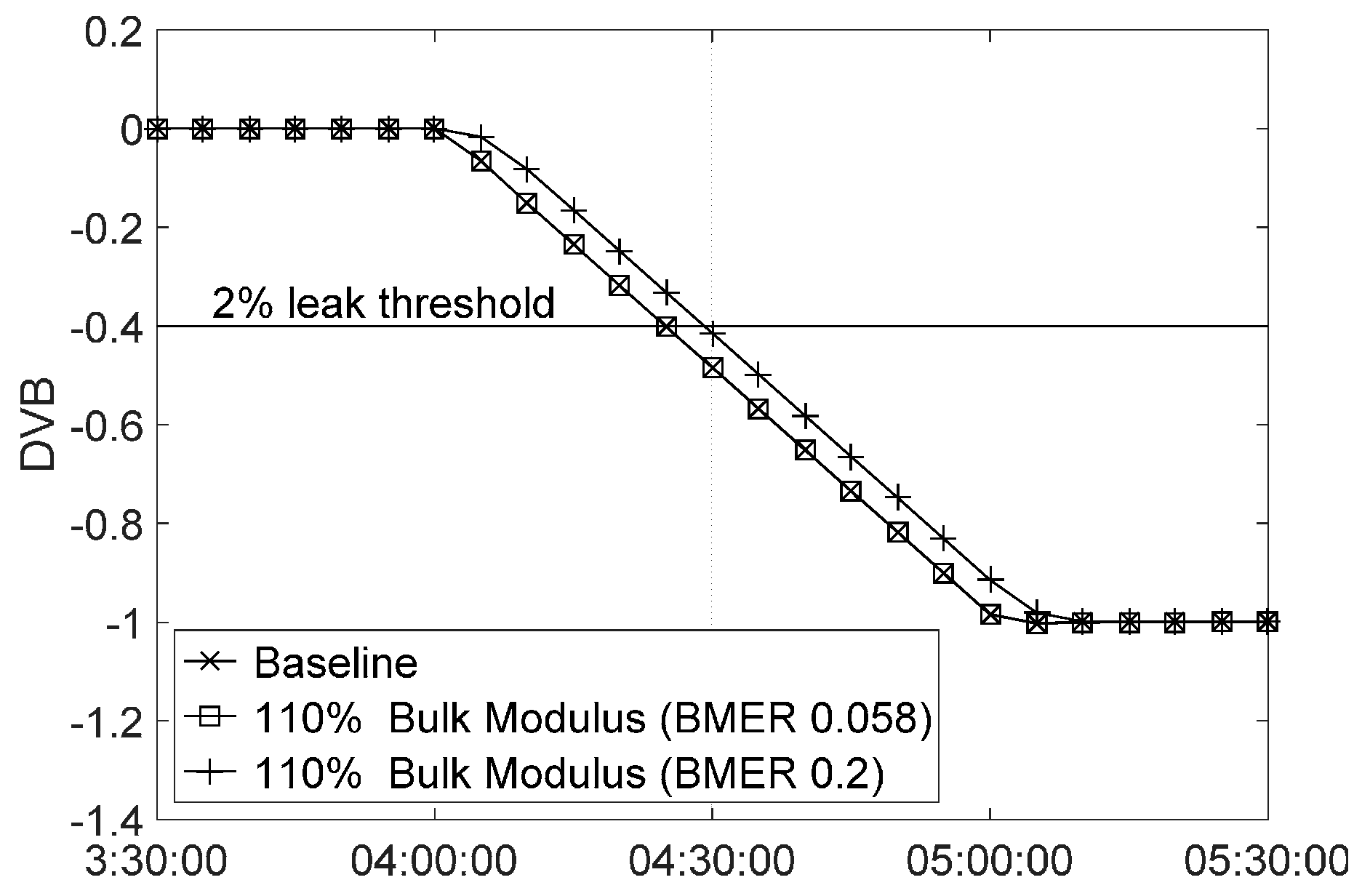
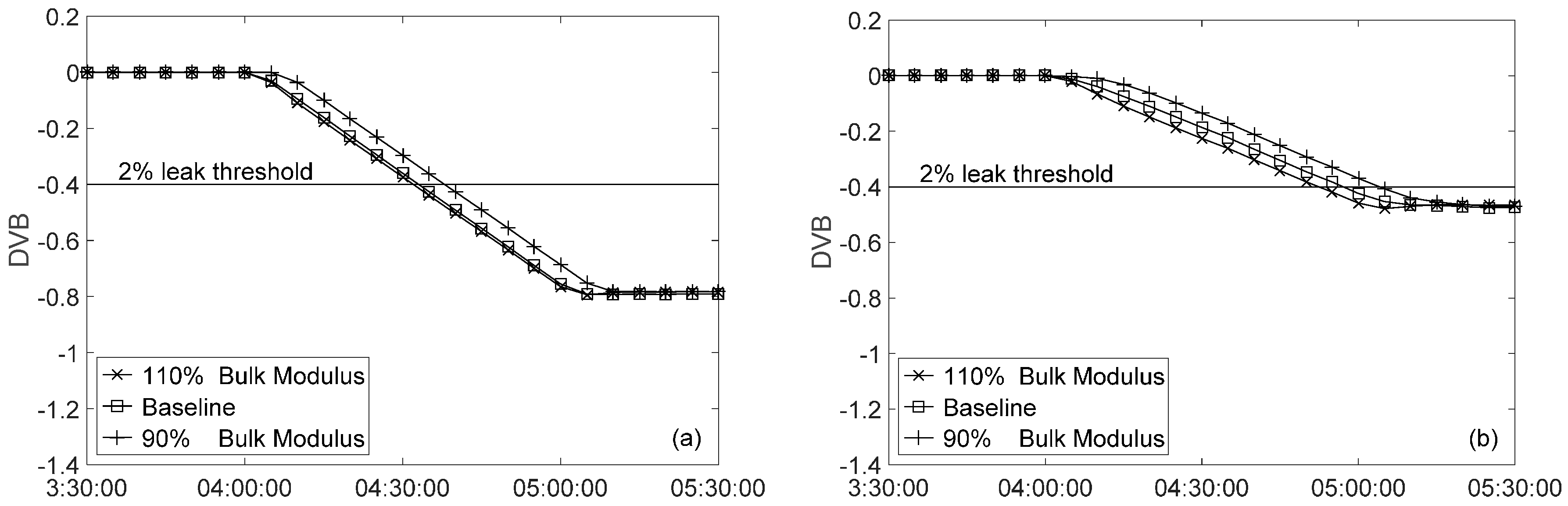
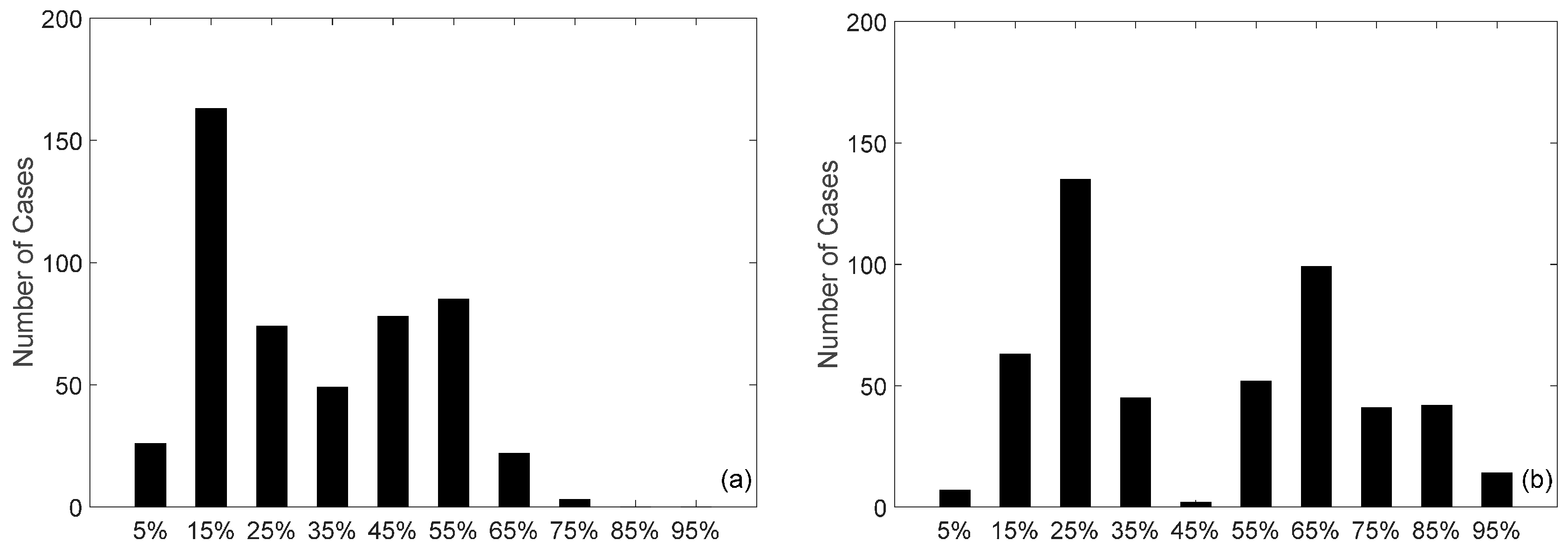
3.1. Uncertainty in R Factor
3.1.1. Viscosity Uncertainty
3.1.2. Bulk Modulus Uncertainty
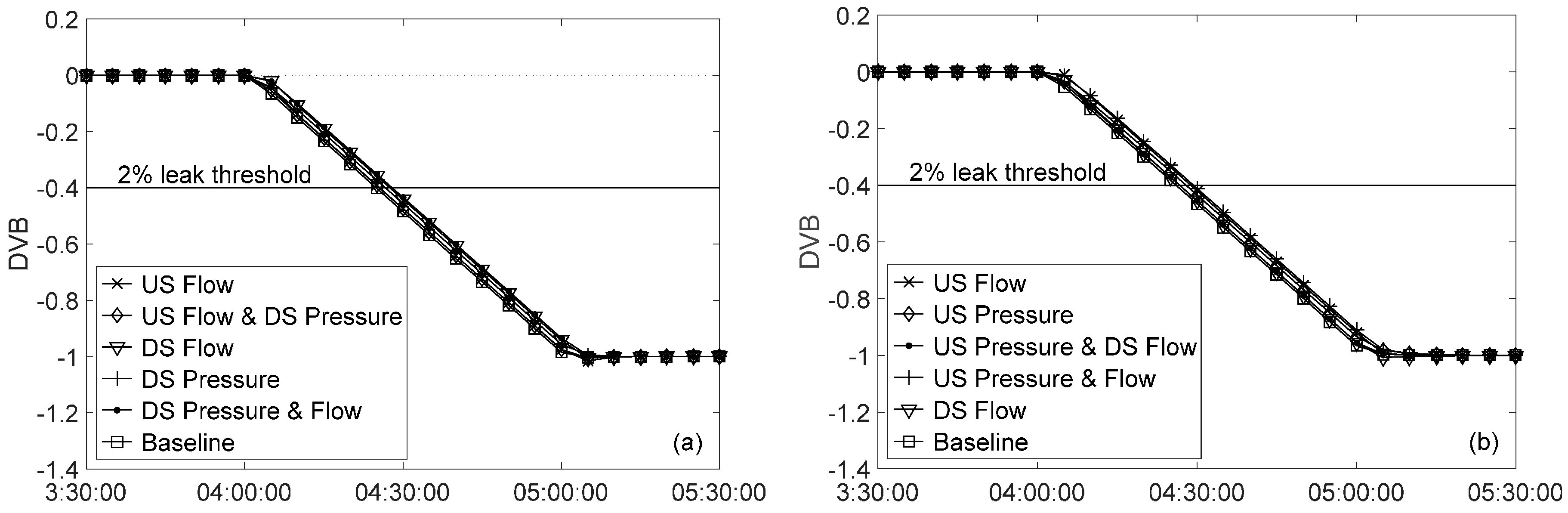
3.2. Uncertainty in Supervisory Control and Data Acquisition Data
3.3. Low R System vs. High R System
3.4. Random Uncertainty Sources
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- National Energy Board. Safety Performance Portal. Available online: https://www.neb-one.gc.ca/sftnvrnmnt/sft/dshbrd/index-eng.html (accessed on 10 October 2016).
- Geiger, G. State-of-the-art in leak detection and localization. Oil Gas Eur. Mag. 2006, 32, 193–198. [Google Scholar]
- Po, A.; Xing, Y. Internal Free Swimming Pipeline Leakage Detection Technology—Smartball. In Proceedings of the International Conference on Pipelines and Trenchless Technology, Xi’an, China, 16–18 October 2011; American Society of Civil Engineers: Reston, VA, USA, 2011; pp. 996–1005. [Google Scholar]
- National Energy Board. Onshore Pipeline Regulations; SOR/99-294; Minister of Justice: Calgary, AB, Canada, 2010.
- Province of Alberta. Pipeline Act; Alberta Queen’s Print: Edmonton, AB, Canada, 2014; p. 32.
- American Petroleum Institute. Computational Pipeline Monitoring for Liquids; American Petroleum Institute Report 1130; American Petroleum Institute: Washington, DC, USA, 2002. [Google Scholar]
- Liou, C.P. Pipeline Leak Detection and Location. In Proceedings of the International Conference on Pipeline Design and Installation, Pipeline Division, American Society of Civil Engineers, Las Vegas, NV, USA, 24–29 September 1990. [Google Scholar]
- Al-Khomairi, A. Leak Detection in Long Pipelines Using the Least Squares Method. ASCE J. Hydraul. Res. 2008, 46, 392–401. [Google Scholar] [CrossRef]
- He, G.; Liang, Y.; Li, Y.; Wu, M.; Sun, L.; Xie, C.; Li, F. A Method for Simulating the Entire Leaking Process and Calculating the Liquid Leakage Volume of A Damaged Pressurized Pipeline. J. Hazard. Mater. 2017, 332, 19–32. [Google Scholar] [CrossRef] [PubMed]
- Al-Zahrani, M. Modeling and Simulation of Water Distribution System: A Case Study. Arab. J. Sci. Eng. 2014, 39, 1621–1636. [Google Scholar] [CrossRef]
- Duan, H.F. Uncertainty Analysis of Transient Flow Modeling and Transient-based Leak Detection in Elastic Water Pipeline Systems. Water Resour. Manag. 2015, 29, 5413–5427. [Google Scholar] [CrossRef]
- American Petroleum Institute. Pipeline Variable Uncertainties and Their Effects on Leak Detectability; American Petroleum Institute Report 1149; American Petroleum Institute: Washington, DC, USA, 1993. [Google Scholar]
- Liou, C.P.; Tian, J. Leak Detection—Transient Flow Simulation Approaches. ASME J. Energy Resour. Technol. 1995, 117, 243–248. [Google Scholar] [CrossRef]
- American Petroleum Institute. Pipeline Variable Uncertainties and Their Effects on Leak Detectability; American Petroleum Institute Report 1149; American Petroleum Institute: Washington, DC, USA, 2015. [Google Scholar]
- DNV GL Group. Stoner Pipeline Simulator (SPS) 9.9.0 Help and Reference; DNV GL Group: Hong Kong, China, 2012. [Google Scholar]
- Wylie, E.B.; Streeter, V.L. Fluid Transient in Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993; ISBN 10:0139344233. [Google Scholar]
- Canadian Standards Association. Z662-07 Oil and Gas Pipeline Systems: Annex E: Recommended Practice for Liquid Hydrocarbon Pipeline System Leak Detection; Canadian Standards Association: Mississauga, ON, Canada, 2007; pp. 388–392. [Google Scholar]
- Vinh, P. Adding Value to CPM Testing; American Petroleum Institute Pipeline Conference and Cybernetics Symposium: Phoenix, AZ, USA, 2012. [Google Scholar]
- Modisette, J. State Estimation of Pipeline Models Using the Ensemble Kalman Filter; Pipeline Simulation Interest Group (PSIG): Prague, Czech Republic, 2013; p. 31. [Google Scholar]
- Arifin, B.; Li, Z.; Shah, S.L. Pipeline Leak Detection Using Particle Filters. IFAC PapersOnLine 2015, 48, 76–81. [Google Scholar] [CrossRef]
- Hung, D.; Mokamati, S. A Novel Approach to Leak Sensitivity Testing of Computational Pipeline Monitoring Systems for Hydrocarbon Liquid Pipelines with Hydraulic Simulators. In Proceedings of the 11th International Pipeline Conference, Calgary, AB, Canada, 26–30 September 2016. [Google Scholar]
- Pabon, S. Sensitivity Study of a Computer Model Based Leak Detection System in Liquid Pipelines. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2015. [Google Scholar]


| Variable | Variable Value | Equivalent Error in R | ||||
|---|---|---|---|---|---|---|
| Lower | Base | Upper | Lower | Base | Upper | |
| Viscosity (mPa·s): R = 2.20 system | 1.31 | 4.57 | 11.53 | −20% | 0 | +20% |
| Viscosity (mPa·s): R = 0.49 system | 1.69 | 4.57 | 9.85 | −20% | 0 | +20% |
| Bulk modulus large (GPa) | 0.86 | 1.45 | 3.31 | +20% | 0 | −20% |
| Bulk modulus realistic (GPa) | 1.30 | 1.45 | 1.59 | +3.5% | 0 | −3.0% |
| Flow Condition | Pressure Sensor with Time Skew | Flow Meter with Time Skew |
|---|---|---|
| Steady State (with leak) | US | none |
| none | DS | |
| US | DS | |
| Flow Decrease | none | US |
| none | DS | |
| DS | None | |
| DS | US | |
| DS | DS | |
| Flow Increase | US | None |
| none | US | |
| none | DS | |
| US | DS | |
| US | US |
| Variables | Range of Uncertainty | Tested Values |
|---|---|---|
| Viscosity | 1.31–11.53 mPa·s | random |
| Bulk modulus | 1.30–1.59 GPa | random |
| Data noise | - | 1%, 2% |
| Time skew | - | 5 s, 10 s |
| Polling time | - | 5 s, 10 s |
| Tuning Weights | Viscosity Error | Bulk Modulus Error | SCADA Error | Random Error |
|---|---|---|---|---|
| W1 | 1 | 1 | 1 | 1 |
| W2 | 1 | 1 | 1 | 1 |
| W3 | 1 | 107 | 107 | 1 |
| W4 | 10 | 10 | 10 | 10 |
| W5 | 500 | 107 | 107 | 500 |
| W6 | 107 | 1 | 107 | 1 |
| W7 | 5 | 5 | 5 | 5 |
| Data Type | Variable | Flow Condition | Level of Uncertainty | Baseline Detection Time (Minutes after Leak Starts) | Change in Detection Time (Min) | ||
|---|---|---|---|---|---|---|---|
| R = 0.49 | R = 2.20 | R = 0.49 | R = 2.20 | ||||
| Perfect Data | Bulk Modulus | Flow Decrease | +10% | 24.2 | 24.9 | 0.7 | 0.0 |
| −10% | 1.7 | 4.9 | |||||
| Flow Increase | +10% | 24.5 | 26.1 | 0.5 | 0.0 | ||
| −10% | 1.4 | 7.0 | |||||
| Steady State | +10% | 24.4 | 25.5 | 0.05 | 0.2 | ||
| −10% | −0.05 | −0.2 | |||||
| Time Skew | Flow Decrease | 10 s | 24.2 | 24.9 | 2.5–3.9 | 0.6–3.1 | |
| Flow Increase | 10 s | 24.5 | 26.1 | 0.8–2.2 | 0.5–3.3 | ||
| Steady State | 10 s | 24.4 | 25.5 | 0.0 | 0.0 | ||
| Noisy Data | Viscosity 1 | Flow Decrease | −20% f | 31.1 | 33.1 | −1.8 | −4.5 |
| +20% f | 0.2 | 0.5 | |||||
| Flow Increase | −20% f | 55.5 | 61.7 | −22.6 | −34.2 | ||
| +20% f | 1.3 | 0.1 | |||||
| Steady State | −20% f | 39.8 | 41.7 | −8.7 | −15.2 | ||
| +20% f | 0.5 | −0.3 | |||||
| Bulk Modulus | Flow Decrease | +10% | 31.1 | 33.1 | 0.1 | −1.0 | |
| −10% | 0.4 | 4.9 | |||||
| Flow Increase | +10% | 55.5 | 61.7 | 0.0 | −4.6 | ||
| −10% | 1.3 | 7.1 | |||||
| Steady State | +10% | 39.8 | 41.7 | 0.05 | 0.2 | ||
| −10% | −0.02 | −0.3 | |||||
| Time Skew | Flow Decrease | 10 s | 31.1 | 33.1 | 28.0 | 35.0 | |
| Flow Increase | 10 s | 55.5 | 61.7 | Undetected | Undetected | ||
| Steady State | 10 s | 39.8 | 41.7 | Undetected | Undetected | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; She, Y.; Loewen, M. A Sensitivity Analysis of a Computer Model-Based Leak Detection System for Oil Pipelines. Energies 2017, 10, 1226. https://doi.org/10.3390/en10081226
Lu Z, She Y, Loewen M. A Sensitivity Analysis of a Computer Model-Based Leak Detection System for Oil Pipelines. Energies. 2017; 10(8):1226. https://doi.org/10.3390/en10081226
Chicago/Turabian StyleLu, Zhe, Yuntong She, and Mark Loewen. 2017. "A Sensitivity Analysis of a Computer Model-Based Leak Detection System for Oil Pipelines" Energies 10, no. 8: 1226. https://doi.org/10.3390/en10081226
APA StyleLu, Z., She, Y., & Loewen, M. (2017). A Sensitivity Analysis of a Computer Model-Based Leak Detection System for Oil Pipelines. Energies, 10(8), 1226. https://doi.org/10.3390/en10081226






