A Full Frequency-Dependent Cable Model for the Calculation of Fast Transients
Abstract
:1. Introduction
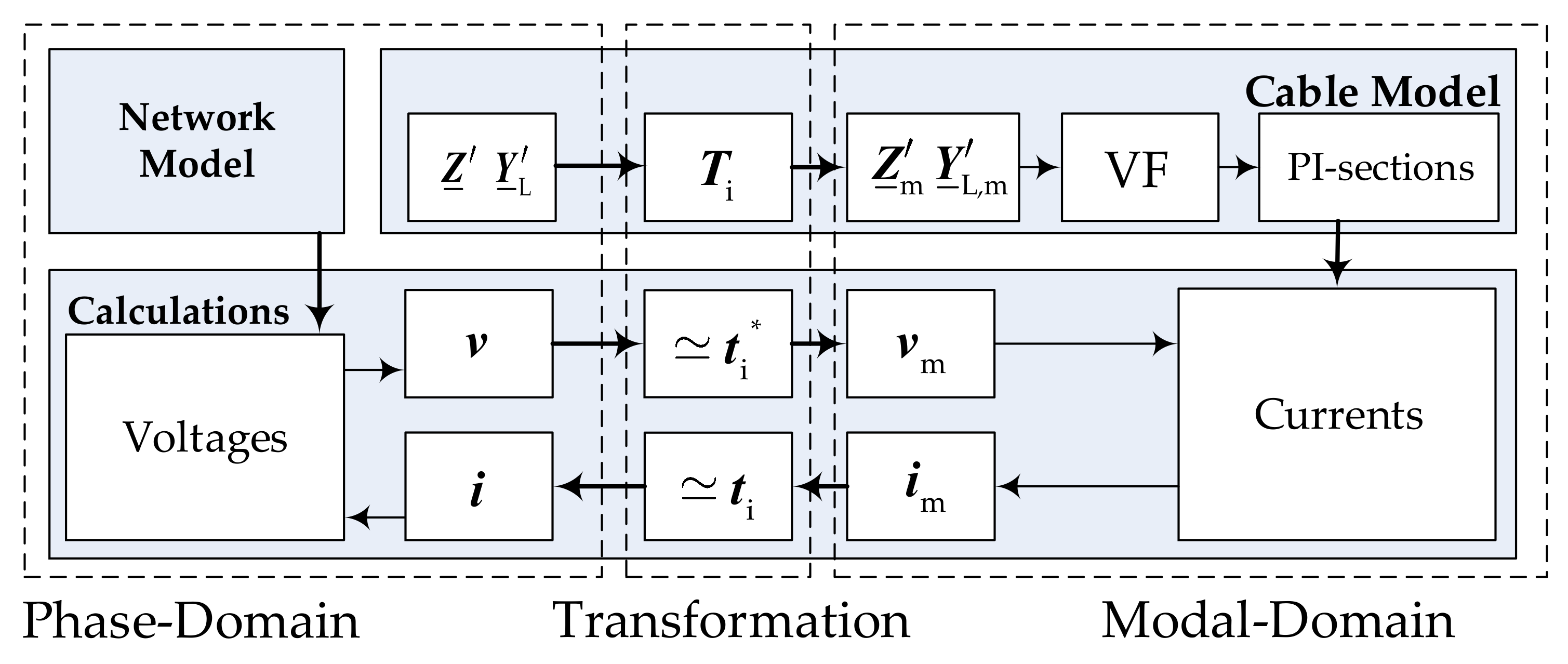
2. Algorithm for Calculation of Frequency-Dependent Cable Parameters
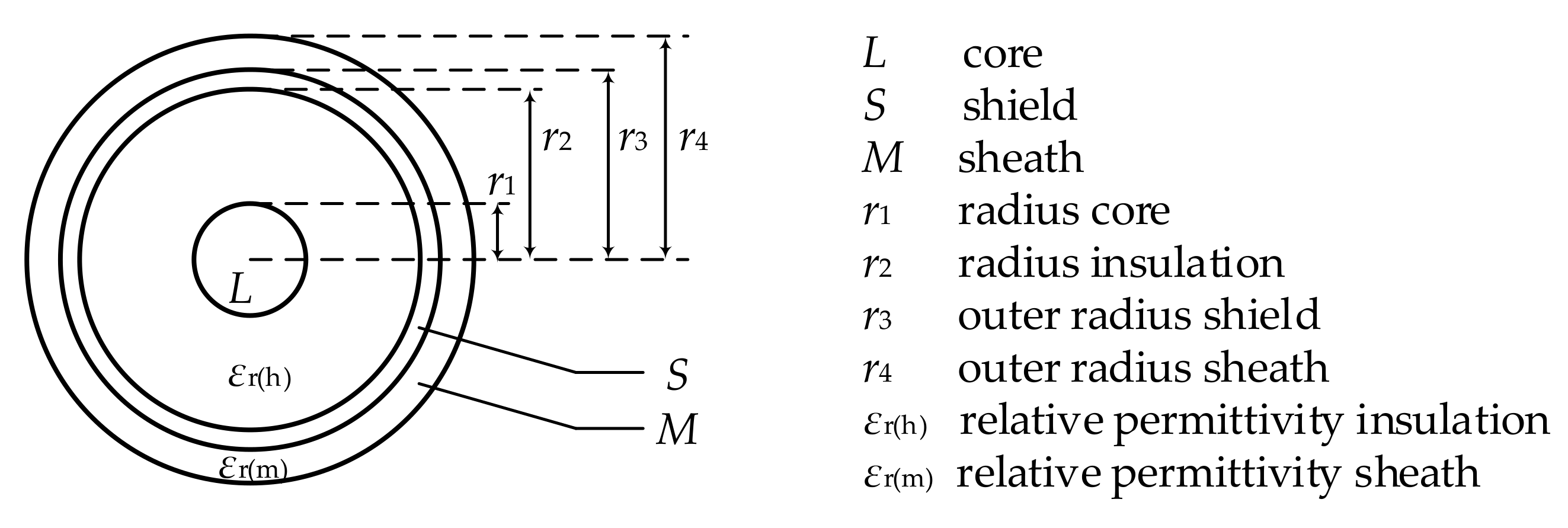
2.1. Fundamentals
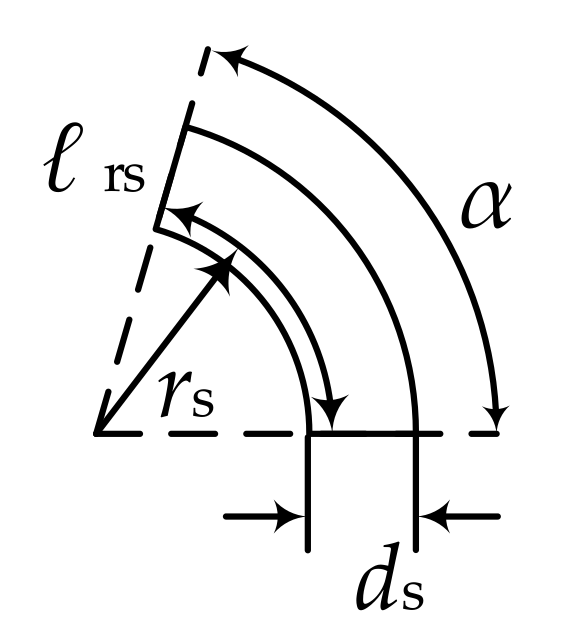
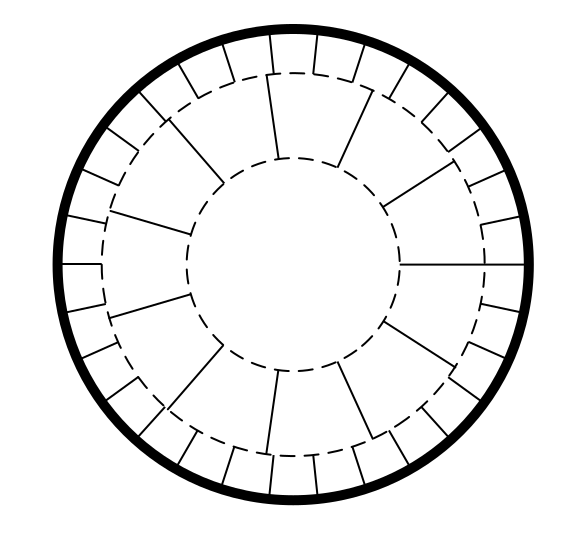
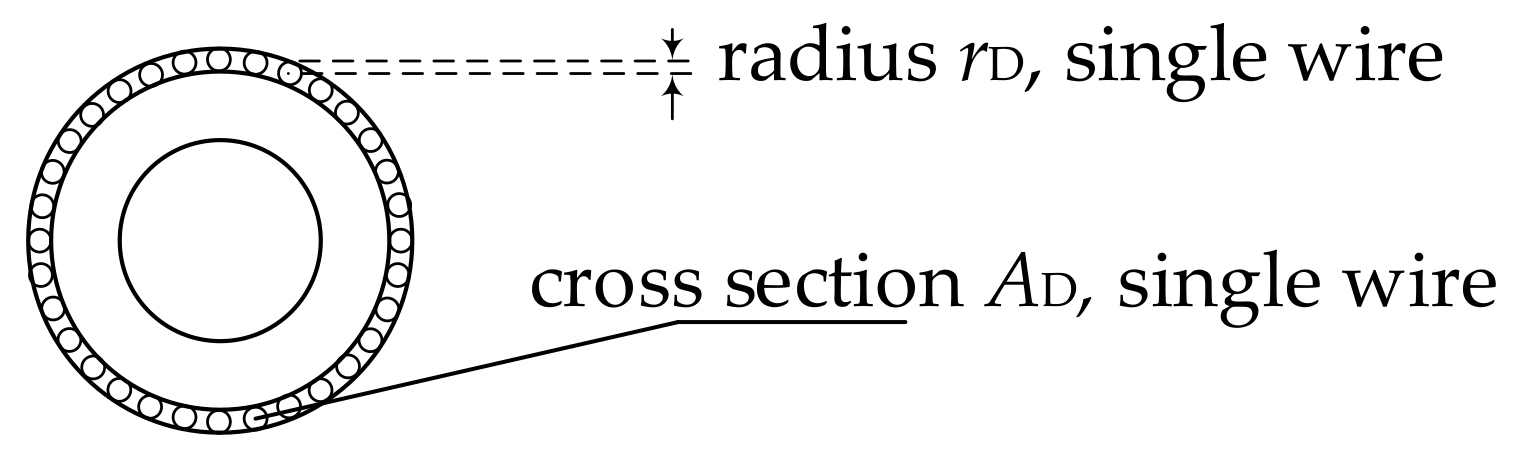
2.2. Partial Subconductor Method
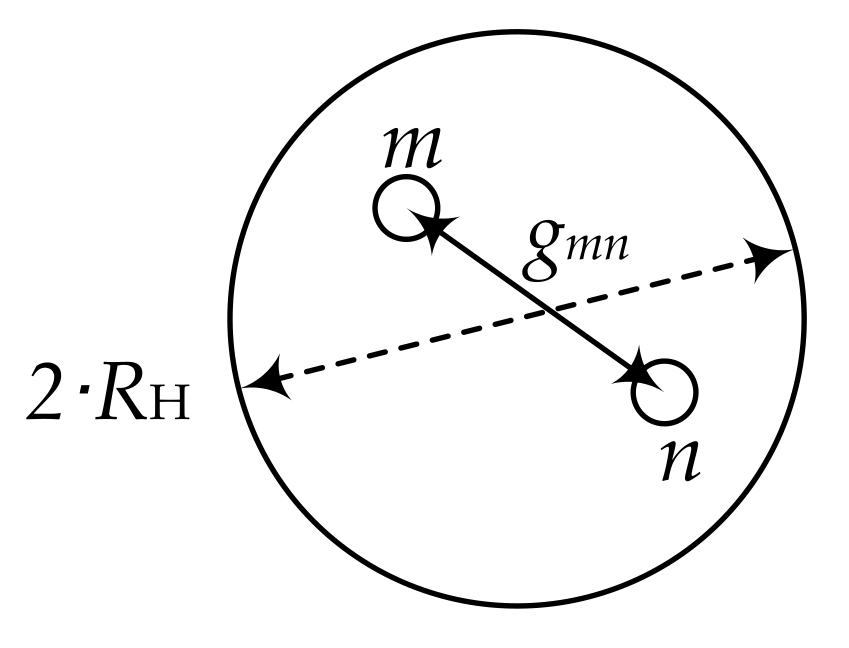
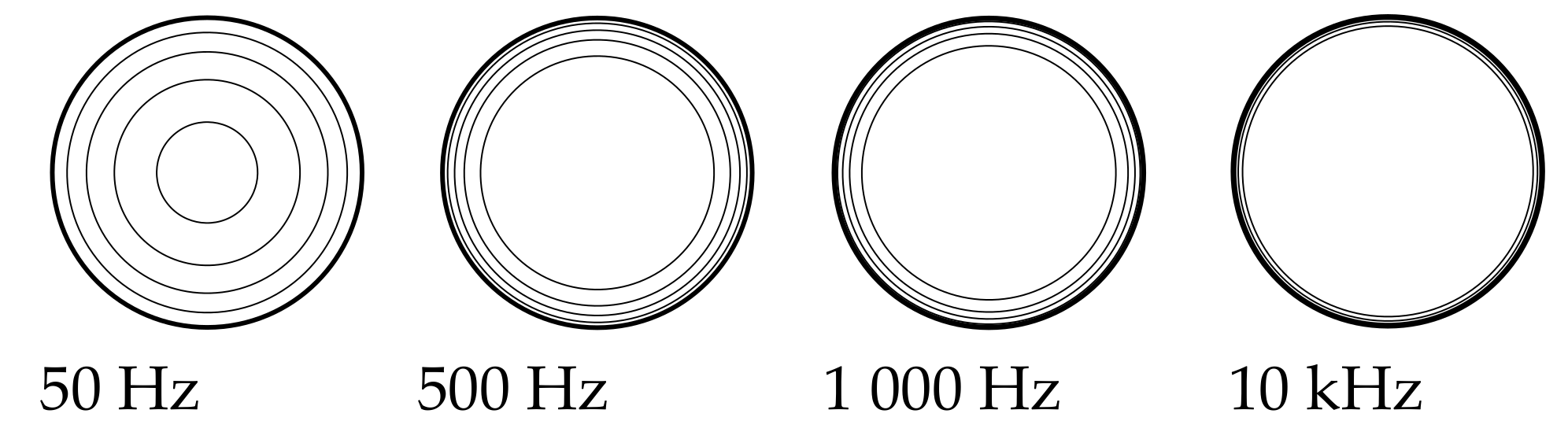
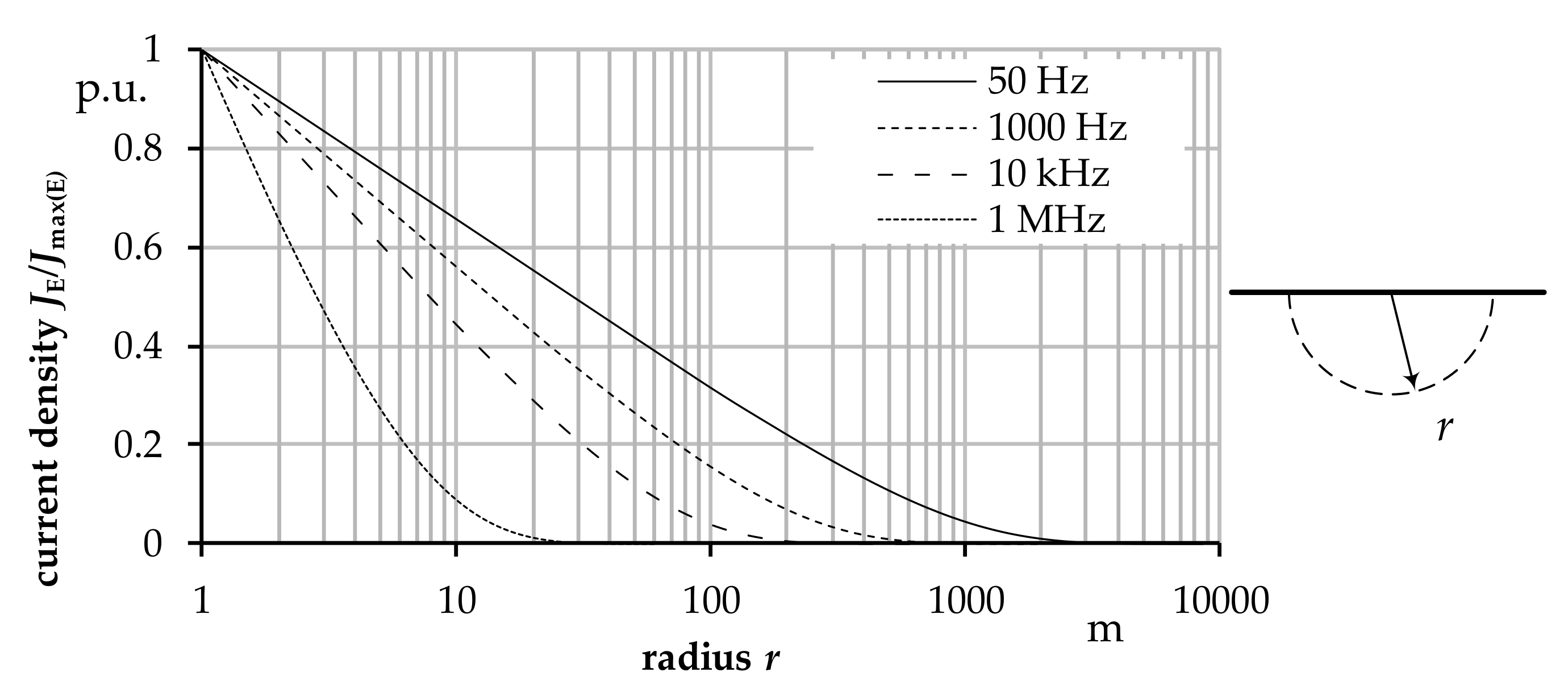
2.3. Frequency-Dependent Segmentation of Conductors
2.4. Earth Segmentation
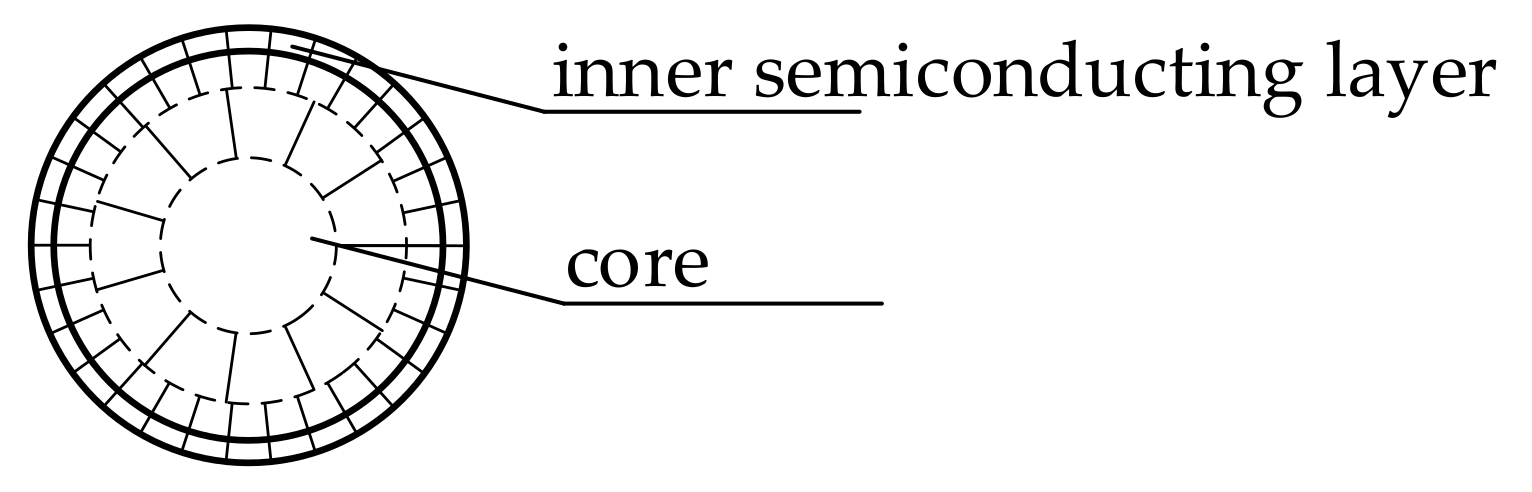
2.5. Shield Segmentation
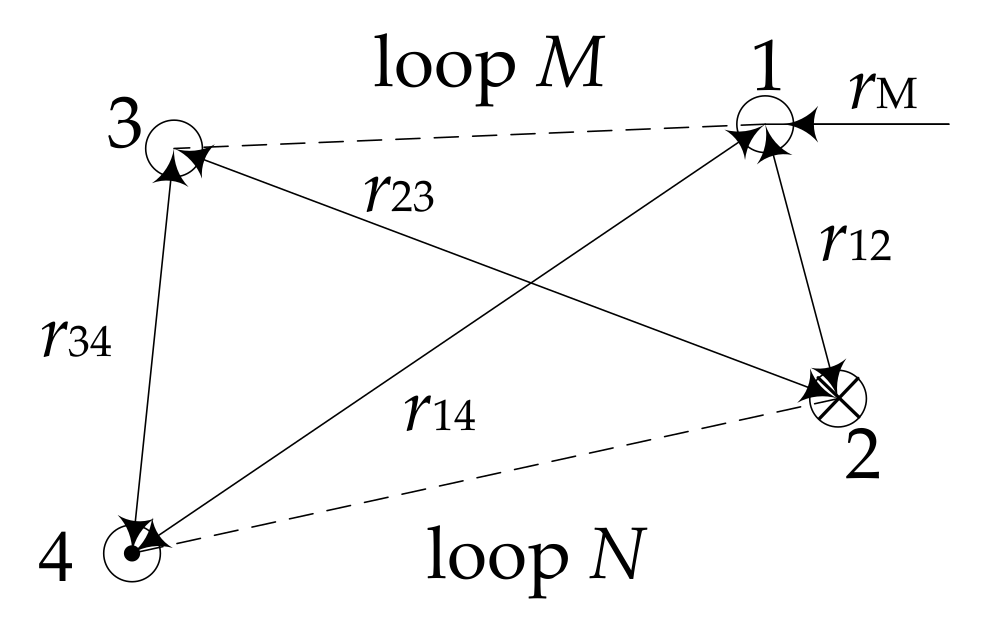
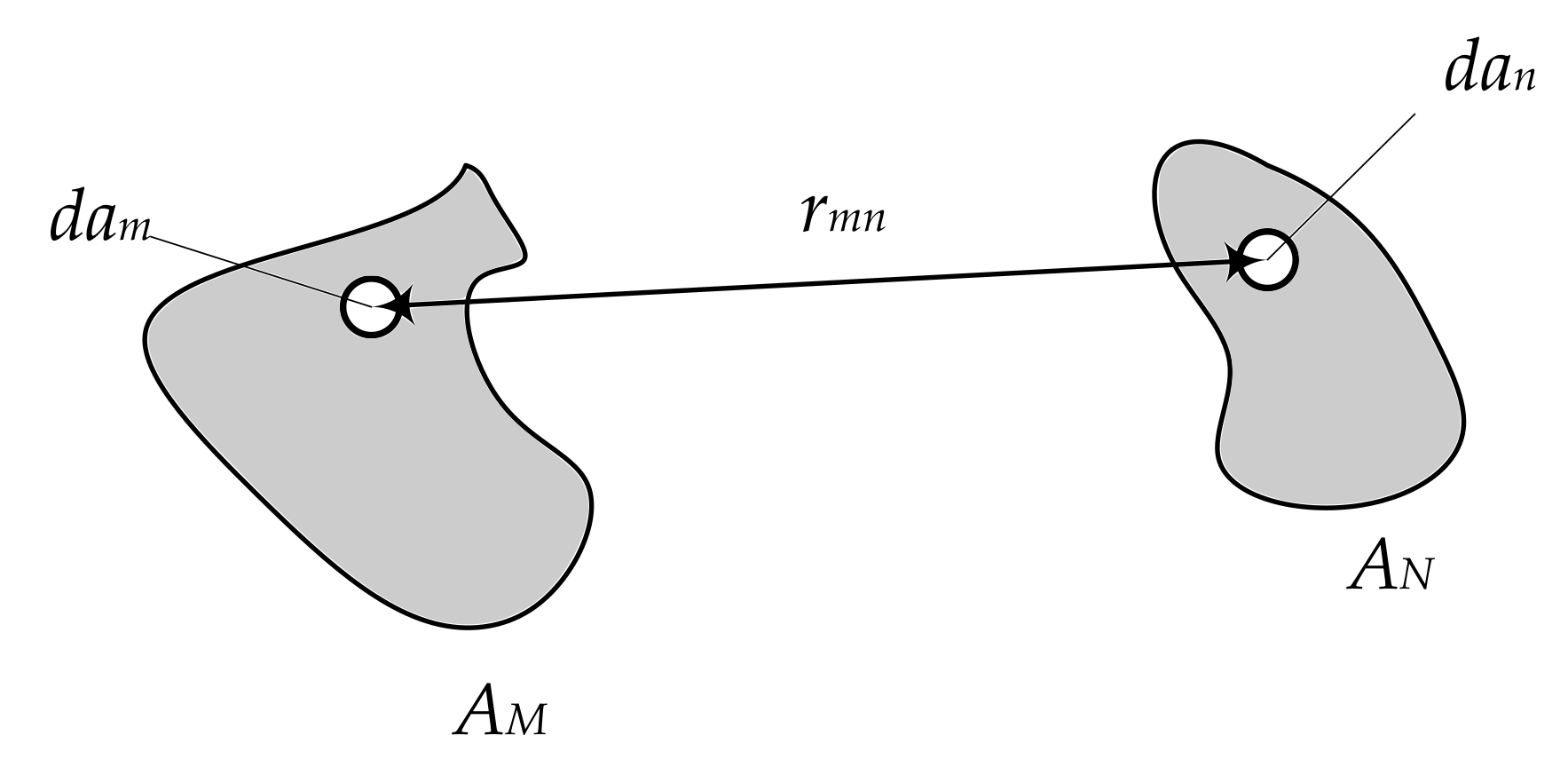
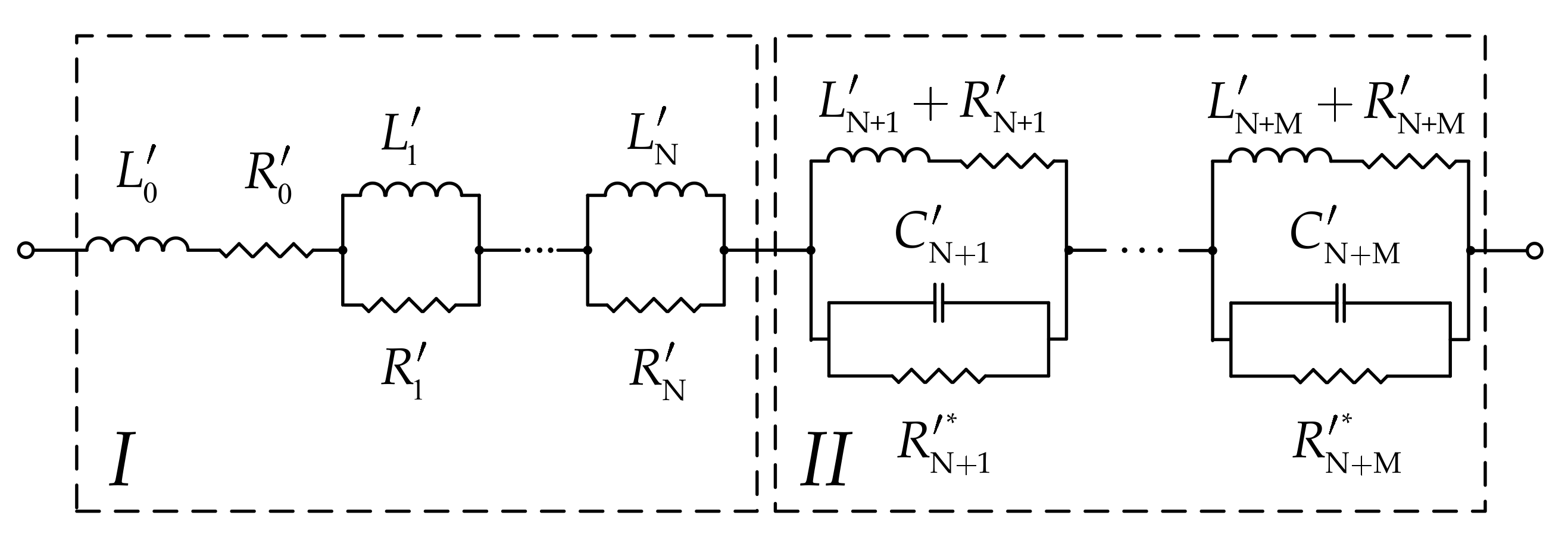
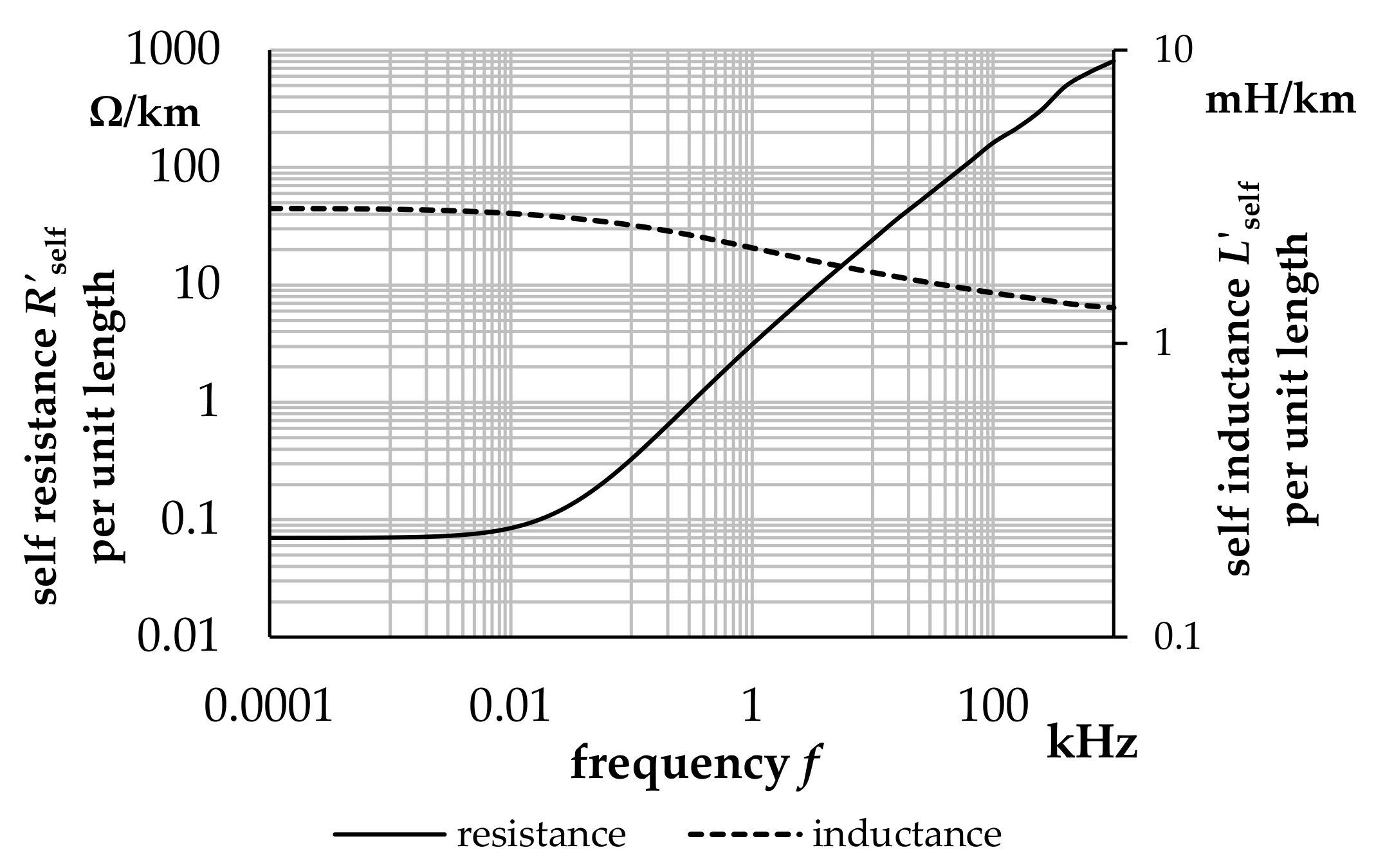
2.6. Calculation of Frequency-Dependent Impedances
2.7. System Impedances
2.8. Impact of Semiconducting Layers
2.9. Main Insulation Capacitance
2.10. Sheath Capacitances
2.10.1. Earth Installation
2.10.2. Air Installation
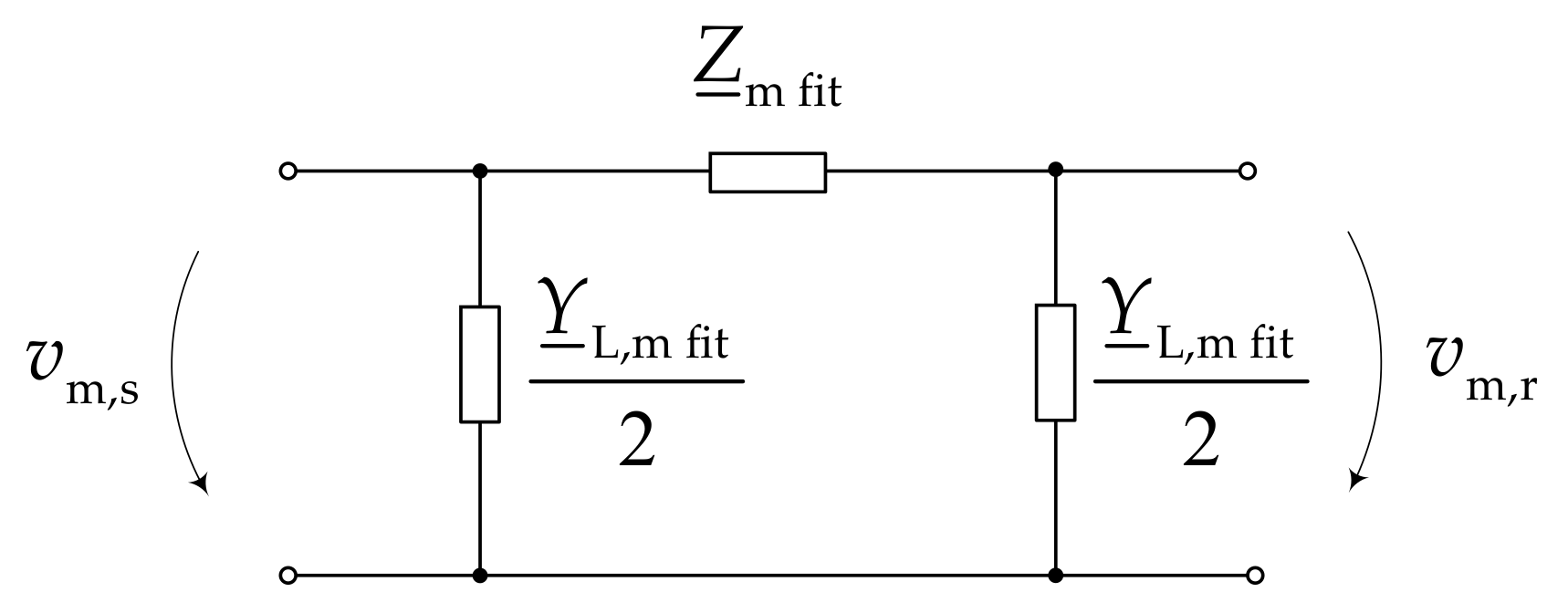
3. Wave Propagation Model
3.1. Approach
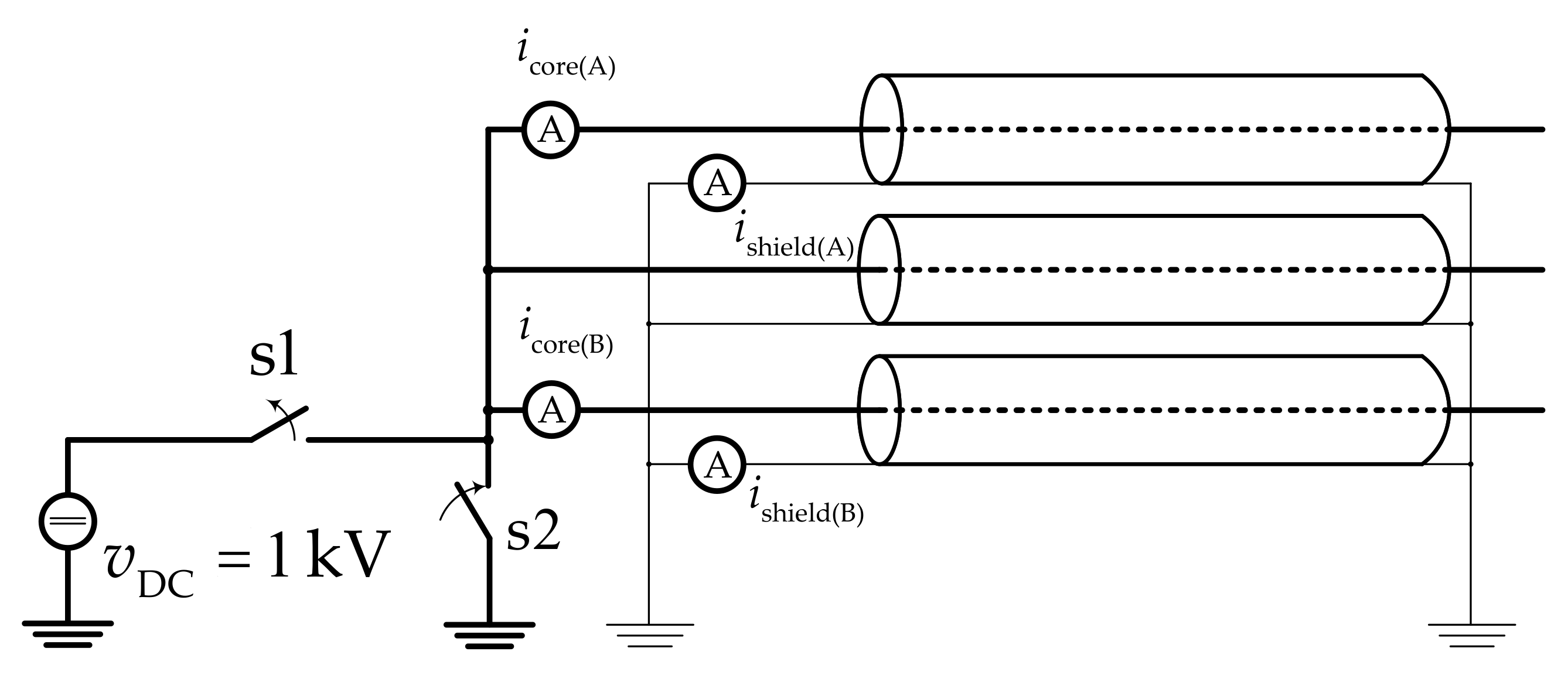
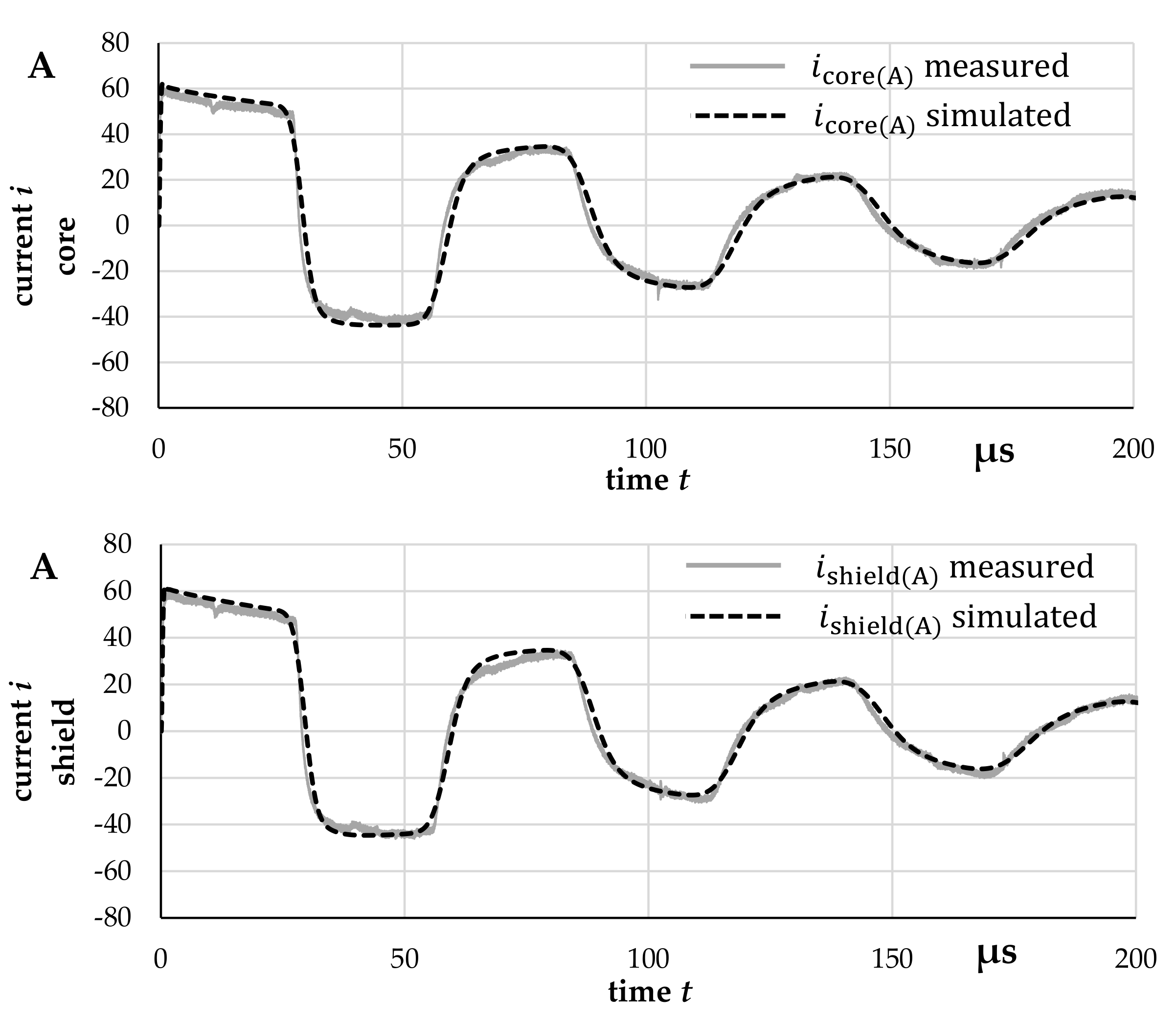
4. Validation of the Full Frequency-Dependent Cable Model
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Ametani, A. A general formulation of impedance and admittance of cables. IEEE Trans. Power Appar. Syst. 1980, PAS-99, 902–909. [Google Scholar] [CrossRef]
- Wedepohl, L.; Wilcox, D. Transient analysis of underground power transmission systems. Proc. IEE 1973, 120, 253–260. [Google Scholar]
- Carson, J.R. Wave propagation in overhead wires with ground return. Bell Syst. Tech. J. 1926, 5, 539–554. [Google Scholar] [CrossRef]
- Pollaczek, F. Über das Feld einer unendlich langen wechselstromdurchflossenen Einfachleitung. Elektr. Nachr. 1926, 3, 339–359. [Google Scholar]
- Schelkunoff, A. The electromagnetic theory of coaxial transmission line and cylindrical shields. Bell Syst. Tech. J. 1934, 13, 532–579. [Google Scholar] [CrossRef]
- Morched, A.; Gustavsen, B.; Manoocher, T. A universal model for accurate calculation of electromagnetic transients on overhead lines and underground cables. IEEE Trans. Power Deliv. 1999, 14, 1032–1038. [Google Scholar] [CrossRef]
- Cgj, L.; Greeff, J.C.; Joubert, S.V. Modelling of telegraph equations in transmission lines. In Proceedings of the Buffelspoort TIME2008, Buffelspoort, South Africa, 22–26 September 2008. [Google Scholar]
- Bekefi, G.; Barrett, H.A. Electromagnetic Vibrations, Waves, and Radiation; MIT Press: Cambridge, MA, USA, 1987. [Google Scholar]
- Rusek, A.; Ganesan, S.; Aloi, N.D. A Friendly Approach to Transient Processes in Transmission Lines. In Proceedings of the 2011 ASEE North Central & Illinois-Indiana Section Conference, Mt. Pleasant, MI, USA, 1–2 April 2011. [Google Scholar]
- Dommel, H.W. Electromagnetic Transients Program Manual (EMTP Theory Book); Bonneville Power Administration: Portland, OR, USA, 1986. [Google Scholar]
- Snelson, J. Propagation of travelling waves on transmission lines-frequency dependent parameters. IEEE Transm. Power Appar. Syst. 1971, PAS-90, 2561–2567. [Google Scholar] [CrossRef]
- Marti, J. Accurate modelling of frequency-dependent lines in electromagnetic transient simulations. IEEE Transm. Power Appar. Syst. 1982, PAS-101, 147–155. [Google Scholar] [CrossRef]
- Marti, L. Simulation of transients in underground cables with frequency dependent modal transformation matrix. IEEE Transm. Power Appar. Syst. 1988, 3, 1099–1110. [Google Scholar] [CrossRef]
- Noda, T.; Nagaoka, N.; Ametani, A. Phase Domain Modeling of Frequency-Dependent transmission Lines by Means of an ARMA Model. IEEE Trans. Power Deliv. 1996, 11, 401–411. [Google Scholar] [CrossRef]
- Gustavsen, B.; Semlyen, A. Rational approximation of frequency domain responses by Vector Fitting. IEEE Trans. Power Deliv. 1995, 21, 1052–1061. [Google Scholar] [CrossRef]
- Gustavsen, B.; Morched, A.; Manoocher, T. Improving the pole relocating properties of vector fitting. IEEE Trans. Power Deliv. 2006, 21, 1587–1592. [Google Scholar] [CrossRef]
- Noda, T. Identification of a multiphase network equivalent for electromagnetic transient calculations using partitioned frequency response. IEEE Trans. Power Deliv. 2005, 20, 1134–1142. [Google Scholar] [CrossRef]
- Noda, T. Application of Frequency-Partitioning Fitting to the Phase-Domain Frequency-Dependent Modeling of Overhead Transmission Lines. IEEE Trans. Power Deliv. 2015, 30, 174–183. [Google Scholar] [CrossRef]
- Noda, T. Application of Frequency-Partitioning Fitting to the Phase-Domain Frequency-Dependent Modeling of Underground Cables. IEEE Trans. Power Deliv. 2016, 31, 1776–1777. [Google Scholar] [CrossRef]
- Kocar, I.; Mahseredjian, J. Accurate Frequency Dependent Cable Model for Electromagnetic Transients. IEEE Trans. Power Deliv. 2016, 31, 1281–1288. [Google Scholar] [CrossRef]
- Hoshmeh, A.; Malekian, K.; Schufft, W.; Schmidt, U. A single-phase cable model based on lumped-parameters for transient calculations in the time domain. In Proceedings of the 15th International Conference on Environment and Electrical Engineering, Rome, Italy, 10–13 June 2015; pp. 731–736. [Google Scholar]
- Küpfmüller, K. Einführung in die Theoretische Elektrotechnik, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1973. [Google Scholar]
- Maxwell, I.C. A Treatise on Electricity and Magnetism, 4th ed.; Oxford University Press: London, UK, 2002; Volume 2. [Google Scholar]
- Brüderlink, R. Induktivität und Kapazität der Starkstrom-Freileitung, 1st ed.; Verlag, G., Ed.; Braun: Karlsruhe, Germany, 1954. [Google Scholar]
- Rees, F. Einfluss des Erdreichs auf das Elektromagnetische und Thermische Verhalten von Hochspannungs- Gleichstrom-Kabeln. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 1977. [Google Scholar]
- Comellini, E.; Invernizzi, A.; Manzoni, G. A computer program for determining electrical resistance and reactance of any transmission line. IEEE Transm. Power Appar. Syst. 1973, PAS-92, 308–314. [Google Scholar] [CrossRef]
- Dommel, H.W. Computation of cable impedances based of subdivision of conductors. IEEE Trans. Power Deliv. 1987, PWRD-2, 21–27. [Google Scholar]
- Lucas, R.; Taluktar, S. Advances in finite elemente techniques for calculation cable resistances and inductances. IEEE Trans. Power Appar. Syst. 1978, PAS-9711, 875–883. [Google Scholar] [CrossRef]
- Schmidt, U.; Shirvani, A.; Probst, R. An improved algorithm for determination of cable parameters based on frequency-dependent conductor segmentation. In Proceedings of the IEEE PES Transmission and Distribution Conference, Orlando, FL, USA, 7–10 May 2012; pp. 241–246. [Google Scholar]
- Schmidt, U. Frequenzabhängige Parameter von Kabeln zur Berechnung von Ausgleichsvorgängen im Zeitbereich. Ph.D. Thesis, Chemnitz Technical University, Chemnitz, Germany, 2013. [Google Scholar]
- Arnold, A.H.M. Proximity effect in solid and hollow round conductors. J. IEE 1941, 88, 349–359. [Google Scholar]
- Brakelmann, H. Analyse der Stromdichteverteilungen von Mehrleiteranordnungen mit einem iterativen Teilleiterverfahren. ETZ Archiv 1989, 11, 369–377. [Google Scholar]
- Ruedenberg, R. Die Ausbreitung der Erdstroeme in der Umgebung von Wechselstromleitungen. Zeitschrift für Angewandte Mathematik und Mechanik 1925, 5, 361–389. [Google Scholar] [CrossRef]
- Dommel, H.W. Digital computer solution of electromagnetic transients in single- and multiphase networks. IEEE Trans. Power Appar. Syst. 1969, PAS-88, 388–399. [Google Scholar] [CrossRef]
- Ametani, A.; Miyamoto, Y.; Nagaoka, N. Semiconducting layer impedance and its effect on cable wave-propagation and transient characteristics. IEEE Trans. Power Deliv. 2004, 19, 1523–1531. [Google Scholar] [CrossRef]
- Liu, T. Dielectric Spectroskopy of Very Low Loss Model Power Cables. Ph.D. Thesis, University of Leicester, Leicester, UK, 2010. [Google Scholar]
- Hadid, S.; Schmidt, U.; Schufft, W.; Rätzke, S. Frequenzabhängigkeit des Verlustfaktors tan δ an VPE-isolierten Kabeln. In Proceedings of the ETG-Fachtagung, Diagnostik Elektrischer Betriebsmittel, Fulda, Germany, 15–16 November 2012. [Google Scholar]
- Wagenaars, P.; Wouters, P.; Wielen, P.; Steenis, E. Approximation of transmission line parameters of single-core and three-core XLPE cables. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 106–115. [Google Scholar] [CrossRef]
- Gustavsen, B.; Sletbak, J.; Henriksen, T. Calculation of electromagnetic transients in transmission cables and lines taking frequency dependent effects accurately into account. IEEE Trans. Power Deliv. 1995, 10, 1076–1084. [Google Scholar] [CrossRef]
- Steinbigler, H. Anfangsfeldstärken und Ausnutzungsfaktoren Rotationssymmetrischer Elektrodenanordnungen in Luft. Ph.D. Thesis, Technische Universität München, Munich, Germany, 1969. [Google Scholar]
- Probst, R. Ermittlung der Kapazitäten des Drehstrom-Kabelsystems. Bachelor’s Thesis, Chemnitz Technical University, Chemnitz, Germany, 2011. [Google Scholar]
- Marti, J. The Problem of Frequency Dependence in Transmission Line Modelling. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 1981. [Google Scholar]
- Chrysochos, A.I.; Papadopoulos, T.A.; Papagiannis, G.K. Robust Calculation of Frequency-Dependent Transmission-Line Transformation Matrices Using the Levenberg Marquardt Method. IEEE Trans. Power Deliv. 2014, 29, 1621–1629. [Google Scholar] [CrossRef]
- Scott-Meyer, W. EMTP—Rule Book; Manual, Bonneviller Power Administration: Portland, OR, USA, 1982. [Google Scholar]


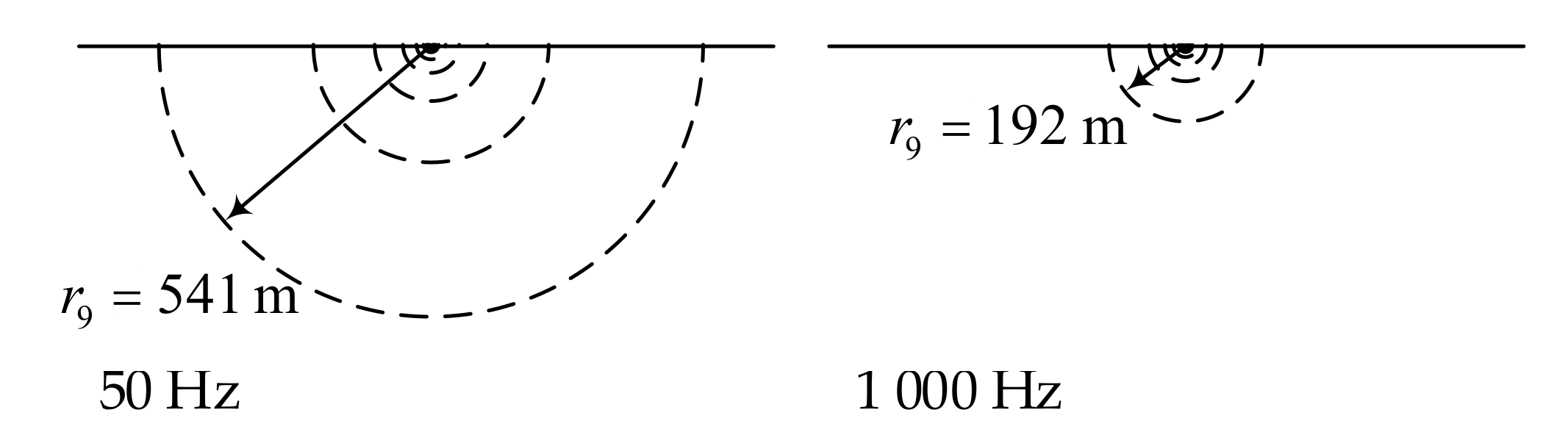

| Polarization | Frequency Range |
|---|---|
| Electronic | ≈ |
| Ionic | ≈ |
| Orientational | ≈ |
| Interfacial |
| Name | Unit | Value |
|---|---|---|
| Outer radius of the core | ||
| Inner radius of the sheath | ||
| Outer radius of the sheath | ||
| Outer insulation radius | ||
| Core resistivity | ||
| Shield resistivity | ||
| Inner insulation | ||
| Outer insulation | ||
| Inner insulation relative permittivity | ||
| Outer insulation relative permittivity | ||
| Relative permeability | ||
| Earth resistivity | 150 | |
| Type of installation | Trefoil | |
| Laying depth (system center) | ||
| Length | ℓ | ≈2.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoshmeh, A.; Schmidt, U. A Full Frequency-Dependent Cable Model for the Calculation of Fast Transients. Energies 2017, 10, 1158. https://doi.org/10.3390/en10081158
Hoshmeh A, Schmidt U. A Full Frequency-Dependent Cable Model for the Calculation of Fast Transients. Energies. 2017; 10(8):1158. https://doi.org/10.3390/en10081158
Chicago/Turabian StyleHoshmeh, Abdullah, and Uwe Schmidt. 2017. "A Full Frequency-Dependent Cable Model for the Calculation of Fast Transients" Energies 10, no. 8: 1158. https://doi.org/10.3390/en10081158
APA StyleHoshmeh, A., & Schmidt, U. (2017). A Full Frequency-Dependent Cable Model for the Calculation of Fast Transients. Energies, 10(8), 1158. https://doi.org/10.3390/en10081158




