Windbreak Effects Within Infinite Wind Farms
Abstract
:1. Introduction
2. Integrated Boundary-Layer Theory for Windbreak Effects in Wind Farms
2.1. Drag Partition for Wind Turbines and Windbreaks
2.1.1. Surface Stress and Windbreak Drag
2.1.2. Turbine Thrust
2.2. Inviscid Speedup from Windbreaks
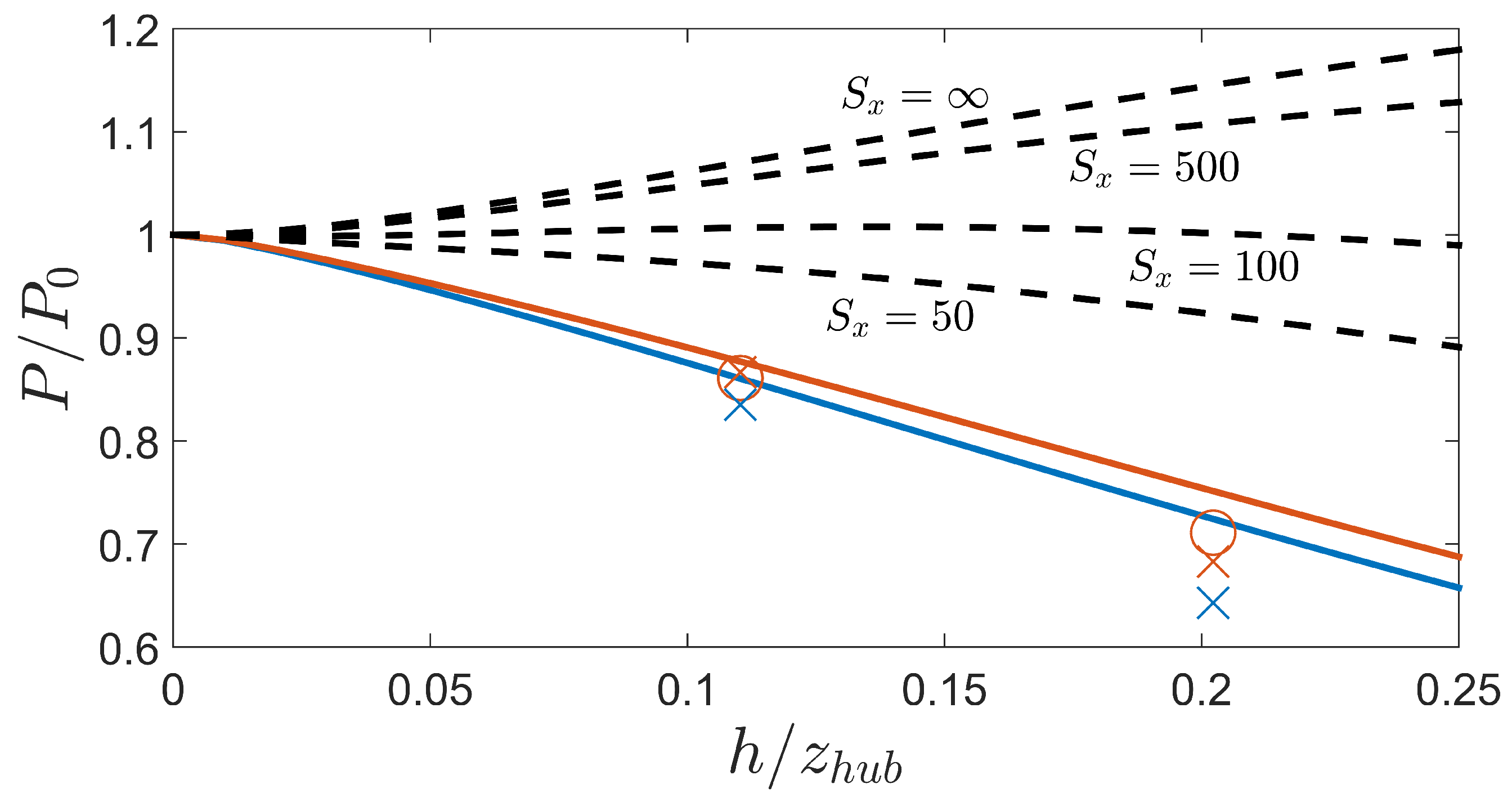
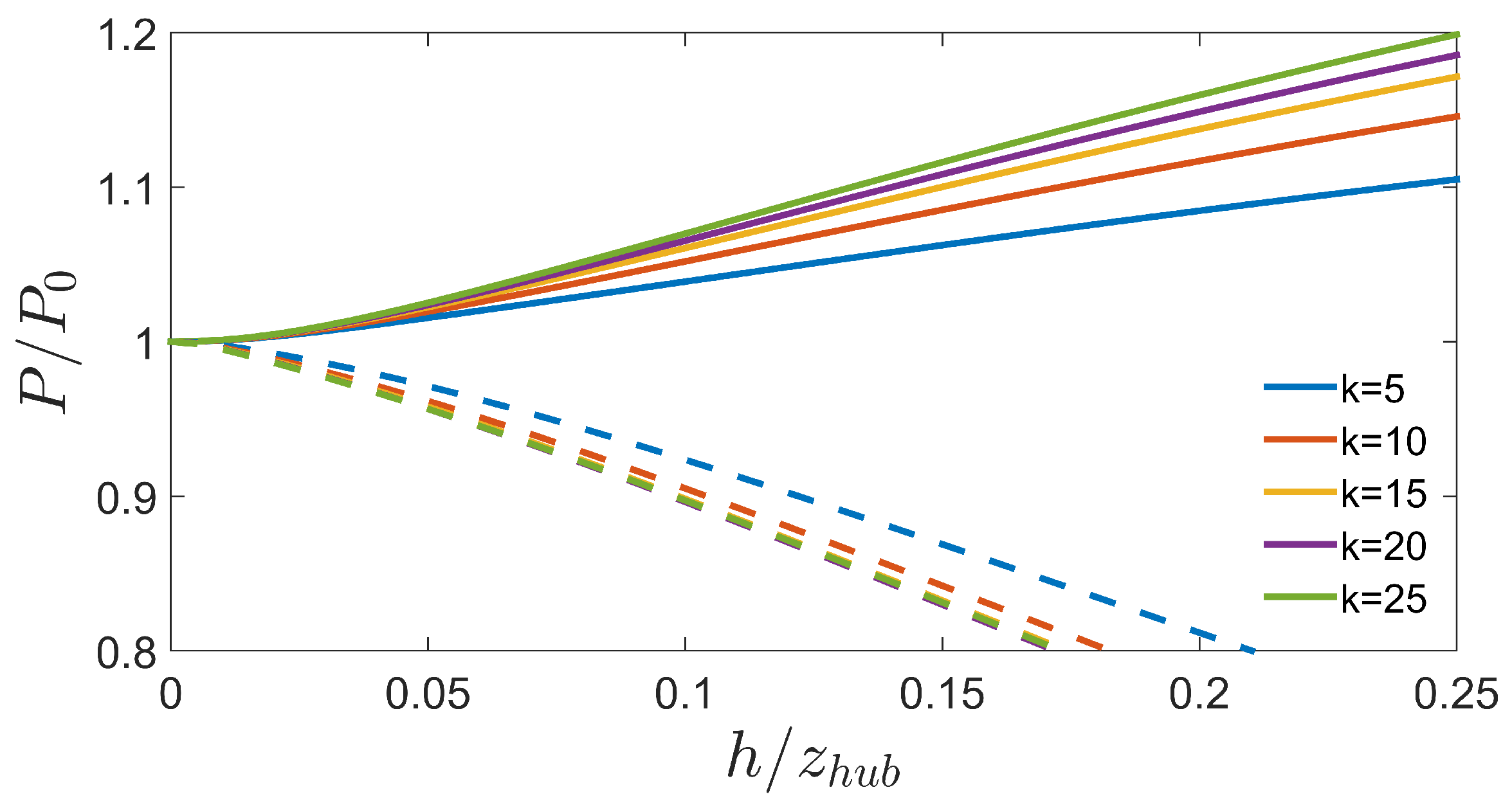
2.3. Total Power Increase
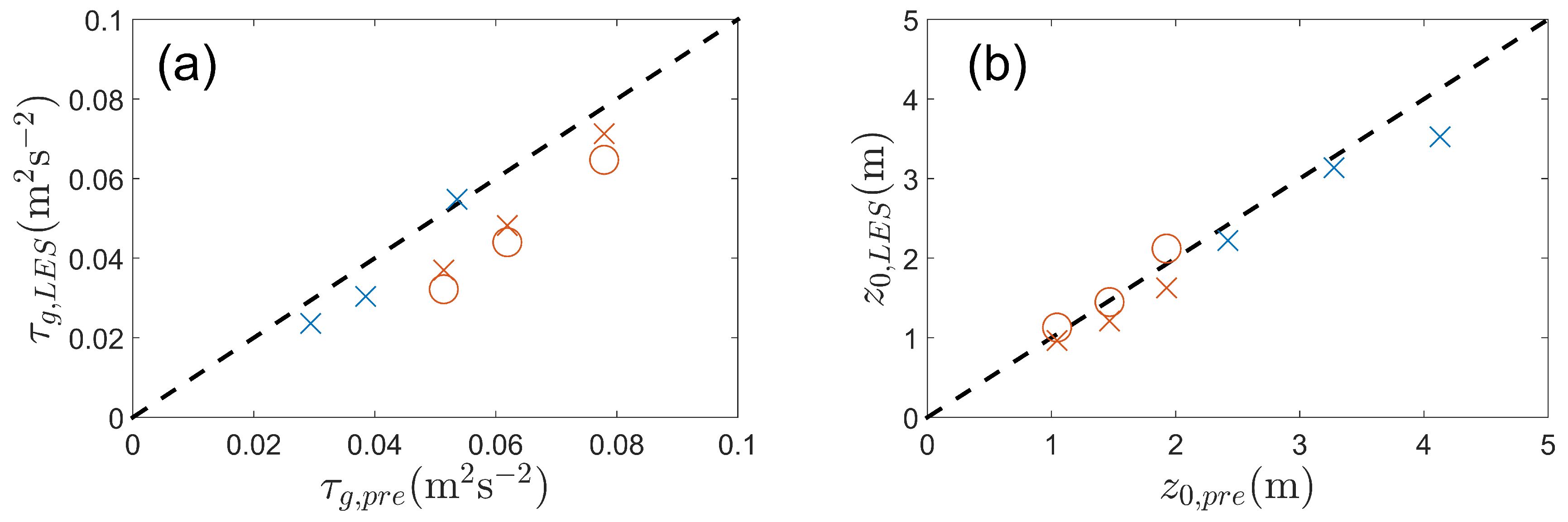
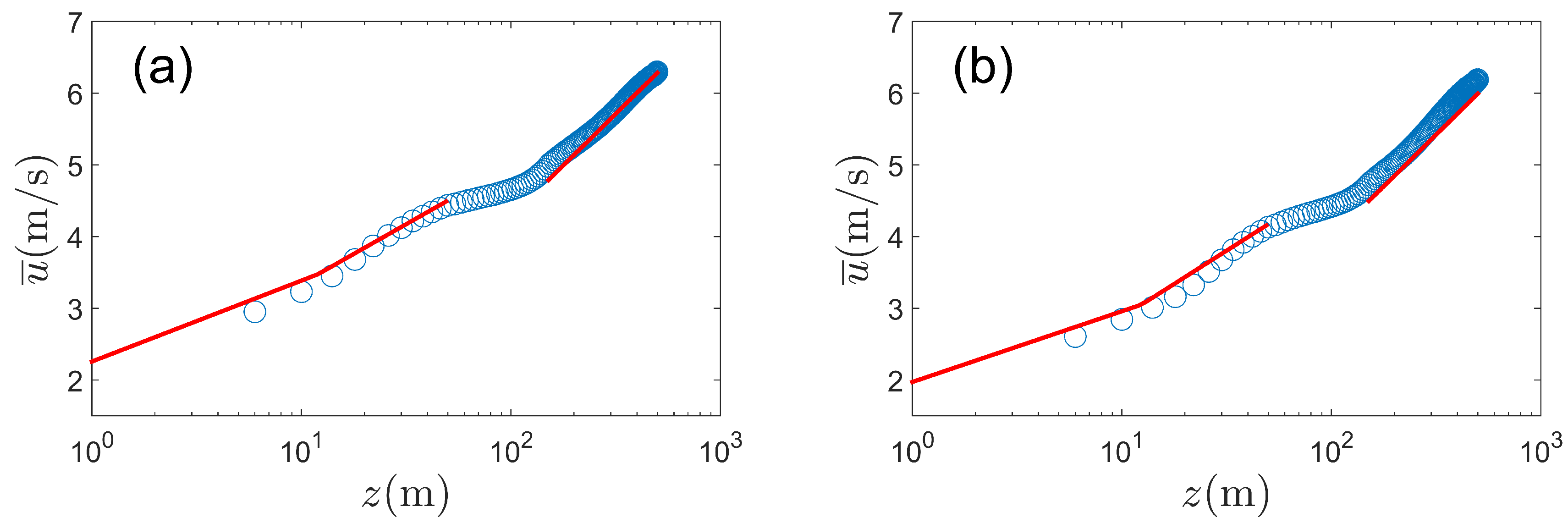
3. Preliminary Validation with Large Eddy Simulations
3.1. Windbreak Flow
3.2. Power Output Measurements
3.3. Impact of Porosity
3.4. Boundary-Layer Predictions
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chamorro, L.P.; Arndt, R.E.A.; Sotiropoulos, F. Turbulent flow properties around a staggered wind farm. Bound.-Layer Meteorol. 2011, 141, 349–367. [Google Scholar] [CrossRef]
- Meyers, J.; Meneveau, C. Optimal turbine spacing in fully developed wind farm boundary layers. Wind Energy 2012, 15, 305–317. [Google Scholar] [CrossRef]
- Palma, J.M.L.M.; Castro, F.A.; Ribeiro, L.F.; Rodrigues, A.H.; Pinto, A.P. Linear and nonlinear models in wind resource assessment and wind turbine micro-siting in complex terrain. J. Wind Eng. Ind. Aerodyn. 2008, 96, 2308–2326. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Tobin, N.; Arndt, R.E.A.; Sotiropoulos, F. Variable-sized wind turbines are a possibility for wind farm optimization. Wind Energy 2014, 17, 1483–1494. [Google Scholar] [CrossRef]
- Fleming, P.A.; Gebraad, P.M.O.; Lee, S.; van Wingerden, J.W.; Johnson, K.; Churchfield, M.; Michalakes, J.; Spalart, P.; Moriarty, P. Evaluating techniques for redirecting turbine wakes using SOWFA. Renew. Energy 2014, 70, 211–218. [Google Scholar] [CrossRef]
- Xie, S.; Archer, C.L.; Ghaisas, N.; Meneveau, C. Benefits of collocating vertical-axis and horizontal-axis wind turbines in large wind farms. Wind Energy 2017, 20, 45–62. [Google Scholar] [CrossRef]
- Tobin, N.; Hamed, A.M.; Chamorro, L.P. Fractional Flow Speed-Up from Porous Windbreaks for Enhanced Wind-Turbine Power. Bound.-Lay. Meteorol. 2017, 163, 253–271. [Google Scholar] [CrossRef]
- Denholm, P.; Hand, M.; Jackson, M.; Ong, S. Land-Use Requirements of Modern Wind Power Plants in the United States; Technical Report No. NREL/TP-6A2-45834; National Renewable Energy Laboratory: Golden, CO, USA, 2009.
- Frandsen, S. On the wind speed reduction in the center of large clusters of wind turbines. J. Wind Eng. Ind. Aerodyn. 1992, 39, 251–265. [Google Scholar] [CrossRef]
- Calaf, M.; Meneveau, C.; Meyers, J. Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 2010, 22, 015110. [Google Scholar] [CrossRef]
- Arya, S.P.S. A drag partition theory for determining the large-scale roughness parameter and wind stress on the Arctic pack ice. J. Geophys. Res. 1975, 80, 3447–3454. [Google Scholar] [CrossRef]
- Stevens, R.J.A.M.; Gayme, D.F.; Meneveau, C. Coupled wake boundary layer model of wind-farms. J. Renew. Sustain. Energy 2015, 7, 023115. [Google Scholar] [CrossRef]
- Yang, X.; Kang, S.; Sotiropoulos, F. Computational study and modeling of turbine spacing effects in infinite aligned wind farms. Phys. Fluids 2012, 24, 115107. [Google Scholar] [CrossRef]
- Dong, Z.; Luo, W.; Qian, G.; Wang, H. A wind tunnel simulation of the mean velocity fields behind upright porous fences. Agric. For. Meteorol. 2007, 146, 82–93. [Google Scholar] [CrossRef]
- Fang, F.M.; Wang, D.Y. On the flow around a vertical porous fence. J. Wind Eng. Ind. Aerodyn. 1997, 67, 415–424. [Google Scholar] [CrossRef]
- Nystrom, N.A.; Levine, M.J.; Roskies, R.Z.; Scott, J. Bridges: A uniquely flexible HPC resource for new communities and data analytics. In Proceedings of the 2015 XSEDE Conference: Scientific Advancements Enabled by Enhanced Cyberinfrastructure, St. Louis, MO, USA, 26–30 July 2015; ACM: New York, NY, USA, 2015; p. 30. [Google Scholar]
- Towns, J.; Cockerill, T.; Dahan, M.; Foster, I.; Gaither, K.; Grimshaw, A.; Hazlewood, V.; Lathrop, S.; Lifka, D.; Peterson, G.D.; et al. XSEDE: Accelerating scientific discovery. Comput. Sci. Eng. 2014, 16, 62–74. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- van Driest, E.R. On Turbulent Flow Near a Wall. J. Aeronaut. Sci. 1956, 23, 1007–1011. [Google Scholar] [CrossRef]
- Laws, E.M.; Livesey, J.L. Flow through screens. Annu. Rev. Fluid Mech. 1978, 10, 247–266. [Google Scholar] [CrossRef]
- Raupach, M.R.; Woods, N.; Dorr, G.; Leys, J.F.; Cleugh, H.A. The entrapment of particles by windbreaks. Atmos. Environ. 2001, 35, 3373–3383. [Google Scholar] [CrossRef]
- Counihan, J.; Hunt, J.C.R.; Jackson, P.S. Wakes behind two-dimensional surface obstacles in turbulent boundary layers. J. Fluid Mech. 1974, 64, 529–564. [Google Scholar] [CrossRef]
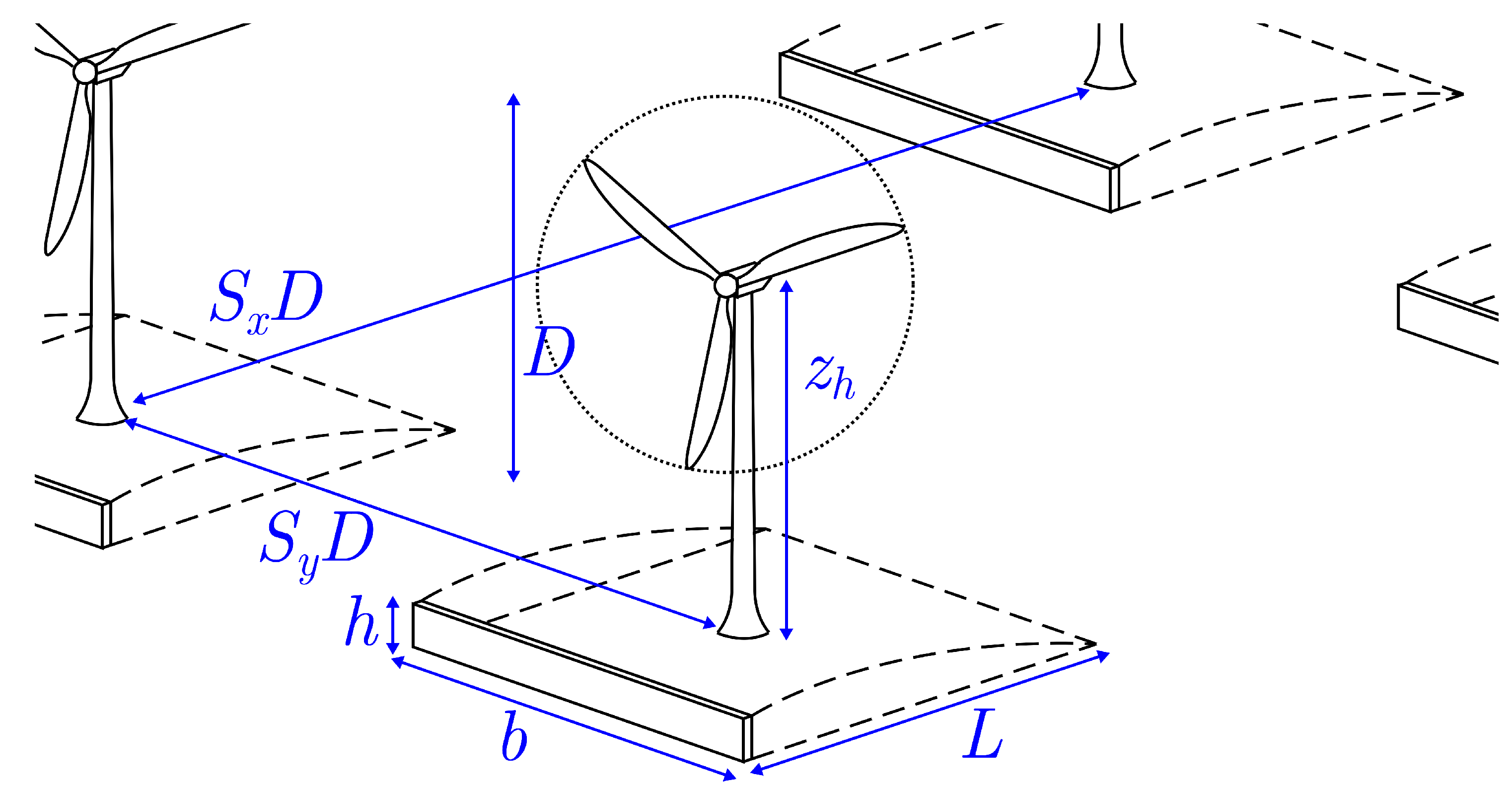
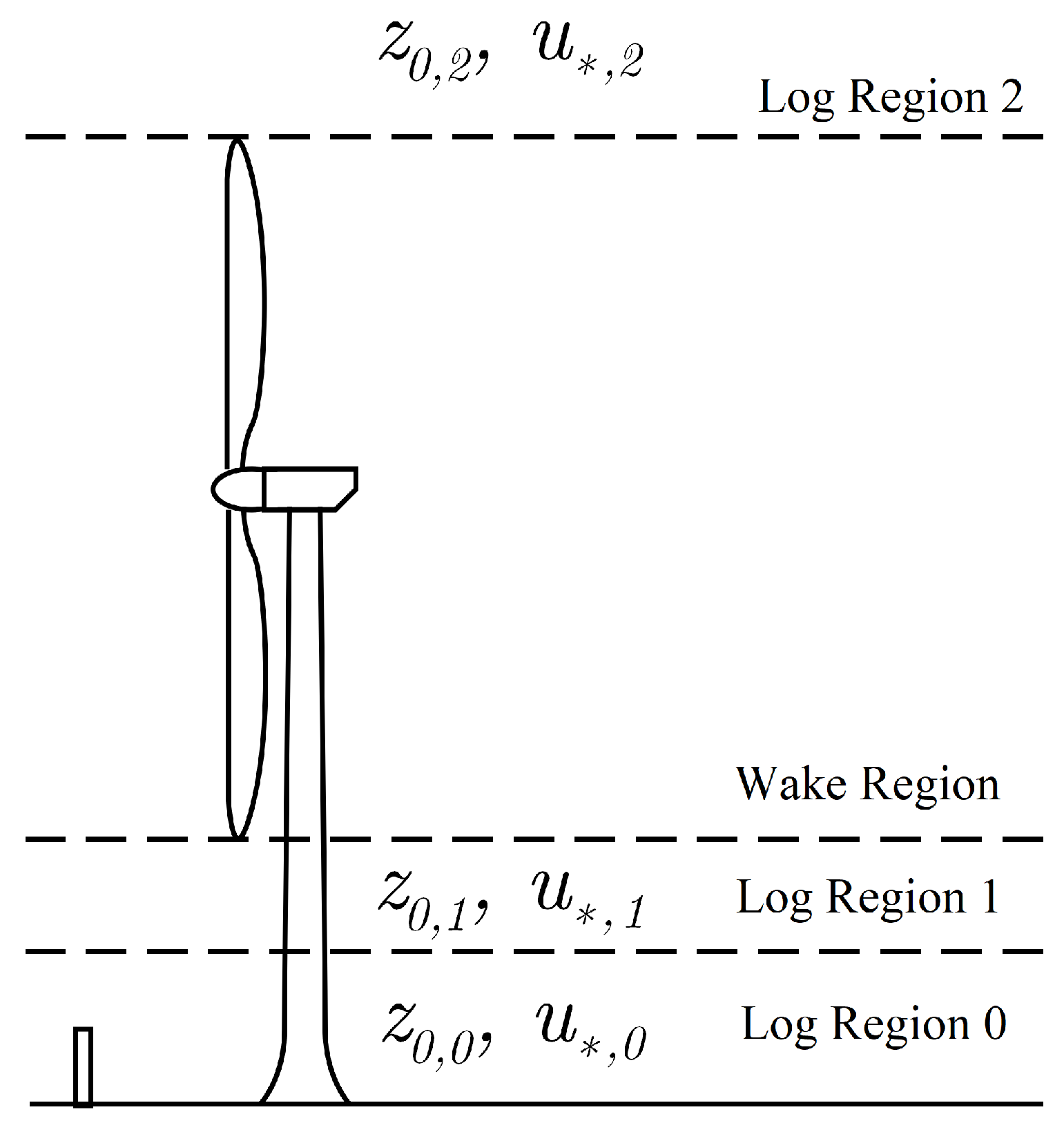
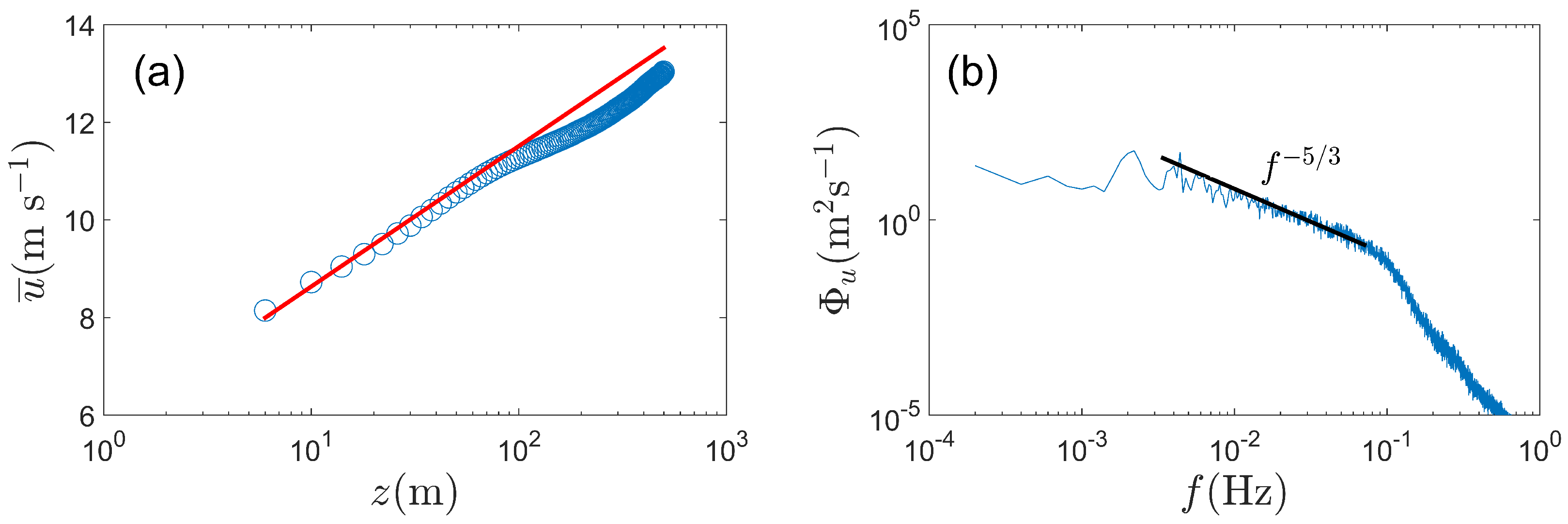
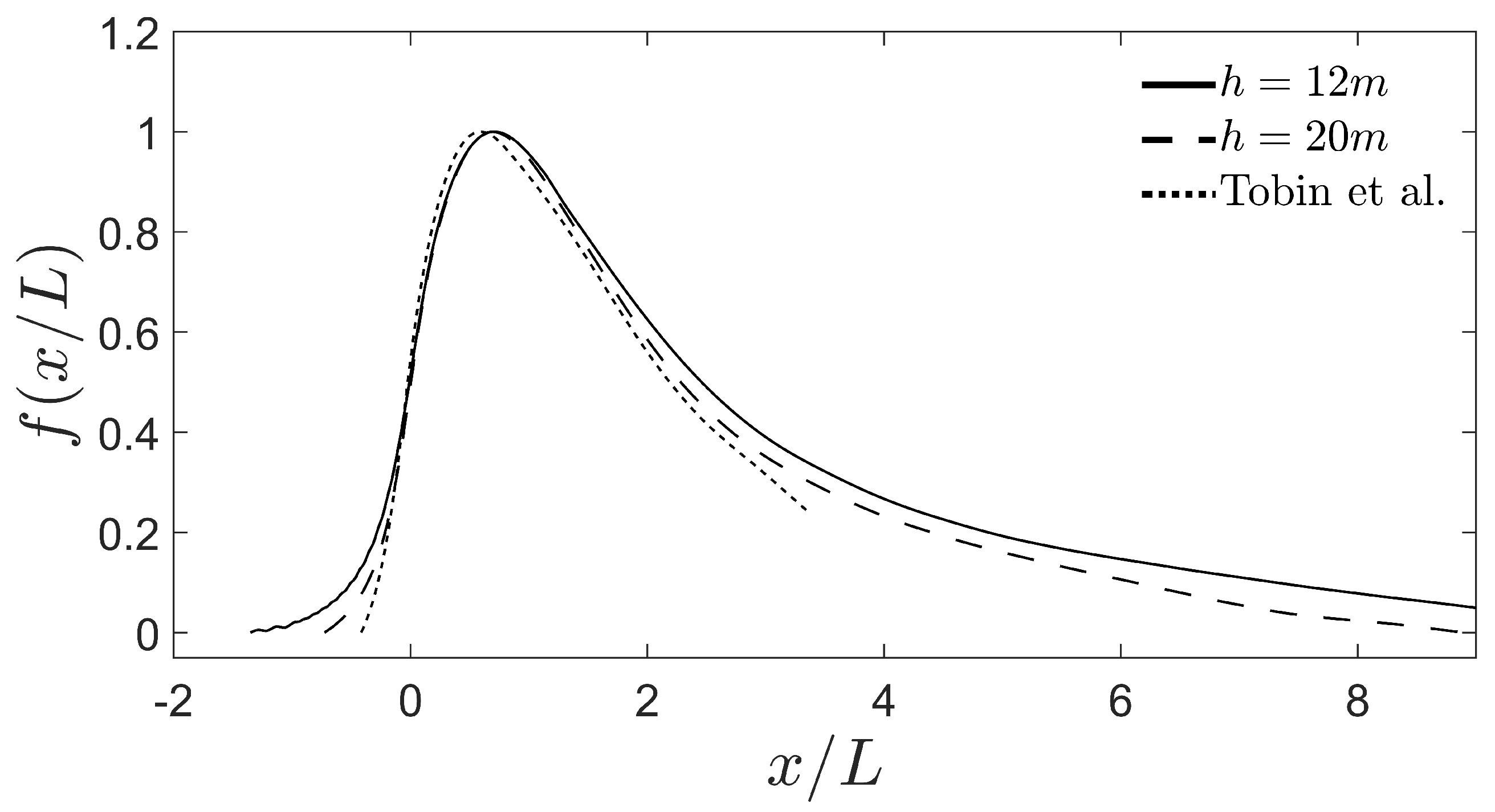
| h (m) | No. of Turbines | Alignment | k | (m) (m) (m) | ||
|---|---|---|---|---|---|---|
| 6 | 5 | 0 | Aligned | 25 | ||
| 6 | 5 | 12 | Aligned | 25 | ||
| 6 | 5 | 20 | Aligned | 25 | ||
| 10 | 5 | 0 | Aligned | 25 | ||
| 10 | 5 | 12 | Aligned | 25 | ||
| 10 | 5 | 2 | Aligned | 25 | ||
| 10 | 5 | 0 | Staggered | 25 | ||
| 10 | 5 | 12 | Staggered | 25 | ||
| - | - | 12 | - | - | 25 | |
| - | - | 20 | - | - | 25 | |
| - | - | 12 | - | - | 20 | |
| - | - | 12 | - | - | 15 | |
| - | - | 12 | - | - | 10 | |
| - | - | 12 | - | - | 5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tobin, N.; Chamorro, L.P. Windbreak Effects Within Infinite Wind Farms. Energies 2017, 10, 1140. https://doi.org/10.3390/en10081140
Tobin N, Chamorro LP. Windbreak Effects Within Infinite Wind Farms. Energies. 2017; 10(8):1140. https://doi.org/10.3390/en10081140
Chicago/Turabian StyleTobin, Nicolas, and Leonardo P. Chamorro. 2017. "Windbreak Effects Within Infinite Wind Farms" Energies 10, no. 8: 1140. https://doi.org/10.3390/en10081140
APA StyleTobin, N., & Chamorro, L. P. (2017). Windbreak Effects Within Infinite Wind Farms. Energies, 10(8), 1140. https://doi.org/10.3390/en10081140






