Development of the IBSAL-SimMOpt Method for the Optimization of Quality in a Corn Stover Supply Chain
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. The Impact of Feedstock Quality
3.2. Interaction Between the Extended IBSAL and the SimMOpt Optimization Method
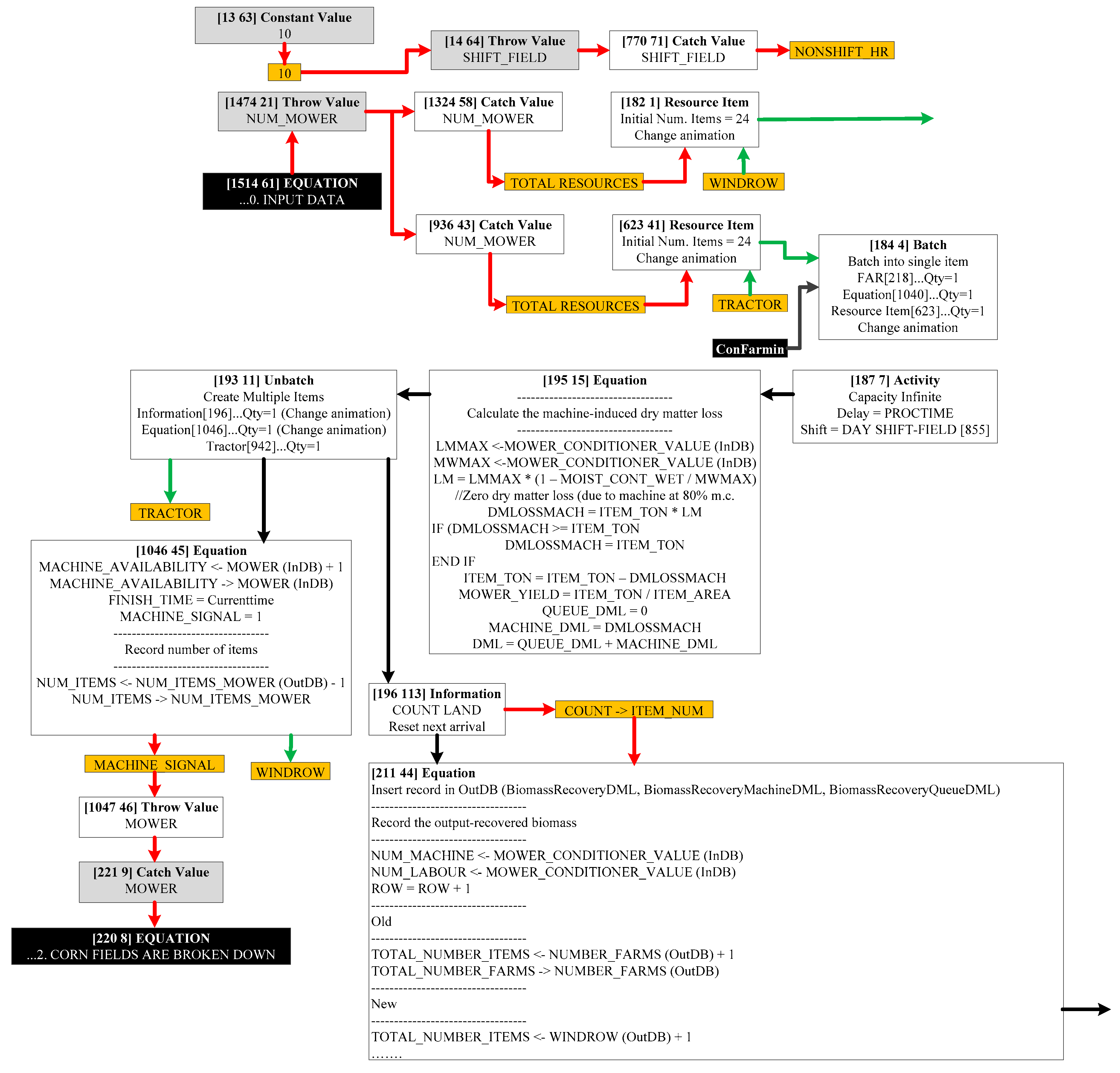
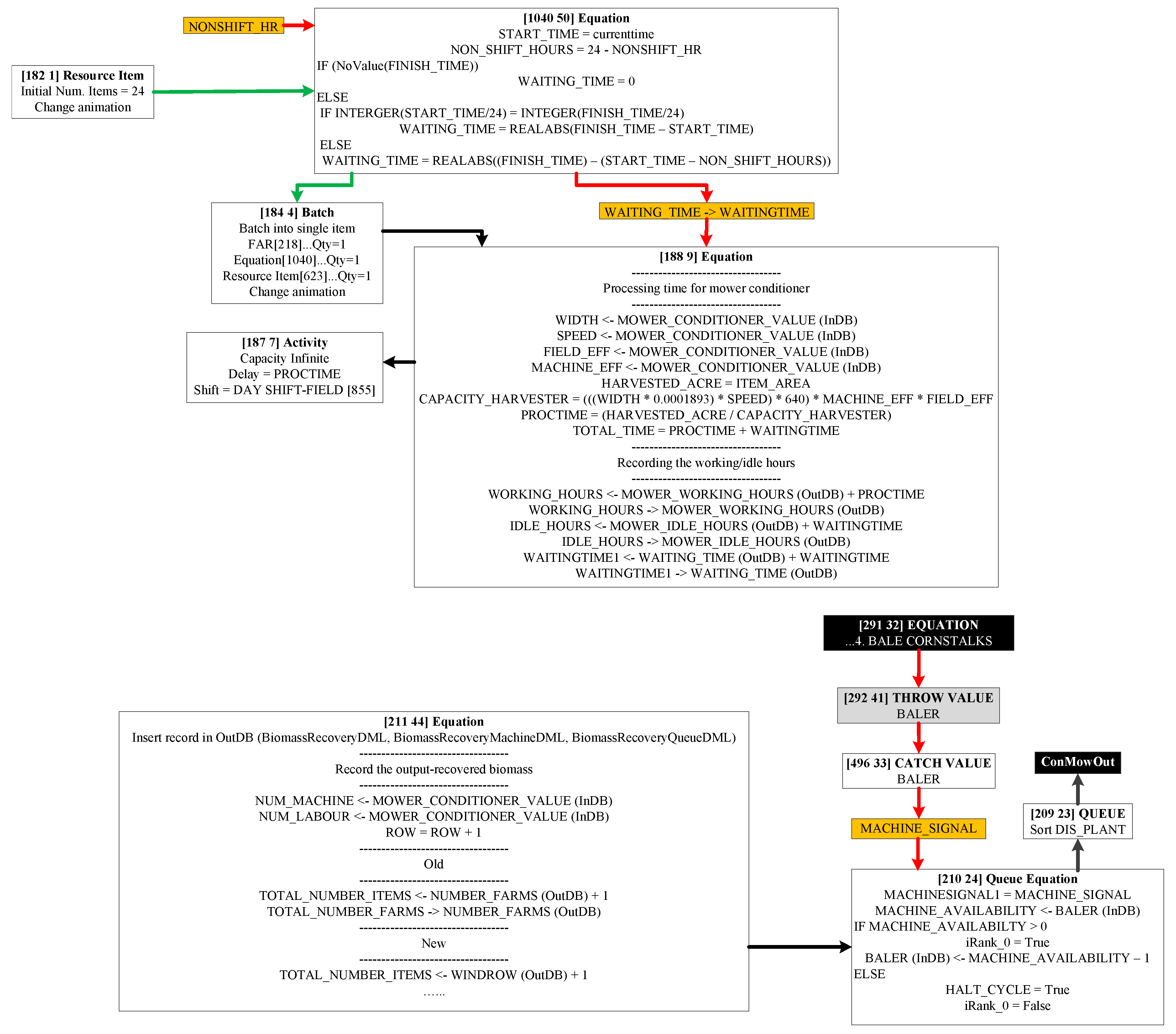
- Extended IBSAL: This research is especially concerned with the costs derived from imperfect quality of feedstock. The IBSAL model is extended so that the cost of imperfect quality of the feedstock is estimated for the corn stover-to-bioethanol SC. For this purpose, blocks were added to the baseline IBSAL for estimating these quality-related costs and other performance measures of interest (e.g., dry matter loss at operations designed to improve the physical characteristics of the feedstock, percentage of moisture, percentage of ash, and probability of having non-conforming stover at the gate of the biorefinery). Extended IBSAL accurately represents the stochastic behavior of elements intervening in the SC and estimates the costs derived from collection, storage, and transportation operations and from having imperfect quality of feedstock.
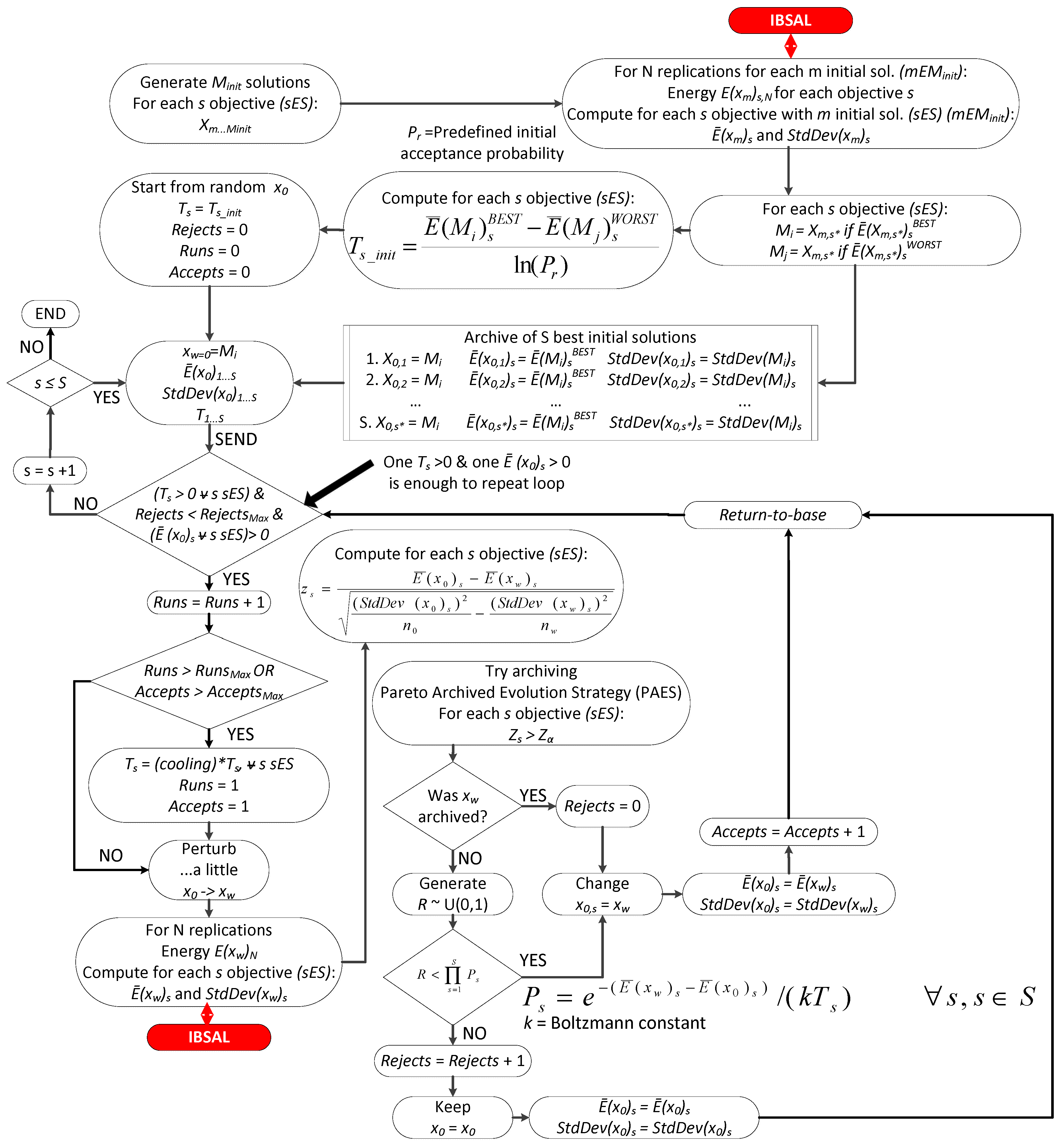
- SimMOpt: The SimMOpt method is inspired on the procedure used by the stochastic Multi-Objective Simulated Annealing (MOSA). It can be expected that the solutions obtained with this method converge to global optima given the appropriate SA schedule. However, just as with any metaheuristic, optimality is not guaranteed. The procedure can be described as follows:
- (a)
- At the initial iteration, a large set of random solutions is computed. The best solutions for each objective of interest determine a cell in the grid of the Pareto front. The initial temperatures are computed.
- (b)
- Solutions are perturbed and several replications of the evaluation of the objectives are computed. This part is where the extended IBSAL connects with the SimMOpt. The extended IBSAL model is used to perform the replication and return the evaluations of the performance measures to the SimMOpt.
- (c)
- The SimMOpt method uses some hypothesis testing techniques and the Pareto Archive Evolution Strategy (PAES) with the evaluations of the performance measures from the extended IBSAL to find good solutions and perturb the solution that will be used in the following iteration.
- (d)
- The procedure is repeated until some conditions are met (e.g., minimum temperature, value of the objectives, maximum number of iterations, maximum number of rejects, and maximum number of accepts).
- The extended IBSAL and the SimMOpt method are coupled (extended IBSAL-SimMOpt) and used to minimize the set of competing objectives.
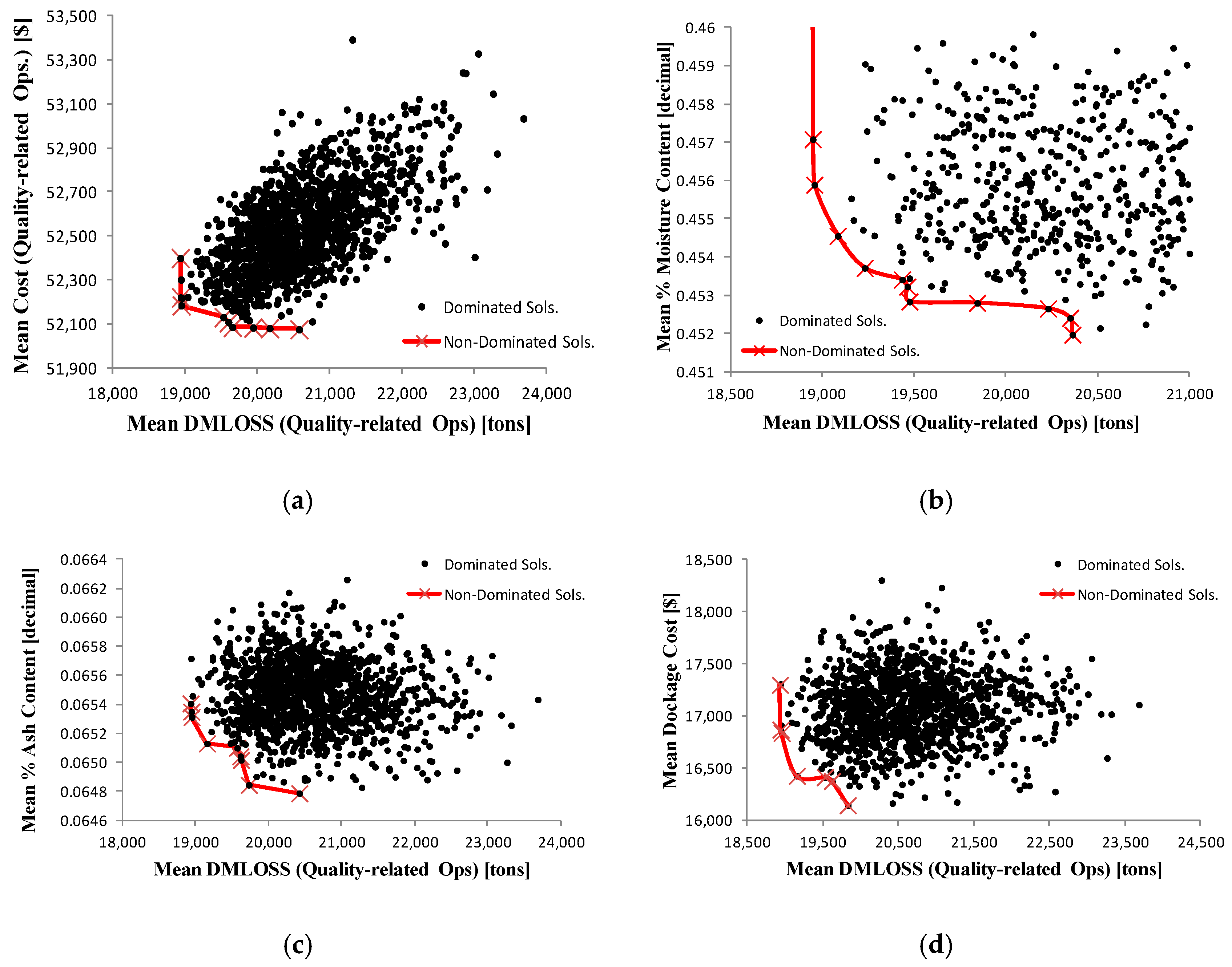
- Non-dominated solutions and Pareto-optimal fronts constructed from these solutions are obtained for multiple SA schedules for the problem in the case study.
- Performances of the Pareto-optimal fronts are evaluated using the hypervolume indicator approach.
3.3. Detailed Description of the SimMOpt Optimization Method
3.4. Extended IBSAL-SimMopt: Quality Related Blocks
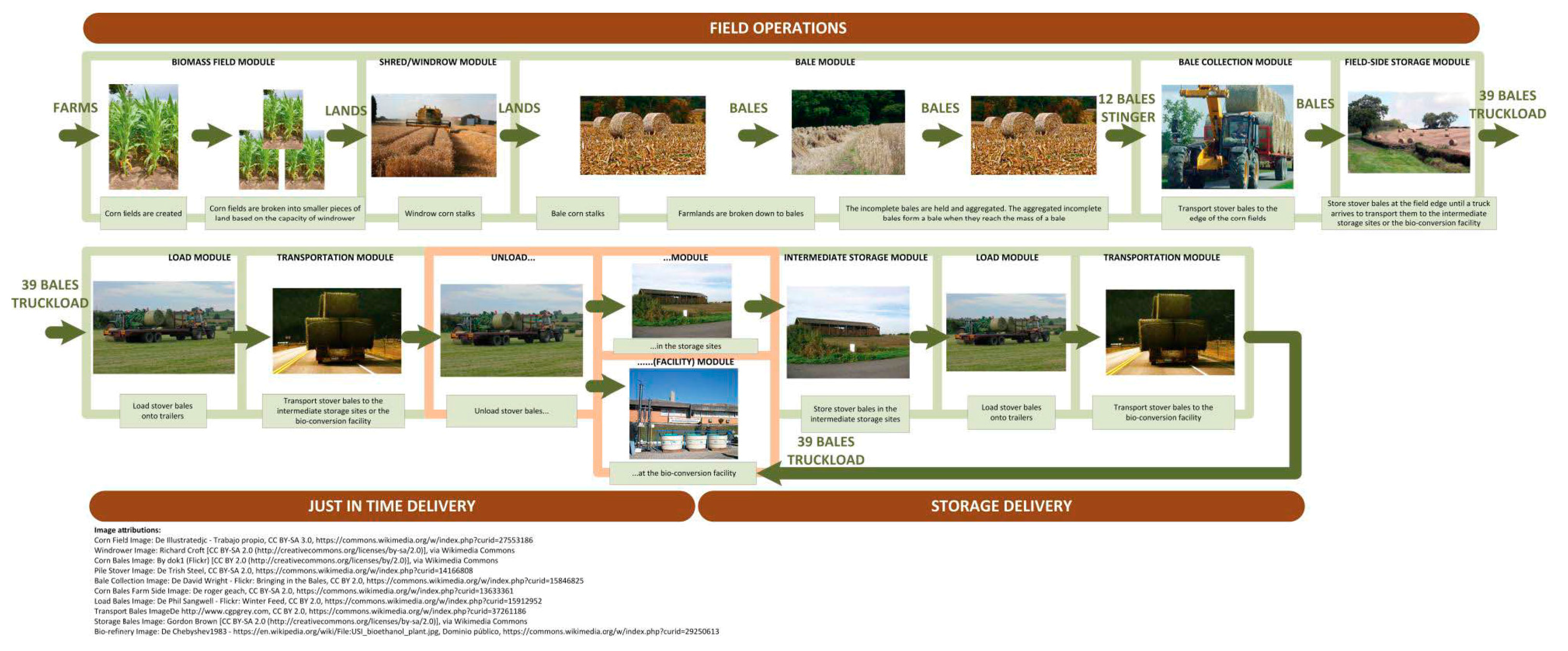
4. Case Study
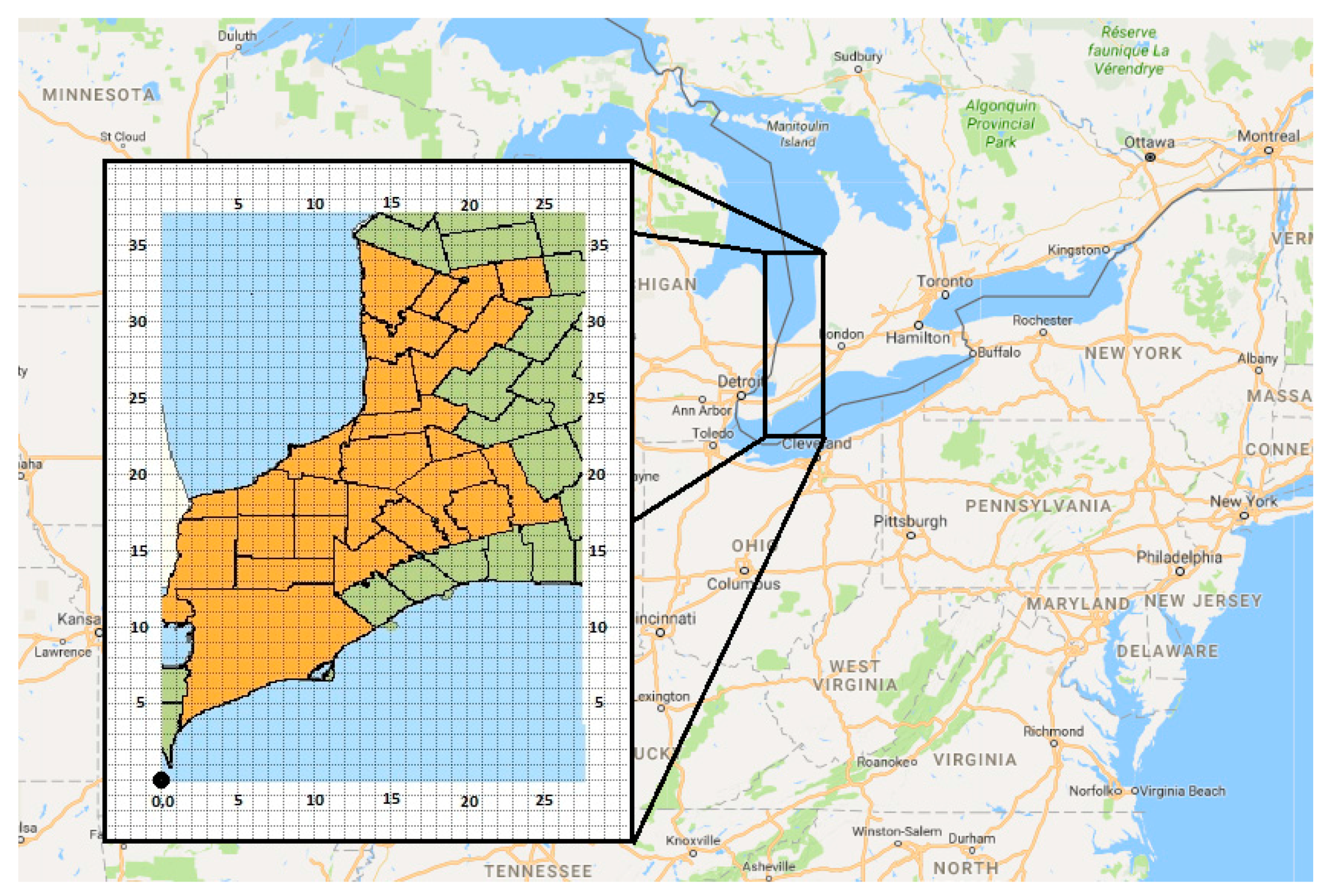
4.1. Geographical Regions and Farm Input Data
4.2. Local Weather Input Data
4.3. Machinery Input Data
4.4. Storage and Other Operational/Quality Input Data
4.5. IBSAL Set Up and Tuning
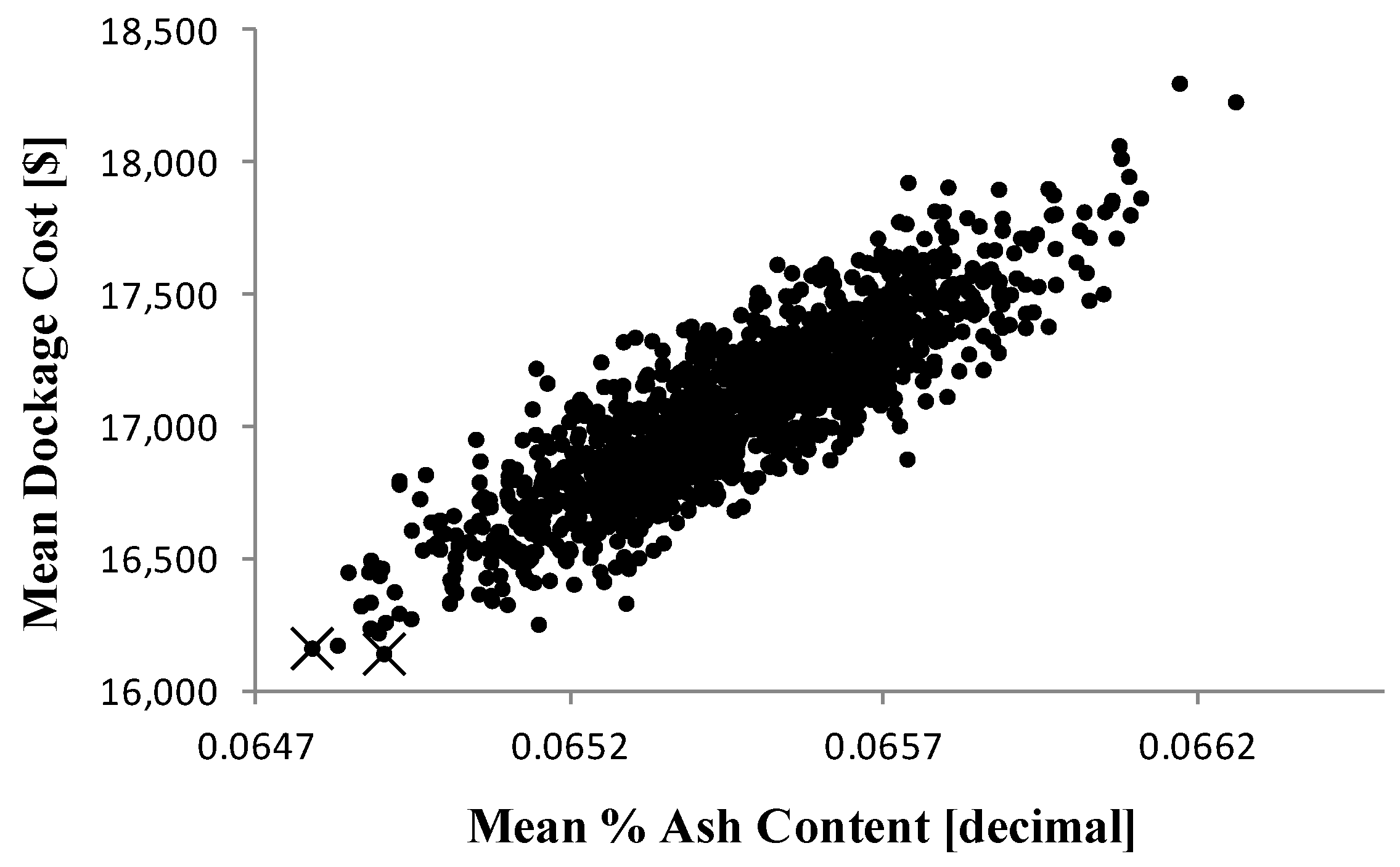
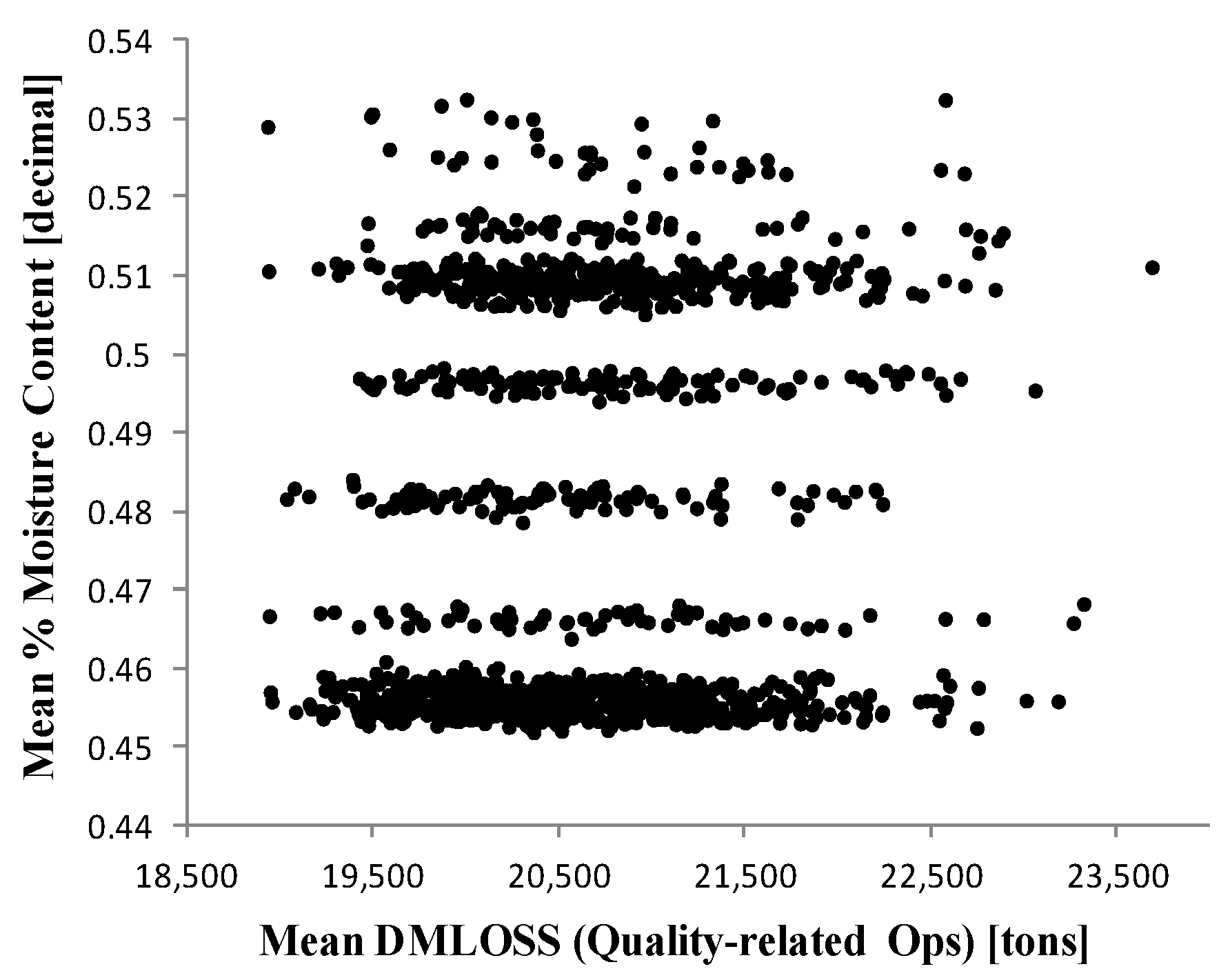
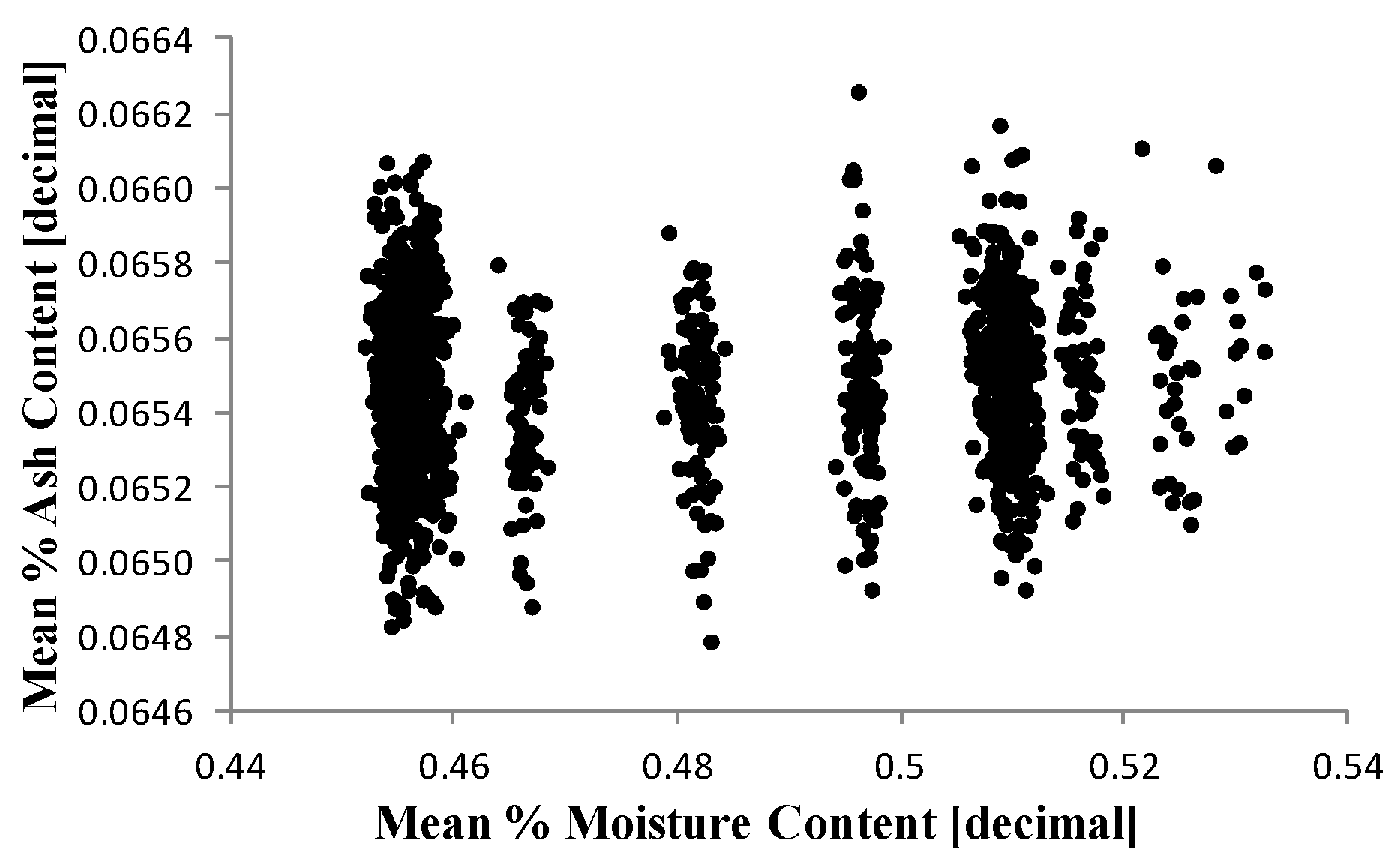
5. Results and Discussion
6. Conclusions
- Provides a novel method for finding near-optimal solutions to the problem of designing biomass supply chains that improve the physical characteristics of the feedstock at an acceptable cost.
- Provides the bioenergy sector and the research community with a simulation-based optimization model with activity-based costing that is capable of representing the stochastic behavior of some elements intervening in the corn stover SC for the production of bioethanol. This analytical model can be used for decision making as well as educational and training purposes since it allows the user to conduct “what if” scenarios.
- Optimizes a set of competing individual objectives that include the cost of having imperfect corn stover quality for the production of bioethanol. The bioenergy industry will potentially benefit from this methodology, which can be adapted to minimize multiple costs in the biomass supply chain (e.g., collection, storage, transportation, and quality-related) as well as other key output measurements (e.g., dry matter loss, moisture content, and ash content) within a computational effort that is sensible for the solution of real problems. Here, the decision maker assigns the priority of objectives when finding a solution.
- Allows modeling complex systems with multiple intertwined stochastic elements; this is one of the most powerful features. The IBSAL-SimMOpt method captures the variability in the behavior of the elements of the biomass SC. Replications of the IBSAL model are performed to represent the stochastic behavior of the system.
- The SimMOpt method interacts with the output from the extended IBSAL model. There are no limitations in terms of the characteristics of the equalities/inequalities representing the objectives and constraints, which is an important concern when using mathematical programming instead of simulation.
- The IBSAL-SimMOpt method can be modified with relative ease using a top-down or bottom-up approach, as required. Therefore, the method can be easily transferred to applications involving biomass SCs with a wider range of feedstock to larger instances.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Symbols | |
| S | Set of objective |
| M | Set of solutions |
| Xm | Solution m (m M) |
| E(Xm)s | Evaluation of objective s by considering solution m (s S, m M) |
| Ts | Temperature related to objective s (s S) |
| NBi | The i-th return-to-base occurs after these many iterations |
| N | Set of replications |
| Minit | Set of initial solutions |
| W | Set of computed solutions |
| Xm | Solution m (m Mini) |
| Mi = Xm,s* | Best initial solution for objective s (m Minit, i Minit, s S) |
| Mj = Xm,s* | Worst initial solution for objective s. (m Minit, j Minit, s S) |
| xw | Solution w computed by a series of perturbations starting from Mi (w W) |
| E(Xw)s | Evaluations of objective s by considering solution Xw (s S, w W) |
| Ts_init | Initial temperature |
| Ts | Temperature |
| Ē(Xw)s | Mean value from evaluations of objective s by considering solution Xw (s S, w W) |
| StdDev(Xw)s | Standard deviation from evaluations of objective s by considering solution Xw (s S, w W) |
| Runsmax | Maximum number of runs (SA schedule) |
| Rejectsmax | Maximum number of rejects (SA schedule) |
| Acceptsmax | Maximum number of accepts (SA schedule) |
| zs | Critical value (Hypotheses testing on the mean of evaluations of objective s for two large samples) (s S) |
| nw | Size of sample consisting of the evaluations of objectives while considering solution Xw (w W) |
| zα | Value from standard normal table corresponding to significance level α. |
| R | Pseudo-random number ~Uniform(0, 1) |
| Ps | Probability of acceptance of solution Xw based on the mean of the evaluations of objective s (s S) |
| K | Boltzmann constant |
| Sched. | SA Schedule |
| Pr | Probability of acceptance of neighbor solution |
| MinTemp | Minimum Temperature—stopping criterion |
| MinOFVal | Minimum value of the objective evaluation—stopping criterion |
| Ali | Number of solutions in the candidate list from which a solution is selected when the SimMOpt returns-to-base |
| Lm | Zero dry matter loss (due to machine) at 80% moisture content |
| Lmmax | Machine biomass loss (decimal) |
| MoistContWet | Moisture content in stover (decimal) |
| Mwmax | Moisture content with zero machine loss (decimal wb) |
| DMLoss | Loss tonnage due to machine (tonne) |
| ItemTom | Tonnage of item (e.g., land) |
| MoistGrainInit | Initial moisture content of the grain (decimal) |
| WindrowDensity | Windrow density (kg/m2) |
| MoistEq(t) | Equilibrium moisture content on the grain (cob) at time t (decimal) |
| RH(t) | relative humidity at time t (decimal) |
| Temp(t) | Ambient air temperature at time t (°C) |
| P(t) | Cumulative harvested fraction at time t (decimal) |
| CumHarvestAreaDay | Cumulative harvested area (considered for all farm lands harvested on the same day) (ac) |
| MoistGrainWet(t) | Grain kernel moisture content at time t (decimal). Assumed ≥ 0.08 |
| MoistContWet | Moisture content of the stover stalk (w.b.) (decimal) |
| Mo | Initial moisture content (decimal) |
| Me | Equilibrium moisture calculated by modified Oswin equation (decimal) |
| K | Drying rate constant (applies to Equations (8) and (9)) |
| AvgRH(t) | Average relative humidity at time t (decimal) |
| VPD(t) | Vapor pressure density at time t |
| Rad(t) | Radiation intensity for the hour at time t (watt/m2) |
| WS(t) | Wind speed at time t (m/s) |
| T | Each day the stover is left on the field for dying (days) |
| StartDayHarvest | Start day of harvest (type of decision variable) |
| DaysInField | Number of days left on the field for drying (type of decision variable) |
| AshCont | Ash content after field drying (decimal) |
| Rainfall(t) | Amount of rain at time t (mm) |
| DMLOSS | Dry matter loss during field drying (decimal) |
| WrappingBales | Binary: wrapping/no wrapping (type of decision variable) |
| DMLOSSWrap | Dry matter loss percentage for wrapped bales (decimal) |
| CostQual | Cost of quality-related operations ($) |
| AirClassification | Binary: classification/no classification |
| CostNoQual | Dockage cost ($) |
| Abbreviations | |
| IBSAL | Integrated Biomass Supply Analysis and Logistics |
| SimMOpt | Simulation-based Multi-Objective Optimization |
| SA | Simulated Annealing |
| NREL | National Renewable Energy Laboratory |
| DES | Discrete Events Simulation |
| SC | Supply Chain |
| ORNL | Oak Ridge National Laboratory |
| DoE | Department of Energy |
| MP | Mathematical Programming |
| QP | Quadratic Programming |
| PROMETHEE | Preference Ranking Organization Method for Enrichment of Evaluations |
| MILP | Mixed-Integer Linear Programming |
| BLM | Biomass Logistic Model |
| FS | Feedstock Supply |
| IBSAL-MC | IBSAL Multi-Crop |
| SD | Systems Dynamics |
| MOSA | Multi-Objective Simulated Annealing |
| PAES | Pareto Archive Evolution Strategy |
| CTL | Central Limit Theorem |
| w.b. | Wet Basis |
Appendix B
References
- Office of Energy Efficiency & Renewable Energy. Available online: http://www.energy.gov/eere/bioenergy/biomass-feedstocks (accessed on 2 August 2017).
- Langholtz, M.H.; Stokes, B.J.; Eaton, L.M. 2016 Billion-Ton Report: Advancing Domestic Resources for a Thriving Bioeconomy, Volume 1: Economic Availability of Feedstocks; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2016.
- Caputo, A.C.; Palumbo, M.; Pelagagge, P.M.; Scacchia, F. Economics of biomass energy utilization in combustion and gasification plants: Effects of logistic variables. Biomass Bioenergy 2015, 28, 35–51. [Google Scholar] [CrossRef]
- Leistritz, F.L.; Hodur, N.M.; Senechal, D.M.; Stowers, M.D.; McCalla, D.; Saffron, C.M. Biorefineries Using Agricultural Residue Feedstock in the Great Plains. Available online: http://ageconsearch.umn.edu/bitstream/7323/2/ae070001.pdf (accessed on 2 August 2017).
- Sadhukhan, J.; Ng, K.S.; Hernandez, E.M. Biorefineries and Chemical Processes: Design, Integration and Sustainability Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Stephen, J.D. Biorefinery Feedstock Availability and Price Variability: Case Study of the Peace River Region, Alberta. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2008. [Google Scholar]
- Sokhansanj, S.; Kumar, A.; Turhollow, A.F. Development and implementation of integrated biomass supply analysis and logistics model (IBSAL). Biomass Bioenergy 2006, 30, 838–847. [Google Scholar] [CrossRef]
- Aslam, T.; Amos, H.N. Multi-objective optimization for supply chain management: A literature review and new development. In Proceedings of the 2010 8th International Conference on Supply Chain Management and Information Systems (SCMIS), Hong Kong, China, 6–8 October 2010; pp. 1–8. [Google Scholar]
- Kumar, A.; Sokhansanj, S.; Flynn, P.C. Development of a multicriteria assessment model for ranking biomass feedstock collection and transportation systems. Appl. Biochem. Biotechnol. 2006, 129, 71–87. [Google Scholar] [CrossRef]
- Kumar, A.; Sokhansanj, S. Switchgrass (Panicum vigratum, L.) delivery to a biorefinery using integrated biomass supply analysis and logistics (IBSAL) model. Bioresour. Technol. 2007, 98, 1033–1044. [Google Scholar] [CrossRef] [PubMed]
- Ravula, P.P.; Grisso, R.D.; Cundiff, J.S. Cotton logistics as a model for a biomass transportation system. Biomass Bioenergy 2008, 32, 314–325. [Google Scholar] [CrossRef]
- Stephen, J.; Sokhansanj, S.; Bi, X.; Sowlati, T.; Kloeck, T.; Townley-Smith, L.; Stumborg, M. The impact of agricultural residue yield range on the delivered cost to a biorefinery in the Peace River region of Alberta, Canada. Biosyst. Eng. 2010, 105, 298–305. [Google Scholar] [CrossRef]
- Sokhansanj, S.; Mani, S.; Tagore, S.; Turhollow, A. Techno-economic analysis of using corn stover to supply heat and power to a corn ethanol plant–Part 1: Cost of feedstock supply logistics. Biomass Bioenergy 2010, 34, 75–81. [Google Scholar] [CrossRef]
- An, H.; Wilhelm, W.E.; Searcy, S.W. A mathematical model to design a lignocellulosic biofuel supply chain system with a case study based on a region in Central Texas. Bioresour. Technol. 2011, 102, 7860–7870. [Google Scholar] [CrossRef] [PubMed]
- Shastri, Y.N.; Rodriguez, L.F.; Hansen, A.C.; Ting, K. Impact of distributed storage and pre-processing on Miscanthus production and provision systems. Biofuels Bioprod. Biorefining 2012, 6, 21–31. [Google Scholar] [CrossRef]
- An, H.; Searcy, S.W. Economic and energy evaluation of a logistics system based on biomass modules. Biomass Bioenergy 2012, 46, 190–202. [Google Scholar] [CrossRef]
- Larasati, A.; Liu, T.; Epplin, F.M. An analysis of logistic costs to determine optimal size of a biofuel refinery. Eng. Manag. J. 2012, 24, 63–72. [Google Scholar] [CrossRef]
- Ebadian, M.; Sowlati, T.; Sokhansanj, S.; Smith, L.T.; Stumborg, M. Development of an integrated tactical and operational planning model for supply of feedstock to a commercial-scale bioethanol plant. Biofuels Bioprod. Biorefining 2014, 8, 171–188. [Google Scholar] [CrossRef]
- Igathinathane, C.; Archer, D.; Gustafson, C.; Schmer, M.; Hendrickson, J.; Kronberg, S.; Faller, T. Biomass round bales infield aggregation logistics scenarios. Biomass Bioenergy 2014, 66, 12–26. [Google Scholar] [CrossRef]
- Searcy, S.W.; Hartley, B.E.; Thomasson, J.A. Evaluation of a modular system for low-cost transport and storage of herbaceous biomass. BioEnergy Res. 2014, 7, 824–832. [Google Scholar] [CrossRef]
- Ren, L.; Cafferty, K.; Roni, M.; Jacobson, J.; Xie, G.; Ovard, L.; Wright, C. Analyzing and comparing biomass feedstock supply systems in China: Corn stover and sweet sorghum case studies. Energies 2015, 8, 5577–5597. [Google Scholar] [CrossRef]
- Chávez, H.; Castillo-Villar, K.K.; Herrera, L.; Bustos, A. Simulation-based multi-objective model for supply chains with disruptions in transportation. Robot. Comput. Integr. Manuf. 2017, 43, 39–49. [Google Scholar] [CrossRef]
- Pinho, T.M.; Coelho, J.P.; Moreira, A.P.; Boaventura-Cunha, J. Modelling a biomass supply chain through discrete-event simulation. IFAC PapersOnLine 2016, 49, 84–89. [Google Scholar] [CrossRef]
- Castillo-Villar, K.K.; Minor-Popocatl, H.; Webb, E. Quantifying the impact of feedstock quality on the design of bioenergy supply chain networks. Energies 2016, 9, 203. [Google Scholar] [CrossRef]
- Sokhansanj, S.; Turhollow, A.; Wilkerson, E. Development of the Integrated Biomass Supply Analysis and Logistics Model (IBSAL); Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2008.
- Ebadian, M.; Sowlati, T.; Sokhansanj, S.; Stumborg, M.; Townley-Smith, L. A new simulation model for multi-agricultural biomass logistics system in bioenergy production. Biosyst. Eng. 2011, 110, 280–290. [Google Scholar] [CrossRef]
- De Meyer, A.; Cattrysse, D.; Rasinmäki, J.; Van Orshoven, J. Methods to optimise the design and management of biomass-for-bioenergy supply chains: A review. Renew. Sustain. Energy Rev. 2014, 31, 657–670. [Google Scholar] [CrossRef]
- Diamond, B. The ExtendSim Optimizer; Imagine That Inc.: San Jose, CA, USA, 2003. [Google Scholar]
- Kadam, K.L.; McMillan, J.D. Availability of corn stover as a sustainable feedstock for bioethanol production. Bioresour. Technol. 2003, 88, 17–25. [Google Scholar] [CrossRef]
- Sokhansanj, S.; Mani, S.; Turhollow, A.; Kumar, A.; Bransby, D.; Lynd, L.; Laser, M. Large-scale production, harvest and logistics of switchgrass (Panicum virgatum L.)—Current technology and envisioning a mature technology. Biofuels Bioprod. Biorefining 2009, 3, 124–141. [Google Scholar] [CrossRef]
- Popp, M.P.; Searcy, S.W.; Sokhansanj, S.; Smartt, J.B.; Cahill, N.E. Influence of weather on the predicted moisture content of field chopped energy sorghum and switchgrass. Appl. Eng. Agric. 2015, 31, 179–190. [Google Scholar]
- Kenney, K.L.; Cafferty, K.G.; Jacobson, J.J.; Bonner, I.J.; Gresham, G.L.; Hess, R.J.; Ovard, L.P.; Smith, W.A.; Thompson, D.N.; Thompson, V.S.; et al. Feedstock Supply System Design and Economics for Conversion of Lignocellulosic Biomass to Hydrocarbon Fuels: Conversion Pathway: Biological Conversion of Sugars to Hydrocarbons; Idaho National Laboratory: Idaho Falls, ID, USA, 2013.
- Kenney, K.L.; Smith, W.A.; Gresham, G.L.; Westover, T.L. Understanding biomass feedstock variability. Biofuels 2013, 4, 111–127. [Google Scholar] [CrossRef]
- Bonner, I.J.; Smith, W.A.; Einerson, J.J.; Kenney, K.L. Impact of harvest equipment on ash variability of baled corn stover biomass for bioenergy. BioEnergy Res. 2014, 7, 845–855. [Google Scholar] [CrossRef]
- Haddock, J.; Mittenthal, J. Simulation optimization using simulated annealing. Comput. Ind. Eng. 1992, 22, 387–395. [Google Scholar] [CrossRef]
- Van Laarhoven, P.J.; Aarts, E.H. Simulated annealing. In Simulated Annealing: Theory and Applications; Springer: Dordrecht, The Netherlands, 1987; pp. 7–15. [Google Scholar]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 6, 721–741. [Google Scholar] [CrossRef] [PubMed]
- Chavez, H.; Castillo-Villar, K.K.; Webb, E. Simulation-based approach for the optimization of a biofuel supply chain. In Proceedings of the Industrial and Systems Engineering Research Conference (ISERC), Pittsburgh, PA, USA, 20–23 May 2017. [Google Scholar]
- Khanchi, A.; Birrell, S.J. Effect of rainfall and swath density on dry matter and composition change during drying of switchgrass and corn stover. Biosyst. Eng. 2017, 153, 42–51. [Google Scholar] [CrossRef]
- Schon, B.; Matt, D. Corn Stover Ash; Iowa State University: Ames, IA, USA, 2014. [Google Scholar]
- Khanchi, A.; Birrell, S. Drying models to estimate moisture change in switchgrass and corn stover based on weather conditions and swath density. Agric. Forest Meteorol. 2017, 237, 1–8. [Google Scholar] [CrossRef]
- Vadas, P.A.; Digman, M.F. Production costs of potential corn stover harvest and storage systems. Biomass Bioenergy 2013, 54, 133–139. [Google Scholar] [CrossRef]
- Thompson, V.S.; Lacey, J.A.; Hartley, D.; Jindra, M.A.; Aston, J.E.; Thompson, D.N. Application of air classification and formulation to manage feedstock cost, quality and availability for bioenergy. Fuel 2016, 180, 497–505. [Google Scholar] [CrossRef]
- Map Data @ 2017 Google United States. Available online: https://www.google.com/maps/@42.2748687,-82.2910045,7.5z (accessed on 4 April 2017).
- Suppapitnarm, A.; Seffen, K.A.; Parks, G.T.; Connor, A.M.; Clarkson, P.J. Multiobjective optimisation of bicycle frames using simulated annealing. In Proceedings of the 1st ASMO/ISSMO Conference on Engineering Design Optimization, Ilkley, UK, 8–9 July 1999. [Google Scholar]
- Cao, Y. Hypervolume Indicator. Available online: https://www.mathworks.com/matlabcentral/fileexchange/19651-hypervolume-indicator (accessed on 2 August 2017).






| Title | Author | Objective/Feedstock | Method | IBSAL |
|---|---|---|---|---|
| Biomass Supply Chains | ||||
| Development of a multicriteria assessment model for ranking biomass feedstock collection and transportation systems | Kumar et al. [9] | Rank alternatives for the collection and transportation of biomass. Feedstock: Biomass (corn stover). | Multicriteria assessment methodology (PROMETHEE I, II) and IBSAL | √ |
| Switchgrass (Panicum vigratum, L.) delivery to a biorefinery using integrated biomass supply analysis and logistics (IBSAL) model | Kumar and Sokhansanj [10] | Evaluate a collection systems of switchgrass and analysis of the related costs, energy input, and carbon emissions. Feedstock: Switchgrass | Discrete event simulation | √ |
| Cotton logistics as a model for a biomass transportation system | Ravula et al. [11] | Determine the operating parameters for reducing the transportation cost of biomass. Feedstock: Cotton gin (analogously to biomass). | Discrete event simulation | |
| The impact of agricultural residue yield range on the delivered cost to a biorefinery in the Peace River region of Alberta, Canada | Stephen et al. [12] | Evaluate the impact of residue yield on the biomass delivered cost. Feedstock: Straw and chaff from wheat, barley, and oats. | Discrete event simulation | √ |
| Techno-economic analysis of using corn stover to supply heat and power to a corn ethanol plant–Part 1: Cost of feedstock supply logistics | Sokhansanj et al. [13] | Propose a supply chain for corn stover to produce heat and power for a dry mill ethanol plant. Feedstock: Corn stover. | Discrete event simulation | √ |
| A mathematical model to design a lignocellulosic biofuel supply chain system with a case study based on a region in Central Texas | An et al. [14] | Maximize the profit of a lignocellulosic biofuel supply chain. Feedstock: Switchgrass. | Multi-commodity flow mathematical model | |
| Impact of distributed storage and pre-processing on Miscanthus production and provision systems | Shastri et al. [15] | Analyze the cost reduction from implementing distributed storage and pre-processing at satellite storage locations. Feedstock: Miscanthus. | Mixed integer linear programming (MILP) (BioFeed) optimization model | |
| Economic and energy evaluation of a logistics system based on biomass modules | An and Searcy [16] | Minimize the feedstock costs in a logistic system by maximizing highway load and minimizing load/unload times. Feedstock: Cotton (analogously to biomass) | Discrete event simulation | √ |
| An analysis of logistic costs to determine optimal size of a biofuel refinery | Larasati et al. [17] | Analyze the impact of logistic costs on the size of cellulosic ethanol biorefineries. Feedstock: Switchgrass. | Variable distance on grids approach | |
| Development of an integrated tactical and operational planning model for supply of feedstock to a commercial-scale bioethanol plant | Ebadian et al. [18] | Integrate the tactical and operational levels in the biomass supply chain for a commercial-scale cellulosic ethanol plant. Feedstock: Multi-biomass. | Discrete event simulation/Mixed-integer linear programming | |
| Biomass round bales infield aggregation logistics scenarios | Igathinathane, et al. [19] | Evaluate logistic scenarios for aggregating biomass bales to a field-edge stack or a storage. Feedstock: Biomass. | Computer simulation | |
| Evaluation of a modular system for low-cost transport and storage of herbaceous biomass | Searcy and Hartley [20] | Optimize the harvest of energy sorghum in the humid southern region by using a modified cotton module builder for the formation of modules. Feedstock: Energy sorghum. | Discrete event simulation | √ |
| Analyzing and comparing biomass feedstock supply systems in China: corn stover and sweet sorghum case studies | Ren et al. [21] | Analyze the harvest, collection, storage, transportation, preprocessing, handling, and queuing operations in the rural China biomass supply system. Feedstock: Corn stover and sweet sorghum. | System’s dynamics. Biomass Logistic Model (BLM) framework (BLM Sino-Feedstock Supply (FS)) | |
| Simulation-based multi-objective model for supply chains with disruptions in transportation | Chavez et al. [22] | Optimize the supply of agricultural products by using a simulation-based optimization model. Feedstock: Agricultural products. | Simulation-based Optimization | |
| Modelling a biomass supply chain through discrete-event simulation | Pinho et al. [23] | Providing a decisions tool for the biomass supply chain management services. Feedstock: Wood chip supply to a co-generation power plant. | Discrete event simulation (SIMEVENTS) | |
| Quantifying the impact of feedstock quality on the design of bioenergy supply chain networks | Castillo-Villar, Minor-Popocatl, and Webb [24] | Present a mixed-integer quadratically constrained programming model that minimizes the bioethanol SC, considering quality related costs. Feedstock: Logging residues. | Mixed-integer quadratic programming | |
| Development of the IBSAL model | ||||
| Development and implementation of integrated biomass supply analysis and logistics model (IBSAL) | Sokhansanj et al. [7] | Describe the development of the IBSAL model. Feedstock: Corn stover. | Discrete event simulation | √ |
| Development of the Integrated Biomass Supply Analysis and Logistics Model (IBSAL) | Sokhansanj, Turhollow, and Wilkerson [25] | Detailed description of the IBSAL model. Feedstock: Corn stover. | Discrete event simulation | √ |
| A new simulation model for multi-agricultural biomass logistics system in bioenergy production | Ebadian et al. [26] | Propose a model for the supply of a mixture of feedstock to a cellulosic ethanol plant. Feedstock: Multi-agricultural. | Discrete event simulation (IBSAL-MC (multi-crop)) | √ |
| Methods to optimise the design and management of biomass-for-bioenergy supply chains: A review | Meyer et al. [27] | Present an overview of the optimization methods and model focusing on the design of biomass SCs. Feedstock: Biomass. | Various methods | |
| The ExtendSim Optimizer | Diamond [28] | Describe the technique used by the ExtendSim Optimizer®™ to find the best set of parameters for a simulation model. Feedstock: N/A. | Simulation optimization | |
| Availability of feedstock and technologies | ||||
| Availability of corn stover as a sustainable feedstock for bioethanol production | Kadam and McMillan [29] | Analyze the potential long-term amount of corn stover available to ethanol plants. Feedstock: Corn stover. | Analysis of a generalized model for stover production and removal | |
| Large-scale production, harvest and logistics of switchgrass (Panicum virgatum L.)—Current technology and envisioning a mature technology | Sokhansanj et al. [30] | Evaluation of technologies for the production, harvest, storage, and transportation. Feedstock: Switchgrass. | Empirical | |
| Evaluation of a modular system for low-cost transport and storage of herbaceous biomass | Searcy and Hartley [20] | Optimize the harvest of energy sorghum in the humid southern region by using a modified cotton module builder for the formation of modules. Feedstock: Energy sorghum. | Discrete event simulation | √ |
| Influence of weather on the predicted moisture content of field chopped energysorghum and switchgrass | Popp et al. [31] | Determine the effect of weather on harvested moisture content. Feedstock: Switchgrass and energy sorghum. | Discrete event simulation | √ |
| Equipment | Input data |
|---|---|
| Mower-Conditioner | Width (ft), field speed average (mph), field efficiency (dec. fraction), machine efficiency, horsepower (hp), custom cost ($/h), annual fixed cost ($), variable cost ($/h), labor cost ($/h), purchase price ($), number of equipment, number of operators, machine biomass loss (decimal), and moisture content with zero machine loss (decimal w.b.) |
| Windrow-Tractor | Power, (hp), total cost ($/h), annual fixed cost ($), variable cost ($/h), labor cost ($/h), and purchase price. |
| Rectangular Baler | Baling pick up width (ft), field average speed (mph), field efficiency (dec. fraction), machine efficiency, power requirement (hp), custom cost ($/h), annual fixed cost ($), variable cost ($/h), labor cost ($/h), purchase price ($), number of equipment, number of operator, machine biomass loss (decimal), moisture content with zero machine loss (decimal w.b.), bale dimension width ( ft), bale dimension height (ft), bale dimension length (ft), bale density (lb/ft3), bales mass (ton), and cost of twine per bale ($/bale). |
| Tractor-Baler | Power (hp), total cost ($/h), annual fixed cost ($), variable cost ($/h), labor cost ($/h), and purchase price (S) |
| Infield-Transporter | Bale size 3x4x8 (volume ft3), bale density (lb/ft3), number of bale per load, load tie time—securing load (min/bale), load efficiency, travel speed full (mph), travel speed empty (mph), efficiency travel, unloading weight and inspection time (min/bale), efficiency unload, power (hp), custom cost ($/h), annual fixed cost ($), variable cost ($/h), labor cost ($/h), purchase price ($), number of equipment, number of operators, machine biomass loss (decimal), moisture content with zero machine loss (decimal w.b.), and winding factor. |
| Loader Storage | Number of bales per load, weight of each bale (ton), loading time per load (min), unloading time per load (min), efficiency, horsepower (hp), custom cost ($/h), annual fixed cost ($), operating cost ($/h), labor cost ($/h), purchase price ($), number of equipment, number of operators, machine biomass loss (decimal), and moisture content with zero machine loss (decimal w.b.) |
| Flatbed Trailer | Bale size 3x4x8 (volume ft3), bale density (lb/ft3), number of bale per load, load tie time—securing load (min/bale), load efficiency, travel speed full (mph), travel speed empty (mph), efficiency travel, unloading weight and inspection time (min/bale), efficiency unload, power (hp), custom cost ($/h), annual fixed cost ($), variable cost ($/h), labor cost ($/h), purchase price ($), number of equipment, number of operators, machine biomass loss (decimal), moisture content with zero machine loss (decimal w.b.), and winding factor. |
| Truck-Tractor | Power (hp), total cost ($/h), annual fixed cost ($), variable cost ($/h), labor cost ($/h), and purchase price |
| Bale Wrapper | Purchase price, stone pad cost ($/m2), cost of plastic wrap per bale, wrapping time (min/bale) |
| Tarp | Tarp cost ($/ft2), labor cost to remove and place tarps ($/ft2), and tarp useful life (years) |
| Sched. | Pr | MinTemp (all) | MinOFVal (all) | Rejectsmax | Runsmax | Acceptsmax | k | Ali | NBi |
|---|---|---|---|---|---|---|---|---|---|
| * | 0.95 | 0.001 | 0.01 | 10 | 10 | 10 | 1 | 10 | 100 |
| ** | 0.6 | 0.001 | 0.01 | 5 | 5 | 5 | 1 | 10 | 10 |
| *** | 0.6 | 0.001 | 0.01 | 10 | 10 | 10 | 1 | 10 | 100 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chavez, H.; Castillo-Villar, K.K.; Webb, E. Development of the IBSAL-SimMOpt Method for the Optimization of Quality in a Corn Stover Supply Chain. Energies 2017, 10, 1137. https://doi.org/10.3390/en10081137
Chavez H, Castillo-Villar KK, Webb E. Development of the IBSAL-SimMOpt Method for the Optimization of Quality in a Corn Stover Supply Chain. Energies. 2017; 10(8):1137. https://doi.org/10.3390/en10081137
Chicago/Turabian StyleChavez, Hernan, Krystel K. Castillo-Villar, and Erin Webb. 2017. "Development of the IBSAL-SimMOpt Method for the Optimization of Quality in a Corn Stover Supply Chain" Energies 10, no. 8: 1137. https://doi.org/10.3390/en10081137
APA StyleChavez, H., Castillo-Villar, K. K., & Webb, E. (2017). Development of the IBSAL-SimMOpt Method for the Optimization of Quality in a Corn Stover Supply Chain. Energies, 10(8), 1137. https://doi.org/10.3390/en10081137





