Abstract
The purpose of this work is to present an adaptive sliding mode Luenberger state observer with improved disturbance rejection capability and better tracking performance under dynamic conditions. The sliding hyperplane is altered by incorporating the estimated disturbance torque with the stator currents. In addition, the effects of parameter detuning on the speed convergence are observed and compared with the conventional disturbance rejection mechanism. The entire drive system is first built in the Simulink environment. Then, the Simulink model is integrated with real-time (RT)-Lab blocksets and implemented in a relatively new real-time environment using OP4500 real-time simulator. Real-time simulation and testing platforms have succeeded offline simulation and testing tools due to their reduced development time. The real-time results validate the improvement in the proposed state observer and also correspond to the performance of the actual physical model.
1. Introduction
The utility of induction motors has risen considerably owing to its integration with power electronic converters, which made variable frequency operation realizable. This, in turn, made the induction motor the workhorse of the industry. Of all the variable frequency control strategies, the vector control or field oriented control principle was the most popular. It provided independent control of torque and flux resulting in fast torque response. The field orientation can be achieved by directly measuring the magnitude and direction of the flux by means of flux sensors or hall effect sensors in the machine (Direct Vector control) or it can be imposed indirectly by a slip frequency component from the rotor dynamics (Indirect Vector control). The latter was more feasible as it did not require the use of additional flux sensors that would occupy additional space and cost. The indirect vector control principle is shown in the phasor diagram expressed as steady state direct current (DC) quantities in Figure 1.
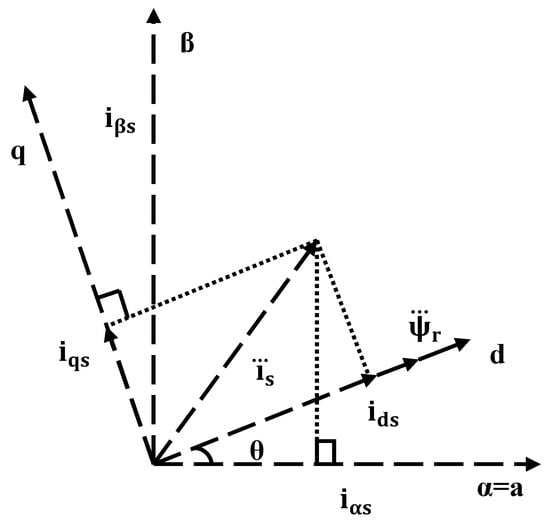
Figure 1.
Indirect vector control principle.
By decoupling the induction motor at synchronously rotating reference frame, and forcing the direct axis stator current component (field producing) in phase with the rotor flux and orthogonal to the quadrature axis stator current’ component (torque producing), independent control of torque and flux is obtained. However, the indirect vector control implementation required the utility of a shaft speed encoder to sense the rotor speed, which was processed along with the speed command to generate the reference torque request for vector control. The presence of the shaft speed encoder implies additional electronics, cost and mounting space. Therefore, to eliminate the shaft speed encoder, the speed estimation techniques were used.
The speed was estimated from either the terminal quantities of the machine or from its rotor saliency. However, speed estimation from the machine model was easier to implement, occupied less computational space and were most effective. Considerable research over the past two decades focused primarily on sensorless control of induction motor [1], with special emphasis on estimation from the machine model [2]. The state estimation schemes are shown in Figure 2.
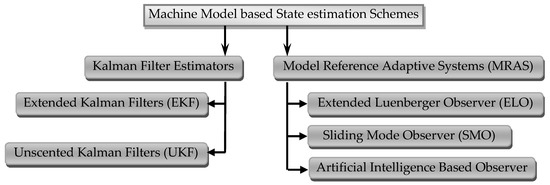
Figure 2.
Machine model based state estimation schemes.
During the earlier stages, extended kalman filter (EKF) based estimators [3,4,5] were widely used for speed estimation, but they give accurate results only if the system dynamics are linearized and had an inherent disadvantage of a high sampling frequency and were computationally expensive. Estimators based on model reference adaptive systems (MRAS), extended luenberger observers (ELO) and sliding mode observers (SMO) [6,7] had a wider utility and were more extensively used owing to ease of use and flexibility. In addition, several configurations varying from lower order to higher order observers, as well as integration of variable structure or artificial intelligence could be developed from the MRAS. All the model based schemes were sensitive to variations or incorrect settings of parameters.
The MRAS and ELO were mainly used for simultaneous state estimation in order to prevent a mismatch between the actual and estimated values of the parameters under all speed ranges. Several studies focused on the performance analysis and parameter estimation [8,9,10] for the drive at low and zero speed regions [11,12,13]. As stated before, variable structure or sliding mode observers (SMO) based on MRAS have been implemented for wide speed bandwidth estimation and faster parameter convergence by constraining the states of the system to the sliding hyperplane [14,15,16,17,18] implements a Luenberger-SMO that estimates the critical parameters online. It is demonstrated by means of hardware in the loop (HIL) simulation setup with an field programmable gate array (FPGA) based controller and an induction motor, in order to verify the robustness of the algorithm. Reference [19] presents a Sliding Mode-MRAS observer based on a super twisting algorithm (STA), where the variations in critical parameters are intentionally considered. In the standard configuration of MRAS, the reference model is replaced by a stator current observer, which is designed based on STA. This, in turn, is insensitive to rotor resistance variations and disturbances when the states converge on the sliding hyperplane. The chattering phenomenon is eliminated and near zero speed operation is realized by means of a parallel identification of stator resistance. In [20], the concept of adaptive Luenberger flux observation is applied for the state estimation of a sensorless symmetrical six phase induction machine subjected to unbalanced operation. In addition to it, the efficacy and performance of the observer is tested by incorporating mechanical and electrical disturbances during the normal operation of the machine. Variation of the inertia up to the maximum value and the loss of one or more stator phases are considered for all the test cases of unbalanced conditions. There are also a certain class of load torque rejection observers that have been implemented. These disturbance observers, either comprised of a mechanical model of the motor or having error components that are dependent on the rotor speed, or gain coefficients dependent on the stator frequency [21,22,23,24]. In [24], the decoupling of current and subsequent control of the current components is applied to induction motor by employing a sliding mode controller and a disturbance observer. The coupled terms are modeled as disturbance, which, after observation, are utilized in the control law. In addition, the rotor speed is estimated based on the magnetizing current and the lyapunov stability criterion is used to ensure closed loop stability. Several of the above categories of observers have been implemented in many experimental platforms and also been verified by means of HIL testing.
The purpose of this paper is to demonstrate the improvement in the rejection of the external load by the proposed observer. The sliding hyperplane is altered and the disturbance estimated from the mechanical model is integrated into the sliding hyperplane along with the real and estimated stator currents [17]. In addition, to add to the nonlinearity of the observer, a Gaussian noise (measurement disturbance) is incorporated at the motor terminals, where the terminal voltages and currents are measured. The observer, along with the drive system, is first built using Matlab/Simulink blocksets and then validated in a comparatively new real-time simulation platform, RT-Lab, developed by Opal-RT (2011, Mathworks, Natick, MA, USA) and the real-time results add more credibility as compared to any other offline simulation platform.
2. General Configuration of Model Reference Adaptive Systems and System Modeling
Adaptive control is mainly used for parameter adaptation. The essence of an adaptive control mechanism is to adapt to the controlled system with parameters that need to be estimated. The concept of parameter adaptive MRAS along with the parallel disturbance torque estimation mechanism is illustrated in Figure 3. There is a reference motor model and the adaptive model as a function of the parameter to be estimated. The adaptive mechanism is used to ensure that the state of the observer (process) converges to the state of the motor (plant). Therefore, we have an optimization criterion X and the error to be constrained:
where Xref and Xadap are outputs of respective models. The adaptation mechanism makes use of the classical Proportional-Integral theory to process the speed tuning signal. A Lyapunov function candidate is used for the speed derivation mechanism.
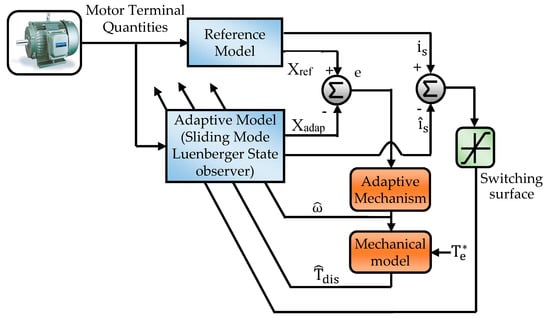
Figure 3.
Basic configuration of parameter adaptive model reference adaptive system (MRAS) scheme with parallel disturbance torque estimation.
2.1. Structure of Sliding Mode Luenberger State Observer
The reduced order sliding mode luenberger observer (SMLO) with the modified switching surface is shown in Figure 4, where “A” is the parameter matrix, “^” is used for estimated parameters, “X” is the state variables comprised of the d and q-axes stator currents and rotor fluxes, “ksw” is the reduced order observer switching gain matrix, chosen in such a way that the eigenvalues of the observer and the machine are maintained proportional to ensure stability under normal operating conditions. “J” is the moment of inertia, “p” is the differential operator, “BV” is the viscous friction coefficient, “” and “” is the reference model electromagnetic torque and the estimated disturbance torque, “k” is an arbitrary positive gain [17]. The purpose of a sliding mode or variable structure strategy is to modify the dynamics of a non linear system state by means of a high frequency switching surface or a sliding hyperplane. The sliding hyperplane is selected in such a way that the Lyapunov function candidate “V” utilized for obtaining the convergence mechanism, and its derivative satisfies the Lyapunov stability criterion [17,25]. “V” is a scalar function of the sliding hyperplane “S”. Therefore,
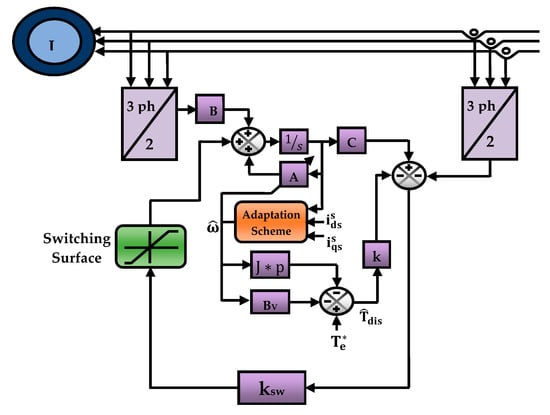
Figure 4.
Proposed state observer with the modified switching hyperplane.
The control law is:
where u(t), ueq(t) and usw(t) represent the control, equivalent control and the switching vector. For stability, the switching vector is obtained [17,26]:
where . η is the switching control gain chosen such that (3) is negative definite, implying , thereby constraining the effect of the external disturbance. However, the high frequency switching plane increases non linearity of the observer, leading to chattering. Therefore, to eliminate the effect of this unwanted phenomenon, a saturation function having boundary layer of width (Φ) is used by replacing sign (S) with sat (S/Φ) and is given by [17]:
Based on the theory of MRAS, the following equations depict the structure of the proposed observer scheme with the conventional and modified sliding hyperplane. The reference and the adaptive model are represented in state space form as they aid in the formulation of control and estimation problems [17,27].
2.1.1. Reference Model (Motor)
- , ,
- , , ,
- , ,
- ,
- ,
- .
2.1.2. Estimation of Disturbance Torque from the Mechanical Model
By exploiting the machine model, the disturbance torque is estimated by utilizing the reference model electromagnetic torque and the estimated speed, respectively:
2.1.3. SMLO 1—Observer with Conventional Disturbance Rejection Mechanism (Adaptive Model)
- ,
- ,
- .
The switching gain “ksw” is designed by the following lower order matrix given by
The switching gain matrix is designed appropriately to make Label (4) stable by means of pole placement. The eigenvalues are designed in such a way that, for the observer, they are comparatively more negative to that of the motor so that they ensure faster convergence of the desired performance to the process. Therefore,
where “m” and “k2” are chosen in such a way that the eigenvalues of the observer are shifted more negative as compared to the eigenvalues of the motor. They also directly affect the dynamics and damping of the observer. “k1” is dependent on the motor parameters.
2.1.4. SMLO 2—Observer with Modified Disturbance Rejection Mechanism (Adaptive Model)
The state dynamic equation is altered by changing the sliding hyperplane, i.e., by including the estimated disturbance torque [17]:
Therefore, the sliding hyperplane becomes, and
2.1.5. Adaptive Mechanism
The Lyapunov function candidate used for speed derivation mechanism and to ensure stability is given by:
where λ is a positive constant.
We have:
where , .
The second and third term of (18) is equalized to realize the expression for the estimated speed given by:
“c” being an arbitrary positive constant. The difference between SMLO 2 and SMLO 1 is the way in which the estimated disturbance is added and constrained in the sliding hyperplane along with the stator current error. The complexity of the observer increases due to the presence of the speed adaptation loop, the disturbance estimation and adaptation loop and the Luenberger observer gain loop, however, by tuning the feedback and switching gains, the dynamic performance and the stability of both the observers can be improved.
2.2. Stability Analysis of Both the Observers by Means of Pole Placement
For the conventional disturbance observer SMLO 1:
The characteristic equation is:
On solving:
The observer poles are:
For the modified disturbance observer SMLO 2:
The characteristic equation is:
On solving:
The observer poles are:
2.3. Structure of Current Regulated Vector Controller
Current regulation or tolerance band current control has a fast torque response and is independent of load parameters. The speed error is processed by a PI controller whose output is the reference torque:
where ec is the speed error, kp and ki are the proportional and integral gains for tuning the speed error, and Ts is the sampling time. For operation in the motoring and flux weakening region, the rotor flux is constant for the former and as a function of the speed for the latter:
The orthogonal direct and quadrature axes stator current components are [1]:
As the slip speed is used for imposing the field orientation, the field angle is determined from the slip speed, therefore:
The three-phase reference currents are obtained from the decoupled reference components of current by means of inverse transformation given as follows:
The three-phase reference current components are compared with the actual sensed three-phase currents by means of hysteresis regulation and the gating pulses for the voltage source inverter (VSI) are generated. The hysteresis band is selected keeping the current and subsequent torque pulsation in mind. The entire sensorless drive scheme is illustrated in Figure 5 [17].
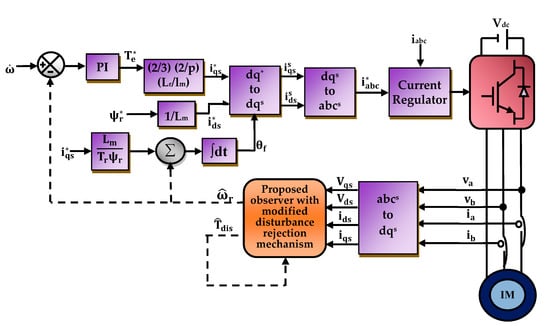
Figure 5.
Voltage source inverter (VSI) fed speed sensorless induction motor drive system.
3. The Concept of Real-Time Simulation
Real-time simulation and test platform is one in which the computer model’s performance corresponds to the performance of the actual physical system [28,29,30,31,32,33,34,35,36]. It would take the same amount of time like any real world application. Unlike many offline simulation platforms, where a variable step solver is used, in real time, a fixed step discrete solver is used. For a given computer model, in a real-time simulation, the processing of inputs, model calculations and the processing of outputs should be less than the fixed step. If it exceeds the fixed step, a phenomenon known as over run would occur. Therefore, it is imperative that the real-time simulator should produce the model calculations and output within the same time interval corresponding to its actual physical counterpart. The applications ranges from mechatronics, power electronic and power system based concepts to gaming and process control.
There are various real-time simulators available such as xPC Target (Mathworks, Natwick, United States), for power electronic system simulation there is eFPGAsim and eDRIVEsim (Opal-RT, Montreal, Canada) and for power system simulation, we have HYPERSIM (Opal-RT, Montreal, Canada) and RTDS (RTDS Technologies Inc., Winnipeg, MB, Canada).
RT-Lab is a distributed real-time platform with features ranging from virtual, control and plant prototyping, model based design, etc. It is flexible and has a fast execution time and can also be utilized for real-time processor-in-loop (PIL) and hardware in the loop (HIL) applications. The package is compatible with various offline platforms such as Matlab/Simulink, Labview, etc. The mathematical and dynamic model of the drive system is built in Simulink environment using sim-power systems toolbox. This acts as the front end interface after which the model is integrated with RT-Lab blocksets. RT-Lab generates the code to be simulated in a single or multiple targets. Here, the real-time simulation target used is OP4500 developed by Opal-RT. It is a multi core target, where the plant and controller can be placed in different cores.
It comprises of analog and digital input/output (I/O) channels with signal conditioning and is also integrated with powerful XILINX Kintex 7 FPGA, which has a very high processing power. The sensorless drive system is modeled and built offline using sim power systems toolbox in Simulink in the workstation. The offline simulink model uses a variable step solver. The RT-Lab integrated real-time platform uses a discretised fixed step time solver with a step size of 50 μs. The workstation is connected to the OP4500 real-time simulator through transmission control protocol/internet protocol (TCP/IP) protocol. The target executes the model and the results are viewed and recorded in the workstation, which is the front end interface. The model is executed and analyzed dynamically for different test cases as presented below.
4. Real-Time Simulation Results: Analysis and Discussion
The motor parameters and ratings used for the real-time simulation are given in Appendix A. In order to emphasize on the improvement in the performance of SMLO 2 over SMLO 1, some results are magnified to present a clearer picture. Parameter estimation of an observer at flux weakening regions is significant, as it indicates its robustness for a wider speed bandwidth as also its tracking performance at a constant power region.
4.1. Performance at Flux Weakening
Here, the observers are tested at a low flux weakening region for a given speed command of 165 rad/s. However, both reach the reference speed at almost identical time, and the estimated speed oscillations are comparatively very high for SMLO 1 as shown in Figure 6a. In the zoomed version shown in Figure 6b, the oscillation is as high as 70 rad/s for the speed command of 165 rad/s, which is almost 42%.
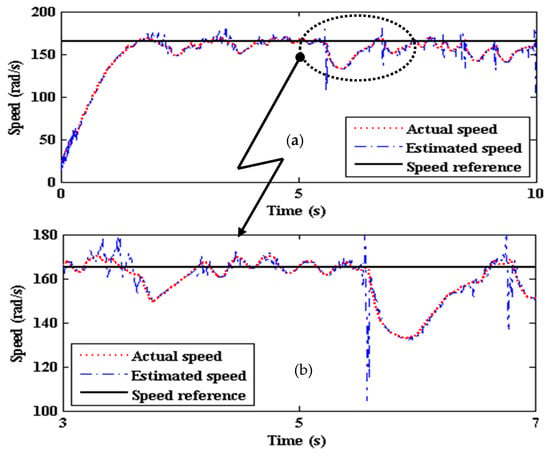
Figure 6.
(a) Estimated speed of conventional sliding mode luenberger observer (SMLO) 1; and (b) zoomed version of (a).
The profiles of the estimated disturbance torque in Figure 7 and the electromagnetic torque in Figure 8 of SMLO1 are almost the same, since the viscous friction coefficient and the inertia constant are of a low value. The estimated rotor flux of SMLO 1 in Figure 9 has more oscillations and the magnitude is increasing with time. As compared to SMLO 1, speed performance of SMLO2 has relatively less oscillations shown in Figure 10a. In Figure 10b, although there is an initial overshoot and undershoot, the oscillation is initially around 20 rad/s, which is around 12%, and gradually dies out after 6 s.
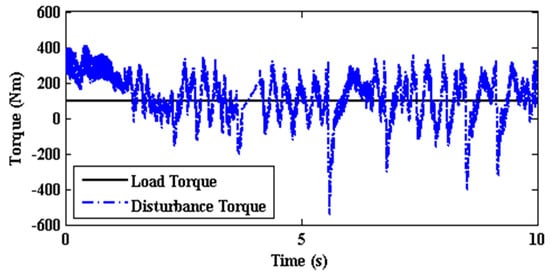
Figure 7.
Estimated disturbance torque of SMLO 1.
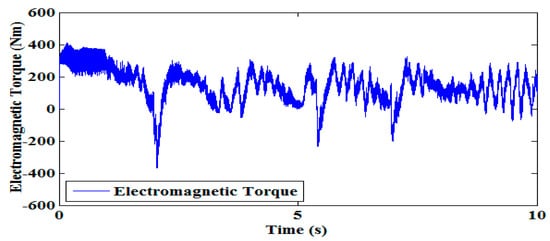
Figure 8.
Electromagnetic torque of SMLO 1.
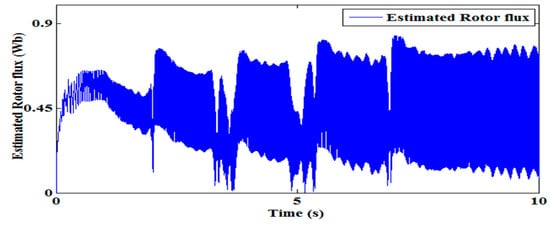
Figure 9.
Estimated rotor flux of SMLO 1.
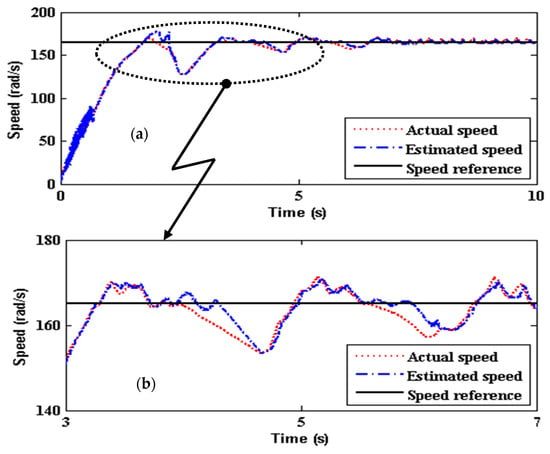
Figure 10.
(a) Estimated speed of Modified Sliding Mode Luenberger Observer (SMLO 2); and (b) zoomed version of (a).
Estimated disturbance torque of SMLO2 shown in Figure 11 has relatively lesser ripples. Again, the electromagnetic torque profile of SMLO2 follows the estimated disturbance torque profile as shown in Figure 12. SMLO2 estimated rotor flux shown in Figure 13 has lesser oscillations. This shows that the SMLO 2 has better reception to flux weakening and operates well in this region.
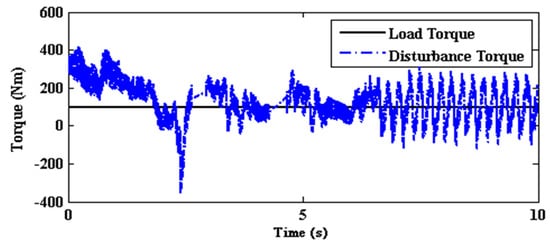
Figure 11.
Estimated disturbance torque of SMLO 2.
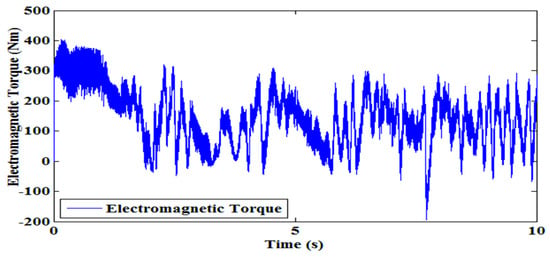
Figure 12.
Electromagnetic torque of SMLO 2.
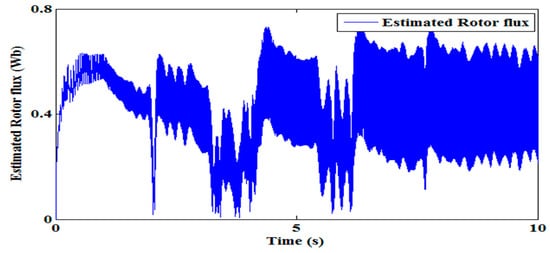
Figure 13.
Estimated rotor flux of SMLO 2.
4.2. Performance at Step Speed Command
The difference is seen more distinctly at step speed command (initially 50 rad/s, after 2 s, stepped upto 150 rad/s, after 7 s, stepped down to 100 rad/s), which covers a wide speed bandwidth. SMLO 1 initially, tracks well for both 50 rad/s and 150 rad/s, but, during deceleration from 150 rad/s to 100 rad/s, there is a very high spike in the estimated speed (of almost 100 rad/s) shown in Figure 14a, which could prove detrimental to the drive system. This is mainly due to the sudden change in the flux level of the motor and SMLO 1, which directly affects its speed convergence. Even after settling down at 100 rad/s, after about 10 s, oscillations persist ranging between 98.5 and 101 rad/s, shown in Figure 14b. SMLO 2 in comparison tracks more smoothly and accurately, even during deceleration as shown in Figure 15a. The oscillations in the estimated speed are greatly reduced as shown in Figure 15b, ranging almost between 99.9 and 100.1 rad/s, which proves that it is near accurate and superior tracking as compared to SMLO 1.
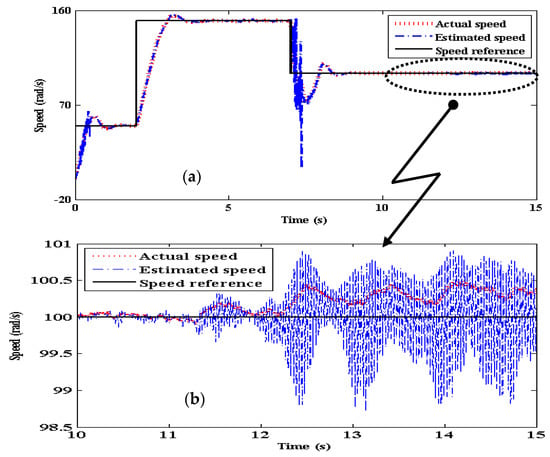
Figure 14.
(a) Estimated speed of SMLO 1; and (b) zoomed version of (a).
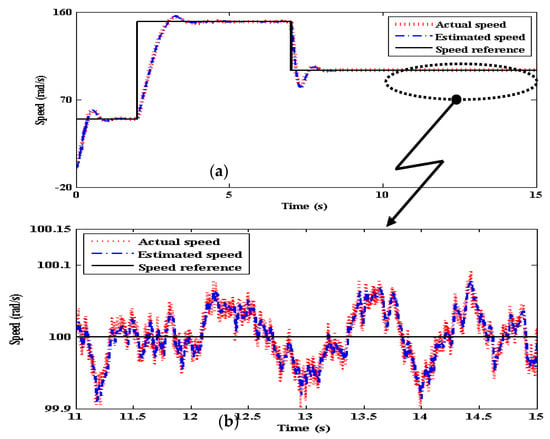
Figure 15.
(a) Estimated speed of SMLO 2 (b); and zoomed version of (a).
Even the estimated disturbance torque profile of SMLO 1 shown in Figure 16a is comparatively less smoother with more pulsations as compared to SMLO 2 shown in Figure 16b. The estimated rotor flux performance for SMLO 1 in Figure 17a and SMLO 2 in Figure 17b can be observed. Here again, the latter gives smoother flux performance in spite of variations in the commanded speed at different time intervals, resulting in better torque holding capability.
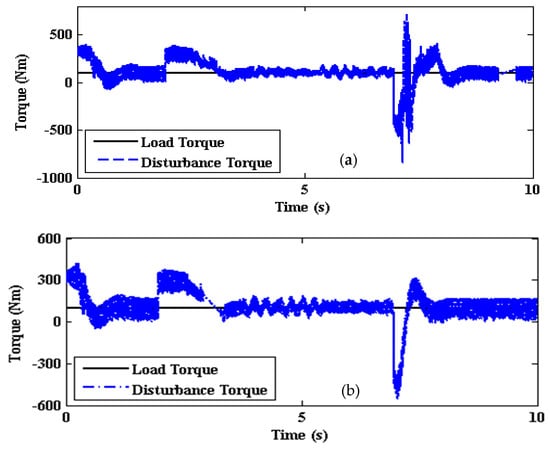
Figure 16.
Estimated disturbance torque of (a) SMLO 1; and (b) SMLO 2.
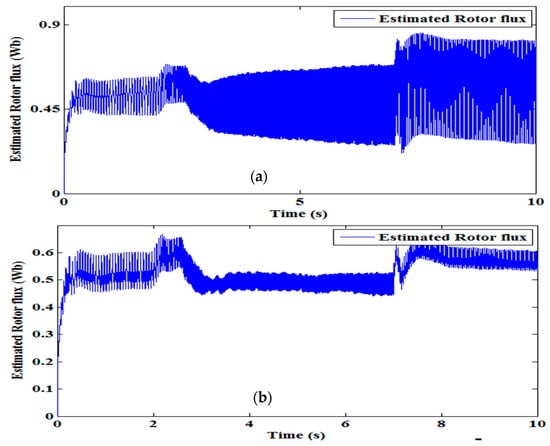
Figure 17.
Estimated rotor flux of (a) SMLO 1; and (b) SMLO 2.
4.3. Performance at Low Speeds
At low speeds (for a speed command of 30 rad/s), SMLO 1 does not track becomes unstable and goes out of bounds. Therefore, the speed bandwidth of SMLO 1 is restricted to a range of 50–150 rad/s. However, the tracking performance of SMLO 2 is shown in Figure 18a, where, after an initial high overshoot for a very small amount of time, it tracks the command accurately, which is more distinct in the zoomed version in Figure 18b.
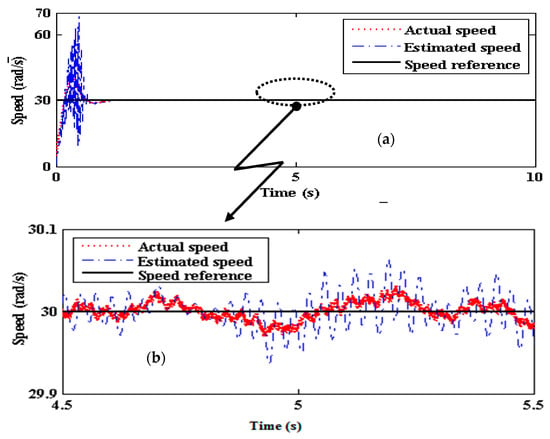
Figure 18.
(a) estimated speed of SMLO 2 (b), zoomed version of (a).
The initial high disturbance torque pulsation shown in Figure 19 is responsible for the high overshoot in estimated speed.
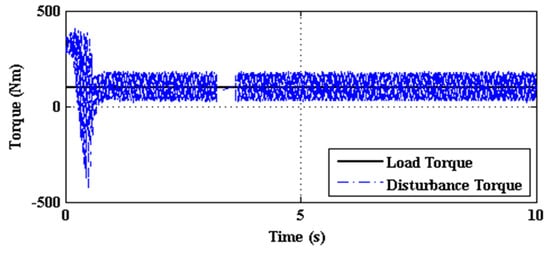
Figure 19.
Estimated disturbance torque of SMLO 2.
4.4. Effect of Parameter Detuning on the Dynamic Performance
The detuning or incorrect setting of parameters plays a significant role in the ability of the adaptive mechanism to converge the states of the observer and motor. The stator resistance and rotor time constant play a critical role in the motor dynamics. Therefore, the speed convergence mechanisms of the observer are tested for incorrect settings of the said parameters. The speed tuning signal for the adaptive mechanism is derived from the difference between the products of the estimated d-axis flux linkages and the q-axis stator current error and q-axis flux linkages and the d-axis stator current error. For 50% incorrect setting in both, the convergence of SMLO 1 is shown in Figure 20a. The speed error gradually increases at the end, thereby affecting its ability to withstand parametric uncertainties, whereas, for SMLO 2, the speed error is approximately zero and consistent with time, as shown in Figure 20b.
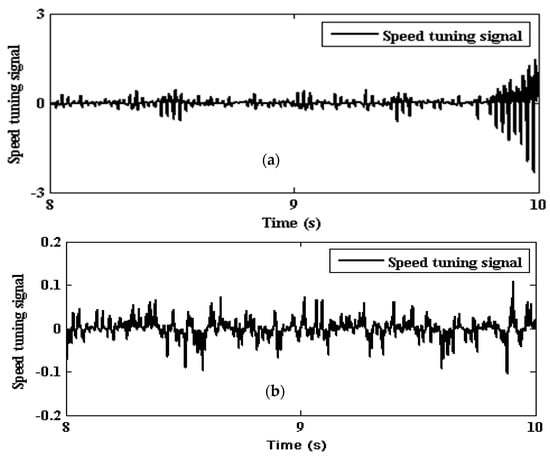
Figure 20.
Speed tuning signal for 50% incorrect setting of stator resistance (Rs) and rotor time constant (Tr) for (a) SMLO 1, and (b) SMLO 2.
Parametric uncertainties can also be treated as model disturbances and this only reflects the ability of SMLO 2 to reject the effect of the disturbances. Again, for nominal setting of Rs and Tr, although the inconsistencies in the speed tuning signal of SMLO 1 has reduced, it is still pertinent, with speed error reaching almost 3 rad/s, as shown in Figure 21a. The speed tuning signal or speed error of SMLO 2 is almost confined to zero, as shown in Figure 21b, indicating faster convergence of the motor and the observer states.
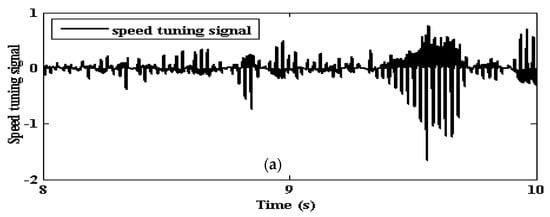
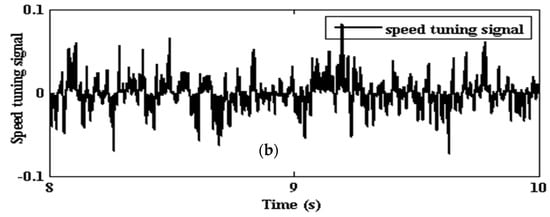
Figure 21.
Speed tuning signal for nominal setting of stator resistance (Rs) and rotor time constant (Tr) for (a) SMLO 1; and (b) SMLO 2.
Now, for 150% incorrect setting in both the parameters, SMLO 1 exhibits a comparatively better convergence than previous cases, as shown in Figure 22a, but, here again, it is observed that SMLO 2 offers a greater and near accurate convergence of states, as shown in Figure 22b.
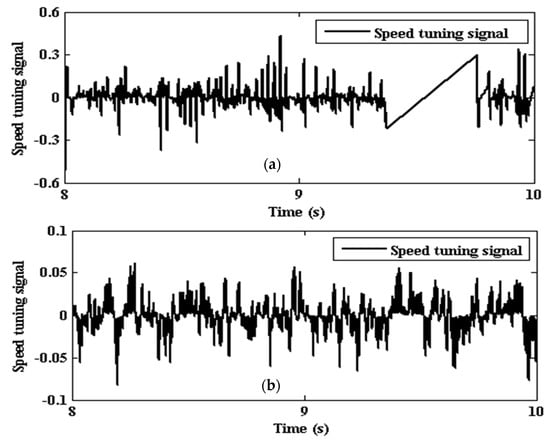
Figure 22.
Speed tuning signal for 150% incorrect setting of stator resistance (Rs) and rotor time constant (Tr) for (a) SMLO 1; and (b) SMLO 2.
4.5. Switching Surface and Convergence of the Stator Current Error
The convergence of the stator current error and the sliding surface is also observed for both the observers. In both the cases, the profile of the sliding surface is identical to that of the stator current error, as both are dependent on each other. The profile of the sliding surface, direct and quadrature axes stator currents, stator current error of SMLO1 are shown in Figure 23a–d. However, as compared to SMLO 1, both the stator current error and the sliding surface of SMLO 2 are slightly displaced in the negative range. This can be primarily due to change in the configuration of the sliding surface, as, along with the stator current error, it also has to constrain the effect of the estimated disturbance torque. The direct and quadrature axes are also obtained. The performance of SMLO2 is shown in Figure 24a–d.
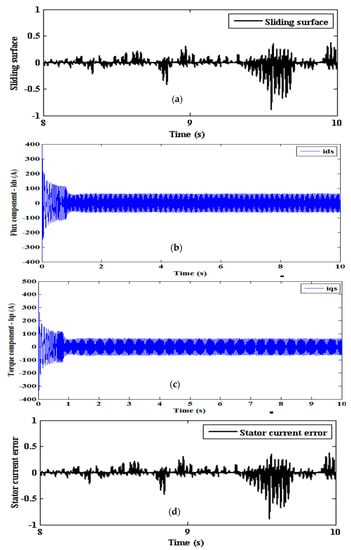
Figure 23.
SMLO 1 (a) sliding surface; (b) flux component of stator current; (c) torque component of stator current; and (d) stator current error.
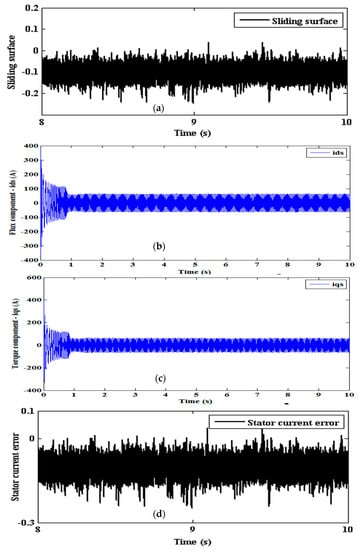
Figure 24.
SMLO 2 (a) sliding surface; (b) flux component of stator current; (c) torque component of stator current; and (d) stator current error.
Although both are similar, the presence of pulsations in the stator current components, both during steady state and transient conditions, give rise to subsequent torque and flux pulsations in the observers. In addition, due to high power rating of the motor, the stator current dynamics play a major role in the torque performance. However, it is seen that the SMLO 2 comparatively displays better dynamic and steady state performance due to its ability to contain the stator current dynamics and ensure that it does not affect the tracking. For the entire study, the load torque was maintained constant at 100 Nm. For the last two test cases, along with the constant load torque, the speed command was also maintained constant at 100 rad/s, respectively.
4.6. Pole Placement Plot of the Modified nd Conventional Disturbance Observers
The pole plot shown in Figure 25 shows that the poles of SMLO 2 are shifted to left of SMLO 1, which indicates comparatively better stability performance of the same in low and flux weakening regions. However, the performance at medium speed regions remains more or less the same.

Figure 25.
Pole placement of SMLO 1 and SMLO 2.
Since hysteresis band current regulation is used, the exact switching frequency cannot be predicted; however, the maximum switching frequency which is realizable by the OP45OO target is (1/(2*time step)), which is 10 kHz. As the model has been successfully executed by the target, it can be safely concluded that the equivalent switching frequency is within 10 kHz. The entire testing and analysis were performed in the motoring mode at low, medium speeds and low flux weakening regions. Although these real-time simulation results can also be considered to be equivalent to the experimental results while testing in model based design paradigm (provided all the model dynamics including uncertainties, plant disturbance etc. have been mathematically modeled), there are some problems which are encountered. While moving from simulations to real-time implementation of the model, in automotive and power applications, (EMI/EMC issues, over-voltages, overcurrent, temperature issues) arise which have to be managed with proper safe circuitry and diagnostic circuitry [30,31,32]. Table 1 summarizes the observations from the above analysis for both the observers.

Table 1.
Salient features of both the observers.
5. Conclusions
This paper presented an improved version of a sliding mode Luenberger observer with comparatively better tracking performance, robustness to the effect of external and model disturbances and a wider speed bandwidth than the conventional one. The drive system along with the proposed observer is executed in real-time using an RT-Lab package and an OP4500 real-time simulator. The real-time results validate the improvement in the disturbance rejection capability for the different test cases presented and also provide more credibility as compared to other offline simulated results. Some significant findings from the study are presented and summarized in a table to add more clarity. They present a realistic view of how the actual physical system would respond just like the virtual system present in the workstation. Furthermore, the plant or the controller can be made to interact in real-time PIL or HIL with the other components of the drive system in the workstation.
Acknowledgments
There were no funding resources.
Author Contributions
Mohan Krishna, Febin Daya, and Sanjeevikumar Padmanaban developed the proposed AC drives research work and implemented it with numerical simulation software and hardware implementation using RT-Lab solutions. Furthermore, Sanjeevikumar Padmanaban and Lucian Mihet-Popa extended the insight and technical expertise to make the work quality in its production. All authors were involved in validating the numerical simulation results with hardware implementation and experimental test results in accordance with the developed theoretical background. All authors were involved and contributed in each part of the article for its final depiction as a research paper.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| idss, iqss, idrr, iqrr | Direct and quadrature axes stator and rotor current components in stationary and rotating frame |
| vdss, vqss | Direct and quadrature stator voltages in stationary frame |
| Tr, Rs, Rr | Rotor time constant, stator and rotor resistance |
| σ, Lr, Lm, Ls | Leakage reactance, rotor, magnetizing and stator self inductance |
| Lls, Llr | Stator and rotor leakage inductances |
| Actual, estimated, reference and base synchronous speed | |
| ψdss, ψqss, ψdrs, ψqrs | Direct and quadrature axes stator and rotor flux linkages in stationary frame |
| Direct and quadrature axes estimated rotor flux linkages | |
| , | Field, slip and rotor angles and Torque reference |
| Direct and quadrature axes stator currents in synchronously rotating frame | |
| Three-phase reference currents |
Appendix A
The ratings of the model considered for the study are: A 50 HP, 415 V, 3Φ, 50 Hz, star connected, four-pole induction motor with equivalent parameters: Rs = 0.087 Ω, Rr = 0.228 Ω, Lls = Llr = 0.8 mH, Lm = 34.7 mH, Inertia, J = 1.662 kgm2, friction factor = 0.1.
References
- Anitha, P.; Badrul, H.C. Sensorless control of inverter-fed induction motor drives. Electr. Power Syst. Res. 2007, 77, 619–629. [Google Scholar]
- Yang, Z.; Yue, Q.; Ye, Y. Induction Motor Speed Control Based on Model Reference. Procedia Eng. 2012, 29, 2376–2381. [Google Scholar]
- Abd El-Halim, A.F.; Abdulla, M.M.; El-Arabawy, I.F. Simulation Aides in Comparison between Different Methodology of Field Oriented Control of Induction Motor Based on Flux and Speed Estimation. In Proceedings of the 22nd International Conference on Computer Theory and Applications, Alexandria, Egypt, 13–15 October 2012. [Google Scholar]
- Sun, D.; Lin, W.; Diao, L.; Liu, Z. Speed Sensorless Induction Motor Drive Based on EKF and Γ-1 Model. In Proceedings of the IEEE International Conference on Computer Distributed Control and Intelligent Environmental Monitoring, Changsha, China, 19–20 February 2011. [Google Scholar]
- Alonge, F.; D’Ippolito, F.; Sferlazza, A. Sensorless Control of Induction-Motor Drive Based on Robust Kalman Filter and Adaptive Speed Estimation. IEEE Trans. Ind. Electron. 2014, 61, 1444–1453. [Google Scholar] [CrossRef]
- Rezgui, S.E.; Benalla, H. MRAS sensorless based control of IM combining sliding-mode, SVPWM, and Luenberger observer. In Proceedings of the International Conference on Computer as a Tool, Lisbon, Portugal, 27–29 April 2011. [Google Scholar]
- Zheng, Y.; Loparo, K.A. Adaptive Flux Observer for Induction Motors. In Proceedings of the American Control Conference, Philadelphia, PA, USA, 24–26 June 1998. [Google Scholar]
- Ticlea, A.; Besancon, G. Observer Scheme for State and Parameter Estimation in Asynchronous Motors with Application to Speed Control. Eur. J. Control 2006, 12, 400–412. [Google Scholar] [CrossRef]
- Mikail, R.; Rahman, K.M. Sensorless Adaptive Rotor Parameter Estimation Method for Three Phase Induction Motor. In Proceedings of the IEEE 5th International Conference on Electrical and Computer Engineering, Dhaka, Bangladesh, 25–27 December 2008. [Google Scholar]
- Levi, E.; Wang, M. Impact of Parameter Variations on Speed Estimation in Sensorless Rotor Flux Oriented Induction Machines. In Proceedings of the IEEE Power Electronics and Variable Speed Drives, London, UK, 21–23 September 1998. [Google Scholar]
- Gadoue, S.M.; Giaouris, D.; Finch, J.W. Performance Evaluation of a Sensorless Induction Motor Drive at Very Low and Zero Speed Using a MRAS Speed Observer. In Proceedings of the IEEE 2008 Region 10 Colloquium and the Third International Conference on Industrial and Information Systems, Kharagpur, India, 8–10 December 2008. [Google Scholar]
- Rashed, M.; Stronach, A.F. A stable back-EMF MRAS-based sensorless low-speed induction motor drive insensitive to stator resistance variation. IEE Proc. Electr. Power Appl. 2004, 151, 685–693. [Google Scholar] [CrossRef]
- Beguenane, B.; Ouhrouche, M.A.; Trzynadlowski, A.M. A new scheme for sensorless induction motor control drives operating in low speed region. Math. Comput. Simul. 2006, 71, 109–120. [Google Scholar] [CrossRef]
- Lascu, C.; Boldea, I.; Blaabjerg, F. A Class of Speed-Sensorless Sliding-Mode Observers for High-Performance Induction Motor Drives. IEEE Trans. Ind. Electron. 2009, 56, 3394–3403. [Google Scholar] [CrossRef]
- Gadoue, S.M.; Giaouris, D.; Finch, J.W. MRAS Sensorless Vector Control of an Induction Motor Using New Sliding-Mode and Fuzzy-Logic Adaptation Mechanisms. IEEE Trans. Energy Convers. 2010, 25, 394–402. [Google Scholar] [CrossRef]
- Zhang, X. Sensorless Induction Motor Drive Using Indirect Vector Controller and Sliding-Mode Observer for Electric Vehicles. IEEE Trans. Veh. Technol. 2013, 62, 3010–3018. [Google Scholar] [CrossRef]
- Krishna, S.M.; Daya, J.L.F. A modified disturbance rejection mechanism in sliding mode state observer for sensorless induction motor drive. Arab. J. Sci. Eng. 2016, 41, 3571–3586. [Google Scholar] [CrossRef]
- Nayeem Hasan, S.M.; Husain, I. A Luenberger-Sliding Mode Observer for Online Parameter Estimation and Adaptation in High-Performance Induction Motor Drives. IEEE Trans. Ind. Appl. 2009, 45, 772–781. [Google Scholar] [CrossRef]
- Albu, M.; Horga, V.; Ratoi, M. Disturbance torque observers for the induction motor drives. J. Electr. Eng. 2006, 6, 1–6. [Google Scholar]
- Krzeminski, Z. Observer of induction motor speed based on exact disturbance model. In Proceedings of the IEEE 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2008. [Google Scholar]
- Krzeminski, Z. A new speed observer for control system of induction motor. In Proceedings of the IEEE International Conference on Power Electronics and Drive Systems, Hong Kong, China, 27–29 July 1999. [Google Scholar]
- Vieira, R.P.; Gabbi, T.S.; Grundling, H.A. Sensorless decoupled IM current control by sliding mode control and disturbance observer. In Proceedings of the IEEE 40th Annual Conference, Dallas, TX, USA, 30 October–1 November 2014. [Google Scholar]
- Comanescu, M. Design and analysis of a sensorless sliding mode flux observer for induction motor drives. In Proceedings of the IEEE International Electric Machines and Drives Conference, Niagara Falls, ON, Canada, 15–18 May 2011. [Google Scholar]
- Krishna, S.M.; Daya, J.L.F. MRAS speed estimator with fuzzy and PI stator resistance adaptation for sesnorless induction motor drives using RT-Lab. Perspect. Sci. 2016, 8, 121–126. [Google Scholar] [CrossRef]
- Krishna, S.M.; Daya, J.L.F. Adaptive Speed Observer with Disturbance Torque Compensation for Sensorless Induction Motor Drives using RT-Lab. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 3792–3806. [Google Scholar] [CrossRef]
- Mikkili, S.; Prattipati, J.; Panda, A.K. Review of real-time simulator and the steps involved for implementation of a model from matlab/simulink to real-time. J. Inst. Eng. India Ser. B. 2014, 96, 179–196. [Google Scholar] [CrossRef]
- Daya, J.L.F.; Sanjeevikumar, P.; Blaabjerg, F.; Wheeler, P.; Ojo, O.; Ertas, A.H. Analysis of Wavelet Controller for Robustness in Electronic Differential of Electric Vehicles—An Investigation and Numerical Developments. J. Electr. Power Compon. Syst. 2016, 44, 763–773. [Google Scholar] [CrossRef]
- Sanjeevikumar, P.; Daya, J.L.F.; Blaabjerg, F.; Wheeler, P.; Oleschuk, V.; Ertas, A.H.; Mir-Nasiri, N. Wavelet-Fuzzy Speed Indirect Field Oriented Controller for Three-Phase AC Motor Drive-Investigation and Implementation. Int. J. Eng. Sci. Technol. 2016, 19, 1099–1107. [Google Scholar]
- Daya, J.L.F.; Subbiah, V.; Iqbal, A.; Sanjeevikumar, P. A Novel Wavelet-Fuzzy based indirect field oriented control of Induction Motor Drives. J. Power Elect. 2013, 13, 656–668. [Google Scholar] [CrossRef]
- Saponara, S.; Fanucci, L.; Bernardo, F.; Falciani, A. Predictive Diagnosis of High-Power Transformer Faults by Networking Vibration Measuring Nodes With Integrated Signal Processing. IEEE. Trans. Instrum. Meas. 2016, 65, 1749–1760. [Google Scholar] [CrossRef]
- Costantino, N.; Serventi, R.; Tinfena, F.; D’Abramo, P.; Chassard, P.; Tisserand, P.; Saponara, S.; Fanucci, L. Design and Test of an HV-CMOS Intelligent Power Switch With Integrated Protections and Self-Diagnostic for Harsh Automotive Applications. IEEE. Trans. Ind. Electron. 2011, 58, 2715–2727. [Google Scholar] [CrossRef]
- Saponara, S.; Petri, E.; Fanucci, L.; Terreni, P. Sensor Modeling, Low-Complexity Fusion Algorithms, and Mixed-Signal IC Prototyping for Gas Measures in Low-Emission Vehicles. IEEE. Trans. Instrum. Meas. 2011, 60, 372–384. [Google Scholar] [CrossRef]
- Sanjeevikumar, P.; Daya, J.L.F.; Wheeler, P.; Blaabjerg, F.; Viliam, F.; Ojo, O. Wavelet Transform with Fuzzy Tuning Based Indirect Field Oriented Speed Control of Three-Phase Induction Motor Drive. Proceedings of 18th IEEE International Conference on Electrical Drives and Power Electronics, Tatranska Lomnica, Slovakia, 21–23 September 2015. [Google Scholar]
- Daya, J.L.F.; Subbiah, V.; Sanjeevikumar, P. Robust Speed Control of an Induction Motor Drive using Wavelet-Fuzzy based Self-tuning Multiresolution Controller. Int. J. Comput. Intell. Syst. 2013, 6, 724–738. [Google Scholar] [CrossRef]
- Sanjeevikumar, P.; Daya, J.L.F.; Blaabjerg, F.; Mir-Nasiri, N.; Ertas, A.H. Numerical Implementation of Wavelet and Fuzzy Transform IFOC for Three-Phase Induction Motor. Int. J. Eng. Sci. Technol. 2016, 19, 96–100. [Google Scholar]
- Daya, J.L.F.; Sanjeevikumar, P.; Blaabjerg, F.; Wheeler, P.; Ojo, O. Implementation of Wavelet Based Robust Differential Control for Electric Vehicle Application. IEEE Trans. Power Electron. 2015, 30, 6510–6513. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).