Analysis of On-Board Photovoltaics for a Battery Electric Bus and Their Impact on Battery Lifespan †
Abstract
:1. Introduction
2. Model Formulation
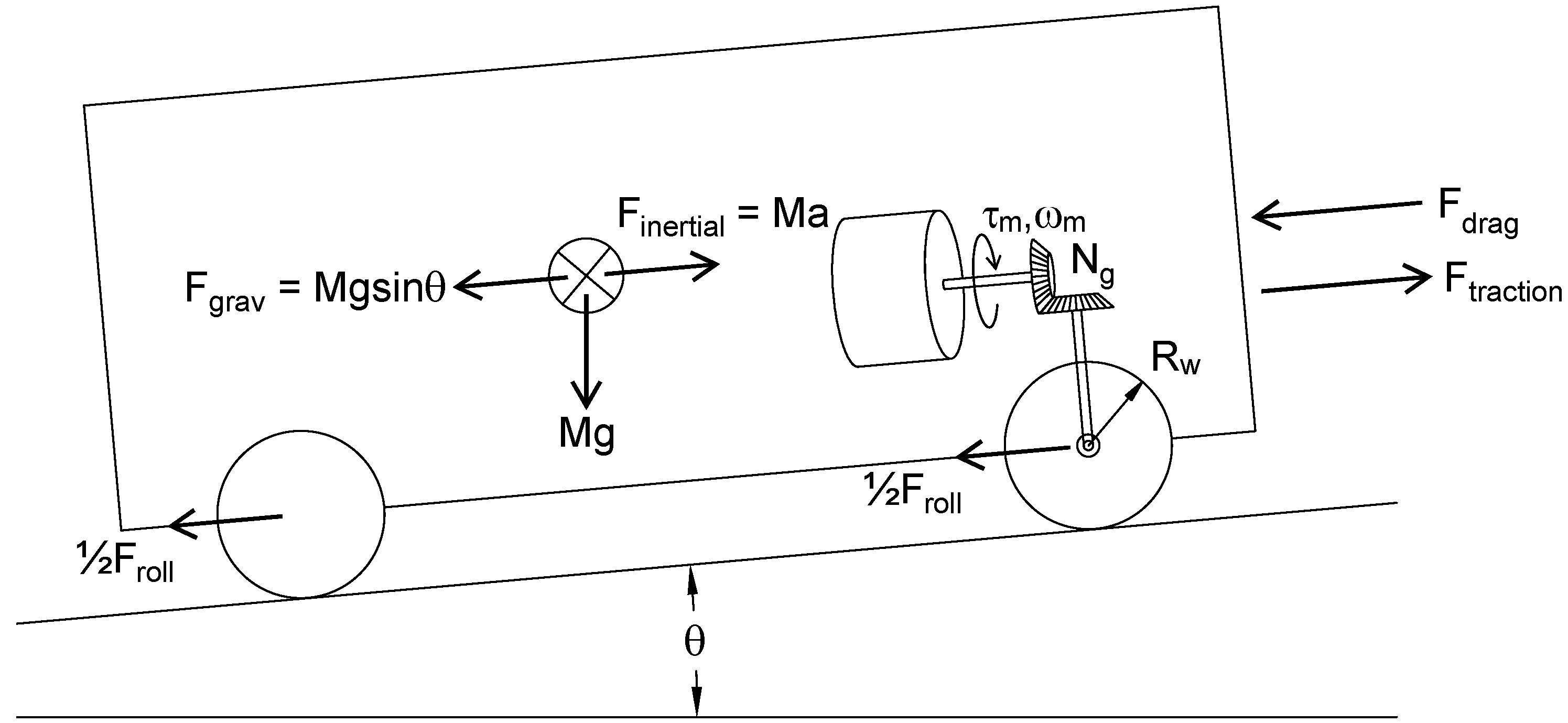
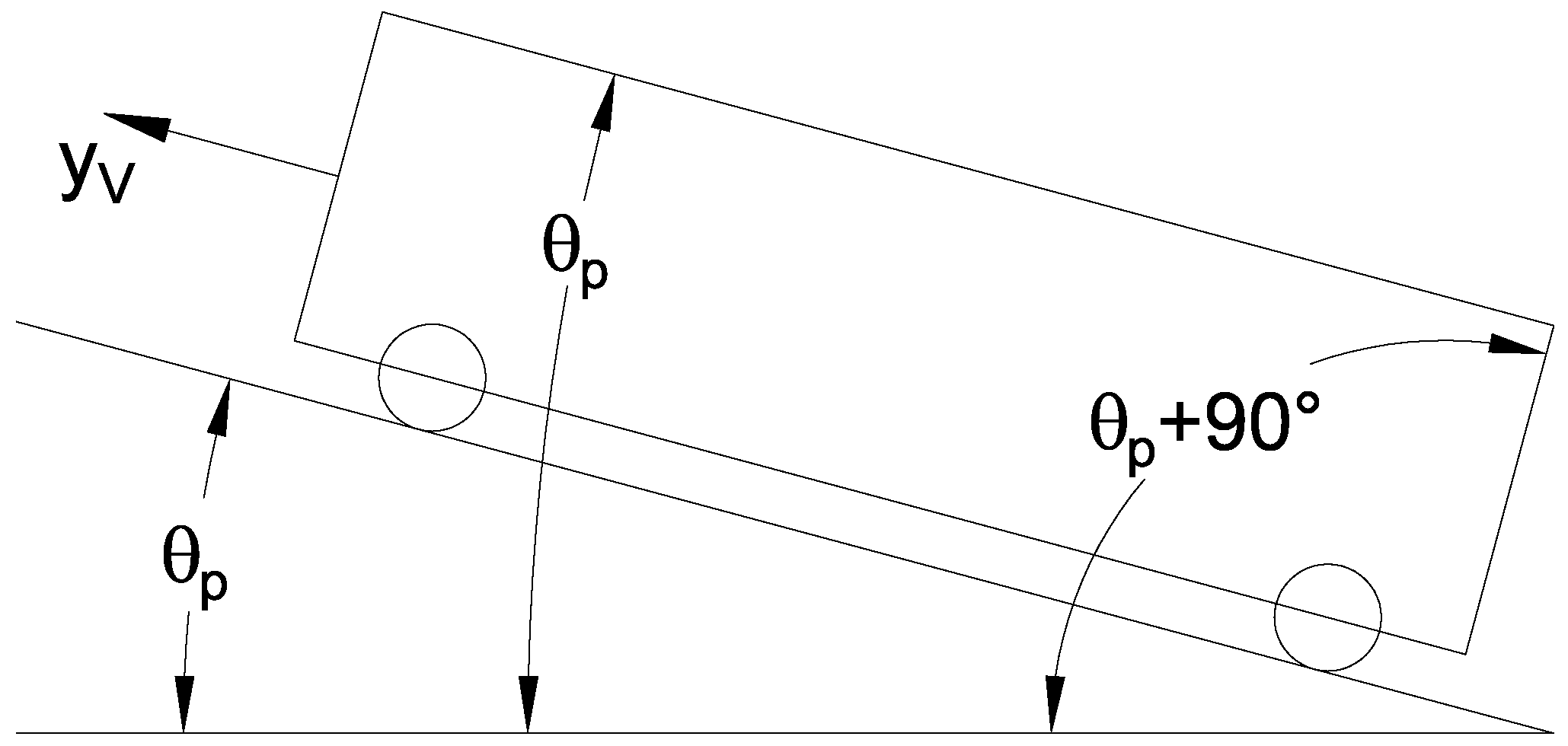
2.1. Vehicle Model
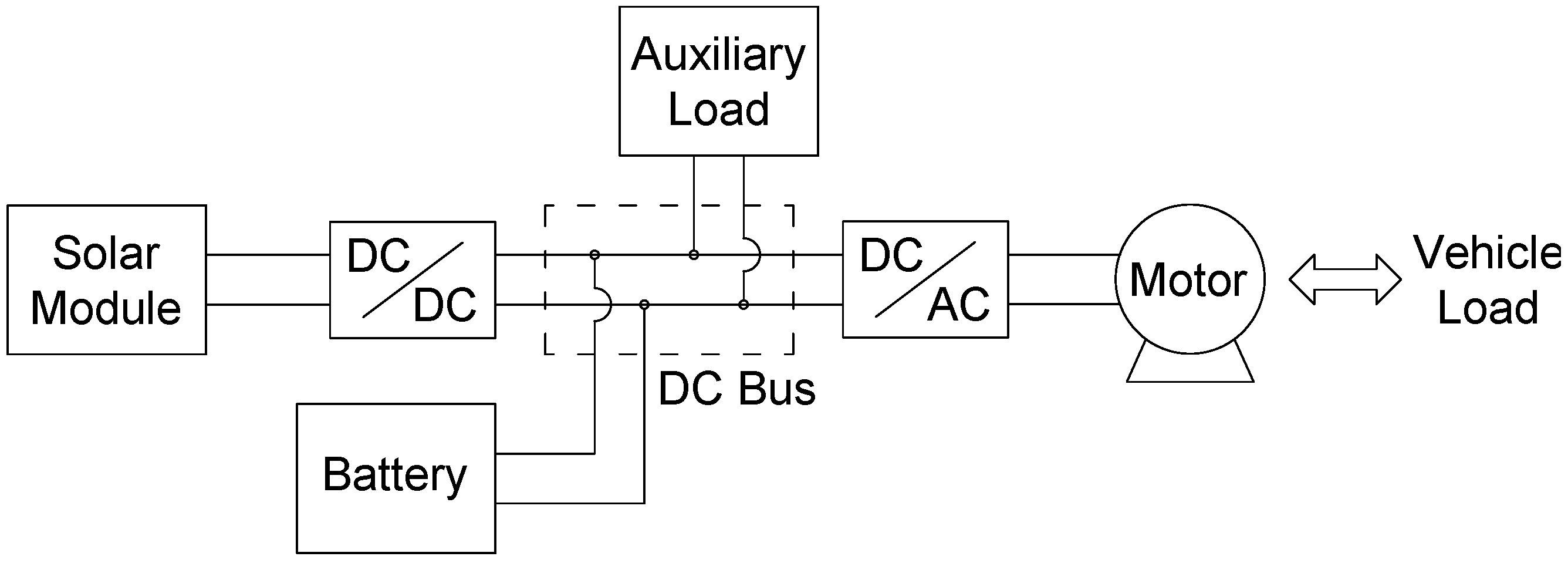
2.2. Motor and Power Electronics Model
2.3. Battery Model
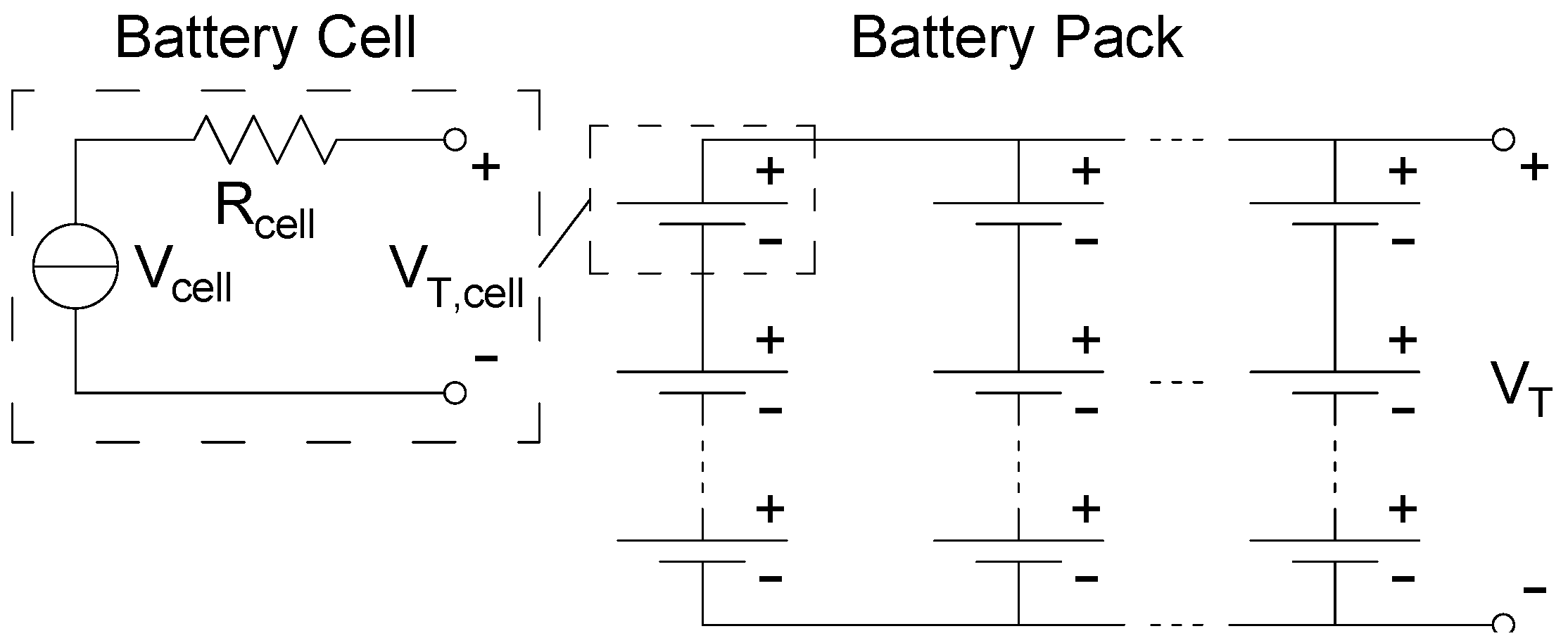
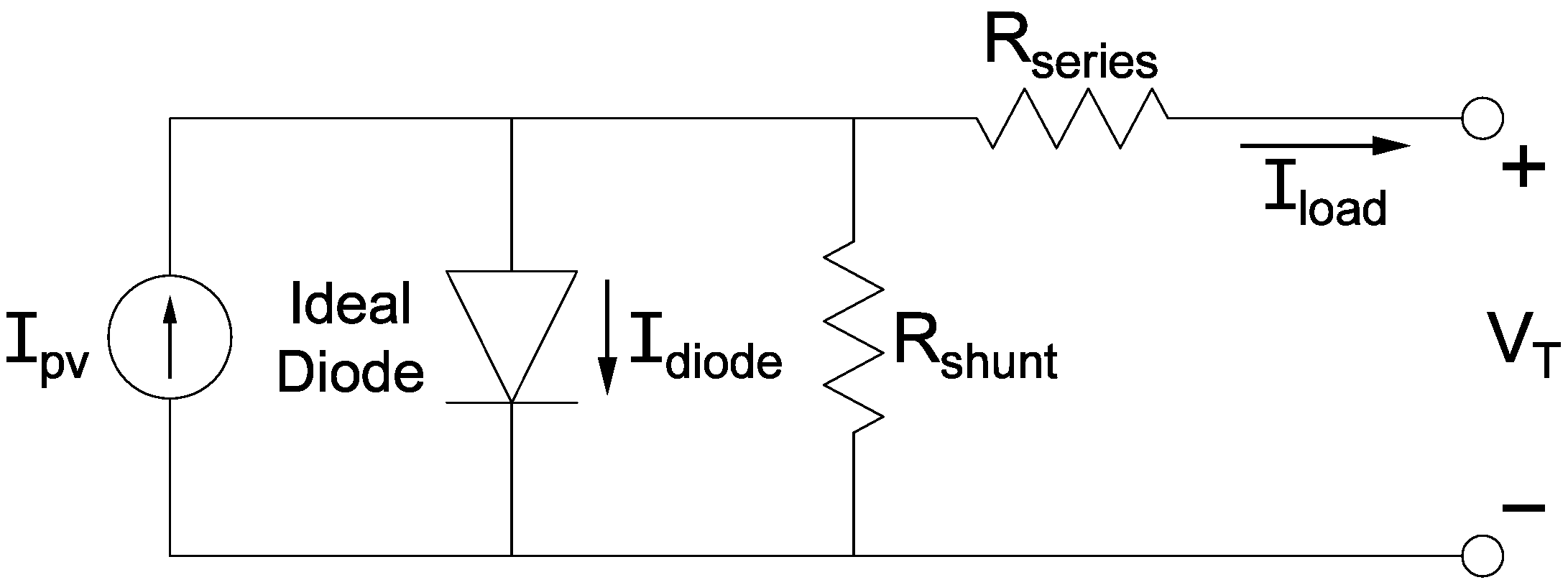
2.3.1. Battery Circuit Model
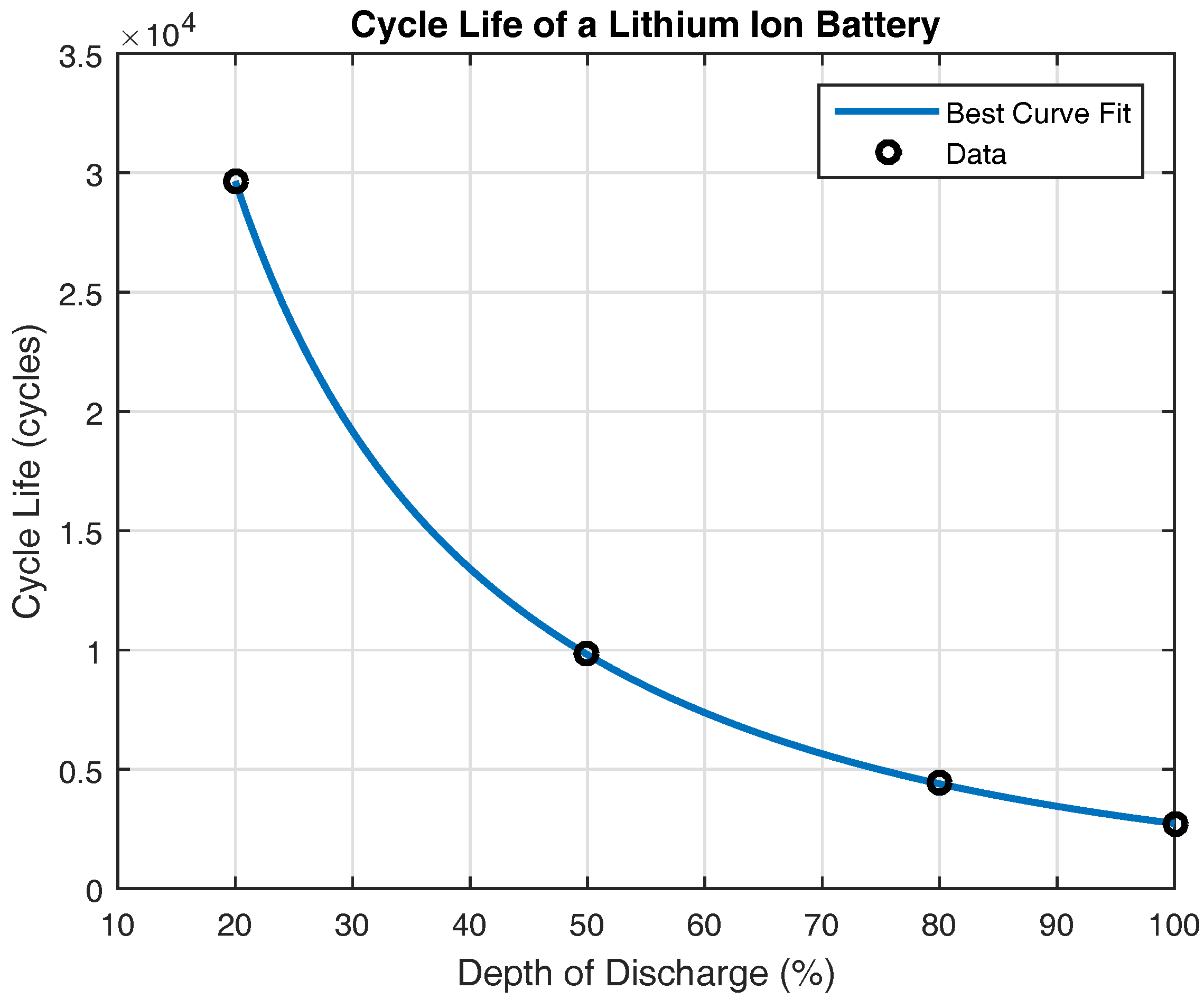
2.3.2. Battery Health Model
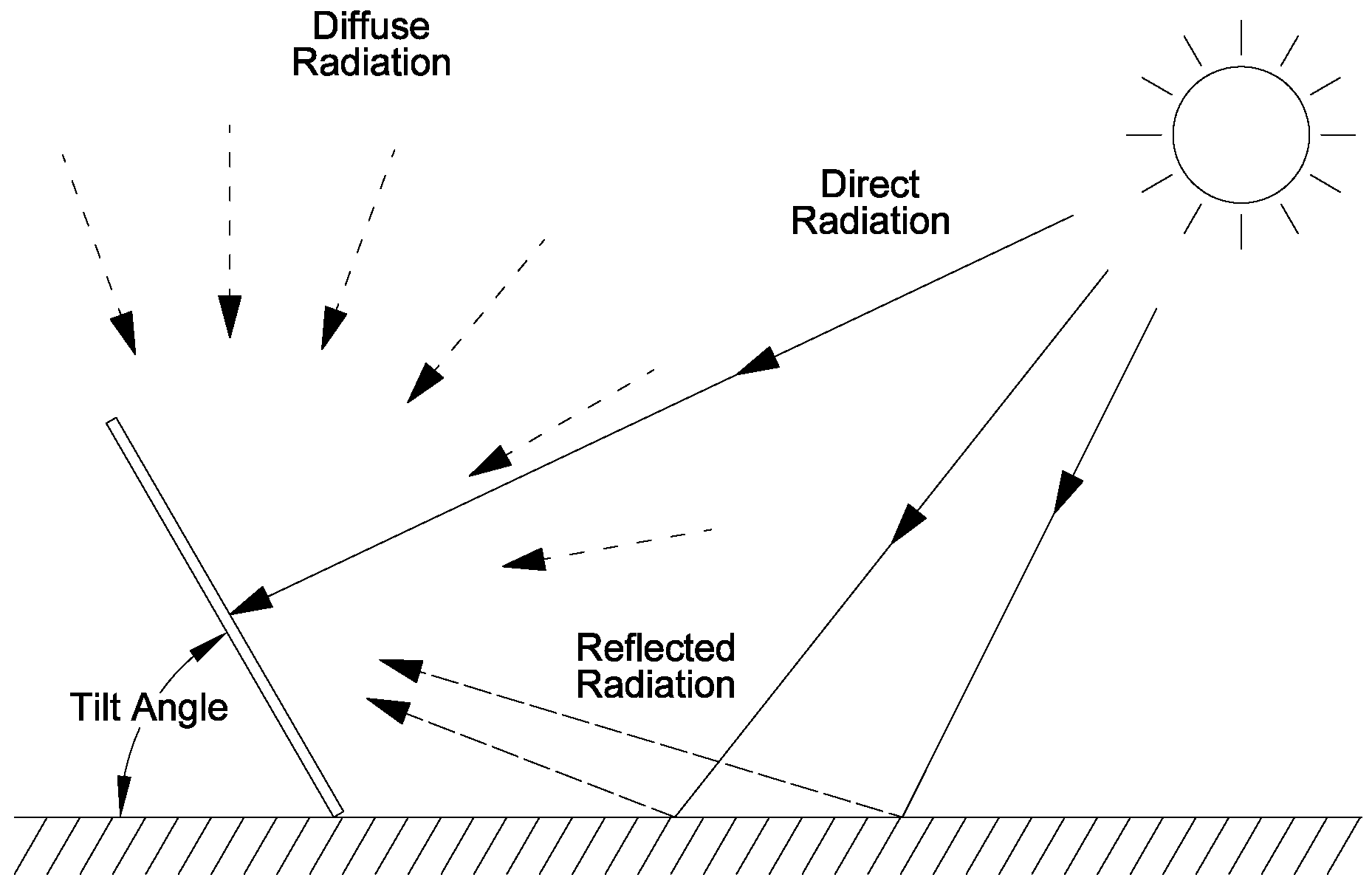
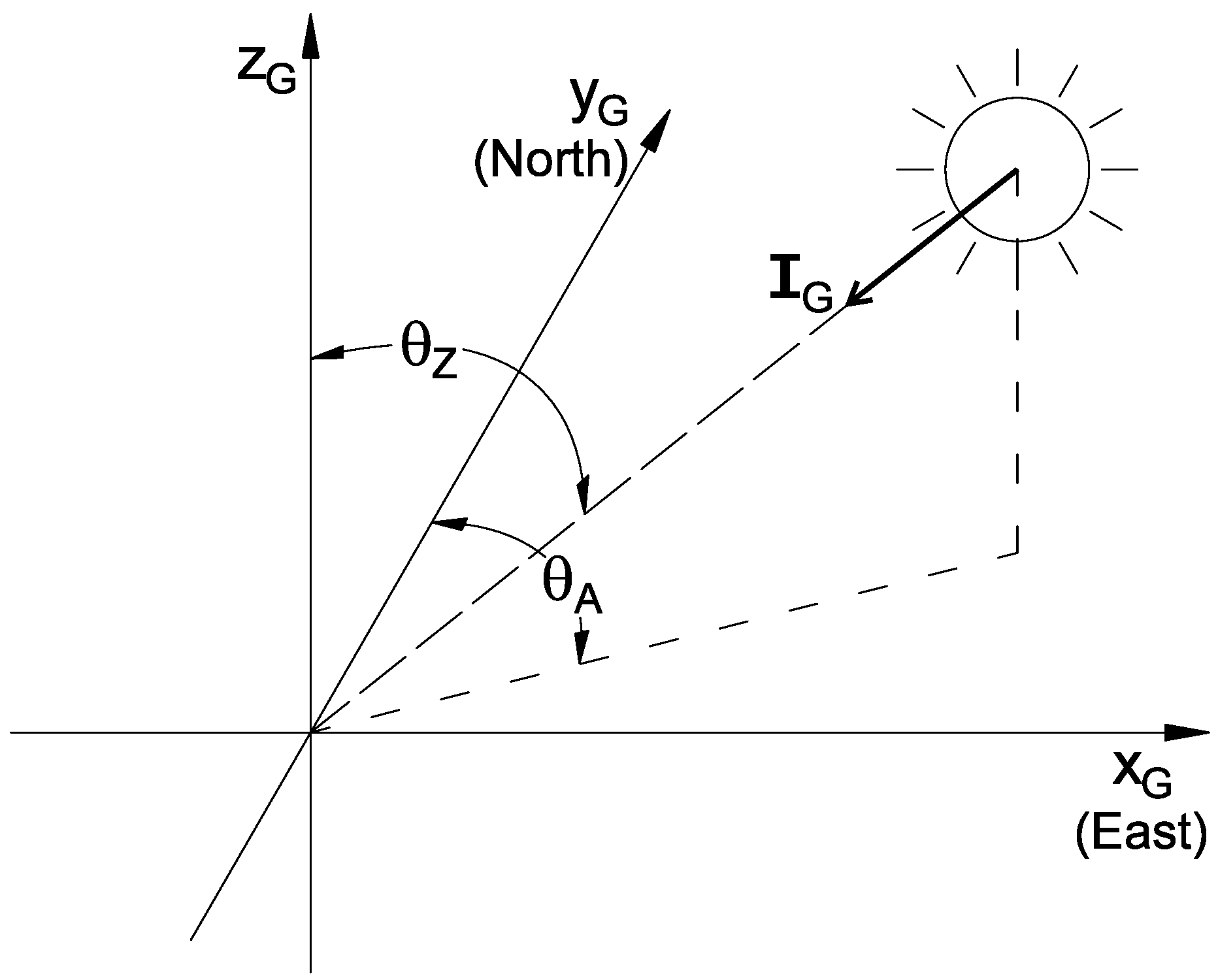
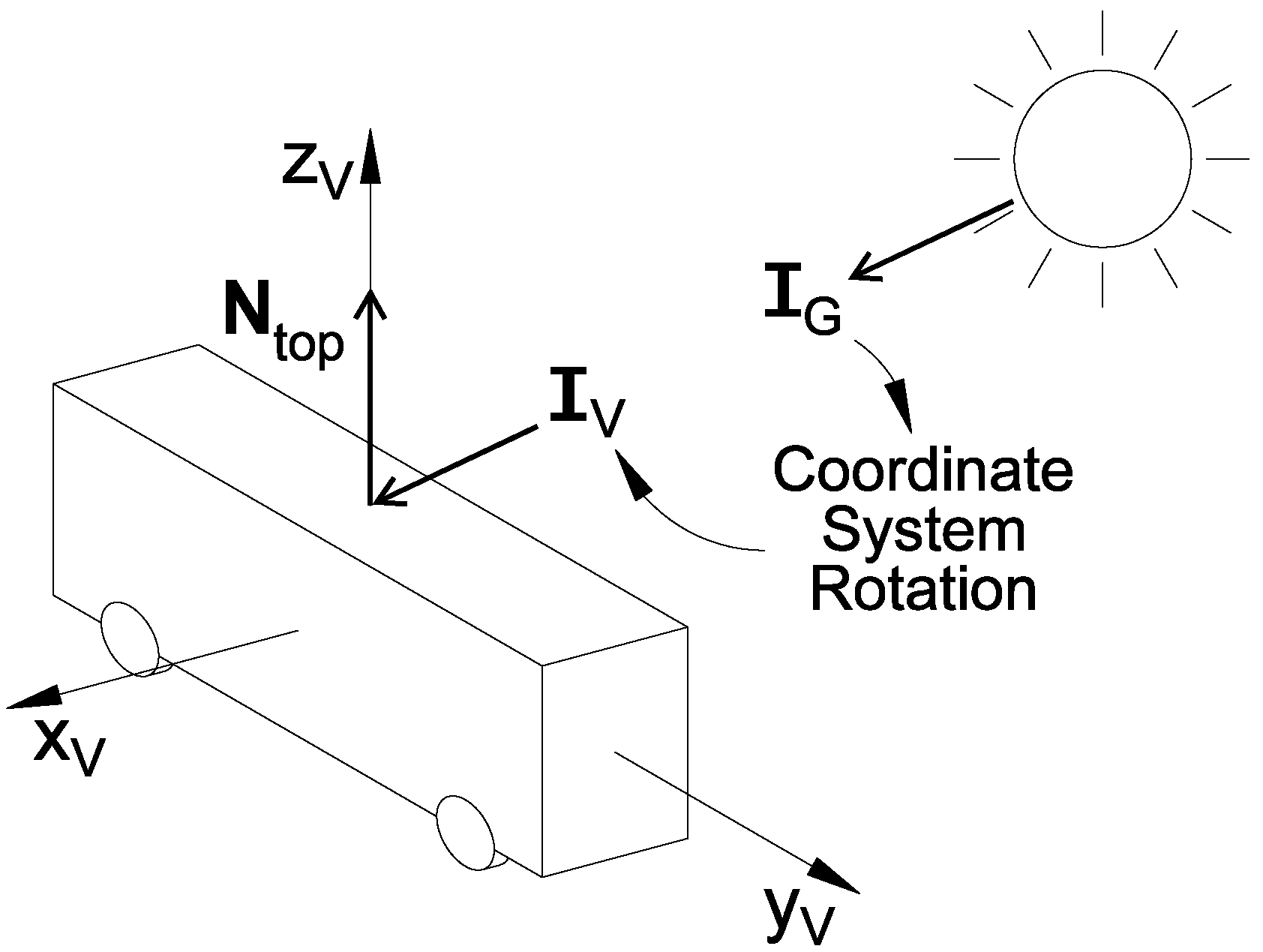
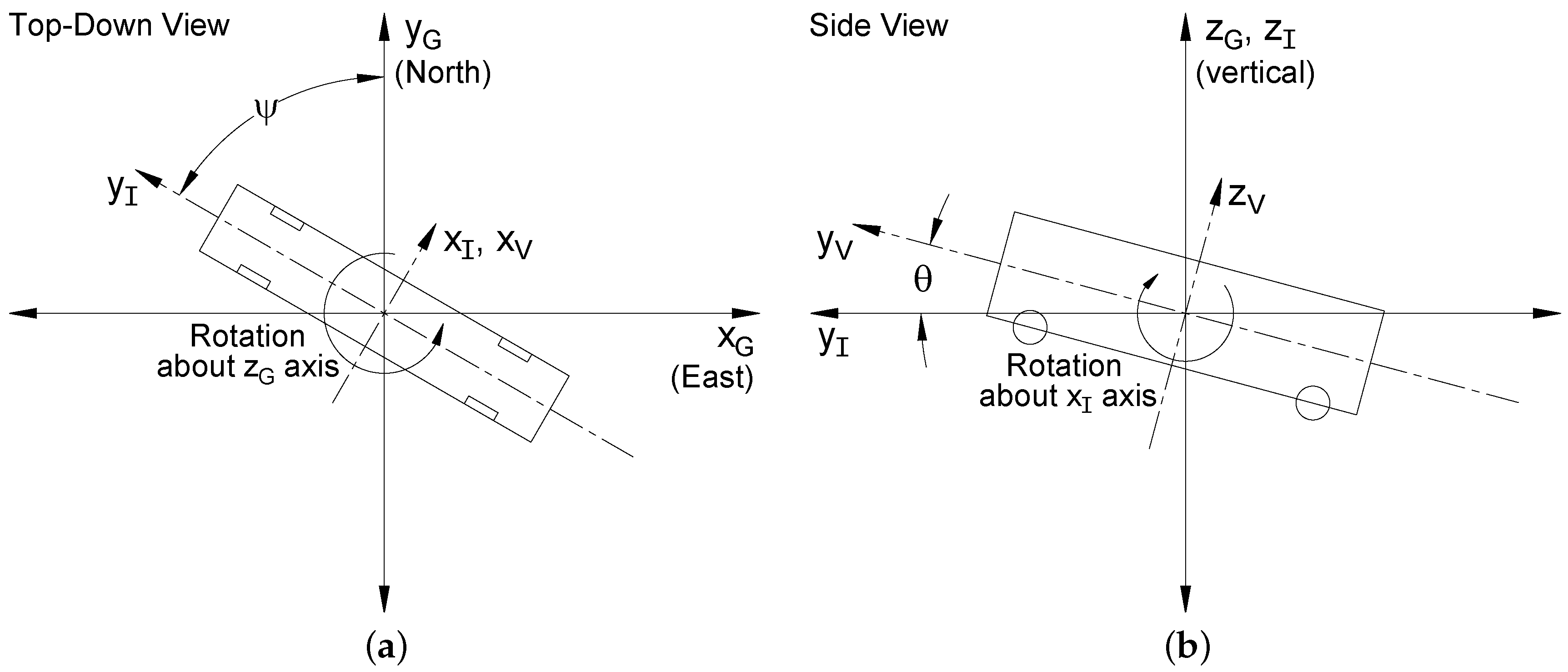
2.4. Solar Radiation and Photovoltaics Model
2.4.1. Module Sizing
2.4.2. Direct Radiation Model
2.4.3. Diffuse Radiation Model
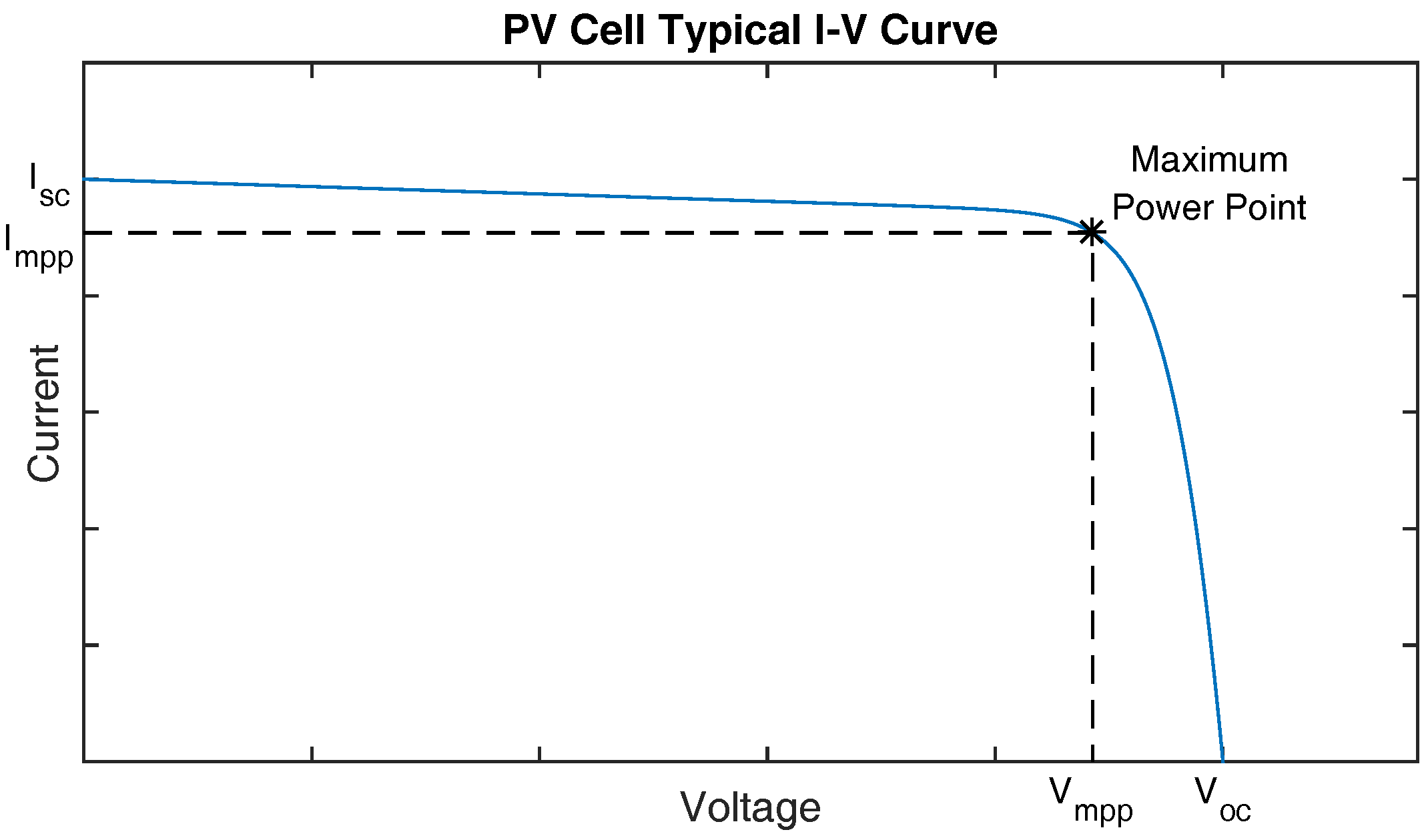
2.4.4. Efficiency Modeling
3. Case Study
3.1. Bus Configurations
3.2. Simulation Location
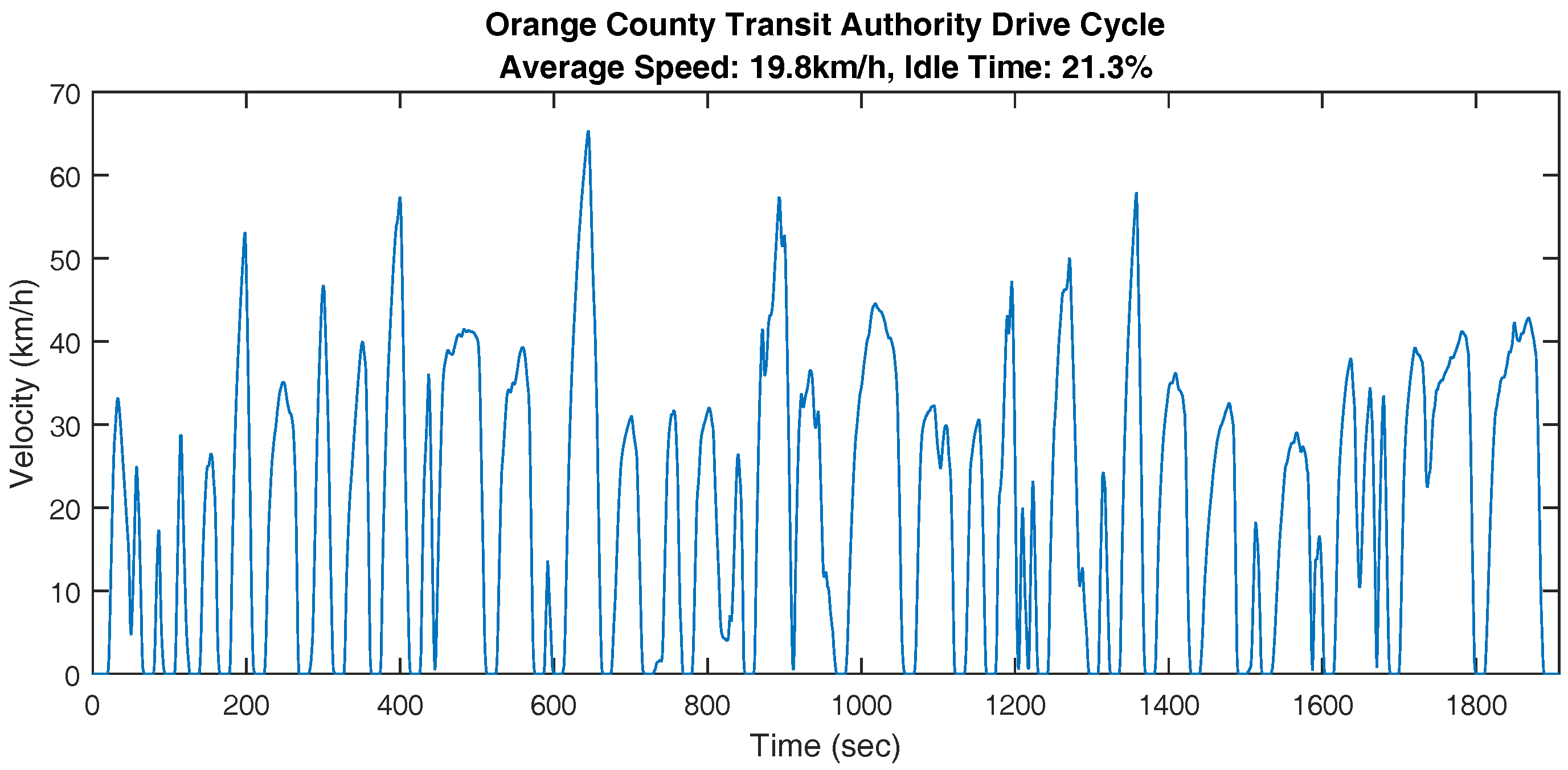
3.3. Drive Cycle
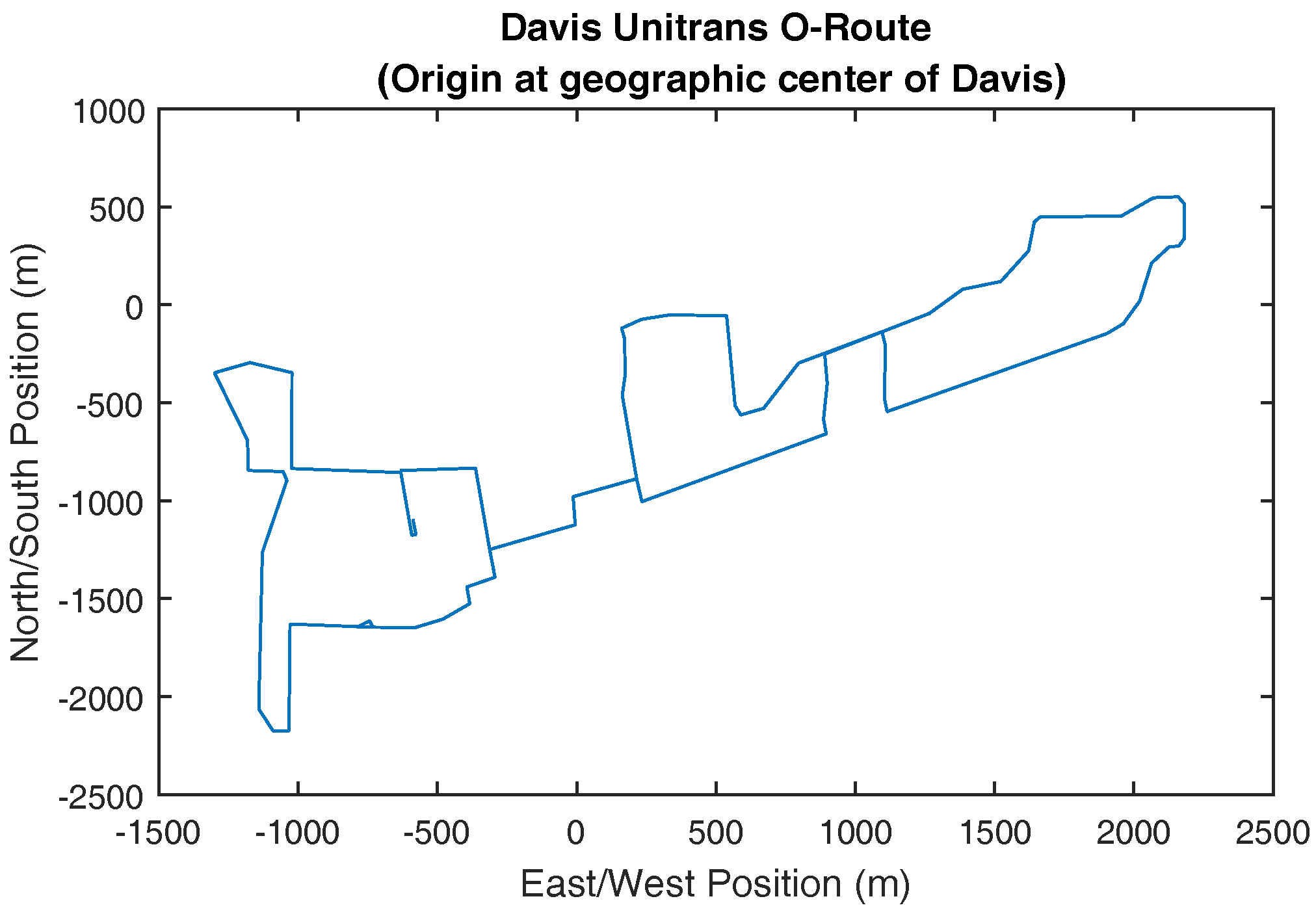
3.4. Route
3.5. Simulation Timespan
4. Results and Analysis
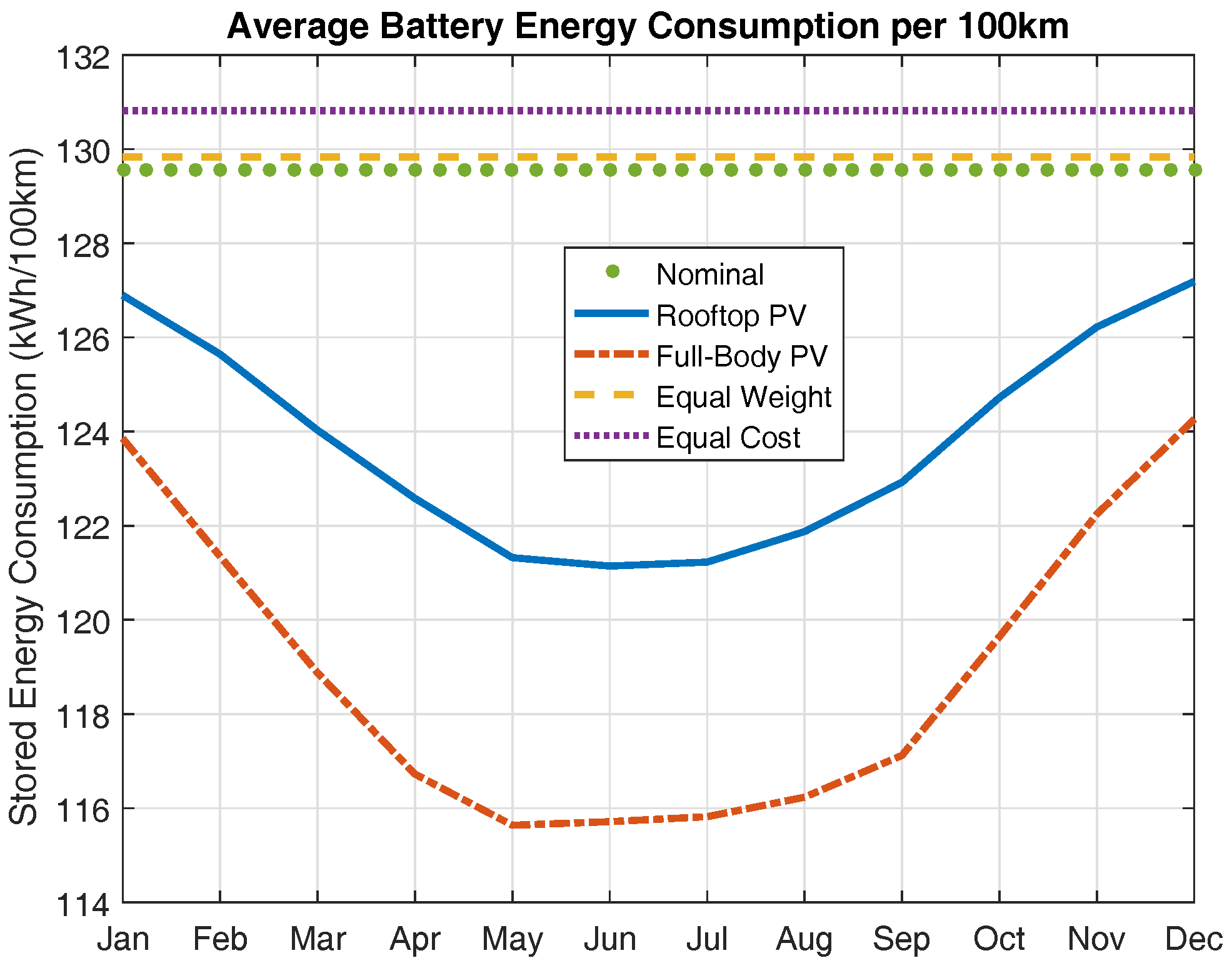
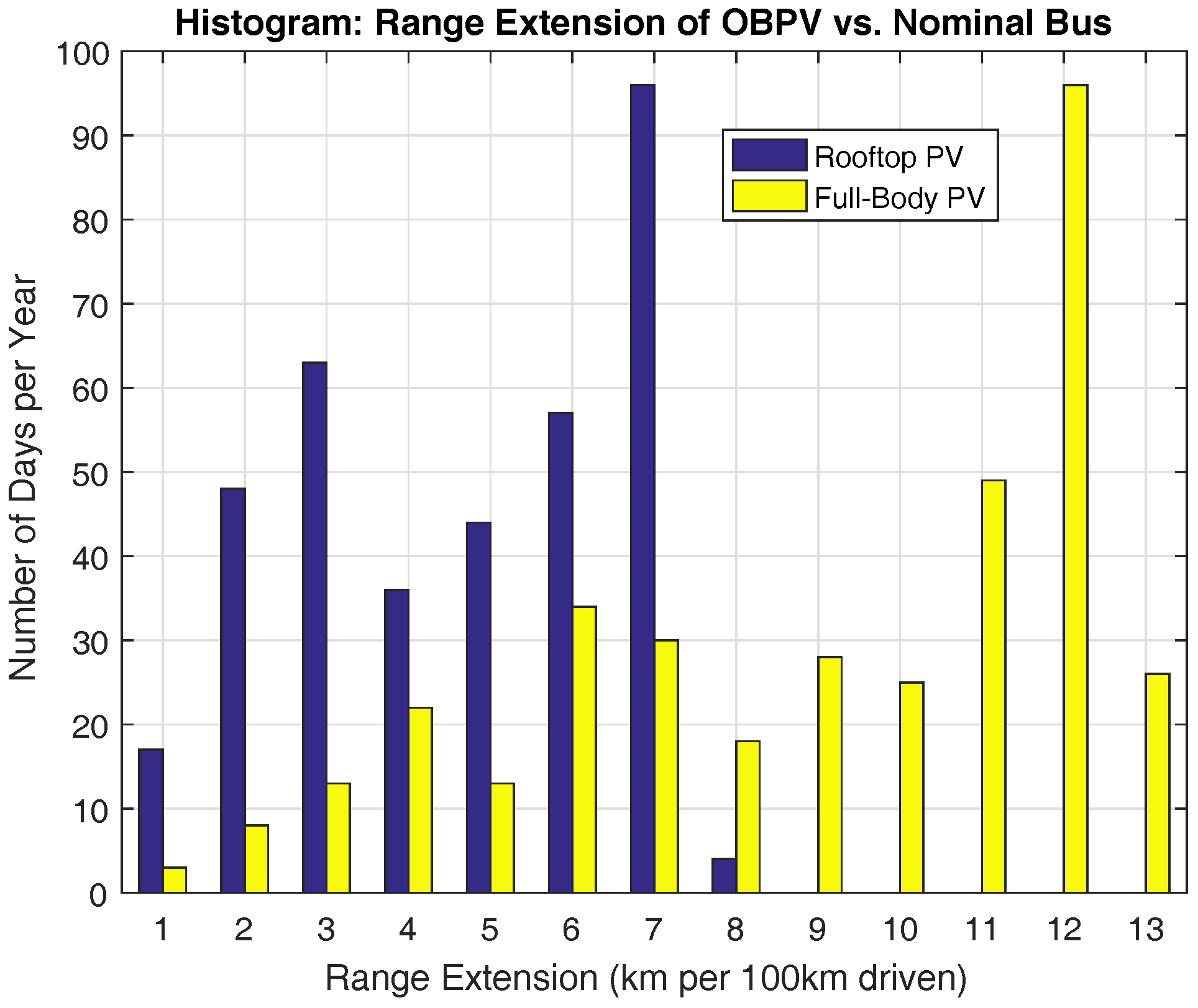
4.1. Range Extension
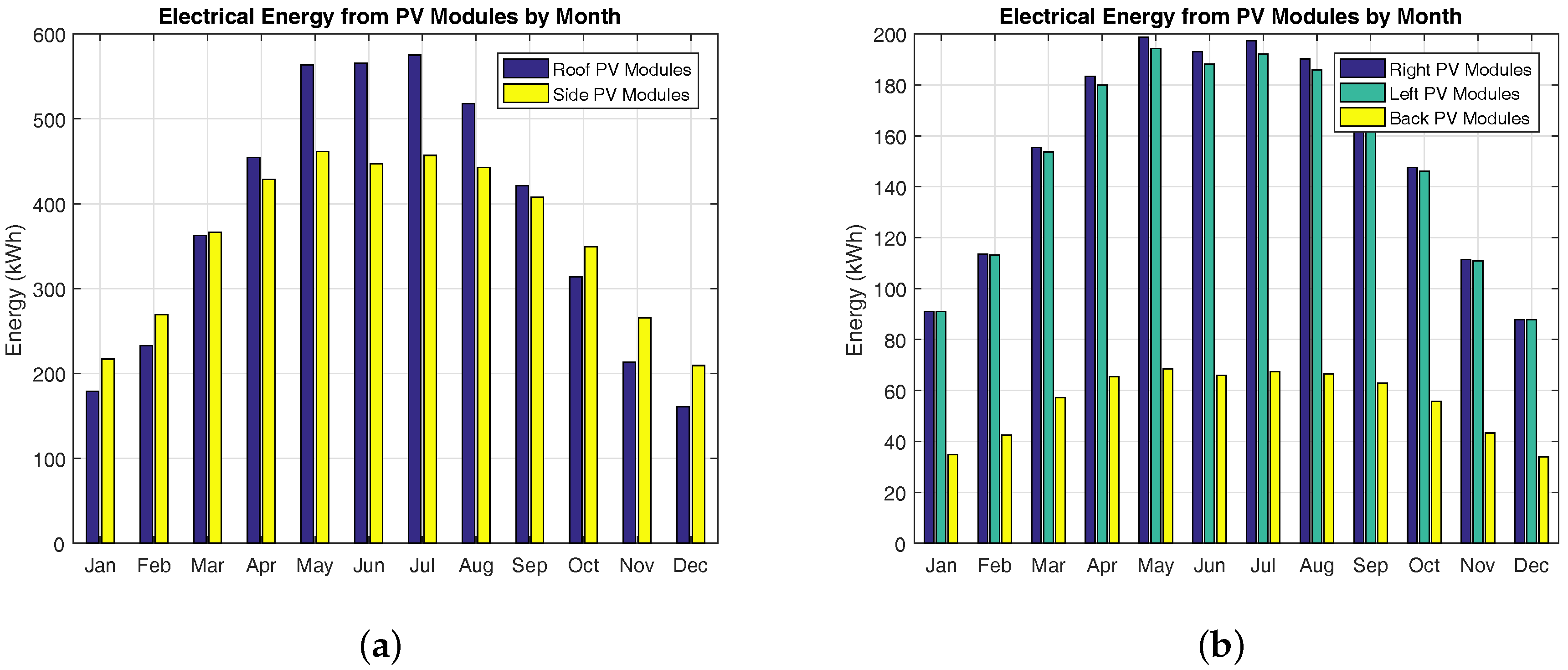
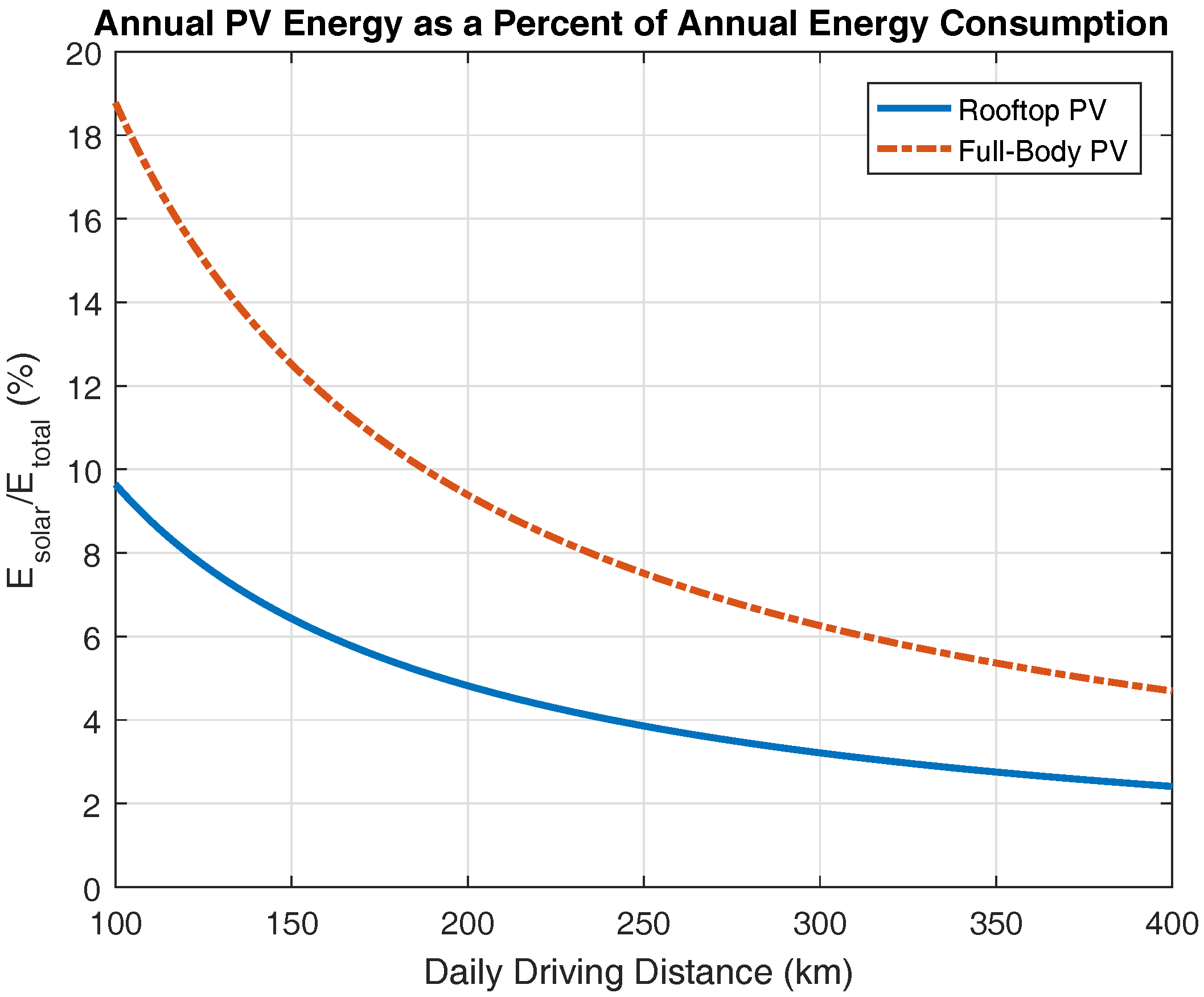
4.2. Photovoltaic Energy
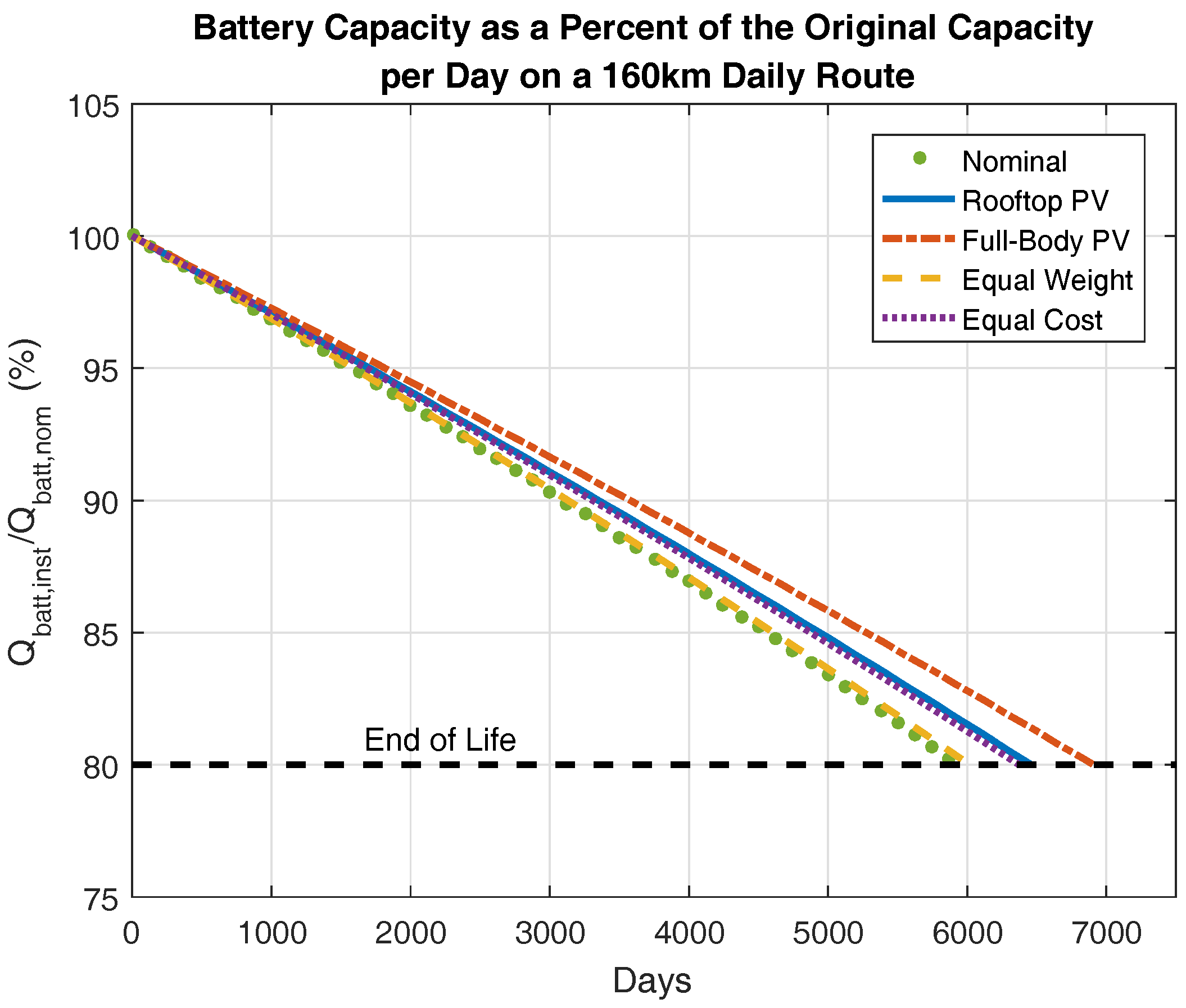
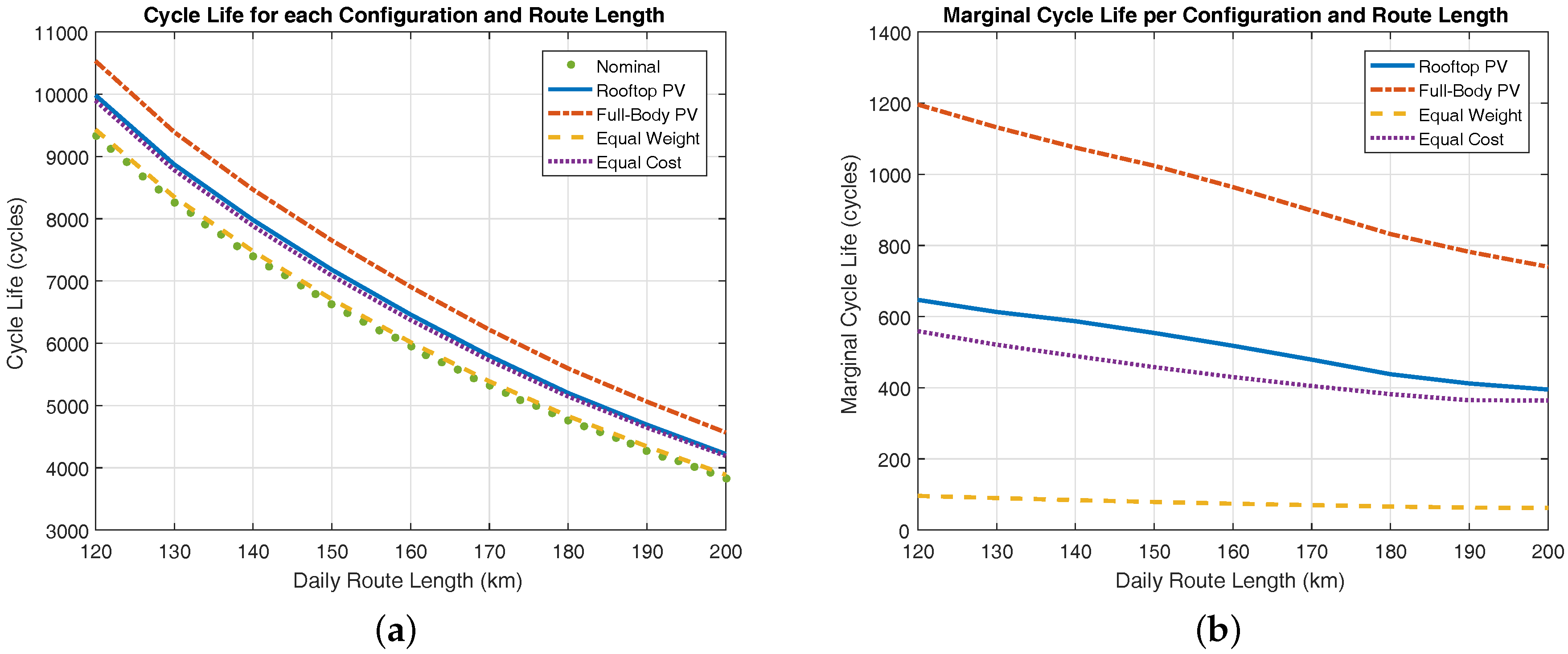
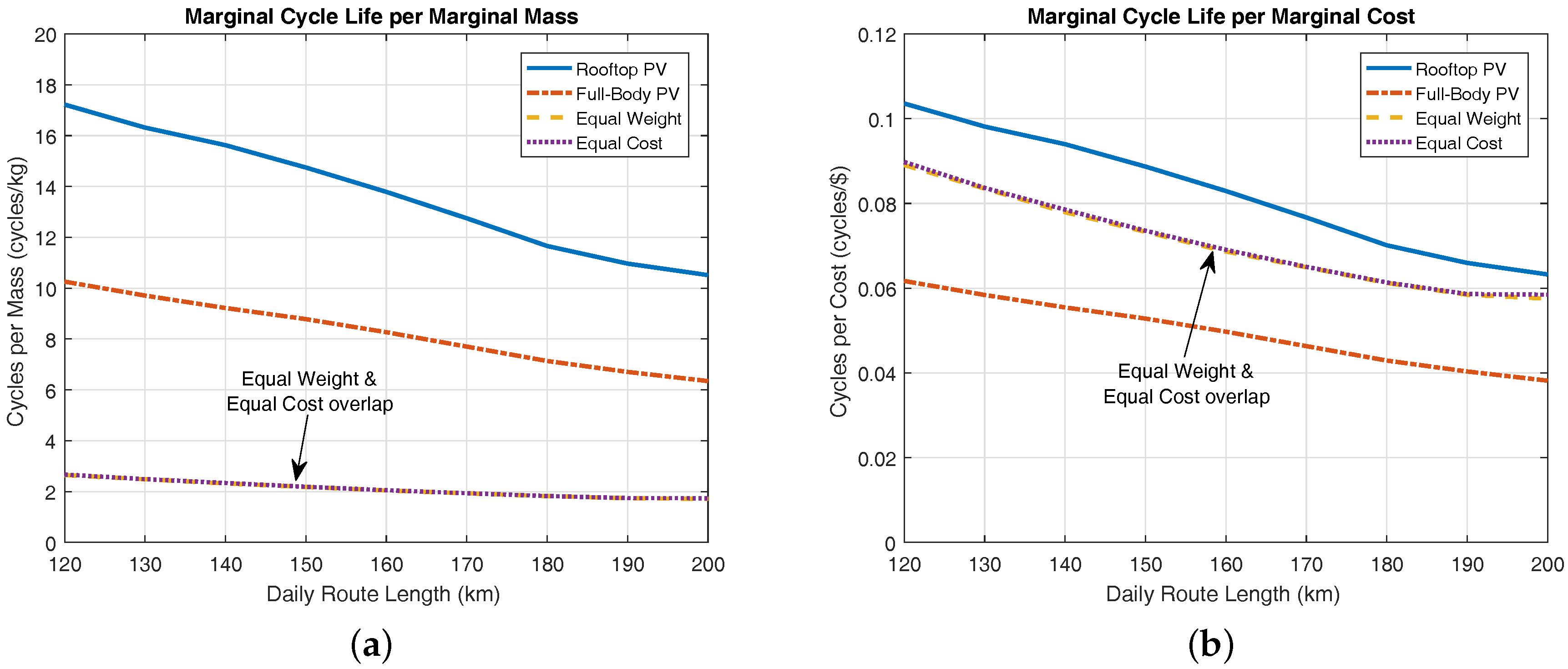
4.3. Battery Aging
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PV | Photovoltaics |
| OBPV | On-Board Photovoltaics |
| DC | Direct Current |
| AC | Alternating Current |
| OCV | Open-Circuit Voltage |
| SOC | State of Charge |
| DOD | Depth of Discharge |
| PM | Palmgren–Miner |
| CL | Cycle Life |
| TMY | Typical Meteorological Year |
| NREL | National Renewable Energy Lab |
| SPD | Surface Power Density |
| AD | Area Density |
| DNI | Direct Normal Irradiance |
| DHI | Diffuse Horizontal Irradiance |
| MPP | Maximum Power Point |
| SRC | Standard Reporting Conditions |
| NOCT | Nominal Operating Cell Temperature |
| OCTA | Orange County Transit Authority |
| ROI | Return On Investment |
References
- Abdel-Rahman, A.A. On the emissions from internal-combustion engines: A review. Int. J. Energy Res. 1998, 22, 483–513. [Google Scholar] [CrossRef]
- Yanowitz, J.; McCormick, R.L.; Graboski, M.S. In-Use Emissions from Heavy-Duty Diesel Vehicles. Environ. Sci. Technol. 2000, 34, 729–740. [Google Scholar] [CrossRef]
- Lee, T.K.; Filipi, Z. Impact of Model-Based Lithium-Ion Battery Control Strategy on Battery Sizing and Fuel Economy in Heavy-Duty HEVs. SAE Int. J. Commer. Veh. 2011, 4, 198–209. [Google Scholar] [CrossRef]
- Geca, M.; Wendeker, M.; Grabowski, L. A City Bus Electrification Supported by the Photovoltaic Power Modules; SAE Technical Paper; SAE International: Birmingham, UK, 2014. [Google Scholar]
- Abdel Dayem, A.M. Set-up and performance investigation of an innovative solar vehicle. J. Renew. Sustain. Energy 2012, 4, 033109:1–033109:18. [Google Scholar] [CrossRef]
- Kimura, K.; Kudo, Y.; Sato, A. Techno-Economic Analysis of Solar Hybrid Vehicles Part 1: Analysis of Solar Hybrid Vehicle Potential Considering Well -to-Wheel GHG Emissions; SAE Technical Paper; SAE International: Birmingham, UK, 2016. [Google Scholar]
- Hara, T.; Shiga, T.; Kimura, K.; Sato, A. Techno-Economic Analysis of Solar Hybrid Vehicles Part 2: Comparative Analysis of Economic, Environmental, and Usability Benefits; SAE Technical Paper; SAE International: Birmingham, UK, 2016. [Google Scholar]
- Abdelhamid, M. A Comprehensive Assessment Methodology Based on Life Cylce Analysis for On-Board Photovoltaic Solar Modeules in Vehicles. Ph.D. Thesis, Clemson University, Clemson, SC, USA, 2014. [Google Scholar]
- Giannouli, M.; Yianoulis, P. Study on the incorporation of photovoltaic systems as an auxiliary power source for hybrid and electric vehicles. Sol. Energy 2012, 86, 441–451. [Google Scholar] [CrossRef]
- Rizzo, G. Automotive Applications of Solar Energy. IFAC Proc. Vol. 2010, 43, 174–185. [Google Scholar] [CrossRef]
- Almonacid, G.; Muñoz, F.J.; de la Casa, J.; Aguilar, J.D. Integration of PV systems on health emergency vehicles. The FIVE project. Prog. Photovolt. Res. Appl. 2004, 12, 609–621. [Google Scholar] [CrossRef]
- Bahaj, A.S.; James, P.A.B. Economics of solar powered refrigeration transport applications. In Proceedings of the Conference Record of the Twenty-Ninth IEEE Photovoltaic Specialists Conference, New Orleans, LA, USA, 19–24 May 2002; IEEE: New Orleans, LA, USA, 2002; pp. 1561–1564. [Google Scholar]
- Kronthaler, L.; Maturi, L.; Moser, D.; Alberti, L. Vehicle-integrated Photovoltaic (ViPV) systems: Energy production, Diesel Equivalent, Payback Time; an assessment screening for trucks and busses. In Proceedings of the 2014 Ninth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 25–27 March 2014; pp. 1–8. [Google Scholar]
- Xue, J. Assessment of agricultural electric vehicles based on photovoltaics in China. J. Renew. Sustain. Energy 2013, 5, 6745–6759. [Google Scholar] [CrossRef]
- Azwan, M.B.; Norasikin, A.L.; Sopian, K.; Abd Rahim, S.; Norman, K.; Ramdhan, K.; Solah, D. Assessment of electric vehicle and photovoltaic integration for oil palm mechanisation practise. J. Clean. Prod. 2017, 140 Pt 3, 1365–1375. [Google Scholar] [CrossRef]
- Assadian, F.; Mallon, K.R.; Fu, B. The Impact of Vehicle-Integrated Photovoltaics on Heavy-Duty Electric Vehicle Battery Cost and Lifespan; SAE Technical Paper; SAE International: Birmingham, UK, 2016. [Google Scholar]
- Mohan, G.; Assadian, F.; Longo, S. Comparative analysis of forward-facing models vs backwardfacing models in powertrain component sizing. In Proceedings of the IET Hybrid and Electric Vehicles Conference 2013 (HEVC 2013), London, UK, 6–7 November 2013; pp. 1–6. [Google Scholar]
- Guzzella, L.; Sciarretta, A. Vehicle Propulsion Systems, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zeng, X.; Yang, N.; Wang, J.; Song, D.; Zhang, N.; Shang, M.; Liu, J. Predictive-model-based dynamic coordination control strategy for power-split hybrid electric bus. Mech. Syst. Signal Process. 2015, 60–61, 785–798. [Google Scholar] [CrossRef]
- Sangtarash, F.; Esfahanian, V.; Nehzati, H.; Haddadi, S.; Bavanpour, M.A.; Haghpanah, B. Effect of Different Regenerative Braking Strategies on Braking Performance and Fuel Economy in a Hybrid Electric Bus Employing CRUISE Vehicle Simulation. SAE Int. J. Fuels Lubr. 2008, 1, 828–837. [Google Scholar] [CrossRef]
- Wang, B.; Luo, Y.; Zhang, J. Simulation of city bus performance based on actual urban driving cycle in China. Int. J. Automot. Technol. 2008, 9, 501–507. [Google Scholar] [CrossRef]
- Proterra. Catalyst 40-Foot Transit Vehicle. Available online: https://www.proterra.com/products/catalyst-40ft/ (accessed on 10 March 2017).
- Lesster, L.E.; Lindberg, F.A.; Young, R.M.; Hall, W.B. An Induction Motor Power Train for EVs—The Right Power at the Right Price. In Advanced Components for Electric and Hybrid Electric Vehicles: Workshop Proceedings; Stricklett, K.L., Ed.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1993; pp. 170–173. [Google Scholar]
- He, H.; Xiong, R.; Fan, J. Evaluation of Lithium-Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Valence Technology, Inc. Lithium Iron Magnesium Phosphate 26650 Power Cell. 2016. Available online: https://www.valence.com/products/cells/26650-power-cells/ (accessed on 10 March 2017).
- Saw, L.H.; Somasundaram, K.; Ye, Y.; Tay, A.A.O. Electro-thermal analysis of Lithium Iron Phosphate battery for electric vehicles. J. Power Sources 2014, 249, 231–238. [Google Scholar] [CrossRef]
- Williamson, S.S. Energy Management Strategies for Electric and Plug-In Hybrid Electric Vehicles; Springer: New York, NY, USA, 2013. [Google Scholar]
- Valence Technology, Inc. Valence Module Range. Available online: https://www.valence.com/wp-content/uploads/2016/11/Valence-Module-Range-113016.pdf (accessed on 10 March 2017).
- Nelson, R.F. Power requirements for batteries in hybrid electric vehicles. J. Power Sources 2000, 91, 2–26. [Google Scholar] [CrossRef]
- DiOrio, N.; Dobos, A.; Janzou, S.; Nelson, A.; Lundstrom, B. Technoeconomic Modeling of Battery Energy Storage in SAM; Technical Report NREL/TP-6A20–64641; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2015. [Google Scholar]
- Ramadesigan, V.; Northrop, P.W.C.; De, S.; Santhanagopalan, S.; Braatz, R.D.; Subramanian, V.R. Modeling and Simulation of Lithium-Ion Batteries from a Systems Engineering Perspective. J. Electrochem. Soc. 2012, 159, R31–R45. [Google Scholar] [CrossRef]
- Pelletier, S.; Jabali, O.; Laporte, G.; Veneroni, M. Battery degradation and behaviour for electric vehicles: Review and numerical analyses of several models. Transp. Res. Part B Methodol. 2017. [Google Scholar] [CrossRef]
- Safari, M.; Morcrette, M.; Teyssot, A.; Delacourt, C. Life-Prediction Methods for Lithium-Ion Batteries Derived from a Fatigue Approach I. Introduction: Capacity-Loss Prediction Based on Damage Accumulation. J. Electrochem. Soc. 2010, 157, A713–A720. [Google Scholar] [CrossRef]
- Valence Technology, Inc. Long Cycle Life Lithium Iron Magnesium Phosphate Battery. 2014. Available online: https://www.valence.com/why-valence/long-lifecycle/ (accessed on 10 March 2017).
- Zhou, C.; Qian, K.; Allan, M.; Zhou, W. Modeling of the Cost of EV Battery Wear Due to V2G Application in Power Systems. IEEE Trans. Energy Convers. 2011, 26, 1041–1050. [Google Scholar] [CrossRef]
- Marano, V.; Onori, S.; Guezennec, Y.; Rizzoni, G.; Madella, N. Lithium-ion batteries life estimation for plug-in hybrid electric vehicles. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–11 September 2009; pp. 536–543. [Google Scholar]
- Millner, A. Modeling Lithium Ion battery degradation in electric vehicles. In Proceedings of the 2010 IEEE Conference on Innovative Technologies for an Efficient and Reliable Electricity Supply, Waltham, MA, USA, 27–29 September 2010; pp. 349–356. [Google Scholar]
- Ma, C.C.Y.; Iqbal, M. Statistical comparison of solar radiation correlations Monthly average global and diffuse radiation on horizontal surfaces. Sol. Energy 1984, 33, 143–148. [Google Scholar] [CrossRef]
- Tracy, C.R.; Hammond, K.A.; Lechleitner, R.A.; Smith, W.J.; Thompson, D.B.; Whicker, A.D.; Williamson, S.C. Estimating clear-day solar radiation: An evaluation of three models. J. Therm. Biol. 1983, 8, 247–251. [Google Scholar] [CrossRef]
- Wilcox, S.; Marion, W. Users Manual for TMY3 Data Sets; Technical Report NREL/TP-581-43156; National Renewable Energy Laboratory: Golden, CO, USA, 2008.
- Arsie, I.; Marotta, M.; Pianese, C.; Rizzo, G.; Sorrentino, M. Optimal Design of a Hybrid Electric Car with Solar Cells. In Proceedings of the 1st AUTOCOM Workshop on Preventive and Active Safety Systems for Road Vehicles, Istanbul, Turkey, 19–20 September 2005. [Google Scholar]
- Emery, K. Measurement and Characterization of Solar Cells and Modules. In Handbook of Photovoltaic Science and Engineering, 2nd ed.; Luque, A., Hegedus, S., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2011; pp. 797–840. [Google Scholar]
- HighFlex Solar, Inc. HF315-6-36b. Available online: http://www.highflexsolar.com/docs/HighFlexSolar_HF315-6-36b_Datasheet_v1.0.pdf (accessed on 10 March 2017).
- Reda, I.; Andreas, A. Solar position algorithm for solar radiation applications. Sol. Energy 2004, 76, 577–589. [Google Scholar] [CrossRef]
- Loutzenhiser, P.G.; Manz, H.; Felsmann, C.; Strachan, P.A.; Frank, T.; Maxwell, G.M. Empirical validation of models to compute solar irradiance on inclined surfaces for building energy simulation. Sol. Energy 2007, 81, 254–267. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Jain, A.; Kapoor, A. Exact analytical solutions of the parameters of real solar cells using Lambert W-function. Sol. Energy Mater. Sol. Cells 2004, 81, 269–277. [Google Scholar] [CrossRef]
- Esram, T.; Chapman, P.L. Comparison of Photovoltaic Array Maximum Power Point Tracking Techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef]
- Bidram, A.; Davoudi, A.; Balog, R.S. Control and Circuit Techniques to Mitigate Partial Shading Effects in Photovoltaic Arrays. IEEE J. Photovolt. 2012, 2, 532–546. [Google Scholar] [CrossRef]
- Emery, K.; Burdick, J.; Caiyem, Y.; Dunlavy, D.; Field, H.; Kroposki, B.; Moriarty, T.; Ottoson, L.; Rummel, S.; Strand, T.; et al. Temperature dependence of photovoltaic cells, modules and systems. In Proceedings of the Conference Record of the Twenty Fifth IEEE Photovoltaic Specialists Conference, Washington, DC, USA, 13–17 May 1996; pp. 1275–1278. [Google Scholar]
- Muller, M. Measuring and Modeling Nominal Operating Cell Temperature (NOCT). Proceedings of PV Performance Modeling Workshop, Albuquerque, NM, USA, 22–23 September 2010. [Google Scholar]
- McCrone, A.; Moslener, U.; d’Estais, F.; Usher, E.; Grüning, C. Global Trends in Renewable Energy Investment 2016; FS-UNEP Collaborating Centre for Climate & Sustainable Energy Finance: Frankfurt am Main, Germany, 2016. [Google Scholar]
- Kahn, S.; Shiao, M.J.; Honeyman, C.; Perea, A.; Jones, J.; Smith, C.; Gallagher, B.; Moskowitz, S.; Baca, J.; Rumery, S.; et al. Solar Market Insight Report 2016 Q2; Solar Energy Industries Association: Washington, DC, USA, 2016. [Google Scholar]
- National Renewable Energy Laboratory. Dynamic Maps, GIS Data, and Analysis Tools—Solar Maps. Available online: http://www.nrel.gov/gis/solar.html (accessed on 10 March 2017).
- National Renewable Energy Laboratory. National Solar Radiation Data Base, and Analysis Tools—Solar Maps. Available online: http://rredc.nrel.gov/solar/old_data/nsrdb/1991-2005/tmy3/by_state_and_city.html (accessed on 23 May 2017).
- California Air Resource Board. Public Transit Bus Fleet Rule and Emission Standards for New Urban Buses. Available online: https://www.arb.ca.gov/regact/bus02/bus02.htm (accessed on 10 March 2017).
- Pacific Gas and Electric Company. Electric Rates. Available online: https://www.pge.com/tariffs/electric.shtml (accessed on 15 April 2017).


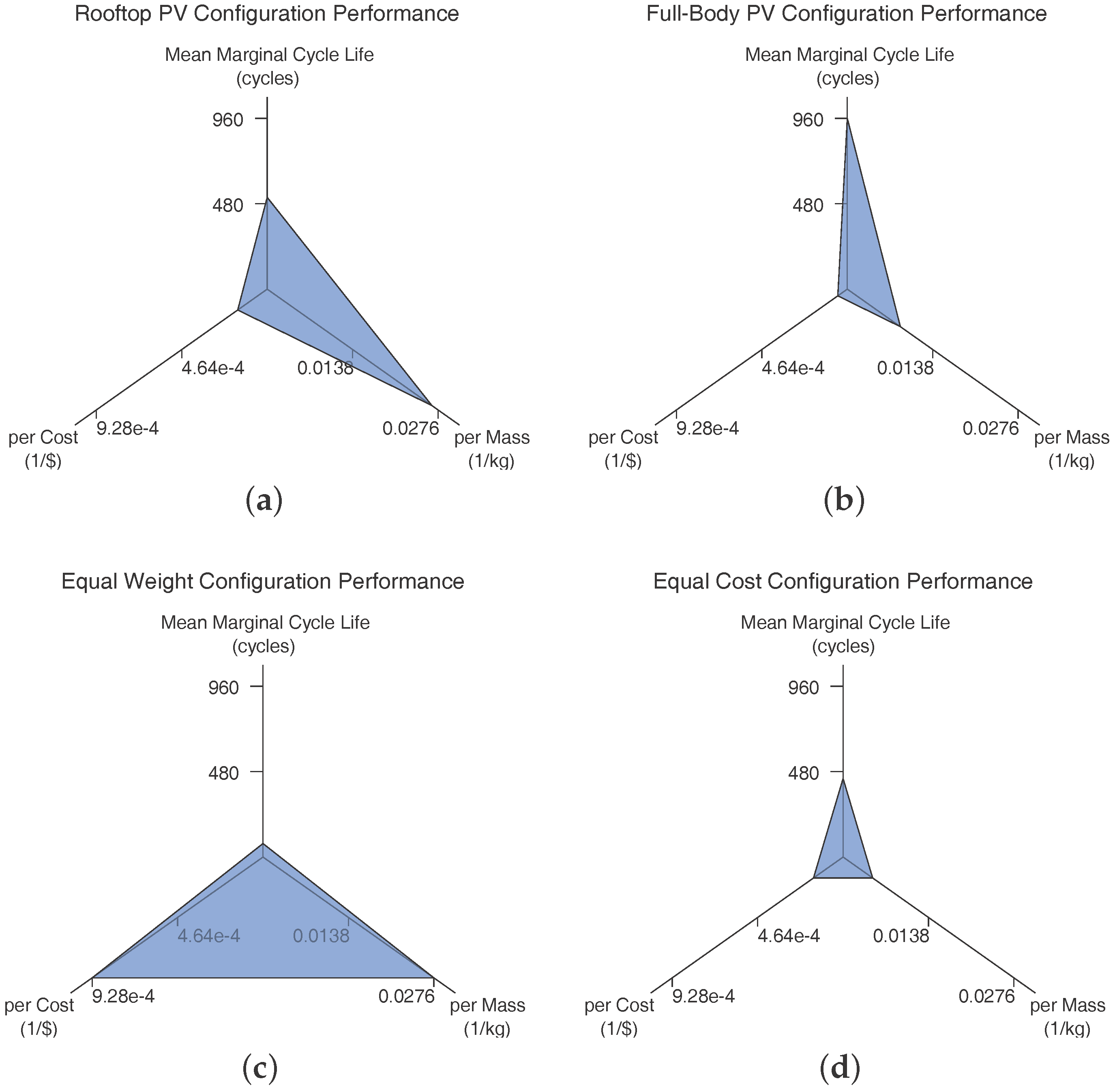
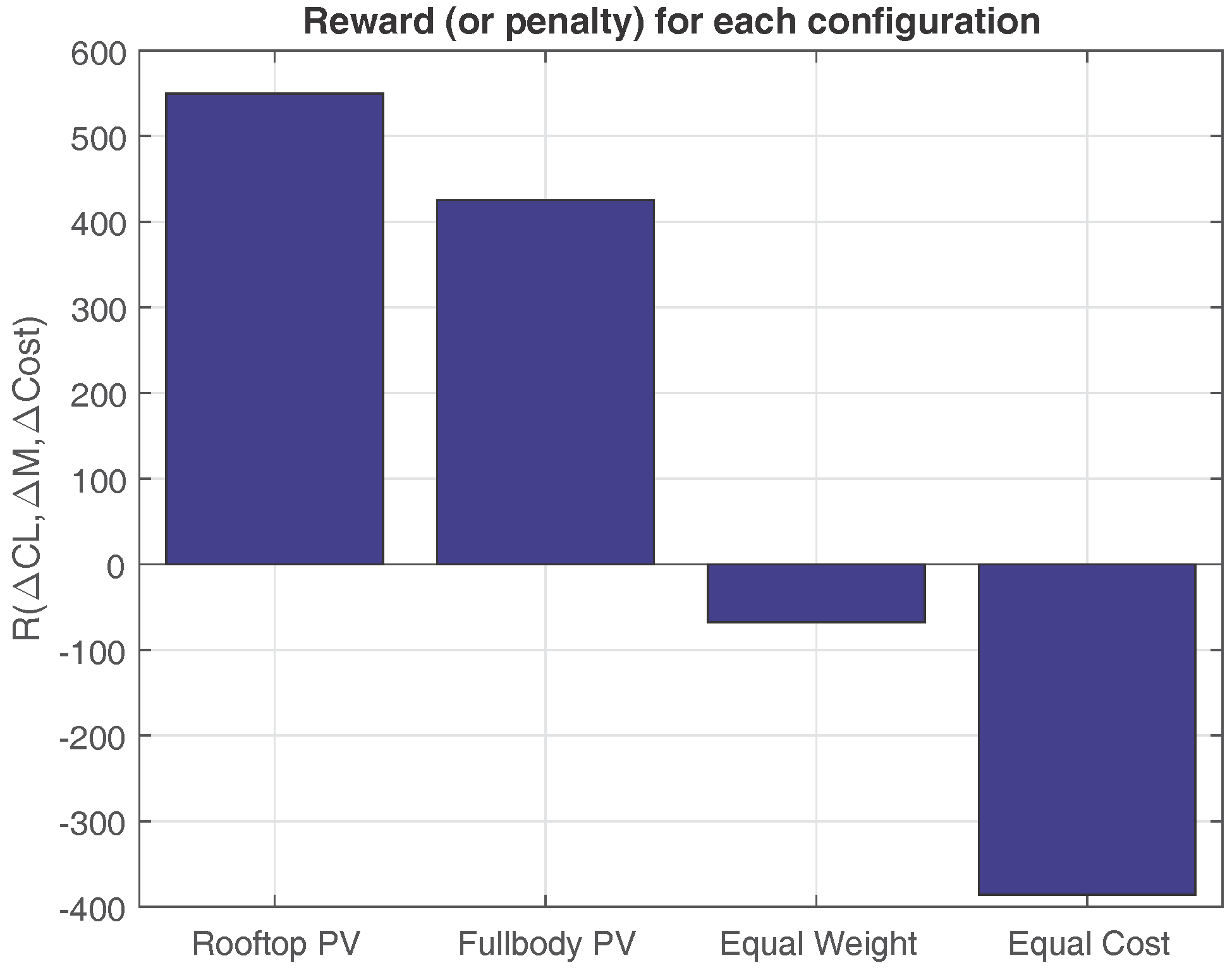
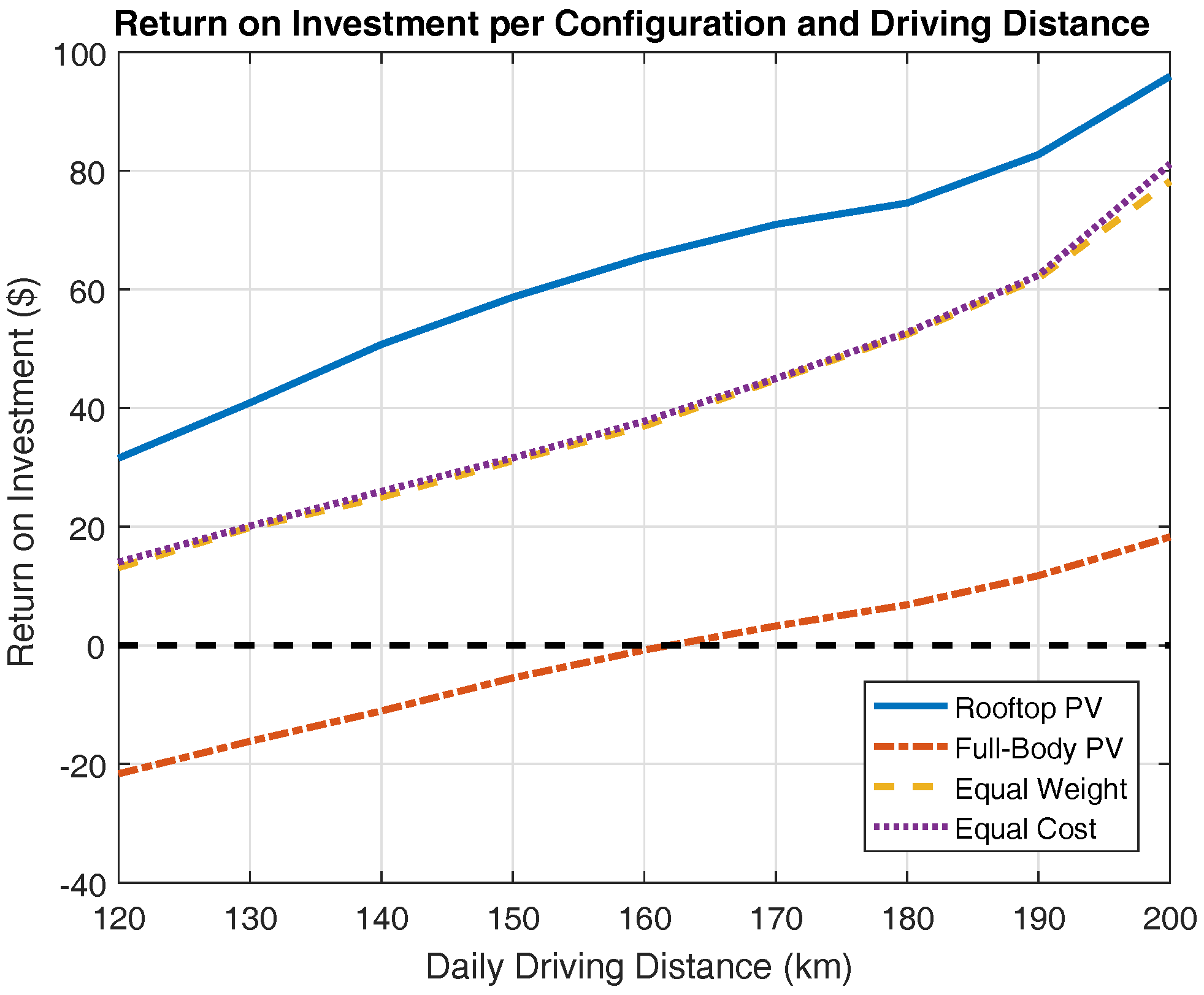
| Parameter | Variable | Value |
|---|---|---|
| Vehicle Mass | 15,500 kg | |
| Frontal Area | 8.02 m | |
| Aerodynamic Drag Coefficient | 0.55 | |
| Rolling Resistance Coefficient | 0.008 | |
| Wheel Inertia | 20.52 kg-m | |
| Motor Inertia | 0.277 kg-m | |
| Wheel Radius | 0.48 m | |
| Final Drive Ratio | 5.5:1 | |
| Gearbox Ratio | 5:1 | |
| Transmission Efficiency | 96% |
| Parameter | Variable | Value |
|---|---|---|
| Open-Circuit Voltage per Cell | 2.0 to 3.4 V | |
| Rated Energy Capacity per Cell | 8 Wh | |
| Rated Charge Capacity per Cell | 2.5 Ah | |
| Battery Cell Equivalent Resistance | 6 m | |
| Battery Cells in Parallel | 385 cells | |
| Parallel Sets in Series | 110 sets | |
| Battery Weight per Cell | 94 g |
| Parameter | Variable | Value |
|---|---|---|
| Vehicle Roof Area | 33.2 m | |
| Vehicle Side Area | 44.1 m | |
| Vehicle Back Area | 8.81 m | |
| Surface Power Density | 165 W/m | |
| Area Density | 1.89 kg/m | |
| Peak Power Temperature Coefficient | −0.43%/C |
| Configuration | PV Modules | Battery Size |
|---|---|---|
| Nominal | None | 338.8 kWh |
| Rooftop PV | Top Only | 338.8 kWh |
| Full-Body PV | Top, Sides, and Back | 338.8 kWh |
| Equal Weight | None | 341.9 kWh |
| Equal Cost | None | 356.6 kWh |
| Configuration | Marginal Mass | Marginal Cost |
|---|---|---|
| Rooftop PV | 37.6 kg | $6247 |
| Full-Body PV | 116.6 kg | $19,386 |
| Equal Weight | 36.2 kg | $1220 |
| Equal Cost | 209.3 kg | $6227 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallon, K.R.; Assadian, F.; Fu, B. Analysis of On-Board Photovoltaics for a Battery Electric Bus and Their Impact on Battery Lifespan. Energies 2017, 10, 943. https://doi.org/10.3390/en10070943
Mallon KR, Assadian F, Fu B. Analysis of On-Board Photovoltaics for a Battery Electric Bus and Their Impact on Battery Lifespan. Energies. 2017; 10(7):943. https://doi.org/10.3390/en10070943
Chicago/Turabian StyleMallon, Kevin R., Francis Assadian, and Bo Fu. 2017. "Analysis of On-Board Photovoltaics for a Battery Electric Bus and Their Impact on Battery Lifespan" Energies 10, no. 7: 943. https://doi.org/10.3390/en10070943
APA StyleMallon, K. R., Assadian, F., & Fu, B. (2017). Analysis of On-Board Photovoltaics for a Battery Electric Bus and Their Impact on Battery Lifespan. Energies, 10(7), 943. https://doi.org/10.3390/en10070943






