Biomass Production from Crops Residues: Ranking of Agro-Energy Regions
Abstract
1. Introduction
2. Methodology
2.1. Multicriteria Methods for Biomass Production
2.2. The ELimination and Et Choix Traduisant la REalite (ELECTRE III) Multicriteria Method
- aPb: The a is strongly preferred to b, where g(a) − g(b) > p
- aQb: The a is meager preferred to b, where q < g(a) − g(b) ≤ p
- aIb: Indifference between a and b, when |g(a) − g(b)| ≤ q
- Agreement Principle: Applies aSb for the majority of the criteria.
- Principle of non-discrepancy: From all the criteria under which it accepted the statement contains no criterion on which this statement is strongly rejected.
- The indifference and preference thresholds for each criterion.
- The criteria weights.
- The difficulties that may arise from comparing two scenarios, the first is significantly better than the second relative to a subset of criteria but inferior compared with the total evaluation.
- When cj(a) − cj(b) ≤ qj, the non-difference between alternatives a and b for the specific criterion j under study is identified. In this case cj(a,b) = 0.
- When cj(a) − Vj(b) > pj, then a is strictly preferred to b for criterion j. In this case cj(a,b) = 1.
2.3. Case Study Area and Criteria
2.3.1. Case Study Area
2.3.2. Criteria
Gross Margin
Income
Variable Cost
Biomass Production
Production of Thermal and Electrical Energy
3. Results and Discussion
Ranking
- A0001: Agro-energy Region of Imathia
- A0002: Agro-energy Region of Thessaloniki
- A0003: Agro-energy Region of Kilkis
- A0004: Agro-energy Region of Pella
- A0005: Agro-energy Region of Pieria
- A0006: Agro-energy Region of Serres
- A0007: Agro-energy Region of Chalkidiki
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vlontzos, G.; Niavis, S.; Manos, B. A DEA approach for estimating the agricultural energy and environmental efficiency of EU countries. Renew. Sustain. Energy Rev. 2014, 40, 91–96. [Google Scholar] [CrossRef]
- European Commision. Horizon 2020. Work Programme 2016–2017. 9. Food Security, Sustainable Agriculture and Forestry, Marine and Maritime and Inland Water Research and the Bioeconomy; European Commision: Brussels, Belgium, 2015. [Google Scholar]
- Fantozzi, F.; Bartocci, P.; D’Alessandro, B.; Arampatzis, S.; Manos, B. Public-private partnerships value in bioenergy projects: Economic feasibility analysis based on two case studies. Biomass Bioenergy 2014, 66, 387–397. [Google Scholar] [CrossRef]
- Manos, B.; Partalidou, M.; Fantozzi, F.; Arampatzis, S.; Papadopoulou, O. Agro-energy districts contributing to environmental and social sustainability in rural areas: Evaluation of a local public-private partnership scheme in Greece. Renew. Sustain. Energy Rev. 2014, 29, 85–95. [Google Scholar] [CrossRef]
- Tziolas, E.; Manos, B.; Bournaris, T. Planning of agro-energy districts for optimum farm income and biomass energy from crops residues. Oper. Res. 2017, 17, 535–546. [Google Scholar] [CrossRef]
- European Commission (EC). Biomass Action Plan; European Commission: Brussels, Belgium, 2005. [Google Scholar]
- Rosillo-Calle, F. The Role of Biomass Energy in Rural Development. Available online: http://www.proceedings.scielo.br/scielo.php?pid=msc0000000022000000100028&script=sci_arttext (accessed on 10 Feburary 2017).
- Best, G. Agro-Energy: A New Function of Agriculture; Latin America Thematic Network on Bioenergy (LAMNET): Morelia, Mexico, 2003. [Google Scholar]
- European Commission (EC). A Strategy for Competitive, Sustainable and Secure Energy; Energy 2020; European Commission: Brussels, Belgium, 2010. [Google Scholar]
- Nishiguchi, S.; Tabata, T. Assessment of social, economic, and environmental aspects of woody biomass energy utilization: Direct burning and wood pellets. Renew. Sustain. Energy Rev. 2016, 57, 1279–1286. [Google Scholar] [CrossRef]
- Bassegio, D.; Zanotto, M.D.; Santos, R.F.; Werncke, I.; Dias, P.P.; Olivo, M. Oilseed crop crambe as a source of renewable energy in Brazil. Renew. Sustain. Energy Rev. 2016, 66, 311–321. [Google Scholar] [CrossRef]
- REN21. Renewable Energy Policy Network for the 21st Century; REN21: Paris, France, 2016. [Google Scholar]
- Bournaris, T.; Moulogianni, C.; Manos, B. A multicriteria model for the assessment of rural development plans in Greece. Land Use Policy 2014, 38, 1–8. [Google Scholar] [CrossRef]
- Manos, B.; Bournaris, T.; Chatzinikolaou, P.; Berbel, J.; Nikolov, D. Effects of CAP policy on farm household behaviour and social sustainability. Land Use Policy 2013, 31, 166–181. [Google Scholar] [CrossRef]
- Xu, J.; Chang, S.; Yuan, Z.; Jiang, Y.; Liu, S.; Li, W.; Ma, L. Regionalized Techno-Economic Assessment and Policy Analysis for Biomass Molded Fuel in China. Energies 2015, 8, 13846–13863. [Google Scholar] [CrossRef]
- Valiakos, A.; Siskos, Y. Multicriteria decision support for the evaluation of agricultural units in Greece. Oper. Res. 2015, 15, 379–393. [Google Scholar] [CrossRef]
- Prišenk, J.; Turk, J.; Rozman, Č.; Borec, A.; Zrakić, M.; Pažek, K. Advantages of combining linear programming and weighted goal programming for agriculture application. Oper. Res. 2014, 14, 253–260. [Google Scholar] [CrossRef]
- Koutroumanidis, T.; Papathanasiou, J.; Manos, B. A multicriteria analysis of productivity of agricultural regions of Greece. Oper. Res. 2002, 2, 339–346. [Google Scholar] [CrossRef]
- Chatzinikolaou, P.; Bournaris, T.; Kiomourtzi, F.; Moulogianni, C.; Manos, B. Classification and ranking rural areas in Greece based on technical, economic and social indicators of the agricultural holdings. Int. J. Bus. Innov. Res. 2015, 9, 455–469. [Google Scholar] [CrossRef]
- Haas, G.; Wetterich, F.; Geier, U. Life Cycle Assessment Framework in Agriculture on the Farm Level. Int. J. Life Cycle Assess. 2000, 5, 345–348. [Google Scholar] [CrossRef]
- Brentrup, F.; Kusters, J.; Kuhlmann, H.; Lammel, J. Application of the Life Cycle Assessment methodology to agricultural production: an example of sugar beet production with different forms of nitrogen fertilisers. Eur. J. Agron. 2001, 14, 221–233. [Google Scholar] [CrossRef]
- Pulighe, G.; Bonati, G.; Fabiani, S.; Barsali, T.; Lupia, F.; Vanino, S.; Nino, P.; Arca, P.; Roggero, P. Assessment of the Agronomic Feasibility of Bioenergy Crop Cultivation on Marginal and Polluted Land: A GIS-Based Suitability Study from the Sulcis Area, Italy. Energies 2016, 9. [Google Scholar] [CrossRef]
- Neri, E.; Cespi, D.; Setti, L.; Gombi, E.; Bernardi, E.; Vassura, I.; Passarini, F. Biomass Residues to Renewable Energy: A Life Cycle Perspective Applied at a Local Scale. Energies 2016, 9. [Google Scholar] [CrossRef]
- Blengini, G.A.; Busto, M. The life cycle of rice: LCA of alternative agri-food chain management systems in Vercelli (Italy). J. Environ. Manag. 2009, 90, 1512–1522. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Tao, J. Economic, energy and environmental evaluations of biomass-based fuel ethanol projects based on life cycle assessment and simulation. Appl. Energy 2009, 86 (Suppl. S1), S178–S188. [Google Scholar] [CrossRef]
- Castillo-Villar, K.; Minor-Popocatl, H.; Webb, E. Quantifying the Impact of Feedstock Quality on the Design of Bioenergy Supply Chain Networks. Energies 2016, 9. [Google Scholar] [CrossRef]
- Fedele, A.; Mazzi, A.; Niero, M.; Zuliani, F.; Scipioni, A. Can the Life Cycle Assessment methodology be adopted to support a single farm on its environmental impacts forecast evaluation between conventional and organic production? An Italian case study. J. Clean. Prod. 2014, 69, 49–59. [Google Scholar] [CrossRef]
- Fagioli, F.F.; Rocchi, L.; Paolotti, L.; Słowiński, R.; Boggia, A. From the farm to the agri-food system: A multiple criteria framework to evaluate extended multi-functional value. Ecol. Indic. 2017, 79, 91–102. [Google Scholar] [CrossRef]
- Micale, R.; Giallanza, A.; Russo, G.; La Scalia, G. Selection of a sustainable functional pasta enriched with Opuntia using ELECTRE III methodology. Sustainability 2017, 9. [Google Scholar] [CrossRef]
- Banias, G.; Achillas, C.; Vlachokostas, C.; Moussiopoulos, N.; Tarsenis, S. Assessing multiple criteria for the optimal location of a construction and demolition waste management facility. Build. Environ. 2010, 45, 2317–2326. [Google Scholar] [CrossRef]
- Banias, G. Development of a System for the Optimal Construction and Demolition Waste Management. Ph.D. Thesis, Aristotle University of Thessaloniki, Thessaloniki, Greece, 2009. [Google Scholar]
- Wang, X.; Triantaphyllou, E. Ranking irregularities when evaluating alternatives by using some ELECTRE methods. Omega 2008, 36, 45–63. [Google Scholar] [CrossRef]
- Buchanan, J.T.; Sheppard, P.J.; Vanderpooten, D. Project Ranking Using ELECTRE III; Department of Management Systems, University of Waikato: Hamilton, New Zealand, 1999. [Google Scholar]
- Roy, B.; Présent, M.; Silhol, D. A programming method for determining which Paris metro stations should be renovated. Eur. J. Oper. Res. 1986, 24, 318–334. [Google Scholar] [CrossRef]
- Roussat, N.; Dujet, C.; Méhu, J. Choosing a sustainable demolition waste management strategy using multicriteria decision analysis. Waste Manag. 2009, 29, 12–20. [Google Scholar] [CrossRef] [PubMed]
- Roy, B.; Bouyssou, D. Aide Multicriterea la Decision: Methods et Cas; Economica: Paris, France, 1993. [Google Scholar]
- Maystre, L.Y.; Pictet, J.; Simos, J.; Roy, B. Méthodes Multicritères ELECTRE: Description, Conseils Pratiques et cas D’application à la Gestion Environnementale; Presses Polytechniques et Universitaires Romandes: Lausanne, Switzerland, 1994. [Google Scholar]
- LAMSADE ELECTRE III e IV Software Official Webpage. Available online: https://www.lamsade.dauphine.fr/spip.php?rubrique64&lang=en (accessed on 15 December 2016).
- Zambon, I.; Colosimo, F.; Monarca, D.; Cecchini, M.; Gallucci, F.; Proto, A.; Lord, R.; Colantoni, A. An Innovative Agro-Forestry Supply Chain for Residual Biomass: Physicochemical Characterisation of Biochar from Olive and Hazelnut Pellets. Energies 2016, 9. [Google Scholar] [CrossRef]
- Di Blasi, C.; Tanzi, V.; Lanzetta, M. A study on the production of agricultural residues in Italy. Biomass Bioenergy 1997, 12, 321–331. [Google Scholar] [CrossRef]
- Menconi, M.E.; Chiappini, M.; Grohmann, D. Implementation of a genetic algorithm for energy design optimization of livestock housing using a dynamic thermal simulator. J. Agric. Eng. 2013, 44, 191–196. [Google Scholar] [CrossRef]
| Crops | Chalkidiki | Imathia | Kilkis | Pella | Pieria | Serres | Thessaloniki |
|---|---|---|---|---|---|---|---|
| Alfalfa | 5548 | 4408.7 | 5518.7 | 3394.6 | 10,175.7 | ||
| Apples | 2614 | ||||||
| Apricots | 1628.7 | ||||||
| Barley | 4265.8 | 1493.5 | 3549.8 | 4064 | 2425.4 | 7825 | 5324.8 |
| Cherries | 7825.1 | ||||||
| Cotton | 16,354.4 | 6814.1 | 11,204.8 | 4614.8 | 14,816.2 | 10,348.6 | |
| Hard Wheat | 16,218 | 4842 | 38,247.8 | 5933.5 | 9498.7 | 33,527 | 30,848.1 |
| Kiwi | 3218.4 | ||||||
| Maize | 5998.3 | 3394.9 | 8498.7 | 1754.5 | 24,135 | 2994.8 | |
| Nectarines | 3914 | 2948.5 | |||||
| Oats | 3214.2 | ||||||
| Olive Trees | 30,847 | 3214.8 | 4623 | 2418.7 | |||
| Peaches | 18,235.7 | 15,898.7 | |||||
| Rapeseed | 2145 | ||||||
| Rice | 1624 | 987.5 | 3104.5 | 17,994.5 | |||
| Set Aside | 11,922.9 | 2778.4 | 9909.9 | 4998.3 | 4358.4 | 8245.8 | 8494.5 |
| Soft Wheat | 3654.1 | 1598.4 | 22,246.3 | 4134.8 | 7914.8 | 11,924.5 | 21,911.2 |
| Sunflower | 1658.1 | 2158.9 | 10,748.5 | 5284.5 | |||
| Tobacco | 4888.8 | 2245 | |||||
| Vetch | 2549.1 | ||||||
| Total | 30,847 | 65,000.7 | 90,730.4 | 72,653.8 | 46,270.7 | 133,515.2 | 105,619.7 |
| Crops | Residues Type | Output of Residues (tn/ha) | Humidity % | Biomass (tn/ha) |
|---|---|---|---|---|
| Alfalfa | Straw | 3 | 0.15 | 2.6 |
| Apples | Pruning | 2.4 | 0.40 | 1.4 |
| Apricots | Pruning | 1.6 | 0.40 | 1 |
| Barley | Straw | 2.7 | 0.15 | 2.3 |
| Cherries | Pruning | 2.5 | 0.40 | 1.5 |
| Cotton | Straw and shell (overground) | 4.2 | 0.40 | 2.5 |
| Cotton | Straw and shell (root) | 1.3 | 0.56 | 0.6 |
| Hard Wheat | Straw | 1.6 | 0.15 | 1.4 |
| Kiwi | Pruning | 1.6 | 0.35 | 1 |
| Maize | Stalks and cobs | 10.5 | 0.55 | 4.7 |
| Nectarines | Pruning | 2.9 | 0.40 | 1.7 |
| Olive Trees | Pruning | 1.7 | 0.50 | 0.9 |
| Peaches | Pruning | 2.9 | 0.40 | 1.7 |
| Rapeseed | Straw | 4 | 0.53 | 1.9 |
| Rice | Straw | 3.8 | 0.25 | 2.9 |
| Set Aside | Not applied | |||
| Soft Wheat | Straw | 2.5 | 0.15 | 2.1 |
| Sunflower | Stalks | 4 | 0.40 | 2.4 |
| Tobacco | Stalks | 2.2 | 0.85 | 0.3 |
| Alternatives Agro-Energy Regions | Criteria | |||||
|---|---|---|---|---|---|---|
| Gross Margin (€) | Income (€) | Variable Cost (€) | Biomass Production | Production of Thermal Energy (MJ) | Production of Electrical Energy (MJ) | |
| Imathia | 82,639,292.18 | 210,811,094.64 | 128,171,802.46 | 153,941.88 | 2,565,940,026.60 | 570,208,894.80 |
| Thessaloniki | 54,904,658.03 | 119,336,134.20 | 64,431,476.17 | 213,695.21 | 3,140,541,839.70 | 697,898,186.60 |
| Kilkis | 48,153,421.10 | 87,650,548.66 | 39,497,127.56 | 160,925.00 | 2,383,266,261.96 | 529,614,724.88 |
| Pella | 174,610,011.65 | 317,328,408.48 | 142,718,396.83 | 161,579.45 | 2,686,299,186.15 | 596,955,374.70 |
| Pieria | 50,209,550.87 | 104,365,027.78 | 54,155,476.91 | 77,115.67 | 1,175,256,301.05 | 261,168,066.90 |
| Serres | 80,164,854.89 | 178,619,541.72 | 98,454,686.83 | 318,397.21 | 4,837,020,975.00 | 1,074,893,550.00 |
| Chalkidiki | 56,526,005.64 | 135,930,670.10 | 79,404,664.46 | 77,969.21 | 1,275,268,402.80 | 283,392,978.40 |
| Criteria | Weights (%) |
|---|---|
| Gross Margin (€) | 7.70 |
| Income (€) | 7.70 |
| Variable Cost (€) | 7.70 |
| Biomass Production | 35.10 |
| Production of Thermal Energy (MJ) | 22.20 |
| Production of Electrical Energy (MJ) | 19.60 |
| Total | 100 |
| Codes | A0001 | A0002 | A0003 | A0004 | A0005 | A0006 | A0007 |
|---|---|---|---|---|---|---|---|
| A0001 | 1 | 0.15 | 0.92 | 0.85 | 0.92 | 0.15 | 0.92 |
| A0002 | 0.85 | 1 | 0.92 | 0.85 | 0.95 | 0.077 | 0.98 |
| A0003 | 0.81 | 0.15 | 1 | 0.67 | 0.98 | 0.077 | 0.9 |
| A0004 | 0.92 | 0.22 | 0.92 | 1 | 0.92 | 0.15 | 0.92 |
| A0005 | 0.077 | 0.21 | 0.15 | 0.077 | 1 | 0.077 | 0.92 |
| A0006 | 0.92 | 0.92 | 0.92 | 0.85 | 0.92 | 1 | 0.92 |
| A0007 | 0.077 | 0.15 | 0.15 | 0.077 | 0.92 | 0.077 | 1 |
| Codes | A0001 | A0002 | A0003 | A0004 | A0005 | A0006 | A0007 |
|---|---|---|---|---|---|---|---|
| A0001 | 1 | 0.15 | 0.92 | 0.85 | 0.92 | 0.15 | 0.92 |
| A0002 | 0.85 | 1 | 0.92 | 0.85 | 0.95 | 0.077 | 0.98 |
| A0003 | 0.81 | 0.15 | 1 | 0.67 | 0.98 | 0.077 | 0.9 |
| A0004 | 0.92 | 0.22 | 0.92 | 1 | 0.92 | 0.15 | 0.92 |
| A0005 | 0.077 | 0.21 | 0.15 | 0.077 | 1 | 0.077 | 0.92 |
| A0006 | 0.92 | 0.92 | 0.92 | 0.85 | 0.92 | 1 | 0.92 |
| A0007 | 0.077 | 0.15 | 0.15 | 0.077 | 0.92 | 0.077 | 1 |
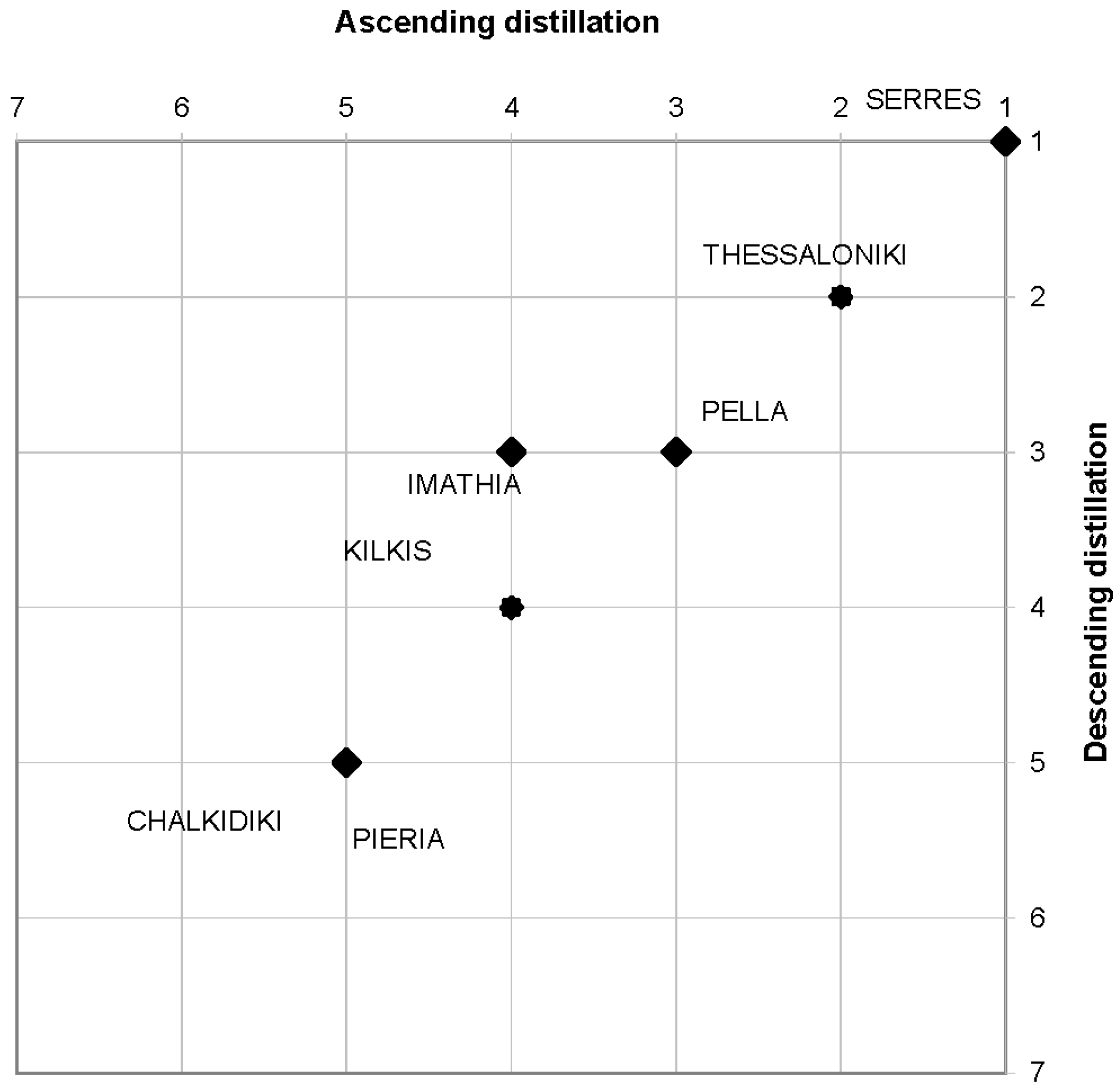
| Ranking | Code | Agro-Energy Region |
|---|---|---|
| 1 | A0006 | Serres |
| 2 | A0002 | Thessaloniki |
| 3 | A0004 | Pella |
| 4 | A0001 | Imathia |
| 5 | A0003 | Kilkis |
| 6 | A0005 and A0007 | Pieria and Chalkidiki |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moulogianni, C.; Bournaris, T. Biomass Production from Crops Residues: Ranking of Agro-Energy Regions. Energies 2017, 10, 1061. https://doi.org/10.3390/en10071061
Moulogianni C, Bournaris T. Biomass Production from Crops Residues: Ranking of Agro-Energy Regions. Energies. 2017; 10(7):1061. https://doi.org/10.3390/en10071061
Chicago/Turabian StyleMoulogianni, Christina, and Thomas Bournaris. 2017. "Biomass Production from Crops Residues: Ranking of Agro-Energy Regions" Energies 10, no. 7: 1061. https://doi.org/10.3390/en10071061
APA StyleMoulogianni, C., & Bournaris, T. (2017). Biomass Production from Crops Residues: Ranking of Agro-Energy Regions. Energies, 10(7), 1061. https://doi.org/10.3390/en10071061







