Flexible Multi-Objective Transmission Expansion Planning with Adjustable Risk Aversion
Abstract
:1. Introduction
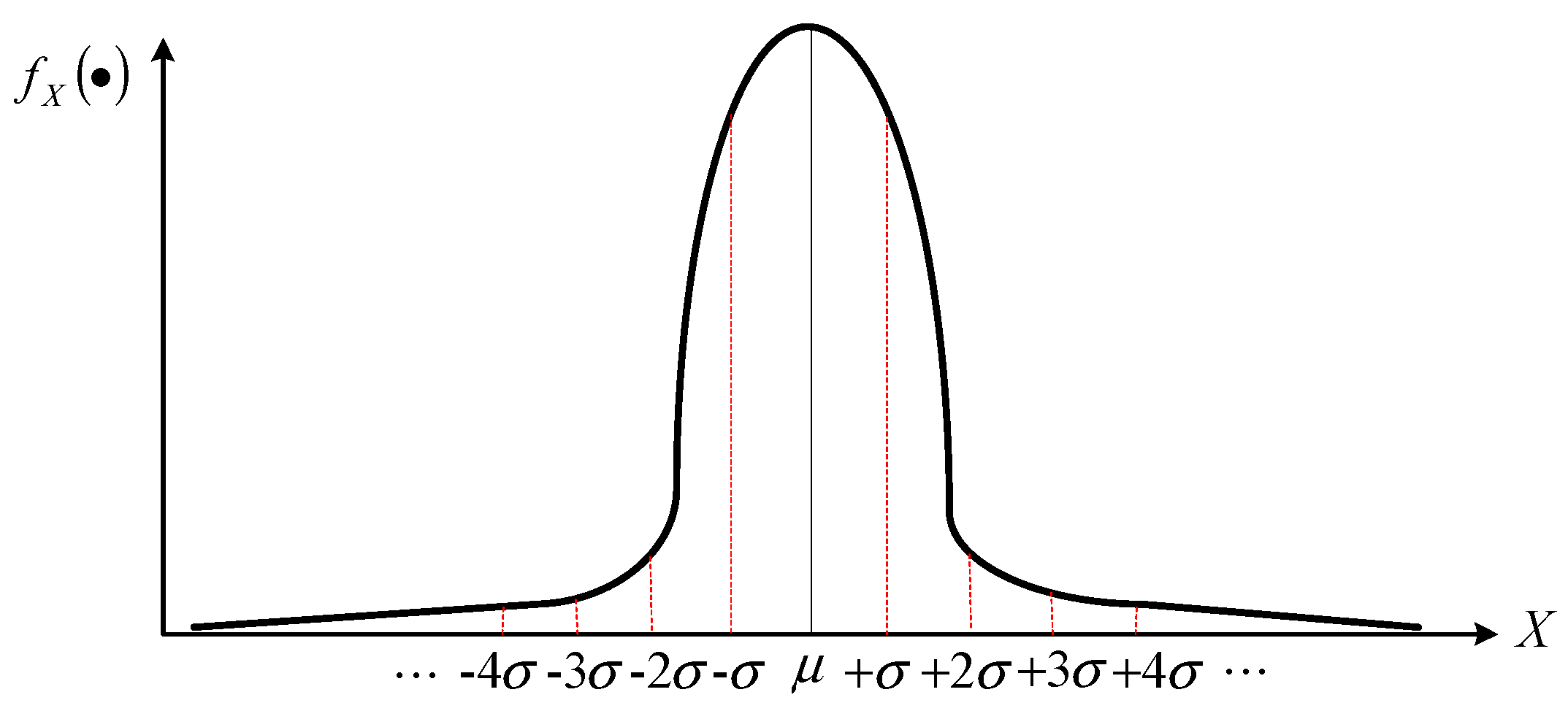
2. Risk Aversion
2.1. Conventional Risk Value
2.2. Defined Risk Value after Risk Aversion
3. Uncertainties
3.1. Wind Power Model
3.2. Load Model
3.3. Component Availability Model
3.4. Incentive-Based Demand Response Model
4. Risk-Averse TEP Model
4.1. Objectives
4.2. Constraints
- (1)
- Power balance constraint
- (2)
- Generator capacity constraint
- (3)
- Branch flow constraint
- (4)
- Ramping constraint
- (5)
- DR or load curtailment constraint
- (6)
- Decision variable constraintwhere denotes power flow between at time ; denotes involuntary load curtailment; denotes the upper limit; , are the number of existing lines and susceptance between ; , denote phase angle at node or at time , respectively; , denote the up and down ramping limits of power generators; and denotes sets of all buses.
4.3. Solution Algorithm
- Step 1:
- Initialization.
- Step 1.1:
- Generate N evenly spread weight vectors: .
- Step 1.2:
- Set EP = Ø, where EP represents the external population, which is used to store non-dominated solutions found during each iteration.
- Step 1.3:
- Calculate Euclidean distances between any two weight vectors and then work out the ξ closest weight vectors of each weight vector. For the ith sub-problem, ∀i ∈ [1, Nsub], let set , where Nsub and are number of sub-problems and the ξ closest weight vectors of λi, respectively.
- Step 1.4:
- Generate an initial population randomly and then set , where represents the vector for objective function values of the ith sub-problem.
- Step 1.5
- Initialize by a problem-specific method.
- Step 2:
- Update solutions of sub-problems.For , perform the following steps.
- Step 2.1:
- Reproduction. Randomly choose two indexes from E(i) and then generate a new solution from and by using a specific operator (e.g., genetic operator).
- Step 2.2:
- Obtain the operation cost and calculate the risk value. Three tasks are completed in this step. (i) For each sampled scenario, solve the optimal power flow (OPF) by a state-of-the-art method (e.g., the interior point method). If no network constraint is violated, calculate the DR cost and generation cost using (24) and (25). If there is any network violation, CC actions are used, and the severity is calculated by (29). (ii) When MC simulations converge, calculate the mean and Std. of the severity using (27) and (28). (iii) For a given , calculate the risk value after risk aversion using (30)–(32).
- Step 2.3:
- Update of the neighboring solutions. For each index , if , then set and .
- Step 2.4:
- Update of EP. Remove from EP all the vectors dominated by . Add to EP if no vectors in EP dominate.
- Step 3:
- Termination.If convergence criterion is satisfied, stop the program and export the EP. Otherwise, go to Step 2. The termination criterion can be: the maximum iteration number is reached, or no changes are found in EP in a number of successive iterations.
- Step 4:
- Solution selectionWith the obtained PF, a final solution can be selected according to practical needs, e.g., Nash equilibrium [31], minimizing the normalized Euclidian distance [21], individual risk preference or engineering judgments [3,32]. In this paper, a fuzzy satisfaction decision-making approach is adopted, and technical details regarding this approach can be found in [33].
5. Case Studies
5.1. Experimental Setting
5.2. Garver’s 6-Bus System
- Case 1:
- The risk objective in (26) is not considered. A single objective TEP approach with a deterministic reliability constraint (i.e., ) as reported in [39].
- Case 2:
- Similar to case 1, without the consideration of DR.
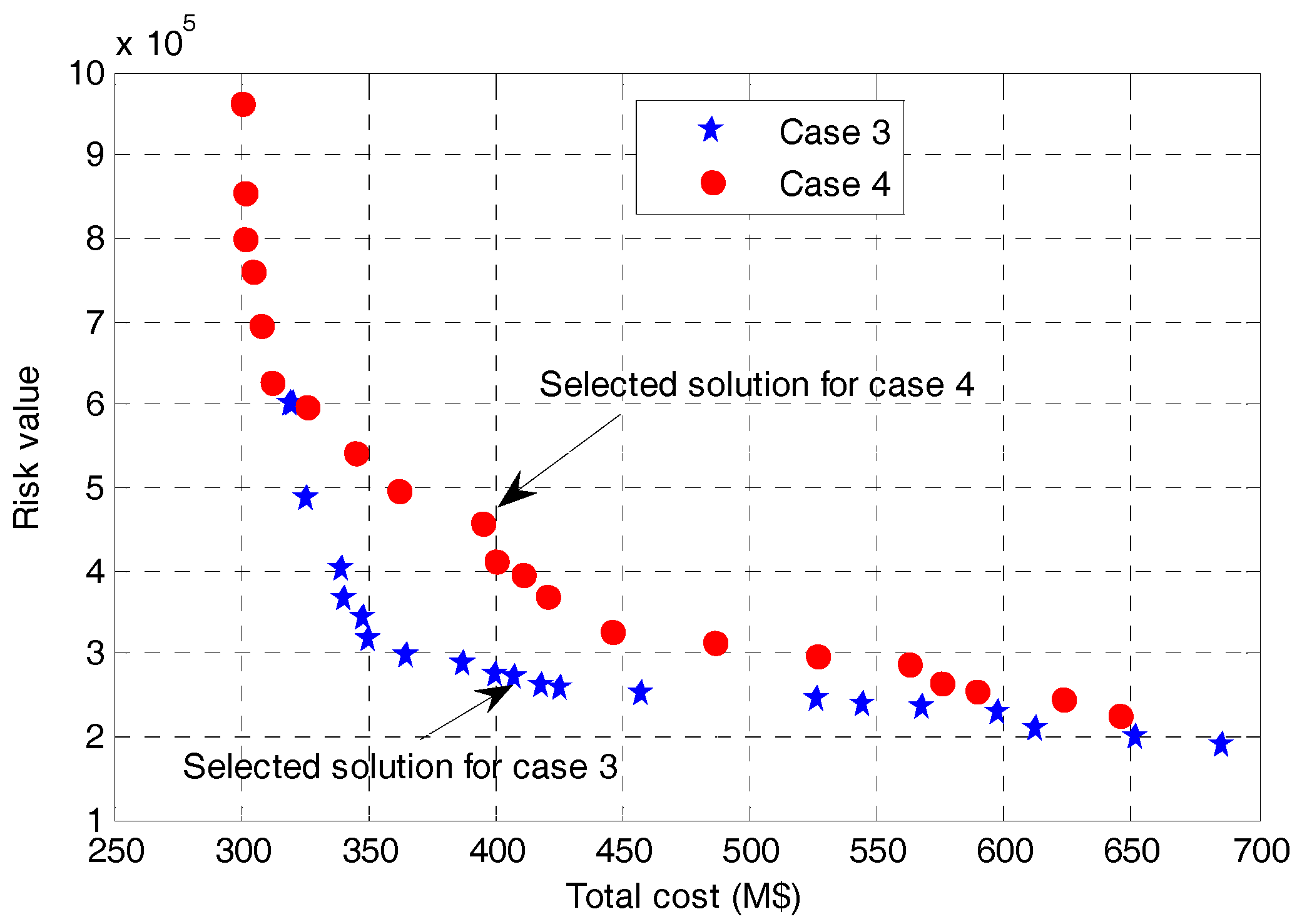
- Case 3:
- The proposed multi-objective TEP approach with DR and with the risk aversion strategy ( is set to be 3).
5.3. IEEE 24-Bus System
- Case 4:
- A multi-objective TEP approach without risk aversion. This means that in the optimization model, the second objective is (27), instead of (30).
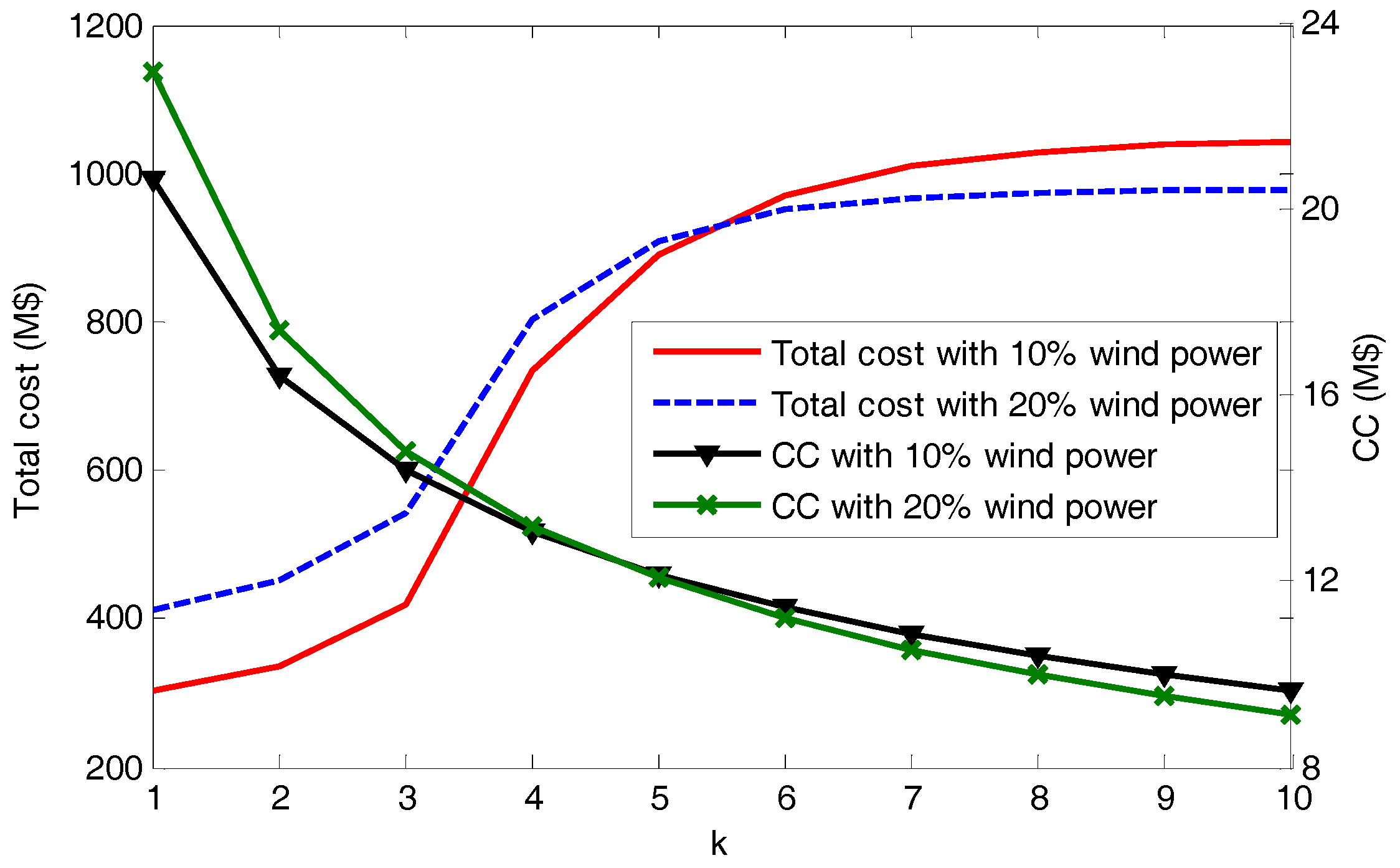
5.4. 2383-Bus Polish System
6. Conclusions
Acknowledgment
Author Contributions
Conflicts of Interest
Nomenclature
| Definitions | Symbols | Descriptions |
| Risk attitude factor | An index that measures to what extent a decision-maker cares about the risk below (when ) or above the expected risk value (when ). | |
| Probability of risk aversion | A probability that measures the occurrence frequency of threats due to a risk-aversion strategy. Theoretically, when , a decision-maker incurs no risk; when , a decision-maker adopts no risk aversion strategies, thus incurring business-as-usual risks. | |
| Probability density function of the risk attitude factor | A function used to specify the probability of the risk attitude factor falling within a particular range of values. This probability density function (PDF) is defined to represent the catastrophic consequences of a low-probability threat event to power networks. | |
| Risk value after risk aversion | A defined risk value that has taken into account the risk attitude factor and the probability of risk aversion, as well as the probability and the severity of threat events. |
References
- Munoz, C.; Sauma, E.; Contreras, J.; Aguado, J.; de la Torre, S. Impact of high wind power penetration on transmission network expansion planning. IET Gener. Trans. Distrib. 2012, 6, 1281–1291. [Google Scholar] [CrossRef]
- Ugranli, F.; Karatepe, E. Multi-objective transmission expansion planning considering minimization of curtailed wind energy. Int. Electr. Power Energy Syst. 2015, 65, 348–356. [Google Scholar] [CrossRef]
- Javadi, M.S.; Saniei, M.; Mashhadi, H.R.; Gutierrez-Alcaraz, G. Multi-objective expansion planning approach: Distant wind farms and limited energy resources integration. IET Renew. Power Gener. 2013, 7, 652–668. [Google Scholar] [CrossRef]
- Hamon, C.; Perninge, M.; Soder, L. An importance sampling technique for probabilistic security assessment in power systems with large amounts of wind power. Electr. Power Syst. Res. 2016, 131, 11–18. [Google Scholar] [CrossRef]
- Park, H.; Baldick, R. Transmission planning under uncertainties of wind and load: Sequential approximation approach. IEEE Trans. Power Syst. 2013, 28, 2395–2402. [Google Scholar] [CrossRef]
- Billinton, R.; Wangdee, W. Reliability-based transmission reinforcement planning associated with large-scale wind farms. IEEE Trans. Power Syst. 2007, 22, 34–41. [Google Scholar] [CrossRef]
- Orfanos, G.A.; Georgilakis, P.; Hatziargyriou, N.D. Transmission expansion planning of systems with increasing wind power integration. IEEE Trans. Power Syst. 2013, 28, 1355–1362. [Google Scholar] [CrossRef]
- Kamalinia, S.; Shahidehpour, M.; Khairuddin, A. Security-constrained expansion planning of fast-response units for wind integration. Electr. Power Syst. Res. 2011, 81, 107–116. [Google Scholar] [CrossRef]
- Li, C.X.; Dong, Z.Y.; Chen, G.; Luo, F.J.; Liu, J. Flexible transmission expansion planning associated with large-scale wind farms integration considering demand response. IET Gener. Trans. Distrib. 2015, 9, 2276–2283. [Google Scholar] [CrossRef]
- Gan, L.; Li, G.; Zhou, M. Coordinated planning of large-scale wind farm integration system and regional transmission network considering static voltage stability constraints. Electr. Power Syst. Res. 2016, 136, 298–308. [Google Scholar] [CrossRef]
- Rahimi, F.; Ipakchi, A. Demand response as a market resource under the smart grid paradigm. IEEE Trans. Smart Grid 2010, 1, 82–88. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Negnevitsky, M.; Groot, M.d. Market-based demand response scheduling in a degregulated environment. IEEE Trans. Smart Grid 2013, 4, 1948–1956. [Google Scholar] [CrossRef]
- Hinojosa, V.H.; Nuques, G.B. A simulated rebounding algorithm applied to the multi-stage security-constrained transmission expansion planning in power systems. Int. J. Electr. Power Energy Syst. 2013, 47, 168–180. [Google Scholar] [CrossRef]
- Foroud, A.A.; Abdoos, A.A.; Keypour, R.; Amirahmadi, M. A multi-objective framework for dynamic transmission expansion planning in competitive electricity market. Int. J. Electr. Power Energy Syst. 2010, 32, 861–872. [Google Scholar] [CrossRef]
- Akbari, T.; Rahimi-Kian, A.; Bina, M.T. Security-constrained transmission expansion planning: A stochastic multi-objective approach. Int. J. Electr. Power Energy Syst. 2012, 43, 444–453. [Google Scholar] [CrossRef]
- Florez, C.A.C.; Ocampo, R.A.B.; Zuluaga, A.H.E. Multi-objective transmission expansion planning considering multiple generation scenarios. Int. J. Electr. Power Energy Syst. 2014, 62, 398–409. [Google Scholar] [CrossRef]
- Yu, H.; Chung, C.Y.; Wong, K.P.; Zhang, J.H. A chance constrained transmission network expansion planning method with consideration of load and wind farm uncertainties. IEEE Trans. Power Syst. 2009, 24, 1568–1576. [Google Scholar] [CrossRef]
- Villumsen, J.C.; Bronmo, G.; Philpott, A.B. Line capacity expansion and transmission switching in power systems with large-scale wind power. IEEE Trans. Power Syst. 2013, 28, 731–739. [Google Scholar] [CrossRef]
- Taherkhani, M.; Hosseini, S.H. Wind farm optimal connection to transmission systems considering network reinforcement using cost-reliability analysis. IET Renew. Power Gener. 2013, 7, 603–613. [Google Scholar] [CrossRef]
- Moeini-Aghtaie, M.; Abbaspour, A.; Fotuhi-Firuzabad, M. Incorporating large-scale distant wind farms in probabilistic transmission expansion planning-part i: Theory and algorithm. IEEE Trans. Power Syst. 2012, 27, 1585–1593. [Google Scholar] [CrossRef]
- Arabali, A.; Ghofrani, M.; Etezadi-Amoli, M.; Fadali, M.S.; Moeini-Aghtaie, M. A multi-objective transmission expansion planning framework in deregulated power systems with wind generation. IEEE Trans. Power Syst. 2014, 29, 3003–3011. [Google Scholar] [CrossRef]
- Ozdemir, O.; Munoz, F.D.; Ho, J.L.; Hobbs, B.F. Economic analysis of transmission expansion planning with price-responsive demand and quadratic losses by successive lp. IEEE Trans. Power Syst. 2016, 31, 1096–1107. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional value-at-risk. J. Risk 2000, 2, 21–41. [Google Scholar] [CrossRef]
- Eydeland, A.; Wolyniec, K. Energy and Power Risk Management; Wiley: Chichester, UK, 2003. [Google Scholar]
- Zhao, J.H.; Wen, F.S.; Dong, Z.Y.; Yue, Y.S.; Wong, K.P. Optimal dispatch of electric vehicles and wind power using enhanced particle swarm optimization. IEEE Trans. Ind. Inform. 2012, 8, 889–899. [Google Scholar] [CrossRef]
- Billinton, R.; Allan, R. Reliability Evaluation of Power Systems, 2nd ed.; Plenum Press: New York, NY, USA, 1996. [Google Scholar]
- Abdi, H.; Dehnavi, E.; Mohammadi, F. Dynamic economic dispatch problem integrated with demand response (DEDDR) considering non-linear responsive load models. IEEE Trans. Smart Grid 2016, 7, 2586–2595. [Google Scholar] [CrossRef]
- Ganguly, S.; Sahoo, N.C.; Das, D. Multi-objective planning of electrical distribution systems using dynamic programming. Int. J. Electr. Power Energy Syst. 2013, 46, 65–78. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Xu, Y.; Dong, Z.Y.; Luo, F.; Zhang, R.; Wong, K.P. Parallel-differential evolution approach for optimal event-driven load shedding against voltage collapse in power systems. IET Gener. Trans. Distrib. 2014, 8, 651–660. [Google Scholar] [CrossRef]
- Xu, Y.; Dong, Z.Y.; Meng, K.; Yao, W.F.; Zhang, R.; Wong, K.P. Multi-objective dynamic var planning against short-term voltage instability using a decomposition-based evolutionary algorithm. IEEE Trans. Power Syst. 2014, 29, 2813–2822. [Google Scholar] [CrossRef]
- Maghouli, P.; Hosseini, S.H.; Buygi, M.O.; Shahidehpour, M. A scenario-based multi-objective model for multi-stage transmission expansion planning. IEEE Trans. Power Syst. 2011, 26, 470–478. [Google Scholar] [CrossRef]
- Maghouli, P.; Hosseini, S.H.; Buygi, M.O.; Shahidehpour, M. A multi-objective framework for transmission expansion planning in deregulated environments. IEEE Trans. Power Syst. 2009, 24, 1051–1061. [Google Scholar] [CrossRef]
- Wu, H.; Shahidehpour, M.; Al-Abdulwahab, A. Hourly demand response in day-ahead scheduling for managing the variability of renewable energy. IET Gener. Trans. Distrib. 2013, 7, 226–234. [Google Scholar] [CrossRef]
- IEEE Reliability Test System. Reliability test system task force of probability methods sub-committee. IEEE Trans. Power Appar. Syst. 1979, 98, 2047–2054. [Google Scholar]
- Matpower 5.0-Description of Case 2383wp. Available online: http://www.pserc.cornell.edu/matpower/docs/ref/matpower5.0/case2383wp.html (accessed on 14 July 2017).
- National Transmission Network Development Plan (NTNDP) Database, Aemo. Available online: https://www.aemo.com.au/Electricity/National-Electricity-Market-NEM/Planning-and-forecasting/National-Transmission-Network-Development-Plan/NTNDP-database (accessed on 14 July 2017).
- Australian Energy Market Operator (AEMO)-Value of Customer Reliability (VCR) Review. Available online: http://www.aemo.com.au/Electricity/National-Electricity-Market-NEM/Planning-and-forecasting/Value-of-Customer-Reliability-review (accessed on 17 July 2017).
- Zhao, J.H.; Dong, Z.Y.; Lindsay, P.; Wong, K.P. Flexible transmission expansion planning with uncertainties in an electricity market. IEEE Trans. Power Syst. 2009, 24, 479–488. [Google Scholar] [CrossRef]


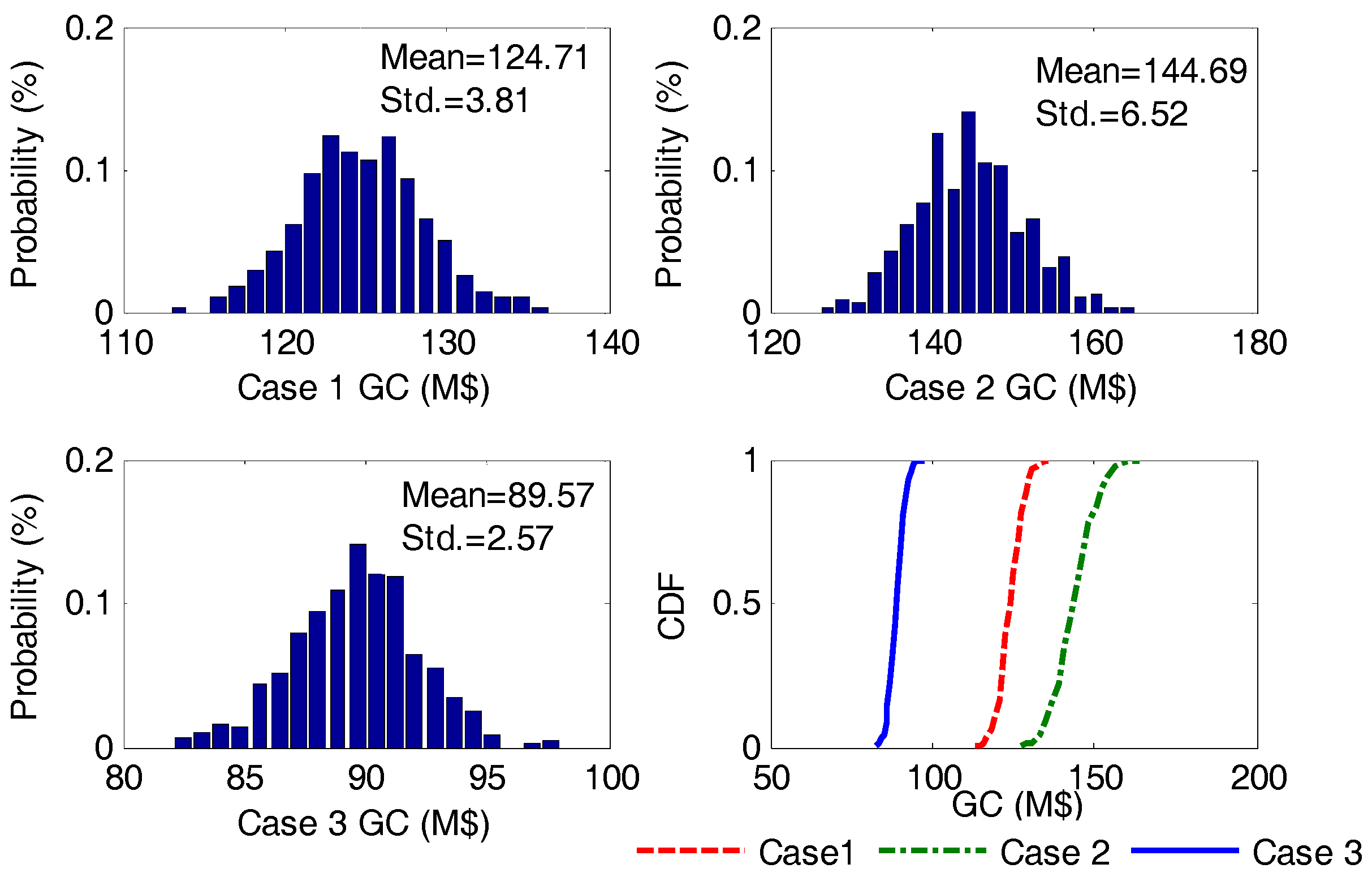

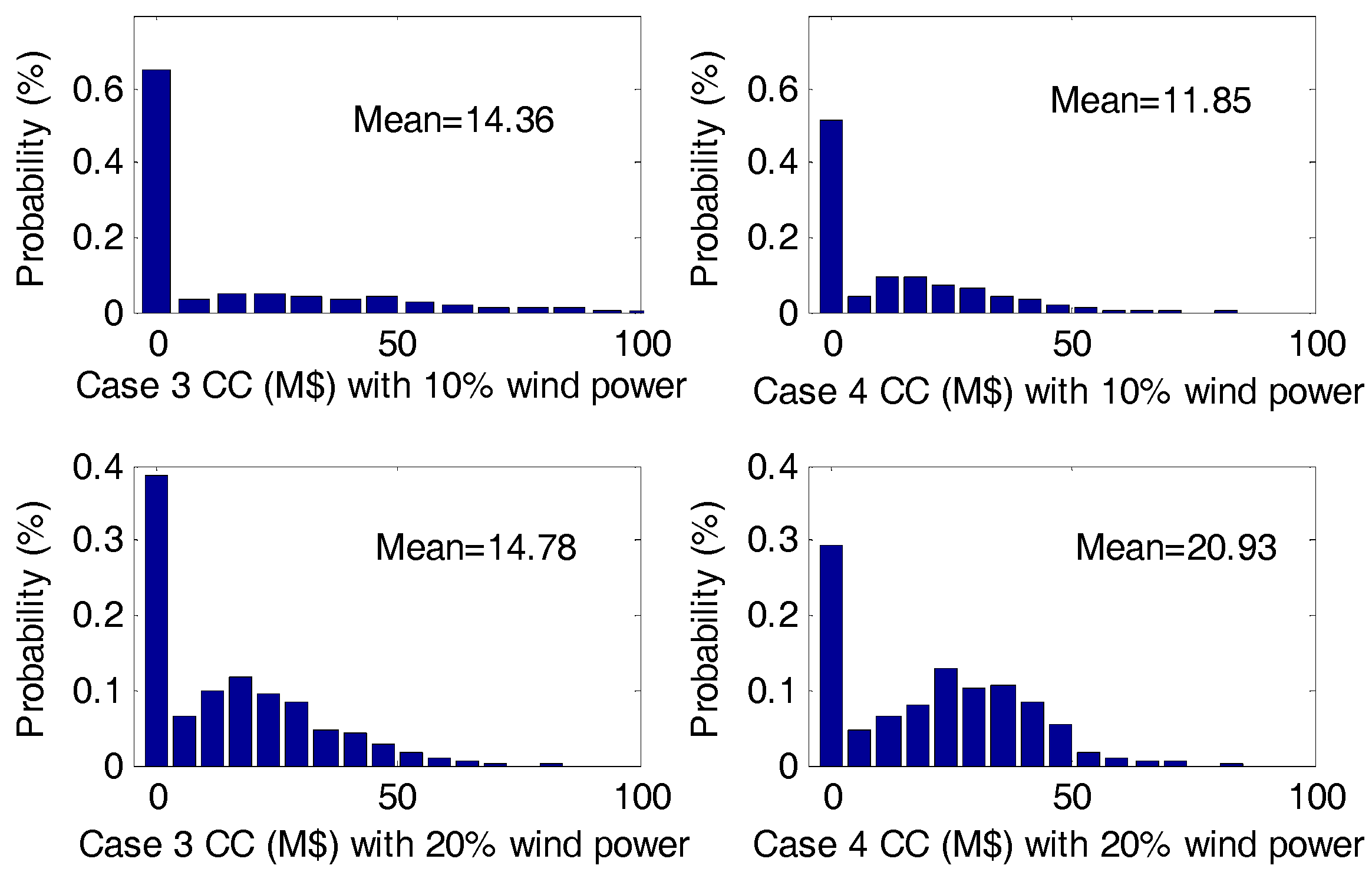

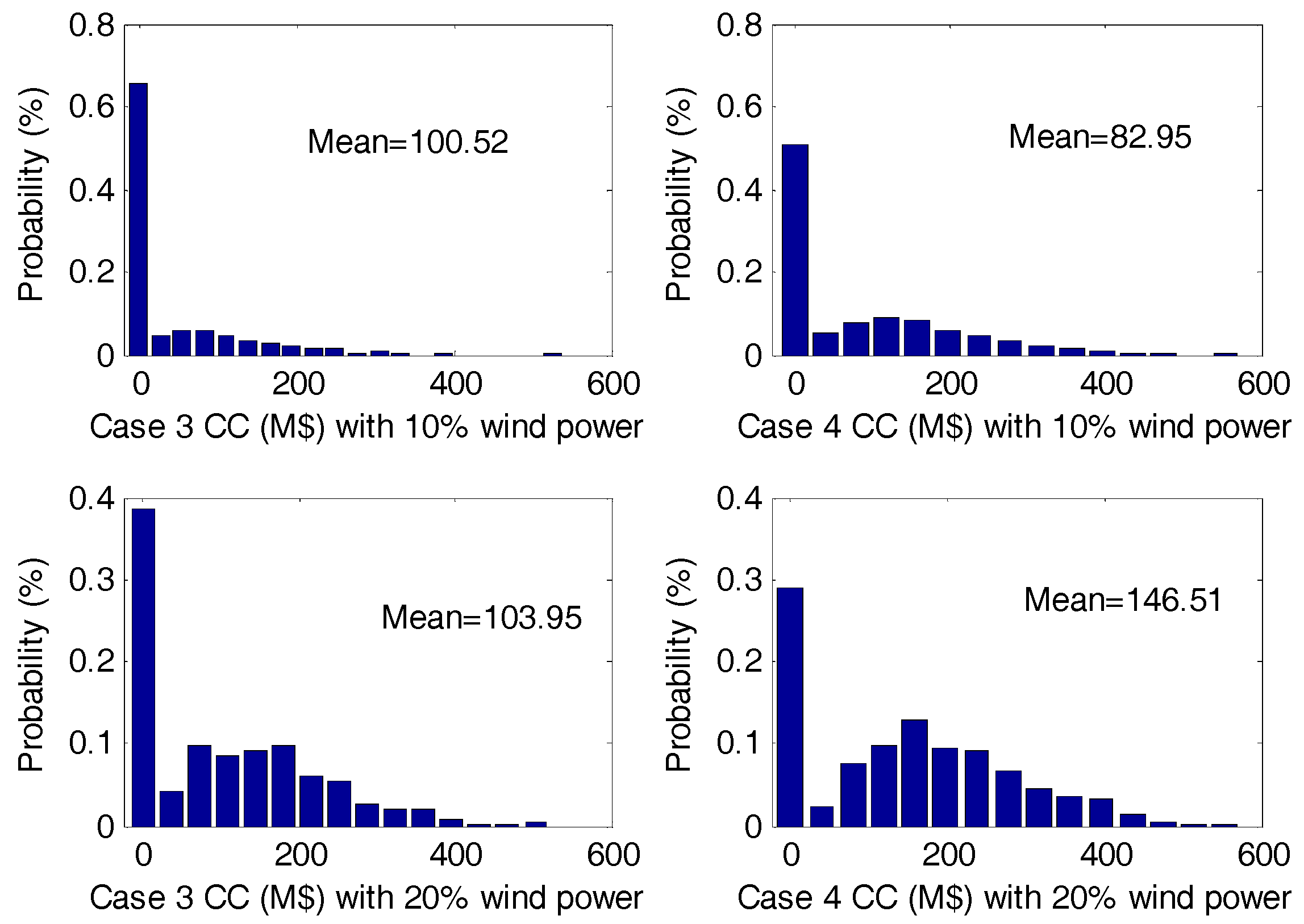
| Case # | GC (M$) | DRC (M$) | IC (M$) | Total Cost (M$) | EENS (%) |
|---|---|---|---|---|---|
| 1 | 124.71 | 6.59 | 136.22 | 267.52 | 0.0194 |
| 2 | 144.69 | - | 165.47 | 310.16 | 0.0196 |
| 3 | 89.57 | 10.26 | 156.61 | 256.44 | 0.0156 |
| Case # | Total Cost (M$) | Energy (GWh) | WPC (GWh) | Peak Load (MW) | EENS (%) | |
|---|---|---|---|---|---|---|
| N-1 | N-2 | |||||
| 1 | 267.52 | 105.68 | 6.82 | 299.41 | 0.0197 | 0.0234 |
| 2 | 310.16 | 103.45 | 13.65 | 325.45 | 0.0199 | 0.0365 |
| 3 | 256.44 | 106.36 | 4.52 | 292.91 | 0.0162 | 0.0196 |
| Case # | Total Cost (M$) | Energy (GWh) | WPC (GWh) | Peak Load (MW) | EENS (%) | |
|---|---|---|---|---|---|---|
| N-1 | N-2 | |||||
| 1 | 275.21 | 105.68 | 8.93 | 299.41 | 0.0199 | 0.0264 |
| 2 | 336.36 | 103.45 | 15.65 | 325.45 | 0.0261 | 0.0398 |
| 3 | 256.58 | 106.36 | 4.56 | 292.91 | 0.0197 | 0.0199 |
| Case # | Identified Planning Schemes |
|---|---|
| 3 | , , , , , , , , , |
| 4 | ,, , , , , , , , , |
| Case # | Total Cost (M$) | Risk Value | WPC (GWh) | Peak Load (MW) | EENS (%) | |
|---|---|---|---|---|---|---|
| N-1 | N-2 | |||||
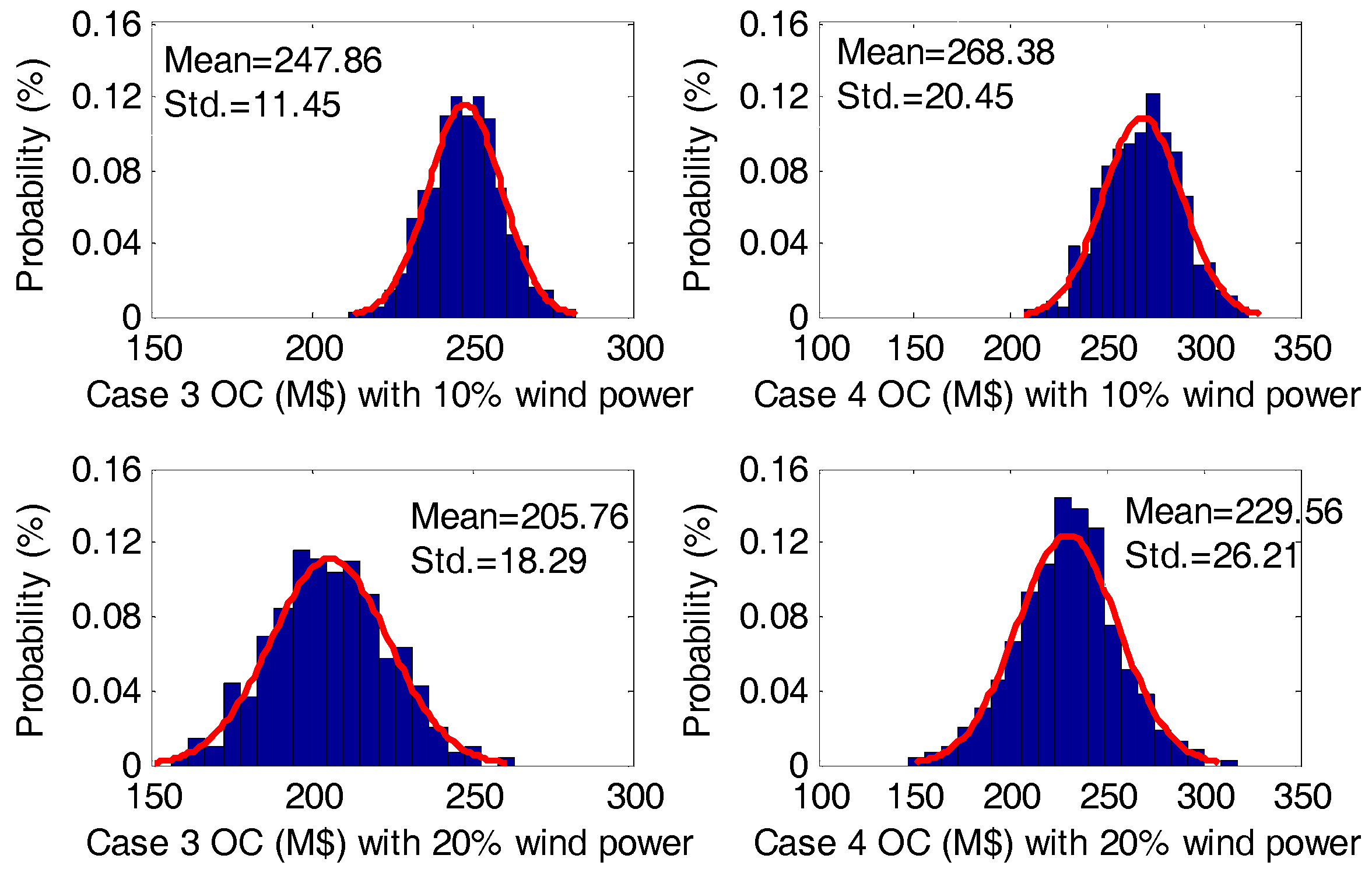
| 3 | 418.26 | 260,995 | 30.54 | 4192.65 | 0.0169 | 0.0185 |
| 4 | 395.18 | 456,236 | 42.36 | 4192.65 | 0.0172 | 0.0189 |
| Case # | Total Cost (M$) | Risk Value | WPC (GWh) | Peak Load (MW) | EENS (%) | |
|---|---|---|---|---|---|---|
| N-1 | N-2 | |||||
| 3 | 419.86 | 303,385 | 30.63 | 4192.65 | 0.0188 | 0.0194 |
| 4 | 420.34 | 652,365 | 44.89 | 4192.65 | 0.0196 | 0.0215 |
| Case # | Total Cost (M$) | Risk Value | WPC (GWh) | EENS (%) | |
|---|---|---|---|---|---|
| N-1 | N-2 | ||||
| 3 | 5049.15 | 7,898,321 | 1098.43 | 0.0176 | 0.0184 |
| 4 | 5223.42 | 13,975,876 | 2009.48 | 0.0188 | 0.0199 |
| Tested Systems | Total Elapsed (s) | Contingency Analysis Elapsed (s) | Iteration Number |
|---|---|---|---|
| 6-bus | 609 | 245 | 2345 |
| IEEE 24-bus | 14,654 | 7643 | 4567 |
| Polish 2383-bus | 37,874 | 18,984 | 7654 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, J.; Zhao, J.; Wang, D. Flexible Multi-Objective Transmission Expansion Planning with Adjustable Risk Aversion. Energies 2017, 10, 1036. https://doi.org/10.3390/en10071036
Qiu J, Zhao J, Wang D. Flexible Multi-Objective Transmission Expansion Planning with Adjustable Risk Aversion. Energies. 2017; 10(7):1036. https://doi.org/10.3390/en10071036
Chicago/Turabian StyleQiu, Jing, Junhua Zhao, and Dongxiao Wang. 2017. "Flexible Multi-Objective Transmission Expansion Planning with Adjustable Risk Aversion" Energies 10, no. 7: 1036. https://doi.org/10.3390/en10071036
APA StyleQiu, J., Zhao, J., & Wang, D. (2017). Flexible Multi-Objective Transmission Expansion Planning with Adjustable Risk Aversion. Energies, 10(7), 1036. https://doi.org/10.3390/en10071036





