Transverse Thermoelectricity in Fibrous Composite Materials
Abstract
:1. Introduction
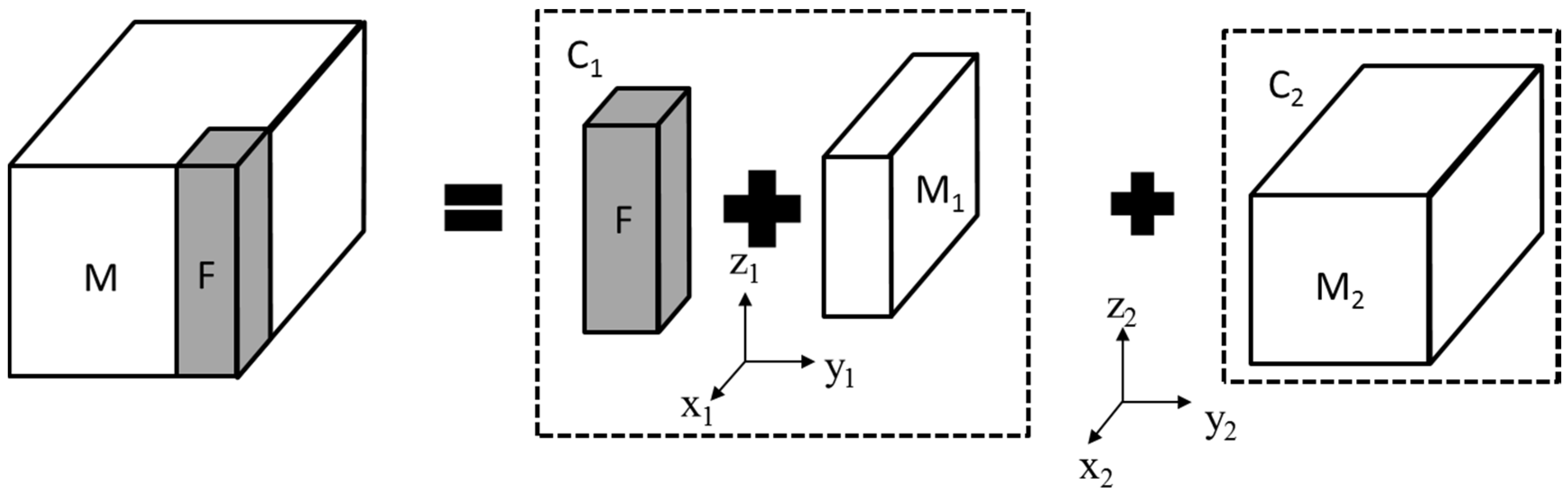
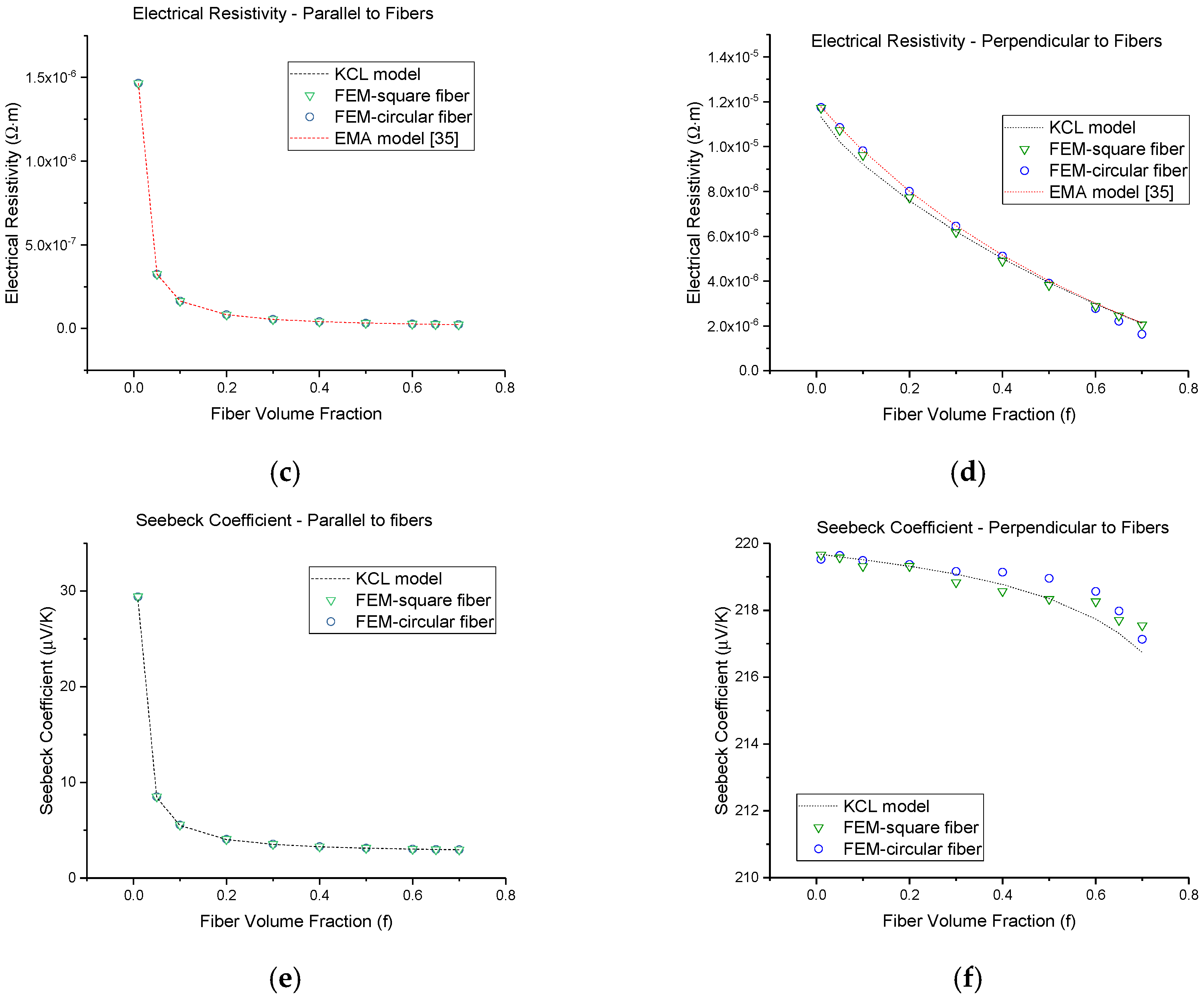
2. Mathematical Modeling
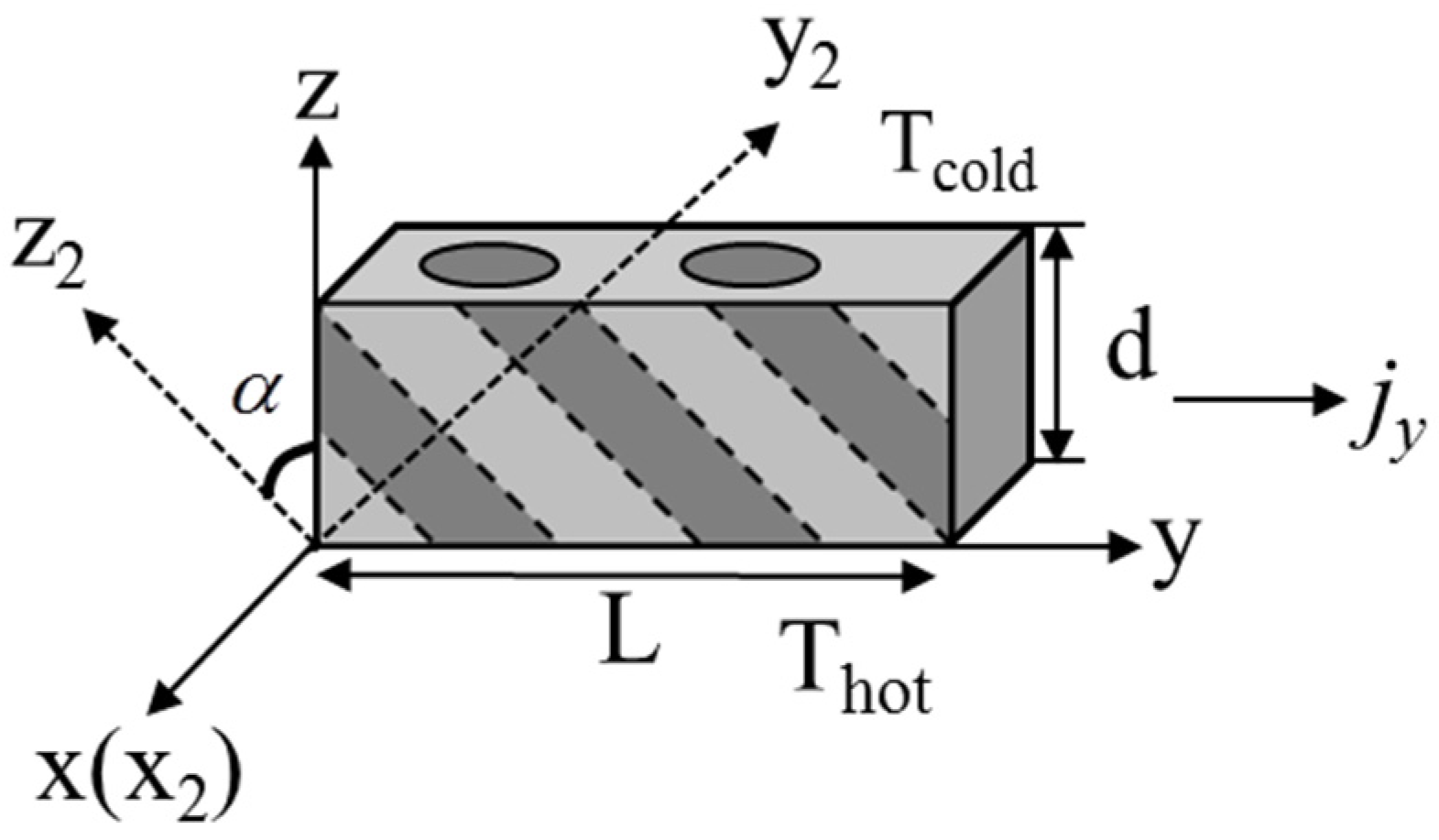
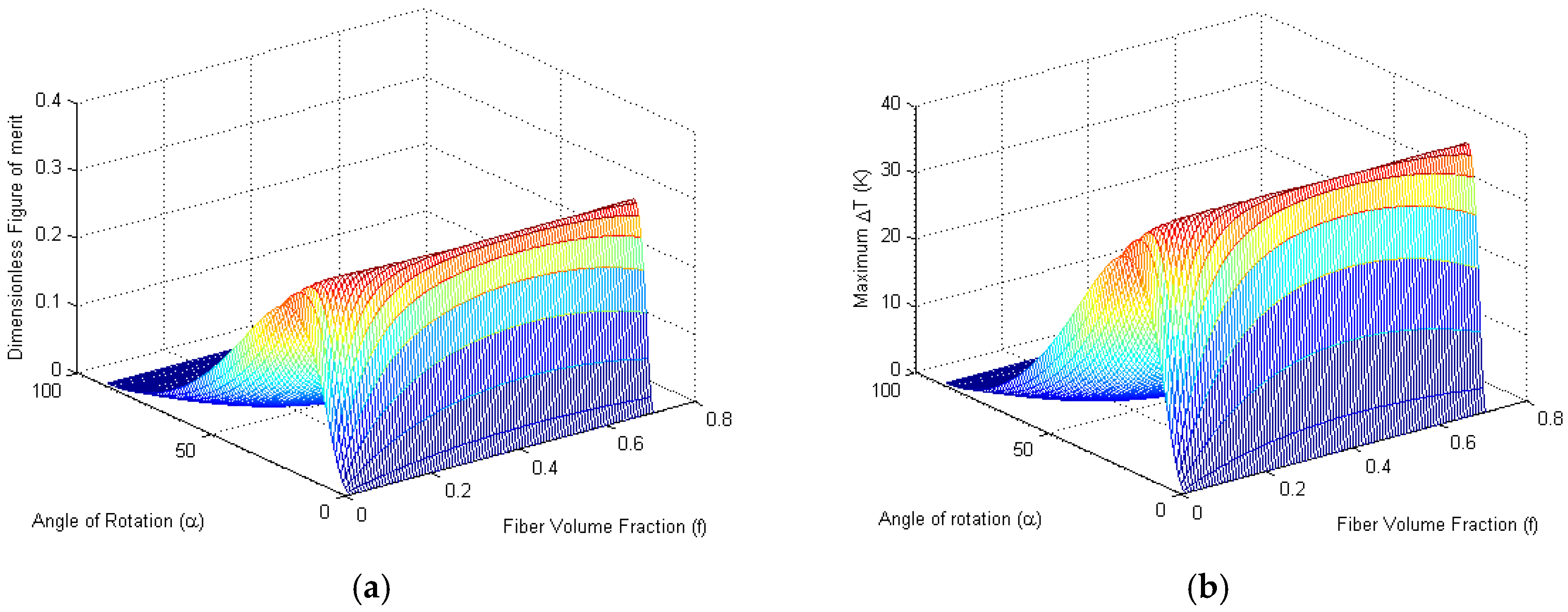
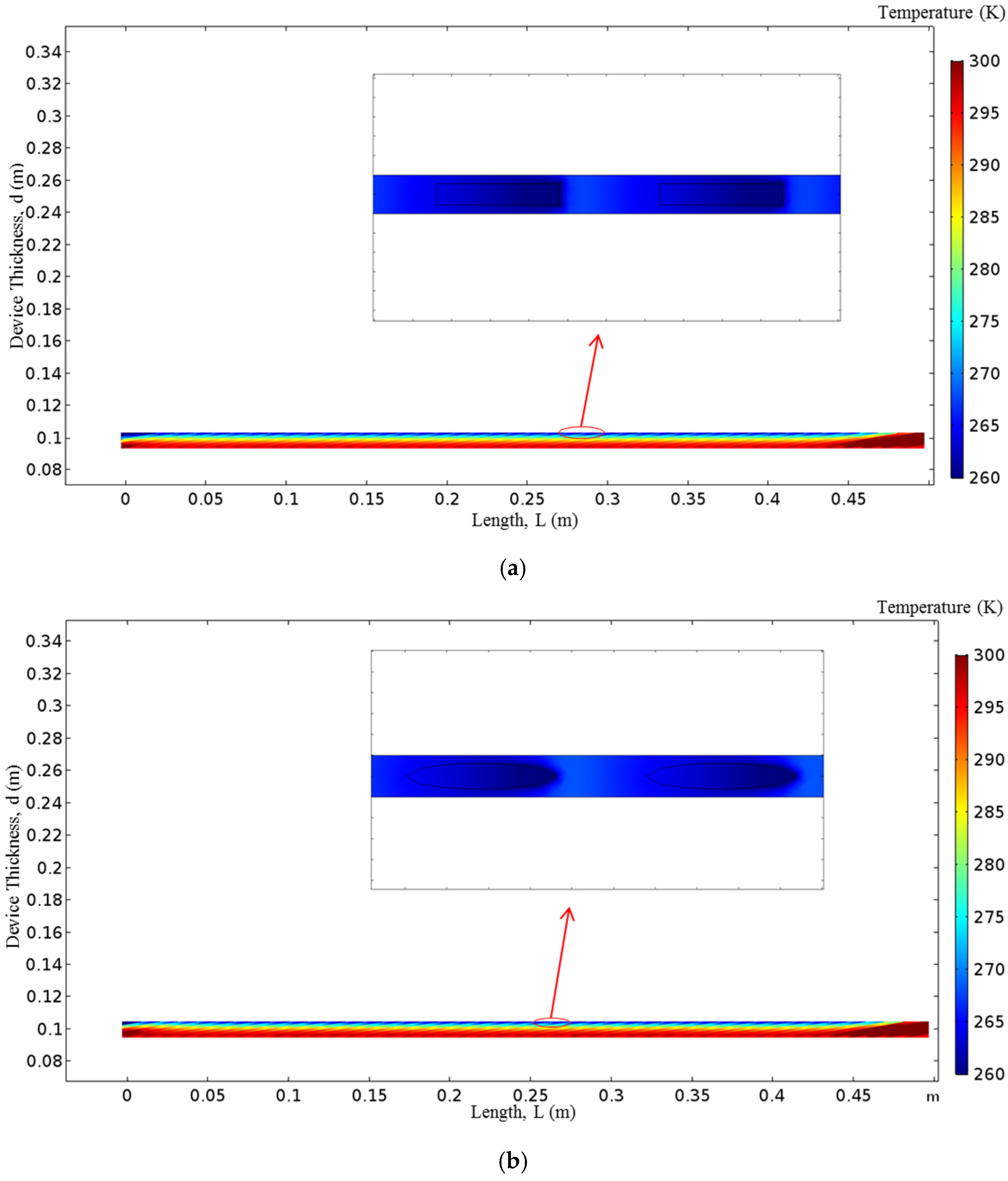
3. Cooling Performance
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| F | Fiber Phase |
| M | Matrix phase |
| KCL | Kirchhoff Circuit Laws |
| COP | Coefficient of performance |
| f | Fiber volume fraction |
| λA | Thermal conductivity of material A |
| ρA | Electrical resistivity of material A |
| SA | Seebeck coefficient of material A |
| λx/y/z | Thermal conductivity in x, y, and z directions |
| ρx/y/z | Electrical resistivity in in x, y, and z directions |
| Sx/y/z | Seebeck coefficient in in x, y, and z directions |
| λij | Elements of thermal conductivity tensor |
| ρij | Elements of electrical resistivity tensor |
| Sij | Elements of Seebeck coefficient tensor |
| P | Material properties (λ, ρ, or S) |
| jy | Current density in y direction |
| L | Device length |
| d | Device thickness |
| α | Rotation angle of aligned fibers |
| Th | Heat sink temperature |
| Tc | Cooling surface temperature |
| ΔT | Temperature difference |
| Ztrans | Transverse figure of merit |
References
- Goldsmid, H.J. Materials for synthetic transverse thermoelectric devices. J. Thermoelectr. 2008, 4, 39–48. [Google Scholar]
- Hamid Elsheikh, M.; Shnawah, D.A.; Sabri, M.F.M.; Said, S.B.M.; Haji Hassan, M.; Ali Bashir, M.B.; Mohamad, M. A review on thermoelectric renewable energy: Principle parameters that affect their performance. Renew. Sustain. Energy Rev. 2014, 30, 337–355. [Google Scholar] [CrossRef]
- Babin, V.P.; Gudkin, T.S.; Dashevskii, Z.M.; Dashevskii, L.D.; Dudkin, E.K.; lordanishvili, E.K.; Kaidanov, V.I.; Kolomoets, N.V.; Narva, O.M.; Stil’bans, L.S. Anisotropic synthetic thermoelements and their maximum capabilities. Sov. Phys. Semicond. 1974, 8, 478–481. [Google Scholar]
- Goldsmid, H.J. Application of the transverse thermoelectric effects. J. Electron. Mater. 2011, 40, 1254–1259. [Google Scholar] [CrossRef]
- Xiong, F.; Zhang, H.; Jiang, Z.M.; Zhang, P.X. Transverse laser-induced thermoelectric voltages in tilted La2−XSrxCuO4 thin films. J. Appl. Phys. 2008, 104, 053118. [Google Scholar] [CrossRef]
- Takahashi, K.; Kanno, T.; Sakai, A.; Adachi, H.; Yamada, Y. Gigantic transverse voltage induced via off-diagonal thermoelectric effect in CaxCoO2 thin films. Appl. Phys. Lett. 2010, 97, 021906. [Google Scholar] [CrossRef]
- Putra, N.; Sukyono, W.; Johansen, D.; Iskandar, F.N. The characterization of a cascade thermoelectric cooler in a cryosurgery device. Cryogenics 2010, 50, 759–764. [Google Scholar] [CrossRef]
- Ma, M.; Yu, J. An analysis on a two-stage cascade thermoelectric cooler for electronics cooling applications. Int. J. Refrig. 2014, 38, 352–357. [Google Scholar] [CrossRef]
- Huber, W.M.; Li, S.T.; Ritzer, A.; Bäuerle, D.; Lengfellner, H.; Prettl, W. Transverse seebeck effect in Bi2Sr2CaCu2O8. Appl. Phys. A 1997, 64, 487–489. [Google Scholar] [CrossRef]
- Gallo, C.F.; Chandrasekhar, B.S.; Sutter, P.H. Transport properties of bismuth single crystals. J. Appl. Phys. 1963, 34, 144–152. [Google Scholar] [CrossRef]
- Zhao, K.; Zeng, H.; Xu, K.; Yu, H.; Li, G.; Song, J.; Shi, X.; Chen, L. Scanning thermoelectric microscopy of local thermoelectric behaviors in (Bi,Sb)2Te3 films. Phys. B Condens. Matter 2015, 457, 156–159. [Google Scholar] [CrossRef]
- Kanno, T.; Yotsuhashi, S.; Sakai, A.; Takahashi, K.; Adachi, H. Enhancement of transverse thermoelectric power factor in tilted Bi/Cu multilayer. Appl. Phys. Lett. 2009, 94, 061917. [Google Scholar] [CrossRef]
- MacDonald, D.K.C. Thermoelectricity: An Introduction to the Principles; Dover Publications: Mineola, NY, USA, 2006. [Google Scholar]
- Korolyuk, S.L.; Pilat, I.M.; Samoilovich, A.G.; Slipchenko, V.N.; Snarskii, A.A.; Tsar’kov, E.F. Anisotropic thermoelements. Sov. Phys. Semicond. 1972, 7, 502–507. [Google Scholar]
- Sampilovic, A.G.; Slipchenko, V.N. Investigation of the efficiency of anisotropic thermoelements. Sov. Phys. Semicond. 1975, 9, 1249–1251. [Google Scholar]
- Qian, B.; Ren, F. Cooling performance of transverse thermoelectric devices. Int. J. Heat Mass Transf. 2016, 95, 787–794. [Google Scholar] [CrossRef]
- Ali, S.A.; Mazumder, S. Computational study of transverse peltier coolers for low temperature applications. Int. J. Heat Mass Transf. 2013, 62, 373–381. [Google Scholar] [CrossRef]
- Lengfellner, H.; Kremb, G.; Schnellbögl, A.; Betz, J.; Renk, K.F.; Prettl, W. Giant voltages upon surface heating in normal YBa2Cu3O7−δ films suggesting an atomic layer thermopile. Appl. Phys. Lett. 1992, 60, 501–503. [Google Scholar] [CrossRef]
- Kanno, T.; Sakai, A.; Takahashi, K.; Omote, A.; Adachi, H.; Yamada, Y. Tailoring effective thermoelectric tensors and high-density power generation in a tubular Bi0.5Sb1.5Te3/Ni composite with cylindrical anisotropy. Appl. Phys. Lett. 2012, 101, 011906. [Google Scholar] [CrossRef]
- Kanno, T.; Takahashi, K.; Sakai, A.; Tamaki, H.; Kusada, H.; Yamada, Y. Detection of thermal radiation, sensing of heat flux, and recovery of waste heat by the transverse thermoelectric effect. J. Electron. Mater. 2014, 43, 2072–2080. [Google Scholar] [CrossRef]
- Sakai, A.; Kanno, T.; Takahashi, K.; Tamaki, H.; Adachi, H.; Yamada, Y. Enhancement in performance of the tubular thermoelectric generator (TTEG). J. Electron. Mater. 2012, 42, 1612–1616. [Google Scholar] [CrossRef]
- Reitmaier, C.; Walther, F.; Lengfellner, H. Power generation by the transverse seebeck effect in Pb-Bi2Te3 multilayers. Appl. Phys. A 2011, 105, 347–349. [Google Scholar] [CrossRef]
- Zahner, T.; Förg, R.; Lengfellner, H. Transverse thermoelectric response of a tilted metallic multilayer structure. Appl. Phys. Lett. 1998, 73, 1364–1366. [Google Scholar] [CrossRef]
- Reitmaier, C.; Walther, F.; Lengfellner, H. Transverse thermoelectric devices. Appl. Phys. A 2010, 99, 717–722. [Google Scholar] [CrossRef]
- Fischer, K.; Stoiber, C.; Kyarad, A.; Lengfellner, H. Anisotropic thermopower in tilted metallic multilayer structures. Appl. Phys. A Mater. Sci. Proc. 2004, 78, 323–326. [Google Scholar] [CrossRef]
- Kyarad, A.; Lengfellner, H. Al-si multilayers: A synthetic material with large thermoelectric anisotropy. Appl. Phys. Lett. 2004, 85, 5613. [Google Scholar] [CrossRef]
- Kyarad, A.; Lengfellner, H. Transverse peltier effect in tilted Pb-Bi2Te3 multilayer structures. Appl. Phys. Lett. 2006, 89, 192103. [Google Scholar] [CrossRef]
- Ren, F.; Wang, H.; Menchhofer, P.A.; Kiggans, J.O. Thermoelectric and mechanical properties of multi-walled carbon nanotube doped Bi0.4Sb1.6Te3 thermoelectric material. Appl. Phys. Lett. 2013, 103, 221907. [Google Scholar] [CrossRef]
- Gaultois, M.W.; Sparks, T.D.; Borg, C.K.H.; Seshadri, R.; Bonificio, W.D.; Clarke, D.R. Data-driven review of thermoelectric materials: Performance and resource considerations. Chem. Mater. 2013, 25, 2911–2920. [Google Scholar] [CrossRef]
- Burkov, A.T.; Vedernikov, M.V. Thermoelectric properties of metallic materials. In CRC handbook of Thermoelectrics; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- CRC Handbook of Chemistry and Physics, 97th ed.; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2017.
- ASM Handbook, Properties of Pure Metals, Properties and Selection: Nonferrous Alloys and Special-Purpose Materials; ASM International: Almere, The Netherlands, 1990; pp. 1099–1201.
- Efunda. Available online: http://www.efunda.com/home.cfm (access on 16 July 2017).
- Nan, C.-W.; Birringer, R.; Clarke, D.R.; Gleiter, H. Effective thermal conductivity of particulate composites with interfacial thermal resistance. J. Appl. Phys. 1997, 81, 6692–6699. [Google Scholar] [CrossRef]
- Nolas, G.S.; Sharp, J.; Goldsmid, H.J. Thermoelectrics: Basic Principles and New Materials Developments; Springer: Berlin, Germany, 2001. [Google Scholar]

| Material | T (K) | S (μV/K) | ρ (Ω·m) | λ (W·m−1·K−1) | Reference |
|---|---|---|---|---|---|
| Bi0.5Sb1.5Te3 | 300 | 220.00 | 1.20 × 10−5 | 1.10 | [28] |
| PbTe | 700 | 236.00 | 2.25 × 10−5 | 1.44 | [29] |
| Si0.2Ge0.8 | 1000 | 232.00 | 2.48 × 10−5 | 2.56 | [29] |
| Bi | 300 | −110.00 | 1.05 × 10−6 | 8.20 | [10] |
| Pb | 300 | −1.05 | 2.13 × 10−7 | 35.30 | [30,31] |
| In | 300 | 1.68 | 8.40 × 10−8 | 83.70 | [30,32] |
| Sn | 300 | −1.00 | 1.05 × 10−7 | 62.50 | [30,32] |
| Al | 300 | −1.66 | 2.62 × 10−8 | 247.00 | [30,32] |
| Ni | 300 | −19.50 | 7.20 × 10−8 | 90.70 | [30,31] |
| 700 | −25.80 | 1.70 × 10−7 | 72.20 | [30,33] | |
| 1000 | −29.90 | 4.20 × 10−7 | 71.80 | [30,33] | |
| Cu | 300 | 1.83 | 1.67 × 10−8 | 400.00 | [30,31] |
| 700 | 2.83 | 3.83 × 10−8 | 372.50 | [30,31] | |
| 1000 | 5.36 | 7.92 × 10−8 | 357.00 | [30,31] | |
| Ag | 300 | 1.51 | 1.63 × 10−8 | 429.00 | [30,31] |
| 700 | 2.82 | 4.21 × 10−8 | 404.00 | [30,31] | |
| 1000 | 7.95 | 6.52 × 10−8 | 379.00 | [30,31] | |
| Au | 300 | 1.94 | 2.01 × 10−8 | 317.00 | [30,31] |
| 700 | 2.86 | 5.82 × 10−8 | 291.00 | [30,31] | |
| 1000 | 3.85 | 8.85 × 10−8 | 270.00 | [30,31] |
| Fiber Volume Fraction (f) | KCL Model | FEA Simulation | |
|---|---|---|---|
| Square Fiber | Circular Fiber | ||
| 0.1 | 38.0 K | 31.8 K | 31.8 K |
| 0.2 | 34.1 K | 31.6 K | 32.7 K |
| 0.3 | 32.0 K | 31.4 K | 31.2 K |
| 0.4 | 31.3 K | 31.2 K | 30. 6 K |
| 0.5 | 31.7 K | 32.3 K | 31.8 K |
| Temperature (K) | Matrix Material | Fiber Material | Fiber Volume Fraction (f) | Rotation Angle (α, Degree) | ZtransT |
|---|---|---|---|---|---|
| 300 K | Bi0.5Sb1.5Te3 | Ni | 0.40 | 12.60 | 0.35 |
| Al | 0.50 | 8.10 | 0.32 | ||
| Au | 0.55 | 7.20 | 0.32 | ||
| Ag | 0.51 | 6.30 | 0.31 | ||
| Cu | 0.56 | 6.30 | 0.31 | ||
| Bi | 0.40 | 34.20 | 0.31 | ||
| In | 0.39 | 13.50 | 0.29 | ||
| Sn | 0.40 | 15.30 | 0.28 | ||
| Pb | 0.38 | 19.80 | 0.27 | ||
| 700 K | PbTe | Ni | 0.36 | 15.30 | 0.42 |
| Au | 0.48 | 7.20 | 0.35 | ||
| Cu | 0.48 | 7.20 | 0.33 | ||
| Ag | 0.43 | 8.10 | 0.33 | ||
| 1000 K | Si0.2Ge0.8 | Ni | 0.37 | 20.70 | 0.27 |
| Au | 0.36 | 10.80 | 0.26 | ||
| Ag | 0.40 | 9.00 | 0.25 | ||
| Cu | 0.37 | 9.90 | 0.25 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, B.; Ren, F. Transverse Thermoelectricity in Fibrous Composite Materials. Energies 2017, 10, 1006. https://doi.org/10.3390/en10071006
Qian B, Ren F. Transverse Thermoelectricity in Fibrous Composite Materials. Energies. 2017; 10(7):1006. https://doi.org/10.3390/en10071006
Chicago/Turabian StyleQian, Bosen, and Fei Ren. 2017. "Transverse Thermoelectricity in Fibrous Composite Materials" Energies 10, no. 7: 1006. https://doi.org/10.3390/en10071006
APA StyleQian, B., & Ren, F. (2017). Transverse Thermoelectricity in Fibrous Composite Materials. Energies, 10(7), 1006. https://doi.org/10.3390/en10071006






