Developing an Input-Output Based Method to Estimate a National-Level Energy Return on Investment (EROI)
Abstract
:1. Introduction
2. A National-Level EROI: The Concept
2.1. Background
2.2. The Benefits of a National-Level EROI
2.3. Conceptual Issues and Choices
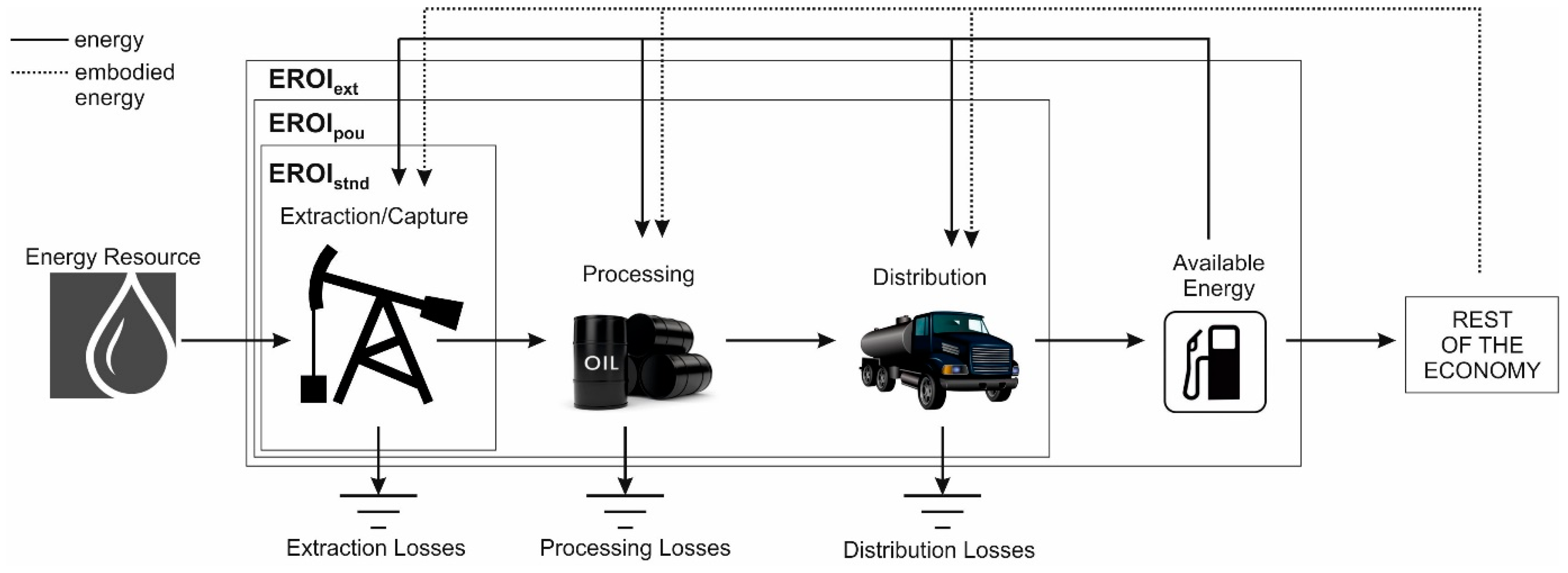
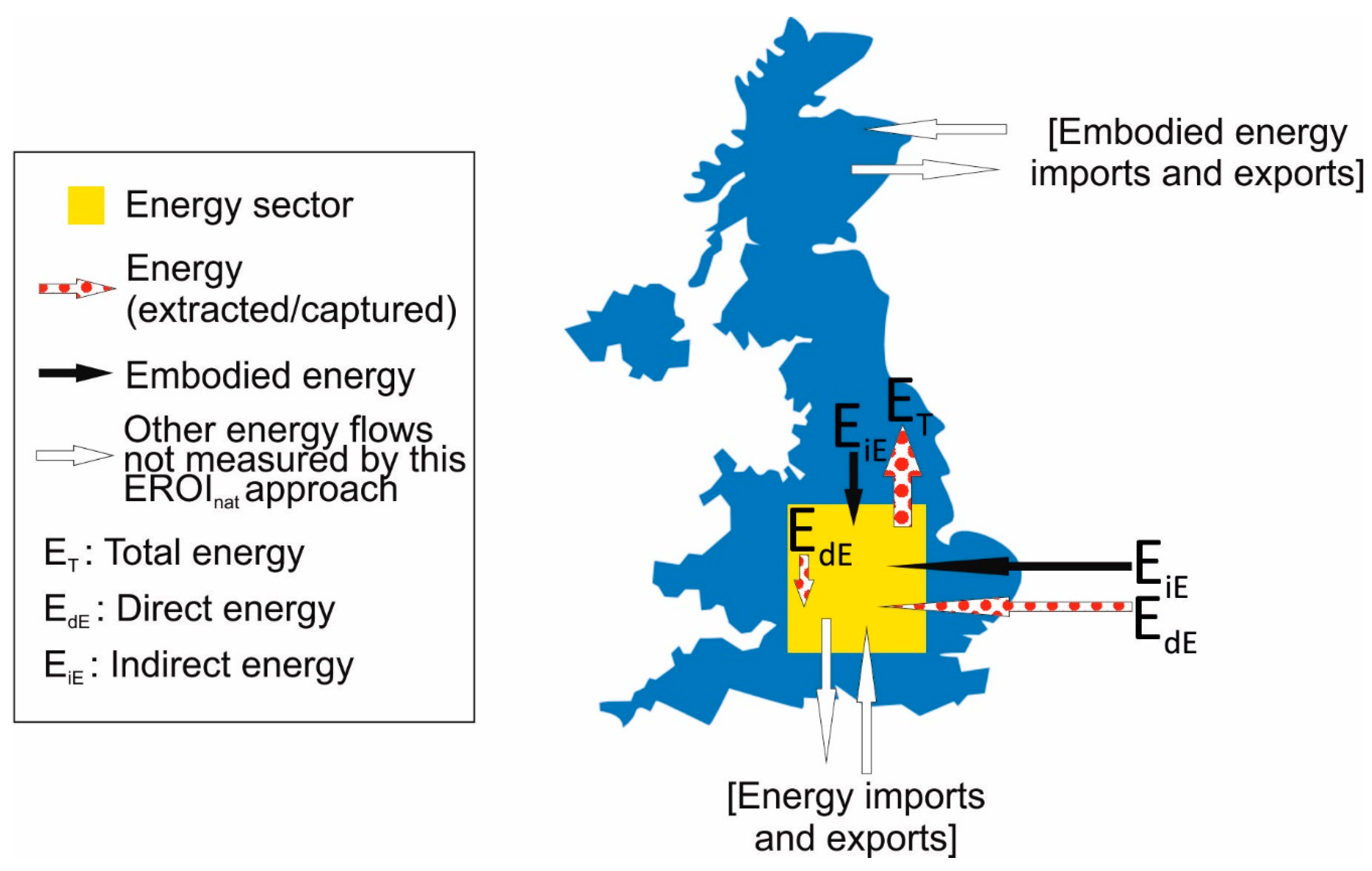
2.3.1. Boundary of Analysis
2.3.2. Accounting for Embodied Energy Inputs
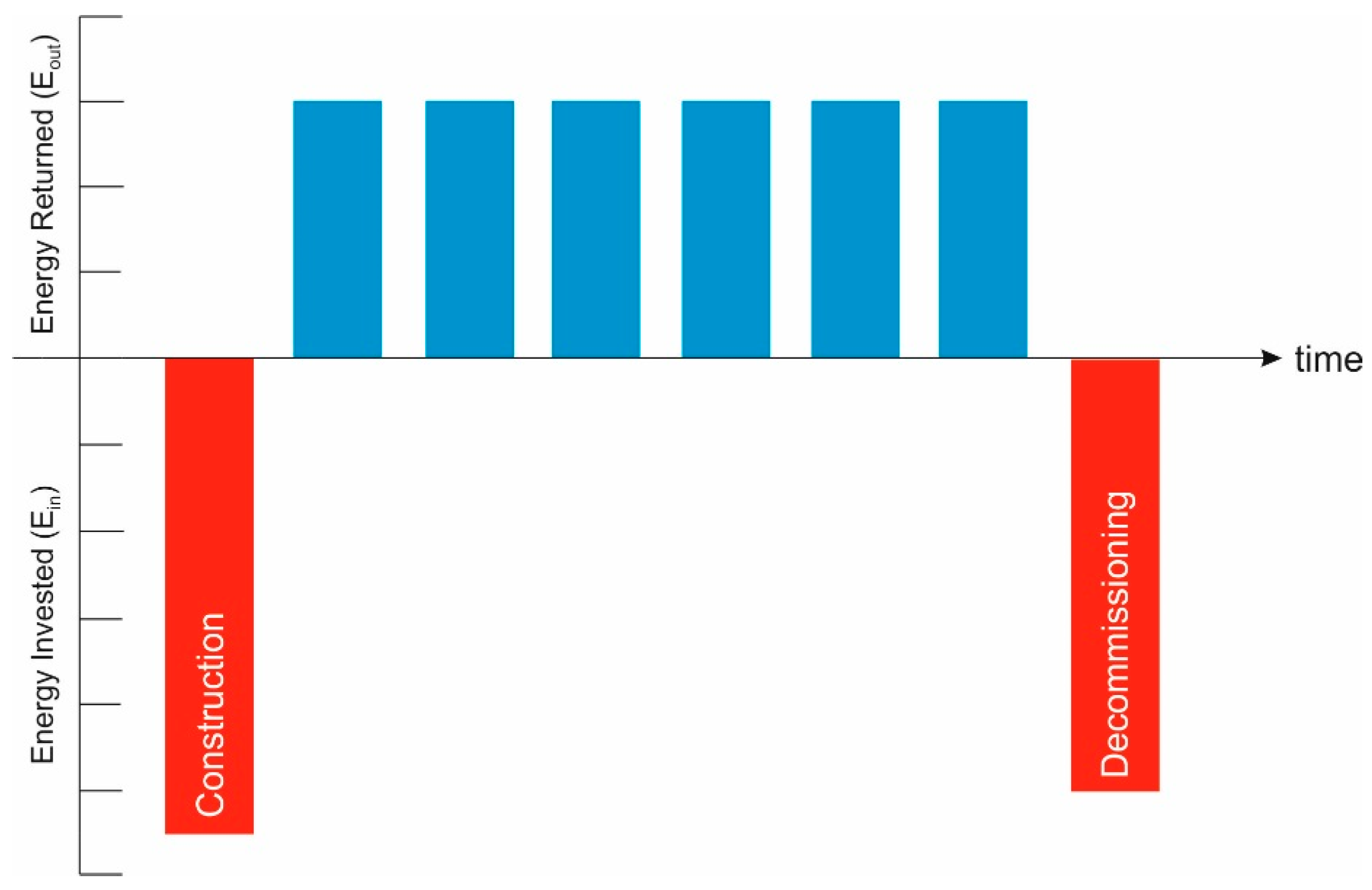
2.3.3. Temporality
2.3.4. Accounting for Energy Quality
3. A national-Level EROI: The Data and the Methodology
3.1. Input-Output and Energy
3.2. EROInat(UK): Data
3.3. EROInat(UK): Methodology
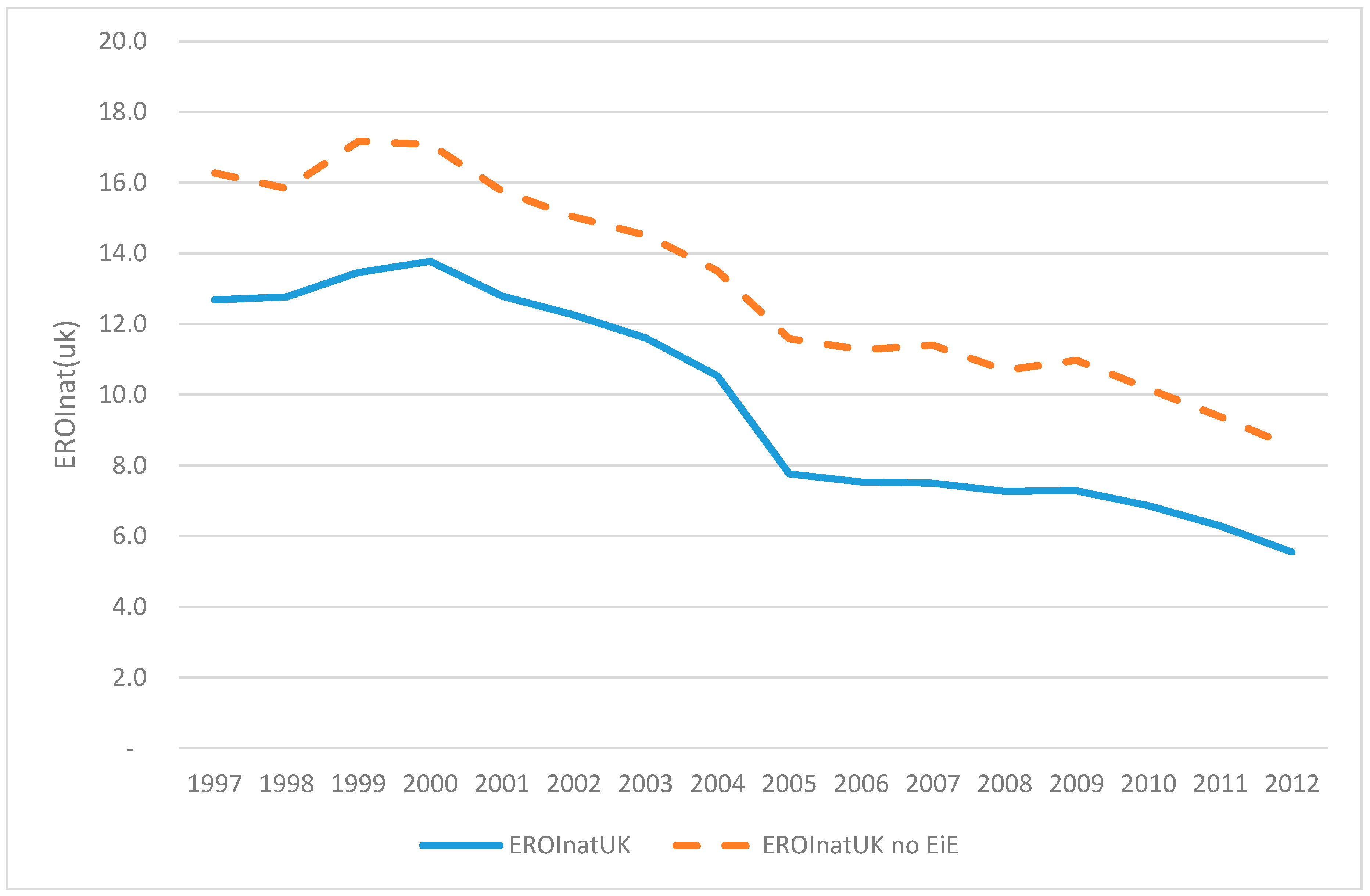
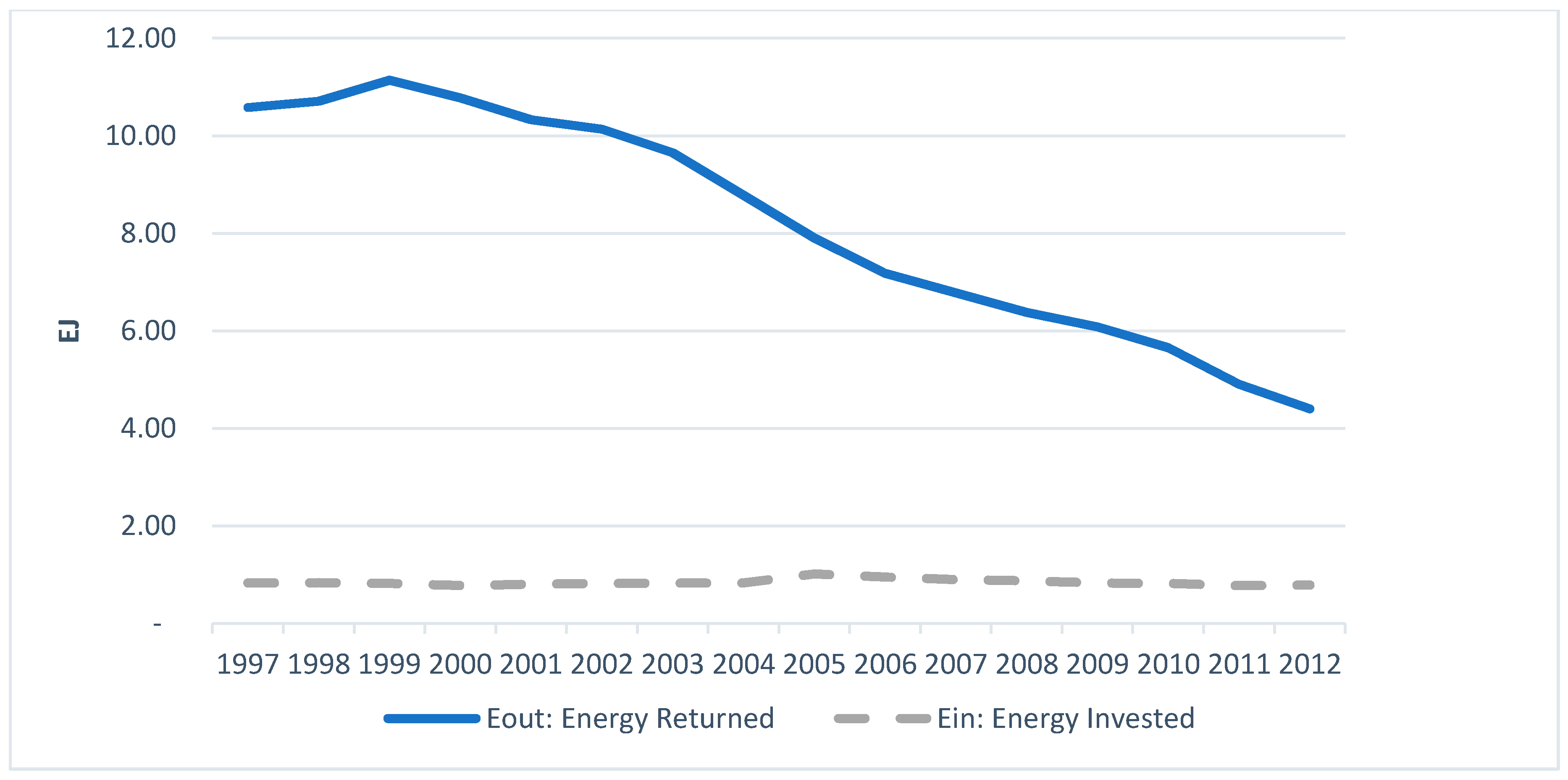
4. Results and Discussion
5. Conclusions and Policy Implications
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
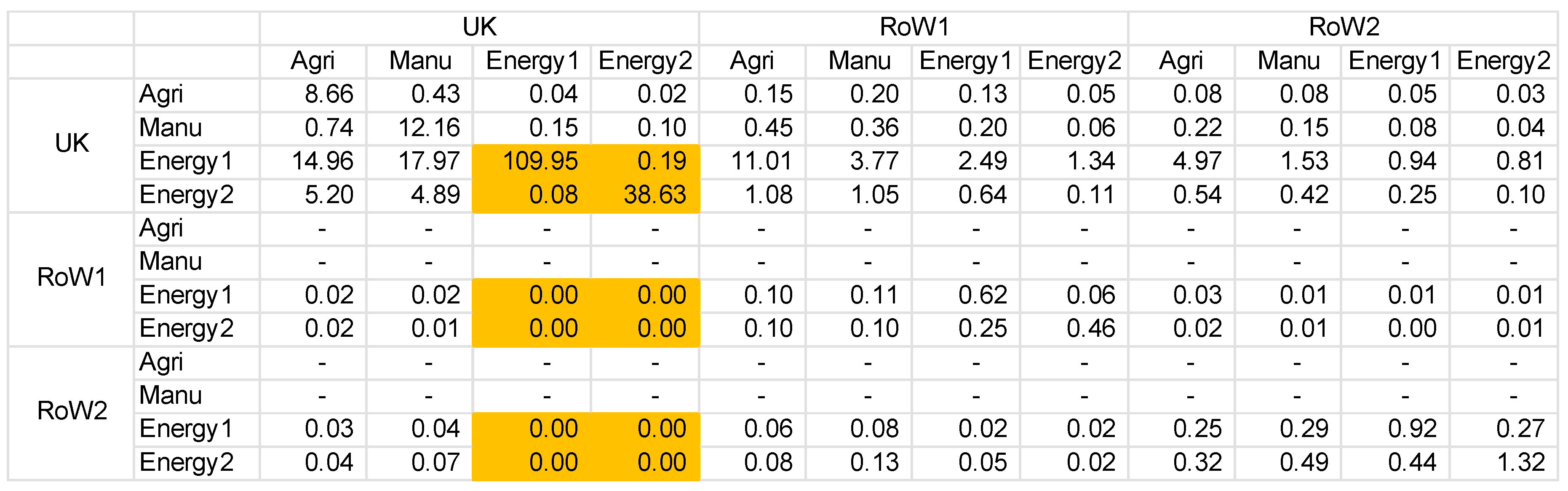
Appendix A
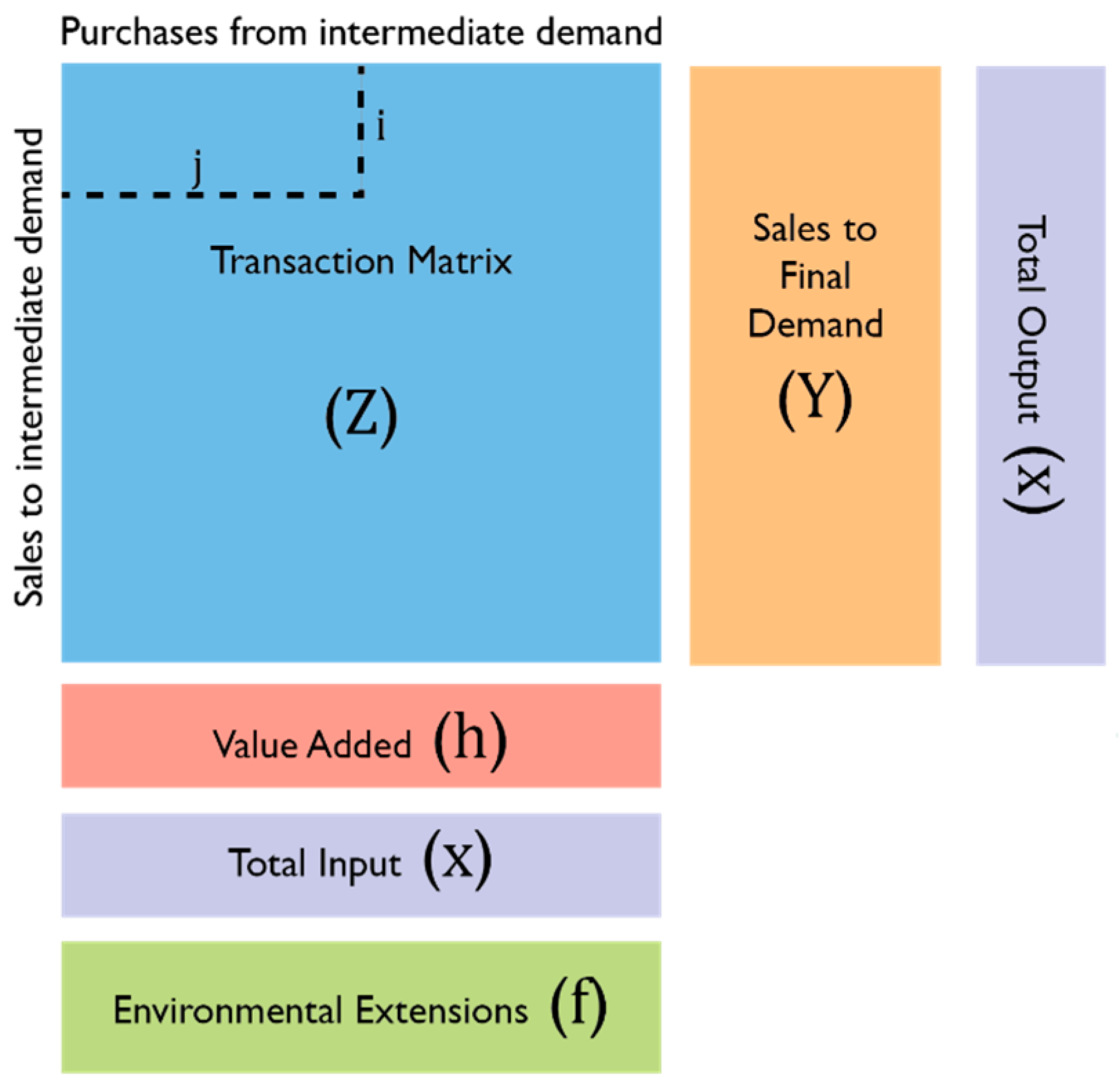
Appendix A.1. A Note on Notation
Appendix A.2. Multi-Regional Input-Output Matrix Structure, with an Energy Extension
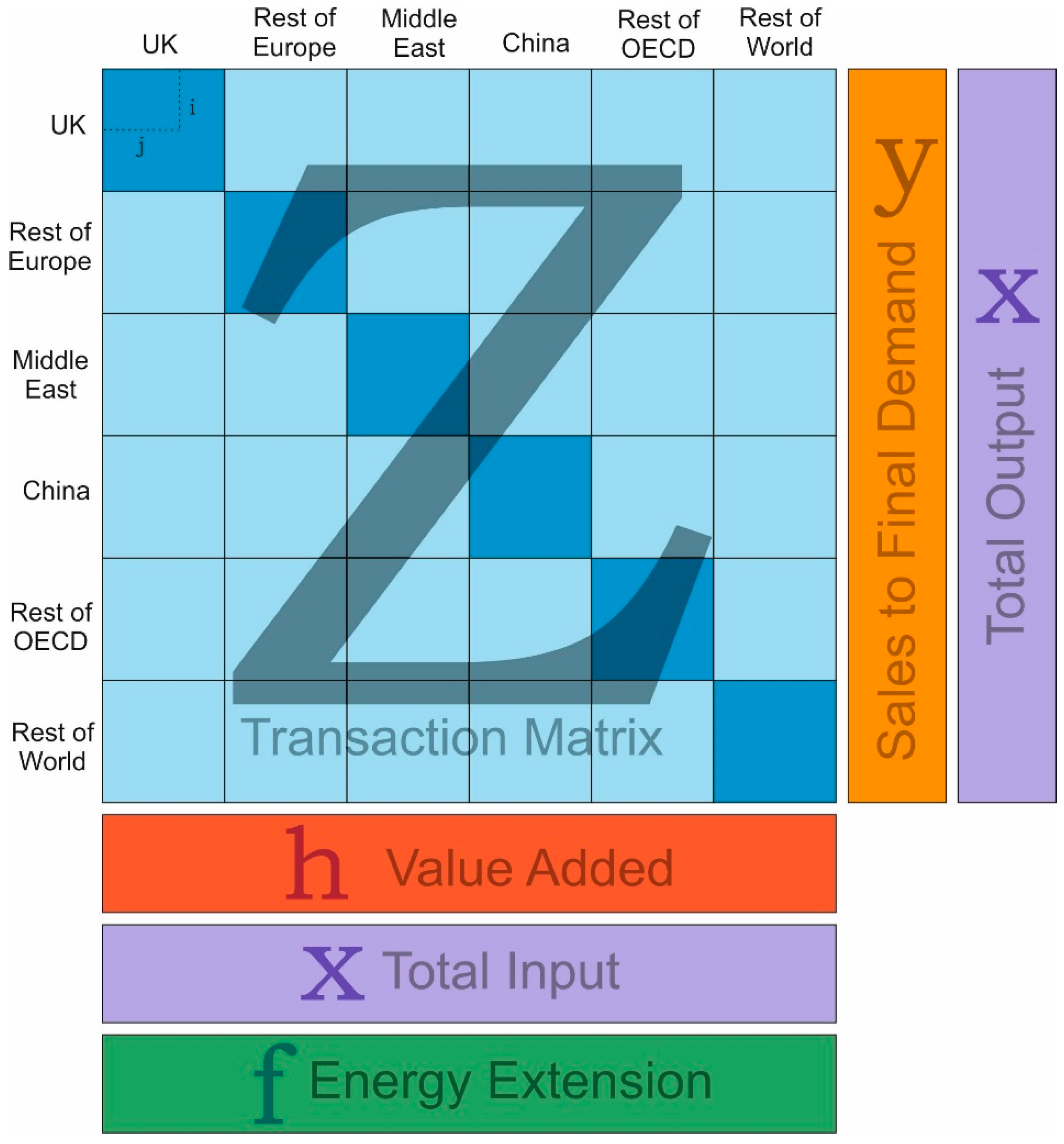
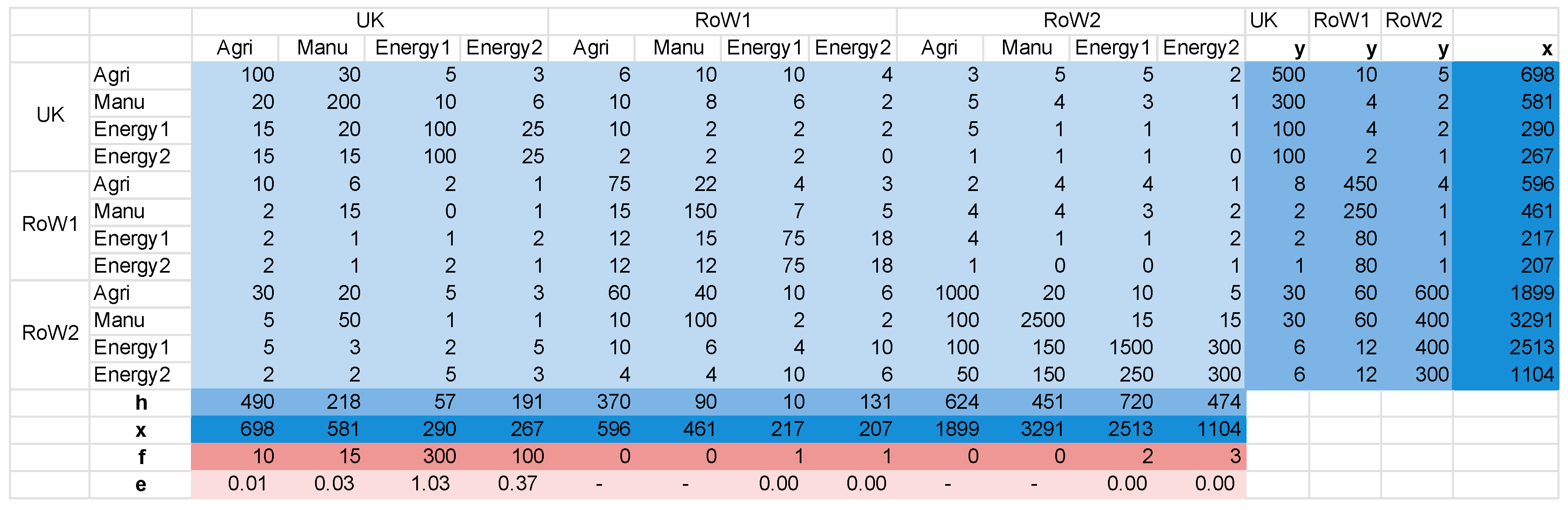
Appendix A.3. Basic Calculations: Obtaining the A, L and F Matrices
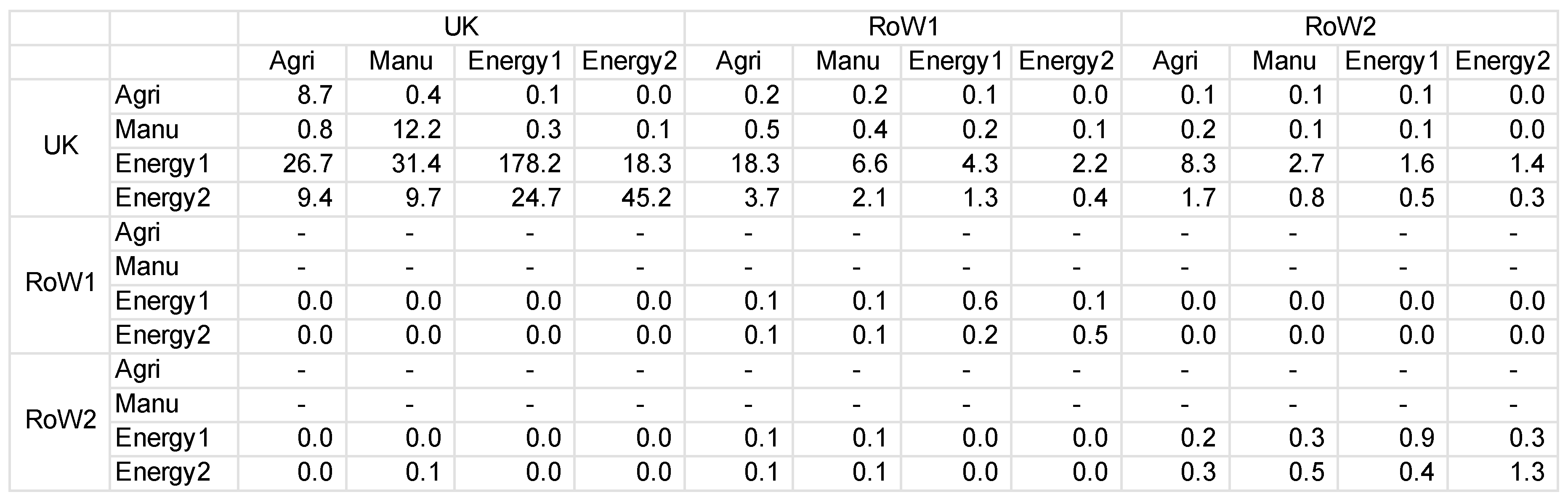
Appendix A.4. EROInat Specific Calculations: Obtaining Indirect Energy
Appendix B
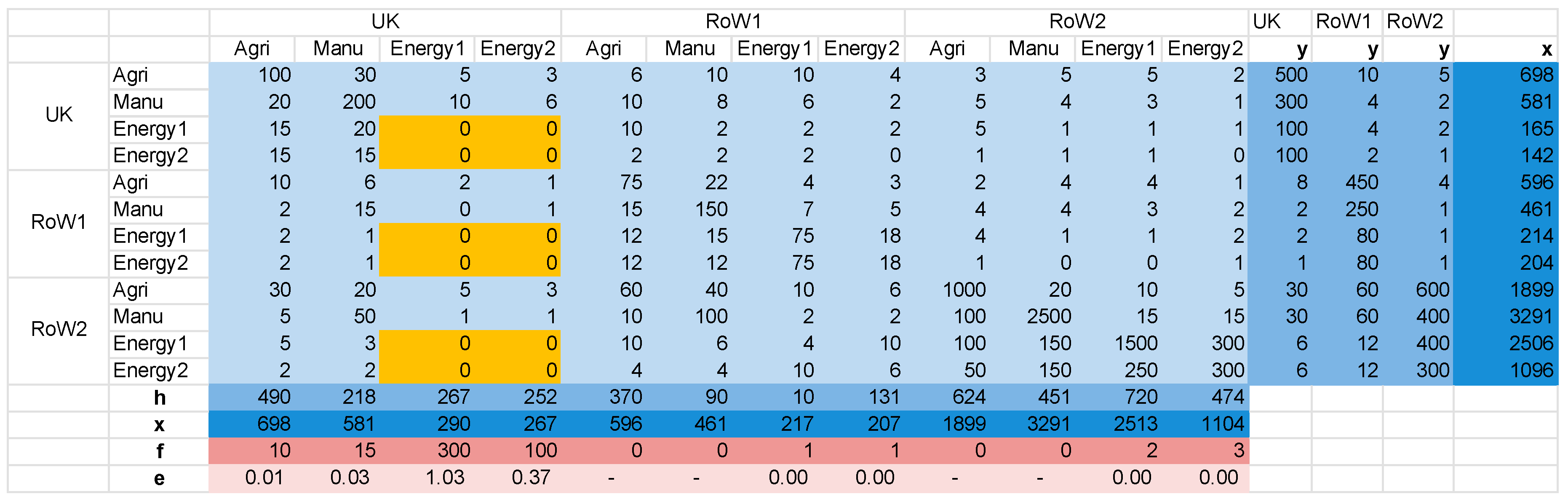
References
- Hall, C.A.S.; Kiltgaard, K.A. Energy and the Wealth of Nations. Understanding the Biophysical Economy; Springer: New York, NY, USA, 2012. [Google Scholar]
- Cleveland, C.J. Biophysical Economics: Historical Perspective and Current Research Trends. Ecol. Modell. 1987, 38, 47–73. [Google Scholar] [CrossRef]
- Dale, M.; Krumdieck, S.; Bodger, P. Net energy yield from production of conventional oil. Energy Policy 2011, 39, 7095–7102. [Google Scholar] [CrossRef]
- Gagnon, N.; Hall, C.A.S.; Brinker, L. A preliminary investigation of energy return on energy investment for global oil and gas production. Energies 2009, 2, 490–503. [Google Scholar] [CrossRef]
- Lambert, J.G.; Hall, C.A.S.; Balogh, S.B. EROI of Global Energy Resources. Status, Trends and Social Implications; Department for International Development: London, UK, 2013. [Google Scholar]
- Hall, C.A.S.; Lambert, J.G.; Balogh, S.B. EROI of different fuels and the implications for society. Energy Policy 2014, 64, 141–152. [Google Scholar] [CrossRef]
- Dale, M.; Benson, S.M. Energy Balance of the Global Photovoltaic (PV) Industry—Is the PV Industry a Net Electricity Producer? Environ. Sci. Technol. 2013, 47, 3482–3489. [Google Scholar] [CrossRef] [PubMed]
- Raugei, M.; Fullana-i-Palmer, P.; Fthenakis, V. The energy return on energy investment (EROI) of photovoltaics: Methodology and comparisons with fossil fuel life cycles. Energy Policy 2012, 45, 576–582. [Google Scholar] [CrossRef]
- Kubiszewski, I.; Cleveland, C.J.; Endres, P.K. Meta-analysis of net energy return for wind power systems. Renew. Energy 2010, 35, 218–225. [Google Scholar] [CrossRef]
- Cleveland, C.J. Net energy from the extraction of oil and gas in the United States. Energy 2005, 30, 769–782. [Google Scholar] [CrossRef]
- Brandt, A.R. Oil depletion and the energy efficiency of oil production: The case of California. Sustainability 2011, 3, 1833–1854. [Google Scholar] [CrossRef]
- Smith, D.M. The yield and energy content of milk and the energetic efficiency of sows on different levels of nutrition during gestation and lactation. New Zeal. J. Agric. Res. 1960, 3, 745–763. [Google Scholar] [CrossRef]
- Hall, C.A.S. Migration and metabolism in a temperate stream ecosystem. Ecology 1972, 53, 585–604. [Google Scholar] [CrossRef]
- Hall, C.A.S.; Lavine, M.; Sloane, J. Efficiency of energy delivery systems: I. An economic and energy analysis. Environ. Manag. 1979, 3, 493–504. [Google Scholar]
- Cleveland, C.J.; Costanza, R.; Hall, C.A.S.; Kaufmann, R.K. Energy and the U.S. Economy: A Biophysical Perspective. Science 1984, 225, 890–897. [Google Scholar] [CrossRef] [PubMed]
- Murphy, D.J.; Hall, C.A.S. Year in review—EROI or energy return on (energy) invested. Ann. N. Y. Acad. Sci. 2010, 1185, 102–118. [Google Scholar] [CrossRef] [PubMed]
- Murphy, D.J.; Hall, C.A.S.; Dale, M.; Cleveland, C.J. Order from Chaos: A Preliminary Protocol for Determining the EROI of Fuels. Sustainability 2011, 3, 1888–1907. [Google Scholar] [CrossRef]
- Murphy, D.J.; Hall, C.A.S. Energy return on investment, peak oil, and the end of economic growth. Ann. N. Y. Acad. Sci. 2011, 52–72. [Google Scholar] [CrossRef] [PubMed]
- Poisson, A.; Hall, C.A.S. Time series EROI for Canadian oil and gas. Energies 2013, 6, 5940–5959. [Google Scholar] [CrossRef]
- Leach, G. Net energy analysis—Is it any use? Energy Policy 1975, 3, 332–344. [Google Scholar] [CrossRef]
- Peet, N.J.; Baines, J.T.; Macdonald, M.G.; Tohili, J.C.; Bassett, R.M. Energy supply and net energy in New Zealand. Energy Policy 1987, 15, 239–248. [Google Scholar] [CrossRef]
- Lambert, J.G.; Hall, C.A.S.; Balogh, S.B.; Gupta, A.; Arnold, M. Energy, EROI and quality of life. Energy Policy 2014, 64, 153–167. [Google Scholar] [CrossRef]
- King, C.W.; Maxwell, J.P.; Donovan, A. ComparingWorld Economic and Net Energy Metrics, Part 2: Total Economy Expenditure Perspective. Energies 2015, 8, 12975–12996. [Google Scholar] [CrossRef]
- King, C.W. Comparing World Economic and Net Energy Metrics, Part 3: Macroeconomic Historical and Future Perspectives. Energies 2015, 8, 12997–13020. [Google Scholar] [CrossRef]
- King, C.W.; Maxwell, J.P.; Donovan, A. ComparingWorld Economic and Net Energy Metrics, Part 1: Single Technology and Commodity Perspective. Energies 2015, 8, 12949–12974. [Google Scholar] [CrossRef]
- Fizaine, F.; Court, V. Energy expenditure, economic growth, and the minimum EROI of society. Energy Policy 2016, 95, 172–186. [Google Scholar] [CrossRef]
- Herendeen, R.A. Connecting net energy with the price of energy and other goods and services. Ecol. Econ. 2015, 109, 142–149. [Google Scholar] [CrossRef]
- Raugei, M.; Leccisi, E. A comprehensive assessment of the energy performance of the full range of electricity generation technologies deployed in the United Kingdom. Energy Policy 2016, 90, 46–59. [Google Scholar] [CrossRef]
- Dale, M.; Krumdieck, S.; Bodger, P. Global energy modelling—A biophysical approach (GEMBA) Part 1: An overview of biophysical economics. Ecol. Econ. 2012, 73, 152–157. [Google Scholar] [CrossRef]
- Heun, M.K.; Santos, J.; Brockway, P.E.; Pruim, R.; Domingos, T.; Sakai, M. From Theory to Econometrics to Energy Policy: Cautionary Tales for Policymaking Using Aggregate Production Functions. Energies 2017, 10, 203. [Google Scholar] [CrossRef]
- Brockway, P.E.; Heun, M.K.; Santos, J.; Barrett, J.R. Energy-Extended CES Aggregate Production : Current Aspects of Their Specification and Econometric Estimation. Energies 2017, 10, 202. [Google Scholar] [CrossRef]
- Kümmel, R. Why energy’s economic weight is much larger than its cost share. Environ. Innov. Soc. Transit. 2013, 9, 33–37. [Google Scholar] [CrossRef]
- Ayres, R.U.; van den Bergh, J.C.J.M.; Lindenberger, D.; Warr, B. The underestimated contribution of energy to economic growth. Struct. Chang. Econ. Dyn. 2013, 27, 79–88. [Google Scholar] [CrossRef]
- Brandt, A.R.; Dale, M. A General Mathematical Framework for Calculating Systems-Scale Efficiency of Energy Extraction and Conversion: Energy Return on Investment (EROI) and Other Energy Return Ratios. Energies 2011, 4, 1211–1245. [Google Scholar] [CrossRef]
- Herendeen, R.A. Net Energy Analysis: Concepts and Methods. Encycl. Energy 2004, 4, 283–289. [Google Scholar]
- International Energy Agency (IEA). Energy Statistics Manual; IEA: Paris, France, 2005. [Google Scholar]
- Brandt, A.R.; Dale, M.; Barnhart, C.J. Calculating systems-scale energy efficiency and net energy returns: A bottom-up matrix-based approach. Energy 2013, 62, 235–247. [Google Scholar] [CrossRef]
- Hall, C.A.S.; Balogh, S.B.; Murphy, D.J. What is the Minimum EROI that a Sustainable Society Must Have? Energies 2009, 2, 25–47. [Google Scholar] [CrossRef]
- Brandt, A.R.; Englander, J.; Bharadwaj, S. The energy efficiency of oil sands extraction: Energy return ratios from 1970 to 2010. Energy 2013, 55, 693–702. [Google Scholar] [CrossRef]
- Harmsen, J.H.M.; Roes, A.L.; Patel, M.K. The impact of copper scarcity on the efficiency of 2050 global renewable energy scenarios. Energy 2013, 50, 62–73. [Google Scholar] [CrossRef]
- Arvesen, A.; Hertwich, E.G. More caution is needed when using life cycle assessment to determine energy return on investment (EROI). Energy Policy 2015, 76, 1–6. [Google Scholar] [CrossRef]
- Dale, M. The Energy Balance of the Photovoltaic (PV) Industry: Is the PV industry a net electricity producer? Environ. Sci. Technol. 2013, 47, 3482–3489. [Google Scholar] [CrossRef] [PubMed]
- Cleveland, C.J.; Kaufmann, R.K.; Stern, D.I. Aggregation and the role of energy in the economy. Ecol. Econ. 2000, 32, 301–317. [Google Scholar] [CrossRef]
- Brockway, P.E.; Barrett, J.R.; Foxon, T.J.; Steinberger, J.K. Divergence of trends in US and UK Aggregate Exergy Efficiencies 1960–2010. Environ. Sci. Technol. 2014, 48, 9874–9881. [Google Scholar] [CrossRef] [PubMed]
- Warr, B.; Ayres, R.U.; Eisenmenger, N.; Krausmann, F.; Schandl, H. Energy use and economic development: A comparative analysis of useful work supply in Austria, Japan, the United Kingdom and the US during 100years of economic growth. Ecol. Econ. 2010, 69, 1904–1917. [Google Scholar] [CrossRef]
- Brockway, P.E.; Steinberger, J.K.; Barrett, J.R.; Foxon, T.J. Understanding China’s past and future energy demand: An exergy efficiency and decomposition analysis. Appl. Energy 2015, 155, 892–903. [Google Scholar] [CrossRef]
- Williams, E.; Warr, B.; Ayres, R.U. Efficiency dilution: Long-term exergy conversion trends in Japan. Environ. Sci. Technol. 2008, 42, 4964–4970. [Google Scholar] [CrossRef] [PubMed]
- Kostic, M.M. Energy: Physics. Encycl. Energy Eng. Technol. 2012, 2, 808–823. [Google Scholar]
- Gaggioli, R.A.; Wepfer, W.J. Exergy economics. Energy 1980, 5, 823–837. [Google Scholar] [CrossRef]
- Wall, G. Exergy—A Useful Concept; Chalmers University of Technology: Göteborg, Sweden, 1986. [Google Scholar]
- Wall, G. Exergy—A Useful Concept within Resource Accounting; Chalmers University of Technology and University of Göteborg: Göteborg, Sweden, 1977. [Google Scholar]
- Wall, G. Exergy tools. Proc. Inst. Mech. Eng. Part A J. Power Energy 2003, 217, 125–136. [Google Scholar] [CrossRef]
- Kanoglu, M.; Cengel, Y.A.; Dincer, I. Efficiency Evaluation of Energy Systems; Springer: London, UK, 2012. [Google Scholar]
- Dincer, I. The role of exergy in energy policy making. Energy Policy 2002, 30, 137–149. [Google Scholar] [CrossRef]
- Rosen, M.A. Benefits of exergy and needs for increased education and public understanding and applications in industry and policy—Part I: Benefits. Int. J. Exergy 2006, 3, 202–218. [Google Scholar] [CrossRef]
- Rosen, M.A. Energy crisis or exergy crisis? Exergy Int. J. 2002, 2, 125–127. [Google Scholar] [CrossRef]
- Sciubba, E.; Wall, G. A brief Commented History of Exergy From the Beginnings to 2004. Int. J. Thermodyn. 2007, 10, 1–26. [Google Scholar]
- IEA. Statistics: Frequently Asked Questions. Available online: http://www.iea.org/statistics/resources/questionnaires/faq/#one (accessed on 2 February 2017).
- Casler, S.; Wilbur, S. Energy Input-Output Analysis. A Simple Guide. Resour. Energy 1984, 6, 187–201. [Google Scholar] [CrossRef]
- Bullard, C.W.; Penner, P.S.; Pilati, D.A. Net energy analysis. Handbook for combining process and input-output analysis. Resour. Energy 1978, 1, 267–313. [Google Scholar] [CrossRef]
- Bullard, C.W.; Herendeen, R.A. The energy cost of goods and services. Energy Policy 1975, 3, 268–278. [Google Scholar] [CrossRef]
- Wright, D.J. Goods and services: An input-output analysis. Energy Policy 1974, 2, 307–315. [Google Scholar] [CrossRef]
- Brandt, A.R. How Does Energy Resource Depletion Affect Prosperity? Mathematics of a Minimum Energy Return on Investment (EROI). Biophys. Econ. Resour. Qual. 2017, 2, 2. [Google Scholar] [CrossRef]
- IEA. World Energy Balances: Extended Energy Balances, 1960–2014. Available online: http://dx.doi.org/10.5257/iea/web/2015 (accessed on 15 October 2015).
- ONS Supply and Use Tables. Available online: http://www.ons.gov.uk/ons/taxonomy/index.html?nscl=Supply+and+Use+Tables (accessed on 6 October 2016).
- Lenzen, M.; Moran, D.; Kanemoto, K.; Geschke, A. Building Eora: A Global Multi-Region Input-Output Database At High Country And Sector Resolution. Econ. Syst. Res. 2013, 25, 20–49. [Google Scholar] [CrossRef]
- Lenzen, M.; Kanemoto, K.; Moran, D.; Geschke, A. Mapping the structure of the world economy. Environ. Sci. Technol. 2012, 46, 8374–8381. [Google Scholar] [CrossRef] [PubMed]
- Roberts, F. The aims, methods and uses of energy accounting. Appl. Energy 1978, 4, 199–217. [Google Scholar] [CrossRef]
- Guevara, Z.H.Z. Three-Level Energy Decoupling: Energy Decoupling at the Primary, Final and Useful Levels of Energy Use; Universidade de Lisboa: Lisboa, Portuguese, 2014. [Google Scholar]
- International Energy Agency (IEA). World Energy Investment Outlook 2014; IEA: Paris, France, 2014. [Google Scholar]
- Berndt, E.R. From Technocracy to Net Energy Analysis: Engineers, Economists and Recurring Energy Theories of Value; Sloan School of Management, Masachusetts Institute of Technology: Cambridge, MA, USA, 1982. [Google Scholar]
- Carbajales-Dale, M.; Barnhart, C.J.; Brandt, A.R.; Benson, S.M. A better currency for investing in a sustainable future. Nat. Clim. Chang. 2014, 4, 524–527. [Google Scholar] [CrossRef]
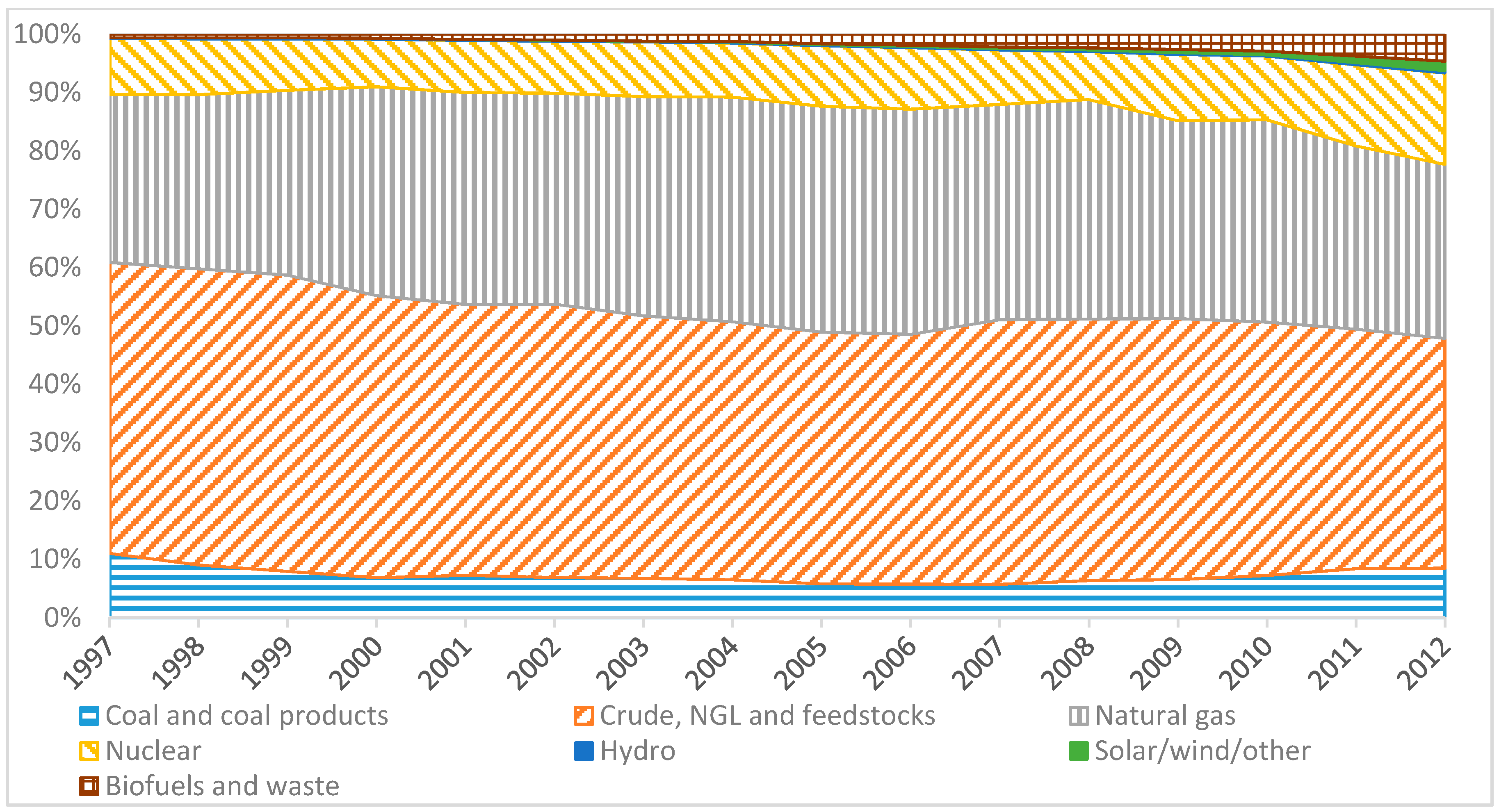
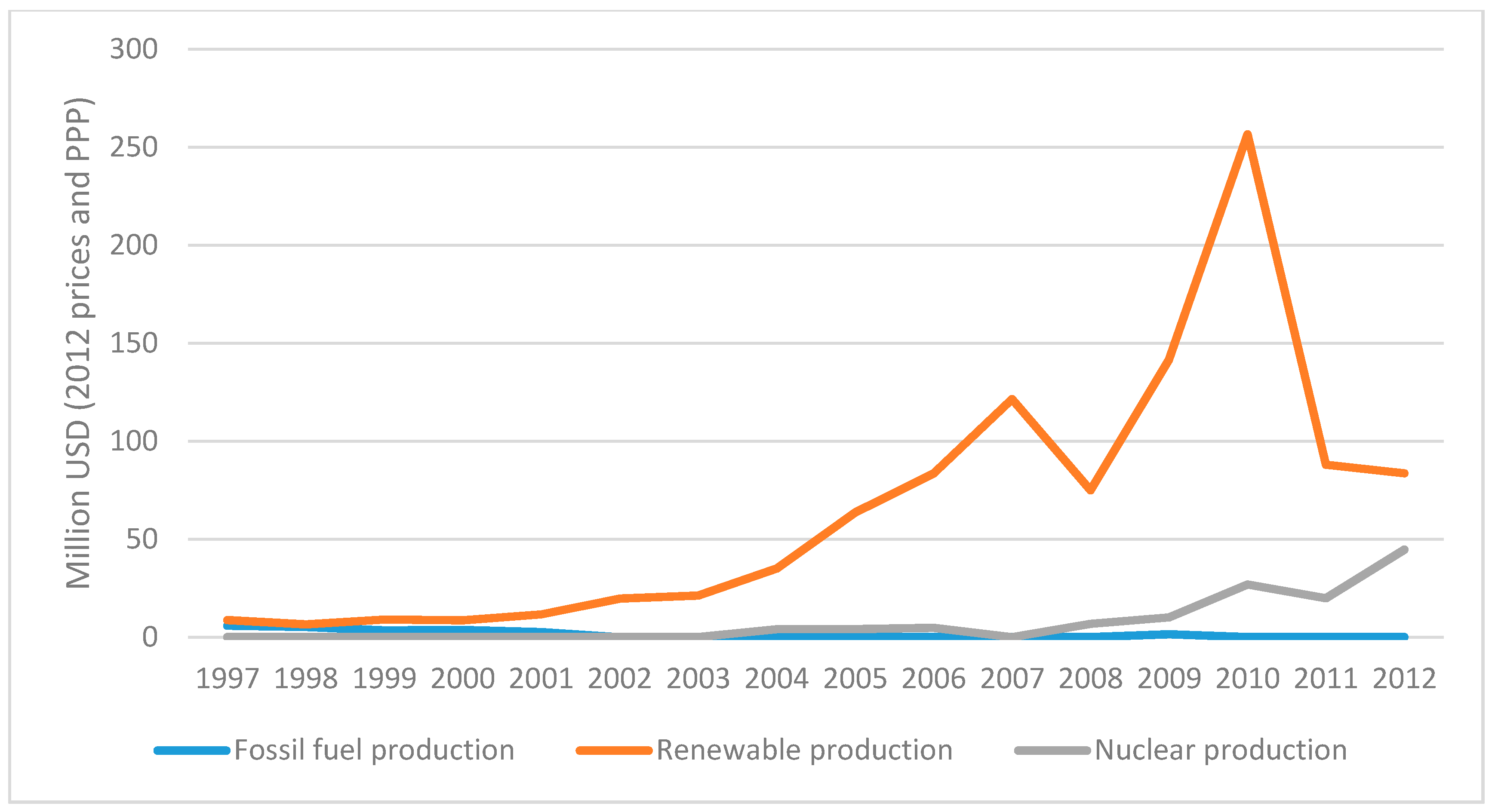
| Energy Source | Change in Production (%) | |
|---|---|---|
| 1997–2010 | 2010–2012 | |
| Coal and coal products | −0.6 | 0.0 |
| Crude, NGL and feedstocks | −0.5 | −0.1 |
| Natural gas | −0.3 | −0.2 |
| Nuclear | −0.4 | 0.1 |
| Hydro | −0.1 | 0.4 |
| Solar/wind/other | 13.5 | 14.2 |
| Biofuels and waste | 1.6 | 0.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brand-Correa, L.I.; Brockway, P.E.; Copeland, C.L.; Foxon, T.J.; Owen, A.; Taylor, P.G. Developing an Input-Output Based Method to Estimate a National-Level Energy Return on Investment (EROI). Energies 2017, 10, 534. https://doi.org/10.3390/en10040534
Brand-Correa LI, Brockway PE, Copeland CL, Foxon TJ, Owen A, Taylor PG. Developing an Input-Output Based Method to Estimate a National-Level Energy Return on Investment (EROI). Energies. 2017; 10(4):534. https://doi.org/10.3390/en10040534
Chicago/Turabian StyleBrand-Correa, Lina I., Paul E. Brockway, Claire L. Copeland, Timothy J. Foxon, Anne Owen, and Peter G. Taylor. 2017. "Developing an Input-Output Based Method to Estimate a National-Level Energy Return on Investment (EROI)" Energies 10, no. 4: 534. https://doi.org/10.3390/en10040534
APA StyleBrand-Correa, L. I., Brockway, P. E., Copeland, C. L., Foxon, T. J., Owen, A., & Taylor, P. G. (2017). Developing an Input-Output Based Method to Estimate a National-Level Energy Return on Investment (EROI). Energies, 10(4), 534. https://doi.org/10.3390/en10040534








