Heat Transfer and Flow of Nanofluids in a Y-Type Intersection Channel with Multiple Pulsations: A Numerical Study
Abstract
:1. Introduction
2. Mathematical Model
2.1. Governing Equations
2.1.1. Conservation of Mass
2.1.2. Conservation of Linear Momentum
2.1.3. Conservation of Nanoparticles Concentration/Flux
2.1.4. Conservation of Energy
2.2. Constitutive Equations
2.2.1. The Stress Tensor
2.2.2. The Particle flux
2.2.3. The Internal Energy
2.2.4. The Heat Flux Vector
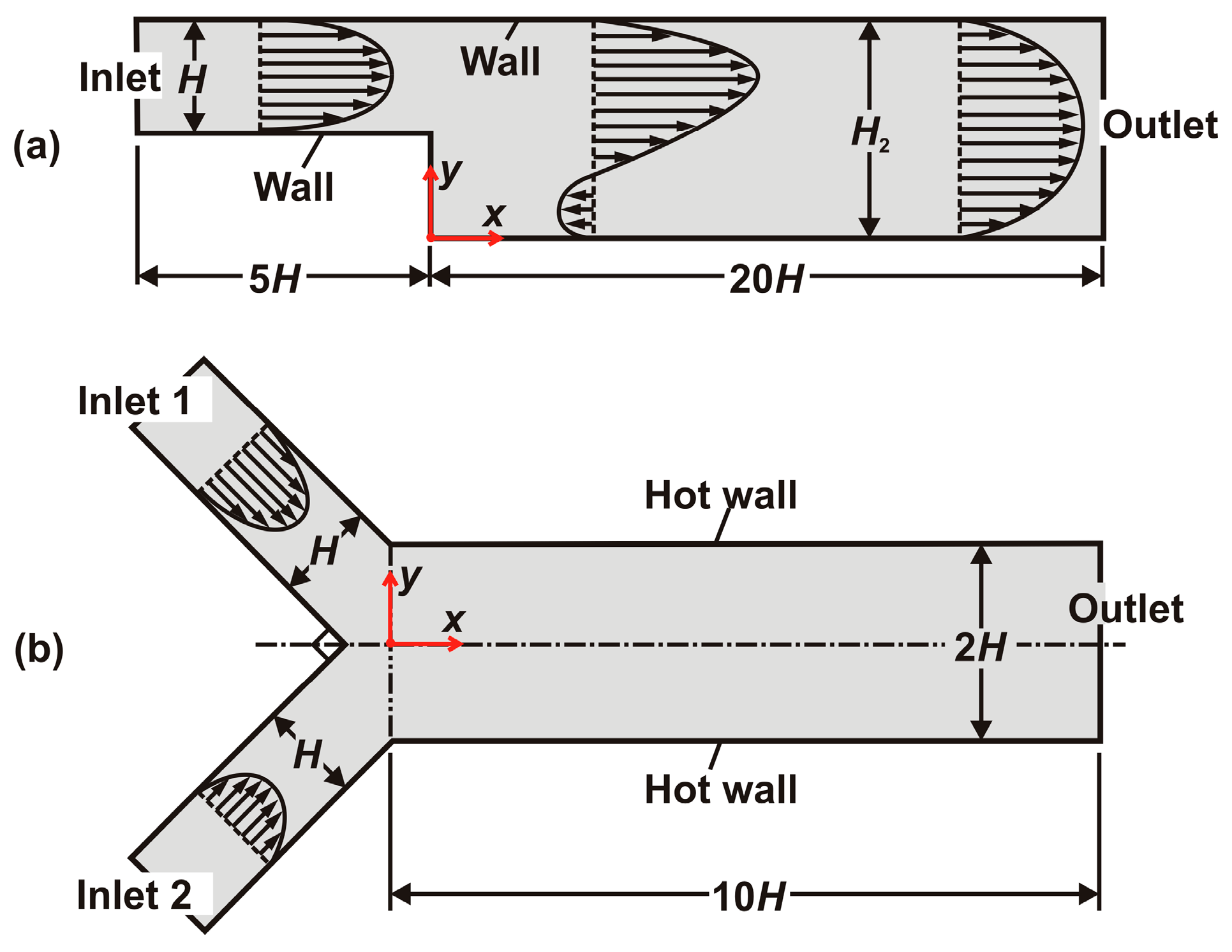
3. The Geometry and the Kinematics of the Physical Problems
4. Results and Discussion
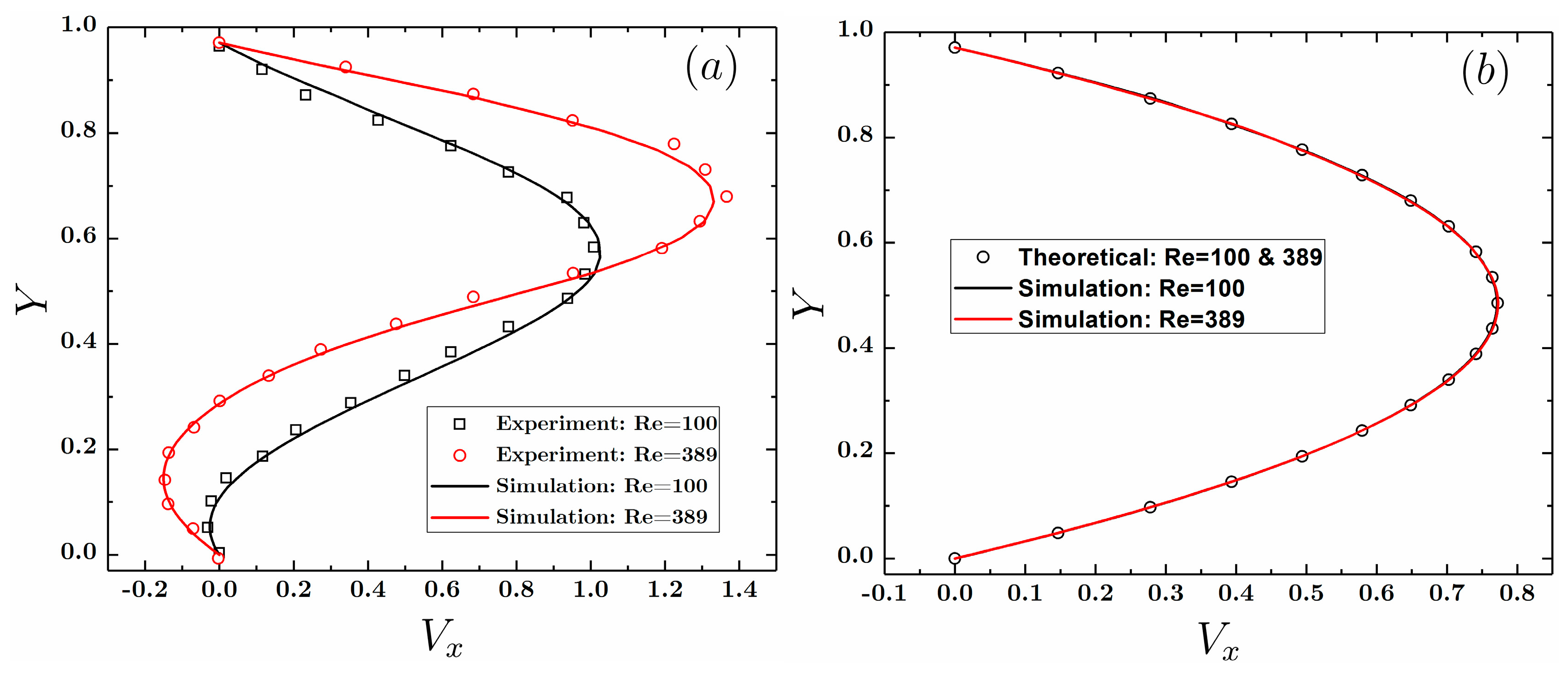
4.1. Steady Flow in a Backward-Step Channel
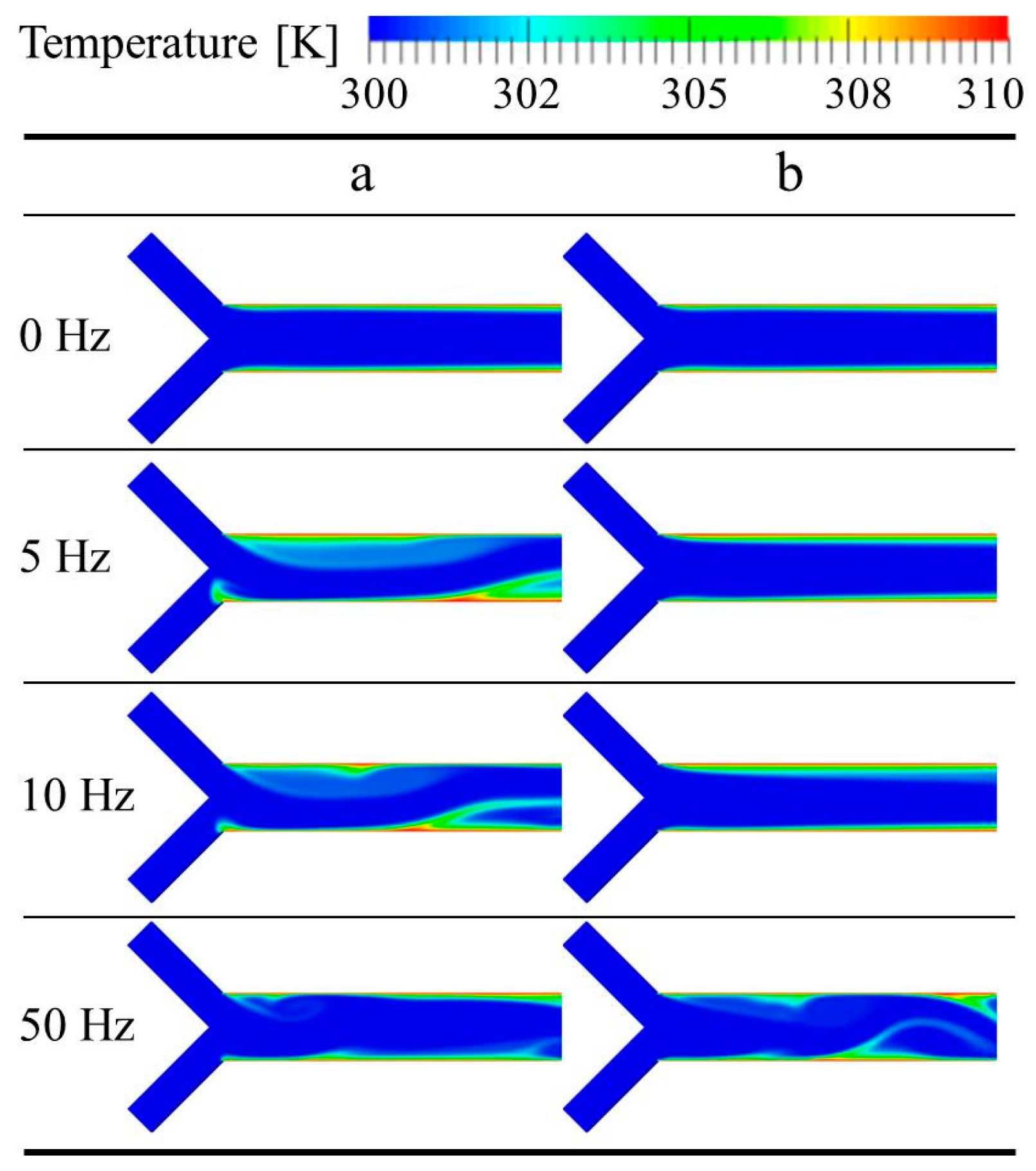
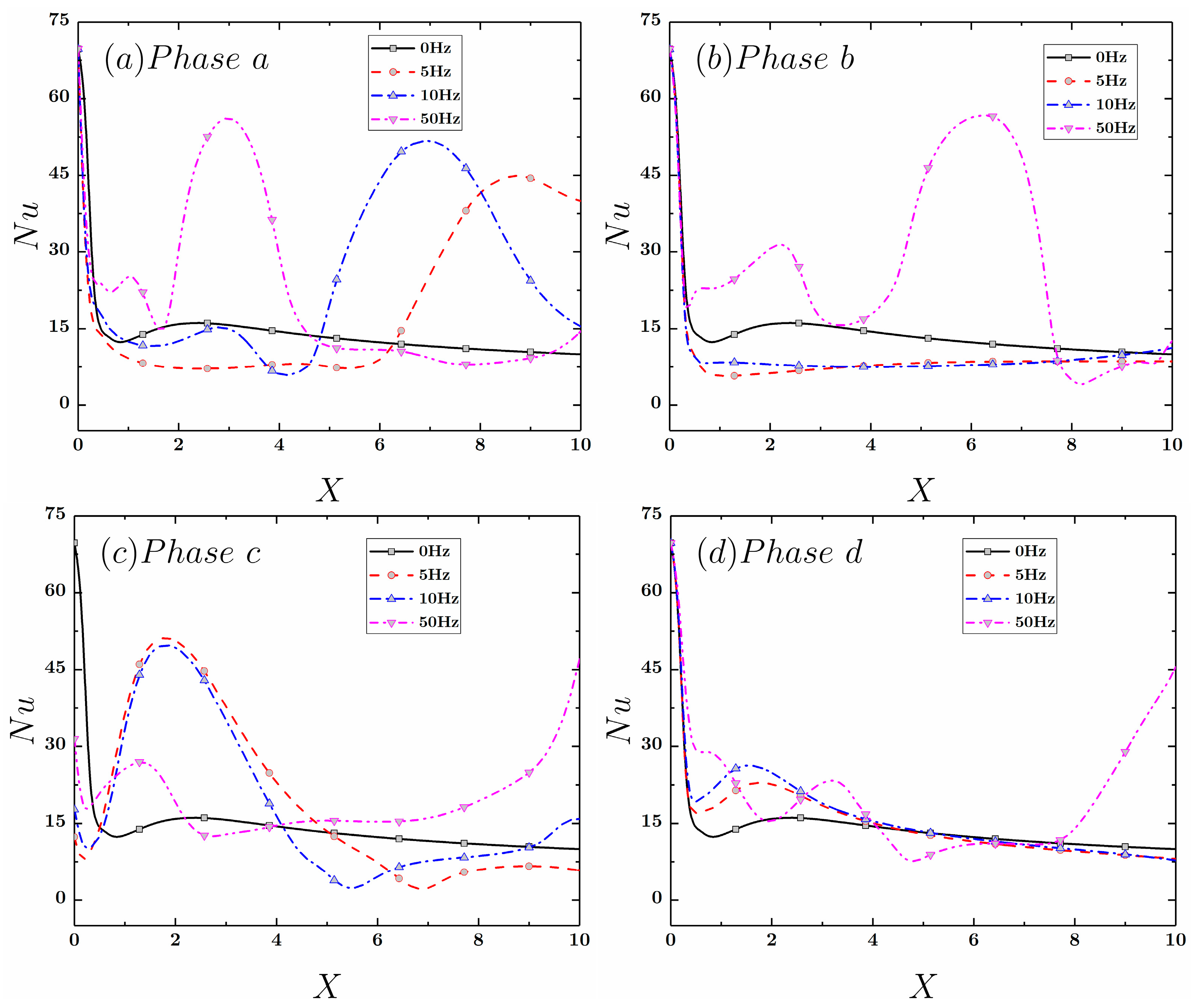
4.2. Heat Transfer Characteristics in a Y-Type Channel with Pulsed Flow
4.2.1. The Effect of Frequency
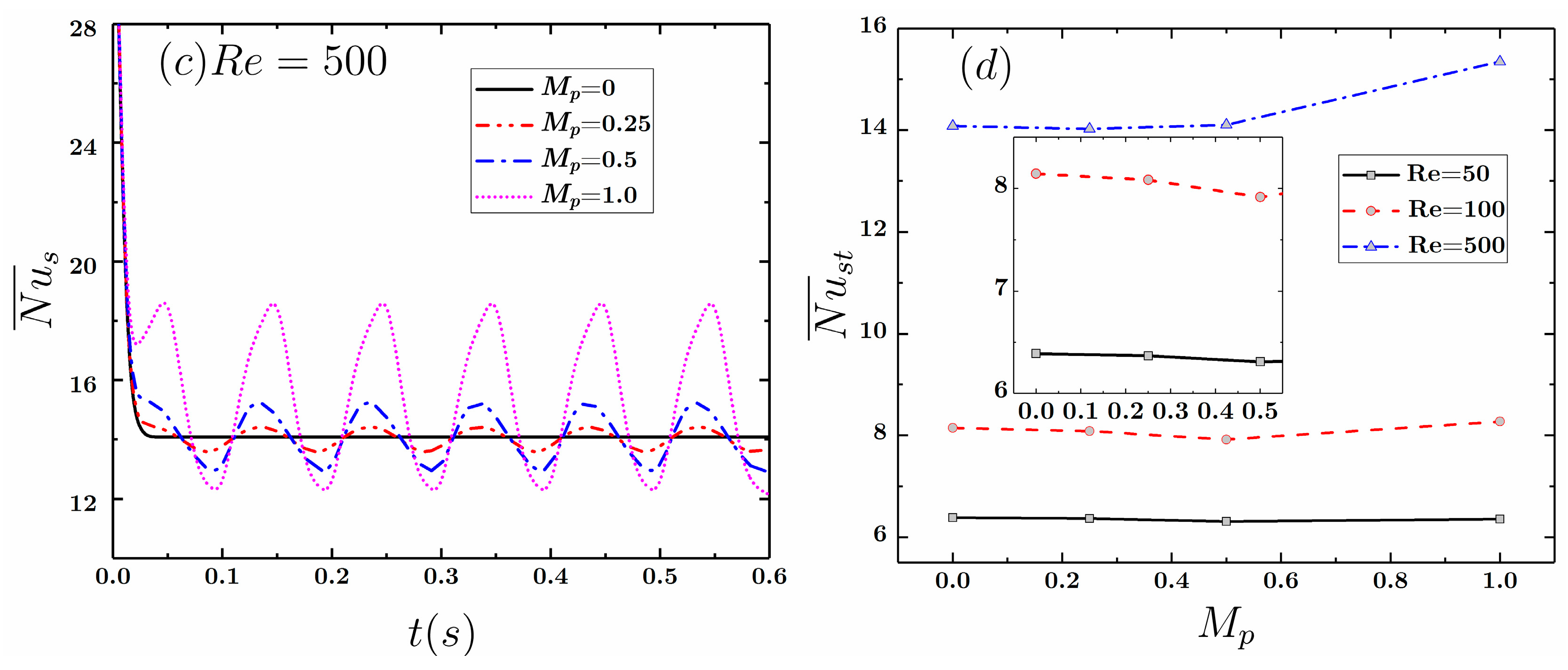
4.2.2. The Effect of the Pulse Amplitude
4.2.3. The Effect of Nanoparticle Concentration
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| body force vector (N/kg) | |
| specific heat of pure fluid (J/(kgK)) | |
| specific heat of nanofluid (J/(kgK)) | |
| specific heat of pure nanoparticles (J/(kgK)) | |
| diameter of nanoparticles (m) | |
| symmetric part of velocity gradient (s−1) | |
| diffusivity of thermophoresis (m2/s) | |
| internal energy (J/m3) | |
| pulse frequency (Hz) | |
| height of the inlet channel (m) | |
| reference length scale (m) | |
| particles flux (kg/(m2s)) | |
| particles flux (thermophoresis) (kg/(m2s)) | |
| particles flux (Brownian motion) (kg/(m2s)) | |
| Boltzmann constant (J/K) | |
| thermal conductivity of pure fluid (W/(mK)) | |
| thermal conductivity of nanofluid (W/(mK)) | |
| thrmal conductivity of particles (W/(mK)) | |
| length of the hot wall (m) | |
| Velocity gradient vector (s−1) | |
| pulse magnitude | |
| dimensionless shape factor | |
| local Nusselt number | |
| Spatial averaged Nusselt number | |
| time and spatial averaged Nusselt number | |
| pressure (Pa) | |
| time | |
| specific radiant energy (W/kg) | |
| heat flux vector (W/m2) | |
| Reynolds number | |
| stress tensor (Pa) | |
| reference velocity (m/s) | |
| velocity vector (m/s) | |
| dimensionless velocity vector | |
| mean inlet velocity (m/s) | |
| velocity at inlet 1 (m/s) | |
| velocity at inlet 2 (m/s) | |
| Cartesian coordinates (m) | |
| position vector (m) | |
| dimensionless Cartesian coordinates | |
| Greek symbols | |
| volume fraction of the base fluid | |
| thermal diffusivity of nanofluid (m2/s) | |
| internal energy density (W/kg) | |
| temperature (K) | |
| inlet fluid temperature (K) | |
| temperature of the hot wall (K) | |
| dynamic viscosity of base fluid (Pa∙s) | |
| dynamic viscosity of nanofluid (Pa∙s) | |
| kinematic viscosity of nanofluid (m2/s) | |
| density of base fluid (kg/m3) | |
| density of nanofluid (kg/m3) | |
| density of pure nanoparticles (kg/m3) | |
| dimensionless time | |
| volume fraction of nanoparticles | |
| thermal conductivity ratio | |
References
- Lienhard, J.H. A Heat Transfer Textbook; Courier Corporation: New York, NY, USA, 2013. [Google Scholar]
- Chen, Q.; Wang, M.; Pan, N.; Guo, Z.-Y. Optimization principles for convective heat transfer. Energy 2009, 34, 1199–1206. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q. Heat transfer enhancement of nanofluids. Int. J. Heat Fluid Flow 2000, 21, 58–64. [Google Scholar] [CrossRef]
- Webb, R.L.; Kim, N.Y. Enhanced Heat Transfer; Taylor and Francis: New York, NY, USA, 2005. [Google Scholar]
- Incropera, F.P.; De Witt, D.P. Fundamentals of Heat and Mass Transfer; John Wiley & Sons, Inc.: New York, NY, USA, 1985. [Google Scholar]
- Li, Q.; Xuan, Y.; Wang, J. Investigation on convective heat transfer and flow features of nanofluids. J. Heat Transf. 2003, 125, 151–155. [Google Scholar]
- Safaei, M.R.; Ahmadi, G.; Goodarzi, M.S.; Safdari Shadloo, M.; Goshayeshi, H.R.; Dahari, M. Heat transfer and pressure drop in fully developed turbulent flows of graphene nanoplatelets–silver/water nanofluids. Fluids 2016, 1, 20. [Google Scholar] [CrossRef]
- Safaei, M.R.; Ahmadi, G.; Goodarzi, M.S.; Kamyar, A.; Kazi, S.N. Boundary layer flow and heat transfer of FMWCNT/water nanofluids over a flat plate. Fluids 2016, 1, 31. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective Transport in Nanofluids. J. Heat Transf. 2006, 128, 240. [Google Scholar] [CrossRef]
- Ho, C.J.; Chung, Y.N.; Lai, C.-M. Thermal performance of Al2O3/water nanofluid in a natural circulation loop with a mini-channel heat sink and heat source. Energy Convers. Manag. 2014, 87, 848–858. [Google Scholar] [CrossRef]
- Kang, Z.; Wang, L. Effect of thermal-electric cross coupling on heat transport in nanofluids. Energies 2017, 10, 123. [Google Scholar] [CrossRef]
- Asirvatham, L.G.; Vishal, N.; Gangatharan, S.K.; Lal, D.M. Experimental study on forced convective heat transfer with low volume fraction of CuO/water nanofluid. Energies 2009, 2, 97–119. [Google Scholar] [CrossRef]
- Patil, M.S.; Kim, S.C.; Seo, J.-H.; Lee, M.-Y. Review of the thermo-physical properties and performance characteristics of a refrigeration system using refrigerant-based nanofluids. Energies 2016, 9, 22. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.-H.; Kang, S.-J.; Lee, M.-Y. Review on synthesis, thermo-physical property, and heat transfer mechanism of nanofluids. Energies 2016, 9, 840. [Google Scholar] [CrossRef]
- Rahgoshay, M.; Ranjbar, A.A.; Ramiar, A. Laminar pulsating flow of nanofluids in a circular tube with isothermal wall. Int. Commun. Heat Mass Transf. 2012, 39, 463–469. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. Proceedings of 1995 International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Thompson, L.J.; Lee, S. Enhanced thermal conductivity through the development of nanofluids. In MRS Proceedings; Cambridge University Press: Cambridge, UK, 1996; Volume 457, p. 3. [Google Scholar]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Yu, W.; Thompson, L.J. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Zhang, Z.G.; Yu, W.; Lockwood, F.E.; Grulke, E.A. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Xie, Y.; Zheng, L.; Zhang, D.; Xie, G. Entropy generation and heat transfer performances of Al2O3-water nanofluid transitional flow in rectangular channels with dimples and protrusions. Entropy 2016, 18, 148. [Google Scholar] [CrossRef]
- Li, P.; Xie, Y.; Zhang, D.; Xie, G. Heat transfer enhancement and entropy generation of nanofluids laminar convection in microchannels with flow control devices. Entropy 2016, 18, 134. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A.; Emam, T.G.; Abdel-Wahed, M.S. Flow and heat transfer over a moving surface with nonlinear velocity and variable thickness in a nanofluid in the presence of thermal radiation. Can. J. Phys. 2013, 92, 124–130. [Google Scholar] [CrossRef]
- Kumar Ch, K.; Bandari, S. Melting heat transfer in boundary layer stagnation-point flow of a nanofluid towards a stretching–shrinking sheet. Can. J. Phys. 2014, 92, 1703–1708. [Google Scholar] [CrossRef]
- Mustafa, I.; Javed, T.; Majeed, A. Magnetohydrodynamic (MHD) mixed convection stagnation point flow of a nanofluid over a vertical plate with viscous dissipation. Can. J. Phys. 2015, 93, 1365–1374. [Google Scholar] [CrossRef]
- Colangelo, G.; Favale, E.; de Risi, A.; Laforgia, D. Results of experimental investigations on the heat conductivity of nanofluids based on diathermic oil for high temperature applications. Appl. Energy 2012, 97, 828–833. [Google Scholar] [CrossRef]
- Mintsa, H.A.; Roy, G.; Nguyen, C.T.; Doucet, D. New temperature dependent thermal conductivity data for water-based nanofluids. Int. J. Therm. Sci. 2009, 48, 363–371. [Google Scholar] [CrossRef]
- Gu, B.; Hou, B.; Lu, Z.; Wang, Z.; Chen, S. Thermal conductivity of nanofluids containing high aspect ratio fillers. Int. J. Heat Mass Transf. 2013, 64, 108–114. [Google Scholar] [CrossRef]
- Nnanna, A.G. Experimental model of temperature-driven nanofluid. J. Heat Transf. 2007, 129, 697–704. [Google Scholar] [CrossRef]
- Lomascolo, M.; Colangelo, G.; Milanese, M.; de Risi, A. Review of heat transfer in nanofluids: Conductive, convective and radiative experimental results. Renew. Sustain. Energy Rev. 2015, 43, 1182–1198. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Nanofluid convective heat transfer using semi analytical and numerical approaches: A review. J. Taiwan Inst. Chem. Eng. 2016, 65, 43–77. [Google Scholar] [CrossRef]
- Fang, X.; Chen, Y.; Zhang, H.; Chen, W.; Dong, A.; Wang, R. Heat transfer and critical heat flux of nanofluid boiling: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 62, 924–940. [Google Scholar] [CrossRef]
- Bigdeli, M.B.; Fasano, M.; Cardellini, A.; Chiavazzo, E.; Asinari, P. A review on the heat and mass transfer phenomena in nanofluid coolants with special focus on automotive applications. Renew. Sustain. Energy Rev. 2016, 60, 1615–1633. [Google Scholar] [CrossRef]
- Kasaeian, A.; Azarian, R.D.; Mahian, O.; Kolsi, L.; Chamkha, A.J.; Wongwises, S.; Pop, I. Nanofluid flow and heat transfer in porous media: A review of the latest developments. Int. J. Heat Mass Transf. 2017, 107, 778–791. [Google Scholar] [CrossRef]
- Jafari, M.; Farhadi, M.; Sedighi, K. Pulsating flow effects on convection heat transfer in a corrugated channel: A LBM approach. Int. Commun. Heat Mass Transf. 2013, 45, 146–154. [Google Scholar] [CrossRef]
- Shahin, G.A. The Effect of Pulsating Flow on Forced Convective Heat Transfer. Master’s Thesis, University of Western Ontario, London, ON, Canada, 1998. [Google Scholar]
- Selimefendigil, F.; Öztop, H.F. Pulsating nanofluids jet impingement cooling of a heated horizontal surface. Int. J. Heat Mass Transf. 2014, 69, 54–65. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. Forced convection with laminar pulsating flow in a channel or tube. Int. J. Therm. Sci. 2007, 46, 551–560. [Google Scholar] [CrossRef]
- Glasgow, I.; Aubry, N. Enhancement of microfluidic mixing using time pulsing. Lab Chip 2003, 3, 114–120. [Google Scholar] [CrossRef] [PubMed]
- Goullet, A.; Glasgow, I.; Aubry, N. Effects of microchannel geometry on pulsed flow mixing. Mech. Res. Commun. 2006, 33, 739–746. [Google Scholar] [CrossRef]
- Elbahjaoui, R.; El Qarnia, H. Transient behavior analysis of the melting of nanoparticle-enhanced phase change material inside a rectangular latent heat storage unit. Appl. Therm. Eng. 2017, 112, 720–738. [Google Scholar] [CrossRef]
- Mashaei, P.R.; Taheri-Ghazvini, M.; Moghadam, R.S.; Madani, S. Smart role of Al2O3-water suspension on laminar heat transfer in entrance region of a channel with transverse in-line baffles. Appl. Therm. Eng. 2017, 112, 450–463. [Google Scholar] [CrossRef]
- Ho, C.J.; Chen, Y.Z.; Tu, F.-J.; Lai, C.-M. Thermal performance of water-based suspensions of phase change nanocapsules in a natural circulation loop with a mini-channel heat sink and heat source. Appl. Therm. Eng. 2014, 64, 376–384. [Google Scholar] [CrossRef]
- Zhou, Z.; Wu, W.-T.; Massoudi, M. Fully developed flow of a drilling fluid between two rotating cylinders. Appl. Math. Comput. 2016, 281, 266–277. [Google Scholar] [CrossRef]
- Slattery, J.C. Advanced Transport Phenomena; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Phillips, R.J.; Armstrong, R.C.; Brown, R.A.; Graham, A.L.; Abbott, J.R. A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids A Fluid Dyn. 1992, 4, 30–40. [Google Scholar] [CrossRef]
- Tzou, D.Y. Thermal instability of nanofluids in natural convection. Int. J. Heat Mass Transf. 2008, 51, 2967–2979. [Google Scholar] [CrossRef]
- Liu, I.-S. Continuum Mechanics; Springer Science & Business Media: Berlin, Germany, 2002. [Google Scholar]
- Govier, G.W.; Aziz, K. The Flow of Complex Mixtures in Pipes; Krieger Pub Co: Malabar, FL, USA, 1977. [Google Scholar]
- Rajagopal, K.R.; Tao, L. Mechanics of Mixtures; Series on Advances in Mathematics for Applied Sciences; World Scientific Publishing: Singapore, 1995; Volume 35. [Google Scholar]
- Massoudi, M. A note on the meaning of mixture viscosity using the classical continuum theories of mixtures. Int. J. Eng. Sci. 2008, 46, 677–689. [Google Scholar] [CrossRef]
- Massoudi, M. A Mixture Theory formulation for hydraulic or pneumatic transport of solid particles. Int. J. Eng. Sci. 2010, 48, 1440–1461. [Google Scholar] [CrossRef]
- Phuoc, T.X.; Massoudi, M.; Chen, R.-H. Viscosity and thermal conductivity of nanofluids containing multi-walled carbon nanotubes stabilized by chitosan. Int. J. Therm. Sci. 2011, 50, 12–18. [Google Scholar] [CrossRef]
- Massoudi, M.; Phuoc, T.X. Remarks on constitutive modeling of nanofluids. Adv. Mech. Eng. 2012, 2012, 927580. [Google Scholar] [CrossRef]
- Wang, X.; Xu, X.; Choi, S.U.S. Thermal conductivity of nanoparticle-fluid mixture. J. Thermophys. Heat Transf. 1999, 13, 474–480. [Google Scholar] [CrossRef]
- Subia, S.R.; Ingber, M.S.; Mondy, L.A.; Altobelli, S.A.; Graham, A.L. Modelling of concentrated suspensions using a continuum constitutive equation. J. Fluid Mech. 1998, 373, 193–219. [Google Scholar] [CrossRef]
- Wu, W.-T.; Massoudi, M. Heat transfer and dissipation effects in the flow of a drilling fluid. Fluids 2016, 1, 4. [Google Scholar] [CrossRef]
- Fourier, J. The Analytical Theory of Heat; Dover Publications: New York, NY, USA, 1955. [Google Scholar]
- Winterton, R.H.S. Early study of heat transfer: Newton and Fourier. Heat Transf. Eng. 2001, 22, 3–11. [Google Scholar] [CrossRef]
- Massoudi, M. On the heat flux vector for flowing granular materials—Part I: Effective thermal conductivity and background. Math. Methods Appl. Sci. 2006, 29, 1585–1598. [Google Scholar] [CrossRef]
- Massoudi, M. On the heat flux vector for flowing granular materials—Part II: Derivation and special cases. Math. Methods Appl. Sci. 2006, 29, 1599–1613. [Google Scholar] [CrossRef]
- Iacobazzi, F.; Milanese, M.; Colangelo, G.; Lomascolo, M.; de Risi, A. An explanation of the Al2O3 nanofluid thermal conductivity based on the phonon theory of liquid. Energy 2016, 116, 786–794. [Google Scholar] [CrossRef]
- Milanese, M.; Iacobazzi, F.; Colangelo, G.; de Risi, A. An investigation of layering phenomenon at the liquid–solid interface in Cu and CuO based nanofluids. Int. J. Heat Mass Transf. 2016, 103, 564–571. [Google Scholar] [CrossRef]
- Sarkar, S.; Selvam, R.P. Molecular dynamics simulation of effective thermal conductivity and study of enhanced thermal transport mechanism in nanofluids. J. Appl. Phys. 2007, 102, 74302. [Google Scholar] [CrossRef]
- Kim, B.H.; Beskok, A.; Cagin, T. Molecular dynamics simulations of thermal resistance at the liquid-solid interface. J. Chem. Phys. 2008, 129, 174701. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.H.; Beskok, A.; Cagin, T. Thermal interactions in nanoscale fluid flow: Molecular dynamics simulations with solid–liquid interfaces. Microfluid. Nanofluid. 2008, 5, 551–559. [Google Scholar] [CrossRef]
- Vo, T.Q.; Park, B.; Park, C.; Kim, B. Nano-scale liquid film sheared between strong wetting surfaces: Effects of interface region on the flow. J. Mech. Sci. Technol. 2015, 29, 1681–1688. [Google Scholar] [CrossRef]
- Colangelo, G.; Favale, E.; Miglietta, P.; Milanese, M.; de Risi, A. Thermal conductivity, viscosity and stability of Al2O3-diathermic oil nanofluids for solar energy systems. Energy 2016, 95, 124–136. [Google Scholar] [CrossRef]
- Sundar, L.S.; Farooky, M.H.; Sarada, S.N.; Singh, M.K. Experimental thermal conductivity of ethylene glycol and water mixture based low volume concentration of Al2O3 and CuO nanofluids. Int. Commun. Heat Mass Transf. 2013, 41, 41–46. [Google Scholar] [CrossRef]
- Hamilton, R.L.; Crosser, O.K. Thermal conductivity of heterogeneous two-component systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Li, S.; Eastman, J.A. Measuring thermal conductivity of fluids containing oxide nanoparticles. J. Heat Transf 1999, 121, 280–289. [Google Scholar]
- Wang, X.-Q.; Mujumdar, A.S. Heat transfer characteristics of nanofluids: A review. Int. J. Therm. Sci. 2007, 46, 1–19. [Google Scholar] [CrossRef]
- OpenFOAM Programmer’s Guide Version 2.1.0; The OpenFOAM Foundation: London, UK, 2011.
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions; Imperial College London (University of London): London, UK, 2002; Volume 1. [Google Scholar]
- Armaly, B.F.; Durst, F.; Pereira, J.C.F.; Schönung, B. Experimental and theoretical investigation of backward-facing step flow. J. Fluid Mech. 1983, 127, 473–496. [Google Scholar] [CrossRef]
- Job, V.M.; Gunakala, S.R. Mixed convection nanofluid flows through a grooved channel with internal heat generating solid cylinders in the presence of an applied magnetic field. Int. J. Heat Mass Transf. 2017, 107, 133–145. [Google Scholar] [CrossRef]
- Barbés, B.; Páramo, R.; Blanco, E.; Pastoriza-Gallego, M.J.; Piñeiro, M.M.; Legido, J.L.; Casanova, C. Thermal conductivity and specific heat capacity measurements of Al2O3 nanofluids. J. Therm. Anal. Calorim. 2013, 111, 1615–1625. [Google Scholar] [CrossRef]
- Sridhara, V.; Satapathy, L.N. Al2O3-based nanofluids: A review. Nanoscale Res. Lett. 2011, 6, 456. [Google Scholar] [CrossRef] [PubMed]
- Touloukian, Y.S.; Powell, R.W.; Ho, C.Y.; Nicolaou, M.C. Thermophysical Properties of Matter-The TPRC Data Series. Volume 10. Thermal Diffusivity; DTIC Document: Bedford, MA, USA, 1974. [Google Scholar]
- Xie, H.; Wang, J.; Xi, T.; Liu, Y.; Ai, F.; Wu, Q. Thermal conductivity enhancement of suspensions containing nanosized alumina particles. J. Appl. Phys. 2002, 91, 4568–4572. [Google Scholar] [CrossRef]







| Boundary Type | Pressure | Velocity | Concentration | Temperature |
|---|---|---|---|---|
| Wall | Fixed flux (0) | Fixed value | Fixed flux (0) | Fixed value or flux |
| Inlet | Fixed value (0) | Fixed value | Fixed value (0) | Fixed value |
| Outlet | Fixed value (0) | Fixed flux (0) | Fixed flux (0) | Fixed flux (0) |
| Physical Property | Value | Physical Property | Value |
|---|---|---|---|
| 1000 kg/m3 [36,75] | 4180 J/(kg∙K) [36,75] | ||
| 3600 kg/m3 [36,76] | 784 J/(kg∙K) [76] | ||
| 60 nm [77] | 0.604 W/(m∙K) [78,79] | ||
| 1.0 cP [36,75] | 76.3 [78,79] |
| Mesh Size | The Nusselt Number, |
|---|---|
| 10,520 | 12.81 |
| 17,221 | 12.65 |
| 21,928 | 12.62 |
| 30,062 | 12.61 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.-T.; Massoudi, M.; Yan, H. Heat Transfer and Flow of Nanofluids in a Y-Type Intersection Channel with Multiple Pulsations: A Numerical Study. Energies 2017, 10, 492. https://doi.org/10.3390/en10040492
Wu W-T, Massoudi M, Yan H. Heat Transfer and Flow of Nanofluids in a Y-Type Intersection Channel with Multiple Pulsations: A Numerical Study. Energies. 2017; 10(4):492. https://doi.org/10.3390/en10040492
Chicago/Turabian StyleWu, Wei-Tao, Mehrdad Massoudi, and Hongbin Yan. 2017. "Heat Transfer and Flow of Nanofluids in a Y-Type Intersection Channel with Multiple Pulsations: A Numerical Study" Energies 10, no. 4: 492. https://doi.org/10.3390/en10040492
APA StyleWu, W.-T., Massoudi, M., & Yan, H. (2017). Heat Transfer and Flow of Nanofluids in a Y-Type Intersection Channel with Multiple Pulsations: A Numerical Study. Energies, 10(4), 492. https://doi.org/10.3390/en10040492







