Automatic J–A Model Parameter Tuning Algorithm for High Accuracy Inrush Current Simulation

Abstract

Inrush current simulation plays an important role in many tasks of the power system, such as power transformer protection. However, the accuracy of the inrush current simulation can hardly be ensured. In this paper, a Jiles–Atherton (J–A) theory based model is proposed to simulate the inrush current of power transformers. The characteristics of the inrush current curve are analyzed and results show that the entire inrush current curve can be well featured by the crest value of the first two cycles. With comprehensive consideration of both of the features of the inrush current curve and the J–A parameters, an automatic J–A parameter estimation algorithm is proposed. The proposed algorithm can obtain more reasonable J–A parameters, which improve the accuracy of simulation. Experimental results have verified the efficiency of the proposed algorithm.

1. Introduction

Power transformers are the most expensive and vital components in electrical power system networks. They are adopted into a variety of configurations and can be switched ON occasionally or frequently. Inrush current [1,2,3] is generated during the energization of a transformer. It is featured by its large magnitude and rich harmonics. Inrush current is caused by the saturation of the iron core [4,5] in the power transformer. Due to the hysteresis characteristic [6,7,8] of the iron core, the transformer can enter severe saturation conditions. Inrush current can cause undesirable effects to the power transformer or even the entire power system, such as maloperation of relay, mechanical stress on windings, noise, reduced power quality, etc.

Since the patterns of inrush current and internal fault signal are similar, it is important to distinguish them in order to perform correct protection operation. Great research effort has been devoted to the discrimination between fault current and inrush current [9,10,11,12,13]. Recently, the data-dependent methods, such as support vector machine (SVM) [14,15], artificial neural network (ANN) [16,17], and random forest (RF) [13], have become more and more popular in tasks of discrimination between inrush current and fault current. These methods treat the discrimination problem as a classification problem and input data are used to satisfy the accuracy requirement. Theoretically, both experimentally measured or simulated current can be used as inputs to train the classifiers. The advantage of the simulated data over measure one is that it can be generated as much as needed in a short time. Therefore, accurate transformer modeling and inrush current simulation is vital to the transformer protection.

The author of [18] built up a low-frequency transformer model based on the equivalent magnetic circuits. In [1], the author proposed a method for simulating magnetizing inrush currents in power transformers by taking the transformer operating conditions, including transformer loading power factors, switching-on angles, and remanent flux into consideration. References [19,20] present a transformer model for low- and mid-frequency transient studies with a focus on the behavior in saturation and the estimation of residual fluxes. A hysteretic core model was implemented to auto initialize residual flux. In [21], the use of a modified J–A model with nonconstant parameters was suggested to improve simulation accuracy. An additional parameter, the peak magnetic field intensity, is added to the J–A parameters to model the power transformer. The inrush current simulated by the new model can match the measured one more precisely. In [22], the sympathetic inrush phenomenon that might occur among several parallel transformers was studied in detail. In addition, a dynamic-simulation-based reconstruction method is proposed for reproducing the phenomenon.

Although various transformer models have been proposed to deal with different problems, there is still room to further improve the performance and adaptivity. Previous methods may have limitations related to the proper representation of the hysteretic behavior of the core, and some others may be too complicated to be implemented and used for practical applicaiton.

A precise transformer model depends on the accurate description of its magnetic characteristics. The characteristics exhibit non-linear, hysteretic, and dynamic behavior due to eddy and anomalous losses in electrically conducting magnetic materials. In this paper, to model the power transformer, the Jiles–Atherton (J–A) model [23,24] was used for its accuracy and ease in numerical implementation. The original J–A model is based on the energy-balance equation, which describes hysteresis loops of soft magnetic materials by simulating the magnetization process by using domain wall motion with pinning effects. By using only five parameters, the J–A model can give a detailed and reasonable expression for the hysteresis characteristics of the soft magnetic materials.

The J–A model is very sensitive to variations in the parameters, thus determining them with reasonable accuracy is a major challenge. Many advanced numerical methods are proposed to determine the correct J–A parameters. For example, in [25], the parameters of the J–A model were identified by using the stochastic optimization method simulated annealing. In [26], the inverse J–A model was used to represent the hysteresis phenomenon in the magnetic core. The parameters of this model are optimally determined using inrush current measurements by the shuffled frog-leaping algorithm.

Different J–A parameters represent different hysteresis characteristics, and thus lead to different inrush currents. The accuracy of inrush current simulation can be improved by using the more accurate J–A parameters.

The direct correlation between J–A parameters and inrush current hasn’t been built up systematically in previous work. In addition, an efficient automatic algorithm for determining the J–A parameters for inrush current simulation needs to be proposed. In this paper, based on the proposed transformer model, the impact of the five J–A parameters are explored in detail. Based on the observation, the key feature of the inrush current signals is extracted. Using the feature as the objective function, an efficient automatic J–A parameter optimization algorithm is proposed. The proposed algorithm is applied to two different types of transformers to verify its efficiency. Experimental results show that the simulated inrush current can match the measure inrush current well, which demonstrates the accuracy and robustness of the proposed algorithm.

The major contribution of this paper lies in four aspects as shown below:

(a)

A J–A theory based transformer model is proposed to simulate the inrush current of the power transformer.

(b)

The impact of each J–A parameter on the inrush current is analysed. It is found that a more accurate inrush current simulation can be achieved by tuning the J–A parameters.

(c)

The most representative feature of the inrush current signals is extracted as the objective function for J–A parameter tuning.

(d)

An automatic J–A parameter tuning algorithm is proposed and verified.

The rest of the paper is organized as follows. Section 2 presents an accurate power transformer model based on J–A theory. The impact of J–A parameters on the inrush current is analyzed in Section 3. An automatic J–A parameter tuning method is presented in Section 4. The experimental results are shown and analyzed in Section 5. Finally, Section 6 concludes the paper.

2. Inrush Current Simulation Model

Transformer models for inrush current simulation can be derived by appropriate equivalent nonlinear magnetic circuits considering the saturation characteristics of iron cores. Furthermore, instead of using basic magnetization curves, the hysteresis models are more appropriate to represent the nonlinear magnetizing characteristic of the iron core. Hysteresis models such as the J–A model can reflect the magnetic hysteresis character of the magnetic material. Therefore, the J–A model is adopted in this paper to model the power transformer.

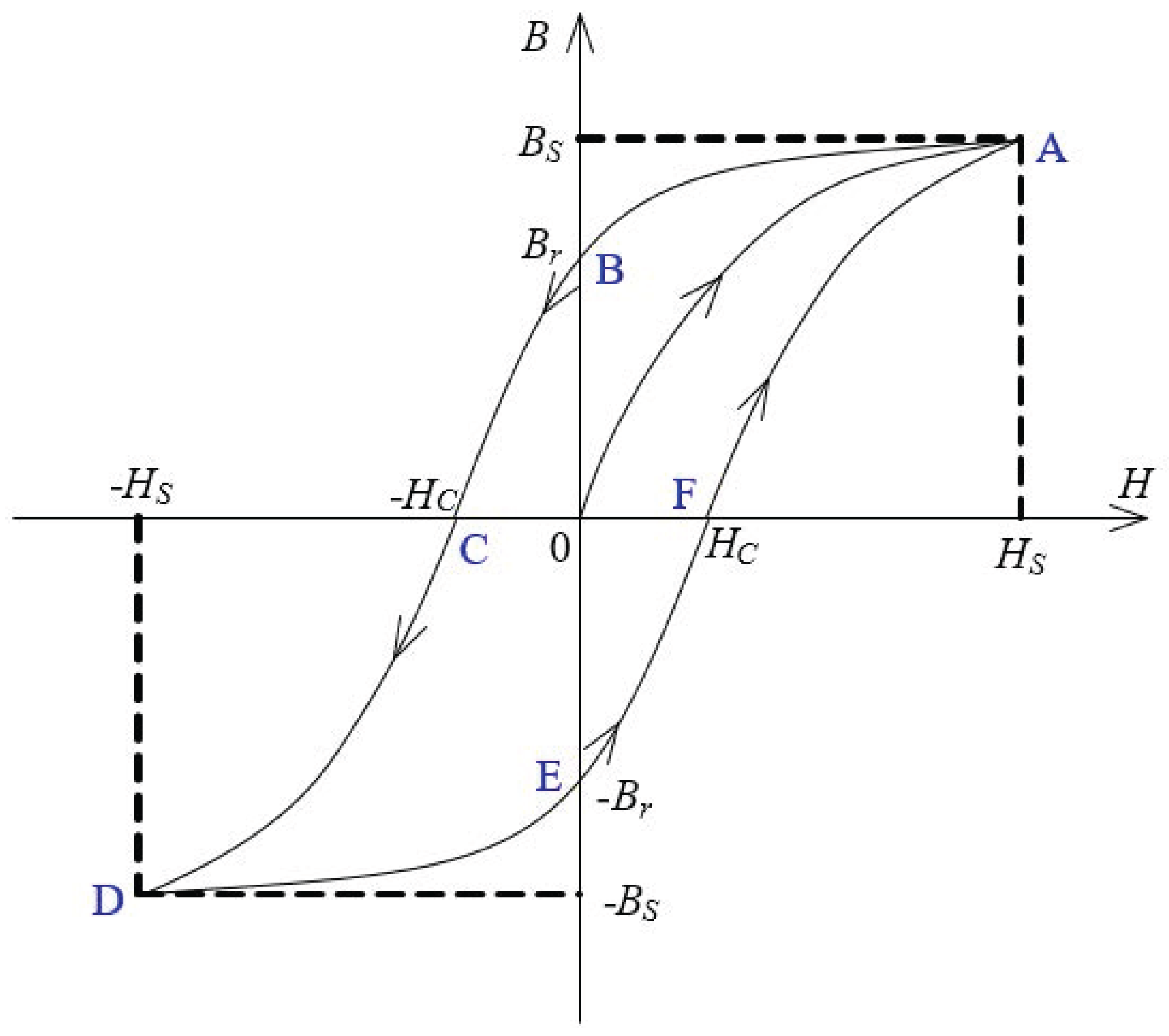
2.1. Jiles–Atherton Model

Ferromagnetic material exhibits nonlinear properties and hysteresis properties that can be described by the hysteresis loop shown in Figure 1. As shown in the figure, the magnetic field intensity H doesn’t increase proportionally with the magnetic flux density B. Due to the continuous rising of the magnetic field intensity, the magnetic flux density tends to reach the saturation state as indicated by the curve between the origin and point A. When the magnetic field intensity decreases, the magnetic flux density decreases by following a different path as shown by the curve connecting points A, B and C. As magnetic field intensity changes periodically, its relationship with the magnetic flux density is expressed by the closed loop, namely, as the hysteresis loop, as shown in Figure 1. $B_r$ is the magnetic flux density when H decreases to zero. $H_c$ is known as coercivity, which is the magnetic field intensity when B increases to zero. The magnetic flux density when the material reaches the saturation state is called the saturation flux density $B_s$. The Jiles–Atherton hysteresis model, which is derived from the physical views of the magnetization process, can simulate the hysteresis phenomenon effectively. The J–A model decomposes the whole magnetization into two components, namely, reversible component $M_{rev}$ and irreversible component $M_{irr}$:

$$M=M_{rev}+M_{irr}$$

(1)

The effective magnetic field within the ferromagnetic material can be described by the J–A model as

$$H_e=H+\alpha M$$

(2)

where H is the external magnetic field, $\alpha$ is the coupling parameter and M is the magnetization intensity. Based on the modified Langevin function, the anhysteretic magnetization intensity $M_{an}$ can be expressed as

$$M_{an}=M_s[coth(\frac{H_e}{a})-\frac{a}{H_e}]$$

(3)

where $M_s$ is the saturation magnetization intensity. The relationship between the reversible magnetization $M_{rev}$, irreversible magnetization $M_{irr}$ and anhysteretic magnetization $M_{an}$ can be expressed as

$$M_{rev}=c(M_{rev}-M_{irr})$$

(4)

where c is the invertible motion parameter. The relationship between the magnetization and magnetic field strength can be derived as follows:

$$\begin{array}{c}\hfill \frac{\partial M}{\partial H}=\frac{c{\displaystyle \frac{\partial M_{an}}{\partial H_e}}-{\displaystyle \frac{(1-c)(M_{an}-M)}{K\delta (1-c)-\alpha (M_{an}-M)}}}{1-\alpha c{\displaystyle \frac{\partial M_{an}}{\partial H_e}}}\end{array}$$

(5)

where $\delta =sgn\left(\frac{\partial H}{\partial t}\right)$. $M_s,a,\alpha ,K$ and c are the parameters to be determined from a measured hysteresis loop. Combined with $B={\mu }_0(H+M)$, the relationship between magnetic flux density B and magnetic field strength H can be interpreted. In order to calculate the inrush current of the transformer, the relationship between the voltage of the magnetizing branch and the inrush current needs to be calculated. The voltage u of the magnetizing branch can be expressed as

$$\begin{array}{c}\hfill u=N\frac{\partial \mathsf{\Phi }}{\partial t}\end{array}$$

(6)

where N is the number of turns in winding and $\mathsf{\Phi }$ is the magnetic flux in the iron core by jointly considering $\mathsf{\Phi }=BS$ and $B={\mu }_0(H+M)$.

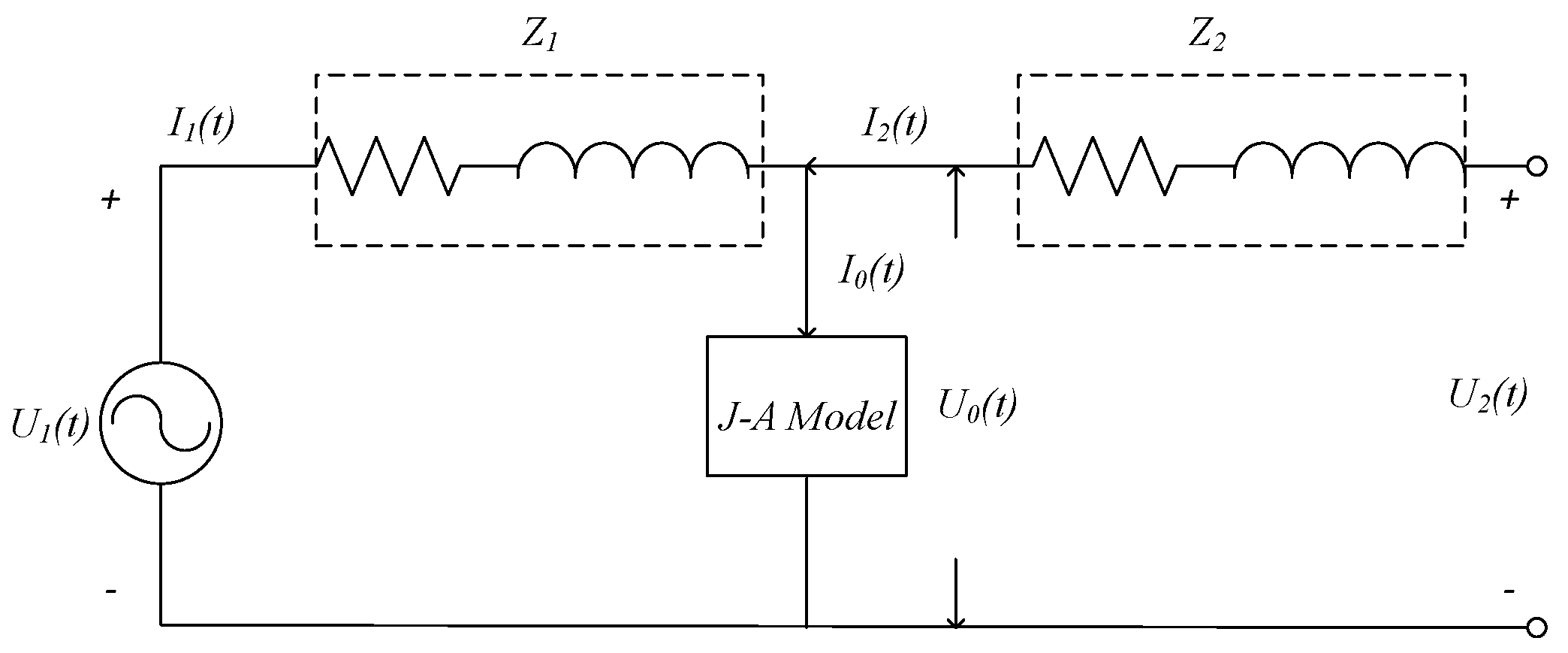
2.2. Power Transformer Simulation Model

The relationship between B and H is given in the J–A model. In order to calculate the inrush current of the power transformer, the relationship between the voltage of the magnetizing branch and the inrush current needs to be calculated. The $T-type$ equivalent circuit as shown in Figure 2 is used to model the power transformer. The module known as the J–A model represents the magnetizing branch. $U_1\left(t\right)$ is the equivalent voltage source, $Z_1$ and $Z_2$ represent the equivalent primary and secondary impedance, respectively, $I_0\left(t\right)$, $I_1\left(t\right)$ and $I_2\left(t\right)$ are excitation current, primary current and secondary current respectively, and $U_0\left(t\right)$ and $U_2\left(t\right)$ represent the voltage of the magnetizing branch and secondary voltage, respectively.

While in no–load excitation, $I_2\left(t\right)=0$, $I_1\left(t\right)$ here is equal to the inrush current $I_0\left(t\right)$. According to the equivalent circuit, we have:

$$\begin{array}{c}\hfill U_0\left(t\right)=N\frac{\partial \varphi }{\partial t}\end{array}$$

(7)

$$\begin{array}{c}\hfill H=N\frac{I_0\left(t\right)}{l}\end{array}$$

(8)

$$\begin{array}{c}\hfill \frac{\partial M}{\partial t}=\frac{\partial M}{\partial H}·\frac{\partial H}{\partial t}\end{array}$$

(9)

Substituting Equations (8) and (9) into Equation (7), the relationship between $U_0\left(t\right)$ and $I_0\left(t\right)$ can be described as follows:

$$\begin{array}{c}\hfill U_0\left(t\right)={\mu }_0{N}^2\frac{S}{l}(1+\frac{\partial M}{\partial H})\frac{\partial I_0\left(t\right)}{\partial t}\end{array}$$

(10)

where N is the number of turns, S is the core equivalent cross–sectional area $\left(m^2\right)$, and l is the equivalent length of the core magnetic path $\left(m\right)$. $\frac{\partial M}{\partial H}$ is described by the J–A model in Equation (5). The inrush current can be achieved by computing Equation (10).

The proposed transformer model was simulated in MatlabR2014a (MathWorks, Natick, MA, USA). An S-Functions Simulation block, which is formulated by its input, state and output was used to simulate the J–A model. The output is a function of the simulation time, the input and the state. As indicated in [27], the state function should in the form of a derivative formula. In the inrush current simulation, the input is the magnetizing branch voltage $U_0\left(t\right)$ and the simulation time t and the output is the inrush current $I_0\left(t\right)$. The state is the magnetization M and the inrush current $I_0\left(t\right)$. Therefore, the derivative formula of the state can be expressed as

$$\begin{array}{c}\hfill \frac{\partial I_0\left(t\right)}{\partial t}=\frac{U_0\left(t\right)}{{\mu }_0{N}^2\frac{S}{l}(1+\frac{\partial M}{\partial H})}\end{array}$$

(11)

and

$$\begin{array}{c}\hfill \frac{\partial M}{\partial t}=\frac{\partial M}{\partial H}·\frac{\partial H}{\partial t}=\frac{\partial M}{\partial H}·\frac{N}{l}·\frac{U_0\left(t\right)}{{\mu }_0{N}^2\frac{S}{l}(1+\frac{\partial M}{\partial H})}\end{array}$$

(12)

Based on Equations (11) and (12), the transformer model based on the J–A theory can be implemented.

3. Inrush Current Characteristics Analysis and Key Feature Extraction

The J–A model is driven by five parameters: $M_s,a,\alpha ,K$ and c. Different combinations of the five parameters represent different magnetic characteristics, which lead to different inrush current curves. As shown in Figure 3b, the hysteresis loop goes through a series of different statuses before it reaches the steady state. The same trend can also be found in the corresponding hysteresis loop as shown in Figure 3a. Various methods have been developed to estimate the J–A parameters from the hysteresis loops. Generally, this is the way to generate the initial J–A parameters for different types of tasks. However, the initial J–A parameters may not be able to generate accurate inrush current. For example, if the J–A parameters are estimated from the hysteresis loops of the steady state, they can hardly be used to simulate the accurate inrush current. Therefore, the initial J–A parameters need to be fine-tuned to fit for different tasks. In this article, in order to obtain a more accurate simulation of the inrush current, the J–A parameters also need to be fine-tuned. In the following paragraph, the characteristics of the J–A parameters are first analyzed. Then, the automatic parameter tuning method is proposed for the more accurate inrush current simulation.

The characteristics of each J–A parameter is studied quantitively. The main concept of this study is to compare the inrush current curves generated by different J–A parameter combinations. Each combination is generated by changing the value of one parameter while fixing the value of the rest. The initial values of the five J–A parameters are set as $M_s=1.65\times {10}^6$, $a=17$, $\alpha =3.7\times {10}^{-5}$, $K=4.5$, and $c=0.28$. The changing rate of each parameter is 25%. For example, the initial value for $M_s$ is $I_{M_s}=1.65\times {10}^6$. Then, the other four different values for $M_s$ are $0.5I_{M_s}$, $0.75I_{M_s}$, $1.25I_{M_s}$ and $1.5I_{M_s}$. The corresponding five inrush current curves for five different $M_s$ are plotted in Figure 4a. $a,\alpha ,K$ and c are fixed at the initial value. The same operation is applied on the rest of the four J–A parameters and the corresponding results are shown in Figure 4b–e, respectively. Parts of the figures are enlarged for better observation.

Several important characteristics can be concluded from the study:

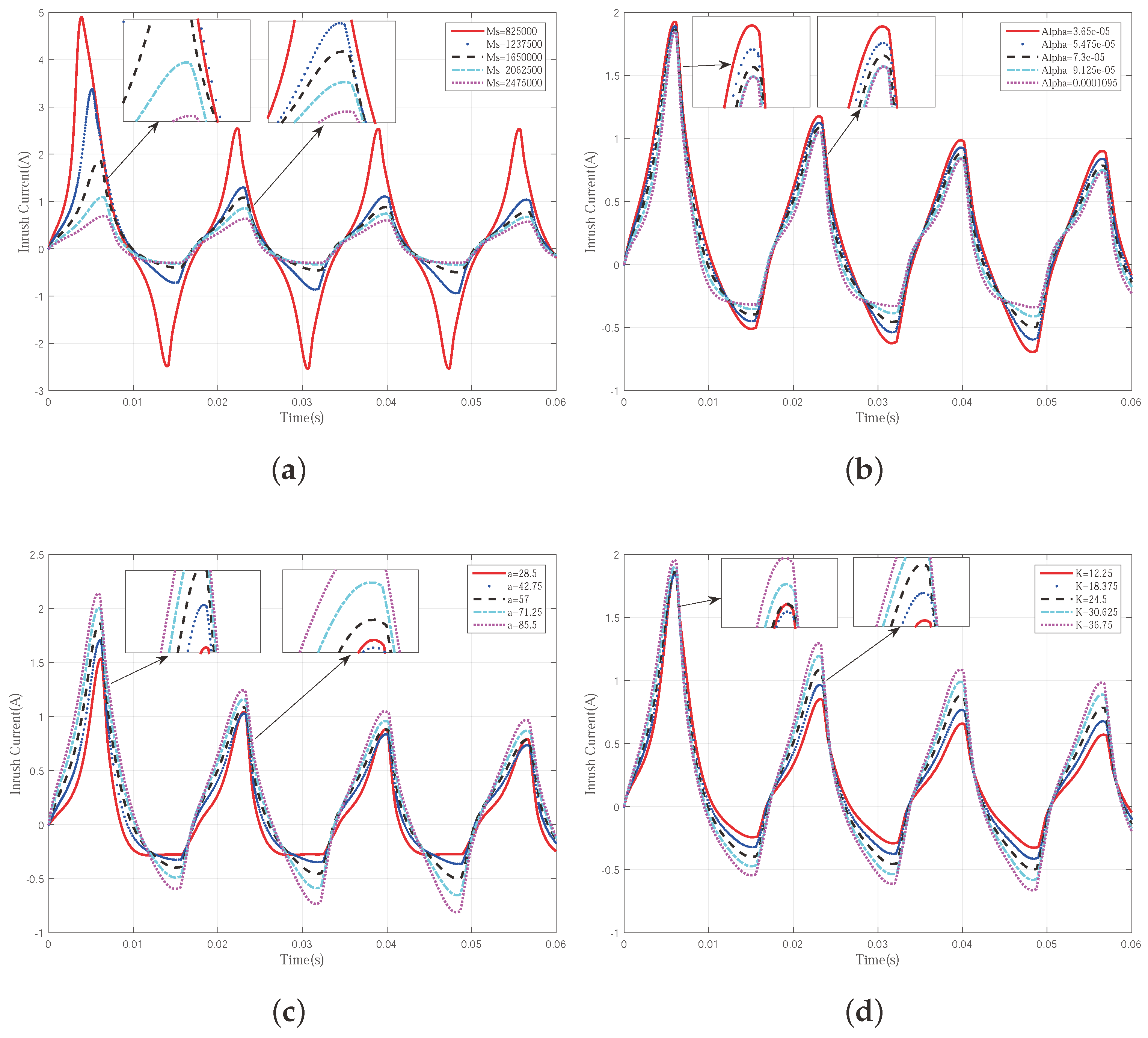
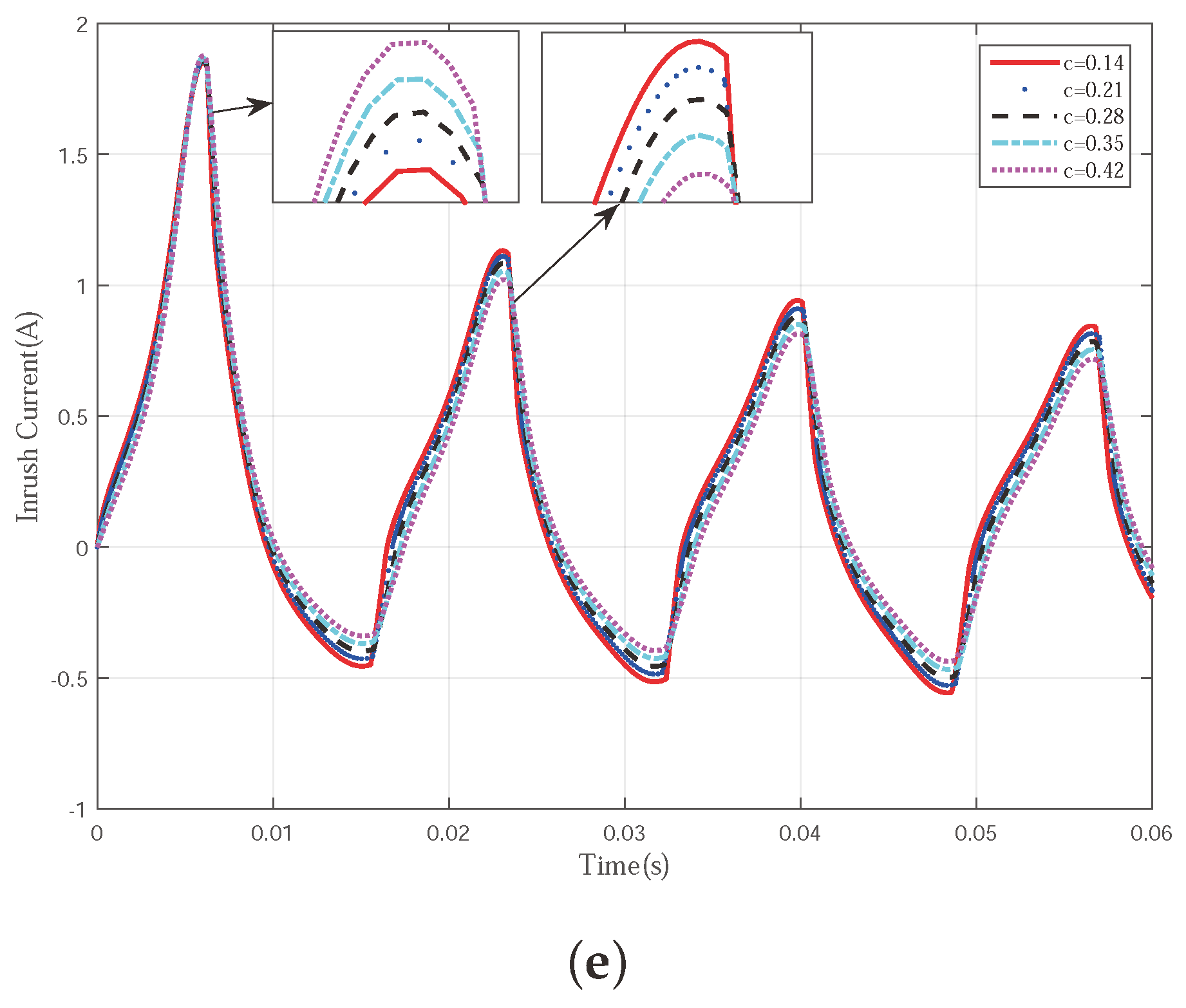
• Relativity: Different J–A parameters generate different inrush current curves. This indicates that by tuning the J–A parameters properly, the corresponding inrush current curve can be changed and thus a more accurate inrush current simulation can be achieved.
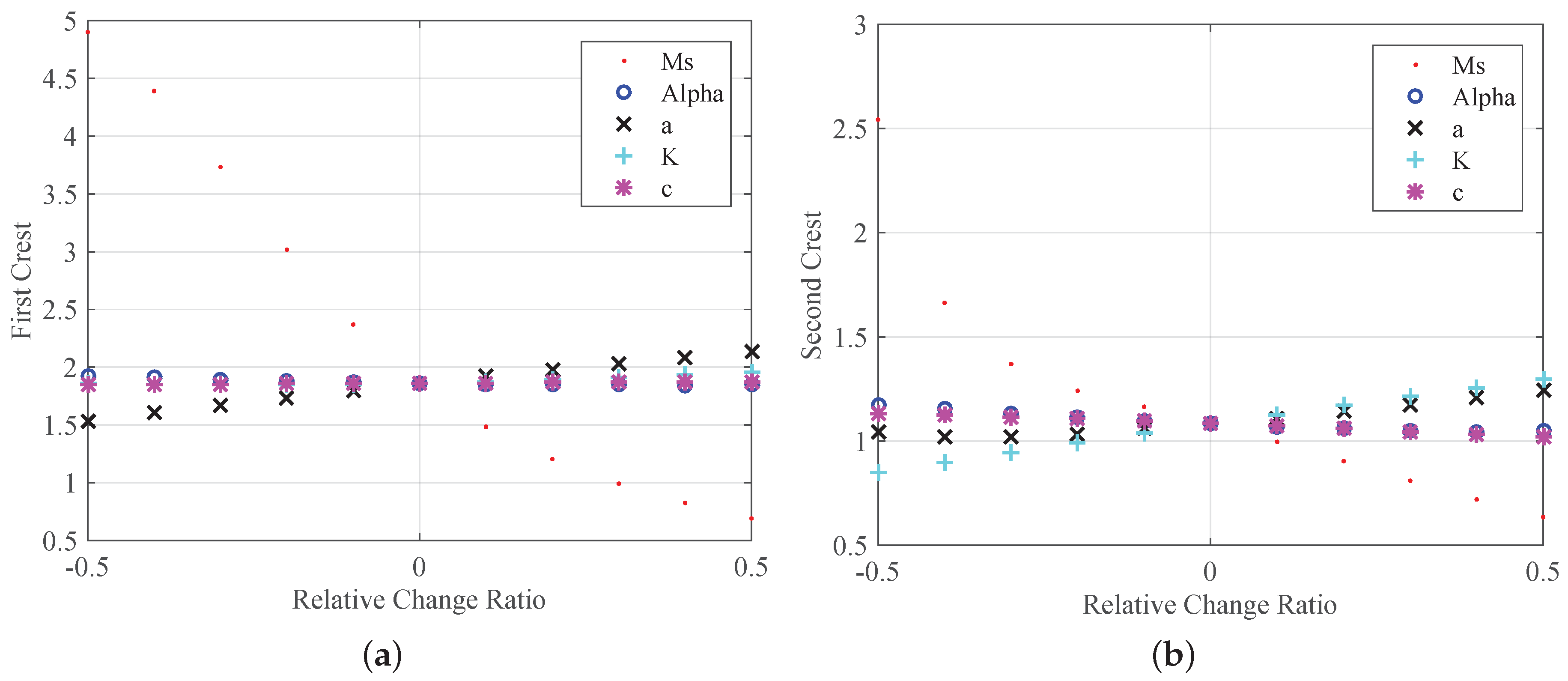
• Sensitivity: The sensitivity of the inrush current to each J–A parameter is different. As can be observed, the first period is more sensitive to the change of $M_s$ and a, while the second period is more sensitive to both $M_s$ and K. This feature indicates that, in order to improve the accuracy of the simulation efficiently, different priority shall be assigned to each of the J–A parameters. The more sensitive parameters shall be tuned first, thus the curve can approach the accurate one more quickly. Then, the small difference between the tuned curve and the true one can be compensated by tuning the less sensitive ones. The whole parameter tuning process can be accelerated significantly by separating the J–A parameters into different groups. The parameters in the primary group should be tuned firstly.
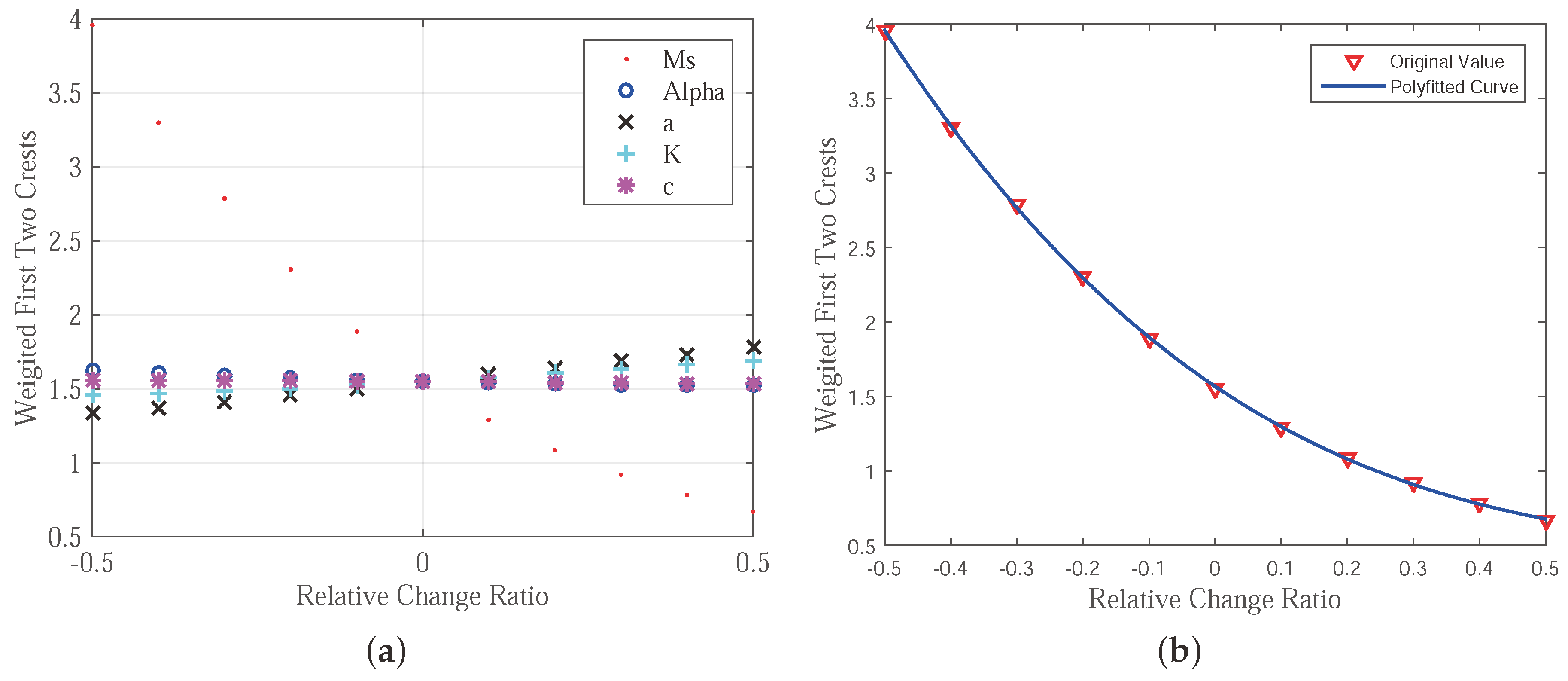
• Key Features: The inrush current curve can be featured by its first two crests. If the first two crests can be simulated precisely, the entire inrush current can be simulated precisely. From our observation, the shape and trend of the inrush current can be represented by the height of its first two crests. Two inrush current curves can be distinguished by comparing their first two crests. If the first two crests of the two curves are similar, then the two curves should also be close to each other. If the crests are far apart from each other, the following parts of the two curves should also be far away from each other. Moreover, if the first and second crests of the inrush current are significantly affected by the J–A parameters, the rest of the curves are also sensitive to the change of the J–A parameters. Furthermore, from our observation, the feature is very robust. It is very hard to find two different inrush currents with the first two crests being similar. The changing of the J–A parameters can be obviously reflected by the first two crests of the inrush current. Another reason for choosing the first two crests as a feature of the efficiency is that it is very easy to collect the data of the first two crest signals. Then, within two periods, the J–A parameters can be adjusted to more accurate values and more precise inrush current signals can be simulated.

Based on the concluded characteristics, the basic principles of J–A parameter tuning for inrush current simulation can be concluded as: (1) by tuning J–A parameters according to the extracted features, the accuracy of the inrush current simulation can be improved obviously; (2) the key features which can serve as the objectives for J–A parameter tuning are the first two crests of the inrush current signal; (3) inrush currents have different sensitivities to different J–A parameters. In the parameter tuning process, the J–A parameters shall be classified into different groups according to their priority.

A more accurate inrush current simulation can be achieved by tuning the corresponding J–A parameters under the key feature’s guidance. An inrush current simulation based on the tuned J–A parameters is demonstrated to verify our conclusion in the next section. The modified parameters can reduce the simulation error and provide accurate matching results. This also verifies the efficiency of the selected features and the parameter classification strategy.

4. Automatic Parameter Tuning Algorithm

4.1. Analysis-Based J–A Parameter Tuning

In order to prove the efficiency of the observed characteristics and the selected key features, the J–A parameters are tuned to improve the simulation accuracy. The inrush current data refers to [21], within which the data is experimentally measured from a 440 V single-phase transformer. The detailed information of the transformer is listed in

Table 1. Transformer [21] specification.

Capacity	Frequency	Rated Voltage Ratio	Turn Ratio	Phase
400 VA	60 Hz	440 V/440 V	727/727	single

.

An initial set of J–A parameters, as is shown in the second row of

Table 2. Initial and modified J–A parameters.

Type	${\mathit{M}}_{\mathit{s}}(\mathbf{A}/\mathbf{m})$	$\mathit{a}(\mathbf{A}/\mathbf{m})$	$\mathit{\alpha }$	$\mathit{K}(\mathbf{A}/\mathbf{m})$	c
Initial J–A Parameters	1,950,000	35	0.000073	10.4	0.391
Modified J–A Parameters	1,650,000	17	0.000037	4.5	0.28

, is estimated from the corresponding hysteresis loops. The inrush current simulated by the initial parameters is compared with the measured one in Figure 3a. As can be observed, the simulated inrush current cannot match the measured one well. The first two crests are not high enough. Parameters that affect the first two crests should be adjusted firstly. According to our analysis of the five J–A parameters in Section 3, we can perform the following actions to make the simulation more accurate.

• The $M_s$ and a are classified as the primary parameters since they have more impact on the first and second crests of the inrush current. The rest of the parameters are classified as the secondary parameters.
• The primary parameters are tuned firstly to reduce the large difference between the simulated inrush current and the measured one. Since the curve is more sensitive to the primary parameters, the simulated one can approach the measured one quickly. In this case, both $M_s$ and a are reduced to increase the height of the first and second crests.
• Tuning the secondary parameters to further reduce the difference between the two curves. In this case, $\alpha$, K and c are all reduced. This can ensure that the simulated curve approaches the measured one and its trough does not go too deep. The small difference generated by the tuned primary parameters can be compensated by the tuned secondary parameters.

Based on the above analysis, the J–A parameters are modified as shown in the third row of Table 2. The corresponding simulated inrush current curve is shown in Figure 5b. As can be observed, the simulation error is effectively reduced and an accurate inrush current simulation can be achieved. This proves the efficiency of the selected features and the concluded characteristics of the J–A parameters. Furthermore, the proposed analysis-based method introduces no more additional parameters, which indicates that the five J–A parameters are capable of representing the transient simulation of the transformer. Previous work on J–A parameter optimization is based on the relationship between the J–A parameters and the hysteresis loop, while, in the proposed method, the parameter modification is based on the direct relationship between the J–A parameters and the inrush current curve. The modeled relationship is more direct and clearer in the proposed method. Thus, the efficiency of the parameter tuning is improved.

4.2. Automatic Algorithm for J–A Parameter Tuning

By observing, comparing and analyzing the simulated and measured inrush current curves, we can estimate more accurate J–A parameters. However, this method is complex, unstable and also needs many manual operations. Meanwhile, as can be observed from Figure 3b, some detailed information of the inrush current curve can not be well simulated. Therefore, in practical operation, an automatic parameter adjustment algorithm needs to be proposed to deal with the parameter tuning efficiently. The details of the proposed algorithm is shown in Algorithm 1.

In Step 2 of Algorithm 1, the sensitivity of the inrush current to each J–A parameter needs to be calculated. Similar to what we have done in Section 4.1, the first two crest values of the inrush current generated by the initial J–A parameter and its neighboring parameters are recorded. The variation trends of the first and second crest in accordance with the relative change ratio of the initial value is shown in Figure 6. The horizontal axis denotes the change ratio of certain J–A parameters and the vertical axis indicates corresponding crest value of the first and second cycles. For example, the point at 0.1 indicates that the corresponding J–A parameter is increased by 10% compared with initial value. From the figure, the sensitivity of each parameter is calculated and thus their priority can be ranked. Based on the rank, the parameters can be classified and tuned accordingly.

In Step 4 of Algorithm 1, the difference between the key feature can be calculated as

$$\begin{array}{c}\hfill {\omega }_1\Delta c_1+{\omega }_2\Delta c_2\end{array}$$

(13)

where $\Delta c_1$ is the difference between the first crest of simulated and measured curves and $\Delta c_2$ is for the second crest. Here, ${\omega }_1$ and ${\omega }_2$ are weights to balance the first and second crests. From our analysis, the first crest is more representative than the second one, thus the weights in this article are set as ${\omega }_1=0.6$ and ${\omega }_2=0.4$. The two thresholds $T_1$ and $T_2$ are used to stop the searching process early when conditions are satisfied. The efficiency can be further improved by using these two thresholds. The specific value of the thresholds depends on the required accuracy of the simulation. If the accuracy requirement of the simulation is high, the value for the thresholds should be small enough.

Algorithm 1: Framework of the proposed algorithm.

Input: 1. Initial J–A parameters, 2. The Measured inrush current, 3. Threshold $T_1$ and $T_2$

Output: The modified J–A parameters

Step 1 Extract the crest of the 1st and 2nd cycles as the key features; Step 2 Classify the J–A parameters into primary parameters and secondary parameters according to their sensitivity characteristics. Add the primary parameters into the searching region; Step 3 Adjust the primary parameters in the searching region according to the polynomial fitted curve and go to Step 4; Step 4

The impact of each J–A parameter on the weighted crest value (${\omega }_1\Delta c_1+{\omega }_2\Delta c_2$) is shown in Figure 7. In order to further improve the efficiency of the searching process, the discrete value shown in Figure 7a can be polyfitted into a continuous polynomial as shown in Figure 7b. The case for $M_s$ is shown in the figure, and the discrete value for $M_s$ can be fitted by the polynomial $M_s=1.16x^3+3x^2-2.99x+1.57$, where x is the relative change ratio. The polynomial method can be treated as a finer and faster searching method. Based on the polynomial function and the measured crests value, the searching range for $M_s$ can be defined as the interval between initial value and target value. Thus, the value for $M_s$ can be modified within the searching region in order to reduce the difference between simulated and measured first and second crests.

In the proposed algorithm, the optimal combination of the primary parameters needs to be searched in order to satisfy the predefined condition (${\omega }_1\Delta c_1+{\omega }_2\Delta c_2<T_1$). Within the searching region defined above, various searching methods can be adopted, such as brute-force search and genetic programming. After the modification of the primary parameters, the simulated inrush current curve is compared with the measured one.

If the simulated curve that is generated by the modified primary parameters can satisfy the first condition (${\omega }_1\Delta c_1+{\omega }_2\Delta c_2<T_1$), the secondary parameters need to be fine-tuned adaptively to satisfy the second condition (${\omega }_1\Delta c_1+{\omega }_2\Delta c_2<T_2$). Here, for the efficiency of the algorithm, the values for primary parameters are fixed. Thus, the problem is also a multi-dimensional searching problem within a certain searching area. A similar searching method can be used in this problem. At the same time, the selected feature, first and second crests, also benefits the efficiency of the algorithm since only the first two periods are needed to run the algorithm.

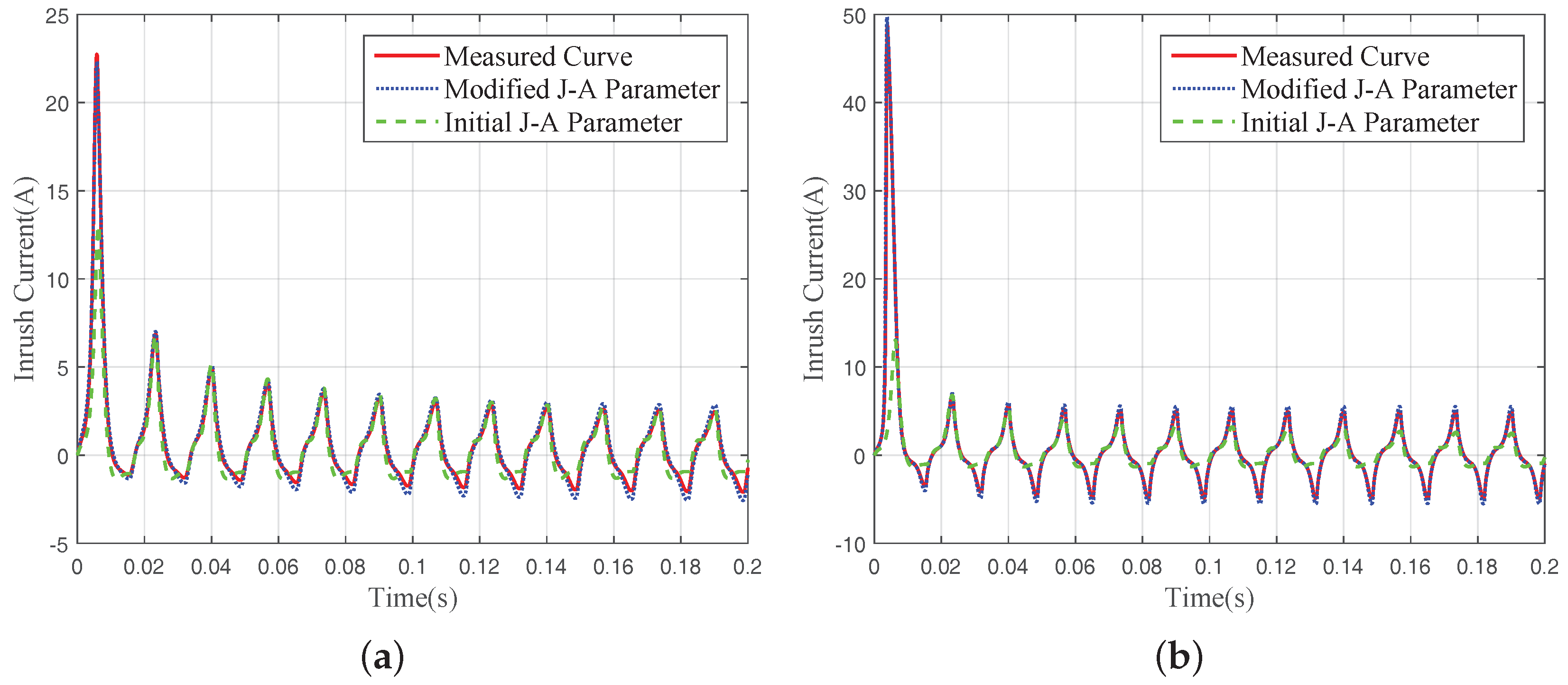
5. Experimental Results and Analysis

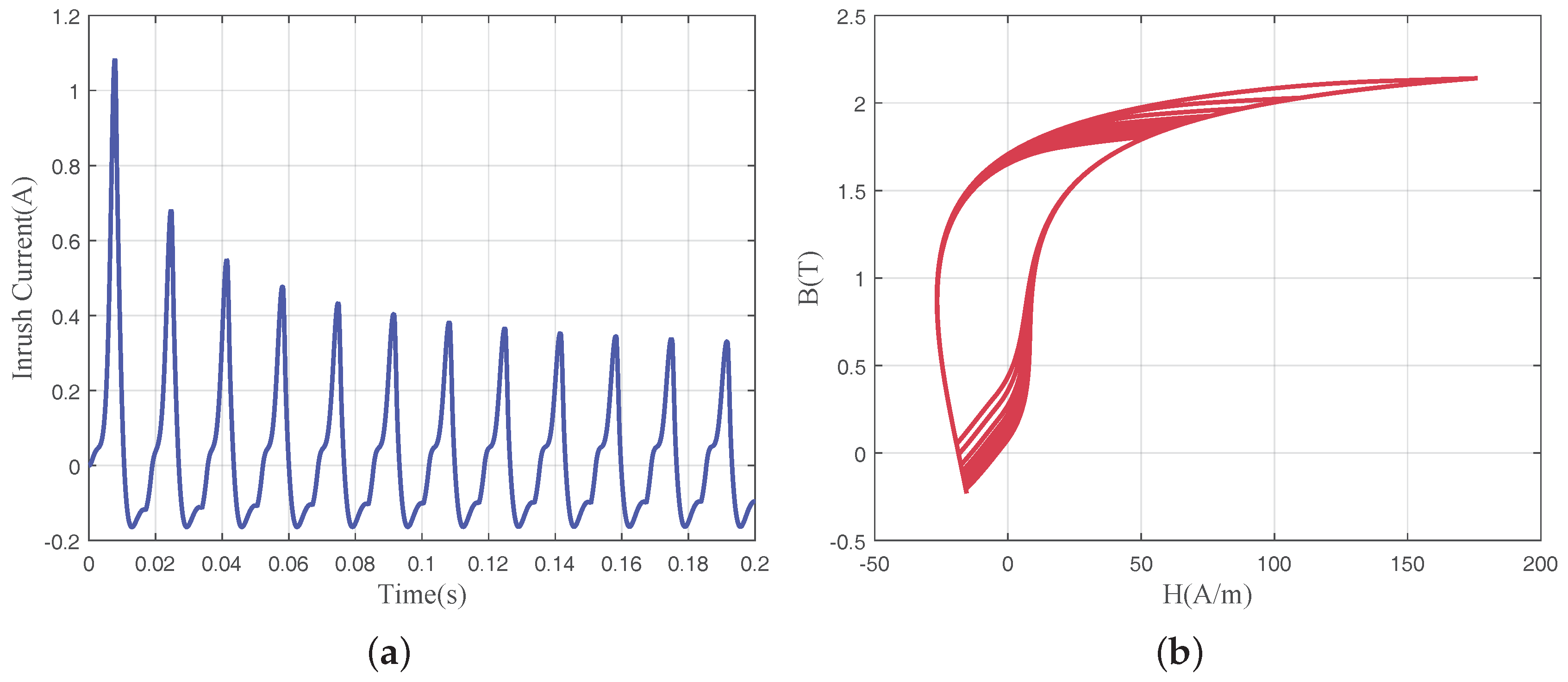
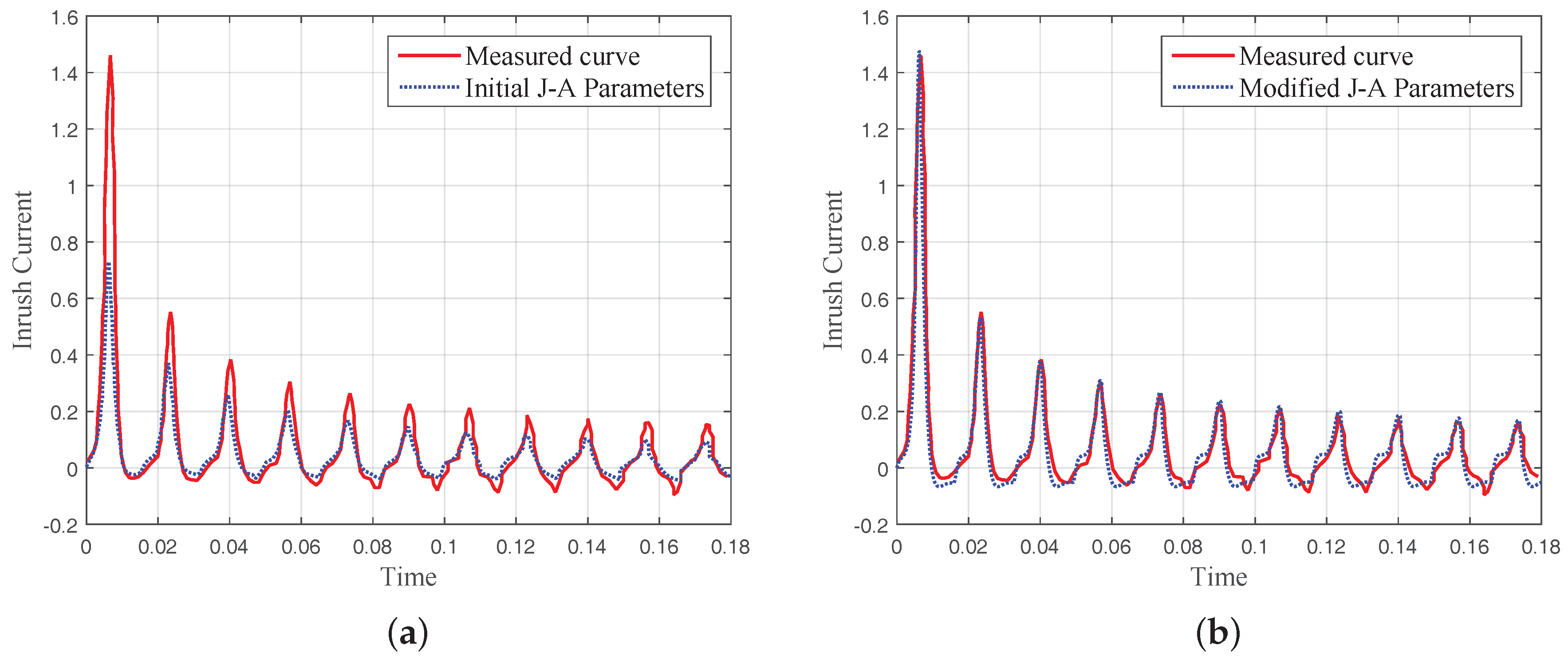
5.1. Experimental Results

Two types of the experimental settings are used for verification of the proposed automatic algorithm.

Set 1: The automatic algorithm is applied with the same experimental settings as shown in Section 4.1. The values of five J–A parameters generated by the proposed automatic algorithm are shown in the second row of

Table 3. J–A parameters generated by the automatic algorithm.

Experiment	${\mathit{M}}_{\mathit{s}}(\mathbf{A}/\mathbf{m})$	$\mathit{a}(\mathbf{A}/\mathbf{m})$	$\mathit{\alpha }$	$\mathit{K}(\mathbf{A}/\mathbf{m})$	c
Set 1	1,733,160	38.5	0.000062	4.1	0.6256
Set 2	1,542,670	40	0.00006	9.1	0.5
Set 2	980,325	20	0.000055	7.1	0.3374

. The simulated inrush current curve using the final modified parameters is compared with the measured one in Figure 8. As can be observed, the simulated curve using the modified parameters can match the measured one precisely. Just like [19], the first crest difference, which describes the difference between the first crests of the two curves, is adopted to measure the simulation accuracy. The first crest difference is reduced to $1.1\%$ from the original $45\%$, which indicates that the modified J–A parameters can generate much more accurate inrush current than the original J–A parameters. The automatically modified parameters can provide more accurate details of the inrush current curve, such as that the inflection points can also be simulated exactly.

Set 2: An inrush current test and analysis system is built up based on our own designed transformer. In the system, a single-phase transformer, as shown in Figure 9, is manufactured and used to carry out no-load switching experiments, and excitation inrush current waveforms are collected. The detailed specification is listed in

Table 4. Specification of the 220 V transformer in experiment set 2.

Capacity	Frequency	Rated Voltage Ratio	Turn Ratio	Phase
1000 VA	50 Hz	220 V/220 V	100/100	single

. Since the inrush current may vary at every single energization, the automatic algorithm is applied to two different measured inrush current curves. In addition, the values of the five J–A parameters generated for each situation by the proposed algorithm are shown in the third and fourth rows of Table 3. The simulated inrush current curves using the modified parameters are compared with measured ones and the ones generated by the initial J–A parameters in Figure 10. Just like the first experiment, the simulated curves, by using the modified J–A parameters, can match the measured one much more precisely than the initial ones. In both cases, the algorithm is able to reach the measured inrush current first crest with less than a $2\%$ difference, while the first crest difference of the original J–A parameters is much larger ( >50%). The automatically modified parameters can provide more accurate details of the inrush current curve, such as the inflection points being able to be simulated exactly. All of this evidence proves that the proposed automatic algorithm is a powerful tool for inrush current simulation and the selected features are effective for representing the entire inrush current curve.

5.2. Analysis and Discussion

Two key factors are considered during the design of the algorithm, accuracy and efficiency. As shown from the experimental results, the transformer models analyzed in this paper can estimate the inrush current with good accuracy. The main reason is due to several aspects. First of all, the hysteresis characteristics of the transformer are modeled by the J–A model. Recent studies [21,28] prove the effectiveness of this approach in the modeling of transformers. Therefore, the inrush current simulation can be modeled as a J–A parameter estimation problem. The assumption made in this paper is that different working statuses of the transformer should be represented by different J–A parameters. The J–A model with non-constant parameters does help to improve the estimation accuracy. In addition, when estimating the J–A parameters, a threshold is set for the parameter tuning procedure, which can help to control the estimation error within a reasonable range.

Except for its capability of representing the hysteresis phenomenon, the J–A model is also selected due to its simpler implementation and reduced computational effort. To further improve the efficiency of the proposed algorithm, the first two crest values of the inrush current are extracted as the feature. These two values can be easily measured within two periods of the signal. Moreover, the five J–A parameters are classified into two groups to accelerate the parameter estimation.

The J–A model has been widely used in many tasks. In [19], the physical topology of the transformer is used to formulate the transformer model. Each of the three main legs and the two outer yokes are modeled with a J–A hysteretic model. The accuracy of the transformer model can be improved by using a more accurate J–A parameter estimation algorithm as proposed in this paper. For the discrimination between fault currents and inrush currents, the proposed simulation model can be used to generate the inrush current data for training the classifier. In addition, the idea of the proposed algorithm can be applied to the discrimination task. Different J–A parameters shall be estimated from different transformer statuses, thus the inrush current and fault current can be distinguished. The interaction of the proposed model and algorithm with other networks or system components needs to be investigated in our future work.

Due to the limitations of the experimental environment, our algorithm is only valid for testing on single-phase two-winding transformers. Our future work also includes the further development of our algorithm for the application on multiwinding single-phase or multiphase transformers.

6. Conclusions

A Jiles–Atherton theory based power transformer model is proposed to simulate the inrush current. The transformer can be implemented easily in practice. The impact of each J–A parameter on the simulated inrush current is explored. It is observed that the inrush current exhibits different sensitivities to different J–A parameters. The efficiency of the simulation model is improved by re-weighting each J–A parameter according to their sensitivity. It is found that the inrush current curve can be precisely featured by its first two crests. Thus, the J–A parameter estimation problem can be formulated as a feature matching problem. An automatic feature matching and parameter tuning algorithm is used to calculate the optimal J–A parameter.

The transient behavior of the proposed transformer model and the automatic algorithm has been verified experimentally with the measured inrush currents. The results show the superiority of the proposed model in inrush current simulation. Experimental results also show that the accuracy of the inrush current simulation can be improved significantly by the proposed automatic algorithm, which takes the key feature as the objective function. This also proves that the selected features are efficient for representing the inrush current of the transformer.