Online Reliable Peak Charge/Discharge Power Estimation of Series-Connected Lithium-Ion Battery Packs
Abstract
:1. Introduction
2. Power Estimation for One Single Battery Cell
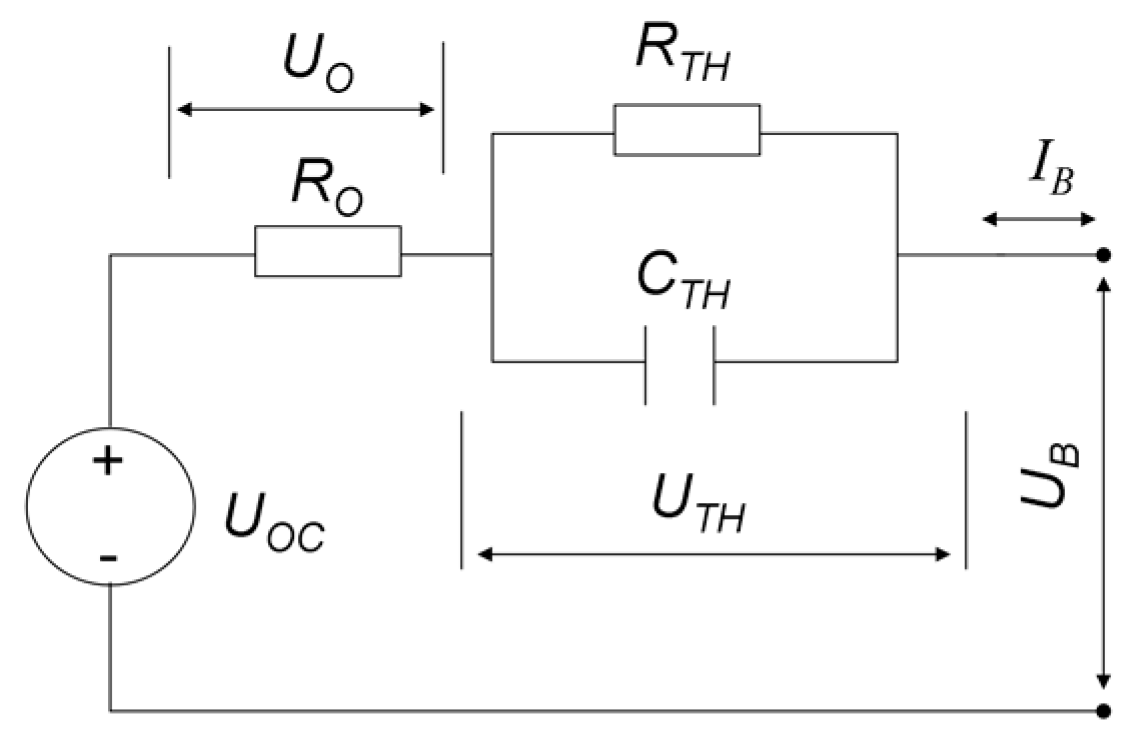
2.1. Lumped Parameter Battery Model
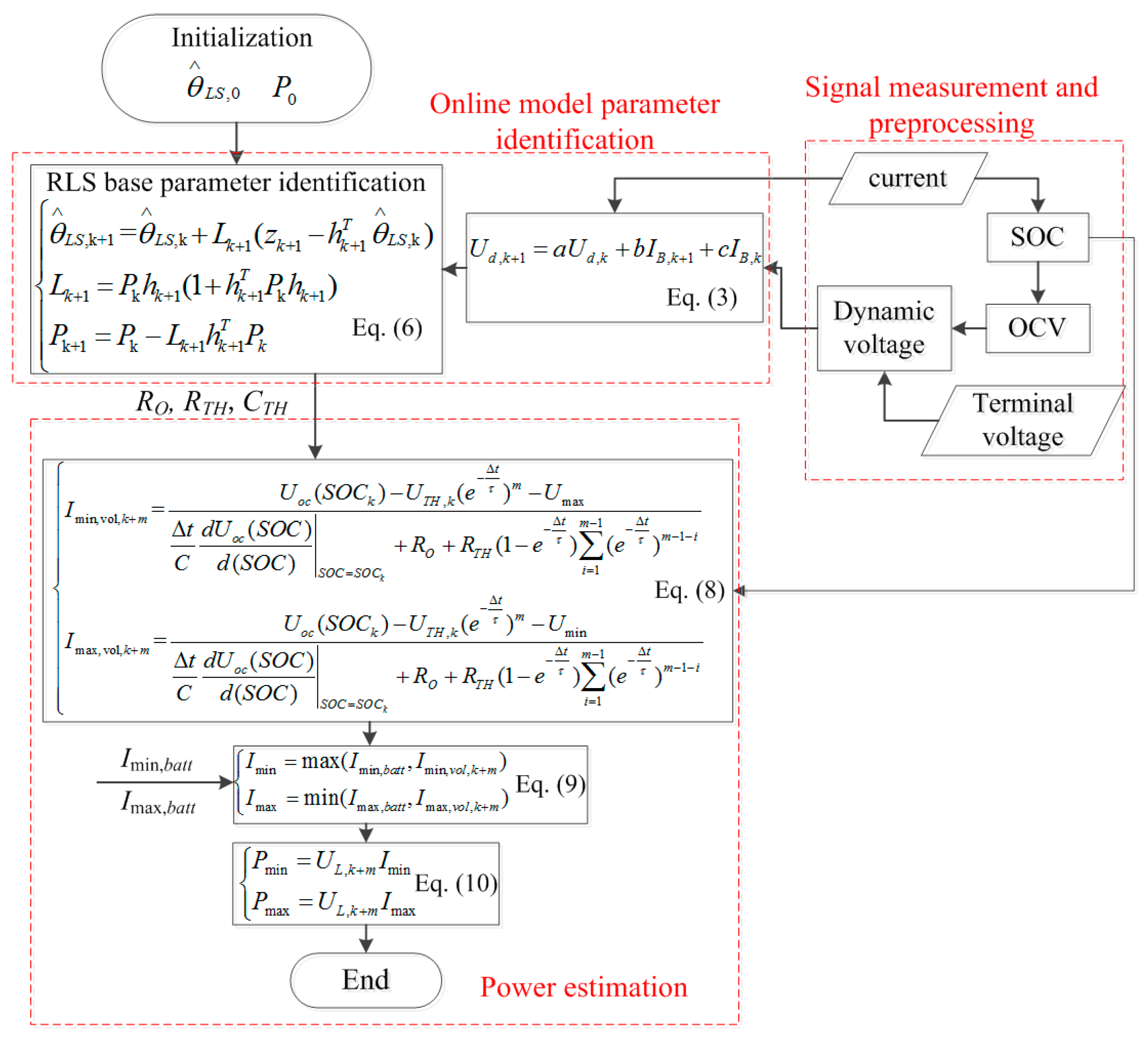
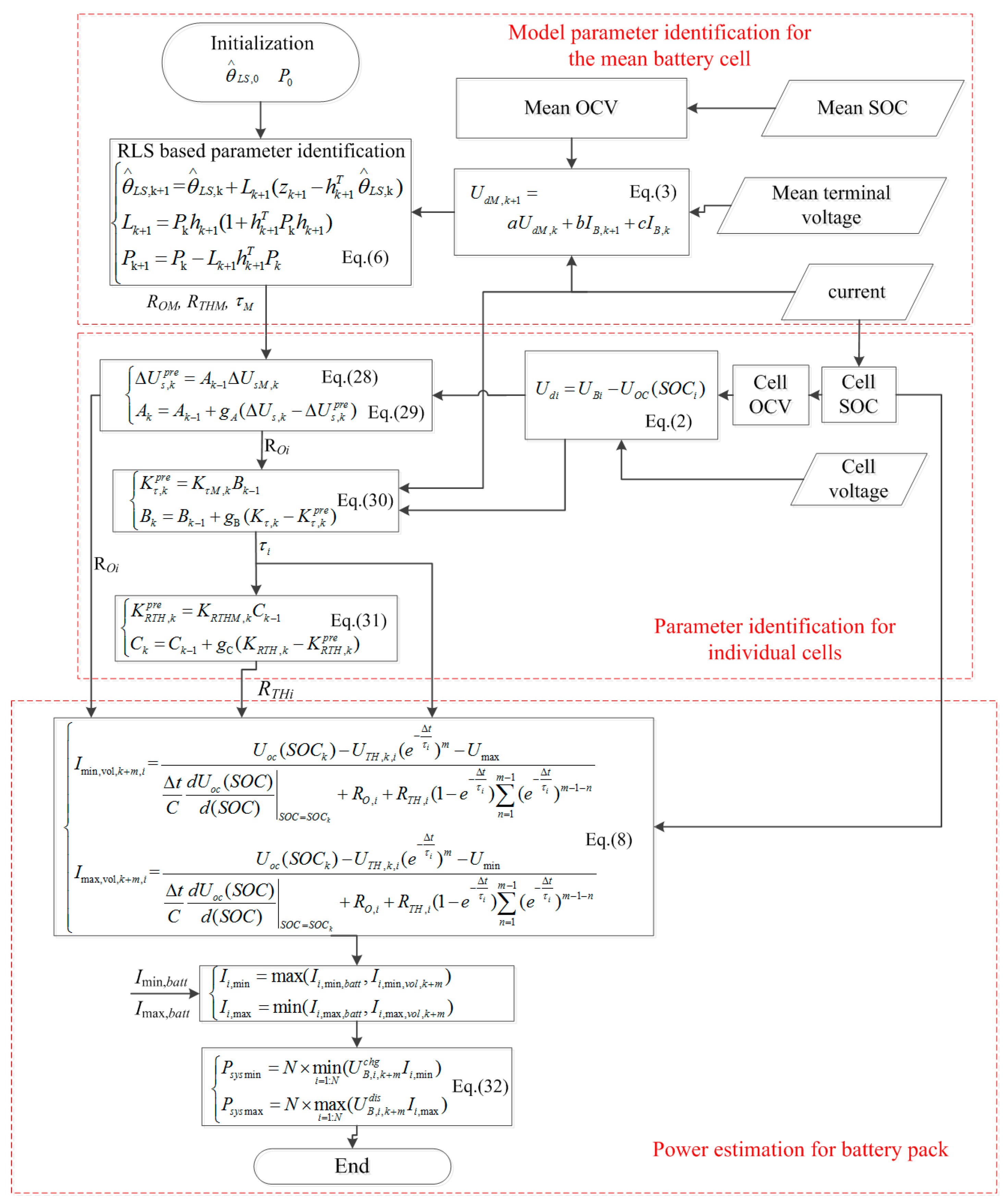
2.2. Online Model Parameter Identification
2.3. Power Estimation
3. Power Prediction of Series-Connected Battery Packs
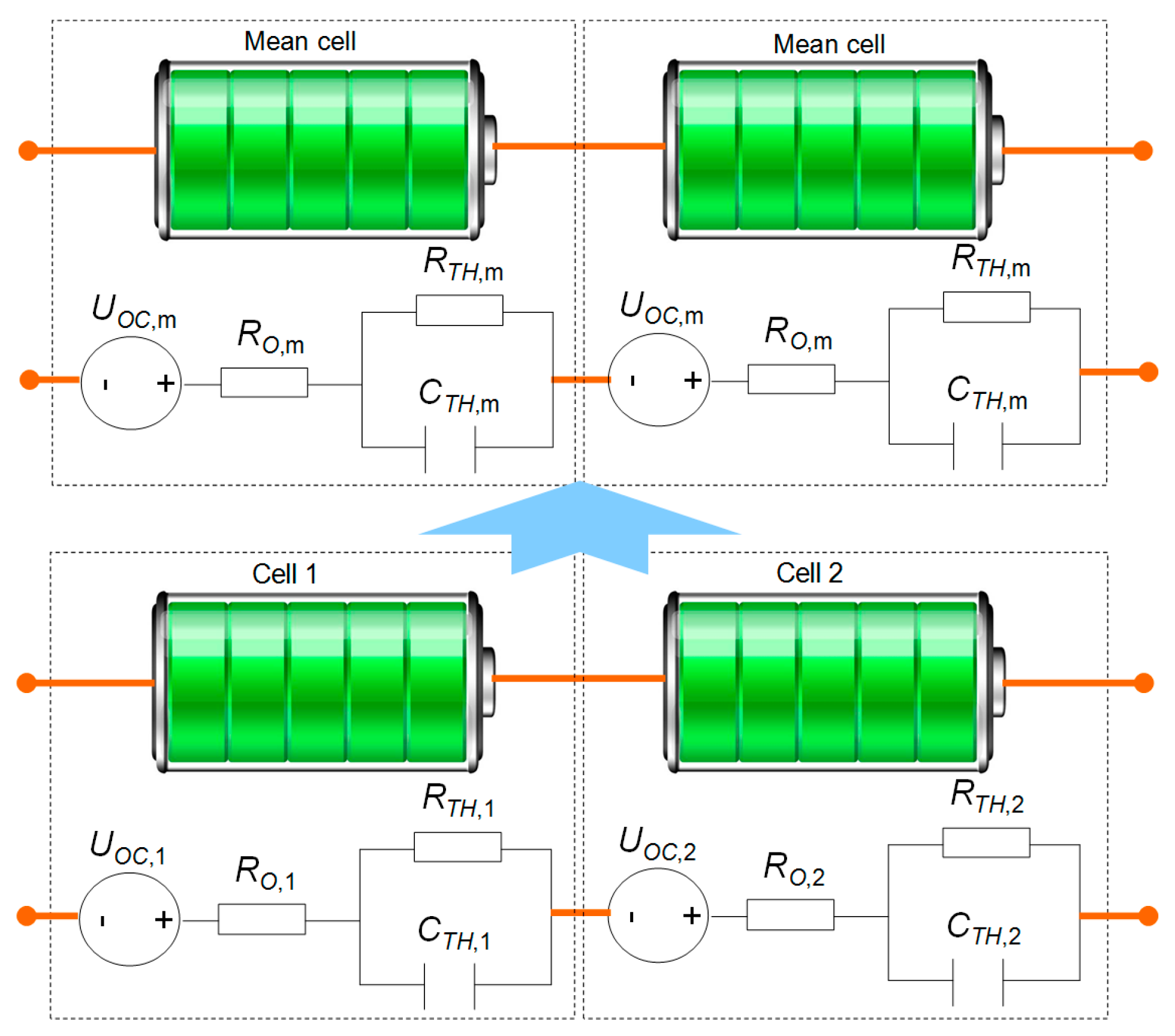
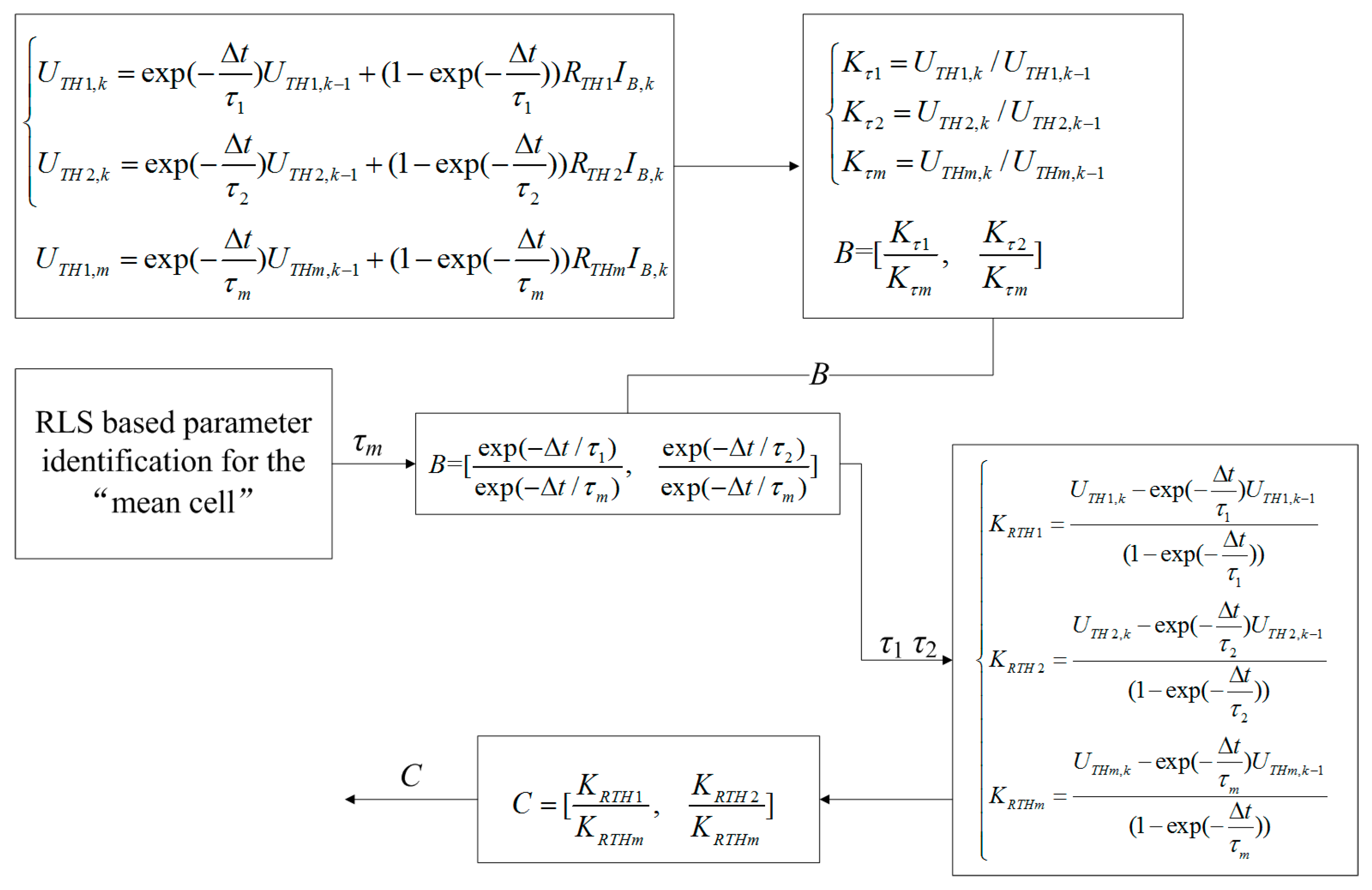
3.1. Improved Parameter Identification for Series Connected Battery Systems
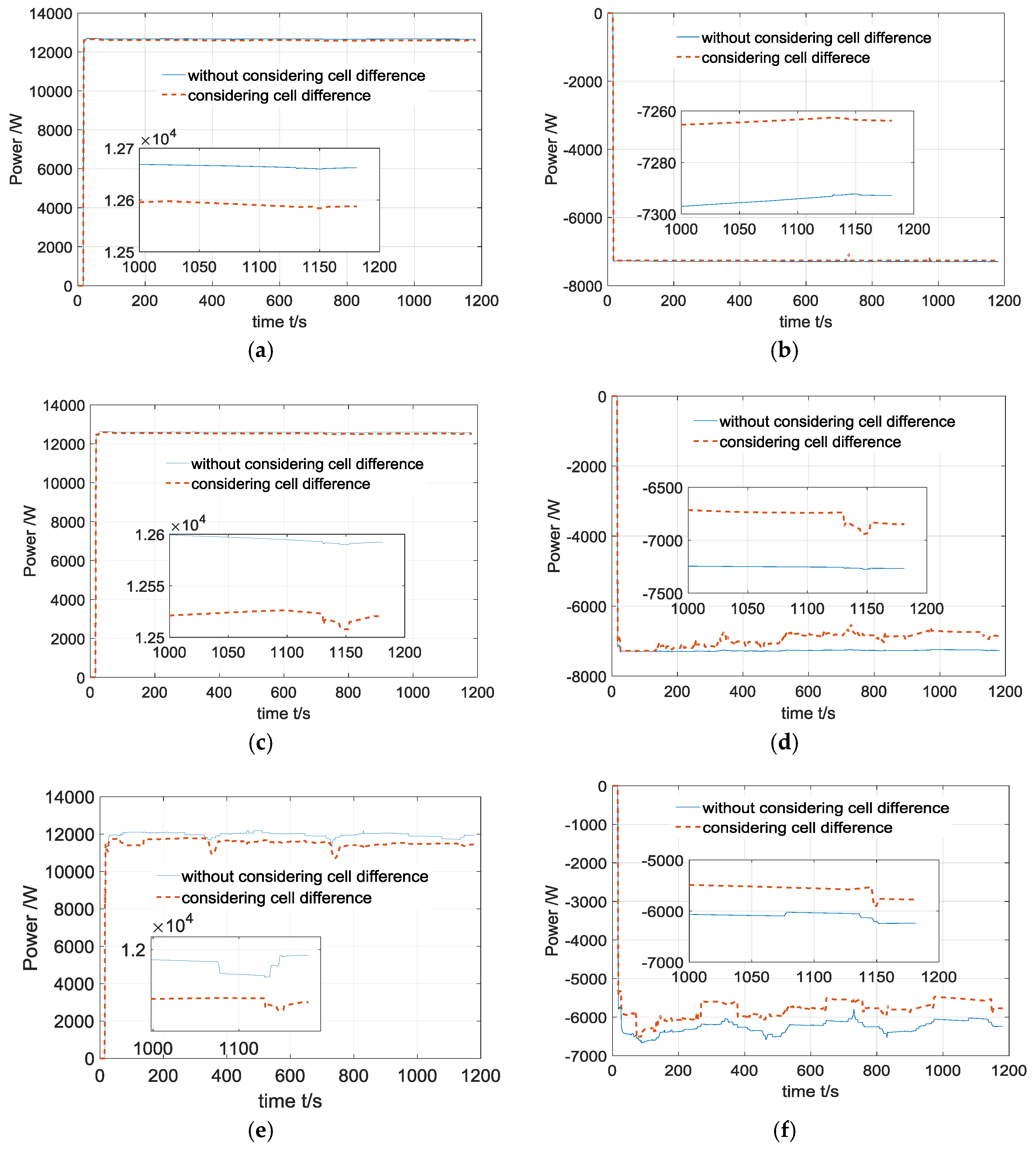
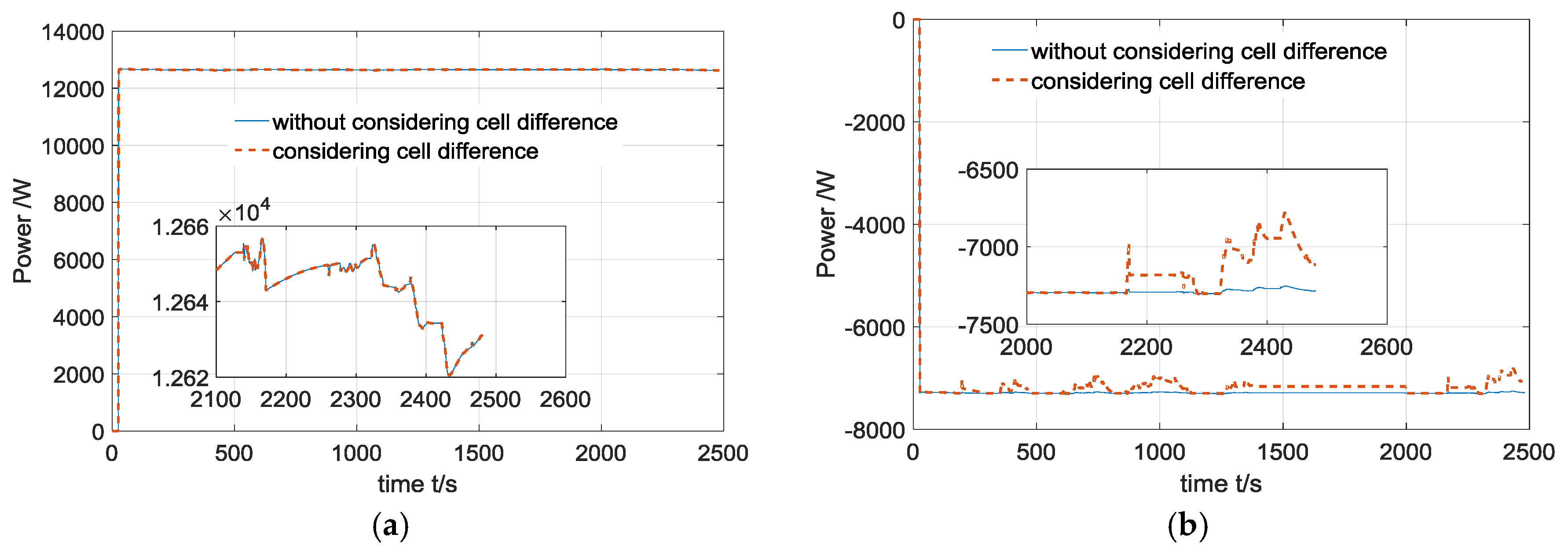
3.2. Power Estimation Considering Cell Difference
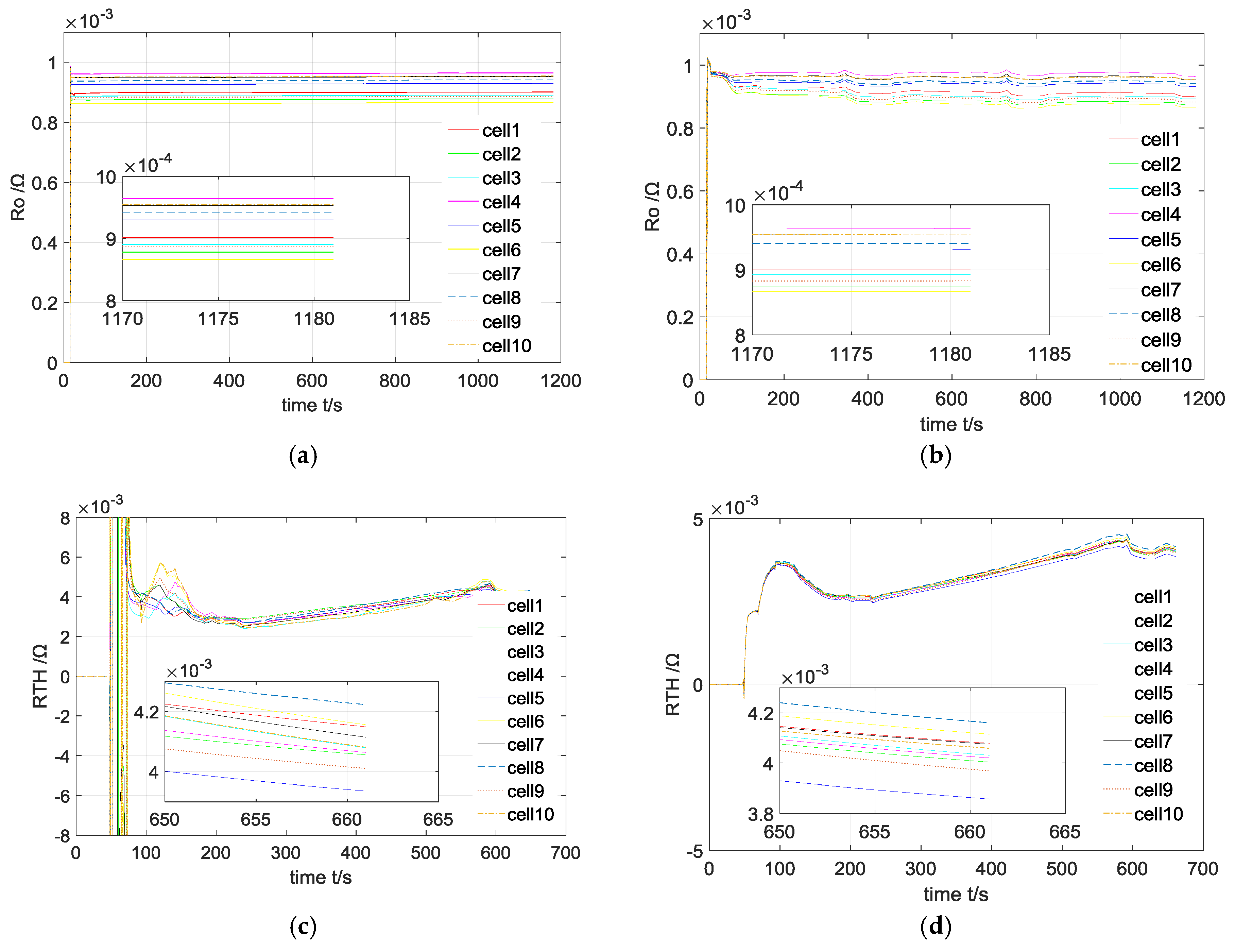
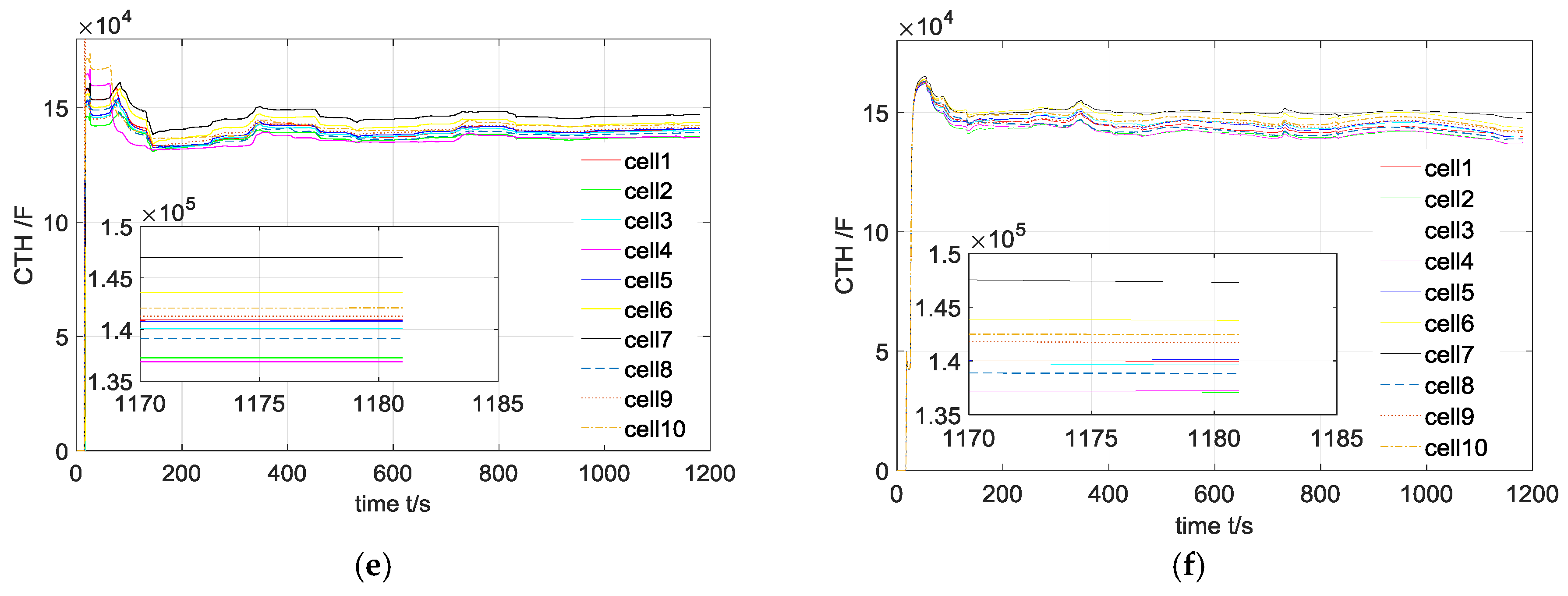
4. Case Study
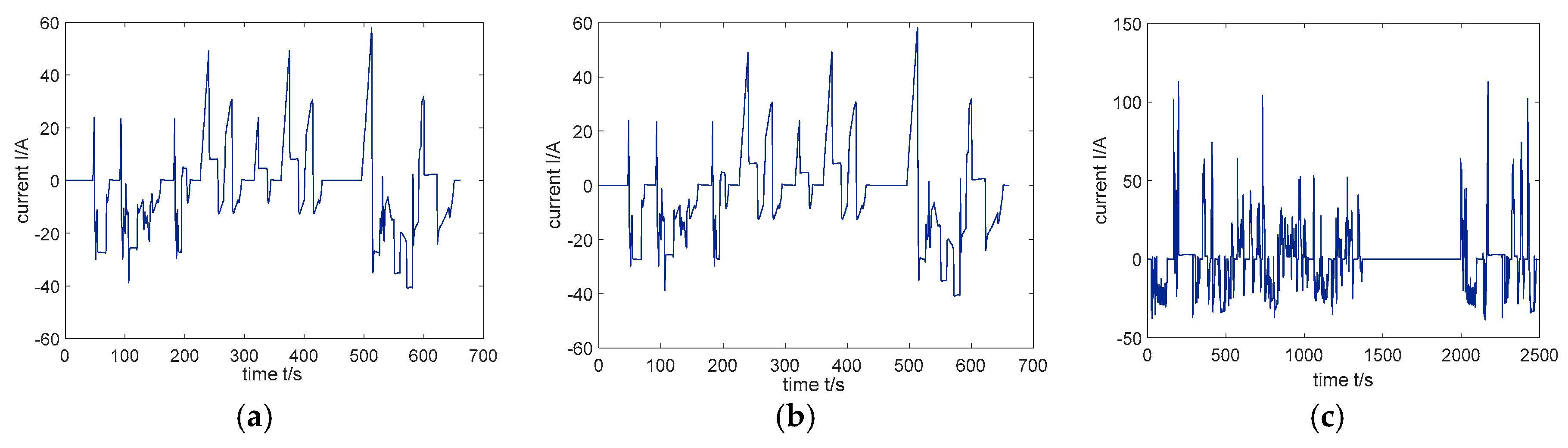
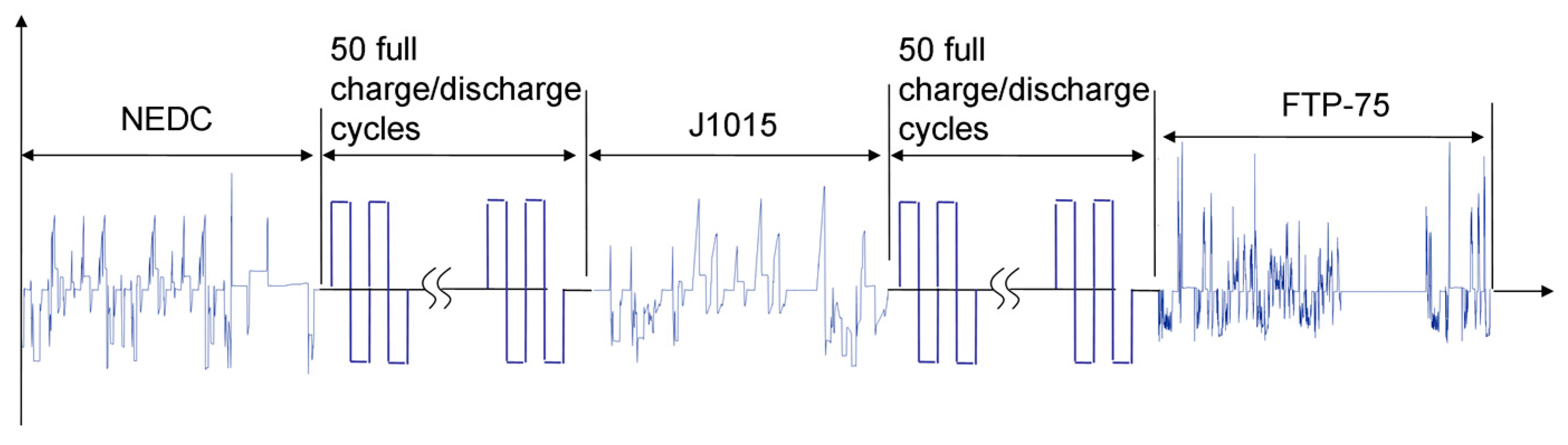
4.1. Experimental Setups
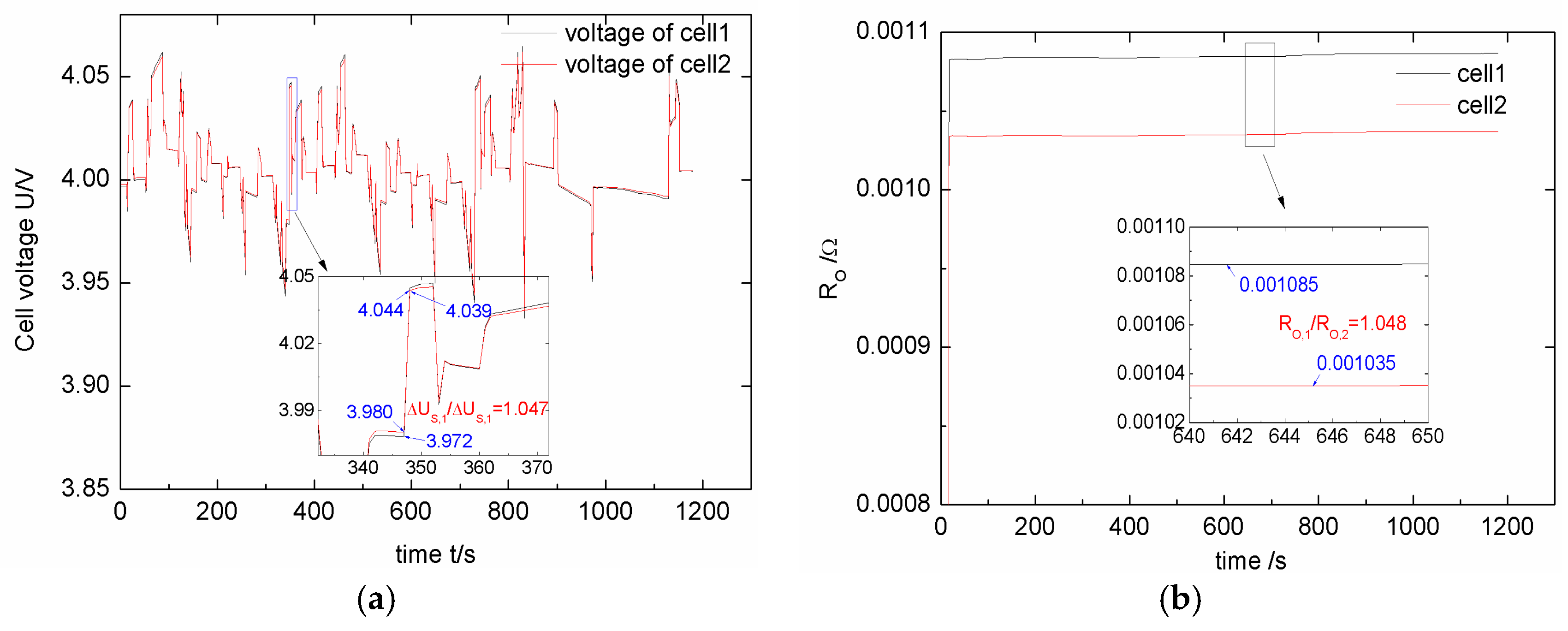
4.2. Results and Discussions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| UB | Battery terminal voltage |
| UOC | Battery open circuit voltage |
| IB | Battery working current |
| RO | Ohmic resistance of the battery |
| UTH | Voltage on network describing the charge transfer effect |
| RTH | Resistance of charge transfer |
| CTH | Double layer capacitor |
| Ud | Dynamic voltage on the impedance under current excitation |
| Δt | Sampling period |
| k | Sampling point |
| θ | Parameter vector of the battery model |
| Umax | Allowed maximum voltage of the battery |
| Umin | Allowed minimum voltage of the battery |
| Imax,batt | Allowed maximum discharge current of the battery suggested by the battery suppliers |
| Imin,batt | Allowed maximum charge current of the battery suggested by the battery suppliers |
| Imax,volt | Allowed maximum discharge current of the battery limited by voltage |
| Imin,volt | Allowed maximum charge current of the battery limited by voltage |
| ROm | Ohmic resistance of the mean battery cell |
| RTHm | Charge transfer resistance of the mean battery cell |
| CTHm | Equivalent capacitor of charge transfer effect of the mean battery cell |
| UO | Voltage on the ohmic resistance under current excitation |
| ΔUsm | Sudden voltage change during current pulse of the mean battery cell |
| ΔUs | Sudden voltage change during current pulse of the battery |
| A | Vector reflecting the difference of ohmic resistance |
| B | Vector reflecting the difference of time constant of charge transfer effect |
| C | Vector reflecting the difference of charge transfer resistance |
| Predicted sudden voltage change during current pulse | |
| N | Number of the battery cells connected in series |
| gA | Adjustment gain for vector A |
| gB | Adjustment gain for vector B |
| gC | Adjustment gain for vector C |
| Psysmin | Maximum charge power of the battery system |
| Psysmax | Maximum discharge power of the battery system |
| Predicted ratio of the charge transfer voltages at sampling point k | |
| Ratio of charge transfer voltages | |
| Ratio of the charge transfer resistance | |
| Predicted ratio of the charge transfer resistance at sampling point |
References
- Lu, L.; Han, X.; Li, J.Q.; Hu, J.F.; Ouyang, M. Review on the key issues for lithium-ion battery management in electric vehicles. J. Power Source 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Castaings, A.; Lhomme, W.; Trigui, R.; Bouscayrol, A. Comparison of energy management strategies of a battery/supercapacitors system for electric vehicle under real-time constraints. Appl. Energy 2016, 163, 190–200. [Google Scholar] [CrossRef]
- PNGV Battery Test Manual: Revision 3; US Department of Energy: Washington, DC, USA, 2001.
- Gregory, L.P. High-performance battery-pack power estimation using a dynamic cell model. IEEE Trans. Veh. Technol. 2004, 53, 1586–1593. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Adaptive on-line prediction of the available power of lithium-ion batteries. J. Power Source 2013, 242, 548–559. [Google Scholar] [CrossRef]
- Sun, F.C.; Xiong, R.; He, H.W.; Li, W.Q.; Aussems, J.E.E. Model-based dynamic multi-parameter method for peak power estimation of lithium-ion batteries. Appl. Energy 2012, 96, 378–386. [Google Scholar] [CrossRef]
- Pei, L.; Zhu, C.B.; Wang, T.S.; Lu, R.G.; Chan, C.C. Online peak power prediction based on a parameter and state estimator for lithium-ion batteries in electric vehicles. Energy 2014, 66, 766–779. [Google Scholar] [CrossRef]
- Burgos-Mellado, C.; Orchard, M.E.; Kazerani, M.; Cardenas, R.; Saez, D. Particle-filtering-based estimation of maximum available power state in lithium-ion batteries. Appl. Energy 2016, 161, 349–363. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.C.; He, H.W.; Nguyen, T.D. A data-driven adaptive state of charge and power capability a data-driven adaptive state of charge and power capability joint estimator of lithium-ion polymer battery used in electric vehicles. Energy 2013, 63, 295–308. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, W.; Ma, Z.Y. Adaptive unscented Kalman filter based state of energy and power capability estimation approach for lithium-ion battery. J. Power Source 2015, 289, 50–62. [Google Scholar] [CrossRef]
- Malysz, P.; Ye, J.; Gu, R.; Yang, H.; Emadi, A. Battery state-of-power peak current calculation and verification using an asymmetric parameter equivalent circuit model. IEEE Trans. Veh. Tech. 2016, 65, 4512–4522. [Google Scholar] [CrossRef]
- Wang, S.Q.; Verbrugge, M.; Wang, J.S.; Liu, P. Power prediction from a battery state estimator that incorporates diffusion resistance. J. Power Source 2012, 214, 399–406. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Source 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Bohlen, O.; Gerschler, J.B.; Sauer, D.U. Robust algorithms for a reliable battery diagnosis-managing batteries in hybrid electric vehicles. In Proceedings of the 22nd Electric Vehicle Symposium (EVS22), Yokohama, Japan, 23–28 October 2006.
- Kim, D.Y.; Jung, D.Y. Method of Estimating Maximum Output of Battery for Hybrid Electric Vehicle. U.S. Patent 7,518,375 B2, 14 April 2009. [Google Scholar]
- Duong, V.H.; Bastawrous, H.A.; Lim, K.C.; See, K.W.; Zhang, P.; Dou, S.X. Online state of charge and model parameters estimation of LiFePO4 battery in electric vehicles using multiple adaptive forgetting factors recursive least-squares. J. Power Source 2015, 296, 215–224. [Google Scholar] [CrossRef]
- Wei, Z.B.; Lim, T.M.; Skyllas-Kazacos, M.; Wai, N.; Tseng, K.J. Online state of charge and model parameter co-estimation based on a novel multi-time scale estimator for vanadium redox flow battery. Appl. Energy 2016, 172, 169–179. [Google Scholar] [CrossRef]
- Plett, L.G. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification. J. Power Source 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Dai, H.F.; Wei, X.Z.; Sun, Z.C. Recursive parameter identification of lithium-ion battery for EVs based on equivalent circuit model. J. Comput. Theor. Nanosci. 2013, 10, 2813–2818. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, X.S.; Ma, H.M.; Li, S.E. Combined state of charge and state of health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Source 2015, 273, 793–803. [Google Scholar] [CrossRef]
- Nejad, S.; Gladwin, D.T.; Stone, D.A. A systematic review of lump-parameter equivalent circuit models for real-time estimation of lithium-ion battery states. J. Power Source 2016, 316, 183–196. [Google Scholar] [CrossRef]
- Feng, T.H.; Yang, L.; Zhao, X.W.; Zhang, H.D.; Qiang, J.X. Online identification of lithium-ion battery parameters based on an improved equivalent-circuit model and its implementation on battery state-of-power prediction. J. Power Source 2015, 281, 192–203. [Google Scholar] [CrossRef]
- Sun, F.; Xiong, R.; He, H. A systematic state-of-charge estimation framework for multi-cell battery pack in electric vehicles using bias correction technique. Appl. Energy 2016, 162, 1399–1409. [Google Scholar] [CrossRef]
- Lim, K.C.; Bastawrous, H.A.; Duong, V.H.; See, K.W.; Zhang, P.; Dou, S.X. Fading Kalman filter-based real-time state of charge estimation in LiFePO4 battery-powered electric vehicles. Appl. Energy 2016, 169, 40–48. [Google Scholar] [CrossRef]
- Partovibakhsh, M.; Liu, G.J. An adaptive unscented Kalman filtering approach for online estimation of model parameters and state-of-charge of lithium-ion batteries for autonomous mobile robots. IEEE Trans. Control Syst. Technol. 2015, 23, 357–363. [Google Scholar] [CrossRef]
- Chen, C.; Xiong, R.; Shen, W. A lithium-ion battery-in-the-loop approach to test and validate multi-scale dual H infinity filters for state of charge and capacity estimation. IEEE Trans. Power Electr. 2017. [Google Scholar] [CrossRef]
- Hua, Y.; Cordoba-Arenas, A.; Warner, N.; Rizzoni, G.A. multi time-scale state-of-charge and state-of-health estimation framework using nonlinear predictive filter for lithium-ion battery pack with passive balance control. J. Power Source 2015, 280, 293–312. [Google Scholar] [CrossRef]
- Dai, H.A.; Wei, X.Z.; Sun, Z.C.; Wang, J.Y.; Gu, W.J. Online cell SOC estimation of Li-ion battery packs using a dual time-scale Kalman filtering for EV applications. Appl. Energy 2012, 95, 227–237. [Google Scholar] [CrossRef]
- Roscher, M.A.; Bohlen, O.S.; Sauer, D.U. Reliable state estimation of multicell lithium-ion battery systems. IEEE Trans. Energy Convers. 2011, 26, 7373–7743. [Google Scholar] [CrossRef]
- Barre, A.; Deguilhem, B.; Grolleau, S.; Gerard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Source 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Waag, W.; Kabitz, S.; Sauer, D.U. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application. Appl. Energy 2013, 102, 885–897. [Google Scholar] [CrossRef]



| No. | Parameter | Value |
|---|---|---|
| 1 | Nominal capacity (Ah) | 80 |
| 2 | Nominal voltage (V) | 3.7 |
| 3 | Discharge cut-off voltage (V) | 2.8 |
| 4 | Charge cut-off voltage (V) | 4.2 |
| 5 | Allowed maximum 30 s pulse discharge current (15%–85% SOC) (A) | 480 |
| 6 | Allowed maximum 30 s pulse charge current (15%–85% SOC) (A) | 240 |
| Test Cycles | Computation time of the RLS (s) | Computation Time of the New Method (s) | Time Reduced (%) |
|---|---|---|---|
| J1015 | 1.46 | 0.67 | 54.1 |
| NEDC | 2.74 | 1.28 | 53.2 |
| FTP75 | 5.71 | 2.66 | 53.4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, B.; Dai, H.; Wei, X.; Zhu, L.; Sun, Z. Online Reliable Peak Charge/Discharge Power Estimation of Series-Connected Lithium-Ion Battery Packs. Energies 2017, 10, 390. https://doi.org/10.3390/en10030390
Jiang B, Dai H, Wei X, Zhu L, Sun Z. Online Reliable Peak Charge/Discharge Power Estimation of Series-Connected Lithium-Ion Battery Packs. Energies. 2017; 10(3):390. https://doi.org/10.3390/en10030390
Chicago/Turabian StyleJiang, Bo, Haifeng Dai, Xuezhe Wei, Letao Zhu, and Zechang Sun. 2017. "Online Reliable Peak Charge/Discharge Power Estimation of Series-Connected Lithium-Ion Battery Packs" Energies 10, no. 3: 390. https://doi.org/10.3390/en10030390
APA StyleJiang, B., Dai, H., Wei, X., Zhu, L., & Sun, Z. (2017). Online Reliable Peak Charge/Discharge Power Estimation of Series-Connected Lithium-Ion Battery Packs. Energies, 10(3), 390. https://doi.org/10.3390/en10030390






