Analytical Calculation of Magnetic Field Distribution and Stator Iron Losses for Surface-Mounted Permanent Magnet Synchronous Machines
Abstract
:1. Introduction
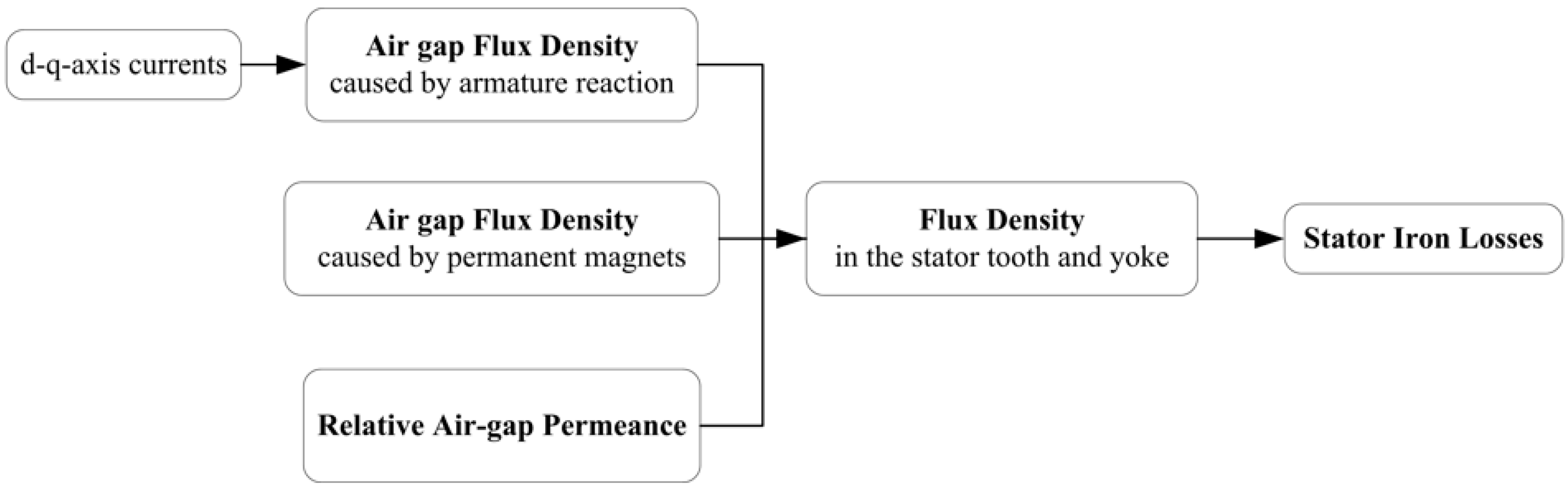
2. Stator Iron Losses Calculation Principle of SPM Machines
3. Analytical Calculation Method
3.1. Air Gap Flux Density Caused by Armature Reaction
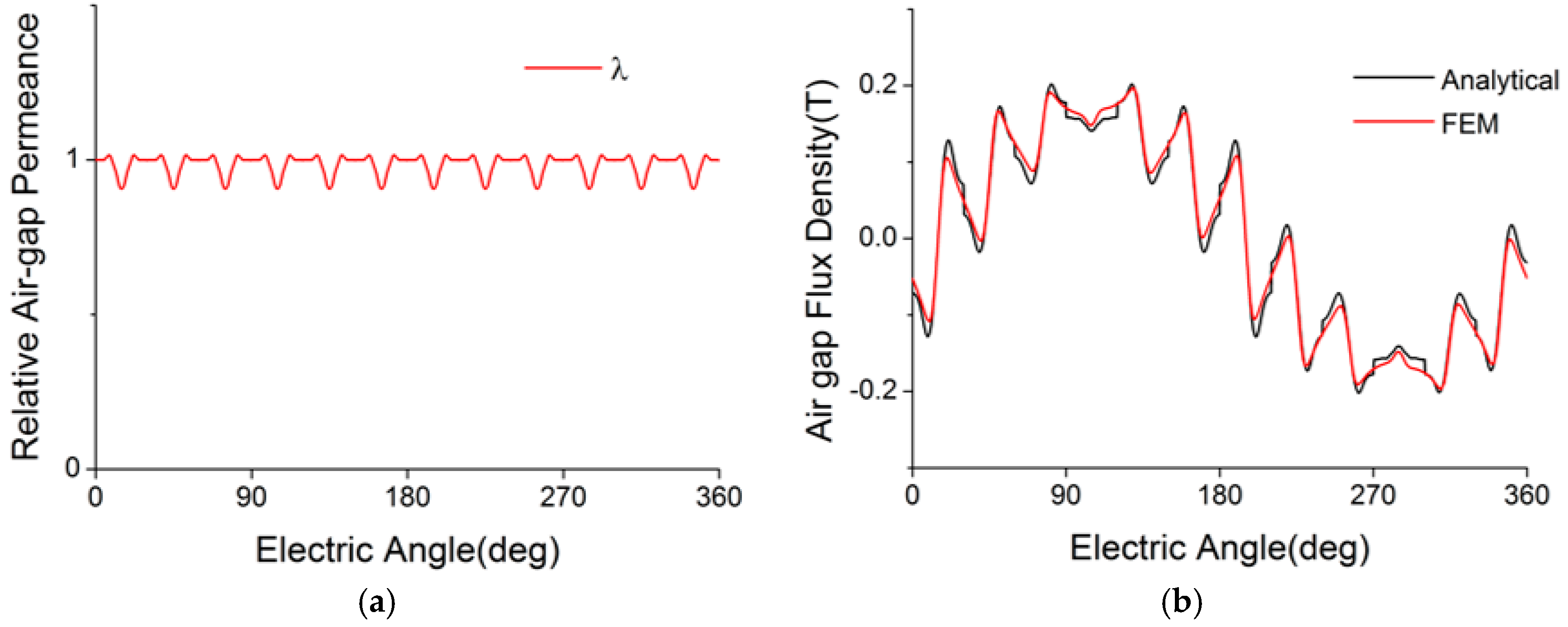
3.2. Relative Air-Gap Permeance
3.3. Air-Gap Flux Density Caused by Permanent Magnets
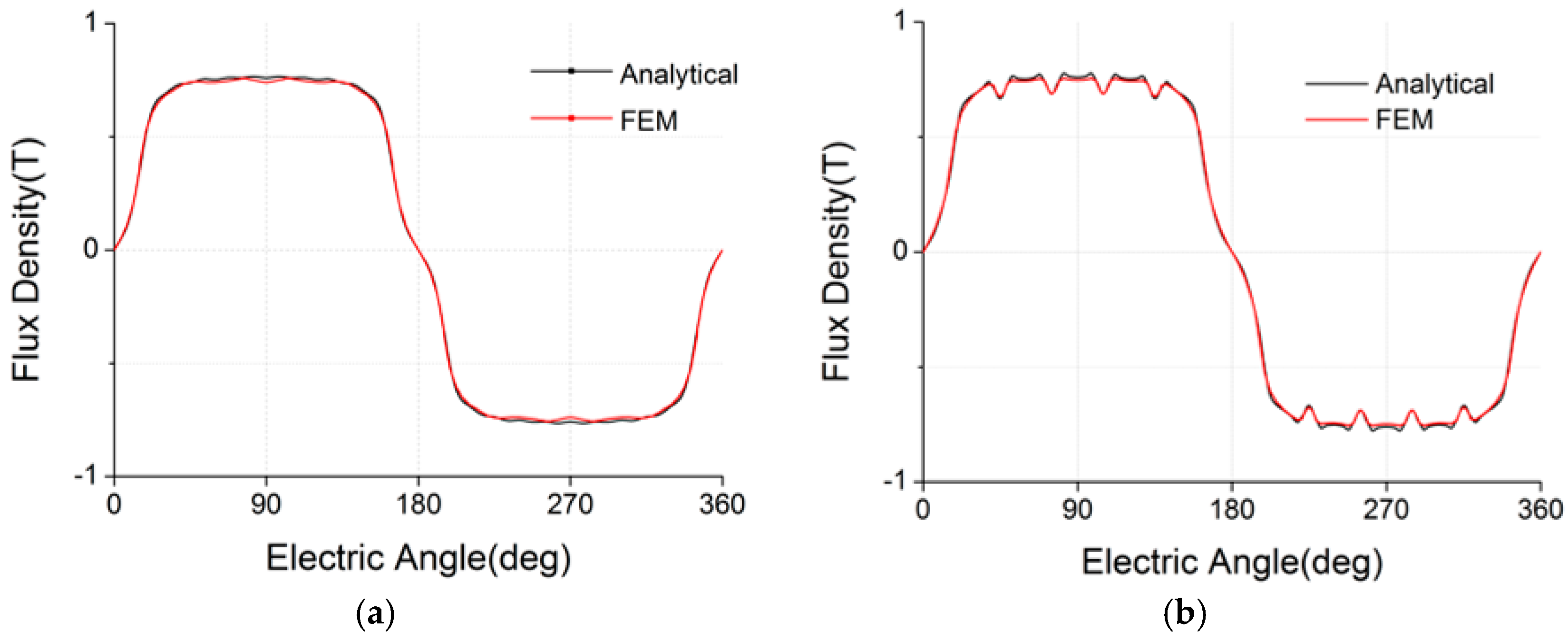
3.4. On-Load Flux Density in Air Gap and Stator
3.5. Stator Iron Losses
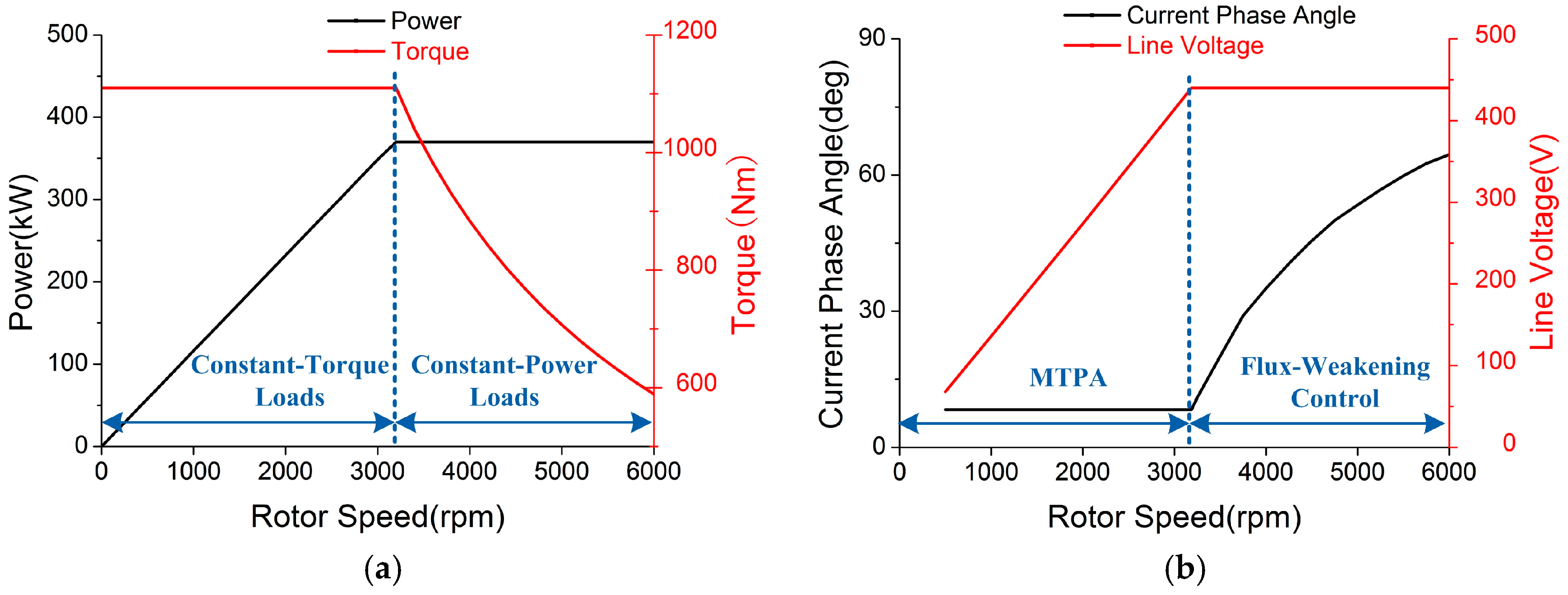
4. Results and Discussions
4.1. Motor Specification
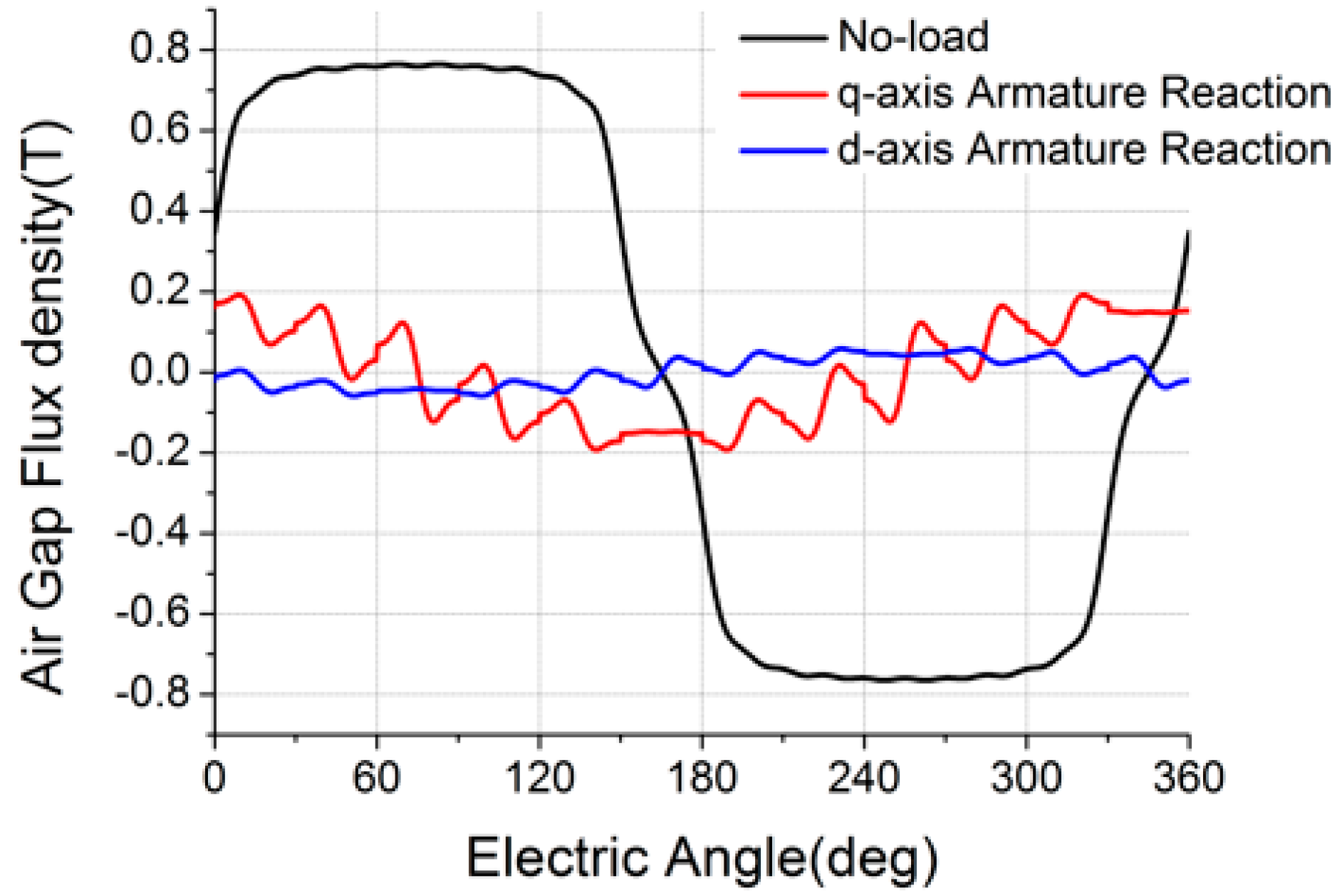
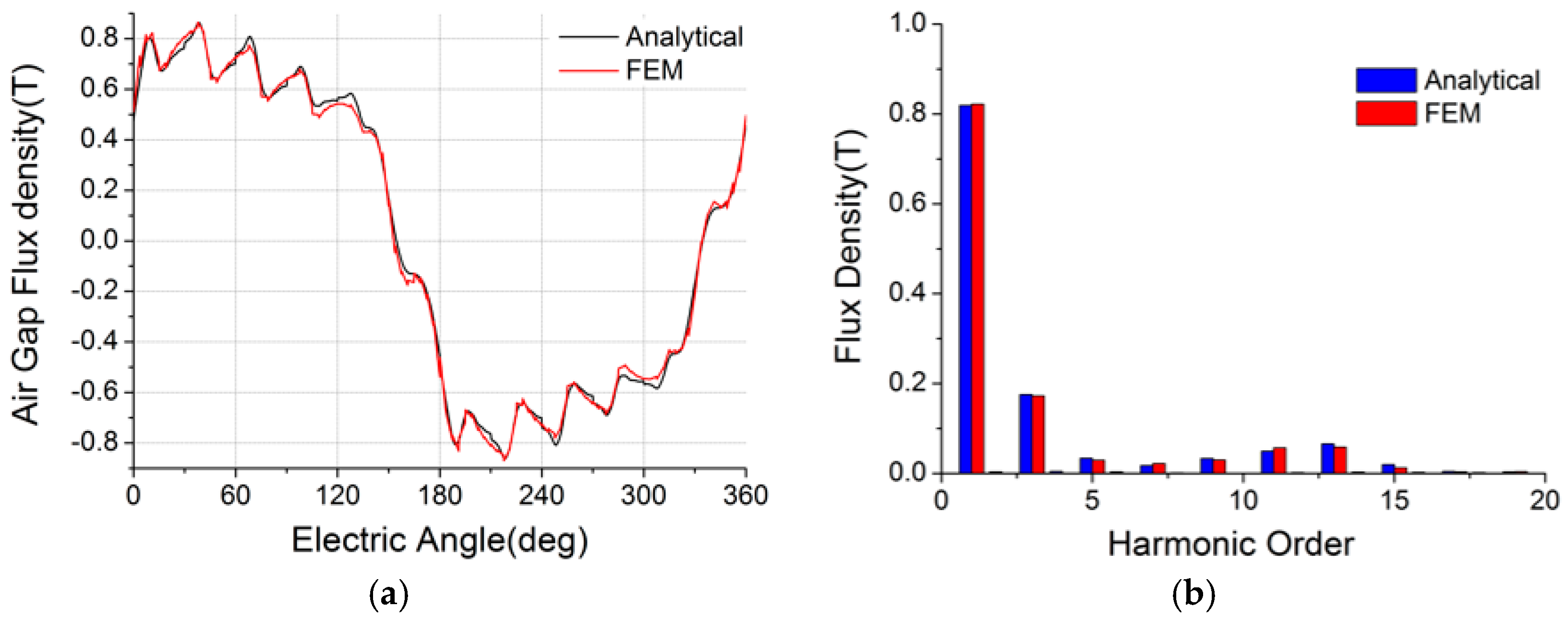
4.2. Relative Air-Gap Permeance and Flux Densities
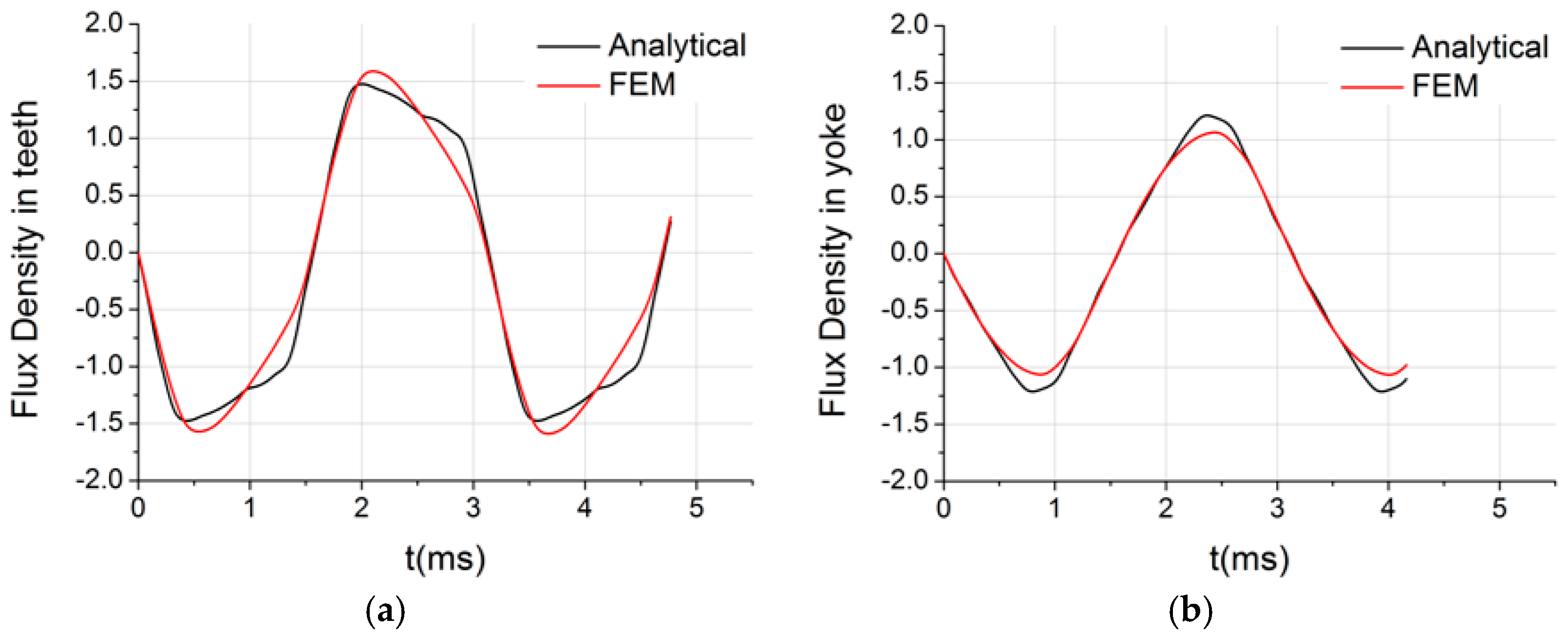
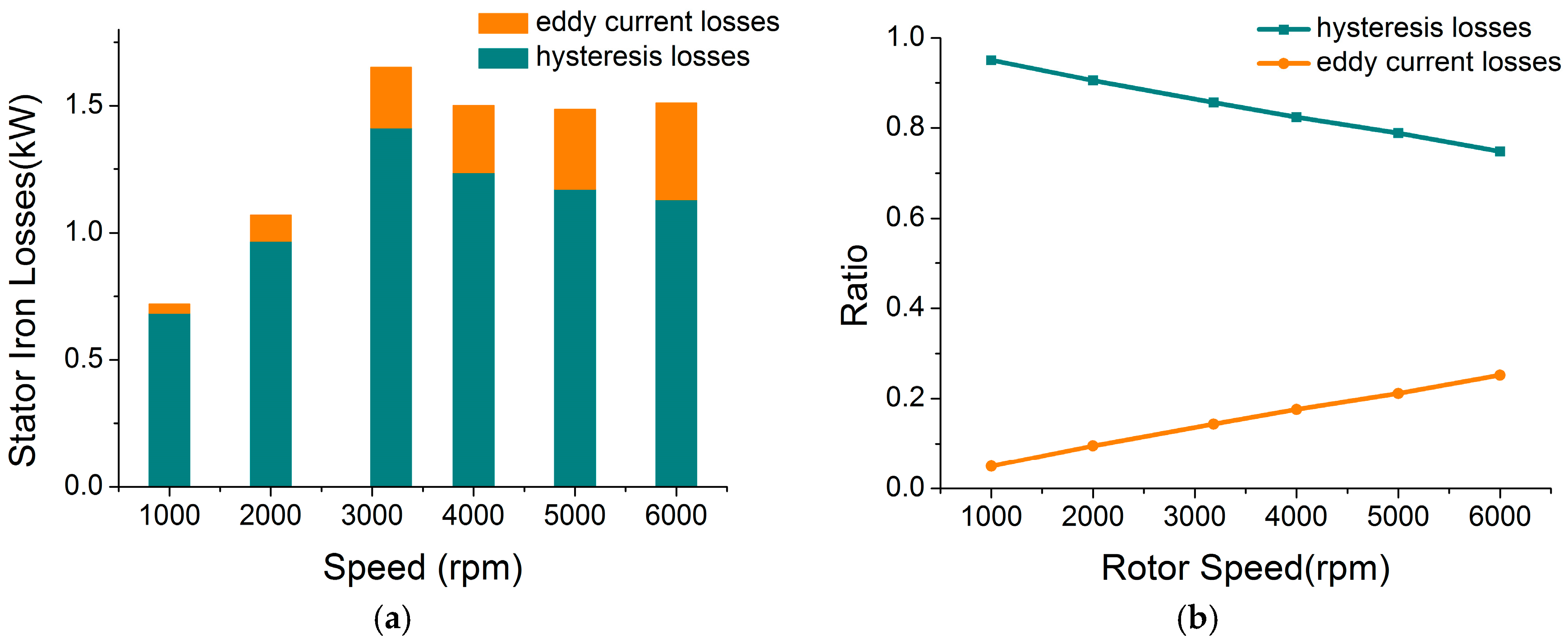
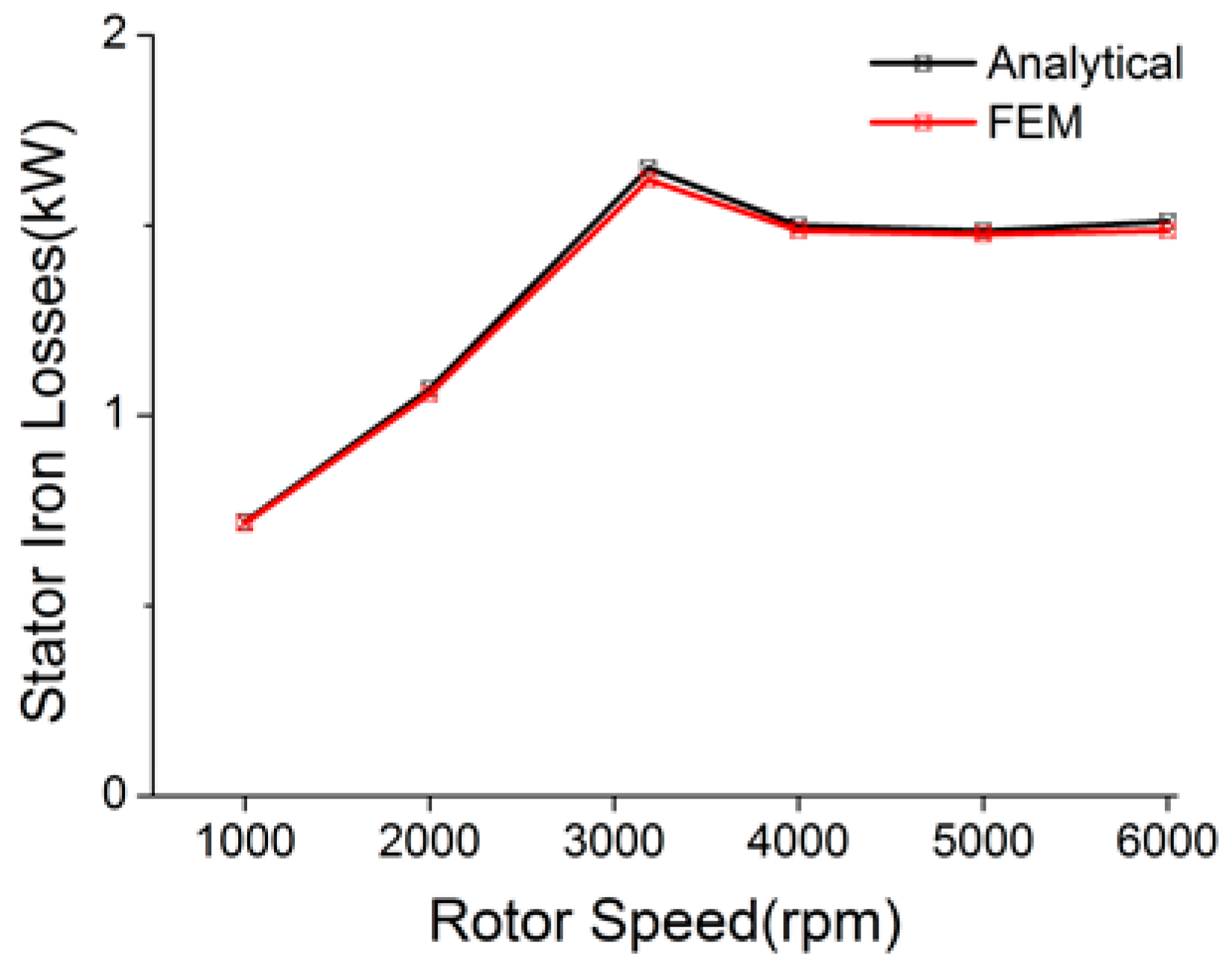
4.3. Stator Iron Losses
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yan, H.; Xu, Y.; Zou, J. A Phase Current Reconstruction Approach for Three-Phase Permanent-Magnet Synchronous Motor Drive. Energies 2016, 9, 853. [Google Scholar] [CrossRef]
- Zhao, J.; Li, B.; Gu, Z. Research on an Axial Flux PMSM with Radially Sliding Permanent Magnets. Energies 2015, 8, 1663–1684. [Google Scholar] [CrossRef]
- Liu, X.; Du, J.; Liang, D. Analysis and Speed Ripple Mitigation of a Space Vector Pulse Width Modulation-Based Permanent Magnet Synchronous Motor with a Particle Swarm Optimization Algorithm. Energies 2016, 9, 923. [Google Scholar] [CrossRef]
- Chu, W.Q.; Zhu, Z.Q.; Chen, J.T. Simplified analytical optimization and comparison of torque densities between electrically excited and permanent-magnet machines. IEEE Trans. Ind. Electron. 2014, 61, 5000–5011. [Google Scholar] [CrossRef]
- Atallah, K.; Zhu, Z.Q.; Howe, D. An improved method for predicting iron losses in brushless permanent magnet DC drives. IEEE Trans. Magn. 1992, 28, 2997–2999. [Google Scholar] [CrossRef]
- Deng, F. An improved iron loss estimation for permanent magnet brushless machines. IEEE Trans. Energy Convers. 1999, 14, 1391–1395. [Google Scholar] [CrossRef]
- Mi, C.; Slemon, G.R.; Bonert, R. Modeling of iron losses of permanent-magnet synchronous motors. IEEE Trans. Ind. Appl. 2003, 39, 734–742. [Google Scholar]
- Bose, B.K. Power Electronics and Variable Frequency Drives. Technology and Applications; IEEE Press: Piscataway, NJ, USA, 1997. [Google Scholar]
- Barcaro, M.; Bianchi, N. Air-gap flux density distortion and iron losses in anisotropic synchronous motors. IEEE Trans. Magn. 2010, 46, 121–126. [Google Scholar] [CrossRef]
- Stumberger, B.; Hamler, A.; Hribernik, B. Analysis of iron loss in interior permanent magnet synchronous motor over a wide-speed range of constant output power operation. IEEE Trans. Magn. 2000, 36, 1846–1849. [Google Scholar] [CrossRef]
- Tang, C.; Soong, W.L.; Liew, G.S.; Ertugrul, N.; Jahns, T.M. Analysis of stator iron loss in interior PM machines under open and short-circuit conditions. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 1227–1234.
- Tangudu, J.K.; Jahns, T.M.; Ayman, E.R. Core loss prediction using magnetic circuit model for fractional-slot concentrated-winding interior permanent magnet machines. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 1004–1011.
- Mi, C.; Slemon, G.R.; Bonert, R. Minimization of iron losses of permanent magnet synchronous machines. IEEE Trans. Energy Convers. 2005, 20, 121–127. [Google Scholar] [CrossRef]
- Zarko, D.; Ban, D.; Lipo, T.A. Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent-magnet motor using complex relative air-gap permeance. IEEE Trans. Magn. 2006, 42, 1828–1837. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D.; Bolte, E.; Ackermann, B. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. I. Open-circuit field. IEEE Trans. Magn. 1993, 29, 124–135. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D.; Chan, C.C. Improved analytical model for predicting the magnetic field distribution in brushless permanent-magnet machines. IEEE Trans. Magn. 2002, 38, 229–238. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. III. Effect of stator slotting. IEEE Trans. Magn. 1993, 29, 143–151. [Google Scholar] [CrossRef]
- Wu, L.; Zhu, Z.Q. Analytical modeling of surface-mounted PM machines accounting for magnet shaping and varied magnet property distribution. IEEE Trans. Magn. 2014, 50, 1–11. [Google Scholar] [CrossRef]
- Li, Q.; Fan, T.; Wen, X. An Improved Model of Estimating Iron Loss for Interior Permanent Magnet Synchronous Machine. In Proceedings of the 2013 IEEE Vehicle Power and Propulsion Conference (VPPC), Beijing, China, 15–18 October 2013; pp. 1–5.
- Li, Q.; Fan, T.; Wen, X. Armature-reaction magnetic field analysis for interior permanent magnet motor based on winding function theory. IEEE Trans. Magn. 2013, 49, 1193–1201. [Google Scholar] [CrossRef]
- Rabinovici, R.; Miller, T.J.E. Eddy-current losses of surface-mounted permanent-magnet motors. IEE Proc.-Electr. Power Appl. 1997, 144, 61–64. [Google Scholar] [CrossRef]
- Tang, R.Y. Modern Permanent Magnet Machines: Theory and Design; China Machine Press: Beijing, China, 1997; pp. 161–215. (In Chinese) [Google Scholar]
- Wang, X. Permanent Magnet Machine; China Electric Power Press: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Lin, F.; Zuo, S.; Ma, C.; Tan, Q. Analytical Calculation of Armature Reaction Field Including Slotting Effects in PMSM with Concentrated Fractional-Slot Winding. Trans. China Electrotech. Soc. 2014, 29, 29–35. (In Chinese) [Google Scholar]

| Specification | Design Results (Parameters) | ||
|---|---|---|---|
| Rated power | 370 kW | Number of poles | 12 |
| Rated speed | 3185 rpm | Number of slots | 72 |
| Rated torque | 1110 Nm | Stator inner diameter | 340 mm |
| DC voltage | 900 V | Stator outer diameter | 482 mm |
| Maximum speed | 6000 rpm | Stack length | 178 mm |
| Maximum output | 555 kW | Airgap length | 4 mm |
| Type of magnet | Sm-Co(Br = 1.06 T) | PM thickness | 13 mm |
| Steel sheet for core | B20AT1500 | Slot depth | 51 mm |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Z.; Zhang, C.; Zhang, S. Analytical Calculation of Magnetic Field Distribution and Stator Iron Losses for Surface-Mounted Permanent Magnet Synchronous Machines. Energies 2017, 10, 320. https://doi.org/10.3390/en10030320
Tian Z, Zhang C, Zhang S. Analytical Calculation of Magnetic Field Distribution and Stator Iron Losses for Surface-Mounted Permanent Magnet Synchronous Machines. Energies. 2017; 10(3):320. https://doi.org/10.3390/en10030320
Chicago/Turabian StyleTian, Zhen, Chengning Zhang, and Shuo Zhang. 2017. "Analytical Calculation of Magnetic Field Distribution and Stator Iron Losses for Surface-Mounted Permanent Magnet Synchronous Machines" Energies 10, no. 3: 320. https://doi.org/10.3390/en10030320
APA StyleTian, Z., Zhang, C., & Zhang, S. (2017). Analytical Calculation of Magnetic Field Distribution and Stator Iron Losses for Surface-Mounted Permanent Magnet Synchronous Machines. Energies, 10(3), 320. https://doi.org/10.3390/en10030320





