Abstract
In recent years, demand side management (DSM) techniques have been designed for residential, industrial and commercial sectors. These techniques are very effective in flattening the load profile of customers in grid area networks. In this paper, a heuristic algorithms-based energy management controller is designed for a residential area in a smart grid. In essence, five heuristic algorithms (the genetic algorithm (GA), the binary particle swarm optimization (BPSO) algorithm, the bacterial foraging optimization algorithm (BFOA), the wind-driven optimization (WDO) algorithm and our proposed hybrid genetic wind-driven (GWD) algorithm) are evaluated. These algorithms are used for scheduling residential loads between peak hours (PHs) and off-peak hours (OPHs) in a real-time pricing (RTP) environment while maximizing user comfort (UC) and minimizing both electricity cost and the peak to average ratio (PAR). Moreover, these algorithms are tested in two scenarios: (i) scheduling the load of a single home and (ii) scheduling the load of multiple homes. Simulation results show that our proposed hybrid GWD algorithm performs better than the other heuristic algorithms in terms of the selected performance metrics.
1. Introduction
In order to make a robust and more reliable power grid, peak demand is taken into account rather than the average demand. As a consequence, natural resources are wasted, and the generation and distribution systems are under-utilized. Fast responding generators (e.g., coal and gas units), which are used to meet the peak demand, are not only expensive, but also have a high carbon emission rate. As a solution, different programs have been presented to shape the energy consumption profiles of users. Such programs aim to efficiently utilize the available generation so that new transmission and new generation infrastructures are minimally installed. These programs, known as demand side management (DSM) programs, aim either at scheduling consumption or reducing consumption [1].
A DSM program provides support towards power grid functionalities in various areas, such as electricity market control, infrastructure maintenance and management of decentralized energy resources [2]. In electricity markets, it informs the load controller about the latest load schedule and possible load reduction capabilities for each time step of the next day. Using this procedure, it schedules the load according to the objectives of interest associated with the power distribution systems [3,4]. The load shapes indicate the daily or seasonal electricity demands of industrial or residential consumers between peak hours (PHs) and off-peak hours (OPHs). These shapes can be modified by six techniques [5,6]: peak clipping, valley filling, load shifting, strategic conservation, strategic load growth and flexible load shape.
Peak clipping and valley filling are direct load control techniques. Peak clipping deals with the reduction of the peak loads, whereas valley filling considers the construction of loads for the off peak demands. Load shifting is the most effective and widely-used technique for load management in current power supply networks. It is concerned with shifting of the load from PHs to OPHs. Strategic conservation [5] applies demand reduction methods at the customer side for achieving optimized load shapes. If there is a larger load demand, then the daily responses are optimized by load growth techniques (distributed energy resources) [5,6,7].
The working of a generic DSM controller is shown in Figure 1. The figure shows that DSM aims for: (i) electricity cost minimization; (ii) energy consumption minimization; (iii) peak to average ratio (PAR) minimization; and (iv) user comfort (UC) maximization. In the literature, many DSM techniques are proposed [8,9,10,11] to achieve the aforementioned objectives. However, UC is not considered in most of these techniques, like [8,10,12,13,14,15,16,17]. In these works, [11,18,19] aim to reduce the electricity cost, and [20,21] focus on minimizing the aggregated power consumption using integer linear programming and mixed integer linear programming. Similarly, electricity bills and aggregated power consumption are reduced in [22] by using mixed integer non-linear programming. However, these techniques do not take into account the large number of different household appliances. Moreover, randomness in user load profiles makes the scheduling task more challenging.
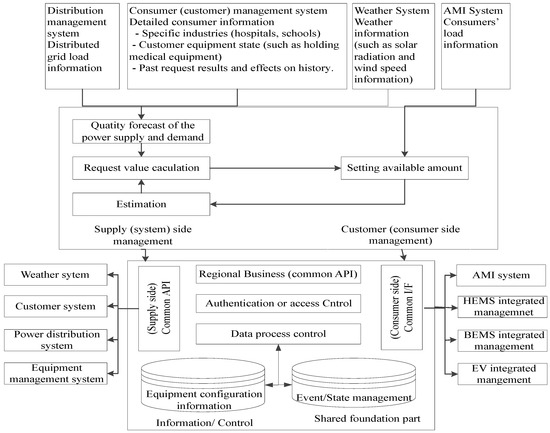
Figure 1.
Working of demand side management (DSM). AMI: Advanced metering infrastructure, HEM: Home Energy Management.
In this paper, a heuristic algorithm-based DSM controller is designed for a residential area in a SG using the RTP scheme. In the designed DSM controller, five heuristic algorithms are implemented; GA, BPSO, wind-driven optimization (WDO), bacterial foraging optimization algorithm (BFOA) and our proposed hybrid genetic wind-driven (GWD) algorithm. These algorithms are chosen for implementation due to their flexibility for specified constraints and their low computational complexity [23]. More distinctively, prioritized load shifting is carried out between PHs and OPHs using a large number of appliances in the residential area. For effective scheduling and ease of implementation, the appliances are divided into two classes: (i) Class A (non-shiftable appliances) and (ii) Class B (shiftable appliances). Simulations are conducted in MATLAB such that all of the selected heuristic algorithms are compared in terms of electricity cost, energy consumption, PAR and UC. Results show that our proposed hybrid GWD performs better than the other compared techniques in terms of the selected performance metrics. It is worth mentioning that the nomenclature and list of abbreviations are given in Table 1 and Table 2, respectively.

Table 1.
Nomenclature.

Table 2.
List of abbreviations.
2. Related Work
In [10], the authors propose a technique for controlling the residential energy loads while maximizing UC and minimizing the electricity bill. A survey of home energy management for the residential customers is presented in [24], where the authors focus on different techniques relating to shiftable, non-shiftable load and peak shaving. They use various pricing schemes, like RTP, TOU, CPP, IBR, etc. In [25], a fully-automated EMSfor residential and commercial buildings is presented. They use the Q-learning algorithm for optimal DR mechanisms. Cristopher et al. [26] design a new framework. They use SMs to decide the appliance schedules based on their load or power consumption. After scheduling, all of the data are transferred to the aggregator module, where the power consumption of all of the appliances is determined. The concept of load clustering is introduced in this approach, which comprises three clusters for scheduling purposes, as the first cluster is from 1 a.m. to 7 a.m., the second from 8 a.m. to 3 p.m. and the third from 3 p.m. to midnight. Two battery scheduling scenarios are used as: (i) the FCFS scheduling policy and (ii) appliance first scheduling policy. In FCFS, requests to consume electricity from clients are assigned priorities based on their arrival, whereas in the appliance first scenario, all electrical devices’ requests are given priority over battery charging.
Another methodology is proposed for minimizing the energy price under the dynamic pricing scheme to avoid PHs in [27]. Its architecture comprises SM, CN, WSN and IHD. AMI controls bidirectional data flow between the utility and SM. The SM operates between MC and AMI. The MC organizes and controls the schedules of both controllable and uncontrollable electrical appliances, such that the optimal schedule is transmitted to each CN via the WSN. IHD invigilates the whole process. In [8], GA is used to solve the scheduling problem under the RTP tariff in residential, commercial and industrial sectors. The authors present a novel approach known as the realistic scheduling mechanisms in [28] for minimizing the customer inconvenience using the TOU pricing scheme. They organize three categories of appliances (ADA, ODA, OIA) and the algorithms relevant to their working times. They also use the BPSO algorithm for the scheduling of these appliances. In [9], the researchers elaborate an efficient energy scheduling model and an algorithm based on artificial intelligence for residential area energy management in order to minimize the electricity cost. BPSO and GA are used for scheduling the optimal time of appliances and also for obtaining the best fitness values of the objective function.
For solving the numerically-constrained optimization problems, a review of BFOA is presented in [29]. The authors discuss the taxonomy of constraint handling techniques, the main steps and adaptations to different schemes, including search space, step size, tumble-swim operator and the elimination-reproduction process. In [30], a case study describes the electric demand model in rural households of Narino. Distributed privacy-friendly DSM is presented in [31], which preserves users’ privacy by integrating data aggregation and perturbation. The authors describe that the users schedule their requests of appliances according to the aggregated energy consumption measurements as an additive white Gaussian process.
The authors in [32] focus on cost and emission minimization approaches in data centers and corresponding cloud network infrastructures. They use renewable energy generation capability to enhance the reliability and energy efficiency in SG. They also improve the latency using the ICTs. The decentralized system framework presents DR mechanisms for the residential users to minimize electricity bills, maximize the UC and privacy in [33]. In this framework, customers’ SMs integrate home load management modules for exchanging the load profiles’ information. Agents exchange information until they find an accurate load profile where the system does not get more improvement in the solution.
In [34], an energy consumption management approach considers household users in which each house consists of two types of requests or demands: (i) essential and (ii) flexible, where flexible demands are further delay sensitive and delay tolerant. To optimize energy for both delay-sensitive and delay-tolerant demands, a new centralized algorithm is presented for scheduling. This approach also aims to minimize the total cost and delay of the flexible demands for obtaining optimal energy decisions. The authors design a cost-efficient demand side day-ahead bidding process and RTP mechanisms by using fractional programming methods in [35].
In [36], the authors present a survey of DSM optimization methods for the residential customers. They classify the DSM techniques into three dimensions as: (i) DSM for individual users and cooperative consumers; (ii) DSM as a deterministic model versus the stochastic method; and (iii) day-ahead DSM versus real-time DSM. The dynamic load priority method presents priorities to modify load priorities during the occurrence of demand response events in [37]. A DR technique formulates the two-stage stochastic problem for energy resource scheduling; inciting the challenges of the renewable sources, electric vehicle and market price uncertainty. It reduces the overall operational cost of the energy aggregator by using stochastic programming [38]. In [39], global load balancing schemes describe the data center power management for minimizing the total electricity cost. They explain different components of the data centers as information technology equipment, the power delivery system and the cooling system in relationship with the SG’s features (power delivery, sustainability, peak shaving, etc.). A multi-objective optimization solution is designed using the market operator and the distributed network operator for a microgrid in [40]. The generation of the price signal from the market operator and the power distribution system is specified using the Pareto-optimal solution. In [41], a novel pricing strategy is proposed to investigate the robustness against renewable energy source power inputs. This scheme also focuses on the marginal befits and marginal cost of the power market using all existing information related to electricity demand, supply and energy imbalance.
In short, the existing optimization techniques in [8,10,12,13,14] are unable to handle the complexity of cost minimization and UC maximization problems due to their non-flexible nature. In fact, the solution of these non-linear problems lead to high computational complexity. Therefore, we use heuristic algorithms (GA, BPSO, WDO and BFOA) to solve these two problems. These algorithms support the multi-objective optimization problems and have flexible constraints and parameters, which are easy to handle. These algorithms are similar to population-based search methods [42], which move from one population to another population in a number of iterations with improvement using a combination of deterministic and probabilistic rules. The comparison of the aforementioned techniques along with their achievements and drawbacks is listed in detail in Table 3.

Table 3.
Recent trends: state of the art work.
3. Problem Formulation
In this work, the major objectives are: (i) to reduce consumers’ electricity cost by optimizing the energy consumption of end users; (ii) to maximize the UC of consumers. Here, the problem is formulated as an optimization problem with fixed, shiftable and elastic loads.
3.1. Cost Minimization
Cost minimization refers to the minimum charges for the consumed loads provided by the utilities to the customers. The elastic and shiftable loads are considered for the cost minimization problem, which is formulated as follows:
such that:
where represents the states of the appliances as ON or OFF (1 = ON and 0 = OFF) and shows the price of the electricity consumed during any time interval t, which is the index for time upper bounded by hours in a day. , where H shows the time for the 24 h of a day, including PHs and OPHs. Here, indicates the PHs and describes the OPHs. i denotes the appliances’ index number, which is taken as .
3.2. UC Maximization
UC is modeled in terms of the minimum delay of appliances and optimal amounts for the electricity bills. Therefore, consumers always expect utilities with minimum delay and cost. Moreover, it also helps in minimizing the customers’ frustrations when the energy consumption is high during the OPHs. In this scenario, the appliances are assigned a specific priority, and high priority appliances are scheduled at the first and foremost available time intervals during the OPHs. The operations of the low priority appliances can be canceled or delayed during the PHs. In this way, appliances’ waiting time is minimized, and UC is achieved maximally. This is the multi-objective problem; several authors handle it using different approaches, as mentioned in the literature [12,13,14,15,16,17]. Here, it is handled by the metaheuristics for scheduling the residential area loads in order to reduce the electricity cost and maximize the UC. Energy cost is weighted at the minimum electricity bill, and UC weights are considered between [0, 1]. It is calculated by using the equations given below,
such that:
α and β are the delay variables. Moreover, is the delay function, and it is restricted to four hours in our scenario. It is worth mentioning that these 4 h are chosen from PHs for elucidating the maximum delay of the appliances. If the delay is greater than 4 h, then the utility pays a penalty by either paying back to customers or providing them with reductions in the electricity bills. According to Constraint (2b.2), the sum of α and β is equal to one because UC ranges between zero and one. is the cost function, and its values are between 20% and 70%. Below 20%, its values are assumed to be negligible, and cost is inconsiderable; and above 70% cost prices are used for the microgrids. is the cost of the appliances during the full day, and is the cost of peak hours of the day; is obtained from the status bits of the appliance x power rating; is also obtained from the hourly information updates. The values of α, β, and are taken from [28].
3.3. Multi-Objective Function
From the objective functions in Equations (1) and (2), it is clear that the optimization problem is multi-objective. We formulate the combined objective function as follows:
where . Here, it is worth mentioning that the combined objective function in Equation (3) is subject to the respective constraints of objective functions in Equations (1) and (2).
4. Proposed Solution
The proposed DSM techniques deal with the load management in a residential area for single and multiple homes. Its architecture consists of the number of homes, SMs, AMI and the utility companies. Let multiple homes be connected with a utility and SMs be installed in all of the homes as shown in Figure 2. The AMI is used for bidirectional communication between SM and the utility. All homes have three types of appliances: (i) fixed; (ii) elastic; and (iii) shiftable. These appliances are also categorized into Class A and Class B based on their fixed or interruptible load profiles. Fixed load appliances are included in Class A, whereas elastic and shiftable are included in Class B. In other words, Class B contains interruptible appliances, which take part in the scheduling process.
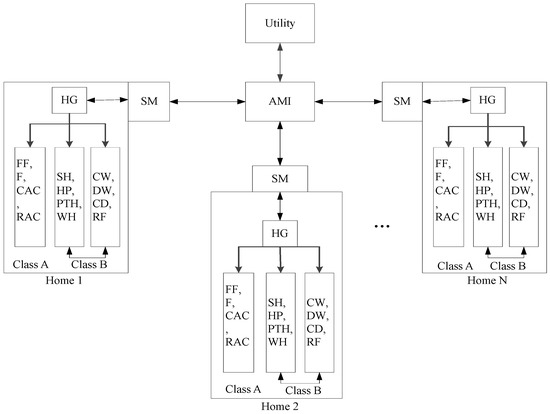
Figure 2.
Proposed system design.
The RTP tariff model is used for tracking the pattern of the total hourly costs of the consumed energy. Figure 3 shows that the appliances are scheduled by the appliances’ handler (EMC) during the specified time intervals using the given frame format. EMC schedules and checks appliances’ PB using the frame format. Each frame format consists of an eight-bit pattern, such that each appliance uses a specified bit pattern relating to its class ID, appliance ID, scheduling bit, interruptible or non-interruptible bit and priority bit. Based on the operational status of an appliance, its hourly cost schedule is tracked. In each class, every attribute uses a single bit, except class ID and appliance schedule, which use three- and two-bit patterns, respectively. This scenario is specific to these sets of the appliances using the given frame format for the proposed system’s test cases; however, it can be further extended to a larger set of appliances, and frame length can also be extended accordingly. Evolutionary algorithms are efficient in terms of computational complexity, however, at the cost of reduced accuracy. We prefer frame tracking over other evolutionary algorithms because it provides simple and efficient procedure in terms of relative accuracy and relative computational complexity. In the following subsections, the algorithms of GA, BPSO, WDO, BFOA and our proposed GWD algorithm are discussed in detail.
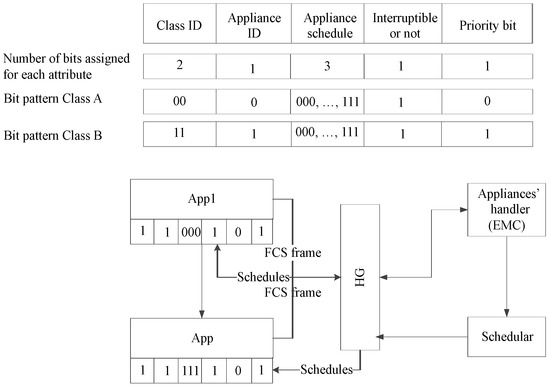
Figure 3.
RTP price tracking system.
4.1. GA, BPSO, WDO and BFOA Algorithms
In this section, we modify the existing versions of GA, WDO, BPSO and BFAO to optimally schedule shiftable appliances. Firstly, the load is shifted to the OPHs subject to electricity cost minimization. In order to reduce peaks during the OPHs, each appliance is assigned a specific PB, which indicates the status (either ON or OFF) of the selected appliance. If an appliance is demanded to run in a specific time slot, its PB = 1; otherwise, its PB = 0. This status bit information is communicated via an RTP frame format.
The authors in [13] have proposed a GA-based home energy management controller for a single home in a residential area using RTP tariffs. In this manuscript, a modified GA (an improved form of [13]) is presented, which is shown in Algorithm 1. Objective functions (refer to Equations (1)–(3)) and their constraints are used by all of the selected optimization algorithms to find feasible solutions. Users input initial parameters for all appliances. GA creates a random population initially, which consists of a number of chromosomes represented by binary strings as the ON/OFF status of each appliance. Each chromosome is evaluated using Equations (1)–(3). RTP is used as the electricity pricing scheme. Key modifications that are implemented in GA (Algorithm 1 [13]) to achieve the objectives in the proposed scheme and its expected outcomes are given in Table 4.

Table 4.
Modifications in GA.
| Algorithm 1: GA algorithm. |
 |
In [15], another energy management model is presented in which BPSO is used to meet the DSM challenges. The goal of this study is to minimize the electricity cost for residential area by scheduling shiftable loads. The authors use the TOU pricing model to calculate electricity bills of customers by investigating DR; however, they have ignored UC. Furthermore, in our proposed work, the objective function is formulated for cost minimization and UC maximization. BPSO is used to solve the designed optimization problem. RTP scheme is used for tracking the real-time behavior of the system. Thus, this proposed work gives a more significant solution for electricity bill minimization, PAR minimization and UC maximization. All steps of the proposed work are shown in Algorithm 2. Compared to [15], BPSO is modified according to the customers’ requirements. Each particle in the generation is represented by a binary string denoted as states of an appliance. The proposed model is applicable for single and multiple homes in residential areas. In Table 5, some suitable modifications and expected results in response to those modifications for the BPSO algorithm are given.

Table 5.
Refinements in BPSO.
| Algorithm 2: BPSO algorithm. |
 |
A WDO-based scheduling technique is presented in [10] for comfort maximization of residential users. By considering appliance classes, user preferences and weather status, they model the UC and electricity cost. The WDO algorithm is used for minimizing electricity cost and maximizing UC. This work also analyses peak cost reduction in electricity bills by considering the TOU tariff. In this proposed work, household appliances are categorized on the basis of LOT and appliance power consumption. In order to make the scheduling process more efficient, delay and PB criteria (which are not considered in [10]) are incorporated here for reducing electricity bills. In this study, WDO is enhanced in which LOT and the energy consumption of each appliance are calculated by evaluating the objective function (refer to Equations (1)–(3)) using constraints. Table 6 shows the enhancements made as per our proposed work and the expected results based on the enhancements. All steps of the implemented WDO algorithm are shown in Algorithm 3.

Table 6.
Adaptations in WDO.
| Algorithm 3: WDO algorithm. |
 |
In [17], the authors propose a BFOA technique for grid resource scheduling. This technique is based on the hyper-heuristic resource scheduling algorithm, which has been designed to effectively schedule jobs on available resources in a grid environment. The authors evaluate the performance of the proposed BFOA algorithm by comparing it with the existing heuristic scheduling algorithms (GA and simulated annealing) using the makespan and cost performance metrics. Experimental results show that the proposed algorithm outperforms the existing algorithms in terms of cost minimization. In comparison to [17], the proposed work introduces a new methodology of appliance scheduling for minimizing electricity cost, energy consumption and PAR, which benefits both customers and the utility. In this study, objective functions (refer to Equations (1)–(3)) and their constraints are modified according to the designed scenario. Table 7 contains the refinements made and their respective expected results. All steps of the proposed work are given in Algorithm 4.

Table 7.
Refinements in BFOA.
| Algorithm 4: BFOA algorithm. |
 |
4.2. Developing a Hybrid GWD Optimization Algorithm
In this algorithm, all of the stages of WDO are performed in a similar way as explained in Section 4.1; however, the velocity updating steps for the global air pressure is replaced with GA’s crossover and mutation operations. In some cases, pressure values are very large, such that the updating velocities become too large, which degrade WDO’s performance. Thus, we replace these with GA’s crossover and mutation values. The scheduling procedure is followed as the same described in GA, BPSO, BFAO and WDO. It is evaluated with the help of the same objective functions (refer to Equations (1)–(3)). Detailed steps of this algorithm are shown in Algorithm 5. Modifications of the hybrid GWD and their respective expected outcomes are given in Table 8 [8,10].

Table 8.
Modifications in GWD.
| Algorithm 5: GWD algorithm. |
 |
The metaheuristic algorithms do not guarantee exact reachability of the global optimum solution. The obtained solution is dependent on the set of random variables generated at the start of the metaheuristic optimization process. In our scenario, PSO, BFOA and WDO suffer from the global optima, and GA is a relatively better suited algorithm for the global optimal solution. In order to filter out the effects of random initializations, simulation runs of these algorithms are increased in number. However, this filtration is achieved at the cost of increased computational time. We have presented the statistical analysis of all of the algorithms with respect to cost and user comfort using the ANOVA in the Results Section after taking the average of the 10 runs.
5. Results and Discussion
In order to evaluate the proposed work, simulations are conducted in MATLAB using the RTP scheme. The 24-h time period is divided into PHs and OPHs for tracking the real-time behavior of the system. Four hours are taken as PHs (from 7 p.m.–10 p.m.) such that the PHs vary from season to season [43]. From December–February, PHs are from 5 p.m.–9 p.m.; from March–May, PHs are 6 p.m.–10 p.m.; from June–August, PHs are 7 p.m.–10 p.m.; and from September-November, these vary accordingly. Four hours are used in this case (from 7 p.m.–10 p.m.) of one season, and the remaining all are included in OPHs.
There are two simulation scenarios that are discussed here: (i) single home and (ii) fifty homes. Each home has 12 appliances, and appliances are categorized into two classes: (i) Class A with fixed load appliances and (ii) Class B with shiftable and elastic load appliances, as shown in Table 9. Figure 4 shows the RTP rates during each hour of the full day. The parameters of GA, BPSO, WDO, BFAO and GWD are given in Table 10, Table 11, Table 12, Table 13 and Table 14, respectively. To evaluate the performance of these algorithms, the following performance metrics are used.
- Cost: Amount of electricity bills for the total number of units consumed per unit time in cents.
- Energy Consumption: It is calculated as the total energy utilized per unit time in kilowatts per hour.
- PAR: It is defined as the total peak load divided by average load during the whole day.
- UC: It is calculated in terms of minimum cost and minimum appliance delay.

Table 9.
Parameters and power ratings.
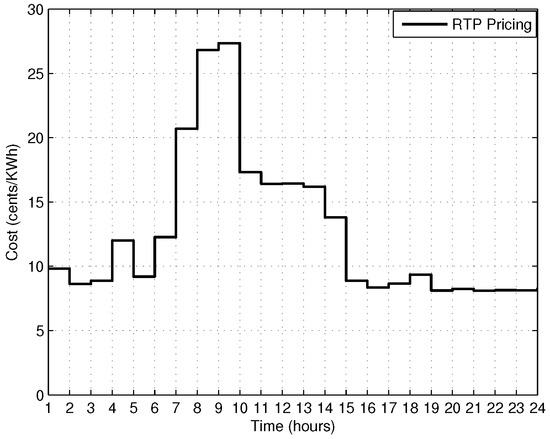
Figure 4.
RTP price signal.

Table 10.
GA parameters and values.

Table 11.
BPSO parameters and values.

Table 12.
WDO parameters and values.

Table 13.
BFAO parameters and values.

Table 14.
GWD parameters and values.
5.1. Single Home
The energy consumption of our proposed scheme hybrid GWD with respect to GA and WDO in unscheduled and scheduled cases is shown in Figure 5. This figure shows that the maximum energy consumption values are 16.2 kWh, 11.8 kWh, 8.2 kWh and 4.1 kWh for the unscheduled case, scheduled GA, WDO and the hybrid GWD approach, respectively. The energy consumption of all algorithms is below their unscheduled cases. The energy consumption in GA, WDO and GWD is 56.89%, 67.18% and 65.87%; which is obtained by dividing the scheduled cost and unscheduled cost with percentage. It is important to note that the hybrid GWD algorithm is better than the simple WDO and GA in terms of energy consumption. GWD uses crossover and mutation operations from the GA, which helps with the faster convergence for achieving optimized results, and WDO uses explicit pressure values; however, when velocities are high, pressure values become extremely large, which leads to performance degradation.
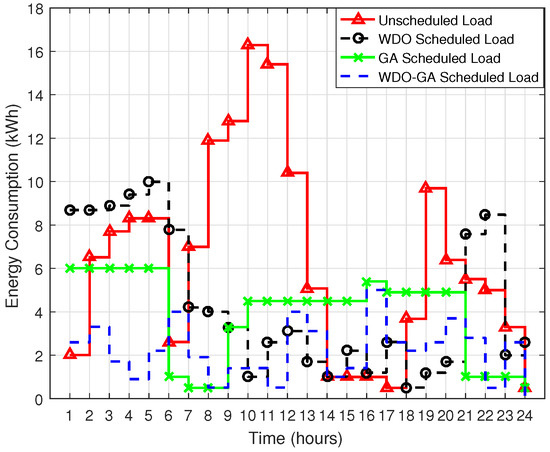
Figure 5.
Energy consumption.
The maximum amount of the electricity bill in the unscheduled case is 318.88 cents, as shown in Figure 6. It is reduced to 78 cents in the case of GA, while it is reduced from 318 cents to 245 cents in WDO and up to 75 cents in GWD. The electricity cost in GA, WDO and GWD is 60%, 62% and 30%, respectively. During PHs, sufficient electricity cost reduction is achieved for all designed algorithms (GA, WDO and GWD). GWD performs better than the other algorithms in terms of the electricity cost reduction due to the amalgamation of crossover and mutation. The WDO’s cost is high due to its high pressure values.
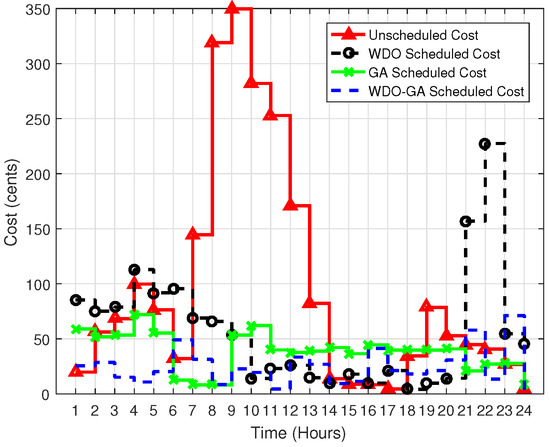
Figure 6.
Total cost.
The PAR performance of all algorithms (GA, WDO and GWD) is shown in Figure 7. This figure shows that PAR is significantly reduced in hybrid GWD as compared to the GA, WDO and unscheduled case. Results prove that our proposed algorithm effectively tackles the peak reduction problem. The PAR graph for GA, WDO and hybrid GWD displays that the power consumption of appliances is optimally distributed without creating peaks during the OPHs and PHs of the day. The PAR in GA, WDO and GWD is 60%, 75% and 40%. WDO has higher PAR than GA because it has higher pressure values of the particles, and GA is more effective in PAR reduction due to its ability to generate new populations of more feasible solutions using crossover and mutation. From these results, it is shown that the hybrid GWD approach outperforms all other schemes, because it uses the best features of both. Peak formation is a major drawback in the traditional electric power system, as it causes customers to pay high electricity bills, and the utility also suffers from high demand, which leads to blackouts or load shedding. The performance of these algorithms in this scenario is improved due to load shifting using appliances’ PBs, which causes utilities to fulfil the demands of customers and gives customers a chance to reduce their electricity bills.
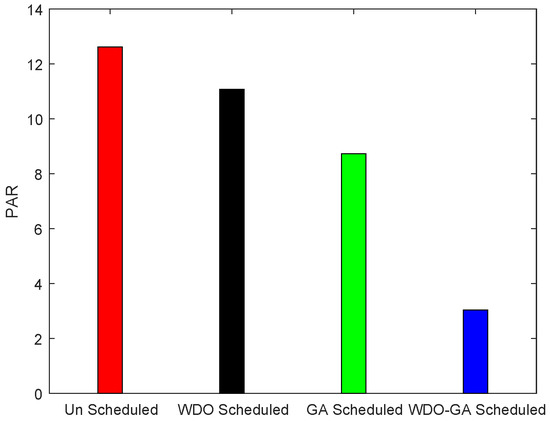
Figure 7.
Scheduled and unscheduled PAR.
In our proposed hybrid scheme, we have achieved the desired UC as shown in Figure 8. It shows that UC is significantly reduced for GWD, GA and WDO as compared to the unscheduled case. By applying priority scheduling on the objective functions (refer to Equations (1)–(3)), this work enhanced the performance in terms of UC. UC of the unscheduled case is 98%, while in schedule WDO, GA and GWD, it is 60%. The maximum delay considered here is 4 h; otherwise, the utility has to pay a penalty for the users. There is a tradeoff in UC of all scheduled algorithms because only one scenario is considered here. However, the performance of this work is much better by considering the priority bits and minimum delay during scheduling.
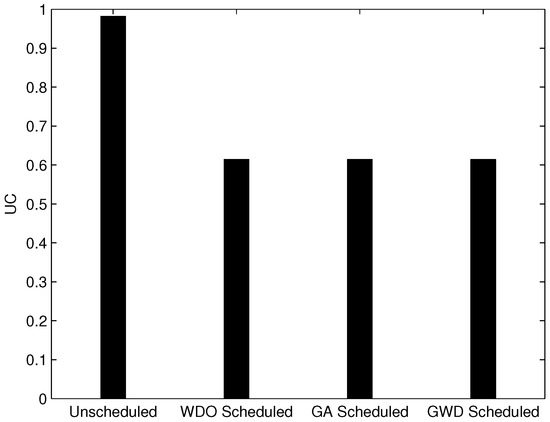
Figure 8.
Scheduled and unscheduled UC.
All above simulations are performed for a single home; however, for testing the effects of the proposed scheme in multiple homes, multiple homes are taken in the next section. All of the modified algorithms (GA, BPSO, WDO and BFOA) are tested for 50 homes to investigate these in terms energy consumption minimization and electricity cost reduction. From Figure 13, it is clear that the proposed work achieves significant results. As these algorithms are designed to satisfy the constraints of the objective function in 24 h, so that residential users get facilitated by reducing their electricity bills and that utilities get the benefit by keeping demand under the power capacity of the grid.
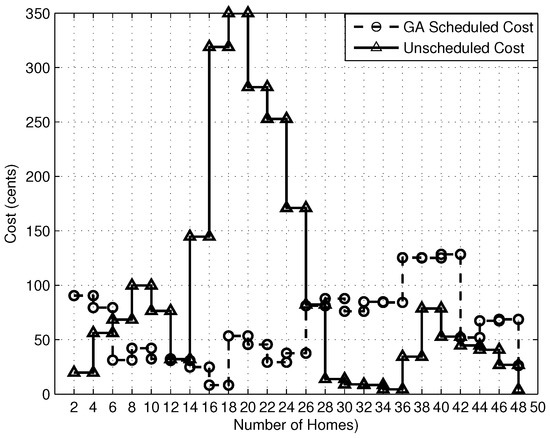
Figure 13.
GA total cost.
5.2. Fifty Homes
The energy consumption of GA, BPSO, WDO and BFOA is 15.00 kWh, 7.90 kWh, 11 kWh and 14.5 kWh, respectively, which is less than the unscheduled case as 16.5 kWh, approximately; as shown in Figure 9, Figure 10, Figure 11 and Figure 12. The energy consumption in GA, BPSO, WDO and BFOA is 79%, 47%, 45% and 88%. GA is efficient among all of the others, though it considers a larger population size. It uses a natural selection operator, which reduces the convergence time towards the efficient solution during scheduling. BFOA is faster than BPSO and consumes less energy because BFOA is faster for a small population size. On the other hand, BPSO is suitable for a larger population size, and it also escapes from the local minima. WDO consumes more energy as compared to BPSO, BFOA and GA, because it has explicit pressure values of particles, causing performance degradation.
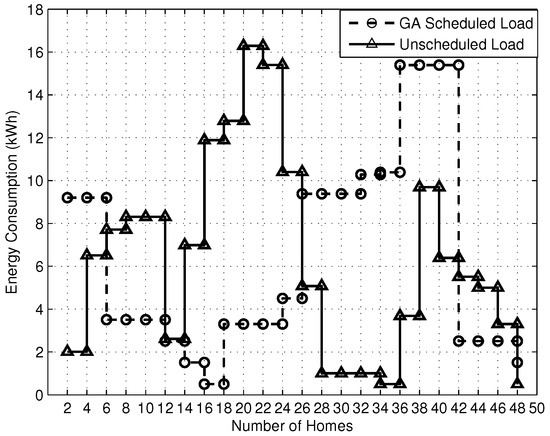
Figure 9.
GA energy consumption.
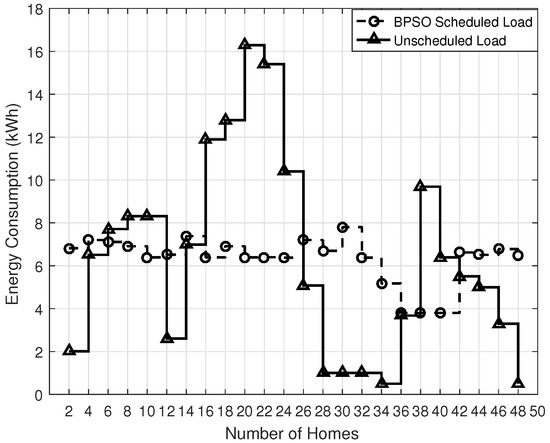
Figure 10.
BPSO energy consumption.
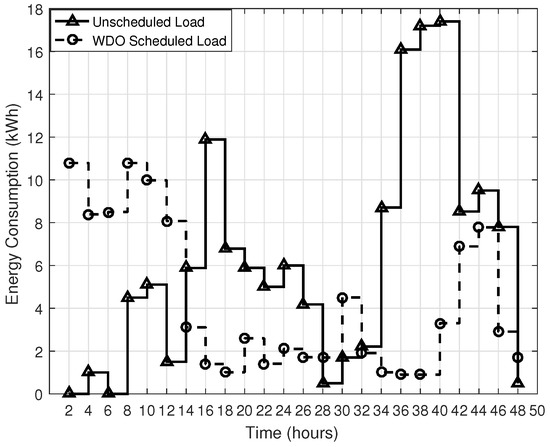
Figure 11.
WDO energy consumption.
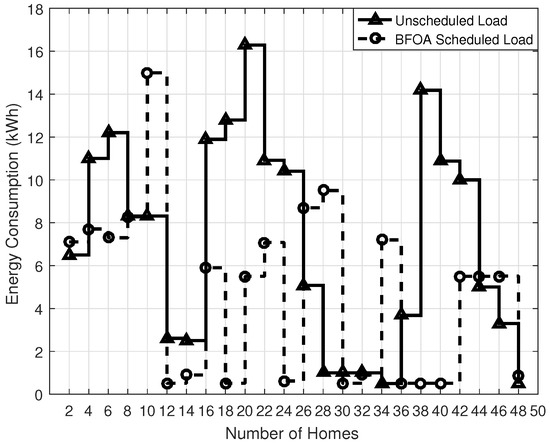
Figure 12.
BFOA Energy Consumption.
The electricity cost of the simulated algorithms is shown in Figure 13, Figure 14, Figure 15 and Figure 16, which is obtained during the scheduling process. In each case, the scheduled costs of all four algorithms, GA, BPSO, WDO and BFOA, are 125.20, 175, 215 and 160 cents, respectively, which are lower than the unscheduled cost of 350. Furthermore, by using the PBs during appliance scheduling, the overall cost is reduced as compared to the unscheduled cases. After scheduling, the obtained electricity cost by using GA, BPSO, WDO and BFOA is 35%, 50%, 61% and 45%, respectively; whereas, in the unscheduled case, it is 100%. In this case, GA is the most effective algorithm even considering a larger population size than the other algorithms. GA uses the crossover and mutation operation, which is efficient in convergence and at finding the global optimal solution. BPSO uses linear and piecewise functions instead of natural selection operators, and it is mostly used for a large population size to avoid local minima. BFOA is suitable for a small population size, and it is more efficient than BPSO and GA in terms of convergence and energy efficiency. WDO suffers from pressure values, so it gives a higher cost than the others.
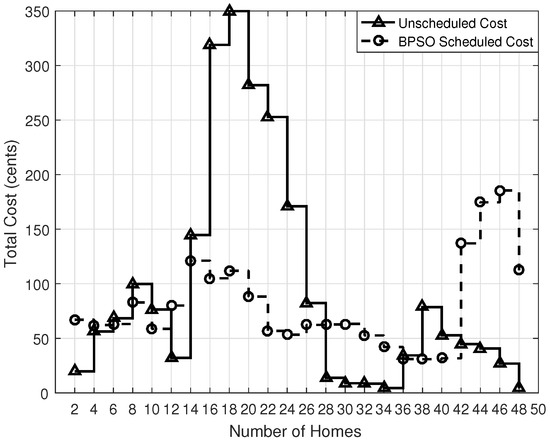
Figure 14.
BPSO total cost.
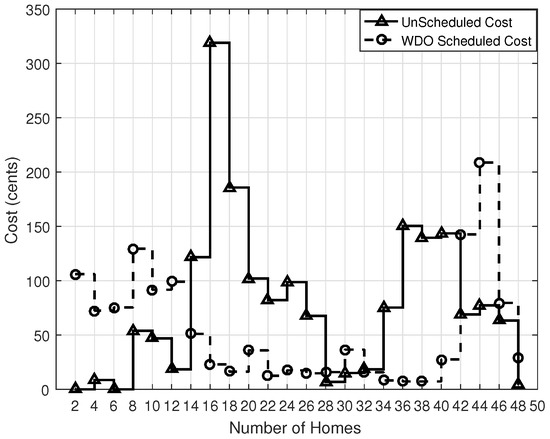
Figure 15.
WDO Total Cost.
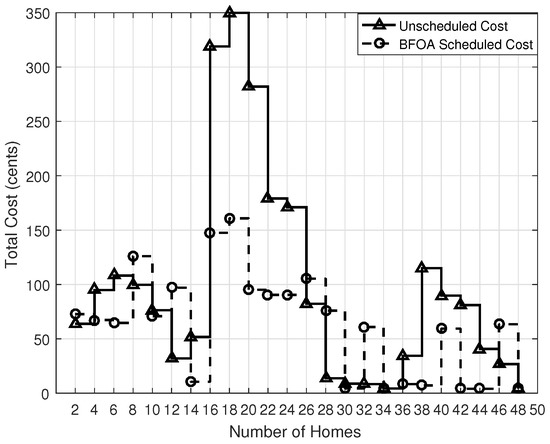
Figure 16.
BFOA total cost.
Overall, the scheduled peak formation rate is better than the unscheduled cases, and the desired results of the load shifting are achieved by the scheduling. The PAR obtained in GA, BPSO, WDO, BFOA and the unscheduled case is 26%, 25%, 12%, 2% and 46%, respectively. All of the high profile appliances are scheduled to low price rate hours. If the consumed energy in OPHs is high (creating peaks), then appliances are scheduled according to their PBs for reducing load and avoiding peak formation even during the low pricing rate hours. PAR in WDO, BPSO and BFOA is better than GA because GA is tested for a large set of populations, whereas all of the others are tested for a small population size, as shown in Figure 17.
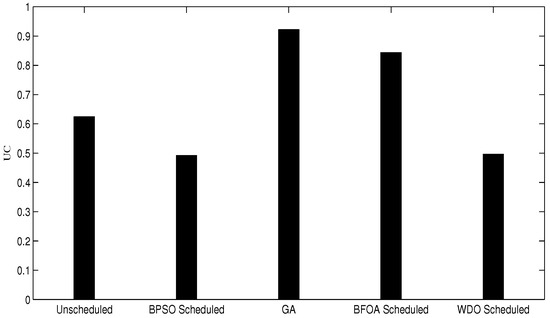
Figure 17.
UC of GA, BPSO, WDO and BFOA.
UC achieved by GA and BFAO is significantly greater than BPSO, WDO and the unscheduled case as shown in Figure 18. The UC achieved in GA is nearly 0.9; BPSO is 0.5; WDO is 0.55; BFAO is 0.85; and it is 90%, 50%, 50% and 85%. Because during scheduling, all high power utilization appliances are shifted to OPHs, which facilitates the customers to pay less on the bill, so UC is maximized in BFOA and GA as compared to WDO and BPSO, which are the desired results obtained by the designed objective functions, and it is also beneficial for both customers and utilities.
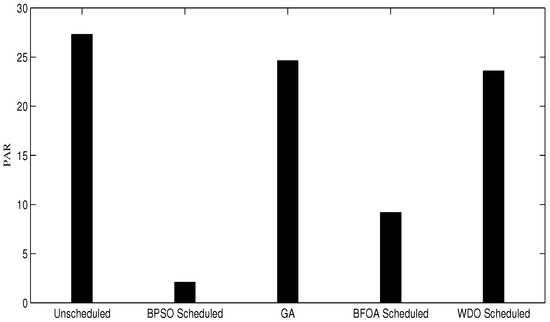
Figure 18.
PAR of GA, BPSO, WDO and BFOA.
In order to quantify the computational burden of the algorithms, we have chosen algorithm execution time (in s) as a performance metric. Figure 19 shows the execution time of the five simulated algorithms: GA, BPSO, WDO, BFOA and GWD. From the figure, it is evident that BPSO has the maximum computational burden (execution time = 88 s), and BFOA has the minimum computational burden (execution time = 8 s); a difference of 80 s. Similarly, GA, WDO and GWD take 13 s, 43 s and 32 s (to execute), respectively. The previous figures in the simulation Results Section show that GWD is relatively better than the compared algorithms in terms of the selected performance metrics, and Figure 19 shows the execution time of GWD as relatively moderate (better than WDO and worse than GA). To sum up, the GWD pays the cost of moderate execution time to achieve a considerable increase in UC and a decrease in both PAR and price.
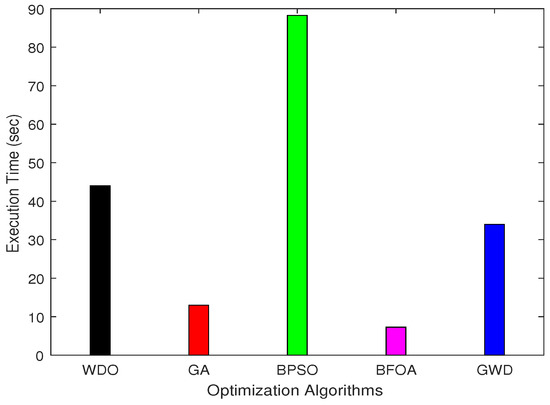
Figure 19.
Execution time of GA, BPSO, WDO, BFOA and GWD.
5.3. Performance Trade-Offs in the Proposed Technique
After conducting the simulations, we have found some trade-offs and achievements. This approach is evaluated with the help of the following parameters: cost minimization, energy consumption minimization, UC maximization and PAR reduction. The achievements and trade-offs are mentioned in Table 15.

Table 15.
Tradeoffs in the proposed algorithms.
5.4. Statistical Validation of GWD and Counter Part Algorithms Using ANOVA
In order to prove the metaheuristic algorithms’ stochastic nature, we have done the statistical analysis for checking their correctness and efficiency. Two algorithms are taken for comparison with our proposed algorithm in terms of the variance. The ANOVA is based on three assumptions [44]: (i) all samples of the populations are normally distributed; (ii) all samples of the populations have equal variance; and (iii) all observations are mutually independent. In the table below, the analysis is described in detail for each sample population generated by the each individual algorithms.
Here, df indicates the degrees of freedom; MS represents the mean square test; and F represents the F test (taken by dividing the sum of squares and MS); and these are calculated using the equations from [44]. We have done the ANOVA of three algorithms including our proposed algorithm. In this way, we have finally estimated that our proposed algorithm varies from them by a significant rate as shown in Table 16 above.

Table 16.
ANOVA results for the proposed algorithm with the existing algorithms.
6. Conclusions
In this work, a DSM controller is designed in which five heuristic algorithms (GA, BPSO, WDO, BFOA and our proposed hybrid GWD) are implemented. The hybrid GWD scheme reduced the electricity cost by approximately 10% in comparison to GA and 33% to WDO. On the other hand, GA provided the global optimal solution in scheduling and faster convergence, even when the population size is large. The GA outperformed BPSO, WDO and BFOA in terms of electricity cost and energy consumption. In contrast to the BPSO, BFOA is suitable for a small population, because it converges at a faster rate when the population size is small. Explicit particle pressure values make WDO the slowest to converge among all of the compared algorithms. The stochastic behavior of these algorithms is analyzed by statistical analysis. Assigning priority to appliances helped with efficient scheduling. Statistical analysis is performed by the ANOVA test, which is used to measure the variation in the algorithms’ performance metrics. In the future, we will focus on enhancing other heuristic algorithms to achieve the desired objectives.
Acknowledgments
This project was full financially supported by the King Saud University, through Vice Deanship of Research Chairs.
Author Contributions
Nadeem Javaid and Sakeena Javaid proposed and implemented the main idea. Wadood Abdul and Imran Ahmed performed the mathematical modeling and wrote the simulation section. Ahmad Almogren, Atif Alamri and Iftikhar Azim Niaz organized and refined the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Logenthiran, T.; Srinivasan, D.; Shun, T.Z. Demand side management in smart grid using heuristic optimization. IEEE Trans. Smart Grid 2012, 3, 1244–1252. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand side management: Demand response, intelligent energy systems, and smart loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Shahidehpour, M.; Yamin, H.; Li, Z. Market overview in electric power systems. In Market Operations in Electric Power Systems: Forecasting, Scheduling, and Risk Management; Wiley-IEEE Press: Hoboken, NJ, USA, 2002; pp. 1–20. [Google Scholar]
- Popovic, Z.N.; Popovic, D.S. Direct load control as a market-based program in deregulated power industries. In Proceedings of the 2003 IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003; Volume 3, pp. 1–4.
- Maharjan, I.K. Demand Side Management: Load Management, Load Profiling, Load Shifting, Residential and Industrial Consumer, Energy Audit, Reliability, Urban, Semi-Urban and Rural Setting; LAP Lambert Academic: Saarbrücken, Germany, 2010. [Google Scholar]
- Gellings, C.W.; Chamberlin, J.H. Demand Side Management: Concepts and Methods; Fairmont: Liburn, GA, USA, 1988. [Google Scholar]
- Kothari, D.P.; Nagrath, I.J. Modern Power System Analysis; Tata McGraw-Hill Education: New Delhi, India, 2003. [Google Scholar]
- Awais, M.; Javaid, N.; Shaheen, N.; Iqbal, Z.; Rehman, G.; Muhammad, K.; Ahmad, I. An Efficient Genetic Algorithm Based Demand Side Management Scheme for Smart Grid. In Proceedings of the 2015 18th International Conference on Network-Based Information Systems (NBiS), Taipei, Taiwan, 2–4 September 2015; pp. 351–356.
- Ullah, I.; Javaid, N.; Khan, Z.A.; Qasim, U.; Khan, Z.A.; Mehmood, S.A. An Incentive-based Optimal Energy Consumption Scheduling Algorithm for Residential User. Procedia Comput. Sci. 2015, 52, 851–857. [Google Scholar] [CrossRef]
- Rasheed, M.B.; Javaid, N.; Ahmad, A.; Khan, Z.A.; Qasim, U.; Alrajeh, N. An Efficient Power Scheduling Scheme for Residential Load Management in Smart Homes. Appl. Sci. 2015, 5, 1134–1163. [Google Scholar] [CrossRef]
- Sousa, T.; Morais, H.; Vale, Z.; Faria, P.; Soares, J. Intelligent energy resource management considering vehicle-to-grid: A simulated annealing approach. IEEE Trans. Smart Grid 2012, 3, 535–542. [Google Scholar] [CrossRef]
- Arabali, A.; Ghofrani, M.; Etezadi-Amoli, M.; Fadali, M.S.; Baghzouz, Y. Genetic algorithm based optimization approach for energy management. IEEE Trans. Power Deliv. 2013, 28, 162–170. [Google Scholar] [CrossRef]
- Khan, M.A.; Javaid, N.; Mahmood, A.; Khan, Z.A.; Alrajeh, N. A generic demand side management model for smart grid. Int. J. Energy Res. 2015, 39, 954–964. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, Y.; Xu, G.; Zhang, Q.; Krundel, L. Home energy management with PSO in smart grid. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 1666–1670.
- Lugo-Cordero, H.M.; Fuentes-Rivera, A.; Guha, R.K.; Ortiz-Rivera, E.I. Particle swarm optimization for load balancing in green smart homes. In Proceedings of the 2011 IEEE Congress of Evolutionary Computation (CEC), New Orleans, LA, USA, 5–8 June 2011; pp. 715–720.
- Narendhar, S.; Amudha, T. A Hybrid Bacterial Foraging Algorithm for Solving Job Shop Scheduling Problems. Int. J. Program. Lang. Appl. (IJPLA) 2012, 2, 1–11. [Google Scholar] [CrossRef]
- Chana, I. Bacterial foraging based hyper-heuristic for resource scheduling in grid computing. Future Gener. Comput. Syst. 2013, 29, 751–762. [Google Scholar]
- Molderink, A.; Bakker, V.; Bosman, M.G.; Hurink, J.L.; Smit, G.J. Domestic energy management methodology for optimizing efficiency in smart grids. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–7.
- Soares, J.; Sousa, T.; Morais, H.; Vale, Z.; Faria, P. An optimal scheduling problem in distribution networks considering V2G. In Proceedings of the 2011 IEEE Symposium on Computational Intelligence Applications In Smart Grid (CIASG), Paris, France, 11–15 April 2011; pp. 1–8.
- Zhu, Z.; Tang, J.; Lambotharan, S.; Chin, W.H.; Fan, Z. An integer linear programming based optimization for home demand side management in smart grid. In Proceedings of the 2012 IEEE PES Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 16–20 January 2012; pp. 1–5.
- Kriett, P.O.; Salani, M. Optimal control of a residential microgrid. Energy 2012, 42, 321–330. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Z.; Zhou, Y.; Dai, J. Optimal dispatching model of smart home energy management system. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Tianjin, China, 21–24 May 2012; pp. 1–5.
- Maringer, D.G. Portfolio Management With Heuristic Optimization; Springer Science and Business Media; Springer: New York, NY, USA, 2006. [Google Scholar]
- Ullah, I.; Javaid, N.; Imran, M.; Khan, Z.A.; Qasim, U.; Alnuem, M.; Bashir, M. A Survey of Home Energy Management for Residential Customers. In Proceedings of the 2015 IEEE 29th International Conference on Advanced Information Networking and Applications, Guwangiu, Korea, 24–27 March 2015; pp. 666–673.
- Wen, Z.; O’Neill, D.; Maei, H. Optimal demand response using device-based reinforcement learning. IEEE Trans. Smart Grid 2015, 6, 2312–2324. [Google Scholar] [CrossRef]
- Adika, C.O.; Wang, L. Smart charging and appliance scheduling approaches to demand side management. Int. J. Electr. Power Energy Syst. 2014, 57, 232–240. [Google Scholar] [CrossRef]
- Shirazi, E.; Jadid, S. Optimal residential appliance scheduling under dynamic pricing scheme via HEMDAS. Energy Build. 2015, 93, 40–49. [Google Scholar] [CrossRef]
- Mahmood, D.; Javaid, N.; Alrajeh, N.; Khan, Z.A.; Qasim, U.; Ahmed, I.; Ilahi, M. Realistic Scheduling Mechanism for Smart Homes. Energies 2016, 9, 202. [Google Scholar] [CrossRef]
- Hernández-Ocana, B.; Mezura-Montes, E.; Pozos-Parra, P. A review of the bacterial foraging algorithm in constrained numerical optimization. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 Junuary 2013; pp. 2695–2702.
- Jiménez, J.B. Electricity demand modeling for rural residential housing: A case study in Colombia. In Proceedings of the 2015 IEEE PES Innovative Smart Grid Technologies Latin America (ISGT LATAM), Montevideo, Uruguay, 5–7 October 2015; pp. 614–618.
- Rottondi, C.; Barbato, A.; Chen, L.; Verticale, G. Enabling Privacy in a Distributed Game-Theoretical Scheduling System for Domestic Appliances. IEEE Trans. Smart Grid 2016, PP, 1–11. [Google Scholar] [CrossRef]
- Erol-Kantarci, M.; Mouftah, H.T. Energy-efficient information and communication infrastructures in the smart grid: A survey on interactions and open issues. IEEE Commun. Surv. Tutor. 2015, 17, 179–197. [Google Scholar] [CrossRef]
- Safdarian, A.; Fotuhi-Firuzabad, M.; Lehtonen, M. Optimal Residential Load Management in Smart Grids: A Decentralized Framework. IEEE Trans. Smart Grid 2016, 7, 1836–1845. [Google Scholar] [CrossRef]
- Liu, Y.; Yuen, C.; Yu, R.; Zhang, Y.; Xie, S. Queuing-based energy consumption management for heterogeneous residential demands in smart grid. IEEE Trans. Smart Grid 2016, 7, 1650–1659. [Google Scholar] [CrossRef]
- Ma, J.; Chen, H.H.; Song, L.; Li, Y. Residential load scheduling in smart grid: A cost efficiency perspective. IEEE Trans. Smart Grid 2016, 7, 771–784. [Google Scholar] [CrossRef]
- Barbato, A.; Capone, A. Optimization models and methods for demand-side management of residential users: A survey. Energies 2014, 7, 5787–5824. [Google Scholar] [CrossRef]
- Fernandes, F.; Morais, H.; Vale, Z.; Ramos, C. Dynamic load management in a smart home to participate in demand response events. Energy Build. 2014, 82, 592–606. [Google Scholar] [CrossRef]
- Soares, J.; Ghazvini, M.A.F.; Borges, N.; Vale, Z. A stochastic model for energy resources management considering demand response in smart grids. Electr. Power Syst. Res. 2017, 143, 599–610. [Google Scholar] [CrossRef]
- Rahman, A.; Liu, X.; Kong, F. A survey on geographic load balancing based data center power management in the smart grid environment. IEEE Commun. Surv. Tutor. 2014, 16, 214–233. [Google Scholar] [CrossRef]
- Chiu, W.Y.; Sun, H.; Poor, H.V. Energy imbalance management using a robust pricing scheme. IEEE Trans. Smart Grid 2013, 4, 896–904. [Google Scholar] [CrossRef]
- Chiu, W.Y.; Sun, H.; Poor, H.V. A multi-objective approach to multimicrogrid system design. IEEE Trans. Smart Grid 2015, 6, 2263–2272. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Yang, R. Intelligent multiagent control system for energy and comfort management in smart and sustainable buildings. IEEE Trans. Smart Grid 2012, 3, 605–617. [Google Scholar] [CrossRef]
- Electricity Tariff. Available online: http://www.lesco.gov.pk/3000063 (accessed on 2 April 2016).
- One-Way Analysis of Variance (ANOVA) Example Problem. Available online: http://cba.ualr.edu/smartstat/topics/anova/example.pdf (accessed on 20 December 2016).
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).