Distributed Economic Dispatch of Virtual Power Plant under a Non-Ideal Communication Network
Abstract
:1. Introduction
2. Economic Dispatch Model
2.1. Objective Function
2.2. Constraints
2.3. Mathematical Reformulation
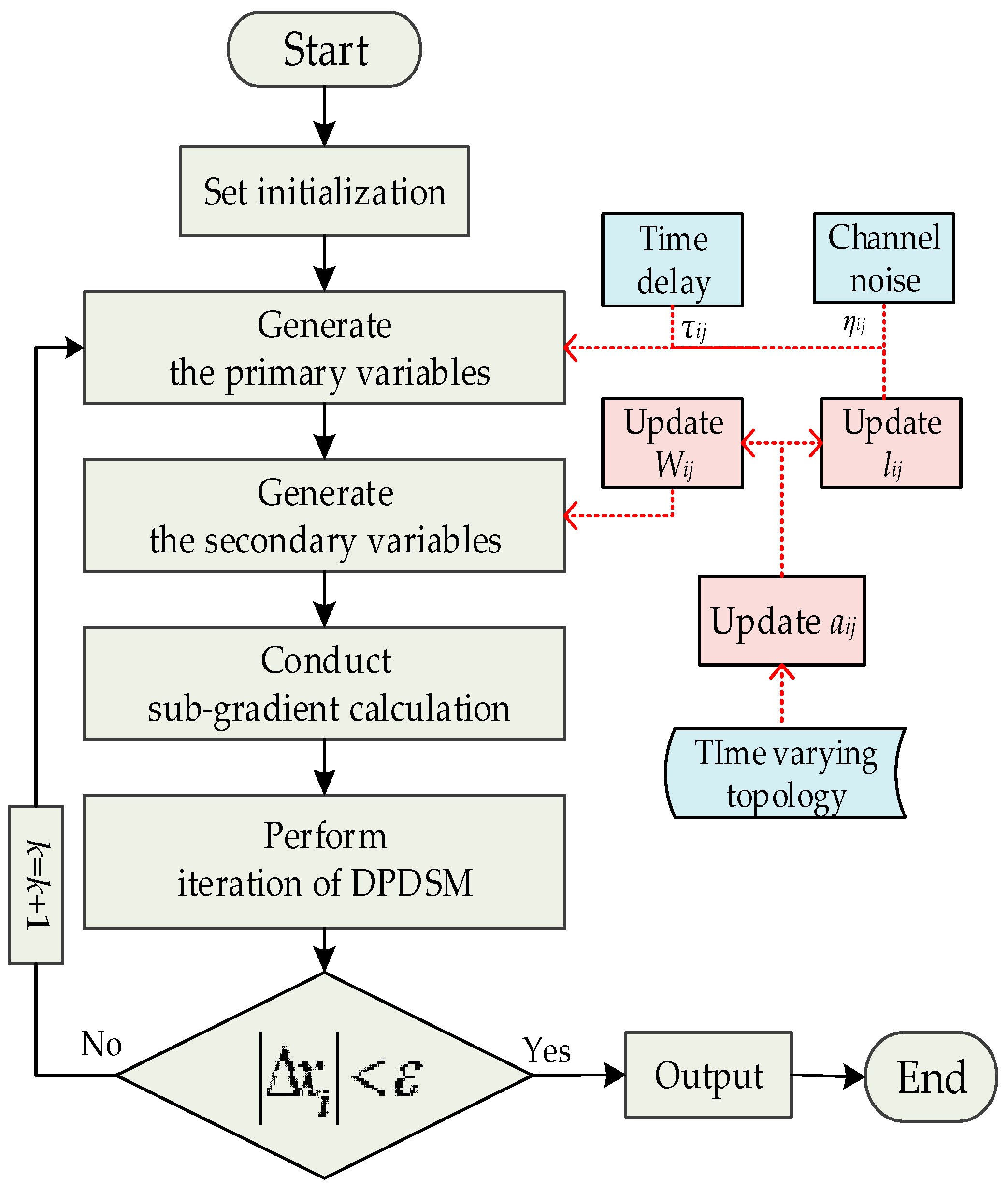
3. Distributed Primal-Dual Sub-Gradient Method (DPDSM)
3.1. Under Ideal Communication Network Conditions
3.2. Under Non-Ideal Communication Network Conditions
4. Numerical Examples
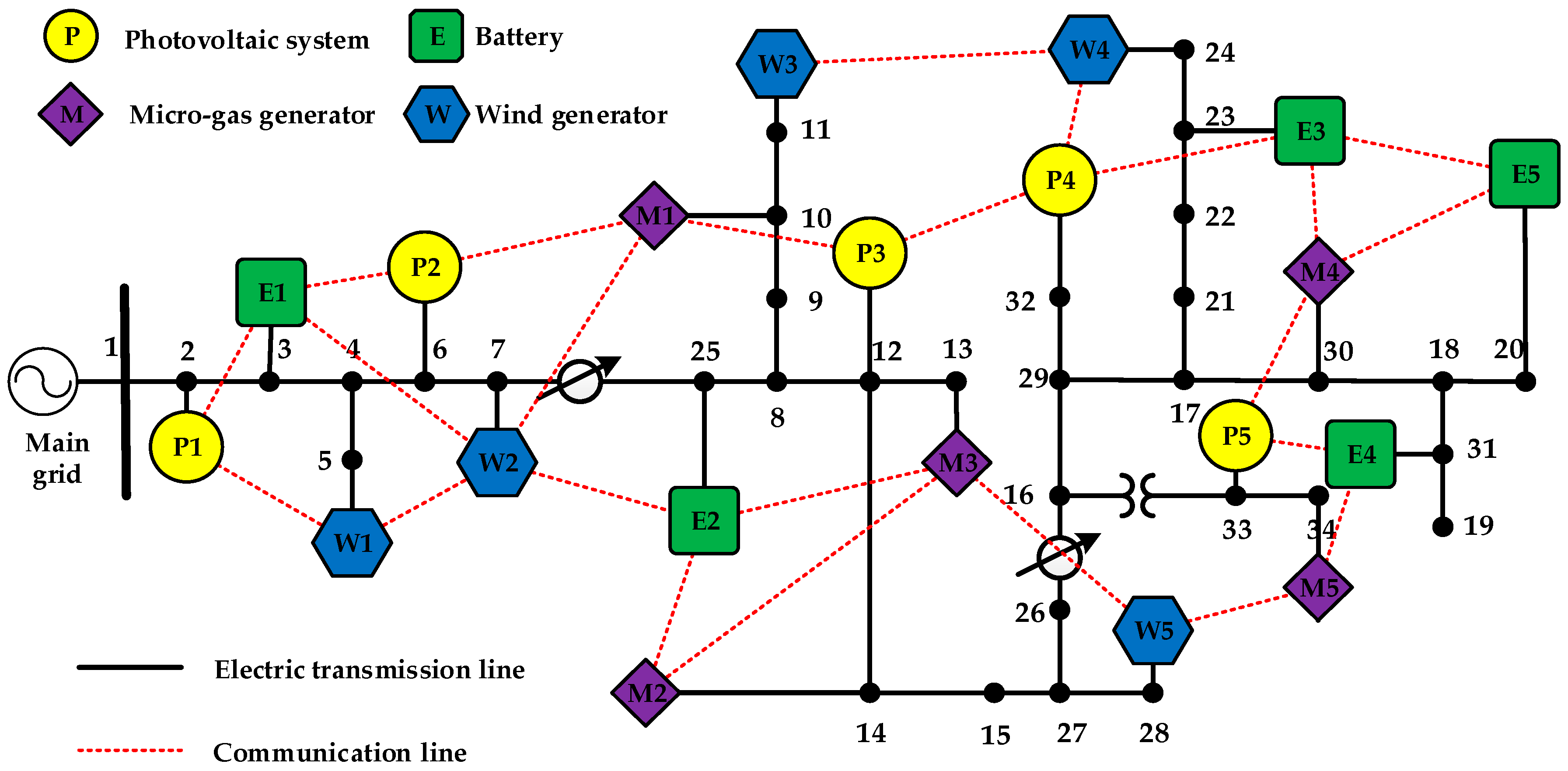
4.1. The Modified IEEE-34 Bus Test System
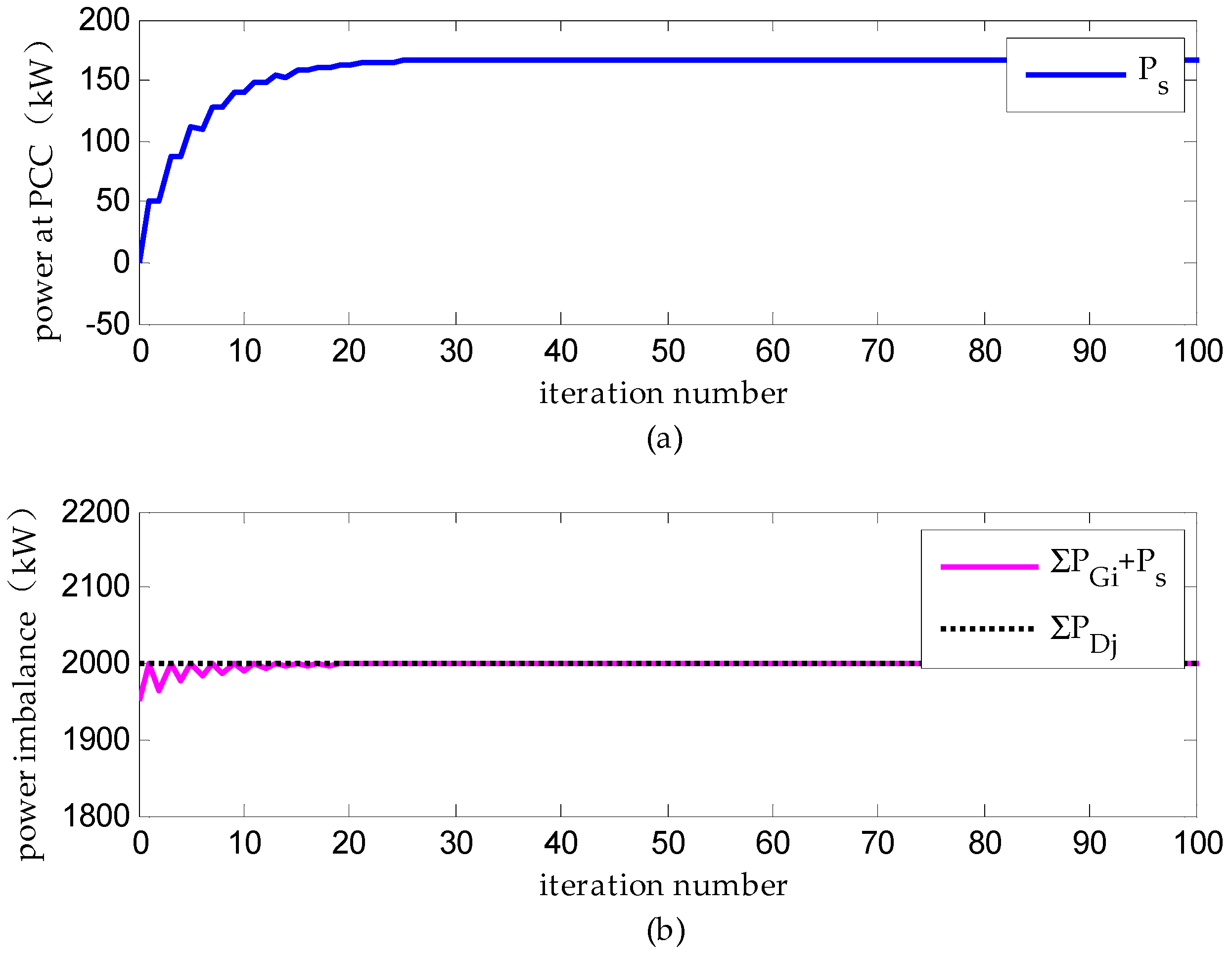
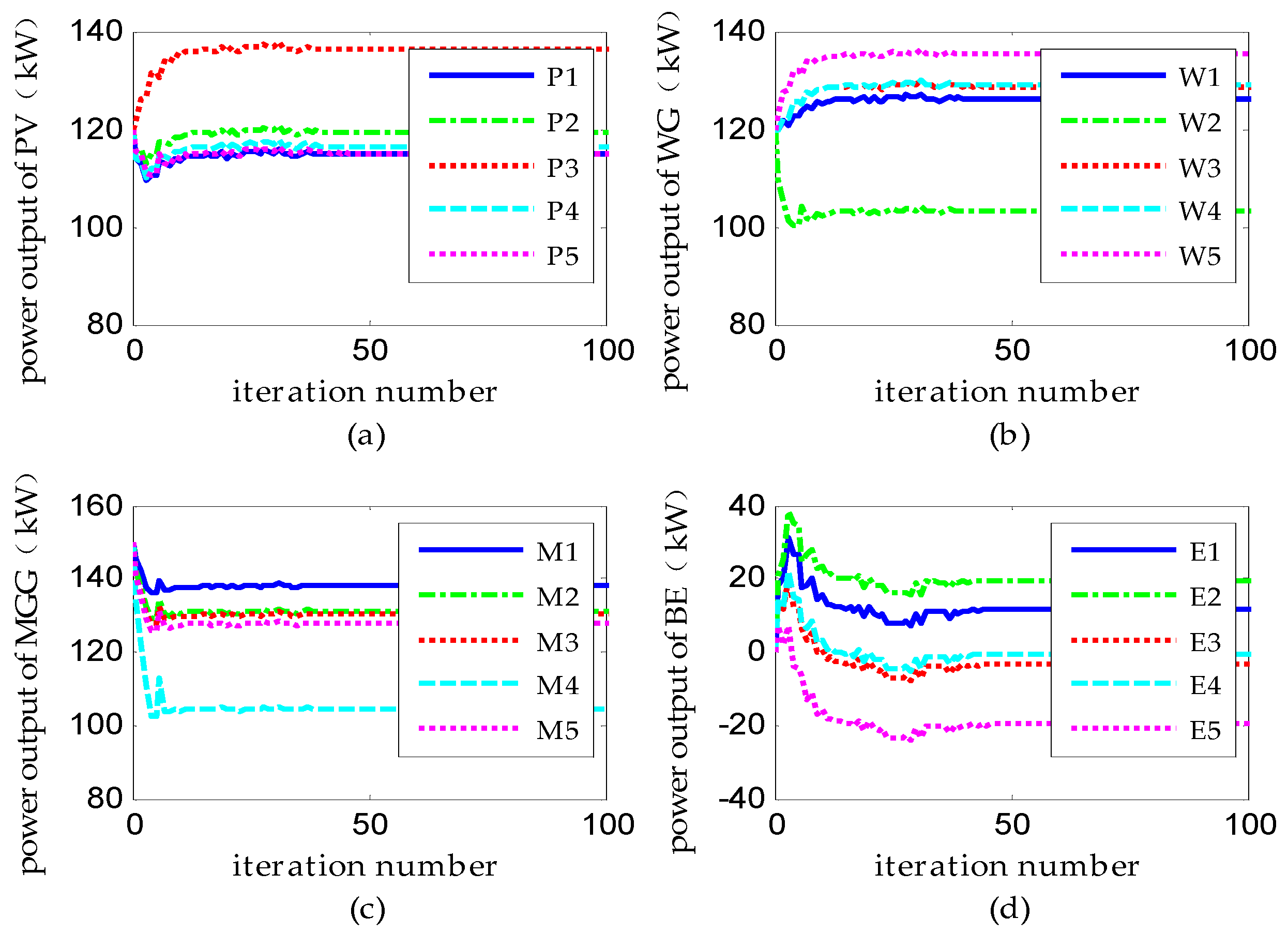
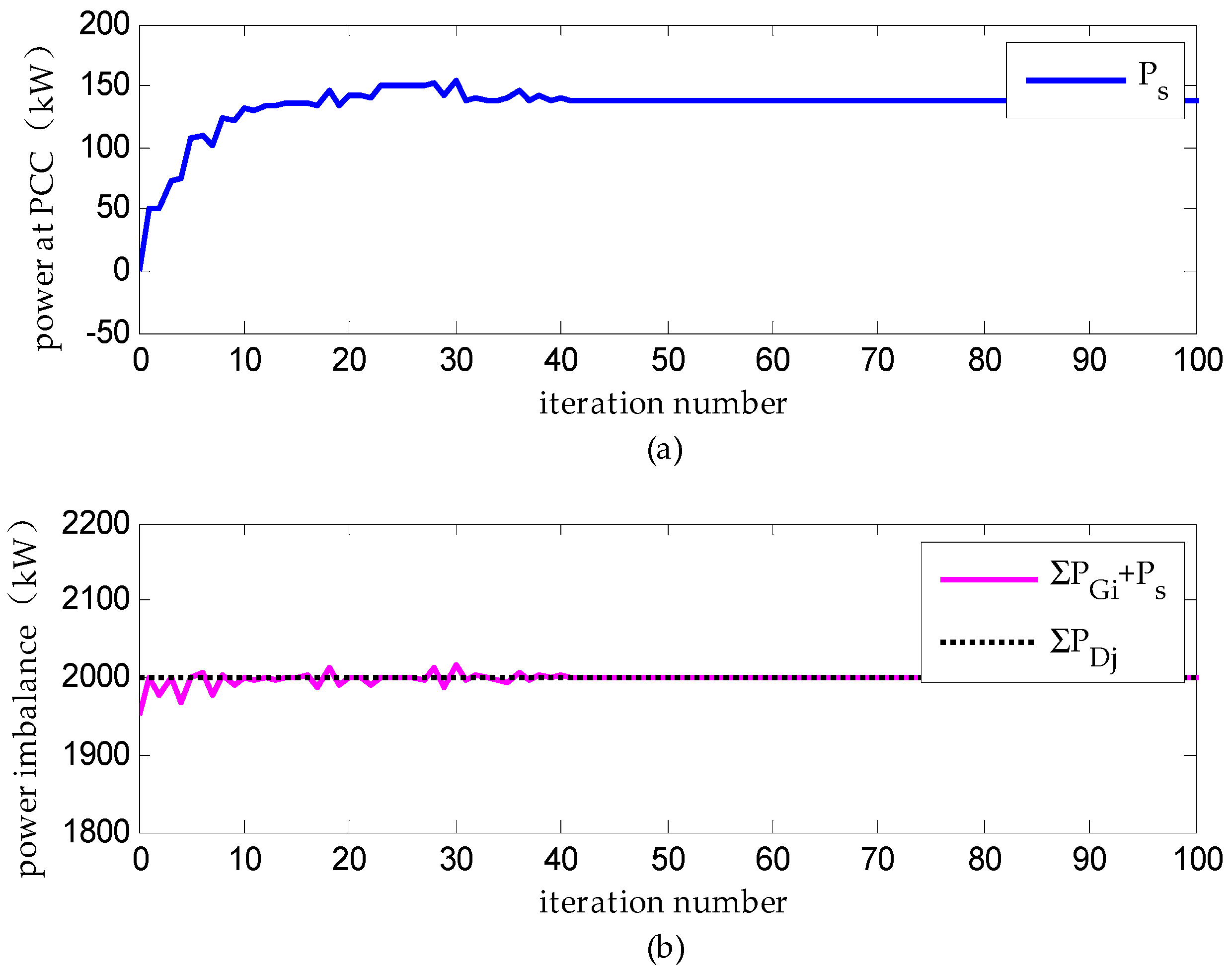
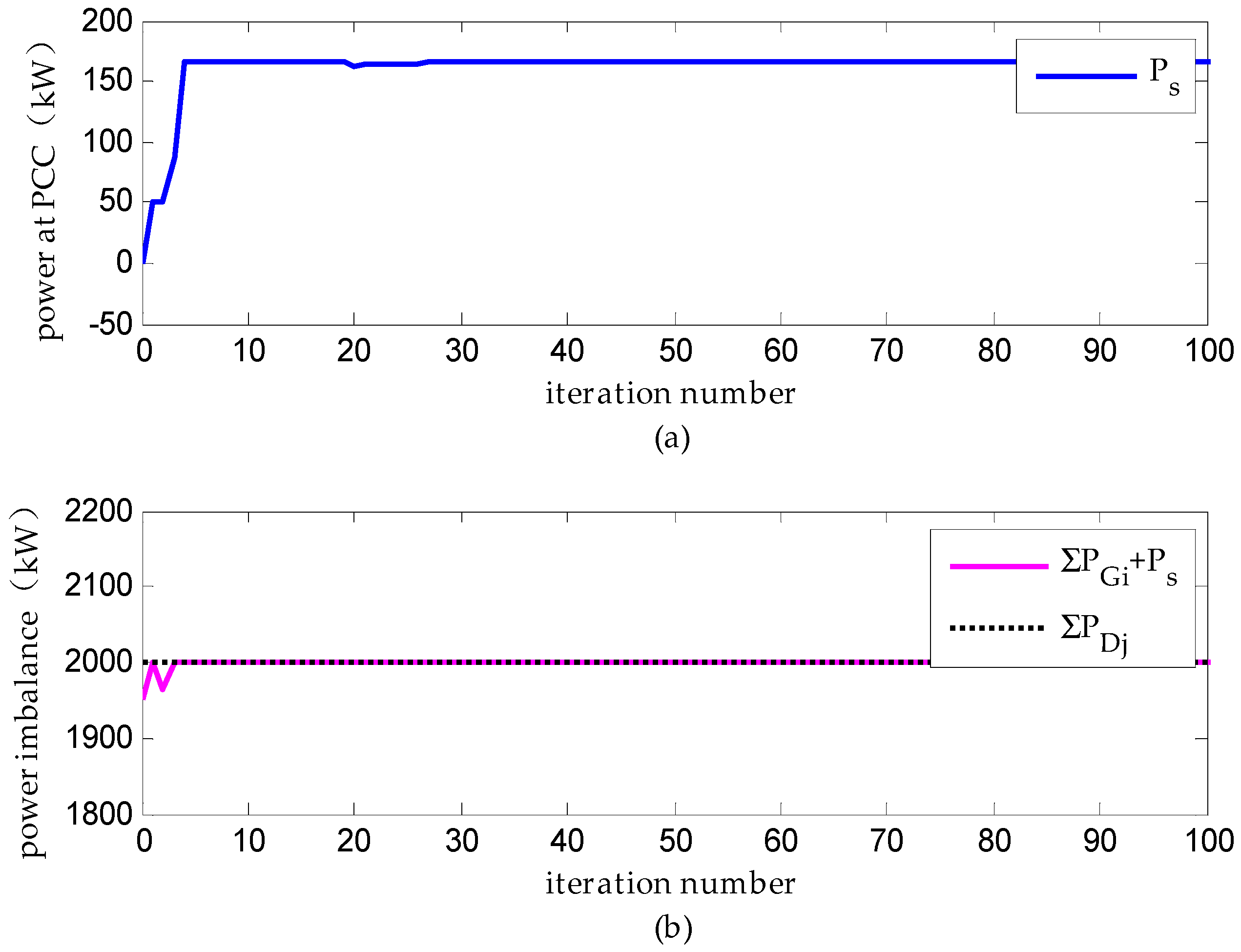
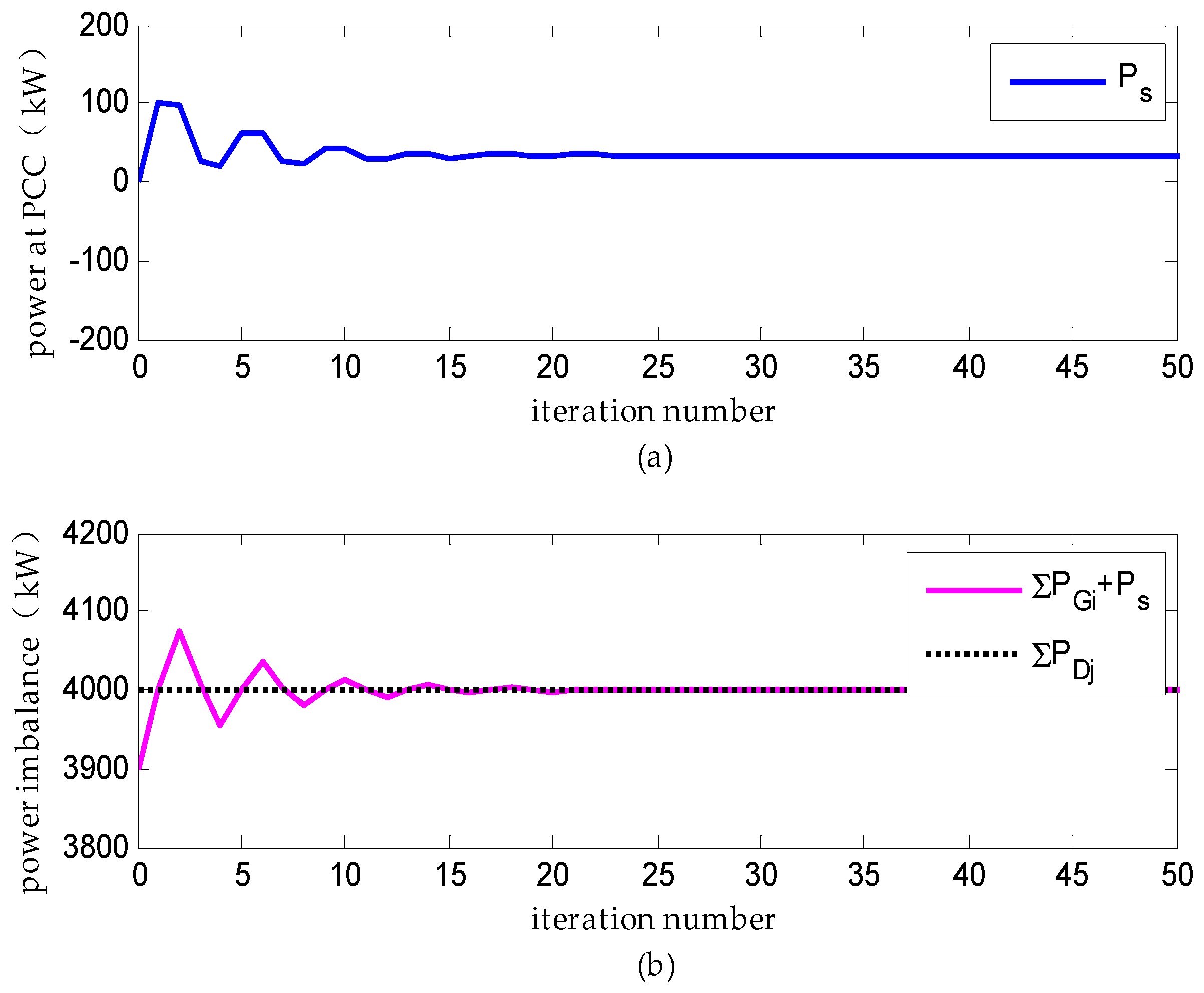
(1) Scenario A: Distributed Dispatch under Ideal Communication
(2) Scenario B: Distributed Dispatch Considering Communication Time Delays and Channel Noises
(3) Scenario C: Distributed Dispatch with a Different Δ
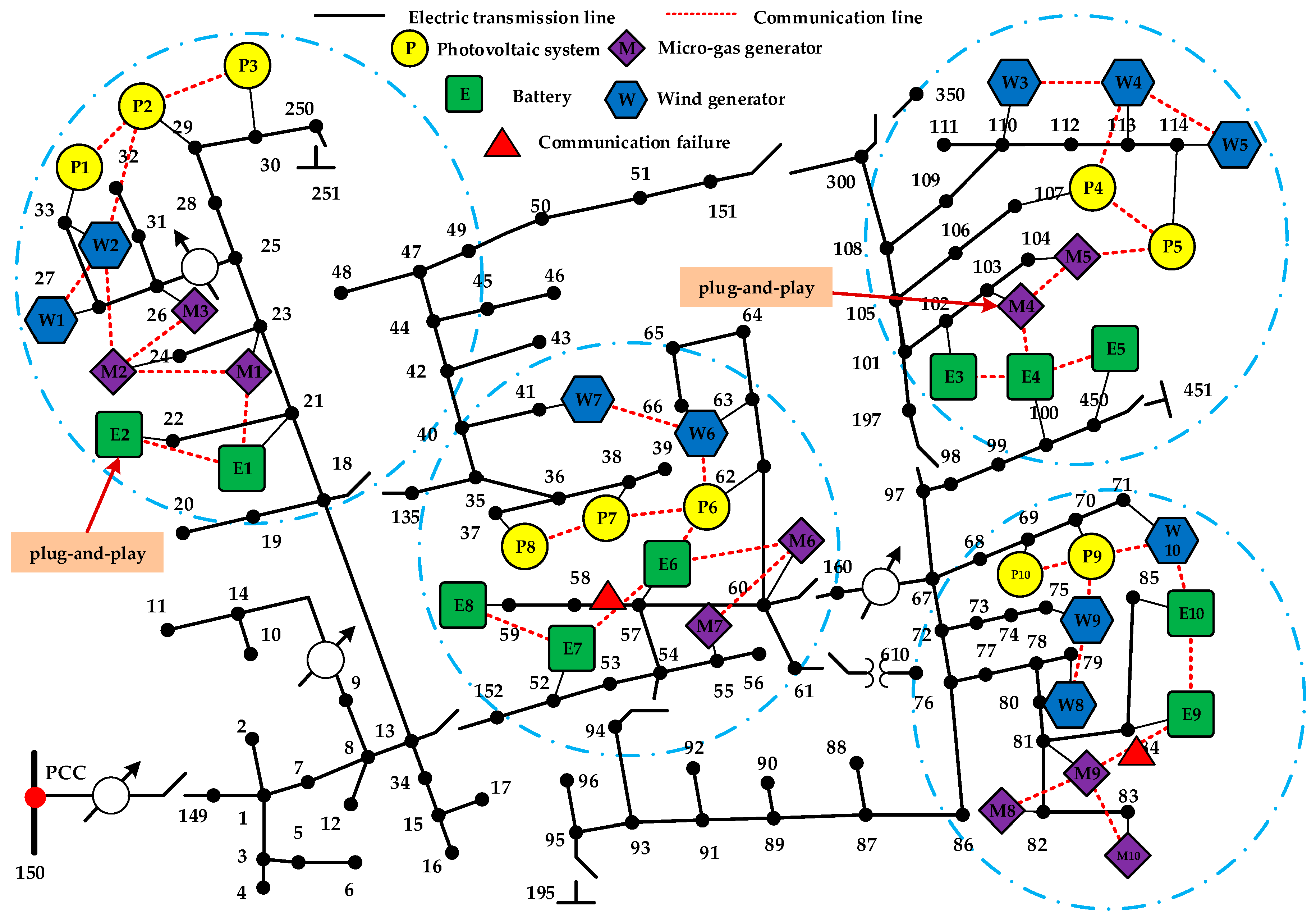
4.2. The Modified IEEE-123 Bus Test System
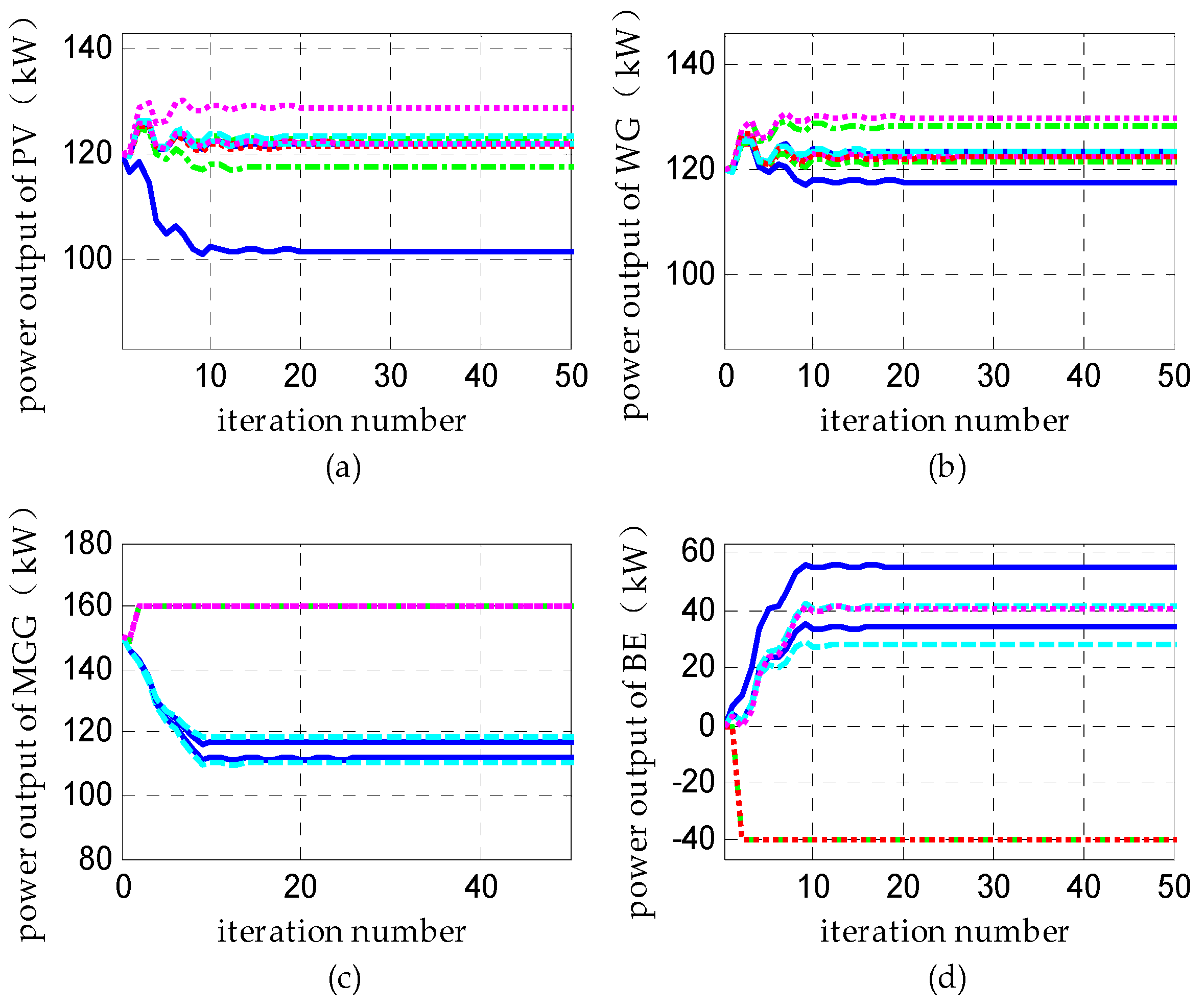
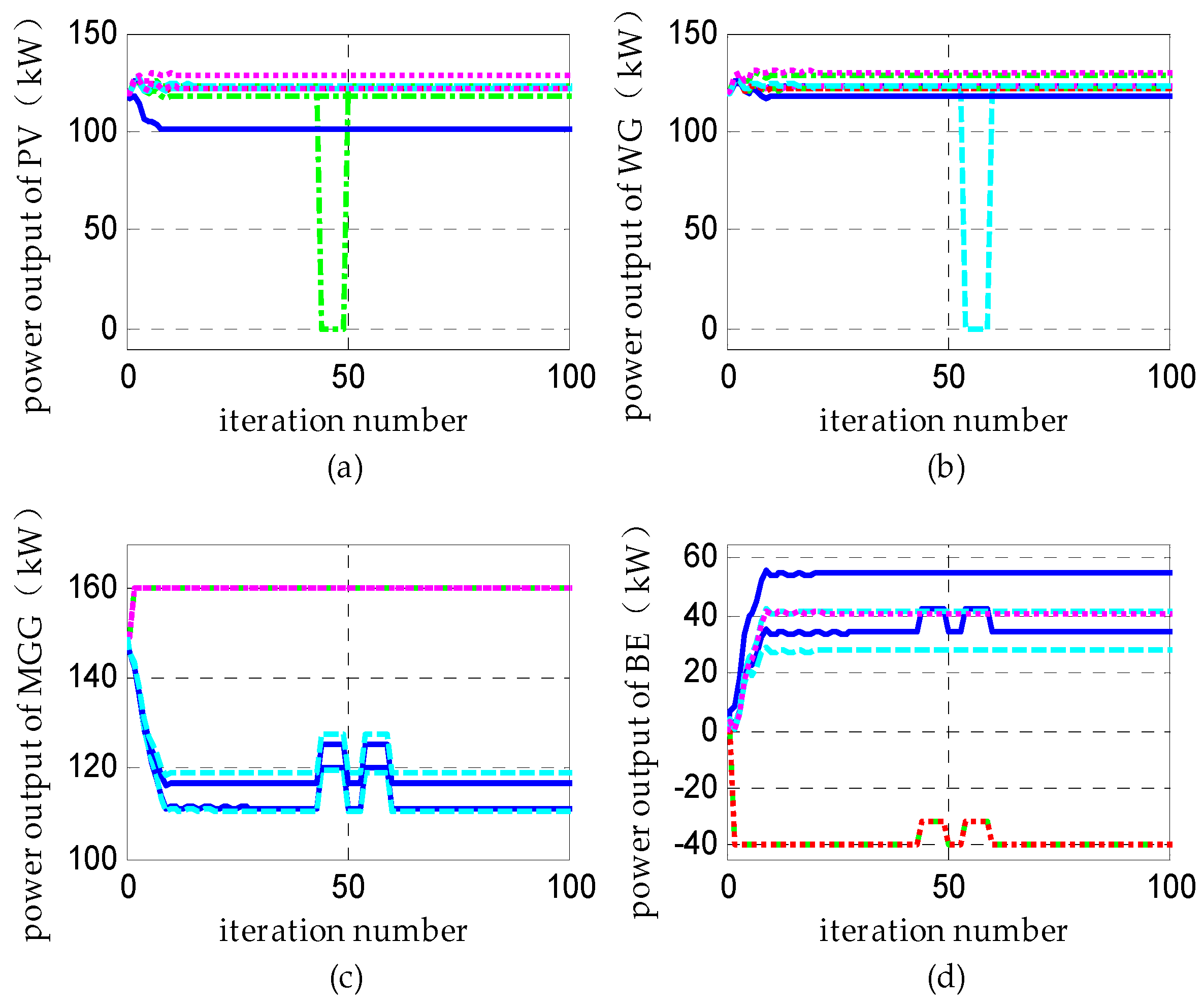
(1) Scenario D: Distributed Dispatch under the Condition of DERs’ Over-Limit
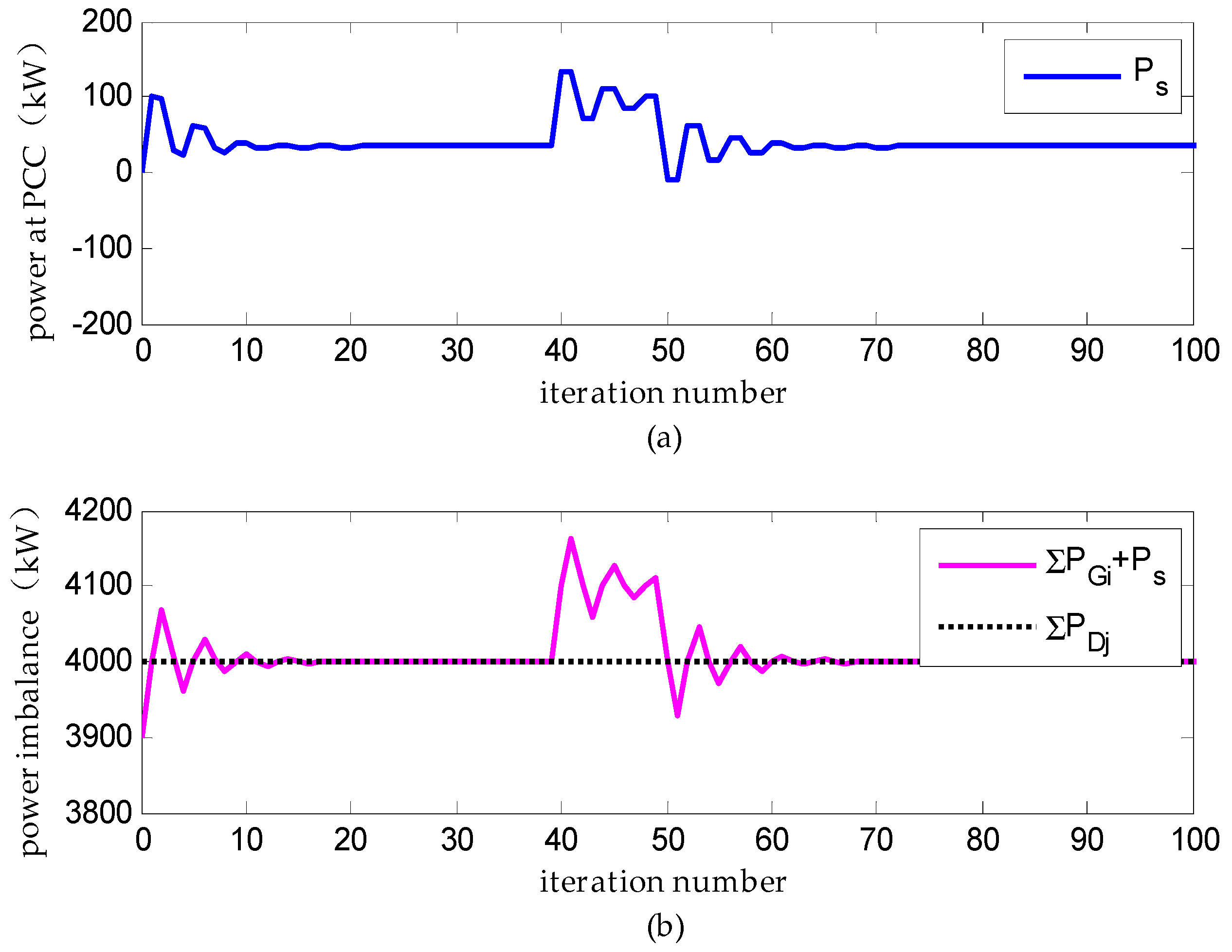
(2) Scenario E: Distributed Dispatch under the Condition of Channel Faults
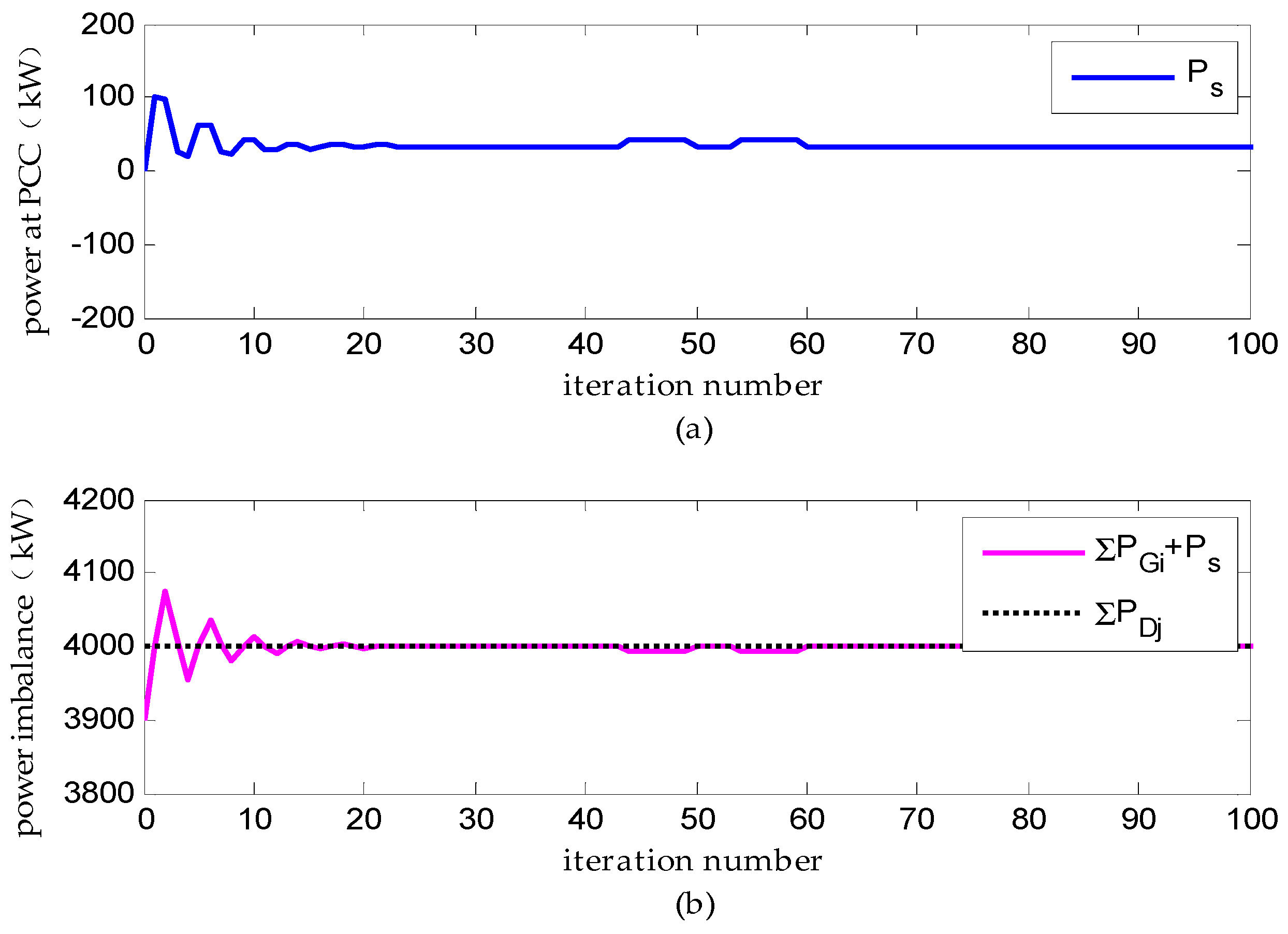
(3) Scenario F: Distributed Dispatch with DERs’ Plug and Play
5. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
- (a)
- Wind generators [23]. The power outputs of WGs are mainly affected by the wind speed and they can be described by the linear model:where Pw is the maximum available power output and Pr is the rated power output of WGs. v, vci, vco, and vr are wind speeds, cut-in wind speeds, cut-out wind speeds, and the rated wind speeds, respectively.
- (b)
- Photovoltaic systems [24]. The PVs’ power outputs are mainly affected by the light intensity and temperature, and the model can be expressed as:where PPV is the maximum available power output of PVs, and represents the maximum output under standard test conditions. GC means the actual light intensity; GCmax is the reference one under standard test conditions. The conversion coefficient of temperature to power is depicted by K. Tc, Tr is the environment temperature and the reference temperature under standard test conditions, respectively.
- (c)
- Storage batteries [10]. In this model, the constraints are mainly considered:where PBE ≥ 0 states the actual power output in the discharging and represents the maximum power output. Consequently, PBE ≤ 0 and can be the same one with the charging state. The state-of-charge (SOC) is also an important constraint. The charging efficiency of BE will be very low if the SOC come to a critical value. To solve the problem, the following formulas are given as:where SOCup and SOCdown are the lower bound and upper bound of BE. This study investigates the transient process of the distributed scheduling, so BEs can work at the two states during this period.
| Parameters | Values |
|---|---|
| Cut-in wind speeds vci | 3.0 m/s |
| Cut-out wind speeds vco | 25 m/s |
| The rated wind speeds vr | 15 m/s |
| The rated power output Pr | 200 kW |
| The capacity of BE | 100 kWh |
| SOCup | 80% |
| SOCdown | 20% |
| PPVmax | 200 kW |
| GCmax | 1 kW/m2 |
| The coefficient Kin (25) | −0.45% |
| Tr | 25 °C |
References
- Malahat, P.H.; Seifi, H.; Eslami, S.E. Decision making of a virtual power plant under uncertainties for bidding in a day-ahead market using point estimate method. Int. J. Electr. Power Energy Syst. 2013, 44, 88–98. [Google Scholar]
- Ali, Z.G.; Alireza, Z.; Shahram, J.; Kazemi, A. Stochastic operational scheduling of distributed energy resources in a large scale virtual power plant. Int. J. Electr. Power Energy Syst. 2016, 82, 608–620. [Google Scholar]
- Xu, H.; Zhang, X.; Yu, T. Robust consensus algorithm for economic dispatch under non-ideal communication network. Autom. Electric Power Syst. 2016, 40, 15–24. (In Chinese) [Google Scholar]
- Hatziargyriou, N.; Asand, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Thavlov, A.; Bindner, H.W. Utilization of flexible demand in a virtual power plant set-up. IEEE Trans. Smart Grid 2015, 6, 640–647. [Google Scholar] [CrossRef]
- Ruiz, N.; Cobelo, I.; Oyarzabal, J. A direct load control model for virtual power plant management. IEEE Trans. Power Syst. 2009, 24, 959–966. [Google Scholar] [CrossRef]
- Khaled, I.H.; Saber, S.M.; Mahmoud, B.M.E. Design of multi-step LC compensator for time-varying nonlinear loads based on genetic algorithm. Int. Trans. Electr. Energy Syst. 2016, 26, 2643–2656. [Google Scholar]
- Amjady Ali, G.; Zakariya, H. Solution of economic load dispatch problem via hybrid particle swarm optimization with time-varying acceleration coefficients and bacteria foraging algorithm techniques. Int. Trans. Electr. Energy Syst. 2013, 23, 1504–1522. [Google Scholar]
- Zhang, W.; Liu, W.; Wang, X. Online optimal generation control based on constrained distributed gradient algorithm. IEEE Trans. Power Syst. 2015, 30, 35–45. [Google Scholar] [CrossRef]
- Yang, H.; Yi, D.; Zhao, J.; Zhao, Y.D. Distributed optimal dispatch of virtual power plant via limited communication. IEEE Trans. Power Syst. 2013, 28, 3511–3512. [Google Scholar] [CrossRef]
- Yang, H.; Yi, D.; Zhao, J.; Luo, F.; Zhao, Y.D. Distributed optimal dispatch of virtual power plant based on ELM transformation. Ind. Manag. Optim. 2014, 10, 1297–1318. [Google Scholar] [CrossRef]
- Xin, H.; Gan, D.; Li, N.; Li, H.; Dai, C. Virtual power plant-based distributed control strategy for multiple distributed generators. IET Control Theory Appl. 2013, 7, 90–98. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, T.; Yin, S.; Gao, H. Data-based optimal control for networked double-layer industrial processes. IEEE Trans. Ind. Electron. 2016. [Google Scholar] [CrossRef]
- Vasirani, M.; Kota, R.; Cavalcante, R.; Ossowski, S.; Jennings, N.R. An agent-based approach to virtual power plants of wind power generators and electric vehicles. IEEE Trans. Smart Grid 2013, 4, 1314–1322. [Google Scholar] [CrossRef]
- Qiu, J.; Gao, H.; Steven, X. Recent advances on fuzzy-model-based nonlinear networked control systems: A survey. IEEE Trans. Ind. Electron. 2016, 63, 1207–1217. [Google Scholar] [CrossRef]
- Yuan, D.; Xu, S.; Zhao, H. Distributed primal–dual sub-gradient method for multi agent optimization via consensus algorithms. IEEE Trans. Syst. Man Cybern. B Cybern. 2011, 41, 1715–1723. [Google Scholar] [CrossRef] [PubMed]
- Angelia, N.; Asuman, O.; Pablo, A.P. Constrained consensus and optimization in multi-Agent networks. IEEE Trans. Autom. Control 2010, 55, 922–938. [Google Scholar]
- Zhu, M.; Martinez, S. On distributed convex optimization under inequality and equality constraints via primal–dual sub-gradient methods. IEEE Trans. Autom. Control 2011, 57, 151–164. [Google Scholar]
- Ali, R.M.; Mahdi, R. Optimal operating strategy of virtual power plant considering plug-in hybrid electric vehicles load. Int. Trans. Electr. Energy Syst. 2016, 26, 236–252. [Google Scholar]
- Rahimiyan, M.; Baringo, L. Strategic bidding for a virtual power plant in the day-ahead and real-time markets: A price-taker robust optimization approach. IEEE Trans. Power Syst. 2016, 31, 2676–2687. [Google Scholar] [CrossRef]
- Kardakos, E.G.; Simoglou, C.K.; Bakirtzis, A.G. Optimal offering strategy of a virtual power plant: A stochastic bi-level approach. IEEE Trans. Smart Grid 2012, 7, 794–806. [Google Scholar] [CrossRef]
- Liu, Y.; Xin, H.; Wang, Z.; Gan, D. Control of virtual power plant in micro grids: A coordinated approach based on photovoltaic systems and controllable loads. IET Gener. Transm. Distrib. 2015, 9, 921–928. [Google Scholar] [CrossRef]
- John, H.; David, C.Y.; Kalu, B. An economic dispatch model incorporating wind Power. IEEE Trans. Energy Convers. 2008, 23, 603–611. [Google Scholar]
- Gavanidou, E.; Bakirtzis, A. Design of a standalone system with renewable energy sources using trade off methods. IET Renew. Power Gener. 1992, 7, 42–48. [Google Scholar]
- Liu, S.; Xie, L.; Zhang, H. Distributed consensus for multi-agent systems with delays and noises in transmission channels. Automatica 2011, 47, 920–934. [Google Scholar] [CrossRef]



| DERs Types | ($/kWh) | PGi[0] (kW) | ||
|---|---|---|---|---|
| ai (10−6) | bi (10−3) | ci | ||
| P1 | 1.182 | 1.498 | 0.0914 | 120 |
| P2 | 1.793 | 1.342 | 0.0945 | 120 |
| P3 | 1.884 | 1.262 | 0.0968 | 120 |
| P4 | 1.916 | 1.328 | 0.0953 | 120 |
| P5 | 1.922 | 1.347 | 0.0938 | 120 |
| W1 | 1.353 | 1.433 | 0.0840 | 120 |
| W2 | 1.171 | 1.517 | 0.0803 | 120 |
| W3 | 1.073 | 1.484 | 0.0865 | 120 |
| W4 | 1.612 | 1.356 | 0.0889 | 120 |
| W5 | 1.405 | 1.388 | 0.0840 | 120 |
| M1 | 6.145 | 0.187 | 0.1011 | 150 |
| M2 | 6.932 | 0.045 | 0.1003 | 150 |
| M3 | 6.642 | 0.128 | 0.1063 | 150 |
| M4 | 6.503 | 0.582 | 0.1006 | 150 |
| M5 | 6.605 | 0.199 | 0.1023 | 150 |
| E1 | 2.503 | 1.645 | 0.0703 | 0 |
| E2 | 2.549 | 1.598 | 0.0747 | 0 |
| E3 | 2.607 | 1.731 | 0.0720 | 0 |
| E4 | 2.720 | 1.694 | 0.0786 | 0 |
| E5 | 2.240 | 1.812 | 0.0765 | 0 |
| DERs Types | PGi (kW) | DERs Types | PGi (kW) | Capacity (kWh) | ||
|---|---|---|---|---|---|---|
| Min | Max | Min | Max | |||
| P1–P5 | 80 | 140 | (charging) | 0 | 40 | 100 kWh |
| W1–W5 | 80 | 140 | E1–E5 | ----- | ----- | ------ |
| M1–M5 | 80 | 160 | (discharging) | 0 | 60 | 100 kWh |
| DERs Types | Scenarios | ||
|---|---|---|---|
| a | b | c | |
| P1 | 111.103 | 114.669 | 111.103 |
| P2 | 115.680 | 119.308 | 115.680 |
| P3 | 132.903 | 136.246 | 132.903 |
| P4 | 113.546 | 116.424 | 113.546 |
| P5 | 106.496 | 115.105 | 106.496 |
| W1 | 120.632 | 126.149 | 120.632 |
| W2 | 103.116 | 103.114 | 103.116 |
| W3 | 128.165 | 128.749 | 128.165 |
| W4 | 126.303 | 128.884 | 126.303 |
| W5 | 132.594 | 135.245 | 132.594 |
| M1 | 128.314 | 137.949 | 128.314 |
| M2 | 123.691 | 131.12 | 123.691 |
| M3 | 123.509 | 130.143 | 123.509 |
| M4 | 89.1574 | 104.548 | 89.1574 |
| M5 | 118.528 | 127.819 | 118.528 |
| E1 | 23.2306 | 11.4967 | 23.2306 |
| E2 | 31.7175 | 19.5987 | 31.7175 |
| E3 | 5.24299 | −3.4207 | 5.24299 |
| E4 | 11.9249 | −0.7296 | 11.9249 |
| E5 | −13.1192 | −19.7492 | −13.1192 |
| Ps | 167.259 | 137.325 | 167.259 |
| Scenarios | The Centralized Dispatch | The Distributed Dispatch |
|---|---|---|
| a | 0.0649 ($/kWh) | 0.0649 ($/kWh) |
| b | 0.0645 ($/kWh) | 0.0645 ($/kWh) |
| c | 0.0649 ($/kWh) | 0.0649 ($/kWh) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, C.; Xie, J.; Yue, D.; Huang, C.; Wang, J.; Xu, S.; Chen, X. Distributed Economic Dispatch of Virtual Power Plant under a Non-Ideal Communication Network. Energies 2017, 10, 235. https://doi.org/10.3390/en10020235
Cao C, Xie J, Yue D, Huang C, Wang J, Xu S, Chen X. Distributed Economic Dispatch of Virtual Power Plant under a Non-Ideal Communication Network. Energies. 2017; 10(2):235. https://doi.org/10.3390/en10020235
Chicago/Turabian StyleCao, Chi, Jun Xie, Dong Yue, Chongxin Huang, Jixiang Wang, Shuyang Xu, and Xingying Chen. 2017. "Distributed Economic Dispatch of Virtual Power Plant under a Non-Ideal Communication Network" Energies 10, no. 2: 235. https://doi.org/10.3390/en10020235
APA StyleCao, C., Xie, J., Yue, D., Huang, C., Wang, J., Xu, S., & Chen, X. (2017). Distributed Economic Dispatch of Virtual Power Plant under a Non-Ideal Communication Network. Energies, 10(2), 235. https://doi.org/10.3390/en10020235







