Robust Clamping Force Control of an Electro-Mechanical Brake System for Application to Commercial City Buses

Abstract

This paper proposes a sensor-less robust force control method for improving the control performance of an electro-mechanical brake (EMB) which is applicable to commercial city buses. The EMB generates the accurate clamping force commanded by a driver through an independent motor control at each wheel instead of using existing mechanical components. In general, an EMB undergoes parameter variation and a backdrivability problem. For this reason, the cascade control strategy (e.g., force-position cascade control structure) is proposed and the disturbance observer is employed to enhance control robustness against model variations. Additionally, this paper proposed the clamping force estimation method for a sensor-less control, i.e., the clamping force observer (CFO). Finally, in order to confirm the performance and effectiveness of a proposed robust control method, several experiments are performed and analyzed.

1. Introduction

As vehicle safety technology has developed, active safety systems with electronic and control technologies are actively proceeding. Especially, among the causes of vehicle and safety device accidents, the brake system represents a significantly large proportion. Thus, the importance of “brake by wire” technology [1,2,3], an electronic brake system which is combined with functions such as an antilock braking system (ABS), traction control system (TCS) and electronic stability program (ESP) is emphasized. Also, its study is consistently evolving. Since the brake by wire system is technology that controls a power of vehicle using electronic signals by eliminating mechanical and hydraulic connection lines, it has received a lot of attention in the automotive industry. Especially, to satisfy the driving stability, a brake by wire system such as electronic hydraulic brake (EHB) [4,5] and electro-mechanical brake (EMB) [6] are considered to be essential elements to develop the braking control system.

Currently, there are two implementation of the brake by wire system, namely EHB and EMB. They also have advantages like light vehicle weight and better utilization of space as compared with past brake systems. However, because an EHB system uses hydraulic power, there are some drawbacks such as the fail-safe problem, the leakage of hydraulic fluid, the lack of power and cost. Compared with an EHB system, an EMB system has some advantages. It is more environmentally friendly than an EHB system. Also, it is possible to realize a faster response due to the fast actuator dynamics and it can control the braking force accurately and precisely.

Due to advantages of EMB systems, they have been studied for a long time. In 2008, [7] presented a method to estimate the clamping force based on other sensory information such as sensor–fusion methods. In 2010, a clamping force control algorithm was suggested along with a consideration of the frictional characteristics and the estimation of the clamping force. A designed model of an EMB system and the use of the triple-loop PI control method were discussed [8,9]. This algorithm can be divided into three parts: current-loop, velocity-loop and pressure-loop. In 2013 [10] introduced the electric parking brake system. This paper also analyzed the modeling and control of the system by designing a nonlinear P controller. Finally, a stability analysis was performed.

Although studies about EMB systems have been widely presented, precisely controlling an EMB system is difficult due to the external disturbance elements such as the generated efficiency deterioration caused by the significantly large gear ratio and friction. To reduce these adverse effects, we suggest the disturbance observer (DOB) algorithm in this paper. A DOB is introduced by Ohnishi [11] for robust control. It has also been analyzed by many researchers [12,13,14,15,16]. A DOB is designed based on a system dynamics model and can estimate the external disturbances and eliminate them in real-time. Due to the good performance of a DOB, it has been applied in a variety of mechatronics fields.

Today, cost reduction is very important in industry applications. Generally, the clamping force in an EMB system is measured by a load cell. It contributes to improving the control performance and accuracy at the same time. However, it is very expensive and makes the system complicated. Furthermore, its signal delay is fatal in control systems requiring fast control response. For these problems, the clamping force observer (CFO) is proposed in this paper. A CFO based on a model dynamics is good solution to replace the load cell and reduce the system costs. Thus, a clamping force estimation is necessary for realizing the cost-effective EMB system.

In this paper, the force sensor-less robust force control method for an EMB system is introduced. The structure of a proposed force control system consists of five parts: (1) a position mode-disturbance observer (P-DOB); (2) a force mode-disturbance observer (F-DOB); (3) a clamping force observer (CFO); (4) a position controller and (5) a force controller. In Section 2, an EMB system dynamics and results for system identification tests are shown. In Section 3, for a sensor-less robust force control, a controller design method is proposed and its performance and effectiveness are shown with several experimental results in Section 4. Finally, the conclusion and future works are presented in Section 5.

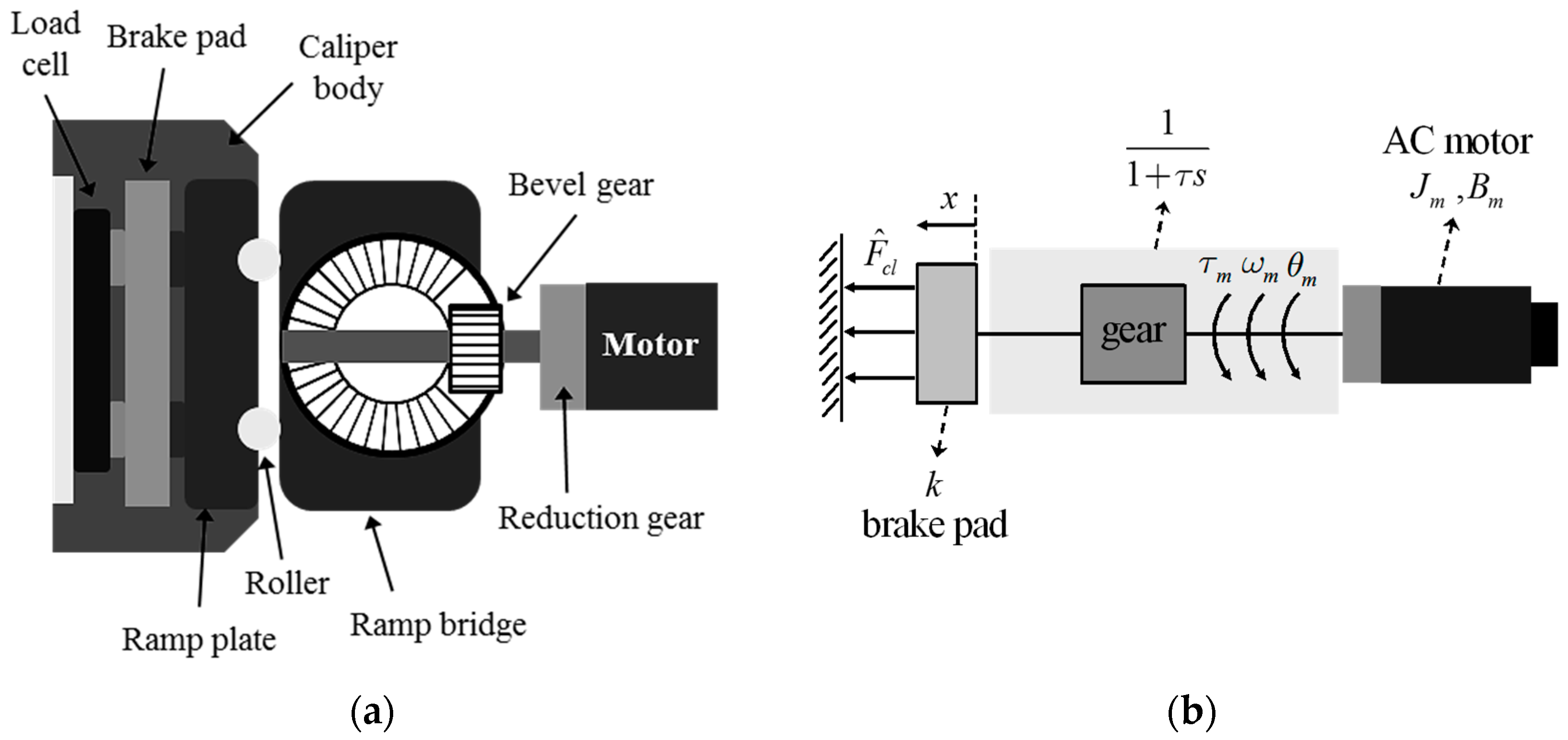
2. System Modeling of an EMB System

This paper suggests the robust clamping force control method without using a force measuring device. However, with this we experience a couple of control problems such as a backdrivability and model variation. In order to overcome these challenging issues, we designed a robust position controller as an inner loop control and a robust force controller as an outer loop control. In order to design the aforemented two controllers, one needs accurate plant model information and model-based control technologies are required for providing the enhanced control performances. In this section, we derived simplified system dynamics for a driving motor and an EMB’s torque transfer mechanism. In addition, those system dynamics models are compared with models obtained from the system identification tests.

Dynamics Model

Figure 1 illustrates a schematic of the proposed EMB system that was developed by Sangsin Brake Co., Ltd. (Daegu, Korea), for commercial city bus applications. Figure 1a represents each component including a driving motor, a reduction gear set, a brake disk, etc. and Figure 1b shows the real view for an EMB system.

In order to describe an EMB system dynamics, we simply modeled an EMB system as shown in Figure 2. For position and force control design, two dynamics models are required. Firstly, a motor dynamics for the precise position control is derived as follows:

$${\tau }_m=J_m{\dot{\omega }}_m+B_m{\omega }_m$$

(1)

$$\frac{{\omega }_m(s)}{{\tau }_m(s)}=\frac{1}{J_{m}s+B_m}$$

(2)

Here, we consider the further dynamics, illustrating the lagging effect between a reduction gear and a brake pad, as a first-order low pass filter. Thus, a system transfer function from input ${\tau }_m$ to the system output ${\omega }_m$ is obtained by

$$P_n(s)=\frac{{\omega }_m}{{\tau }_m}=\frac{1}{J_{m}s+B_m}\times \frac{1}{1+\tau s}$$

(3)

To confirm the model validity, system identification tests were performed and results are represented in Figure 3. A green thick line in Figure 3 is the frequency response for the model Equation (3) and other results are for experimentally-obtained frequency responses with different input voltages.

Secondly, we need to obtain the dynamics for designing the force controller which has a motor angle as an input and a clamping force as an output. Considering that a clamping force and a motor angle has a proportional relationship (i.e., a proportional gain $K$ is obtained from the reduction gear ratio and mechanical stiffness), it is reasonable to choose a simple first order model as below:

$$P_m(s)=\frac{{\widehat{F}}_{cl}}{{\theta }_m}\approx \frac{K}{1+\tau s}.$$

(4)

where a linear transfer function $P_m$ is the relationship between a motor angle ${\theta }_m$ and a clamping force ${\widehat{F}}_{cl}$, $\tau$ is the model cut-off frequency that is the same value used in Equation (3).

To get a representative model $P_m$ used in a force tracking controller, system identification tests were performed and results are represented in Figure 4. A blue thin line is the estimated clamping force and a red thick line is the linear model that we designed (i.e., Equation (4)). Since a force-mode disturbance observer is designed based on this model, a modeling error shown in Figure 4 is properly compensated and a real plant is nominalized to the linear model we designed.

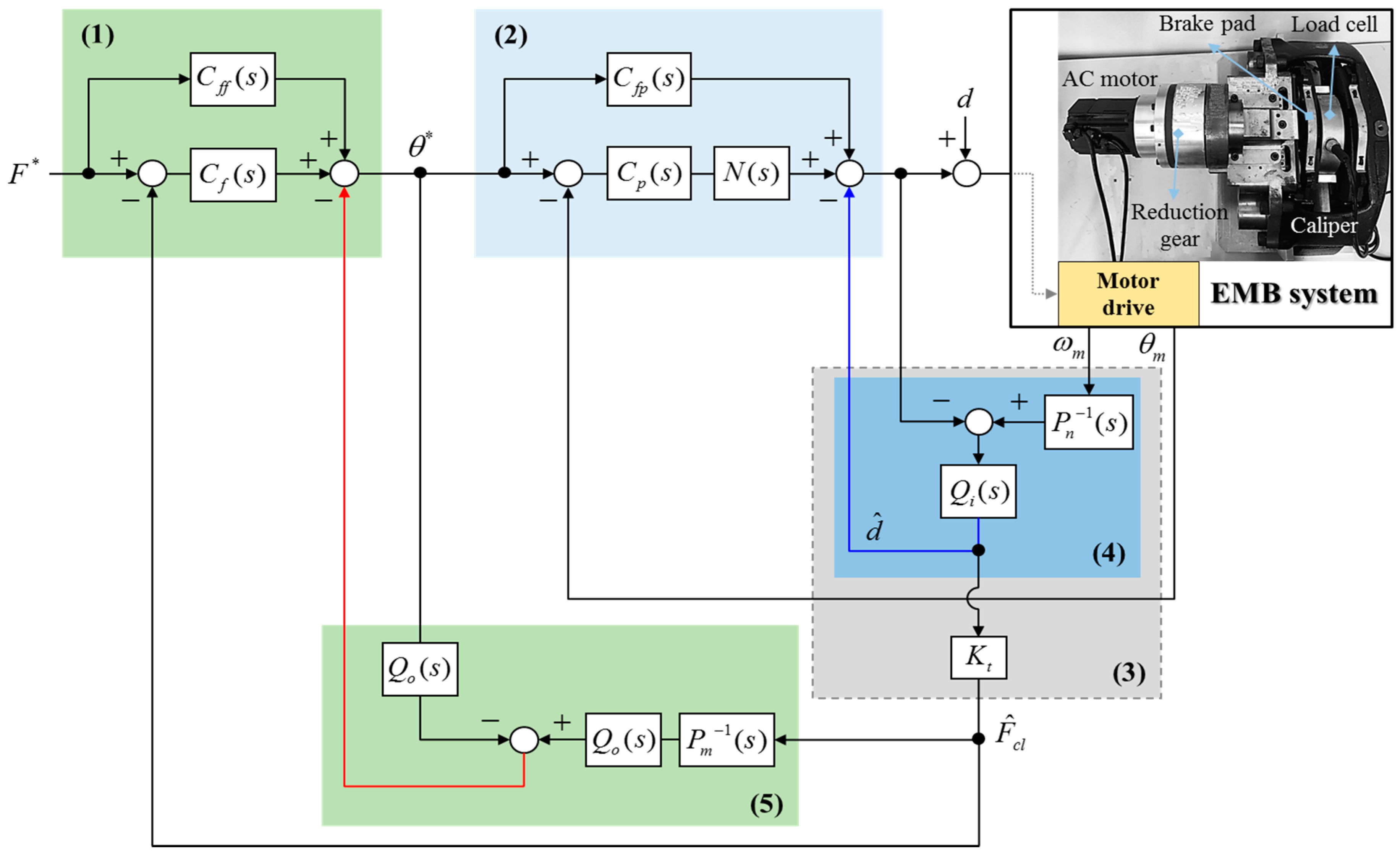
3. Design of a Sensor-Less Robust Controller

In this paper, we focus on two control objectives: (1) design of more robust and accurate position and force controllers for enhancing the braking force control performance; and (2) design of a practical clamping force observer to reduce the system cost. Thus, we propose the force sensor-less robust force control method. The overall control structure is shown in Figure 5. The control scheme is given as follows.

• First, the desired clamping force $F^{*}$ is generated by a driver’s brake pedal command. Note that the desired clamping force can be calculated by using the brake pedal stroke sensor.
• Second, the 2-degree-of-freedom position controller is designed based on the defined nominal motor model for improving the position tracking performances and an inner-loop disturbance observer (i.e., called a position-mode DOB) is designed for making the position controller robust against external disturbances.
• Third, a CFO is designed based on a nominal motor model and a reduction gear ratio.
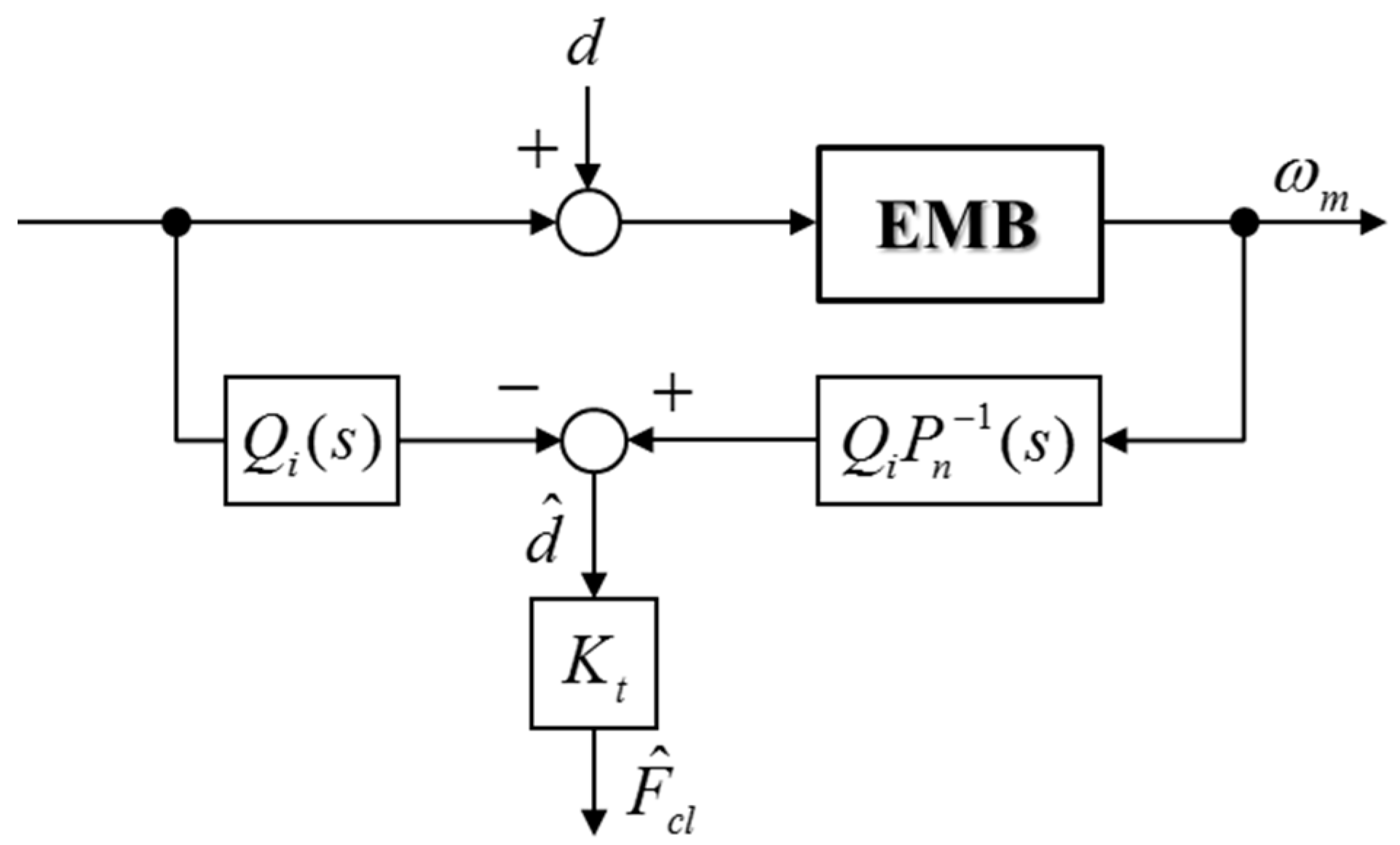
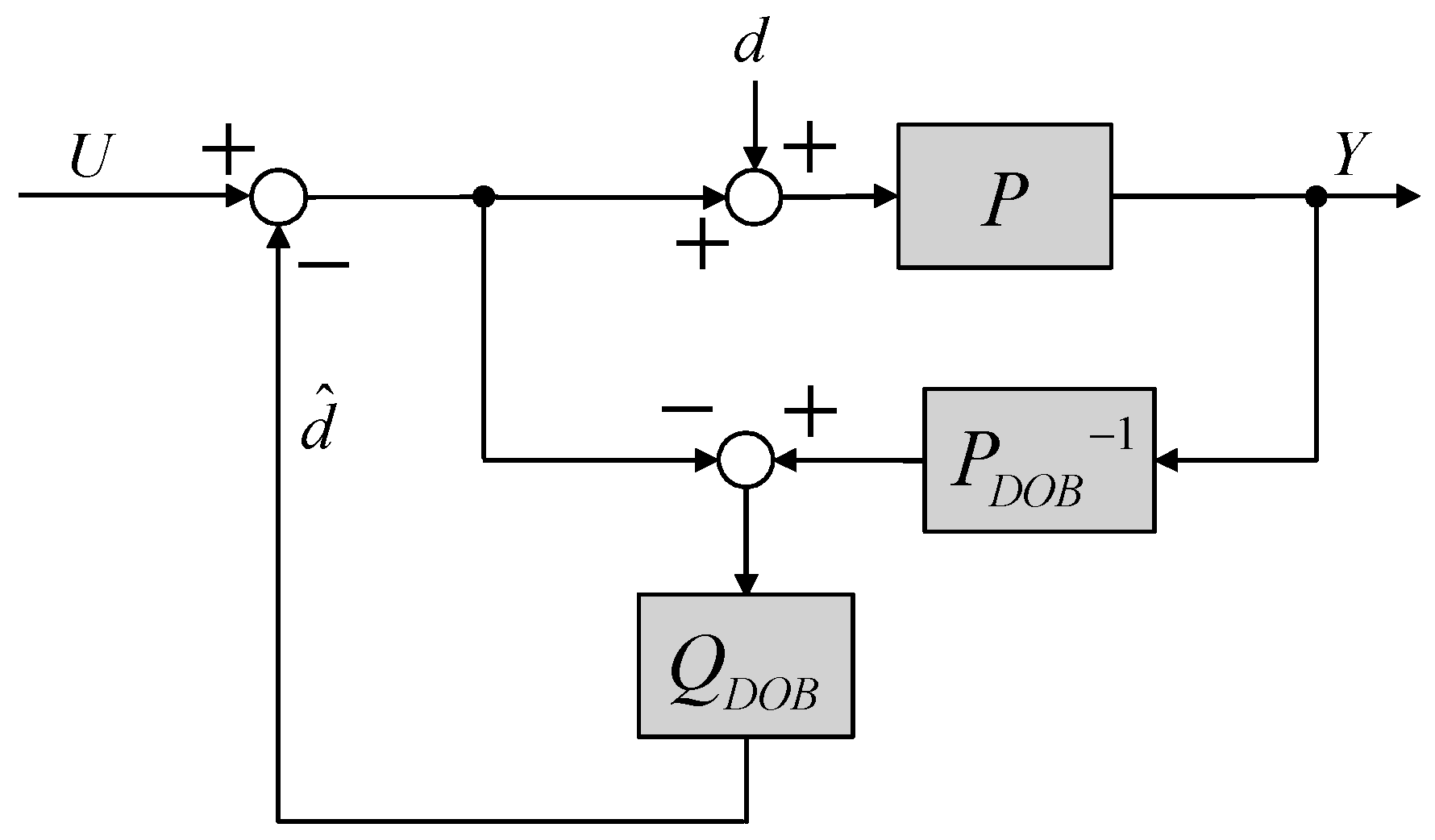
• Forth, the outer-loop disturbance observer (i.e., called a force-mode DOB) is designed to compensate for model variations and to reject undesired disturbances. A F-DOB makes the complicated calmping force dynamics behave as a defined nominal clamping force model.
• Finally, the 2-degree-of-freedom clamping force controller is designed by using the nominal clamping force model.

3.1. Design of a Clamping Force Observer (CFO)

In the operation of an EMB, it is very important to know the clamping force in real time. Even if a load cell or force sensor can be used to measure the clamping force, it entails extra cost and space. Therefore, in order to estimate the clamping force, we proposed a CFO based on a nominal model $P_n$ and the second-order low pass filter $Q_i(s)$ as shown in Figure 6:

$$Q_i(s)=\frac{{{\omega }_i}^2}{s^2+2{\omega }_{i}s+{{\omega }_i}^2}$$

(5)

The estimation result for the CFO is shown in Figure 7. It is confirmed that the estimated clamping force (i.e., a red thin line in Figure 7) tracks the sensor measurement without a noticeable error. Note that a reduction gear mechanism with a high gear ratio (i.e., 100:1) is applied in a proposed EMB system, the nonlinear effects, caused by gear backlash or friction, affect the estimation performance.

3.2. Design of an Inner-Loop Controller: Position Controller

In this section, a robust position controller used as an inner-loop controller is introduced and its control effectiveness is explained from experimental results. A DOB-based inner-loop position control is required to track the reference with a high control bandwidth and to make control system robust against external disturbances and nonlinear effects. The structure is shown in Figure 8.

In order to accomplish the control goal, firstly, A P-DOB is designed to compensate the external disturbance and thereby makes the closed position control system robust. Secondly, a 2-DOF position controller (i.e., a feedback controller, $C_p(s)$ and feed-forward controller, $C_{fp}(s)$) is designed to enhance the reference tracking performance and a residual vibration compensator (i.e., $N(s)$) is additionally designed based on frequency analysis for the tracking error. A transfer function between the reference position, ${\theta }^{*}$, and the output ${\theta }_m$ is expressed as:

$$\frac{{\theta }_m}{{\theta }^{*}}=\frac{C_{p}P}{1-Q_i+C_{p}P+P{P}_n^{-1}{Q}_i},$$

(6)

where, if $Q_i\approx 1$ and $P=P_n$, Equation (6) can be simplified as:

$$\frac{{\theta }_m}{{\theta }^{*}}\approx \frac{C_p{P}_n}{1+C_p{P}_n}=\frac{{\omega }_p}{s+{\omega }_p}$$

(7)

Here, in order to satisfy the Equation (7) condition, a feedback controller, designed based on a pole-zero cancellation method, should have a following form:

$$C_p(s)=\frac{K_{pp}s+K_{ip}+K_{dp}{s}^2}{s}$$

(8)

where, proportional, integral, and derivative gains are chosen as $K_{pp}={\omega }_p(J_m+B_m\tau )$, and $K_{dp}={\omega }_p{J}_m\tau$, respectively, ${\omega }_p$ is the cut-off frequency deciding the position control bandwidth.

In addition, an inverse model-based feed-forward controller is added to achieve fast response in the transient region as follows:

$$C_{fp}(s)=\frac{{{\omega }_1}^{3}s(J_{m}s+B_m)(1+\tau s)}{{(s+{\omega }_1)}^3},$$

(9)

where, ${\omega }_1$ is the cut-off frequency of a feed-forward filter that is required to reject noises caused by numerical differentiation.

To alleviate overshoot phenomenon at a certain frequency, a residual vibration compensator is applied and it is given by:

$$N(s)=\frac{s^2+2\zeta {\omega }_{c}s+{\omega }_c^2}{s^2+2{\omega }_{c}s+{\omega }_c^2},$$

(10)

where, $\zeta$ and ${\omega }_c$ are the damping coefficient and resonance frequency, respectively, and these values are obtained from the repeated experiment under various operating conditions.

Several experiments are performed to confirm the frequency response for designed control system and those results are shown in Figure 9. It is examined that a maximum overshoot occurs in the vicinity of 12 Hz (i.e., a driving motor is the most oscillatory.). One can see that a vibration compensator,$N(s)$, contributes to reducing the maximum magnitude of the closed-loop frequency response by 45%.

3.3. Design of an Outer-Loop Controller: Force Controller

The EMB control is challenged by the nonlinearities in the reduction gear mechanism, model uncertainty, and low backdrivability. To compensate for such undesired factors and unpredictable terms, a DOB has been used in this study. In general, the DOB is used for rejecting disturbance and compensating for variation of plant dynamics by treating the variations as an equivalent disturbances. In the design of DOB, the selection of the low pass filter called a Q-filter is very important. It is required to select $Q_{DOB}(s)$ such that $Q_{DOB}(s)P_{DOB}{(s)}^{-1}$ is realizable. In general, the $Q_{DOB}(s)$ is designed as a low-pass filter, which has the dc gain of one, such that the closed-loop system has a good disturbance rejection performance at low frequencies. From the general framework of a DOB shown in Figure 10, characteristics of the DOB is analytically explained. A transfer function of a DOB, i.e., from the input $U$ to the ouput $Y$, is expressed as:

$$\begin{array}{l}\frac{Y}{U}=\frac{P{P}_{DOB}}{P_{DOB}+P{Q}_{DOB}-Q_{DOB}{P}_{DOB}}\approx P_{DOB}\\ (If,Q_{DOB}\approx 1)\end{array}.$$

(11)

The transfer function of the input $d$ to the output $Y$ is expressed as follows:

$$\begin{array}{l}\frac{Y}{d}=\frac{P{P}_{DOB}(1-Q_{DOB})}{P_{DOB}+P{Q}_{DOB}-Q_{DOB}{P}_{DOB}}\approx 0\\ (If,Q_{DOB}\approx 1)\end{array}.$$

(12)

Based on a nominal clamping force model (i.e., Equation (4)), a F-DOB is designed and it contributed to alleviating the hysteresis effect during brake apply and release. In similar manner, a 2-DOF controller is designed by pole placement based on given control performance specifications and two feedback gains (i.e., a proportional and integration gains) are chosen to make a closed-loop transfer function to be a 1st low-pass filter with a cut-off frequency of ${\omega }_f$:

$$\frac{{\widehat{F}}_{cl}}{F^{*}}=\frac{C_{f}P}{1-Q_o+C_{f}P+P{P}_n^{-1}{Q}_o}\approx \frac{C_{f}P}{1+C_{f}P}=\frac{{\omega }_f}{s+{\omega }_f}$$

(13)

$$C_f=\frac{K_{pf}s+K_{if}}{s}$$

(14)

where, $K_{pf}=\frac{{\omega }_f\tau }{k}$, $K_{if}=\frac{{\omega }_f}{k}$.

A feed-forward controller is also designed based on an inverse nominal model, i.e., ${P_m}^{-1}(s)=K^{-1}(1+\tau s)$, and 1st low-pass filter, i.e., ${\omega }_2/(s+{\omega }_2)$, is used for rejecting the amplified noise:

$$C_{ff}(s)=\frac{{\omega }_2(1+\tau s)}{K(s+{\omega }_2)}$$

(15)

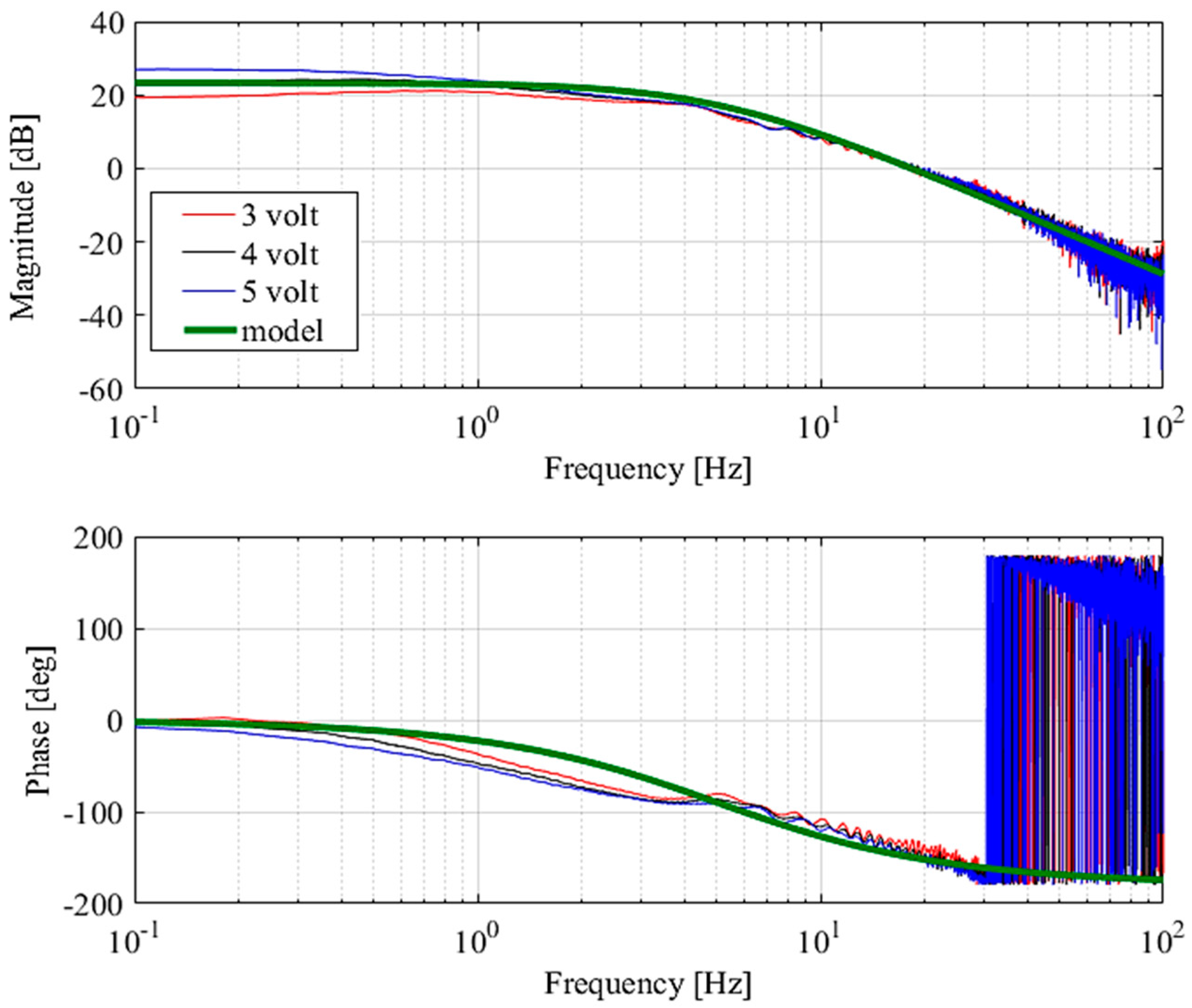
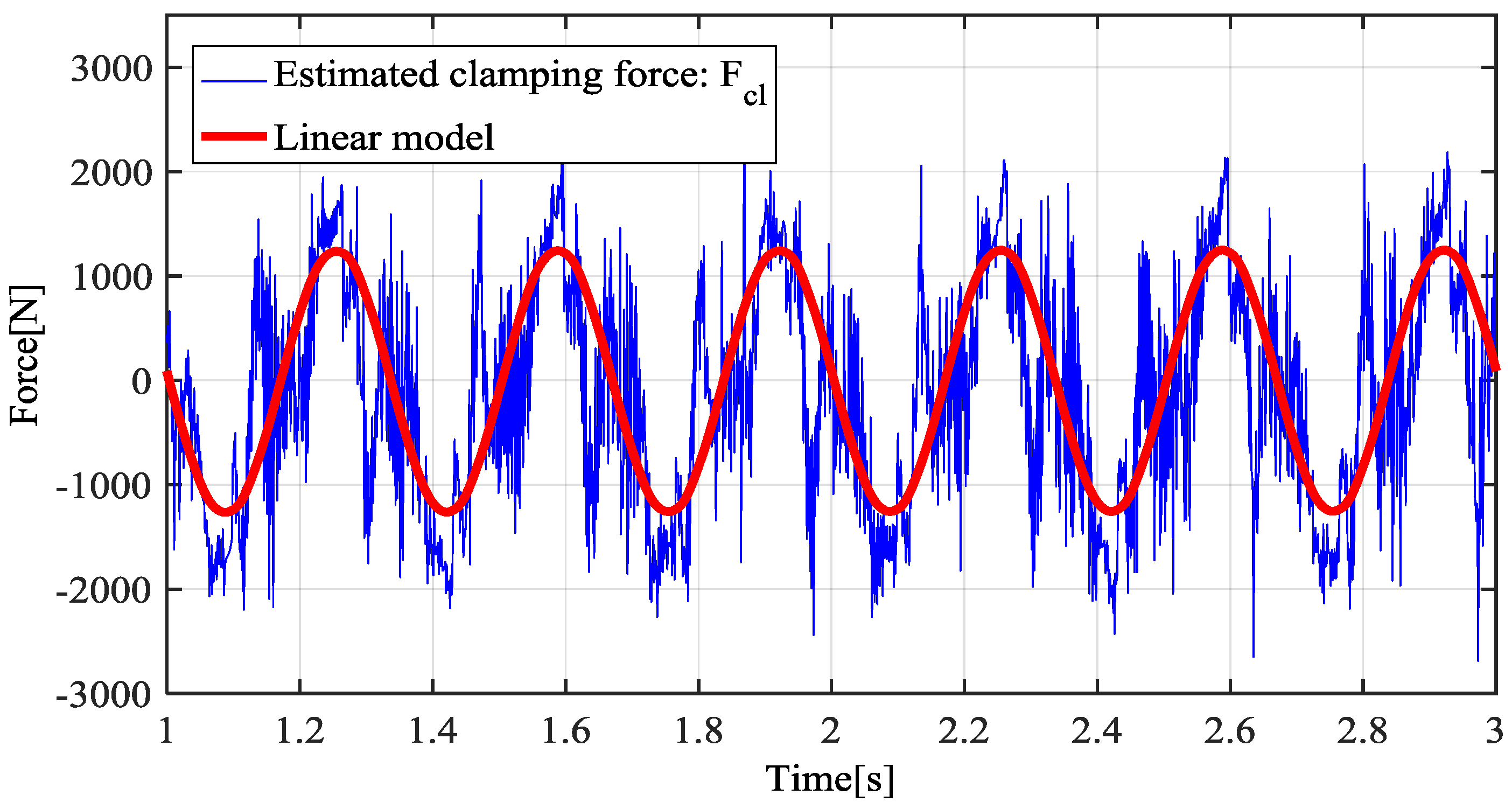
4. Experiments

In this section, an experimental setup for the EMB system is introduced and experimental results are presented to confirm the tracking performance of a proposed controller.

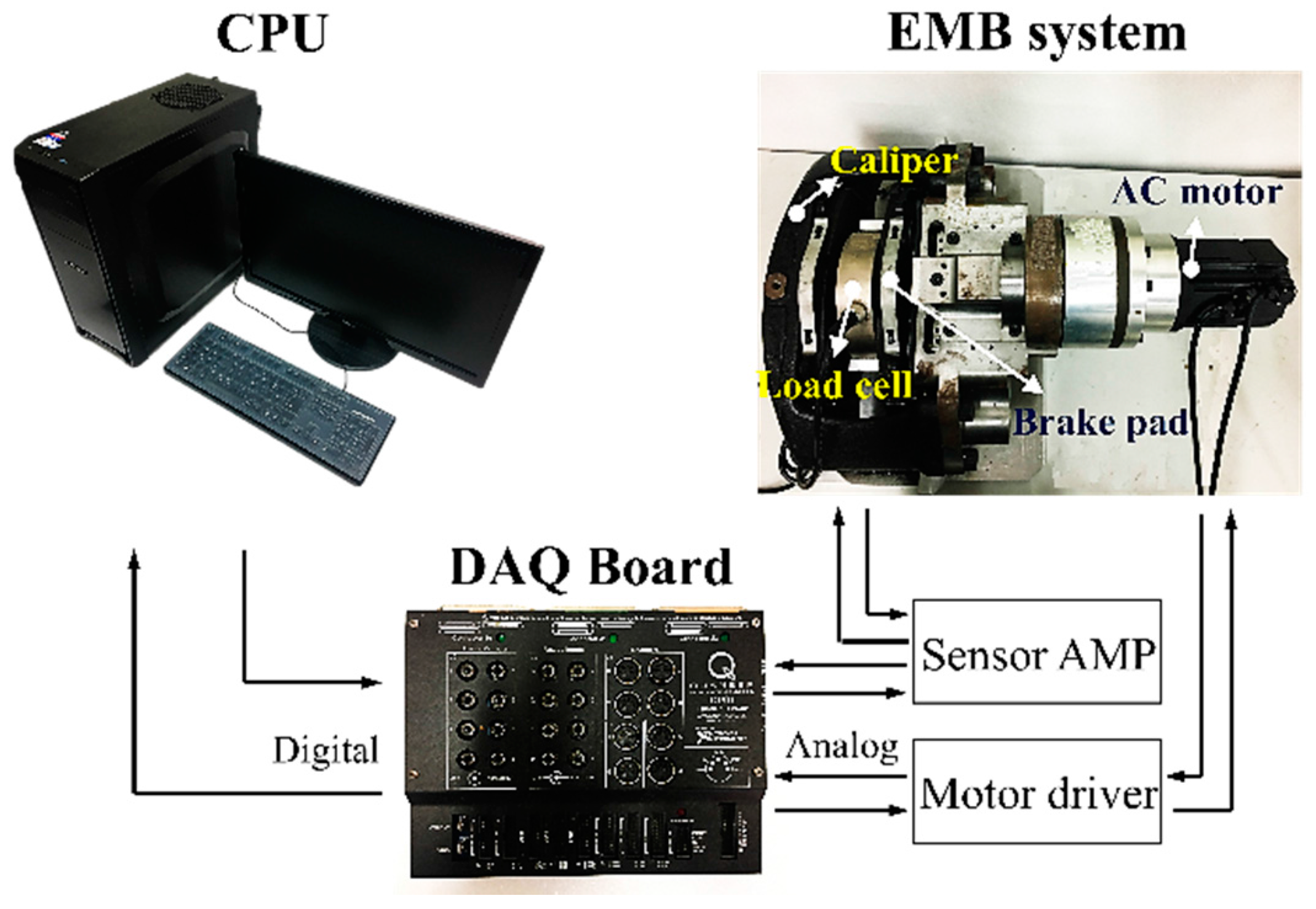
4.1. Experimental Setup

Figure 11 shows the experimental setup for the EMB system. An EMB system consists of an AC motor, mechanical brake components and a load cell. It should be noted that a load cell is very expensive, e.g., more than $1000. In this paper, it is only used as a reference for validating the proposed clamping force estimation algorithm. The MATLAB/SIMULINK software is used to realize the real-time control. Additionally, in order to measure the data, a Quanser DAQ board from Quanser Company (Markham, ON, Canada) is used.

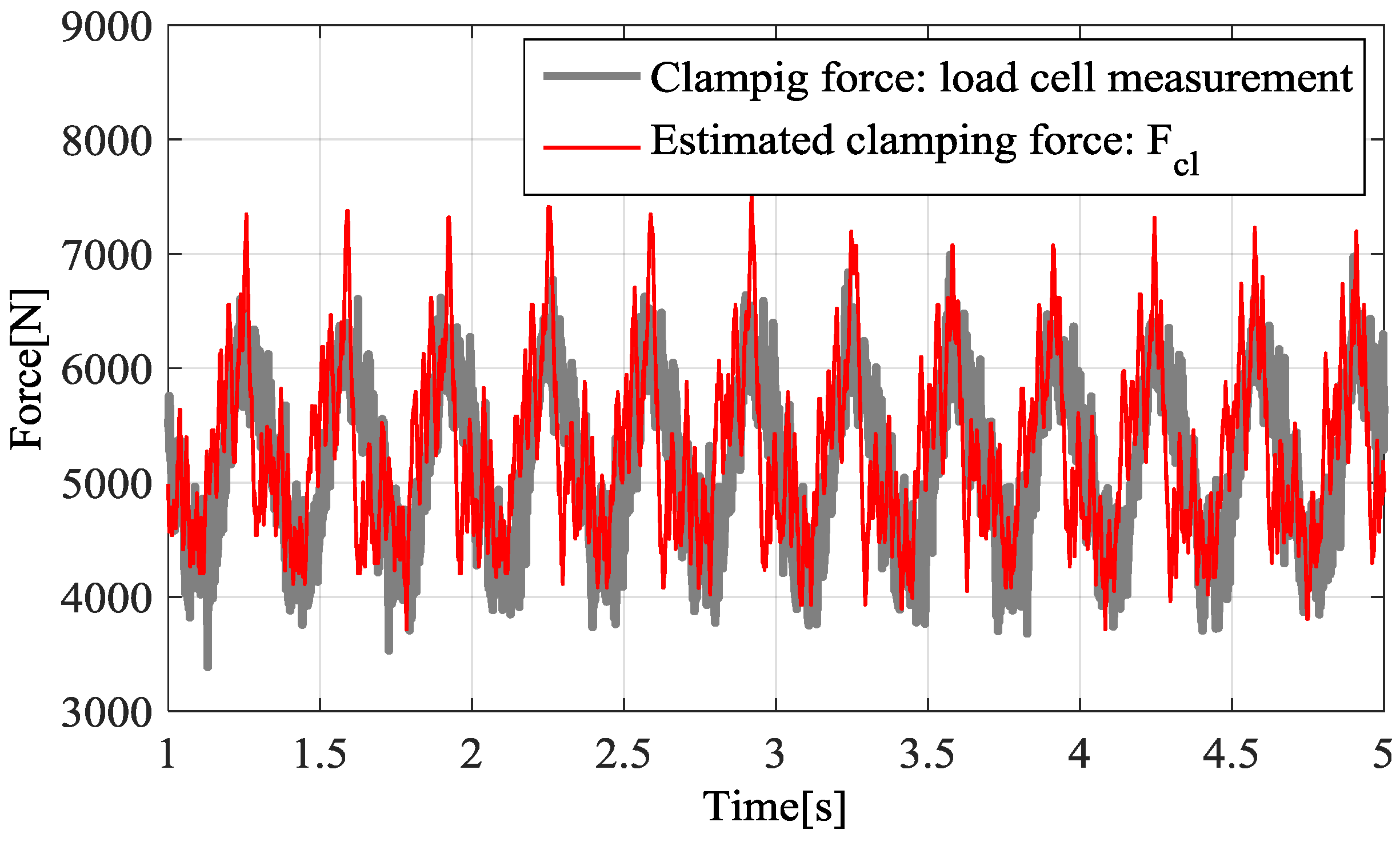
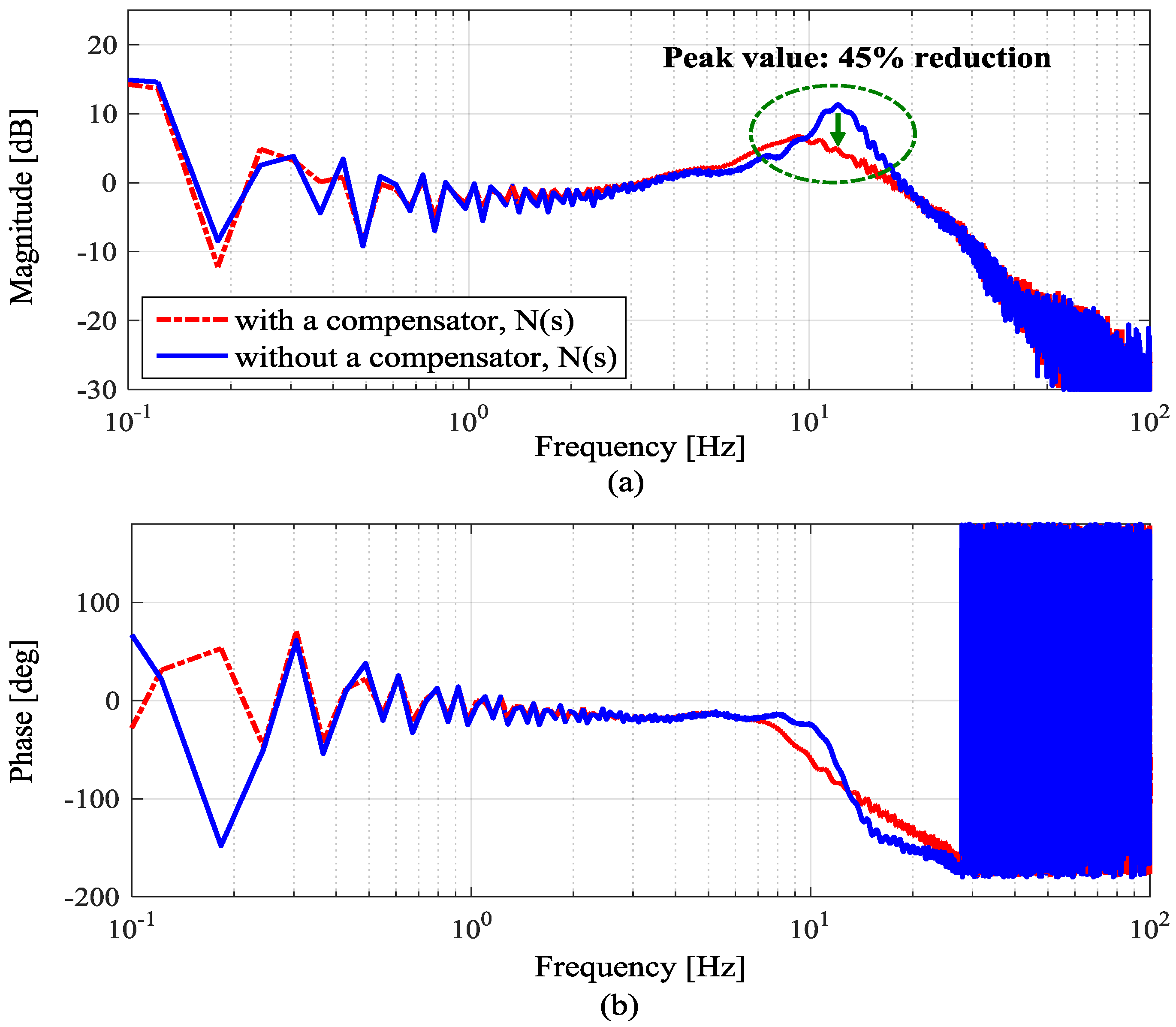
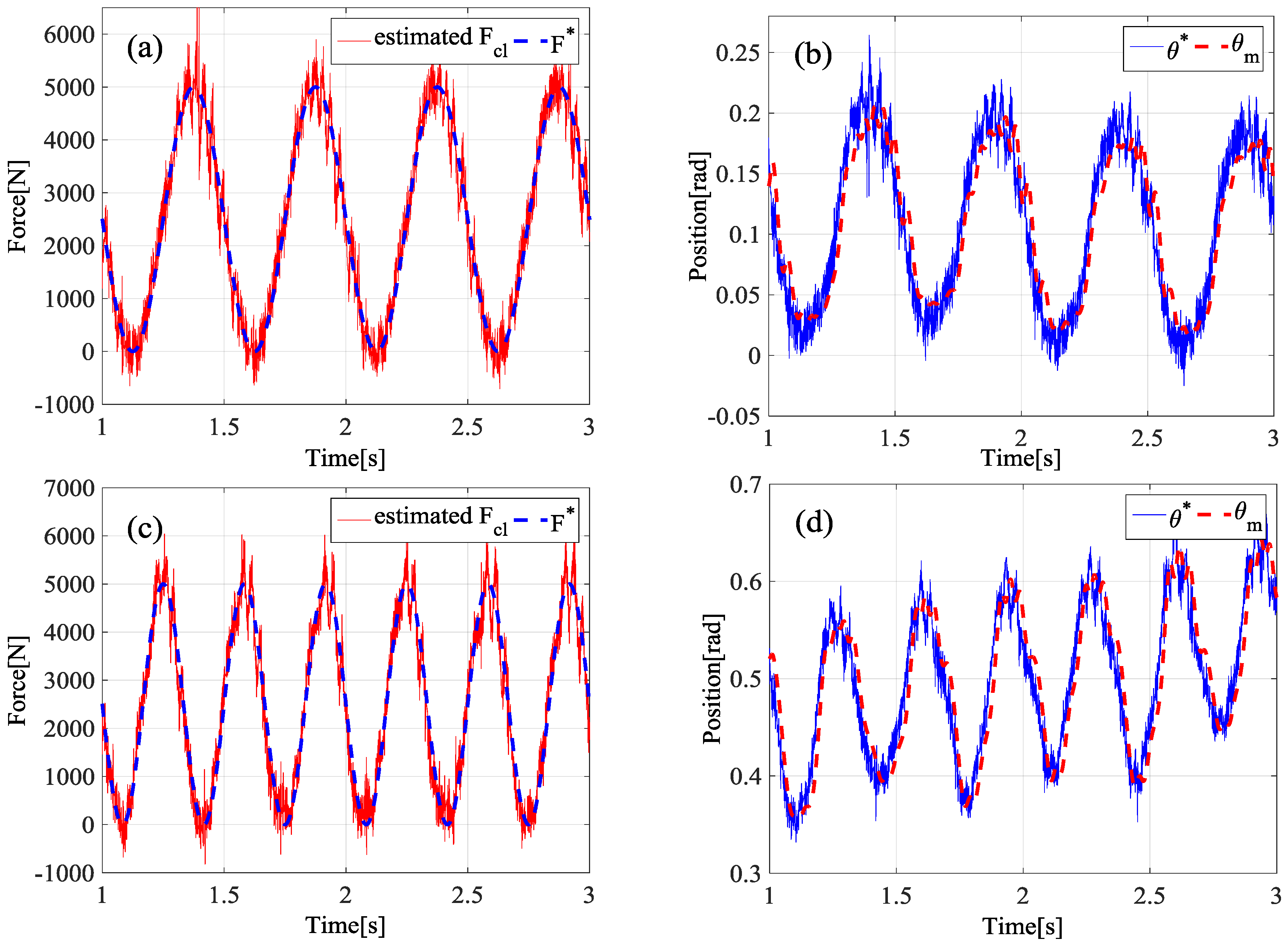
4.2. Experimental Results

A proposed estimation and clamping force control methods, illustrated in Figure 5, are implemented on an EMB system shown in Figure 11. To simulate the driver’s brake command, the sinusoidal braking maneuver has been done under various frequency conditions (e.g., 2 Hz sinusoidal command, 3 Hz sinusoidal command). Considering the possible foot-braking frequency that a driver makes is about 0–3 Hz, test scenarios are reasonable. Figure 12 represents the test results for a proposed clamping force control. Figure 12a–d are the results for the control with a 2 Hz and a 3 Hz clamping force commands, respectively. We can see that the estimated clamping force (i.e., a feedback variable) well tracks the generated clamping force command from Figure 12a. Also, under the same test conditions, a driving motor’s angle tracks the control angle command generated from the outer-loop force controller as shown in Figure 12b. From the similar control results, Figure 12c,d, it is confirmed that a propose EMB control system shows the satisfactory reference tracking performance without noticeable errors. Considering that the braking control bandwidth in commercial ABS for heavy vehicles is under 3 Hz, it is expected that control performances of an ABS, based on a proposed EMB control systems, are significantly improved. As aforementioned, most of the EMB systems undergo the backdrivability problem and have challenging control issues accordingly. In this paper, to overcome that problem, we proposed a dual loop control strategy and its effectiveness is verified from test results, i.e., Figure 12. In addition, it is confirmed that the force sensor-less force control method is practically applicable to an EMB control system.

5. Conclusions

This paper has presented a robust clamping force control method for EMB control system applications. In order to overcome challenging issues in precise force control, a dual loop control technique is employed and its performance is verified by several control results. Since the EMB undergoes parameter variations and a backdrivability problem under various operating conditions, a disturbance compensation technique based on a DOB is used for enhancing the robustness and a 2-DOF control method is used to improve the reference tracking performance. Additionally, a model-based clamping force estimation method for realizing the sensor-less control is proposed and its effectiveness is also verified by brake apply-release tests. Although there exists an estimation error that is caused by nonlinear effects such as gear backlash or friction, the trajectory of the estimate is well-matched with that of the sensor measurement without any noticeable errors. As a cost-effective control solution, proposed estimation and control methods can be practically applied to EMB systems for commercial city buses. In future works, precise friction modeling should be done and non-linear clamping force estimation methods will be studied. In addition, the closed-loop stability analysis will be done by employing the robust stability theorem as shown in the authors’ other publication [17].