Abstract
Plug-in hybrid electric vehicles (PHEVs) can be considered as a hybrid system (HS) which includes the continuous state variable, discrete event, and operation constraint. Thus, a model predictive control (MPC) strategy for PHEVs based on the mixed logical dynamical (MLD) model and short-term vehicle speed prediction is proposed in this paper. Firstly, the mathematical model of the controlled PHEV is set-up to evaluate the energy consumption using the linearized models of core power components. Then, based on the recognition of driving intention and the past vehicle speed data, a nonlinear auto-regressive (NAR) neural network structure is designed to predict the vehicle speed for known driving profiles of city buses and the predicted vehicle speed is used to calculate the total required torque. Next, a MLD model is established with appropriate constraints for six possible driving modes. By solving the objective function with the Mixed Integer Linear Programming (MILP) algorithm, the optimal motor torque and the corresponding driving mode sequence within the speed prediction horizon can be obtained. Finally, the proposed energy control strategy shows substantial improvement in fuel economy in the simulation results.
1. Introduction
Focusing on plug-in hybrid electric vehicles (PHEVs), which are a typical hybrid system (HS) [1], an accurate system model is mandatory to study their control strategy. Commonly used hybrid system modeling methods include hierarchical model [2], Petri net model based on the proposed network diagram [3], the “unified model” of hybrid dynamic systems by Branicky et al. [4] and the Piecewise Affine (PWA) switching model [5]. All these models are relatively complex and inconvenient compared to the conventional control technology. In [6], Bemporad and Morari proposed the mixed logical dynamical (MLD) model that includes interdependent physical laws, logic rules and operational constraints, to apply the conventional control methods (e.g., optimization and prediction) to the hybrid system. The MLD model also uses differential equations to avoid the complex conditions in hybrid systems and could be transferred into mixed integer linear programming (MILP) [7] for a solution.
The control strategy for PHEVs aims to find an appropriate power and torque distribution between the combustion engine and the electric motor to improve the fuel economy and emission performance [8]. Among various control strategies, the rule-based control method [9] is the most widely used, but it relies on experience to a greater extent, which makes it difficult to adapt to dynamic changes in the driving cycles and to optimize the fuel economy of the vehicle. The optimization-based control strategy [10] includes instantaneous optimization and global optimization. The instantaneous optimization control strategy [11] for an equivalent minimal fuel consumption does not give sufficient consideration to the vehicle state in the future; while for the global optimization [12], complete statistical information on driving cycles must be provided, including road conditions, which makes it hard to compute fast and it lacks adaptability, and eventually cannot be applied directly to real-time control of the vehicle. If the vehicle state information is predicted accurately beforehand, global optimization within this time could be applied to overcome the disadvantages of inadaptability. This could also form the basis of the Model Predictive Control (MPC) method for a hybrid electric vehicle. In [13], a generalized predictive optimal control framework is proposed, and MILP methodology is utilized, which enables the control strategy to get better economy than instantaneous strategies. However, it assumes the traffic pattern and terrain are known in advance without any prediction.
In this paper, the required vehicle torque is calculated based on the predicted vehicle speed. Commonly used vehicle speed prediction methods are the model-based method [14], Kalman filter [15], hidden Markov models [16] and neural network models [17], etc. The non-linear auto-regressive (NAR) model neural network [18,19] has advantages of solving time variant and nonlinear problems, making it suitable for vehicle speed prediction. For training the neural network, most researchers have only used global positioning system (GPS) data from or statistical analysis data from the vehicle driving cycle [20,21,22], but ignored the driver’s operation such as accelerator pedal and braking pedal operations which can reflect the future speed variation trends. Therefore, a vehicle speed prediction method using a NAR neutral network based on the combination of past speed data and driving intention data recognized by fuzzy inference is proposed.
Based on the analysis above, this paper focuses on a parallel plug-in hybrid electric city bus, and the powertrain model is set-up firstly. Then, the driving intention is recognized by using fuzzy inference to analyze the pedal operation. A vehicle speed prediction method using a NAR neutral network based on the combination of driving intention and the past speed data is proposed to predict the future short-term vehicle running state and calculate the required vehicle torque. Afterwards, the MLD model is established for the PHEV powertrain. Combined with MILP algorithm and aiming at the minimal equivalent fuel consumption, a mixed logic dynamical-model predictive control (MLD-MPC) strategy based on vehicle speed prediction is proposed. Finally, the simulation results are presented to validate the proposed energy control strategy.
2. Modeling of Powertrain System
In this part, the vehicle powertrain is modeled. It is used to calculate the total vehicle torque demand, and to evaluate the engine and motor energy consumption quickly for the control strategy, similar torque-speed modelling method could also be found in literature [12,23,24]. Parallel powertrain and transmission system of PHEV [25] adopted in this paper are shown in Figure 1. The mathematical models of each part in powertrain are described as follows. The speed and torque models of wheels are described in Equation (1):
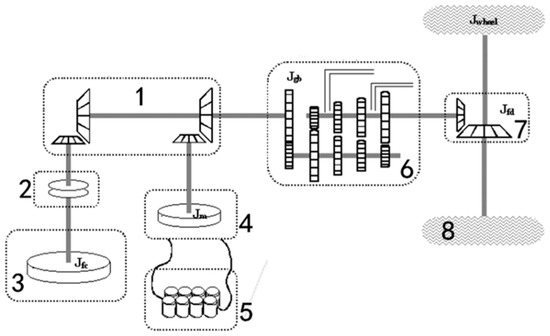
Figure 1.
Parallel plug-in hybrid electric vehicle (PHEV) powertrain and transmission system (1—Touque Coupler; 2—Clutch; 3—Engine; 4—Motor; 5—Energy Storage System; 6—Gearbox; 7—Final Drive; 8—Wheels).
In Equation (1), is the vehicle velocity in m/s, is the air density (1.2258 kg/m3), is the radius of wheel in m, is the wheel rotating speed in rad/s, is the wheel torque in , is the frontal area in , is the drag coefficient, represents tire rolling resistance coefficient, m is the vehicle mass in kg, represents total vehicle rotational inertia in , is vehicle slope angle in rad, is the acceleration in m/s2. Model of transmission torque and speed is given in Equation (2), where is the required input rotating speed of transmission in rad/s; is the total transmission ratio; is the required input torque of transmission in ; is the efficiency from transmission input to tire [26]. The model of engine fuel consumption rate is given in Equation (3), where is the engine fuel consumption rate, which is a function of its rotation speed and torque :
According to the engine fuel consumption data, the relationship between fuel consumption rate and torque under different rotating speed is curve-fitted using the least squares method and is plotted in Figure 2. In Equation (4), and are the fitting coefficients in linear expression (see Appendix A).
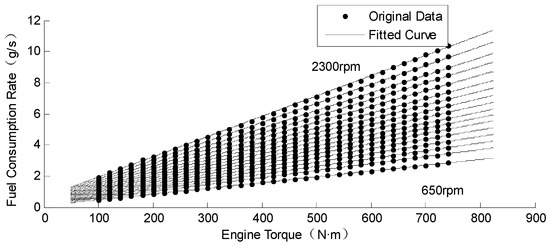
Figure 2.
Linear fitting curve of engine fuel consumption rate and torque.
Equation (5) is the model of equivalent fuel consumption rate of electric motor, where is the rate of fuel consumption which is equivalent to the electric power the motor used, is the mass calorific value of diesel (43,000 kJ/kg), is the motor speed in rad/s, and is the motor torque in N·m, is the open-circuit voltage in V, I is the battery output current in A. is the equivalent fuel factor of the battery power, it is decided by the ratio of electricity and fuel price as can be seen in Equation (6), is the fuel price (5.6 RMB/L), is the electricity price (1 RMB/kWh), is the fuel density (835 kg/L), is the efficiency of the charging pile.
According to the battery output current [27] given by Equation (7), the relationship between motor torque and the rate of change of state of charge (SOC) of the battery under a certain motor speed is plotted in Figure 3, and the approximate linear function obtained using least square method is given by Equation (8), where is the rate of change of SOC, and are the fitting coefficients (see Appendix A). is the equivalent resistance of the battery in , and is the capacity of the battery in C:
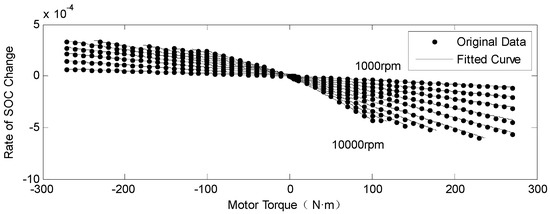
Figure 3.
Fitted curves of motor torque and state of charge (SOC) change.
3. Short-Term Vehicle Speed Prediction
3.1. Driving Intention Identification
Driving intention depends on the driving environment, the vehicle running state and the driver’s driving habits, etc. It is a typical empirical model with characteristics of fuzziness. Given the obvious advantages of fuzzy theory in dealing with the empirical models, a fuzzy logic inference system was developed to identify the driving intention.
Driving intention, in general, can be divided into acceleration intention and braking intention. Based on the urgency of accelerating, accelerating intention is divided into slow acceleration, relatively slow acceleration, normal acceleration, relatively rapid acceleration, and rapid acceleration. When no operation on the accelerator pedal it can be considered as braking intention and is divided into general braking and coasting based on whether the braking pedal is operated or not. Based on the urgency of general braking, general braking intention is divided into slow braking, relatively slow braking, normal braking, relatively rapid braking, and rapid braking.
Drivers operate the accelerator pedal and braking pedal directly according to the driving environment and the running state of the vehicle, so as to realize their driving intention. Therefore, the acceleration pedal travel and the braking pedal travel are used as the two main identification parameters. However, the pedal travel cannot completely reflect the urgency of driving intention. Hence the rate of change of acceleration pedal travel and braking pedal travel are also considered to identify the driving intention.
The acceleration intention is identified by fuzzy inference, and its identification parameters are acceleration pedal travel and rate of change of acceleration pedal travel, membership functions of which are shown in Figure 4a,b respectively. The membership functions of the acceleration intention are shown in Figure 4c. The fuzzy rules for the acceleration intention identification are shown in Table 1.
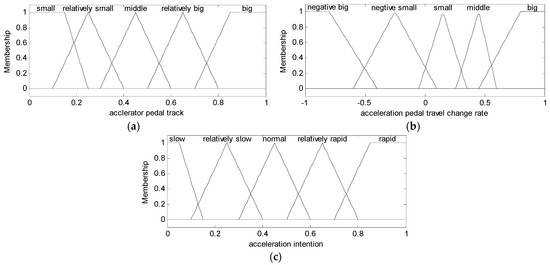
Figure 4.
(a) Membership functions of acceleration pedal travel; (b) membership functions of rate of change of acceleration pedal travel; and (c) membership functions of acceleration intention.

Table 1.
The fuzzy rules for identification of the acceleration intention.
The braking intention is identified by fuzzy inference, and its identification parameters are braking pedal travel and rate of change of braking pedal travel, membership functions of which are showed in Figure 5a,b respectively. The membership functions of the braking intention are shown in Figure 5c. The fuzzy rules for the braking intention identification are shown in Table 2.
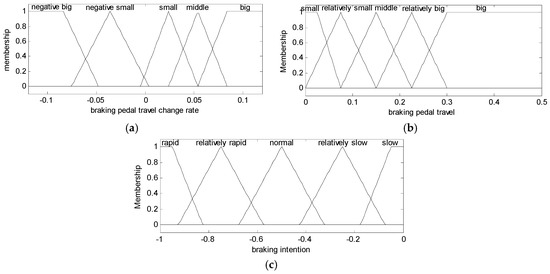
Figure 5.
(a) Membership functions of braking pedal travel; (b) membership functions of rate of change of braking pedal travel; and (c) membership functions of braking intention.

Table 2.
The fuzzy rules for identification of the braking intention.
In this paper, the United Kingdom Bus (UKBUS) driving cycle is considered as an example, and the driving intention identification is carried out. Figure 6 shows the speed segment of UKBUS driving cycle. The acceleration intention identification results are in the range of 0–1, the closer that this value is to 1, the more urgent the acceleration intention is. The braking intention identification results are in the range of −1–0, the closer that this value is to −1, the more urgent the braking intention is. Besides, the driving intention is identified as coasting when there are no operations on both accelerator pedal and braking pedal. The resultant values are a continuous time sequence ranging from −1 to 1, based on which the driving intention can be distinguished between acceleration or braking at each and every moment, as well as the urgency of the driving intention. Then the obtained driving intention time sequence, as well as the vehicle speed time sequence, are given as inputs to the NAR neural network. The acceleration calculated through the real velocity is normalized in −1–1 and it is used as the real driving intention intensity. The comparison of the driving intention identified by fuzzy inference and the real driving intention intensity is shown in Figure 7. The mean absolute error (MAE) of the driving intention recognition result is 0.16 when the data ranges from −1 to 1. This fuzzy recognition result with sufficient accuracy could be used as input for the speed prediction neural network to improve the prediction precision.
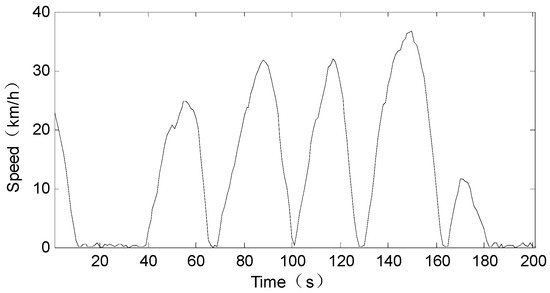
Figure 6.
The speed segment of United Kingdom Bus (UKBUS) driving cycle.
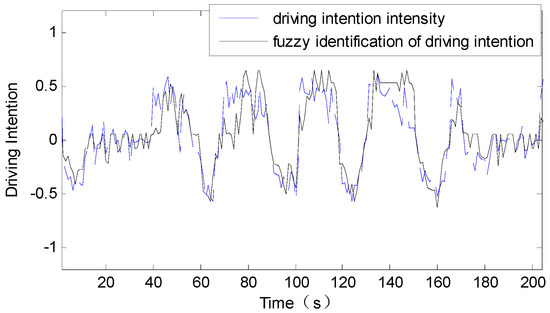
Figure 7.
The driving intention identification result comparison.
3.2. Short-Term Vehicle Speed Prediction Using Nonlinear Auto-Regressive Neural Network
The NAR neural network is a kind of dynamic neural network, which could add the output memory to the input automatically to calculate the output at the next instance. As the driver’s operation can reflect the future speed variation trend, the obtained time series of driving intention are provided as input to the network together with the past vehicle speed data.
Definition of the prediction model is given in Equation (9):
where is the output at a time t, f is the nonlinear mapping, is the output memory order. The output at the time (t + 1), i.e., depends on the former steps of output , as the predicted values could be fed back to the input, the long-term predictions can be achieved.
The NAR neural network structure, consisting a hidden layer, an output layer, and an output feedback layer, is given in Figure 8. As shown in Figure 8, the hidden and the output layer include 15 and 1 neurons respectively. The order of output memory is 5. is the connection weight between input and output layer neuron, is the threshold of the layer, is the transfer function of the hidden layer, is the connection weight between hidden layer and output layer, is the threshold of output layer and is the transfer function of output layer.
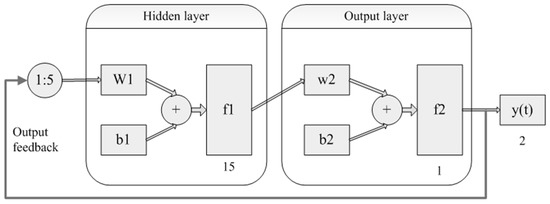
Figure 8.
Nonlinear auto-regressive (NAR) neural network structure.
This paper uses a Bayesian algorithm to train the network, choosing Tan-sigmoid transfer function as hidden layer function, and purelin linear function for the output layer. In this paper, a plug-in hybrid electric city bus is studied which is running on pre-determined routes, thus the speed prediction method is for known driving profiles. Taking the UKBUS driving cycle as an example, the driving intention time series corresponding to the conditions are obtained by the aforementioned driving intention identification method. A total of 3288 samples of vehicle speed-intention data, choosing 2788 samples as training samples among which 75% is considered as training data, and the remaining 25% is used as validation data and test data. The remaining 500 samples which didn’t participate in the training are used to test the network’s predictive ability.
The predicted speed segmentation with a receding horizon of 5 s is shown in Figure 9. As can be observed, the NAR-based speed predictor predicts the micro-trip behaviors effectively.
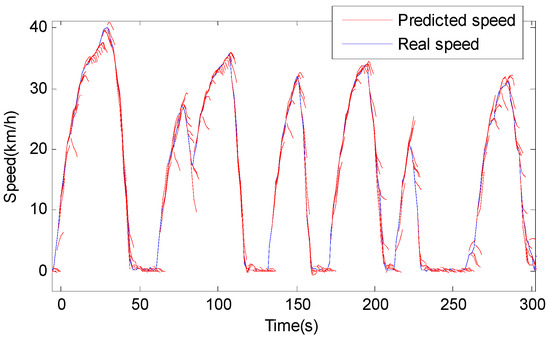
Figure 9.
Short-term predicted speed compared with the real speed.
Root mean square error (RMSE) is used in this paper to estimate the error between the prediction value and the actual value. Smaller the RMSE means higher prediction accuracy. In Figure 10, the comparison between the real value and the single-step prediction value of vehicle velocity segment is given. It can be seen in the figure that the error falls into (−2.5, 2.5) km/h and has good prediction results, based on which the length of the step is increased further. The RMSE results within different prediction horizon are shown in Table 3. Along with the increase in estimation time of vehicle velocity, the prediction error is in the increasing trend. And in order to verify the effect of introducing driving intention data as NAR input, the RMSE results of the NAR prediction model with the same parameters which only use the past speed data are also shown in Table 3. As can be seen, the RMSE results of prediction model without using driving intention data is higher, which reflects that the introduction of driving intention recognition results as NAR input can improve the prediction accuracy.
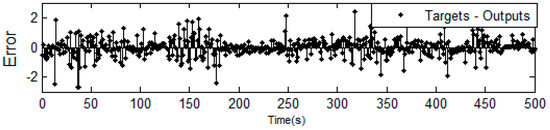
Figure 10.
Error of single-step prediction.

Table 3.
Prediction results comparison of NAR neural network at different prediction horizon.
4. Mixed Logic Dynamical Model Predictive Control Strategy
4.1. Modeling of Mixed Logic Dynamical Predictive Control Strategy
The short-term future vehicle speed in each receding horizon can be obtained through the proposed speed prediction method in Section 3. Then the predicted vehicle speed is used to calculate the vehicle required torque at each moment within the receding horizon. The proposed MLD-MPC control strategy aims to distribute the vehicle required torque between motor and engine reasonably at each moment within the prediction horizon to achieve optimal fuel economic. Thus MLD model is established to tackle this optimization problem with the objective function of equivalent fuel consumption, the control variable of motor torque u(k) and the state variable of SOC x(k). The optimal control variable sequence are obtained by minimizing the total equivalent fuel consumption in the receding horizon through MLD model and only the first control variable need to be applied in the controlled PHEV model at the present moment. The MLD-MPC receding horizon control procedure is described as follows:
- (1)
- at time k, predict the short-term future speed profile for the current control horizon (k–k + N, where N is the receding horizon) and calculate the corresponding required torque through Equations (1) and (2);
- (2)
- the MLD model calculates the optimal control policy (u(k)–u(k + N)) for the current prediction horizon (k–k + N);
- (3)
- apply the first time-step of the optimal control policy u(k) in the controlled PHEV model;
- (4)
- update the state variable and system constraints, repeat the computation procedure 1–3 at the next time instant (time k + 1).
MLD model is suitable for solving problems combining binary variables and continuous variables. In [28], a constrained optimal problem is formulated and solved based on MPC using the simplified MLD model for DC-DC boost converter. Similarly, in our PHEV energy management control strategy, based on the simplified powertrain model in Section 2, the state transition equation and evaluation equation of MLD model can be described in Equation (10):
where,
The inequality constraint of the six operation modes for PHEV presented in Table 4 includes electric power mode, fuel consumption mode, mixed driven mode, drive charging mode, regenerate braking mode and stopping mode. The constraint describes the relationship of motor torque u and the vehicle required torque in each operation mode. In Table 4, and are the maximum motor torque and vehicle required torque respectively; and are the maximum engine torque and motor torque respectively; is the maximum regenerative braking torque; ; is the machine accuracy, = 0.0001; is the required torque, which can be can be calculated from Equations (1) and (2); is the logic variable representing the operation mode of the vehicle (if , it means that the vehicle is running under the operation mode i); Consider the inequality constraints above into time sequence k and transfer them into the unified matrix inequality as follows, where E1, E2, E3 and E4 are all the coefficients in the form of Matrix converted from Table 4.

Table 4.
Constraints during various operation mode for PHEV.
Applying receding horizon optimization based predictive control theory to the MLD model, and the optimal model is set-up as given in Equations (13) and (14), where the optimization metric is the sum of equivalent fuel consumption in the receding horizon at time k, the state transition and evaluation equality constraint are from Equation (10), the inequality constraints are taken from Equation (12):
s.t.
within it, B1, B2, D1, D2 is the same as Equation (10), and E1, E2, E3, E4, is defined as follows:
In the equation, N is the prediction horizon, k is the specific second in the prediction horizon, and are the upper and lower limit of SOC accessible domains respectively at time k. Considering the values of matrices B1, B2, D1, D2, E1, E2, E3 and E4 at every sampling time k and according to the objective function of minimal equivalent fuel consumption, Equations (13) and (14) can be converted into a MILP problem.
4.2. Solution of Mixed Integer Linear Programming
The MILP problem can be modeled using YALMIP toolbox in the Matlab platform and solved using the Gurobi optimizer. The optimal control variable sequence (u(k)–u(k + N)) in the prediction horizon (k–k + N) can be calculated at time k, and the first value of the optimal control variable sequence u(k) is applied to the controlled object. Then utilizing the receding horizon optimization method, the former solving steps are repeated to get a new control value at time k + 1 to realize the PHEV MPC. In the process of updating the model state variable, SOC, the original nonlinear model as shown in Equation (6) is used instead of the simplified linear equality constraint model in MILP to obtain a better estimate of the true SOC value at the end of the control time domain. The obtained value is considered as the initial state value to the next receding horizon optimization, so as to realize the feedback correction in predictive control.
Heuristic rules for some special driving conditions are set to reduce the range of feasible solution of MILP and improve the real-time performance of the control strategy. The introduced heuristic rules are presented in Table 5. While the condition in the first column is satisfied, the corresponding operation mode and motor torque can be decided respectively. Total required torque can be used as a measure to judge whether the car is braking or stopping. Based on the value of total required torque, whether it is less than or equal to zero, the vehicle can choose regenerate braking mode or stop mode directly, and the corresponding control variable value can be determined directly. When the vehicle is in urgent acceleration or at high speed, and the total inquired torque is larger than the maximum engine torque at that speed, the vehicle can choose mixed driven mode directly. Otherwise, the control strategy can switch among four modes, i.e., electric power mode, fuel consumption mode, mixed driven mode, drive charging mode. The control variable value in electric power mode and fuel consumption mode can be directly obtained. The control variable in the mixed driven mode and drive charging mode can be selected through the optimization of the objective function. These heuristic rules can significantly reduce the search space of MILP and thus improve the efficiency of the algorithm.

Table 5.
Heuristic rules.
When SOC approaches to the lower limit, once the required torque is larger than the maximum torque of the engine and the objective function in MLD-MPC is not modified, the motor needs to output the power which would make the SOC of the battery to exceed the lower limit. This violates the constraints defined in MILP problem and cannot find a feasible solution. Thus, when SOC is around the lower limit, the heuristic rule is applied to solve the control problem. First, estimate the highest SOC at each step in the prediction horizon under the assumption that the engine outputs its maximum torque. If the estimated highest SOC is higher than the lower limit of SOC, the current SOC constraints are imposed in MILP, otherwise the corresponding SOC constraints will be removed. When the current SOC is lower than the lower limit of SOC, the algorithm will stop solving the MILP problem and change to the heuristic solver mode. In this mode, the maximum charging torque (or the minimum discharging torque) of the motor is calculated directly while the engine is set to output its maximum torque. After the SOC rises to a certain value higher than the lower limit of SOC, the MILP solver will be restarted.
5. Simulation Experiments and Analysis
5.1. Simulation Experiments
Parameters of the PHEV are given in Table 6. The diesel engine displacement is 7.3 L with a rated power of 177 kW, and maximum engine speed is 2300 r/min.

Table 6.
Parameters of the PHEV.
The type of motor is AC induction motor, with rated power of 124 kW, and maximum motor speed of 10,000 r/min. The type of battery used is a lithium battery with a rated capacity of 90 . Mm is 272 N·m, and Min is 1170 N·m. Fitting coefficients of engine and motor are listed in the Appendix A. ADVISOR (Advanced Vehicle Simulator, 2002, National Renewable Energy Laboratory, Golden, CO, USA) is used to simulate the UKBUS driving cycle as shown in Figure 11, with an initial SOC value of 0.7 (), prediction horizon N of 15 s and sampling period of 1 s (the effect of predict time domain is discussed in Section 5.2). The simulation results are presented in Figure 12. Figure 12a is the comparison of the SOC curves between the MLD-MPC control strategy proposed in this paper and Charge Depleting-Charge Sustaining (CD-CS) control strategy. As can be observed, the CD-CS strategy consumes the battery energy within 8000 s, and then sustains SOC around 0.3 for the remainder of the trip. In the MLD-MPC control strategy, the battery energy is completely consumed by the end of the trip. Compared to CD-CS control strategy, the proposed MLD-MPC strategy can make more reasonable use of battery energy. Figure 12b is the comparison of the fuel consumption between the MLD-MPC control strategy presented in this paper and CD-CS control strategy. As seen in the picture, the CD-CS control strategy makes full use of battery energy and does not consume fuel within the first 8000 s, then the fuel consumption grow rapidly during the Charge-Sustaining mode, while the MLD-MPC control strategy maintains a relatively slow fuel consumption rate. Up to the end of the whole driving cycle, the fuel consumption is 12.93 L, and the end value of SOC is 0.3043 for the MLD-MPC control strategy, while the fuel consumption is 15.39 L, and the end value of SOC is 0.3125 for the CD-CS control strategy. It can be concluded from this results that under the same driving cycle conditions, the MLD-MPC control strategy reduces the fuel consumption of a PHEV. Figure 13 shows the comparison of engine operation points of these two control strategies. As can be observed, the engine operation points of the CD-CS control strategy spread out on a much larger area, and a lot of operation points in the low efficiency area. While the engine operation points of MLD-MPC control strategy is relatively centralized and most of them are in the high efficiency area which will improve fuel economic.
Figure 11.
Vehicle speed curve.
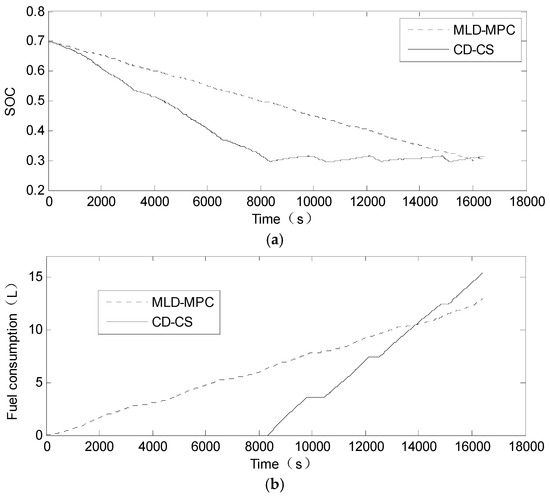
Figure 12.
(a) comparison of SOC curves of two strategies; and (b) comparison of the fuel consumption of two strategies.
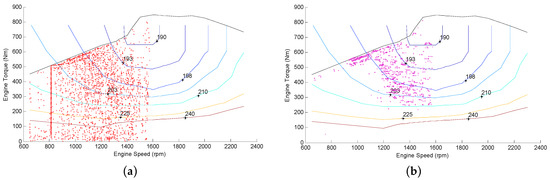
Figure 13.
(a) Engine operation points of charge depleting-charge sustaining (CD-CS) strategy; and (b) engine operation points of mixed logic dynamical-model predictive control (MLD-MPC) Strategy.
Besides the simulation of UKBUS driving cycle, driving cycles of Orange County Bus Cycle (OCC) and New European Drive Cycle (NEDC) are simulated as well. The results can be seen in Table 7, which shows that the fuel economy of PHEV under these driving cycles is improved to a noticeable extent.

Table 7.
Fuel consumption under two control strategies. NEDC: New European Drive Cycle; OCC: Orange County Bus Cycle.
5.2. Influence of Prediction Horizon for Mixed Logic Dynamical-Model Predictive Control (MLD-MPC) Strategy
Two key steps are included in the MLD-MPC control strategy proposed in this paper, which are NAR neural network based vehicle speed prediction and minimal fuel consumption objective function-based MLD model prediction control. With an increase in prediction horizon, the accuracy of prediction results will decrease compared to the actual speed and thus affect the accuracy of the MPC solution and increase the fuel consumption. The MPC uses the online receding horizon optimization within the limited horizon, and when the optimal horizon increases, the optimization performance index also increases which leads to better results. Therefore, it is important to find out the proper prediction horizon for the optimal fuel consumption simulation.
Here, NEDC is used to study the effect of prediction horizon length on target equivalent fuel consumption. And the same NAR neural network training method as for UKBUS is utilized for NEDC. With a total of 1190 samples of vehicle speed-intention data, the first 900 samples are chosen as training samples, and the remaining 290 samples which didn’t participate in the training are used to test the network’s predictive ability. When the value of SOC does not drop to the lower limit value, the constraints of state variable SOC are not activated. The optimal control variable can be solved independently, and the function of prediction horizon cannot be reflected, as the state association of each second is not restricted by constraints within the prediction horizon. The function of prediction horizon is realized only when the value of SOC is going to cross the lower limit. Therefore, initial SOC value of 0.7 is selected and the lower limit of SOC is set to 0.67 to simulate the condition that SOC is going to reach the lower limit. In this phase, heuristic solver mode will be activated to recharge the batteries up to 0.68 when SOC falls below 0.67 and then MILP solver mode will be selected.
Figure 14 shows the battery SOC curve under different prediction horizons, and the corresponding time to reach the lower limit of SOC value is shown in Table 8. It can be seen that the time to reach the lower limit of SOC is extended as the prediction horizon increases. That is to say, in the process of optimization with MILP, it can predict in advance that SOC is about to reach the lower limit so the strategy can choose to save electricity in advance and improve the fuel efficiency. Figure 15 shows the equivalent fuel consumption per hundred kilometers corresponding to the different prediction horizons.
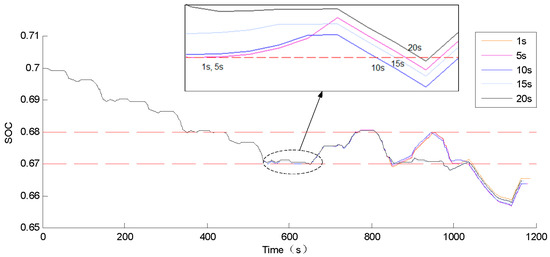
Figure 14.
Battery SOC curve under different prediction horizons.

Table 8.
SOC bottoming time under different prediction horizons.
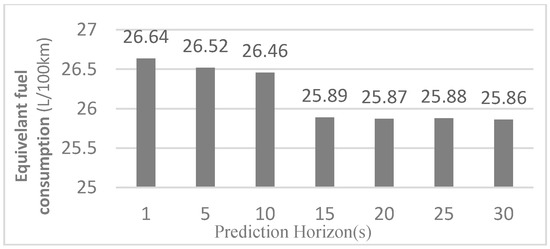
Figure 15.
Equivalent fuel consumption under different prediction horizons.
The change of RMSE of the predicted speed with different prediction horizons is shown in Figure 16. Compared to Figure 15, with an increase in prediction horizon, the equivalent fuel deceases continuously until the prediction horizon reaches 15 s, while the equivalent fuel consumption deceased only a little when the prediction horizon is increased from 15 s to 30 s. However, RMSE of the predicted speed is significant increased when the prediction horizon is increased from 15 s to 30 s. Therefore, a prediction horizon of 15 s is chosen in this paper.
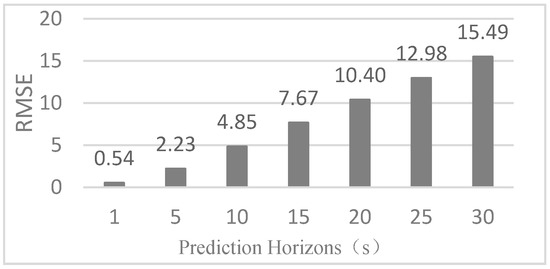
Figure 16.
Root mean square error (RMSE) under different prediction horizons.
6. Conclusions
A MPC strategy for PHEV based on a MLD model and vehicle speed prediction was proposed in this paper. Firstly, to convert the PHEV control problem into a linear programming problem, the energy consumption model of engine and motor were both linearized. After that, focusing on a city bus which usually has determined routes and known velocity profiles, a vehicle speed prediction method using a NAR neural network based on the combination of driving intention and historical speed data was proposed, in which the driving intention is recognized by using fuzzy inference to analyze the driver’s pedal operation. Then, a vehicle MLD model is established with constraints in six possible driving modes and an objective function of minimum equivalent fuel consumption. With the predicted vehicle speed, a MPC method was utilized and the energy management problem was converted to a MILP problem, and the optimal motor torque and the corresponding driving mode sequence within the speed prediction horizon can be solved. The simulation was carried out under three driving cycles, and the effect of prediction horizon on the result of the simulation is analyzed, the simulation results verified the feasibility and effectiveness of the vehicle speed prediction based MLD-MPC strategy.
Acknowledgments
This project is supported by the National Natural Science Foundation of China (Grant Nos. 61473057, 61203171) and the China Fundamental Research Funds for the Central Universities (Grant No. DUT15LK13).
Author Contributions
All authors contributed to the paper, Jing Lian is the main author of this work, Shuang Liu and Linhui Li designed the experiments; Xuanzuo Liu and Fan Yang performed the experiments; Yafu Zhou and Lushan Yuan analyzed the data; Jing Lian wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Engine speed index:
FC_V = [650 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100 2200 2300]
Engine fitting coefficients:
- a1 = [0.0037, 0.0045, 0.0050, 0.0055, 0.0060, 0.0065, 0.0069, 0.0073, 0.0078, 0.0083, 0.0088, 0.0094, 0.0100, 0.0107, 0.0113, 0.0122, 0.0130];
- a0 = [0.1021, 0.1232, 0.1372, 0.1513, 0.1654, 0.1795, 0.2258, 0.2771, 0.3053, 0.3347, 0.3685, 0.4039, 0.4412, 0.4800, 0.5453, 0.5856, 0.6275]
Motor speed index:
| M_V = | [1000 2000 3000 4000 5000 6000 7000 8000 9000 10000]; |
| [–1000 –2000 –3000 –4000 –5000 –6000 –7000 –8000 –9000 –10000] |
Battery SOC change fitting coefficients:
| b1 | = | 1.0 × 10−5 × [−0.0406, −0.0751, −0.1120, −0.1591, −0.2056, −0.2582, −0.2989, −0.3413, −0.3779, −0.4234]; |
| 1.0 × 10−5 × [−0.0246, −0.0535, −0.0805, −0.1002, −0.1222, −0.1396, −0.1626, −0.1862, −0.2117, −0.2355]; | ||
| b0 | = | 1.0 × 10−4 × [0.0046, 0.0002, 0.0132, 0.0604, 0.0824, 0.1037, 0.0777, 0.0600, 0.0435, 0.0343]; |
| 1.0 × 10−4 × [0.0074, 0.0047, 0.0255, 0.0857, 0.1048, 0.1310, 0.1194, 0.1005, 0.0888, 0.0668] |
References
- Benveniste, A.; Bourke, T.; Caillaud, B.; Pouzet, M. Non-standard semantics of hybrid systems modelers. J. Comput. Syst. Sci. 2012, 78, 877–910. [Google Scholar] [CrossRef]
- Matos, R.; Araujo, J.; Oliveira, D.; Maciel, P.; Trivedi, K. Sensitivity analysis of a hierarchical model of mobile cloud computing. Simul. Model. Pract. Theory 2015, 50, 151–164. [Google Scholar] [CrossRef]
- Little, S.; Seegmiller, N.; Walter, D.; Myers, C. Verification of analog/mixed-signal circuits using labeled hybrid petri nets. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2011, 30, 617–630. [Google Scholar] [CrossRef]
- Branicky, M.S.; Borkar, V.S.; Mitter, S.K. A unified framework for hybrid control: Model and optimal control theory. IEEE Trans. Autom. Control 1998, 43, 31–45. [Google Scholar] [CrossRef]
- Kruglikov, B.; Rypdal, M. A piece-wise affine contracting map with positive entropy. Discret. Contin. Dyn. Syst. 2005, 16, 393–394. [Google Scholar]
- Bemporad, A.; Morari, M. Control of systems integrating logic, dynamics, and constraints. Automatica 1999, 35, 407–427. [Google Scholar] [CrossRef]
- Rueda-Medina, A.C.; Franco, J.F.; Rider, M.J.; Padilha-Feltrin, A.; Romero, R. A mixed-integer linear programming approach for optimal type, size and allocation of distributed generation in radial distribution systems. Electr. Power Syst. Res. 2013, 97, 133–143. [Google Scholar] [CrossRef]
- Wirasingha, S.G.; Emadi, A. Classification and review of control strategies for plug-in hybrid electric vehicles. IEEE Trans. Veh. Technol. 2011, 60, 111–122. [Google Scholar] [CrossRef]
- Padmarajan, B.; Mcgordon, A.; Jennings, P. Blended rule based energy management for PHEV: System structure and strategy. IEEE Trans. Veh. Technol. 2016, 65, 8757–8762. [Google Scholar] [CrossRef]
- Wu, L.; Wang, Y.; Yuan, X.; Chen, Z. Multiobjective optimization of HEV fuel economy and emissions using the self-adaptive differential evolution algorithm. IEEE Trans. Veh. Technol. 2011, 60, 2458–2470. [Google Scholar] [CrossRef]
- Tianheng, F.; Lin, Y.; Qing, G.; Yanqing, H.; Ting, Y.; Bin, Y. A supervisory control strategy for plug-in hybrid electric vehicles based on energy demand prediction and route preview. IEEE Trans. Veh. Technol. 2014, 64, 1691–1700. [Google Scholar] [CrossRef]
- Wang, X.; He, H.; Sun, F.; Zhang, J. Application study on the dynamic programming algorithm for energy management of plug-in hybrid electric vehicles. Energies 2015, 8, 3225–3244. [Google Scholar] [CrossRef]
- Salman, M.; Chang, M.F.; Chen, J.S. Predictive energy management strategies for hybrid vehicles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Chicago, IL, USA, 7–9 September 2005; pp. 21–25.
- Ngoduy, D. Application of gas-kinetic theory to modelling mixed traffic of manual and ACC vehicles. Transportmetrica 2012, 8, 43–60. [Google Scholar] [CrossRef]
- Hodgson, D.; Mecrow, B.C.; Gadoue, S.M.; Slater, H.J. Effect of vehicle mass changes on the accuracy of Kalman filter estimation of electric vehicle speed. IET Electr. Syst. Transp. 2013, 3, 67–78. [Google Scholar] [CrossRef]
- Wu, J.; Cui, Z.-M.; Zhao, P.-P.; Chen, J.-M. Traffic vehicle behavior prediction using hidden markov models. In Proceedings of International Conference on Artificial Intelligence and Computational Intelligence, Chengdu, China, 26–28 October 2012; pp. 383–390.
- Chan, K.Y.; Dillon, T.S.; Singh, J.; Chang, E. Neural-network-based models for short-term traffic flow forecasting using a hybrid exponential smoothing and Levenberg-Marquardt algorithm. IEEE Trans. Intell. Transp. Syst. 2012, 13, 644–654. [Google Scholar] [CrossRef]
- Benmouiza, K.; Cheknane, A. Forecasting hourly global solar radiation using hybrid k-means and nonlinear autoregressive neural network models. Energy Convers. Manag. 2013, 75, 561–569. [Google Scholar] [CrossRef]
- Ozcelik, R.; Diamantopoulou, M.J.; Crecente-Campo, F.; Eler, U. Estimating Crimean juniper tree height using nonlinear regression and artificial neural network models. Forest Ecol. Manag. 2013, 306, 52–60. [Google Scholar] [CrossRef]
- Park, J.; Li, D.; Murphey, Y.L.; Kristinsson, J. Real time vehicle speed prediction using a neural network traffic model. IJCNN 2011, 42, 2991–2996. [Google Scholar]
- Yang, J.Y.; Chou, L.D.; Tung, C.F.; Huang, S.M.; Wang, T.W. Average-speed forecast and adjustment via VANETs. IEEE Trans. Veh. Technol. 2013, 62, 4318–4327. [Google Scholar] [CrossRef]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transp. Res. Part C Emerg. Technol. 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Zou, Y.; Liu, T.; Sun, F.; Peng, H. Comparative study of dynamic programming and Pontryagin’s minimum principle on energy management for a parallel hybrid electric vehicle. Energies 2013, 6, 2305–2318. [Google Scholar]
- Zhang, C.; Vahidi, A. Route preview in energy management of plug-in hybrid vehicles. IEEE Trans. Control Syst. Technol. 2012, 20, 546–553. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Z. Dynamic Analysis and multivariable transient control of the power-split hybrid powertrain. IEEE/ASME Trans. Mechatron. 2015, 20, 3085–3097. [Google Scholar] [CrossRef]
- Beck, R.; Bollig, A.; Abel, D. Comparison of two real-time predictive strategies for the optimal energy management of a hybrid electric vehicle. Oil Gas Sci. Technol.-Rev. IFP 2007, 62, 635–643. [Google Scholar] [CrossRef]
- Son, H.; Kim, H. Development of near optimal rule-based control for plug-in hybrid electric vehicles taking into account drivetrain component losses. Energies 2016, 9, 420. [Google Scholar] [CrossRef]
- Ren, H.P.; Zheng, M.M.; Li, J. A simplified mixed logical dynamic model and model predictive control of boost converter with current reference compensator. In Proceedings of the 2015 IEEE 24th International Symposium on Industrial Electronics (ISIE), Rio de Janeiro, Brazil, 3–5 June 2015; pp. 61–65.
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).