Investigation of the Magnetic Circuit and Performance of Less-Rare-Earth Interior Permanent-Magnet Synchronous Machines Used for Electric Vehicles
Abstract
:1. Introduction
2. No-Load Magnetic Circuit Analysis
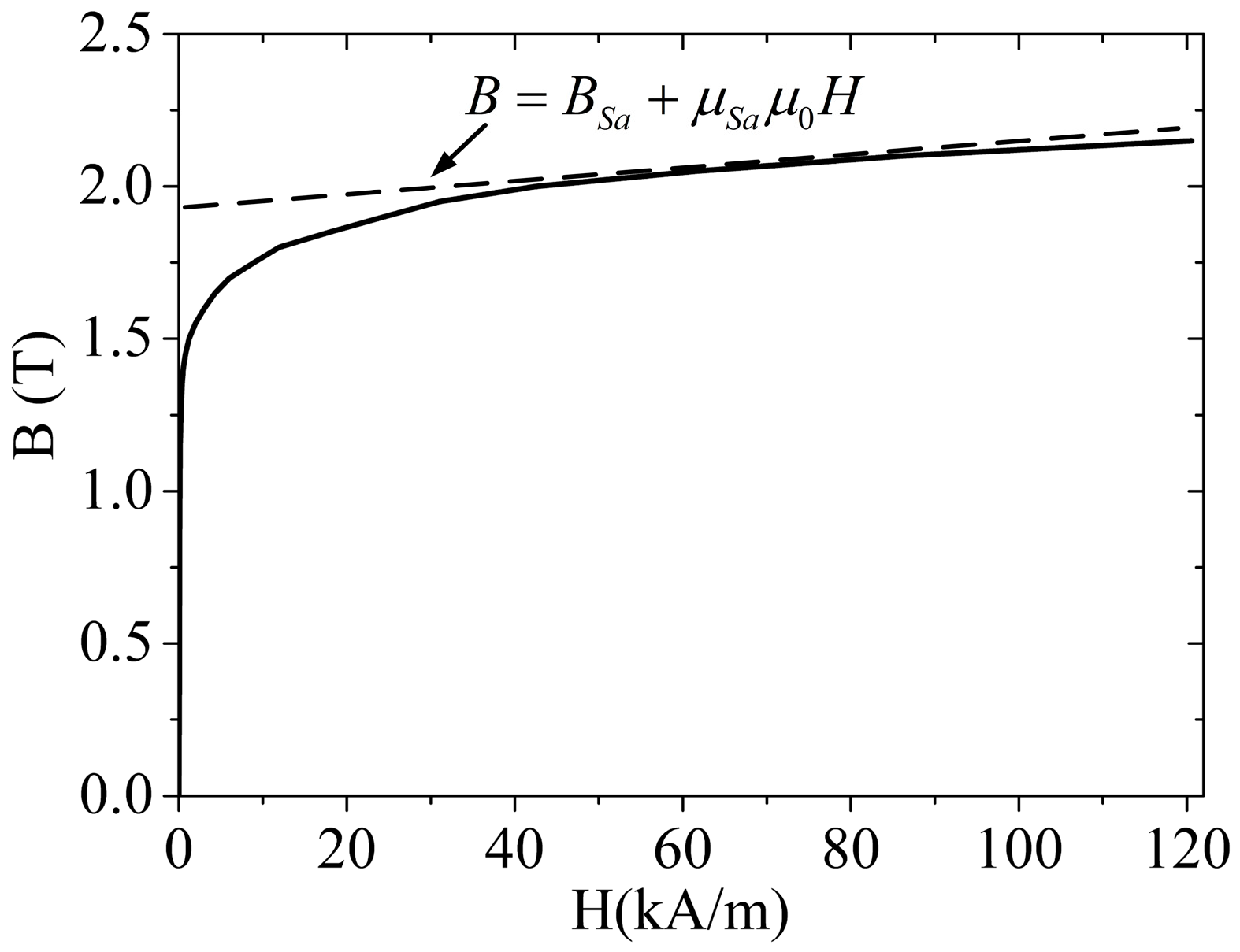
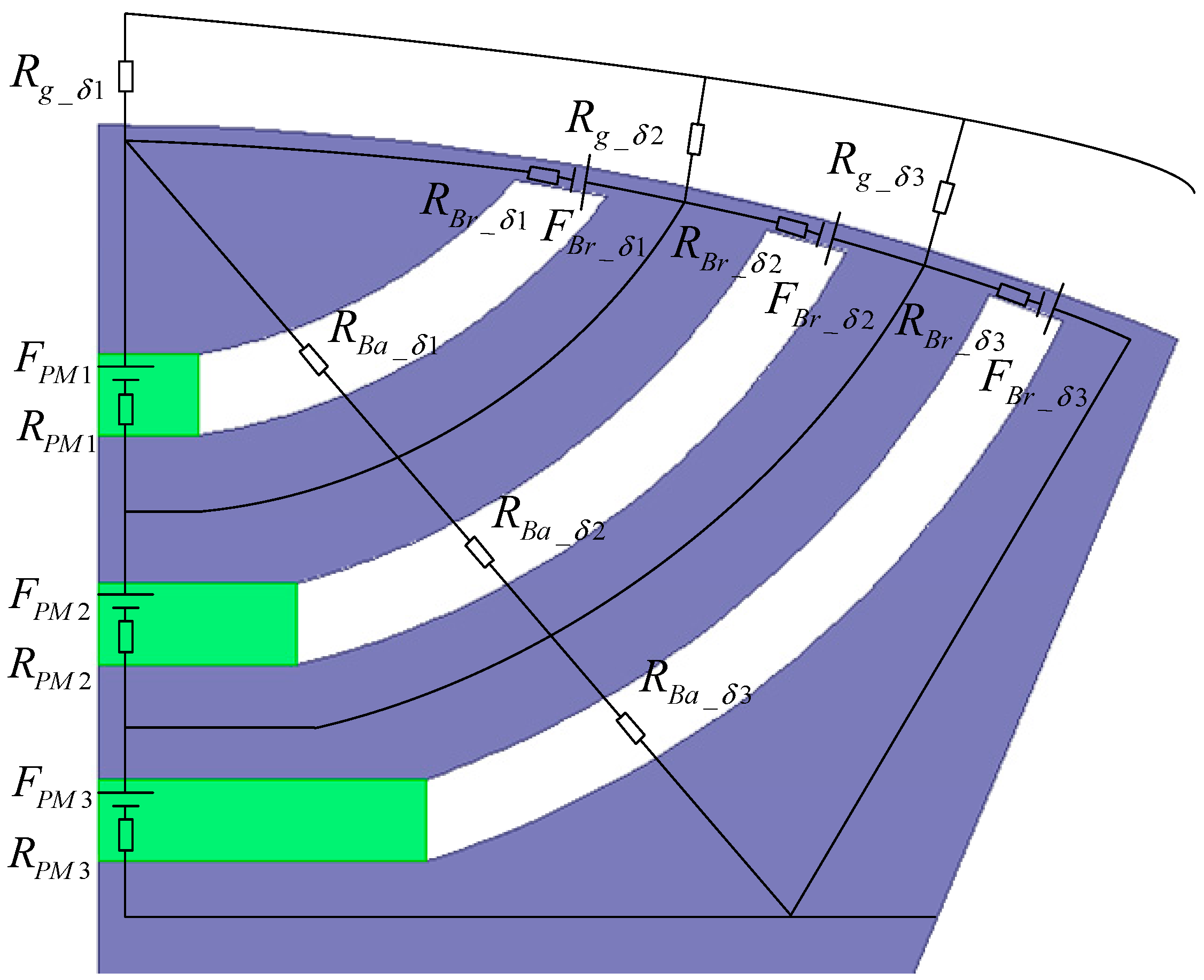
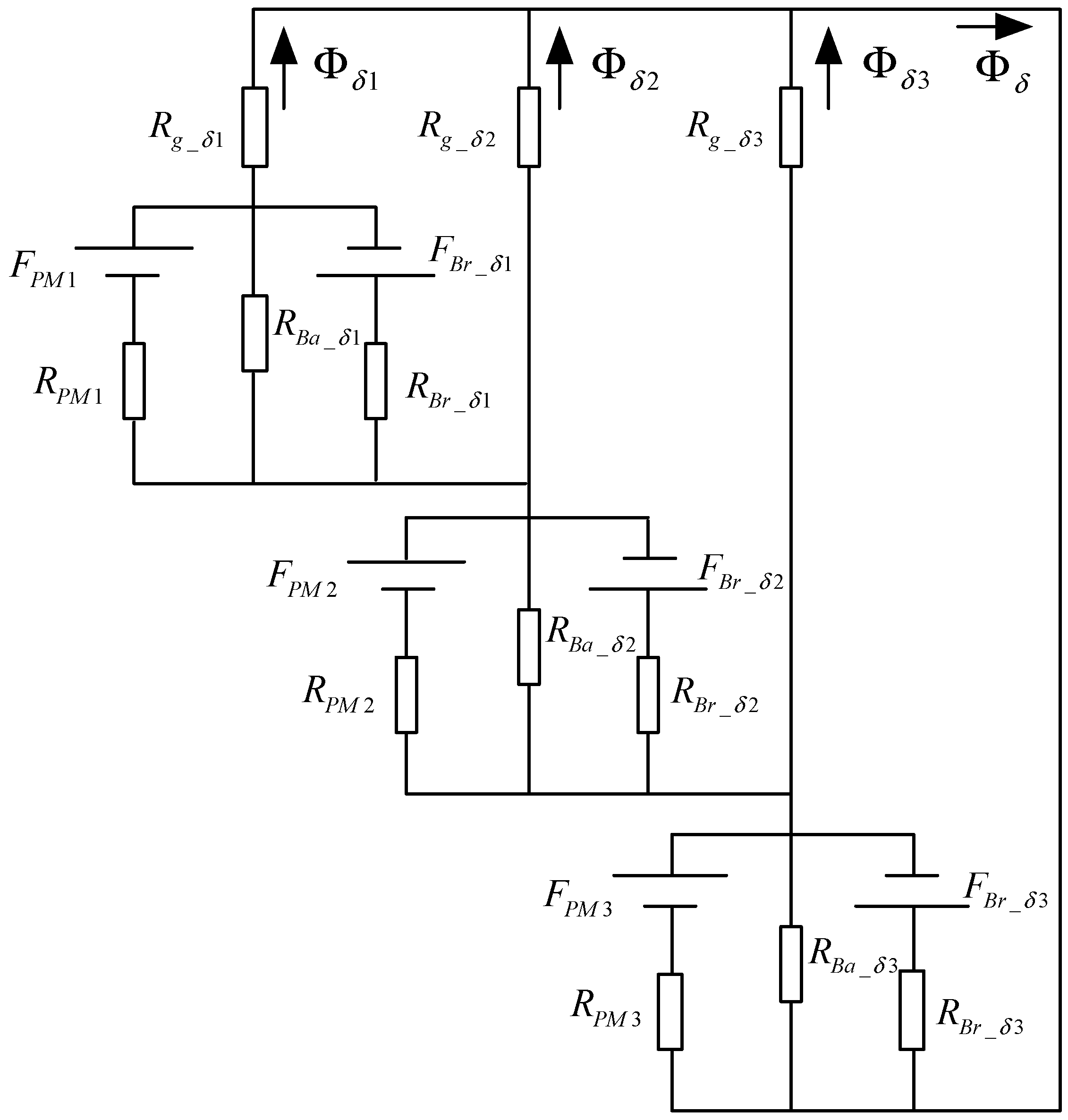
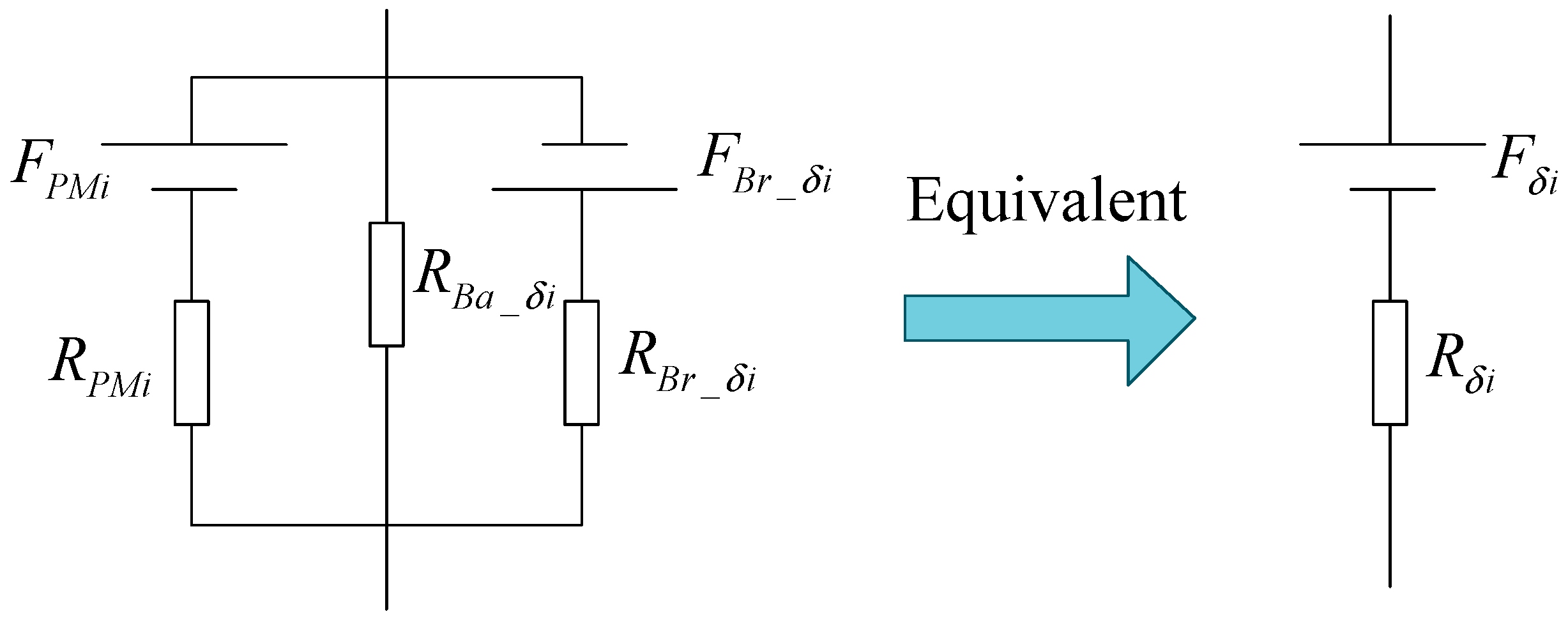
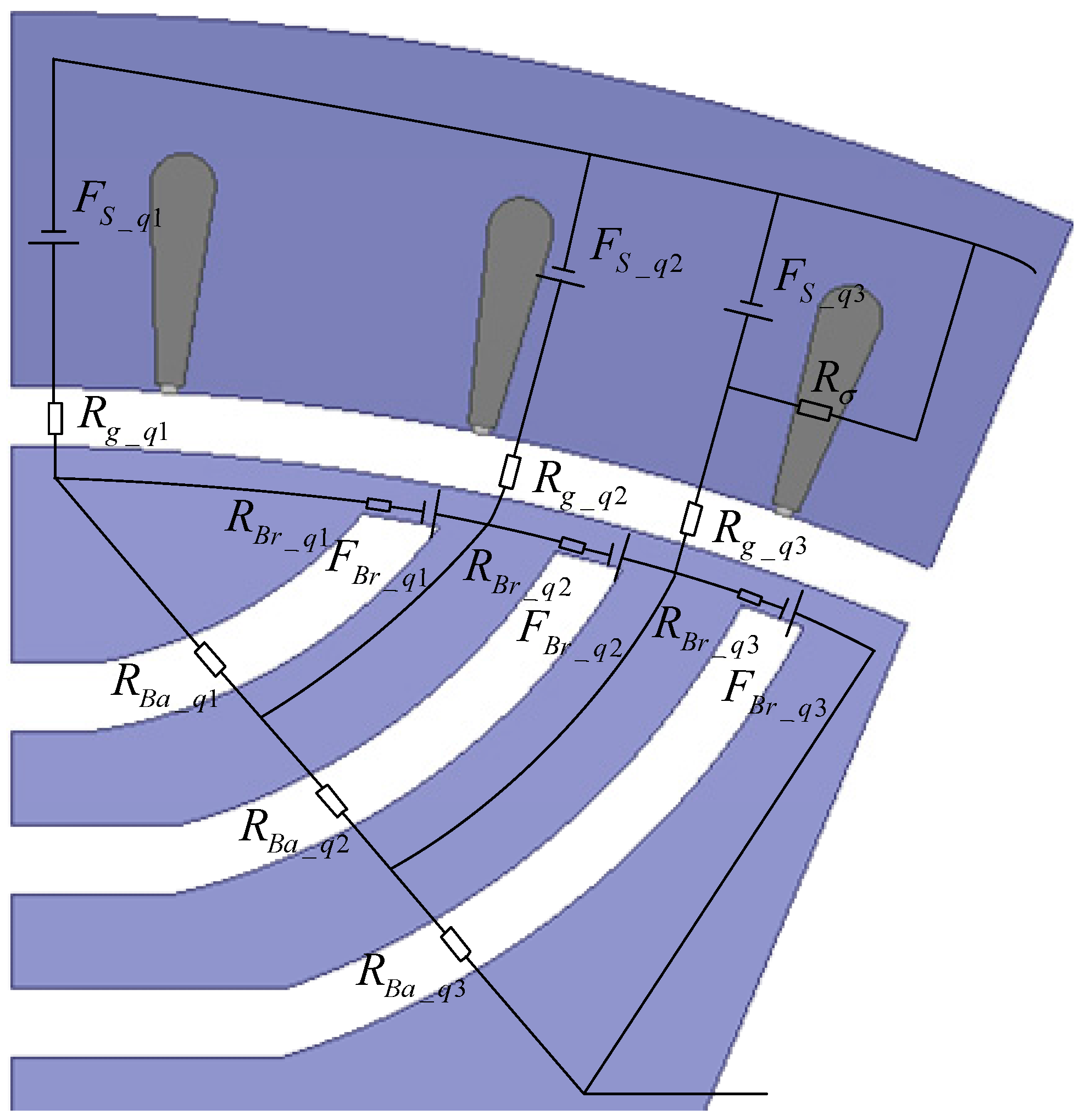
2.1. No-Load Magnetic Circuit Model
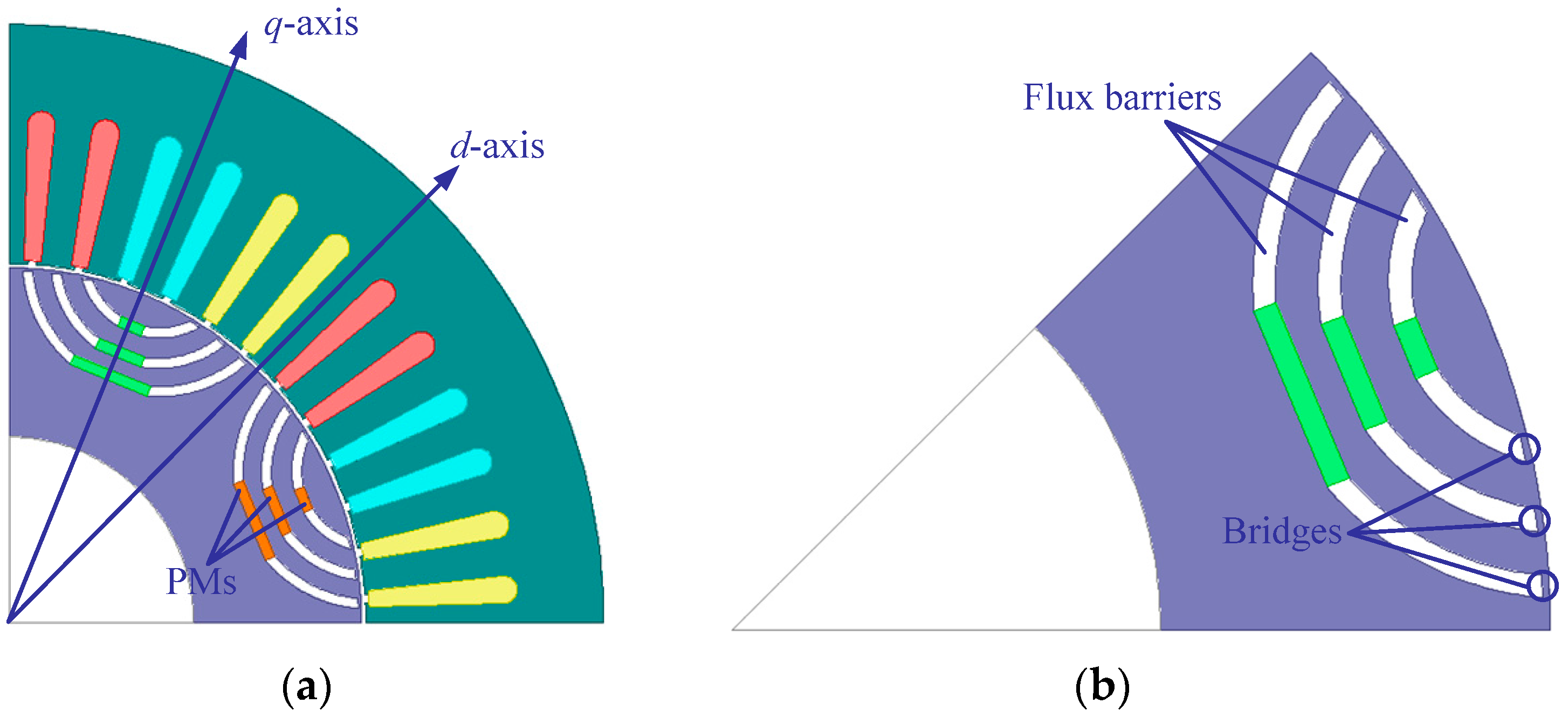
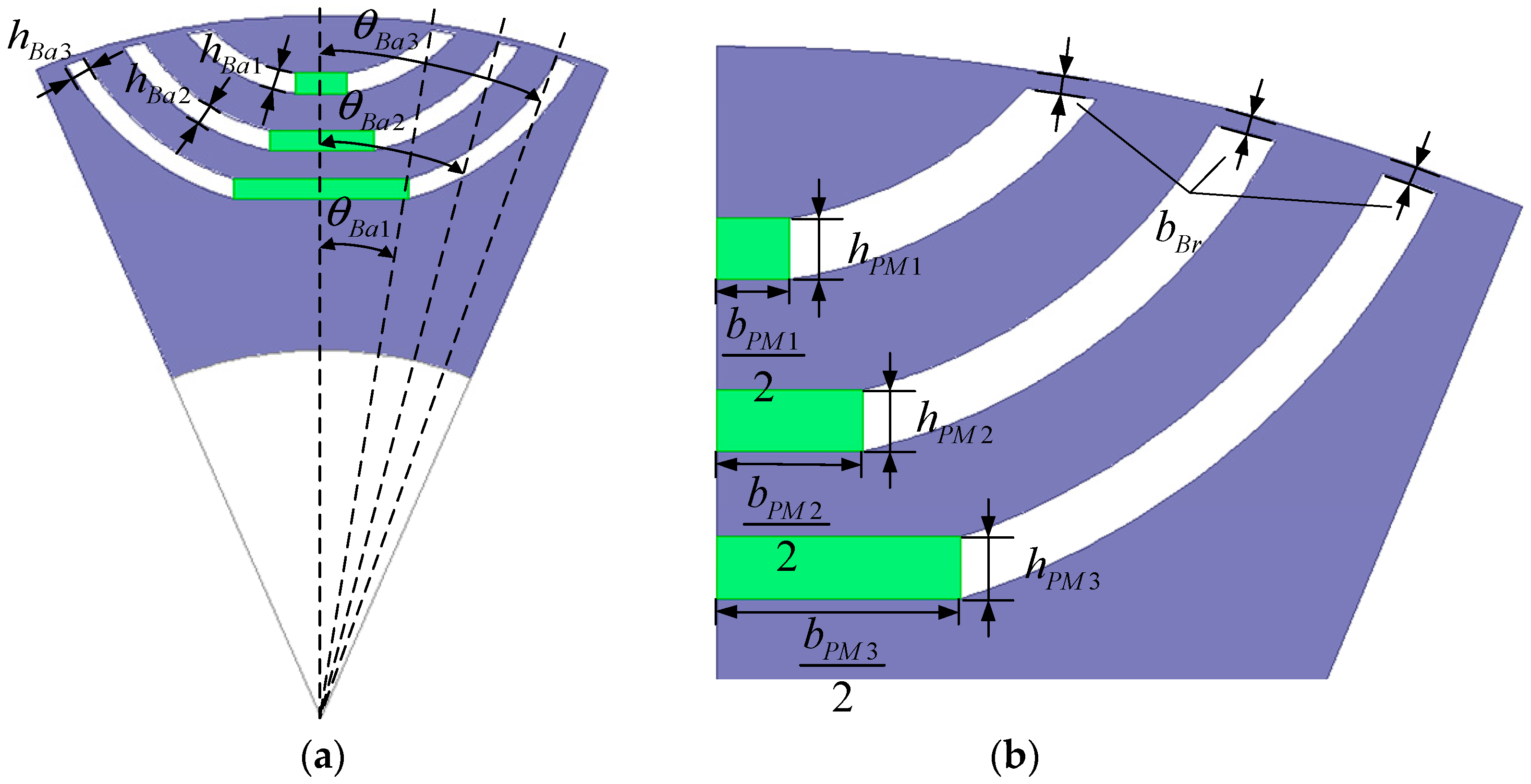
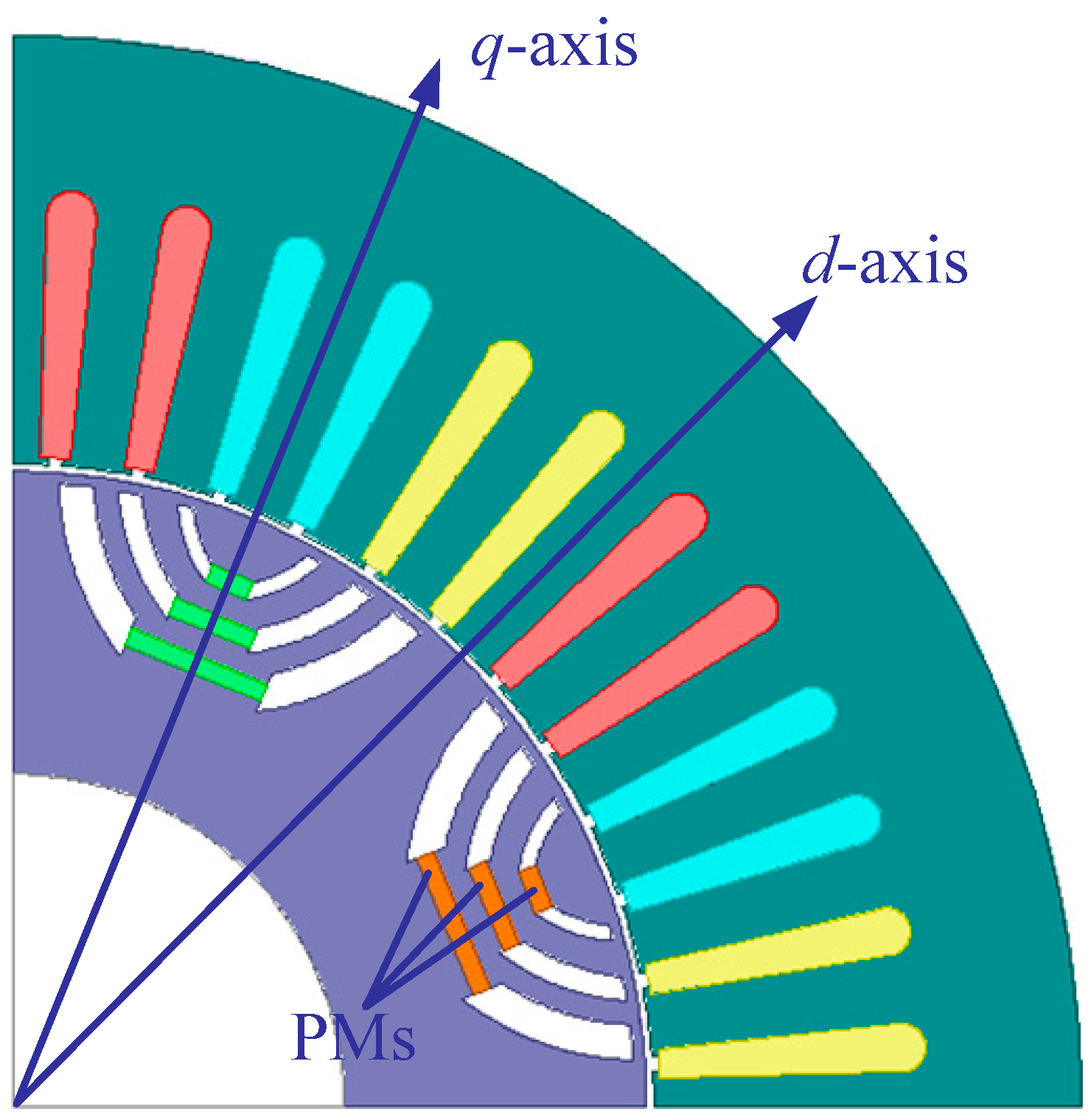
2.2. Geometric Parameters of the LRE-IPMSM
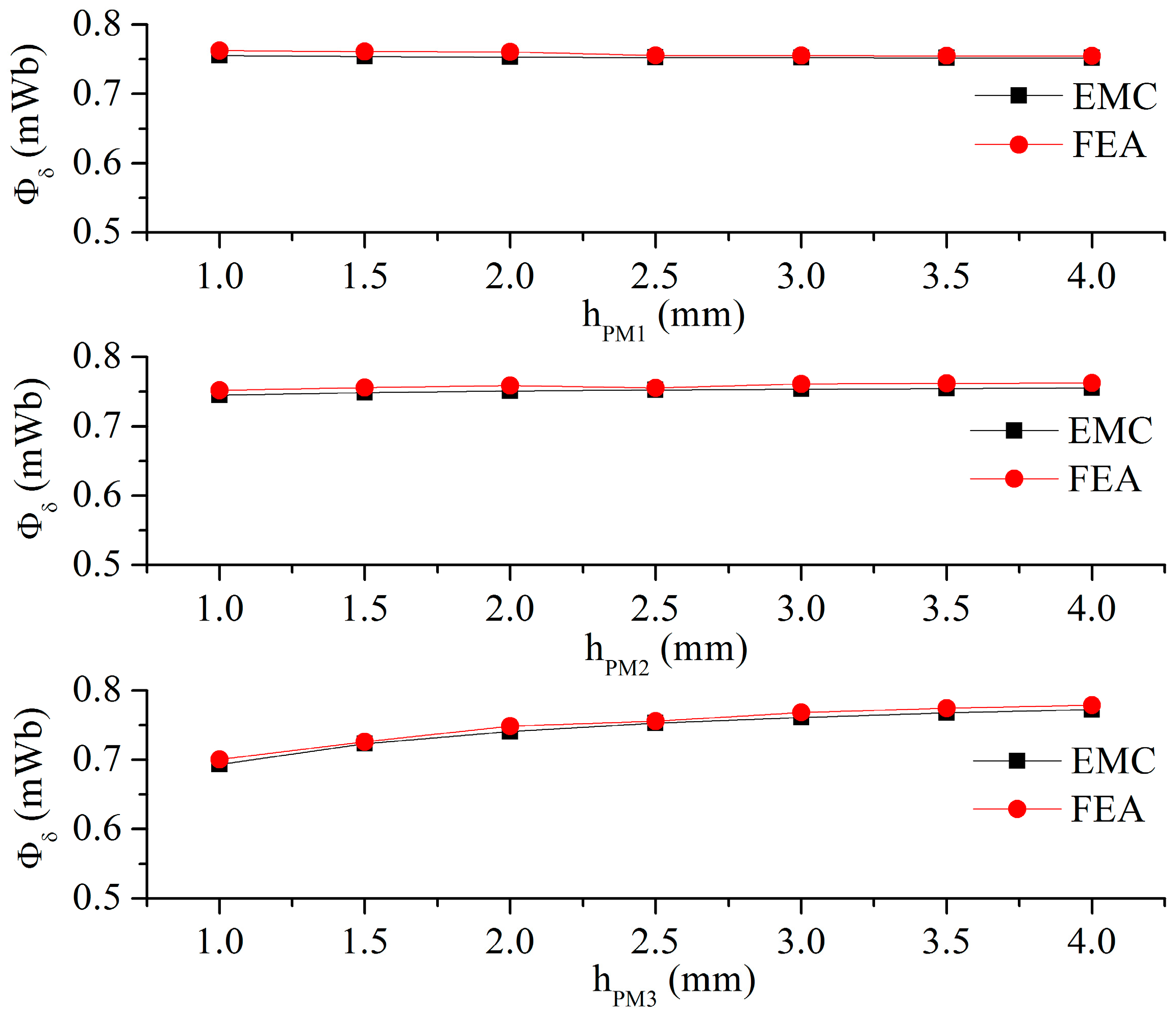
2.3. Effect of PM Thickness on No-Load Flux
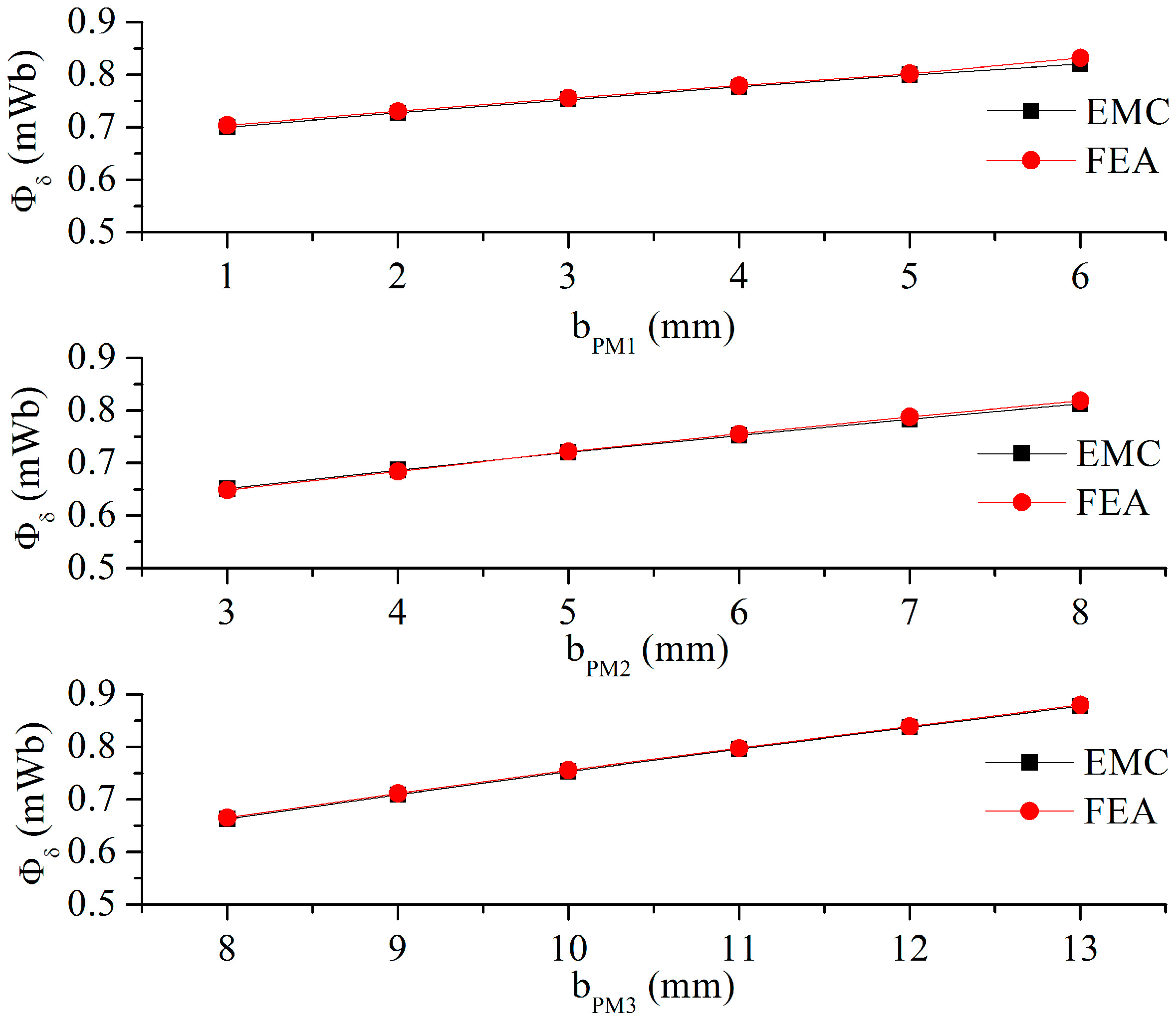
2.4. Effect of PM Width on No-Load Flux
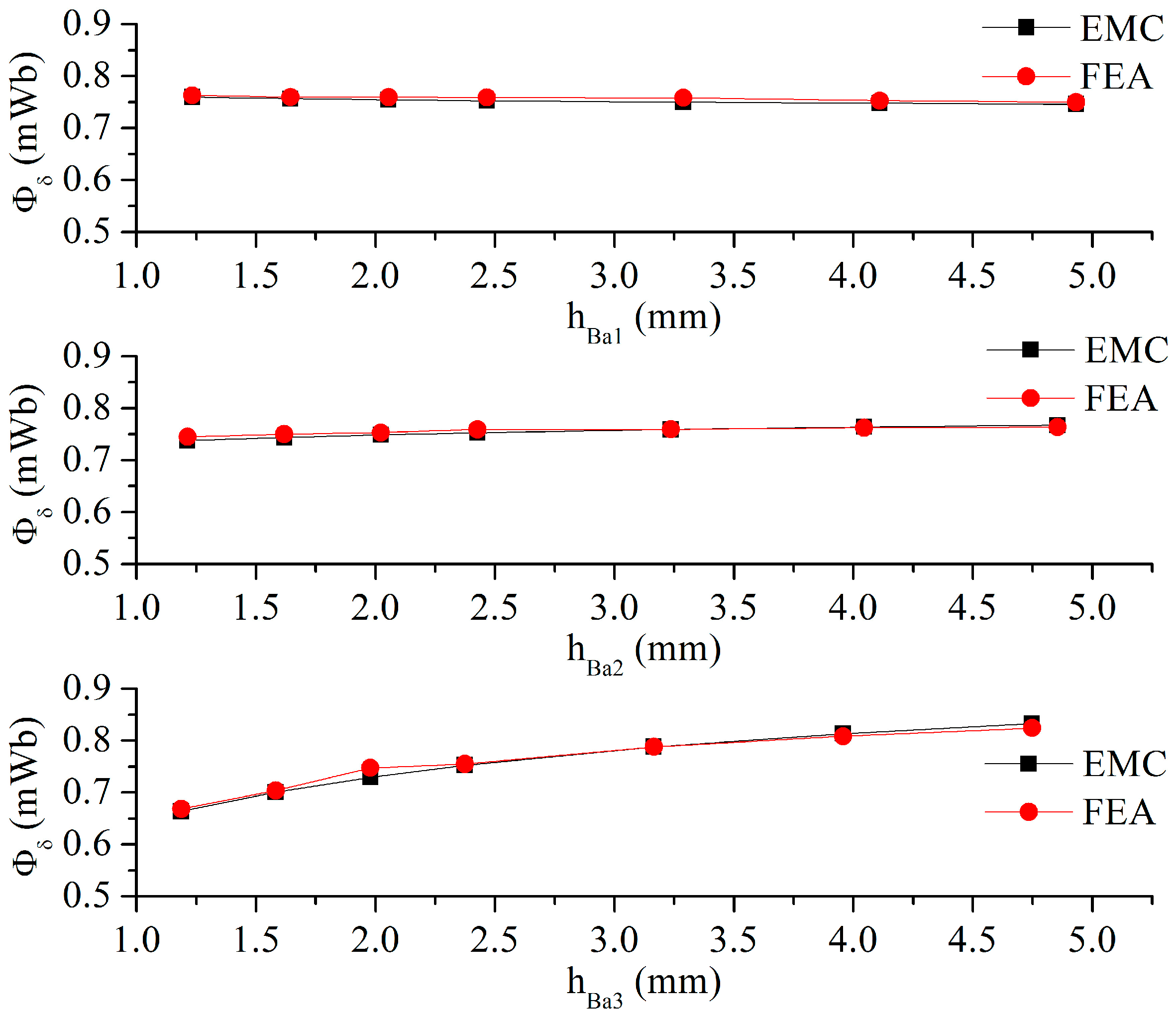
2.5. Effect of Flux Barrier Thickness on No-Load Flux
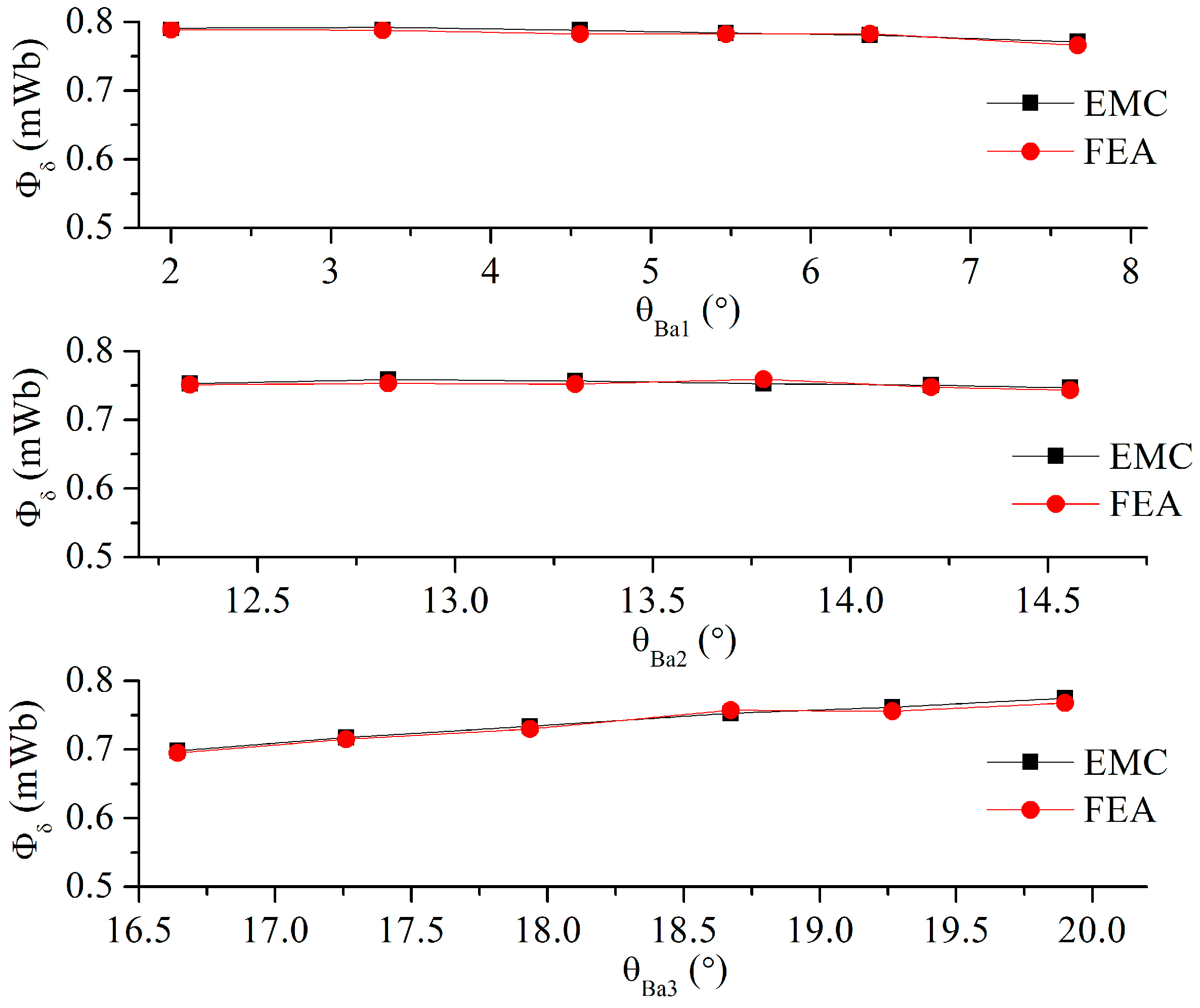
2.6. Effect of Flux Barrier Span Angle on No-Load Flux
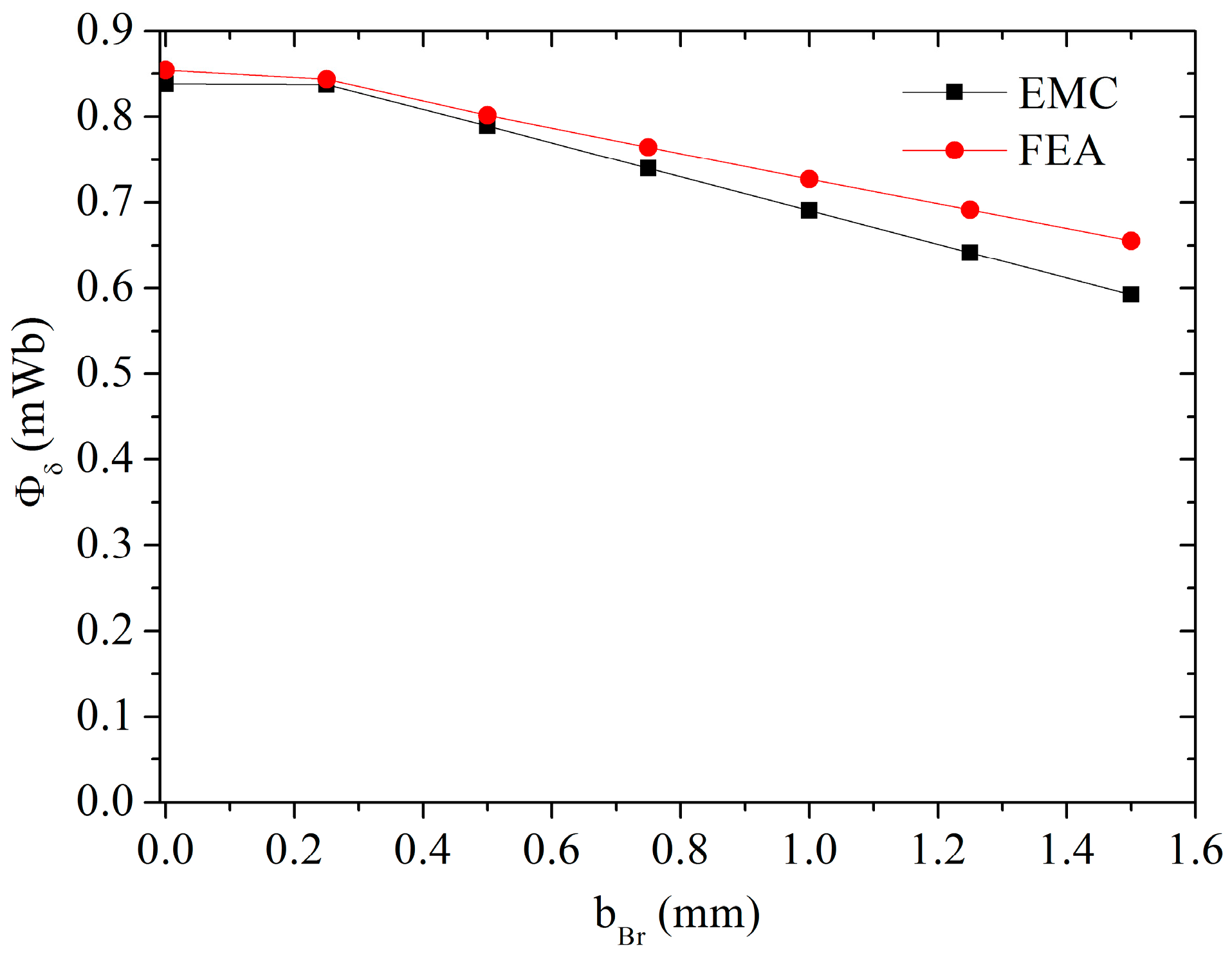
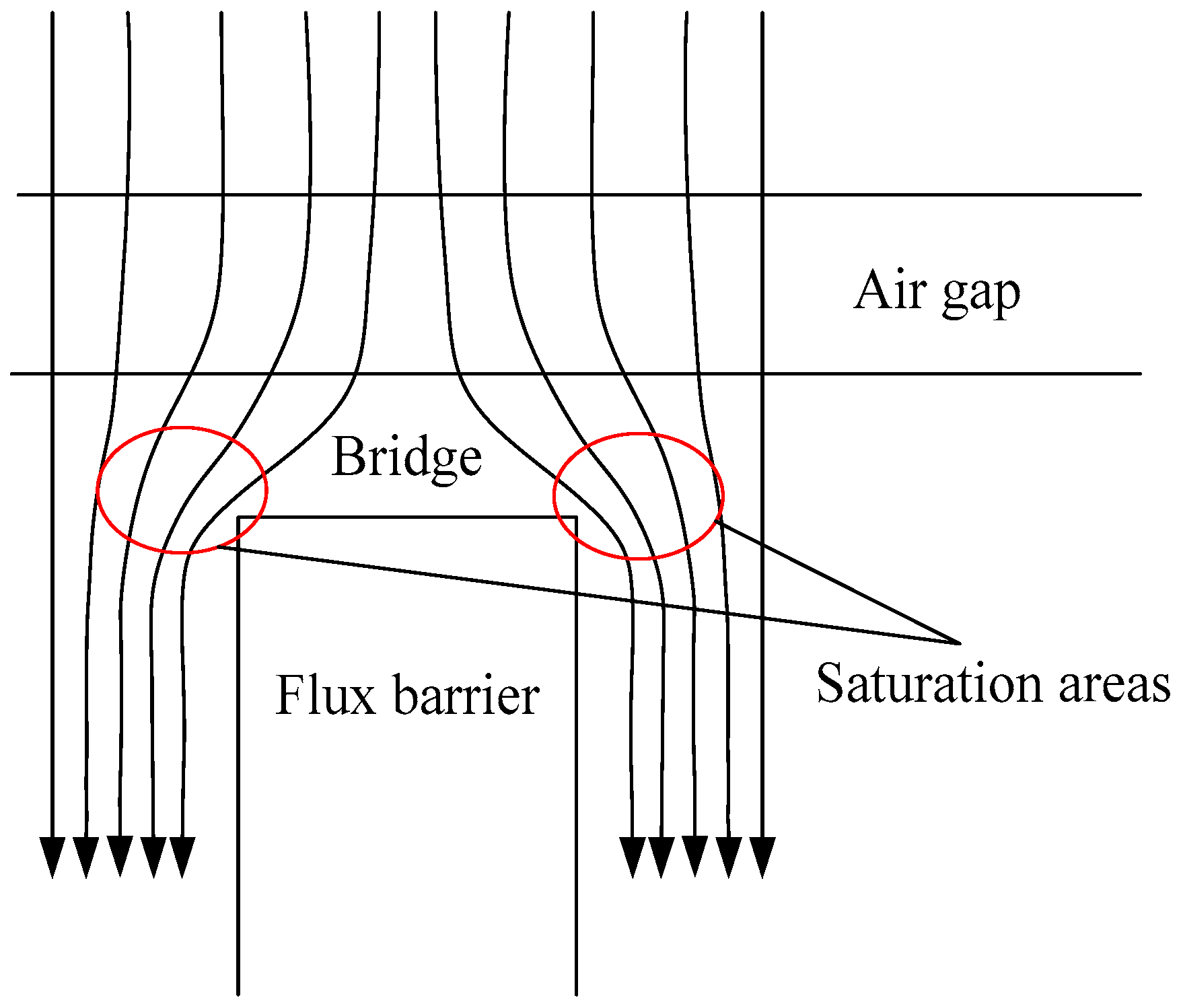
2.7. Effect of Bridge Width on No-Load Flux
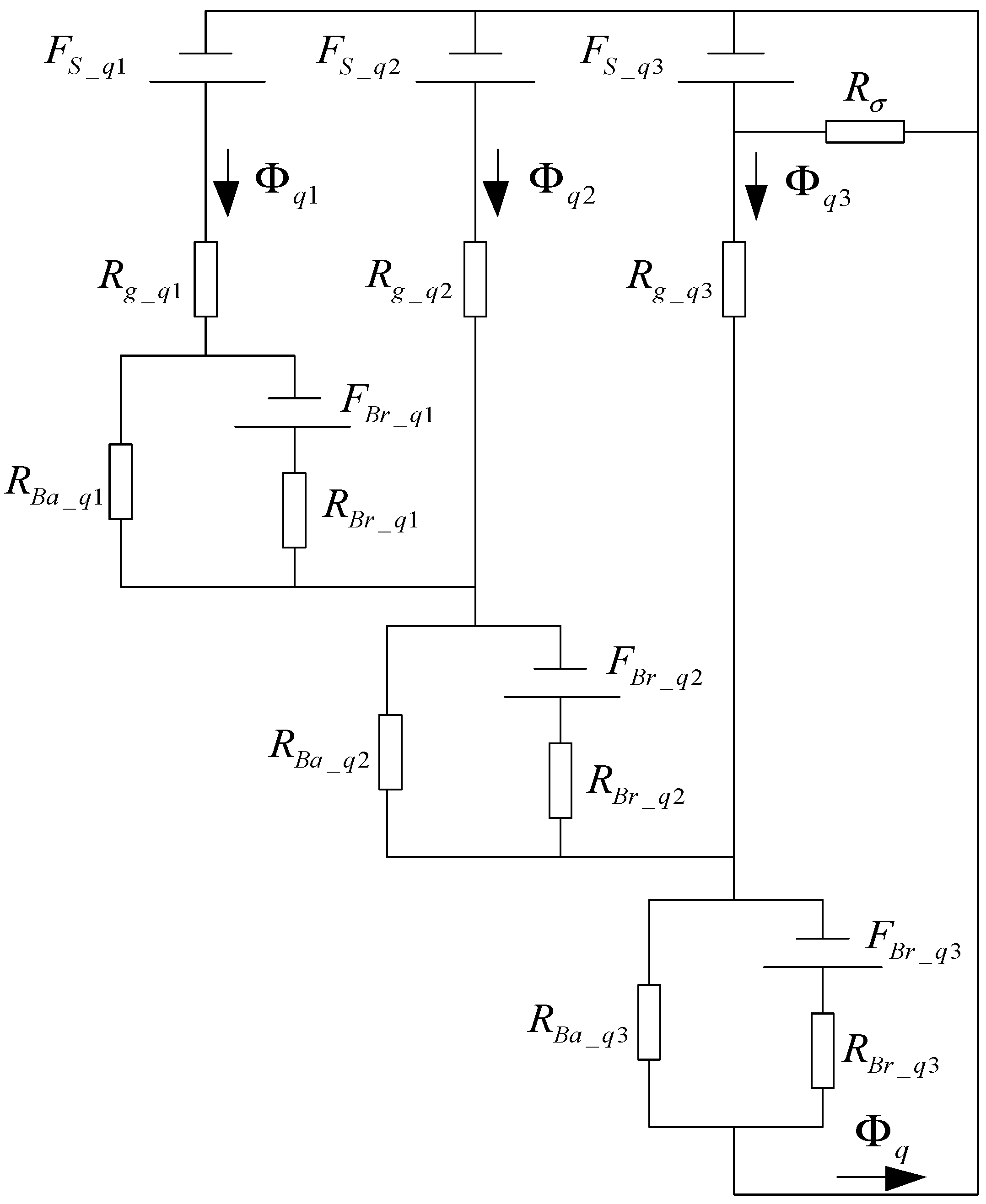
3. q-Axis Magnetic Circuit Analysis
3.1. q-Axis Magnetic Circuit Model
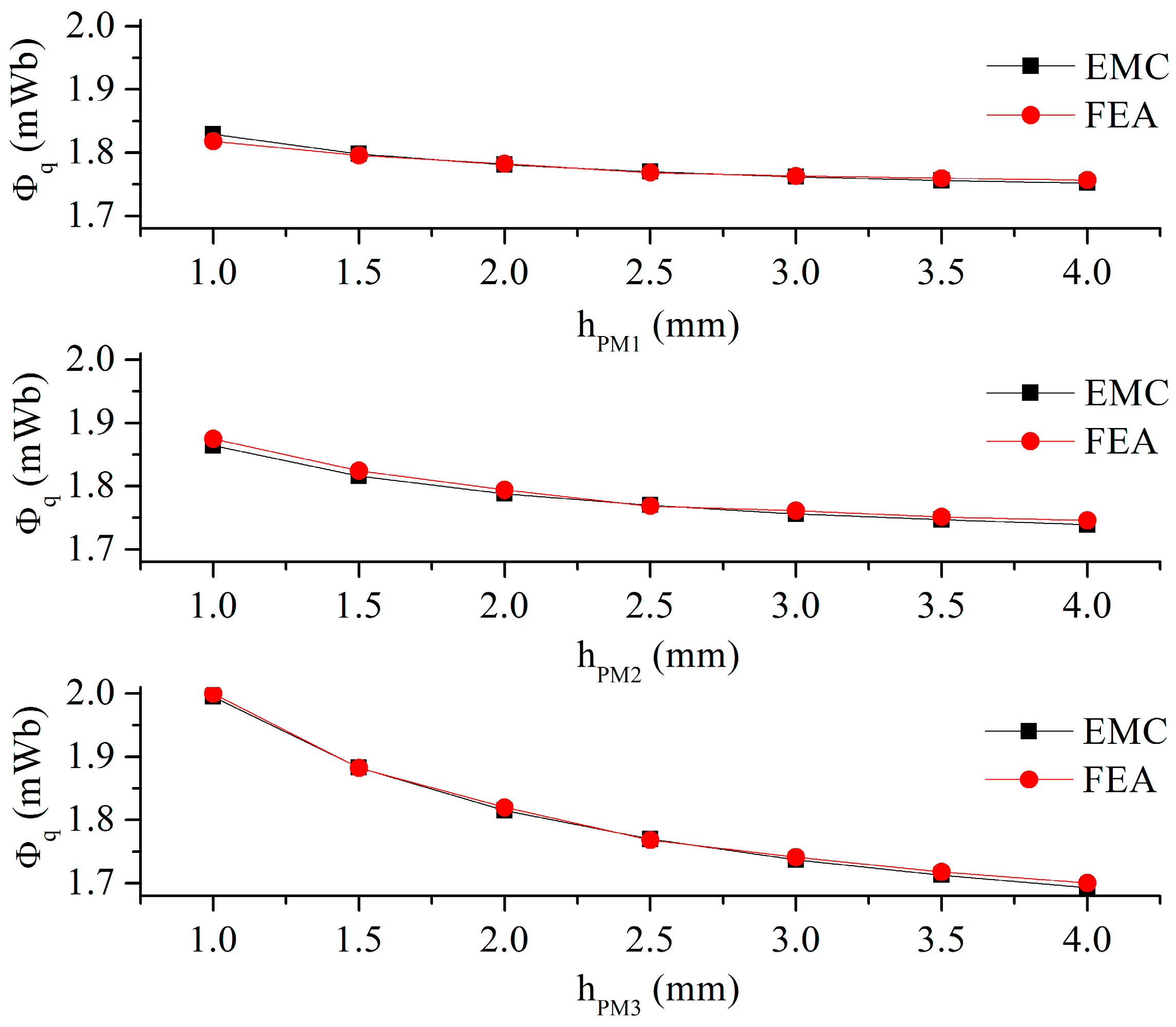
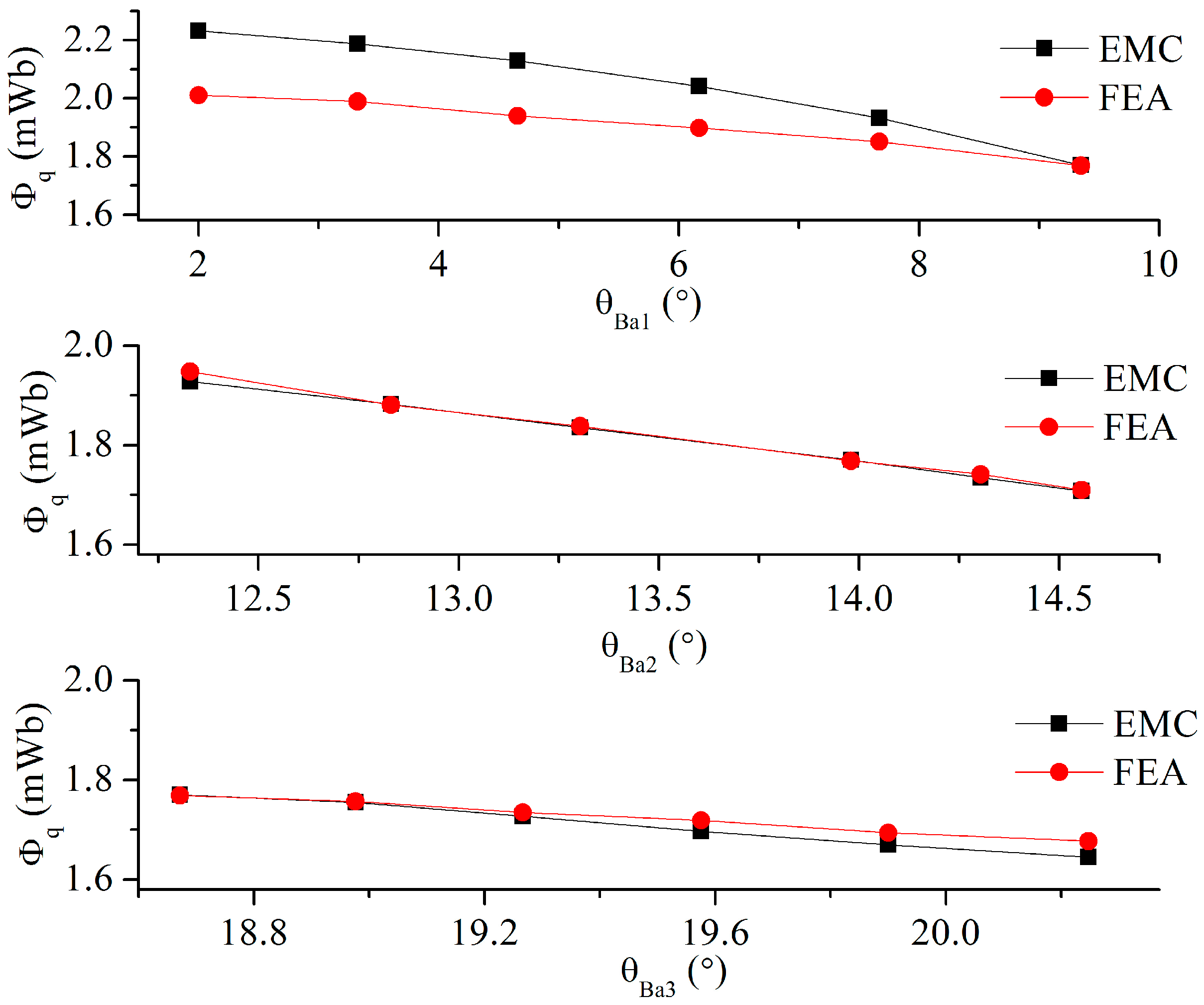
3.2. Effect of PM Thickness on q-Axis Flux
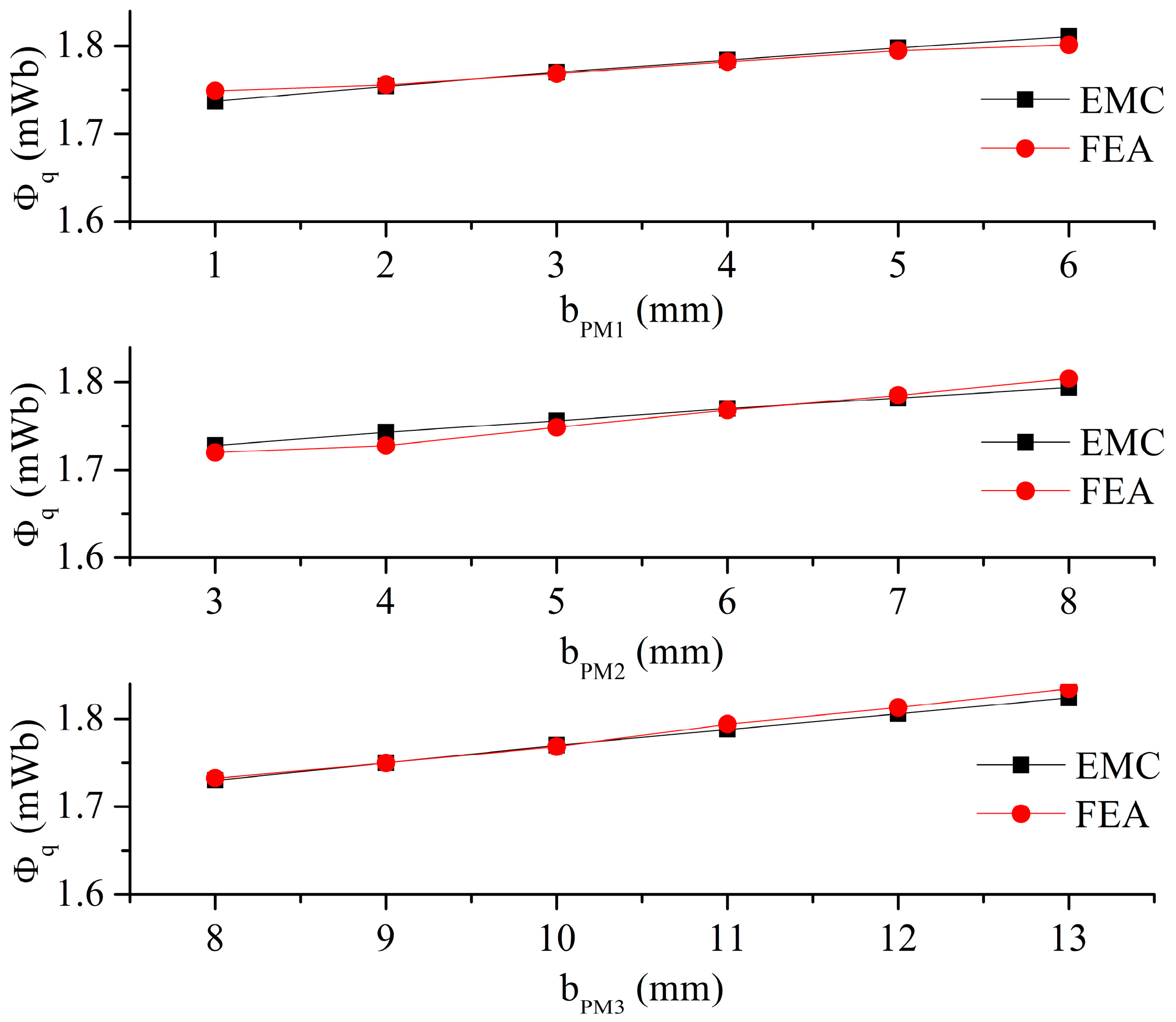
3.3. Effect of PM Width on q-Axis Flux
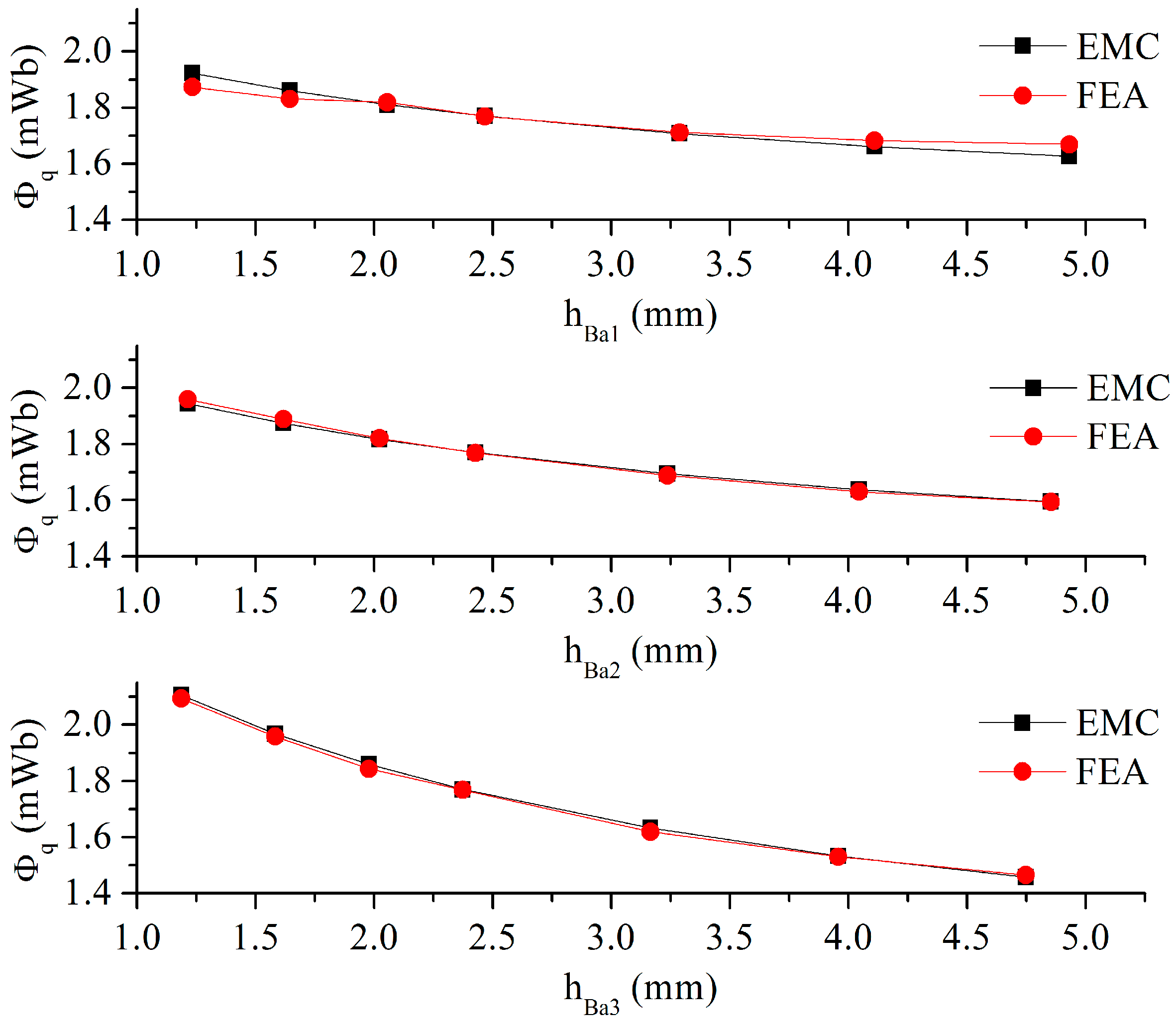
3.4. Effect of Flux Barrier Thickness on q-Axis Flux
3.5. Effect of Flux Barrier Span Angle on q-Axis Flux
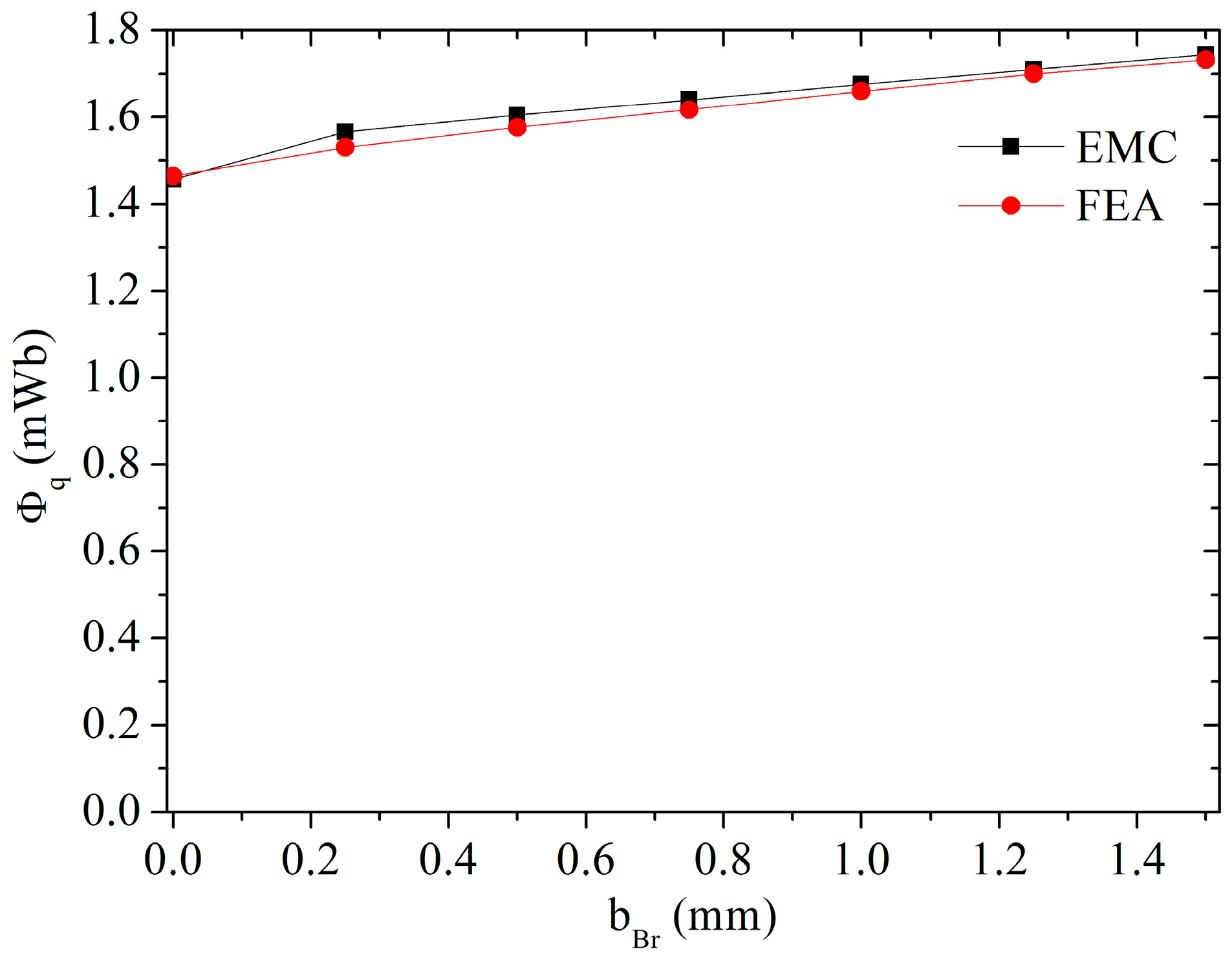
3.6. Effect of Bridge Width on q-Axis Flux
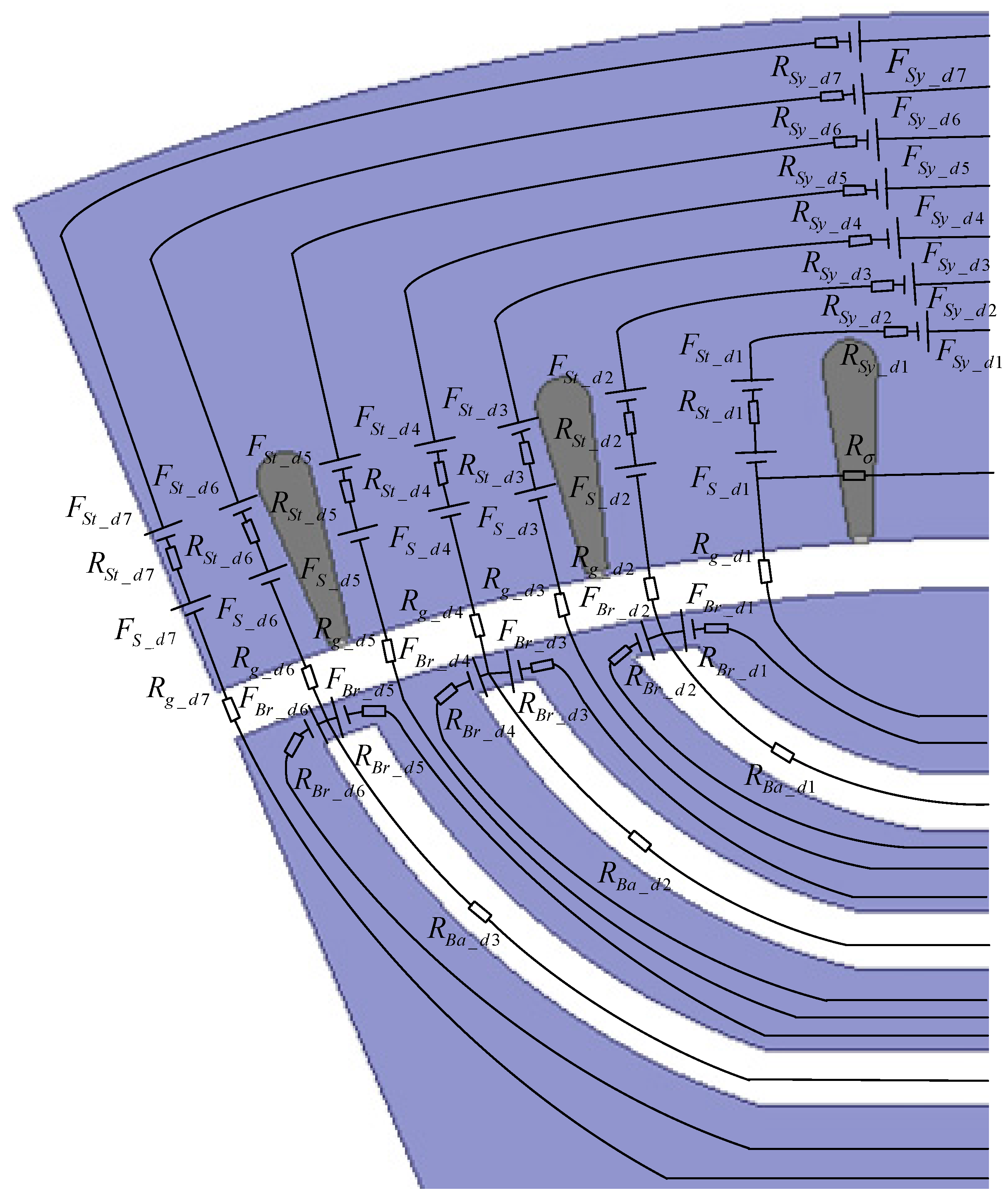
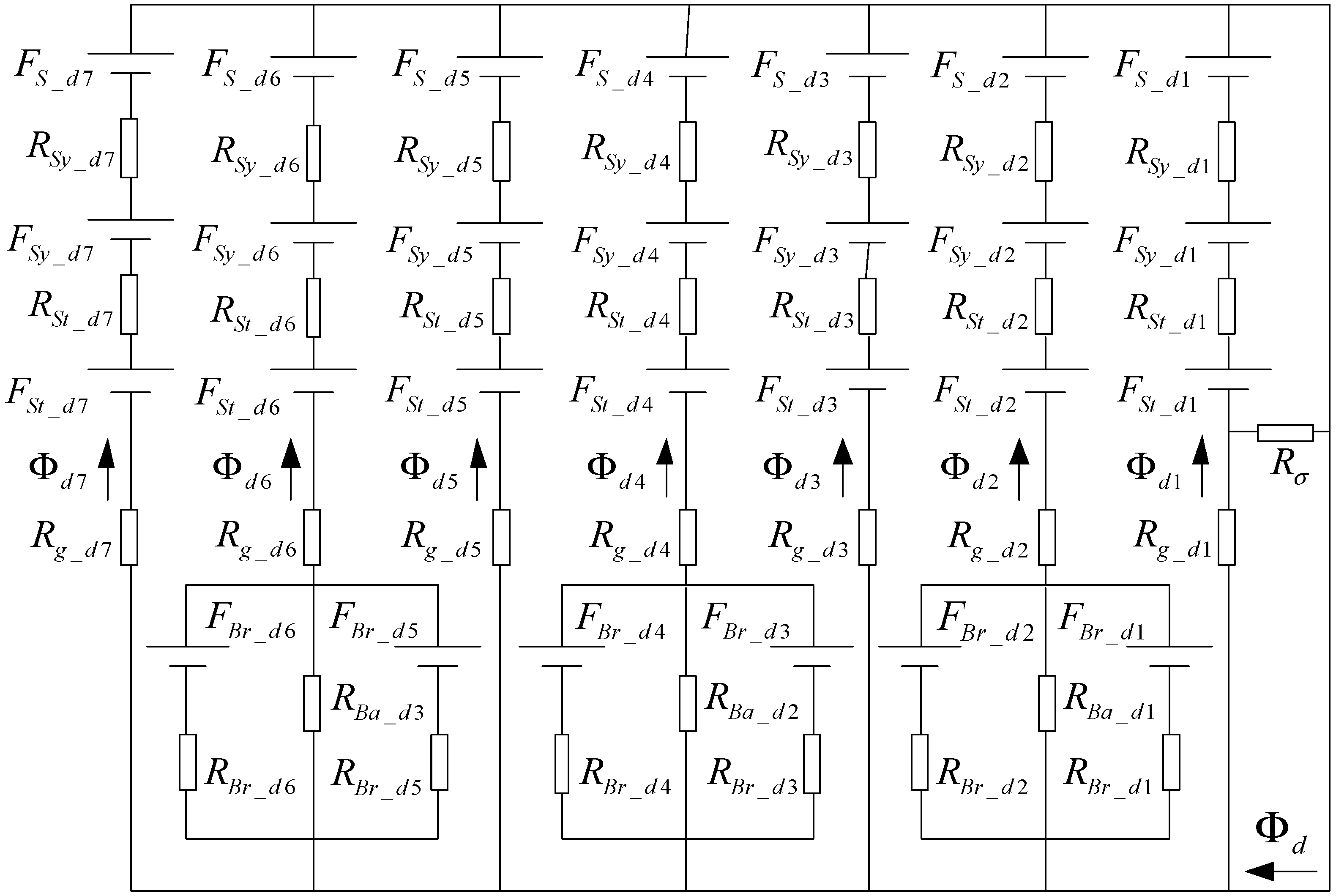
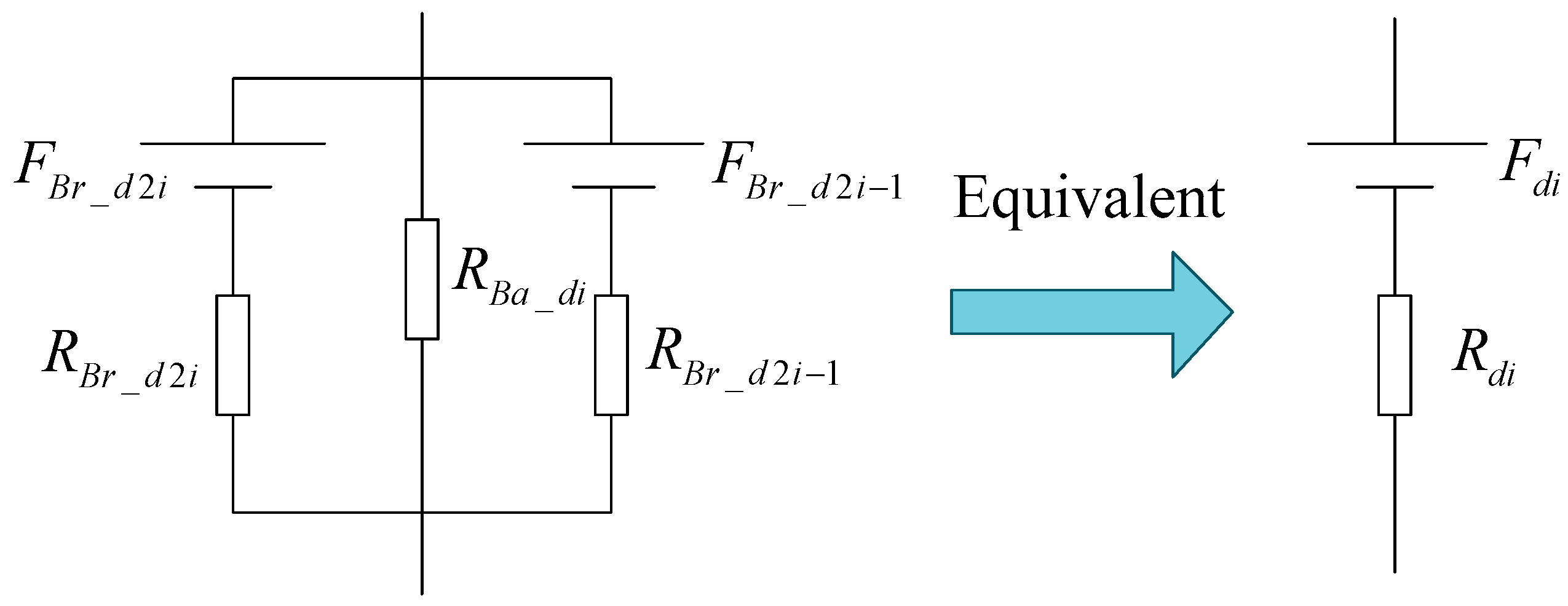
4. d-Axis Magnetic Circuit Analysis
4.1. d-Axis Magnetic Circuit Model
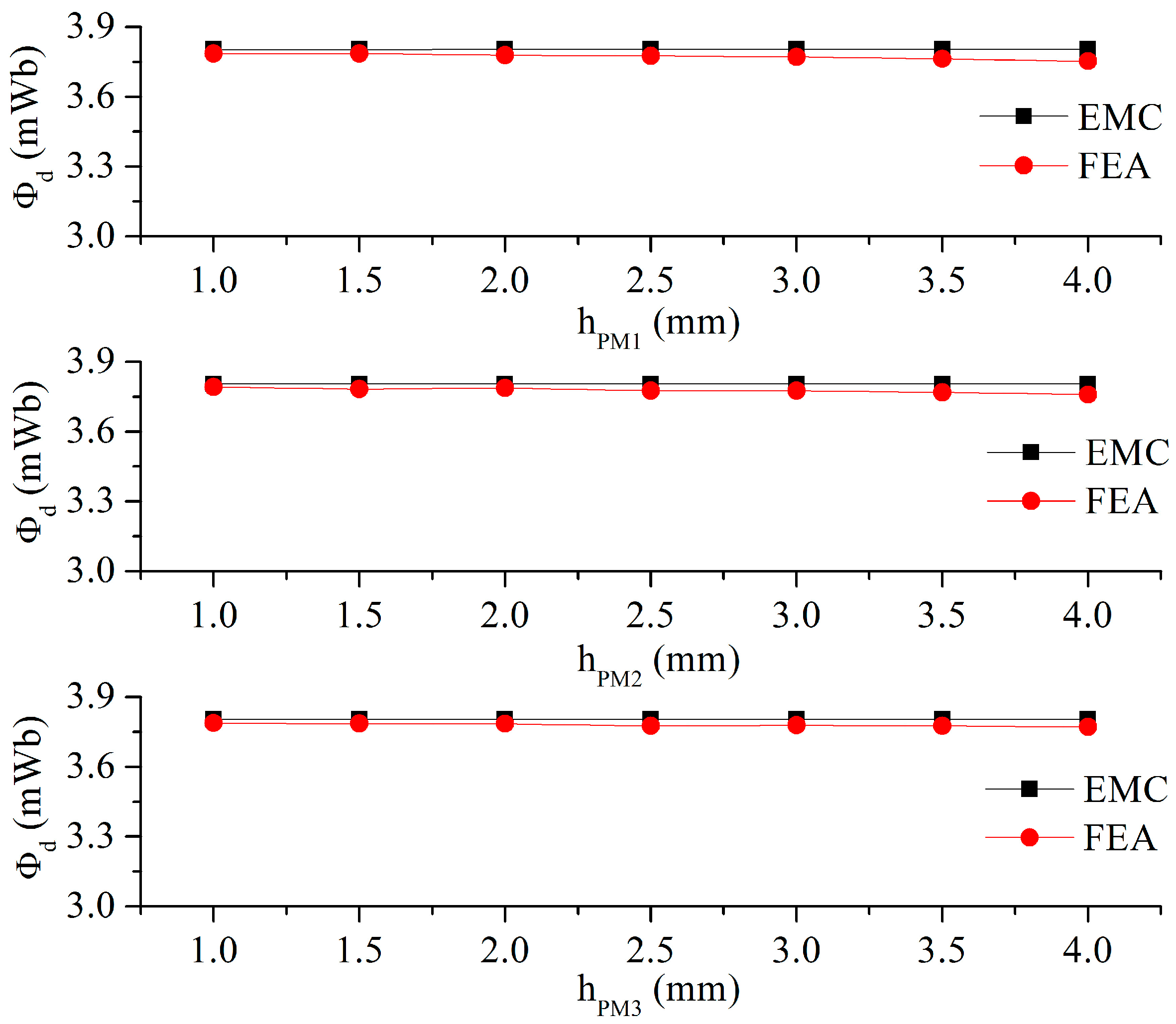
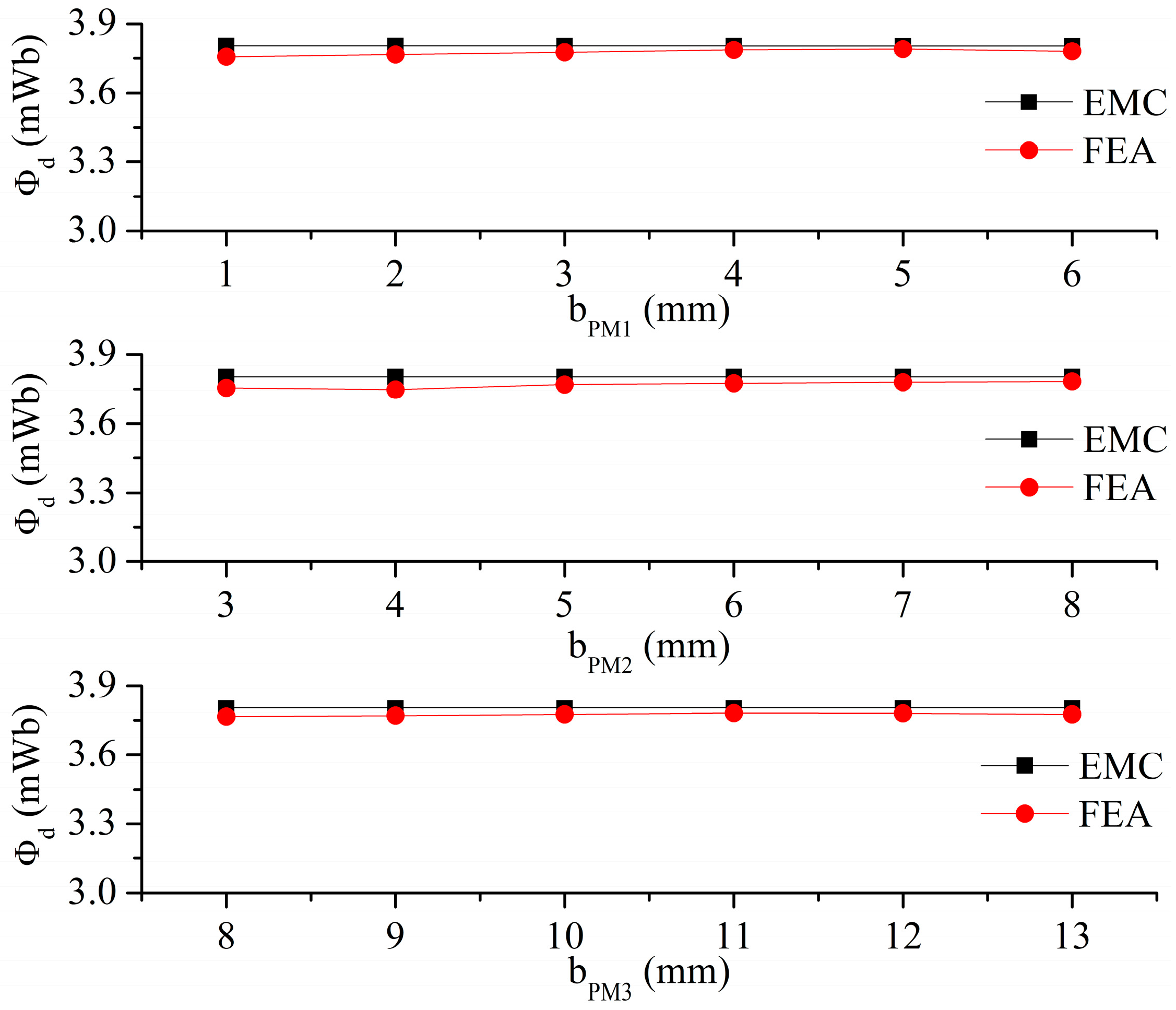
4.2. Effect of PM Thickness on d-Axis Flux
4.3. Effect of PM Width on d-axis Flux
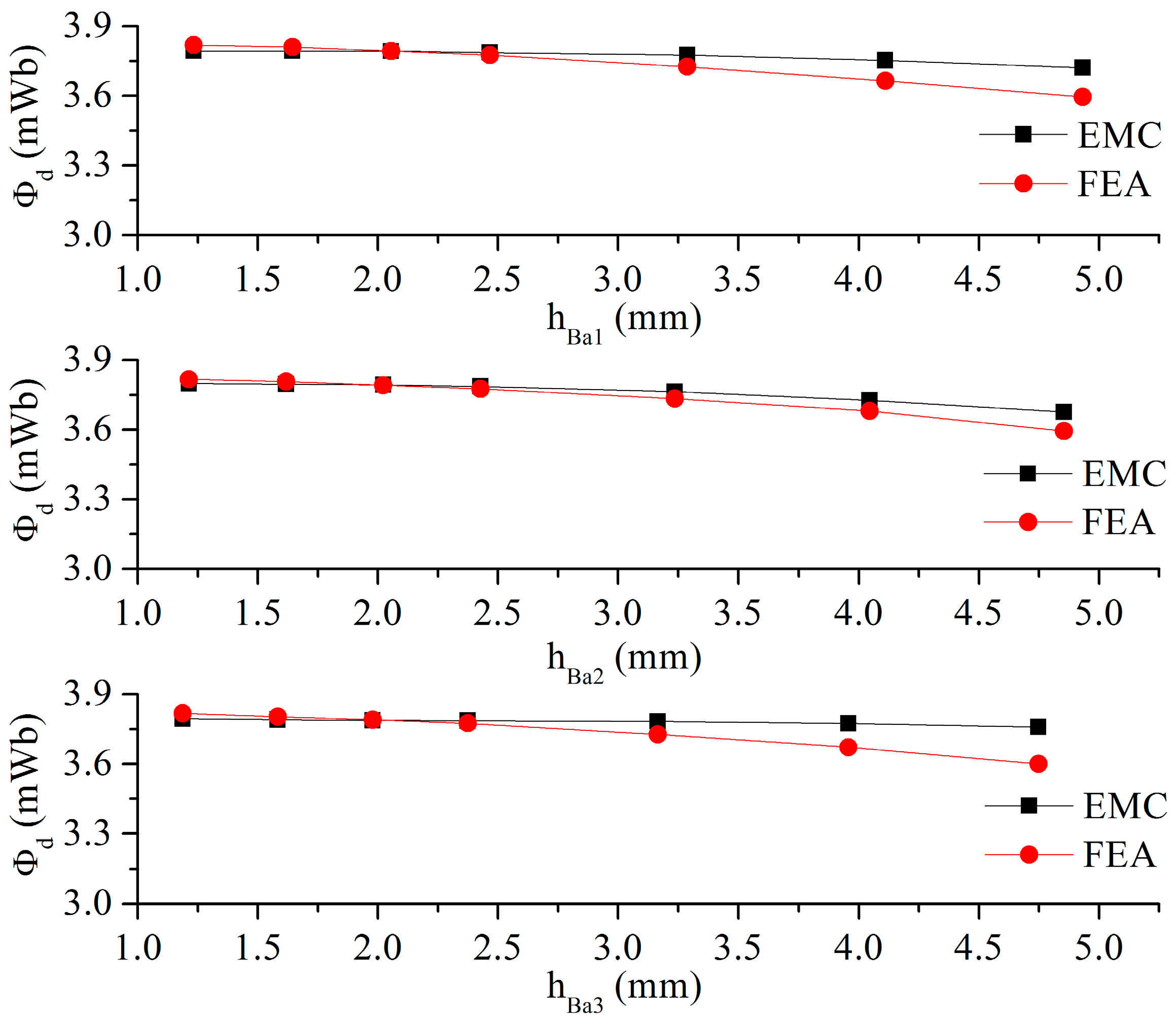
4.4. Effect of Flux Barrier Thickness on d-Axis Flux
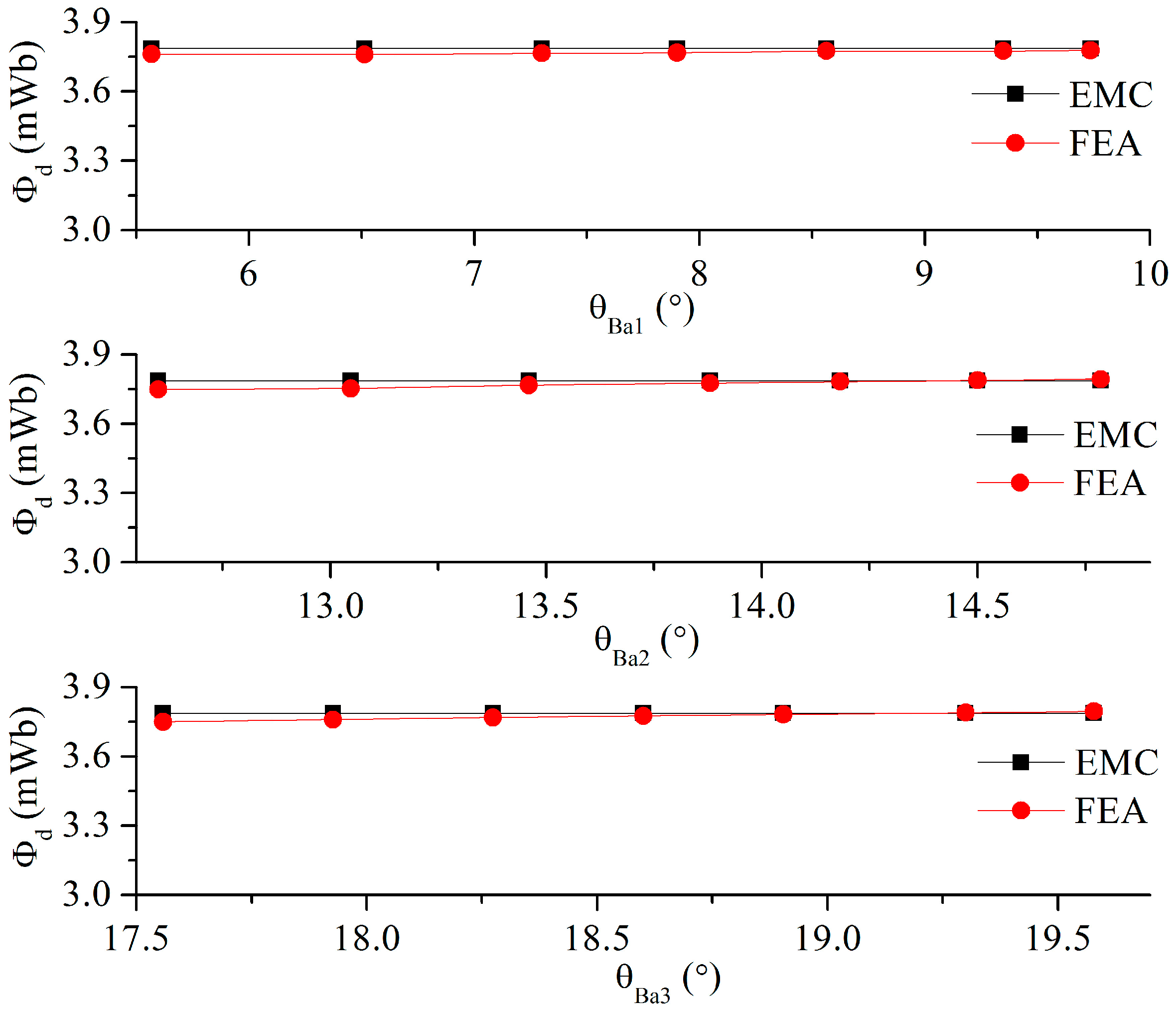
4.5. Effect of Flux Barrier Span Angle on d-Axis Flux
4.6. Effect of Bridge Width on d-Axis Flux
5. Electromagnetic Performance Analyses
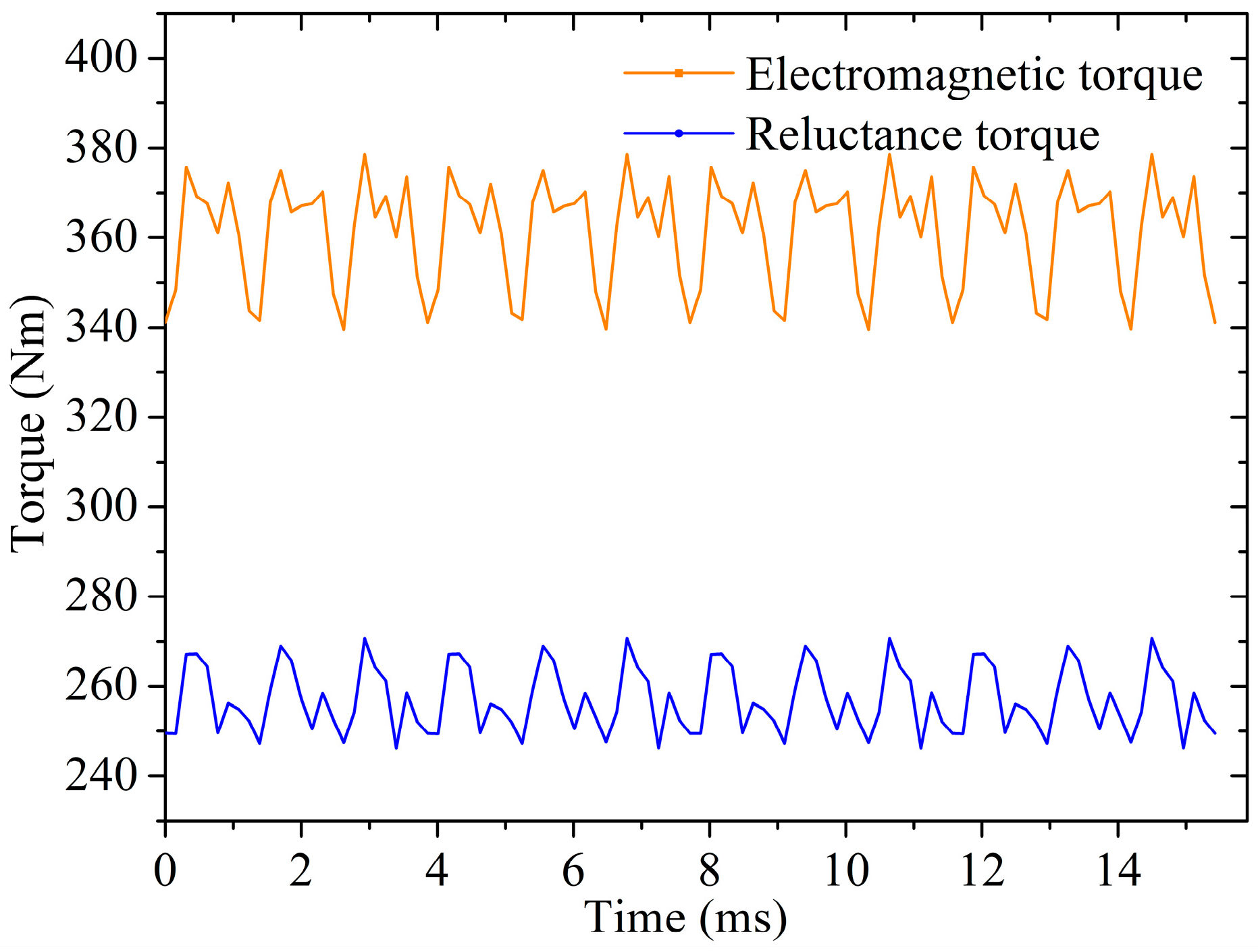
5.1. Torque Characteristics
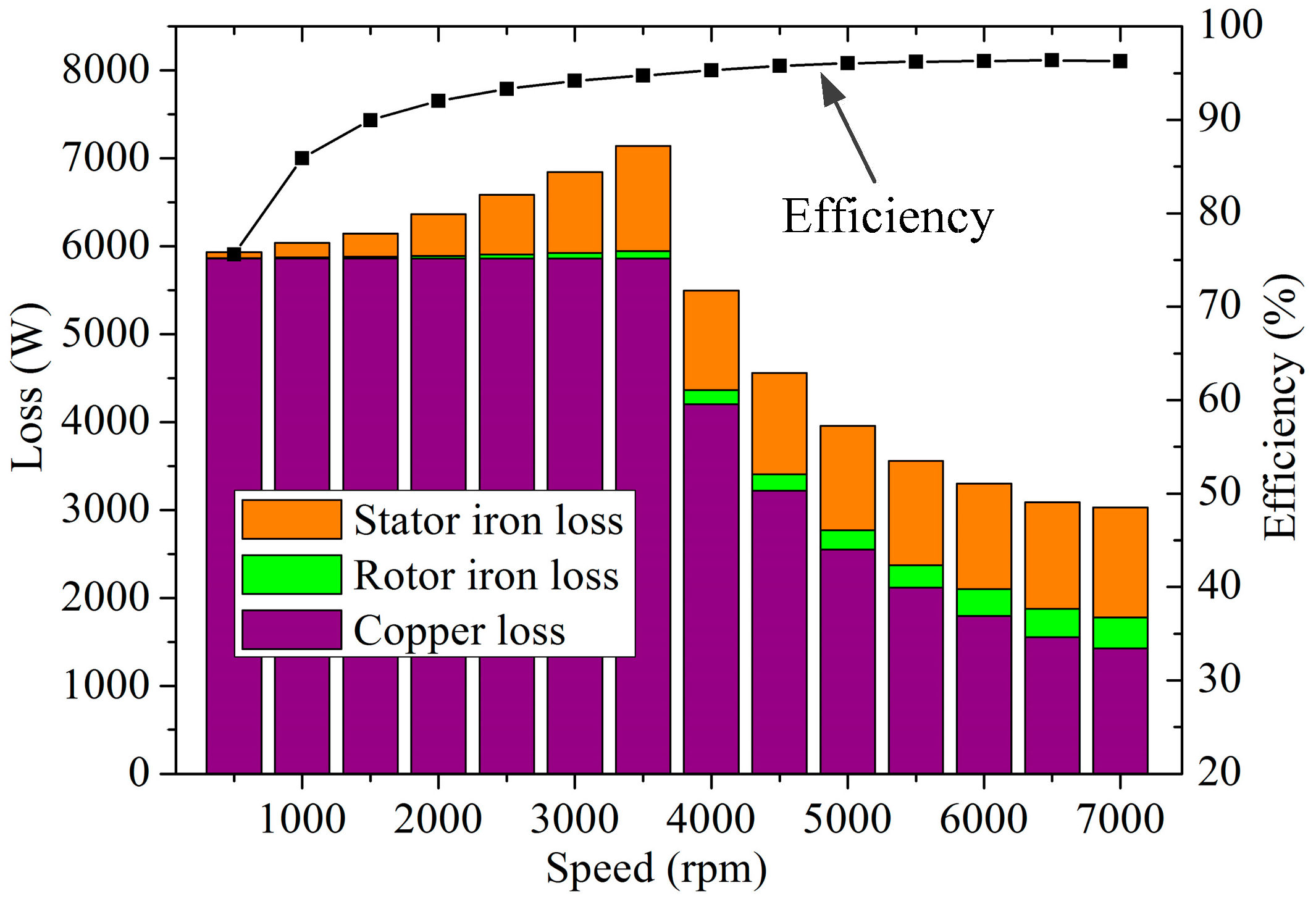
5.2. Loss and Efficiency Characteristics
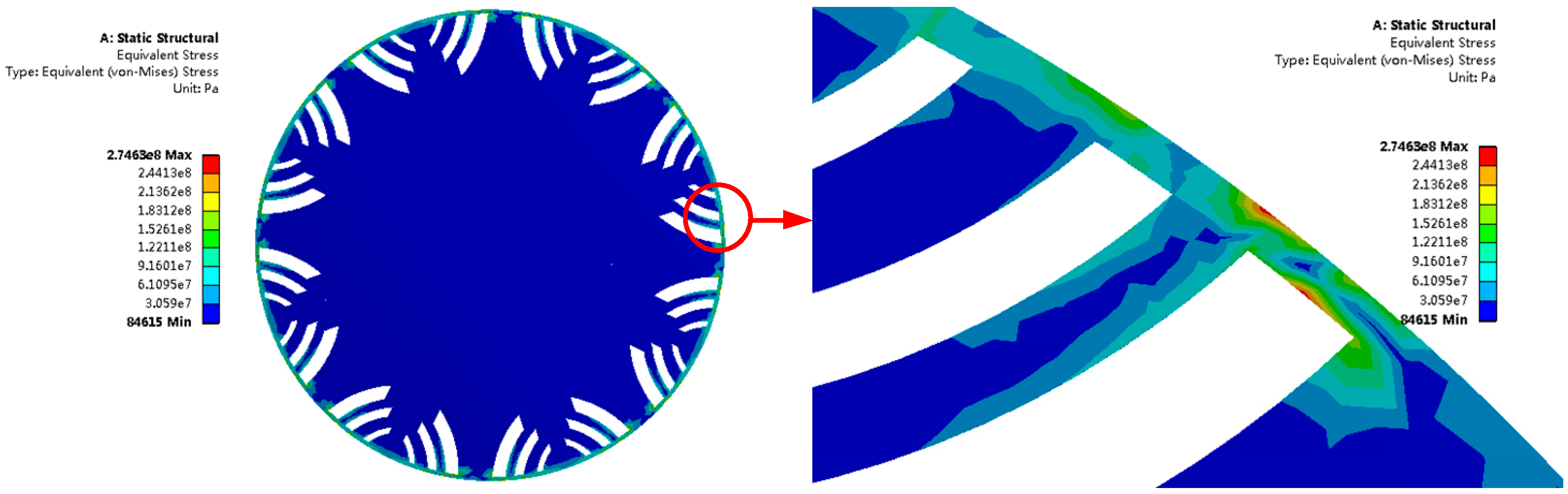
6. Mechanical Strength Verification
7. Conclusions
- (1)
- The PM width has a significant influence on the no-load flux, but the PM thickness does not. Thickening the third flux barrier and increasing the third flux barrier span angle can increase the no-load flux.
- (2)
- Thickening the PM and flux barrier, as well as increasing the flux barrier span angle, can decrease the q-axis flux, while widening the PM increases the q-axis flux.
- (3)
- The PM width and PM thickness, as well as the flux barrier span angle, affect the d-axis flux negligibly. The rotor saturation results in d-axis flux reduction as the flux barrier thickness increases continuously.
- (4)
- Widening the bridge can decrease the no-load flux and increase the q-axis flux obviously. However, the bridge width affects the d-axis flux negligibly because the saturation area of the bridge end is far smaller than that of the stator teeth and yoke.
- (5)
- The analyses of the EMC models can be extended to the rotor structure with a different number of poles and different layers of the flux barriers, as well as various types of materials. However, when the stator current changes, the accuracy of EMC models declines (especially in the d-axis model) because of the variation of the saturation level. Hence, the accuracy of torque calculation by the EMC method declines as the stator current changes.
- (6)
- It is shown by the electromagnetic performance of the optimized LRE-IPMSM that the electromagnetic torque reaches 361.69 Nm and the electromagnetic torque ripple is 5.39% under MTPA control of 371 A. The efficiency reaches the maximum of 96.4% at 6500 rpm. The stress distribution of the optimized LRE-IPMSM at maximum speed is obtained. The result shows that the optimized LRE-IPMSM satisfies the requirement of mechanical strength.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Boldea, I.; Tutelea, L.; Parsa, L.; Dorrell, D. Automotive electric propulsion systems with reduced or no permanent magnets: An overview. IEEE Trans. Ind. Electron. 2014, 61, 5696–5711. [Google Scholar] [CrossRef]
- Degano, M.; Carraro, E.; Bianchi, N. Selection criteria and robust optimization of a traction PM-assisted synchronous reluctance motor. IEEE Trans. Ind. Appl. 2015, 51, 4383–4391. [Google Scholar] [CrossRef]
- Vagati, A.; Boazzo, B.; Guglielmi, P.; Pellegrino, G. Design of ferrite-assisted synchronous reluctance machines robust toward demagnetization. IEEE Trans. Ind. Appl. 2014, 50, 1768–1779. [Google Scholar] [CrossRef]
- Morimoto, S.; Ooi, S.; Inoue, Y.; Sanada, M. Experimental evaluation of a rare-earth-free PMASynRM with ferrite magnets for automotive applications. IEEE Trans. Ind. Electron. 2014, 61, 5749–5756. [Google Scholar] [CrossRef]
- Boazzo, B.; Vagati, A.; Pellegrino, G.; Armando, E.; Guglielmi, P. Multipolar ferrite-assisted synchronous reluctance machines: A general design approach. IEEE Trans. Ind. Electron. 2015, 62, 832–845. [Google Scholar] [CrossRef]
- Lazari, P.; Wang, J.; Sen, B. 3-D effects of rotor step-skews in permanent magnet-assisted synchronous reluctance machines. IEEE Trans. Magn. 2015, 51, 8112704. [Google Scholar] [CrossRef]
- Wang, Y.; Ionel, D.M.; Jiang, M.; Stretz, S.J. Establishing the relative merits of synchronous reluctance and PM-assisted technology through systematic design optimization. IEEE Trans. Ind. Appl. 2016, 52, 2971–2978. [Google Scholar] [CrossRef]
- Bianchi, N.; Fornasiero, E.; Ferrari, M.; Castiello, M. Experimental comparison of PM-assisted synchronous reluctance motors. IEEE Trans. Ind. Appl. 2016, 52, 163–171. [Google Scholar] [CrossRef]
- Carraro, E.; Morandin, M.; Bianchi, N. Traction PMASR motor optimization according to a given driving cycle. IEEE Trans. Ind. Appl. 2016, 52, 209–216. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Bon, D.; Pré, M.D. Rotor flux-barrier design for torque ripple reduction in synchronous reluctance and PM-assisted synchronous reluctance motors. IEEE Trans. Ind. Appl. 2009, 45, 921–928. [Google Scholar] [CrossRef]
- Obata, M.; Morimoto, S.; Sanada, M.; Inoue, Y. Performance evaluation of high power and low torque ripple structure of rare-earth free PMASynRM with ferrite magnet. In Proceedings of the 10th IEEE International Conference on Power Electronics and Drive Systems (PEDS), Kitakyushu, Japan, 22–25 April 2013; pp. 714–719. [Google Scholar]
- Ooi, S.; Morimoto, S.; Sanada, M.; Inoue, Y. Performance evaluation of a high-power-density PMASynRM with ferrite magnets. IEEE Trans. Ind. Appl. 2013, 49, 1308–1315. [Google Scholar] [CrossRef]
- Carraro, E.; Degano, M.; Bianchi, N. Permanent magnet volume minimization in permanent magnet assisted synchronous reluctance motors. In Proceedings of the 8th International Conference and Exhibition on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 27–30 March 2013; pp. 1–4. [Google Scholar]
- Guglielmi, P.; Boazzo, B.; Armando, E.; Pellegrino, G.; Vagati, A. Permanent-magnet minimization in PM-assisted synchronous reluctance motors for wide speed range. IEEE Trans. Ind. Appl. 2013, 49, 31–41. [Google Scholar] [CrossRef]
- Calvo, E.S.; Potoradi, D. Synchronous reluctance motors with and without permanent magnets for high performance low cost electrical drives. In Proceedings of the 5th International Electric Drives Production Conference (EDPC), Nuremberg, Germany, 15–16 September 2015; pp. 1–7. [Google Scholar]
- Zhu, L.; Jiang, S.Z.; Zhu, Z.Q.; Chan, C.C. Analytical modeling of open-circuit air-gap field distributions in multisegment and multilayer interior permanent-magnet machines. IEEE Trans. Magn. 2009, 45, 3121–3130. [Google Scholar] [CrossRef]
- Bianchi, N.; Mahmoud, H. An analytical approach to design the PM in PMAREL motors robust toward the demagnetization. IEEE Trans. Energy Convers. 2016, 31, 800–809. [Google Scholar] [CrossRef]
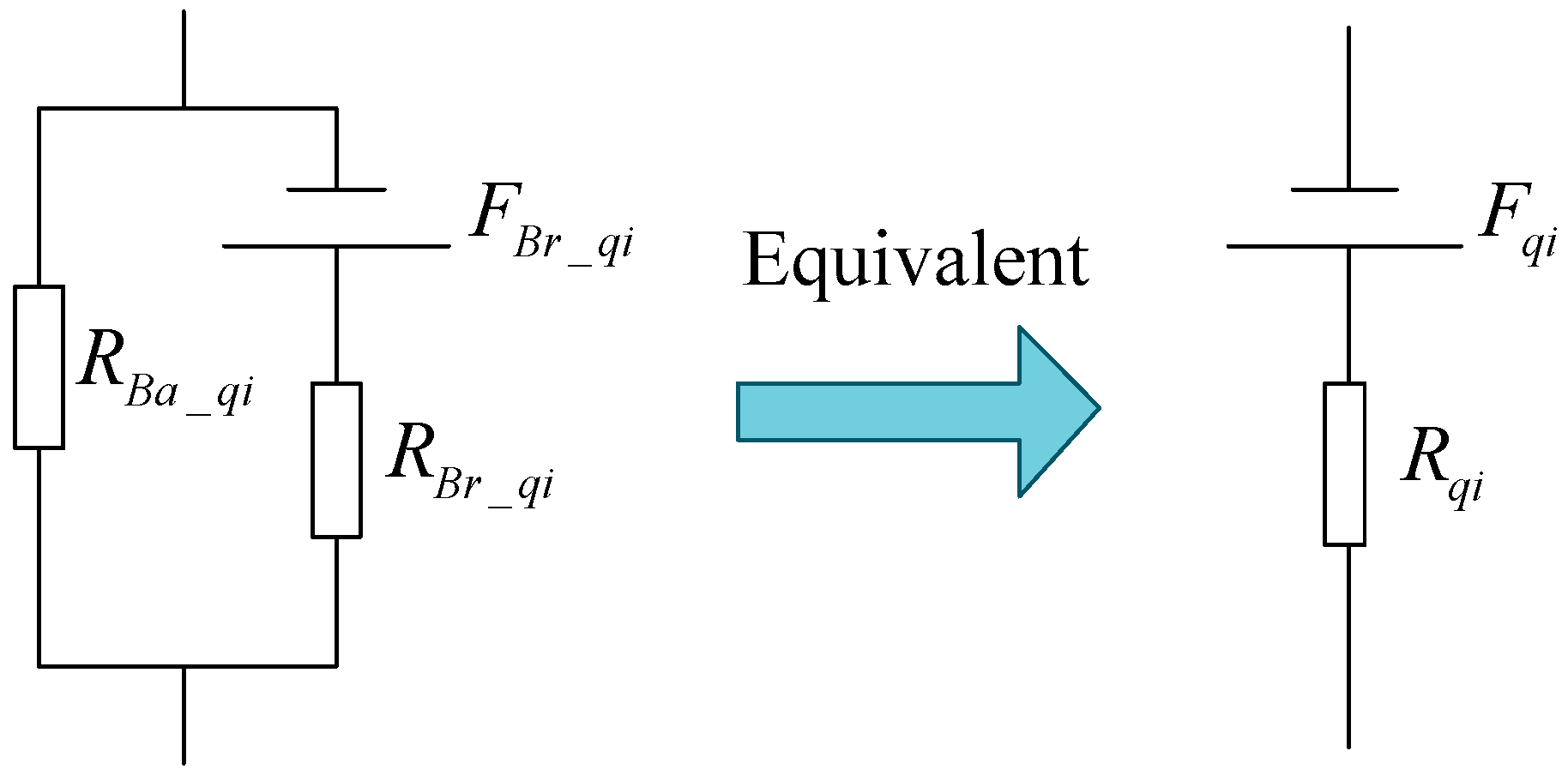


| Parameters | Unit | Value |
|---|---|---|
| Stator outer diameter | mm | 290 |
| Rotor outer diameter | mm | 172 |
| Air gap length | mm | 1 |
| Stack length | mm | 106 |
| Maximum speed | rpm | 7000 |
| Maximum torque | Nm | 344 |
| Maximum efficiency | % | 96 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, P.; Wang, W.; Wang, M.; Liu, Y.; Fu, Z. Investigation of the Magnetic Circuit and Performance of Less-Rare-Earth Interior Permanent-Magnet Synchronous Machines Used for Electric Vehicles. Energies 2017, 10, 2173. https://doi.org/10.3390/en10122173
Zheng P, Wang W, Wang M, Liu Y, Fu Z. Investigation of the Magnetic Circuit and Performance of Less-Rare-Earth Interior Permanent-Magnet Synchronous Machines Used for Electric Vehicles. Energies. 2017; 10(12):2173. https://doi.org/10.3390/en10122173
Chicago/Turabian StyleZheng, Ping, Weinan Wang, Mingqiao Wang, Yong Liu, and Zhenxing Fu. 2017. "Investigation of the Magnetic Circuit and Performance of Less-Rare-Earth Interior Permanent-Magnet Synchronous Machines Used for Electric Vehicles" Energies 10, no. 12: 2173. https://doi.org/10.3390/en10122173
APA StyleZheng, P., Wang, W., Wang, M., Liu, Y., & Fu, Z. (2017). Investigation of the Magnetic Circuit and Performance of Less-Rare-Earth Interior Permanent-Magnet Synchronous Machines Used for Electric Vehicles. Energies, 10(12), 2173. https://doi.org/10.3390/en10122173





