Abstract
Energy consumption for multiple trains on the urban subway line is predominantly affected by the operation strategy. This paper proposed an energy-saving operation strategy for multiple trains, which is suitable for various line conditions and complex train schedules. The model and operation modes of the strategy are illustrated in detail, aiming to take full use of regenerative braking energy in complex multi-train systems with different departure intervals and dwell times. The computing method is proposed by means of the heuristic algorithm to obtain the optimum operation curve for each train. The simulation result based on a real urban subway line is provided to verify the correctness and effectiveness of the proposed energy-saving operation strategy.
1. Introduction
Energy consumption of public transportations is highly concerning due to the global energy crisis. Urban subway, acting as an essential part of public transportation, is rapidly becoming a hot research area for the energy-saving strategy under complex operating environments and various influences.
Recently, with the development of energy-saving research, the focus of the research has been transferred from a single train to multi-train system. The operation strategy and the driving curves with specific line and dispatch constraints are mainly concerned with the single-train energy-saving research. According to the latest research, the optimal operation strategy, based on Pontryagin maximum principle and adjoint variables to find switching points, has the best performance on the single train [1,2,3,4]. However, the multi-train system may not obtain the best performance when each train operates independently.
Minimizing tractive energy consumption and maximizing the utilization of regenerative energy are two main energy-saving operation methods [5], and the energy-saving research on single train cares more about tractive energy consumption, so the research on multi-train system concentrates on maximizing the utilization of regenerative energy. A method that modifies the schedule of two trains is proposed to realize minimum energy consumption and safe separation of the trains [6]. However, the method has limitations that the train schedule is affected by many factors and the regenerative energy is not entirely used. A series of studies on how to reduce total tractive energy consumption and total travel time is made [7,8,9,10], and the accelerating and braking action functions of trains are built by using integrated metro timetable and optimizing speed profile. However, the study still focuses more on the schedule adjustment with little change in speed profile. Moreover, the different headways are discussed to adjust the train arrival time at stations [11], but the study has the same problem that it cannot fully use the regenerative energy, and the result has a conflict with train dispatch.
An integrated optimization approach with adaptive cycle time is proposed based on the passenger demand [12,13], and an integer programming model is built to determine the schedule and speed profile with minimum net energy consumption. The proposed method has better performance compared to the schedule optimization method and integrated energy-efficient (IEE) optimization model [14,15]. However, the analytical solution of the complex mathematical model is needed that makes it more suitable for offline calculation rather than online calculation.
Recently, we proposed an energy-saving control strategy that combines the schedule and speed profile [16] to fully use the regenerative energy. The optimum driving curve for each train can be easily calculated online based on the heuristic algorithm and has no conflict with dispatch. However, the research is based on a two-train system, and the dwell time for each train and signaling block system are not considered, thus further research is needed.
Besides, to ensure the safety of multi-train operation, the problem of minimizing energy consumption also focuses on signaling block system in urban subway system [17]. The moving block signaling system method becomes more and more important for maintaining the required safety margins. A nonlinear programming method is proposed to optimize the energy-saving operation curve for the leading and following train in moving block signaling system [18,19,20]. However, the research is based on simulation and is not sufficient to consider the speed profile for the multi-train system.
In conclusion, the operation strategy for the single train is not suitable for the multi-train system; the adjustment of train schedules cannot fully use the regenerative energy; and the studies that combine schedule optimization and the speed profile are either too complicated to calculate or insufficient to consider all constraints. In this paper, based on the previous research of the single train and two-train system, an energy-saving operation strategy for multiple trains is proposed, and all the related factors are carefully considered. Different departure intervals and different dwell times are discussed in detail, and the optimum operation strategy can be obtained to minimize total energy consumption. Moreover, a computing method related to the operation strategy, which can calculate the driving mode and driving curves for the multi-train system with signaling block system and limiting-velocity curve, is proposed in the following sections. The computing method is based on the heuristic algorithm, which is very important for guiding and evaluating the operation strategy. Finally, the simulation results based on Beijing Subway Line 4 are given to show the correctness and effectiveness of the proposed energy-saving operation strategy.
This paper is organized as follows: Section 2 introduces the previous study on single train and two-train system, and also introduces Beijing Subway Line 4 to make the explanation clear; Section 3 first builds the model of multi-train system, then proposes the energy-saving operation strategy under different departure intervals and dwell times, and finally illustrates the computing method to calculate the driving mode and driving curves for multiple trains; Section 4 presents and analyzes the simulation results of the energy-saving operation strategy for multiple trains based on Beijing Subway Line 4; and Section 5 presents the conclusion.
2. Introduction of the Multi-Train System and the Previous Study for the Single Train and Two-Train System
In recent years, energy consumption of urban subway has been highly concerning, and the energy-saving operation strategies of the single train and two-train system have been studied by us for a while. Several research achievements have been published in the energy-saving journals [1,17,21]. Previous research results on the single train and two trains are introduced in this section as the fundamental of multi-train system research, and the deficiencies of the study are also illustrated. To make the illustration clear, an example of the multi-train system based on Beijing Subway Line 4 is introduced. The subway train parameters and the traction substation parameters are introduced separately. The example has the same kinds of constraints as other urban lines, so it has universal significance and can be replaced by any other urban line.
2.1. Parameters of the Subway Train 100% Low Floor Train
The low floor train (C type Metro vehicle) produced by Tangshan Railway Vehicle Co., Ltd. (Tangshan, China) is the subway train for Beijing Subway Line 4. Its marshaling mode is -Mc+M+Tp+Mc-, as shown in Figure 1. Mc stands for motor car with cabin, M for motor car, and Tp for trailer car with pantograph. The total length Ltrain is 37.34 m. The maximum speed Vmax is 70 km/h. The mass of the train in the AW2 case is 70 T.
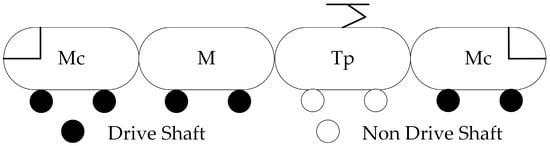
Figure 1.
Configurations of the 100% low floor train.
The traction force Ft(v) with respect to the speed v is described as:
The braking force Fb(v) with respect to the speed v is described as:
Then, the relationship between the running resistance and the speed v is described as:
2.2. Parameters of the Traction Substation—Beijing Subway Line 4
There are some traction substations on one line, and there are some stations in one traction substation. According to the urban subway system, the traction substation of Beijing Subway Line 4 contains three subway stations from Anheqiao North to Xiyuan. Meanwhile, two-side feeding is used, and its voltage is 750 V. The structure of this traction substation system is given in Figure 2 [22]. Station A stands for Anheqiao North, Station B for Beigongmen, and Station C for Xiyuan. Each traction substation contains at most three trains.
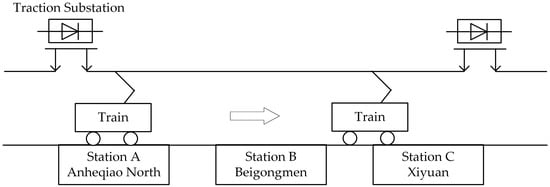
Figure 2.
The structure of the traction substation system.
The line conditions are shown in Table 1. The unit gradient resistance for the train is wg = gi, where g is the gravitational acceleration and i is the gradient. The unit curve resistance is wc = 600/R, where R is the curve radius.

Table 1.
The line conditions.
According to parameters of the train dispatch, the dwell time for each station is 30 s, 35 s, 40 s, 45 s or 50 s in Beijing Subway Line 4 based on the current passenger volume of each station.
The traction force, braking force, running resistance, unit gradient resistance and unit curve resistance are important parameters while calculating the driving curves for multi-train system. Detailed algorithm will be explained in Section 3.3.
2.3. Energy-Saving Operation Strategy for the Single Train
The energy-saving operation strategy for single train is trying to solve the switching points and driving curve between two stations of the single train with a fixed travel time, and to obtain the minimum energy consumption. Based on the modern optimal control theory and Pontryagin maximum principle, the single train adopting four-mode operation consumes the minimum energy [1]. Four-mode operation means that the train runs in four conditions in turn: maximum power, speed holding, coasting and maximum braking. The time point that the train operates from one condition to another is called switching point. The switching points and driving curve for the single train can also be determined by the heuristic algorithm.
Based on Beijing Subway Line 4, the driving curve is calculated and presented in Figure 3. The single train departs from Station A, travels for 109 s and stops at Station B. Then, it departs again from Station B, travels for 93 s and finally stops at Station C. The horizontal axis is the distance between Station A and Station C, and the vertical axis is the velocity of the single train. The red curve is limiting velocity curve, of which the solid line is the actual limits of velocities, and the dotted line means no limit. The train first runs with maximum traction power, and then holds its speed for a while; after that, the train coasts without traction power; and, finally, the train operates with maximum braking power. The tractive energy consumption, regenerative braking energy, and energy consumption of the single train are calculated and presented in Table 2.
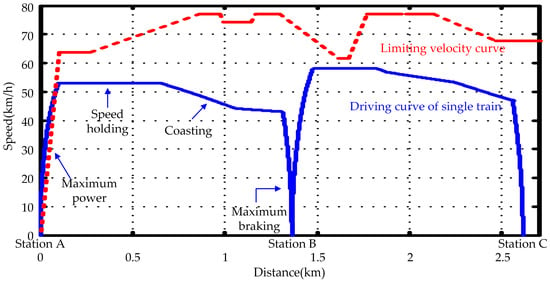
Figure 3.
Energy-saving operation curve and limiting velocity curve.

Table 2.
Energy consumption of the single train.
2.4. Energy-Saving Operation Strategy for the Two-Train System
The operation strategy for the two-train system is trying to solve driving curves of two trains and fully use the regenerate energy. The 1st train departs from Station A and travels on its way to Station B, and the 2nd departs from Station A after a certain departure interval. Based on energy-saving operation strategy of two trains in the previous study [17], the 1st train still operates under four-mode operation. For different departure intervals, the 2nd train can adopt two driving modes to minimize the total energy consumption: four-mode operation and five-mode operation. Five-mode operation means that the train runs in five conditions in turn: maximum power, coasting, maximum power, coasting and maximum braking. The 2nd train operates under four-mode operation when its departure interval is close to or after the switching point that the 1st train starts to brake. The 2nd train operates under five-mode operation when its departure is before the 1st train braking switching point. The first coasting condition for the 2nd train is added to make the second maximum power condition overlap with the maximum braking condition of the 1st train to entirely use the regenerated energy. An example based on Beijing Subway Line 4 is presented, and the energy-saving operation curves for two trains are calculated and shown in Figure 4. The departure interval of the 2nd train is 92 s. The horizontal axis is the time of the train, and the vertical axis represents the speed.
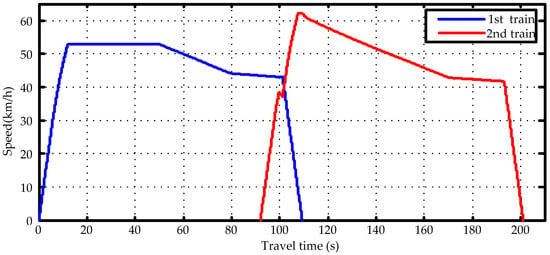
Figure 4.
Optimal energy-saving operation curve of two trains.
The 2nd train coasts at 100 s to fully use the regenerated energy by the second maximum power condition. Under the same departure interval, the results that the 2nd train operates under five-mode operation and operates independently are presented in Table 3.

Table 3.
Results between energy-saving strategies for the two-train system and single train.
However, the energy-saving strategy for two trains is not suitable for multiple trains, as more factors should be considered for the multi-train system. In this paper, the study focuses on the energy-saving operation strategy for the multi-train system in one traction substation with three stations. The 3rd train is added to the system, which reaches the maximum volume of the traction substation. The study on three trains is enough to illustrate the strategy for multiple trains. The main factors contain the departure interval for the 3rd train and dwell time for the 1st train. To guarantee the safe operation of these trains, the following train should keep absolute braking distance after the leading train in moving automatic block system.
3. The Energy-Saving Operation Strategy for Multi-Train System
3.1. The Model of Multi-Train Cooperative Operation
The model for the cooperative operation of the multi-train system is established first to find the energy-saving driving strategy. Assume that there is no energy-saving device on the power supply network, and the regenerative energy can only be reused by other trains. The excess regenerative energy will be consumed through braking resistors on the power supply network. This study takes three-train cooperative operation at the same traction substation as an example to define an objective function. The 1st train departs from Station A to Station B. Then, the 2nd train departs from Station A after the 1st train departs, which can use regenerative braking energy produced by the 1st train. The driving curves for these two processes are based on two-train energy-saving operation strategy. Moreover, the 3rd train departs from Station A behind the 2nd train, which can use the regenerative braking energy produced by the 2nd train. Meanwhile, after certain dwell time, the 1st train departs from Station B again to Station C, which can also use the regenerative braking energy produced by the 2nd train.
Therefore, total energy consumption of the traction substation is:
where Ejtrac is tractive energy consumption for the jth train, and Ejregen is the available regenerative braking energy for the jth train that can be reused by other trains.
The line conditions of traction substation are shown in Table 1, and the various constraints of cooperative operation are shown as follows in unit time Tunit_i (i = 0, 1, 2, …, n). n is the total number of unit times during the travel time (for example, if travel time is 109 s, and unit time Tunit_i is 0.01 s for the algorithm, n is 10,900).
The constraint of speed is: 0 ≤ vi ≤ Vlimit_i, v0 = 0, vn = 0.
The constraint of travel time is: 0 ≤ ti ≤ T, t0 = 0, tn = T.
The constraint of travel distance is: 0 ≤ si ≤ S, s0 = 0, sn = S.
v0, t0 and s0 are the speed, travel time and travel distance when the train starts at one station, and vn, tn and sn are the speed, travel time and travel distance when the train arrives at a new station, respectively.
The constraint of traction coefficient is: 0 ≤ nt ≤ 1.
The constraint of braking force coefficient is: 0 ≤ nb ≤ 1.
The constraint of mode transformation is that maximum power condition and maximum braking condition cannot transform to each other directly unless using coasting mode in the middle.
Traction energy consumption of jth train in unit time etrac_j_i can be calculated as:
The braking energy of jth train in unit time eb_j_i can be calculated as:
where μ is the feedback coefficient of braking. When the braking energy of jth train is more than the total traction energy in unit time, the available regenerate energy of jth train (eregen_j_i) equals to the total traction energy, and vice versa. Moreover, eregen_j_i can be calculated as:
Then Ejtrac and Ejregen of Equation (4) can be calculated as:
All the constraints are important parameters when calculating the driving curves, and the total energy consumption of Equation (4) is the key indicator for the optimum driving strategy.
3.2. Energy-Saving Driving Strategy of Multiple Trains
Based on the model of multi-train cooperative operation, the energy-saving operation strategy for the multi-train system is aiming to minimize the total energy consumption under one traction substation. Based on the two-train energy-saving operation strategy, the 1st train has already finished its first trip and stopped at Station B, and the 2nd train is on its trip to Station B. The research for multi-train system tries to find the available regenerate energy made by the 2nd train that can be used for the 3rd train and the 1st train. The constraint of the 3rd train is departure interval, which is affected by the passenger flow of the line, and the constraint of the 1st train is dwell time, which is affected by the passenger flow of Station B.
The 3rd train and the 1st train are discussed separately. The energy-saving operation strategy is designed to ensure that the 3rd train uses the regenerate energy preferentially. According to the two-train energy-saving strategy, the 3rd train, operating under four-mode operation or five-mode operation, can make full use of the 2nd train’s regenerate energy.
The driving curves for the multi-train system when the 3rd train operates under four-mode operation are presented in Figure 5. ttrm_k is the kth switching point for train m. TA is the travel time from Station A to Station B, and TB is the travel time from Station B to Station C. TDB is the dwell time of Station B. TI2 is the departure interval for the 2nd train, and TI3 is the departure interval for the 3rd train. If the departure interval for the 3rd train ttr3_1(TI3) is little before ttr2_5 and enables the 3rd train to accelerate with the regenerate energy from the 2nd train, four-mode operation is suitable for the 3rd train. In addition, if the departure interval for the 3rd train ttr3_1(TI3) is after ttr2_5, four-mode operation is also suitable for the 3rd train, and the 3rd train can use the regenerated energy as much as possible.
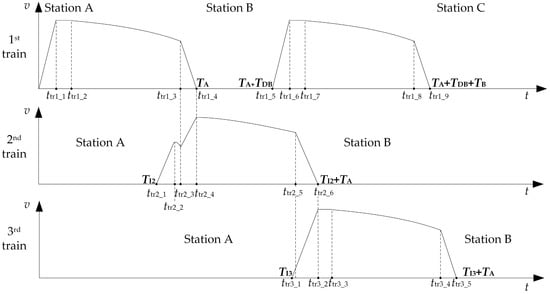
Figure 5.
The driving curves for multi-train system when the 3rd train operates under four-mode operation.
If departure interval for the 3rd train ttr3_1(TI3) is far before ttr2_5, as shown in Figure 6, the 3rd train can operate in coasting condition for a while to make the second maximum power condition overlap with the braking condition for the 2nd train. Thus, the 3rd train operates under five modes (maximum power, coasting, maximum power, coasting and maximum braking) during the trip. For this circumstance, five-mode operation is suitable for the 3rd train. After starts at ttr3_1, the 3rd train coasts from ttr3_2 to ttr3_3, and traction from ttr3_3(ttr2_5) to ttr3_4(ttr2_6).
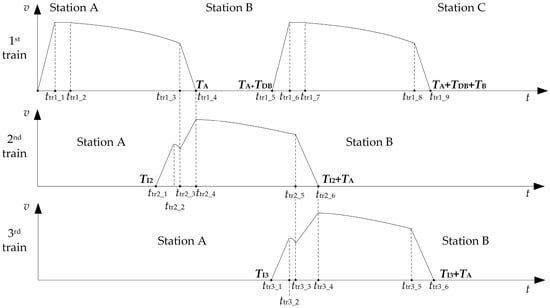
Figure 6.
The driving curves for multi-train system when the 3rd train operates under five-mode operation.
When the 3rd train operates using the regenerated energy, the available energy for the 1st train departing again from Station B is discussed. The different dwell times are considered. The 1st train only operates under four-mode operation so the departure can be regarded as a new beginning of circulation for the multi-train system operation, and the 2nd train and the 3rd train can be determined. The traction curves for different dwell times are shown in Figure 7 when the 3rd train operates in four-mode operation.
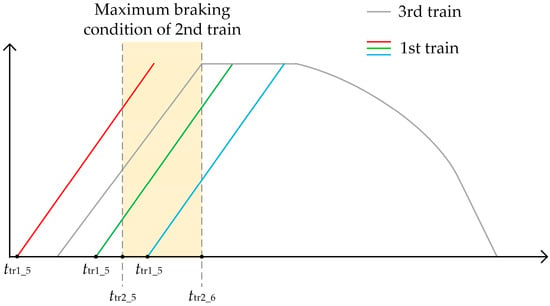
Figure 7.
The traction curves of the 1st train when the 3rd train operates in four-mode operation.
The colored lines are the different traction curves for the 1st train. The silver curve is the driving curve for the 3rd train. The orange background is the period that the 2nd train operates in maximum braking condition. The ttr1_5 equals to the travel time from Station A to Station B plus dwell time at Station B (TA + TDB). There are four situations for the 1st train to use the regenerative braking energy produced by the 2nd train. Define the ttr1_start and ttr1_end to be the start time and end time for the 1st train to use the regenerative energy. The 2nd train’s switching points are chosen for discussion.
- When ttr1_5 ≤ ttr2_5 ≤ ttr1_6, the 1st train can use regenerative braking energy provided by the 2nd train. Meanwhile, the overlapping period is from ttr1_start = ttr2_5 to ttr1_end = ttr1_6.
- When ttr1_5 ≤ ttr2_5 ≤ ttr2_6 ≤ ttr1_6, the 1st train can use regenerative braking energy provided by the 2nd train. Meanwhile, the overlapping period is from ttr1_start = ttr2_5 to ttr1_end = ttr2_6.
- When ttr2_5 ≤ ttr1_5 ≤ ttr2_6, the 1st train can use regenerative braking energy provided by the 2nd train. Meanwhile, the overlapping period is from ttr1_start = ttr1_5 to ttr1_end = ttr2_6.
- Otherwise, there is no available regenerative braking energy when the 1st train departs from Station B again.
The traction curves for different dwell times are shown in Figure 8 when the 3rd train operates in five-mode operation. The 3rd train’s switching points are chosen for discussion because the 3rd train is the main train that needs to be adjusted.
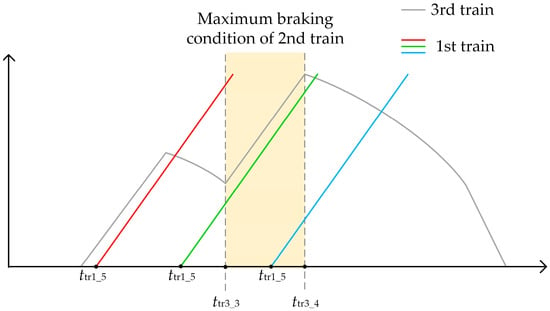
Figure 8.
The traction curves of the 1st train when the 3rd train operates in five-mode operation.
- When ttr1_5 ≤ ttr3_3 ≤ ttr1_6, the 1st train can use regenerative braking energy provided by the 2nd train. Meanwhile, the overlapping period is from ttr1_start = ttr3_3 to ttr1_end = ttr1_6.
- When ttr1_5 ≤ ttr3_3 ≤ ttr3_4 ≤ ttr1_6, the 1st train can use regenerative braking energy provided by the 2nd train. Meanwhile, the overlapping period is from ttr1_start = ttr3_3 to ttr1_end = ttr3_4.
- When ttr3_3 ≤ ttr1_5 ≤ ttr3_4, the 1st train can use regenerative braking energy provided by the 2nd train. Meanwhile, the overlapping period is from ttr1_start = ttr1_5 to ttr1_end = ttr3_4.
- Otherwise, there is no available regenerative braking energy when the 1st train departs from Station B again.
Based on the discussion above, the main idea for the proposed energy-saving operation strategy for the multi-train system is:
- The 3rd train operates under four-mode operation or five-mode operation and is ensured to use the regenerate energy firstly.
- The 1st train under different dwell time tries to use the regenerate energy of the 2nd train as much as possible.
- The energy-saving operation strategy only provides the available operation modes (four-mode operation and five-mode operation) for the multi-train system, which can be regarded as the guidance for the computing method. The computing method solves the switching points and the drive curves under different modes and finally chooses the optimum drive curves and the optimum operation mode for the multi-train system.
The computing method is as important as the energy-saving operation strategy because the drive curves are the final demand for the operation of trains. Accordingly, a computing method based on heuristic algorithm is proposed to evaluate the energy-saving operation strategy.
3.3. Computing Method for Energy-Saving Driving Strategy of Multiple Trains
Although the operation modes of the 3rd train can be chosen based on the departure interval, it cannot be determined directly. The computing method is needed to calculate energy consumption under both operation modes to determine which one is optimum. The computing method for the energy-saving operation strategy is to find the best driving mode and driving curves for the multi-train system. Based on the heuristic algorithm and the energy-saving operation strategy for the two-train system, the whole algorithm of the proposed computing method is described in Figure 9.
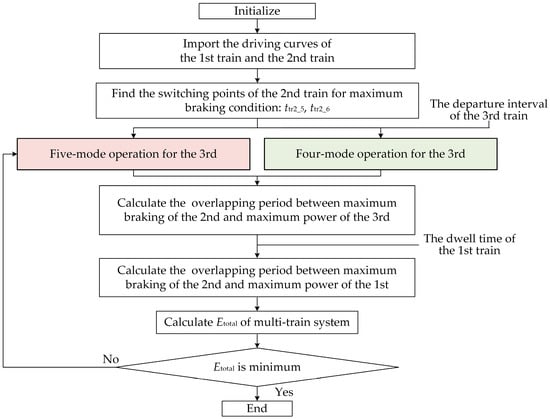
Figure 9.
The whole algorithm of the proposed computing method.
The details of the algorithm for the computing method are described as follows:
- Initialize. Determine the parameters of urban subway train and traction substation.
- Import the line conditions (including the limiting velocity, the unit curve and slope resistance).
- Import the driving curves of the 1st train and the 2nd train which can be obtained based on the energy-saving operation strategy for the two-train system.
- Find the switching points ttr2_5 and ttr2_6 (directly obtain from the driving curves).
- Based on different operation modes, calculate the minimum energy consumption of the 3rd train(E3trac). The calculating processes of five-mode operation and four-mode operation for the 3rd train are illustrated in Figure 10 and Figure 11 in detail.
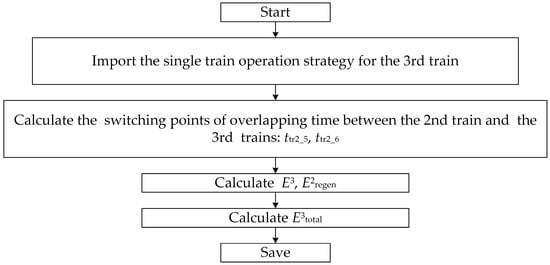 Figure 10. The calculation process of the 3rd train under four-mode operation.
Figure 10. The calculation process of the 3rd train under four-mode operation.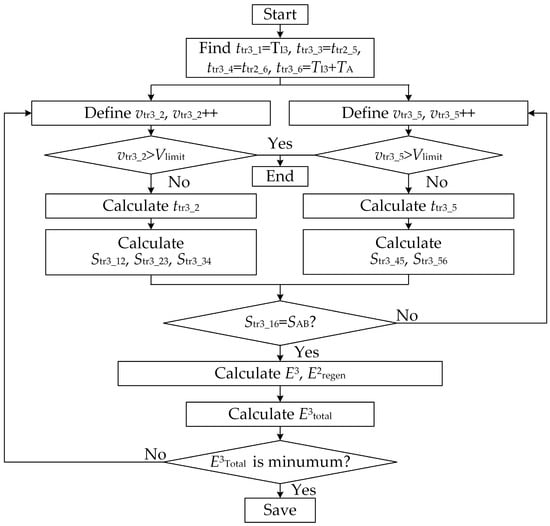 Figure 11. The calculation process of the 3rd train under five-mode operation.
Figure 11. The calculation process of the 3rd train under five-mode operation. - Calculate Etotal. The calculating progress can be realize by Equations (4)–(9). Choose minimum energy consumption (Emin) and determine the optimum driving mode and driving curves for the 1st train and the 3rd train.
The calculation process of the 3rd train under four-mode operation is shown in Figure 10. The driving curve and switching points for the 3rd train can be directly obtained because it is same as the 1st train according to the single train operation strategy. Then, the overlapping time between the 2nd train’s maximum braking condition and the 3rd train’s maximum power condition can be calculated. Total energy consumption of the 3rd train can be obtained.
If the 3rd train adopts the driving strategy of five-mode operation to take full advantage of regenerative braking energy, it needs to operate under maximum power condition when the 2nd train operates under maximum braking condition. Since there is not just one driving curve under five-mode operation for a specific departure interval of the 3rd train, the calculating process based on the heuristic algorithm is proposed to find minimum energy consumption, as shown in Figure 11. The key to obtain the optimum driving curves is the calculation of switching points. The calculating process is corresponding to Figure 6. The vtrm_k is the velocity at ttrm_k for train m. Strm_ij is the distance traveled by the mth train in the period (ttrm_i, ttrm_j).
The details of the calculating process are described as follows:
- Determine the known switching points of the 3rd train. ttr3_1 equals to the departure interval of the 3rd train (TI3), ttr3_3 is the switching point when the 2nd train starts braking (ttr2_5), ttr3_4 is the switching point when the 2nd train stops braking (ttr3_6), and ttr3_6 equals to the departure interval plus the travel time from Station A to Station B (TI3 + TAB). The unknown switching points are ttr3_2 and ttr3_5.
- Two loops are built to gain the unknown switching points. Firstly, define the vtr3_2. Then, ttr3_2 can be calculated based on the line conditions. Since the ttr3_1, ttr3_2, ttr3_3 and ttr3_4 are known, the Str3_12, Str3_23 and Str3_34 can be calculated.
- Under the circumstance that the vtr3_2 is determined, define vtr3_5. The ttr3_5 can be calculated. Since the ttr3_4, ttr3_5 and ttr3_6 are known, the Str3_45 and Str3_56 can be calculated.
- If the total travel distance Str3_16(Str3_12 + Str3_23 + Str3_34 + Str3_45 + Str3_56) does not equals to the distance SAB between Station A and Station B, the vtr3_5 will be added with a small increment and back to the Step 3 of the process. Moreover, if Str3_16 equals the S, the current (ttr3_2, vtr3_2) and (ttr3_5, vtr3_5) will be saved as one solution for the five-mode operation.
- Calculate total energy consumption of the 3rd train E3total.
- A small increment is added to vtr3_2, and back to step 2, 3, 4 again.
- Choose minimum energy consumption of the 3rd train, and the corresponding driving curve is defined as the optimum driving curve for the 3rd train under five-mode operation.
To keep absolute braking distance between two trains, we must modify current speed before they crash. Based on the diagram of absolute braking distance in moving automatic block system, which is shown in Figure 12, the tracing distance Ltrace can be obtained as:
where v is the speed of the train, Vmax is the maximum speed, and b is the deceleration coefficient of the train, its unit is m/s2. Lsafety is the safe distance between the parking target position for the following train and the parking position of the leading train, Ltrain is the length of the train.
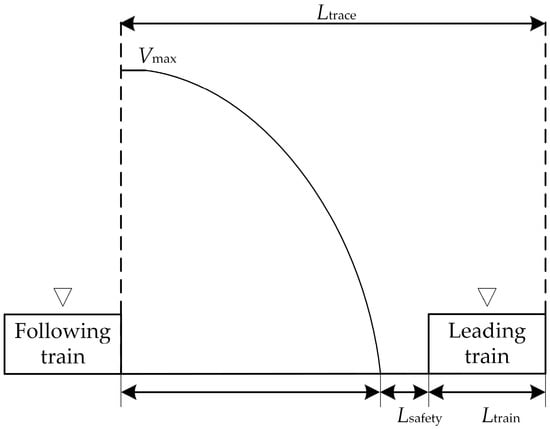
Figure 12.
Diagram of absolute braking distance in moving automatic block system.
Meanwhile, in moving automatic block, it can lead to an intensive queue in the same traction substation when the dwell time is too long. If two trains depart at the same time, the peak power will suddenly increase so that the power supply network may overload. To avoid the problem, the following train is scheduled to depart before or after 10 s when the leading train starts.
The calculating process of modifying speed in the multi-train system is shown in Figure 13. The vlast and vcurrent are the velocities of last unit time and current unit time, and the Slast and Scurrent are the travel distances of last unit time and current unit time. The ΔS is the distance between two trains. The vcurrent and ΔS in the calculating process are verified to modify the velocity.
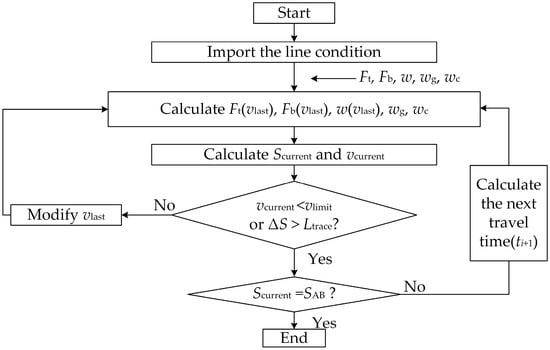
Figure 13.
Process of modifying speed in multi-train system.
The velocity of current unit time vcurrent can be calculated as:
where M is the mass of the train, and the traction force Ft(v), braking force Fb(v), running resistance w(v), unit gradient resistance wg and unit curve resistance wc can be obtained from Section 2.1 and Section 2.2. The travel distance of current unit time Scurrent can be calculated as:
The total energy can be calculated by Equations (4)–(9). Then, the computing method for energy-saving driving strategy of multiple trains is ready to obtain the optimum driving curves and the minimum energy consumption.
3.4. Conclusion of the Energy-Saving Operation Strategy
The conclusion of the proposed energy-saving operation strategy is shown in Figure 14. The 3rd train departures from Station A under the specific departure interval, and the 1st train departures from Station B again under the specific dwell time. Based on the energy-saving strategy for the two-train system, the driving modes for the 1st train and the 3rd train are designed by the energy-saving operation strategy for multi-train system to fully use the regenerate energy of the 2nd train. The driving curves under different operation modes are obtained by the computing method considering the line conditions and moving automatic block system. The driving curve with minimum energy consumption is chosen as the optimum curve; at the same time, the corresponding operation mode is chosen as the optimum energy-saving operation strategy. In some papers, the energy-saving operation strategy and the computing method are collectively called energy-saving strategy, which is not much different. Moreover, the computing method can also calculate total energy consumption under different departure intervals and dwell times, which can also adjust the train dispatch to a certain degree.
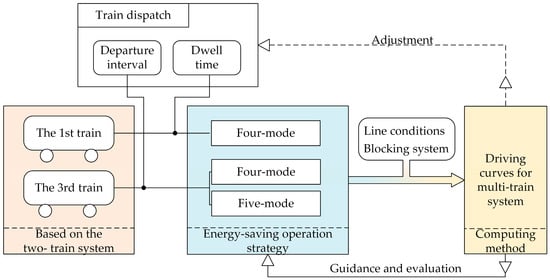
Figure 14.
The conclusion of proposed energy-saving operation strategy.
4. Simulation Results and Analysis
Based on the energy-saving operation strategy described above, a simulation platform based on Beijing Subway Line 4 is built. The driving curves for the two-train system shown in Figure 4 are the preconditions for the simulation platform. The 1st train departs from Station A based on single train strategy and stops at Station B after 109 s. The 2nd train also departs from Station A under five-mode operation. Then, energy consumption results under different departure internals and operation modes for the 3rd train are presented, and the dwell time for the 1st train is maintained at 30 s to make the results clearly for the moment. Then, energy consumption under three different dwell times (30 s, 40 s and 50 s) are presented. The analysis of the simulation results is given, and the correctness and validity of the proposed energy-saving operation strategy are verified.
4.1. Results of Simulation
When the departure interval of the 3rd train is between 110 s and 190 s, the five-mode operation is available for the 3rd train. The dwell time of the 1st train is maintained at 30 s.
Results of energy consumption for the 1st train and the 3rd train are shown in Figure 15a. The relationship between total energy consumption and the departure intervals of the 3rd train in traction substation is presented in Figure 15b. The relationship between the energy-saving efficiency and the departure intervals of the 3rd train is also illustrated in the same figure. During 129 to 148 s, the 3rd train does not depart to avoid peak power problem when the 1st train starts, as shown in Figure 15. Hence, there is no energy consumption of the 3rd train.
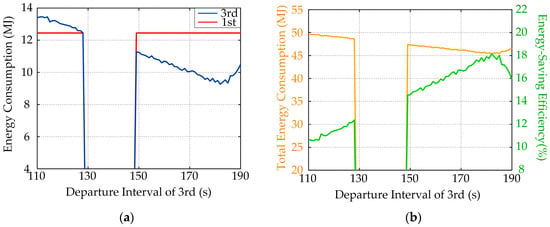
Figure 15.
Results under five-mode operation: (a) energy consumption of the 1st train and the 3rd train; and (b) total energy consumption and energy-saving efficiency.
The 3rd train adopting the driving strategy with four-mode operation is available when the departure interval of the 3rd train is between 110 s and 210 s. Results of energy consumption for the 1st train and the 3rd train are shown in Figure 16a. The relationship between total energy consumption and the departure intervals of the 3rd train in traction substation is illustrated in Figure 16b. The relationship between the energy-saving efficiency and the departure intervals of the 3rd train is also illustrated in the same figure. Similarly, as shown in Figure 16, the 3rd train does not depart during 129 to 148 s. Hence, there is no energy consumption of the 3rd train.
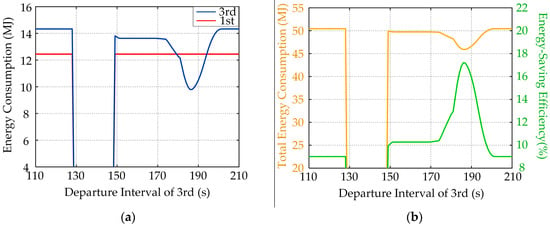
Figure 16.
Results under four-mode operation: (a) energy consumption of the 1st train and the 3rd train; and (b) total energy consumption and energy-saving efficiency.
The energy consumption results under different dwell times are also obtained based on the same strategy and computing method. The dwell time is mainly determined by the passenger flow of each station, and 30 s, 40 s and 50 s are the actual dwell times of Beijing Subway Line 4 at different times of the day. The total energy consumption and energy-saving efficiency results of different dwell times are elaborated in Table 4.

Table 4.
Total energy consumption under different dwell times of 1st train.
4.2. Analysis
Based on the simulation results, analysis of the energy-saving operation strategy for multiple trains is illustrated in detail as follows:
- When the departure interval and the dwell time are certain, the optimum operation mode and driving curves for the multi-train system can be obtained by the proposed energy-saving operation strategy. For example, when the dwell time of the 1st train is 30 s, and the departure interval is between 110 s and 186 s, the five-mode operation is suitable for the 3rd train, and, when the departure interval is after 186 s, four-mode operation is suitable for the 3rd train. The driving curves can be obtained by the corresponding computing method.
- When the dwell time is specified and the departure interval is adjustable, the optimum departure interval can be obtained to realize minimum energy consumption for the multi-train system by the proposed energy-saving operation strategy. For example, when the dwell time of the 1st train is 30 s, the optimum departure interval for the 3rd train is 182 s and the current energy-saving efficiency is 18.15%.
- When the dwell time is adjustable, the optimum dwell time for the 1st train can be obtained to make full use of the 2nd train’s regenerate energy. For example, when the dwell time is 50 s, the total energy consumption is the minimum, and the energy-saving efficiency is 18.24%.
- The computing method can work under complex circumstance considering the line conditions and the moving automatic block system. For example, the 3rd train is not allowed to depart when the 1st train starts accelerating.
- The proposed energy-saving operation strategy is suitable for both online and offline operation. When the departure interval and the dwell time are given by train dispatch, the operation strategy with velocity adjustment and moving automatic block system can gain the driving curves quickly. Moreover, the strategy is also suitable for offline calculation because energy consumption results under different departure intervals and dwell times can be calculated to guide and adjust the train dispatch.
- The proposed energy-saving operation strategy not only can be applied to the three-train system but can also be generalized to other multi-train systems. As in the previous example, one traction substation contains at most three trains, so the three trains can be regarded as a group. All the trains on one subway line depart by groups. For the three-train group, after the 1st train departs again from Station B, the whole system can be regarded to operate for a new circulation, so the energy-saving operation strategy is fit for the 2nd train and the 3rd train departing from station B again. For other multi-train systems that one traction substation contains more than three trains, the computing method is also able to calculate the driving curves for rest of the trains under different dwell times and departure intervals.
5. Conclusions
In this paper, an energy-saving operation strategy for multiple trains system is proposed. The strategy, aiming to fully use the regenerate energy, can obtain the optimum operation mode and driving curves for the multi-train system under complex operation conditions. The novelty of this paper is that the proposed strategy can take full use of the regenerated energy, and the algorithm of computing method is easy that can be calculated both online and offline, at the same time all the constraints such as line conditions, velocity limitation and moving automatic block system can be considered. Firstly, the paper introduced the previous research on the single train and two-train system combined with a real example (Beijing Subway Line 4). The research is fundamental for the study of the multi-train system. Then, the model of the multi-train system is built. Based on the model, the energy-saving operation strategy under different circumstances is discussed. The operation modes under different departure intervals for the 3rd train and the utilization of regenerate energy under different dwell time of the 1st train are illustrated in detail. Meanwhile, the computing method based on the heuristic algorithm is proposed to obtain the driving curves. The method can obtain energy consumption results under different situations. The driving mode and driving curve that can save the most energy are chosen as the optimum. The results for different departure intervals and dwell times are also instructive for train dispatch. Finally, a simulation platform based on Beijing Subway Line 4 is built. The results show the validity and efficiency of the proposed energy-saving operation strategy. The proposed strategy of the multi-train system can save 18.24% energy at most, and solve the problems brought by previous studies that either concentrate on a single train, or not fully consider the complex contrasts. The strategy can realize both online and offline calculation with simple algorithm under complex circumstances and can be easily generalized to other multi-train systems.
Acknowledgments
This research was supported by Chinese National Key Research and Development (R & D) Program 2017YFB1201304-04 and the Fundamental Research Funds for the Central Universities E15JB00220.
Author Contributions
Jianqiang Liu conceived and designed the experiments; Nan Zhao performed the experiments; Nan Zhao and Jianqiang Liu analyzed the data; and Nan Zhao wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Ft(v) | Traction force |
| w(v) | Running resistance |
| wc | Unit curve resistance |
| Ejtrac | Tractive energy consumption for the jth train |
| Tunit_i | Unit time |
| vi | Speed |
| si | Travel distance |
| nb | Braking force coefficient |
| eb_j_i | Braking energy of jth train in unit time |
| TX | Travel time from Station X to next station |
| TIm | Departure interval for the train m |
| Strm_ij | Distance traveled by the mth train in the period (ttrm_i, ttrm_j) |
| Vmax | Maximum speed |
| Ltrain | Length of the train |
| vlast | Velocity of last unit time |
| Slast | Travel distance of last unit time |
| ΔS | Distance between two trains |
| Fb(v) | Braking force |
| wg | Unit gradient resistance |
| Etotal | Total energy consumption |
| Ejregen | Available regenerative braking energy for the jth train |
| n | Total number of unit times |
| ti | Travel time |
| nt | Traction coefficient |
| etrac_j_i | Traction energy consumption of jth train in unit time |
| ttrm_k | kth switching point for train m |
| TDX | Dwell time of Station X |
| vtrm_k | Velocity at ttrm_k for train m |
| Ltrace | Tracing distance |
| Lsafety | Safe distance |
| b | Deceleration coefficient |
| vcurrent | Velocity of current unit time |
| Scurrent | Travel distance of current unit time |
| M | Mass of the train |
References
- Liu, J.; Wei, Y.; Hu, H. research on the optimization control method of energy-saving operation for high-speed train. China Railw. Soc. 2014, 36, 7–12. (In Chinese) [Google Scholar]
- Albrecht, A.R.; Howlett, P.G.; Pudney, P.J.; Vu, X. Energy-efficient train control: From local convexity to global optimization and uniqueness. Automatica 2013, 49, 3072–3078. [Google Scholar] [CrossRef]
- Howlett, P.G.; Pudney, P.J.; Vu, X. Local energy minimization in optimal train control. Automatica 2009, 45, 2692–2698. [Google Scholar] [CrossRef]
- Wang, Q.; Feng, X. Optimal switching for control conditions of punctual and energy efficient operation of train. China Railw. Soc. 2016, 37, 91–98. (In Chinese) [Google Scholar]
- Yang, X.; Li, X.; Ning, B.; Tang, T. A Survey on energy-efficient train operation for urban rail transit. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2–13. [Google Scholar] [CrossRef]
- Albrecht, A.R.; Howlett, P.G.; Pudney, P.J.; Vu, X.; Zhou, P. Energy-efficient train control: The two-train separation problem on level track. J. Rail Trans. Plan. Manag. 2015, 5, 163–182. [Google Scholar] [CrossRef]
- Yang, X.; Li, X.; Gao, Z.; Wang, H.; Tang, T. A cooperative scheduling model for timetable optimization in subway systems. IEEE Trans. Intell. Transp. Syst. 2013, 14, 438–447. [Google Scholar] [CrossRef]
- Yang, X.; Li, X.; Ning, B.; Tang, T. An optimisation method for train scheduling with minimum energy consumption and travel time in metro rail systems. Transp. B Transp. Dyn. 2015, 3, 79–98. [Google Scholar] [CrossRef]
- Yang, X.; Chen, A.; Li, X.; Ning, B.; Tang, T. An energy-efficient scheduling approach to improve the utilization of regenerative energy for metro systems. Transp. Res. Part C 2015, 57, 13–29. [Google Scholar] [CrossRef]
- Yang, X.; Chen, A.; Ning, B.; Tang, T. A stochastic model for the integrated optimization on metro timetable and speed profile with uncertain train mass. Transp. Res. Part B Methodol. 2016, 91, 424–445. [Google Scholar] [CrossRef]
- Bin, N.; Jing, X.; Shigen, G.; Lingying, Z. An integrated control model for headway regulation and energy saving in urban rail transit. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1469–1478. [Google Scholar]
- Li, X.; Lo, H.K. An energy-efficient scheduling and speed control approach for metro rail operations. Transp. Res. Part B 2014, 64, 73–89. [Google Scholar] [CrossRef]
- Li, X.; Lo, H.K. Energy minimization in dynamic train scheduling and control for metro rail operations. Transp. Res. Part B 2014, 70, 269–284. [Google Scholar] [CrossRef]
- Su, S.; Li, X.; Tang, T.; Gao, Z. A subway train timetable optimization approach based on energy-efficient operation strategy. IEEE Trans. Intell. Transp. Syst. 2013, 14, 883–893. [Google Scholar] [CrossRef]
- Su, S.; Tang, T.; Li, X.; Gao, Z. Optimization of multitrain operations in a subway system. IEEE Trans. Intell. Transp. Syst. 2014, 15, 673–685. [Google Scholar]
- Liu, J.; Guo, H.; Yu, Y. Research on the cooperative train control strategy to reduce energy consumption. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1134–1142. [Google Scholar] [CrossRef]
- Liu, H.; Mao, B.; He, T.; Ding, Y.; Wang, X. Study on tracking operations between trains of difference block modes and simulation system. China Railw. Soc. 2005, 27, 121–125. (In Chinese) [Google Scholar]
- Gu, Q.; Tang, T.; Song, Y. A survey on energy-saving operation of railway transportation systems. Meas. Control 2010, 43, 209–211. [Google Scholar] [CrossRef]
- Gu, Q.; Tang, T.; Cao, F.; Song, Y. Energy-efficient train operation in urban rail transit using real-time traffic information. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1216–1233. [Google Scholar] [CrossRef]
- Gu, Q.; Meng, Y.; Ma, F. Energy saving for automatic train control in moving block signaling system. China Commun. 2014, 11, 12–22. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, J.Q.; Tian, W.; Shahidehpour, M.; Krishanurthy, M. Harvesting for the electrification of railway stations: Getting a charge from the regenerative braking of trains. IEEE Electr. Mag. 2014, 2, 39–48. [Google Scholar] [CrossRef]
- Zhen, T.; Zhang, M. Design and calculation of traction power supply system. In Traction Power Supply System for Urban Rail Transit, 1st ed.; Su, G.R., Ed.; China Railway Publishing House: Beijing, China, 2003; Volume 6, pp. 134–143. ISBN 978-7-11-303674-4. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).