Comparative Performance Analysis of Optimal PID Parameters Tuning Based on the Optics Inspired Optimization Methods for Automatic Generation Control

Abstract

The Optics Inspired Optimization (OIO) algorithm is a new metaheuristic optimization method. In this paper, the OIO algorithm was proposed for automatic production control parameters in electrical power systems. The performance of the proposed algorithm was realized on two power systems that have different structures. The first structure is a two-area interconnected thermal reheat power system and the other one is a two-area interconnected multi-unit hydro-thermal power system. The results obtained with the proposed algorithm were compared with an artificial bee colony and particle swarm optimization, initial values are randomly defined that are commonly used in literature. The results were examined using four different cost functions based on area control error. Considering the obtained results, the proposed algorithm reached to the global minimum value with less number of iterations and is more suitable for online optimization. According to the results obtained with this novel method, it has a better performance for maximum overshoot and settling time values when the test systems are implemented.

1. Introduction

The amount of electrical energy consumed per person shows the level of development of a country and the quality of this energy consumed by people is also an important criterion. The system frequency and voltage are the two most important parameters that determine the power quality. Controlling the frequency takes longer than controlling the voltage and it is a more dominant parameter in the power system. Therefore, the primary parameter that should be controlled is frequency [1]. The interconnected power system is created by integration of many areas. Any power changes (supply or demand) that will occur in any of these areas will affect other areas that are connected in terms of frequency and power. In addition, characteristic of the connecting line between the areas connected to the power system is another factor affecting the frequency change. When changes in the frequency of the power system exceeds the limits set, they may create serious instability problems in electrical power system, stop of the plants connected to the system and even black-out of the system at later stages. In such a case, the area feeding from the system will remain de-energized and there will be huge economic losses. Black-outs affected 77 million people in 2015 in Turkey, 150 million people in 2014 in Bangladesh and 620 people in 2012 in India some examples of these huge losses [2]. Therefore, considering these huge economic losses caused by system failures, the load-frequency control is a crucial issue that should be taken into consideration in order to prevent such losses.

Behaviors of systems/living creatures such as nature, society, culture, politics, and human have been the source of inspiration of most of the algorithms created from the 1970s until today. Metaheuristic is used for combination of randomness and rules of natural phenomena that are imitated. In recent years, metaheuristic methods have attracted the attention of researchers in many disciplines.

This interest has increased further with the implementation of the actual optimization problems particularly in engineering applications and many other industrial areas. Different metaphors are used for search processes of each metaheuristic optimization. For example, particle swarm optimization algorithm, that is called the PSO in literature, introduced by Eberhart in 1995, models herd behavior of birds [3]; harmony search algorithm, called the HAS, introduced by Geem et al. in 2001, searches for the perfect harmony by using the musical process [4]; bacteria foraging optimization algorithm, called the BFOA, introduced by Passino and Biomimicry in 2002, models the process of the search of a single bacteria for food with the lowest energy [5]. The bacteria chemotaxis algorithm, called the BC, introduced by Muller et al. in 2002, shows reaction tendency of bacteria towards chemical agents in the concentration trend [6]. The artificial bee colony algorithm, called the ABC, proposed by Karaboğa in 2005, simulates foraging behaviors of honey bee swarms [7]. The center power optimization algorithm, called the CFO, proposed by Formato in 2007, makes an analogy between the search operation in the decision space for maximum value of objective function and moving searches along the physical space under the effect of gravity [8].

The firefly algorithm, called the FA, proposed by Yang in 2010, is performed based on idealization of light emission characteristics of fireflies [9]. The league championship algorithm, called the LCA, introduced by Kashan in 2009, is based on simulating league games with modelling game analysis methods using experiences of the coaches [10]. The group search optimization, called the GSO, introduced by He et al. in 2009, simulates search behaviors of animals such as feeding, breeding, egg spread and nidification [11]. The gravitational search algorithm, called the GSA, announced by Rashedi et al. in 2009, was established based on the concept of mass interactions and the law of gravity [12]. The teaching-learning based optimization, called the TLBO, announced by Rao et al. in 2011, imitates the teaching-learning process in the classroom between teachers and students [13]. Krill herd algorithm, called the KH, announced by Gandomi et al. in 2012, works by performing simulations of gathering krill swarms together in response to specific biological and environmental processes [14].

Optimization methods have been applied to many problems in power systems such as automatic voltage regulation [15], load frequency control [15,16,17,18,19,20], and optimal power flow [21,22,23]. In the power systems, conventional proportional integral derivative controls (PID) are widely used for Automatic Generation Control. Many studies were conducted to determine the best PID parameters. Metaheuristic methods Bacteria Foraging [24,25,26,27], PSO [28,29,30,31,32,33], Ant Colony Optimization [34], Artificial Bee Colony [35] and Orthogonal Learning Artificial Bee Colony [36] are used in the determination of controller gains. Although these methods seem to be good methods for determining the controller gains, they have problems such as slow convergence and local minimums in the step of global minimum search. Optics inspired optimization (OIO), which is a new metaheuristic method, is found to be showing better performance in terms of these aspects [37,38].

In the literature, the main aim of the current study is to design and implement a new metaheuristic method for optimal design of a PID controller to solve an LFC problem. In this paper, the OIO algorithm was proposed in order to identify the optimal PID controller parameters which is controlling the frequency of an electrical power systems. For this purpose, two different test systems were investigated and named as test system-1 and test system-2 in this paper. The rest of the paper is organized as follows:

Section 1 discusses how PID controller gains were determined by using OIO, PSO, ABC, and other heuristic algorithms in literature and their performances were compared to each other. In Section 2, the mathematical model and block diagram of a two-area test power systems are given. In Section 3, the proposed OIO optimization method is discussed. In Section 4, the integral of squared error (ISE), the Integral of absolute error (IAE), the integral of time multiply squared error (ITSE) and the integral of time multiply absolute error (ITAE) cost functions were used as the performance index. Frequency changes in the two regions and simulation results of the power variation of collection line is obtained for each performance index. Finally, we discuss conclusions in Section 5.

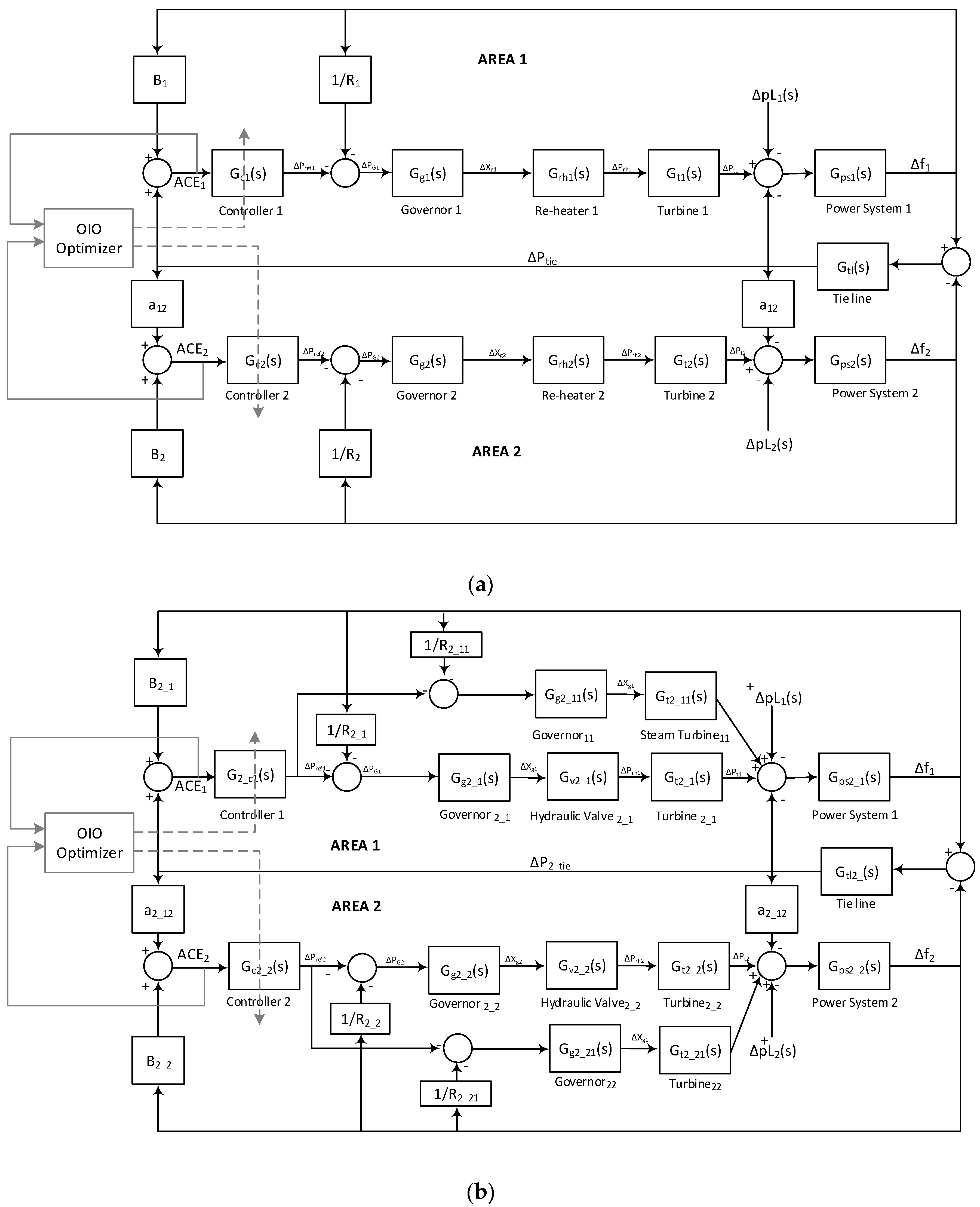
2. Power System Model

Potential/Kinetic energy is converted into mechanical energy by means of turbines and then the mechanical energy is converted into electrical energy via generators in a power plant, which has rotating machines. The simplified equation of motion belonging to this principle is written:

$$T_m-T_e=J\frac{d\omega }{dt}$$

(1)

where, $T_m$ is mechanical momentum, $T_e$ is load moment, J is the moment of inertia, and ω is angular velocity.

An interconnected power system consists of areas connected to each other with tie-line. It is assumed that generator groups, which exist in each of the areas, have a composite structure. The frequency deviations can occur in some areas of the power system. Deviations cause a variation in power flow in the tie-line. In the present case, the variation and area frequency are required to be controlled. Each area provides its own users with energy and the tie-line allows inter-area power flow. Therefore, when there is a sudden load change in an area, frequency in other areas and power flow in tie-lines are affected. Controllers need information about the transient state of each area to return the system to the required steady state. Thus, it could return frequency of the system to the required steady state. If losses in the tie-line are ignored, the power flow in the tie-line can be written as:

$$P_{\mathrm{line}12}=\frac{\left|V_1\right|\cdot \left|V_2\right|}{X_{12}}\sin ({\delta }_1-{\delta }_2)$$

(2)

where V₁ and V₂ are voltage amplitude of the first and second areas, respectively, Δ₁ and Δ₂ are corresponding phase angles, and X₁₂ is the impedance of the tie-line between the two areas. Where the phase angle deviation for each area is written as:

$$\Delta \delta =2\pi {\displaystyle \int \Delta fdt}$$

(3)

Power flow deviation between areas will be:

$$\Delta P_{12}=\frac{\left|V_1\right|\cdot \left|V_2\right|}{X_{12}}\cos ({\delta }_1-{\delta }_2)(\Delta {\delta }_1-\Delta {\delta }_2)=T_{12}(\Delta {\delta }_1-\Delta {\delta }_2)$$

(4)

where the synchronizing moment coefficient of the tie-line is:

$$T_{12}=\frac{\left|V_1\right|\cdot \left|V_2\right|}{X_{12}}\cos ({\delta }_1-{\delta }_2)$$

(5)

When the moment coefficient is written in its place in (4), the power deviation of the tie-line will be:

$$\Delta P_{\mathrm{tie}}=T_{12}(\Delta {\delta }_1-\Delta {\delta }_2)$$

(6)

In consequence of power deviation, $\Delta P_L$ of the system, frequency deviation, power deviation, and control error (Area Control Error—ACE) are as follows:

$$\Delta f=\frac{-\Delta P_{L1}}{\frac{1}{R_1}+\frac{1}{R_2}+D_1+D_2},$$

(7)

$$\Delta P_{\mathrm{tie}}=\frac{-\Delta P_{L1}(\frac{1}{R_2}+D_2)}{\frac{1}{R_1}+\frac{1}{R_2}+D_1+D_2},$$

(8)

$${\mathrm{ACE}}_1=\Delta P_{\mathrm{tie}}+B_1\cdot \Delta f_1,$$

(9)

$${\mathrm{ACE}}_2=B_2\cdot \Delta f_2+a_{12}\cdot \Delta P_{\mathrm{tie}}.$$

(10)

Block diagram of the test system-1 and test system-2 are depicted in Figure 1.

Transfer function of each block is given below:

Governors:

$$\begin{gathered} G_{g1}(s)=G_{g2}(s)=\frac{K_h}{T_h\cdot s+1}, \\ {G}_{g2\_11}(s)=G_{g2\_21}(s)=\frac{K_{2\_1h}}{T_{2\_1h}\cdot s+1}, \\ {G}_{g2\_1}(s)=G_{g2\_2}(s)=\frac{K_{2\_h}}{T_{2\_h}\cdot s+1}. \end{gathered}$$

(11)

Re-heater:

$$G_{rh1}(s)=G_{rh2}(s)=\frac{(K_{r12}\cdot T_{r11})\cdot s+1}{T_{r1}\cdot s+1}.$$

(12)

Turbine:

$$\begin{gathered} \mathrm{Steam}:G_{t1}(s)=G_{t2}(s)=\frac{K_{st1}}{T_t\cdot s+1},G_{t2\_11}(s)=G_{t2\_21}(s)=\frac{K_{st2}}{T_{2t}\cdot s+1}. \\ \mathrm{Hydraulic}:G_{t2\_1}(s)=G_{t2\_2}(s)=\frac{1-s{T}_w}{1+0.5s{T}_w}. \end{gathered}$$

(13)

Valve:

$$G_{V2\_1}(s)=G_{V2\_2}(s)=\frac{T_{Vr}\cdot s+1}{T_{V2}\cdot s+1}.$$

(14)

Power system:

$$\begin{gathered} G_{ps1}(s)=G_{ps2}(s)=\frac{K_g}{T_g\cdot s+1}, \\ {G}_{ps2\_1}(s)=G_{ps2\_2}(s)=\frac{K_{g\_2}}{T_{g\_2}\cdot s+1}. \end{gathered}$$

(15)

Tie-line:

$$\begin{gathered} G_{tl}(s)=\frac{2\pi \cdot T_{12}}{s}, \\ {G}_{tl2\_}(s)=\frac{2\pi \cdot T_{2\_12}}{s}. \end{gathered}$$

(16)

Test system-1 [39,40] and test system-2 [41,42] are widely employed in literature. System parameters used for test system-1 and test system-2 are given below:

Parameters of Test System-1:

Rating of each area = 2000 MW, base power = 2000 MVA, f = 60 Hz, P_r1 = P_r2 = 1000 MW, K_g = 120 Hz/p.u. MW, T_g = 20.0 s, K_r12 = 0.5, T_r1 = T_r2 = 10.0 s, T_g1 = T_g2 = 0.086 s, T_t1 = T_t2 = 0.3 s, R₁ = R₂ = 2.43 Hz/p.u. MW, B₁ = B₂ = 0.425 p.u. MW/Hz, a₁₂ = −1, T₁₂ = 0.0707, ΔP_L1 = 0.01 p.u. MW.

Parameters of Test System-2:

Rating of each area = 2000 MW, base power = 2000 MVA, f = 50 Hz, P_r1 = P_r2 = 1000 MW, K_{2_h} = 1, T_{2_h} = 48.7 s, K_{2_1h} = 1, T_{2_1h} = 0.08 s, K_st2 = 1, T_2t = 0.3 s, T_vr = 5 s, T_v2 = 0.513 s, T_w = 1 s, R_{2_11} = R_{2_21} = 2 Hz/p.u. MW, R_{2_1} = R_{2_2} = 2.4 Hz/p.u. MW, K_{g_2} = 100, T_{g_2} = 20 s, B_{2_1} = B_{2_2} = 0.425 p.u. MW/Hz, a_{2_12} = −1, T_{2_12} = 0.0707 s.

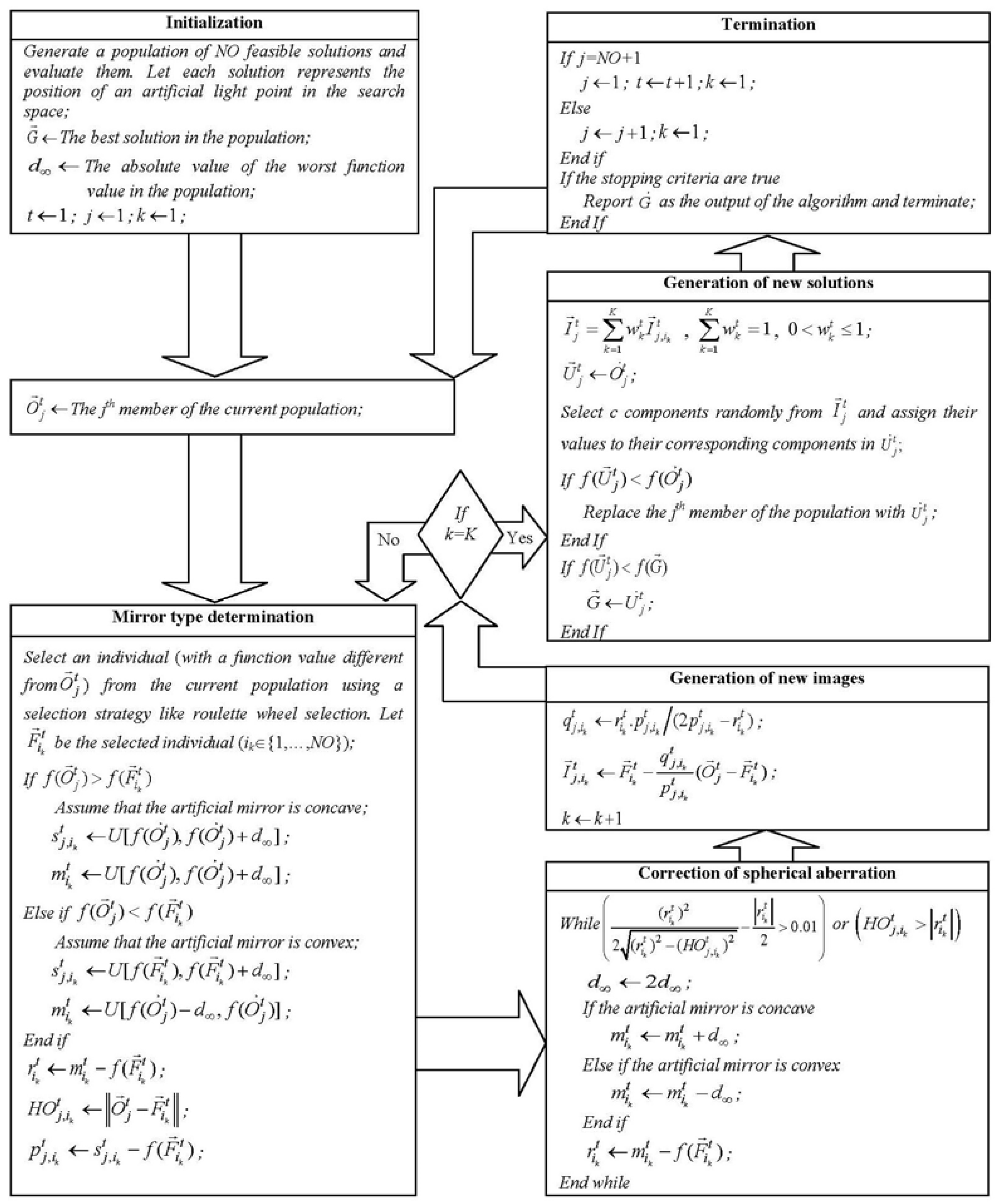
3. Optics Inspired Optimization

OIO algorithm is a physics-based heuristic algorithm introduced by Ali Husseinzadeh Kashan in 2014 [38]. It was developed by being inspired from optics, which is one of the laws of physics. OIO is an algorithm assuming that there are a series of artificial light points (points at Rⁿ⁺¹ matching at Rⁿ are potential solutions to the problem) of an artificial mirror reflecting the image. Each bump is accepting as a convex reflecting surface and each concave is considered as a concave reflecting surface. In this way, an artificial light coming from an artificial light point is reflected back from the function surface of a part of convex or convey surface. Artificial image point (like a new solution in the search area at Rⁿ⁺¹ matching at Rⁿ) is either straight (in the direction of position of light point in the search space) or reverse (outward from position of light point in the search space).

$f(\overrightarrow{X}=[X_1{X}_2\dots X_n])$ is a numerical function that can be minimized with n variables in the n-dimensional decision space defined with $I_d\le X_d\le U_d$, d = 1,… n_i. Let’s remember that $f:R^n\to R,$ we are looking for the general minimum of f finding ${\overrightarrow{X}}^{\ast }\in R^n$ where $f({\overrightarrow{X}}^{\ast })\le f(\overrightarrow{X})$ for $\forall \overrightarrow{X}\in R^n$.

It should be noted that common search and objective space is a vector in ${[X_1{X}_2\dots X_{n}f(\overrightarrow{X})]}_{1\times (n+1)}$ and it is a subset of $R^{n+1}$.

-

${\overrightarrow{O}}_j^t={[o_{j1}^t{o}_{j2}^t\dots o_{jn}^t]}_{1\times n}$ indicates the position of j artificial point of light in the t iteration and n-dimensional space (i.e., j th solution in the population).

-

${\overrightarrow{F}}_{i_k}^t={[f_{i_{k1}}^t{f}_{i_{k2}}^t\dots f_{i_{kn}}^t]}_{1\times n}$ specifies a different point in the search space passing through its own artificial axis (an individual in position). Artificial mirror peak position is determined by ${[f_{i_{k1}}^t{f}_{i_{k2}}^t\dots f_{i_{kn}}^{t}f({\overrightarrow{F}}_{i_k}^t)]}_{1\times n}$ vector. $i_k$ index is randomly selected from $\left\{1,\dots ,NO\right\}$ NO is the number of artificial light points.

-

${\overrightarrow{I}}_{j,i_k}^t={[i_{j1}^t{i}_{j2}^t\dots i_{jn}^t]}_{1\times n}$ specifies location of an image of j artificial point of light in the t iteration in the search space. The artificial image is created through ${\overrightarrow{F}}_{i_k}^t$ by an artificial mirror passing through the main axis.

-

${\overrightarrow{S}}_{j,i_k}^t$ specifies the position of j artificial light point on function/objective axis (objective space) in t iteration. The position of j artificial light point in common search and objective space is given by ${[o_{j1}^t{o}_{j2}^t\dots o_{jn}^t{s}_{j,i_k}^t]}_{1\times (n+1)}$ vector.

-

$P_{j,i_k}^t$ is the distance between j artificial light point on function/objective axis (objective space) and vertex of the artificial mirror $(f({\overrightarrow{F}}_{i_k}^t))$ in t iteration.

-

$q_{j,i_k}^t$ is the distance between j artificial light point on function/objective axis and position of vertex of the artificial mirror on function/objective axis $(f({\overrightarrow{F}}_{i_k}^t))$.

-

$r_{i_k}^t$ is the radius of curvature of an artificial mirror that can pass through the center of curvature of an artificial mirror on the main axis through ${\overrightarrow{F}}_{i_k}^t$.

-

$m_{i_k}^t$ is the position of the center of curvature on function/objective axis (in the objective space).

-

$H{O}_{j,i_k}^t$ is the height of j artificial light point from the artificial main axis in t iteration.

-

$H{I}_{j,i_k}^t$ is the height of image of j artificial light point from the artificial main axis in t iteration.

-

$K_{j,i_k}^t$ is the value of lateral deviation on artificial mirror reflecting the image of j artificial light point in t iteration.

It is possible to express the general mechanism of the OIO as follows: first, NO individuals are randomly generated to create the initial positions of artificial light points in the search space; then, each j artificial light point in the search space of t iteration and ${\overrightarrow{O}}_j^t=[o_{j1}^t{o}_{j2}^t\dots o_{jn}^t]$ $(j=1,\dots ,NO)$ is put in front of the artificial mirror with a distance of $P_{j,i_k}^t$ from the corner of the mirror (in the common search and objective space positioned at $[o_{j1}^t{o}_{j2}^t\dots o_{jn}^t{s}_{j,i_k}^t]$ and its artificial image is created in the search and objective space with a distance of $q_{j,i_k}^t$ from the main axis (on function/objective axis) where ${\overrightarrow{F}}_{i_k}^t$ point passes the axis (${\overrightarrow{F}}_{i_k}^t$ is randomly selected from the population in case $f({\overrightarrow{F}}_{i_k}^t)$ differs from $f({\overrightarrow{O}}_j^t))$. The radius of curvature of the artificial mirror is $r_{i_k}^t$. The position of the artificial image is produced by an artificial image position ${\overrightarrow{I}}_{j,i_k}^t$ that can be a new solution to the problem in the search space by matching with the solution space. The flow chart of OIO algorithm is shown in Figure 2.

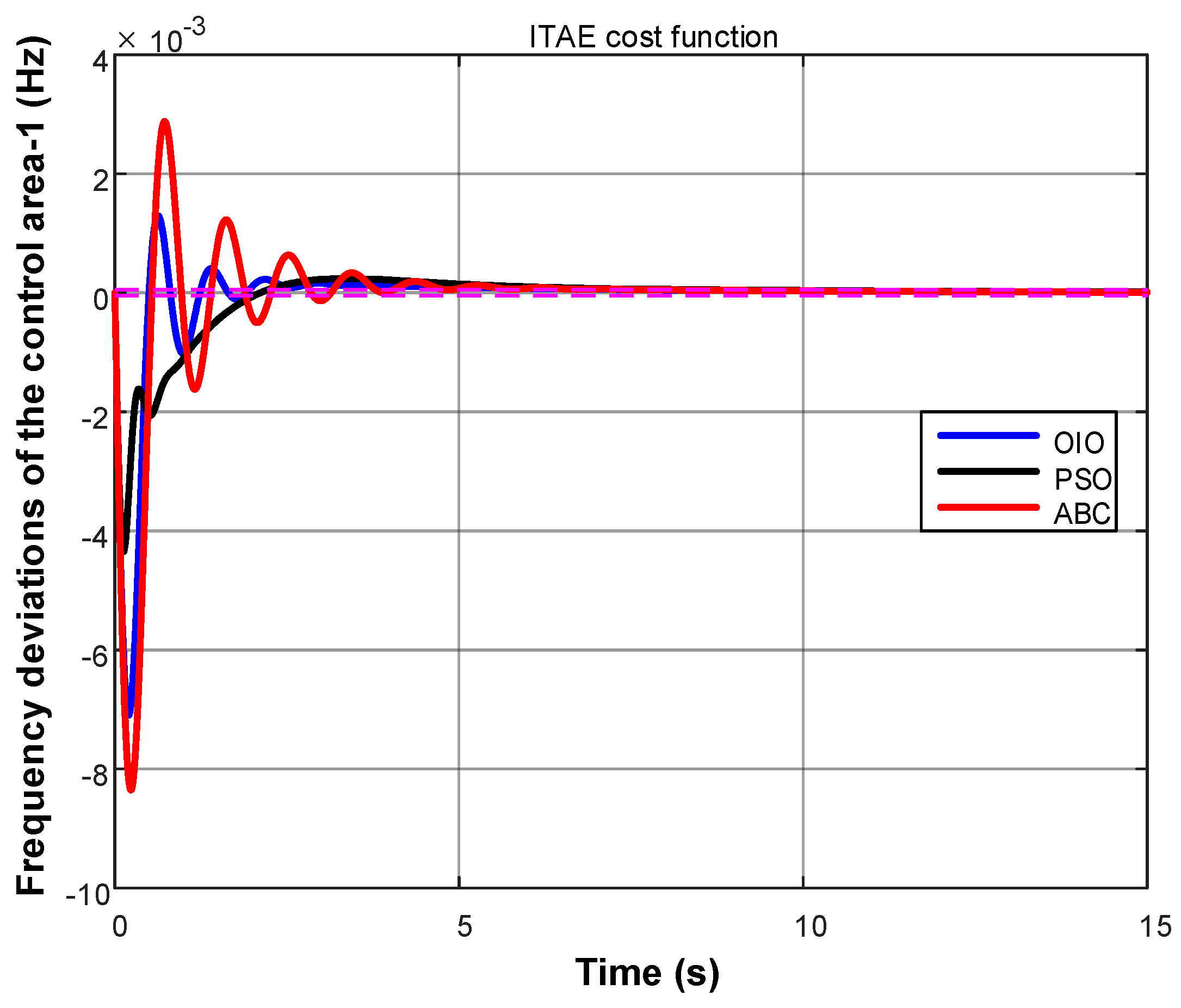
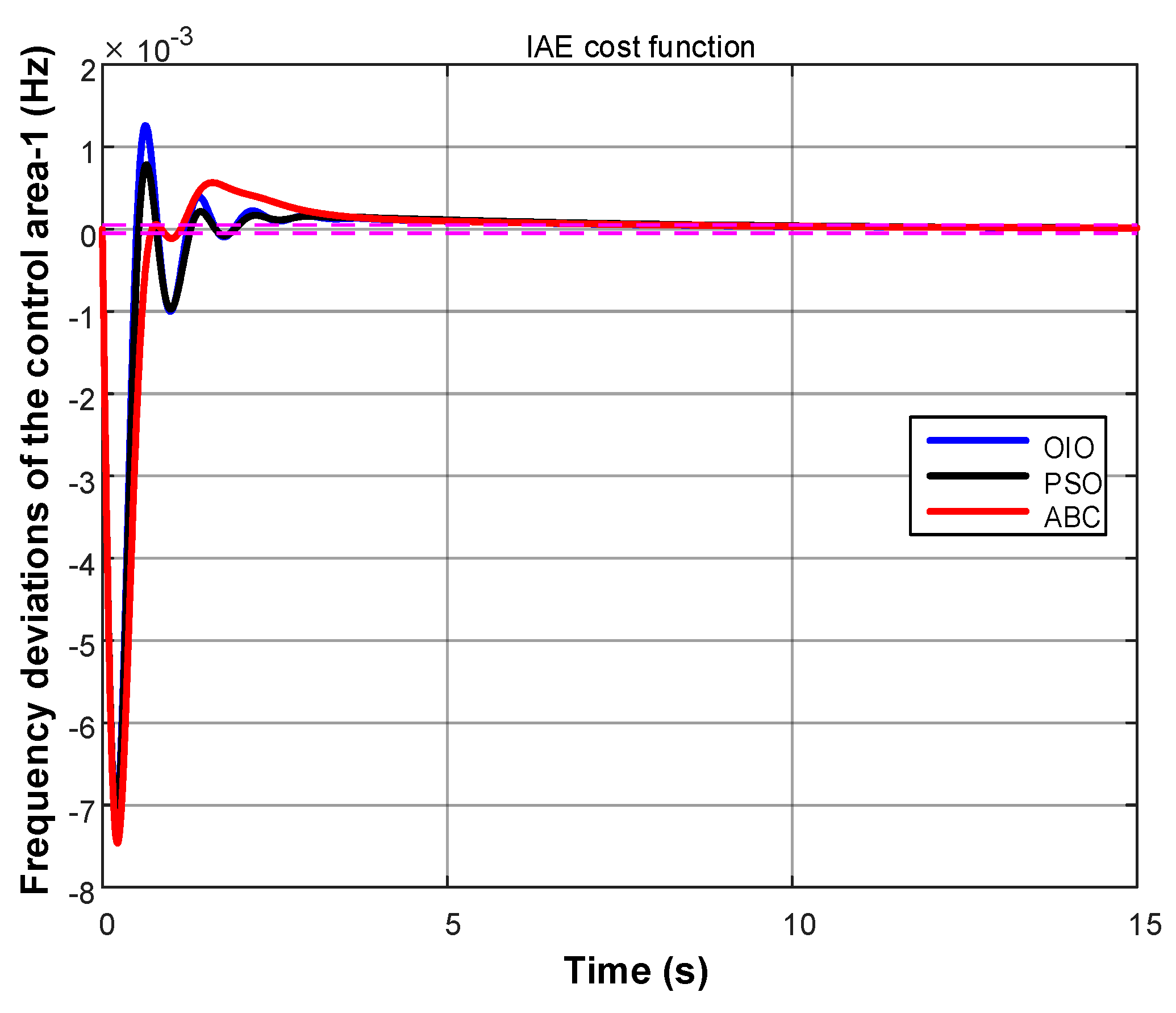
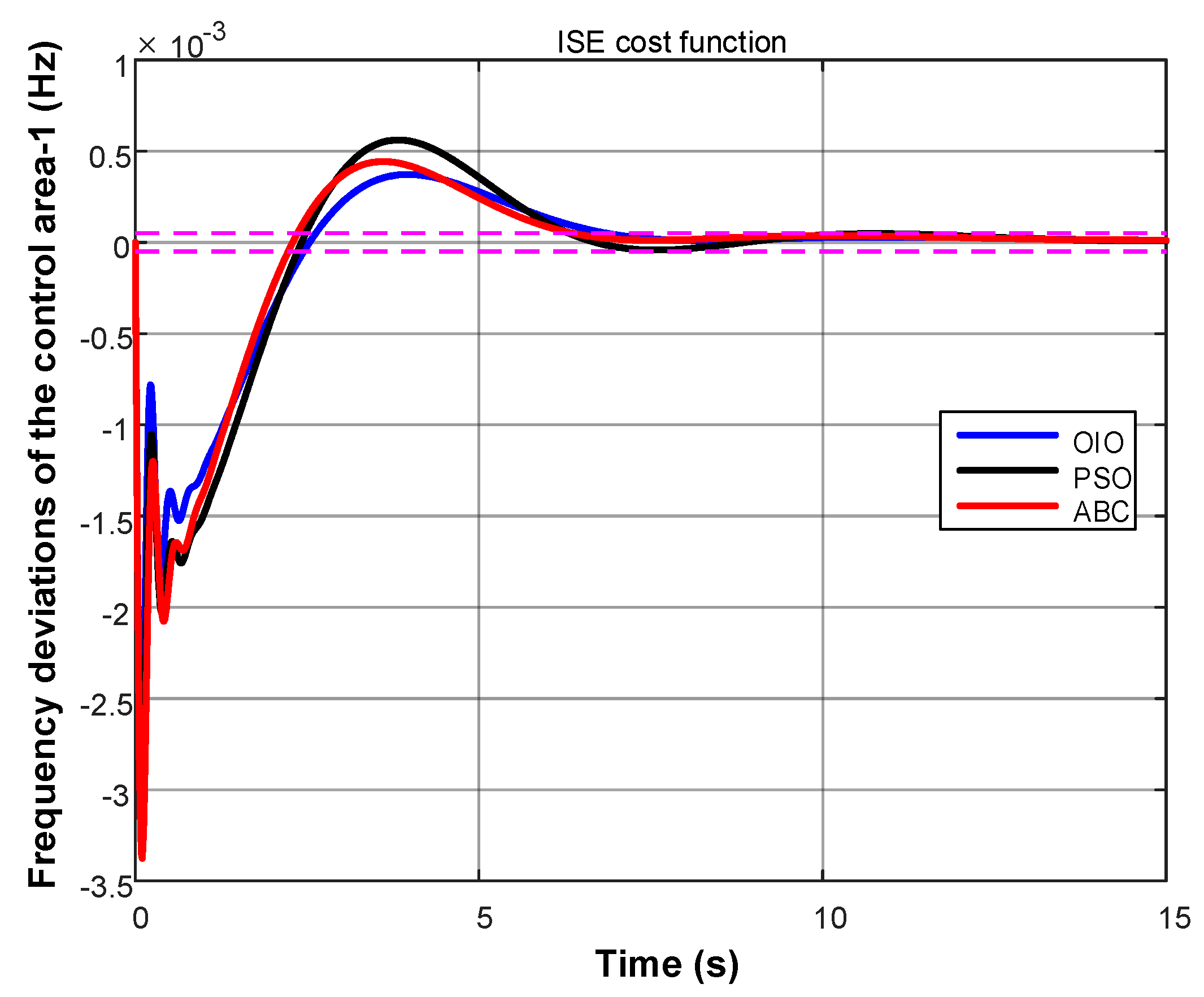
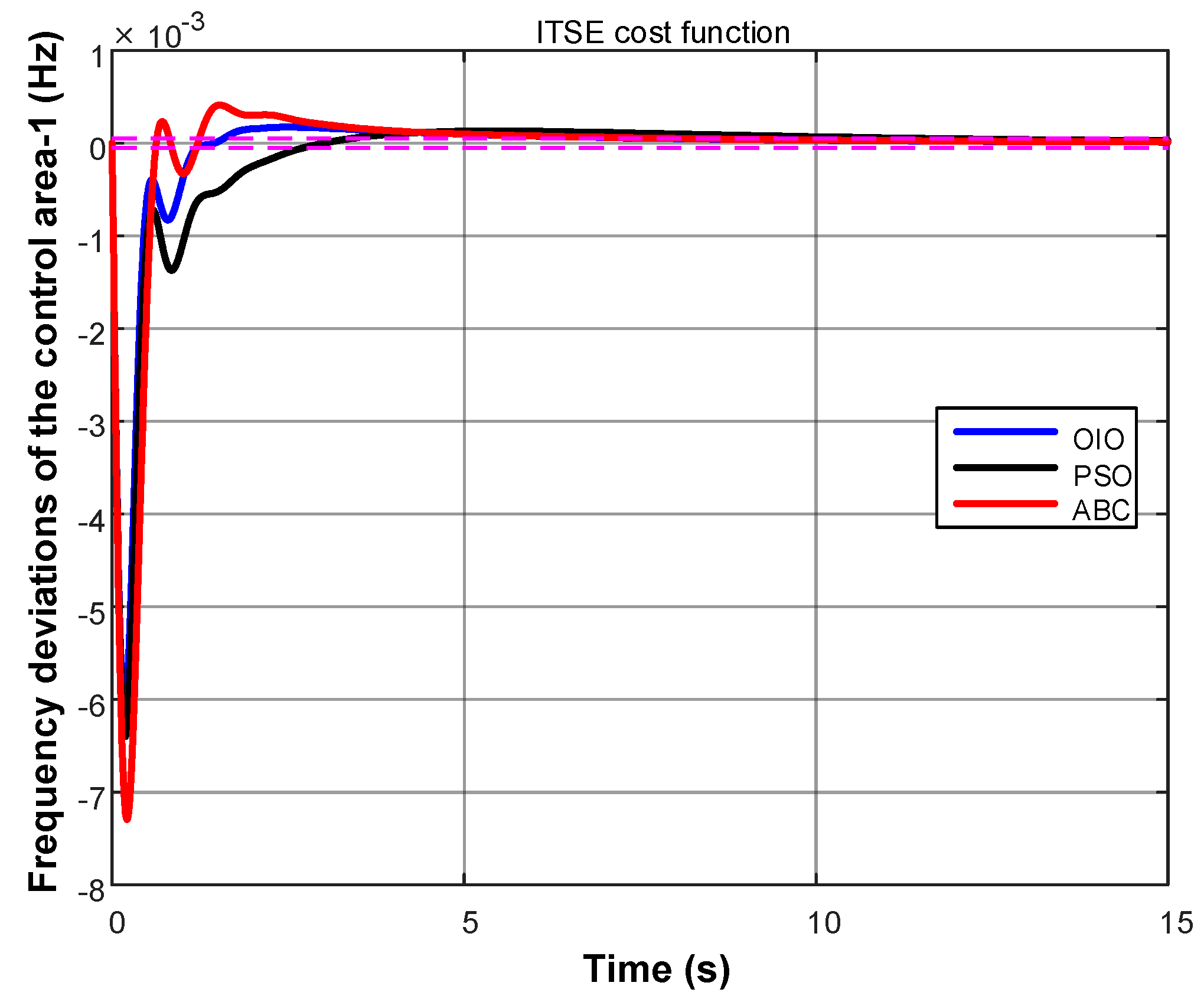
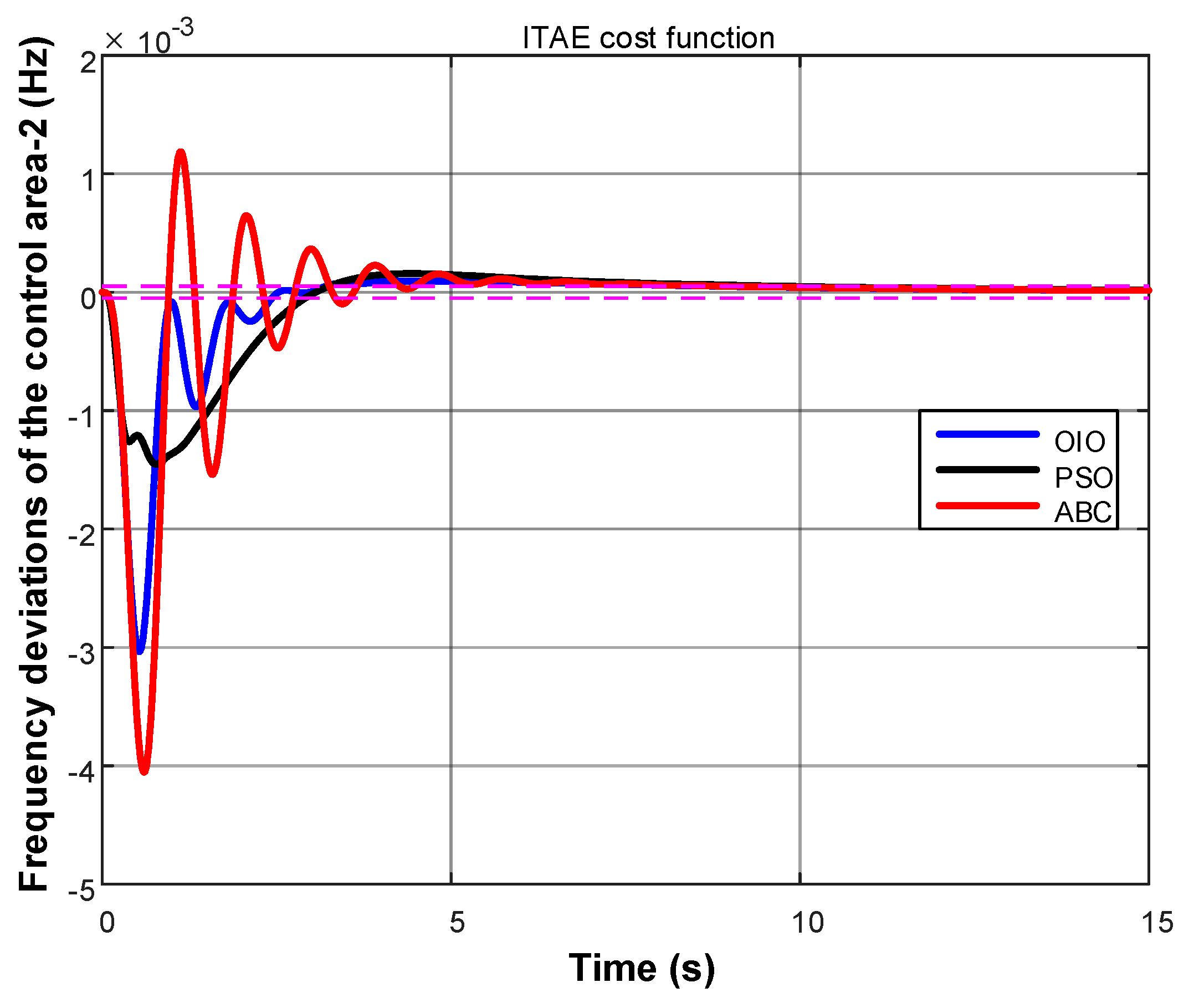
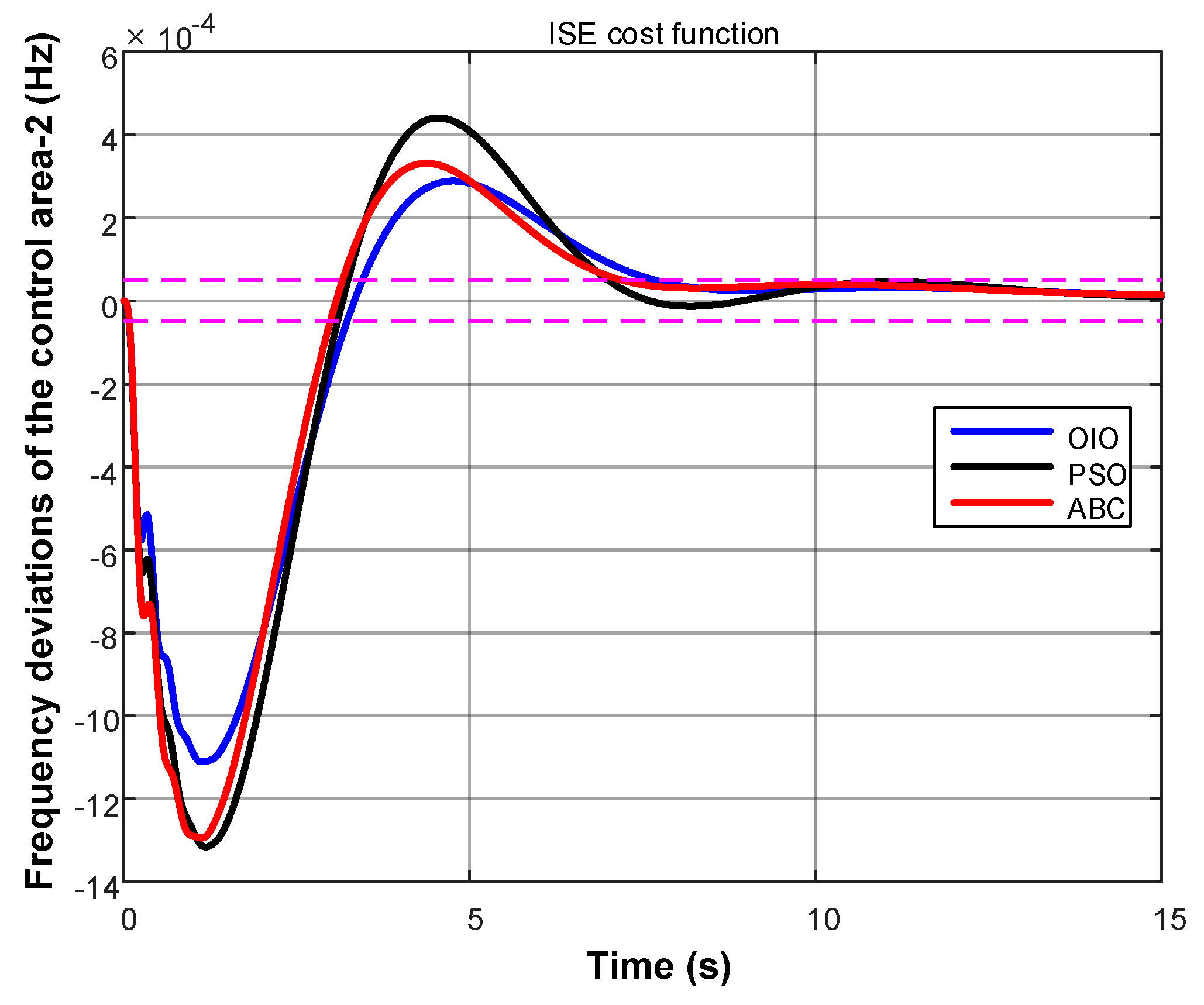
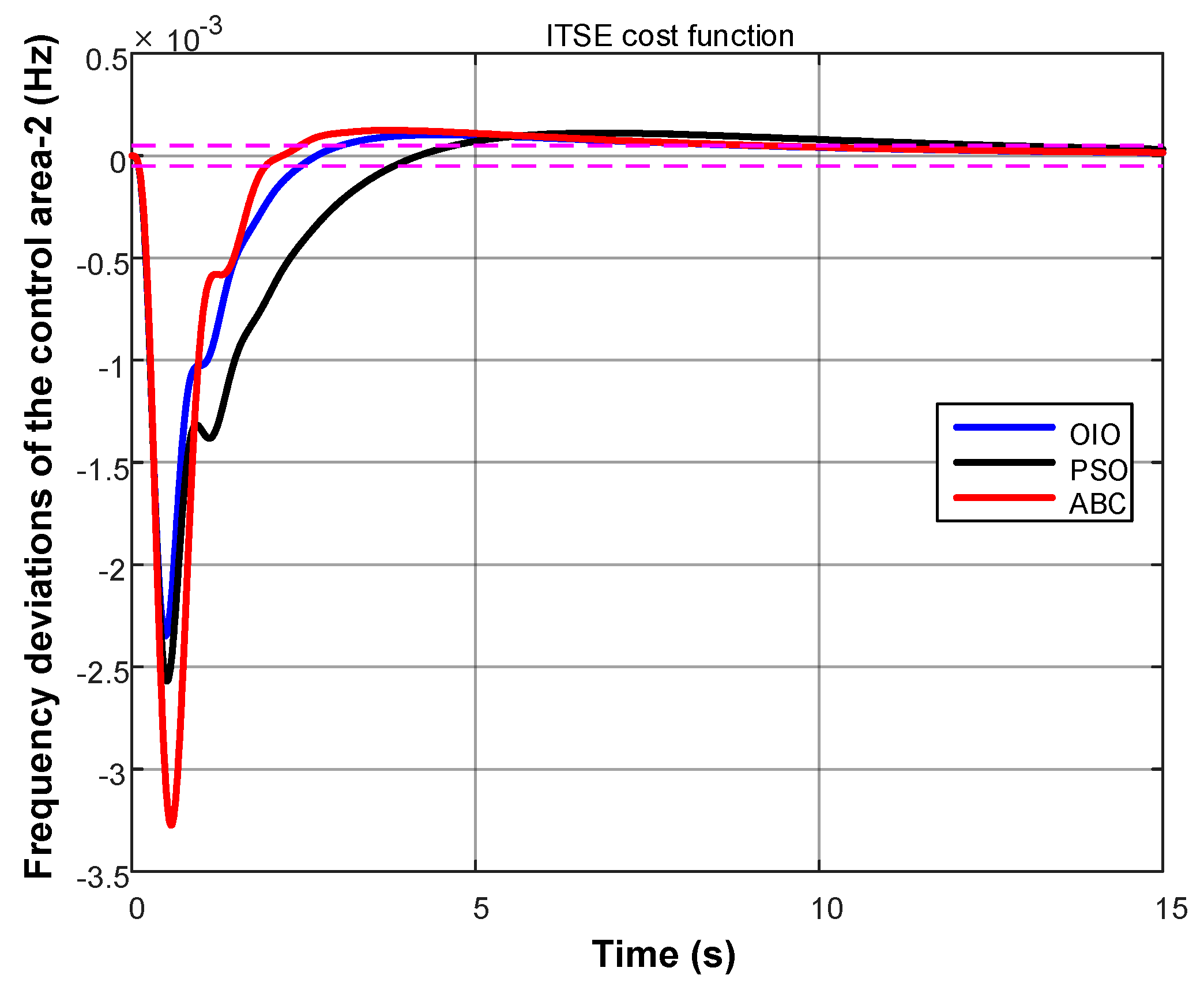
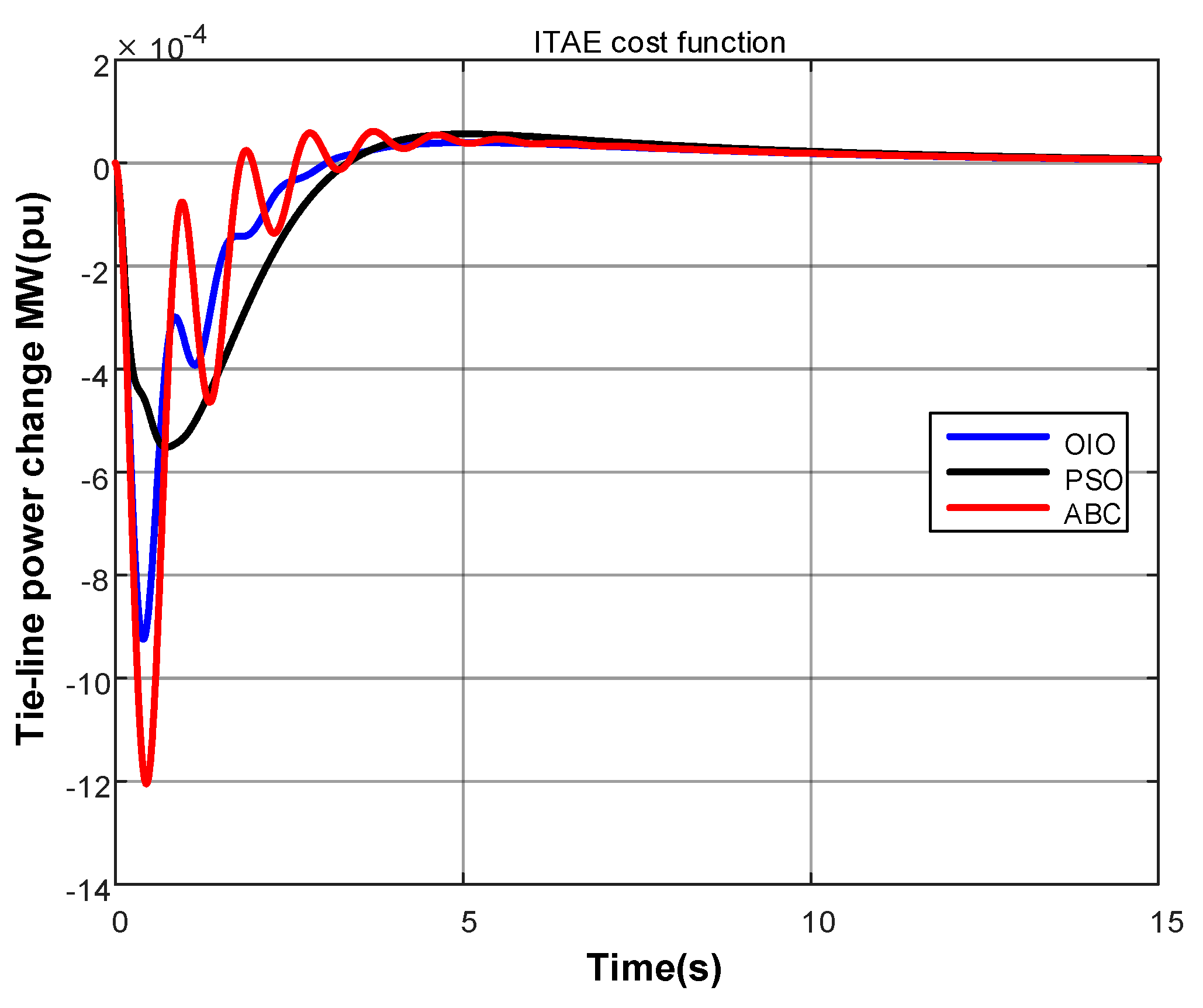
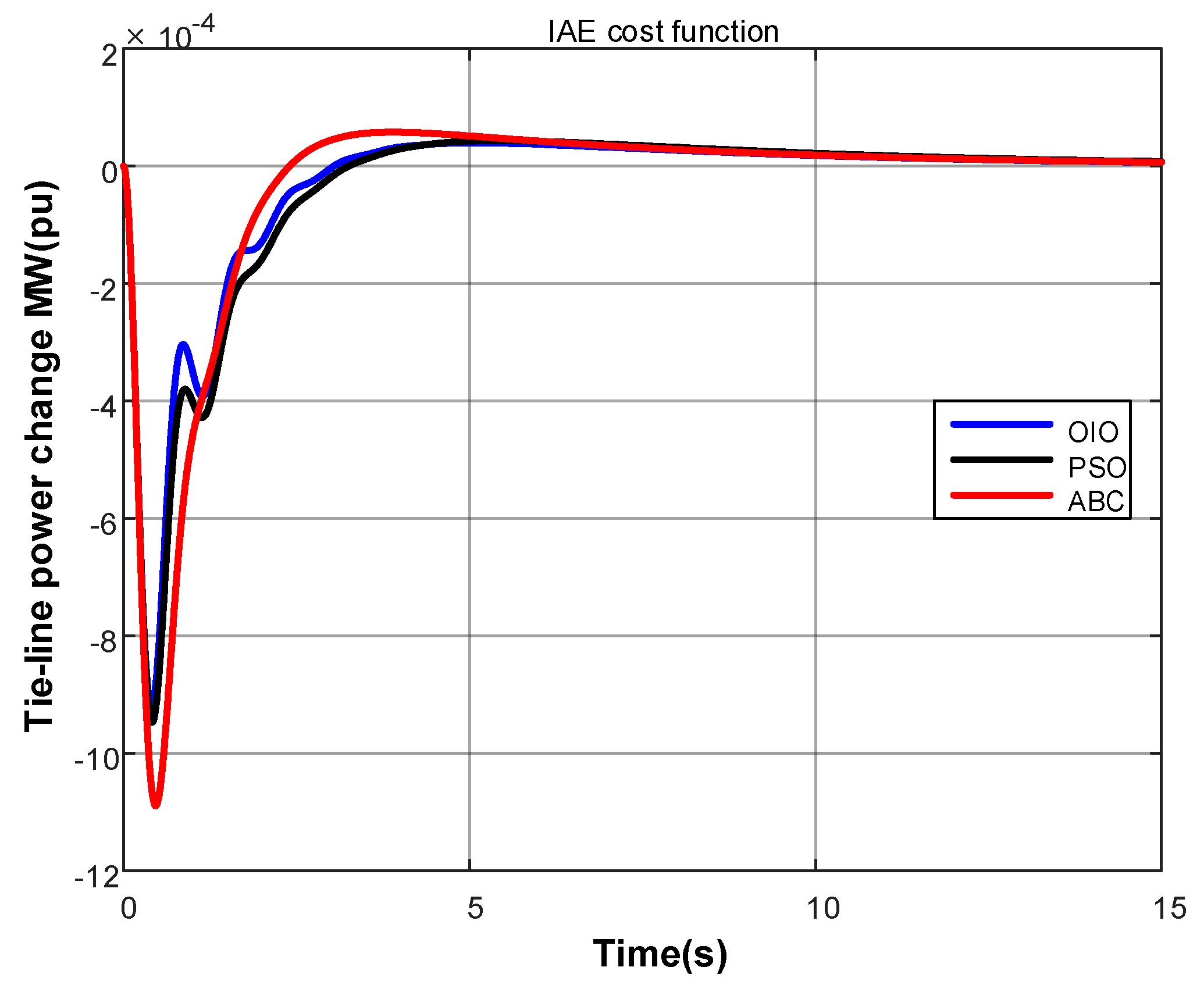
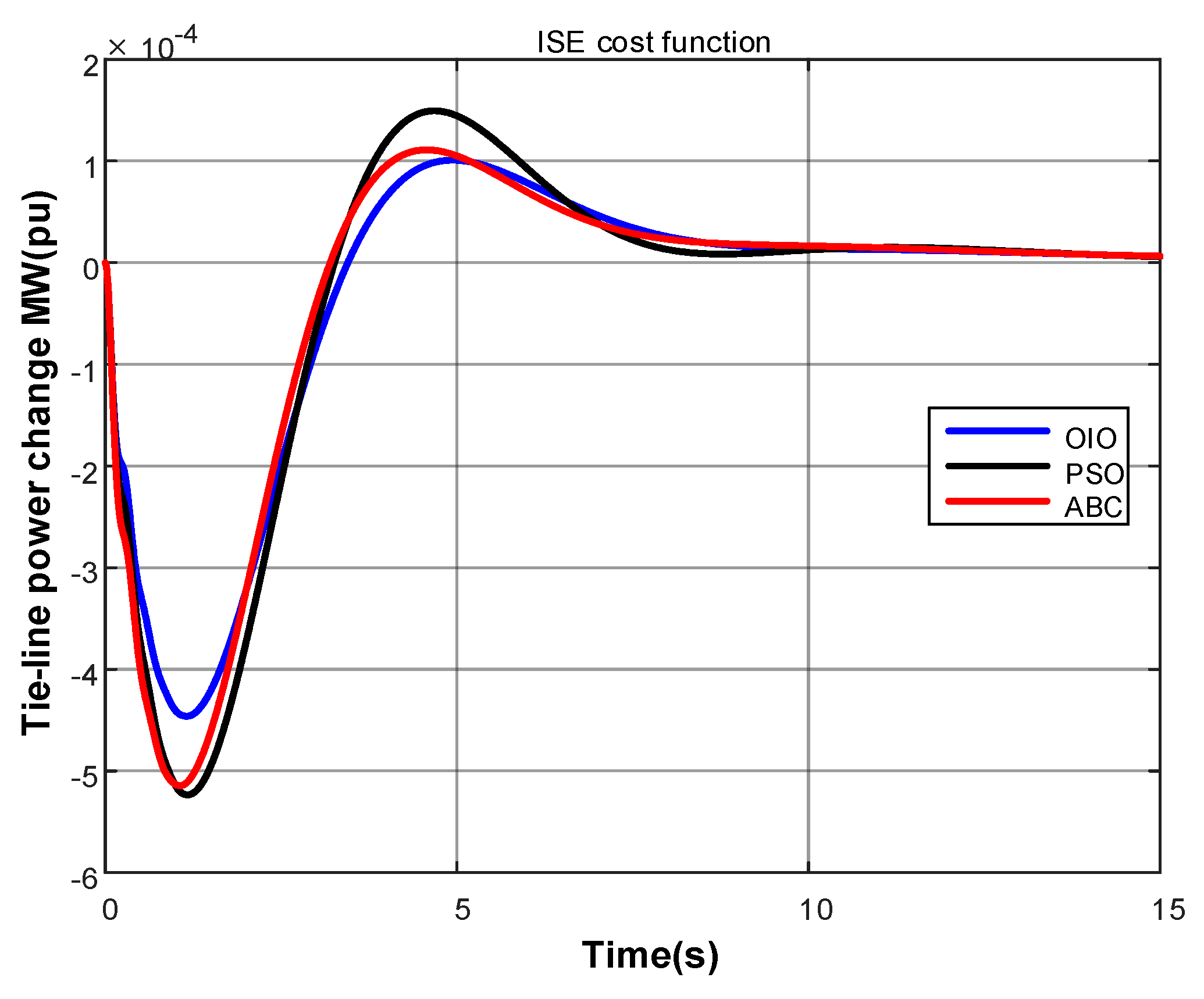
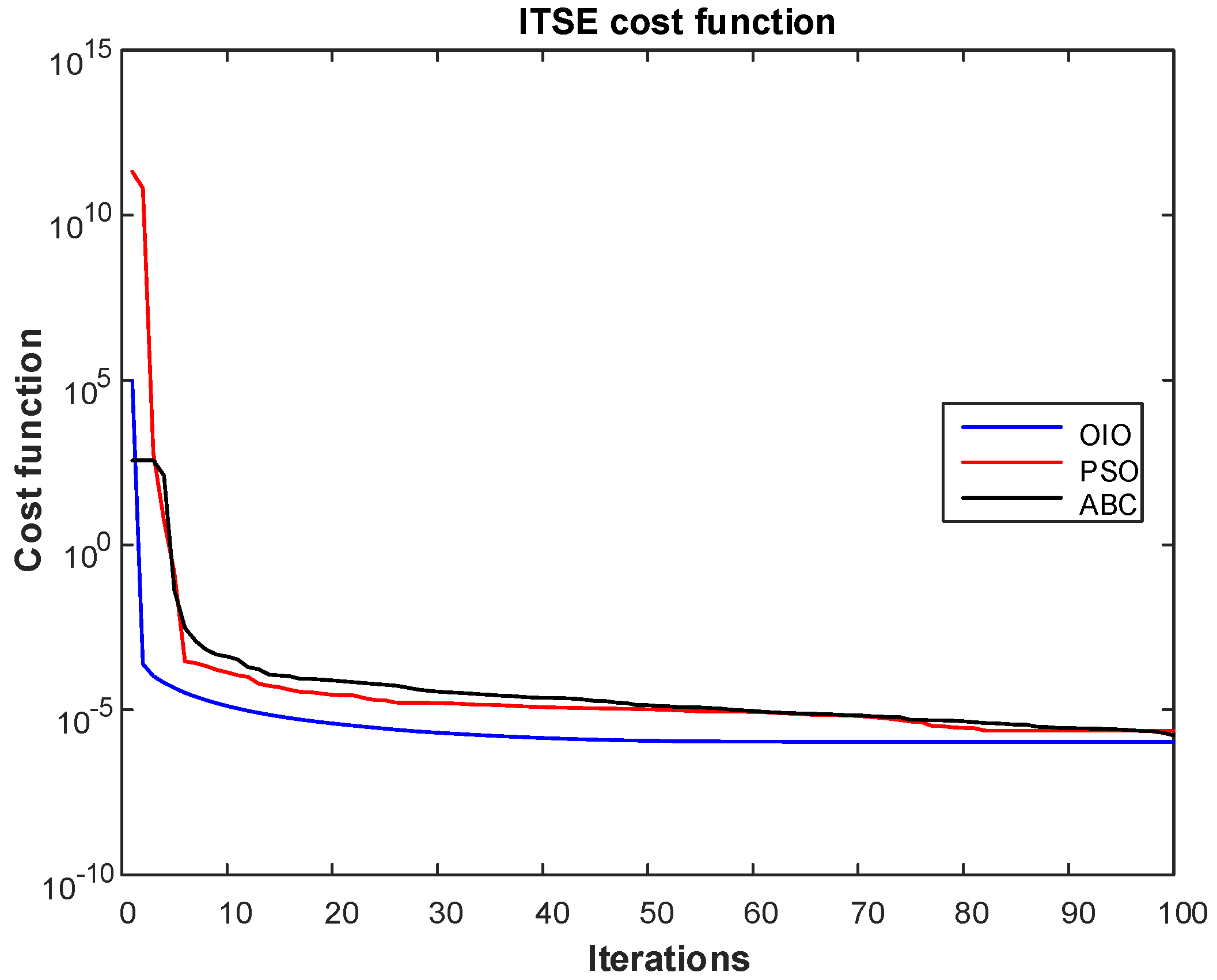
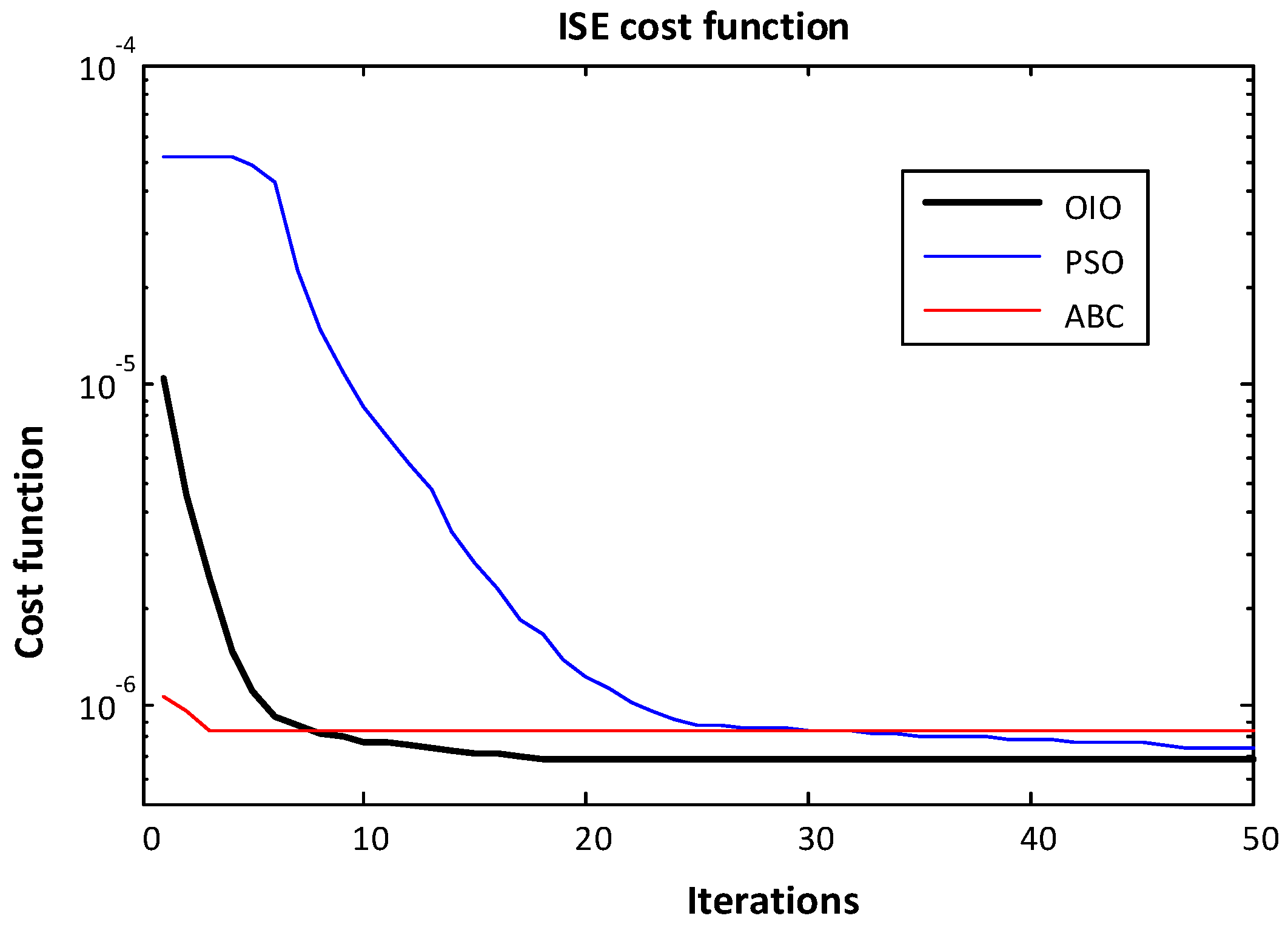
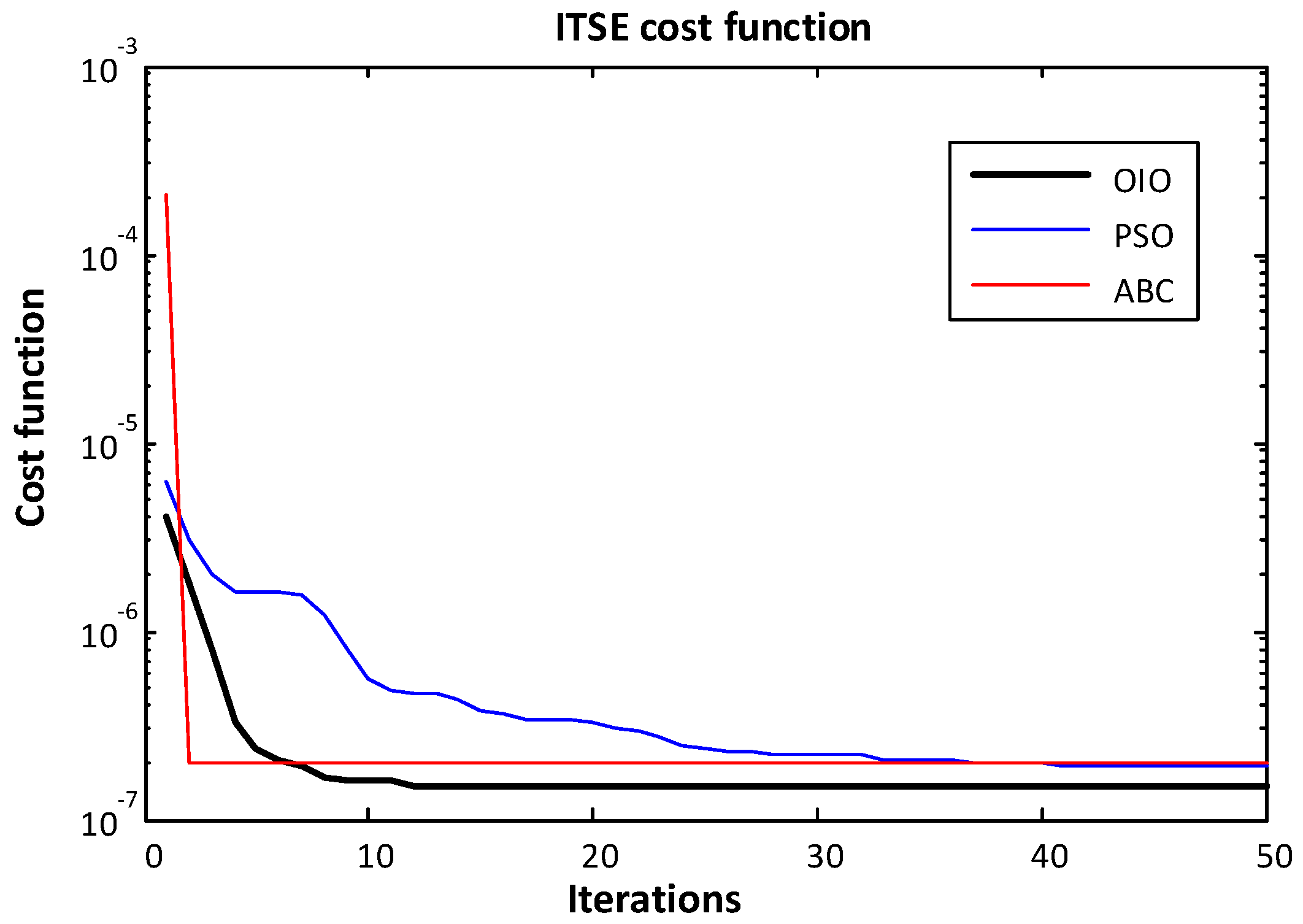
4. Results

In the simulations, the power change occurred in the connection line while frequency change occurred in two areas in response to a ∆P_L1 change in the first area is costed by using various performance indices that are ISE, IAE, ITAE, and ITSE. The mathematical expressions are shown below.

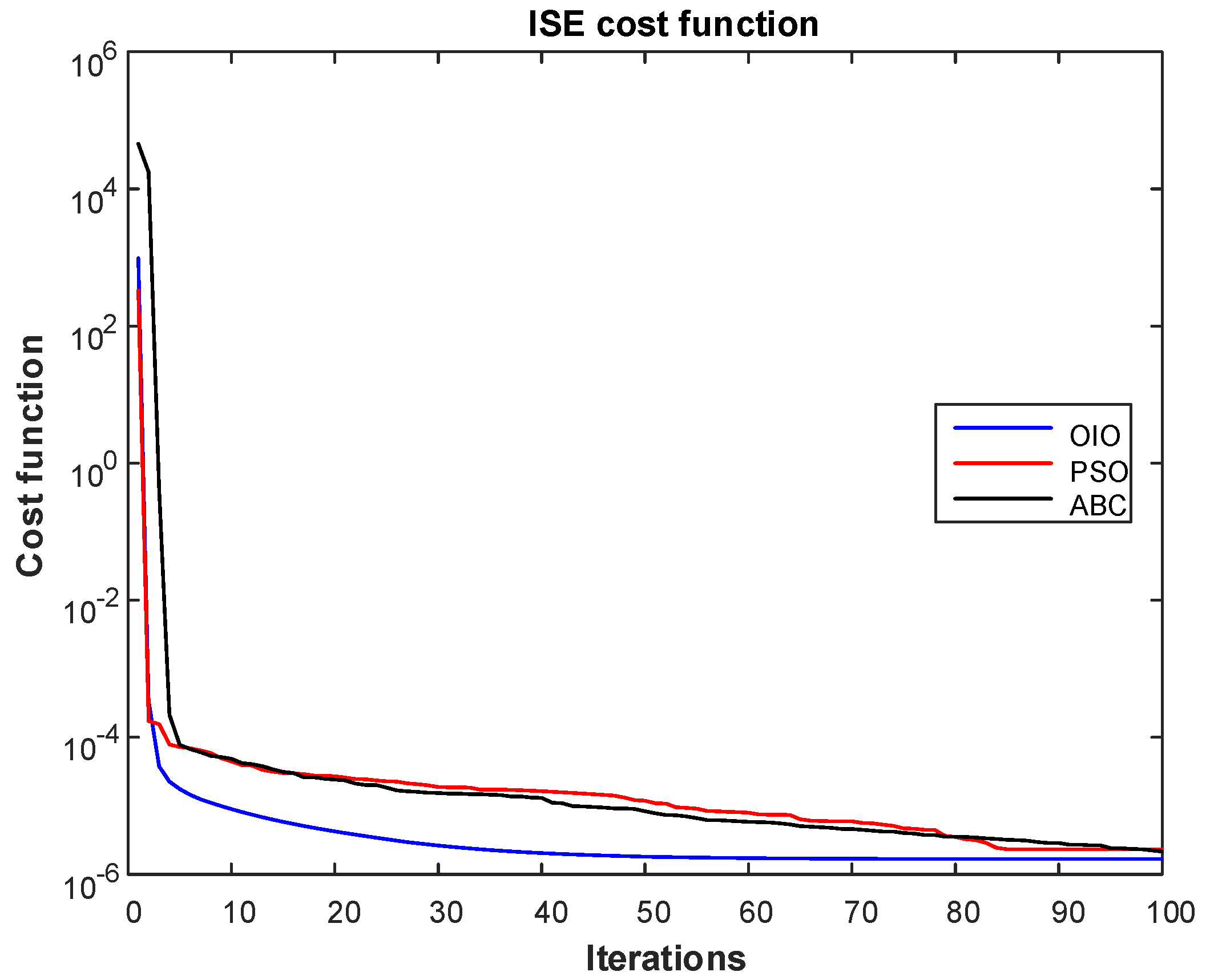
• Integral of square error (ISE)

  $$\mathrm{ISE}={\displaystyle \underset{0}{\overset{\infty }{\int }}{[e(t)]}^{2}dt}.$$
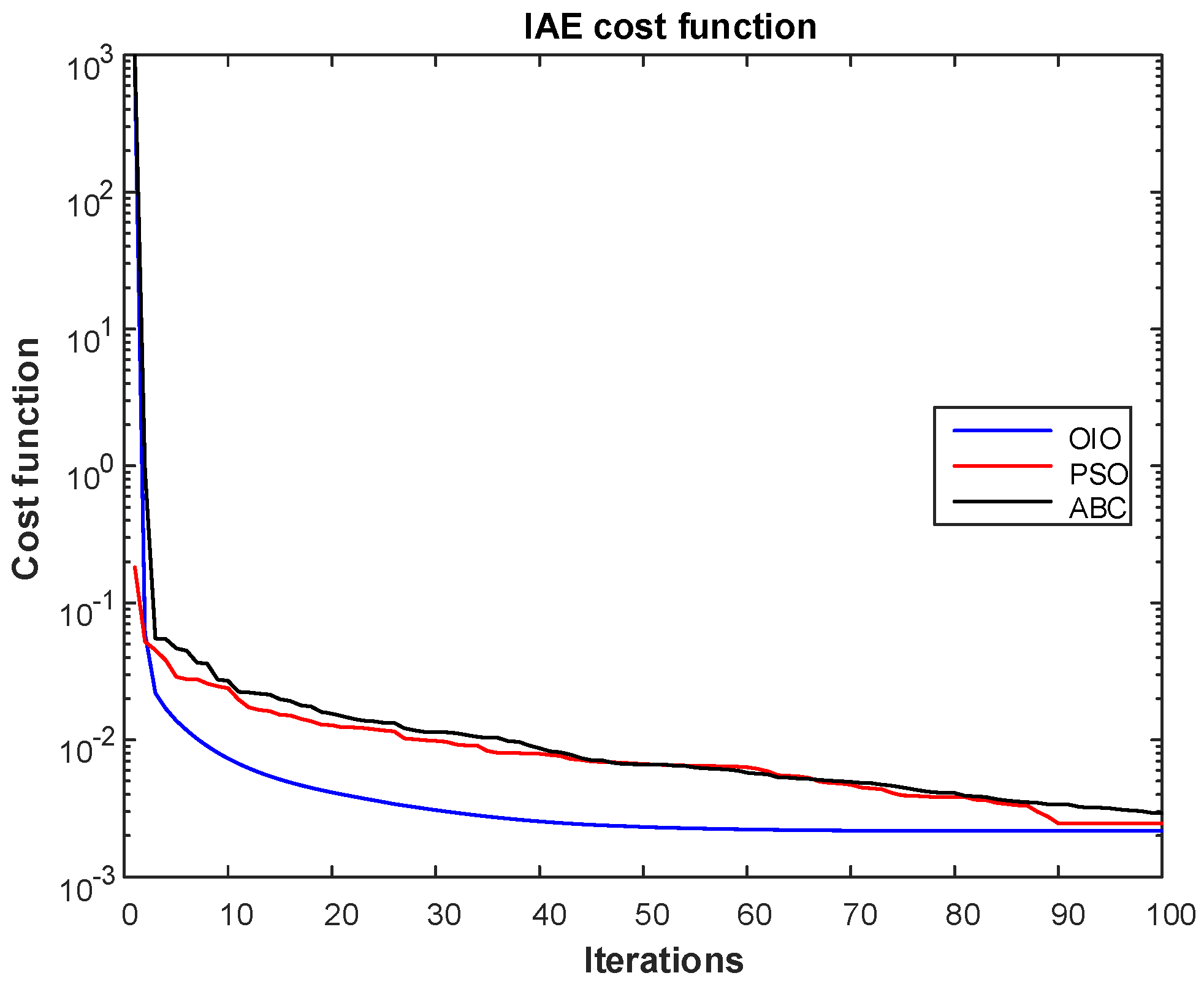
• Integral of absolute value of error (IAE)

  $$\mathrm{IAE}={\displaystyle \underset{0}{\overset{\infty }{\int }}\left|e(t)\right|dt}.$$
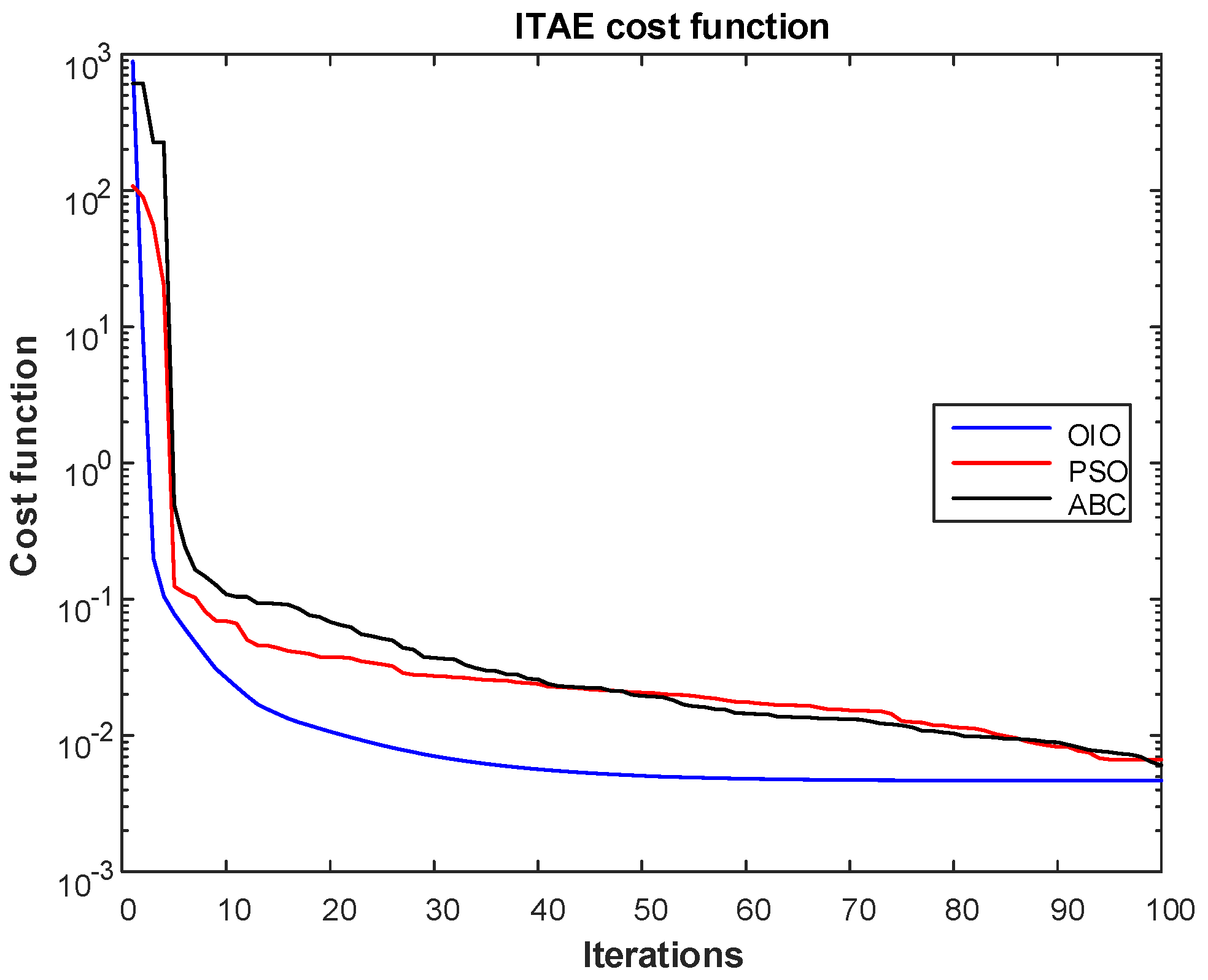
• Time-weighted ITAE

  $$\mathrm{ITAE}={\displaystyle \underset{0}{\overset{\infty }{\int }}t\left|e(t)\right|dt}.$$
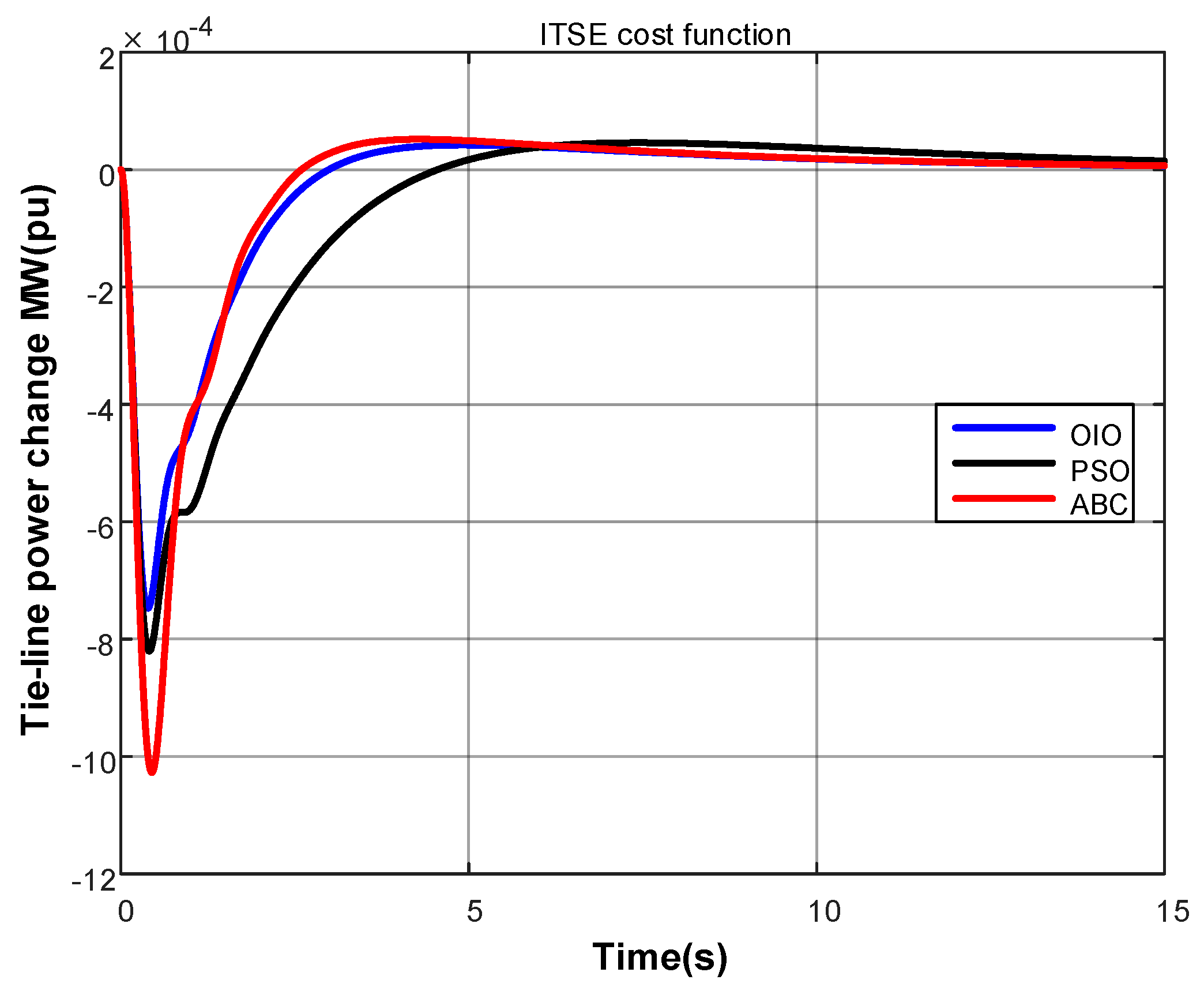
• Time-weighted ITSE

  $$\mathrm{ITAE}={\displaystyle \underset{0}{\overset{\infty }{\int }}t{[e(t)]}^{2}dt}.$$

In the simulations, the results of power change occurred in the connection line while frequency change occurred in two areas in response to a change of $\Delta P_{L1}=0.01$ at t = 0 are given in tables and time domain simulations. The controller parameters used in the results are determined according to OIO, PSO, and ABC. The model created and m files are performed in MATLAB R2013a. The lower and upper limits of K_p, K_i, and K_d values, which are the controller gains, are given in

Table 1. Limits of Controller Parameters.

Controller Gain Limits	Kp	Ki	Kd
Upper Limits	0	0	0
Lower Limits	10	10	10

.

The controller parameters optimized by four different performance indices with the limitations seen in Table 1 are given in

Table 2. Optimal parameters of the PID controllers for test system-1 and test system-2.

System	Algoritm	Controller Gains	IAE	ISE	ITSE	ITAE
Test system 1	OIO	Kp	9.999	9.999	9.999	9.997
		Ki	9.999	9.999	9.998	9.999
		Kd	1.765	1.778	9.861	2.524
	PSO	Kp	9.874	9.342	7.505	9.505
		Ki	8.479	8.614	9.454	5.68
		Kd	4.934	1.793	8.915	2.305
	ABC	Kp	8.062	6.405	8.580	7.331
		Ki	9.510	9.047	9.461	9.214
		Kd	1.225	1.791	7.817	1.821
Test system 2	OIO	Kp	5.571	4.969	4.061	4.545
		Ki	5.789	3.001	3.903	2.211
		Kd	1.312	1.487	1.965	1.497
	PSO	Kp	2.093	5.782	5.277	4.592
		Ki	7.341	9.998	1.273	7.141
		Kd	0.545	1.520	1.774	1.149
	ABC	Kp	5.818	4.327	6.358	4.191
		Ki	1.483	3.026	9.998	7.119
		Kd	1.263	1.458	1.547	1.128

.

The time domain simulation results, Figure 3 and the following 14 figures, are given only for test system-1. Similar results are not given for test system-2. However, the performances of all simulation results are given with all tables Table 2 and the following 4 tables. In Figure 3, Figure 4, Figure 5 and Figure 6, the frequency changes occurred in the first area as a result of the simulation performed with controller parameters optimized for ITAE, IAE, ISE, and ITSE performance indices are shown. The frequency changes of the second area are given in Figure 7, Figure 8, Figure 9 and Figure 10. In Figure 11, Figure 12, Figure 13 and Figure 14, the power change in the connecting line is given. The maximum overshoot and settlement times are given in

Table 3. Settling times and maximum overshoots (max. oversht.) of the frequency deviation of the control area-1.

System	Algoritm	Step Response	IAE	ISE	ITSE	ITAE
Test system 1	OIO	Max. oversht.	7.07 × 10−3	2.94 × 10−3	6.09 × 10−3	7.09 × 10−3
		Settling times	8.056390	6.860694	8.030881	8.056704
	PSO	Max. oversht.	7.12 × 10−3	3.14 × 10−3	6.40 × 10−3	4.34 × 10−3
		Settling times	8.905854	6.310906	11.743802	8.887682
	ABC	Max. oversht.	7.46 × 10−3	3.37 × 10−3	7.29 × 10−3	8.35 × 10−3
		Settling times	8.168429	6.364761	8.183634	8.223559
Test system 2	OIO	Max. oversht.	2.74 × 10−3	2.62 × 10−3	2.35 × 10−3	2.62 × 10−3
		Settling times	1.788248	1.996599	2.913395	1.865132
	PSO	Max. oversht.	4.15 × 10−3	2.59 × 10−3	2.44 × 10−3	2.92 × 10−3
		Settling times	1.409041	2.447668	2.249040	2.547392
	ABC	Max. oversht.	2.78 × 10−3	2.65 × 10−3	2.56 × 10−3	2.95 × 10−3
		Settling times	1.892082	2.25415	2.662097	2.4863540

and

Table 4. Settling times and maximum overshoots of the frequency deviation of the control area-2.

System	Algoritm	Step Response	IAE	ISE	ITSE	ITAE
Test system 1	OIO	Max. oversht.	3.02 × 10−3	1.11 × 10−3	2.35 × 10−3	3.04 × 10−3
		Settling times	8.934293	7.677125	8.929580	8.934334
	PSO	Max. oversht.	3.08 × 10−3	1.32 × 10−3	2.57 × 10−3	1.45 × 10−3
		Settling times	9.801351	6.999126	12.630685	9.904835
	ABC	Max. oversht.	3.45 × 10−3	1.29 × 10−3	3.27 × 10−3	4.05 × 10−3
		Settling times	9.111831	7.201539	9.121439	8.941476
Test system 2	OIO	Max. oversht.	9.77 × 10−5	8.79 × 10−5	8.30 × 10−5	9.50 × 10−5
		Settling times	3.939263	5.523281	4.862744	5.94255
	PSO	Max. oversht.	2.75 × 10−4	1.13 × 10−4	1.09 × 10−4	1.32 × 10−4
		Settling times	6.158258	7.257616	6.807813	7.61831
	ABC	Max. oversht.	1.09 × 10−4	9.04 × 10−5	1.14 × 10−4	1.34 × 10−4
		Settling times	6.573563	5.447564	7.339555	7.529223

according to the time-domain simulations.

Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 are given data with the aim of better illustrating the data given in Table 3 and Table 4 which are the tables that include maximum overshoot and settling time in every area. In these tables when the results of test system-1 are considered, apparently it is seen that OIO gives better result for maximum overshoot and settling times. In the first area, the best result was obtained with PSO in terms of the maximum overshoot for ITAE performance index, whereas the best settlement result was obtained by OIO method. According to settling time values while the best results are found with the help of OIO for IAE, ITSE, and ITAE values, PSO found better results for ISE. The results of the second area are similar with the results of the first area.

As the results of test system-2 are considered, apparently it is seen that OIO gives better result for maximum overshoot and settling times. In the first area, the best result was obtained with PSO in terms of the maximum overshoot for ISE performance index, whereas the best settlement result was obtained by OIO method. According to settling time OIO is the best result for ISE and ITAE and PSO becomes prominent for ITSE and ISE. The results of the second area are similar with the results of the first area.

The best results are obtained with OIO method in both first and second areas in maximum overshoot and settling times for IAE, ISE, and ITSE performance indices.

In Figure 15, Figure 16, Figure 17 and Figure 18. The change of cost function values for four different performance indices are given for Test system-1 and Figure 19, Figure 20, Figure 21 and Figure 22. For Test system-2. The final values of these changes are shown in

Table 5. Value of cost function for OIO, PSO, and ABC.

System	Algoritm	IAE	ISE	ITSE	ITAE
Test system 1	OIO	2.16 × 10−3	1.68 × 10−6	1.05 × 10−6	4.67 × 10−3
	PSO	2.46 × 10−3	2.34 × 10−6	2.29 × 10−6	6.65 × 10−3
	ABC	2.78 × 10−3	2.12 × 10−6	1.59 × 10−6	5.56 × 10−3
Test system 2	OIO	7.22 × 10−4	6.80 × 10−7	1.50 × 10−7	2.16 × 10−3
	PSO	8.75 × 10−4	7.40 × 10−7	1.90 × 10−7	2.46 × 10−3
	ABC	7.59 × 10−4	8.40 × 10−7	2.00 × 10−7	2.78 × 10−3

. Considering these figures and the data given in tables. It is clearly seen that OIO algorithm finds smaller values earlier than other methods.

Total optimization times for each method and algorithm are given in

Table 6. Total computation time table in second.

System	Algoritm	IAE	ISE	ITSE	ITAE
Test system 1	OIO	389.5745	391.4756	391.1157	389.4153
	PSO	497.208	489.2443	477.7997	492.3465
	ABC	552.9799	559.9015	553.7232	560.1486
Test system 2	OIO	199.1631	198.4873	197.0914	195.9271
	PSO	249.3927	243.8966	243.0222	250.9786
	ABC	277.4441	280.5757	278.4784	281.0236

. OIO algorithm realized optimization process in a shorter time for both test systems. The number of mirror used in OIO algorithm corresponds to the number of population. The number of mirror was specified as 2 in implemented optimizations. The number of population for artificial bee colony for is 3 and 4 for particle swarm optimization. When the number of population is decreased it is seen that the methods occur to have the problem of convergence. All parameters used in all three algorithms are presented in Appendix A.

In Figure 19, Figure 20, Figure 21 and Figure 22 optimization histories are given for test system-2. Although the ABC algorithm has a higher convergence speed, it is seen that it cannot find global minimum. When time domain results and Table 5 are considered, the speed of convergence and reached global minimum values for OIO algorithm are better.

5. Conclusions

In this paper, the OIO algorithm was proposed for optimizing controller gains in load frequency controls in electrical power systems. The reason to use the method developed by Kashan is that it reaches the global minimum value faster. The method was compared with PSO and ABC methods which are widely used in literature. The idea behind choosing these methods is that their initial conditions are randomly defined. These three methods were optimized with two different test systems and four different cost functions. According to the results obtained, OIO algorithm converges to the global minimum value with ten iterations in average. The results obtained from these two test systems can be ordered as follows:

• OIO algorithm has found lowest cost value.
• OIO algorithm reaches to the global minimum value in short time.
• OIO can converge with less number of population.
• OIO algorithm has the total lowest optimization time.

As the authors conclude from the results explained above, they propose OIO algorithm in specifying PID gains online for a two-area power systems in laboratory applications for future studies.