1. Introduction
Over the last decade, the exponential demand growth and the ever-increasing number of connected devices have forced the necessity to look to the next evolution of wireless data communications [
1]. The adoption of 5G networks, expected by 2020, will allow handling more traffic in dense environments, providing higher data rates and reduced end-to-end latency [
2]. In this scenario, achieving energy efficiency becomes even more concerning and challenging. For instance, according to [
3], by 2025, the global Internet will be responsible for more than 10% of the world’s electricity consumption. To face this steadily rising power consumption, a strongly related Key Performance Indicator (KPI) to be addressed by the 5G generation is precisely the energy efficiency [
4]. Accordingly, an effective energy management, as well as enhanced network performance, are essential design goals to fulfill the requirements of future 5G systems for heterogeneous applications and services. However, some of these requirements may be in conflict, and specific strategies must be developed. Precisely, the existing trade-off between energy efficiency and network performance was investigated as part of a conference paper in [
5] and is now further expanded in this article.
Energy consumption concern in 5G system has currently attracted a great deal of attention from networking researchers. Several papers have been proposed with solutions enabling significant energy efficiency gains in the mobile networks division [
6,
7,
8]. Although 5G is mostly perceived as wireless access by the user, different communication facilities and users need to be connected through backhaul networks—either using optical fiber networks or radio links—and backbone networks. Apart from being key enablers for a successful deployment of this complex architecture, these network segments are of paramount importance to reduce the energy consumption of 5G systems. Therefore, this paper is conceived to tackle the energy consumption problem in 5G backbone networks.
Software-Defined Networking (SDN) is expected to play a major role in 5G systems in order to provide a more intelligent use of the underlying transport networks [
9]. Moreover, this technology, together with Network Function Virtualization (NFV), can provide the required tools to support network slicing in order to accommodate the wide range of demanded services over a common infrastructure simultaneously [
10,
11,
12]. The basic idea of SDN [
13]—control and data planes separation—makes network environments more manageable. The logically centralized control plane in SDN provides global knowledge of the network state information, which allows for end-to-end visualization. Moreover, it can manage network tasks and perform device programming without needing any additional software or hardware-based intelligence in each one of the switching elements. Meanwhile, interconnection devices follow the rules set by the controller to forward the traffic. Consequently, the use of an underlying SDN architecture will facilitate the introduction and deployment of new applications and services, making it easier than with classical hardware-dependent standards. Another advantage of exploiting SDN is the possibility to dynamically adapt control decisions to comply with diverse QoS requirements to handle heterogeneous application-driven networks.
Given that in practice, the energy consumption of network equipment is not in proportion with their traffic load, the reduction of the number of active elements is an effective and widely-accepted strategy to decrease the consumption of data networks [
14]. This feature can be implemented by putting into sleep mode (i.e., a low-power state) unused networks elements such as line cards or port interfaces. Although turning off entire interconnection devices improves the energy efficiency, this possibility is not considered in this work given the resilience concerns in the case of network events. Nevertheless, due to the link over-provisioning typically considered in the design and operation of backbone networks, substantial energy can still be saved putting into sleep mode port interfaces that are not transferring data. Within this context, SDN architecture is very well-suited to perform an energy-aware routing and to manage the state of unused switch interfaces in a coordinated and centralized way. Therefore, the implementation of an energy-aware solution in the control plane is a valuable opportunity to solve the power consumption problem in data networks.
Despite consistent efforts to improve the network power efficiency, energy-aware techniques may lead to performance degradations if QoS requirements are neglected [
15,
16]. Inspired by this reality, this paper introduces a new energy-aware strategy and evaluates its impact on different performance metrics. Instead of restricting the path selection and potential improvements in terms of energy efficiency to meet some specific metric bound, this work aims to gain insight into potential energy savings and to quantify the existing trade-off between power consumption and several performance indicators, as one crucial issue for communication systems nowadays.
Throughout this work, we consider an SDN architecture with multiple controllers and, similar to previous works [
17,
18,
19], in-band control traffic. In this operational mode, links are shared between data and control plane traffic. Hence, control messages are exchanged without the need for additional links. In this way, the proposed energy-aware routing can be applied when implementing a dedicated control network is not feasible either for physical or cost-related restrictions. In large backbone networks, this is a more realistic scenario since additional links dedicated to directly connect controllers and forwarding devices are impractical and cost-inefficient.
Specifically, the major contributions of this work are as follows:
An Integer Linear Problem (ILP) is formulated to optimize the number of active links in SDN, considering multiple controllers and links shared between data and control plane traffic.
For large network topologies, we propose a novel energy-aware mechanism that reduces the time complexity of our approach and allows allocating the traffic demands in real time as it comes.
Two solution modules were conceived of in this mechanism, exploiting knowledge of the network topology and traffic engineering techniques to reduce the overall power consumption.
Using real topologies and traffic demands, we provide a performance comparison analysis of our proposal with another routing approach.
The remainder of this paper is structured as follows. In
Section 2, previous related studies about different strategies to tackle the problem of power consumption are discussed. In
Section 3, the energy consumption optimization problem is formalized through a general mathematical formulation fully compatible with SDN environments using multiple controllers and in-band control traffic. In
Section 4, we explain the main characteristics of our low-complexity energy-aware approach together with a detailed description of its two comprised modules. The simulations strategies and the obtained results are presented and analyzed in
Section 5. Finally, in
Section 6, we provide the conclusion of our work and outline future research guidelines.
3. The Energy-Aware Routing Problem in SDN
To formalize the energy consumption optimization problem, we consider an SDN represented by a directed graph , being V, E and C the set of nodes, links and controllers respectively, where . We use to denote the capacity of a link . The set of interconnection devices is defined as .
Considering F as the entire set of traffic flows existing in the network between any pair of nodes, we use D to denote the subset of data plane communications. For the control plane, let T denote the subset of communications between network controllers and switches, while H is used as the subset of communications between controllers. Accordingly, . Each flow from source to destination , has its associated throughput, denoted by .
To minimize the number of links needed to route a given traffic demand matrix, we develop an ILP model, according to the following binary variables:
- :
describes the state of a link
.
- :
describes the selection of a link
to route a flow
.
- :
describes the association of each forwarding device
with a controller
.
Considering the complete set of demands fixed and known in advance, a global optimization process can jointly compute all the required optimal control and data paths minimizing the energy efficiency. Using the aforementioned binary variables, the optimization model can be formulated as:
To manage each forwarding device in the network
, a single controller is selected.
Additionally, the number of switches associated with each controller cannot exceed the controller capacity. In this expression, we use
to denote the computational and networking resources, in terms of number of devices that can be supported for a controller
.
To avoid additional traffic load through network controllers, data plane communications (i.e.,
) cannot be routed through these devices. Furthermore, control traffic between controllers and switches (i.e.,
) will not pass through any other controller (i.e., except for those being the source or target of the traffic). The same must hold true for communications between controllers (i.e.,
). In these constraints, we use
to denote the set of neighbors of a node
i and
to identify the forwarding device involved in the source/target pair of traffic flow
.
The routing of data plane communications and control traffic exchange between controllers follows the traditional flow conservation constraints.
Meanwhile, for the subset of communications between controllers and switches
, these constraints are modified to assure that every switch exchanges control messages only with its controller. Similarly, the forwarding device and controller involved in the source/target pair of traffic flow
, are denoted with
and
, respectively.
A link
is active if it is used by some traffic flow
. Furthermore, the total traffic in each active link must be less than its assigned capacity.
Using this model, the centralized controller can determine all the optimal routes and set the corresponding flow rules on each interconnection device in the network before the traffic arrival. Although this formulation allows the attainment of optimal solutions for the energy consumption problem in SDN, it becomes highly challenging to solve on large or even medium-scale topologies. This is because the complexity of the energy-aware routing problem is NP-hard [
35], so the required computational time and resources grow exponentially with the network size.
4. Energy-Aware Approach
Given the high complexity of the proposed optimization problem in large real-world networks, in this section, we present a hybrid solution for the energy efficiency problem in SDN comprising the main advantages of the two aforementioned solution types. More precisely, we exploit specific network topological properties combined with the use of traffic engineering to reduce the overall power consumption.
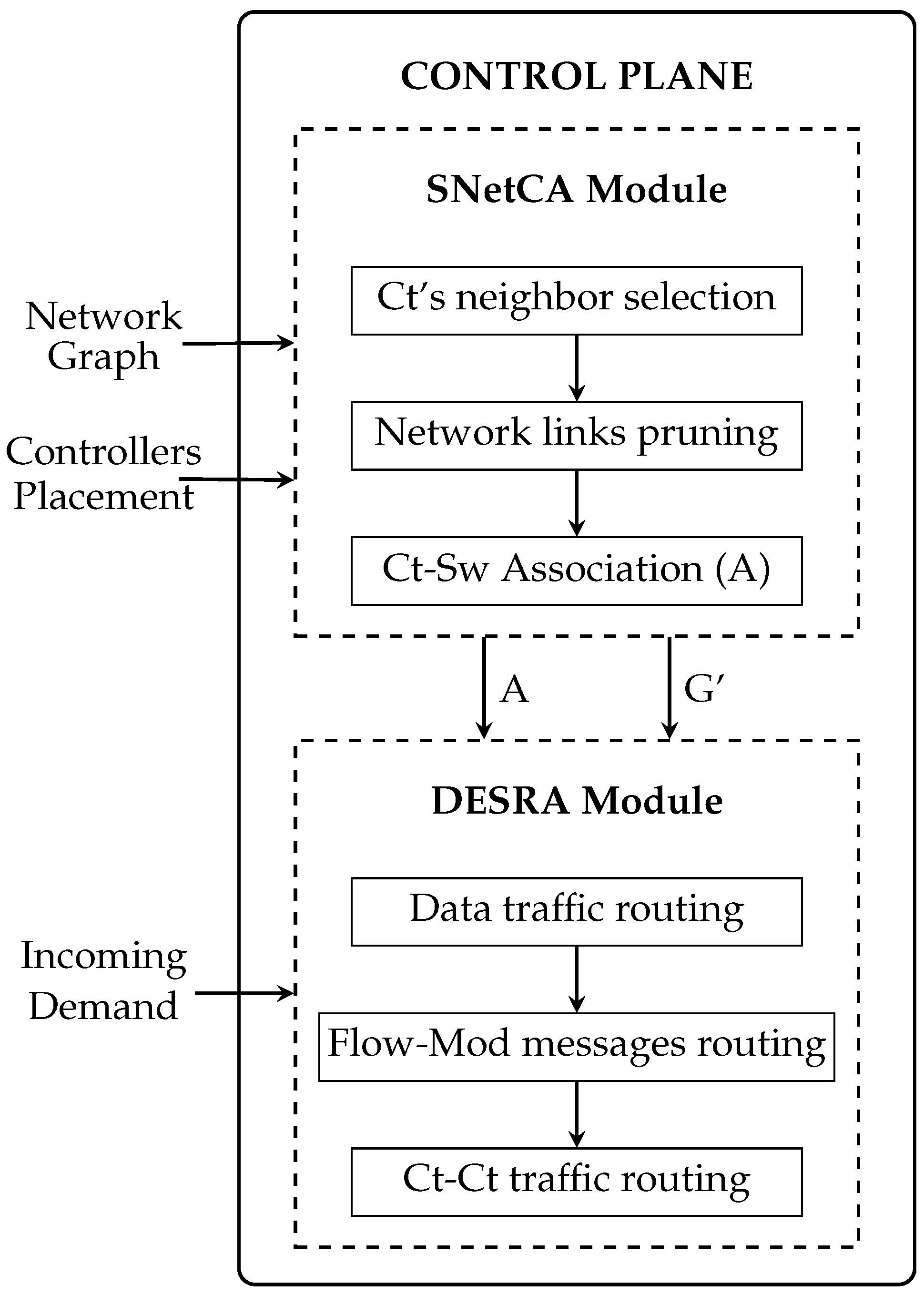
An illustrative diagram of this strategy is shown in
Figure 1. The first component, denoted as Static Network Configuration Algorithm (SNetCA), is a topology-based solution intended to be statically activated at specific instances as a planned operation. On the other hand, the traffic-based module, denoted as Dynamic Energy Saving Routing Algorithm (DESRA), is activated by the arrival of each incoming traffic demand. Therefore, an accurate prediction of incoming traffic is not needed.
In essence, this approach finds the routes between network elements that minimize the number of active links used, being the links shared between data and control plane traffic (i.e., in-band mode). Therefore, control paths between controllers and switches (in both senses) and between controllers are also established.
Additionally, given the controllers placement in the network topology, an ideal distribution of switches between controllers is determined by our model. This is done in terms of energy efficiency, while considering as well the controllers capacity to support forwarding devices. Moreover, our energy-aware approach avoids the routing of additional traffic load through controllers. Therefore, admissible control paths do not traverse any other controller, but the source or target of the traffic and data plane communications cannot be routed through any of these devices.
The two main parts enclosed within the proposed energy-aware approach are described in more details in the following subsections.
4.1. Static Network Configuration Algorithm
By considering the typical link redundancy of backbone networks, we design a Static Network Configuration Algorithm, denoted as SNetCA, which aims to prune as many links as possible in order to stress the importance of energy saving. Additionally, the most favorable switch-controller associations in terms of energy efficiency and load balance are determined in this stage.
The algorithm, described in the Algorithm 1 pseudo-code, is composed of three steps:
selecting one of the controller’s neighbors, as the node that will remain connected to it in the outcome topology;
identifying the links that do not disconnect the graph to be put into sleep mode;
associating each node with one controller and computing the control path between them.
| Algorithm 1 SNetCA | |
| Require: | |
| Ensure: , A, | |
| 1: Set of neighbors of controller | |
| 2: NULL | ▹ Array of selected switch for each controller |
| 3: | |
| 4: for do | |
| 5: NULL | ▹ Array of betweenness values |
| 6: Set of shortest paths from controller | |
| 7: for do | |
| 8: if then | |
| 9: continue | |
| 10: end if | |
| 11: | |
| 12: for do | |
| 13: if then | |
| 14: | |
| 15: end if | |
| 16: end for | |
| 17: end for | |
| 18: according to decreasing order of B | |
| 19: for do | |
| 20: if c not already in then | |
| 21: | |
| 22: end if | |
| 23: Remove links and from | |
| 24: end for | |
| 25: end for | |
| 26: for do | |
| 27: if or then | |
| 28: continue | |
| 29: end if | |
| 30: | |
| 31: Remove controllers from | |
| 32: Remove link from | |
| 33: if remains strongly connected then | |
| 34: Remove link from | |
| 35: end if | |
| 36: end for | |
| 37: for do | |
| 38: if s is already associated with another then | |
| 39: continue | |
| 40: end if | |
| 41: PathSelector() | |
| 42: Update , A, X, U | |
| 43: end for | |
| 44: for the rest of do | |
| 45: PathSelector() | |
| 46: Update , A, X, U | |
| 47: end for | |
The input of Algorithm 1 is the network topology with controllers’ placement, and its outputs are a pruned network with a reduced number of links, denoted as , an array keeping the controller-switch associations, denoted as A, and the control paths from each node to its controller, denoted as . Additionally, we use X to denote the set of active links and U to store the utilization of network links.
In the first step, the algorithm iterates over the set of network controllers in order to evaluate each one of its neighbors. The selection of one neighbor node for each controller is based on the betweenness centrality (), which measures the intermediary role of a node in the network. In the proposed approach, we use a simplified version of this metric considering only the shortest paths from a controller to every switch.
In particular, after computing the shortest paths from one controller as the single source, the algorithm determines whether a neighbor node belongs to each path and increases the associated with that node (Lines 7–17). For each controller, a list of neighbor devices, sorted in decreasing order of , is stored in L. This list is used to identify the neighbor with the highest betweenness centrality. This will be the node that will remain connected to the controller in the resulting pruned topology. Thus, the controller considered in the current iteration and the selected neighbor, are stored in .
For the remaining nodes in L, the links between them and the controller are removed from the resulting network graph. This means that they are put into sleep mode in the original graph. Notice that when a controller’s neighbor is another controller, the link between them is not considered as a candidate to be pruned (Lines 8–10).
In the next step, the algorithm iterates over the set of directional links in the pruned network that do not have any controller as its extreme nodes. At each iteration, the algorithm attempts to increase the number of switched-off edges.
A new link is removed only when the resulting graph remains being strongly connected, i.e., at least one path exists between every pair of nodes in the network. To accomplish this, a temporal graph without any controller, denoted as , is created. This graph is used to check the required connectivity between all the forwarding devices. After validating that the possibility to reach any node in the network is not affected, the considered link is removed from the resulting graph.
The last step of the algorithm is intended to determine a control path from each forwarding device to one controller. To achieve this goal, the algorithm starts evaluating the pairs of controller-switch already stored in (Line 37). For each pair, the algorithm first determines whether the considered switch is still available. If this is the case, an admissible control path minimizing the number of active links is computed using the method PathSelector described in Algorithm 2, which will be further explained below. As stated previously, admissible control paths do not pass through any other controller that does not act as the source or target of the considered traffic. The remaining forwarding devices are then considered. Notice that in this case, the algorithm takes into account the control paths to all controllers in the network. Precisely, the path computed by the PathSelector in this step defines the controller for the rest of forwarding devices.
Using this initial control plane configuration, switches send to the controller packet_in requests when a new traffic flow arrives, as well as statistics and failure notifications. Consequently, there is an initial set of active links in the network before the ingress of traffic flows, as well as some link utilization.
The PathSelector method, described in Algorithm 2, performs the energy-aware path selection. In essence, this function is used to select the best admissible route between a pair of nodes, aiming to minimize the total number of active links in the network. The key idea of this function is to perform a low-complexity greedy evaluation between all the admissible paths to select the most suitable route in terms of energy-efficiency, while guaranteeing a balanced load of switches between controllers and capacity constraint of links. Since this method works over the pruned network with a reduced number of links (i.e., ), the set of admissible paths considered is significantly smaller than in the original topology, and the solution can be found after fewer iterations. When this function is asked to find the path between each forwarding device and one controller (i.e., using the set of controllers as the traffic destination), the controller load is considered (Line 4–8). In addition, a candidate path is selected as long as it has sufficient link capacity to route the required traffic volume.
| Algorithm 2 PathSelector() |
- 1:
- 2:
- 3:
for Get_All_Admissible_Paths do - 4:
if then - 5:
if p is to an already loaded controller then - 6:
continue - 7:
end if - 8:
end if - 9:
off ← number of links in p that are not in X - 10:
if off and p has sufficient bandwidth then - 11:
off - 12:
- 13:
end if - 14:
end for
|
4.2. Dynamic Energy Saving Routing Algorithm
When a new traffic demand arrives, a routing request is sent from the input node to its associated controller using the path between both devices previously computed during the static network configuration phase. Based on its global knowledge of the network topology, this controller calculates the required data path minimizing the number of links that need to be activated for this connection request and creates the flow forwarding rules.
The proposed dynamic energy-aware routing is shown in Algorithm 3. For an incoming demand d from source to destination , the algorithm starts storing in the controller associated with the source node. This controller is the main responsible of managing this traffic request.
Using the PathSelector method, the most favorable admissible data path in terms of energy consumption is computed. This is done considering that admissible paths do not go through any controller in the network. Then, a loop is used to establish the required control plane communications for each node along this path.
| Algorithm 3 DESRA |
- Require:
, A, d incoming traffic request - Ensure:
, , data and control paths, X active links, U links utilization - 1:
- 2:
PathSelector() - 3:
Update , X, U - 4:
for do - 5:
- 6:
PathSelector() - 7:
Update , X, U - 8:
if then - 9:
PathSelector() - 10:
Update , X, U - 11:
end if - 12:
end for
|
After identifying the controller associated with each node in the data path, a control path is computed between them. These paths are used to set the flow forwarding rules in each switch using the flow_mod messages. Given the multi-domain scenario considered, the nodes traversed by the data traffic may be associated with different controllers. When a node is not associated with , an additional control message is sent from this controller to the other, in order to inform the second controller of the flow forwarding rule that needs to be installed in one of its managed nodes.
4.3. Complexity Analysis
Considering that the computation of the shortest paths from each single controller is done in
using the Dijkstra algorithm, the selection of one controller’s neighbor in the fist step of Algorithm 1 has a worst run-time complexity equal to
, where
N is the number of total network nodes and
S is the number of forwarding devices. Given that this operation is performed
C times, being
C the number of controllers, the complexity of Step 1 becomes
. Pruning as many links as possible without disconnecting the network graph during the second step has a complexity equal to
, where
E is the number of links and
refers to the connectivity checking process [
36]. The complexity of last step is determined by
, where
M indicates the worst-case complexity of Algorithm 2. It should be noticed that after pruning the network topology, the number of admissible paths and the consequent computation complexity of this method are significantly reduced with respect to the original graph. Therefore, the SNetCA complexity can be expressed as
.
The overall complexity of the proposed dynamic routing solution, mixing together both Algorithms 2 and 3, is since the maximum length of a data path is precisely the number of forwarding devices given the routing restriction avoiding data traffic through network controllers. Given that M is usually a small number after pruning the network topology and will not grow rapidly along with the network topology size, running the algorithm upon each flow request is a reasonable approach.
5. Simulations and Results
In this section, we describe the evaluation of our energy-aware approach and analyze the achieved results. We used the linear programming solver Gurobi Optimizer [
37] for the ILP model. Meanwhile, the proposed control framework described in
Section 4 was implemented using the programming language Python to develop the heuristic algorithms. A computer with 3.30 GHz Intel Core i7 and 16GB RAM was used to carried out all computations. To conduct our simulations, we use real-world network topologies and traffic demands collected from SNDlib [
38]. Each router in the network was considered as an SDN node or as a tentative controller location. Since the topologies used in our experiments are backbone networks, for the sake of simplicity and without loss of generality, we opted to compute the communications delay as the propagation latency.
Specifically, we use three of the most link-redundant network topologies in SNDlib in order to assess the effectiveness of the proposed scheme. The mentioned topologies are New York, Geant and Norway, and their main characteristics are summarized in
Table 2.
Table 2 presents, apart from the topological properties, a general description of the provided traffic load for each studied topology. Specifically, for New York and Norway, we use the default traffic matrices provided, while for Geant, we select the subset of available traffic matrices measured at 00:00 on 5 May 2005.
As we are considering an in-band scenario, after placing the controllers in each simulation instance, we have deleted the data traffic demands from/to them. The network load being an important parameter that impacts the efficiency of any energy-aware solution, we also compute the average network load
, defined as follows:
Where the traffic flowing on each link was obtained routing each traffic demand using the shortest path. Results from this early analysis confirm that the real scenarios considered present a low network traffic load. More in detail, the average network loads of the three network topologies are less than 0.05, New York links being particularly lightly loaded (i.e., ). This behavior is typical in real backbone topologies where capacity planning strategies aim to always ensure a significant over-provisioning in core links relative to the offered average load. This is done as an attempt to avoid the congestion in case of peak load and to allow the fulfillment of Service Level Agreement (SLA) requirements. Intuitively, low loaded networks are suitable scenarios for deploying energy-aware solutions that concentrate traffic and turn off unused network links. Therefore, this analysis suggests that substantial energy savings are possible. Moreover, we can deduce that potential energy benefits will be more limited by the required connectivity and topological properties than by the network traffic load.
An average rate of 1.7 Mbps was assumed for the control traffic [
39]. Considering a homogeneous scenario, where all controllers have the same computational and networking capabilities, in our simulations, we set the maximum number of forwarding devices that can be associated with each controller as follows:
In this way, switches are evenly distributed, and the load of switches is balanced among controllers.
To analyze the performance of our energy-aware approach, five groups of evaluations are presented varying the number of controllers in the considered topologies. In the first part, the performance of our heuristic algorithms with respect to the optimal model is analyzed in order to fix an upper bound for the energy saving capabilities of proposed solutions. In the second part, the potential of SNetCA to prune a network topology is investigated. Then, we compare our solution with the four strategies of another energy-aware method proposed in the literature. Next, we analyze the impact of our model on crucial network performance metrics, such as latency, link utilization and TCAM occupation. Finally, we provide an initial analysis exploring the existing trade-off between energy savings and network resilience.
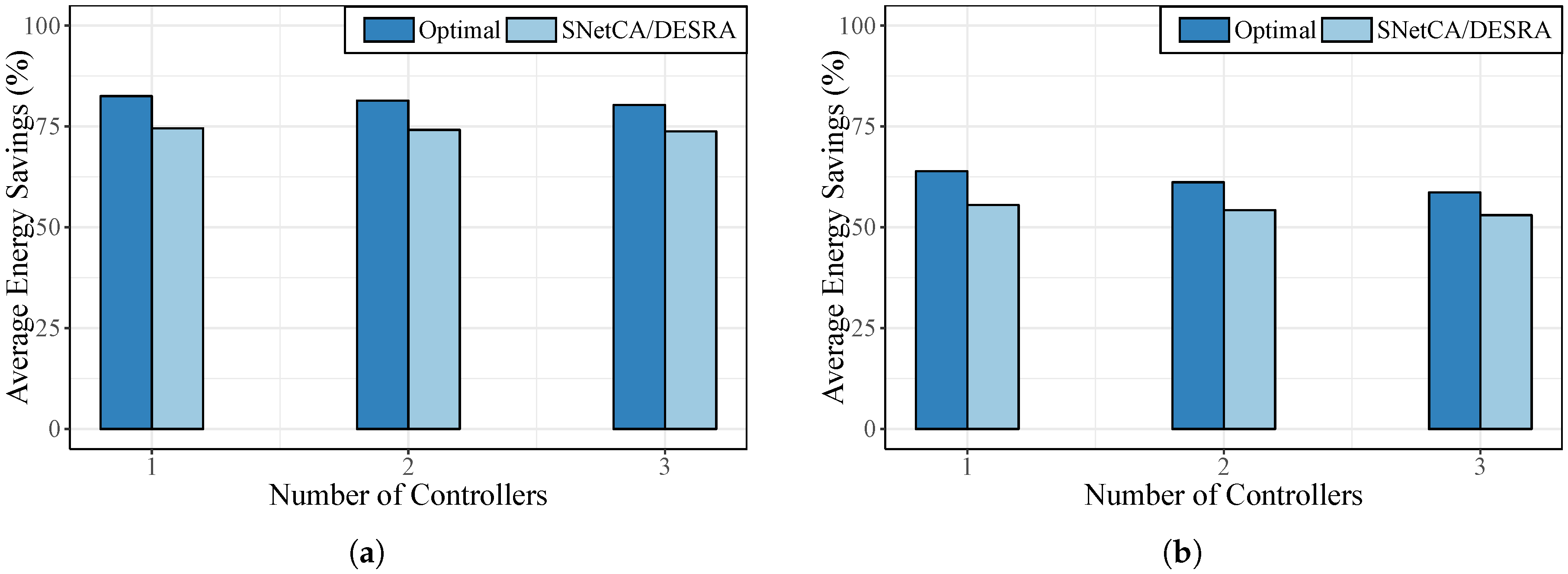
5.1. Optimal vs. Heuristic Solutions
To assess the performance of proposed heuristic algorithms against the optimal solution achieved by the ILP model, we show their behaviors in
Figure 2 using the New York and Geant topologies.
In both networks, we consider all admissible controller placements and compute the average energy savings for different numbers of controllers. Notice that a controller placement is admissible when the assumptions established in this proposal to avoid the routing of additional traffic load through network controllers can be kept (i.e., the network graph without any controller is strongly connected). We compute energy savings as the proportion of links in sleep mode with respect to the total amount of network links.
As shown in
Figure 2, the energy savings reached by the optimization model are up to 64% and 83% in Geant and New York topologies, respectively. On the other hand, the heuristic strategy (denoted in the figure as SNetCA/DESRA) allows attaining close-to-optimal energy savings, with a maximum gap of 9%.
We can also see that while the number of controllers grows energy savings decrease. This is due to the fact that in our approach data plane communications are not routed through network controllers. Therefore, as the number of network controllers is increased, a higher number of links (i.e., links directly connected to the controllers) is likely to be used to route control traffic, but not for data plane communications. A similar decreasing behavior can be noticed in the gap between optimal and heuristic results since, as the amount of network controllers grows, a lesser number of feasible possibilities can be considered by the linear solver.
Table 3 shows the average execution times of the optimal model and heuristic algorithms in the three network topologies considered in our experimental simulations. While the SNetCA column shows the execution times required to prune the network, the two others contains how many seconds are spent by each routing approach to compute all the required control and data paths according to the incoming traffic. As is shown, in both approaches, computation times mostly tend to decrease as the number of controllers grows. The reason for this is that in these energy-aware approaches, the routing of additional traffic load through network controllers is avoided. Therefore, an increase of network controllers implies that fewer alternate paths between each pair of nodes are considered in the simulation.
Although in all cases, the proposed strategy outperforms the optimal model in terms of computation time, a higher improvement is achieved as the network size grows. For instance, in the Norway topology, the processing times required by the optimal model increase dramatically. The ILP model in this topology can take more than two hours on average to find a solution, which is a great limitation in current networking environments. Meanwhile, it is always less than 10 s for the heuristic strategy, i.e., almost a three order of magnitude improvement. This comparison validates the improvements achieved by the heuristic proposal in terms of computation time and clearly justifies its necessity.
For the Norway topology, only the case of having one and two controllers is shown. The required convergence time for solving the exact model beyond this limit became unfeasible, since the number of possible combinations of nodes as controllers’ placement grows exponentially.
5.2. SNetCA Performance
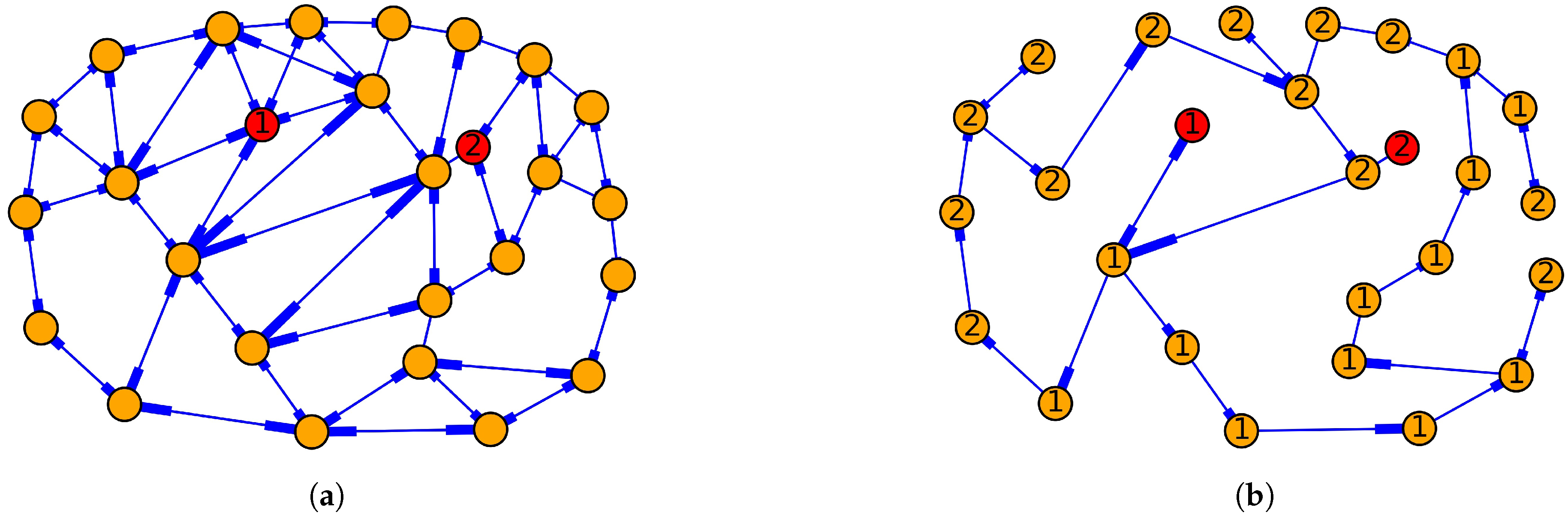
In order to evaluate the effectiveness of the proposed topology-based module,
Figure 3 shows an example of the performance of SNetCA on the Norway topology, considering two network controllers placed at nodes denoted as 1 and 2 and emphasized with a different color in the figure. The distribution of switches between controllers is depicted through the use of labels in each node, indicating the controller number to which the node is associated. Here, we focus our attention on the Norway topology, but similar results have been obtained for the two remaining topologies considered.
A comparison between the original network and the resulting graph illustrated in
Figure 3a,b respectively, shows a difference of 67 edges, which represents more than 65% of total network links. These links are pruned by our algorithm guaranteeing that the resulting graph remains strongly connected and avoiding additional traffic load through network controllers.
Additionally, as a result of applying SNetCA on the Norway topology, switches are distributed between controllers minimizing the number of required active links and ensuring a balanced controllers load. For instance, 12 switches are associated with Controller 1, while the remaining 13 are managed by Controller 2.
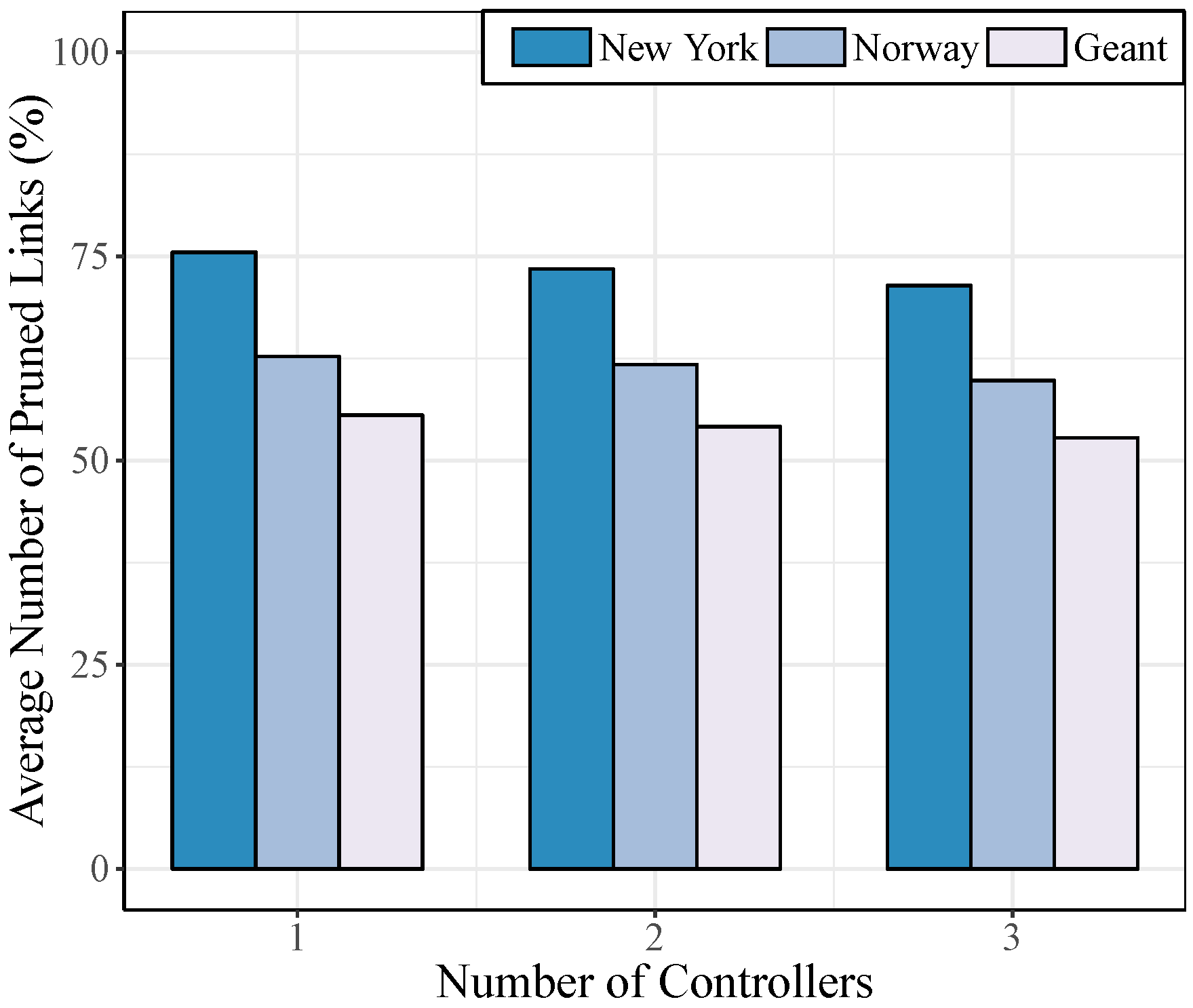
To provide a more general perspective,
Figure 4 shows, for the three considered topologies, the average number of links pruned by SNetCA, which contribute directly to the energy efficiency achieved by this proposal. In this analysis, we also consider all the admissible placements of one to three controllers.
As is shown, an important number of links is pruned in all the topologies considered, but the highest energy savings are achieved in the New York topology. The reason for this is that New York has much more link redundancy than Geant and Norway. Therefore, a higher number of links can be pruned while guaranteeing the network connectivity. In general, the more redundant the network, the higher number of links are put into sleep mode applying this strategy.
5.3. Assessment of Energy Saving Potential
SGH [
25] is an energy-aware routing solution based on knowledge of the incoming traffic requests. This proposal selects, using a pre-calculated set of shortest paths, the most suitable path in terms of energy savings to allocate each traffic demand, as long as it has enough capacity. To do so, traffic demands are ordered according to the following four different strategies:
Node pairs with the shortest Shortest Path First (SPF)
Node pairs with Longest shortest Paths First (LPF)
Node pairs with Smallest Demand First (SDF)
Node pairs with Highest Demand First (HDF).
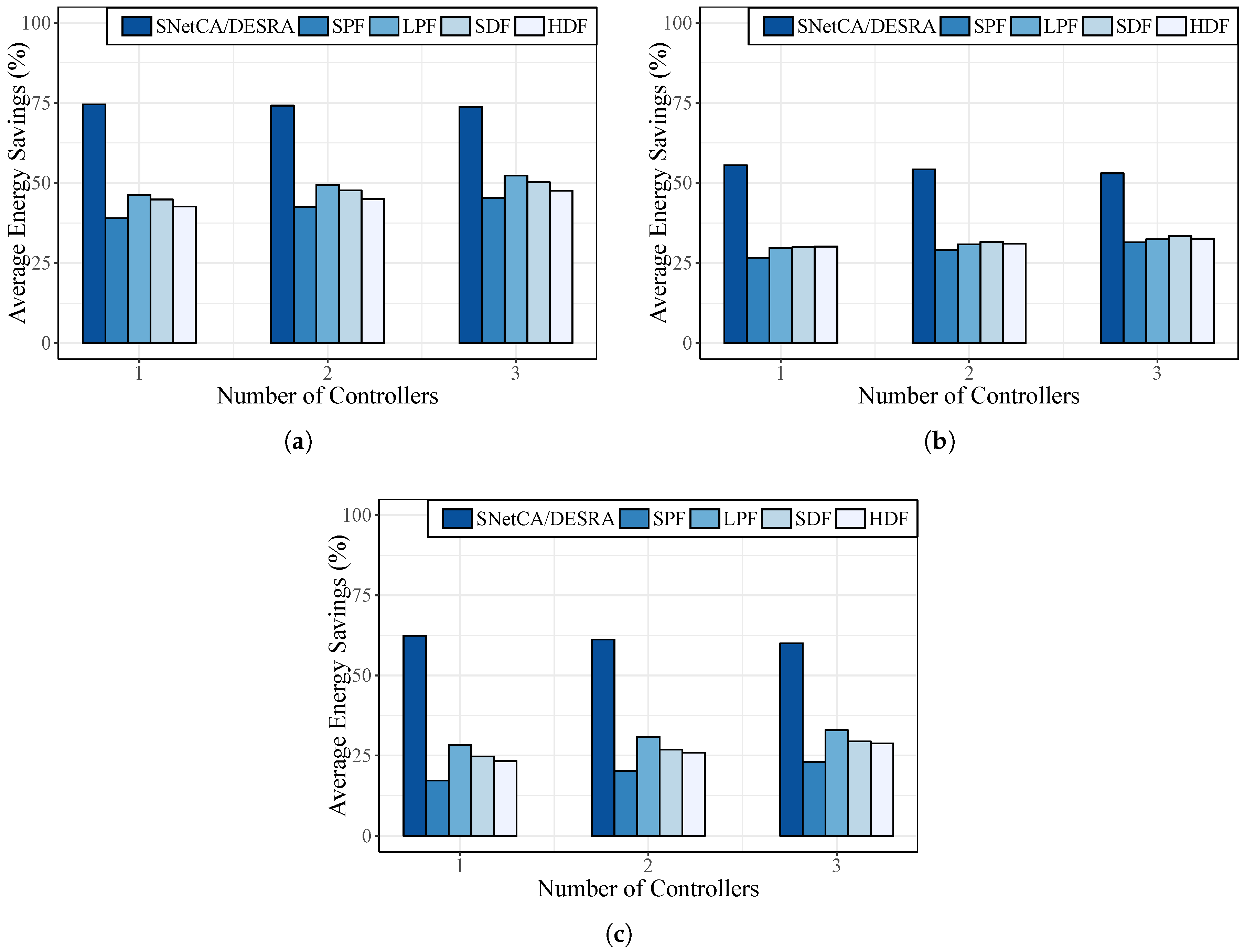
Figure 5 shows the average performance in terms of energy savings of the two-module based strategy SNetCA/DESRA with respect to the four different versions of SGH in the three real topologies analyzed for different amounts of controllers.
As we are considering an in-band SDN with multiple controllers, the traffic matrix provided to SGH includes, together with the data demands, a control traffic flow for each pair of associated controller-switch and for each pair of controllers in the network. In this way, required control plane communications are also established by SGH. This is done taking into account the distribution of switches between controllers obtained from SNetCA. Additionally, the routing restrictions established in this proposal to avoid additional traffic load through network controllers are considered in the computation of the pre-calculated shortest paths. On the other hand, given that DESRA is an online routing strategy, the connection requests are sequentially allocated as they appear in the considered traffic matrix.
In
Figure 5a–c, we can see that SNetCA/DESRA performs better than the remaining algorithms. While similar results are obtained by the four different versions of SGH, the proposed strategy achieves notable improvements in the three considered topologies. For instance, differences up to 35%, 29% and 45% of energy savings are reached in the New York, Geant and Norway topologies, respectively. Such significant differences are mostly due to the operation of SNetCA before the traffic arrival, which is able to prune a great number of links without affecting the network capabilities to manage the incoming requests. Additionally, the routing decisions performed by SGH are limited to a predefined number of pre-computed shortest paths and fail to extensively exploit the energy saving potential of each topology. Therefore, even without a prior arrangement of demands based on accurate knowledge about the incoming traffic, the proposed scheme in this paper puts to sleep mode a higher percentage of links, being able to save substantially more energy.
5.4. Impact on Network Performance
It is to be emphasized that in our energy-aware approach, Quality of Service (QoS) constraints and performance metric boundaries are not considered. This is not a limitation, but a choice; since we intend to measure the impact of our proposal on the network performance metrics as a trade-off with the energy saving improvements. In fact, we are presenting an effective and easy to implement green routing mechanism that emphasizes the importance of energy efficiency in the operation of current data networks.
In order to assess the impact of our energy-aware approach on the network performance, we adapt two well-known state-of-the-art routing algorithms: Shortest Path Routing (SPR) and Load Balancing (LB) for their use in the considered in-band SDN environment. Additionally, the rule space being a significant issue of concern in SDN, we include in this analysis an algorithm balancing the number of rules installed in each forwarding device, denoted here as TCAM Occupation Balancing (TOB). In general, these algorithms are greedy heuristics that follow the procedure described in Algorithm 4.
More precisely, these algorithms will evaluate every candidate admissible path and find the one prioritizing some performance metric such as: traffic latency, link utilization or TCAM occupation. According to the approach used, the selected path will be:
- SPR
The one minimizing the propagation latency
- LB
The one minimizing the maximum link utilization
- TOB
The one minimizing the maximum TCAM occupation
It is clear that, in each of these metrics, the corresponding baseline algorithm will have better performance than our energy-aware approach. However, the purpose of this evaluation is to use these algorithms as a reference point to illustrate the energy-aware solution impact on network performance. All of them follow the assumptions established in this proposal to avoid the routing of additional traffic load through network controllers. Similarly, SNetCA is still used to determine the distribution of switches between controllers. Although we may focus our attention on some specific network for the different performance metrics, the derived conclusions are general and independent of the specific considered topology. Thus, they hold whichever network is examined.
| Algorithm 4 Greedy_baselines |
- Require:
G, A, D - 1:
for do - 2:
Find_Best_Data_Path - 3:
Update network metrics - 4:
for do - 5:
if no control path is already established between s and its controller in A then - 6:
Find_Best_Control_Path - 7:
Update network metrics - 8:
end if - 9:
end for - 10:
end for
|
5.4.1. Traffic Latency
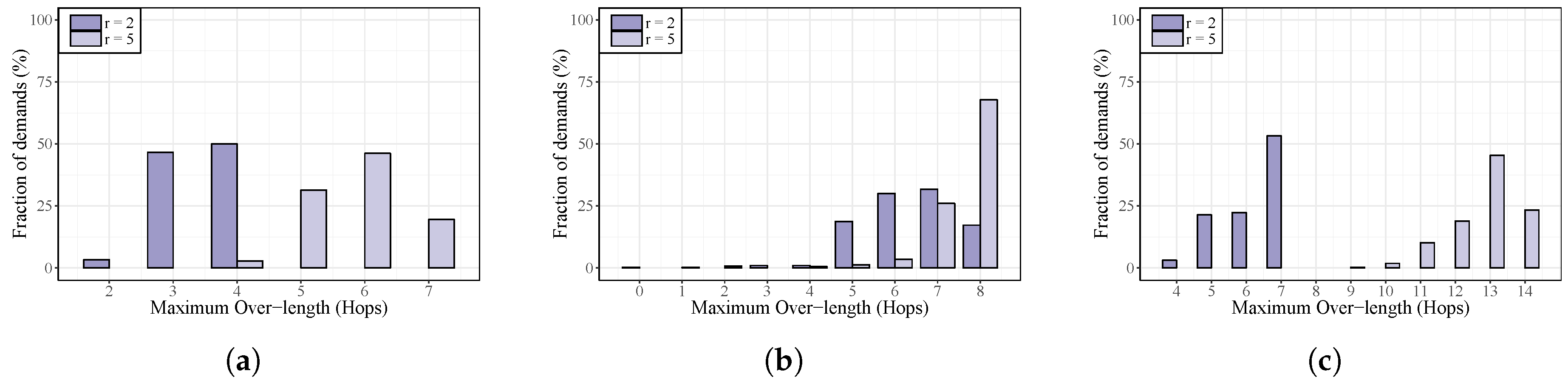
In the first set of simulations, we analyze how the data and control paths latency is affected by routing decisions made.
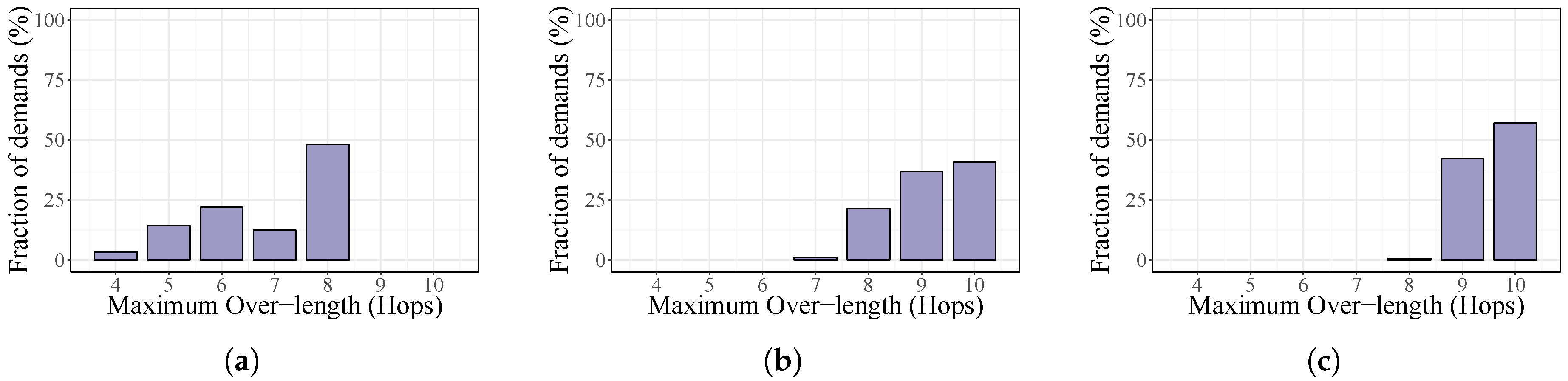
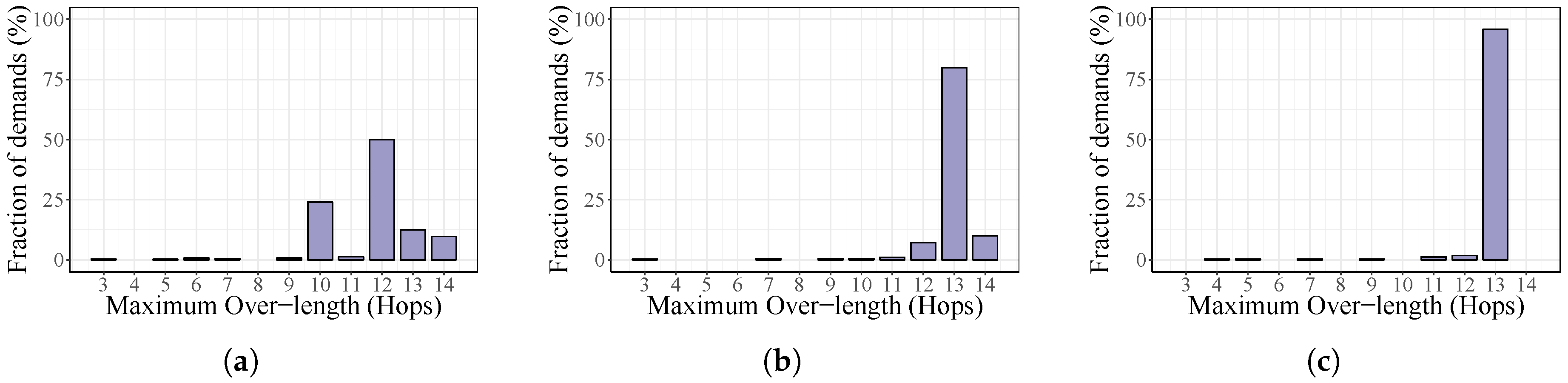
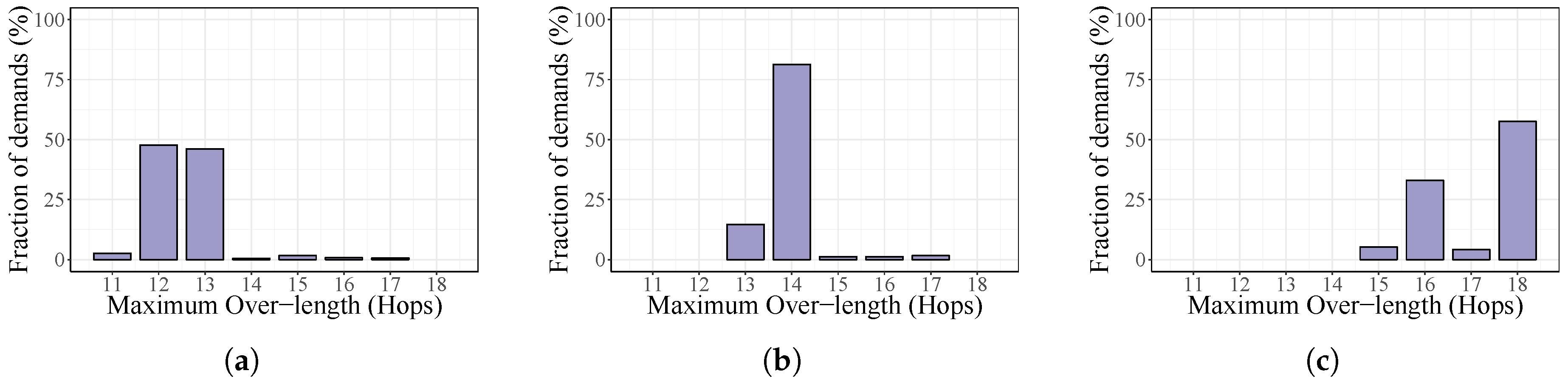
To evaluate the impact of our algorithm on control path delay, we collect, for each traffic demand, the length of its associated control paths and the corresponding shortest paths. The notation Maximum Over-length is used to denote the maximum number of additional hops (with respect to the length of the corresponding shortest path) among the routing solutions for the required control paths. For instance, when this value is equal to zero, it means that every control traffic is routed using exactly the shortest path.
Figure 6,
Figure 7 and
Figure 8 show this behavior for the three studied topologies considering all possible placements for different amounts of controllers.
As is shown, in all cases when the number of controllers grows, the control traffic is routed using a larger number of hops for a higher fraction of demands. Norway being the largest one in terms of network size (number of nodes and links), control paths in this topology are increased by a higher number of hops.
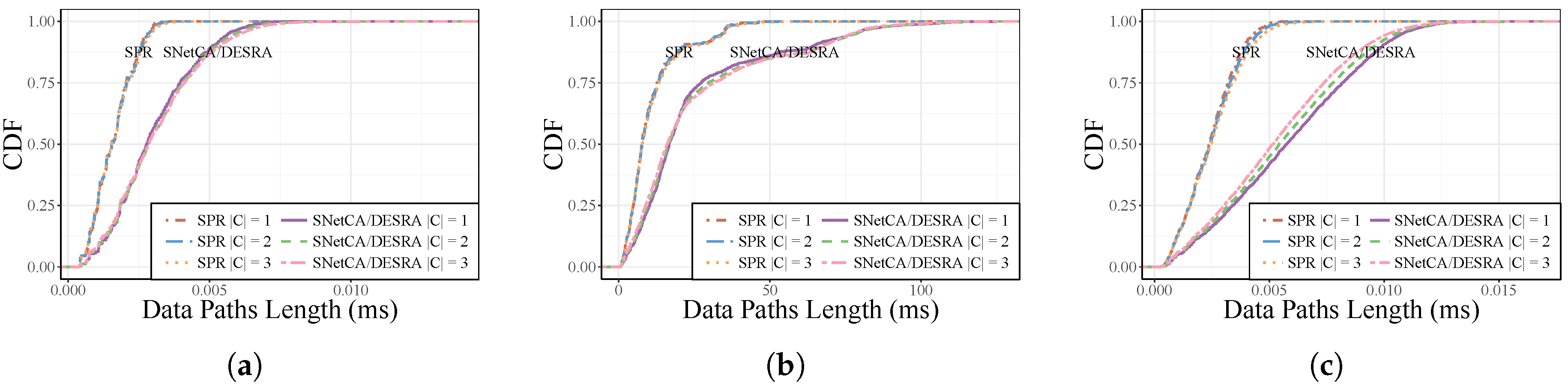
To take a closer look at the data plane, we draw in
Figure 9 the Cumulative Distribution Function (CDF) of data paths’ latency for the three topologies considering all possible locations of one to three controllers.
As shown in
Figure 9a–c, the CDFs of data paths’ latencies for different amounts of controllers are quite similar. However, we can see that under the energy-aware routing, data path delay is affected since larger data paths are used in order to minimize the number of active links. For instance, in
Figure 9b, only 87% of data paths exhibit delays lower than 50 ms, meanwhile all control paths in the SPR case are under this value. This performance degradation is less critical in the two other topologies, which are deployed in smaller geographic areas compared to Geant. In general, the larger the network (in terms of geographic length), the more increase in latency is incurred.
Despite the presented latency degradations with respect to SPR, the solution performances observed in
Figure 9a,c are suitable for supporting latency critical services in 5G networks demanding end-to-end delays lower than 10 ms [
40], such as robotics and telepresence, virtual reality, health care, among others. Likewise, less demanding applications and use case scenarios to be addressed in 5G networks, such as intelligent transport systems and smart grid, with latency requirements up to 100 ms [
40], could be conceived of and deployed in Geant-like environments.
These latency degradations confirm that, according to traffic requirements, specific performance bounds may be required. In order to ensure the suitability of the proposed algorithm for delay-critical services, we include in this analysis the evaluation of a delay-constrained version. To do so, we now restrict the number of links that can be initially pruned by SNetCA. Specifically, network links belonging to the shortest path between any pair of nodes are not removed during the static network configuration phase. In this way, the shortest path will always be available if it is needed for allocating the incoming traffic with DESRA. In both modules, the path latency is now taken into account for the PathSelector mechanism in order to satisfy given delay bounds.
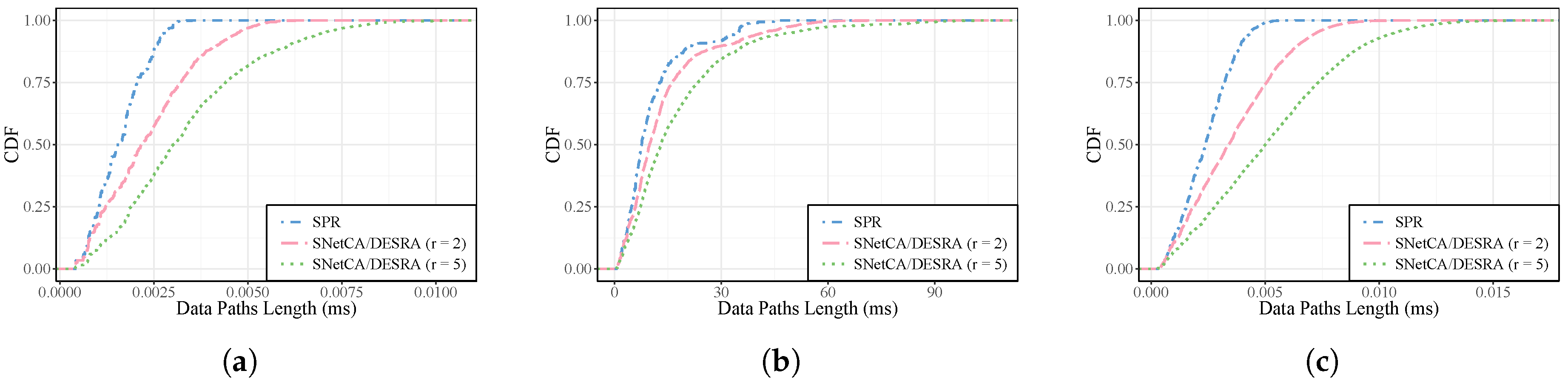
Figure 10 and
Figure 11 show the performance of the delay-constrained version considering data and control paths latency bounded by the factor
r. This latency threshold is used to denote the relation among the delay requirement and the shortest path propagation latency for every established path. For instance, when
every path latency will be, at most, twice that of the shortest path.
As is shown in
Figure 10 under the delay-constrained approach, the control traffic can be routed incurring smaller over-lengths with respect to the performance-agnostic approach. Similarly,
Figure 11 shows that the data paths latency are less compromised when more restrictive possibilities in terms of latency (
and 5) are considered. In general, the more restrictive is the latency bound used, the better the performance in terms of delay can be achieved.
On the other hand, considering a latency restriction during paths’ selection will negatively impact the potential improvements in terms of energy efficiency. To validate this affirmation, the energy savings achieved by the delay-constrained version using
are shown in
Table 4. In this table, optimal and heuristic values are depicted as well as the energy saving differences between the performance-agnostic results shown in
Figure 2 and the delay-constrained version.
Optimal values were obtained after adding to the ILP model presented in
Section 3 the following constraint, where
and
denote the link propagation delay and the traffic maximum latency bound, respectively.
Significant reductions in terms of achieved energy saving values can be seen in
Table 4 for the both considered topologies as a consequence of restricting the path selection to meet the delay requirements. However, even considering such restricted thresholds, where no traffic can be routed using a path longer than twice the shortest path length (in terms of propagation delay), substantial energy savings can still be reached by the proposed heuristic strategy.
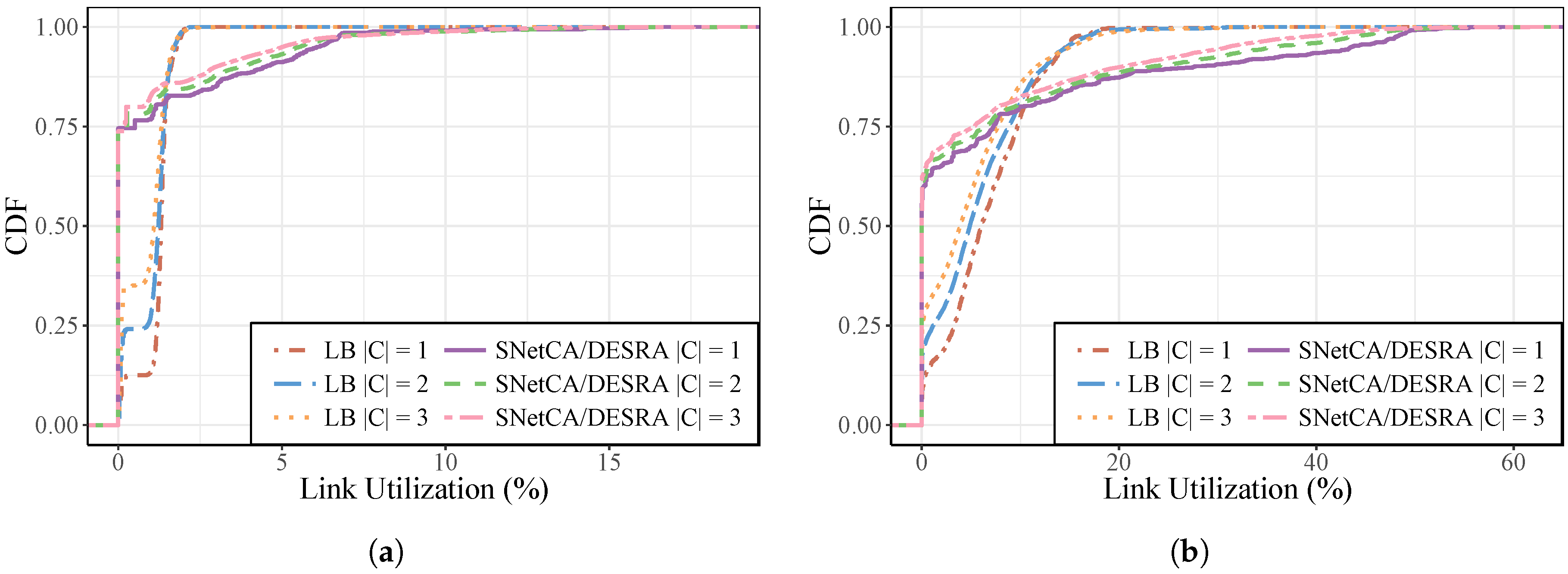
5.4.2. Links Utilization
The selection of routing paths minimizing the energy consumption has a direct influence on the traffic load of all the network links. To better showcase this situation, we use the New York and Geant topologies and the LB algorithm.
Figure 12 provides the CDF of link utilization under both algorithms considering all possible locations of one to three controllers in both topologies.
As expected, the fairness of traffic distribution is altered by the energy-aware routing, since under this approach, traffic is concentrated in a fewer number of links. Therefore, there is a subset of active links that is more overloaded than the others. For instance, in
Figure 12b, the link utilization of some links in Geant is increased to more than twice the value achieved by the LB algorithm. Nevertheless, even in the more loaded cases, the link utilization in this topology is under 60%. A less concerning situation can be observed in
Figure 12a since the given traffic load in the New York topology is very low.
5.4.3. TCAM Occupation
Intuitively, energy-aware routing would affect the allocation of flow rules, a practical constraint in OpenFLow devices, given that traffic flows are redirected to minimize the number of active links.
In
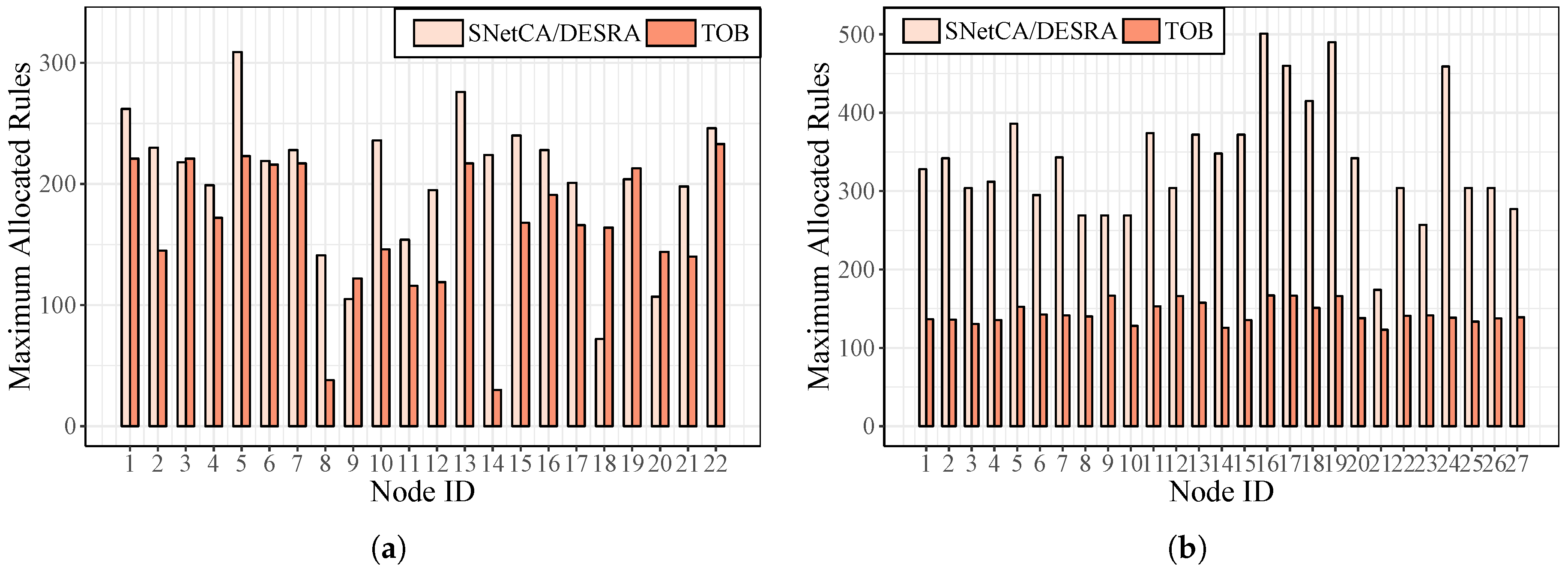
Figure 13, we evaluate the impact of our approach on TCAM occupation with respect to the TOB algorithm using the Geant and Norway topologies and all possible locations of two network controllers.
As expected, the number of installed rules is raised by the energy-aware routing since new paths are more likely to be allocated over the most loaded devices instead of activating a new one. For instance, this increase is observed in all network devices in Norway topology and in 17 out of 22 nodes in Geant topology, in some cases being more than twice the value obtained by the TOB algorithm. However, an accurate explanation about these numbers is difficult since the energy-aware proposal does not care at all about the use of rule capacity. Furthermore, the SNetCA/DESRA performance in both topologies is still physically acceptable considering that a routing table can support around a few thousands of rules [
23].
5.4.4. Energy Savings
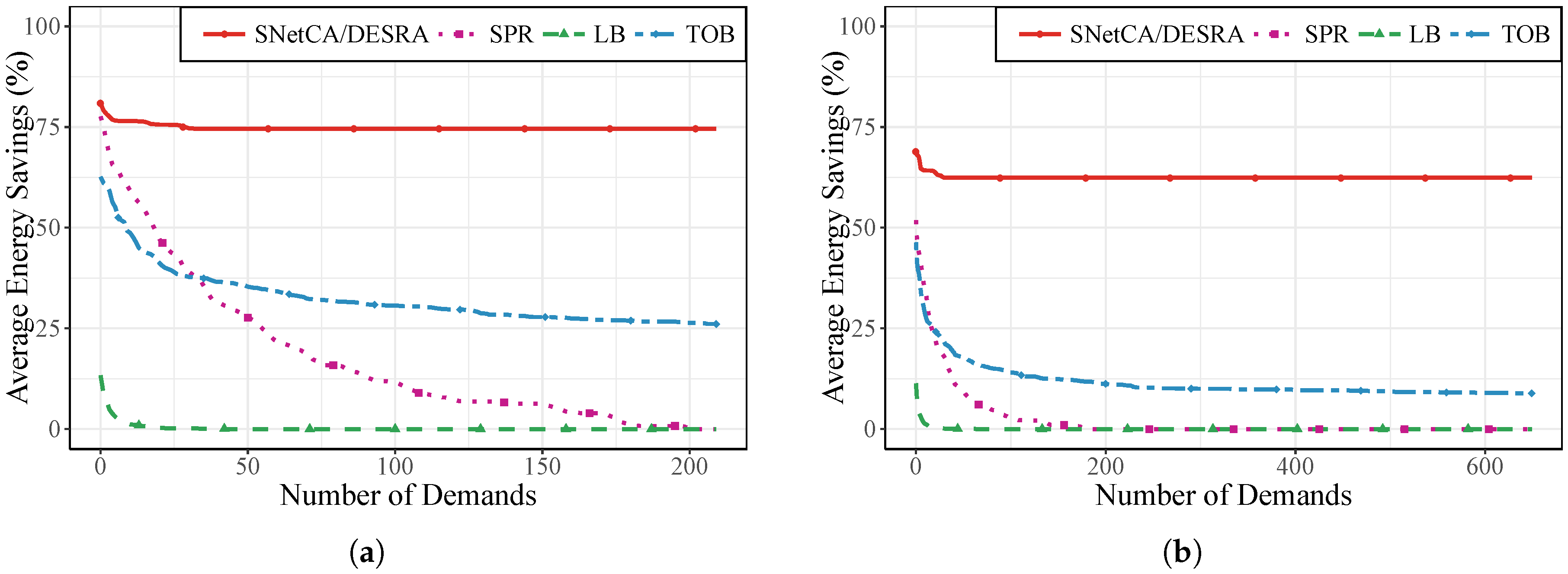
Finally, to get a sense of the other side of the trade-off between energy efficiency and network performance,
Figure 14 shows the average energy performance of all the considered routing models in the New York and Norway topologies for the case of one centralized controller in the network.
As expected, in all cases, energy savings decrease while the number of demands grows. This is due to the fact that new paths need to be established to accommodated such traffic. The flat tendency of energy savings achieved by the power-aware solution despite the increase in allocated demands is possible given the low network load discussed at the beginning of this section. Moreover, the proposed strategy greatly outperforms SPR, LB and TOB in terms of energy saving. In general, SNetCA/DESRA is able to achieve significant energy savings, but bigger improvements with respect to the other approaches are reached when the traffic grows.
5.5. Resilience Concerns
While SNetCA allows important gains in terms of energy efficiency by pruning as many links as possible and leaving available only the minimum number of links needed to support the incoming traffic, the remaining subnetwork is more vulnerable to resource failures and sudden traffic bursts. To ensure an adequate network reliability while keeping low energy consumption, resilience constraints should be taken into account.
Given that the largest Laplacian eigenvalue of a graph is a widely-accepted metric to assess network robustness with respect to link and node removals [
41], we use it (referred to here as
) to control the resulting resilience after applying SNetCA. Several papers about graph theory [
42,
43] sustain that a network is more resilient the higher the largest eigenvalue of its Laplacian matrix. In general, these networks are more robust since they have small diameters, higher numbers of nodes and link disjoint paths and are likely to expand faster.
In order to provide an initial investigation exploring the existing trade-off between energy savings and network reliability, in this analysis, we evaluate a resilience-constrained version of SNetCA, which enables us to limit the admissible reduction rate due to the link removal process. Additionally, to improve the redundancy for the control paths, the amount of neighbors that will remain connected to the controller is relaxed using different bounds (from one to the controller degree).
Table 5 presents some of the obtained results using the three considered topologies with one centralized controller. The presented results validate the impact of varying these two criteria (i.e., controller connectivity and
reduction rate) on energy savings and network robustness.
While the controller connectivity (denoted as
) is bounded by a number of neighbors between one and the controller degree, the allowed
reduction rate (denoted as
) was normalized according to the following expression, where the term SNetCA’ denotes the resilience-constrained version:
As is shown in
Table 5 when
and
, the resilience-constrained version of SNetCA behaves exactly as the resilience-agnostic one. However, less energy can be saved as more restrictive values of
and
are imposed, since each of these elements determines that a fewer number of links could be put into sleep mode by the pruning function of SNetCA.
Inversely, when no resilience degradation is allowed (i.e., ), higher values of are obtained. More importantly, we can observe that considerable energy savings can still be reached by the proposed heuristic strategy, while ensuring the original network reliability.
Although higher values of are expected when the bound of nodes that will remain connected to the controller is increased, this is not always the behavior that can be appreciated in the table for the three network scenarios considered. The reason for this is that every network node, which is considered in one particular instance of the simulation as the controller, does not have the same node degree. Thus, for each considered possibility of , different amounts of nodes are part of the presented average values.
We stress that the impact of switching off network links on SDN reliability is even more critical for networks with in-band control traffic where any link/node failure will affect not only data plane communications, but the connection with the controller. Hence, a further analysis about this crucial issue will be done in follow-on work.
6. Conclusions
In this work, 5G is considered as the broad context where several recent technologies, such as SDN, will be leveraged to fulfil functional and performance requirements of heterogeneous services and devices. At the same time, the unprecedented number of devices together with the rate-demanding services and the high energy efficiency expected in 5G networks are decisive drivers motivating this research. Undoubtedly, to gain insight into the existing trade-off between energy efficiency and network performance is a valuable contribution on the road to 5G. Precisely, this is the aim of this paper, conceived to highlight this crucial issue and to tackle the energy consumption problem in 5G backbone networks.
More in details, in this paper, we proposed an energy-aware strategy that reduces the number of active links used to handle the incoming traffic suitable for SDN environments with in-band control traffic and multiple controllers. To achieve such a goal, we first provided a link-based formulation of the optimization problem, integrating the routing requirements for data and control traffic. Given the overall complexity of the exact model in large-scale topologies and the fact that new devices with less predictable traffic patterns will join the 5G broadband network, a heuristic hybrid approach is conceived, comprising two algorithms: a static network configuration and a dynamic energy-aware routing. In this way, the number of links to be considered in the paths’ computation is significantly reduced by the first component, which contributes to decreasing the computation times, and traffic demands can be allocated by the second module in real-time as they come. Based on experimental simulations with real-world topologies and traffic matrices, energy savings between around 50% and 80% are reached by the proposed energy-aware approaches. The heuristic strategy attains results very close to the optimal values. In addition, the proposed algorithms are able to converge much faster and handle larger network sizes for which the exact model fails to find solutions in a reasonable time.
Apart from providing an effective power-aware scheme able to achieve notable improvements in terms of energy saving, the most significant added value of this proposal is the insightful analysis presented to evaluate the impact on network performance. Extensive simulations validate that crucial network parameters such as control traffic delay, data path latency, link utilization and TCAM occupation are affected by the performance-agnostic energy-aware model. Therefore, this paper stands as a valuable proposal in the design of online energy-aware strategies suitable for control planes of current programmable networks. Moreover, the intrinsic trade-off between environmental and performance concerns is disclosed and investigated using the proposed approach. As future work, we plan to extend the analysis about the impact of energy-aware solutions based on the reduction of active network elements on SDN reliability, considering in-band control traffic.