Fuzzy Logic Based MPPT Controller for a PV System
Abstract
:1. Introduction
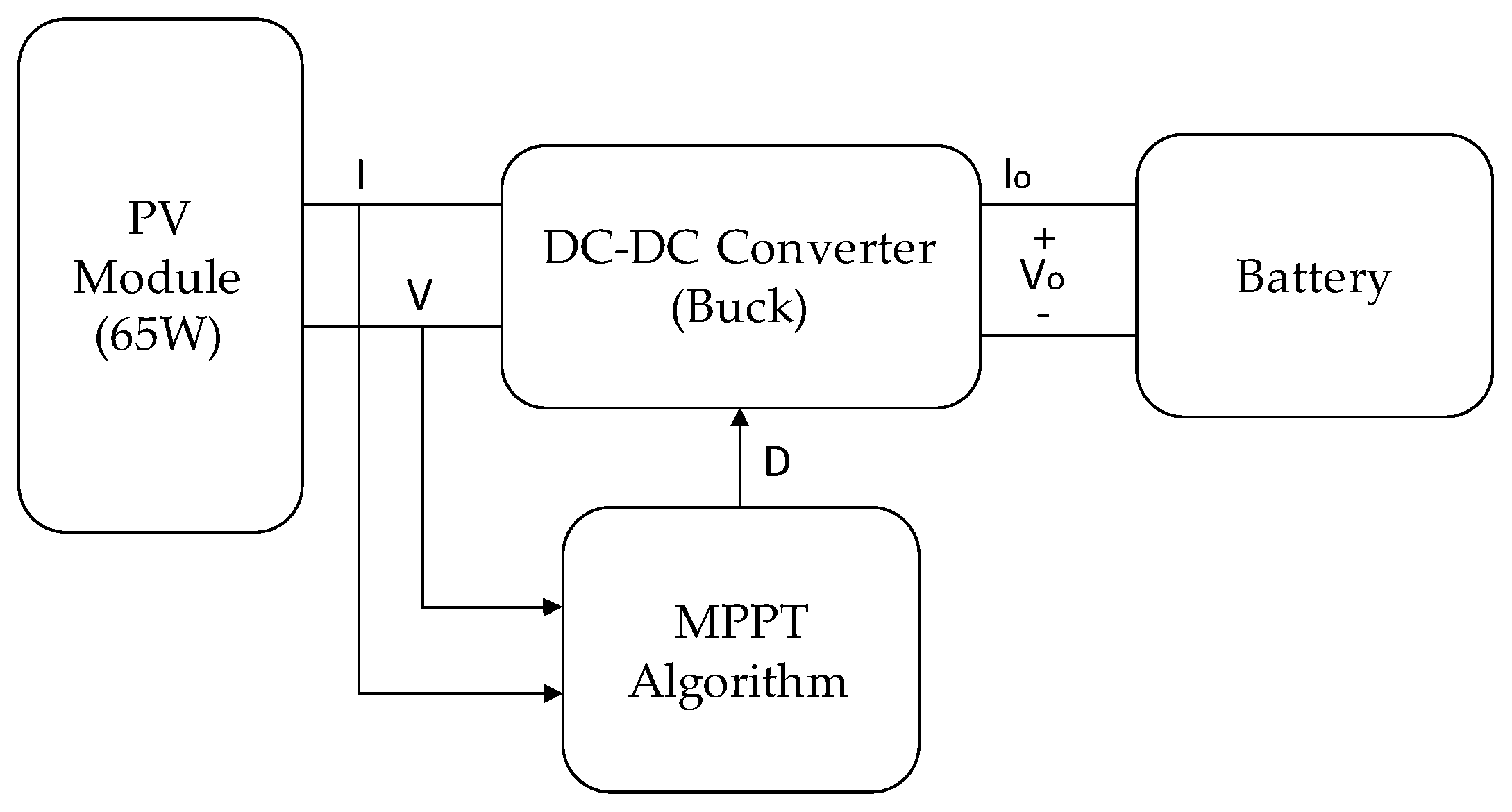
2. Design and Modeling of PV System
2.1. Modeling of the PV Module
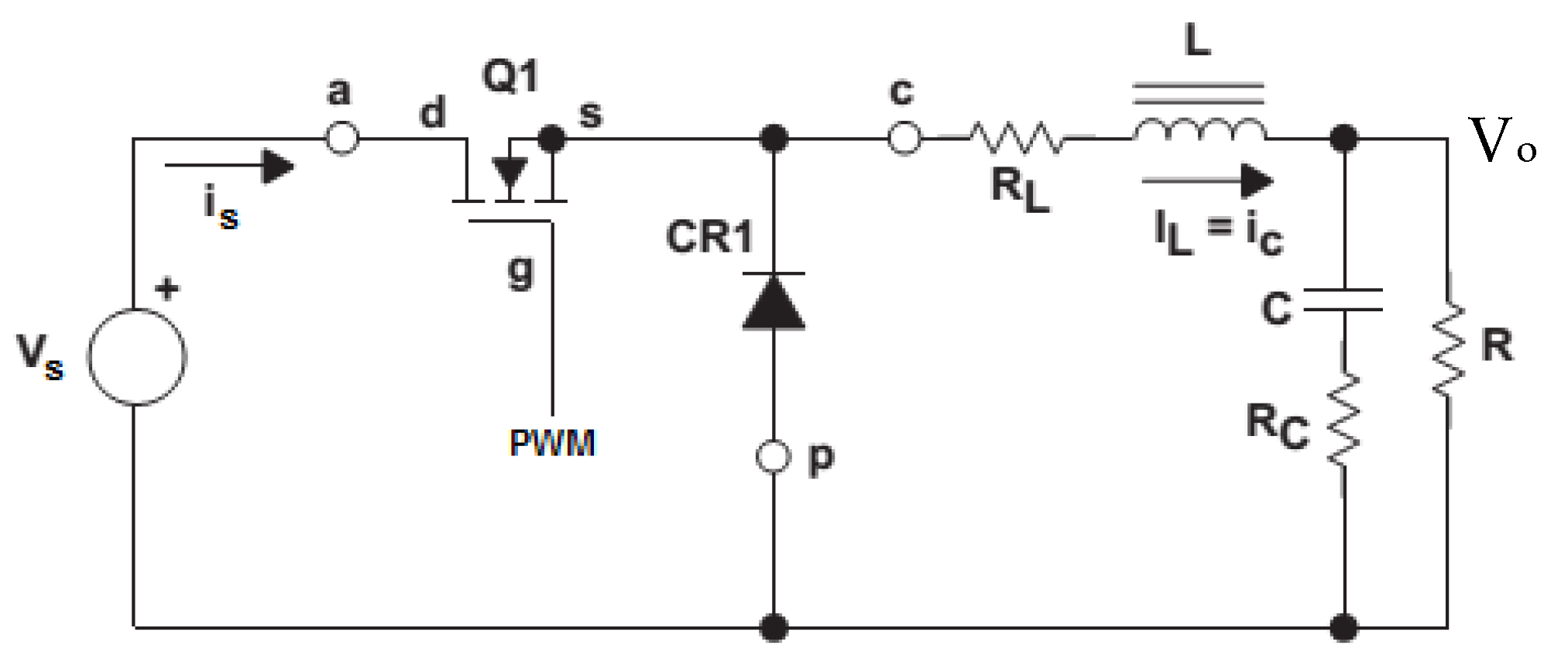
2.2. DC-DC Converter Model
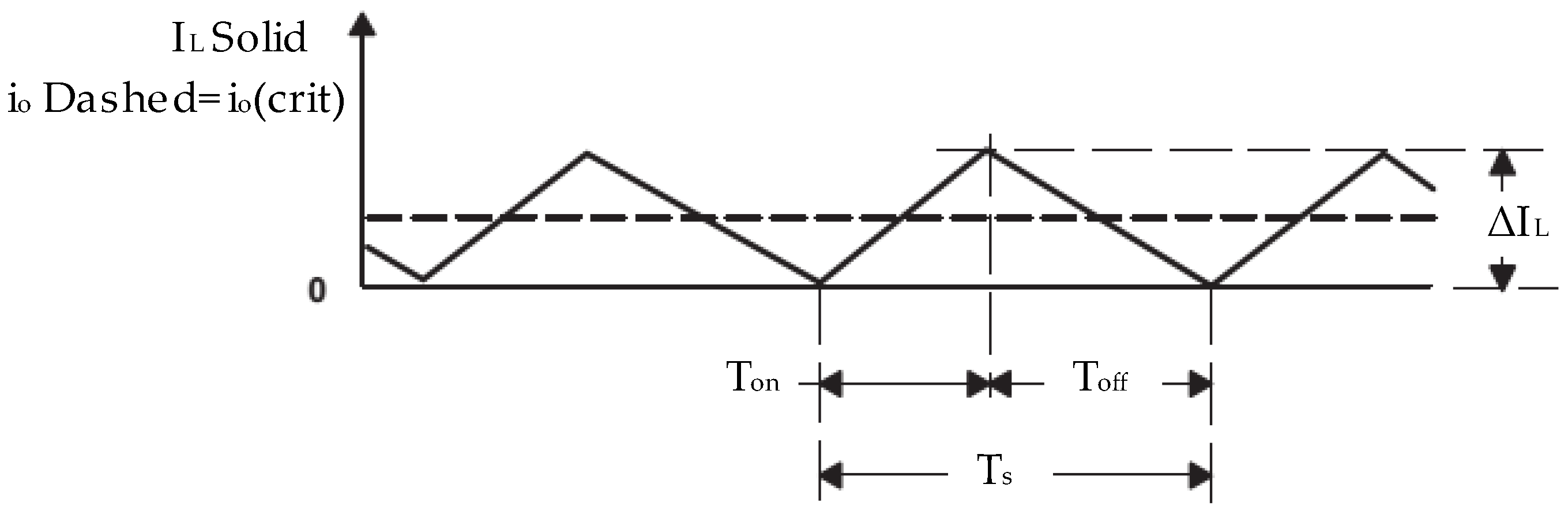
2.2.1. Inductor Design
2.2.2. Capacitor Design
2.2.3. Modelling of Buck Converter
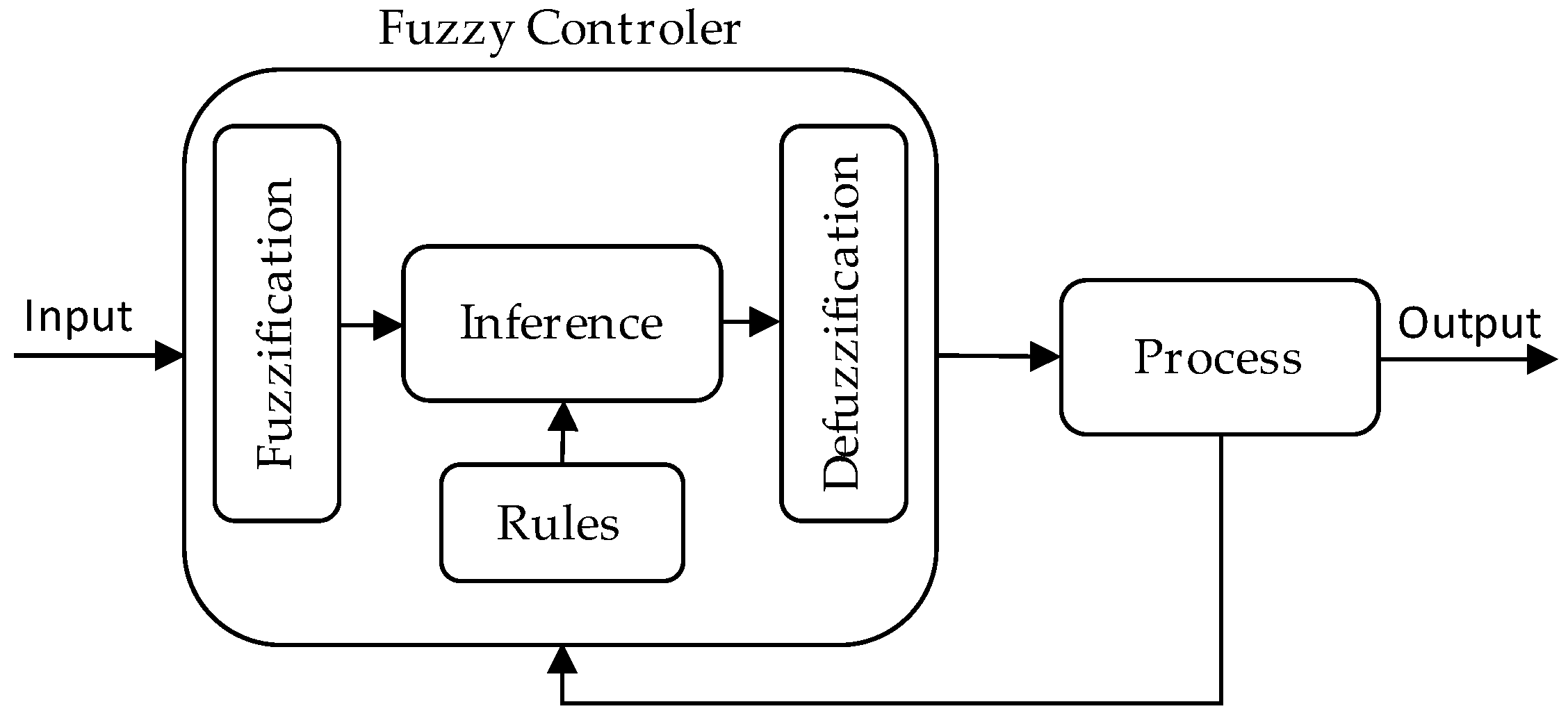
2.3. Fuzzy Controller Design
2.3.1. Membership Functions
2.3.2. Fuzzy Rules
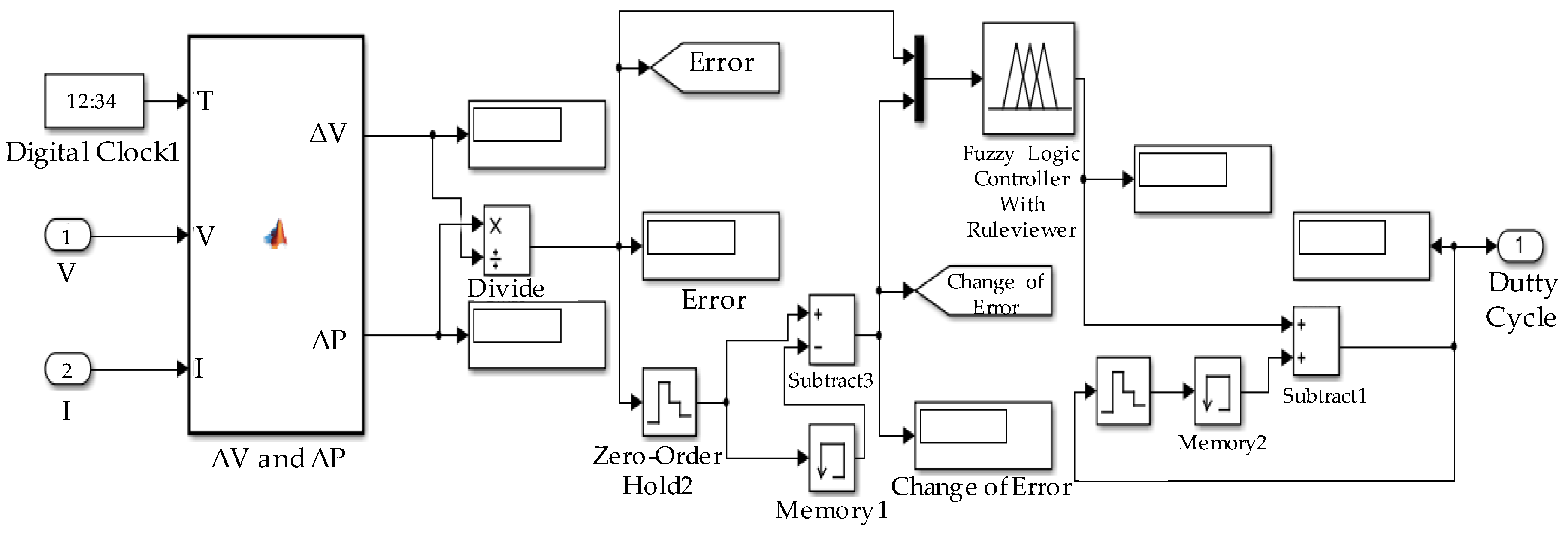
2.3.3. Fuzzy Controller Modelling
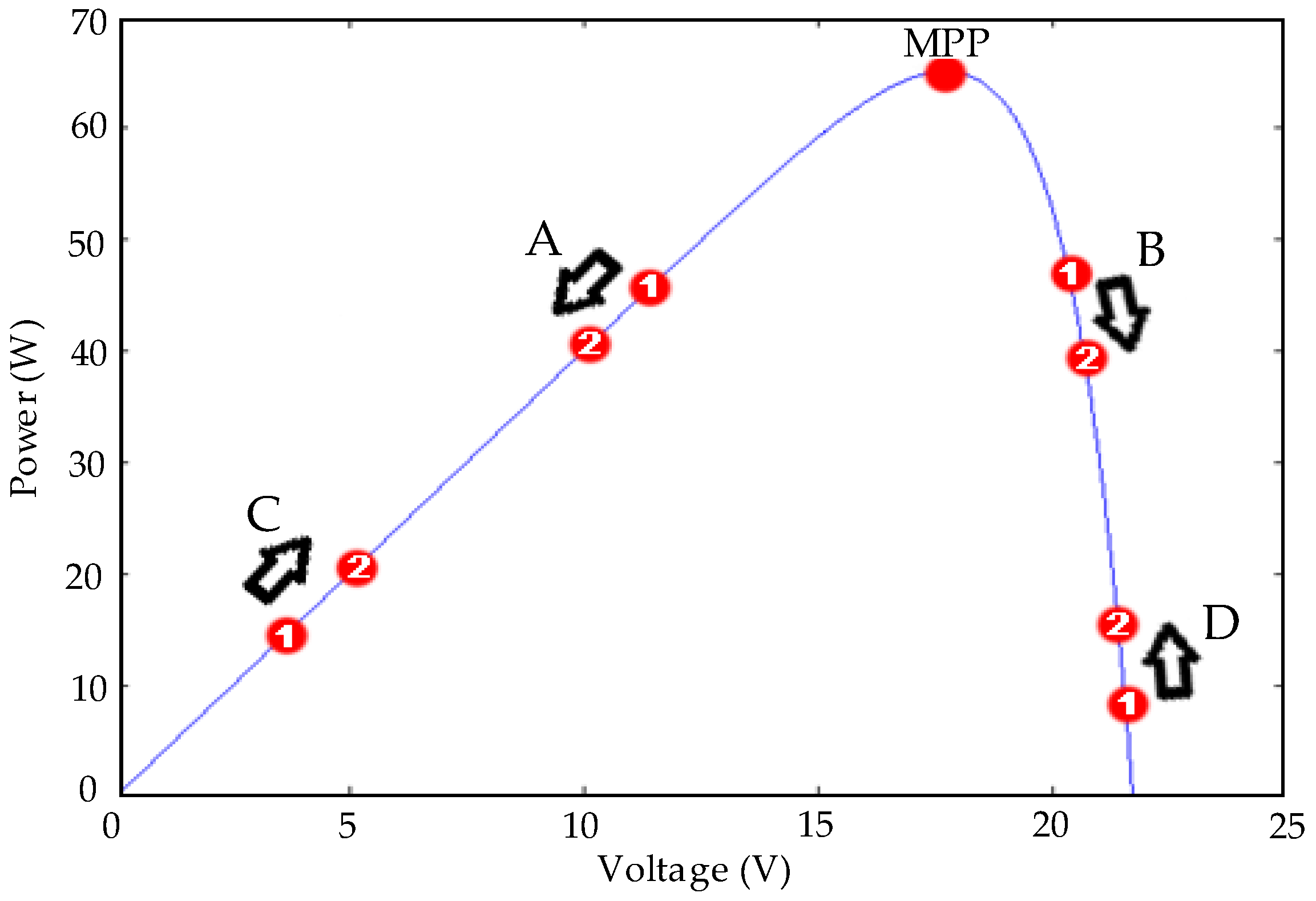
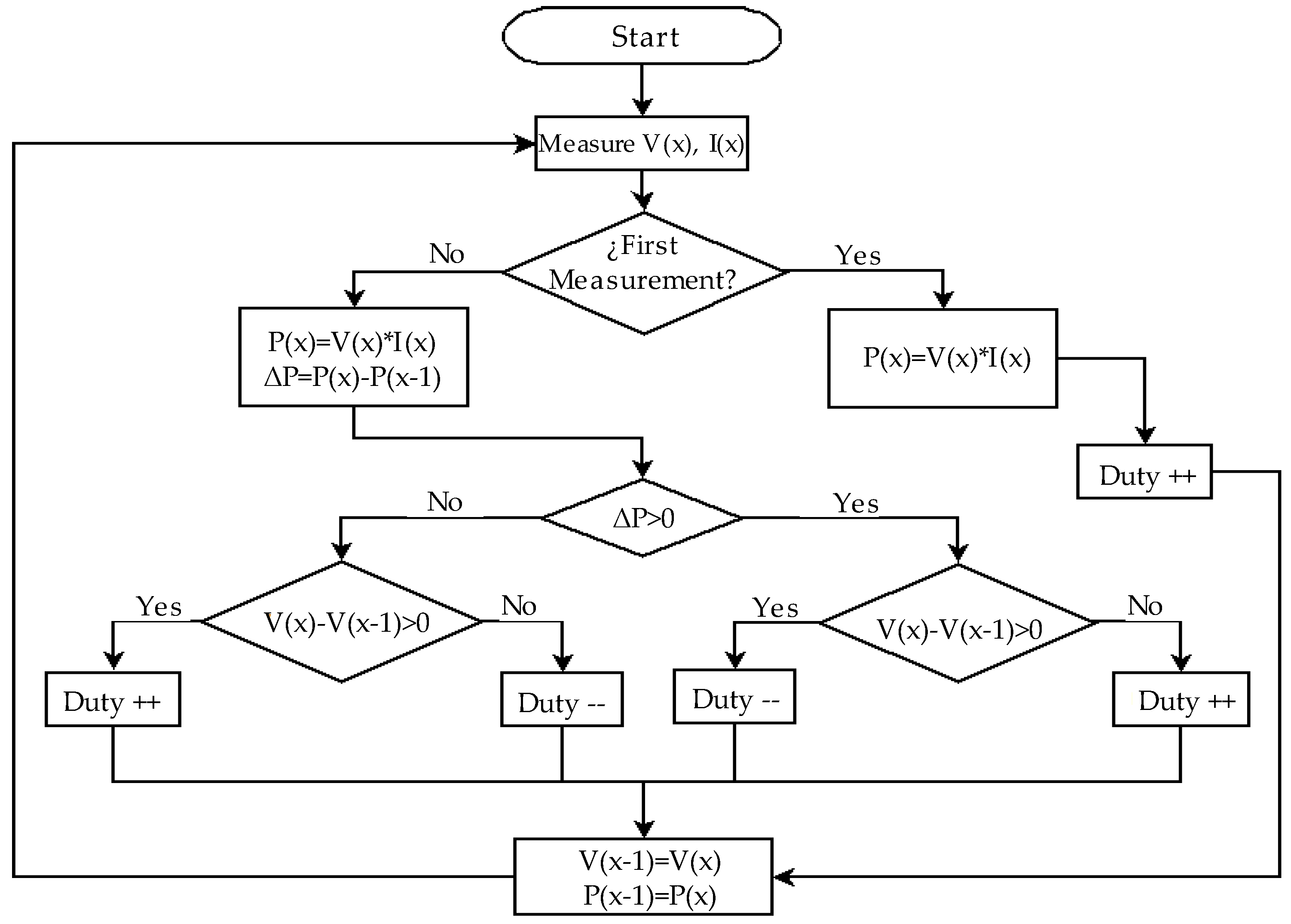
2.4. P&O Controller Design
- Case A: ΔP < 0 y ΔV < 0.
- Case B: ΔP < 0 y ΔV > 0.
- Case C: ΔP > 0 y ΔV > 0.
- Case D: ΔP > 0 y ΔV < 0.
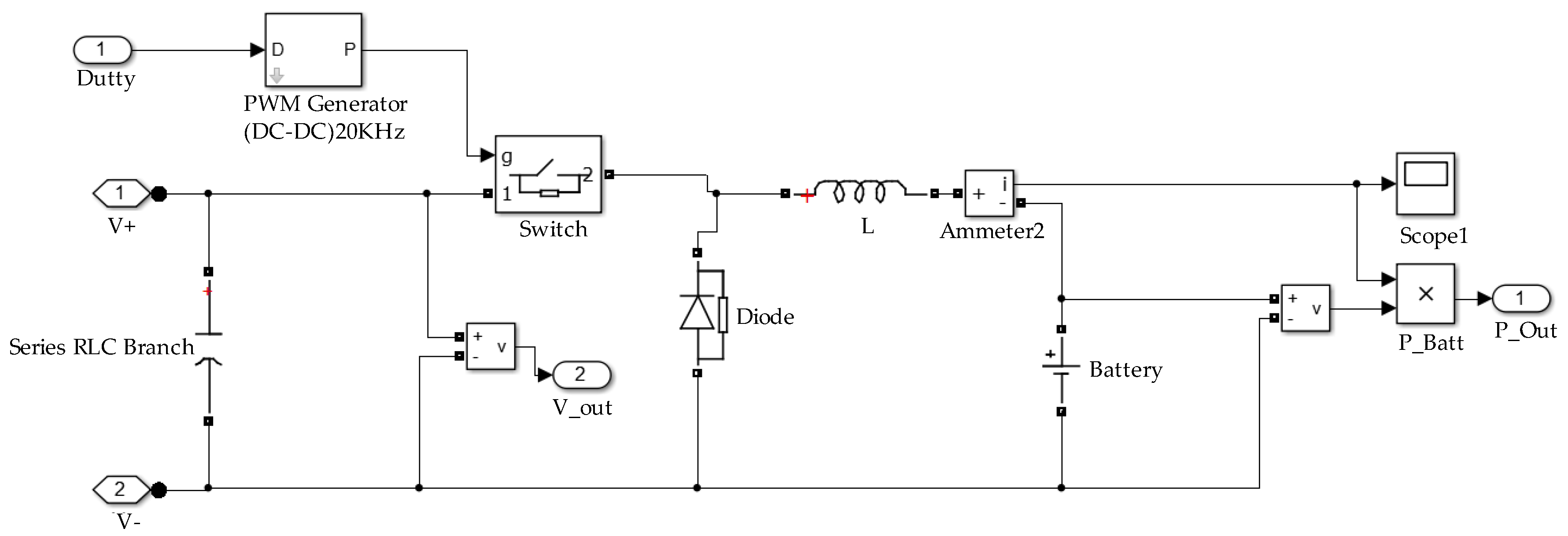
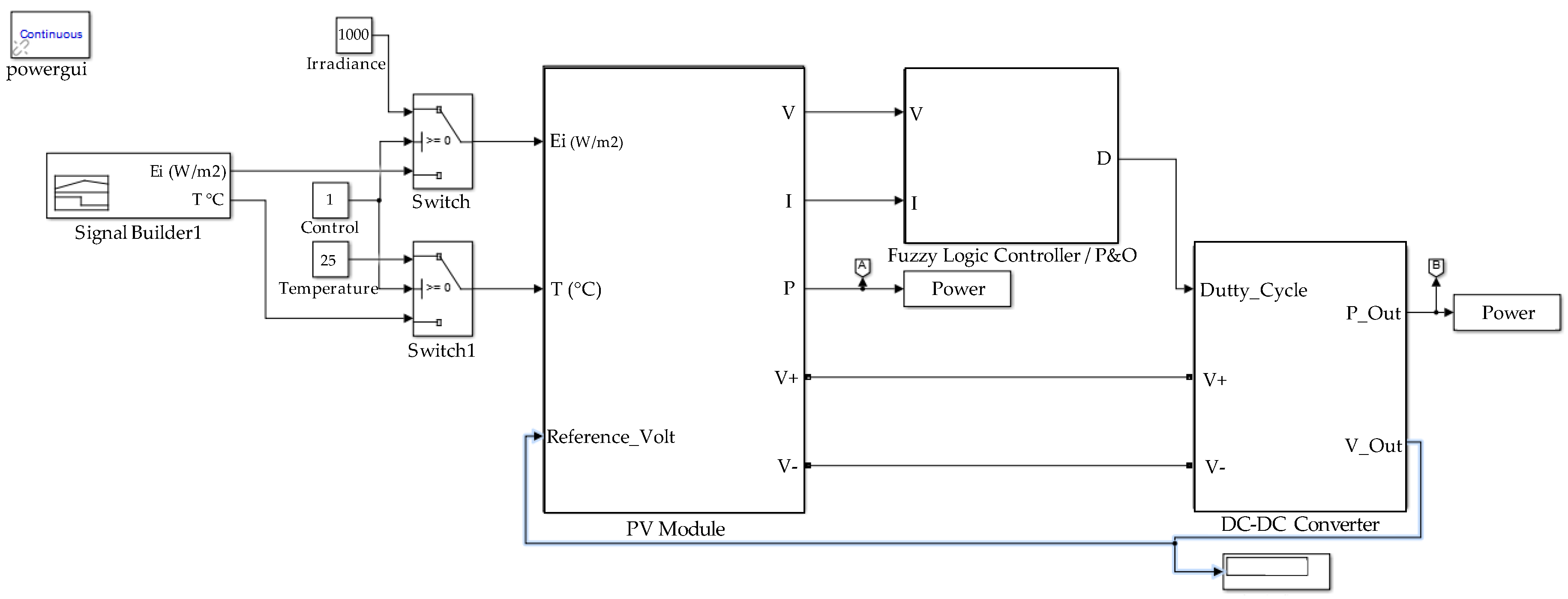
2.5. PV System Modelling
2.6. Limitations
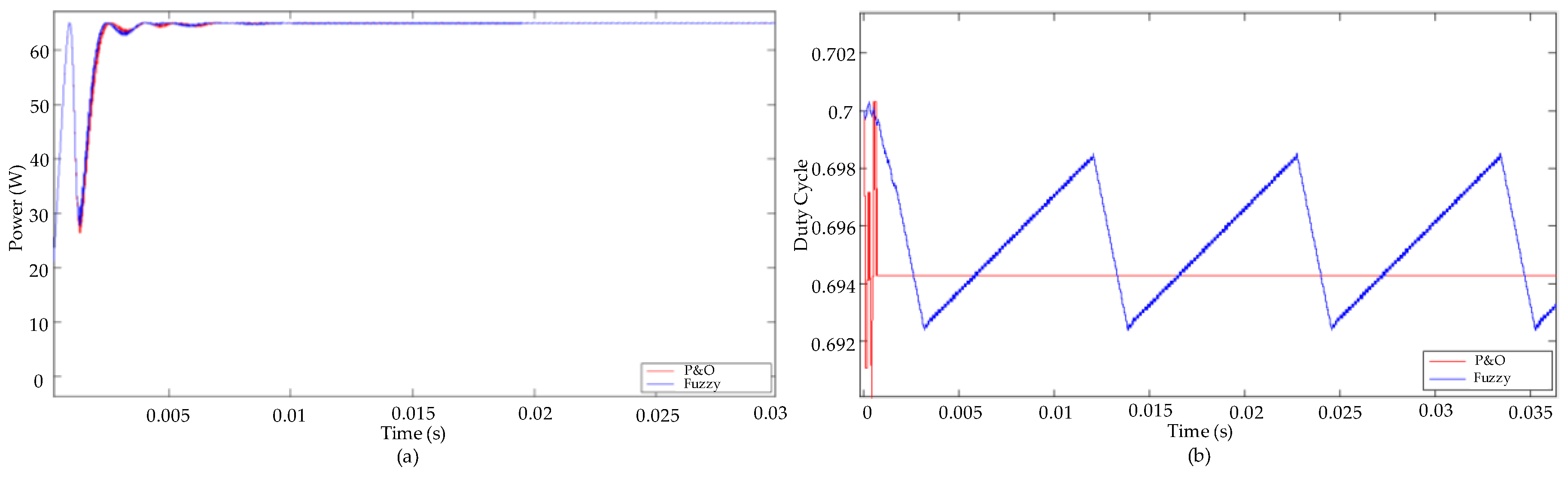
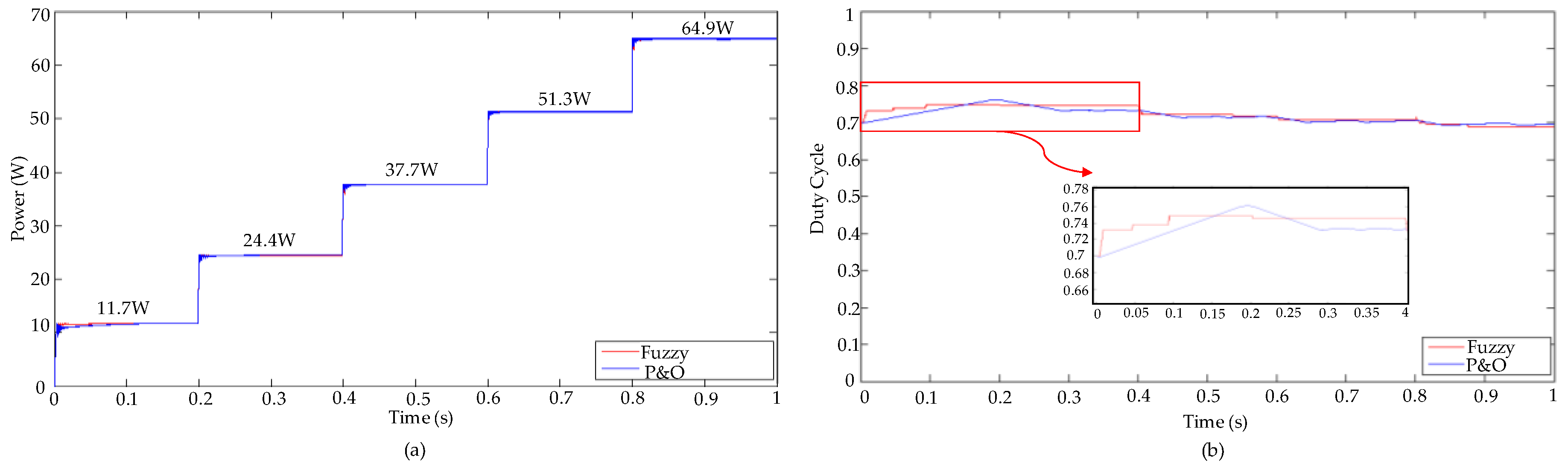
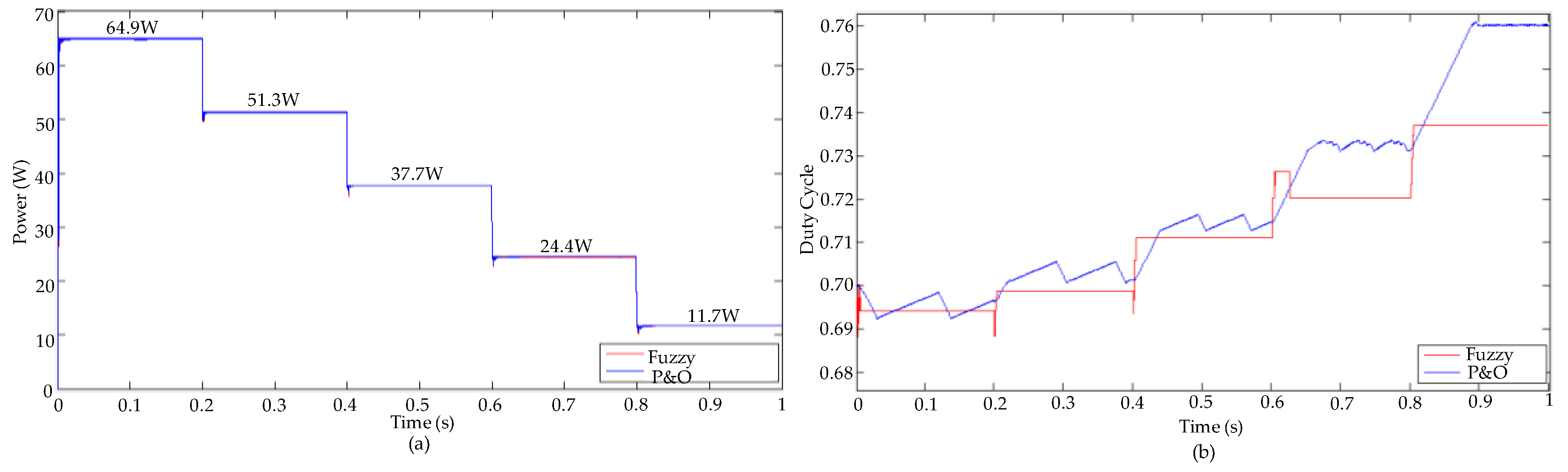
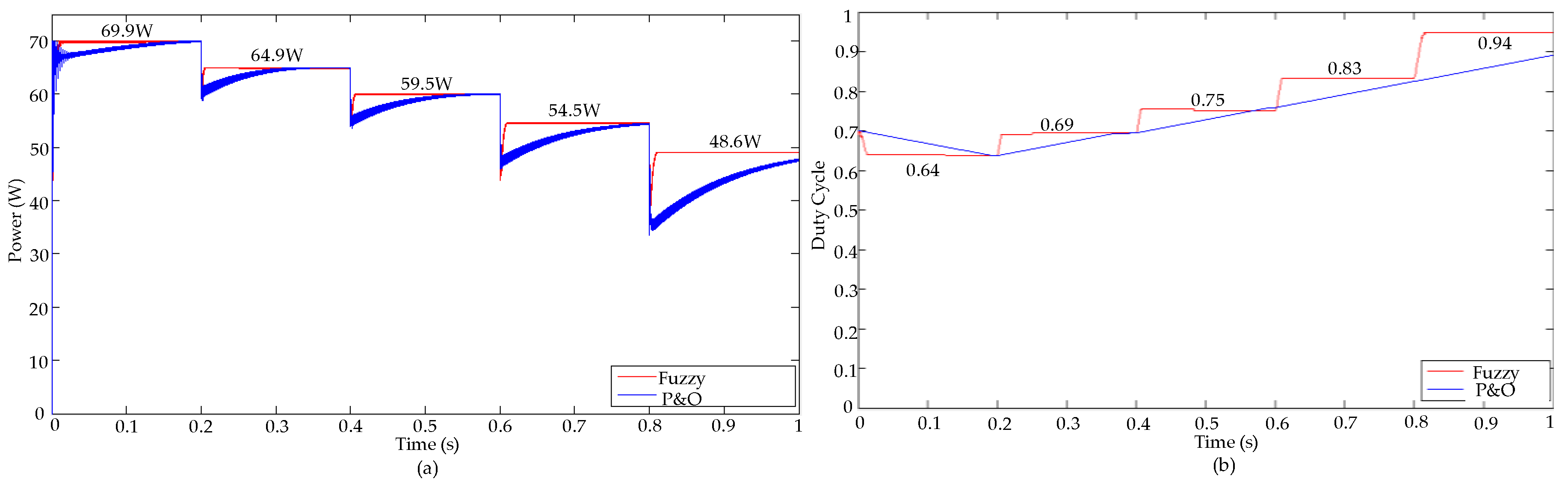
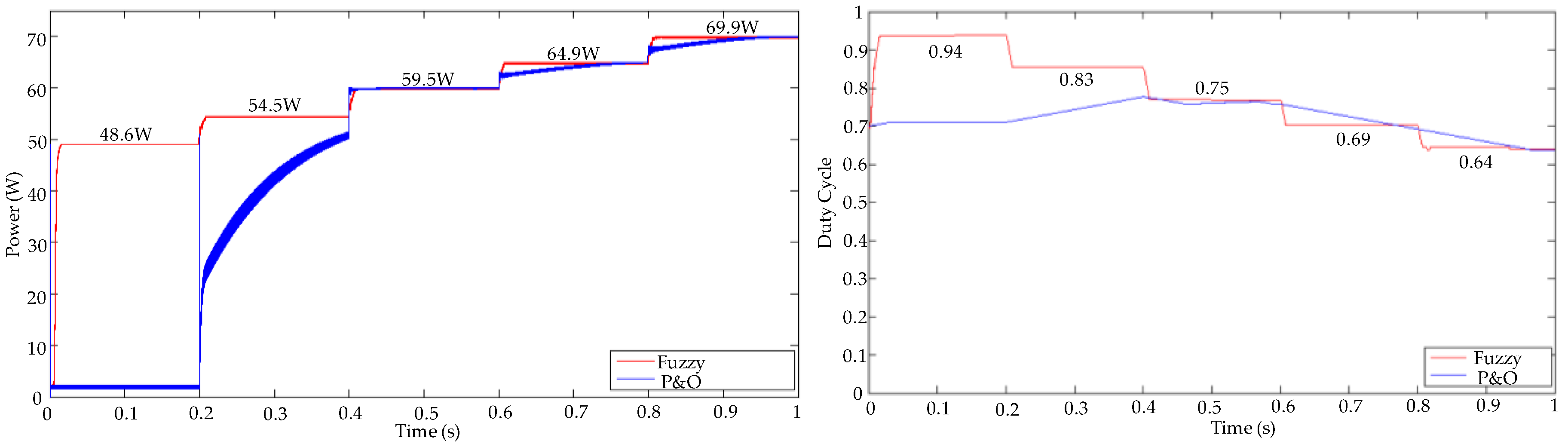
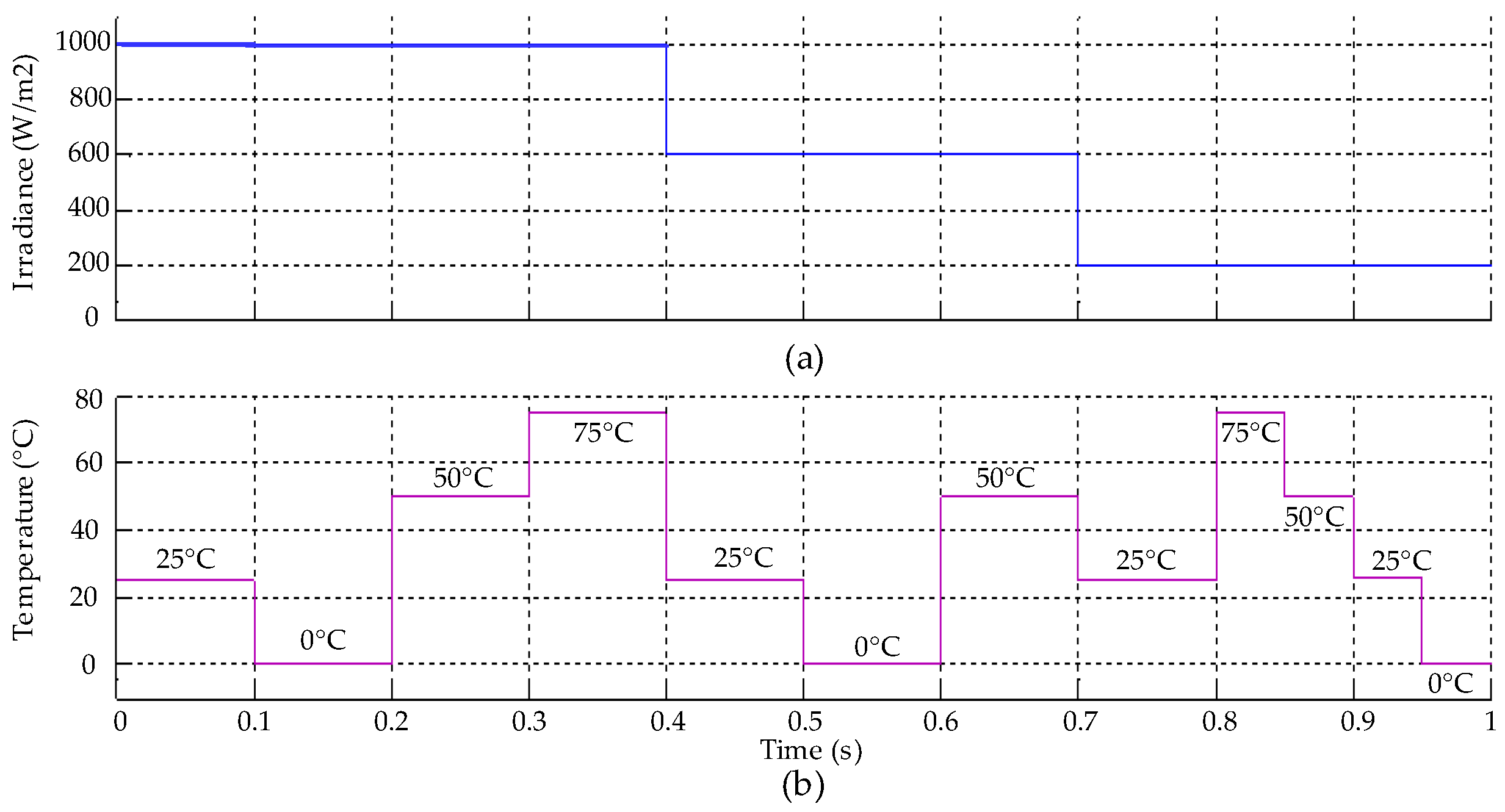
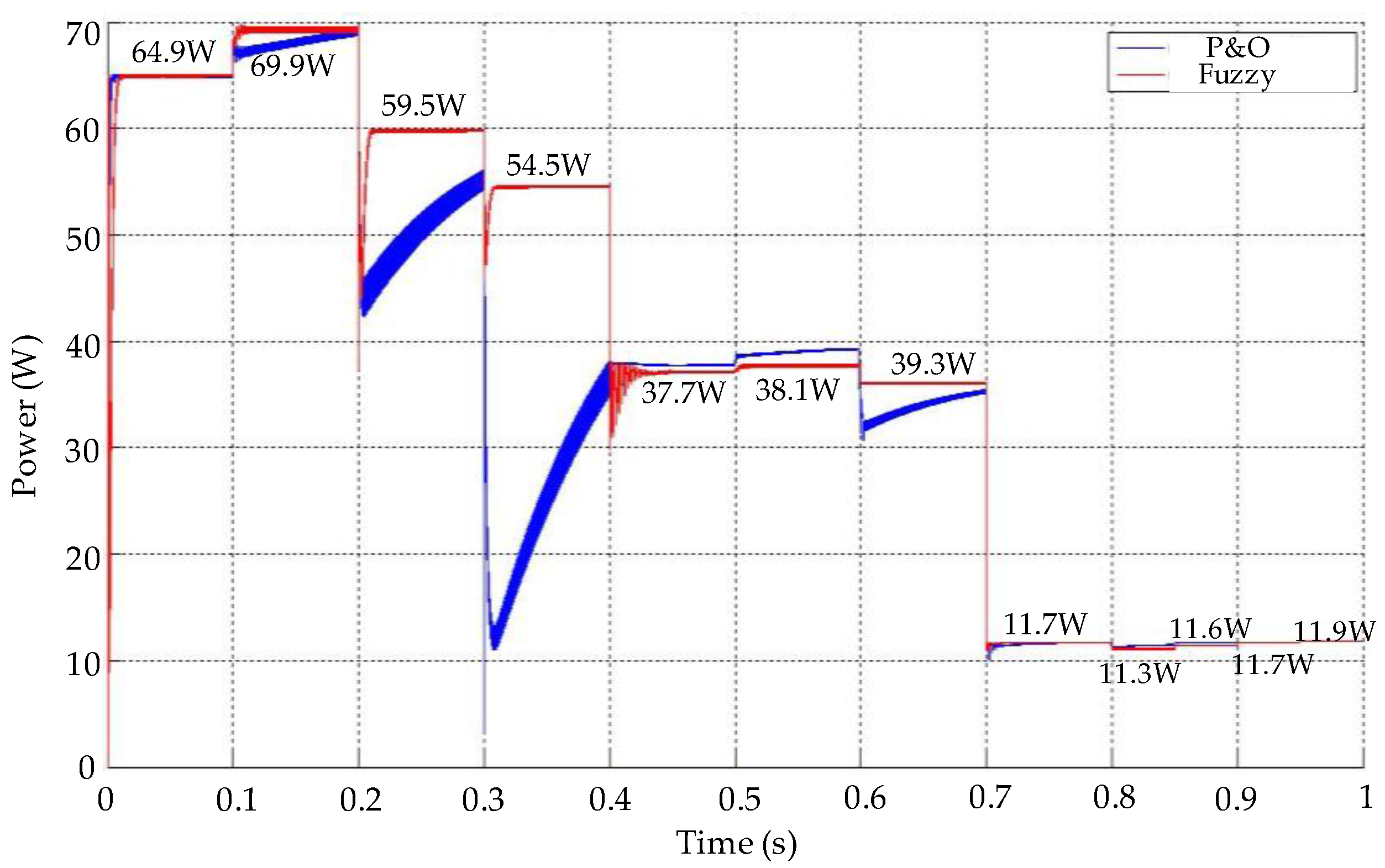
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Vx | Open circuit voltage for variable values of solar irradiance and operating temperature. |
| Ix | Short-circuit current for variable values of solar irradiance and operating temperature. |
| MPP | Maximum power point of the PV module. |
| Pmax | Maximum power of the PV module. |
| Vmpp | Voltage at Pmax. |
| Impp | Current at Pmax. |
| s | Number of PV modules connected in series. |
| p | Number of PV modules connected in parallel. |
| Ei | Effective irradiation of the PV module. |
| EiN | Irradiation constant of 1000 W/m2. |
| T | Temperature of the PV module. |
| TN | Temperature constant of 25 °C. |
| Tcv | Temperature coefficient of voltage. |
| Tci | Temperature coefficient of current. |
| Voc | Open circuit voltage. |
| Isc | Short-circuit current. |
| Vmax | Voltage for irradiations under 200 W and operating temperature of 25 °C. |
| Vmin | Voltage for irradiations over 1200 W and operating temperature of 25 °C. |
| VL | Voltage in the inductor. |
| RL | Internal resistance of the inductor. |
| Rc | Internal resistance of the capacitor. |
| Ton | The on time in the dc-dc converter. |
| Toff | The off time in the dc-dc converter. |
| Ts | Sampling time. |
| D | Duty cycle. |
| Vs | Input voltage in dc-dc converter. |
| Vdc | Transistor voltage in the on mode. |
| Vd | Diode forward voltage. |
| Vo | Output voltage of the dc-dc converter. |
| ΔIL | Ripple current in the inductor. |
| ΔIL(+) | Ripple current in Ton. |
| ΔIL(−) | Ripple current in Toff. |
| Io | Critical output current. |
| ΔQ | Charge variation in the capacitor. |
| ΔV | Voltage variation in the capacitor. |
References
- Karami, N.; Moubayed, N.; Outbib, R. General review and classification of different MPPT Techniques. Renew. Sustain. Energy Rev. 2017, 68, 1–18. [Google Scholar] [CrossRef]
- Mohapatra, A.; Nayak, B.; Das, P.; Mohanty, K.B. A review on MPPT techniques of PV system under partial shading condition. Renew. Sustain. Energy Rev. 2017, 80, 854–867. [Google Scholar] [CrossRef]
- Bianconi, E.; Calvente, J.; Giral, R.; Mamarelis, E.; Petrone, G.; Ramos, C.A.; Spagnuolo, G.; Vitelli, M. Perturb and Observe MPPT algorithm with a current controller based on the sliding mode. Int. J. Electr. Power 2013, 44, 346–356. [Google Scholar] [CrossRef]
- Chen, M.; Ma, S.; Wu, J.; Huang, L. Analysis of MPPT Failure and Development of an Augmented Nonlinear Controller for MPPT of Photovoltaic Systems under Partial Shading Conditions. Appl. Sci. 2017, 7, 95. [Google Scholar] [CrossRef]
- Kwan, T.H.; Wu, X. High performance P&O based lock-on mechanism MPPT algorithm with smooth tracking. Sol. Energy 2017, 155, 816–828. [Google Scholar] [CrossRef]
- Alik, R.; Jusoh, A. Modified Perturb and Observe (P&O) with checking algorithm under various solar irradiation. Sol. Energy 2017, 148, 128–139. [Google Scholar] [CrossRef]
- Bounechba, H.; Bouzid, A.; Snani, A.; Lashab, A. Real time simulation of MPPT algorithms for PV energy system. Int. J. Electr. Power 2016, 83, 67–78. [Google Scholar] [CrossRef]
- Huang, Y.P.; Hsu, S.Y. A performance evaluation model of a high concentration photovoltaic module with a fractional open circuit voltage-based maximum power point tracking algorithm. Comput. Electr. Eng. 2016, 51, 331–342. [Google Scholar] [CrossRef]
- Cortajarena, J.A.; Barambones, O.; Alkorta, P.; De Marcos, J. Sliding mode control of grid-tied single-phase inverter in a photovoltaic MPPT application. Sol. Energy 2017, 155, 793–804. [Google Scholar] [CrossRef]
- Tobón, A.; Peláez-Restrepo, J.; Villegas-Ceballos, J.P.; Serna-Garcés, S.I.; Herrera, J.; Ibeas, A. Maximum Power Point Tracking of Photovoltaic Panels by Using Improved Pattern Search Methods. Energies 2017, 10, 1316. [Google Scholar] [CrossRef]
- Loukriz, A.; Haddadi, M.; Messalti, S. Simulation and experimental design of a new advanced variable step size Incremental Conductance MPPT algorithm for PV systems. ISA Trans. 2016, 62, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Mellit, A.; Rezzouk, H.; Messai, A.; Medjahed, B. FPGA-based real time implementation of MPPT-controller for photovoltaic systems. Renew. Energy 2011, 36, 1652–1661. [Google Scholar] [CrossRef]
- Ramalu, T.; Mohd Radzi, M.A.; Mohd Zainuri, M.A.A.; Abdul Wahab, N.I.; Abdul Rahman, R.Z. A Photovoltaic-Based SEPIC Converter with Dual-Fuzzy Maximum Power Point Tracking for Optimal Buck and Boost Operations. Energies 2016, 9, 604. [Google Scholar] [CrossRef]
- Hassan, S.Z.; Li, H.; Kamal, T.; Arifoğlu, U.; Mumtaz, S.; Khan, L. Neuro-Fuzzy Wavelet Based Adaptive MPPT Algorithm for Photovoltaic Systems. Energies 2017, 10, 394. [Google Scholar] [CrossRef]
- Nabipour, M.; Razaz, M.; Seifossadat, S.; Mortazavi, S. A new MPPT scheme based on a novel fuzzy approach. Renew. Sustain. Energy Rev. 2017, 74, 1147–1169. [Google Scholar] [CrossRef]
- Bendib, B.; Krim, F.; Belmili, H.; Almi, M.F.; Boulouma, S. Advanced Fuzzy MPPT Controller for a Stand-alone PV System. Energy Procedia 2014, 50, 383–392. [Google Scholar] [CrossRef]
- Belaidi, R.; Haddouche, A.; Fathi, M.; Larafi, M.M.; Kaci, G.M. Performance of grid-connected PV system based on SAPF for power quality improvement. In Proceedings of the International Renewable and Sustainable Energy Conference (IRSEC), Marrakech, Morocco, 14–17 November 2016; pp. 1–4. [Google Scholar]
- Chekired, F.; Larbes, C.; Rekioua, D.; Haddad, F. Implementation of a MPPT fuzzy controller for photovoltaic systems on FPGA circuit. Energy Procedia 2011, 6, 541–549. [Google Scholar] [CrossRef]
- Na, W.; Chen, P.; Kim, J. An Improvement of a Fuzzy Logic-Controlled Maximum Power Point Tracking Algorithm for Photovoltic Applications. Appl. Sci. 2017, 7, 326. [Google Scholar] [CrossRef]
- Messaltia, S.; Harrag, A.; Loukriz, A. A new variable step size neural networks MPPT controller: Review, simulation and hardware implementation. Renew. Sustain. Energy Rev. 2017, 68, 221–233. [Google Scholar] [CrossRef]
- Dounis, A.I.; Kofinas, P.; Papadakis, G.; Alafodimos, C. A direct adaptive neural control for maximum power point tracking of photovoltaic system. Sol. Energy 2015, 115, 145–165. [Google Scholar] [CrossRef]
- Muthuramalingam, M.; Manoharan, P.S. Comparative analysis of distributed MPPT controllers for partially shaded stand alone photovoltaic systems. Energy Convers. Manag. 2014, 86, 286–299. [Google Scholar] [CrossRef]
- Jin, Y.; Hou, W.; Li, G.; Chen, X. A Glowworm Swarm Optimization-Based Maximum Power Point Tracking for Photovoltaic/Thermal Systems under Non-Uniform Solar Irradiation and Temperature Distribution. Energies 2017, 10, 541. [Google Scholar] [CrossRef]
- Titri, S.; Larbes, C.; Toumi, K.Y.; Benatchba, K. A new MPPT controller based on the Ant colony optimization algorithm for Photovoltaic systems under partial shading conditions. Appl. Soft Comput. 2017, 58, 465–479. [Google Scholar] [CrossRef]
- Jiang, L.L.; Maskell, D.L.; Patra, J.C. A novel ant colony optimization-based maximum power point tracking for photovoltaic systems under partially shaded conditions. Energy Build. 2013, 58, 227–236. [Google Scholar] [CrossRef]
- Benyoucef, A.S.; Chouder, A.; Kara, K.; Silvestre, S.; Sahed, O.A. Artificial bee colony based algorithm for maximum power point tracking (MPPT) for PV systems operating under partial shaded conditions. Appl. Soft Comput. 2015, 32, 38–48. [Google Scholar] [CrossRef]
- Fathy, A. Reliable and efficient approach for mitigating the shading effect on photovoltaic module based on Modified Artificial Bee Colony algorithm. Renew. Energy 2015, 81, 78–88. [Google Scholar] [CrossRef]
- Atawi, I.E.; Kassem, A.M. Optimal Control Based on Maximum Power Point Tracking (MPPT) of an Autonomous Hybrid Photovoltaic/Storage System in Micro Grid Applications. Energies 2017, 10, 643. [Google Scholar] [CrossRef]
- Ou, T.-C.; Hong, C.-M. Dynamic operation and control of microgrid hybrid power systems. Energy 2014, 66, 314–323. [Google Scholar] [CrossRef]
- Hong, C.-M.; Ou, T.-C.; Lu, K.-H. Development of intelligent MPPT (maximum power point tracking) control for a grid-connected hybrid power generation system. Energy 2013, 50, 270–279. [Google Scholar] [CrossRef]
- Shiau, J.-K.; Wei, Y.-C.; Lee, M.-Y. Fuzzy Controller for a Voltage-Regulated Solar-Powered MPPT System for Hybrid Power System Applications. Energies 2015, 8, 3292–3312. [Google Scholar] [CrossRef]
- Ou, T.-C.; Su, W.-F.; Liu, X.-Z.; Huang, S.-J.; Tai, T.-Y. A Modified Bird-Mating Optimization with Hill Climbing for Connection Decisions of Transformers. Energies 2016, 9, 671. [Google Scholar] [CrossRef]
- Ou, T.-C. A novel unsymmetrical faults analysis for microgrid distribution systems. Electr. Power Energy Syst. 2012, 43, 1017–1024. [Google Scholar] [CrossRef]
- Ou, T.-C. Ground fault current analysis with a direct building algorithm for microgrid distribution. Electr. Power Energy Syst. 2013, 53, 867–875. [Google Scholar] [CrossRef]
- Ou, T.-C.; Lu, K.-H.; Huang, C.-J. Improvement of Transient Stability in a Hybrid Power Multi-System Using a Designed NIDC (Novel Intelligent Damping Controller). Energies 2017, 10, 488. [Google Scholar] [CrossRef]
- Robles Algarín, C.; Callejas Cabarcas, J.; Polo Llanos, A. Low-Cost Fuzzy Logic Control for Greenhouse Environments with Web Monitoring. Electronics 2017, 6, 71. [Google Scholar] [CrossRef]
- Ortiz, E. Modeling and Analysis of Solar Distributed Generation. Ph.D. Thesis, Michigan State University, Michigan, MI, USA, 2006. [Google Scholar]
- Gil, O. Modelado Y Simulación de Dispositivos Fotovoltaicos. Master’s Thesis, Universidad de Puerto Rico, San Juan, Puerto Rico, 2008. [Google Scholar]
- Robles, C.; Ospino, A.; Casas, J. Dual-Axis Solar Tracker for Using in Photovoltaic Systems. Int. J. Renew. Energy Res. IJRER 2017, 10, 137–145. [Google Scholar]



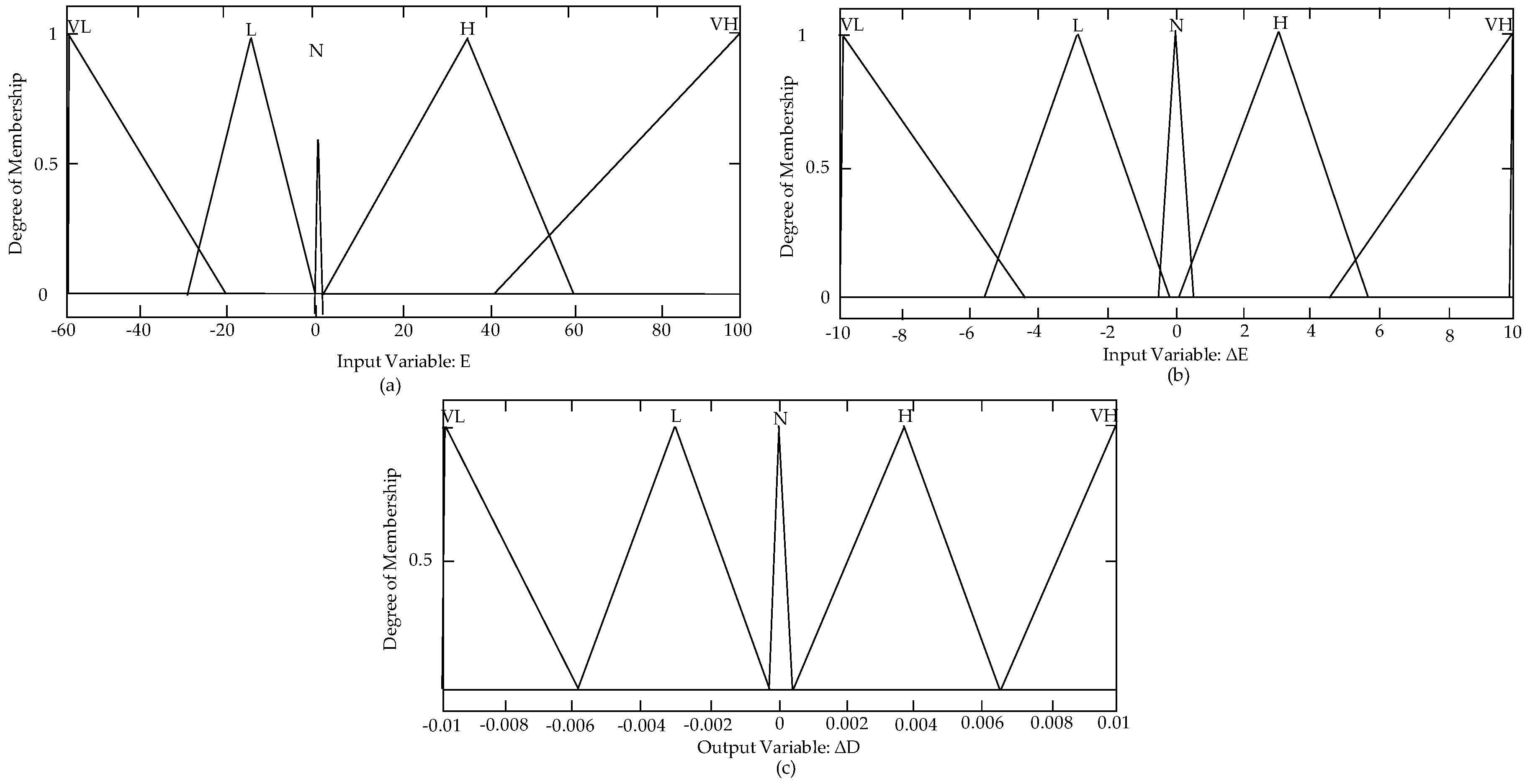


| Parameter | Value |
|---|---|
| Short-circuit current (Isc) | 4 A |
| Open circuit voltage (Voc) | 21.7 V |
| Voltage at Pmax (Vmpp) | 17.5 V |
| Current at Pmax (Impp) | 3.71 A |
| Temperature coefficient of voltage (Tcv) | −0.0802 V/°C |
| Temperature coefficient of current (Tci) | 0.0024 A/°C |
| Maximum voltage (Vmax) | 22.35 V |
| Minimum voltage (Vmin) | 18.44 V |
| Parameter | 1000 W/m2 | 800 W/m2 | 600 W/m2 | 400 W/m2 | 200 W/m2 |
|---|---|---|---|---|---|
| Short-circuit current Isc (A) | 4.0 | 3.2 | 2.4 | 1.6 | 0.8 |
| Open circuit voltage Voc (V) | 21.70 | 21.42 | 21.02 | 20.44 | 19.62 |
| Voltage at Pmax Vmpp (V) | 17.66 | 17.55 | 17.37 | 16.78 | 16.08 |
| Current at Pmax Impp (A) | 3.679 | 2.924 | 2.171 | 1.459 | 0.730 |
| Maximum Power Point (W) | 64.98 | 51.31 | 37.72 | 24.48 | 11.75 |
| Parameter | 0 °C | 25 °C | 50 °C | 75 °C |
|---|---|---|---|---|
| Short-circuit current Isc (A) | 3.94 | 4.00 | 4.06 | 4.12 |
| Open circuit voltage Voc (V) | 23.71 | 21.7 | 19.69 | 17.69 |
| Voltage at Pmax Vmpp (V) | 19.39 | 17.66 | 16.47 | 14.47 |
| Current at Pmax Impp (A) | 3.606 | 3.679 | 3.617 | 3.771 |
| Maximum Power Point (W) | 69.92 | 64.98 | 59.59 | 54.55 |
| E/ΔE | Very Low | Low | Neutral | High | Very High |
|---|---|---|---|---|---|
| Very Low | VH | VH | H | VL | VL |
| Low | H | H | H | VL | L |
| Neutral | H | H | N | L | L |
| High | H | H | L | L | VL |
| Very High | H | H | L | L | VL |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robles Algarín, C.; Taborda Giraldo, J.; Rodríguez Álvarez, O. Fuzzy Logic Based MPPT Controller for a PV System. Energies 2017, 10, 2036. https://doi.org/10.3390/en10122036
Robles Algarín C, Taborda Giraldo J, Rodríguez Álvarez O. Fuzzy Logic Based MPPT Controller for a PV System. Energies. 2017; 10(12):2036. https://doi.org/10.3390/en10122036
Chicago/Turabian StyleRobles Algarín, Carlos, John Taborda Giraldo, and Omar Rodríguez Álvarez. 2017. "Fuzzy Logic Based MPPT Controller for a PV System" Energies 10, no. 12: 2036. https://doi.org/10.3390/en10122036
APA StyleRobles Algarín, C., Taborda Giraldo, J., & Rodríguez Álvarez, O. (2017). Fuzzy Logic Based MPPT Controller for a PV System. Energies, 10(12), 2036. https://doi.org/10.3390/en10122036





