Optimization of a Heliostat Field Layout on Annual Basis Using a Hybrid Algorithm Combining Particle Swarm Optimization Algorithm and Genetic Algorithm
Abstract
1. Introduction
2. Mathematical Model
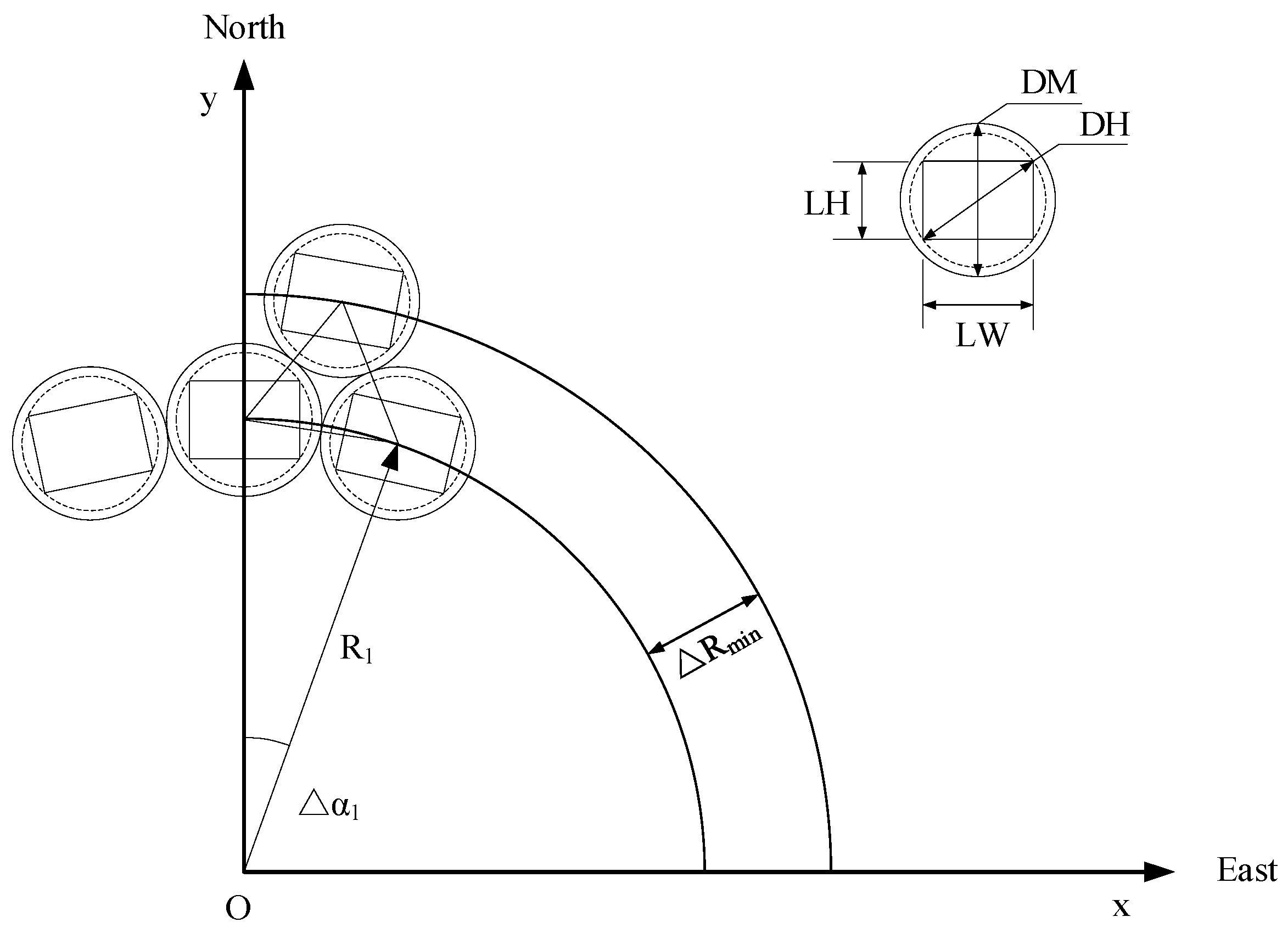
2.1. A Preliminary Heliostat Field Generation
2.2. Optical Efficiency Calculation
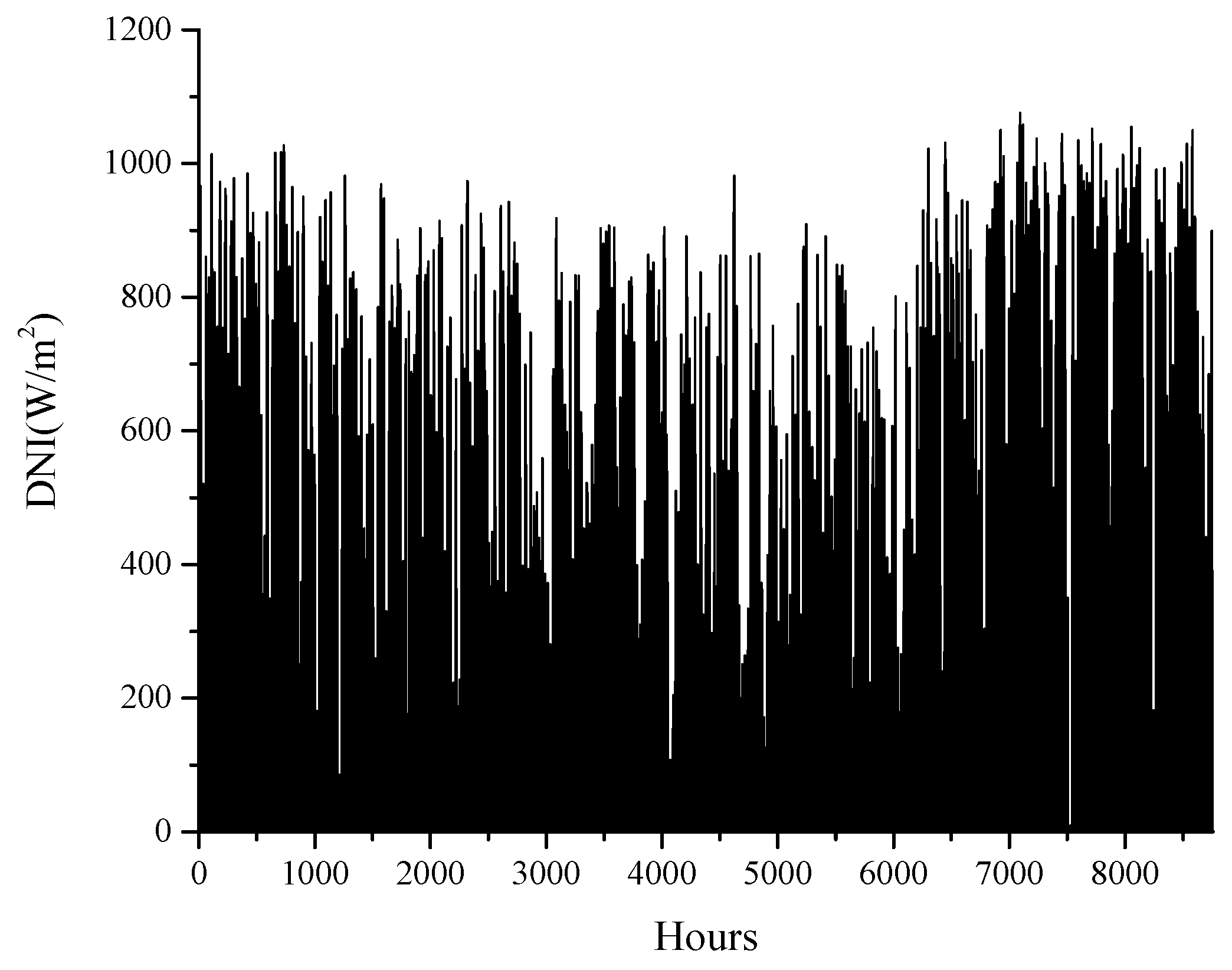
2.3. Annual Averaged Efficiency and Annual Energy Collected Per Unit Cost
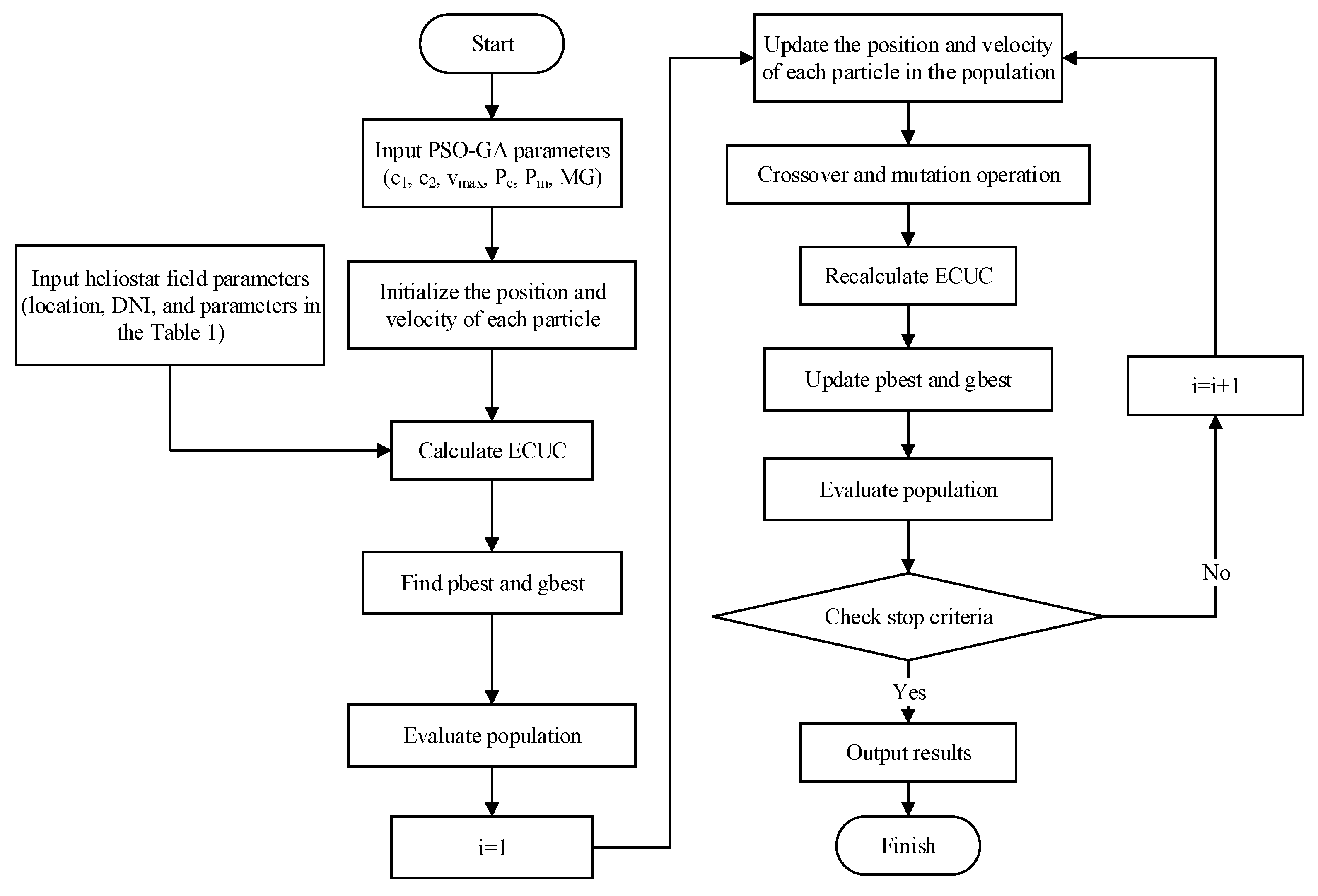
2.4. Hybrid PSO-GA Algorithm
3. Results and Discussion
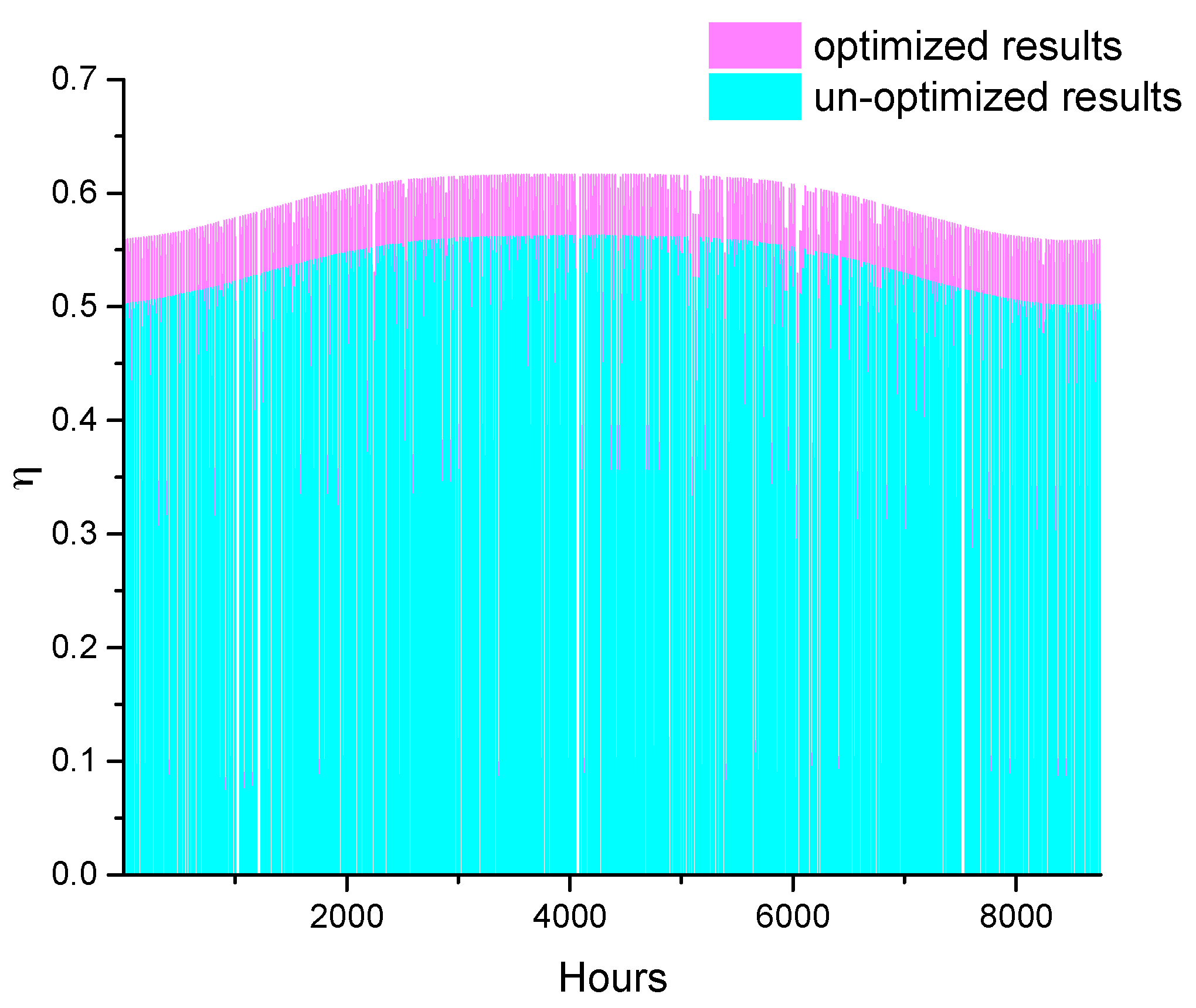
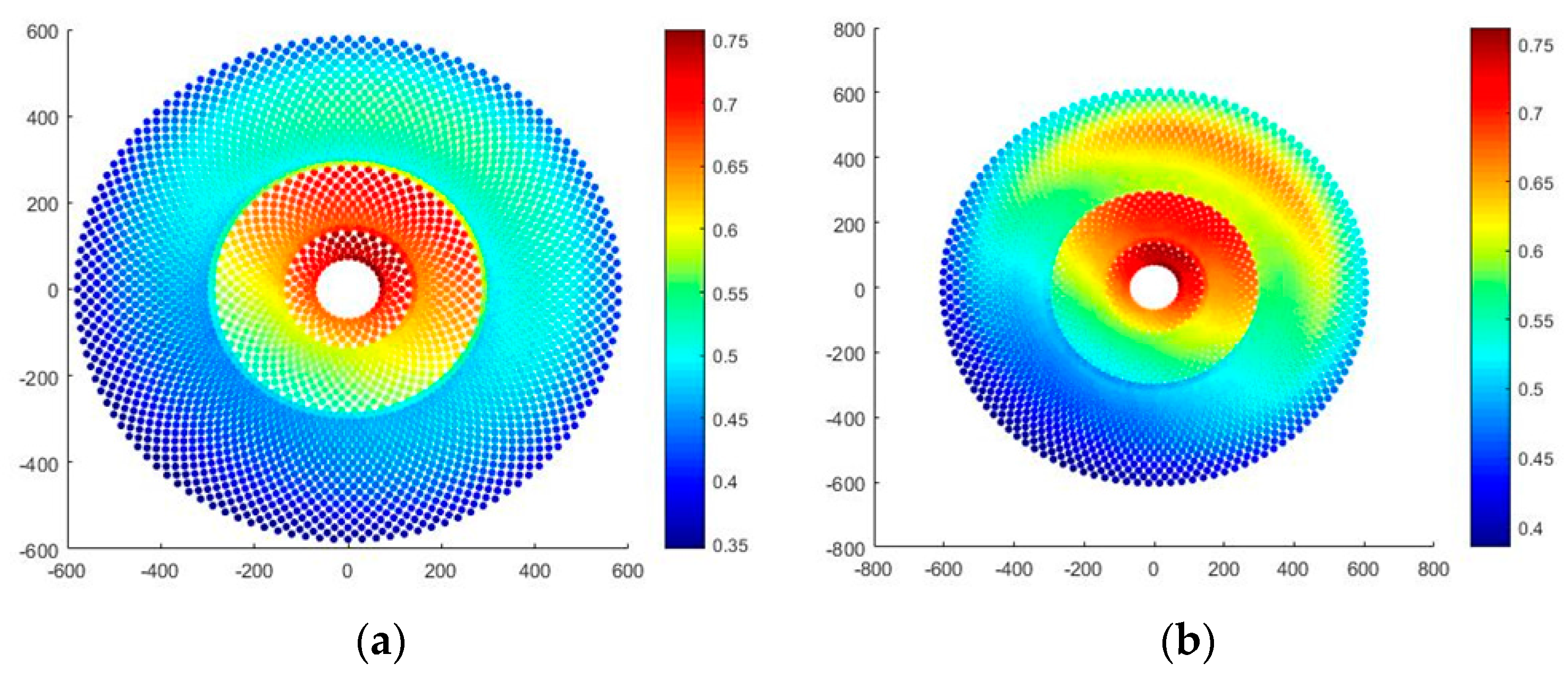
3.1. Optimized Results
3.2. Sensitivity Analysis
3.2.1. Effect of Nhel1
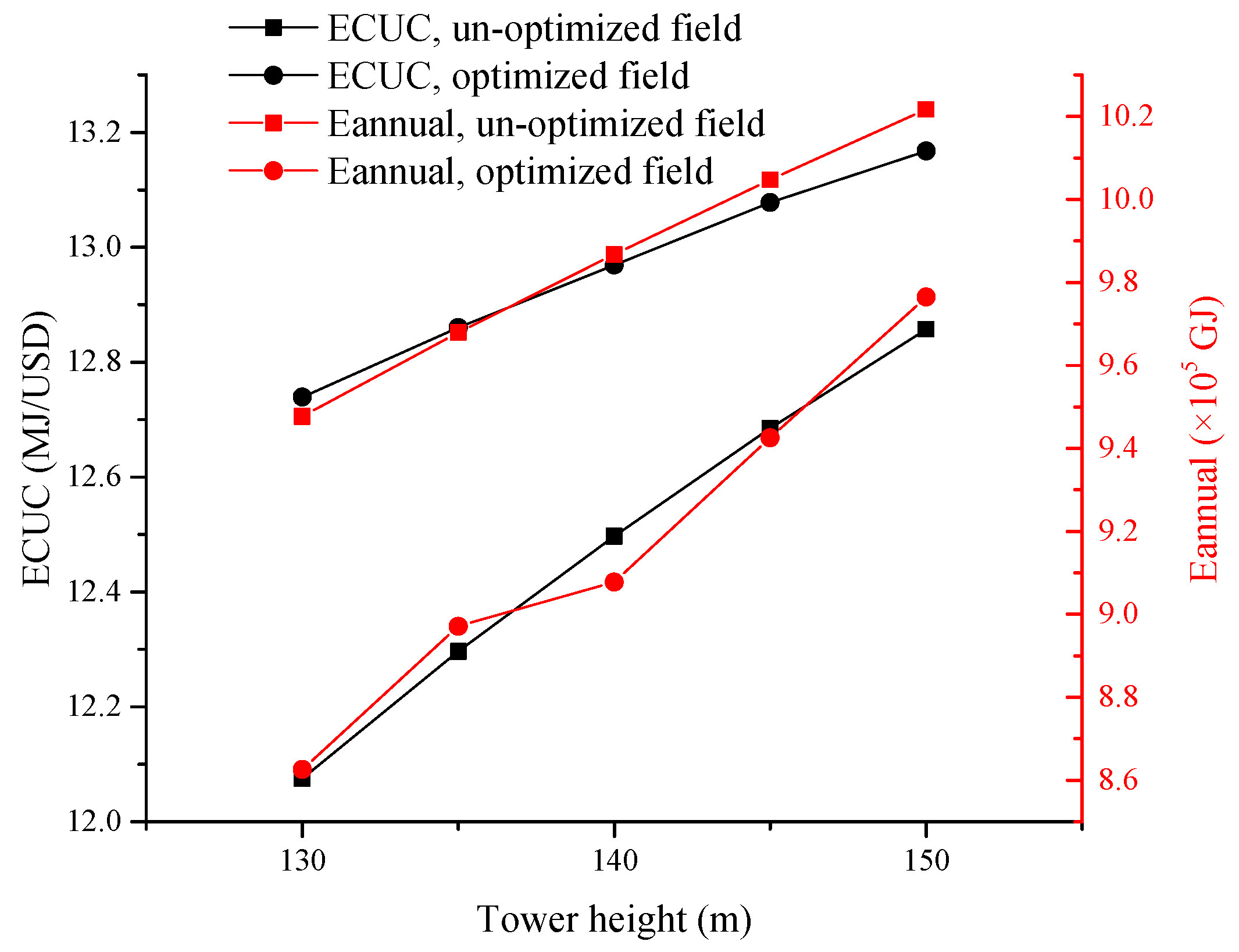
3.2.2. Effect of Tower Height
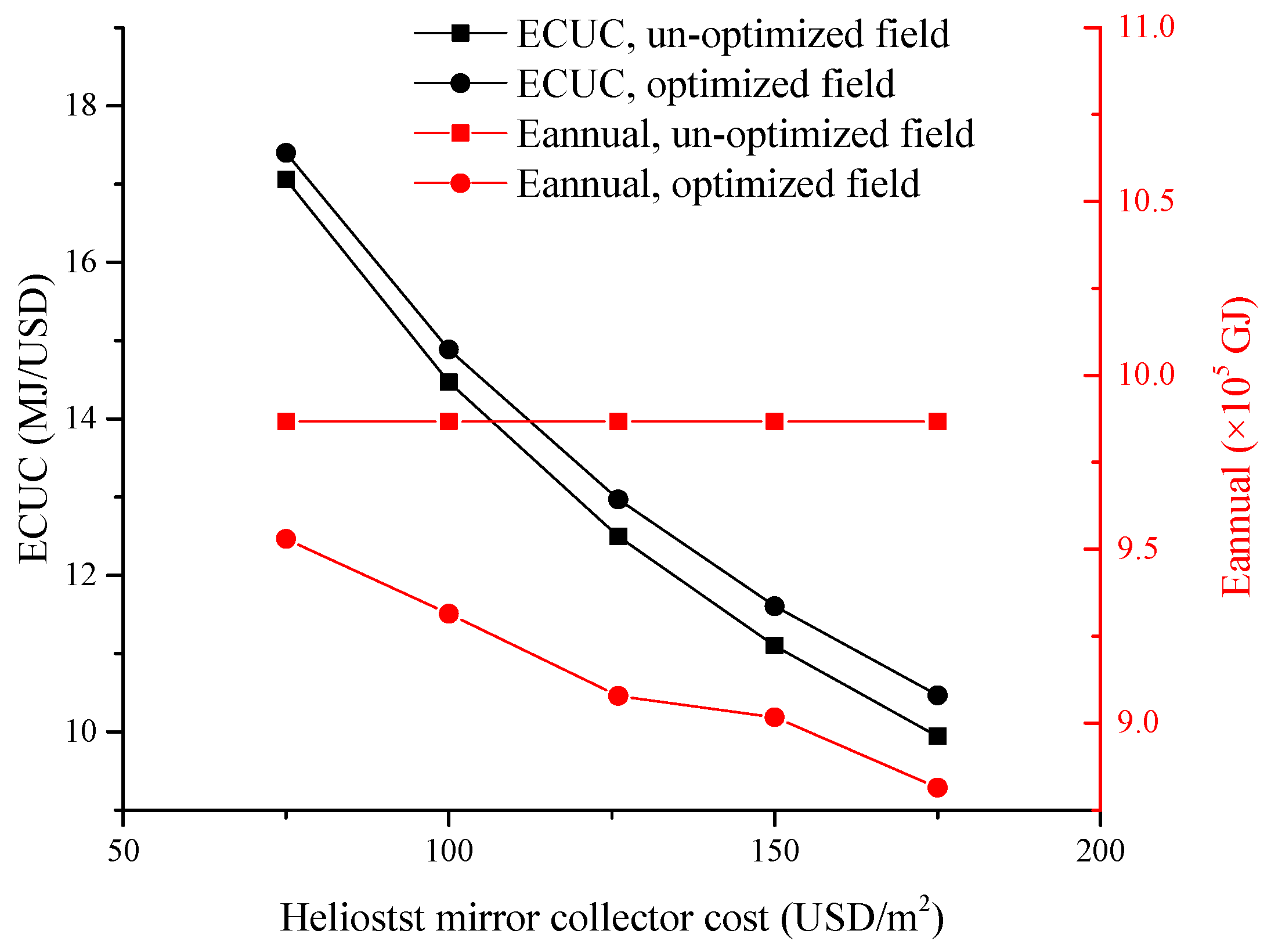
3.2.3. Effect of Heliostat Mirror Collector Cost
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Ah | area of a heliostat, m2 |
| Area | land area of the heliostat field, m2 |
| c1 and c2 | acceleration coefficient |
| ccol | unit cost of heliostat mirror collector, USD/m2 |
| cland | unit cost of land purchase, USD/m2 |
| cos | cosine factor |
| DH | diagonal of heliostat, m |
| DM | distance between the center of two contiguous heliostats, m |
| DNI | Direct Normal Irradiance, W/m2 |
| D | general dimension of the heliostat, m |
| desp | additional separation distance, m |
| dhr | distance between the heliostat and the receiver, m |
| E | daily energy collected, MJ |
| Eannual | annual energy collected, GJ |
| ECUC | energy collected of unit cost, MJ/USD |
| fat | atmospheric attenuation factor |
| fint | intercept factor |
| fsb | shadowing and blocking factor |
| fit | fitness of the calculated particle |
| GA | genetic algorithm |
| gbest | best solution found by the whole swarm |
| Hcol | heliostat pedestal height, m |
| Htow | tower height, m |
| Icol | investment of heliostat mirror collector, USD |
| Ifield | investment of the heliostat field, USD |
| Iland | investment of land purchase, USD |
| Ireceiver | investment of the receiver, USD |
| Itower | investment of the central tower, USD |
| LH | height of the heliostat, m |
| LW | width of the heliostat, m |
| MG | maximum generation |
| m | self-adaptive weight |
| Nheli | number of heliostats in each row in the ith zone |
| Nrowsi | number of rows in the ith zone |
| Num | number of heliostats of the heliostat field |
| n | number of the calculating day in the year |
| pbest | best solution found by particle itself |
| PSO | particle swarm optimization algorithm |
| R | reflect vector |
| Ri | radius of the first row in the ith zone, m |
| Rlast | radius of the last row in the third zone |
| RH | receiver height, m |
| RW | receiver radius, m |
| r1 and r2 | random number |
| S | incident vector |
| SPTT | solar tower power plant |
| t | solar time |
| vi | velocity of the ith particle |
| x | optimization parameter of desp |
| xi | position of the ith particle |
| yi | optimization parameter of radial distance in different zones |
| List of Greek Symbols | |
| α | altitude angle of the sun, rad |
| β | azimuth angle of the sun, rad |
| δ | solar declination, rad |
| ∆αi | azimuthal spacing between adjacent heliostats in different zones, rad |
| ∆Rmin | minimum radial increment, m |
| ∆Ri | radial distance in the ith zone, m |
| η | instantaneous optical efficiency of a heliostat |
| ηannual | annual averaged efficiency of the heliostat field |
| ηhel,daily | daily averaged efficiency of a heliostat |
| ηzonei | annual averaged efficiency of the ith zone in the heliostat field |
| ω | hour angle, rad |
| φ | latitude of the location, ° |
| ρ | reflectivity of the heliostat |
| σtot | total standard deviation of the incident ray on the receiver |
References
- Ye, B.; Zhang, K.; Jiang, J.; Miao, L.; Li, J. Towards a 90% renewable energy future: A case study of an island in the South China Sea. Energy Convers. Manag. 2017, 142, 28–41. [Google Scholar] [CrossRef]
- Ye, B.; Yang, P.; Jiang, J.; Miao, L.; Shen, B.; Li, J. Feasibility and economic analysis of a renewable energy powered special town in China. Resour. Conserv. Recycl. 2017, 121, 40–50. [Google Scholar]
- Piroozmand, P.; Boroushaki, M. A computational method for optimal design of the multi-tower heliostat field considering heliostats interactions. Energy 2016, 106, 240–252. [Google Scholar]
- Emes, M.J.; Arjomandi, M.; Nathan, G.J. Effect of heliostat design wind speed on the levelised cost of electricity from concentrating solar thermal power tower plants. Sol. Energy 2015, 115, 441–451. [Google Scholar] [CrossRef]
- Zeyghami, M.; Khalili, F. Performance improvement of dry cooled advanced concentrating solar power plants using daytime radiative cooling. Energy Convers. Manag. 2015, 106, 10–20. [Google Scholar] [CrossRef]
- Reyes-Belmonte, M.A.; Sebastián, A.; Romero, M.; González-Aguilar, J. Optimization of a recompression supercritical carbon dioxide cycle for an innovative central receiver solar power plant. Energy 2016, 112, 17–27. [Google Scholar]
- Besarati, S.M.; Yogi Goswami, D. A computationally efficient method for the design of the heliostat field for solar power tower plant. Renew. Energy 2014, 69, 226–232. [Google Scholar] [CrossRef]
- Wei, X.; Lu, Z.; Wang, Z.; Yu, W.; Zhang, H.; Yao, Z. A new method for the design of the heliostat field layout for solar tower power plant. Renew. Energy 2010, 35, 1970–1975. [Google Scholar] [CrossRef]
- Schwarzbözl, P.; Schmitz, M.; Pitz-Paal, R. Visual HFLCAL—A Software Tool for Layout and Optimisation of Heliostat Fields. In Proceedings of the Solarpaces 2009, Berlin, Germany, 15–18 Septmeber 2009. [Google Scholar]
- Leary, P.L.; Hankins, J.D. User’s Guide for MIRVAL: A Computer Code for Comparing Designs of Heliostat-Receiver Optics for Central Receiver Solar Power Plants; Central Receivers; Sandia National Laboratories (SNL-CA): Livermore, CA, USA, 1979.
- Kistler, B.L. A user’s manual for DELSOL3: A computer code for calculating the optical performance and optimal system design for solar thermal central receiver plants. In Proceedings of the 3rd Central-European Workshop on Services and their Composition (ZEUS), Karlsruhe, Germany, 21–22 February 2011; pp. 24–25. [Google Scholar]
- Collado, F.J.; Guallar, J. A review of optimized design layouts for solar power tower plants with campo code. Renew. Sustain. Energy Rev. 2013, 20, 142–154. [Google Scholar] [CrossRef]
- Cádiz, P.; Frasquet, M.; Silva, M.; Martínez, F.; Carballo, J. Shadowing and blocking effect optimization for a variable geometry heliostat field. Energy Procedia 2015, 69, 60–69. [Google Scholar]
- Wei, X.; Lu, Z.; Yu, W.; Wang, Z. A new code for the design and analysis of the heliostat field layout for power tower system. Sol. Energy 2010, 84, 685–690. [Google Scholar] [CrossRef]
- Kim, S.; Lee, I.; Lee, B.J. Development of performance analysis model for central receiver system and its application to pattern-free heliostat layout optimization. Sol. Energy 2017, 153, 499–507. [Google Scholar] [CrossRef]
- Noone, C.J.; Torrilhon, M.; Mitsos, A. Heliostat field optimization: A new computationally efficient model and biomimetic layout. Sol. Energy 2012, 86, 792–803. [Google Scholar] [CrossRef]
- Gadalla, M.; Saghafifar, M. Thermo-economic and comparative analyses of two recently proposed optimization approaches for circular heliostat fields: Campo radial-staggered and biomimetic spiral. Sol. Energy 2016, 136, 197–209. [Google Scholar] [CrossRef]
- Eddhibi, F.; Ben Amara, M.; Balghouthi, M.; Guizani, A. Design and analysis of a heliostat field layout with reduced shading effect in southern Tunisia. Int. J. Hydrogen Energy 2017, 42, 28973–28996. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, L.; Xu, C.; Du, X. An efficient code to optimize the heliostat field and comparisons between the biomimetic spiral and staggered layout. Renew. Energy 2016, 87, 720–730. [Google Scholar] [CrossRef]
- Li, C.; Zhai, R.; Liu, H.; Yang, Y.; Wu, H. Optimization of a heliostat field layout using hybrid PSO-GA algorithm. Appl. Therm. Eng. 2018, 128, 33–41. [Google Scholar] [CrossRef]
- Lipps, F.W. Theory of Cellwise Optimization for Solar Central Receiver System; No. SAND-85-8177; Houston University: Houston, TX, USA, 1985. [Google Scholar]
- Collado, F.J.; Guallar, J. Campo: Generation of regular heliostat fields. Renew. Energy 2012, 46, 49–59. [Google Scholar] [CrossRef]
- Lipps, F.W.; Vant-Hull, L.L. A cellwise method for the optimization of large central receiver systems. Sol. Energy 1978, 20, 505–516. [Google Scholar] [CrossRef]
- Lipps, F.W.; Vanthull, L.L. Shading and blocking geometry for a solar tower concentrator with rectangular mirrors. In Proceedings of the American Society of Mechanical Engineers, Winter Meeting, New York, NY, USA, 17–22 November 1974; pp. 57–58. [Google Scholar]
- Atif, M.; Al-Sulaiman, F.A. Development of a mathematical model for optimizing a heliostat field layout using differential evolution method. Int. J. Energy Res. 2015, 39, 1241–1255. [Google Scholar] [CrossRef]
- Saghafifar, M.; Gadalla, M. Thermo-economic analysis of air bottoming cycle hybridization using heliostat field collector: A comparative analysis. Energy 2016, 112, 698–714. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Collado, F.J. Design of solar tower plants heliostat by heliostat: The shadowing and blocking factor. In Proceedings of the Solarpaces 2011, Granada, Spain, 20–23 Septmeber 2011. [Google Scholar]
- Sassi, G. Some notes on shadow and blockage effects. Sol. Energy 1983, 31, 331–333. [Google Scholar] [CrossRef]
- Wagner, M.J. Simulation and Predictive Performance Modeling of Utility-Scale Central Receiver System Power Plants; University of Wisconsin: Madison, WI, USA, 2008. [Google Scholar]
- Saghafifar, M.; Gadalla, M. Thermo-economic optimization of hybrid solar Maisotsenko bottoming cycles using heliostat field collector: Comparative analysis. Appl. Energy 2017, 190, 686–702. [Google Scholar] [CrossRef]
- Modi, A.; Kærn, M.R.; Andreasen, J.G.; Haglind, F. Thermoeconomic optimization of a Kalina cycle for a central receiver concentrating solar power plant. Energy Convers. Manag. 2016, 115, 276–287. [Google Scholar] [CrossRef]
- Yu, S.; Zhang, J.; Zheng, S.; Sun, H. Provincial carbon intensity abatement potential estimation in China: A PSO–GA-optimized multi-factor environmental learning curve method. Energy Policy 2015, 77, 46–55. [Google Scholar] [CrossRef]
- Klein, S.A. Calculation of monthly average insolation on tilted surfaces. Sol. Energy 1977, 19, 325–329. [Google Scholar] [CrossRef]
- Pfahl, A.; Coventry, J.; Röger, M.; Wolfertstetter, F.; Vásquez-Arango, J.F.; Gross, F.; Arjomandi, M.; Schwarzbözl, P.; Geiger, M.; Liedke, P. Progress in heliostat development. Sol. Energy 2017, 152, 3–37. [Google Scholar] [CrossRef]

| Parameter | Value | Unite |
|---|---|---|
| Tower optical height | 140 | m |
| Receiver radius | 4.0 | m |
| Receiver height | 9.0 | m |
| Heliostat total height | 9.752 | m |
| Heliostat total width | 12.305 | m |
| Heliostat pedestal height | 5 | m |
| Standard deviation surface error | 0.94 | mrad |
| Standard deviation tracking error | 0.63 | mrad |
| Standard deviation of sunshape | 2.51 | mrad |
| Effective reflectivity | 0.88 × 0.95 | - |
| Number of zones in the field | 3 | - |
| Number of heliostats in first row | 30 | - |
| Month | Average Day of Month (Date) | Day of the Year |
|---|---|---|
| January | 17 | 17 |
| February | 16 | 47 |
| March | 16 | 75 |
| April | 15 | 105 |
| May | 15 | 135 |
| June | 11 | 162 |
| July | 17 | 198 |
| August | 16 | 228 |
| September | 15 | 258 |
| October | 15 | 288 |
| November | 14 | 318 |
| December | 10 | 344 |
| Parameters | Number of Generations | |
|---|---|---|
| Nhel1 change | 25 | 127 |
| 28 | 82 | |
| 30 | 120 | |
| 32 | 111 | |
| 34 | 70 | |
| Tower height change | 130 | 124 |
| (m) | 135 | 121 |
| 145 | 75 | |
| 150 | 129 | |
| Heliostat mirror cost change | 75 | 85 |
| (USD/m2) | 100 | 125 |
| 150 | 147 | |
| 175 | 145 |
| Un-Optimized Field | Optimized Field | |
|---|---|---|
| y1 | 1.0000 | 1.0000 |
| y2 | 1.0000 | 1.0000 |
| y3 | 1.0000 | 1.2971 |
| x | 0.0000 | 0.0785 |
| Num | 3450 | 2850 |
| Area (×106 m2) | 1.10 | 1.20 |
| ηannual | 0.5074 | 0.5648 |
| ηzone1 | 0.6907 | 0.6924 |
| ηzone2 | 0.6281 | 0.6311 |
| ηzone3 | 0.4669 | 0.5339 |
| Eannual (×105 GJ) | 9.87 | 9.08 |
| ECUC (MJ/USD) | 12.50 | 12.97 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Zhai, R.; Yang, Y. Optimization of a Heliostat Field Layout on Annual Basis Using a Hybrid Algorithm Combining Particle Swarm Optimization Algorithm and Genetic Algorithm. Energies 2017, 10, 1924. https://doi.org/10.3390/en10111924
Li C, Zhai R, Yang Y. Optimization of a Heliostat Field Layout on Annual Basis Using a Hybrid Algorithm Combining Particle Swarm Optimization Algorithm and Genetic Algorithm. Energies. 2017; 10(11):1924. https://doi.org/10.3390/en10111924
Chicago/Turabian StyleLi, Chao, Rongrong Zhai, and Yongping Yang. 2017. "Optimization of a Heliostat Field Layout on Annual Basis Using a Hybrid Algorithm Combining Particle Swarm Optimization Algorithm and Genetic Algorithm" Energies 10, no. 11: 1924. https://doi.org/10.3390/en10111924
APA StyleLi, C., Zhai, R., & Yang, Y. (2017). Optimization of a Heliostat Field Layout on Annual Basis Using a Hybrid Algorithm Combining Particle Swarm Optimization Algorithm and Genetic Algorithm. Energies, 10(11), 1924. https://doi.org/10.3390/en10111924





