Studies on Cup Anemometer Performances Carried out at IDR/UPM Institute. Past and Present Research

Abstract

In the present work, the research derived from a wide experience on cup anemometer calibration works at IDR/UPM Institute (Instituto Universitario de Microgravedad “Ignacio Da Riva”) is summarized. This research started in 2008, analyzing large series of calibrations, and is focused on two main aspects: (1) developing a procedure to predict the degradation level of these wind sensors when working on the field and (2) modeling cup anemometer performances. The wear and tear level of this sensor is evaluated studying the output signal and its main frequencies through Fourier analysis. The modeling of the cup anemometer performances is carried out analyzing first the cup aerodynamics. As a result of this process, carried out through several testing and analytical studies since 2010, a new analytical method has been developed. This methodology might represent an alternative to the classic approach used in the present standards of practice such as IEC 64000-12.

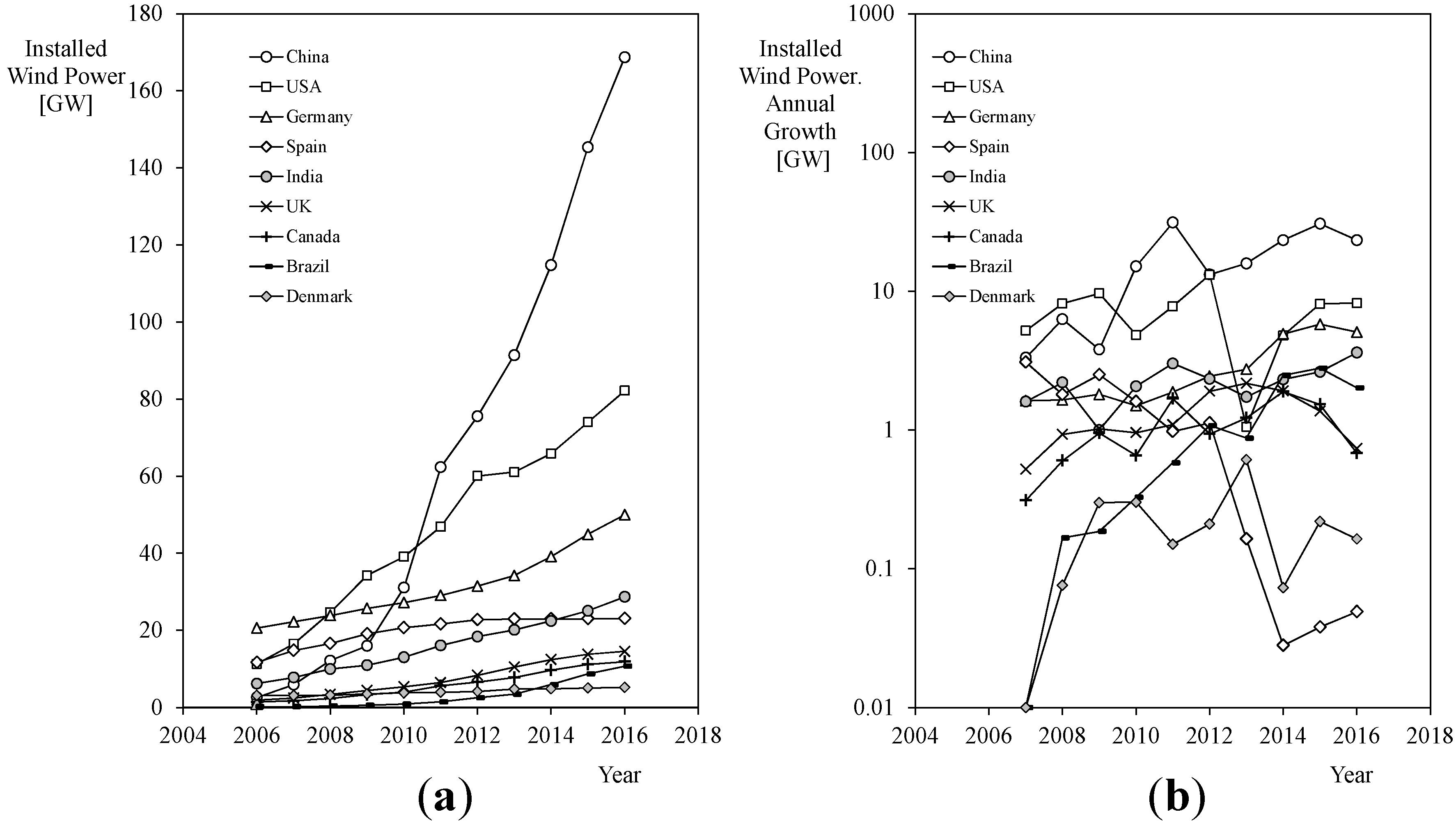
1. Introduction

Since 1997, the IDR/UPM Institute (Instituto Universitario de Microgravedad “Ignacio Da Riva”) has performed high level standardized calibrations to wind speed sensors, mainly for the wind energy sector and Spanish meteorology institutions. LAC-IDR/UPM is the calibration laboratory within this research institute, which is accredited according to ISO/IEC 17025 standard and is a member of the Measuring Network of Wind Energy Institutes (MEASNET) since 2003.

The line of work related to wind speed sensors calibration represents, together with space engineering [1,2,3,4,5,6,7,8,9,10,11], wind engineering [12,13,14,15,16,17], and different high education degree programs such as the Master in Space Systems [18,19,20,21], the core of the activities being carried out by the IDR/UPM research institute’s staff.

With regard to the aforementioned wind speed sensors calibration, this line of work has produced a strong research, mainly focused on cup anemometers (see Figure 1) [22,23,24,25,26,27,28,29,30,31,32,33,34]. Additionally, some relevant research devoted to sonic anemometers has been carried out at IDR/UPM [35,36,37,38,39]. Although other wind speed sensors such as the aforementioned sonic anemometer, LIDAR, SODAR, and nacelle anemometers, have been thoroughly developed and studied in order to substitute the cup anemometer along the past decades [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59], this old fashioned but robust and reliable instrument (see Figure 1) developed by T.R. Robinson in the 19th century [60,61,62,63], remains the most demanded and used wind sensor for meteorologists and within the wind energy sector.

In addition, it should be pointed out that the demand of cup anemometers might increase, as the wind energy installed power has been continuously growing in the last years (see Figure 2). This fact also involves a huge demand for calibration of these sensors because any lack of accuracy in relation to the measured wind speed by an anemometer installed on a wind generator will have a major impact on the economic revenue (the extractable wind power is proportional to third power of the wind speed).

In this work, the research activities related to cup anemometer performance analysis carried out at IDR/UPM are reviewed. The work is organized as follows: the experimental analyses and results based on the huge calibrations database of the LAC-IDR/UPM are described in Section 2. In Section 3, the analytical models and procedures developed at IDR/UPM to study the cup anemometer are reviewed. Finally, conclusions are summarized in Section 4.

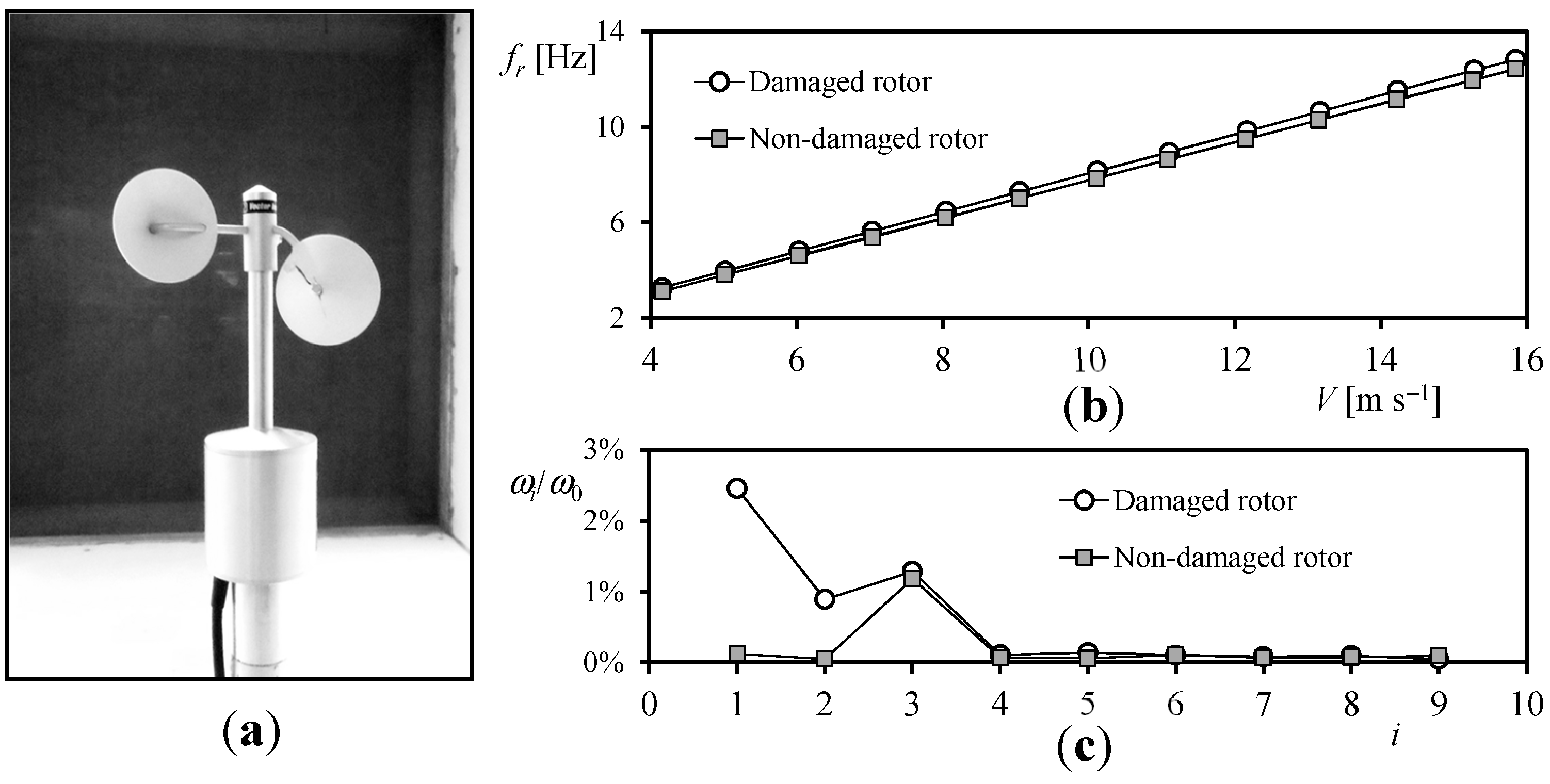
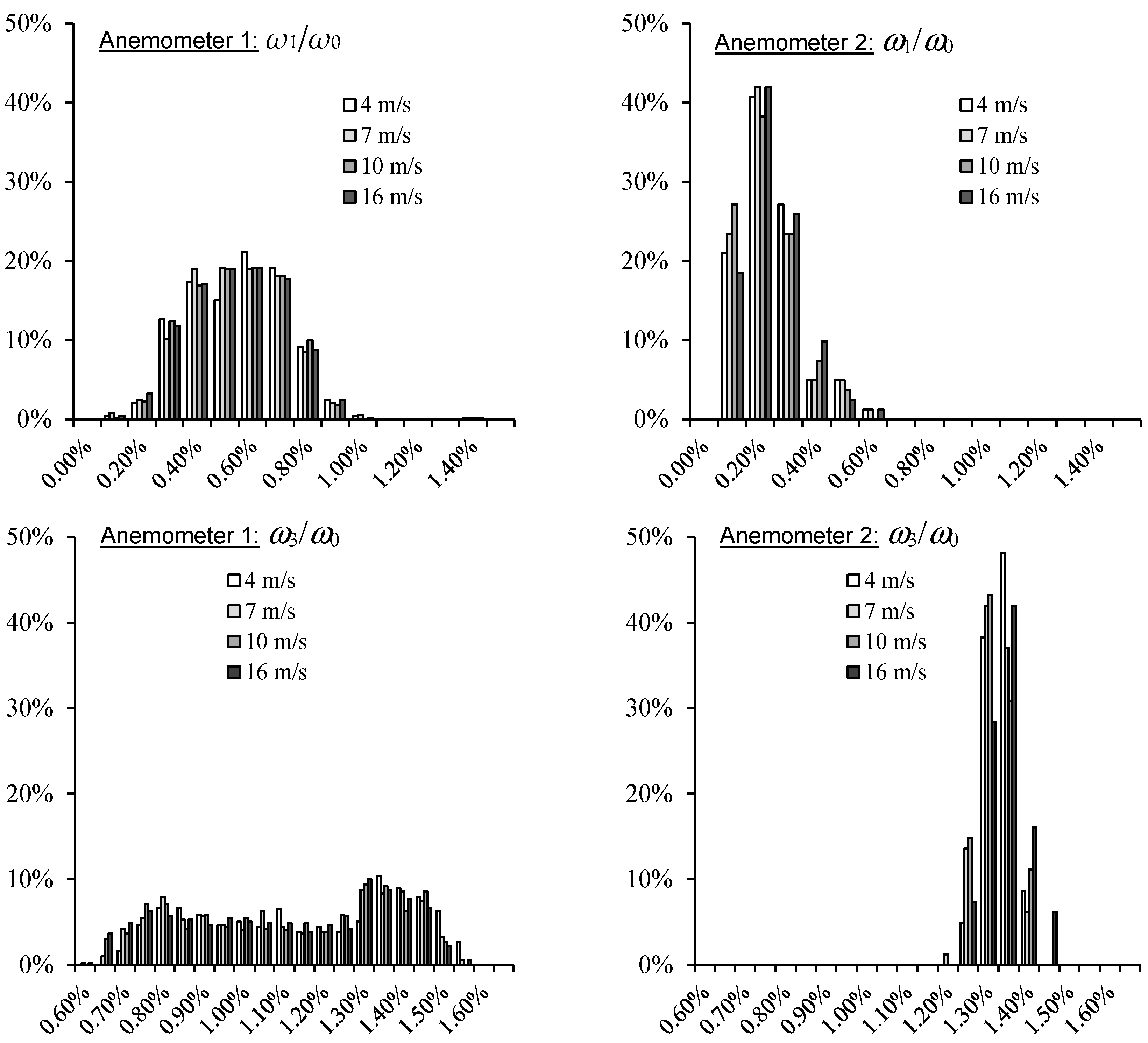
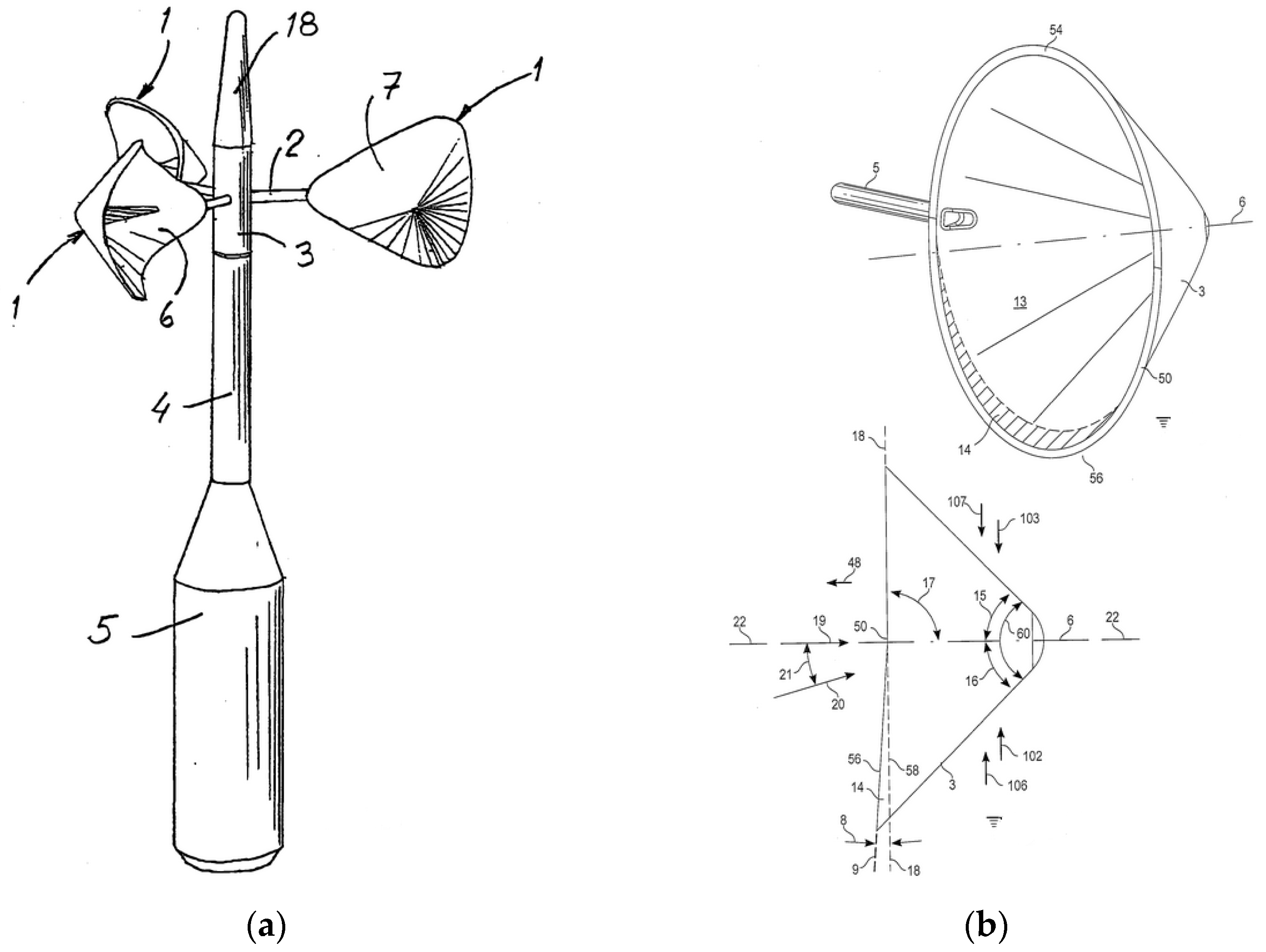
2. Experimental Analyses of Cup Anemometer Performances

Historically, the first analyses of cup anemometer performance were carried out based on experimental results, analyzing the performances [64,65,66,67] or searching for the optimum configuration (number of cups, size…) [68,69,70,71]. A thorough review of the literature was carried out in previous works [29,31].

In a first approach to anemometer performances, more than 3500 calibrations (performed at IDR/UPM on 25 different cup anemometer models) were studied by Pindado et al. [22]. The calibration of an anemometer involves the definition of its transfer function, which relates the measured wind speed, V, to the cup anemometer’s output frequency, f.

$$V=\mathrm{A}f+\mathrm{B}.$$

(1)

In the above equation, constants A (slope) and B (offset) are the ones that need to be defined by means of a proper calibration. However, it should be pointed out that normally the output frequency is not equal to the cup anemometer’s rotation frequency, f_r, due to the different electronic systems used to measure the rotation rate, which give a different number of pulses, m, along one turn of the rotor. Therefore, Equation (1) should be referred to f_r, in order to analyze the aerodynamic performances properly (obviously, A_r = m·A in the above equation).

$$V={\mathrm{A}}_r{f}_r+\mathrm{B}.$$

(2)

In Figure 3, the results of two different calibration procedures, performed on the same Thies 4.3350 cup anemometer, are shown. The first procedure, the AC calibration procedure, strictly follows MEASNET [72,73] requirements (13 measurement points taken within a wind speed bracket from 4 m·s⁻¹ to 16 m·s⁻¹), whereas the second one, the AD calibration procedure, is an internal procedure performed at the IDR/UPM Institute within a larger wind speed range and with less measurement points taken (nine measurement points taken within a wind speed bracket from 4 m·s⁻¹ to 23 m·s⁻¹). This AD calibration procedure was developed at customers’ request.

Two important conclusions were derived as a result of this work:

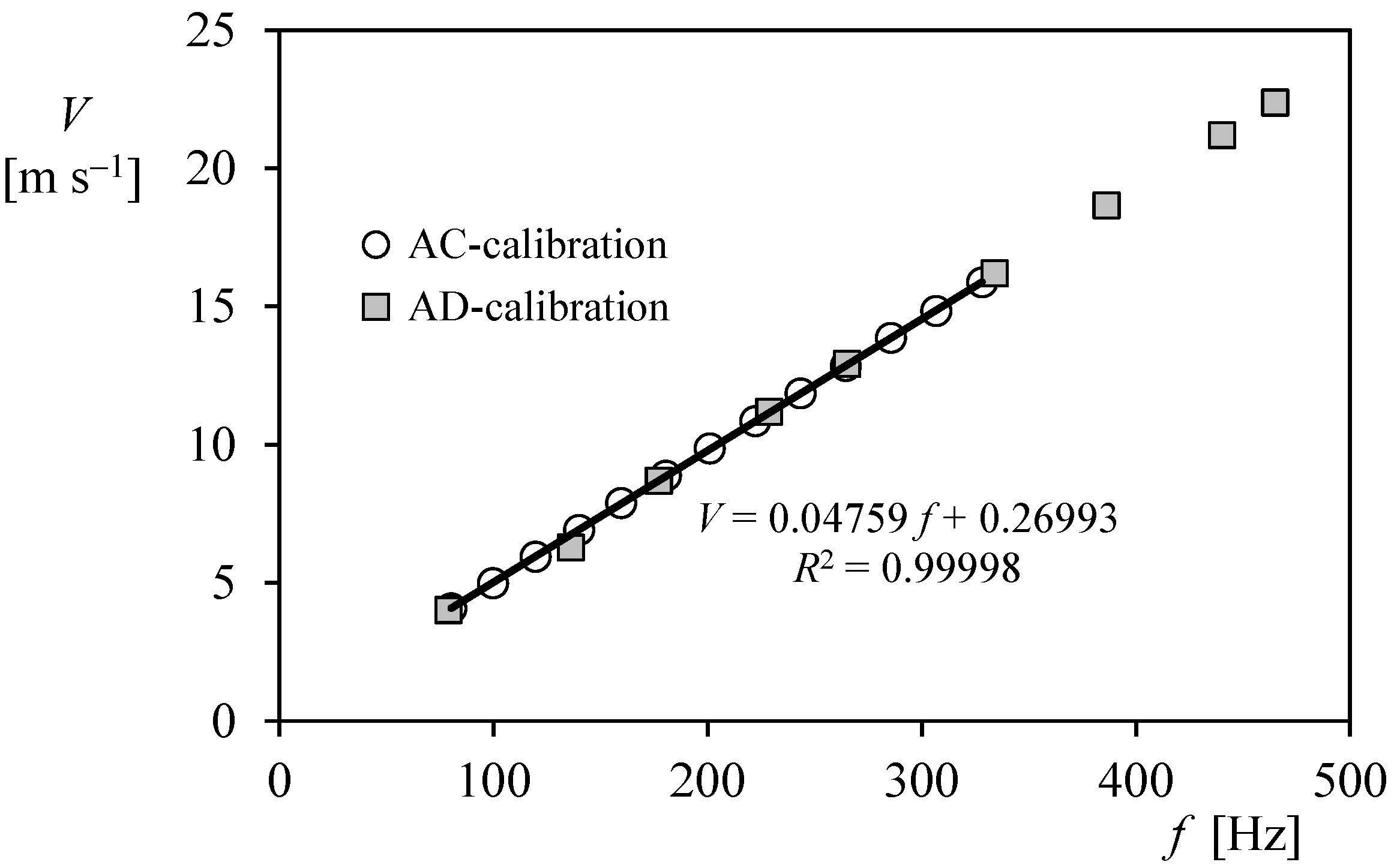
• The differences between the AC and AD calibration procedures were negligible in terms of both wind speed (with 2.6%, 0.88%, and 0.31% deviation at 5 m·s⁻¹, 10 m·s⁻¹, and 15 m·s⁻¹ wind speed for the Thies anemometer referred in Figure 3) and wind power generator Annual Energy Production (AEP);
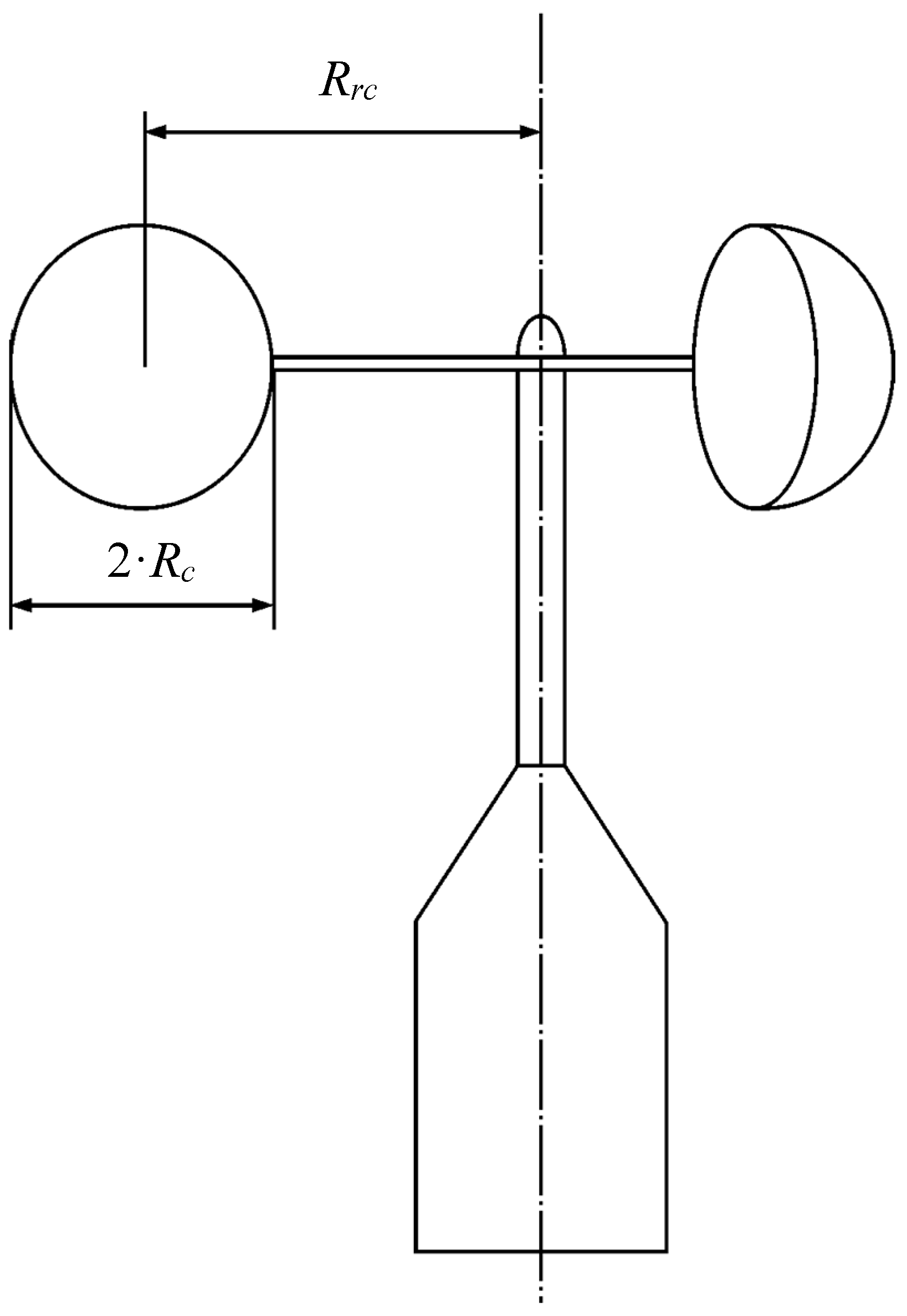
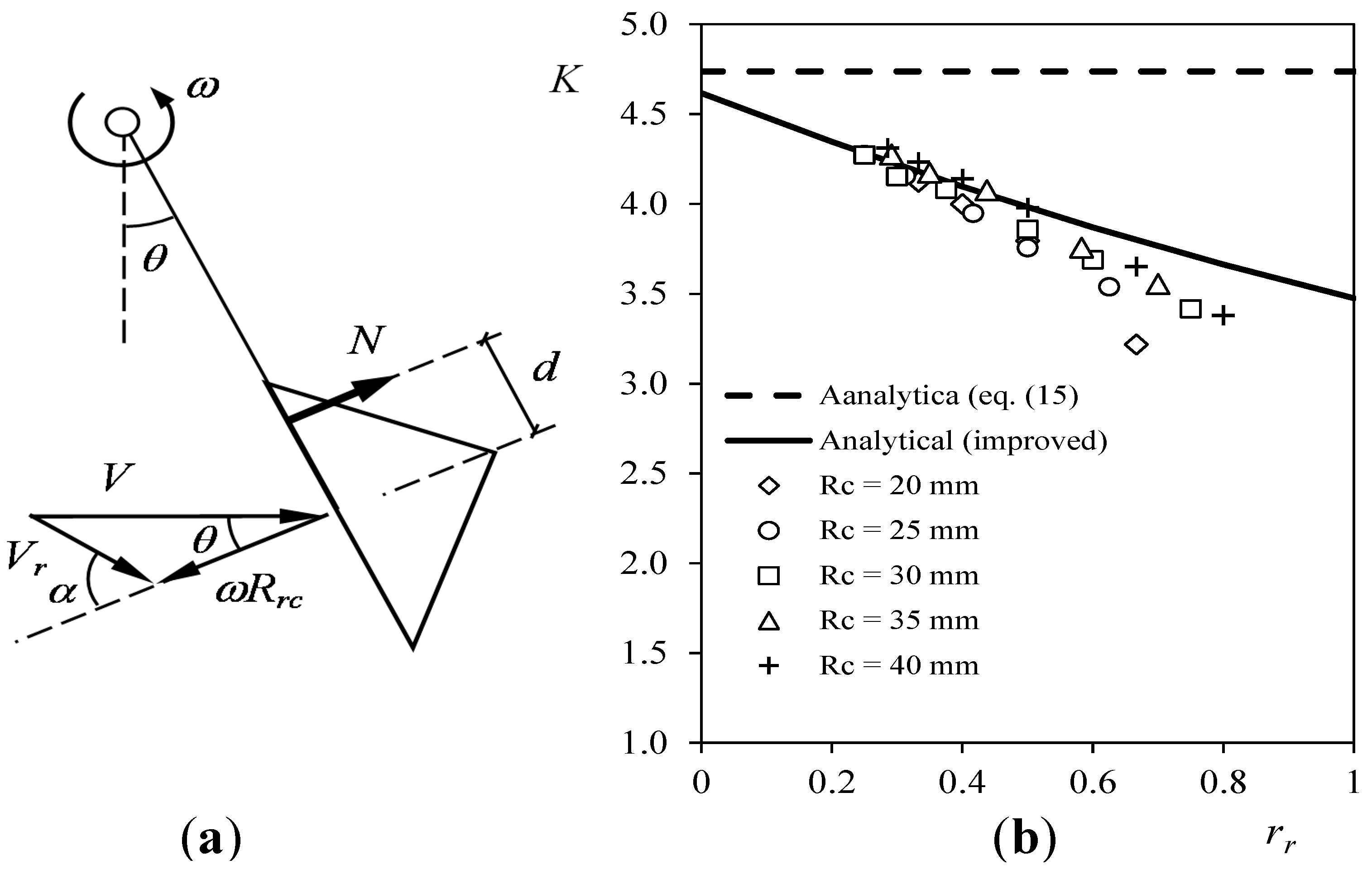
• The slope of the calibration curve, A_r, seemed (in that work) to have a direct relationship with the cups’ center rotation radius, R_rc, (that is, with the anemometer’s rotor radius). This relationship was also proven with an analytical model of the cup anemometer performance.

This last conclusion was checked with further studies at the IDR/UPM Institute by Pindado et al. [24] and Sanz-Andres et al. [29]. In these works, the calibration constants were proven to be dependent on geometric parameters of cup anemometer rotors, the following equations being derived:

$${\mathrm{A}}_r=\frac{{\mathrm{dA}}_r}{\mathrm{d}{R}_{rc}}{R}_{rc}+{\mathrm{A}}_{r0}=\frac{{\mathrm{dA}}_r}{\mathrm{d}{R}_{rc}}{R}_{rc}-S_c\left(\mathsf{\zeta }+\mathsf{\eta }{S}_c^{-\mathsf{\xi }}\right),$$

(3)

$$\mathrm{B}=\frac{\mathrm{dB}}{\mathrm{d}{R}_{rc}}{R}_{rc}+{\mathrm{B}}_0=\left(\mathsf{\epsilon }+\mathsf{\varphi }{S}_c^{-\mathsf{\gamma }}\right)R_{rc}-\mathsf{\mu }{S}_c^{-\mathsf{\psi }},$$

(4)

where R_rc is the cups’ center rotation radius, S_c, stands for the cups front area, and R_c is the cups radius (see Figure 4). The other terms present in the above equations: ζ η, ξ, ε, φ, γ, μ, and ψ are parameters to be extracted from experimental data.

In the mentioned work by Pindado et al. [24], two anemometers (Climatronics 100075 and Ornytion 107A, see pictures in Figure 5), were calibrated several times equipped with different rotors (varying the size of the same conical-shape cups and their distance to the rotation axis, i.e., R_rc). One of the most relevant conclusions of this study was that the slope dA_r/dR_rc only depends on the cups shape and not on their size (see Figure 5). Furthermore, in the analysis carried out by Sanz-Andres et al. [29], another important fact was revealed. The aerodynamic force on the cups is not acting on their center and even more, the center of the cup is not the average location of the aerodynamic center during one turn of the rotor (this has a quite important effect on the analytical modeling of cup anemometer performances).

Additionally, both the effect of the climatic conditions during the calibration process and cup anemometer performance degradation after several months working on the field were analyzed in the works by Pindado et al. [23,25]. The results of these analyses were as follows:

• Calibration constants, A and B, are affected by changes in air density, which, on the other hand, is driven mostly by changes in air temperature;
• These changes have a quite relevant impact on Annual Energy Production (AEP) estimations, depending on the selected wind sensor. Deviations of AEP up to 18% and 8% at 4 m·s⁻¹, and 7 m·s⁻¹ wind speeds were calculated for 0.1 kg·m⁻³ air density variations and first class anemometers;
• The anemometers degrade in large storage periods;
• Even showing a quite high level of wear and tear, it is quite difficult to establish degradation patterns of anemometers working on the field.

The output signal of cup anemometers has been also thoroughly studied at IDR/UPM Institute [26,30,31,34]. In steady wind the multi-pulse signal can be translated into a periodic rotation speed that shows three accelerations (and three decelerations) per turn of the rotor (see Figure 6). Therefore, from the pulsed-signal, it is possible to decompose the rotation rate of the anemometer, ω, into a Fourier series within one rotation period (see Figure 6).

$$\begin{array}{c}\omega \left(t\right)={\omega }_0+{\omega }_1\sin \left({\omega }_{0}t+{\phi }_1\right)+{\omega }_2\sin \left(2{\omega }_{0}t+{\phi }_2\right)+{\omega }_3\sin \left(3{\omega }_{0}t+{\phi }_3\right)\dots =\hfill \\ {\omega }_0+{\displaystyle \sum _{i=1}^{\infty }{\omega }_i\sin \left(i{\omega }_{0}t+{\phi }_i\right)}\hfill \end{array},$$

(5)

where i is the number of the harmonic term, ω_i its magnitude, and φ_i its phase angle (or angular deviation).

In the above equation, two important facts should be taken into account. First of all, the most relevant harmonic terms are the ones which are multiples of three, since due to the shape of the rotor (equipped with three cups) it accelerates three times per turn. Besides, all the other terms are noise due to turbulence or the wake downstream the anemometer’s body interaction with the rotor, with the obvious exception of the constant term, ω₀, that gives the average rotation speed, and the first harmonic term, ω₁, which reflects the perturbations that are repeated periodically once per turn. See the previous works by IDR/UPM Institute researchers [26,30,31].

The analysis of this first harmonic term has revealed itself as a very promising way to monitor the anemometer working condition. A quite relevant percentage of anemometers that are removed from a wind power generator for a recalibration process are damaged [74]. In Figure 7, a damaged A100 LK cup anemometer is shown, together with its calibration curve. This curve is compared to the one obtained with the anemometer equipped with a non-damaged rotor. In the top-right graph included in Figure 7, it can be observed that only a slight difference in the calibration curve is obtained, although the economic impact of this tiny deviation on a wind power plant could be huge. On the other hand, the damage is perfectly revealed by the first harmonic term (shown in the bottom-right graph of the figure).

Furthermore, a damaged cup anemometer might remain in a static position, that is, not-rotating, under normal or strong winds if one of the cups is missing or severely damaged. This can be a quite relevant problem, as the anemometer could still generate a pulsed signal that might be translated by the data-logger into a wind speed. The pulsed signal is generated by a small rotor-oscillation movement produced by the wake of the anemometer’s neck interacting with the rotor. Even worse, this completely wrong signal depends linearly on the wind speed and could induce a wind power generator to work out of the maximum efficiency point in case this problem is not anticipated, as shown by Pindado et al. [32].

Finally, the harmonic distribution of the rotor movement in steady wind speed represents a signature that defines a cup anemometer. Analyzing large series of two commercial cup anemometers calibrated at IDR/UPM facility, different patterns of the first and third harmonic terms statistical distribution were observed [34] (see Figure 8). The analysis of these frequency histograms might be used for quality control processes related to cup anemometer industrial production, as the best quality processes ensure a lower level of deviation among performances of different units of the same model (that is, a larger deviation of the harmonic histograms indicates greater differences on the unit’s performances).

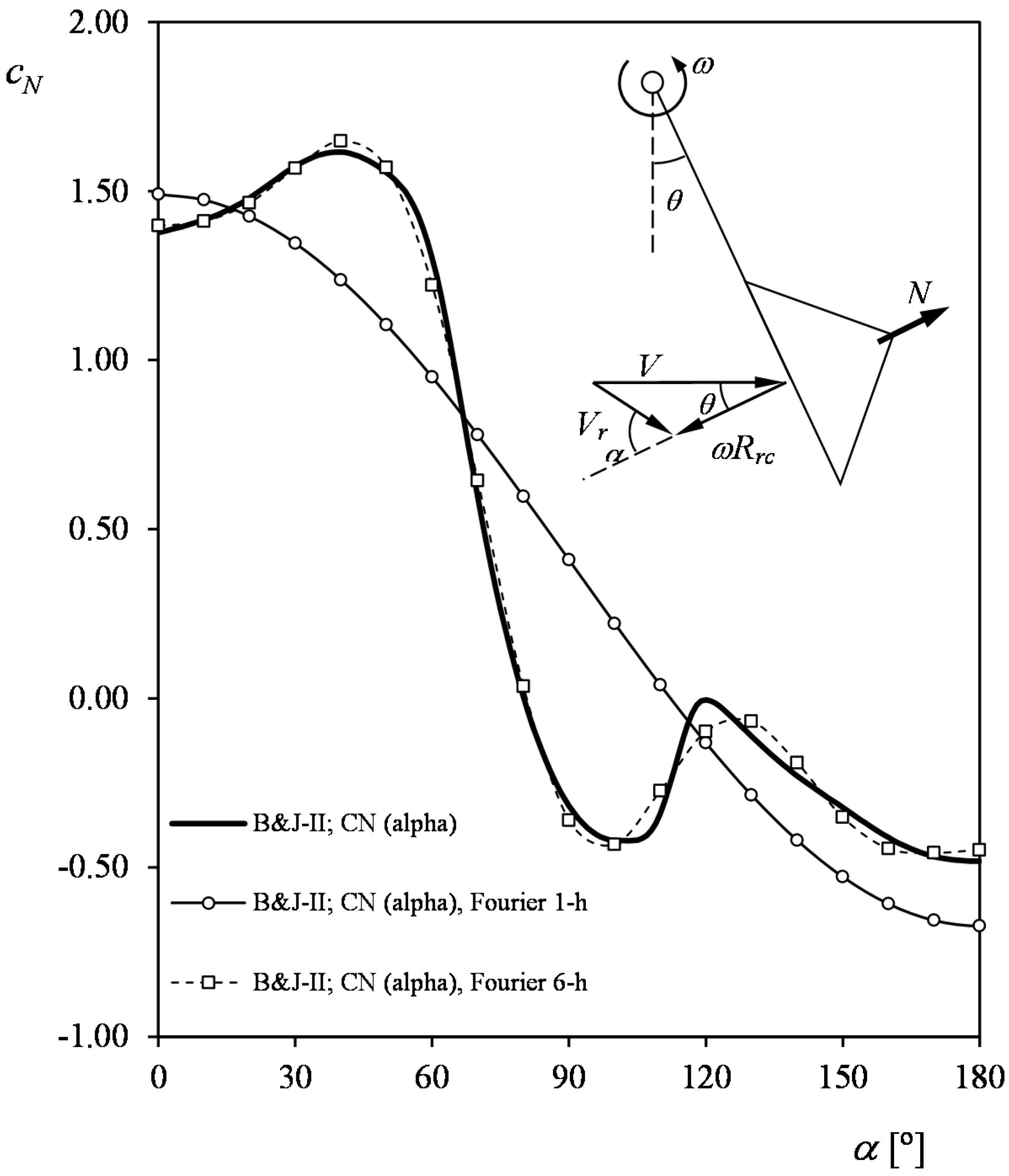
3. Modeling Cup Anemometer Performances

As far as the authors’ knowledge, the first analytical model developed to study cup anemometer performances was proposed by Chree by the end of the 19th century [75]. After that, Schrenk [76] developed the classic model that was initially used by the IDR/UPM staff to study the cup anemometer behavior [22,29]. Since 2012, a new analytical model that takes into account the aerodynamic forces on the three cups of the rotor has been developed at IDR/UPM Institute [24,27,31,33]. At this point, it might be necessary to underline the importance of the analytical models. These models reproduce the behavior of complex processes (related to mechanics, thermodynamics, fluid mechanics, etc.), with quite simple equations that preserve the physics of the problem. In the present case, the goal is to analyze the performance of a rotor based on the cups’ aerodynamics.

The aforementioned model, developed in our previous works, is derived from the equation that defines the performance, that is, the rotation rate, ω, of a cup anemometer.

$$I\frac{\mathrm{d}\omega }{\mathrm{d}t}=Q_A+Q_f,$$

(6)

where I is the moment of inertia of the rotor, Q_A is the aerodynamic torque, and Q_f is the frictional torque that depends on the air temperature and the rotation rate [31]. The frictional torque is normally neglected, as its effect is only important at very low wind speeds (out of the calibration range). If the three cups of the rotor are taken into account the previous equation can be rewritten as follows:

$$\begin{array}{l}I\frac{\mathrm{d}\omega }{\mathrm{d}t}=\frac{1}{2}\rho S_c{R}_{rc}{V}_r^2\left(\theta \right)c_N\left(\alpha \left(\theta \right)\right)+\frac{1}{2}\rho S_c{R}_{rc}{V}_r^2\left(\theta +{120}^{\circ }\right)c_N\left(\alpha \left(\theta +{120}^{\circ }\right)\right)+\\ +\frac{1}{2}\rho S_c{R}_{rc}{V}_r^2\left(\theta +{240}^{\circ }\right)c_N\left(\alpha \left(\theta +{240}^{\circ }\right)\right)\end{array},$$

(7)

where V_r is the wind speed relative to the cups, c_N is the aerodynamic normal force coefficient, α is the wind direction with respect to the cups, and θ is the angle of the rotor with respect to a reference line (see sketch in Figure 9). The relative-to-the-cup wind speed can be expressed as:

$$V_r\left(\theta \right)=\sqrt{V^2+{\left(\omega R_{rc}\right)}^2-2V\omega R_{rc}\cos \left(\theta \right)}.$$

(8)

On the other hand, it is possible to derive an equation that correlates both the wind direction angle, α, and the position angle θ.

$$\tan \left(\alpha \right)=\frac{K\sin \left(\theta \right)}{K\cos \left(\theta \right)-1}.$$

(9)

In the above equation, the constant K is called the anemometer factor and it represents the ratio between the wind speed and the speed of the center of the cups.

$$K=\frac{V}{\omega R_{rc}}=\frac{{\mathrm{A}}_r{f}_r+\mathrm{B}}{2\pi f_r{R}_{rc}}=\frac{{\mathrm{A}}_r}{2\pi R_{rc}}\frac{1}{1-\left(\frac{\mathrm{B}}{V}\right)}.$$

(10)

Taking into account that the offset B is below 0.6 m·s⁻¹ for most commercial anemometers in the wind energy sector [22], it can be assumed that

$$K=\frac{{\mathrm{A}}_r}{2\pi R_{rc}}.$$

(11)

The aerodynamic force coefficient related to the cups, c_N, can be obtained, in a first approximation, from static measurements (that is, with no rotation of the cup) in wind tunnel [77]. However, this approach does not take into account the aerodynamic effect produced by the rotating flow over the cup. The aerodynamic force coefficient, c_N, can be expressed in terms of Fourier series, as it is a periodic function. See in Figure 9 the 1-harmonic and 6-harmonic terms Fourier series compared to the coefficient related to a conical cup experimentally measured. If the 1-harmonic equation is considered,

$$c_N\left(\alpha \right)=c_0+c_1\cos \left(\alpha \right).$$

(12)

Besides, the relationship between α and θ angles, previously defined by Equation (9), can be approximated as follows:

$$\cos \left(\alpha \right)={\eta }_0+{\eta }_1\cos \left(\theta \right)+{\eta }_2\cos {\left(\theta \right)}^2+{\eta }_3\cos {\left(\theta \right)}^3\dots$$

(13)

where:

$${\eta }_0=\frac{-1}{\sqrt{1+K^2}};{\eta }_1=\frac{K}{\sqrt{1+K^2}}-\frac{1}{K^2-1};{\eta }_2=\frac{1}{\sqrt{1+K^2}};{\eta }_3=\frac{K^2}{K^2-1}-\frac{K}{\sqrt{1+K^2}}.$$

(14)

Taking into account the above equations, the following expression can be derived from (7) in order to relate the anemometer factor, K, to the aerodynamic coefficients of the rotor cups:

$$0=\left(1+\frac{1}{K^2}\right)\left(1-\frac{1}{2}\frac{c_1}{c_0}\frac{1}{\sqrt{1+K^2}}\right)-\frac{1}{4}\frac{c_1}{c_0}\frac{1}{K}\left(\frac{K}{\sqrt{1+K^2}}+\frac{3K^2-4}{K^2-1}\right).$$

(15)

In Figure 10 the anemometer factor of several cases that were measured in wind tunnel (one anemometer, Climatronics 100075, equipped with different rotors in which the characteristics of the cups have been varied) are compared to the above equation. Results from of Equation (15) seem to reflect the tendencies shown by the testing results, with 13% average error [27].

However, this model presents a drawback, as it gives a single value of K without taking into account the geometric characteristics of the rotor (that affects the anemometer performance, as shown by Equations (3) and (4)). This was already observed in previous research campaigns at IDR/UPM, in which the effect of the ratio of the cups’ radius, R_c, to the cups’ center rotation radius, R_rc, defined as:

$$r_r=\frac{R_c}{R_{rc}},$$

(16)

was observed. In order to improve the model two effects were considered after an analysis campaign carried out by using Computer Fluid Dynamics (CFD) [78]. First of all, a phase angle δ was considered in relation to the aerodynamic force coefficient.

$$\begin{array}{l}{c}_N\left(\alpha \right)=c_0+c_1\cos \left(\alpha +\delta \right)=c_0+c_1\cos \left(\delta \right)\cos \left(\alpha \right)-c_1\sin \left(\delta \right)\sin \left(\alpha \right)=\\ c_0+c_{11}\cos \left(\alpha \right)-c_{12}\sin \left(\alpha \right)\end{array}.$$

(17)

Additionally, the aerodynamic force on the cup was not considered to be applied on the cups center, a deviation from the center (see sketch in Figure 11) being introduced in the model instead. This deviation d was also considered to be displaced a phase angle γ with respect to the cup position angle α in relation to the wind.

$$\begin{array}{l}\frac{d\left(\alpha \right)}{R_c}=e\sin \left(\alpha +\gamma \right)=e\cos \left(\gamma \right)\sin \left(\alpha \right)+e\sin \left(\gamma \right)\cos \left(\alpha \right)=\\ e_{11}\sin \left(\alpha \right)+e_{12}\cos \left(\alpha \right)\end{array}.$$

(18)

This approach takes into account the aerodynamic forces produced by cup rotation, together with the aforementioned forces derived from the cup direction with respect to the wind (that is, the aforementioned aerodynamic forces measured in static position). Making reasonable assumptions, this model was compared to testing results [33]. As it can be observed in Figure 11, the model was able to predict cup anemometer performances quite accurately, taking into account the effect of the geometric variable r_r. Furthermore, it is also fair to mention that the model seems to be less accurate for r_r > 0.45, that is, for rotors in which the cups are closer to the rotation axis (in relation to the cups size). In these cases, the rotation produces higher variations on the local wind speed around the cups, and probably causes this deviation.

Going back to the cup anemometer’s signal in steady wind and bearing in mind the work carried out in [31], it should be also pointed out that its Fourier series decomposition (Equation (5)) can be introduced in the general equation of the cup anemometer (Equation (7)), generating an interesting equation that takes into account the third harmonic term.

$$\begin{array}{l}\frac{I}{\frac{3}{2}\rho S_c{R}_{rc}{V}^2}\frac{\mathrm{d}\omega }{\mathrm{d}t}=-\frac{I3{\omega }_0{\omega }_3}{\frac{3}{2}\rho S_c{R}_{rc}{V}^2}\sin \left(3{\omega }_{0}t+{\phi }_3\right)\\ =\left(\left(1+\frac{1}{K^2}\right)(c_0+c_1({\eta }_0+\frac{1}{2}{\eta }_2))-\frac{1}{K}{c}_1({\eta }_1+\frac{3}{4}{\eta }_3)\right)\\ +\left(\left(1+\frac{1}{K^2}\right){\eta }_3-\frac{2}{K}{\eta }_2\right)\frac{c_1}{4}\cos \left(3\theta \right)\end{array}.$$

(19)

As it is obvious, the second term at the right side of the above equation is indeed the Equation (15), which gives the average rotation speed of the cup anemometer as a function of the ratio c₁/c₀. Additionally, the remaining terms give information on the third harmonic term of the rotation rate. The following equation can then be derived:

$$\begin{array}{l}\frac{{\omega }_3}{{\omega }_0}=\left(\frac{\pi }{8}\right)\left(\frac{\rho R_{rc}^5}{I}\right)\left|\left(\left(K^2+1\right){\eta }_3-2K{\eta }_2\right)\right|c_1{r}_r^2\\ \approx \left(\frac{\pi }{8}\right)\left(\frac{\rho R_{rc}^5}{I}\right)\left(0.5308{\left(\frac{c_1}{c_0}-1\right)}^{-1.599}-0.5\right)c_1{r}_r^2\end{array}$$

(20)

This is an important result that suggests the existence of a theoretical minimum for this third harmonic term for c₁/c₀ ≈ 2.05.

Finally, the importance of modeling cup anemometer performances should be emphasized in order to produce new improvements and designs that could increase the accuracy of the wind speed measurements. In this sense, it is worth mentioning the work by Dahlberg et al. [79] that produced in 2001 a new rotor design (Patent No.: US 2004/0083806 A1 [80], see Figure 12), or the one from Thies Clima (Patent No.: EP 1489427 B1 [81]), or the more recent development by Hong in 2012 [82] (Patent No.: US 2012/0266692 A1, see Figure 12).

4. Conclusions

In the present work, the research on cup anemometer performances carried out at IDR/UPM has been summarized. This research has been focused on the following two aspects, although both are related:

• The analysis of the performance based on experimental results as follows:

  ○

  Force on isolated cups;

  ○

  Calibrations performed on both commercial anemometers and anemometers equipped with special-design rotors;

  ○

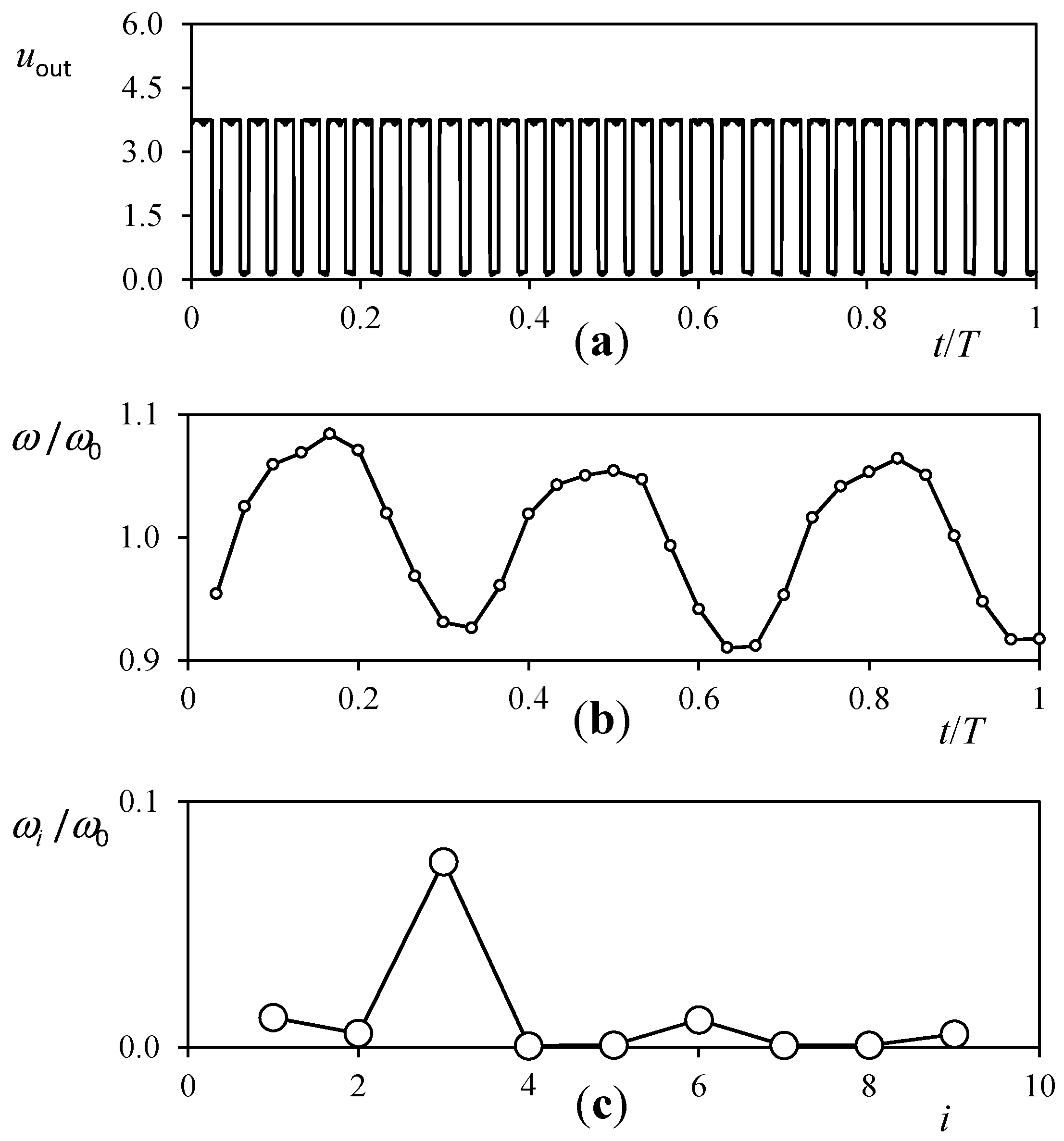
  The output signal of the cup anemometers.

• The analytical study of the cup anemometer performances with a new methodology developed consequently. All expertise gained with the analysis of testing results was a fundamental basis for this analytical work. It should be underlined the importance of analytical models in order to produce better sensors in the future, as by using these models, a reduction of costs (measured in time and calculation resources) can be achieved in the first stages of the designing process.

For future works, some of them being in progress at the IDR/UPM Institute, it could be interesting to analyze the performances of working-on-the-field cup anemometers, taking into account the evolution of the rotation rate harmonic terms after long service periods of the wind sensor. Besides, it should be also of great interest to understand the aerodynamic forces and pressure distribution on rotating cups by means of experimental testing and CFD analysis.