Evaluation of Electrical Tree Degradation in Cross-Linked Polyethylene Cable Using Weibull Process of Propagation Time
Abstract
:1. Introduction
2. Test Specimens and Experimental Setup
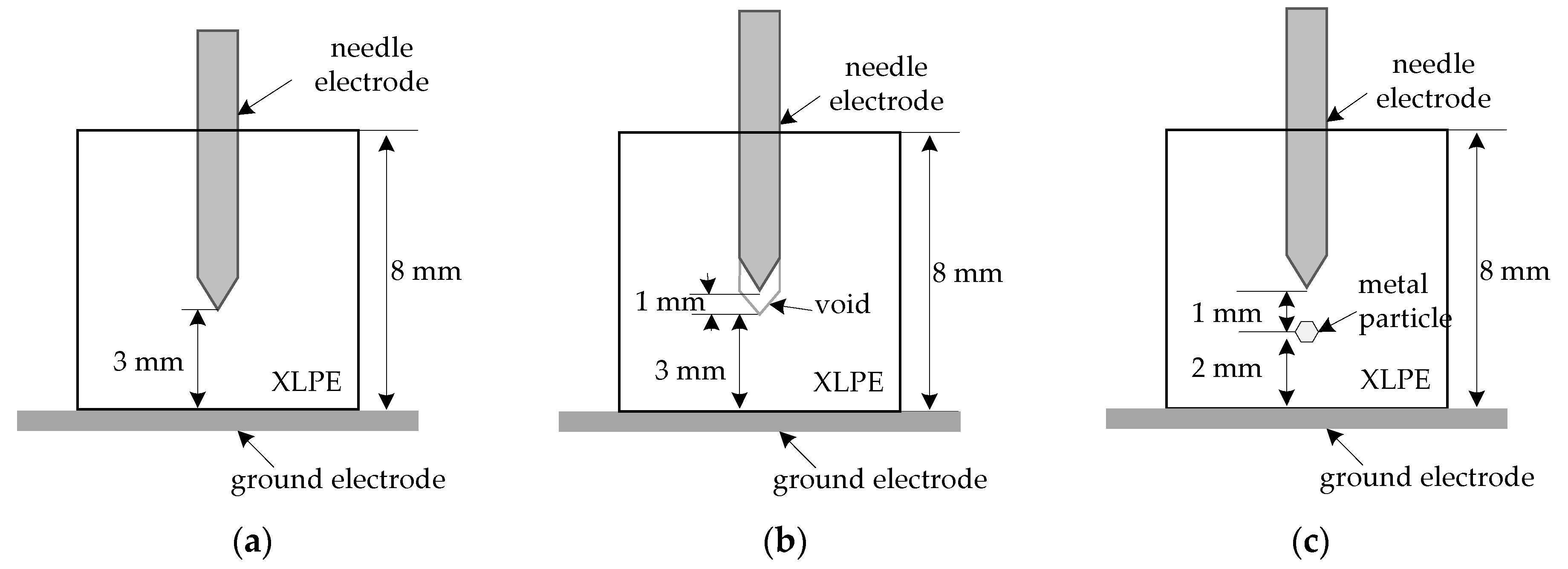
2.1. Artificial Electrical Tree Model
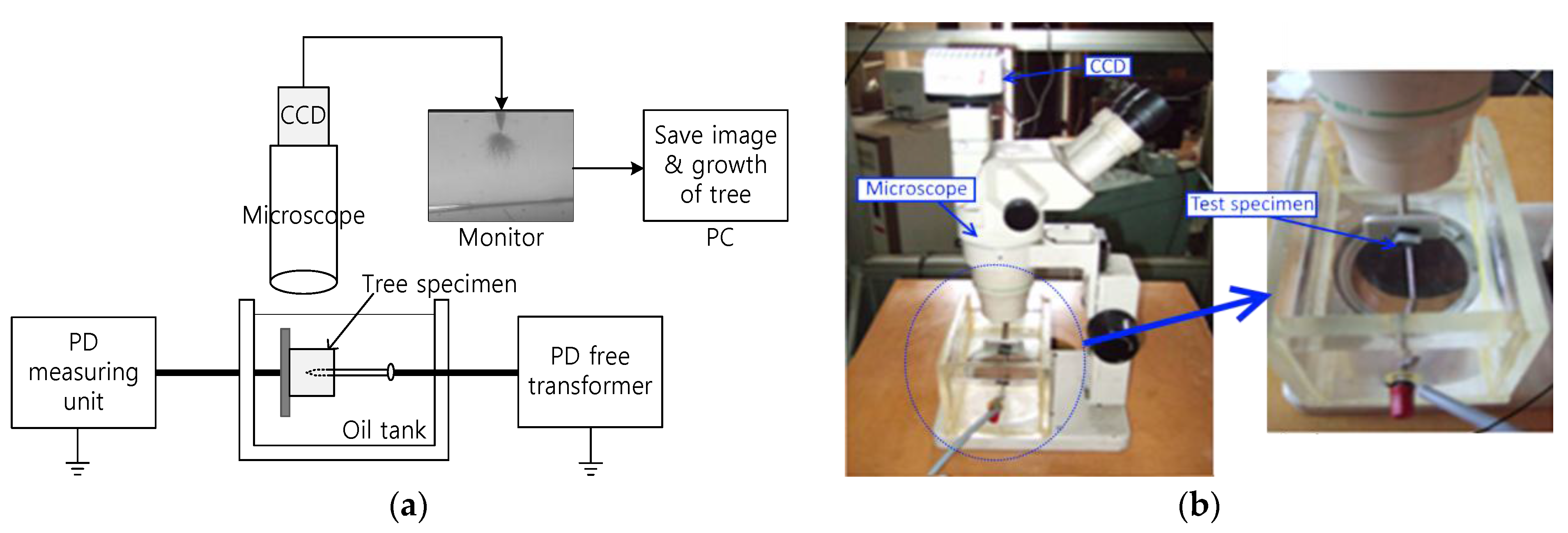
2.2. Experimental Method and Data Processing
2.2.1. Partial Discharge Measurement
2.2.2. Observation of Tree Propagation
2.2.3. Tree Growth and Degradation Stage
3. Experimental Results
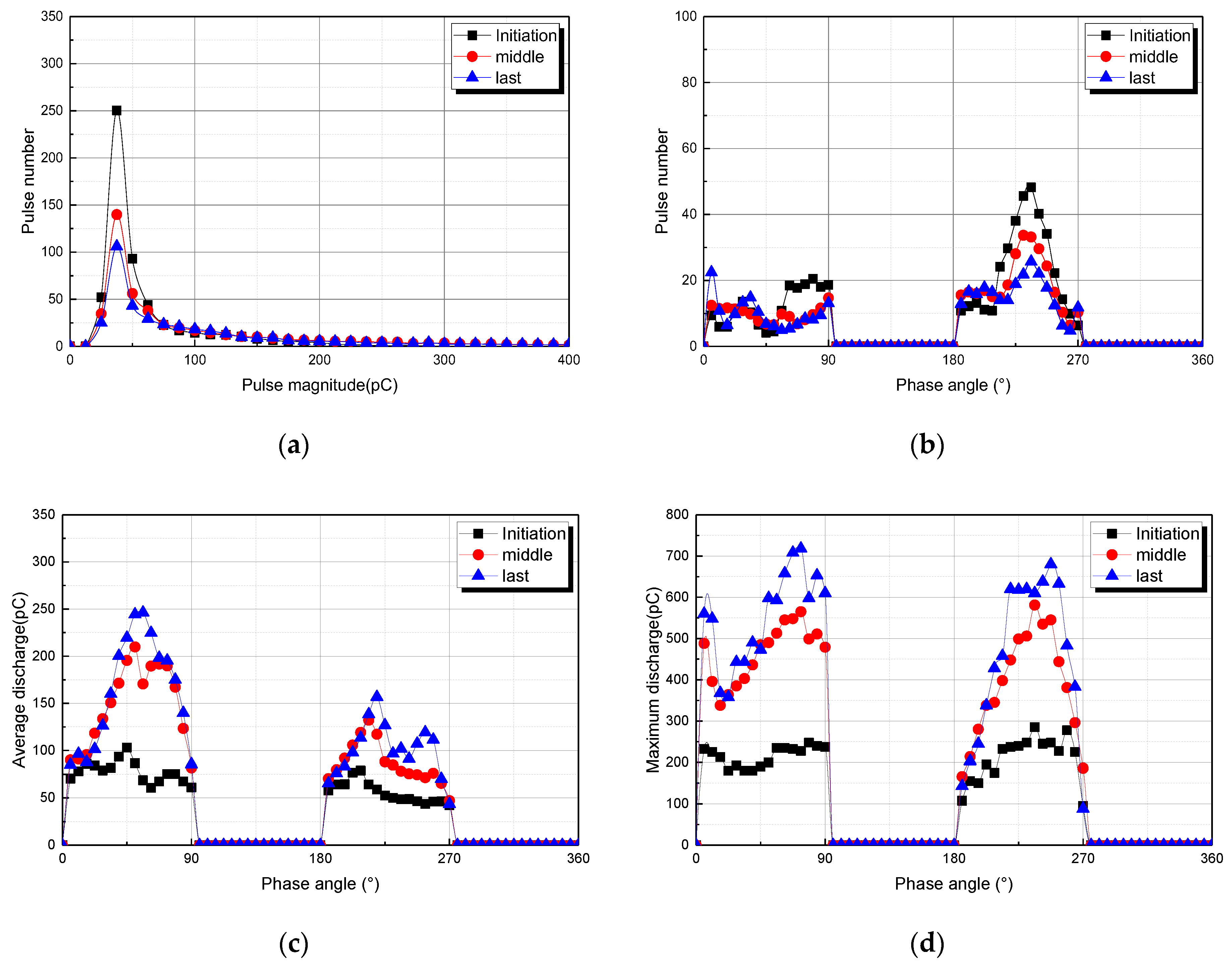
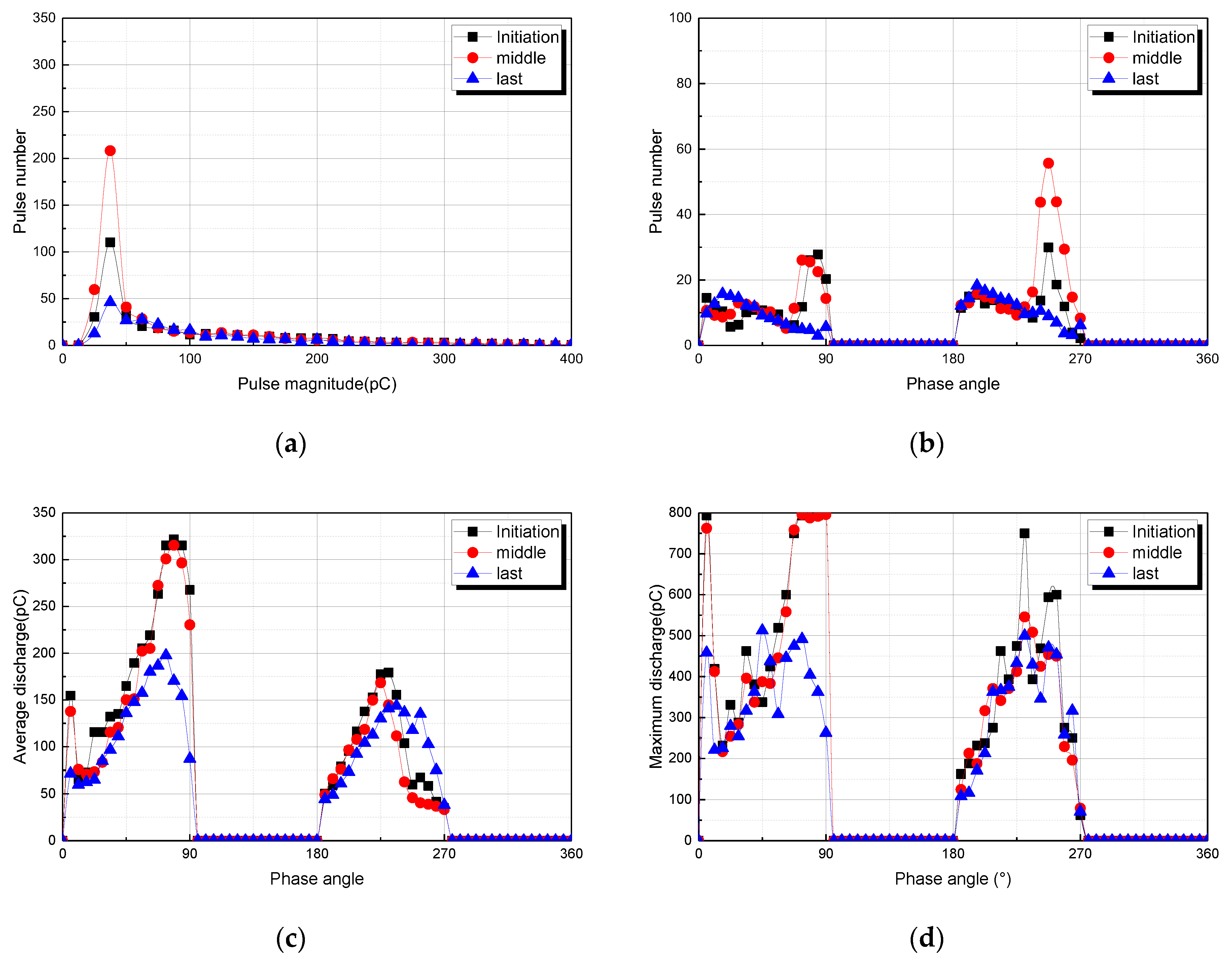
3.1. Partial Discharge Distributions for Tree Model 1
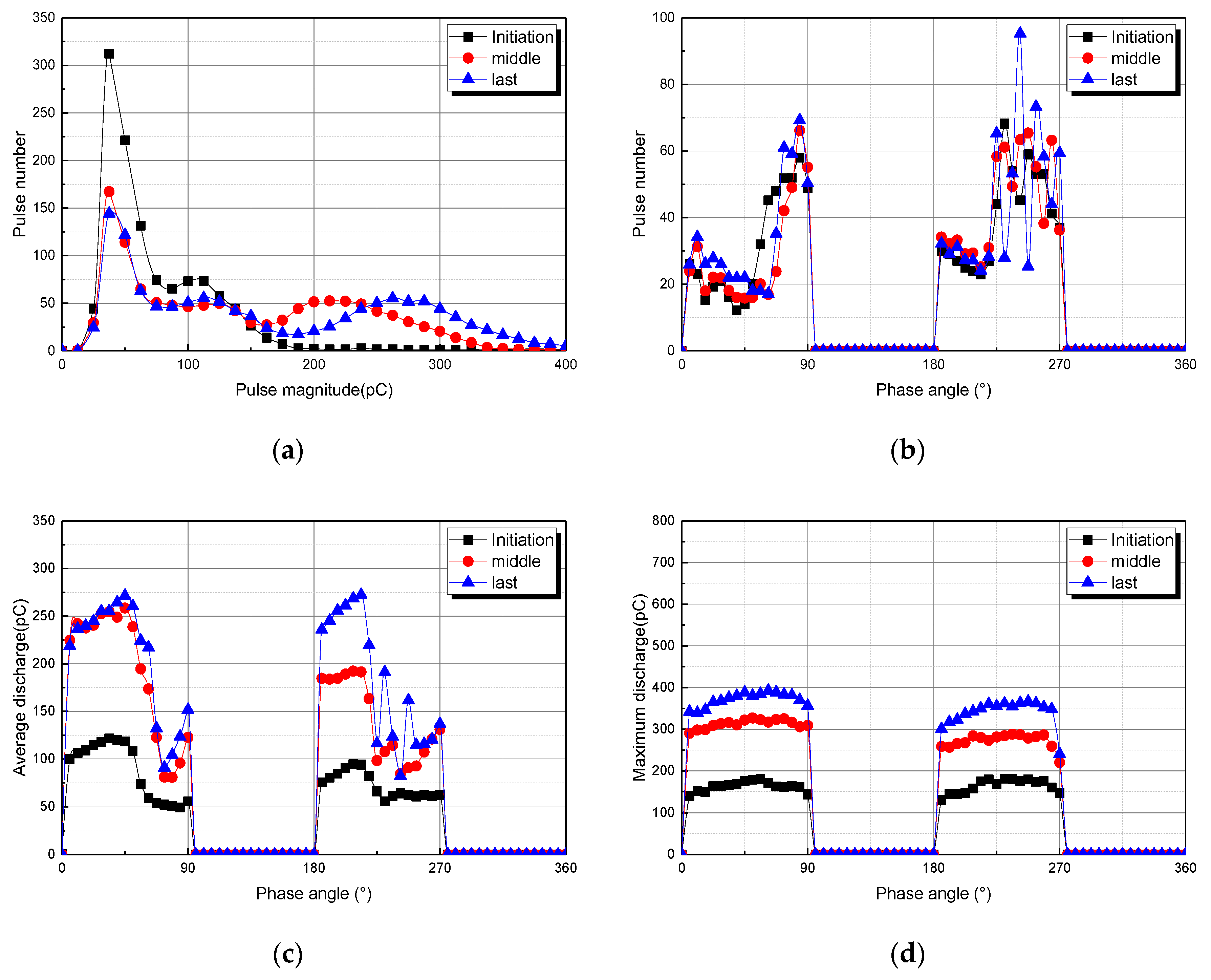
3.2. Partial Discharge Distributions for Tree Model 2
3.3. Partial Discharge Distributions for Tree Model 3
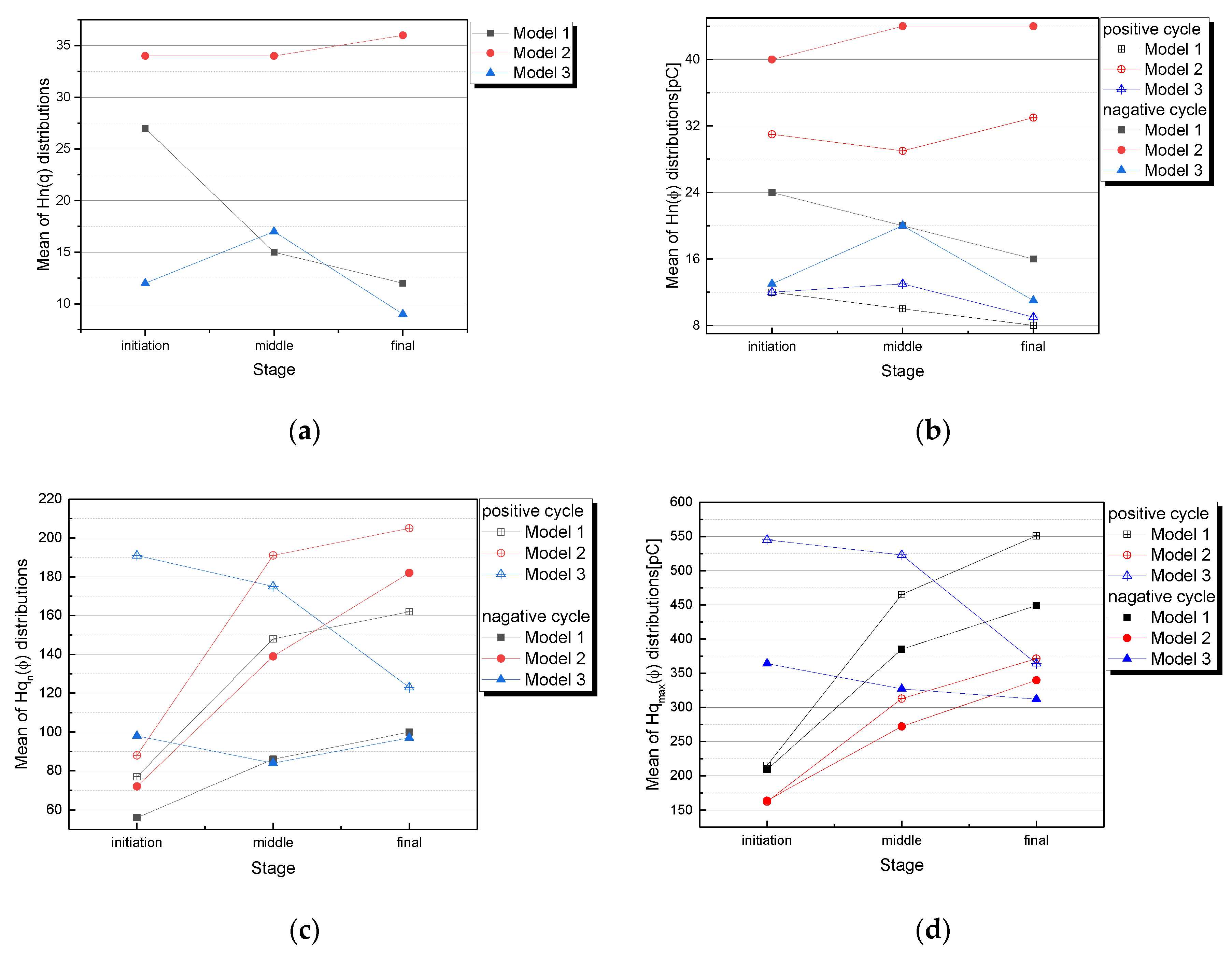
3.4. Tendeny of Statistical Distributions of PD According to Tree Propagation
3.5. Evaluation of the Degradation Degree of XLPE Cable Using Weibull Analysis
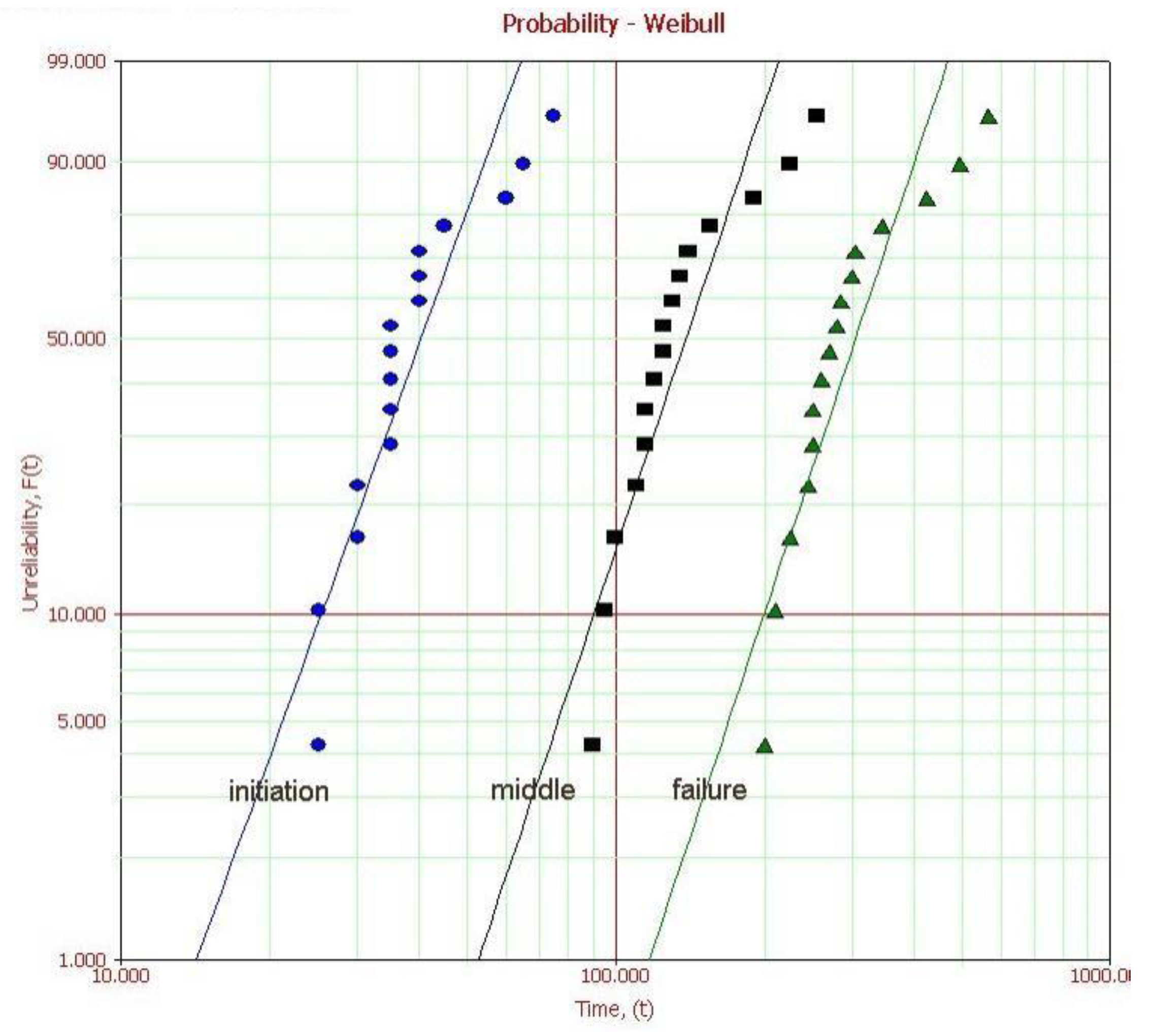
3.5.1. Weibull Analysis
3.5.2. Examination of the Electrical Tree Propagation Time
4. Discussion
5. Conclusions
- This paper analyzed the characteristics of the partial discharge distributions at each tree propagation stage in each simulated electrical tree model.
- Shape and scale parameters tended to increase as the electrical tree degradation proceeded in Tree Models 1 and 2, whereas the values of shape and scale parameters tended to decrease when the electrical tree propagation proceeded towards the final stage in Model 3.
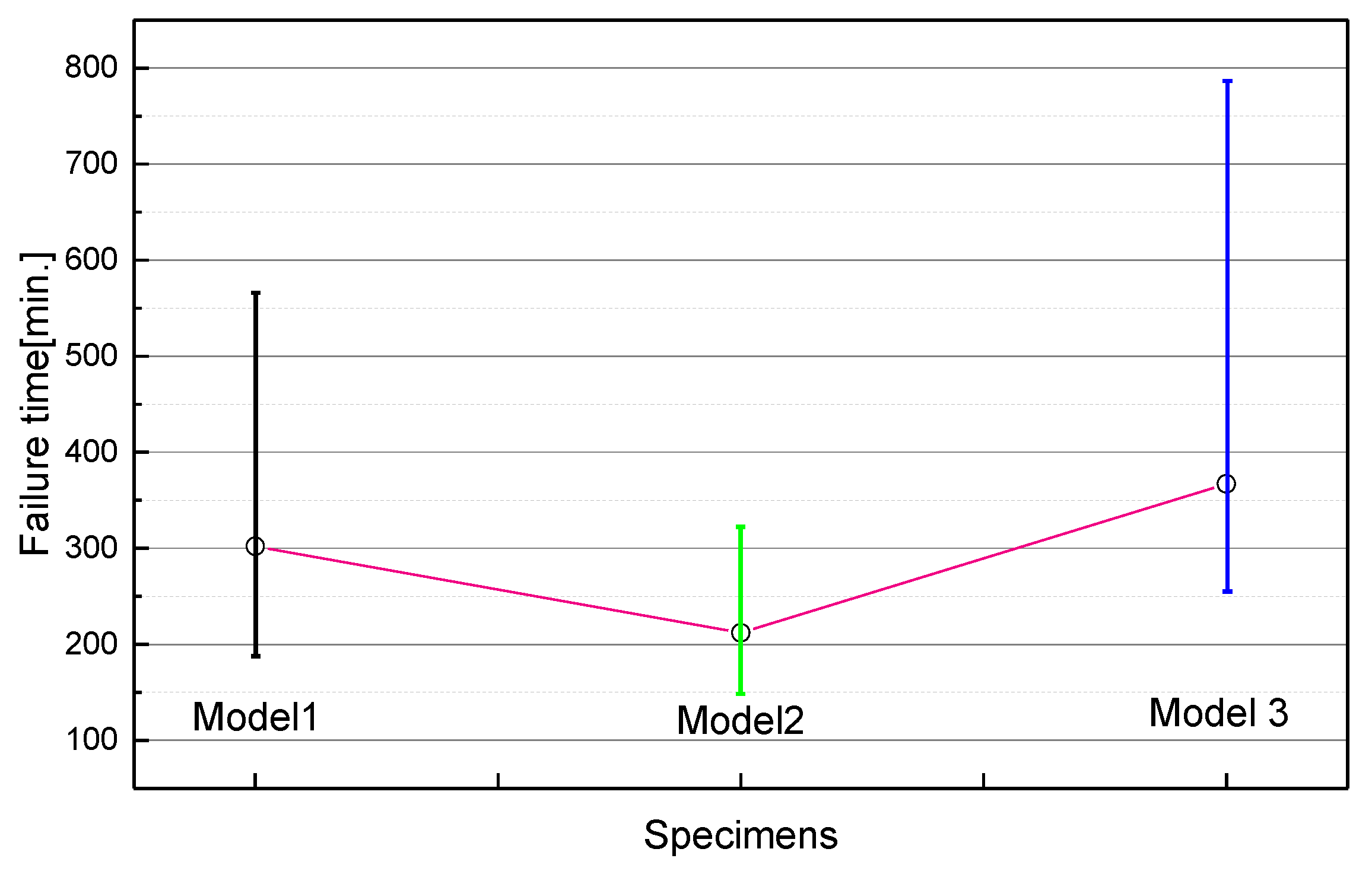
- The failure time of each specimen was measured in order to determine the degradation degree of the electrical trees by means of F(t) which uses the relevant time as a variable. The failure times in each model were measured and written by the degradation stage, and the shape parameters, the scale parameters and MTTF for each model and each stage were also estimated by means of these measurement results. The time difference between the degradation stages could be calculated, and the remaining lifetime of trees was estimated by means of such time differences.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kreuger, F.H.; Gulski, E.; Krivda, A. Classification of Partial Discharge. IEEE Trans. Electr. Insul. 1993, 28, 917–931. [Google Scholar] [CrossRef]
- Gulski, E. Computer-aided Measurement of Partial Discharges in HV Equipment. IEEE Trans. Electr. Insul. 1993, 28, 969–976. [Google Scholar] [CrossRef]
- Shimizu, N.; Laurent, C. Electrical Tree Initiation. IEEE Trans. Dielectr. Electr. Insul. 1998, 5, 651–659. [Google Scholar] [CrossRef]
- Du, B.X.; Xue, J.S.; Sum, J.G.; Han, T. Effects of ambient temperature on electrical tree in epoxy resin under repetitive pulse voltage. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1527–1536. [Google Scholar] [CrossRef]
- Bamji, S.S.; Bulinski, A.T.; Chen, Y.; Densley, R.J. Photodegradation versus hot-electron impact for electrical tree inception at low electric fields. In Proceedings of the 3rd International Conference on Properties and Applications of Dielectric Materials, Tokyo, Japan, 8–12 July 1991; Volume 1, pp. 51–54. [Google Scholar] [CrossRef]
- Jiang, Y.; Min, H.; Luo, J.H.; Li, Y.; Jiang, X.J.; Xia, R.; Li, W.J. Partial Discharge Pattern Characteristic of HV Cable Joints with Typical Artificial Defect. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference (APPEEC), Chengdu, China, 28–31 March 2010. [Google Scholar]
- Wang, L.; Liang, X.; Guan, Z.; Que, W. Research on 500 kV Phase to Phase Composite Spacer for Compact Lines. In Proceedings of the 6th International Conference on Properties and Applications of Dielectric Materials, Xi’an, China, 21–22 June 2000; pp. 346–349. [Google Scholar]
- Guastavino, F.; Cerutti, B. Tree growth monitoring by means of digital partial discharge measurements. IEEE Trans. Dielectr. Electr. Insul. 2003, 10, 65–72. [Google Scholar] [CrossRef]
- Tian, Y.; Lewin, P.L.; Wilkinson, J.S.; Sutton, S.J.; Swingler, S.G. Continuous on-line monitoring of partial discharges in high voltage cables. In Proceedings of the Conference Record of the 2004 IEEE International Symposium on Electrical Insulation, Indianapolis, IN, USA, 19–22 September 2004; pp. 454–457. [Google Scholar] [CrossRef]
- Fabiani, D.; Simoni, L. Discussion on Application of the Weibull Distribution to Electrical Breakdown of Insulating Materials. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 6–11. [Google Scholar] [CrossRef]
- Shimizu, N.; Sato, H. Role of Electron Impact in AC Electrical Tree Initiation. In Proceedings of the IEEE Transactions on Properties and Applications of Dielectric Materials, Seoul, Korea, 25–30 May 1997; pp. 414–417. [Google Scholar]
- Nelson, W. Applied Life Data Analysis; John Wiley & Sons: New York, NY, USA, 1982. [Google Scholar]
- Sarathi, R.; Oza, K.H.; Pavan Kumar, C.L.G.; Tanaka, T. Electrical treeing in XLPE cable insulation under harmonic AC voltages. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 3177–3185. [Google Scholar] [CrossRef]
- Jarvid, M.; Johansson, A.; Bjuggren, J.M.; Wutzel, H.; Englund, V.; Gubanski, S.; Müller, C.; Andersson, M.R. Tailored side-chain architecture of benzil voltage stabilizers for enhanced dielectric strength of cross-linked polyethylene. J. Polym. Sci. Part B Polym. Phys. 2014, 52, 1047–1054. [Google Scholar] [CrossRef]
- Bahadoorsingh, S.; Rowland, S. Investigating the impact of harmonics on the breakdown of epoxy resin through electrical tree growth. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 1576–1584. [Google Scholar] [CrossRef]
- Park, S.H. Classification of Defects and Evaluation of Electrical Tree Degradation in Cable Insulation Using Pattern Recognition Method and Weibull Process of Partial Discharge. Ph.D. Thesis, Chungbuk National University, Cheongju, Korea, 2007. [Google Scholar]
- Woojin, K.; Jeong, J.H.; Kim, Y.; Lim, W.C.; Kim, J.H.; Park, J.H.; Shin, H.J.; Park, Y.S.; Kim, K.S.; Park, S.H. Classification of defects and evaluation of electrical tree degradation in cable insulation using pattern recognition method and weibull process of partial discharge. In Proceedings of the 2008 International Conference on Condition Monitoring and Diagnosis, Beijing, China, 21–24 April 2008; pp. 101–104. [Google Scholar]
- Park, S.H.; Lim, K.J.; Kang, S.H. Comparison of Classification Rate for PD Sources using Different Classification Schemes. J. Electr. Eng. Technol. 2006, 1, 257–262. [Google Scholar] [CrossRef]
- Park, S.H.; Jang, D.U.; Kang, S.H.; Lim, K.J. Off-line PD Model Classification of Traction Motor Stator Coil Using BP. KIEE Int. Trans. Electrophys. Appl. 2005, 5-C, 223–227. [Google Scholar]
- Steennis, F.; Wagenaars, P.; van der Wielen, P.; Wouters, P.; Li, Y.; Broersma, T.; Harmsen, D.; Bleeker, P. Guarding MV cables on-line: With travelling wave based temperature monitoring, fault location, PD location and PD related remaining life aspects. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1562–1569. [Google Scholar] [CrossRef]

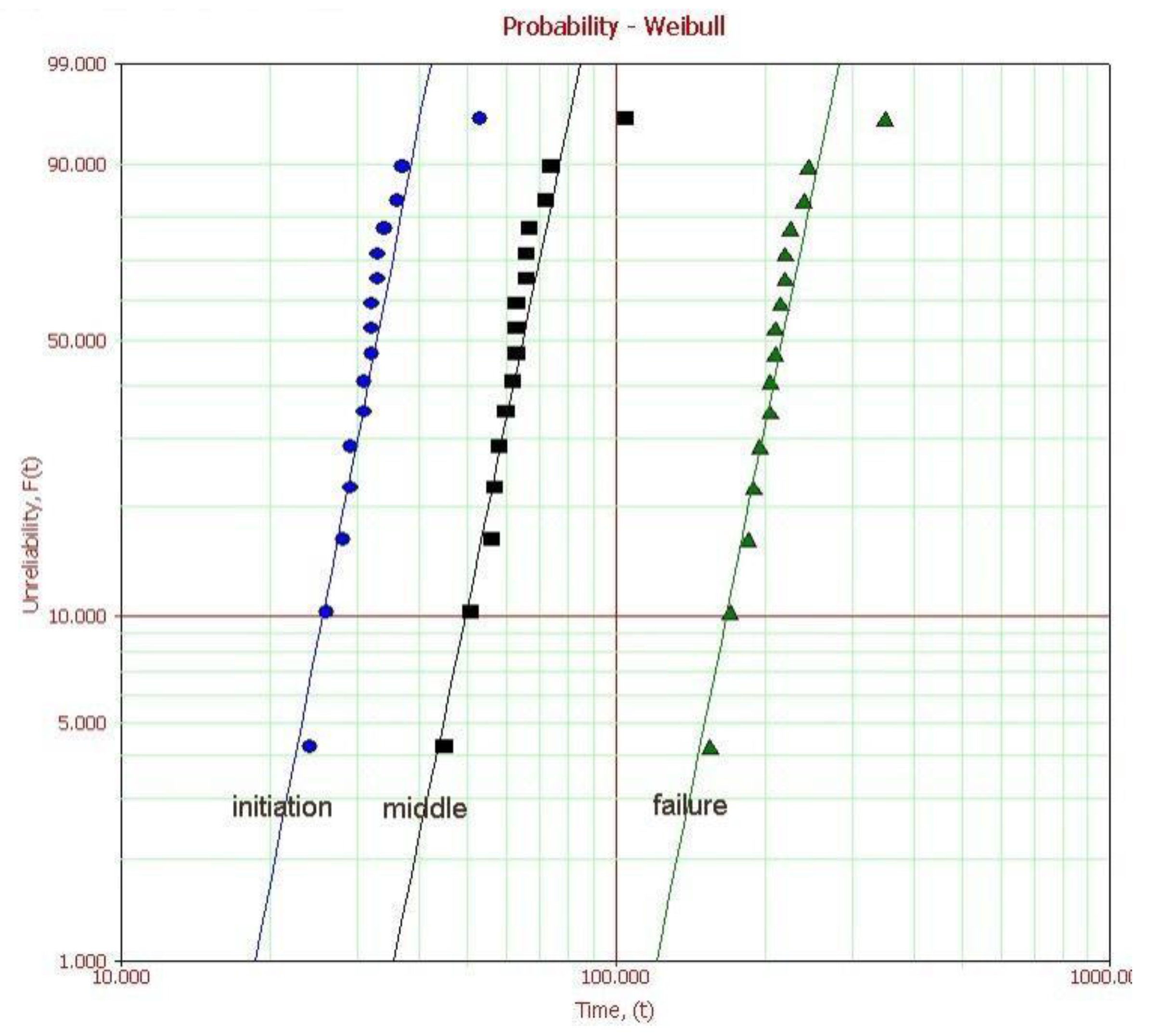
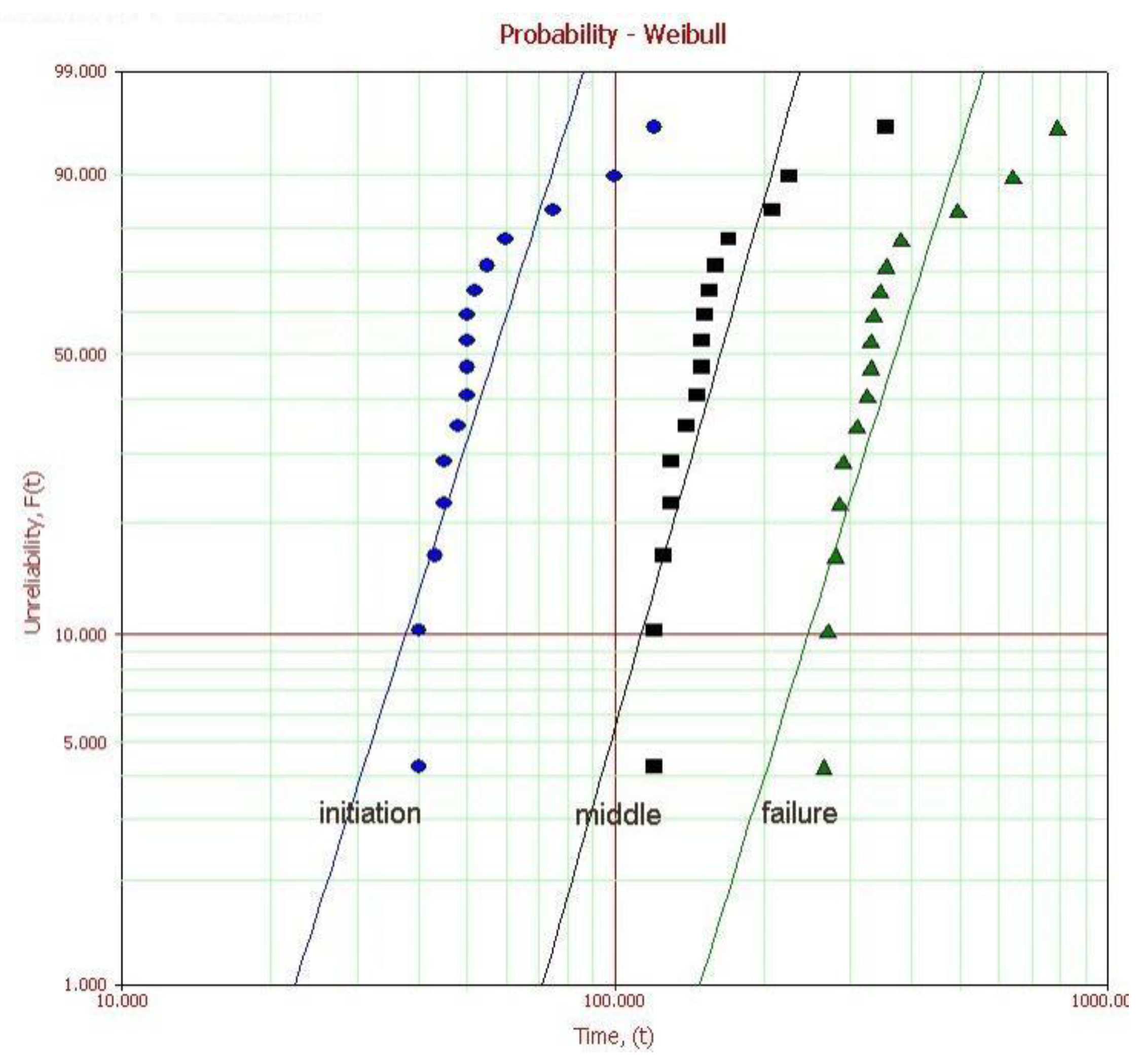
| Specimen Number | Initiation (Min.) | Middle (Min.) | Failure (Min.) |
|---|---|---|---|
| 1 | 25 | 90 | 200 |
| 2 | 30 | 100 | 225 |
| 3 | 30 | 110 | 245 |
| 4 | 25 | 95 | 210 |
| 5 | 35 | 125 | 270 |
| 6 | 40 | 140 | 305 |
| 7 | 40 | 135 | 300 |
| 8 | 75 | 255 | 565 |
| 9 | 35 | 115 | 250 |
| 10 | 35 | 120 | 260 |
| 11 | 65 | 225 | 495 |
| 12 | 45 | 155 | 345 |
| 13 | 60 | 190 | 425 |
| 14 | 35 | 115 | 250 |
| 15 | 35 | 125 | 280 |
| 16 | 40 | 130 | 285 |
| Average time | 41 | 139 | 307 |
| Parameter | Initiation | Middle | Failure | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Grouping | Shape | Scale (Min.) | MTTF (Min.) | Shape | Scale (Min.) | MTTF (Min.) | Shape | Scale (Min.) | MTTF (Min.) | |
| subpopulation 1 | 6.3 | 37 | 41 | 8.4 | 124 | 137 | 8 | 271 | 302 | |
| subpopulation 2 | 7.5 | 70 | 3.3 | 212 | 4.6 | 495 | ||||
| Specimen Number | Initiation (Min.) | Middle (Min.) | Failure (Min.) |
|---|---|---|---|
| 1 | 32 | 63 | 210 |
| 2 | 26 | 51 | 170 |
| 3 | 29 | 60 | 195 |
| 4 | 33 | 66 | 220 |
| 5 | 36 | 72 | 240 |
| 6 | 32 | 63 | 210 |
| 7 | 24 | 45 | 155 |
| 8 | 31 | 62 | 205 |
| 9 | 37 | 74 | 245 |
| 10 | 34 | 63 | 225 |
| 11 | 53 | 105 | 350 |
| 12 | 33 | 67 | 220 |
| 13 | 29 | 57 | 190 |
| 14 | 28 | 56 | 185 |
| 15 | 32 | 66 | 215 |
| 16 | 31 | 58 | 205 |
| Average time | 33 | 64 | 215 |
| Initiation | Middle | Failure | ||||||
|---|---|---|---|---|---|---|---|---|
| Shape | Scale (Min.) | MTTF (Min.) | Shape | Scale (Min.) | MTTF (Min.) | Shape | Scale (Min.) | MTTF (Min.) |
| 7.5 | 34 | 32 | 7.03 | 68 | 64 | 7.64 | 226 | 212 |
| Specimen Number | Initiation (Min.) | Middle (Min.) | Failure (Min.) |
|---|---|---|---|
| 1 | 45 | 130 | 285 |
| 2 | 45 | 125 | 280 |
| 3 | 60 | 170 | 380 |
| 4 | 40 | 120 | 270 |
| 5 | 43 | 130 | 290 |
| 6 | 52 | 155 | 345 |
| 7 | 50 | 152 | 335 |
| 8 | 75 | 225 | 495 |
| 9 | 50 | 147 | 325 |
| 10 | 120 | 355 | 790 |
| 11 | 50 | 150 | 330 |
| 12 | 48 | 140 | 310 |
| 13 | 100 | 208 | 640 |
| 14 | 55 | 160 | 355 |
| 15 | 40 | 120 | 265 |
| 16 | 50 | 150 | 330 |
| Average time | 58 | 165 | 377 |
| Parameter | Initiation | Middle | Failure | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Grouping | Shape | Scale (Min.) | MTTF (Min.) | Shape | Scale (Min.) | MTTF (Min.) | Shape | Scale (Min.) | MTTF (Min.) | |
| Subpopulation 1 | 10.8 | 50 | 56 | 9.1 | 150 | 161 | 9.3 | 329 | 367 | |
| Subpopulation 2 | 2.9 | 98 | 2.9 | 293 | 4.1 | 700 | ||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, D.; Park, S. Evaluation of Electrical Tree Degradation in Cross-Linked Polyethylene Cable Using Weibull Process of Propagation Time. Energies 2017, 10, 1789. https://doi.org/10.3390/en10111789
Jang D, Park S. Evaluation of Electrical Tree Degradation in Cross-Linked Polyethylene Cable Using Weibull Process of Propagation Time. Energies. 2017; 10(11):1789. https://doi.org/10.3390/en10111789
Chicago/Turabian StyleJang, Donguk, and Seonghee Park. 2017. "Evaluation of Electrical Tree Degradation in Cross-Linked Polyethylene Cable Using Weibull Process of Propagation Time" Energies 10, no. 11: 1789. https://doi.org/10.3390/en10111789
APA StyleJang, D., & Park, S. (2017). Evaluation of Electrical Tree Degradation in Cross-Linked Polyethylene Cable Using Weibull Process of Propagation Time. Energies, 10(11), 1789. https://doi.org/10.3390/en10111789





