The Thermoelectric Analysis of Different Heat Flux Conduction Materials for Power Generation Board
Abstract
:1. Introduction
2. Theory Analysis of TEG
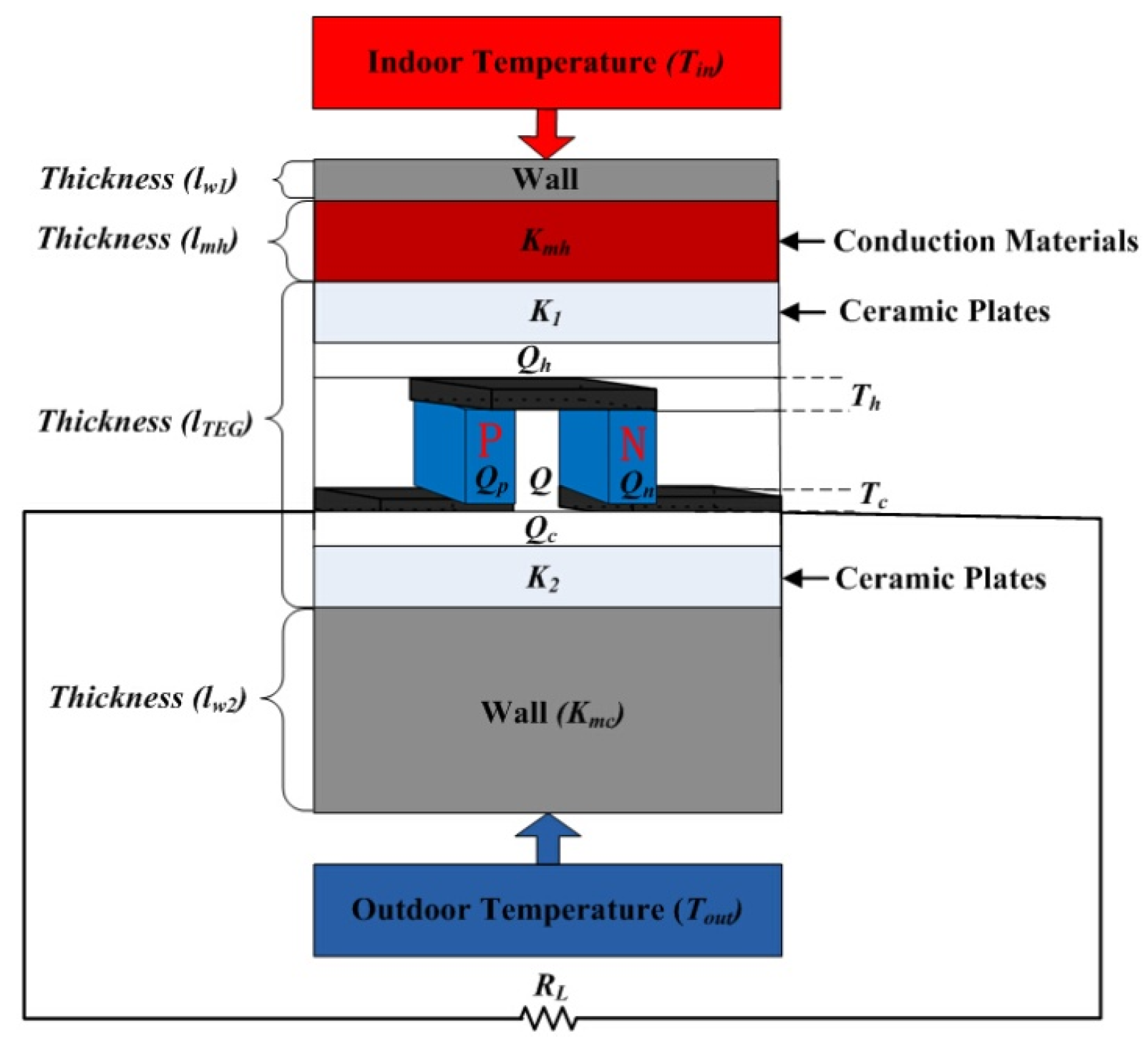
2.1. Thermal Model of TE Board
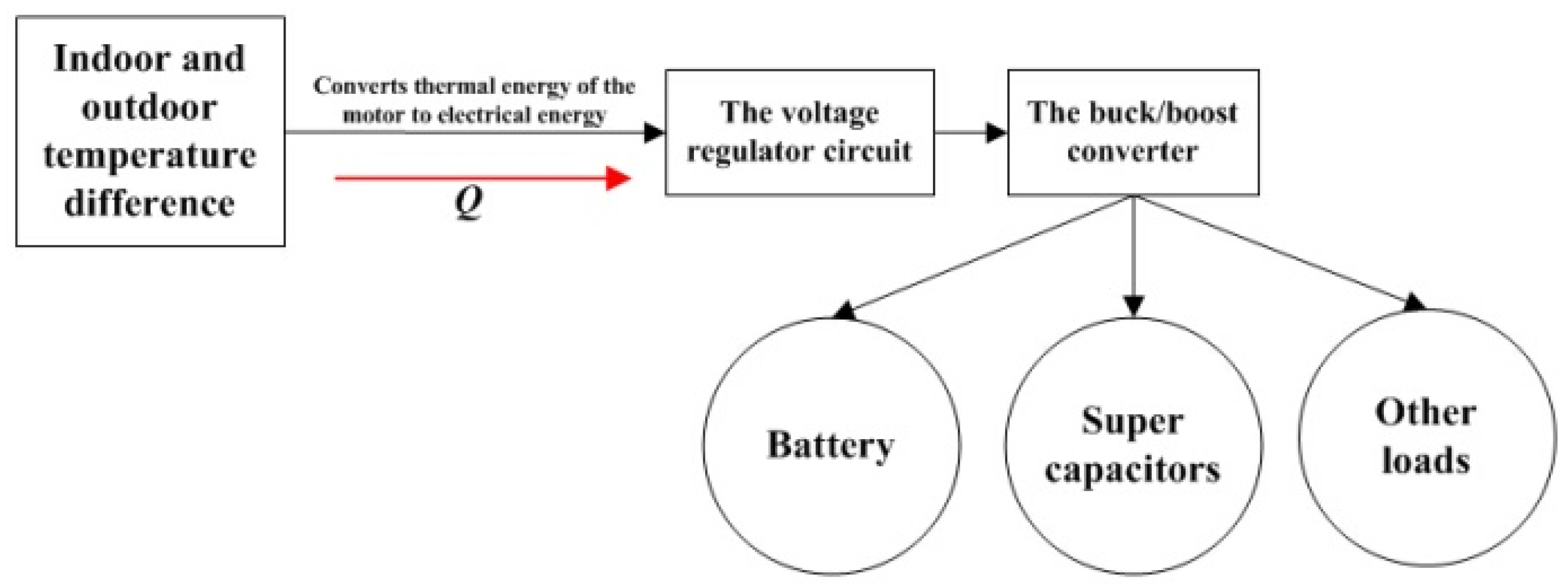
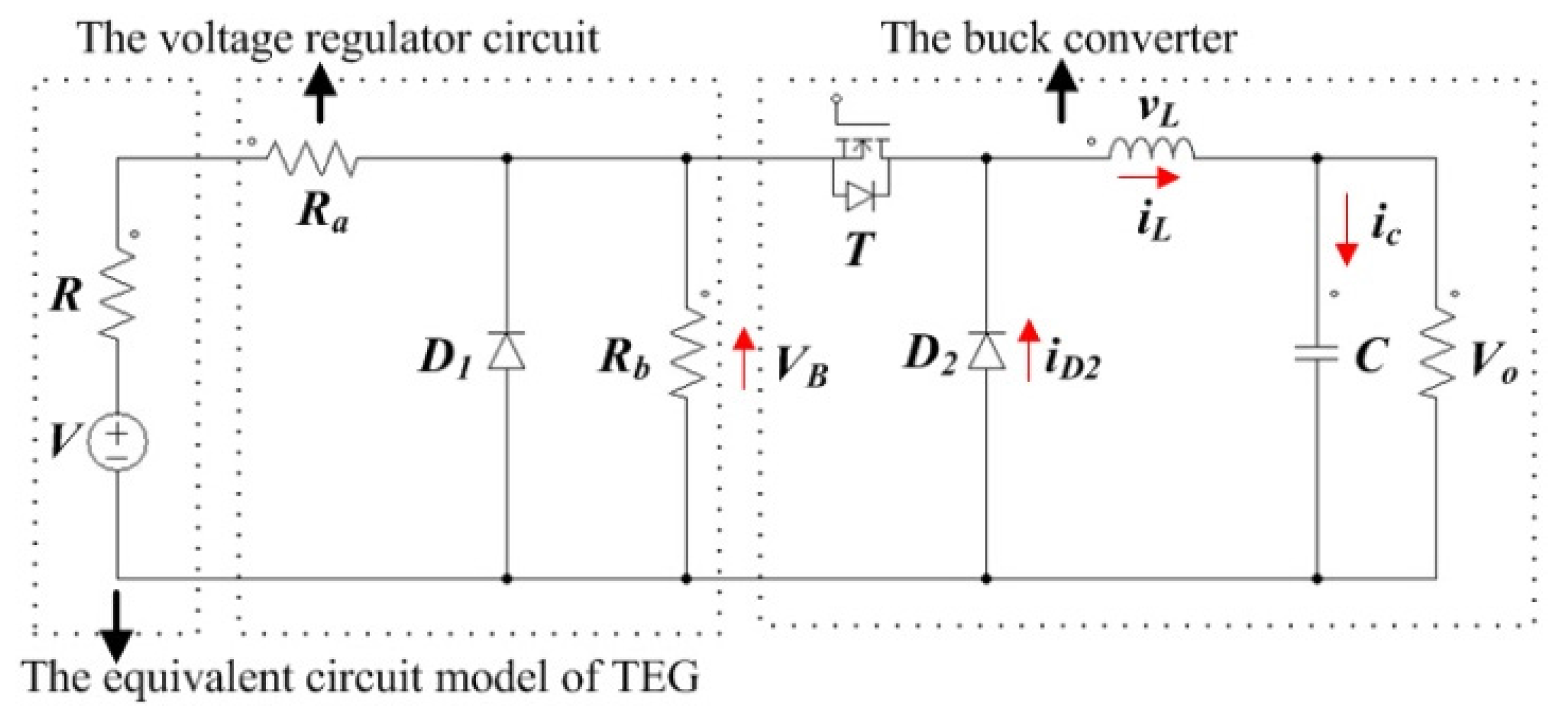
2.2. Control and Electrical Model of TE Board
3. Analysis and Comparison of Thermally Conductive Materials with TEGs
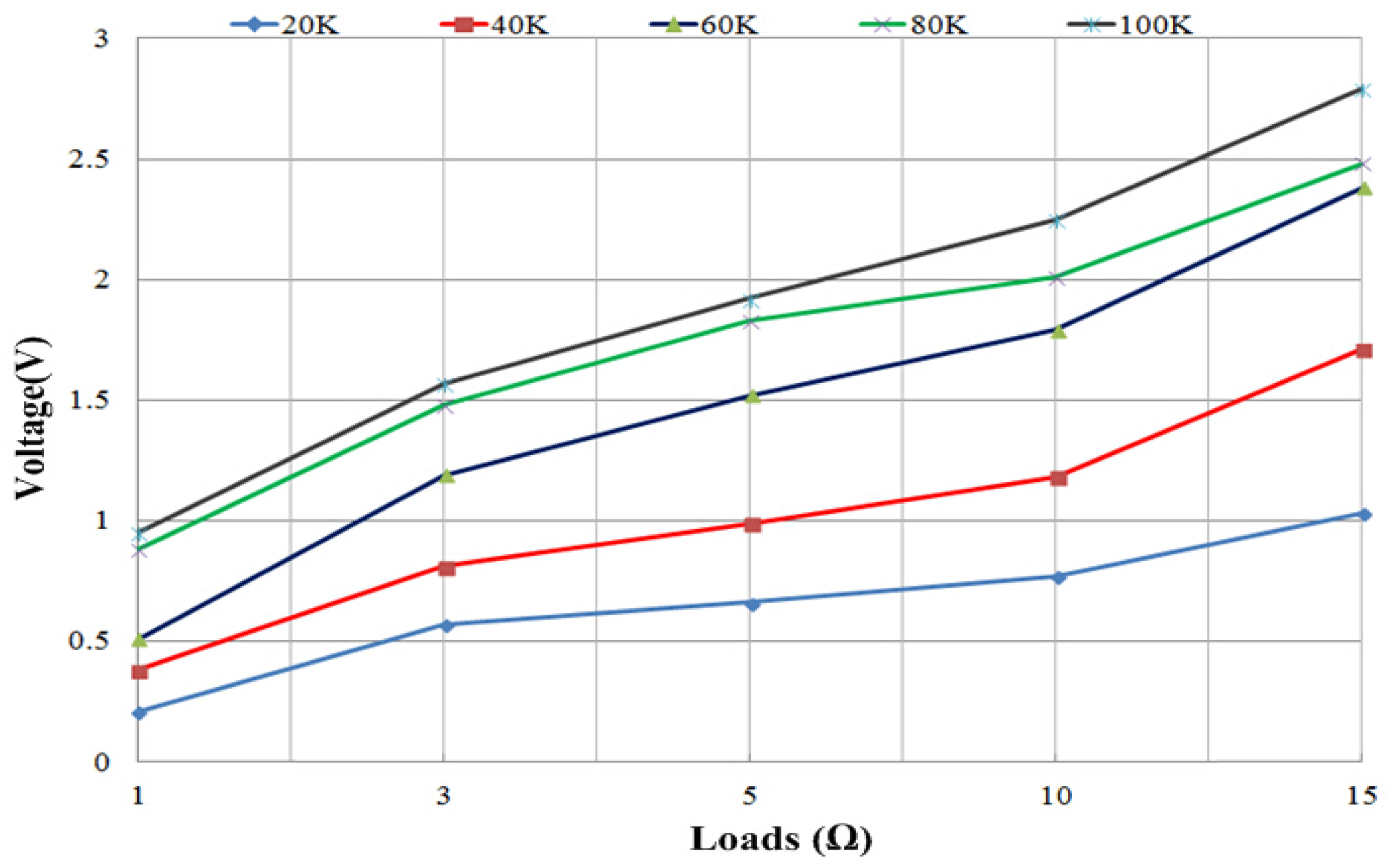
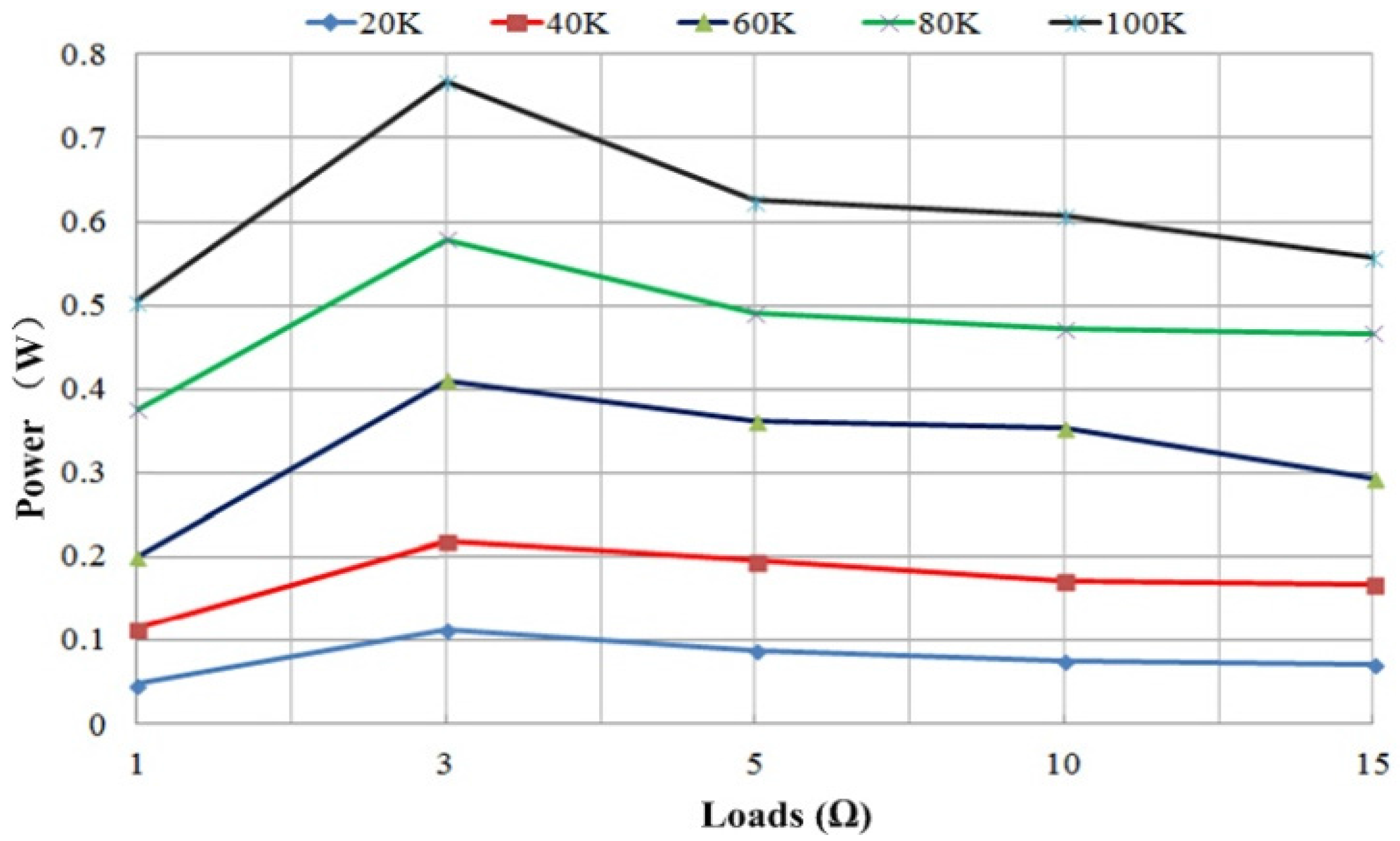
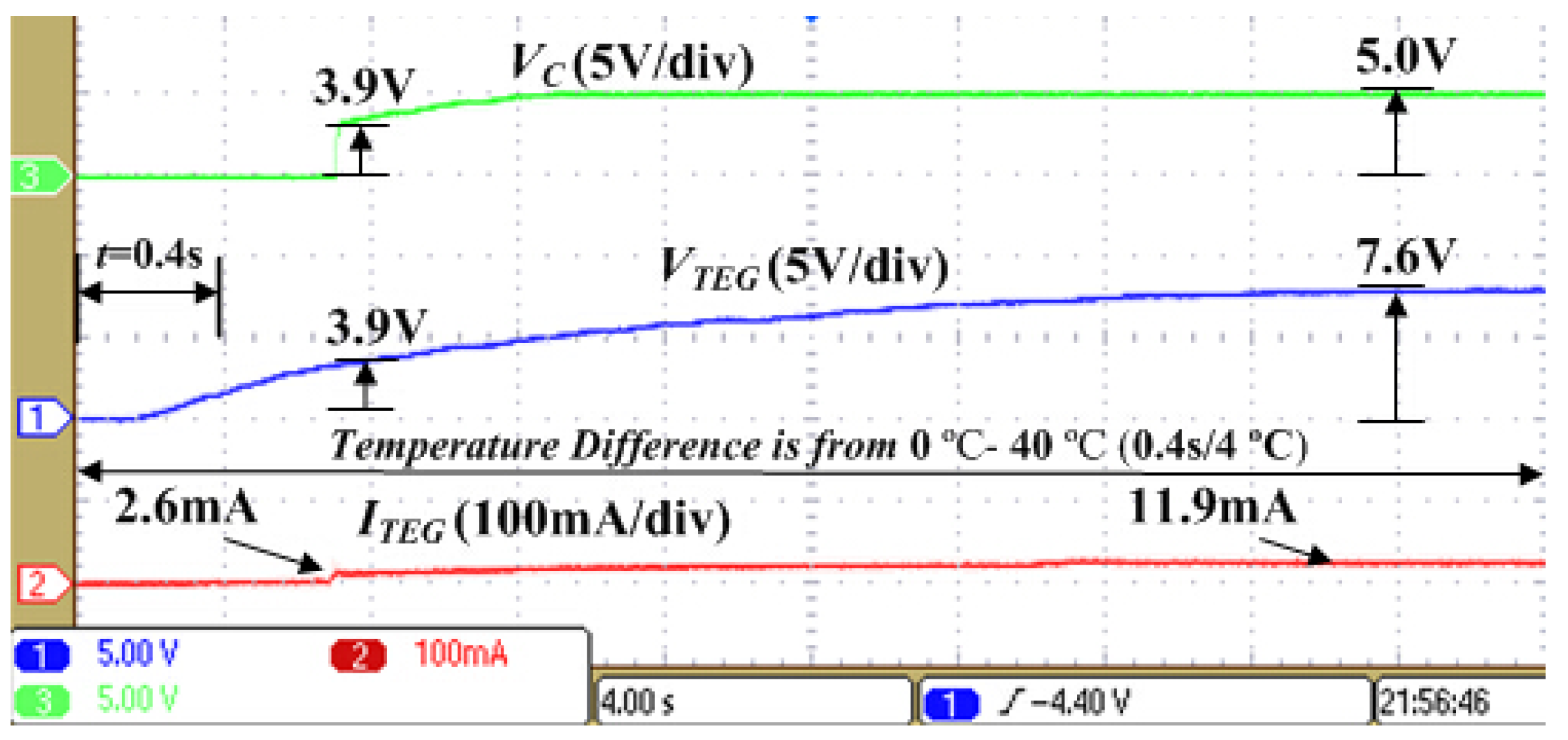
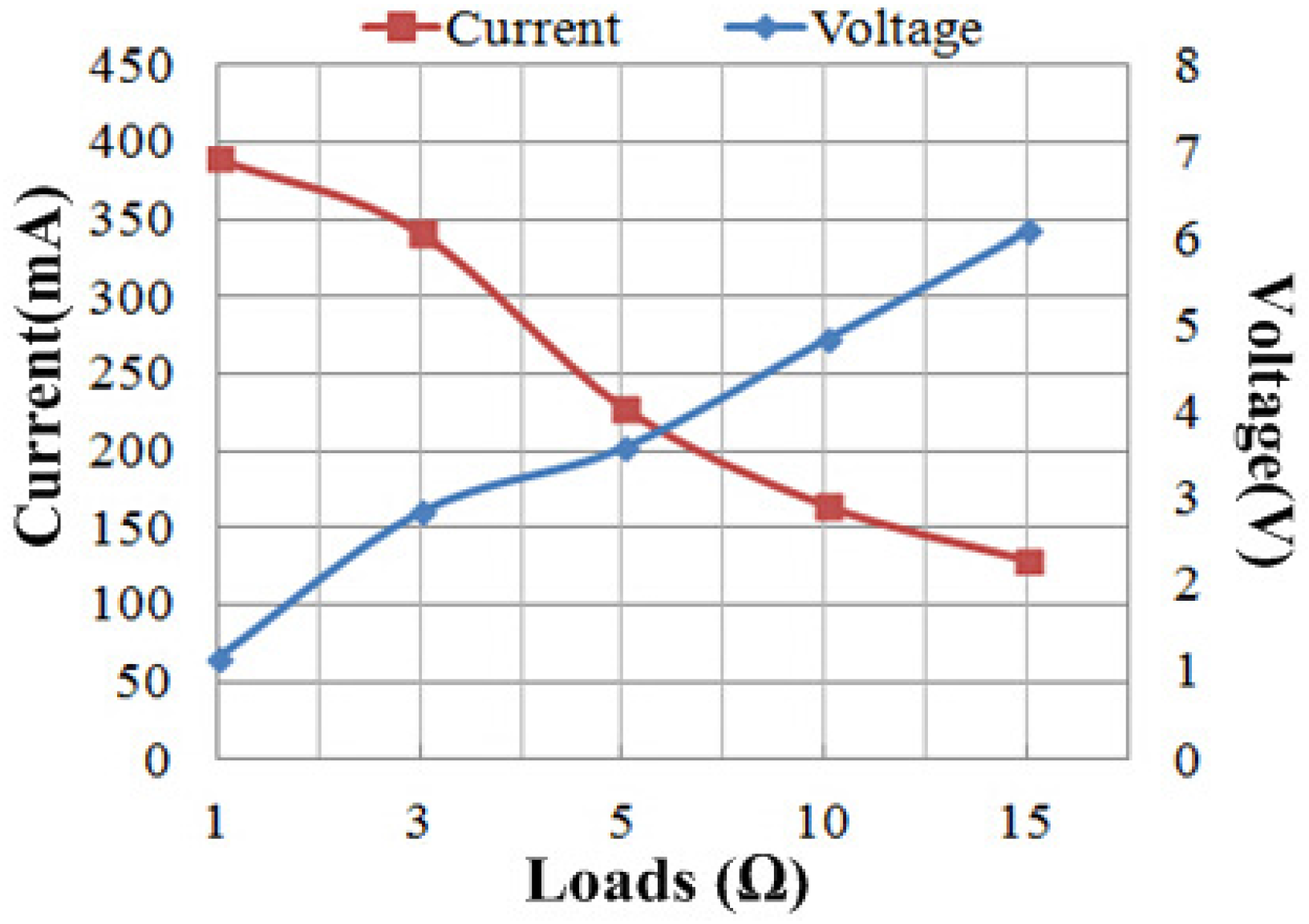
3.1. Analysis of the Characteristics of TEG
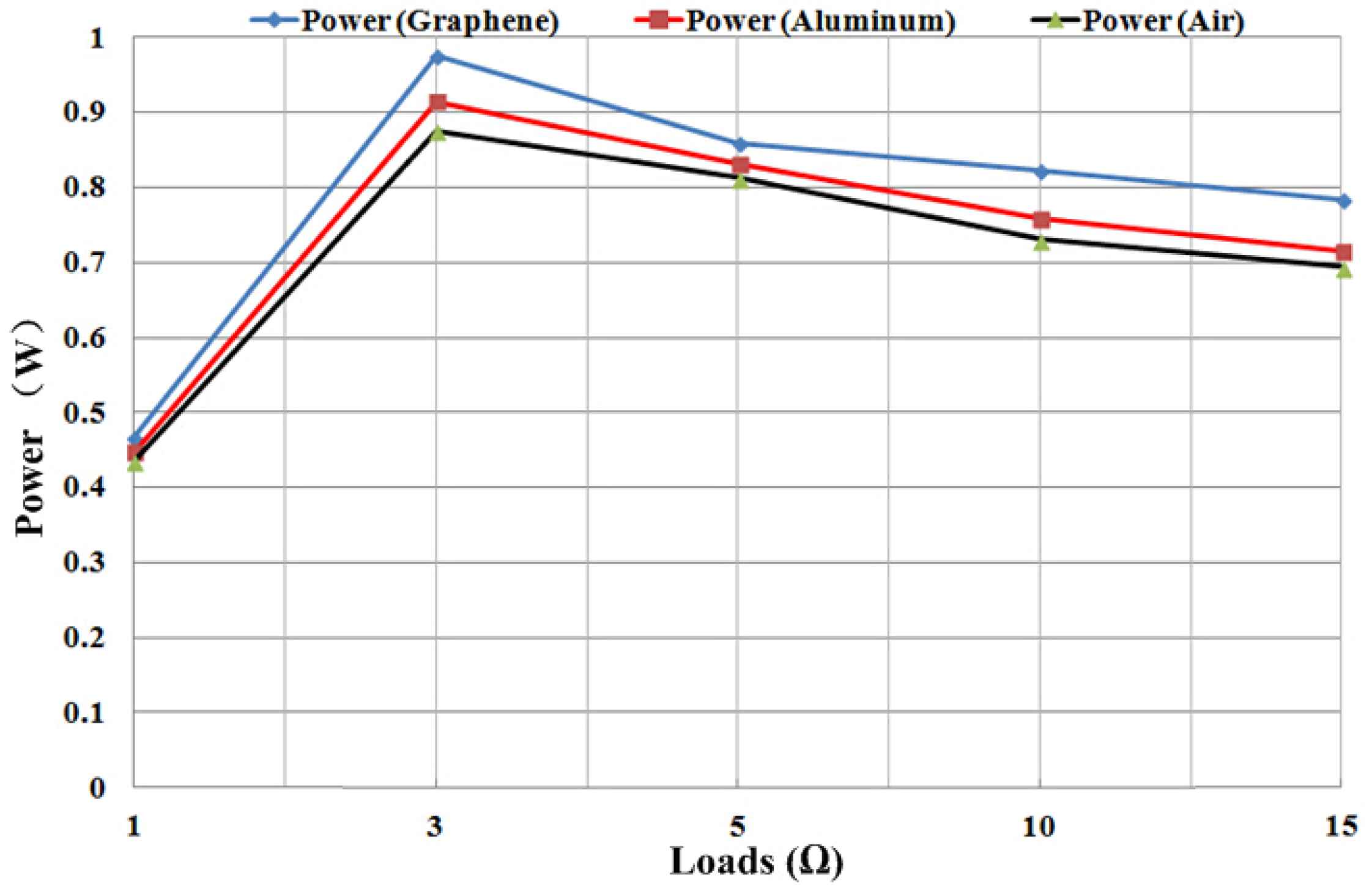
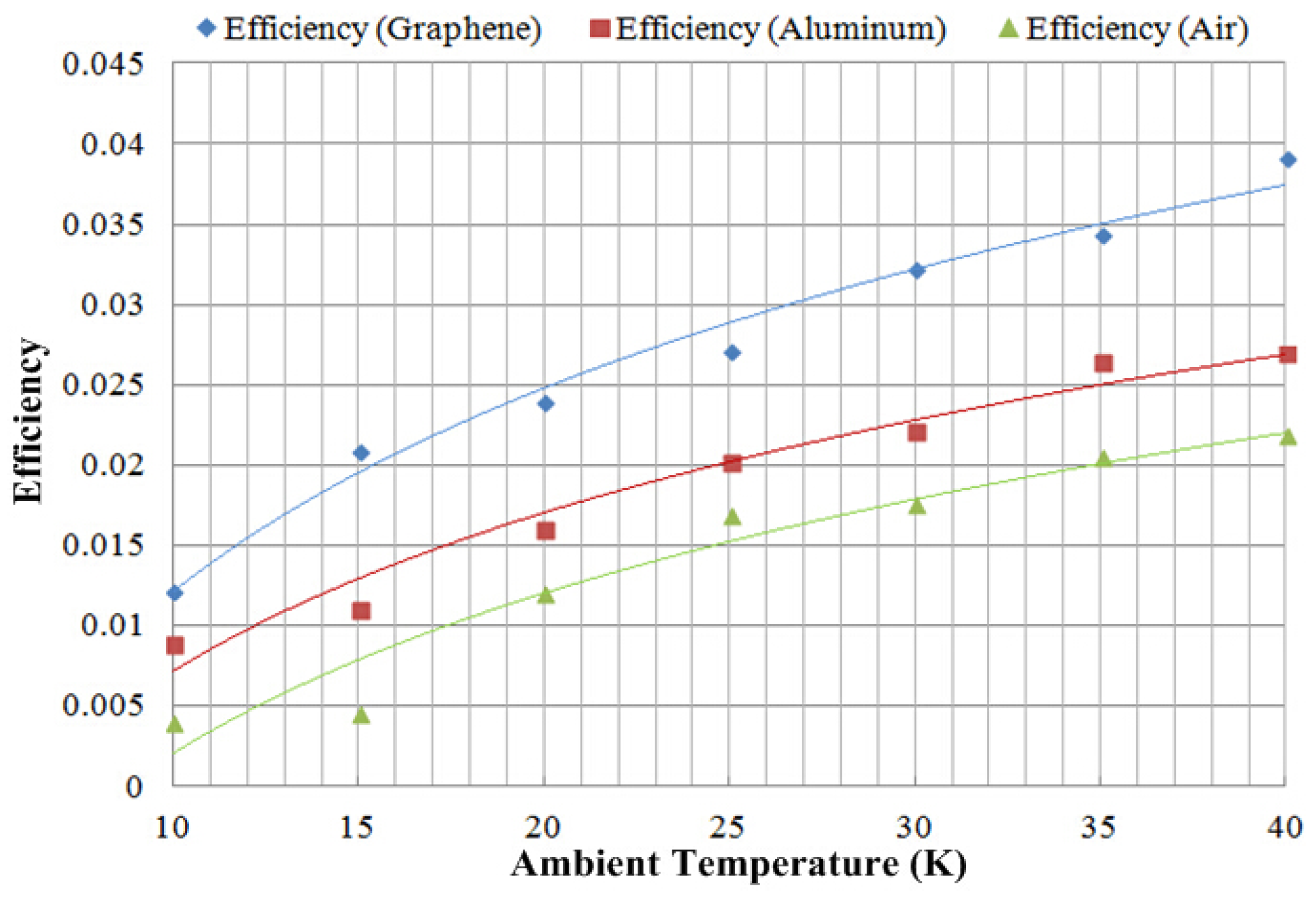
3.2. Analysis of the Characteristics of TEG with Different Thermally Conductive Materials
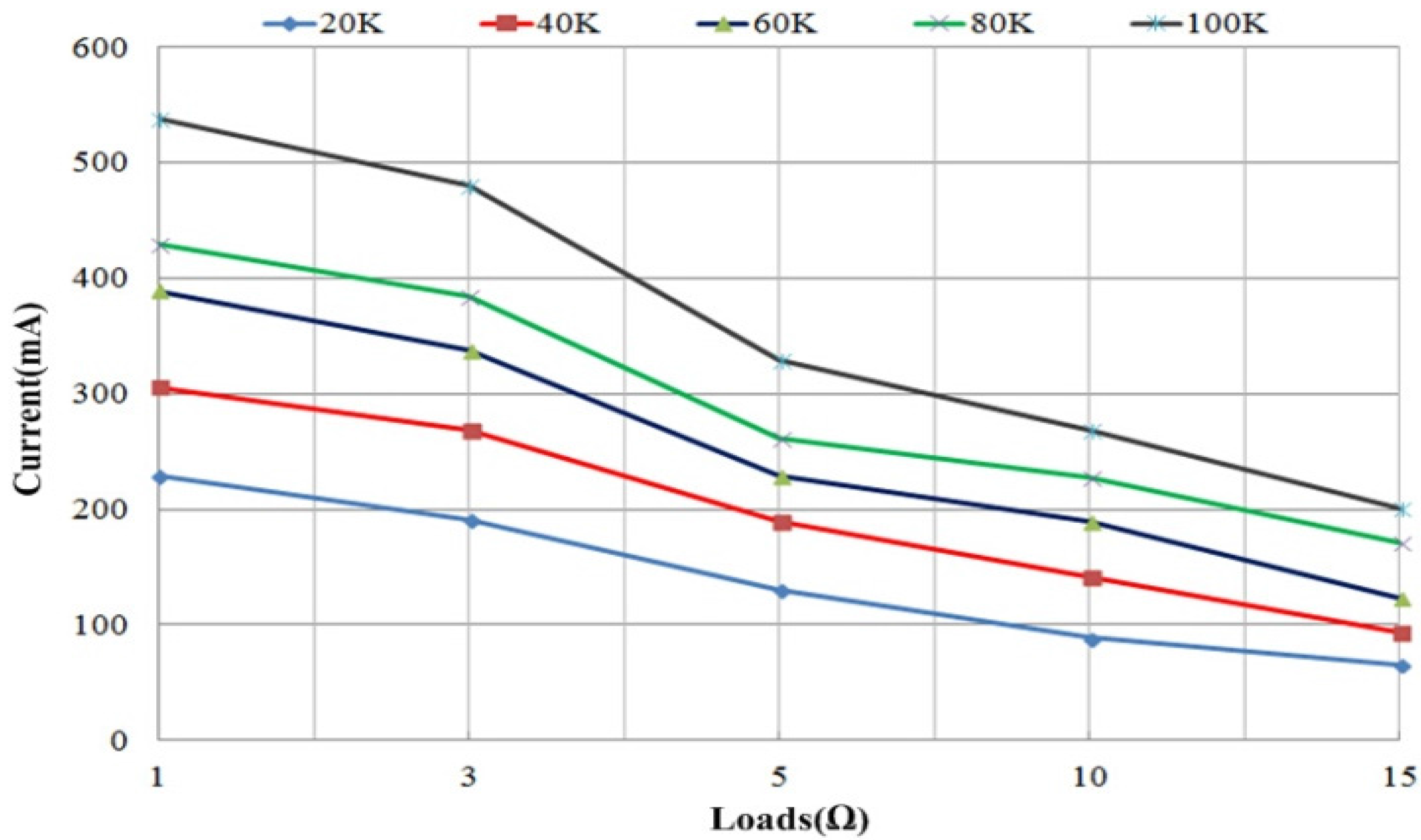
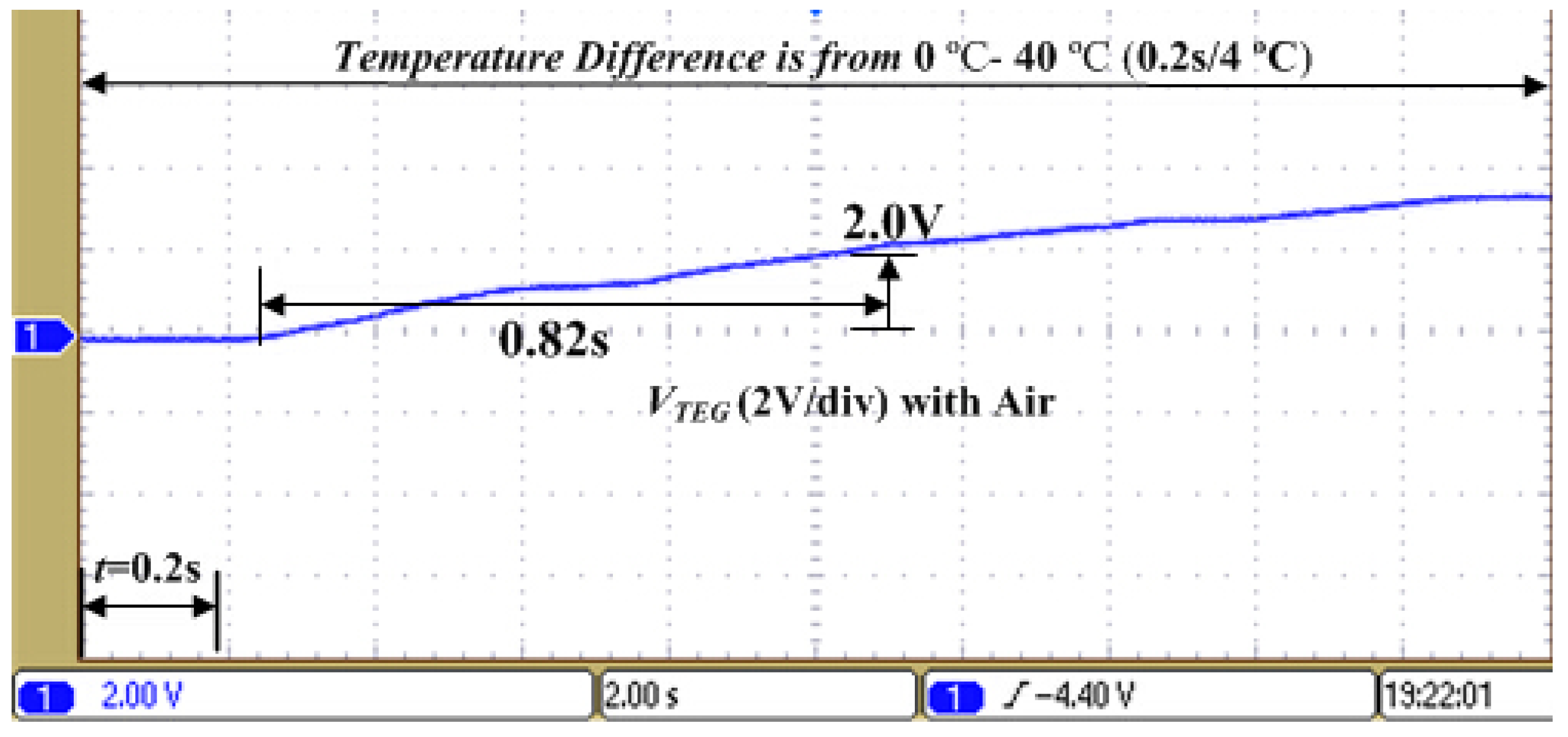
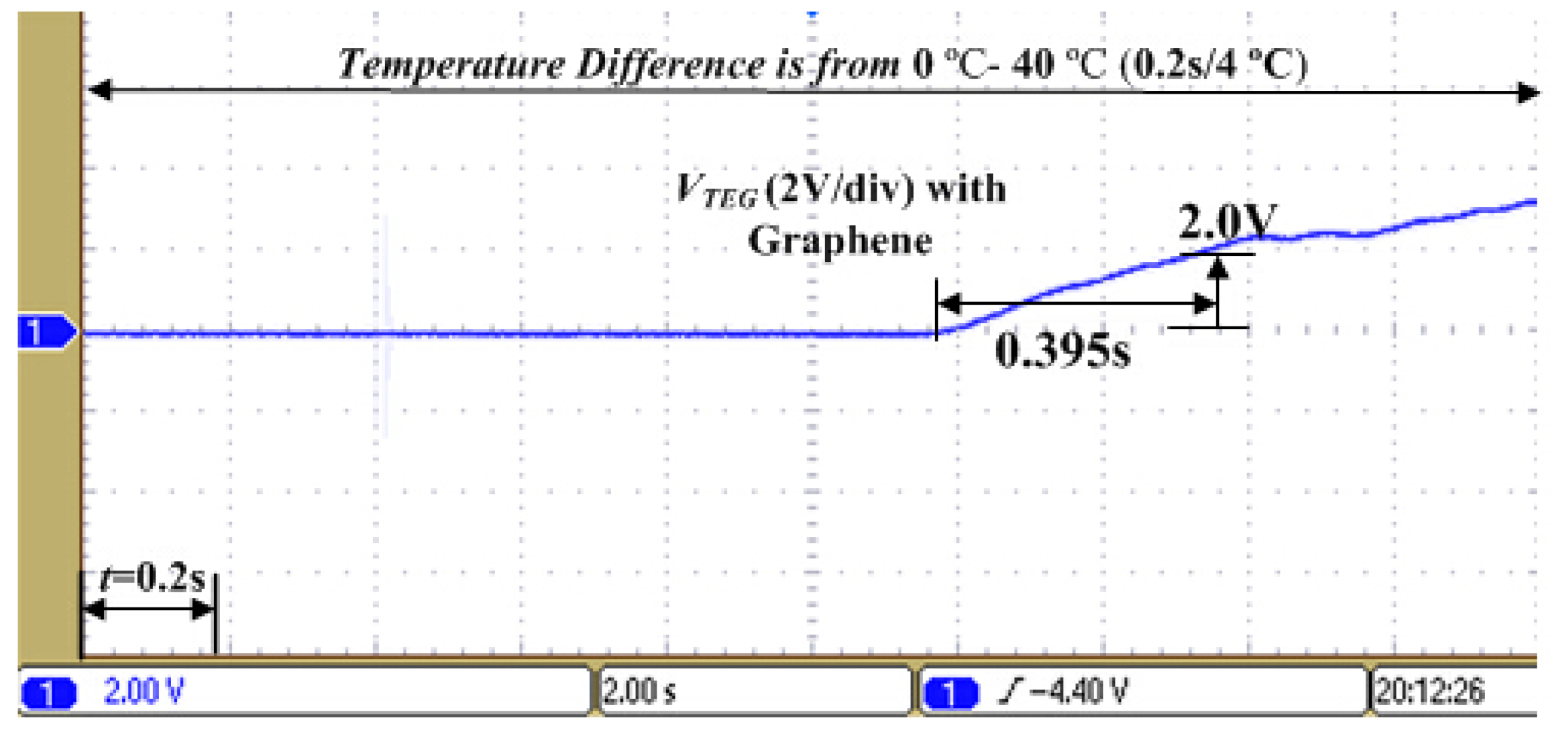
4. Experimental Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zou, Y.; Cheng, K.W.E. A Vertical Flux-Switching Permanent Magnet Based Oscillating Wave Power Generator with Energy Storage. Energies 2017, 10, 887. [Google Scholar] [CrossRef]
- Singh, M.; Singh, J.; Garg, A. Efficient autonomous solar panel and thermo-electric Generator (TEG) integrated hybrid energy harvesting system. In Proceedings of the Progress in Electromagnetic Research Symposium (PIERS), 8–11 August 2016; pp. 1764–1768. [Google Scholar]
- Harihara Krishnan, S.; Ezhilarasi, D.; Uma, G.; Umapathy, M. Pyroelectric-based solar and wind energy harvesting system. IEEE Trans. Sustain. Energy 2014, 5, 73–81. [Google Scholar] [CrossRef]
- Su, S.H.; Chen, J.C. Simulation investigation of high-efficiency solar thermoelectric generators with in homogeneously doped nonmaterial. IEEE Trans. Ind. Electron. 2015, 62, 3569–3575. [Google Scholar]
- Yang, D.J.; Yin, H.M. Energy conversion efficiency of a novel hybrid solar system for photovoltaic, thermoelectric, and heat flux utilization. IEEE Trans. Energy Convers. 2011, 26, 662–670. [Google Scholar] [CrossRef]
- Rodriguez, R.; Preindl, M.; Emadi, A.; Cotton, J. Maximum power point tracking for thermoelectric generators with high frequency injection. In Proceedings of the 41st Annual Conference of the IEEE Industrial Electronics Society (IECON 2015), Yokohama, Japan, 9–12 November 2015; pp. 4127–4132. [Google Scholar]
- Wang, Y.; He, H.M.; Wang, J.; Bai, B.D. Research of novel water cooling jacket for explosion-proof motor. In Proceedings of the 2013 International Conference on Electrical Machines and Systems (ICEMS), Busan, Korea, 26–29 October 2013; pp. 691–694. [Google Scholar]
- Moon, S.H.; Yun, J.H.; Kim, W.G.; Kim, J.P. Thermal-flow analysis and cooling performance enhancement of a totally enclosed fan-cooled motor. In Proceedings of the 2013 International Conference Electrical Machines and Systems (ICEMS), Busan, Korea, 10–12 August 2014; pp. 2028–2030. [Google Scholar]
- Deng, F. Wearable thermoelectric power generators combined with flexible supercapacitor for low-power human diagnosis devices. IEEE Trans. Ind. Electron. 2017, 64, 1477–1485. [Google Scholar] [CrossRef]
- Wakitani, S.; Deng, M.; Ichikawa, A. Operator based MPPT scheme of power generation system using thermoelectric devises. In Proceedings of the 2014 International Conference on Advanced Mechatronic Systems (ICAMechS) 2014 Int. Conf. Adv. Mechatron. Systems, Kumamoto, Japan, 10–12 August 2014; pp. 382–386. [Google Scholar]
- Siyang, L.; Lam, K.H.; Cheng, K.W.E. Development of a motor waste heat flux power generation system based on thermoelectric generators. In Proceedings of the 2016 International Symposium on Electrical Engineering (ISEE), Hong Kong, China, 14 December 2016. [Google Scholar]
- Kyono, T.; Suzuki, R.O.; Ono, K. Conversion of unused heat flux energy to electricity by means of thermoelectric generation in condenser. IEEE Trans. Energy Convers. 2013, 18, 330–334. [Google Scholar] [CrossRef]
- Masuda, C.; Deng, M. Thermoelectric generation system design with considering heat flux output dynamics and its application to motor car. In Proceedings of the 54th Annual Conference of the IEEE, Hangzhou, China, 28–30 July 2015. [Google Scholar]
- Anamaria, E.; Schaltz, E.; Rosendahl, L.; Rezaniakolaei, A.; Platzek, D. A High Temperature Experimental Characterization Procedure for Oxide-Based Thermoelectric Generator Modules under Transient Conditions. Energies 2015, 8, 12839–12847. [Google Scholar]
- Ming, T.Z.; Wang, Q.K.; Peng, K.Y.; Wei, Z.C.; Tang, Y.J.; Wu, Y.; Gong, T.R. The Influence of Non-Uniform High Heat Flux on Thermal Stress of Thermoelectric Power Generator. Energies 2015, 8, 12584–12602. [Google Scholar] [CrossRef]
- Goldsmid, H.J. Conversion Efficiency and Figure-of-Merit, CRC Handbook of Thermoelectric; Rowe, M.M., Ed.; Chemical Rubber Company: Cleveland, OH, USA, 1995; pp. 19–25. [Google Scholar]
- Krutov, V. (Ed.) Technical Thermo Dynamics; Vishaya Shkola: Moscow, Russian, 1971. (In Russian) [Google Scholar]
- Wang, Y.; Ajit, K.; Vallabhaneni, B.Q.; Ruan, X.L. Two-dimensional thermal transport in graphene: A review of numerical modeling studies. Nanosci Microsc. Thermophys. Eng. 2014, 18, 155–182. [Google Scholar] [CrossRef]
- Qiu, B.; Wang, Y.; Zhao, Q.; Ruan, X.L. The effects of diameter and chirality on the thermal transport in free-standing and supported carbon-nanotubes. Appl. Phys. Lett. 2012, 23, 633–638. [Google Scholar]
- Chen, M.; Rosendahl, L.A.; Condra, T.C.; Pedersen, J.K. Numerical modelling of thermoelectric generators with varing material properties in a circuit simulator. IEEE Trans. Energy Convers. 2009, 24, 112–124. [Google Scholar]
- Lineykin, S.; Ben-Yaakov, S. Modelling and analysis of thermoelectric modules. IEEE Trans. Ind. Appl. 2015, 43, 505–512. [Google Scholar] [CrossRef]
- Ye, Y.-M.; Eric Cheng, K.W. Quadratic boost converter with low buffer capacitor stress. IET Power Electron. 2014, 7, 1162–1170. [Google Scholar] [CrossRef]
- Law, K.K.; Eric Cheng, K.K. Examination of the frequency modulation and lifting techniques for the generalized power factor correction switched-capacitor resonant converter. Int. J. Circuit Theor. Appl. 2007, 36, 839–855. [Google Scholar] [CrossRef]
- Li, S.; Cheng, K.W.E.; Ye, Y.M.; Shi, Z.G. Wide input and wide output topology analysis for tapped-inductor converters with consideration of parasitic elements. IET. Power Electron. 2016, 9, 1952–1961. [Google Scholar] [CrossRef]
- Siouane, S.; Jovanovic, S.; Poure, P. Equivalent Electrical Circuit of Thermoelectric Generators under Different Operating Conditions. Energies 2017, 10, 386. [Google Scholar] [CrossRef]
- Cheng, K.W.E. Storage energy for classical switched mode power converters. IEE Proc.-Electr. Power Appl. 2003, 150, 439–446. [Google Scholar] [CrossRef]





© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Lam, K.H.; Cheng, K.W.E. The Thermoelectric Analysis of Different Heat Flux Conduction Materials for Power Generation Board. Energies 2017, 10, 1781. https://doi.org/10.3390/en10111781
Li S, Lam KH, Cheng KWE. The Thermoelectric Analysis of Different Heat Flux Conduction Materials for Power Generation Board. Energies. 2017; 10(11):1781. https://doi.org/10.3390/en10111781
Chicago/Turabian StyleLi, Siyang, Kwok Ho Lam, and Ka Wai Eric Cheng. 2017. "The Thermoelectric Analysis of Different Heat Flux Conduction Materials for Power Generation Board" Energies 10, no. 11: 1781. https://doi.org/10.3390/en10111781
APA StyleLi, S., Lam, K. H., & Cheng, K. W. E. (2017). The Thermoelectric Analysis of Different Heat Flux Conduction Materials for Power Generation Board. Energies, 10(11), 1781. https://doi.org/10.3390/en10111781






