A Game Theory Approach to Multi-Agent Decentralized Energy Management of Autonomous Polygeneration Microgrids
Abstract
1. Introduction
2. Materials and Methods
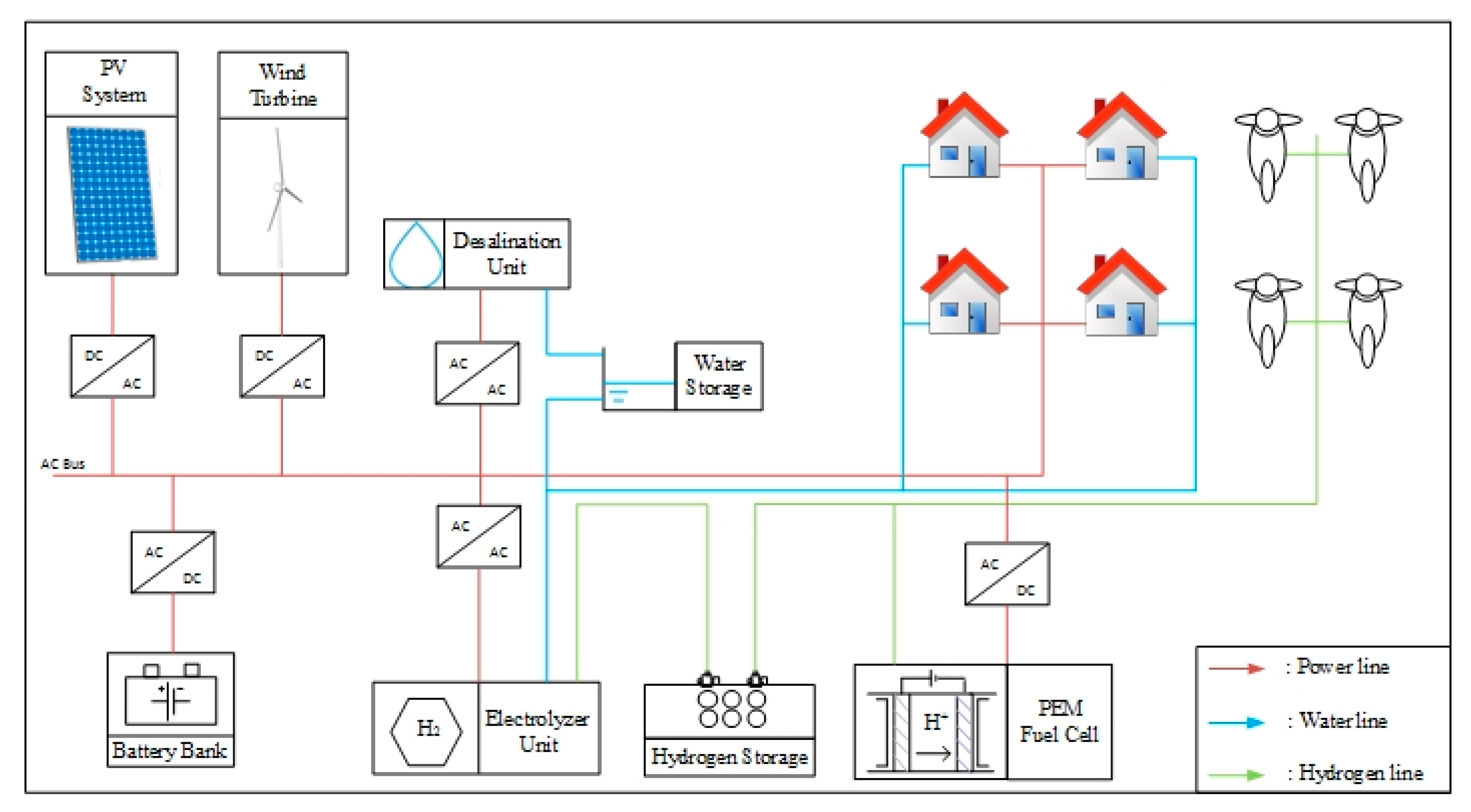
2.1. Microgrid Configuration
- Distributed energy sources: A typical monocrystalline silicon photovoltaic array installed on a vertical tracker, a horizontal axis wind turbine and a typical Proton Exchange Membrane (PEM) fuel cell were considered.
- Storage devices: A deep discharge solar lead acid 48 VDC battery bank, a water tank and a metal hydride tank were considered.
- Energy consumptions units: Household electrical consumptions (e.g., lighting, refrigeration, cooking appliances etc.), a reverse osmosis desalination unit and hybrid fuel cell-battery scooters were considered.
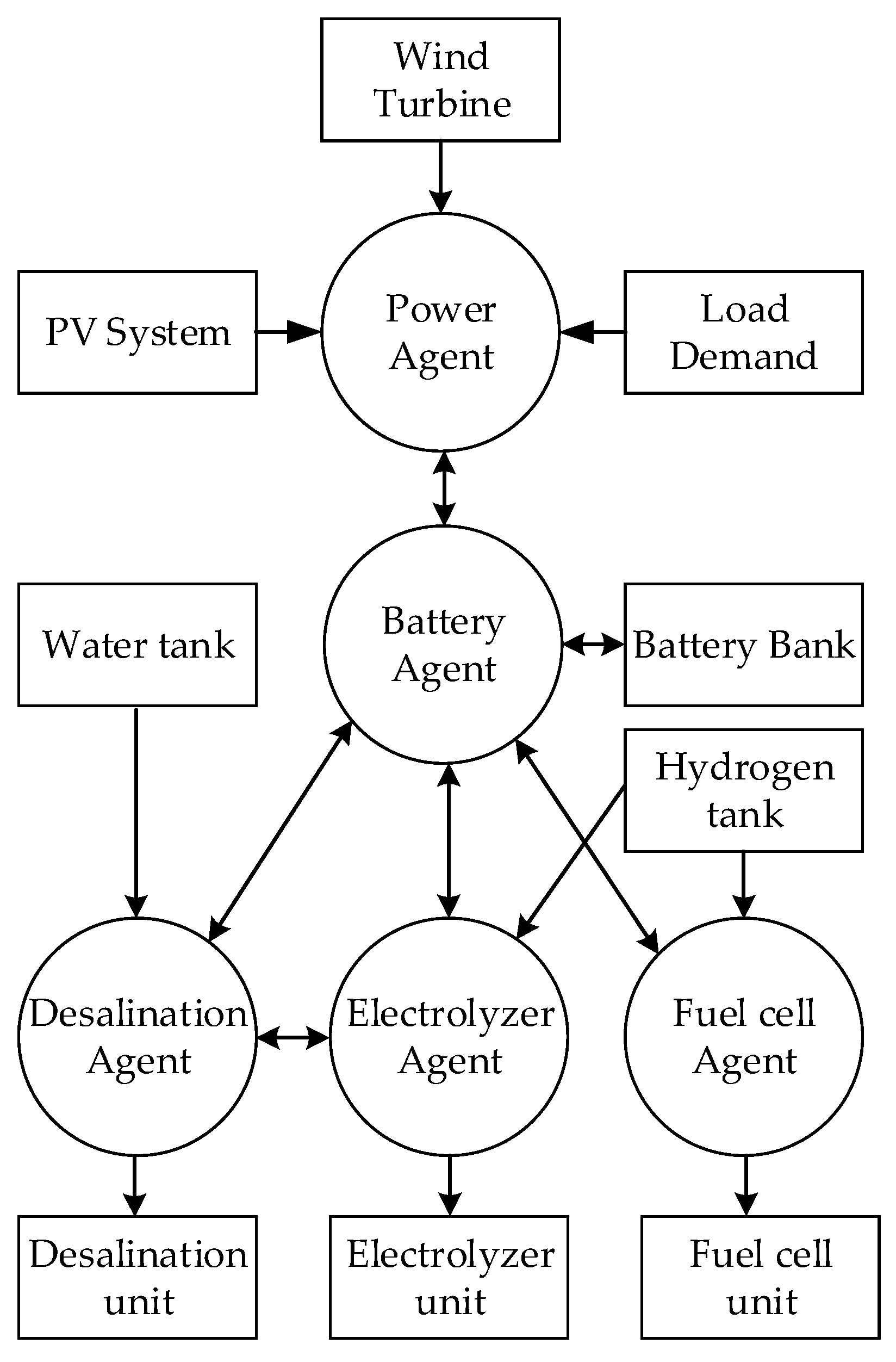
2.2. Intelligent Agents
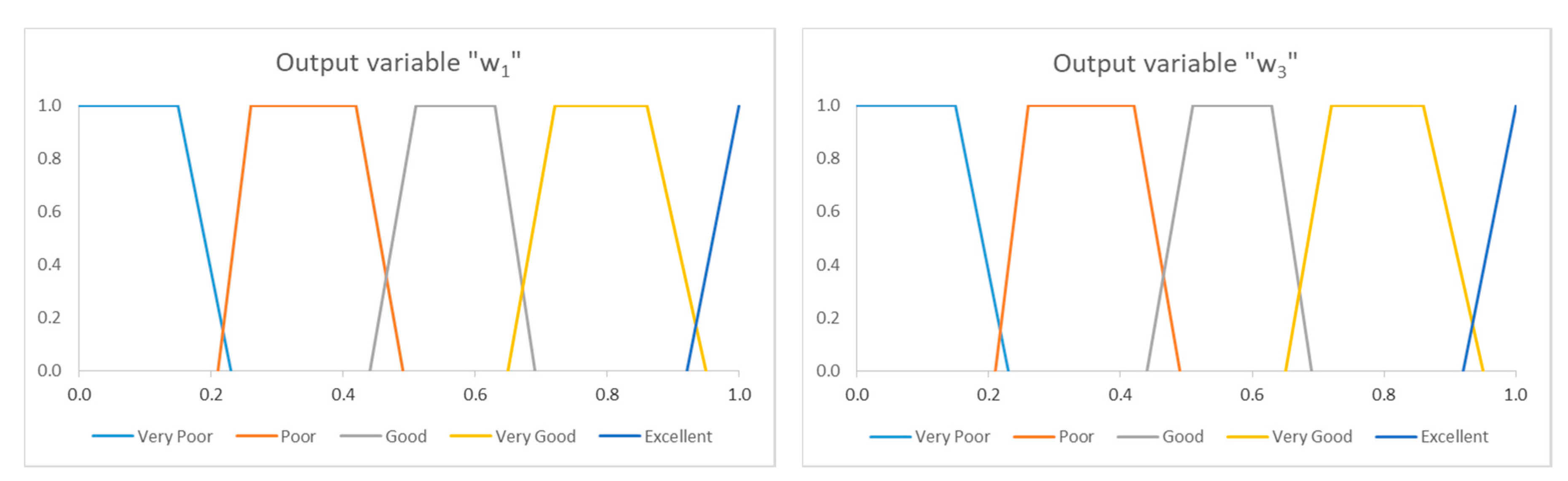
2.3. Game Theory Analysis
- N is the set of players
- Ai is the set of actions of player i where
- is the utility function of player i which can be a profit (maximize) or a cost (minimize)
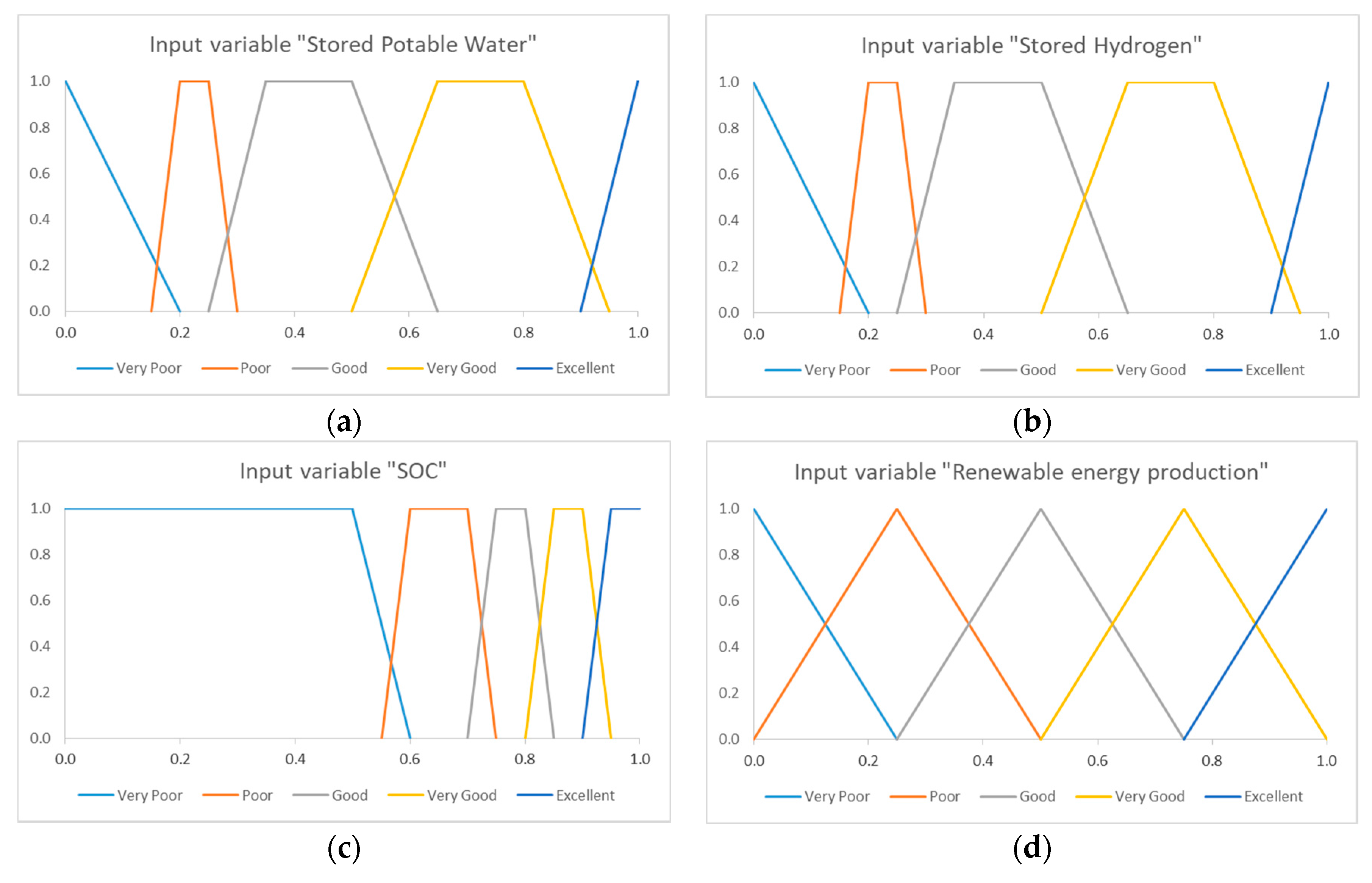
2.4. Optimization Method
2.5. Modeling, Simulation and Optimization Platform
3. MAS-DEMS of the Microgrid
3.1. Overview
3.2. Intelligent Agents Overview
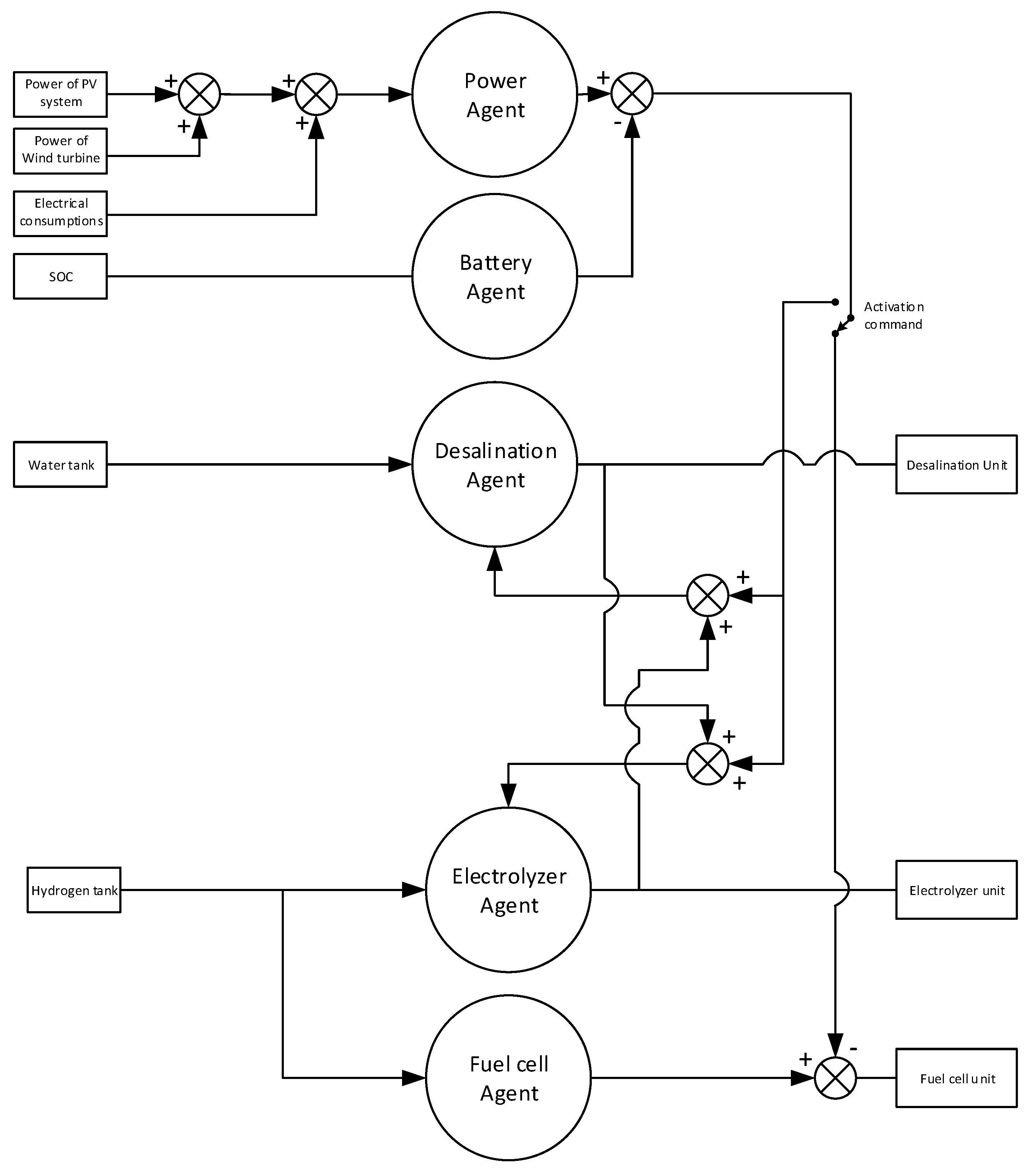
3.2.1. Power Agent
3.2.2. Battery Agent
3.2.3. Desalination Agent
3.2.4. Electrolyzer Agent
3.2.5. Fuel Cell Agent
3.3. Game Theory for MAS
3.3.1. Energy Control Games
First Game Model
Second Game Model
4. Optimization Parameters
- All household electrical consumptions must be covered at 100% throughout the year.
- The potable water tank must never get empty.
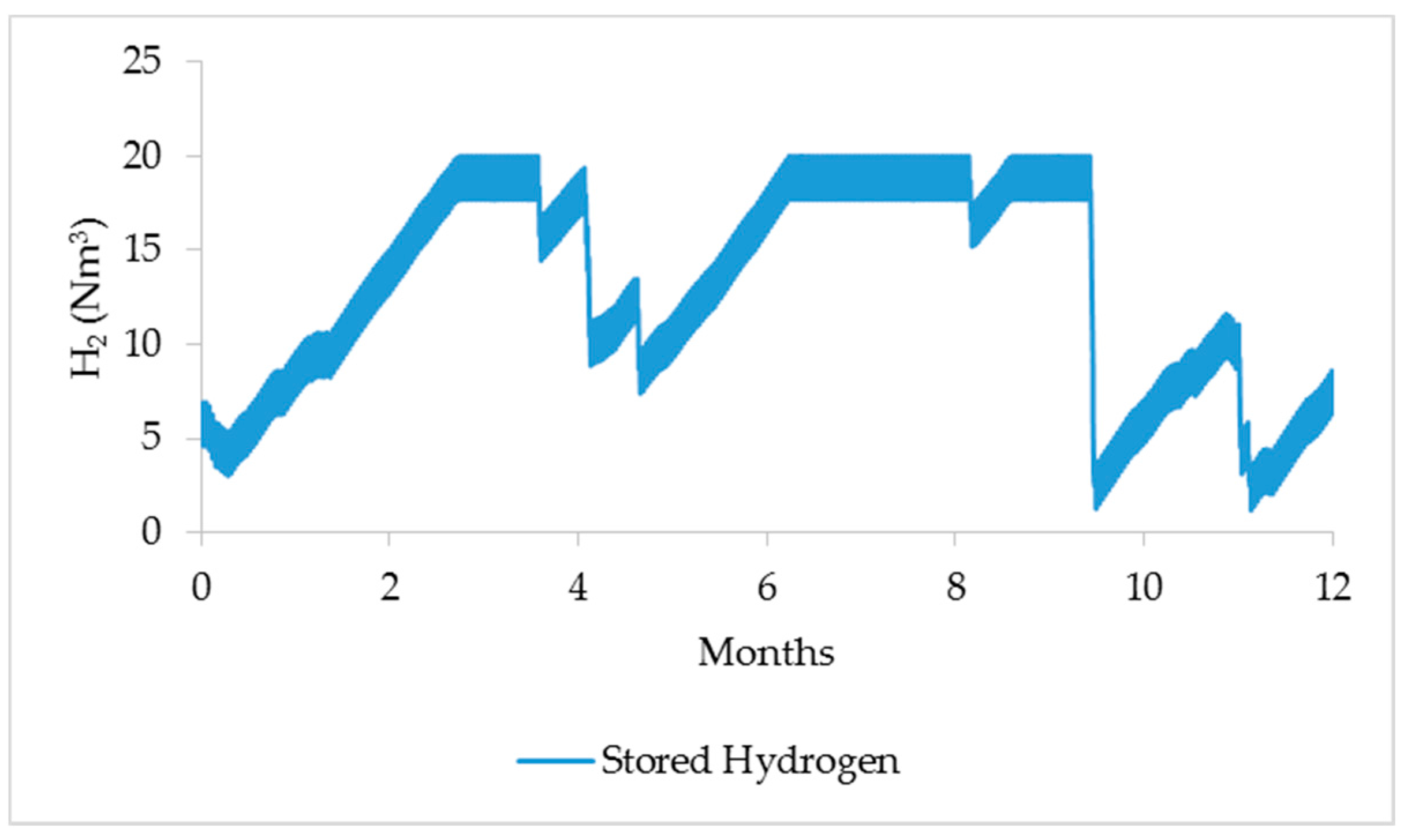
- The hydrogen tank must never get empty.
- The stored potable water and hydrogen at the end of the year ought to be equal or higher than the stored water and hydrogen at the beginning of the year.
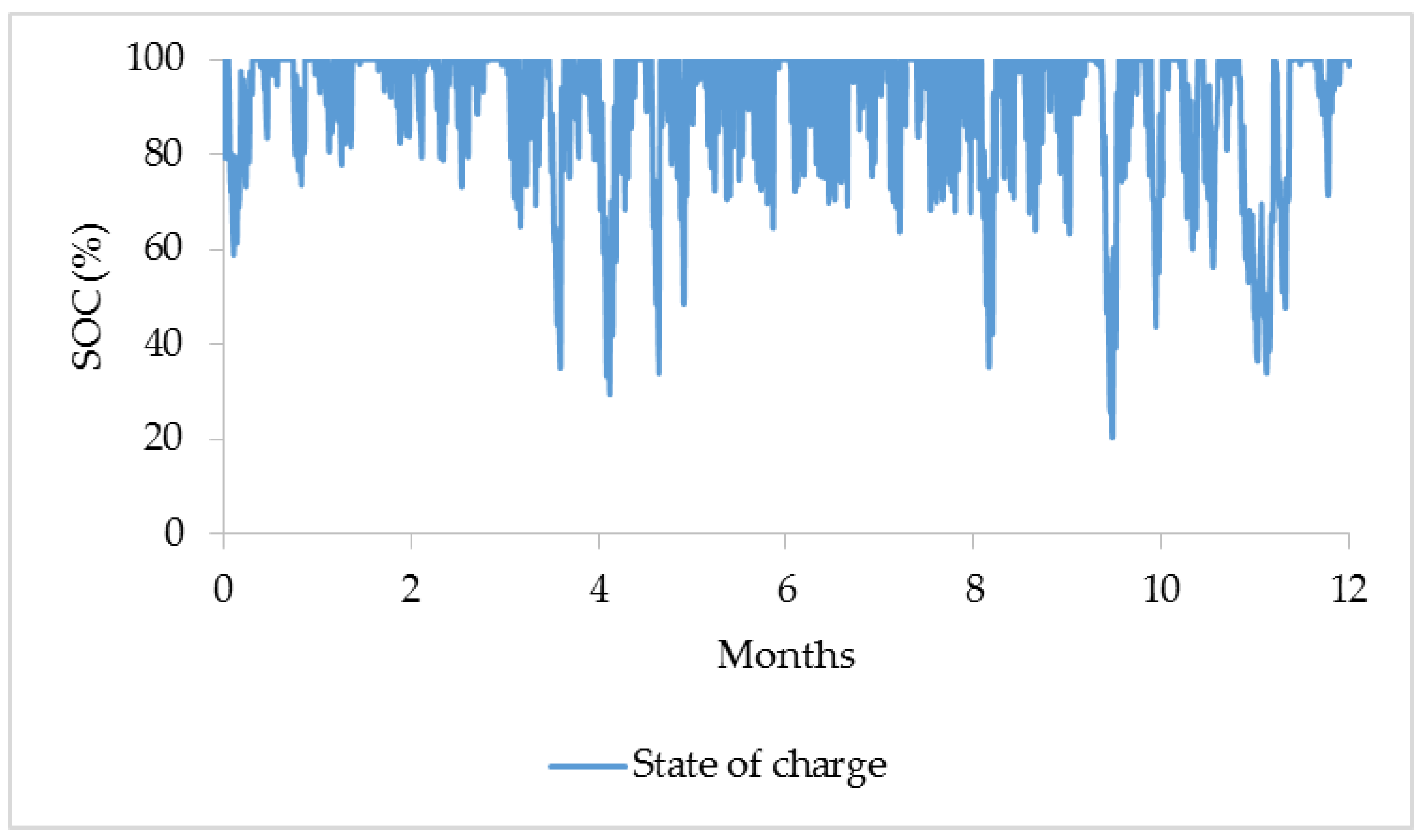
- The battery bank ought not to be deep discharged. The SOC of the battery bank should not drop under 20% at any time.
5. Simulation and Results
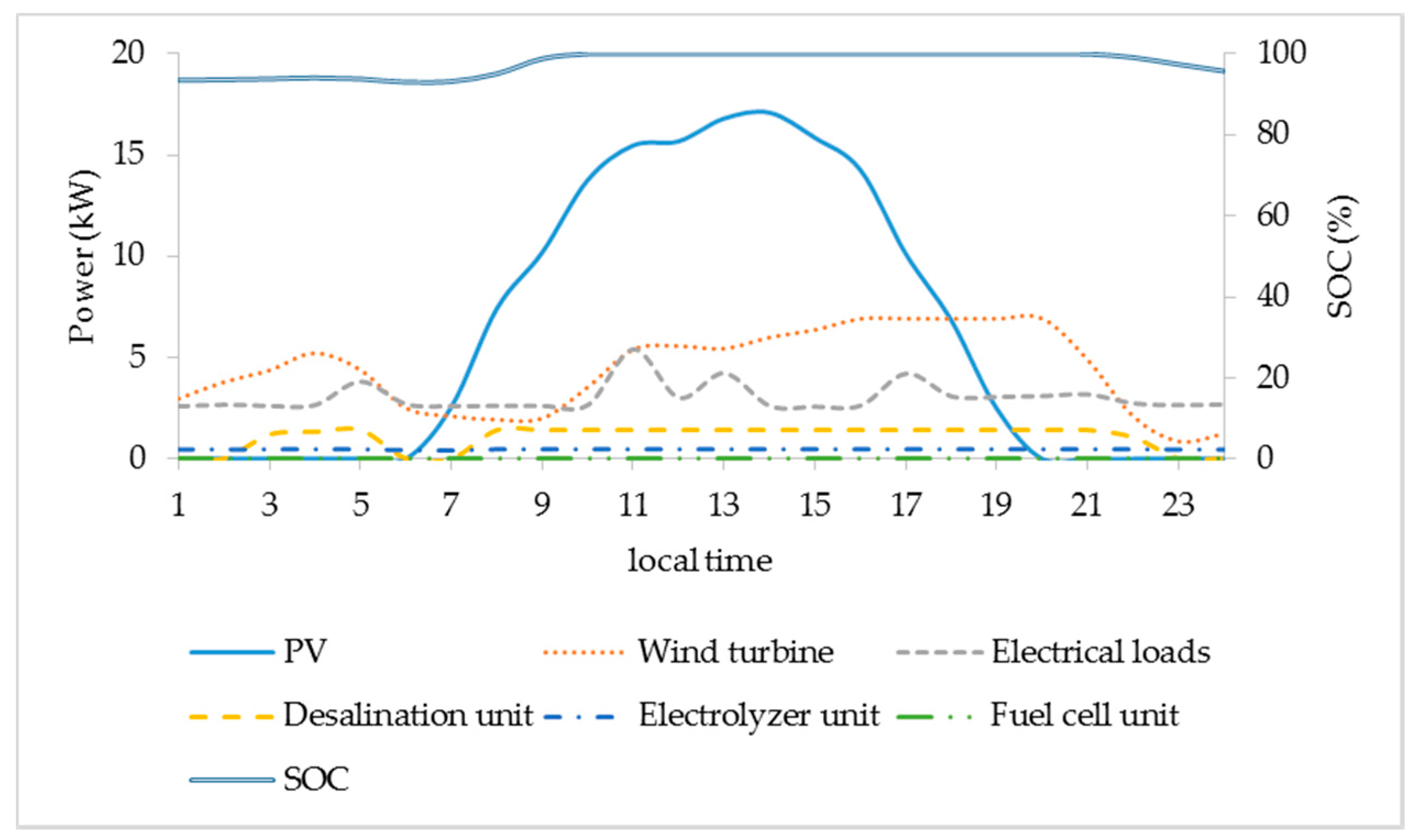
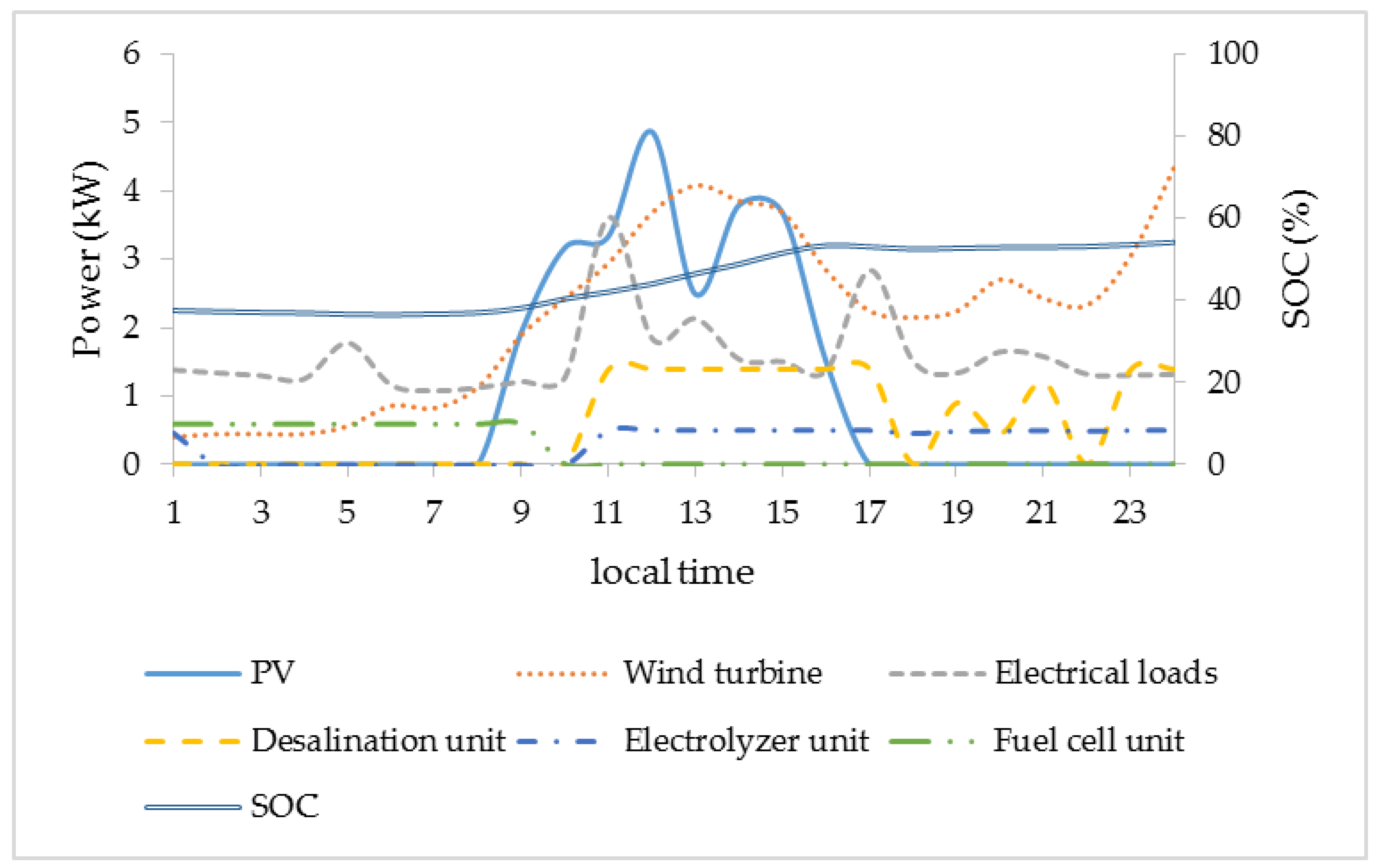
5.1. Simulation Results
5.2. Microgrid Performance Evaluation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| CF | Cost function |
| DOD | Depth of discharge |
| Pb | Battery penalty |
| EBAT | Operating energy capacity |
| EBAT,max | Nominal energy capacity of the battery bank |
| PDES | The operation power of the desalination unit |
| PDES,nom | The nominal power of the desalination unit |
| PELE | The operation power of the electrolyzer unit |
| PELE,nom | The nominal power of the electrolyzer unit |
| PFUEL | The operation power of the fuel cell unit |
| PH2 | Hydrogen penalty |
| PH2T | Metal hydride tank penalty |
| Pload | Power consumption |
| Ploss | Power losses |
| Ppv | Power generation by the photovoltaic array |
| Pprod | Total energy production |
| Pcons | Total energy consumption |
| Pw | Water penalty |
| Pwind | Power generation of the wind turbine |
| Pwt | Water tank penalty |
| SOC | State of charge |
| StoredH2 | The hydrogen stored in the metal hydride tank |
| ΔE | Surplus energy |
Abbreviations
| APM | Autonomous polygeneration microgrid |
| CEMS | Centralized energy management system |
| DEMS | Decentralized energy management system |
| EMS | Energy management system |
| FCM | Fuzzy cognitive maps |
| ΙΑ | Intelligent agent |
| MAS | Multi agent system |
| NPC | Net present cost |
| PAGE | Percepts, actions, goals and environment |
| PSO | Particle swarm optimization |
| RES | Renewable energy sources |
References
- Chen, C.; Wang, J.; Qiu, F.; Zhao, D. Resilient distribution system by microgrids formation after natural disasters. IEEE Trans. Smart Grid 2016, 7, 958–966. [Google Scholar] [CrossRef]
- Karavas, C.-S.; Papadakis, G. Renewable energy driven small-scale sea water reverse osmosis desalination systems: A survey. J. Fundam. Renew. Energy Appl. 2017, 7, e115. [Google Scholar] [CrossRef]
- Dimitriou, E.; Mohamed, E.S.; Karavas, C.; Papadakis, G. Experimental comparison of the performance of two reverse osmosis desalination units equipped with different energy recovery devices. Desalinat. Water Treat. 2014, 55, 1–8. [Google Scholar] [CrossRef]
- Kosmadakis, G.; Landelle, A.; Lazova, M.; Manolakos, D.; Kaya, A.; Huisseune, H.; Karavas, C.-S.; Tauveron, N.; Revellin, R.; Haberschill, P.; et al. Experimental testing of a low-temperature organic Rankine cycle (ORC) engine coupled with concentrating PV/thermal collectors: Laboratory and field tests. Energy 2016, 117, 222–236. [Google Scholar] [CrossRef]
- Franzitta, V.; Curto, D.; Rao, D.; Viola, A. Hydrogen production from sea wave for alternative energy vehicles for public transport in Trapani (Italy). Energies 2016, 9, 850. [Google Scholar] [CrossRef]
- Kyriakarakos, G.; Dounis, A.I.; Rozakis, S.; Arvanitis, K.G.; Papadakis, G. Polygeneration microgrids: A viable solution in remote areas for supplying power, potable water and hydrogen as transportation fuel. Appl. Energy 2011, 88, 4517–4526. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, R.; Hatziargyriou, N.; Dimeas, A. Microgrids management. IEEE Power Energy Mag. 2008, 6, 78–94. [Google Scholar] [CrossRef]
- Jiang, Q.; Xue, M.; Geng, G. Energy management of microgrid in grid-connected and stand-alone modes. IEEE Trans. Power Syst. 2013, 28, 3380–3389. [Google Scholar] [CrossRef]
- Lidula, N.W.A.; Rajapakse, A.D. Microgrids research: A review of experimental microgrids and test systems. Renew. Sustain. Energy Rev. 2011, 15, 186–202. [Google Scholar] [CrossRef]
- Meng, L.; Sanseverino, E.R.; Luna, A.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Microgrid supervisory controllers and energy management systems: A literature review. Renew. Sustain. Energy Rev. 2016, 60, 1263–1273. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Dimeas, A.; Tsikalakis, A. Centralized and decentralized control of microgrids. Int. J. Distrib. Energy Resour. 2005, 1, 197–212. [Google Scholar]
- Conti, S.; Nicolosi, R.; Rizzo, S.; Zeineldin, H. Optimal dispatching of distributed generators and storage systems for MV islanded microgrids. IEEE Trans. Power Deliv. 2012, 27, 1243–1251. [Google Scholar] [CrossRef]
- Etemadi, A.H.; Davison, E.J.; Iravani, R. A decentralized robust control strategy for multi-DER microgrids—Part I: Fundamental concepts. IEEE Trans. Power Deliv. 2012, 27, 1843–1853. [Google Scholar] [CrossRef]
- Karavas, C.-S.; Kyriakarakos, G.; Arvanitis, K.G.; Papadakis, G. A multi-agent decentralized energy management system based on distributed intelligence for the design and control of autonomous polygeneration microgrids. Energy Convers. Manag. 2015, 103, 166–179. [Google Scholar] [CrossRef]
- Torreglosa, J.; García, P.; Fernández, L.; Jurado, F. Hierarchical energy management system for stand-alone hybrid system based on generation costs and cascade control. Energy Convers. Manag. 2014, 77, 514–526. [Google Scholar] [CrossRef]
- Kyriakarakos, G.; Dounis, A.I.; Arvanitis, K.G.; Papadakis, G. A fuzzy logic energy management system for polygeneration microgrids. Renew. Energy 2012, 41, 315–327. [Google Scholar] [CrossRef]
- Kyriakarakos, G.; Dounis, A.I.; Arvanitis, K.G.; Papadakis, G. A fuzzy cognitive maps-petri nets energy management system for autonomous polygeneration microgrids. Appl. Soft Comput. 2012, 12, 3785–3797. [Google Scholar] [CrossRef]
- Chang, H.-H. Genetic algorithms and non-intrusive energy management system based economic dispatch for cogeneration units. Energy 2011, 36, 181–190. [Google Scholar] [CrossRef]
- Anh, H.P.H. Implementation of supervisory controller for solar PV microgrid system using adaptive neural model. Int. J. Electr. Power Energy Syst. 2014, 63, 1023–1029. [Google Scholar] [CrossRef]
- McArthur, S.D.; Davidson, E.M.; Catterson, V.M.; Dimeas, A.L.; Hatziargyriou, N.D.; Ponci, F.; Funabashi, T. Multi-agent systems for power engineering applications—Part I: Concepts, approaches, and technical challenges. IEEE Trans. Power Syst. 2007, 22, 1743–1752. [Google Scholar] [CrossRef]
- McArthur, S.D.; Davidson, E.M.; Catterson, V.M.; Dimeas, A.L.; Hatziargyriou, N.D.; Ponci, F.; Funabashi, T. Multi-agent systems for power engineering applications—Part II: Technologies, standards, and tools for building multi-agent systems. IEEE Trans. Power Syst. 2007, 22, 1753–1759. [Google Scholar] [CrossRef]
- Kyriakarakos, G.; Piromalis, D.D.; Dounis, A.I.; Arvanitis, K.G.; Papadakis, G. Intelligent demand side energy management system for autonomous polygeneration microgrids. Appl. Energy 2013, 103, 39–51. [Google Scholar] [CrossRef]
- Dou, C.-X.; Wang, W.-Q.; Hao, D.-W.; Li, X.-B. MAS-based solution to energy management strategy of distributed generation system. Int. J. Electr. Power Energy Syst. 2015, 69, 354–366. [Google Scholar] [CrossRef]
- Fudenberg, D.; Tirole, J. Game Theory; The MIT Press: Cambridge, MA, USA, 1991; p. 12. [Google Scholar]
- Mei, S.; Wang, Y.; Liu, F.; Zhang, X.; Sun, Z. Game approaches for hybrid power system planning. IEEE Trans. Sustain. Energy 2012, 3, 506–517. [Google Scholar]
- Wang, Y.; Saad, W.; Han, Z.; Poor, H.V.; Başar, T. A game-theoretic approach to energy trading in the smart grid. IEEE Trans. Smart Grid 2014, 5, 1439–1450. [Google Scholar] [CrossRef]
- Khan, M.R.B.; Jidin, R.; Pasupuleti, J. Multi-agent based distributed control architecture for microgrid energy management and optimization. Energy Convers. Manag. 2016, 112, 288–307. [Google Scholar] [CrossRef]
- Agarwal, T.; Cui, S. Noncooperative Games for Autonomous Consumer Load Balancing over Smart Grid (GAMENETS); Springer: Berlin, Germany, 2012; pp. 163–175. [Google Scholar]
- Yin, H.; Zhao, C.; Li, M.; Ma, C.; Chow, M.-Y. A tem. IEEE Trans. Ind. Electr. 2016, 63, 4266–4277. [Google Scholar] [CrossRef]
- Stephens, E.R.; Smith, D.B.; Mahanti, A. Game theoretic model predictive control for distributed energy demand-side management. IEEE Trans. Smart Grid 2015, 6, 1394–1402. [Google Scholar] [CrossRef]
- Atzeni, I.; Ordóñez, L.G.; Scutari, G.; Palomar, D.P.; Fonollosa, J.R. Demand-side management via distributed energy generation and storage optimization. IEEE Trans. Smart Grid 2013, 4, 866–876. [Google Scholar] [CrossRef]
- Saad, W.; Han, Z.; Poor, H.V.; Basar, T. Game-theoretic methods for the smart grid: An overview of microgrid systems, demand-side management, and smart grid communications. IEEE Signal Process. Mag. 2012, 29, 86–105. [Google Scholar] [CrossRef]
- Russell, S. Artificial Intelligence: A Modern Approach Author: Stuart Russell, Peter Norvig; Prentice Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Wooldridge, M. An Introduction to Multiagent Systems; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Osborne, M.J.; Rubinstein, A. A Course in Game Theory; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Aristidou, P.; Dimeas, A.L.; Hatziargyriou, N.D. Microgrid Modelling and Analysis Using Game Theory Methods, ICST E-Energy; Springer: Berlin, Germany, 2010; pp. 12–19. [Google Scholar]
- Ito, T.; Zhang, M.; Robu, V.; Fatima, S.; Matsuo, T. Advances in Agent-Based Complex Automated Negotiations; Springer: Berlin, Germany, 2009; Volume 233. [Google Scholar]
- Fakhrzad, M.; Khademi Zare, H. Combination of genetic algorithm with Lagrange multipliers for lot-size determination in multi-stage production scheduling problems. Expert Syst. Appl. 2009, 36, 10180–10187. [Google Scholar] [CrossRef]
- Fadaee, M.; Radzi, M. Multi-objective optimization of a stand-alone hybrid renewable energy system by using evolutionary algorithms: A review. Renew. Sustain. Energy Rev. 2012, 16, 3364–3369. [Google Scholar] [CrossRef]
- Wang, G.-G.; Hossein Gandomi, A.; Yang, X.-S.; Hossein Alavi, A. A novel improved accelerated particle swarm optimization algorithm for global numerical optimization. Eng. Comput. 2014, 31, 1198–1220. [Google Scholar] [CrossRef]
- Khare, A.; Rangnekar, S. A review of particle swarm optimization and its applications in solar photovoltaic system. Appl. Soft Comput. 2013, 13, 2997–3006. [Google Scholar] [CrossRef]
- Shakib, S.E.; Amidpour, M.; Aghanajafi, C. Simulation and optimization of multi effect desalination coupled to a gas turbine plant with HRSG consideration. Desalination 2012, 285, 366–376. [Google Scholar] [CrossRef]
- Clarke, D.P.; Al-Abdeli, Y.M.; Kothapalli, G. Multi-objective optimisation of renewable hybrid energy systems with desalination. Energy 2015, 88, 457–468. [Google Scholar] [CrossRef]
- Klein, A.; Beckman, A.; Mitchell, W.; Duffie, A.; Duffie, N.; Freeman, T. TRNSYS 17-a Transient System Simulation Program; Solar Energy Laboratory, University of Wisconsin: Madison, WI, USA, 2011. [Google Scholar]
- Mondol, J.D.; Yohanis, Y.G.; Norton, B. Optimising the economic viability of grid-connected photovoltaic systems. Appl. Energy 2009, 86, 985–999. [Google Scholar] [CrossRef]
- Kyriakarakos, G.; Dounis, A.I.; Arvanitis, K.G.; Papadakis, G. Design of a Fuzzy Cognitive Maps variable-load energy management system for autonomous PV-reverse osmosis desalination systems: A simulation survey. Appl. Energy 2017, 187, 575–584. [Google Scholar] [CrossRef]
- Yilanci, A.; Dincer, I.; Ozturk, H.K. Performance analysis of a PEM fuel cell unit in a solar-hydrogen system. Int. J. Hydrogen Energy 2008, 33, 7538–7552. [Google Scholar] [CrossRef]
- Barbir, F. PEM electrolysis for production of hydrogen from renewable energy sources. Sol. Energy 2005, 78, 661–669. [Google Scholar] [CrossRef]
- Wetter, M. GenOpt, Generic Optimization Program, User Manual, version 3; Lawrence Berkeley National Laboratory, University of California: Oakland, CA, USA, 2008. [Google Scholar]
- Thermal Energy System Specialists; TESS Libraries: Madison, WI, USA, 2008.
- Anuphappharadorn, S.; Sukchai, S.; Sirisamphanwong, C.; Ketjoy, N. Comparison the economic analysis of the battery between lithium-ion and lead-acid in PV stand-alone application. Energy Procedia 2014, 56, 352–358. [Google Scholar] [CrossRef]
- Shen, J.; Dusmez, S.; Khaligh, A. Optimization of sizing and battery cycle life in battery/ultracapacitor hybrid energy storage systems for electric vehicle applications. IEEE Trans. Ind. Inform. 2014, 10, 2112–2121. [Google Scholar] [CrossRef]
- Dimitriou, E.; Mohamed, E.S.; Kyriakarakos, G.; Papadakis, G. Experimental investigation of the performance of a reverse osmosis desalination unit under full-and part-load operation. Desalinat. Water Treat. 2015, 53, 3170–3178. [Google Scholar] [CrossRef]
- Bindner, H.; Cronin, T.; Lundsager, P.; Manwell, J.F.; Abdulwahid, U.; Baring-Gould, I. Lifetime Modelling of Lead Acid Batteries; University of Massachusetts: Boston, MA, USA, 2005. [Google Scholar]

| Topology | Lbest |
|---|---|
| Size | 3 |
| Particles | 20 |
| Generations | 100 |
| Seed | 0 |
| Cognitive acceleration constant | 2.05 |
| Social acceleration constant | 2.05 |
| Maximum velocity discrete gain | 0.5 |
| Maximum velocity continuous gain | 0 |
| Constriction gain | 0.729 |
| Page of the MAS | |
|---|---|
| Percepts | Produced power by the PVs and wind turbine, produced energy by the fuel cell, state of charge of the battery bank, available potable water in the water tank and available hydrogen in the metal hydride tank |
| Actions | Activate or deactivate the desalination unit, electrolyzer and fuel cell and determine theirs operation points. |
| Goals | Fully meet the load demand, water and fuel needs and exploiting the highest possible potable water production and hydrogen production in a cost and energy effective way. |
| Environment | All the components of the system |
| Variable | Lowest Value | Highest Value | Step | Optimal Value |
|---|---|---|---|---|
| System Components | ||||
| Capacity rating of each of the 2 V batteries. 24 are used for a 48 V DC bus (Wh) | 800, 1000, 1200, 1500, 1600, 2000 | 1500 | ||
| Typical multicrystalline modules rated at 180 Wp each in series | 90 | 125 | 1 | 120 |
| Rated Power of the Fuel Cell (W) | 300 | 1200 | 100 | 600 |
| Rated Power of the Electrolyzer Unit (W) | 400 | 1700 | 100 | 500 |
| Low pressure Hydrogen Tank Storage Capacity (Nm3 of H2) | 18 | 30 | 1 | 20 |
| Potable Water Tank Volume (m3) | 18 | 35 | 1 | 27 |
| Rated Power of the Desalination Unit (W) | 700 | 1700 | 100 | 1400 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karavas, C.-S.; Arvanitis, K.; Papadakis, G. A Game Theory Approach to Multi-Agent Decentralized Energy Management of Autonomous Polygeneration Microgrids. Energies 2017, 10, 1756. https://doi.org/10.3390/en10111756
Karavas C-S, Arvanitis K, Papadakis G. A Game Theory Approach to Multi-Agent Decentralized Energy Management of Autonomous Polygeneration Microgrids. Energies. 2017; 10(11):1756. https://doi.org/10.3390/en10111756
Chicago/Turabian StyleKaravas, Christos-Spyridon, Konstantinos Arvanitis, and George Papadakis. 2017. "A Game Theory Approach to Multi-Agent Decentralized Energy Management of Autonomous Polygeneration Microgrids" Energies 10, no. 11: 1756. https://doi.org/10.3390/en10111756
APA StyleKaravas, C.-S., Arvanitis, K., & Papadakis, G. (2017). A Game Theory Approach to Multi-Agent Decentralized Energy Management of Autonomous Polygeneration Microgrids. Energies, 10(11), 1756. https://doi.org/10.3390/en10111756







