1. Introduction
The distribution system is the final interconnection between the bulk power system and consumers. There is a large number of buses and lines with a high R/X ratio, which results into high power losses in distribution systems. These losses are even more significant at heavy loads. Moreover, the voltage of buses, farther from the substation, decreases. It is important to optimize the operation of distribution systems by reducing the losses and enhancing the voltages profile. To assure these improvements reconfiguration and capacitor placement have been employed earlier but in recent decade the placement of dispersed generation has attracted the researchers. Dispersed Generators (DGs) are small-scale generators that are located near to load centers. The size of DGs varies from less than a kW to tens of MW. The DGs have additional advantage of meeting load demand along with reduction in losses and improvement of voltage profile. To maximize these benefits, DG of optimal size should be placed at optimal site. Several optimization techniques have been utilized for DG placement by optimizing various objective functions, as single objective and multi-objective optimization problem.
The placement of DG as single objective optimization is carried out through various optimization techniques for loss minimization, cost minimization, profit maximization. These methods include Particle Swarm Optimization (PSO) [
1,
2], Genetic Algorithm (GA) [
3], Artificial Bee Colony (ABC) [
4], Improved Bat Algorithm [
5], and Analytical expression based heuristics [
6,
7,
8,
9]. The limitation of analytical expression based heuristics is inability to handle multiple objectives and multiple DGs.
The optimal placement of DG has been investigated through PSO [
1,
2] to minimize losses in distribution system. The effectiveness of three different types of DGs have been analyzed [
1]. The DG that is capable of supplying both active and reactive power is most effective for loss reduction. Loss minimization has been investigated by integrating multiple DGs [
2]. The realistic nature of loads has been accounted by time-varying characteristics. GA [
3] has been applied to optimally allocate DGs to minimize losses. It has been concluded that the benefit of loss minimization by DG placement is limited up to certain locations only and after that trend reverses. The problem of DG placement to minimize losses has been solved by ABC algorithm [
4] for two different load scenarios. Multiple DG placement has been obtained by Bat Algorithm [
5] to achieve maximum reduction in annual energy losses in distribution system.
An analytical heuristic based on exact loss formula has been derived to attain the optimal size and location of DG [
6] to reduce the power losses in distribution system. The location of DG, capable of supplying only active power, is found by sensitivity loss factors. The heuristic proposed in [
6] is elaborated to consider different types of DG [
7]. Another classical technique utilizes loss formula based on bus-injection to branch-current (BIBC) and branch-current to bus-voltage (BCBV) matrices [
8] to calculate the optimal size and site of DG. This method does not require calculation of impedance matrix. Another technique based on analytical expressions [
9] obtain the optimal site and size of four different types of DG by minimizing the losses. A decision making approach [
10] based on exhaustive load flow has been employed to allocate wind and photovoltaic (PV) based DGs in distribution system to reduce the power losses and improve voltage profile. The PV based DG is found more influential in voltage profile improvement in comparison to wind based DG.
The multi-objective optimization problem has been solved by two different approaches i.e., by representing multi-objective optimization as single objective optimization using weighed sum approach or by handling multiple objectives simultaneously. The common objectives for multi-objective DG placement are minimization of power loss, voltage deviation, customer interruptions, cost of purchased energy and cost of DG.
The weighted sum approach has been used in [
11,
12,
13,
14,
15] to find the optimal size and optimal site of DG. The allocation has been investigated through GA [
11] where the multi-objective problem is changed to single objective by assigning weights to four objectives namely real and reactive power loss index, voltage profile index and Mega Volt Ampere (MVA) capacity index. In addition to these four objectives short-circuit current is also considered as objective in [
12]. The optimization has been carried out using PSO after changing the multi-objective problem to single objective problem. Optimal site of DG for predefined size has been obtained by Simulated Annealing [
13] for minimizing power loss, emissions and contingency. Optimal allocation of multiple DGs based on wind turbine and PV array has been done by PSO [
14] for minimizing power loss and improving voltage stability. The multi-objective optimization problem is converted to single objective by assigning weights, where the weights were updated iteratively. Weighted sum approach has also been utilized in [
15] for optimal sizing and siting of voltage controlled DG for balanced as well as unbalanced distribution networks for objectives as real and reactive power loss index, voltage profile index and reserve capacity of conductor index. The optimization has been attempted by supervised big-bang crunch method. The limitation of weighted sum approach is that the solution is dependent on weight assigned to each objective or the decision maker who assigns the weights to the objectives, influences the solution. Such solutions may be non-optimal solutions.
Multi-objective optimization problem has been solved by ε-constrained technique in [
16,
17,
18] to suggest optimal allocation of DG in which one objective is selected as main objective and rest of objectives are treated as constraints. Minimization of cost of energy losses, voltage profile and power quality index are selected as objectives in [
16] to attempt optimization by ε-constrained technique. The ε-constrained technique has been combined with GA [
17] for optimal allocation of DG by minimizing four costs network upgrading, purchased energy, energy losses, energy not supplied. The combination of ε-constrained technique and GA [
18] has been employed to allocate DG optimally considering voltage dependent loads. The minimization of interruptions to customers, cost of active power losses, cost of energy purchased, bus voltage deviation and maximization of security margin has been considered as multiple objectives.
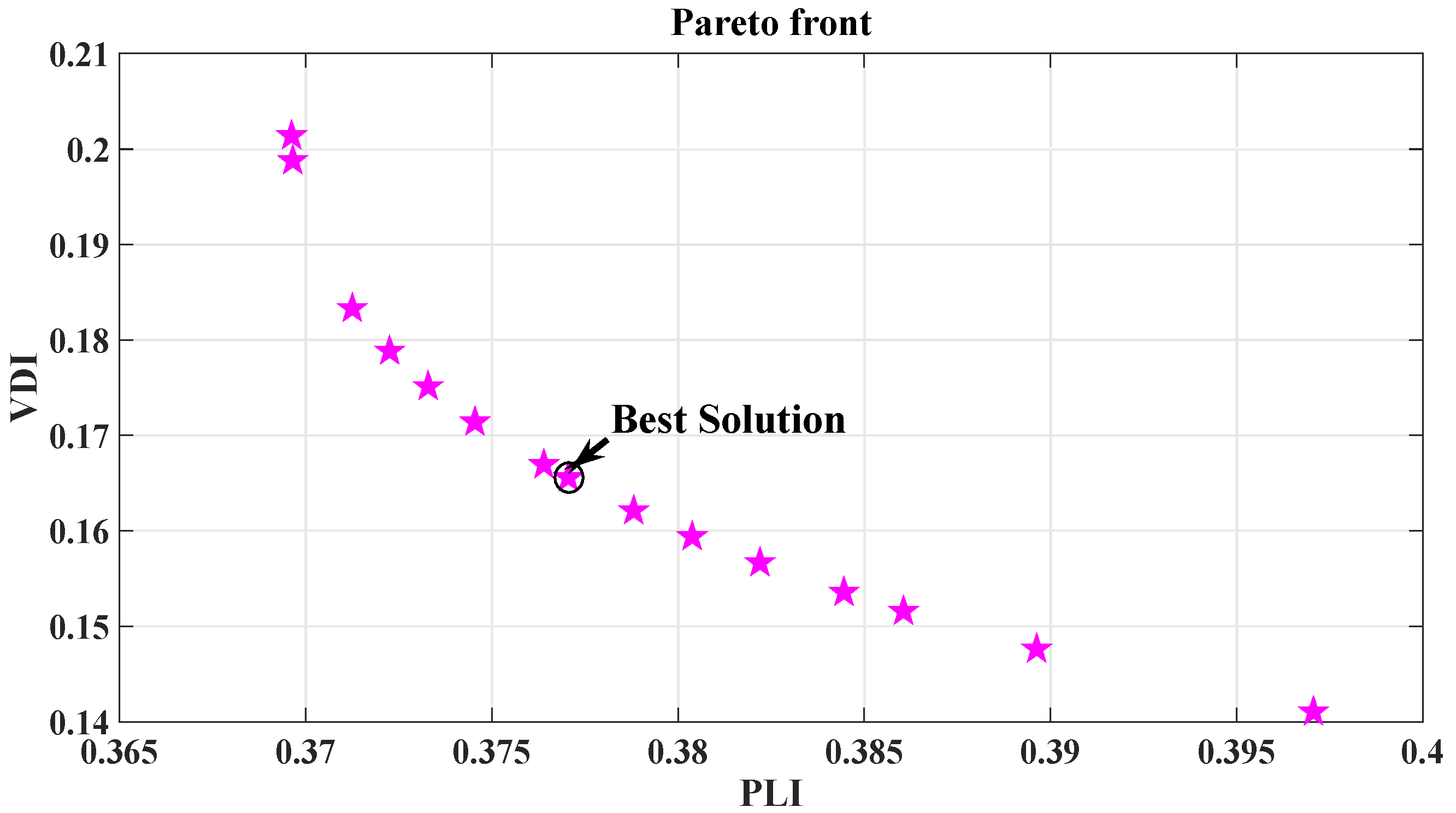
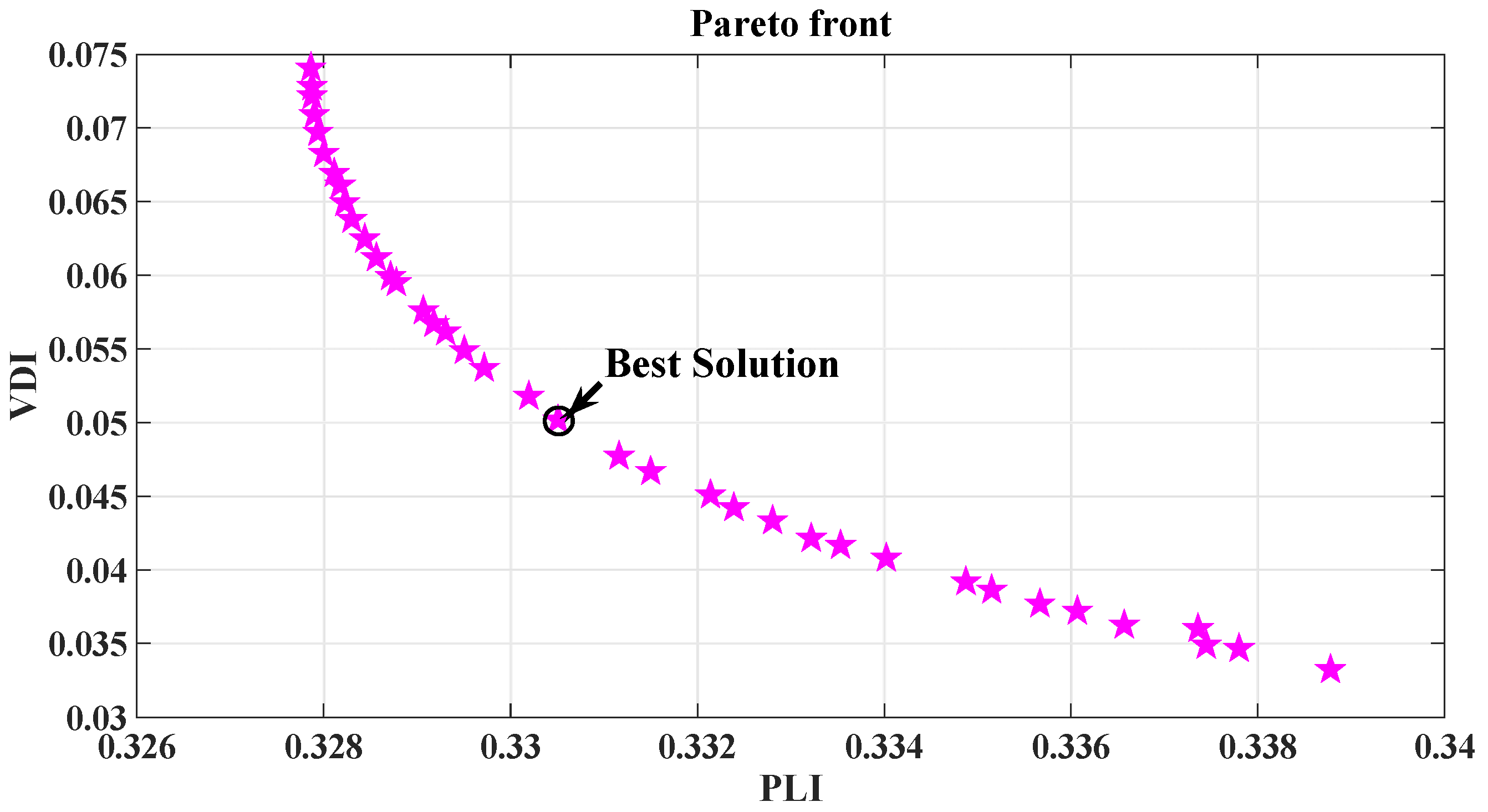
Optimal location and size of DG has been obtained by Strength Pareto Evolutionary Algorithm and Non-dominated Sorting GA-II in [
19] and Shuffled frog leaping algorithm in [
20] to minimize real power loss and cost of DG. Optimization of weight factor is additional parameter to be optimized in [
20] which balances the two main objectives. In addition to minimization of real power losses of system and cost of DG, voltage deviation minimization is also considered as objective in [
21]. Non-dominated Sorting GA-II was used to solve the problem of optimal allocation of specified number of DGs of multiple types. The pareto front is obtained for simultaneous optimization of three objectives and final solution is selected from non-dominated solutions by normalized membership functions. Optimal allocation of DG models has been done by minimizing voltage deviation index, real and reactive power loss index, line loading index and short-circuit index using fuzzy embedded GA [
22]. The multi-objective problem is simplified by assigning fuzzy membership function to each index. Goal optimization algorithm [
23] has been used for optimal allocation of DG in distribution system by achieving the set goal for the indices used in [
22]. In [
24] combination of GA and PSO has been utilized by where optimal site is obtained by GA and size of DG is obtained by PSO. Multiple DGs of optimal size has been placed to minimize losses, improve voltage profile and to optimize voltage stability index. Enhanced multi-objective PSO has been proposed to optimally allocate multiple DGs by minimizing power losses and maximize voltage stability index [
25,
26]. Fuzzy decision-making has been employed to select single solution from Pareto front. Sequential quadratic programming has been employed in [
27] to obtain set of optimal solutions to minimize total real power loss and cost of DG. In addition to loss and voltage deviation minimization, cost minimization is also considered as objective [
28]. Shuffled Bat algorithm has been employed in solving optimization. Pareto front has been obtained in both and compromised solution has been selected from set of solutions. The best solution has been selected by fuzzy decision-making in [
27] and while it has been done by max-min technique in [
28].
The GA and PSO are commonly used techniques for optimal placement of DG. The PSO has better diversity and exploration in comparison to GA and its convergence is fast due to momentum effect on particles [
29]. Therefore, the optimization in the presented work is carried out through PSO.
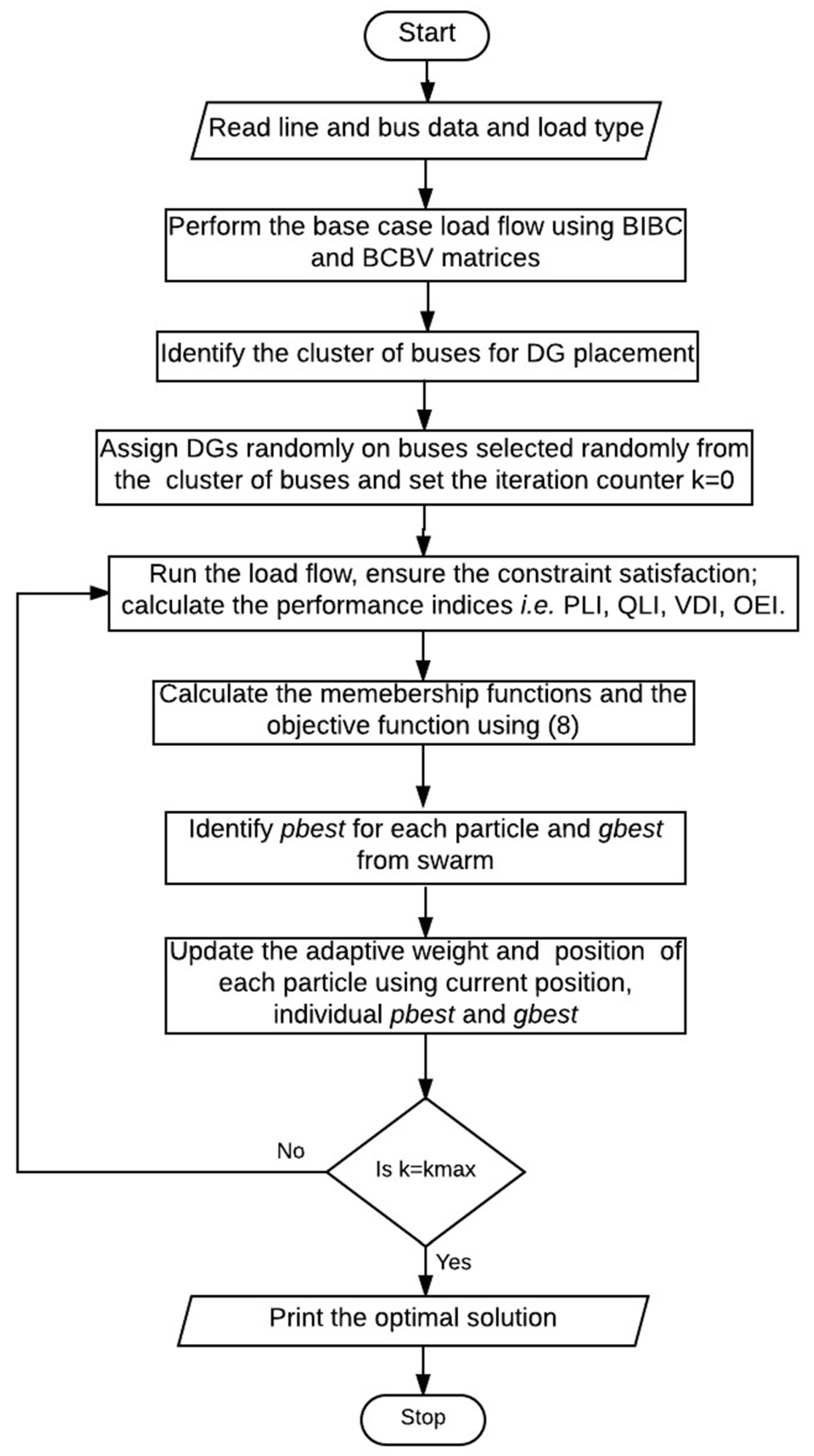
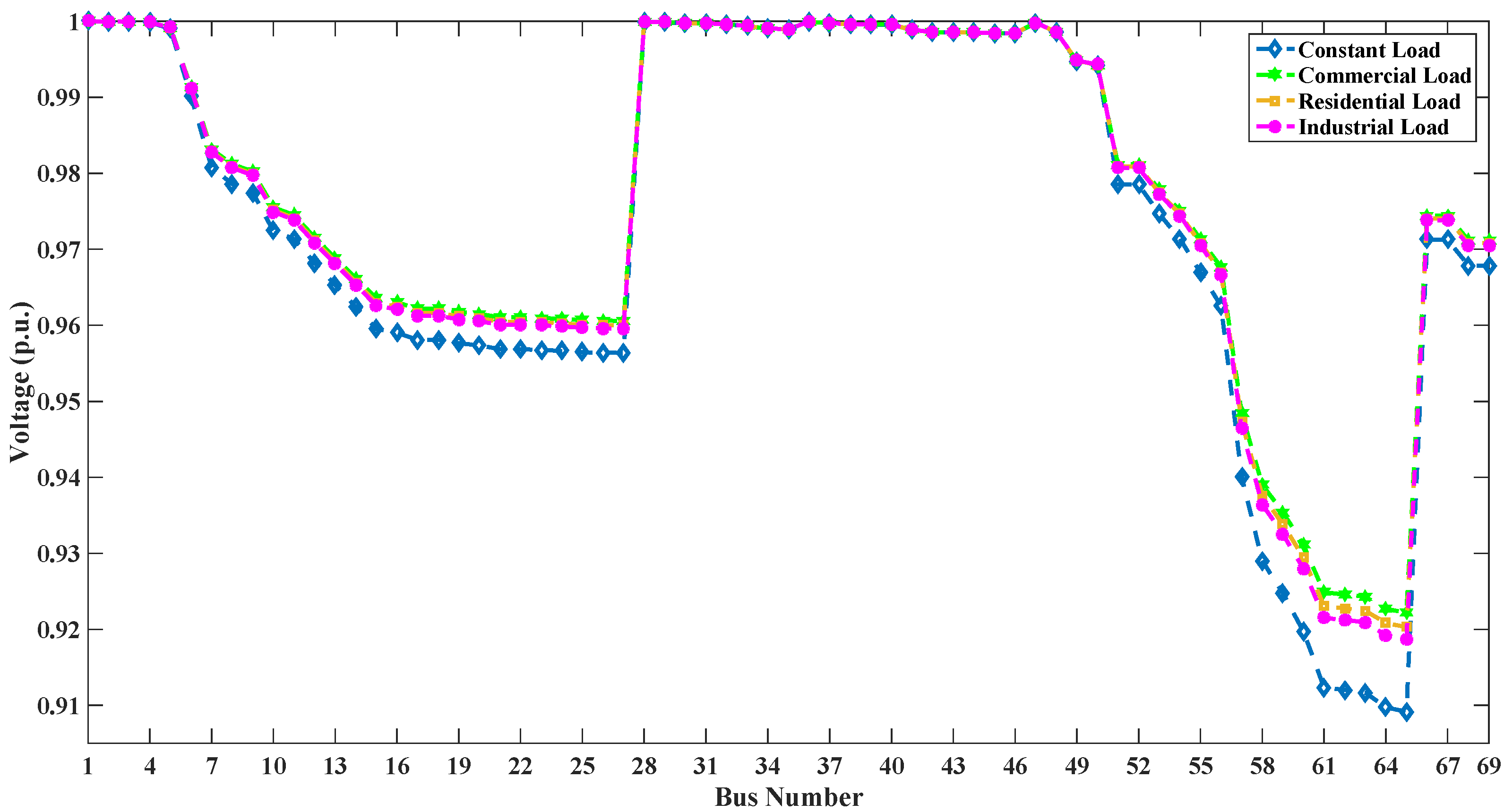
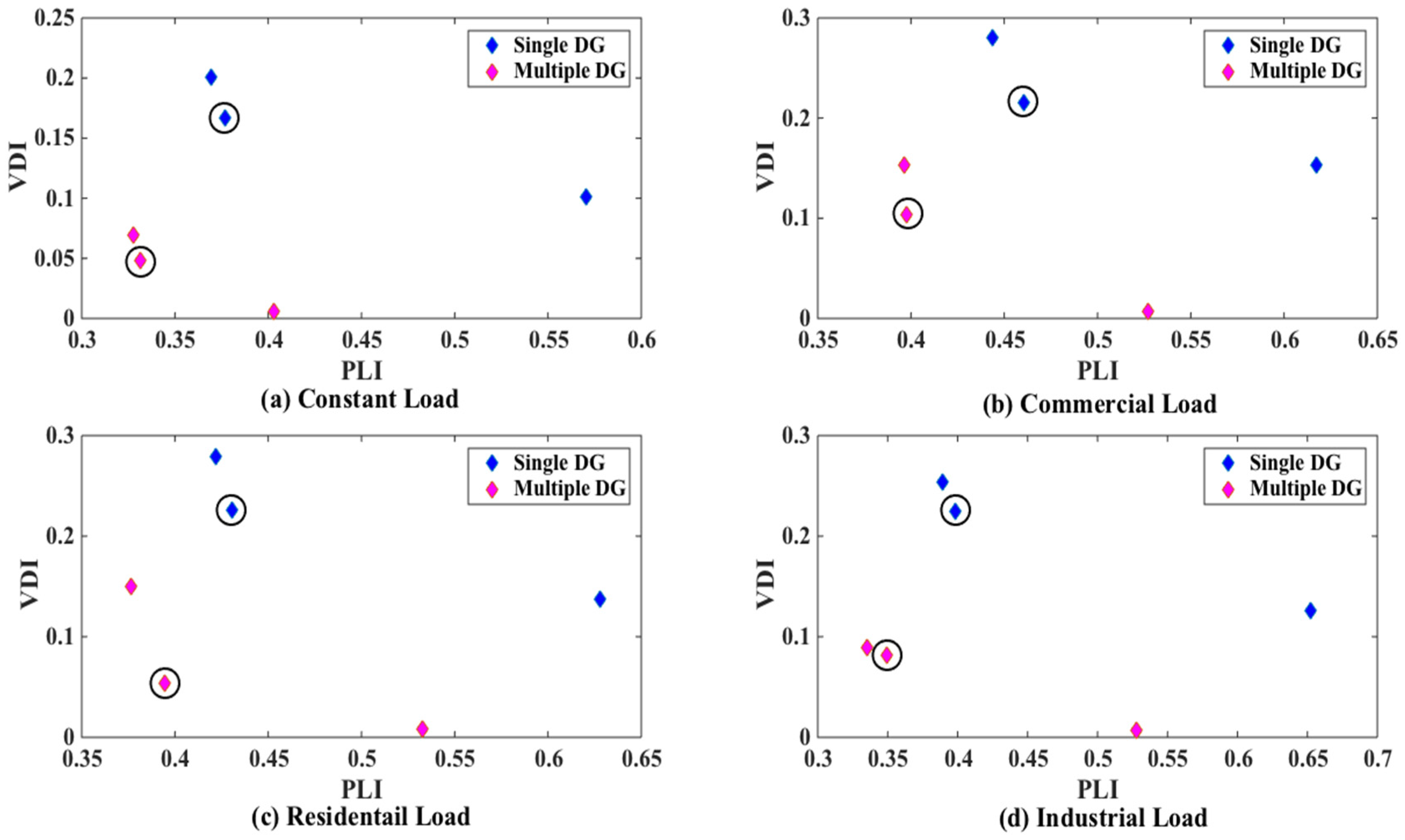
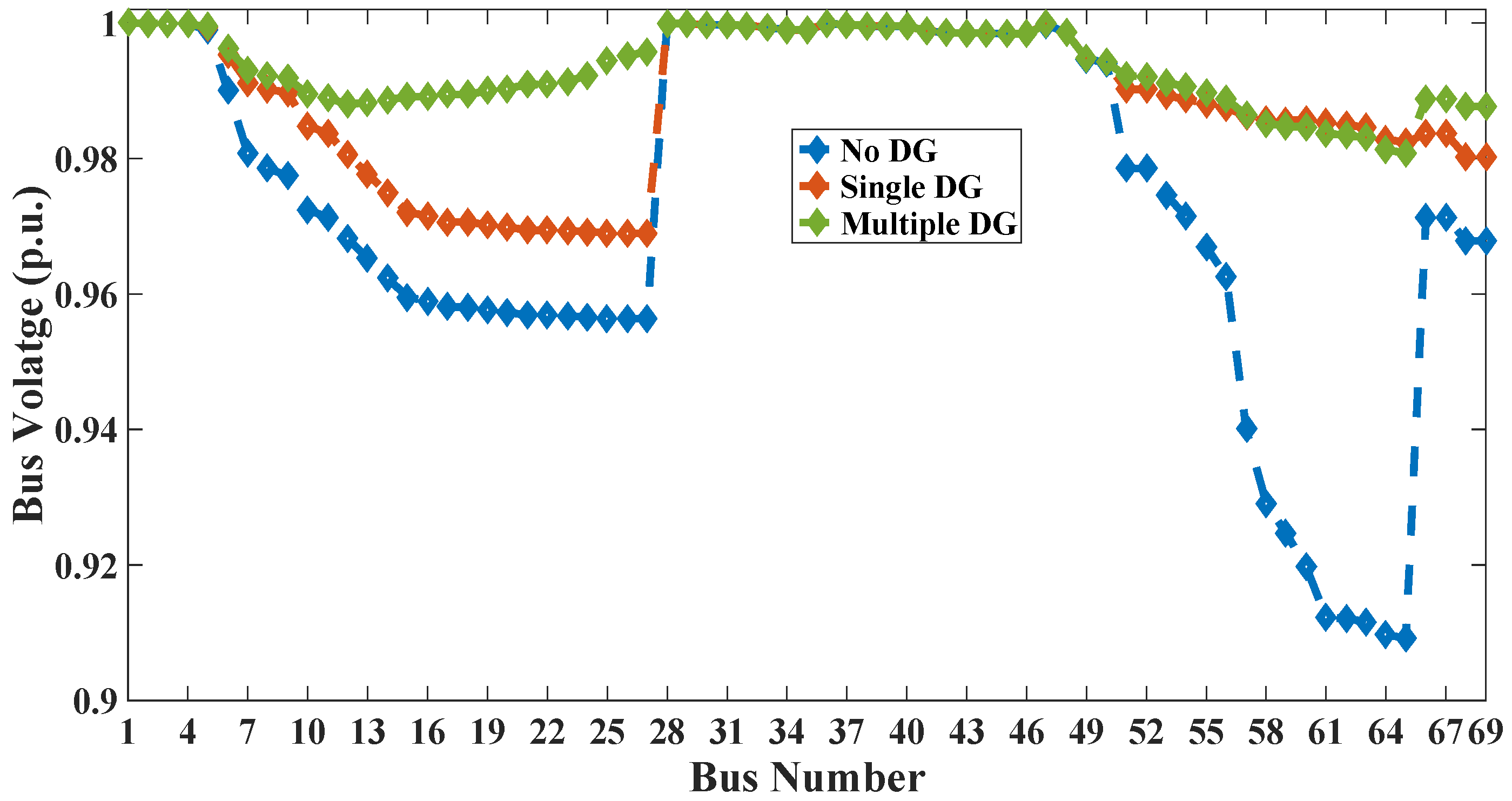
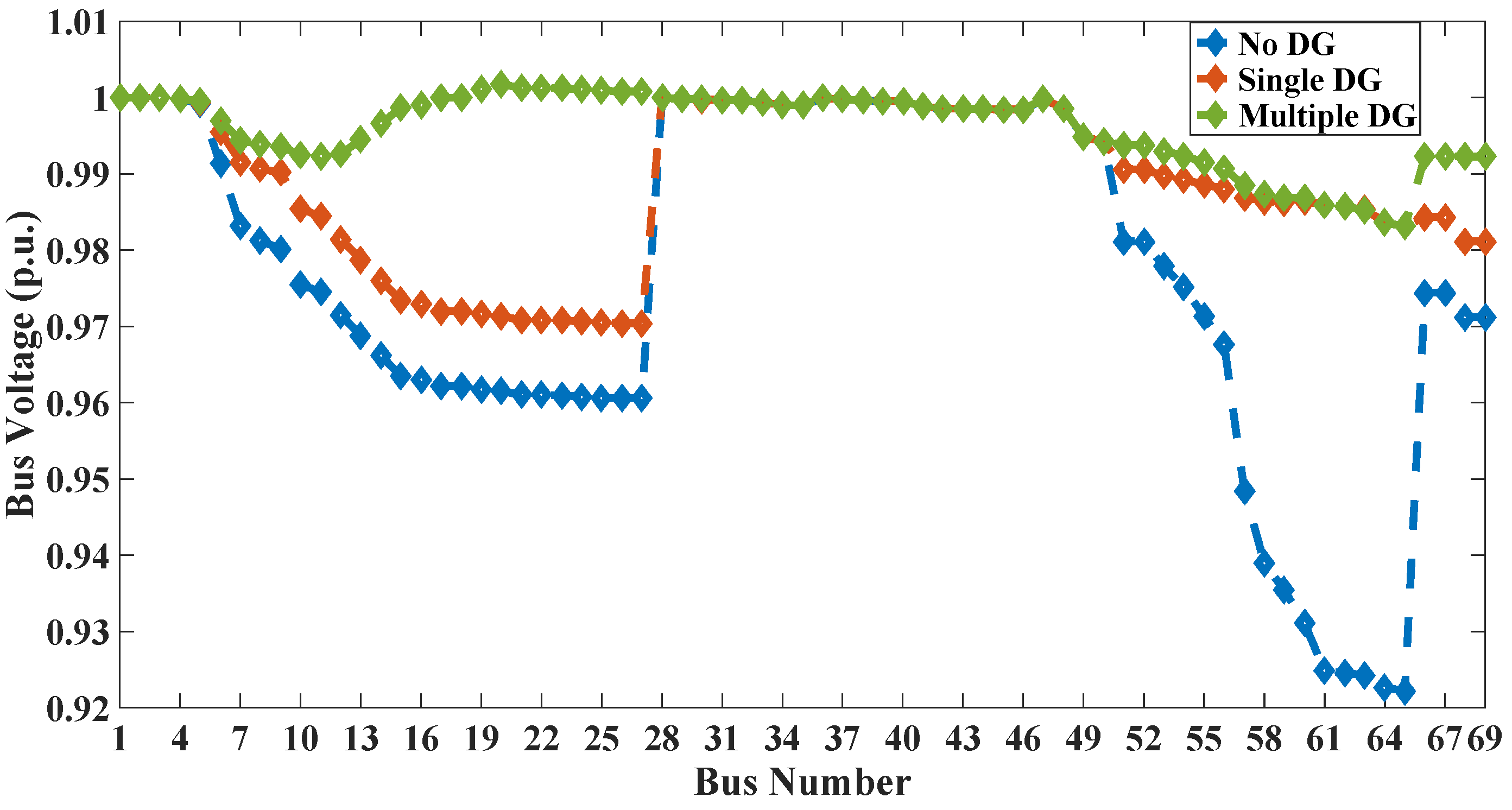
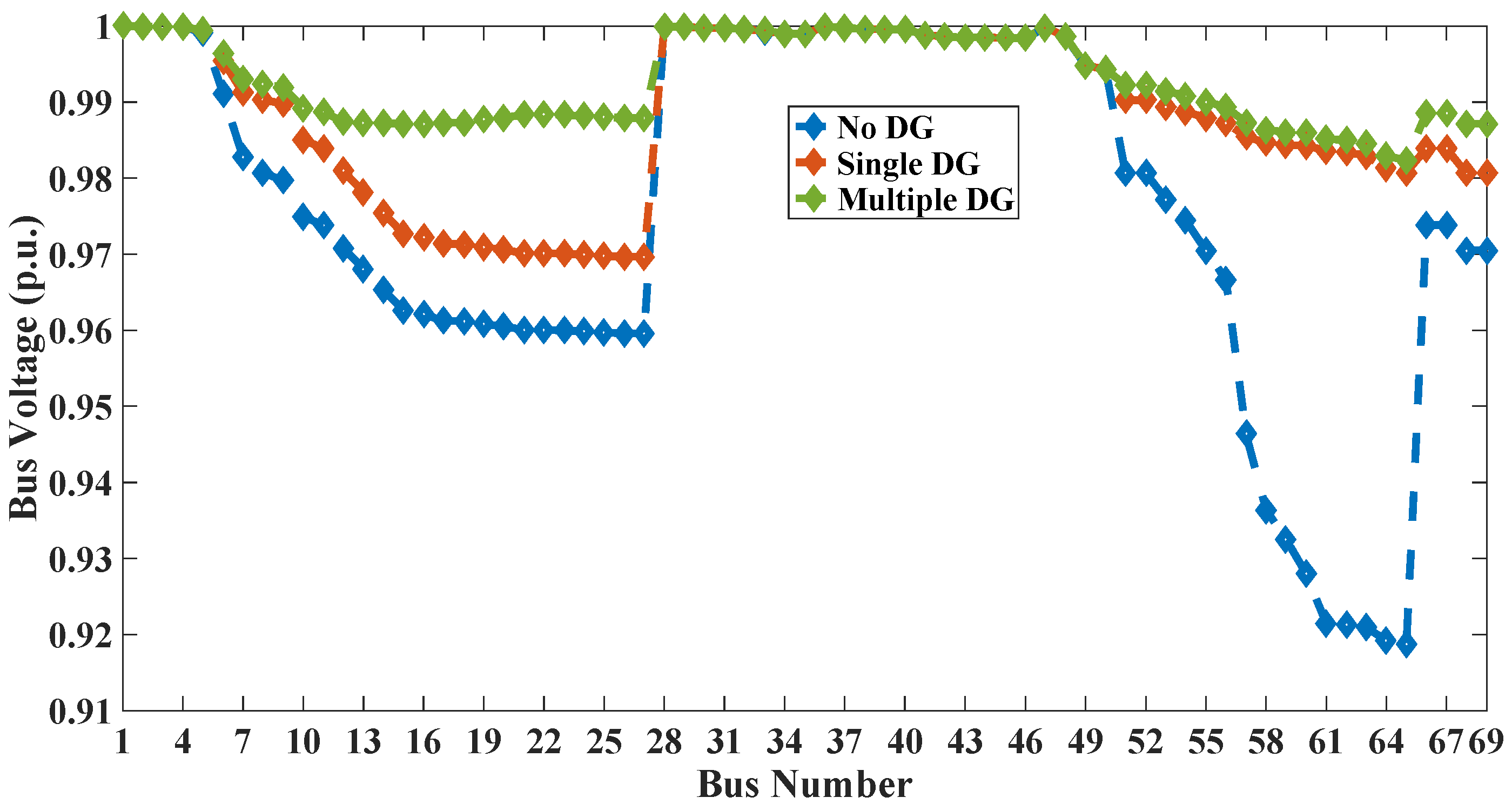
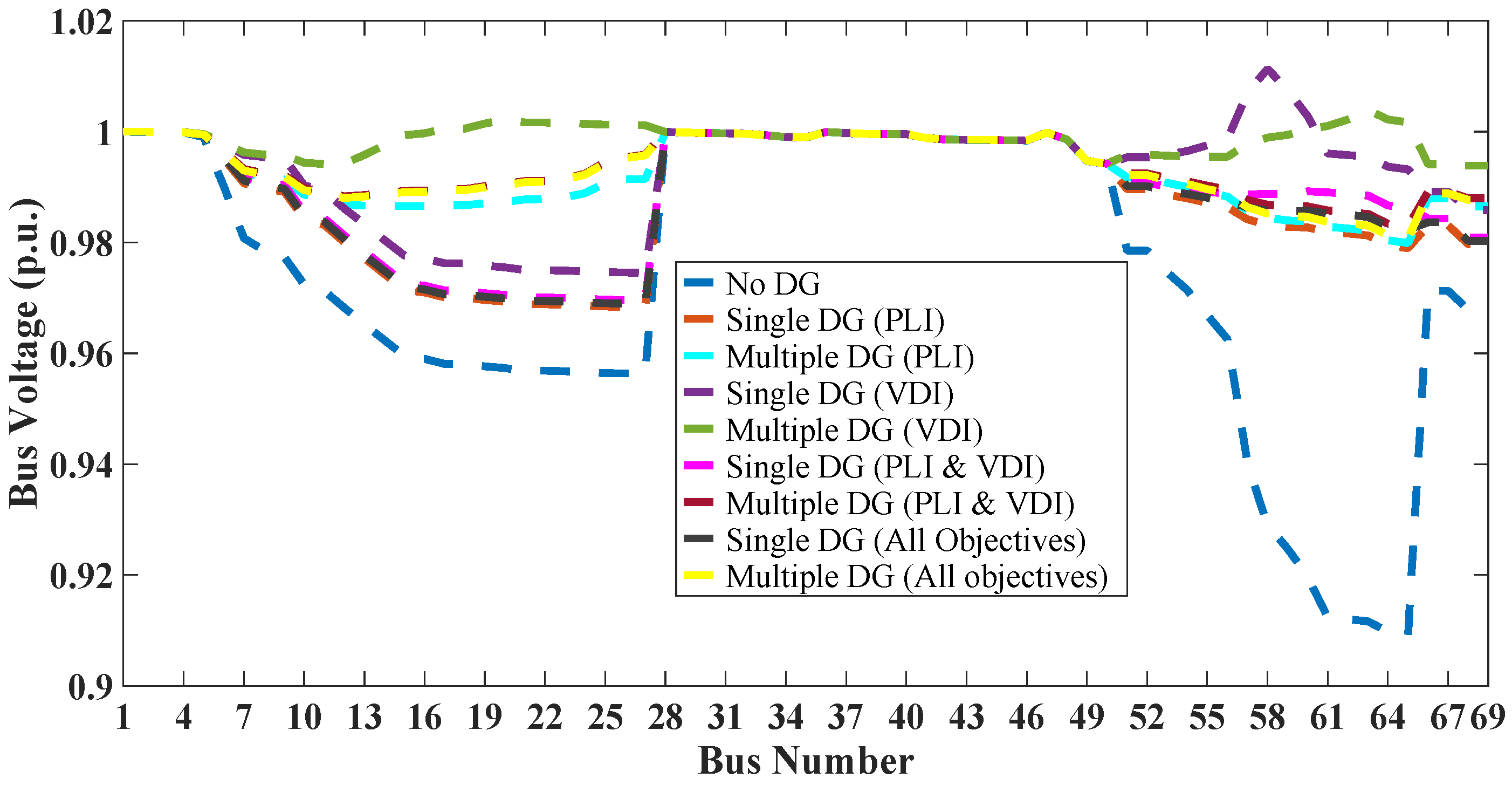
In this paper the four indices are selected for allocation of DG of optimal size at optimum location in radial distribution system (RDS). These indices are active power loss index (PLI), reactive power loss index (QLI), voltage deviation index (VDI) and overall economy index (OEI). The multi-objective optimization is implemented using fuzzy decision approach by assigning fuzzy memberships to these indices and optimizing the resultant membership. The optimal sizes and sites of DGs are obtained through PSO for voltage dependent residential, commercial and industrial loads. The optimization is carried out for placement of single as well as multiple DGs. The clustering of buses based on base case load flow is done to reduce the search space.