Metaheuristic Techniques in Enhancing the Efficiency and Performance of Thermo-Electric Cooling Devices
Abstract
:1. Introduction
1.1. Problem Statement
1.2. Objectives and Motivations of the Study
- ▪
- To investigate using metaheuristic stand-alone techniques like SA and DE for STEC and TTEC.
- ▪
- To develop hybrid techniques for STEC and TTEC.
- ▪
- To validate the all the techniques (stand-alone and hybrid) on STEC and TTEC.
2. Background
2.1. Basic Structure and Operation Principle of TEC
- ▪
- Seebeck Effect: If A and B: two dissimilar semiconductors are joined at two points and the temperature difference ΔT is maintained between the two junctions, then an open-circuit potential difference ΔV will be developed. This is called the Seebeck effect. The equation is presented in Equation (1) defines the differential Seebeck coefficient α between two dissimilar conductors:For small ΔT, a linear relation occurs. If the coefficient of Seebeck is known, the temperature difference can be measured through measuring Seebeck voltage. The sign regarding αAB is positive when the ΔV causes a current to flow in a clockwise direction as around the circuit.
- ▪
- Peltier Effect: Peltier is briefly the principal effect concerned with thermo-electric refrigeration of heat pumping. At the time A and B: two different conductors are joined together and electric current flows through the one direction, heat will be generated or absorbed at the junction at a constant rate. The Peltier coefficient is determined based on Equation (2):Q is known as Peltier heat or heat generation. The rate at which heat is absorbed is proportional to the current and associated with the nature of the two materials, which comprises the junction. Comparing with the Seebeck effect, where heat flow induces an electric current, the Peltier effect is opposite, with an electric current induced a heating or cooling effect. These two thermo-electric effects are thermodynamically related by means of so-called Kelvin relation as shown in Equation (3):
- ▪
- Thomson Effect: As the last of the thermo-electric effects, the Thomson effect is associated with the rate of generation of reversible heat Q resulting from the passage of a current along a portion of a single conductor along which there is a ΔT. The Thomson effect is not of primary importance in thermo-electric device but it should not be neglected in detailed calculations.
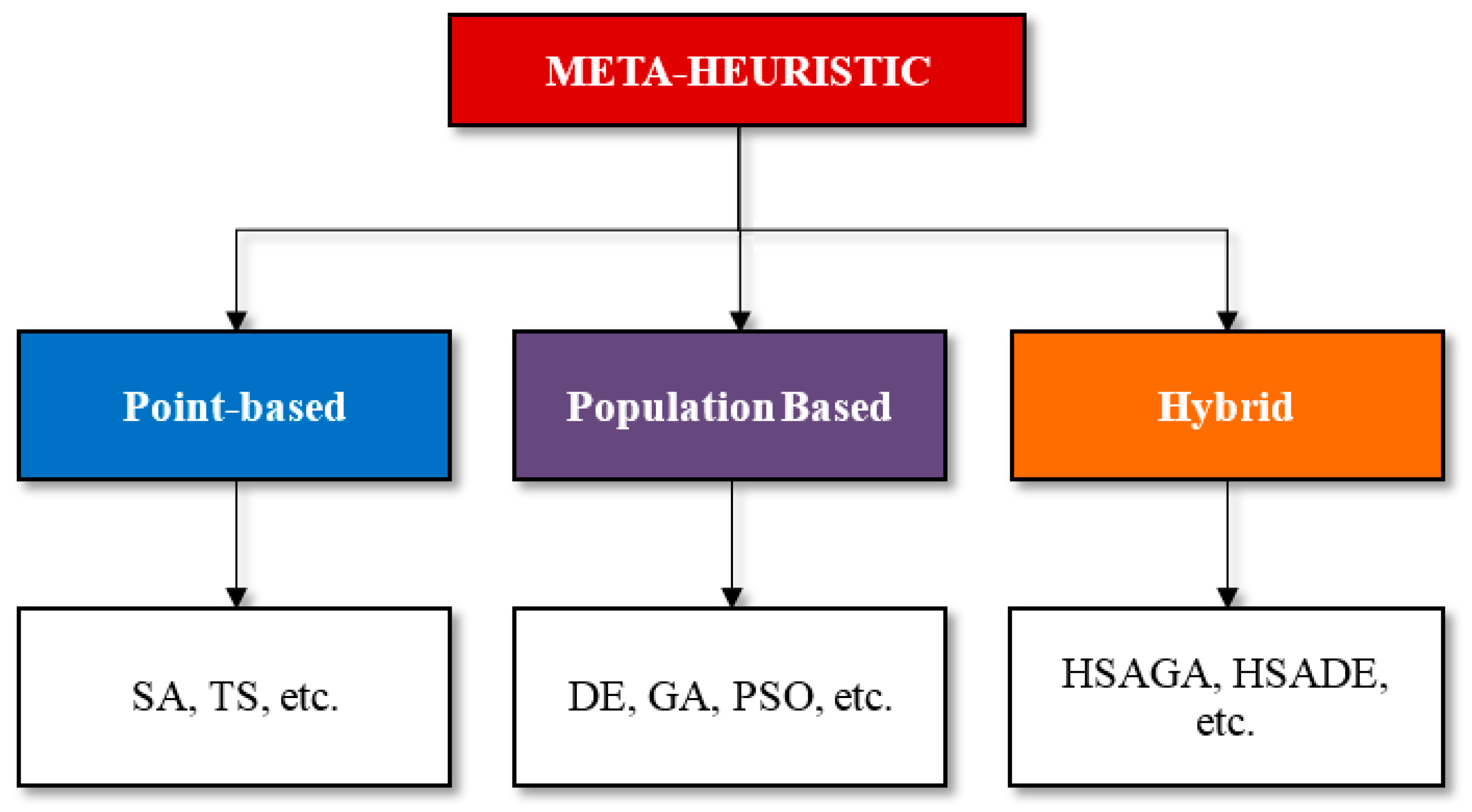
2.2. Metaheuristic Optimization Algorithms
- ▪
- Point-based: Point-based methods focus on a single solution at the start and then moves away from it, drawing a trajectory within the search space [21]. Some algorithms like SA (Simulated Annealing), and TS (Tabu Search) are popular point-based metaheuristic techniques.
- ▪
- Population-based: Population-based methods focused on a set (or similarly called group) of solutions rather than just a single solution [22]. Some of the most popular population-based methods are GA (Genetic Algorithms), DE (Differential Evolution) and PSO (Particle Swarm Optimization).
- ▪
- Hybrid optimization: Hybrid optimization methods are one of the most interesting research trends nowadays. Hybridized algorithms are not just the combination of different point-based or population-based metaheuristics [23]. The combination can benefit from the advantages and strengths of each employed algorithm so as to improve algorithm performance, overcome the individual weaknesses and be more effective and efficient during problem-solving processes [24].
2.3. Literature Review
- ▪
- Operating temperature Tc and Th, the needed output voltage V, current I, and power output P are known as the specifications. These are usually provided by customers according to requirements within a specific application.
- ▪
- The material parameters are based on the status of current materials and the technologies regarding module fabrication. As a result of the effect of material properties on TEC performance, many research works were realized during the past ten years in order to find new materials and structures for use in a green system with highly efficient cooling and also energy conversion. With the highest value figure of merit (ZT), bismuth-telluride (Bi2Te3) is among the best thermo-electric materials [26]. By doping or alloying some other elements in several fabrication processes, there has been a remarkable effort to raise the ZT of bulk materials based on Bi2Te3. At the end, it has been seen that the ZT value was not much more than one and seems insufficient to improve the cooling efficiency. That is because of the difficulty of increasing the electrical conductivity or Seeback coefficient without realizing a corresponding increase in the thermal conductivity [27]. The work by Poudel et al. describes recent advances in improving ZT values [28]. They have achieved a peak ZT of 1.4 at 100 °C suing a bismuth antimony telluride (BiSbTe) p-type nanocrystalline bulk alloy. This material is an alloy of Bi2Te3 and generally obtained by hot pressing nanopowders, which are ball-milled from crystalline ingots. These materials are useful for microprocessor cooling applications because ZT is about 1.2 at room temperature and peaks at about 1.4 at 100 °C.
- ▪
- Eventually, TEC design aims to determine a set of design parameters appropriate for the necessary specifications or effective on achieving the best performance at aminimum cost. Table 1 lists details regarding the optimization techniques used in the optimization of TECs.
2.4. Critical Analysis
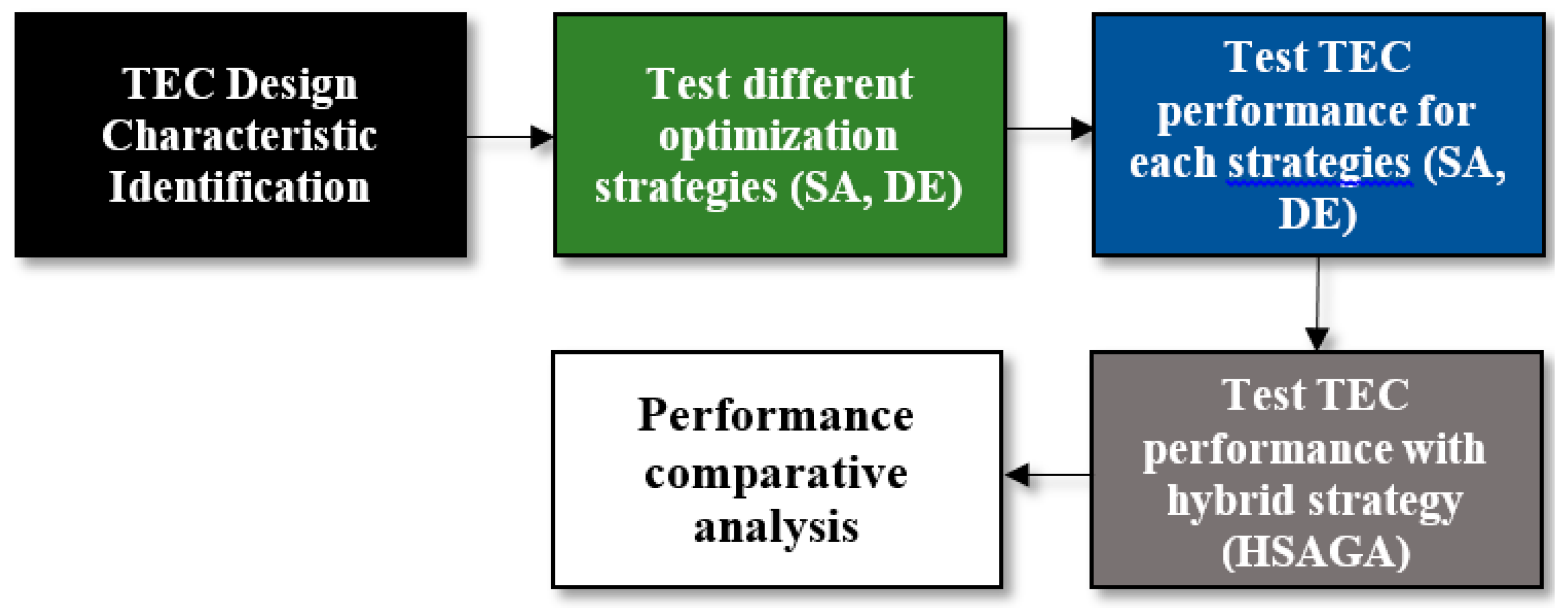
3. Methodology
3.1. Mathematical Modelling of STECs
- ▪
- Impact of operating conditions: For a TEC having a specific geometry, cooling rate and COP are all based on its operating conditions such as the temperature difference ΔT, and the applied current. Base on the work of Huang [31], the authors claimed that by using a fixed ΔT, cooling rate and COP are increased firstly and decreased then as the supplied current is increased. For the same supplied current, the maximum cooling rate and maximum COP cannot always be reached simultaneously. Similarly, for the same operating conditions, as the TEC geometry is varied, cooling rate and COP both vary, but maybe cannot simultaneously reach their maximum values [42].
- ▪
- Impact of geometric properties: From the Equations (4) and (5), the maximum cooling rate increases with the decrease of semiconductor length until it reaches a maximum and then decreases with a further reduction of the thermo-element length [31]. The COP increases following the increase in thermo-element length. As the COP increases with the semiconductor area, the cooling rate may decrease. That is because of the limited total available volume. When the semiconductor area is reduced, the cooling rate generally increases. A smaller semiconductor area and a greater number of them results in a greater cooling capacity. At the time when the semiconductor length is below this related lower bound, the cooling capacity declines enormously [43]. Like the contact resistance, other elements have an effect on the performance of the TEC, but it’s very small so it can be neglected in some calculation.
- ▪
- Impact of material properties: TEC performance is highly based on the thermo-electric materials used [31]. Here, a good thermo-electric material should come with a large Seebeck coefficient for getting low electrical resistance in order to minimize Joule heating [44], low thermal conductivity for reducing the conduction from the hot side and back to the cold side, and finally the greatest possible temperature difference per given amount of electrical potential (voltage). Pure metalshavea low Seebeck coefficient and that causes low thermal conductivity while in insulators electrical resistivity is low, which causes higher Joule heating. The performance evaluation index of thermo-electric materials is the figure of merit (Z) or dimensionless figure of merit (ZT = α2T/ρк) combining the properties above. The increase in Z or ZT causes improvement in the cooling efficiency of Peltier modules. At this point, material properties are considered to be associated with the average temperature of the cold side and hot side temperatures of each stage. Values of them can be calculated via Equations (8)–(10) as follows [29]:
3.2. Mathematical Modelling of TTECs
3.3. Effect of Thermal Resistance on the Performance of TTECs
3.4. Methodology and Materials in the Study
3.4.1. Optimization Parameters
- ▪
- Group 1—Objective functions: the objective function is maximum cooling rate and/or COP. For STEC, the equations of cooling rate and COP were presented before in Equation (4) and Equation (7), respectively. For TTEC, the equations of cooling rate and COP were presented before in Equation (11) and Equation (21). These objectives can be optimized individually or simultaneously based on single-objective optimization or multi-objective optimization approach.
- ▪
- Group 2—Variables: For STECs, the design parameters are: length of the semiconductor element (L), cross-sectional area of semiconductor element (A), and number of semiconductor elements (N). For TTECs, the design parameters are: supplied current to hot stage (Ih) and cold stage (Ic) of TTEC, and ratio number of semiconductor elements (r) between the hot stage and cold stage TTEC.
- ▪
- Group 3—Fixed parameters: For STECs, some fixed parameters need to be determined as follows: total volume in which STEC can be placed which is determined by the total cross-sectional area (S) and its height (H) and operating conditions such as applied current I and required temperature at hot side Th and cold side Tc of STEC. Then, the material properties are calculated based on Equations (18)–(20). For TTECs, fixed parameters are as follows: total number of semiconductor elements (Nt) in both stages of the TTEC, and operating condition of the system such as required temperature at hot side of the hot stage Th,h and cold side of the cold stage Tc,c of the TTEC.
- ▪
- Group 4—Constraints: For both types of TEC, the constraints can be: boundary constraints over the design variables, and the requirement of satisfying a required value of COP (COP > COPmin) and a limited value of the manufacturing cost (cost < costmax).
3.4.2. Single-Objective and Multi-Objective Optimization
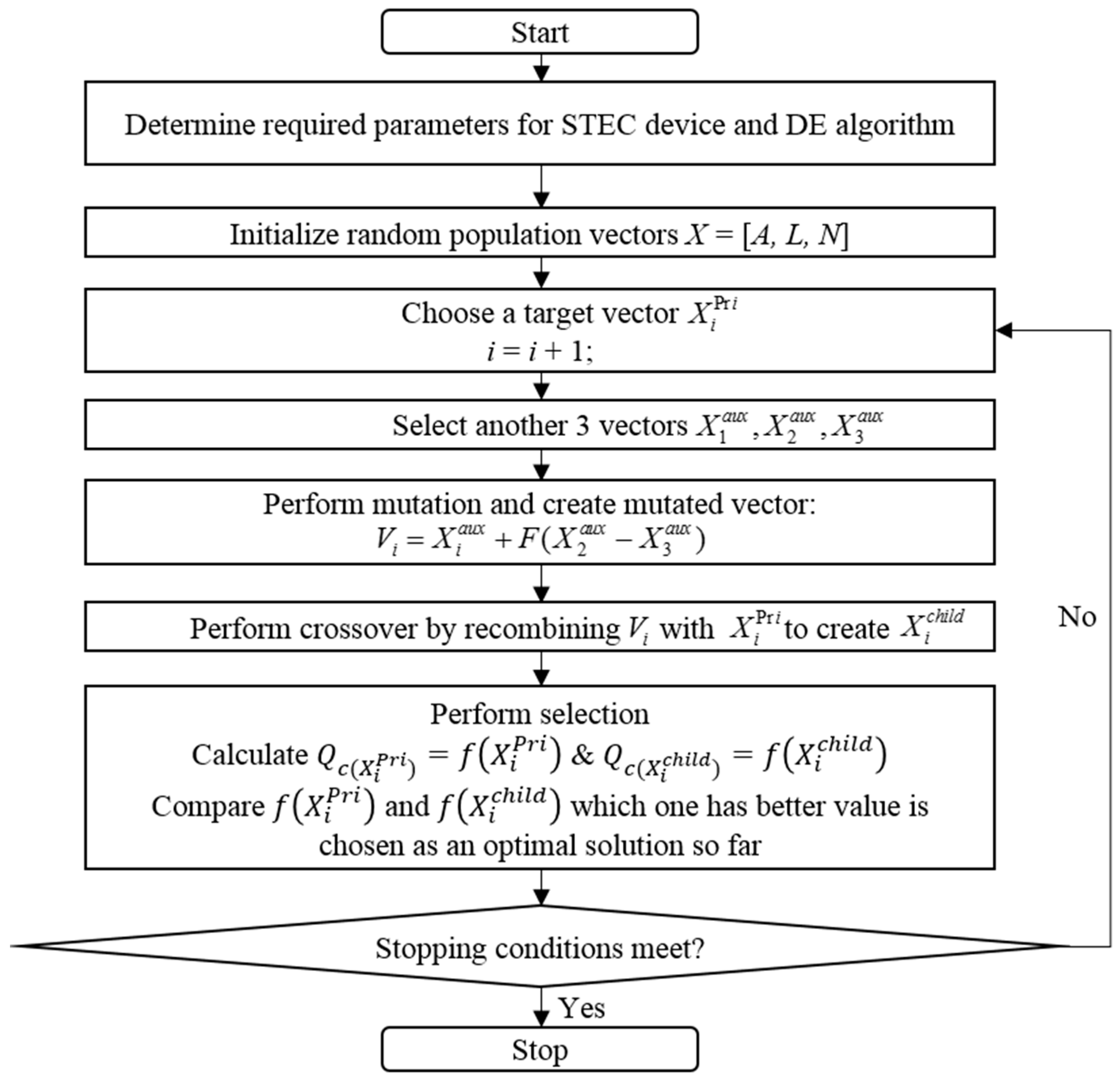
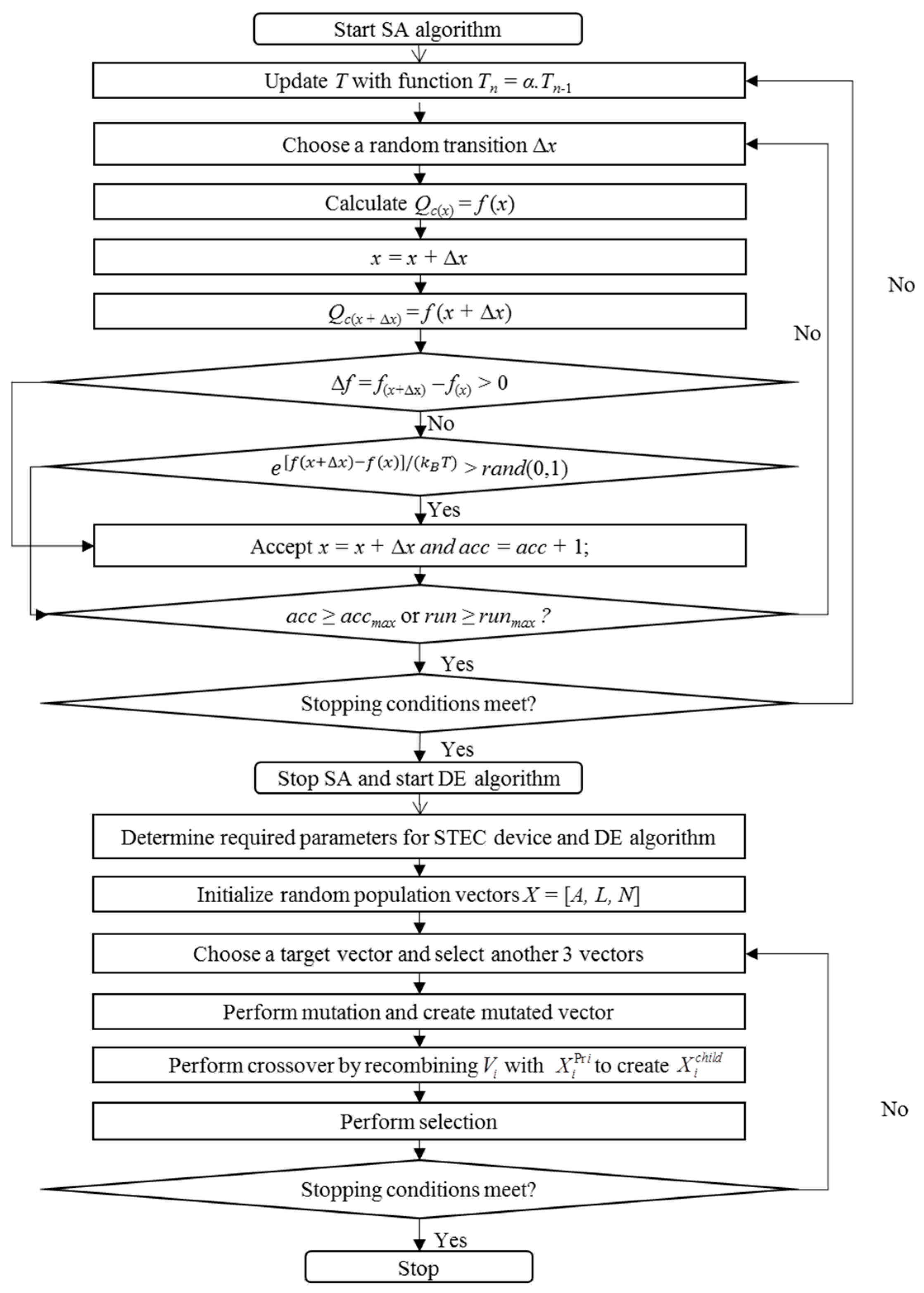
3.4.3. Differential Evolution Algorithm
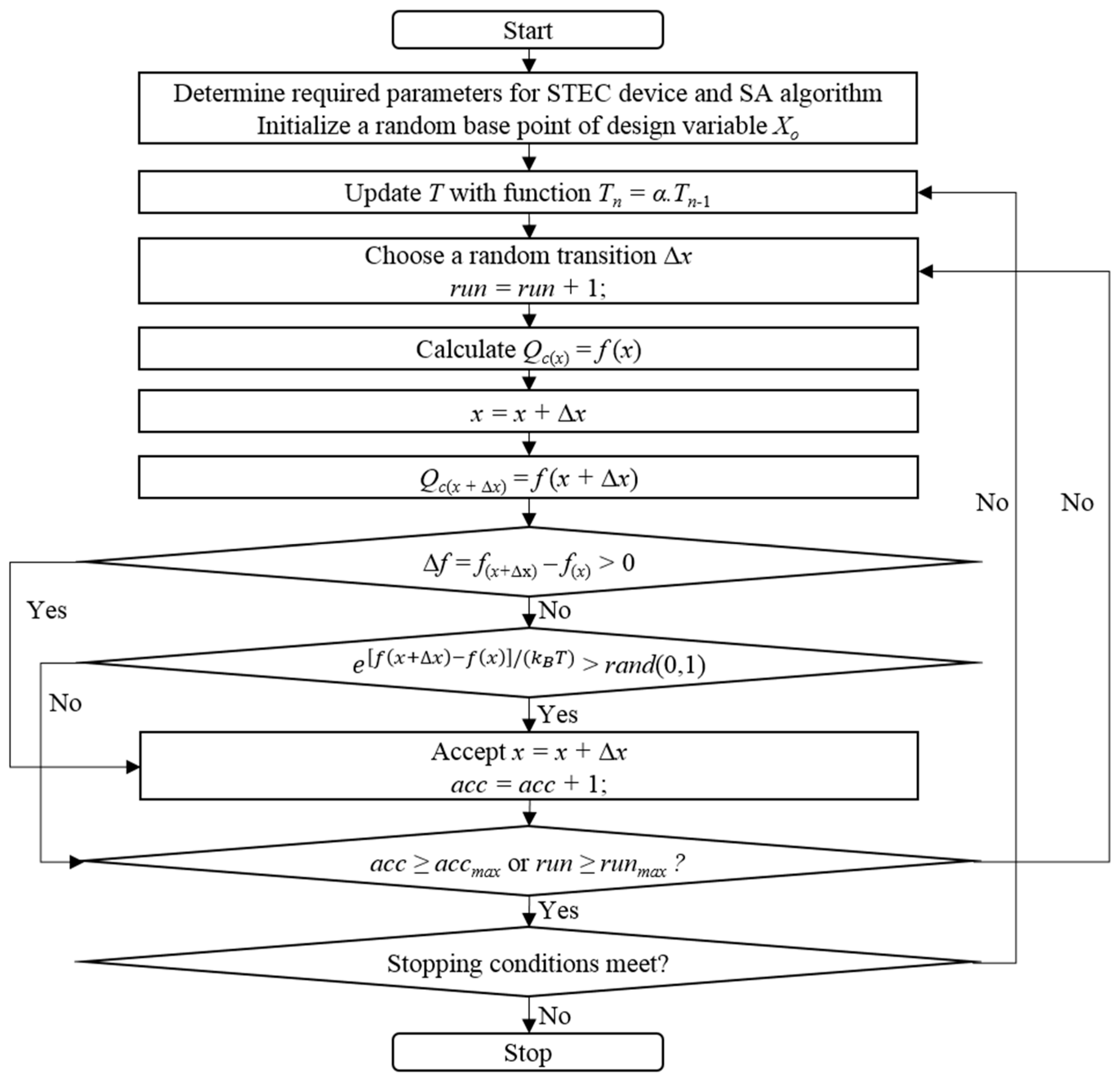
3.4.4. Simulated Annealing Optimization Algorithm
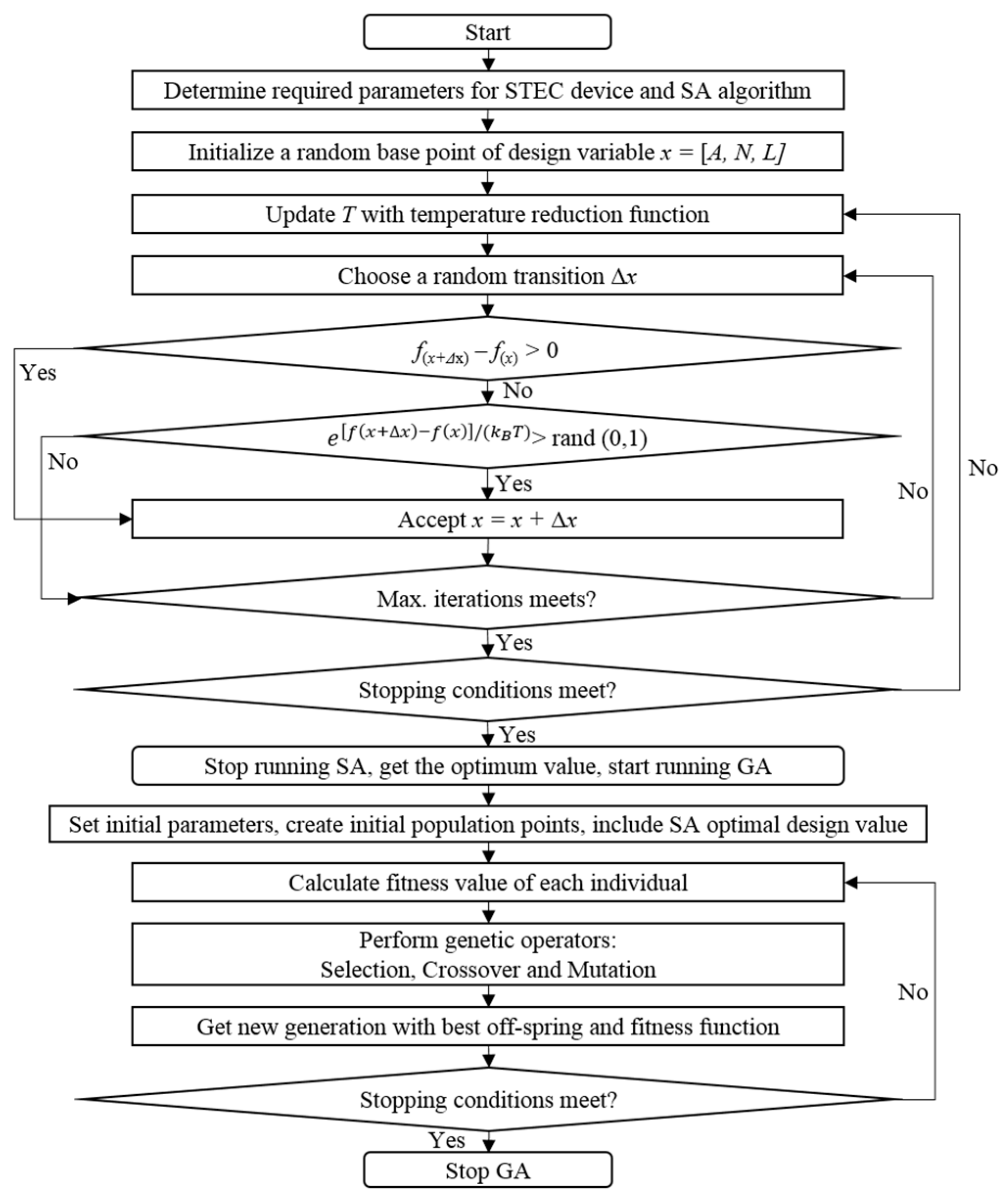
3.4.5. Hybrid Techniques Such as HSAGA and HSADE
3.4.6. Tests for Evaluating the Algorithms
- ▪
- Fast—the optimization technique has the capability to produce high-quality solutions quicker than other optimization approaches.
- ▪
- Simple—the algorithm code is easy to implement with less parameter setting than other optimization approaches.
- ▪
- Accurate—the optimization technique is able to identify higher quality solutions than other optimization approaches.
- ▪
- High impact—the optimization technique can solve a new or important—remarkable problem more accurately and faster than other approaches.
- ▪
- Robustness—the optimization technique is less sensitive to differences taking place in the problem features, tuning parameters, and data quality, according to other approaches.
3.4.7. Parameter Selection of TEC
- ▪
- Test case-1: The STEC model is optimized under the constraints of total limited area S = 100 mm2 and maximum cost of material $385. The parameter setting follows Table 6 but the requirement of COP is ignored.
- ▪
- Test case-2: The STEC model is optimized under the requirement of satisfying the condition that the COP is equal to 1. The purpose is to test the capability of solving non-linear equality constraint problem of both algorithms.
- ▪
- Test case-3: The STEC model is optimized under all the constraints in test cases 1 and 2. The capability of handling both inequality and equality constraints is tested to see which algorithm performs slightly better. The parameter setting follows Table 6.
- ▪
- Test case-4: The TTEC model is optimized with considering Qc,c as objective function under boundary constraint conditions, not too complicated as compared to the above test cases. The parameter setting follows Table 7.
- ▪
- Test case-5: The TTEC model is optimized with considering COP as objective function. The parameter setting follows Table 7.
4. Applications—Tests
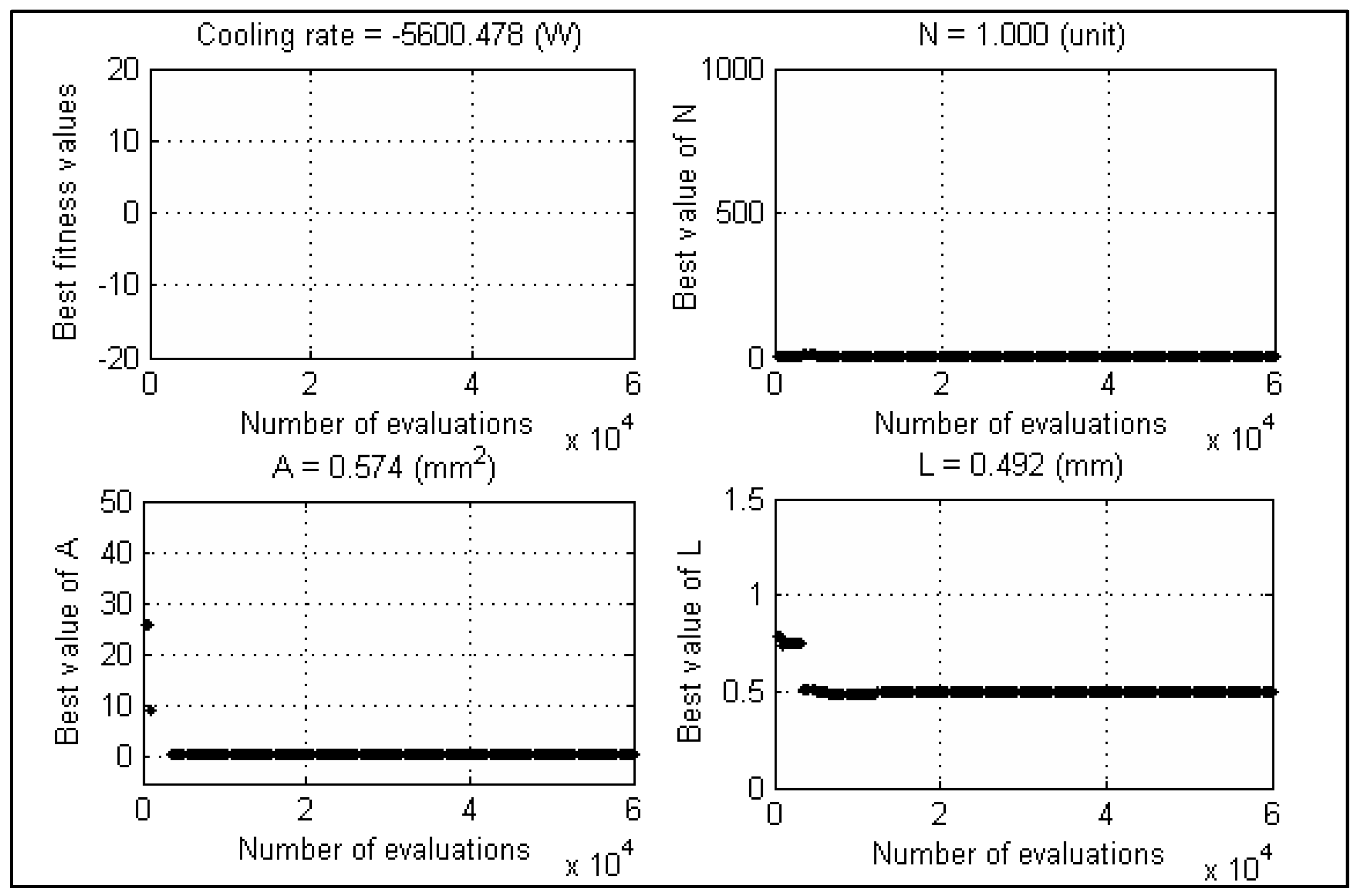
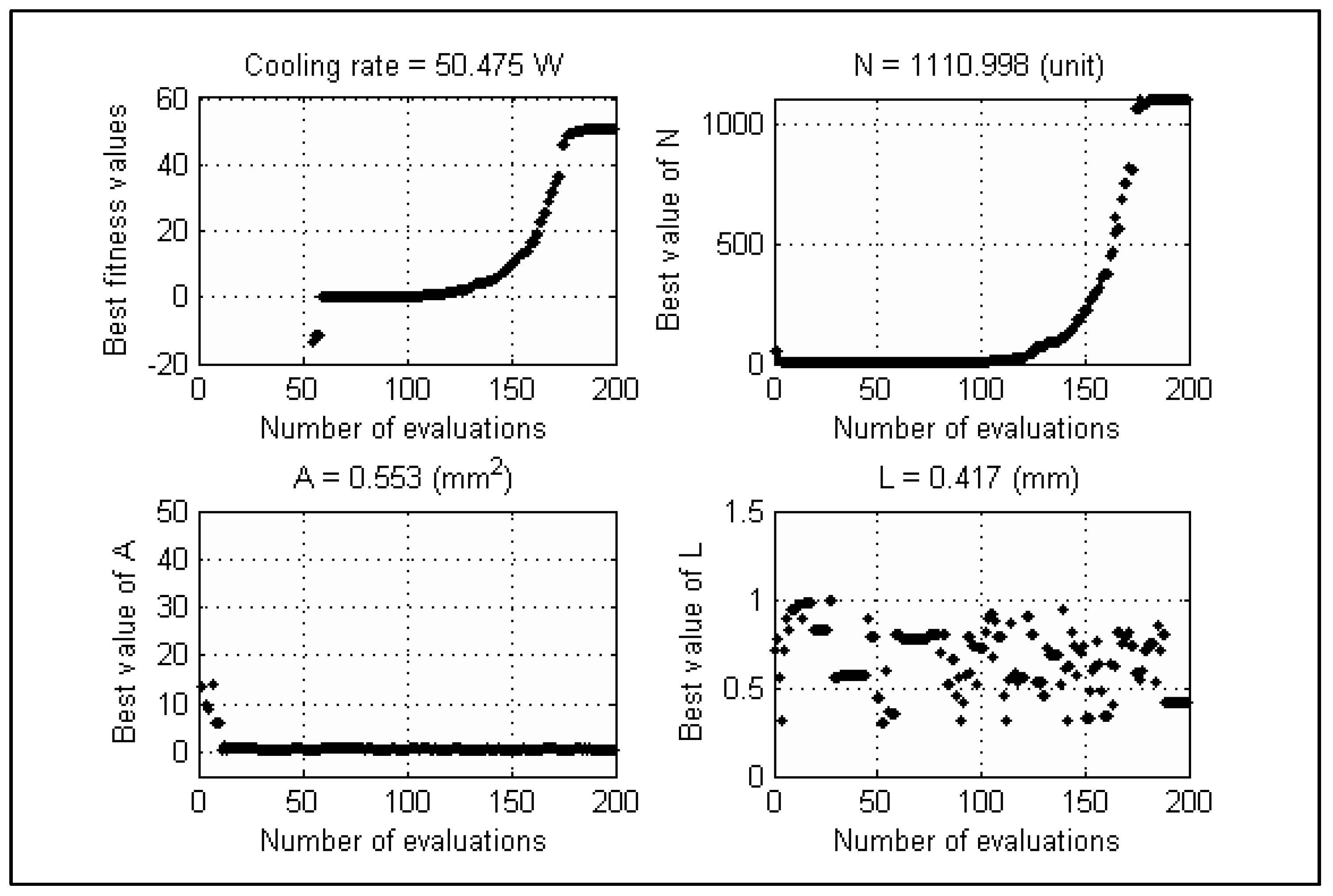
4.1. Convergence Speed Test
4.1.1. Test Case-1
4.1.2. Test Case-2
4.1.3. Test Case-3
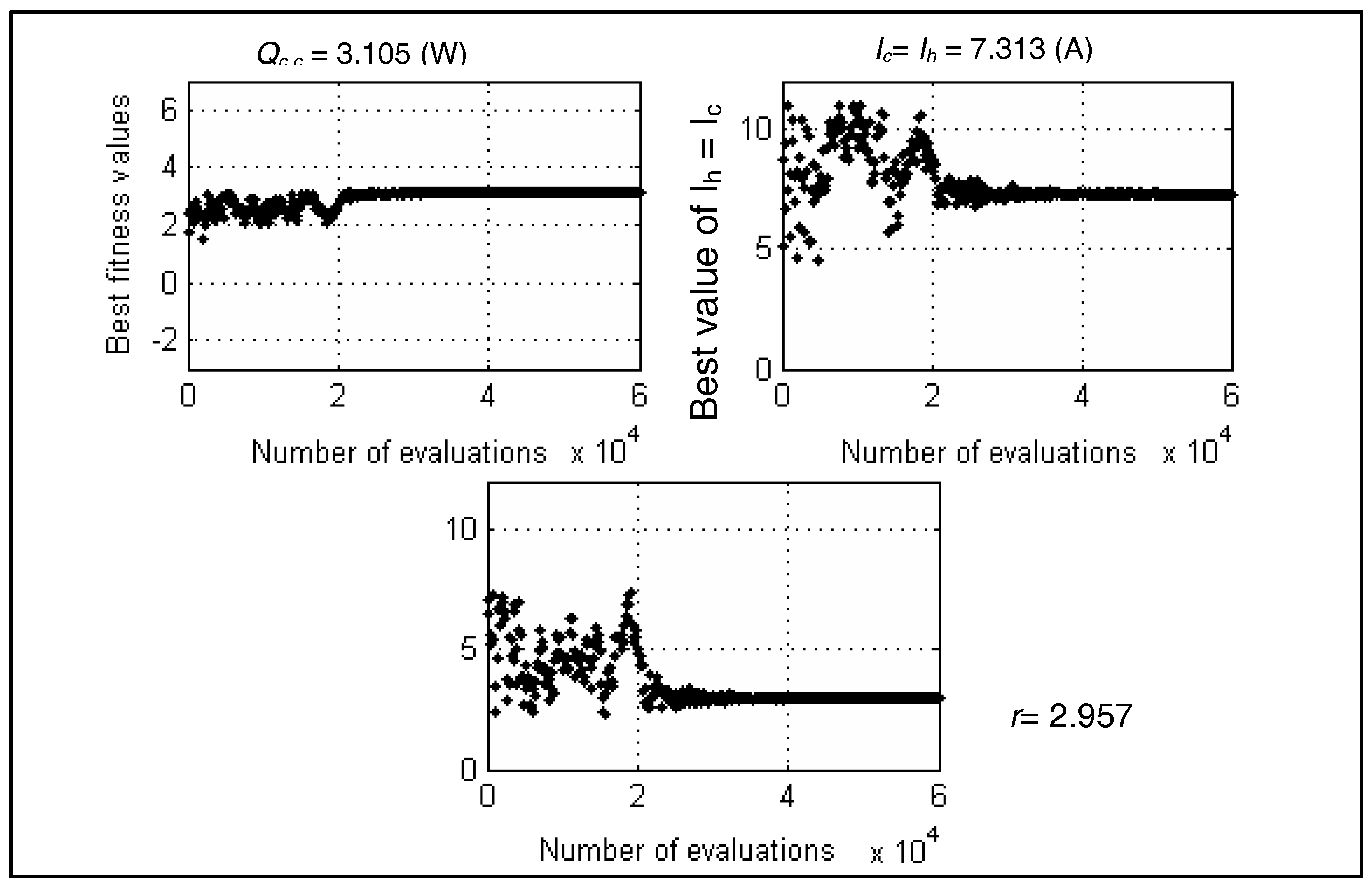
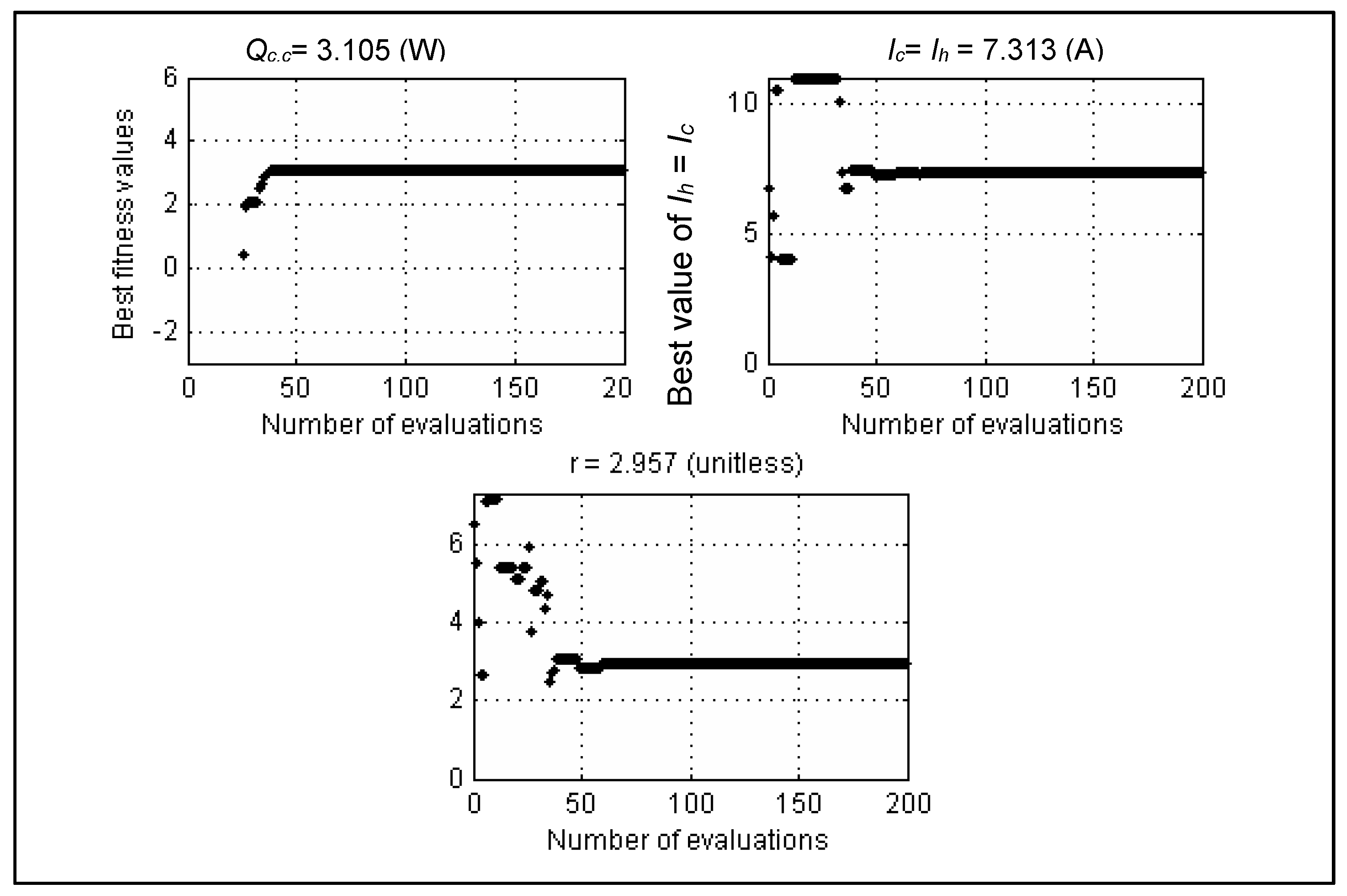
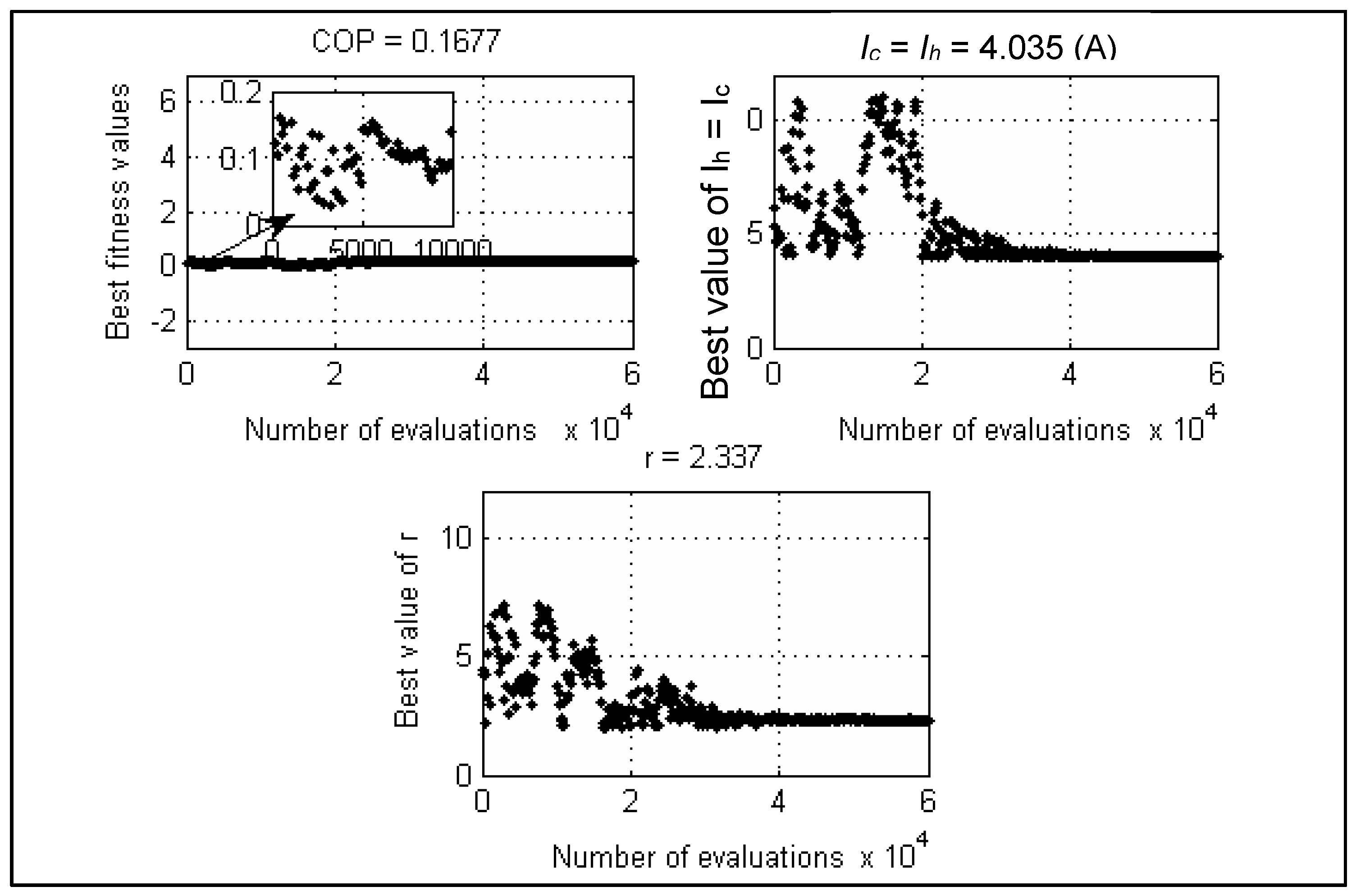
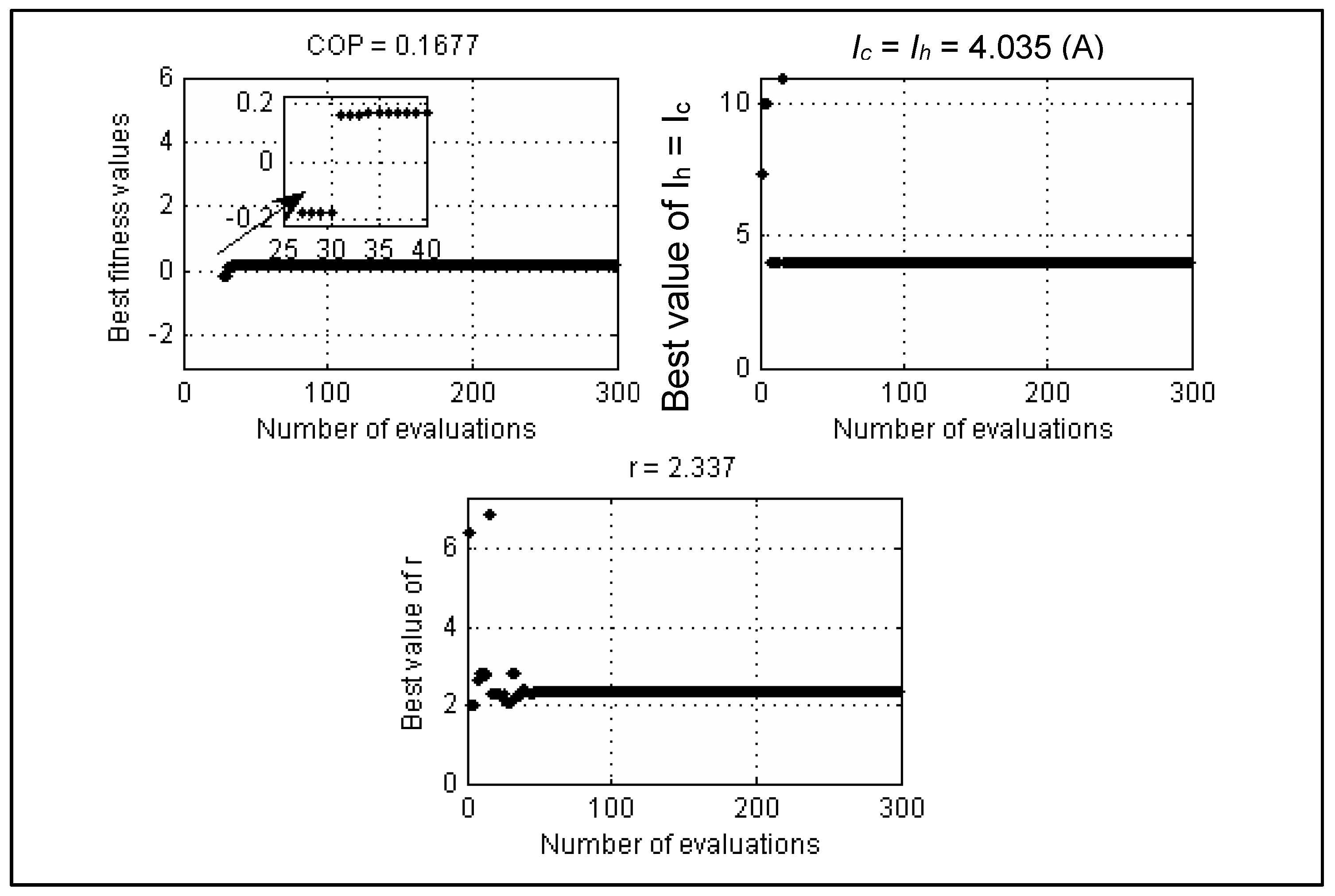
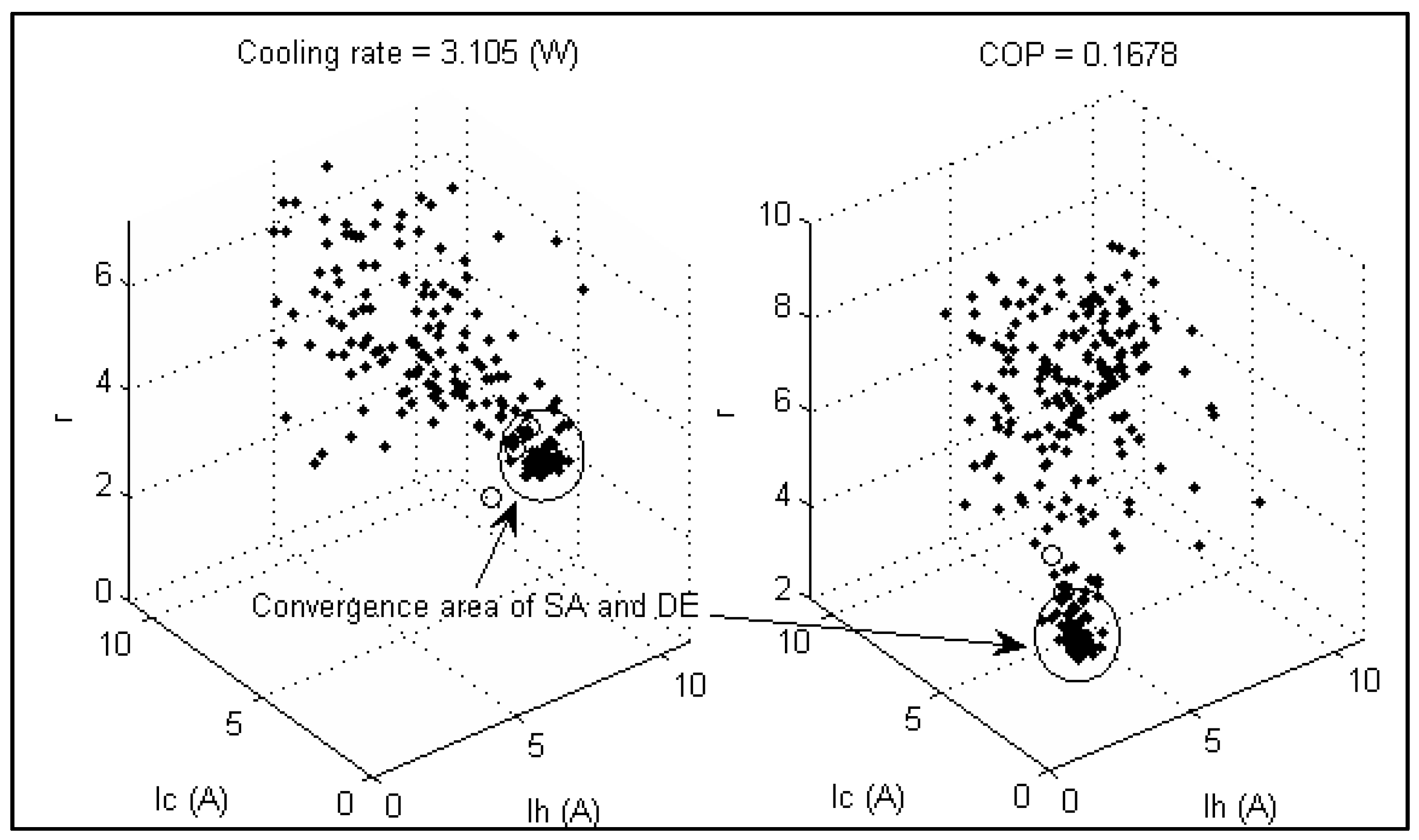
4.1.4. Test Case-4 and Test Case-5
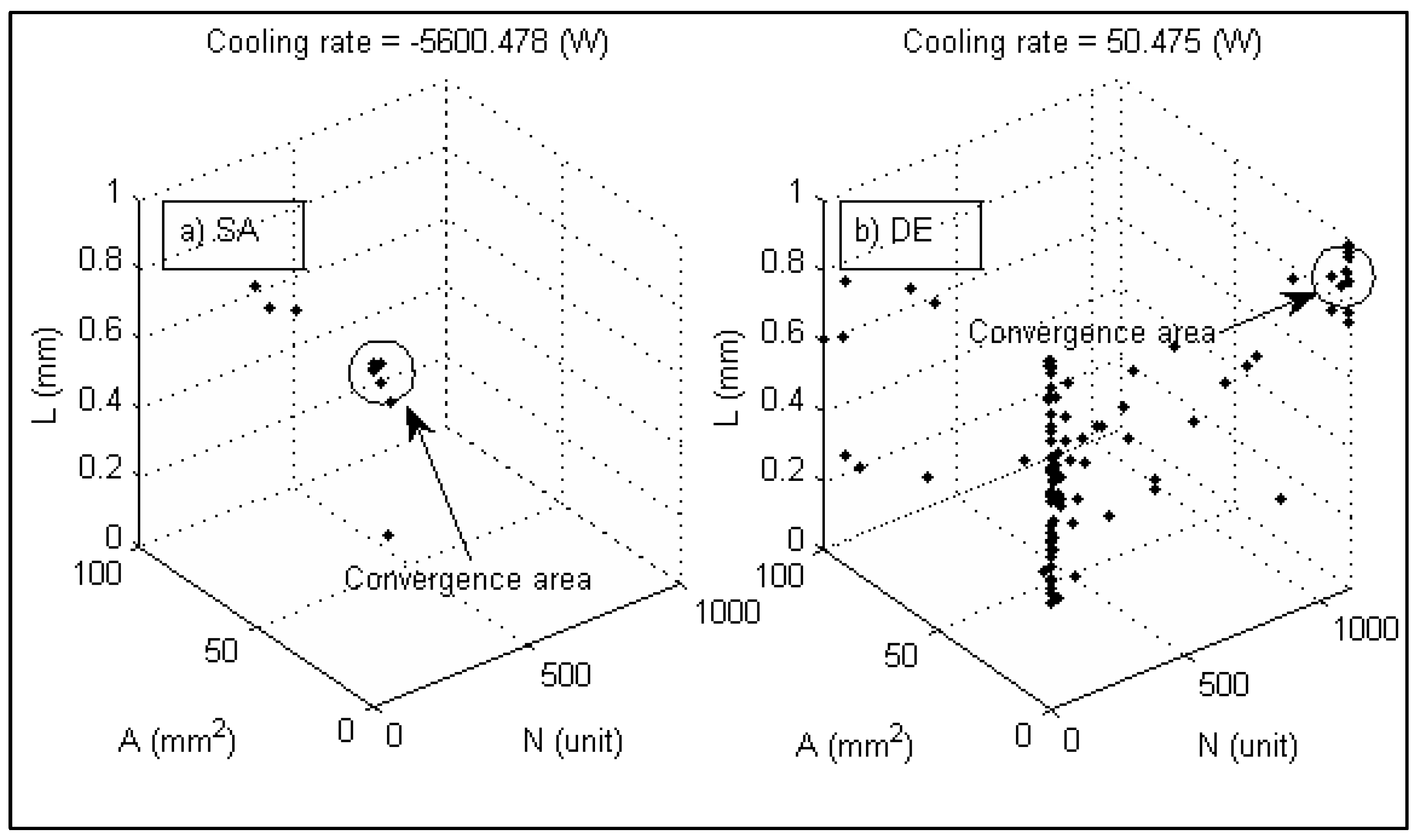
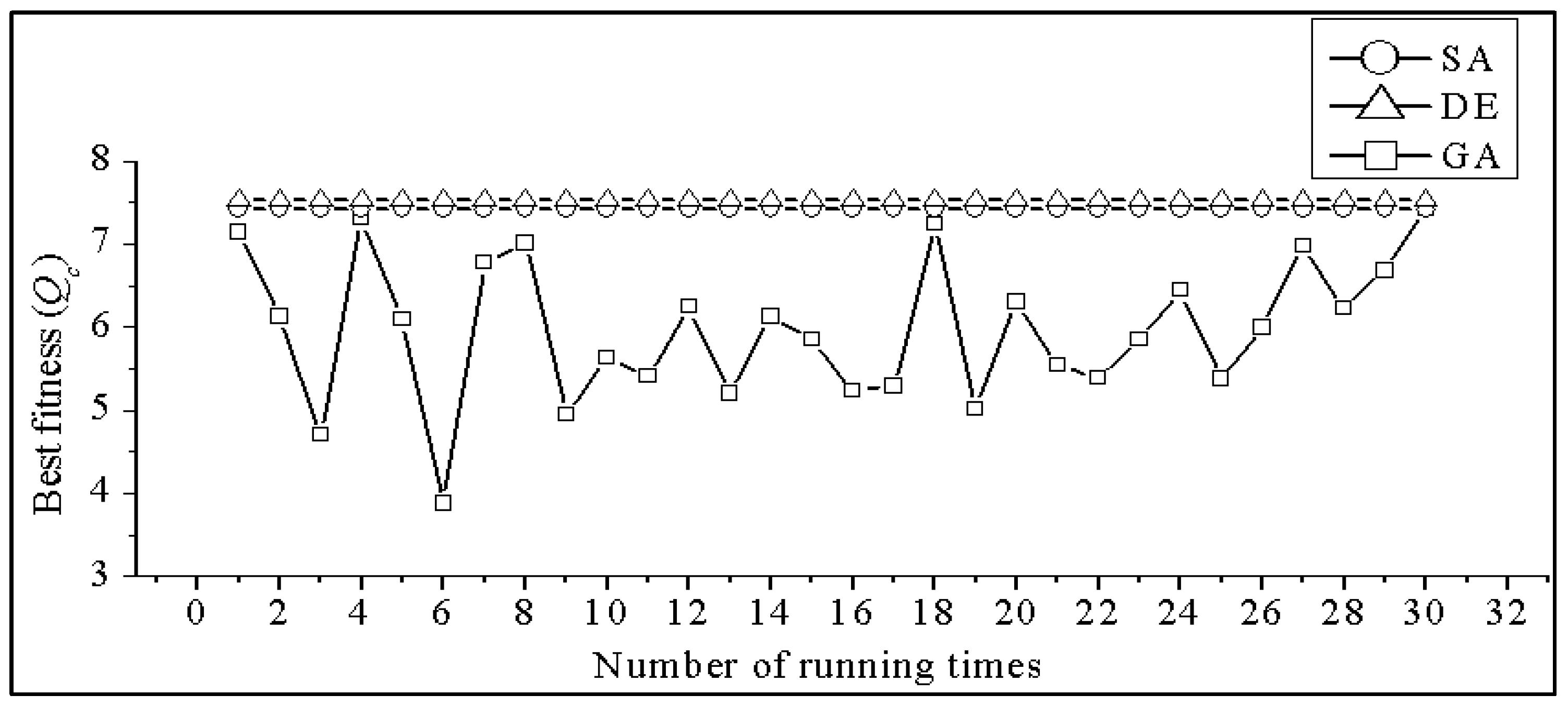
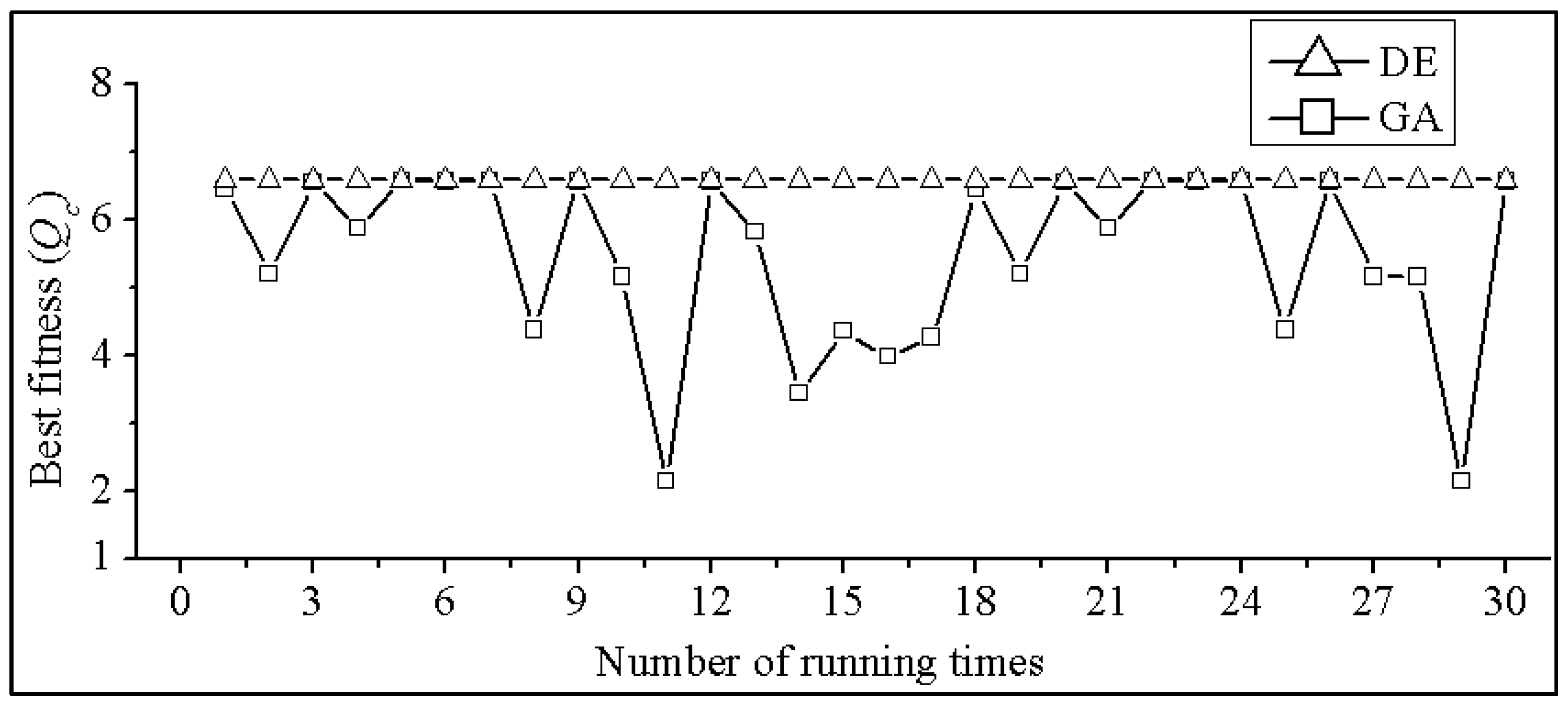
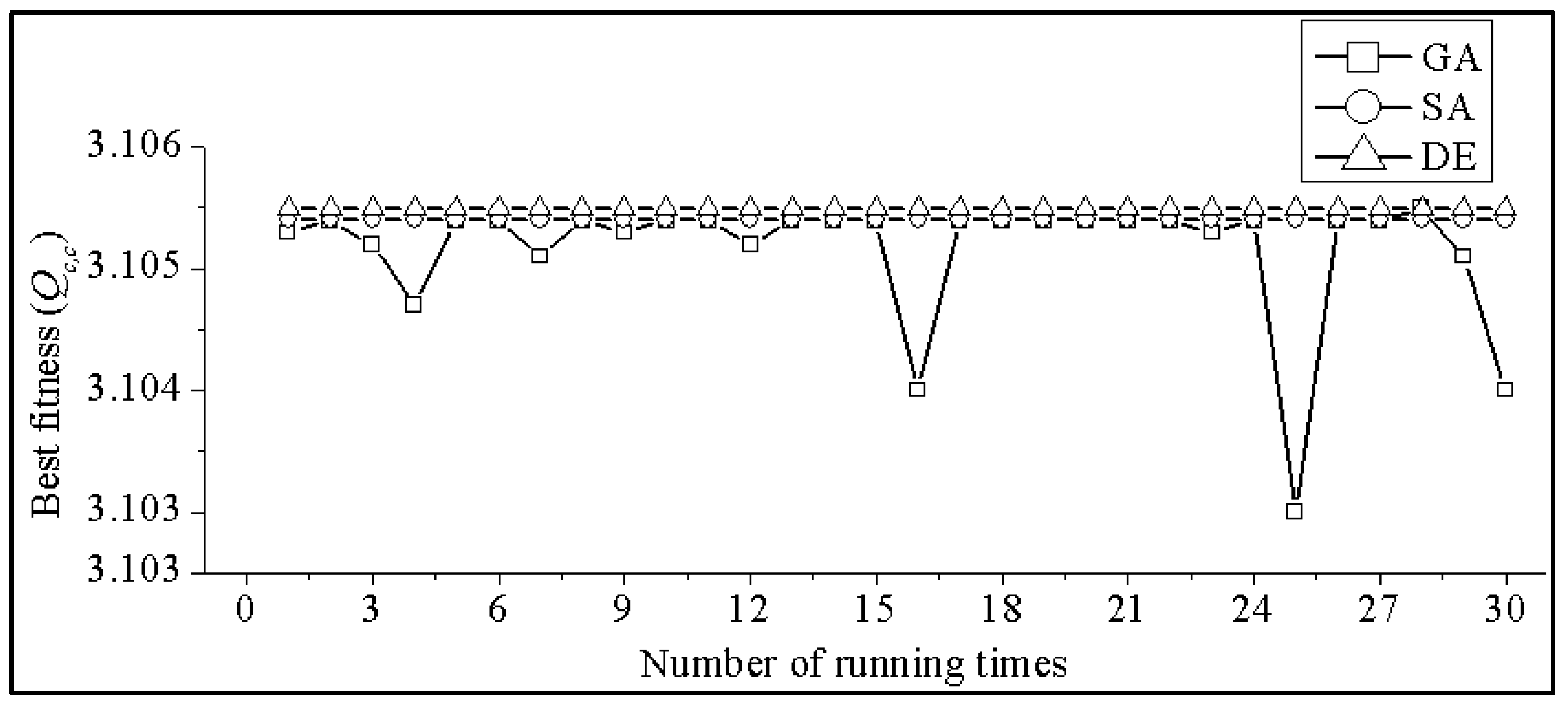
4.2. Stability Test
- Test case-1: Best fitness of STEC after 30 trial runs under two in equality constraints using GA, SA and DE.
- Test case-3: Best fitness of STEC after 30 trial runs under three constraints using GA and DE. SA can’t perform this test under equality constraints.
- Test case-4: Optimal Qc,c of STEC after 30 trial runs using GA, SA and DE.
- Test case-5: Optimal COP of STEC after 30 trial runs using GA, SA and DE.
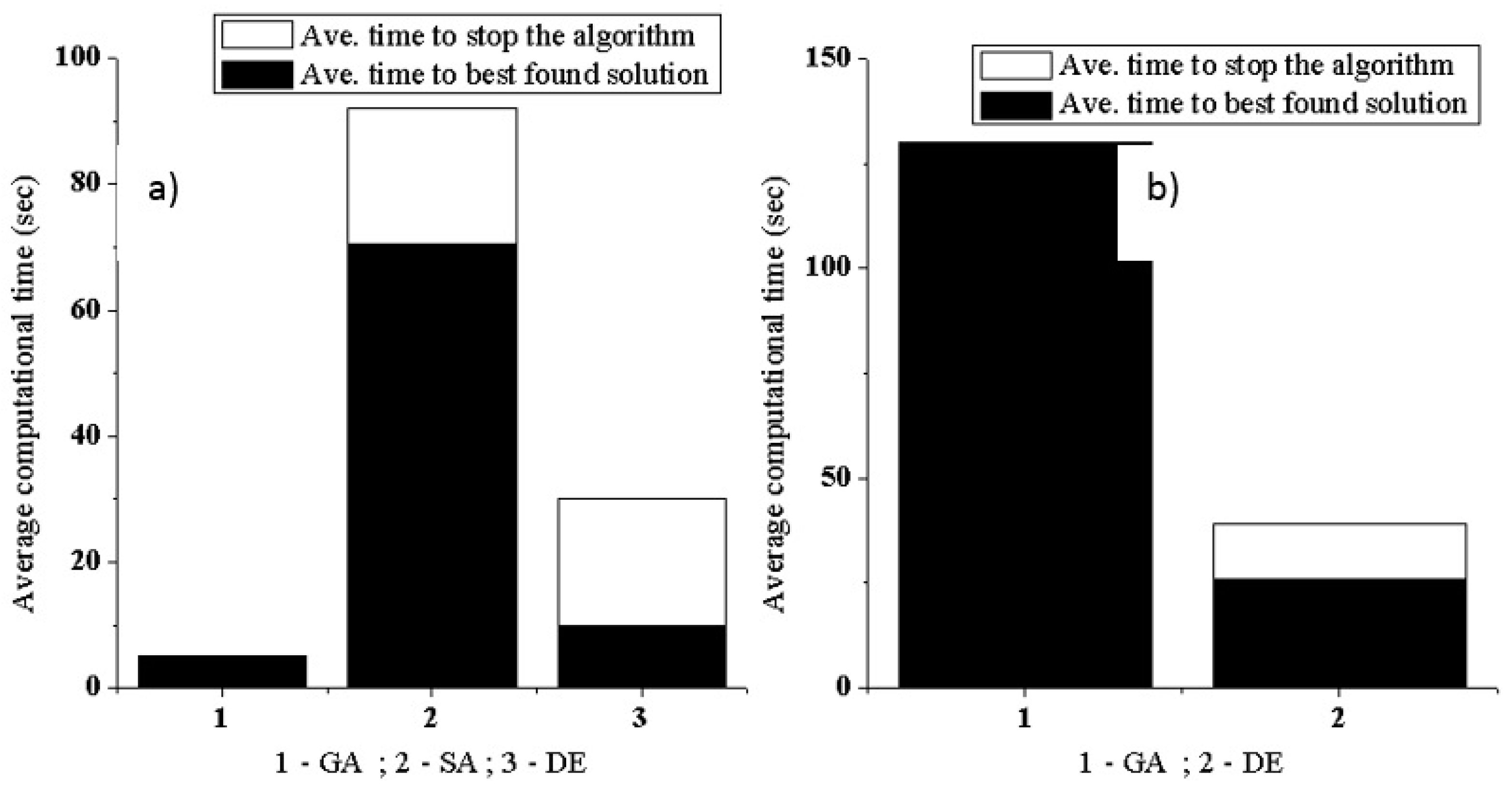
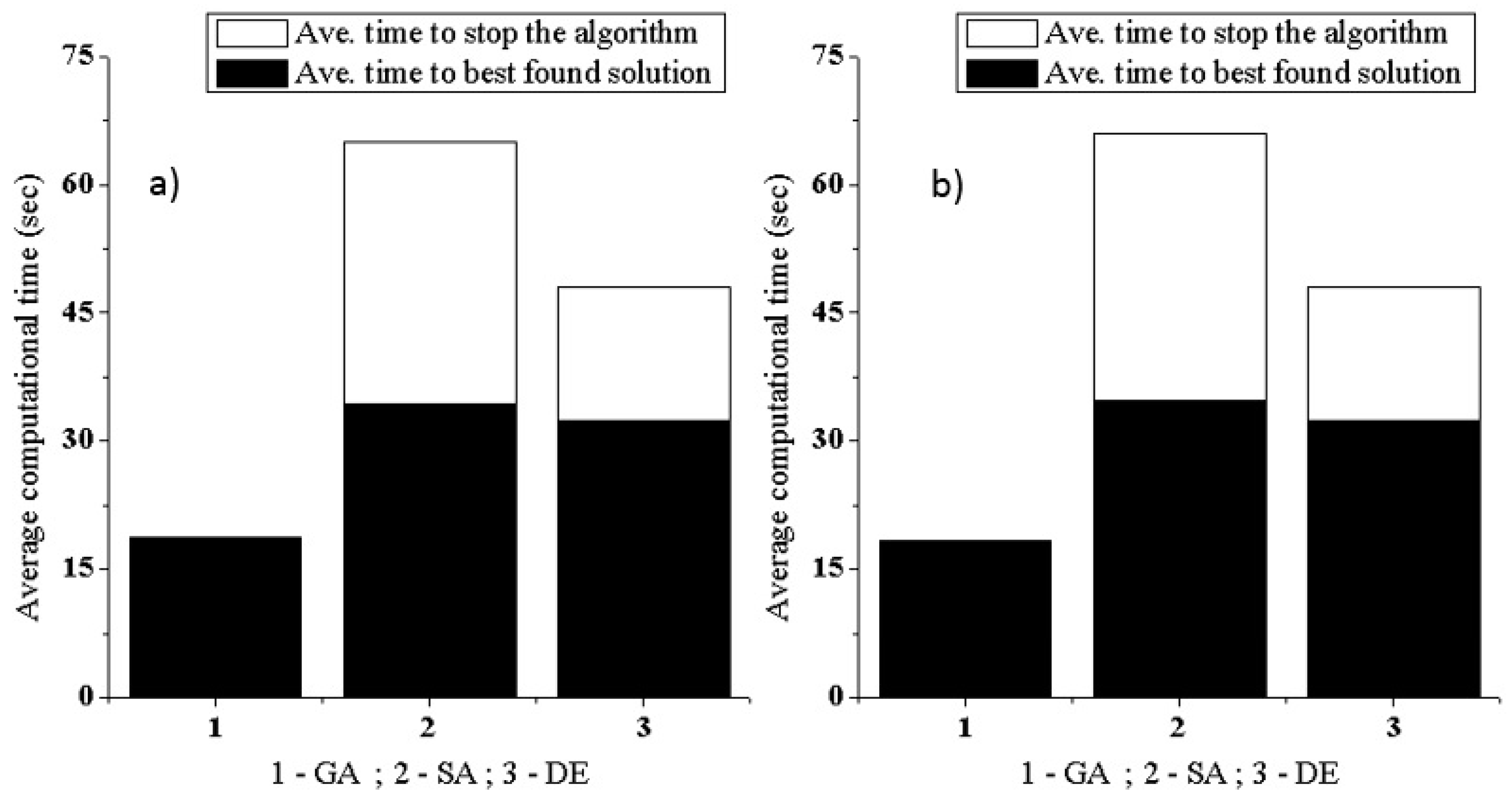
4.3. Computational Efficiency Test
4.4. Robustness Test
4.5. Test on HSAGA and HSADE
4.6. Optimization Results
- ▪
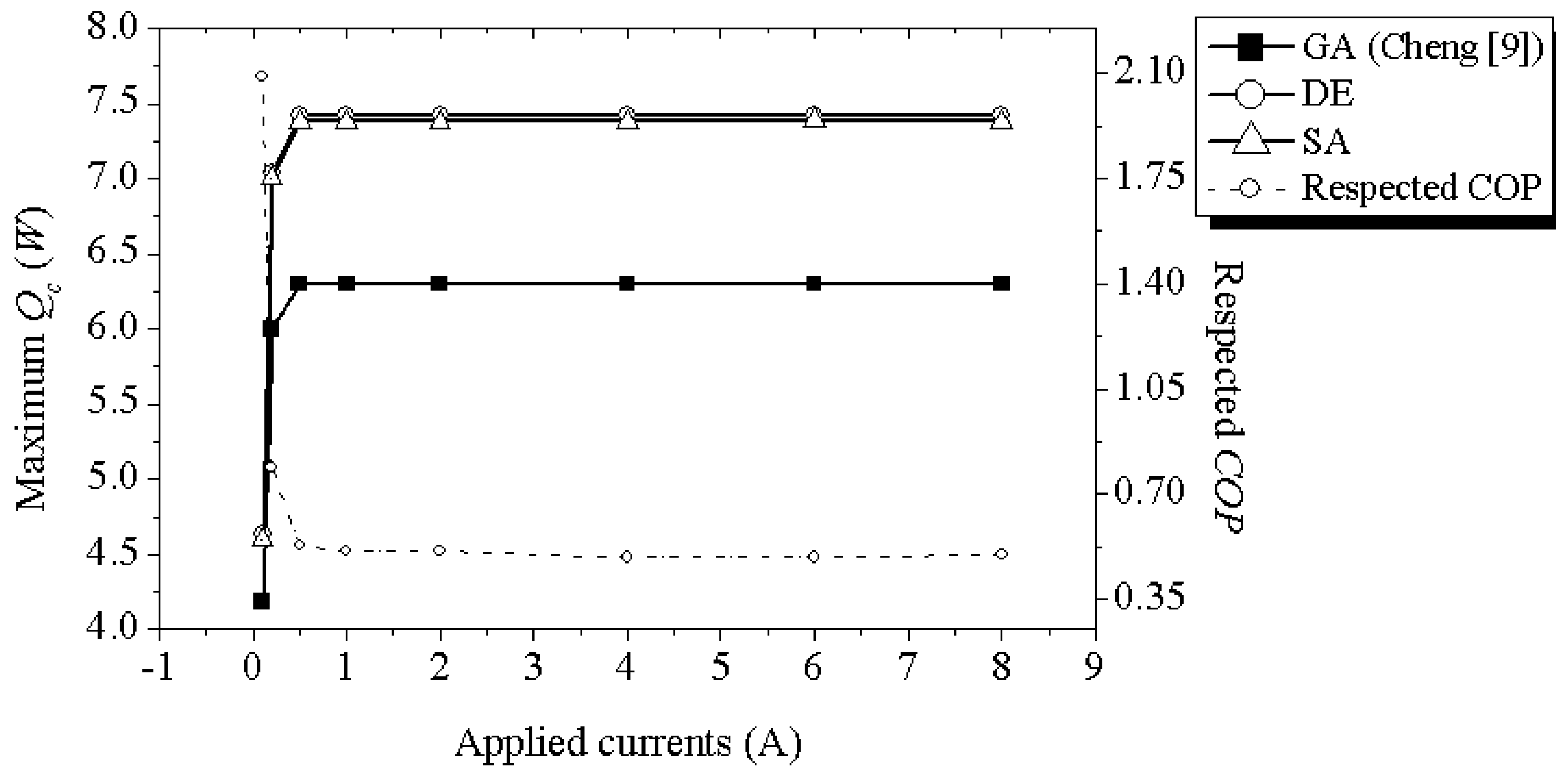
- Case-1: The parameter settings of the STEC model follow Table 6 and SA and DE are applied to find an optimal STEC geometric design under the limitation of total area S = 100 mm2 and the maximum cost for material is $385. However, the applied current is varied from 0.1 A to 8 A, hot side and cold side temperature are set as Th = Tc = 323 °K, the requirement of COP is neglected. With ΔT = 0 °K, the maximum cooling rate for every specific value of applied DC current can be achieved. Because COP is not considered, SA can provide good performance and is run under the same conditions, and the results from the Cheng’s work employing GA are used for the comparison.
- ▪
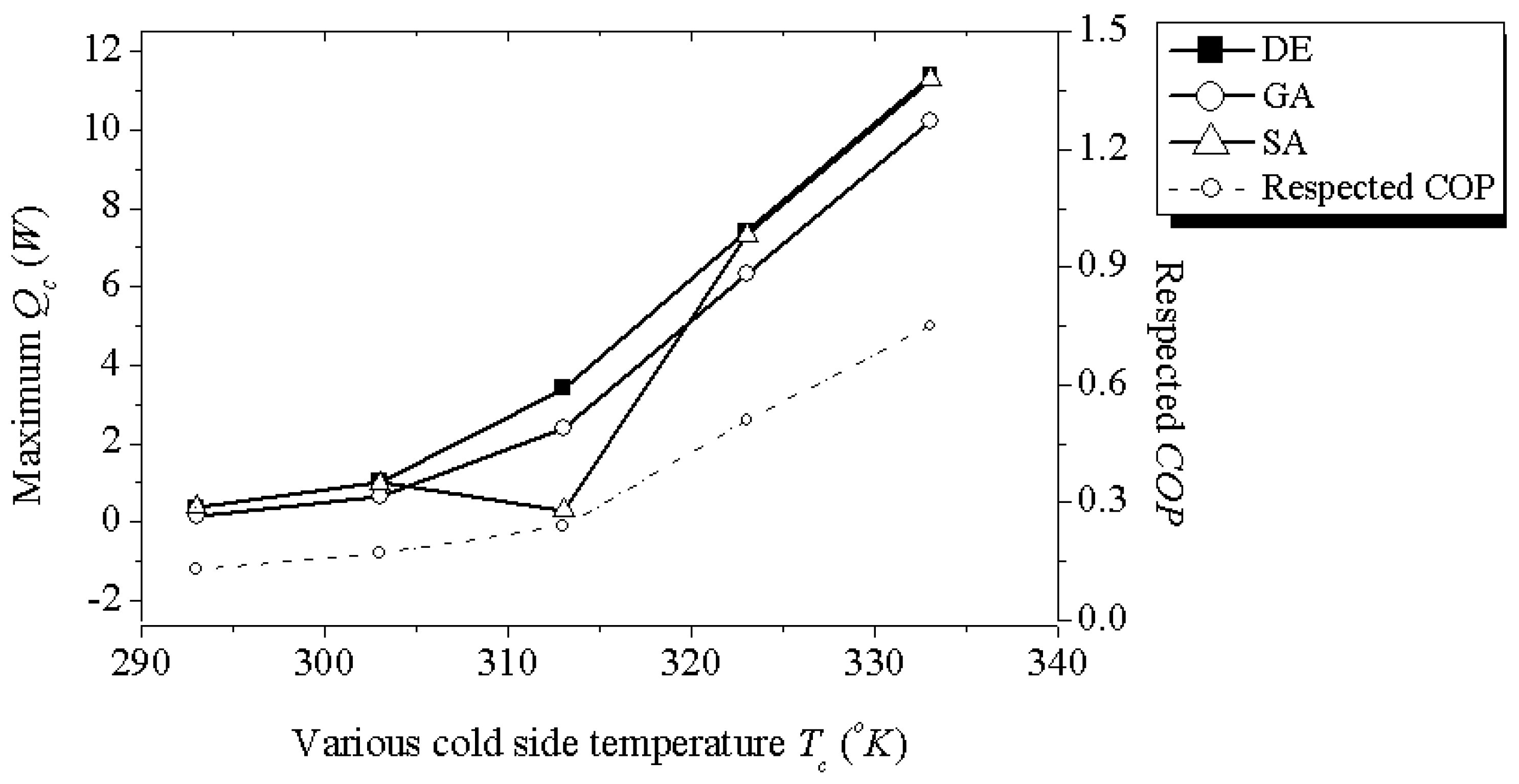
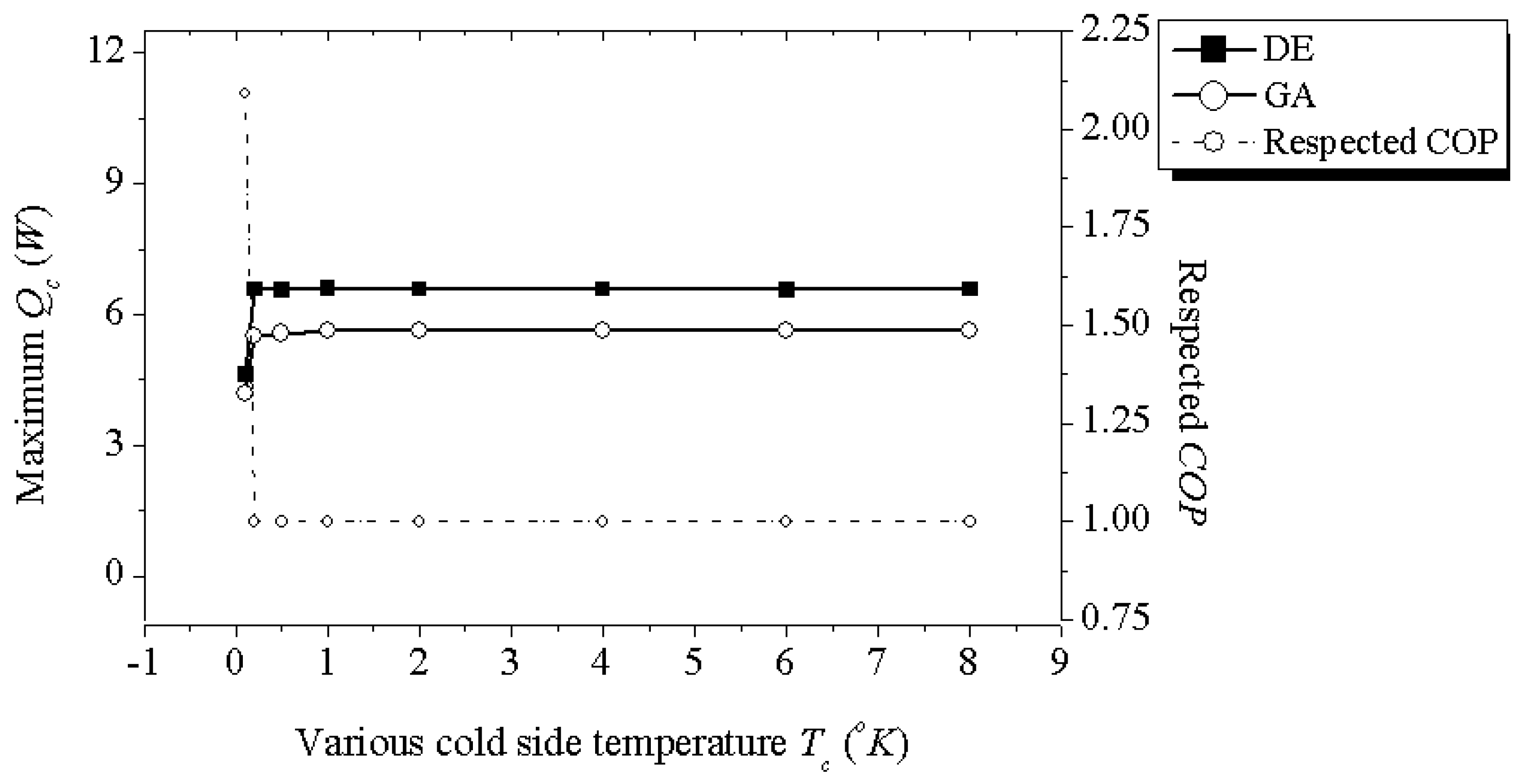
- Case-2: Same condition settings as Case-1 but with the cold side temperature Tc is varied from 283 °K to 323 °K and hot side temperature Th still remains in 323 °K and the applied current is kept in 1 A. The obtained results are useful for designers to choose a suitable STEC geometric design which yields enough cooling capacity and satisfies the required temperature difference ΔT with a defined input current.
- ▪
- Case-3: Same condition settings as Case-1. In this case, COP is not considered as a requirement though it has an important role in STEC performance. Considering cooling rate as an objective function which is single-objective optimization, in this case, the requirement of COP is required as a constraint condition which has a value equal to 1.
- ▪
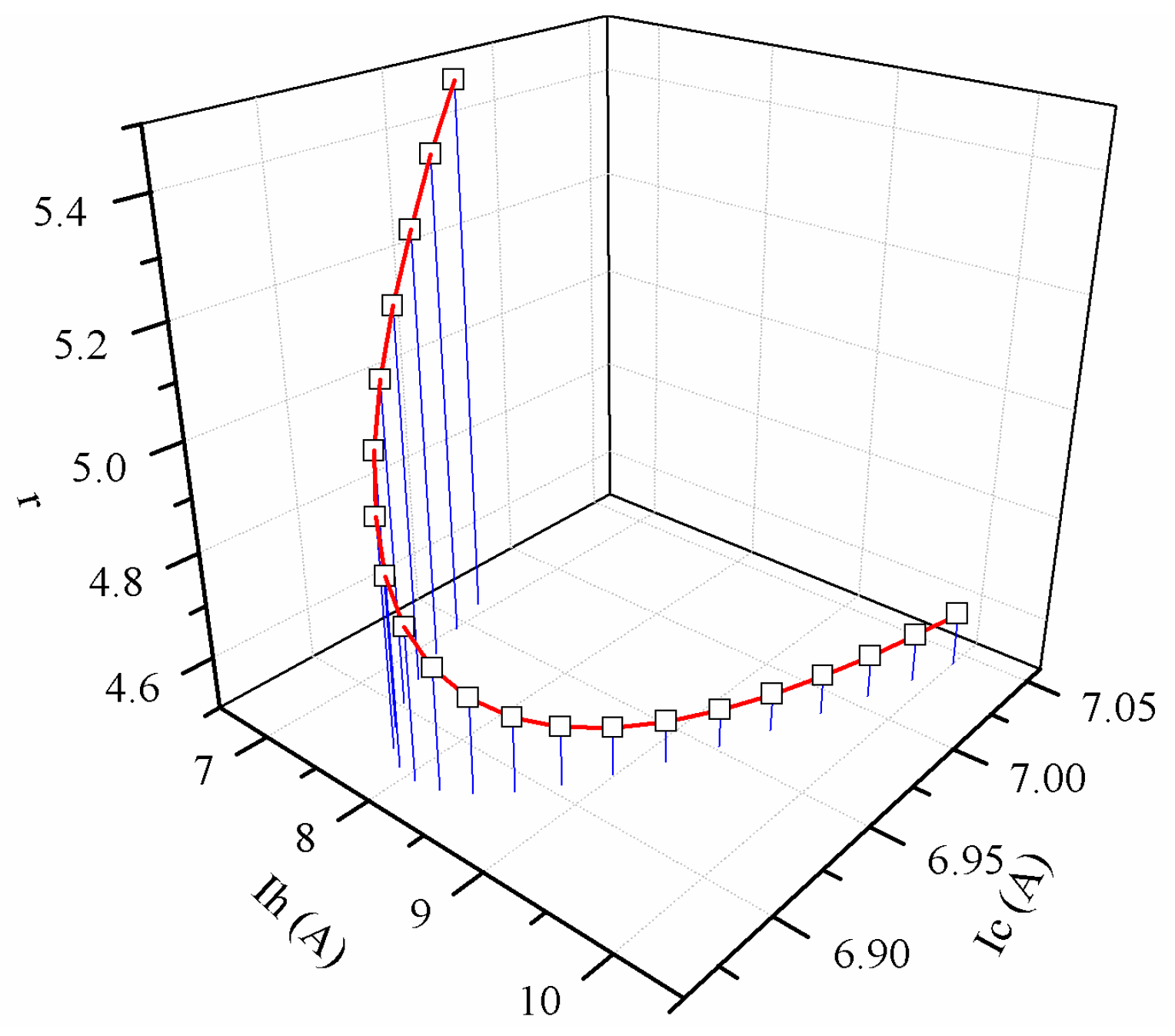
- Case-4: In this study, the parameters settings of TTEC follows Table 7 but the total number of semiconductor elements N is changed to 200 to compare with the results of Cheng [29]. The first type of TTEC as connected electrically in series (Ih = Ic) and second type of TTEC is separated electrically in series (Ih ≠ Ic) are used, Tc,c is varied from 210 °K to 230 °K and Tc,h is kept in 240 °K.
- ▪
- Case-5: In this case, the effect of contact and spreading resistance are taken into consideration. The parameter settings of two types of TTEC follow Table 14 and the calculations from Section 3.2.3, which are preferred from Rao [33] and Cheng’s work [30] with the consideration of contact and spreading thermal resistance. TTEC is used to produce temperature Tc,c = 210 °K at a temperature of Th,h = 300 °K is needed to be optimized for maximizing Qc,c and COP separately. The total number of semiconductor elements of TTEC is Nt = 100 units and the ratio of cross-sectional area to the semiconductor element is G = 0.0018. Thermal resistance is presented at the interface of TEC. Alumina with a thermal conductivity kh,s equal to 30 W/m°K is a substrate for considering the spreading resistance. The thickness of the substrate Sh,s is equal to 0.1 cm. In order to consider the contact resistance, which is between the two stages, the joint resistance RSj is varied from 0.02 to 2 cm2K/W.
- ▪
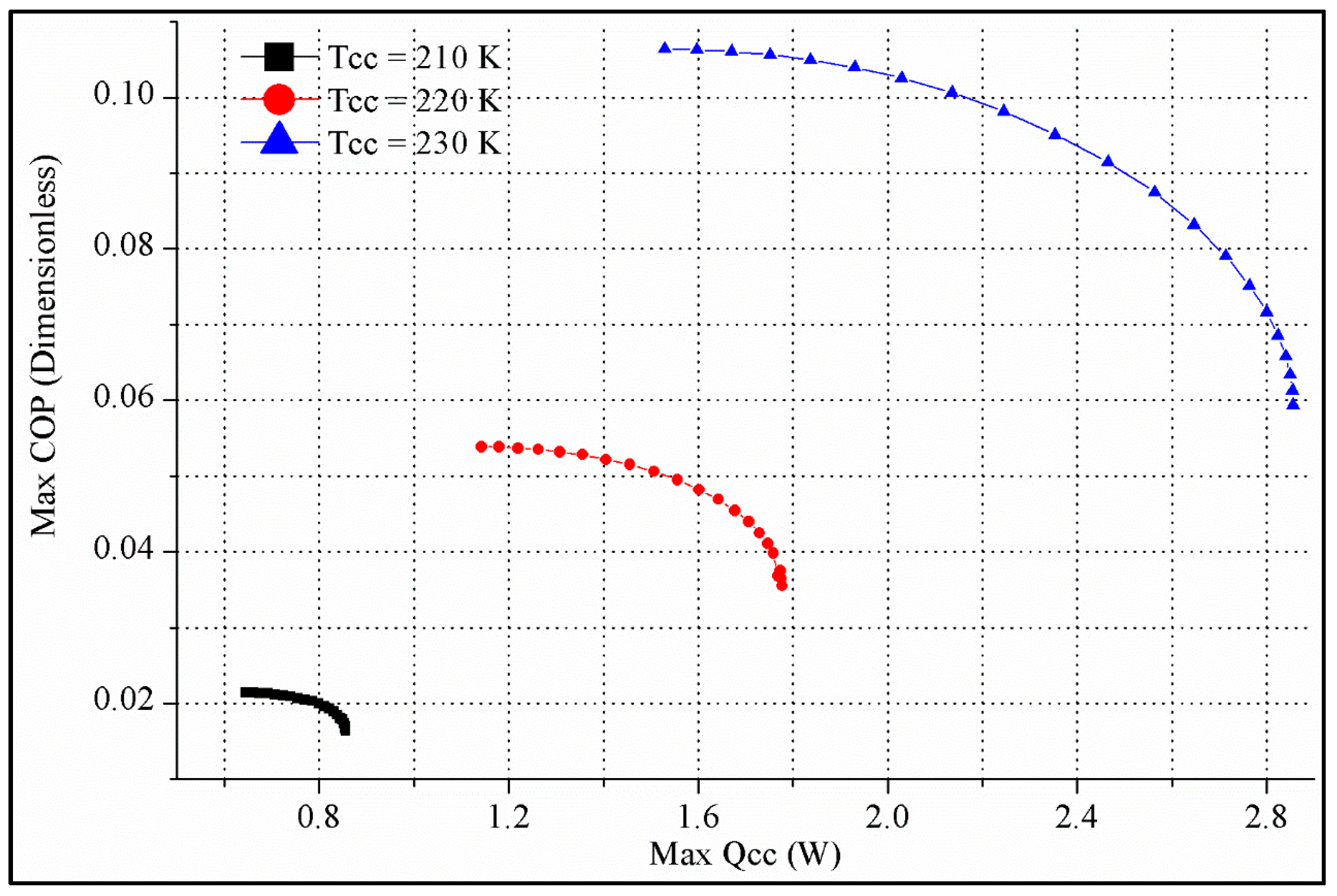
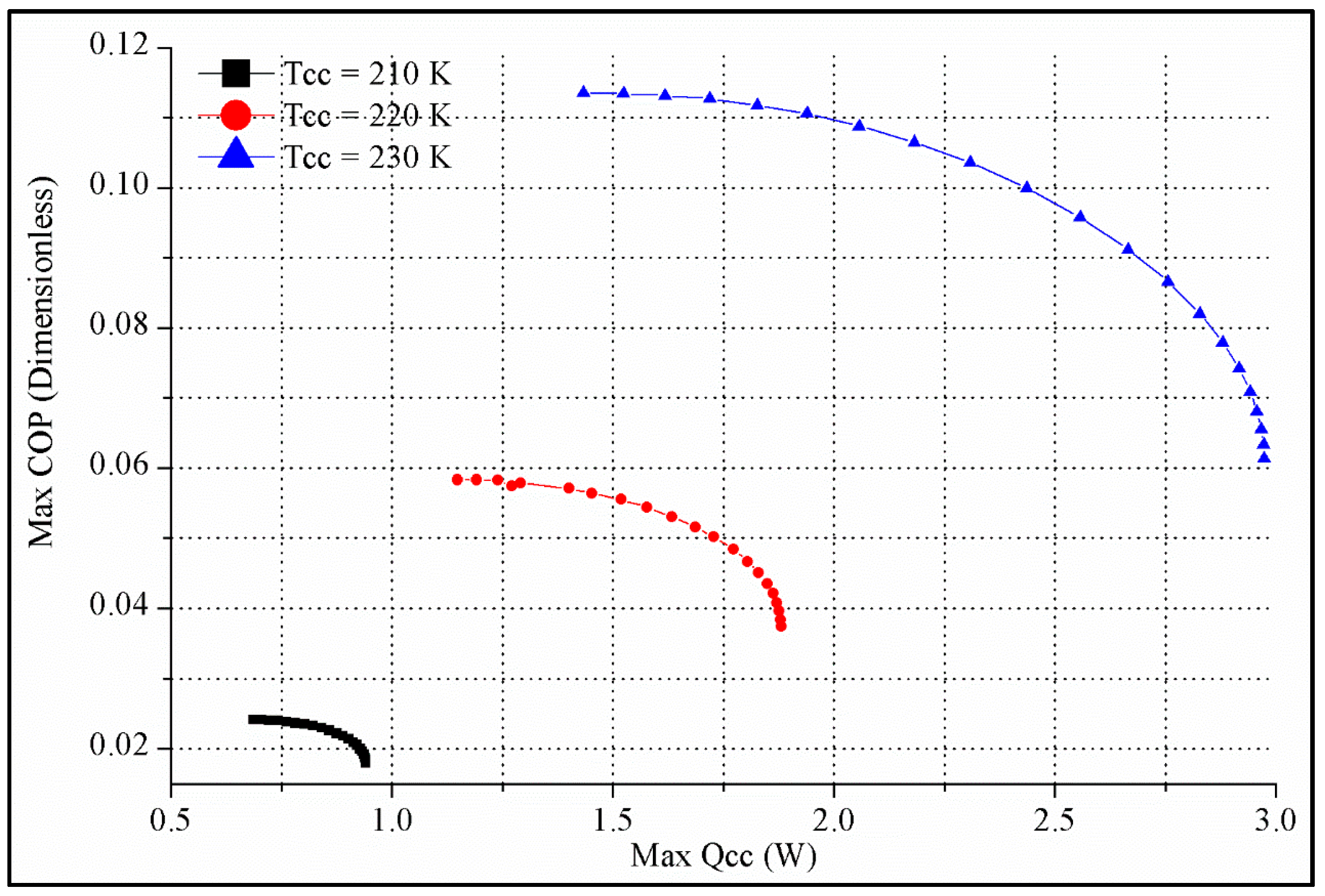
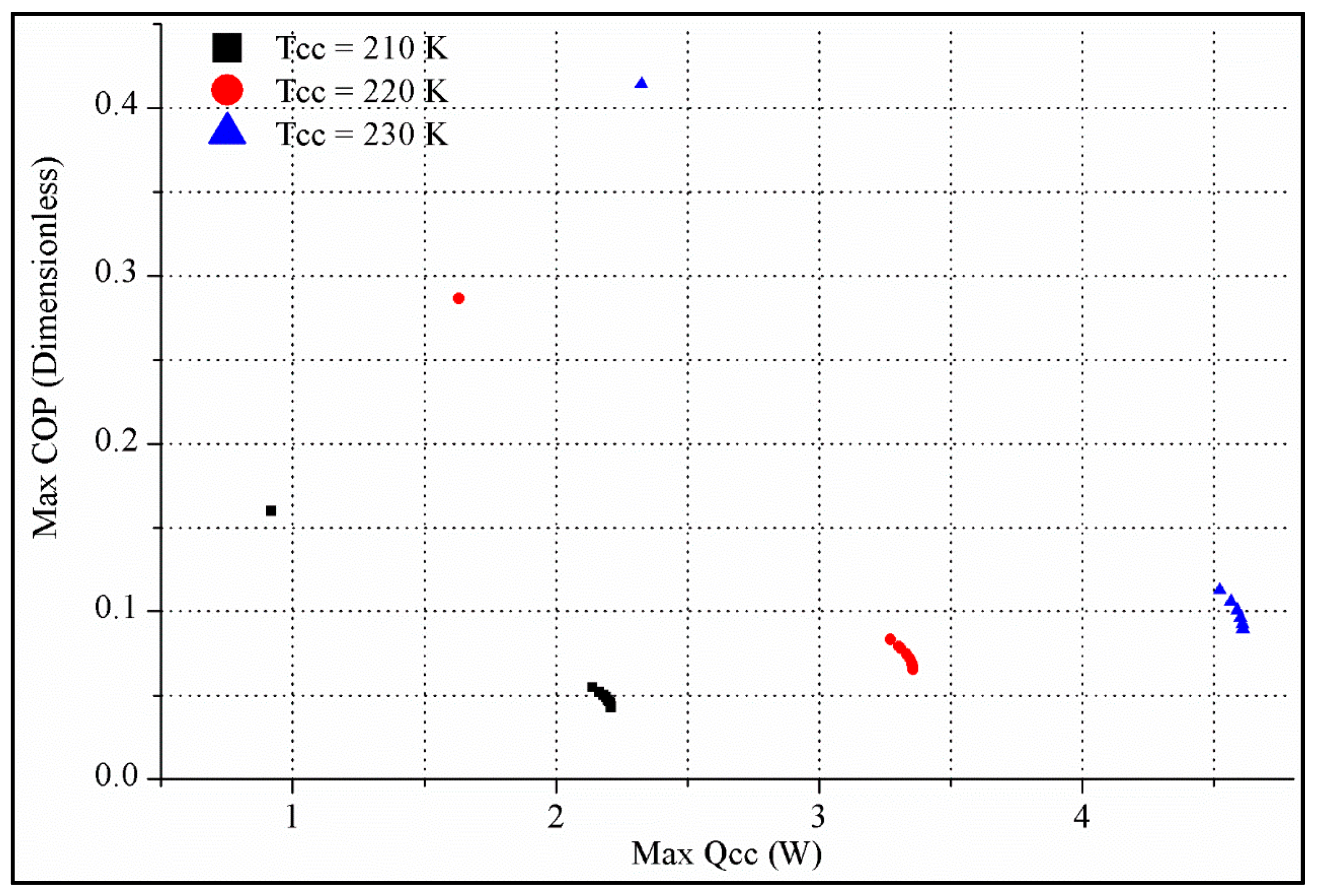
- Case-6: In this case, multi-objective optimization maximizing Qc,c and COP simultaneously to create the Pareto frontier. Following the parameter settings of Table 14, the TTEC type with better performance from Case-5 is chosen to form the Pareto front graph. TTEC designs with the balance of maximum Qc,c and maximum COP are suggested.
4.6.1. Single-Objective Optimization Results
4.6.2. Multi-Objective Optimization Results
5. Discussion
- ▪
- Results provided here are some proofs of the success of SA and DE in solving single-objective and multi-objective optimization problems.
- ▪
- Results of this study contribute to the previous findings in the literature (and also ideas in this study) regarding the better optimization performance of both SA and DE than GA.
- ▪
- The study here provided a wide examination of the optimization problems of TECs by focusing on the stability, reliability, robustness and computational efficiency of the techniques used. These are important to have accurate ideas about also the success of SA and DE according to objective tests—problems and performance of the GA.
- ▪
- According to the obtained findings (results), it is possible to indicate that the objectives of the study have been met. In detail, our investigation on using metaheuristic stand-alone techniques like SA and DE for STECs and TTECs has been successful. Following that, the research has proven that the development of hybrid techniques for STECs and TTECs has resulted in positive findings. Finally, validation of all the techniques used (stand-alone and hybrid ones) on STECs and TTECs has been done through the explained methodology—research process.
- ▪
- Multi-objective optimization approaches discussed in this study are useful for the designer to find the suitable design parameters of TECs balancing the important role of cooling rate and COP.
- ▪
- For the interested readers, the results reported here open doors to further investigations of STECs and TTECs using additional alternative metaheuristic and stand-alone techniques, and also alternative methods for them. Additionally, it is good to run alternative design optimizations by using the same SA and DE stand-alone techniques and also hybrid techniques developed with them.
- ▪
- Optimization is a process occurring in life itself and especially hard problems require the use of effective and accurate techniques to obtain the desired optimal results. Currently, metaheuristic techniques are important ways to deal with such problems. There are many unsolved hard problems or problems requiring better solution methods waiting for researchers to perform the necessary investigations on them.
6. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cohen, J.; Rogers, D.J.; Malcore, E.; Estep, J. The Qwest for High Temperature MWD and LWD Tools; GasTIPS: Vancouver, BC, Canada, 2002. [Google Scholar]
- Sinha, A.; Joshi, Y.K. Downhole Electronics Cooling Using a Thermoelectric Device and Heat Exchanger Arrangement. J. Electron. Packag. 2011, 133, 041005. [Google Scholar] [CrossRef]
- Goldsmid, H.J. The Thermoelectric and Related Effects. In Introduction to Thermoelectricity; Springer: Berlin, Germany, 2009; pp. 1–6. [Google Scholar]
- Karimi, G.; Culham, J.R.; Kazerouni, V. Performance analysis of multi-stage thermoelectric coolers. Int. J. Refrig. 2011, 34, 2129–2135. [Google Scholar] [CrossRef]
- Deb, K. Multi-objective optimization. In Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2001; pp. 13–46. [Google Scholar]
- Davis, L. Handbook of Genetic Algorithms; Van Nostrand Reinhold: New York, NY, USA, 1991; Volume 115. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, W.; Hansen, K.M. An evaluation of the NSGA-II and MOCell genetic algorithms for self-management planning in a pervasive service middleware. In Proceedings of the 2009 14th IEEE International Conference on Engineering of Complex Computer Systems, Potsdam, Germany, 2–4 June 2009; pp. 192–201. [Google Scholar]
- Van Laarhoven, P.J.; Aarts, E.H. Simulated Annealing; Springer: Berlin, Germany, 1987. [Google Scholar]
- Rutenbar, R.A. Simulated annealing algorithms: An overview. IEEE Circuits Devices Mag. 1989, 5, 19–26. [Google Scholar] [CrossRef]
- Wah, B.W.; Chen, Y.X. Optimal anytime constrained simulated annealing for constrained global optimization. In Principles and Practice of Constraint Programming–CP 2000; Springer: Berlin, Germany, 2000; pp. 425–440. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces; International Computer Science Institute (ICSI): Berkeley, CA, USA, 1995. [Google Scholar]
- Ali, M.; Pant, M.; Abraham, A. Simplex differential evolution. Acta Polytech. Hung. 2009, 6, 95–115. [Google Scholar]
- Mezura-Montes, E.; Velázquez-Reyes, J.; Coello, C.A.C. A comparative study of differential evolution variants for global optimization. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, Seattle, WA, USA, 8–12 July 2006; pp. 485–492. [Google Scholar]
- Enescu, D.; Virjoghe, E.O. A review on thermoelectric cooling parameters and performance. Renew. Sustain. Energy Rev. 2014, 38, 903–916. [Google Scholar] [CrossRef]
- Zhao, D.; Tan, G. A review of thermoelectric cooling: Materials, modeling and applications. Appl. Therm. Eng. 2014, 66, 15–24. [Google Scholar] [CrossRef]
- Rowe, D. Thermoelectric Handbook; Chemical Rubber Company: Boca Raton, FL, USA, 1995; p. 407. [Google Scholar]
- Boussaïd, I.; Lepagnot, J.; Siarry, P. A survey on optimization metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Saka, M.P.; Geem, Z.W. Mathematical and metaheuristic applications in design optimization of steel frame structures: An extensive review. Math. Prob. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Yang, X. Nature-Inspired Metaheuristic Algorithm; Luniver Press: Frome, UK, 2010. [Google Scholar]
- Baghel, M.; Agrawal, S.; Silakari, S. Survey of Metaheuristic Algorithms for Combinatorial Optimization. Int. J. Comput. Appl. 2012, 58, 21–31. [Google Scholar] [CrossRef]
- Burke, E.K.; Gendreau, M.; Hyde, M.; Kendall, G.; Ochoa, G.; Özcan, E.; Qu, R. Hyper-heuristics: A survey of the state of the art. J. Oper. Res. Soc. 2013, 64, 1695–1724. [Google Scholar] [CrossRef]
- Bahrammirzaee, A. A comparative survey of artificial intelligence applications in finance: Artificial neural networks, expert system and hybrid intelligent systems. Neural Comput. Appl. 2010, 19, 1165–1195. [Google Scholar] [CrossRef]
- Marques, A.; García, V.; Sanchez, J. A literature review on the application of evolutionary computing to credit scoring. J. Oper. Res. Soc. 2012, 64, 1384–1399. [Google Scholar] [CrossRef]
- Lee, K.Y.; El-Sharkawi, M.A. Modern Heuristic Optimization Techniques: Theory and Applications to Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 39. [Google Scholar]
- Yamashita, O.; Sugihara, S. High-performance bismuth-telluride compounds with highly stable thermoelectric figure of merit. J. Mater. Sci. 2005, 40, 6439–6444. [Google Scholar] [CrossRef]
- Rodgers, P. Nanomaterials: Silicon goes thermoelectric. Nat. Nano 2008, 3, 76. [Google Scholar] [CrossRef] [PubMed]
- Poudel, B.; Hao, Q.; Ma, Y.; Lan, Y.; Minnich, A.; Yu, B.; Yan, X.; Wang, D.; Muto, A.; Vashaee, D.; et al. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science 2008, 320, 634–638. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.H.; Lin, W.K. Geometric optimization of thermoelectric coolers in a confined volume using genetic algorithms. Appl. Therm. Eng. 2005, 25, 2983–2997. [Google Scholar] [CrossRef]
- Cheng, Y.H.; Shih, C. Maximizing the cooling capacity and COP of two-stage thermoelectric coolers through genetic algorithm. Appl. Therm. Eng. 2006, 26, 937–947. [Google Scholar] [CrossRef]
- Huang, Y.X.; Wang, X.D.; Cheng, C.H.; Lin, D.T.W. Geometry optimization of thermoelectric coolers using simplified conjugate-gradient method. Energy 2013, 59, 689–697. [Google Scholar] [CrossRef]
- Nain, P.; Sharma, S.; Giri, J. Non-dimensional multi-objective performance optimization of single stage thermoelectric cooler. In Simulated Evolution and Learning; Springer: Berlin, Germany, 2010; pp. 404–413. [Google Scholar]
- Rao, R.V.; Patel, V. Multi-objective optimization of two stage thermoelectric cooler using a modified teaching–learning-based optimization algorithm. Eng. Appl. Artif. Intell. 2013, 26, 430–445. [Google Scholar]
- Xuan, X.C.; Ng, K.C.; Yap, C.; Chua, H.T. Optimization of two-stage thermoelectric coolers with two design configurations. Energy Convers. Manag. 2002, 43, 2041–2052. [Google Scholar] [CrossRef]
- Nain, P.K.S.; Giri, J.M.; Sharma, S.; Deb, K. Multi-objective Performance Optimization of Thermo-Electric Coolers Using Dimensional Structural Parameters. In Swarm, Evolutionary, and Memetic Computing; Panigrahi, B., Das, S., Suganthan, P., Dash, S., Eds.; Springer: Berlin Heidelberg, 2010; Volume 6466, pp. 607–614. [Google Scholar]
- Blum, C.; Roli, A.; Sampels, M. Hybrid Metaheuristics: An Emerging Approach to Optimization; Springer Science & Business Media: Berlin, Germany, 2008; Volume 114. [Google Scholar]
- Deb, K. Optimization for Engineering Design: Algorithms and Examples; PHI Learning Pvt. Ltd.: Delhi, India, 2012. [Google Scholar]
- Sohrabi, B. A comparison between Genetic Algorithm and Simulated Annealing Performance in preventive part replacement. Management 2006, 72, 112–120. [Google Scholar]
- Franconi, L.; Jennison, C. Comparison of a genetic algorithm and simulated annealing in an application to statistical image reconstruction. Stat. Comput. 1997, 7, 193–207. [Google Scholar] [CrossRef]
- Liu, K.; Du, X.; Kang, L. Differential Evolution Algorithm Based on Simulated Annealing. In Advances in Computation and Intelligence; Kang, L., Liu, Y., Zeng, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4683, pp. 120–126. [Google Scholar]
- Yan, J.Y.; Ling, Q.; Sun, D.M. A Differential Evolution with Simulated Annealing Updating Method. In Proceedings of the 2006 International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006; pp. 2103–2106. [Google Scholar]
- Goldsmid, H.J. Introduction to Thermoelectricity; Springer Science & Business Media: Berlin, Germany, 2009; Volume 121. [Google Scholar]
- Rowe, D.; Min, G. Design theory of thermoelectric modules for electrical power generation. IEE Proc.-Sci. Meas. Technol. 1996, 143, 351–356. [Google Scholar] [CrossRef]
- Yamashita, O.; Tomiyoshi, S. Effect of annealing on thermoelectric properties of bismuth telluride compounds doped with various additives. J. Appl. Phys. 2004, 95, 161–169. [Google Scholar] [CrossRef]
- Song, S.; Au, V.; Moran, K.P. Constriction/spreading resistance model for electronics packaging. In Proceedings of the 4th ASME/JSME Thermal Engineering Joint Conference, Lahaina, HI, USA, 19–24 March 1995; pp. 199–206. [Google Scholar]
- Bryan, K.; Shibberu, Y. Penalty Functions and Constrained Optimization; Department of Mathematics, Rose-Hulman Institute of Technology: Terre Haute, IN, USA; Available online: http://www.rose-hulman.edu/~bryan/lottamath/penalty.pdf (accessed on 28 June 2017).
- Kim, I.Y.; de Weck, O. Adaptive weighted sum method for multiobjective optimization: A new method for Pareto front generation. Struct. Multidiscip. Optim. 2006, 31, 105–116. [Google Scholar] [CrossRef]
- Babu, B.; Angira, R. New strategies of differential evolution for optimization of extraction process. In Proceedings of the International Symposium & 56th Annual Session of IIChE (CHEMCON-2003), Bhubaneswar, India, 19–22 December 2003. [Google Scholar]
- Deb, K. Multi-objective optimization. In Search Methodologies; Springer: Berlin, Germany, 2014; pp. 403–449. [Google Scholar]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Guo, H.; Li, Y.; Li, J.; Sun, H.; Wang, D.; Chen, X. Differential evolution improved with self-adaptive control parameters based on simulated annealing. Swarm Evol. Comput. 2014, 19, 52–67. [Google Scholar] [CrossRef]
- Blum, C.; Roli, A. Hybrid metaheuristics: An introduction. In Hybrid Metaheuristics; Springer: Berlin, Germany, 2008; pp. 1–30. [Google Scholar]
- Vasant, P.; Barsoum, N. Hybrid Simulated Annealing and Genetic Algorithms for industrial production management problems. AIP Conf. Proc. 2009, 1159, 254–261. [Google Scholar]
- Abbasi, B.; Niaki, S.T.A.; Khalife, M.A.; Faize, Y. A hybrid variable neighborhood search and simulated annealing algorithm to estimate the three parameters of the Weibull distribution. Expert Syst. Appl. 2011, 38, 700–708. [Google Scholar] [CrossRef]
- Vasant, P. Hybrid LS–SA–PS methods for solving fuzzy non-linear programming problems. Math. Comput. Model. 2013, 57, 180–188. [Google Scholar] [CrossRef]
- Chen, D.; Lee, C.Y.; Park, C.H. Hybrid genetic algorithm and simulated annealing (HGASA) in global function optimization. In Proceedings of the 17th IEEE International Conference on Tools with Artificial Intelligence, 2005 (ICTAI 05), Hong Kong, China, 14–16 November 2005; pp. 126–133. [Google Scholar]
- Barr, R.; Golden, B.; Kelly, J.; Resende, M.C.; Stewart, W., Jr. Designing and reporting on computational experiments with heuristic methods. J. Heuristics 1995, 1, 9–32. [Google Scholar] [CrossRef]
- Vasant, P. Meta-Heuristics Optimization Algorithms in Engineering, Business, Economics, and Finance; IGI Global: Hershey, PA, USA, 2012. [Google Scholar]
- Purnomo, H.D.; Wee, H. Metaheuristics Methods for Configuration of Assembly Lines: A Survey. In Handbook of Research on Novel Soft Computing Intelligent Algorithms: Theory and Practical Applications; Vasant, P., Ed.; IGI Global: Hershey, PA, USA, 2014; pp. 165–199. [Google Scholar] [CrossRef]
- Roeva, O.; Slavov, T.; Fidanova, S. Population-Based vs. Single Point Search Meta-Heuristics for a PID Controller Tuning. In Handbook of Research on Novel Soft Computing Intelligent Algorithms: Theory and Practical Applications; Vasant, P., Ed.; IGI Global: Hershey, PA, USA, 2014; pp. 200–233. [Google Scholar] [CrossRef]
- Vasant, P.; Alparslan-Gok, S.Z.; Weber, G. Handbook of Research on Emergent Applications of Optimization Algorithms (2 Volumes); IGI Global: Hershey, PA, USA, 2017–2018. [Google Scholar] [CrossRef]







| Author | Application | Advantages and Disadvantages |
|---|---|---|
| Cheng [29] | GA is applied to optimize the geometric design of STECs | GA proves fast convergence speed and effective search, but GA parameter setting is not suggested or discussed. |
| Cheng [30] | GA is applied to optimize the design parameter of TTECs | GA was applied successfully to solve a heavier TTEC problem, but the robustness of GA when applied to for TTEC model is not very deterministic. |
| Huang [31] | Applies a conjugate-gradient method to optimize the geometric design of STECs | Effects regarding applied current and temperature on the optimum geometry are generally discussed. Performance analysis of the technique applied for STEC was not conducted. The base area of the studied STEC was small and not practical. |
| Nain [32] | Uses NSGA-II to optimize the geometric design of STECs | Multi-objective optimization is performed by optimizing cooling rate and COP simultaneously. Parameters of NSGA-II were chosen based on the authors’ experience, but the obtained findings are not reliable because of the unstable performance of the algorithm. |
| Rao [33] | Uses TLBO to optimize the design parameters of TTECs | Multi-objective optimization is performed. The performance of TLBO is evaluated and compared to GA, PSO by using some defined criteria, however, parameter selection for TLBO was not implemented. |
| No. | Parameter | Specified Value |
|---|---|---|
| 1 | Number of population member | P = 30 |
| 2 | Scaling factor | F = 0.85 |
| 3 | Crossover probability constant | CR = 1 |
| 4 | Variable number | D = 3 |
| 4 | Maximum iteration | imax = 300 |
| No. | Parameter | Specific Values |
|---|---|---|
| 1 | Initial temperature | To = 100 |
| 2 | Maximum number of runs | runmax = 250 |
| 3 | Maximum number of acceptance | accmax = 125 |
| 4 | Maximum number of rejection | rejmax = 125 |
| 5 | Temperature reduction value | α = 0.95 |
| 6 | Boltzmann annealing | kB = 1 |
| 7 | Stopping criteria | Tfinal = 10−10 |
| No. | Parameters | Specific Values |
|---|---|---|
| 1 | Population size | 100 |
| 2 | Function for fitness scaling | Fitness scaling ranking |
| 3 | Function for selection | Selection tournament-4 |
| 4 | Function for crossover | Arithmetic crossover |
| 5 | Crossover fraction | 0.6 |
| 6 | Function for mutation | Mutation Adaptive Feasible |
| 7 | Stopping criteria of GA | Maximum number of generations 300 |
| No. | Test Type | Purpose of the Test |
|---|---|---|
| 1 | Convergence speed test | Measure how fast the algorithm converge by counting the number of iterations |
| 2 | Computational effort | Measure time consuming of every running time of optimization technique |
| 3 | Stability test | Measure how stable & accurate the algorithm obtain after a number of trial runs |
| 4 | Robustness test | Measure ability to realize well many test problems & parameters |
| No. | Parameters | Description |
|---|---|---|
| 1 | Objective function | Single-objective optimization—Maximize Qc |
| 2 | Variables | L—Height of semiconductor element (mm) |
| A—Area of semiconductor element (mm2) | ||
| N—Total number of semiconductor elements (unit) | ||
| 3 | Fixed parameter | Th = Tc = 323 °K→Tave = 323 °K |
| I = 1 (A) | ||
| rc = 10−8 (Ωm2) | ||
| 4 | Constraints | 1. Boundary constraint: - 0.03 mm ≤ L ≤ 1 mm - 0.09 mm2 ≤ A ≤ 100 mm2 - 1 unit ≤ N ≤ 1111 unit |
| 2. Inequality constraint: - Limited total surface area S = 100 mm2 - Production cost of material $385 | ||
| 3. Equality constraint: - Minimum requirement COP = 1 |
| No. | Parameters | Description |
|---|---|---|
| 1 | Objective function | Single-objective optimization—Maximize Qc,c or maximize COP |
| 2 | Variables | Ic—Input current to the cold stage (A) |
| Ih—Input current to the hot stage (A) | ||
| r—ratio number for semiconductor elements between the hot stage and the cold stage | ||
| 3 | Fixed variable | Nt = 100 (unit) |
| G = 0.0018 m | ||
| Th,h = 300 °K | ||
| Tc,c = 240 °K | ||
| 4 | Boundary constraint | 4 A ≤ Ih ≤ 11 A |
| 4 A ≤ Ic ≤ 11 A | ||
| 2 ≤ r ≤ 7.33 |
| Technique Used | GA | SA | DE |
|---|---|---|---|
| Test case 1 | Qc (W) | Qc (W) | Qc (W) |
| Standard deviation of best fitness | 0.8616 | 0.0025 | 0 |
| Average value of best fitness | 5.982 | 7.417 | 7.421 |
| Minimum value of best fitness | 3.880 | 7.410 | 7.421 |
| Maximum value of best fitness | 7.417 | 7.420 | 7.421 |
| Technique Used | GA | SA | DE |
|---|---|---|---|
| Test Case-3 | Qc(W) | Qc(W) | Qc(W) |
| Standard deviation of best fitness | 1.3251 | SA can’t solve this test case | 0 |
| Average value of best fitness | 5.487 | 6.596 | |
| Minimum value of best fitness | 2.154 | 6.596 | |
| Maximum value of best fitness | 6.595 | 6.596 |
| Technique Used | GA | SA | DE | |||
|---|---|---|---|---|---|---|
| Test cases 4 and 5 | Qc,c (W) | COP | Qc,c (W) | COP | Qc,c (W) | COP |
| Standard deviation | 5.5 × 10−4 | 8.584 × 10−5 | 0 | 0 | 0 | 0 |
| Ave. of best fitness | 3.1052 | 0.1677 | 3.1055 | 0.1677 | 3.1055 | 0.1677 |
| Min. of best fitness | 3.1030 | 0.1673 | 3.1055 | 0.1677 | 3.1055 | 0.1677 |
| Max. of best fitness | 3.1055 | 0.1677 | 3.1055 | 0.1677 | 3.1055 | 0.1677 |
| Ave. computational time | 18 s | 18 s | 66 s | 66 s | 48 s | 48 s |
| No. | (F, CR, P) | Test Case-1 | Test Case-3 | Test Case-4 | Test Case-5 |
|---|---|---|---|---|---|
| (Ave. Qc, Std Qc) | (Ave. Qc, Std Qc) | (Ave. Qc,c, Std Qc,c) | (Ave. COP, Std COP) | ||
| 1 | 0.95, 0.95, 30 | (7.421 W, 0) | (6.596 W, 0) | (3.105 W, 0) | (0.1677, 0) |
| 2 | 1.0, 1.0, 35 | (7.421 W, 0) | (6.596 W, 0) | (3.105 W, 0) | (0.1677, 0) |
| 3 | 0.97, 0.97, 30 | (7.421 W, 0) | (6.596 W, 0) | (3.105 W, 0) | (0.1677, 0) |
| 4 | 0.93, 0.97, 27 | (7.421 W, 0) | (6.596 W, 0) | (3.105 W, 0) | (0.1677, 0) |
| 5 | 0.93, 0.93, 25 | (7.421 W, 0) | (6.596 W, 0) | (3.105 W, 0) | (0.1677, 0) |
| 6 | 0.91, 0.91, 23 | (7.421 W, 0) | (6.596 W, 0) | (3.105 W, 0) | (0.1677, 0) |
| 7 | 0.85, 0.9, 21 | (7.421 W, 0) | (6.596 W, 0) | (2.720 W, 0.25) | (0.1377, 0.046) |
| 8 | 0.80, 0.2, 19 | (7.339 W, 0.10) | - | - | - |
| 9 | 0.75, 0.18, 19 | (6.981 W, 0.804) | - | - | - |
| No. | (To, nmax, α, Tfinal) | Test Case 1 | Test Case 4 | Test Case 5 |
|---|---|---|---|---|
| (Ave. Qc, Std Qc) | (Ave. Qc, Std Qc) | (Ave. Qc, Std Qc) | ||
| 1 | (100, 300, 0.95, 10−10) | (7.417 W, 0.0025) | (3.105 W, 0) | (0.1677, 0) |
| 2 | (102, 310, 0.9, 10−10) | (6.918 W, 1.049) | (3.105 W, 0) | (0.1677, 0) |
| 3 | (98, 290, 0.9, 10−10) | (6.9015 W, 1.588) | (3.105 W, 0) | (0.1677, 0) |
| 4 | (96, 285, 0.85, 10−10) | (6.769 W, 1.465) | (3.105 W, 0) | (0.1677, 0) |
| 5 | (94, 280, 0.85, 10−9) | (6.68 W, 1.674) | (3.105 W, 0) | (0.1677, 0) |
| 6 | (92, 275, 0.8, 10−9) | (5.141 W, 2.342) | (3.105 W, 0) | (0.1677, 0) |
| 7 | (90, 270, 0.8, 10−8) | (6.277 W, 1.834) | (3.105 W, 0) | (0.1677, 0) |
| 8 | (88, 265, 0.75, 10−8) | (5.396 W, 2.451) | (3.105 W, 0) | (0.1677, 0) |
| Technique Used | HSAGA | HSADE | ||
|---|---|---|---|---|
| Test Case | (1) Qc (W) | (3) Qc (W) | (1) Qc (W) | (3) Qc (W) |
| Standard deviation | 0.0269 | 0.5409 | 0 | 0 |
| Average value of best fitness | 7.38 | 5.916 | 7.421 | 6.596 |
| Minimum value of best fitness | 7.42 | 4.907 | 7.421 | 6.596 |
| Maximum value of best fitness | 7.33 | 6.95 | 7.421 | 6.596 |
| No. | Parameters | Description |
|---|---|---|
| 1 | Objective function | Case 5: Single-obj. opt.—Maximize Qc,c or maximize COP. |
| Case 6: Multi-obj. opt.—Maximize Qc,c and COP | ||
| 2 | Variables | Ic—Input current to the cold stage TTEC (A) |
| Ih—Input current to the hot stage TTEC (A) | ||
| r—ratio number for TE modules between the hot stages and the cold stage (unitless) | ||
| 3 | Fixed variable | Nt = 100 (unit) |
| G = 0.0018 (m) | ||
| RSj = 0.02; 0.2; 2 (cm2K/W) | ||
| Sh,s = 0.1 (cm) | ||
| a = 0.02 (cm2) | ||
| kh,s = 0.3 (W/cmK) | ||
| Th,h = 300 (°K) | ||
| Tc,c = 210 °K, 220 °K, 230 °K, 240 °K | ||
| 4 | Boundary constraint | 4 (A) ≤ Ih ≤ 11 (A) |
| 4 (A) ≤ Ic ≤ 11 (A) | ||
| 2 ≤ r ≤ 7.33 |
| I (A) | DE | SA | COP | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Qc (W) | N (unit) | A (mm2) | L (mm) | Qc (W) | N (unit) | A (mm2) | L (mm) | ||
| 0.1 | 4.63 | 842 | 0.09 | 0.3 | 4.63 | 841 | 0.09 | 0.3 | 2.09 |
| 0.2 | 7.04 | 842 | 0.09 | 0.3 | 7.04 | 841 | 0.09 | 0.3 | 0.79 |
| 0.5 | 7.42 | 437 | 0.17 | 0.3 | 7.42 | 437 | 0.17 | 0.3 | 0.5 |
| 1 | 7.42 | 217 | 0.35 | 0.3 | 7.42 | 221 | 0.34 | 0.3 | 0.51 |
| 2 | 7.42 | 108 | 0.7 | 0.3 | 7.42 | 108 | 0.7 | 0.3 | 0.51 |
| 4 | 7.42 | 55 | 1.39 | 0.3 | 7.42 | 55 | 1.39 | 0.3 | 0.49 |
| 6 | 7.42 | 36 | 2.09 | 0.3 | 7.41 | 36 | 2.08 | 0.3 | 0.49 |
| 8 | 7.42 | 27 | 2.82 | 0.3 | 7.42 | 27 | 2.82 | 0.3 | 0.5 |
| Tc (°K) | DE | SA | COP | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Qc (W) | N (unit) | A (mm2) | L (mm) | Qc (W) | N (unit) | A (mm2) | L (mm) | ||
| 283 | - | - | - | - | - | - | - | - | - |
| 293 | 0.37 | 45 | 0.51 | 1 | 0.37 | 45 | 0.51 | 1 | 0.13 |
| 303 | 1.03 | 82 | 0.44 | 0.62 | 1.02 | 77 | 0.45 | 0.66 | 0.17 |
| 313 | 3.42 | 209 | 0.36 | 0.3 | 0.30 | 44 | 0.13 | 0.7 | 0.24 |
| 323 | 7.42 | 221 | 0.34 | 0.3 | 7.42 | 221 | 0.34 | 0.30 | 0.51 |
| 333 | 11.38 | 226 | 0.335 | 0.3 | 11.38 | 226 | 0.33 | 0.30 | 0.75 |
| I (A) | DE | COP | |||
|---|---|---|---|---|---|
| Qc (W) | N (unit) | A (mm2) | L (mm) | ||
| 0.1 | 4.63 | 842 | 0.09 | 0.3 | 2.09 |
| 0.2 | 6.59 | 723 | 0.1 | 0.3 | 1 |
| 0.5 | 6.59 | 288 | 0.26 | 0.3 | 1 |
| 1 | 6.59 | 145 | 0.52 | 0.3 | 1 |
| 2 | 6.59 | 72 | 1.04 | 0.3 | 1 |
| 4 | 6.59 | 36 | 2.09 | 0.3 | 1 |
| 6 | 6.59 | 24 | 3.15 | 0.3 | 1 |
| 8 | 6.59 | 19 | 4.18 | 0.3 | 1 |
| First Type TTEC | Optimal Design Variables | DE and SA | GA— [29] | |||
|---|---|---|---|---|---|---|
| Tc,c (°K) | Nc | Nh | Ic (A) | Ih (A) | Max. Qc,c (W) | Max. Qc,c (W) |
| 230 | 44 | 156 | 7.487 | 7.487 | 4.25 | 4.25 |
| 220 | 36 | 164 | 7.719 | 7.719 | 2.49 | 2.49 |
| 210 | 25 | 175 | 8.028 | 8.028 | 1.07 | 1.07 |
| Tc,c (°K) | Nc | Nh | Ic (A) | Ih (A) | Max. COP | Max. COP |
| 230 | 50 | 150 | 4.908 | 4.908 | 0.1 | 0.1 |
| 220 | 39 | 171 | 5.587 | 5.587 | 0.044 | 0.04 |
| 210 | 26 | 173 | 6.886 | 6.886 | 0.02 | 0.02 |
| Second Type TTEC | Optimal Design Variables | DE and SA | GA— [29] | |||
|---|---|---|---|---|---|---|
| Tc,c (°K) | Nc | Nh | Ic (A) | Ih (A) | Max. Qc,c (W) | Max. Qc,c (W) |
| 230 | 60 | 140 | 5.439 | 9.957 | 5.18 | 5.16 |
| 220 | 48 | 152 | 5.874 | 9.925 | 3.09 | 3.07 |
| 210 | 33 | 167 | 6.508 | 9.883 | 1.36 | 1.35 |
| Tc,c (°K) | Nc | Nh | Ic (A) | Ih (A) | Max. COP | Max. COP |
| 230 | 55 | 145 | 4.619 | 5.212 | 0.09 | 0.09 |
| 220 | 56 | 144 | 5.459 | 6.286 | 0.05 | 0.04 |
| 210 | 30 | 170 | 6.358 | 7.479 | 0.02 | 0.02 |
| First Type TTEC | Optimal Design Variables | DE and SA | GA— [30] | |||
|---|---|---|---|---|---|---|
| RSj (cm2K/W) | Nc | Nh | Ic (A) | Ih (A) | Max. Qc,c (W) | Max. Qc,c (W) |
| 0.02 | 14 | 86 | 8.266 | 8.266 | 0.723 | 0.73 |
| 0.2 | 14 | 86 | 8.395 | 8.395 | 0.816 | 0.818 |
| 2 | 19 | 81 | 9.883 | 9.883 | 2.185 | 2.123 |
| RSj (cm2K/W) | Nc | Nh | Ic (A) | Ih (A) | Max. COP | Max. COP |
| 0.02 | 15 | 85 | 6.920 | 6.920 | 0.021 | 0.019 |
| 0.2 | 16 | 84 | 6.934 | 6.934 | 0.024 | 0.020 |
| 2 | 21 | 79 | 7.086 | 7.086 | 0.064 | 0.048 |
| Second Type TTEC | Optimal Design Variables | DE and SA | GA— [30] | |||
|---|---|---|---|---|---|---|
| RSj (cm2K/W) | Nc | Nh | Ic (A) | Ih (A) | Max. Qc,c (W) | Max. Qc,c (W) |
| 0.02 | 21 | 79 | 6.864 | 9.967 | 0.856 | 0.755 |
| 0.2 | 18 | 82 | 7.043 | 10.004 | 0.940 | 0.838 |
| 2 | 20 | 80 | 9.311 | 10.510 | 2.210 | 2.103 |
| RSj (cm2K/W) | Nc | Nh | Ic (A) | Ih (A) | Max. COP | Max. COP |
| 0.02 | 16 | 84 | 6.740 | 7.121 | 0.021 | 0.019 |
| 0.2 | 15 | 85 | 6.962 | 6.901 | 0.024 | 0.021 |
| 2 | 12 | 88 | 11 | 4 | 0.160 | 0.061 |
| Second Type TTEC | w1 | Ih (A) | Ic (A) | r | Max. Qc,c | Max. COP |
|---|---|---|---|---|---|---|
| RSj = 0.02 cm2K/W Tc,c = 210 °K | 0 | 7.1213 | 6.7396 | 5.3969 | 0.6457 | 0.0214 |
| 0.5 | 8.5062 | 6.7056 | 4.7398 | 0.799 | 0.02 | |
| 1 | 9.9673 | 6.8638 | 4.6913 | 0.8555 | 0.0164 | |
| RSj = 0.02 cm2K/W Tc,c = 220 °K | 0 | 5.8037 | 5.9636 | 3.8962 | 1.1424 | 0.0538 |
| 0.5 | 7.8384 | 5.8902 | 3.0916 | 1.6011 | 0.0482 | |
| 1 | 10.011 | 6.2804 | 3.1262 | 1.7767 | 0.0355 | |
| RSj = 0.02 cm2K/W Tc,c = 230 °K | 0 | 4.5574 | 5.296 | 3.3146 | 1.5295 | 0.1064 |
| 0.5 | 7.1472 | 5.1585 | 2.294 | 2.4651 | 0.0915 | |
| 1 | 10.0444 | 5.8688 | 2.4079 | 2.8554 | 0.0594 | |
| RSj = 0.2 cm2K/W Tc,c = 210 °K | 0 | 6.9015 | 6.9622 | 5.4852 | 0.6865 | 0.0241 |
| 0.5 | 8.4447 | 6.8835 | 4.6794 | 0.8744 | 0.0222 | |
| 1 | 10.0038 | 7.0427 | 4.6041 | 0.94 | 0.018 | |
| RSj = 0.2 cm2K/W Tc,c = 220 °K | 0 | 5.5202 | 6.2531 | 4.1809 | 1.148 | 0.0583 |
| 0.5 | 7.7598 | 6.0721 | 3.1288 | 1.6855 | 0.0516 | |
| 1 | 10.0486 | 6.4637 | 3.1317 | 1.8805 | 0.0374 | |
| RSj = 0.2 cm2K/W Tc,c = 230 °K | 0 | 4.1216 | 5.7414 | 3.9161 | 1.4334 | 0.1136 |
| 0.5 | 7.0816 | 5.3424 | 2.3521 | 2.5569 | 0.0958 | |
| 1 | 10.0835 | 6.0516 | 2.434 | 2.973 | 0.0614 | |
| RSj = 2 cm2K/W Tc,c = 210 °K | 0 | 4 | 11 | 7.33 | 0.9207 | 0.1596 |
| 0.5 | 4 | 11 | 7.33 | 0.9207 | 0.1596 | |
| 1 | 10.5099 | 9.3109 | 3.9839 | 2.2097 | 0.0429 | |
| RSj = 2 cm2K/W Tc,c = 220 °K | 0 | 4 | 11 | 7.33 | 1.6316 | 0.2866 |
| 0.5 | 4 | 11 | 7.33 | 1.6316 | 0.2866 | |
| 1 | 10.5716 | 8.7926 | 3.1648 | 3.3572 | 0.0651 | |
| RSj = 2 cm2K/W Tc,c = 230 °K | 0 | 4 | 11 | 7.33 | 2.3244 | 0.4142 |
| 0.5 | 4 | 11 | 7.33 | 2.3244 | 0.4142 | |
| 1 | 10.6264 | 8.3924 | 2.6641 | 4.6084 | 0.0897 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasant, P.; Kose, U.; Watada, J. Metaheuristic Techniques in Enhancing the Efficiency and Performance of Thermo-Electric Cooling Devices. Energies 2017, 10, 1703. https://doi.org/10.3390/en10111703
Vasant P, Kose U, Watada J. Metaheuristic Techniques in Enhancing the Efficiency and Performance of Thermo-Electric Cooling Devices. Energies. 2017; 10(11):1703. https://doi.org/10.3390/en10111703
Chicago/Turabian StyleVasant, Pandian, Utku Kose, and Junzo Watada. 2017. "Metaheuristic Techniques in Enhancing the Efficiency and Performance of Thermo-Electric Cooling Devices" Energies 10, no. 11: 1703. https://doi.org/10.3390/en10111703
APA StyleVasant, P., Kose, U., & Watada, J. (2017). Metaheuristic Techniques in Enhancing the Efficiency and Performance of Thermo-Electric Cooling Devices. Energies, 10(11), 1703. https://doi.org/10.3390/en10111703






