Comparison of Modelled and Measured Tilted Solar Irradiance for Photovoltaic Applications
Abstract
1. Introduction
2. Instruments and Methods
2.1. IMUK Measurements
- Global Horizontal Irradiance (GHI) from January 2014 to December 2016, measured by a CMP11 pyranometer (Kipp & Zonen, Delft, The Netherlands),
- Diffuse Horizontal Irradiance (DHI) from January 2014 to December 2016, measured by a CMP11 pyranometer with a shadow ball (Figure 1a),
- Global Tilted Irradiance (GTI) measured at a 40° inclined plane facing south by a CM11 pyranometer from January to December 2016,
- Global Tilted Irradiances from January 2014 to December 2016 measured by at various orientations by 14 crystalline silicon PV device with individual temperature sensors (Mencke & Tegtmeyer GmbH, Hameln, Germany). Seven of those silicon sensors (SiS) were facing south, tilted at 0°, 10°, 20°, 30°, 40°, 50°, 60°, 70°, six sensors were tilted vertically facing N, S, E, W, SE and SW and a single sensor was oriented horizontally (Figure 1b).
2.2. NREL Measurements
- 1
- Global Horizontal Irradiance (GHI) measured by a CMP11 pyranometer,
- 2
- Diffuse Horizontal Irradiance (DHI), measured by a CMP11 pyranometer,
- 3
- Global Tilted Irradiance (GTI) measured at a 40° inclined plane facing south by a CMP11 pyranometer,
- 4
- Global Tilted Irradiances measured by a silicon pyranometer LI-200 (LI-COR Inc., Lincoln, NE, USA), facing S, tilted at 40° and vertically tilted sensors facing N, S, E and W,
- 5
- Albedo measurements, measured by two silicon pyranometers LI-200.
2.3. Preprocessing and Quality Control
2.4. Transposition Models
2.4.1. Liu and Jordan Model
2.4.2. Klucher Model
2.4.3. Hay and Davies Model
2.4.4. Reindl Model
2.4.5. Perez Model
3. Results and Discussion
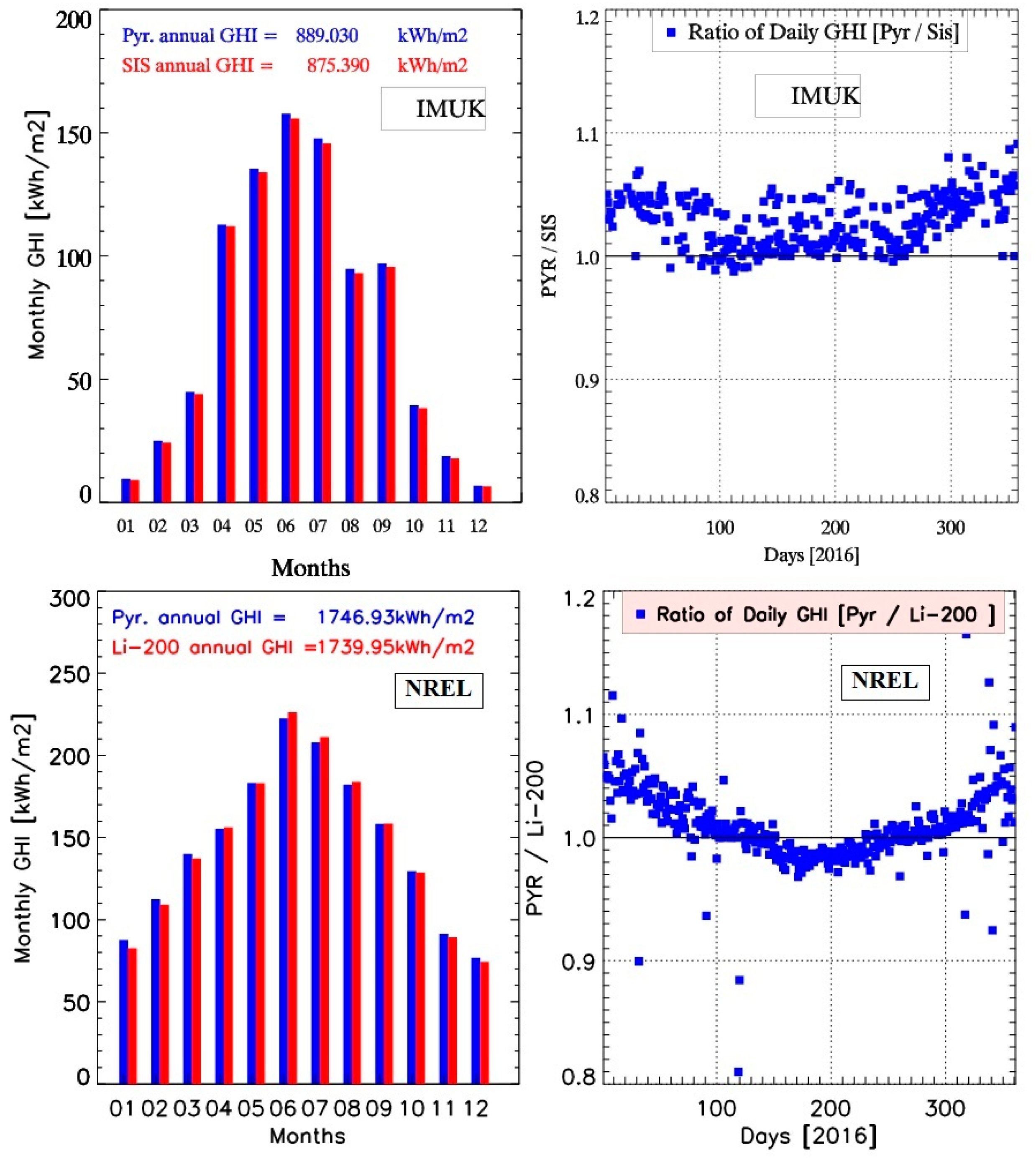
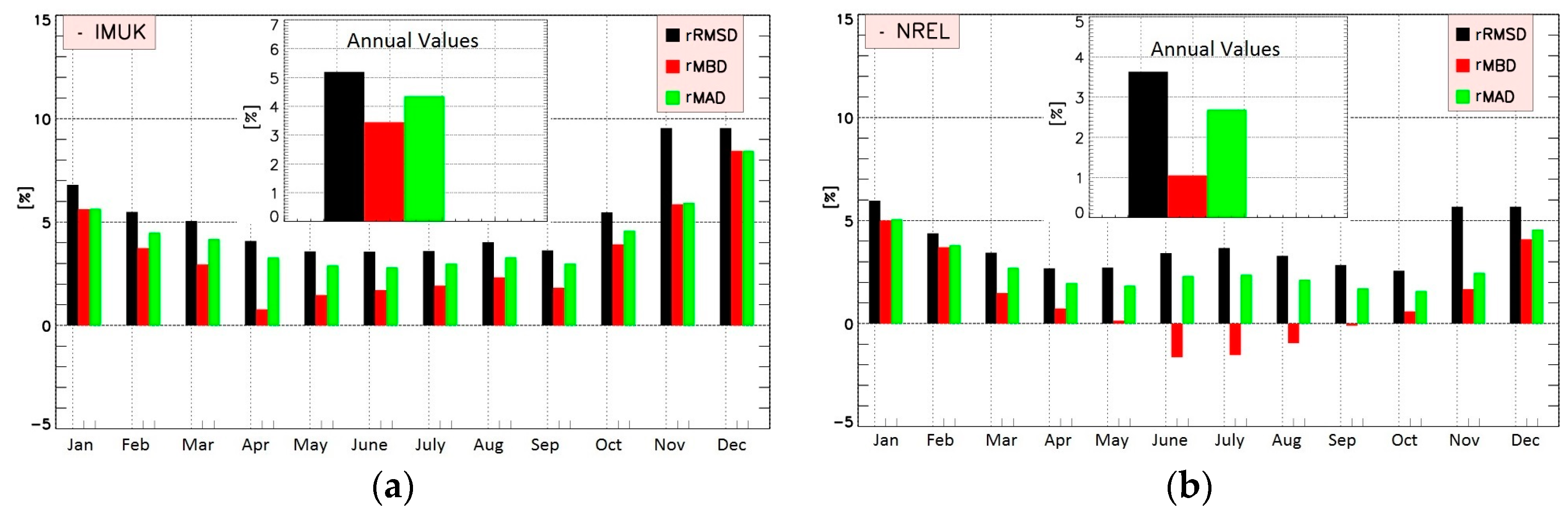
3.1. Measurement Validation
3.1.1. Uncertainty Resulting from Using Different Sensors
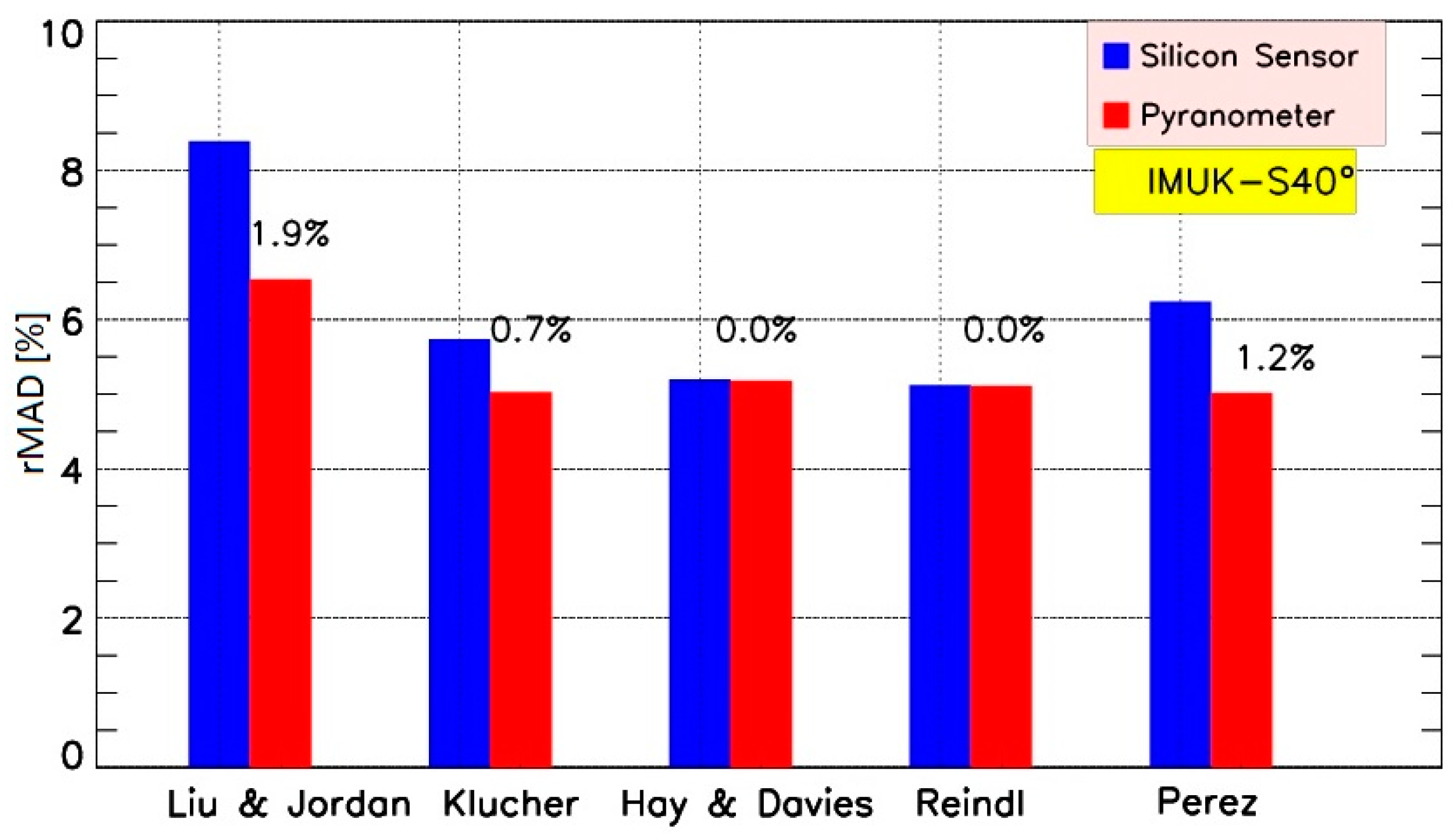
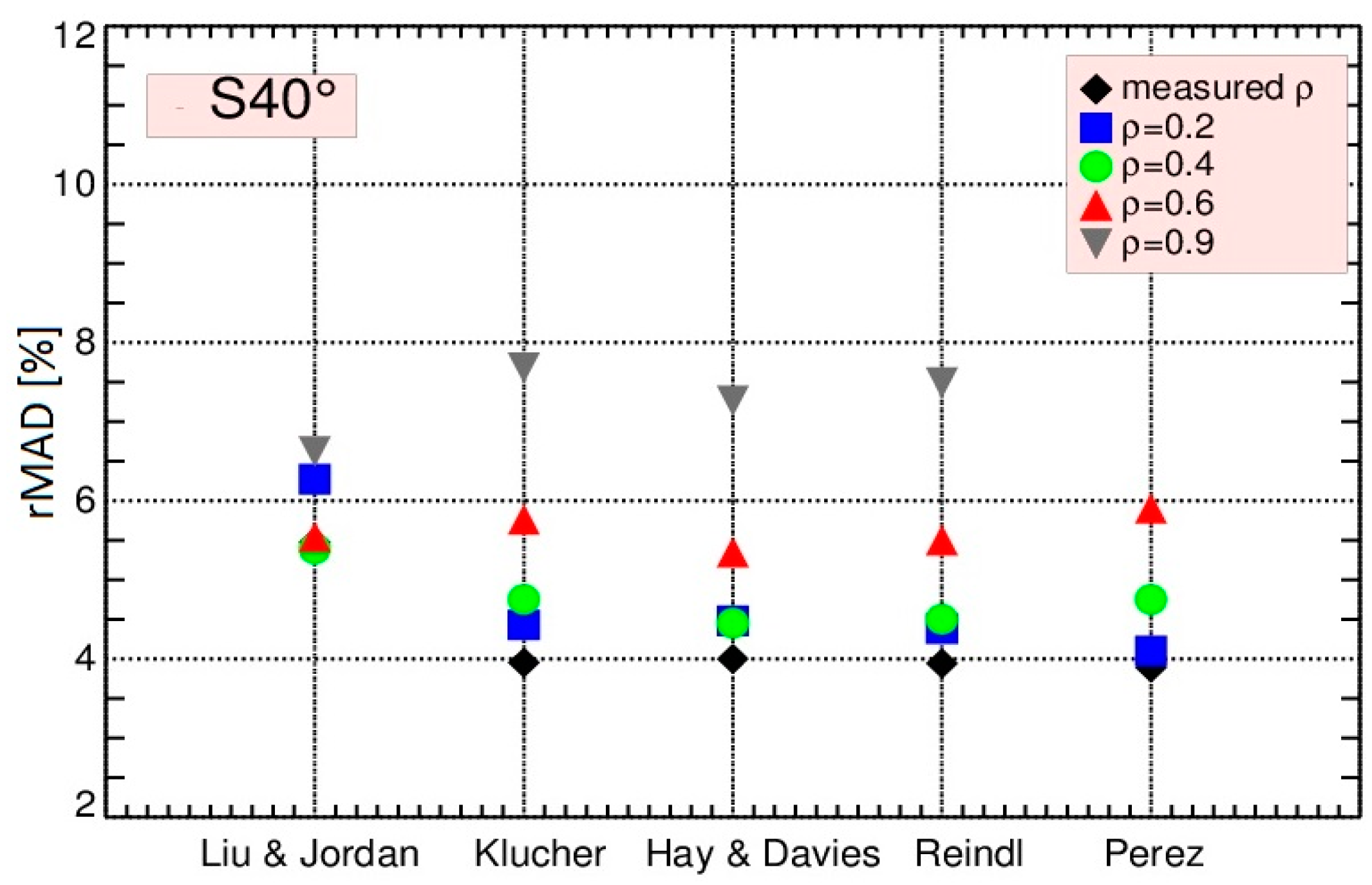
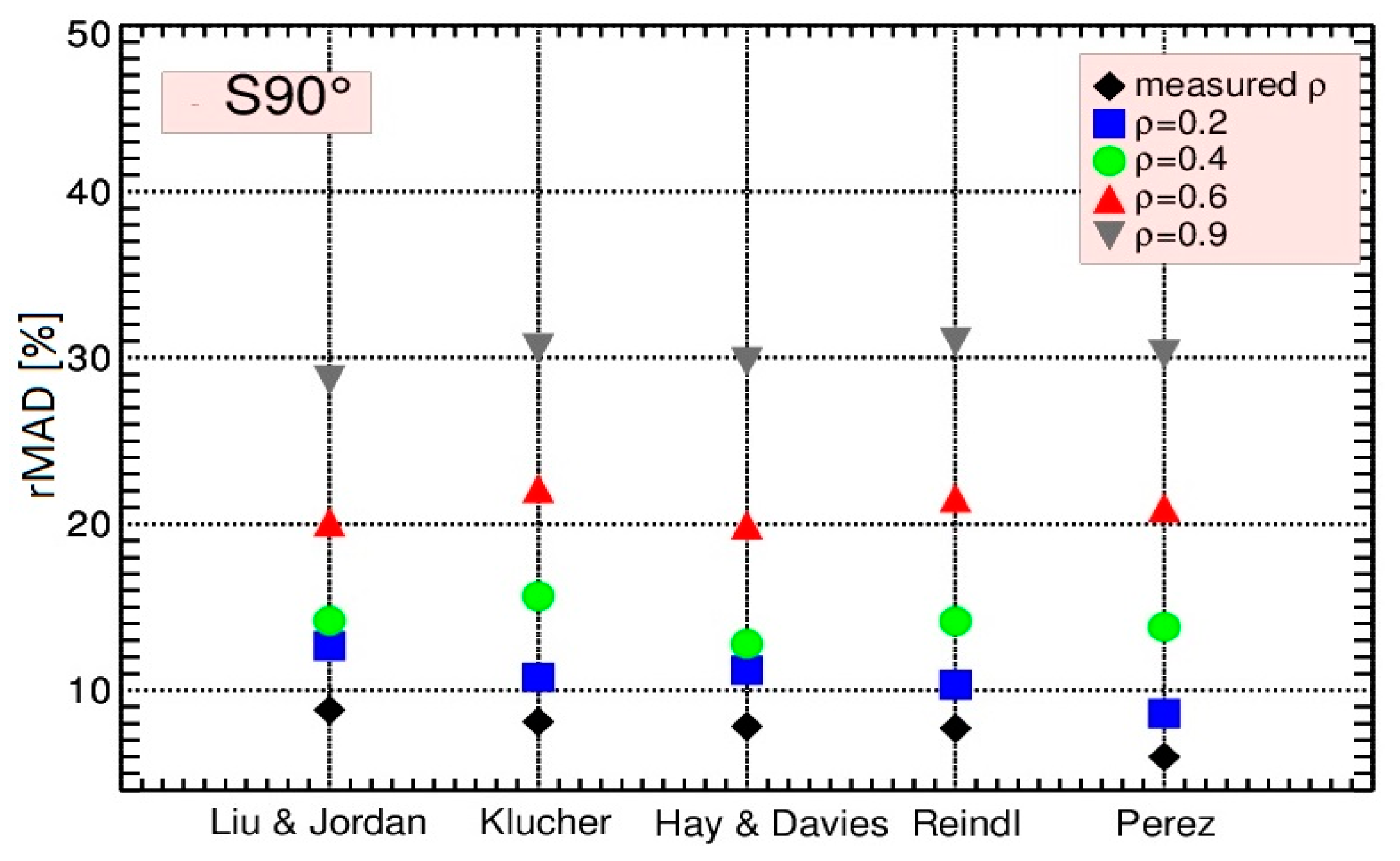
3.1.2. Albedo and Seasonal Effects
3.2. Model Validation
4. Conclusions
- -
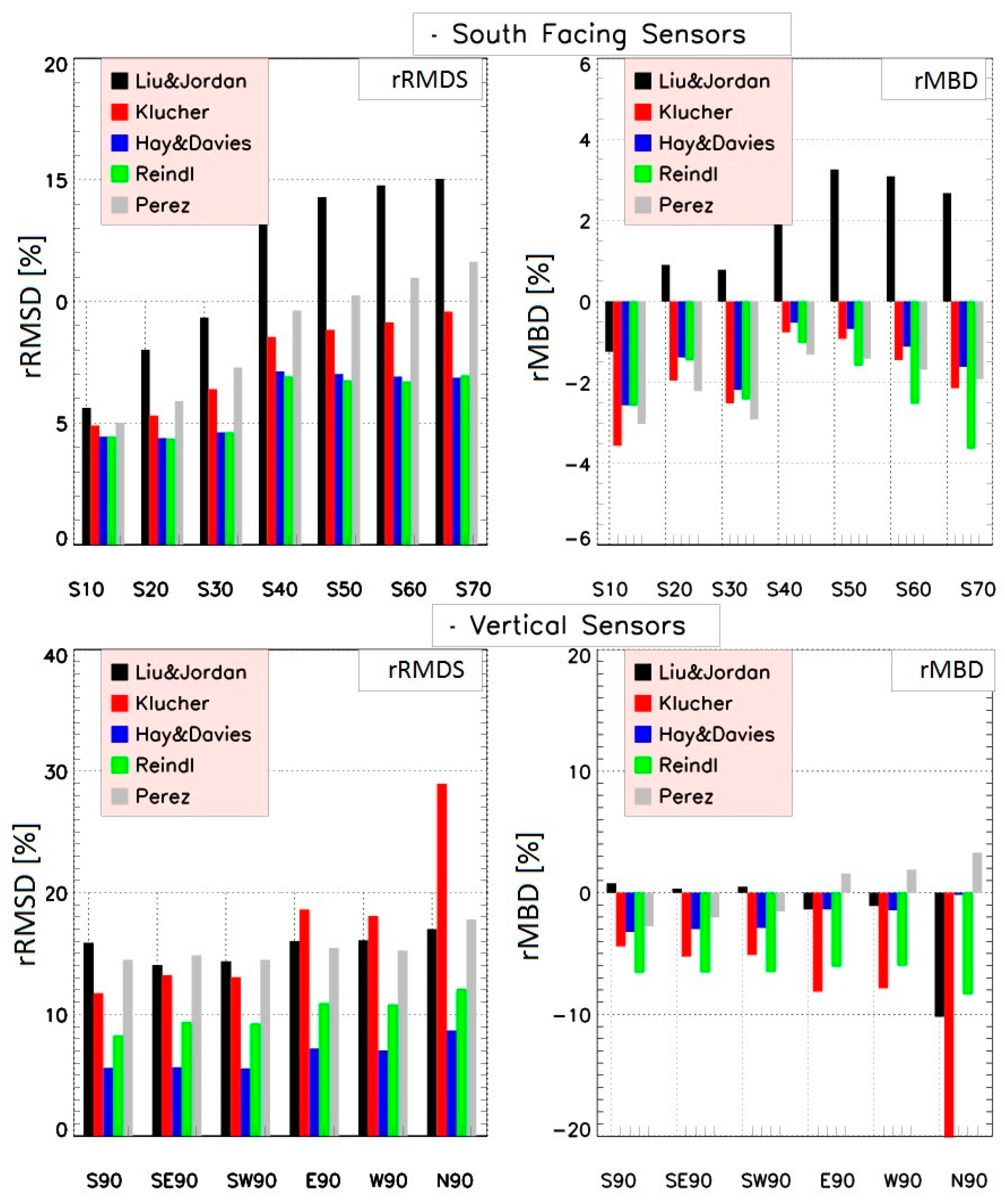
- Best results are provided by the models from Hay and Davies and Reindl, when horizontal pyranometer measurements and a constant albedo value of 0.2 are used. This agreement of the two may relate to the anisotropic index used by both models to weight the circumsolar and isotropic components.
- -
- The anisotropic models overestimate the south tilted irradiance and most of vertical tilted irradiance. In contrast, the isotropic model underestimates the tilted irradiance in most directions.
- -
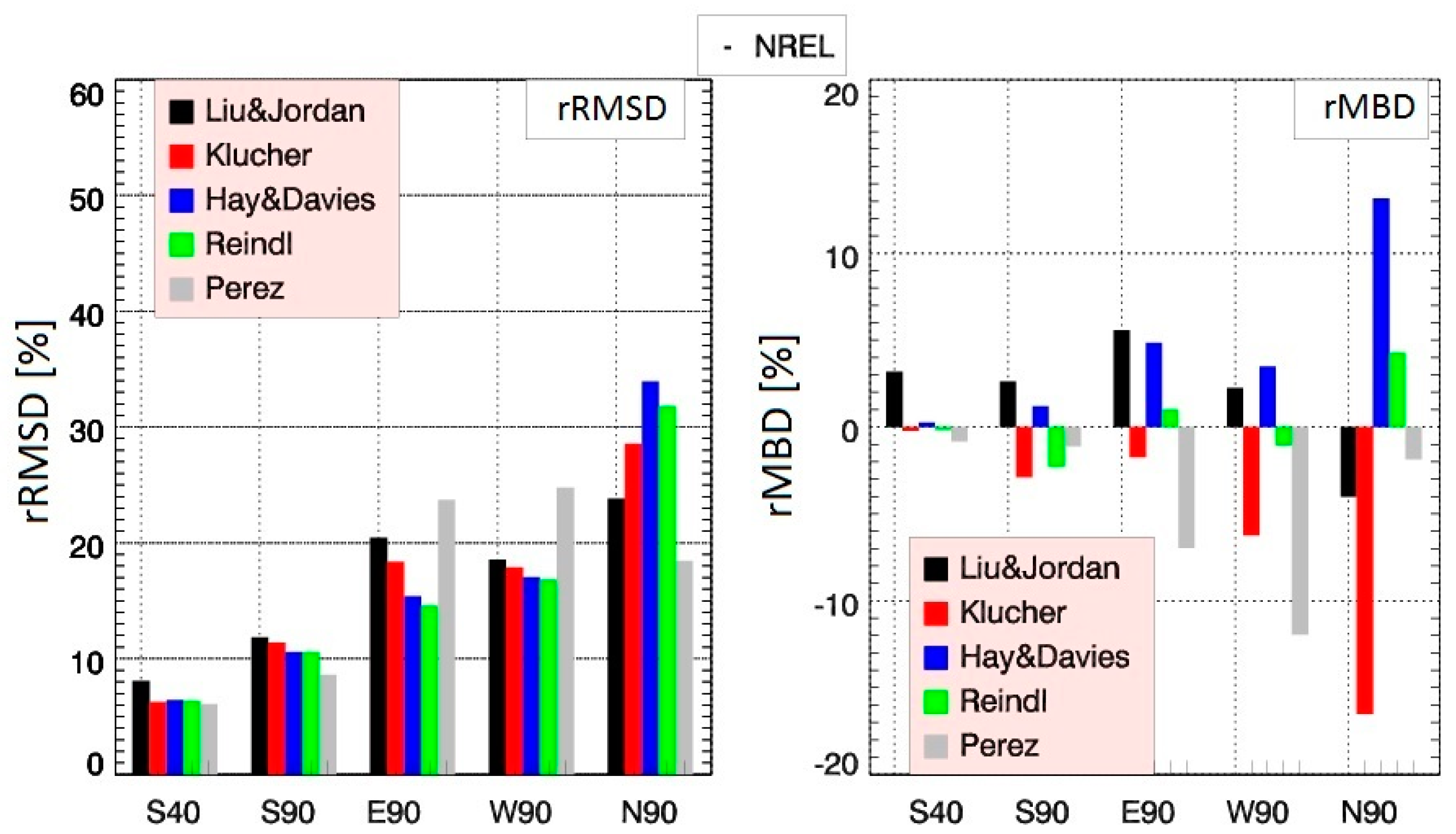
- For the NREL location, when measured albedo is used, the Perez model provides the best estimates of global tilted irradiance.
- -
- The deviations of the anisotropic models from the measurements increase with increasing deviation from the south direction. In this case, the ratio of direct to diffuse radiation decreases and the uncertainty in modelling the diffuse irradiance becomes dominant.
- -
- An uncertainty is introduced when using horizontal pyranometer measurements to estimate the irradiance absorbed by tilted PV modules. Depending on the used model, this uncertainty has only a small or even no effect on the calculated irradiance.
- -
- The influence of albedo value on the calculated tilted irradiance increases as the tilt angle increases. The use of a constant albedo value of 0.2, which is widely accepted and used in most applications, leads to an increase in the rMAD that ranges between 0.2% and 0.8% at 40° tilt and reaches up to 3.8% at 90° tilt angle. If there are surfaces with higher reflectance in the vicinity of the PV system, rMAD is significantly higher.
- -
- The models of Hay and Davies and Reindl is recommended to estimate the tilted irradiance for south-facing modules in regions with mainly cloudy conditions and when albedo measurements are not available. The Hay and Davies model would also be useful for vertical surfaces (e.g., facades and glazing) whereas the Perez model is recommended for sunny sites and when albedo measurements are available.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Δ | sky’s brightness, as in Perez model |
| ρ | ground albedo |
| β | tilt angle (rad) |
| θ | incidence angle (rad) |
| solar zenith angle (rad) | |
| ε | sky’s clearness, as in Perez model [21] |
| a, b | sky geometry parameters, as in Perez model |
| A | transmittance of beam irradiance through atmosphere, as in Hay & Davies model |
| c-Si | crystalline silicon |
| F | Klucher’s modulating factor |
| F1, F2 | degree of circumsolar and horizon anisotropy, in the simplified Perez model |
| , , ,, | Perez model coefficients for irradiance |
| direct-normal solar irradiance (DNI) (W/m2) | |
| beam horizontal irradiance (BHI) (W/m2) | |
| global horizontal irradiance (GHI) (W/m2) | |
| diffuse horizontal irradiance (DHI) (W/m2) | |
| beam tilted irradiance (BTI) (W/m2) | |
| diffuse tilted irradiance (DTI) (W/m2) | |
| ground-reflected irradiance (W/m2) | |
| direct extraterrestrial normal irradiance (W/m2) | |
| global tilted irradiance (GTI) (W/m2) | |
| MAD | mean absolute difference |
| MBD | mean bias difference |
| PV | photovoltaic |
| α | temperature coefficient |
| factor that accounts for direction of beam radiation, | |
| RMSD | root mean square difference |
| SiS | silicon sensor |
References
- Mehleri, E.D.; Zervas, P.L.; Sarimveis, H.; Palyvos, J.A.; Markatos, N.C. A new neural network model for evaluating the performance of various hourly slope irradiation models: Implementation for the region of Athens. Renew. Energy 2010, 35, 1357–1362. [Google Scholar] [CrossRef]
- Kudish, A.I.; Evseev, E.G. Prediction of solar global radiation on a surface tilted to the south. In Proceedings of the Optical Modeling and Measurements for Solar Energy Systems II, San Diego, CA, USA, 11 September 2008; p. 704603. [Google Scholar]
- Riechelmann, S.; Schrempf, M.; Seckmeyer, G. Simultaneous measurement of spectral sky radiance by a non-scanning multidirectional spectroradiometer (MUDIS). Meas. Sci. Technol. 2013, 24, 125501. [Google Scholar] [CrossRef]
- Liu, B.; Jordan, R. Daily insolation on surfaces tilted towards equator. ASHRAE J. 1961, 10, 526–541. [Google Scholar]
- Duffie, J.A.; Beckman, W.A.; Worek, W.M. Solar Engineering of Thermal Processes, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- Badescu, V. 3D isotropic approximation for solar diffuse irradiance on tilted surfaces. Renew. Energy 2002, 26, 221–233. [Google Scholar] [CrossRef]
- Grant, R.H.; Heisler, G.M. Obscured Overcast Sky Radiance Distributions for Ultraviolet and Photosynthetically Active Radiation. J. Appl. Meteorol. 1997, 36, 1336–1345. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Psiloglou, B.E.; Gueymard, C. Measurements and models for total solar irradiance on inclined surface in Athens, Greece. Sol. Energy 1994, 53, 177–185. [Google Scholar] [CrossRef]
- Gueymard, C. An anisotropic solar irradiance model for tilted surfaces and its comparison with selected engineering algorithms. Sol. Energy 1987, 38, 367–386. [Google Scholar] [CrossRef]
- Hay, J.E. Calculation of monthly mean solar radiation for horizontal and inclined surfaces. Sol. Energy 1979, 23, 301–307. [Google Scholar] [CrossRef]
- Reindl, D.T.; Beckman, W.A.; Duffie, J.A. Evaluation of hourly tilted surface radiation models. Sol. Energy 1990, 45, 9–17. [Google Scholar] [CrossRef]
- Skartveit, A.; Asle Olseth, J. Modelling slope irradiance at high latitudes. Sol. Energy 1986, 36, 333–344. [Google Scholar] [CrossRef]
- Notton, G.; Cristofari, C.; Poggi, P. Performance evaluation of various hourly slope irradiation models using Mediterranean experimental data of Ajaccio. Energy Convers. Manag. 2006, 47, 147–173. [Google Scholar] [CrossRef]
- Gueymard, C.A. Advanced solar irradiance model and procedure for spectral solar heat gain calculation. ASHRAE Trans. 2007, 113 Pt 1, 149–164. [Google Scholar]
- Gueymard, D.R.; Myers, C.A. Validation and Ranking Methodologies for Solar Radiation Models; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Yang, D. Solar radiation on inclined surfaces: Corrections and benchmarks. Sol. Energy 2016, 136, 288–302. [Google Scholar] [CrossRef]
- Li, D.H.W.; Lam, J.C.; Lau, C.C.S. A new approach for predicting vertical global solar irradiance. Renew. Energy 2002, 25, 591–606. [Google Scholar] [CrossRef]
- Cucumo, M.; De Rosa, A.; Ferraro, V.; Kaliakatsos, D.; Marinelli, V. Experimental testing of models for the estimation of hourly solar radiation on vertical surfaces at Arcavacata di Rende. Sol. Energy 2007, 81, 692–695. [Google Scholar] [CrossRef]
- Chirarattananon, S.; Rukkwansuk, P.; Chaiwiwatworakul, P.; Pakdeepol, P. Evaluation of vertical illuminance and irradiance models against data from north Bangkok. Build. Environ. 2007, 42, 3894–3904. [Google Scholar] [CrossRef]
- Loutzenhiser, P.G.; Manz, H.; Felsmann, C.; Strachan, P.A.; Frank, T.; Maxwell, G.M. Empirical validation of models to compute solar irradiance on inclined surfaces for building energy simulation. Sol. Energy 2007, 81, 254–267. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Seals, R.; Michalsky, J.; Stewart, R. Modeling daylight availability and irradiance components from direct and global irradiance. Sol. Energy 1990, 44, 271–289. [Google Scholar] [CrossRef]
- De Miguel, A.; Bilbao, J.; Aguiar, R.; Kambezidis, H.; Negro, E. Diffuse solar irradiation model evaluation in the North Mediterranean Belt area. Sol. Energy 2001, 70, 143–153. [Google Scholar] [CrossRef]
- Pandey, C.K.; Katiyar, A.K. A comparative study of solar irradiation models on various inclined surfaces for India. Appl. Energy 2011, 88, 1455–1459. [Google Scholar] [CrossRef]
- Demain, C.; Journée, M.; Bertrand, C. Evaluation of different models to estimate the global solar radiation on inclined surfaces. Renew. Energy 2013, 50, 710–721. [Google Scholar] [CrossRef]
- Khalil, S.A.; Shaffie, A.M. Performance of Statistical Comparison Models of Solar Energy on Horizontal and Inclined Surface. Int. J. Energy Power 2013, 2, 8–25. [Google Scholar]
- Wattan, R.; Janjai, S. An investigation of the performance of 14 models for estimating hourly diffuse irradiation on inclined surfaces at tropical sites. Renew. Energy 2016, 93, 667–674. [Google Scholar] [CrossRef]
- Klucher, T.M. Evaluation of models to predict insolation on tilted surfaces. Sol. Energy 1979, 23, 111–114. [Google Scholar] [CrossRef]
- Martin, N.; Ruiz, J.M. Annual angular reflection losses in PV modules. Prog. Photovolt. Res. Appl. 2005, 13, 75–84. [Google Scholar] [CrossRef]
- Lave, M.; Hayes, W.; Pohl, A.; Hansen, C.W. Evaluation of global horizontal irradiance to plane-of-array irradiance models at locations across the United States. IEEE J. Photovolt. 2015, 5, 597–606. [Google Scholar] [CrossRef]
- Maxwell, E.; Wilcox, S. Users Manual for SERI QC Software, Assessing the Quality of Solar Radiation Data; National Renewable Energy Laboratory: Golden, CO, USA, 1993.
- Hay, J.E.; Davies, J.A. Calculation of the solar radiation incident on an inclined surface. In Proceedings of the First Canadian Solar Radiation Data Workshop, Toronto, ON, Canada, 17–19 April 1978; pp. 59–72. [Google Scholar]
- Woyte, A.; Richter, M.; Moser, D.; Mau, S.; Reich, N.; Jahn, U. Monitoring of Photovoltaic Systems: Good Practices and Systematic Analysis. J. Chem. Inf. Model. 2013, 53, 1689–1699. [Google Scholar]
- Woyte, A.; Richter, M.; Moser, D.; Reich, N.; Green, M.; Mau, S.; Beyer, H. Analytical Monitoring of Grid-Connected Photovoltaic Systems—Good Practices for Monitoring and Performance Analysis; Technical Report; IEA-PVPS: St. Ursen, Switzerland, 2014. [Google Scholar]
- Glotzbach, T.; Schulz, B.; Zehner, M.; Fritze, P.; Schlatterer, M.; Vodermayer, C.; Wotruba, G.; Mayer, M. Round-Robin-Test of Irradiance Sensors. In Proceedings of the 23th PVSEC, Valencia, Spain, 1–5 September 2008. [Google Scholar]
- King, D.L.; Myers, D.R. Silicon-photodiode pyranometers: operational characteristics, historical experiences, and new calibration procedures. In Proceedings of the Conference Record of the Twenty-Sixth IEEE Photovoltaic Specialists Conference, Anaheim, CA, USA, 29 September–3 October 1997; pp. 1285–1288. [Google Scholar]
- Garg, H.P.; Prakash, J. Solar Energy Fundamentals and Applications; Tata McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Perez, R.; Seals, R.; Ineichen, P.; Stewart, R.; Menicucci, D. A new simplified version of the perez diffuse irradiance model for tilted surfaces. Sol. Energy 1987, 39, 221–231. [Google Scholar] [CrossRef]
- Hofmann, M.; Seckmeyer, G. A New Model for Estimating the Diffuse Fraction of Solar Irradiance for Photovoltaic System Simulations. Energies 2017, 10, 248. [Google Scholar] [CrossRef]


| ε | ||||||
|---|---|---|---|---|---|---|
| [1, 1.065] | −0.008 | 0.588 | −0.062 | −0.06 | 0.072 | −0.022 |
| [1.065, 1.23] | 0.13 | 0.683 | −0.151 | −0.019 | 0.066 | −0.029 |
| [1.23, 1.5] | 0.33 | 0.487 | −0.221 | 0.055 | −0.064 | −0.026 |
| [1.5, 1.95] | 0.568 | 0.187 | −0.295 | 0.109 | −0.152 | −0.014 |
| [1.95, 2.8] | 0.873 | −0.392 | −0.362 | 0.226 | −0.462 | 0.001 |
| [2.8, 4.5] | 1.132 | −1.237 | −0.412 | 0.288 | −0.823 | 0.056 |
| [4.5, 6.2] | 1.06 | −1.6 | −0.359 | 0.264 | −1.127 | 0.131 |
| [6.2, ∞] | 0.678 | −0.327 | −0.25 | 0.156 | −1.377 | 0.251 |
| Specifications | Pyranometer CMP11 | Silicon Sensor SiS | Silicon Sensor Li-200 |
|---|---|---|---|
| Spectral sensitivity range (nm) | 285–2800 | 350–1100 | 350–1100 |
| Response time (s) | 5 | <0.001 | <0.001 |
| Offset (W/m2) | 2 | 0 | 0 |
| Temperature dependence (−10–40 °C) (%) | <1 | 0.2 | ±0.15 |
| Uncertainty (W/m2) | <5 | ± 5 | <5 |
| Non-linearity (100 to 1000 W/m2) (%) | <0.5 | ±0.5 | <1.0 |
| Measurements | Model | |||||
|---|---|---|---|---|---|---|
| Parameter | Description | Measuring Sensor | Parameter | Description | Inputs | Measuring Sensor |
| GTI south facing (IMUK) | Tilt: 10°, 20°, 30°, 40°, 50°, 60°, 70° | SiS | GTI south facing | Tilt: 10°, 20°, 30°, 40°, 50°, 60°, 70° | GHI DHI Albedo | CMP11 CMP11 Const. 0.2 |
| GTI Vertical (IMUK) | E, S, W, N, SE, SW | SiS | GTI Vertical | E, S, W, N, SE, SW | GHI DHI Albedo | CMP11 CMP11 Const. 0.2 |
| GTI south facing (IMUK) | Tilt: 40° | CMP11 | GTI south facing | Tilt: 40° | GHI DHI Albedo | CMP11 CMP11 Const. 0.2 |
| GTI south facing (NREL) | Tilt: 40° | Li-200 | GTI south facing | Tilt: 40° | GHI DHI Albedo | CMP11 CMP11 Li-200 |
| GTI Vertical (NREL) | E, S, W, N | Li-200 | GTI Vertical | E, S, W, N | GHI DHI Albedo | CMP11 CMP11 Li-200 |
| GTI south facing (NREL) | Tilt: 40° | CMP11 | GTI south facing | Tilt: 40° | GHI DHI Albedo | CMP11 CMP11 Li-200 |
| GTI south facing (NREL) | Tilt: 40° | Li-200 | GTI south facing | Tilt: 40° | GHI DHI Albedo | CMP11 CMP11 Li-200 |
| GTI Vertical (NREL) | S | Li-200 | GTI Vertical | S | GHI DHI Albedo | CMP11 CMP11 Li-200 |
| IMUK | Liu & Jordan | Klucher | Hay & Davies | Reindl | Perez | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Azimuth/Tilt | rMBD | rMAD | rRMSD | rMBD | rMAD | rRMSD | rMBD | rMAD | rRMSD | rMBD | rMAD | rRMSD | rMBD | rMAD | rRMSD |
| ss10 | −1.24 | 4.32 | 5.62 | −3.56 | 4.06 | 4.98 | −2.56 | 3.67 | 4.44 | −2.57 | 3.67 | 4.44 | −3.02 | 3.94 | 5.01 |
| ss20 | 0.90 | 5.61 | 8.01 | −1.95 | 4.08 | 5.30 | −1.38 | 3.51 | 4.38 | −1.45 | 3.51 | 4.36 | −2.21 | 4.19 | 5.90 |
| ss30 | 0.78 | 6.55 | 9.33 | −2.51 | 4.95 | 6.39 | −2.18 | 3.75 | 4.62 | −2.41 | 3.77 | 4.61 | −2.91 | 5.08 | 7.28 |
| ss40 | 3.03 | 8.71 | 13.49 | −0.76 | 6.54 | 8.54 | −0.52 | 5.11 | 07.12 | −1.02 | 5.04 | 06.91 | −1.31 | 6.40 | 09.62 |
| ss50 | 3.25 | 9.11 | 14.29 | −0.92 | 6.20 | 08.83 | −0.68 | 5.06 | 07.02 | −1.58 | 5.01 | 06.74 | −1.41 | 6.88 | 10.24 |
| ss60 | 3.08 | 9.37 | 14.76 | −1.44 | 6.46 | 09.13 | −1.11 | 5.04 | 06.91 | −2.52 | 5.15 | 06.70 | −1.68 | 7.41 | 10.97 |
| ss70 | 2.57 | 10.96 | 15.03 | −2.14 | 6.47 | 09.58 | −1.61 | 5.05 | 06.86 | −3.63 | 5.16 | 06.95 | −1.93 | 8.05 | 11.63 |
| ss90 | 0.76 | 08.04 | 15.89 | −4.41 | 08.04 | 11.74 | −3.22 | 04.14 | 05.60 | −6.57 | 6.70 | 09.27 | −2.75 | 10.25 | 14.48 |
| se90 | 0.32 | 08.56 | 14.06 | −5.26 | 08.42 | 13.20 | −2.99 | 04.00 | 05.64 | −6.55 | 06.65 | 09.38 | −2.02 | 10.73 | 14.85 |
| sw90 | 0.50 | 08.70 | 14.36 | −5.12 | 08.43 | 13.05 | −2.98 | 03.96 | 05.55 | −6.51 | 06.60 | 09.26 | −1.54 | 10.43 | 14.47 |
| ee90 | −1.37 | 10.29 | 16.02 | −8.14 | 12.66 | 18.63 | −1.38 | 05.21 | 07.20 | −6.07 | 07.69 | 10.92 | 1.57 | 11.36 | 15.46 |
| ww90 | −1.09 | 10.46 | 16.10 | −7.86 | 12.50 | 18.09 | −1.43 | 05.13 | 07.02 | −6.01 | 07.67 | 10.80 | 1.98 | 11.27 | 15.24 |
| nn90 | −10.20 | 10.48 | 17.00 | −20.13 | 20.28 | 28.94 | −0.17 | 06.81 | 08.67 | −8.34 | 08.97 | 12.08 | 3.47 | 14.45 | 17.81 |
| pyr40 | 4.66 | 6.64 | 8.69 | 0.74 | 5.03 | 6.74 | 1.45 | 5.68 | 7.59 | 1 | 5.49 | 7.37 | 0.23 | 5.08 | 6.66 |
| NREL | Liu & Jordan | Klucher | Hay & Davies | Reindl | Perez | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Azimuth/Tilt | rMBD | rMAD | rRMSD | rMBD | rMAD | rRMSD | rMBD | rMAD | rRMSD | rMBD | rMAD | rRMSD | rMBD | rMAD | rRMSD |
| S 40 | 2.89 | 5.47 | 7.85 | −0.45 | 3.95 | 6.08 | 0.08 | 4.0 | 6.26 | −0.36 | 3.94 | 6.18 | −0.96 | 3.98 | 6.0 |
| S 90 | 2.40 | 8.81 | 11.76 | −3.06 | 8.11 | 11.46 | 1.09 | 7.82 | 10.63 | −2.41 | 7.72 | 10.68 | −1.13 | 5.99 | 8.72 |
| E 90 | 5.48 | 13.87 | 20.5 | −1.75 | 13.1 | 18.64 | 4.70 | 11.18 | 15.50 | 0.91 | 10.5 | 14.8 | −6.88 | 17.07 | 24.02 |
| W 90 | 2.28 | 13.58 | 18.8 | −6.1 | 13.25 | 18.2 | 3.50 | 13.49 | 17.3 | −1.02 | 13.05 | 17.1 | −11.78 | 17.75 | 25.15 |
| N 90 | −4.60 | 18.3 | 24.10 | −16.7 | 21.00 | 29.05 | 12.33 | 28.20 | 33.78 | 3.47 | 25.85 | 31.8 | −2.65 | 14.31 | 18.89 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mubarak, R.; Hofmann, M.; Riechelmann, S.; Seckmeyer, G. Comparison of Modelled and Measured Tilted Solar Irradiance for Photovoltaic Applications. Energies 2017, 10, 1688. https://doi.org/10.3390/en10111688
Mubarak R, Hofmann M, Riechelmann S, Seckmeyer G. Comparison of Modelled and Measured Tilted Solar Irradiance for Photovoltaic Applications. Energies. 2017; 10(11):1688. https://doi.org/10.3390/en10111688
Chicago/Turabian StyleMubarak, Riyad, Martin Hofmann, Stefan Riechelmann, and Gunther Seckmeyer. 2017. "Comparison of Modelled and Measured Tilted Solar Irradiance for Photovoltaic Applications" Energies 10, no. 11: 1688. https://doi.org/10.3390/en10111688
APA StyleMubarak, R., Hofmann, M., Riechelmann, S., & Seckmeyer, G. (2017). Comparison of Modelled and Measured Tilted Solar Irradiance for Photovoltaic Applications. Energies, 10(11), 1688. https://doi.org/10.3390/en10111688





