Multi-Objective Optimal Design of Stand-Alone Hybrid Energy System Using Entropy Weight Method Based on HOMER
Abstract
:1. Introduction
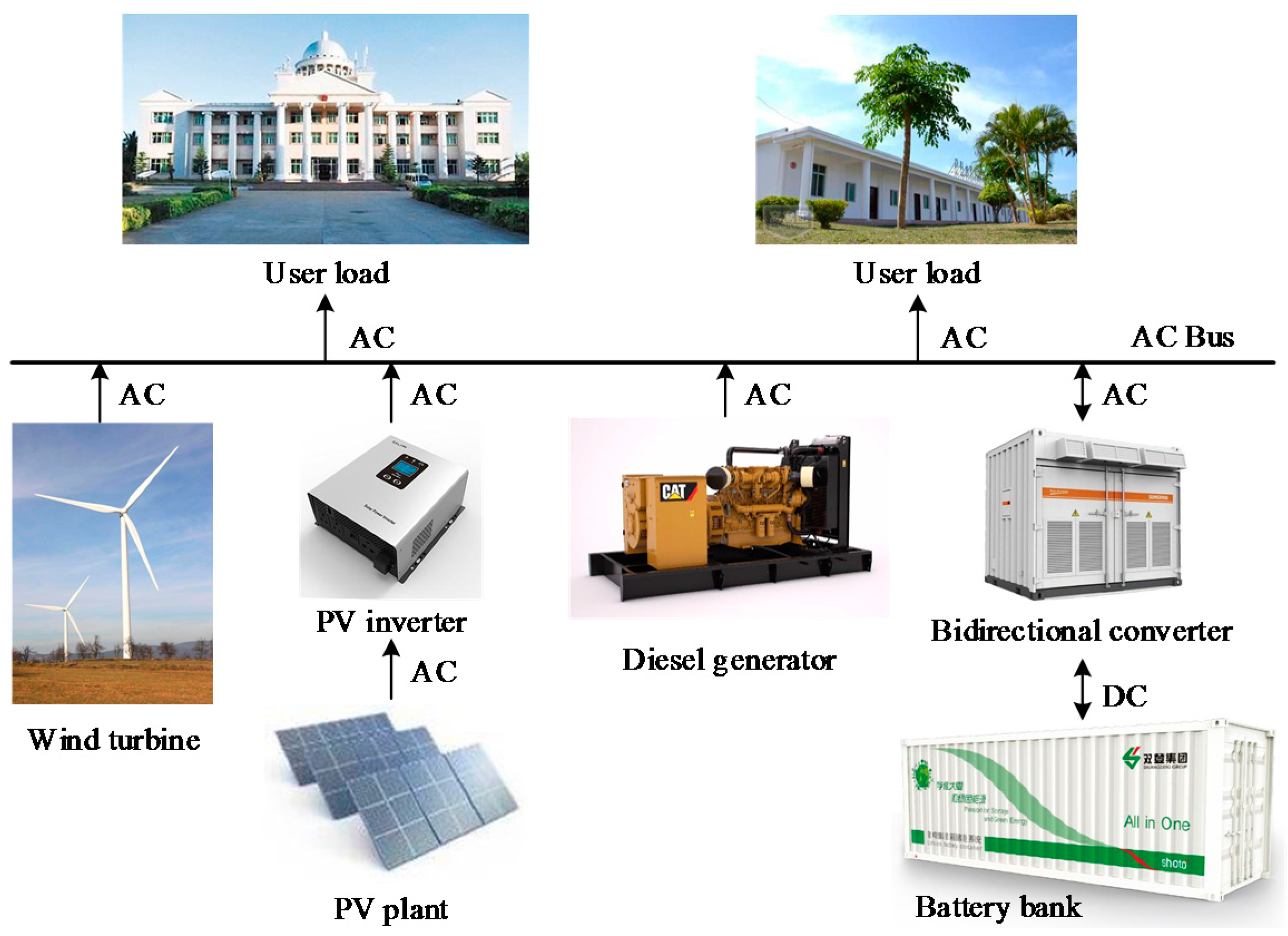
2. Description of HES
2.1. Mathematical Model of Major Components
2.1.1. Model of Photovoltaic (PV) Panel
2.1.2. Model of Wind Turbine (WT)
2.1.3. Model of Battery Bank
2.1.4. Model of Diesel Generator
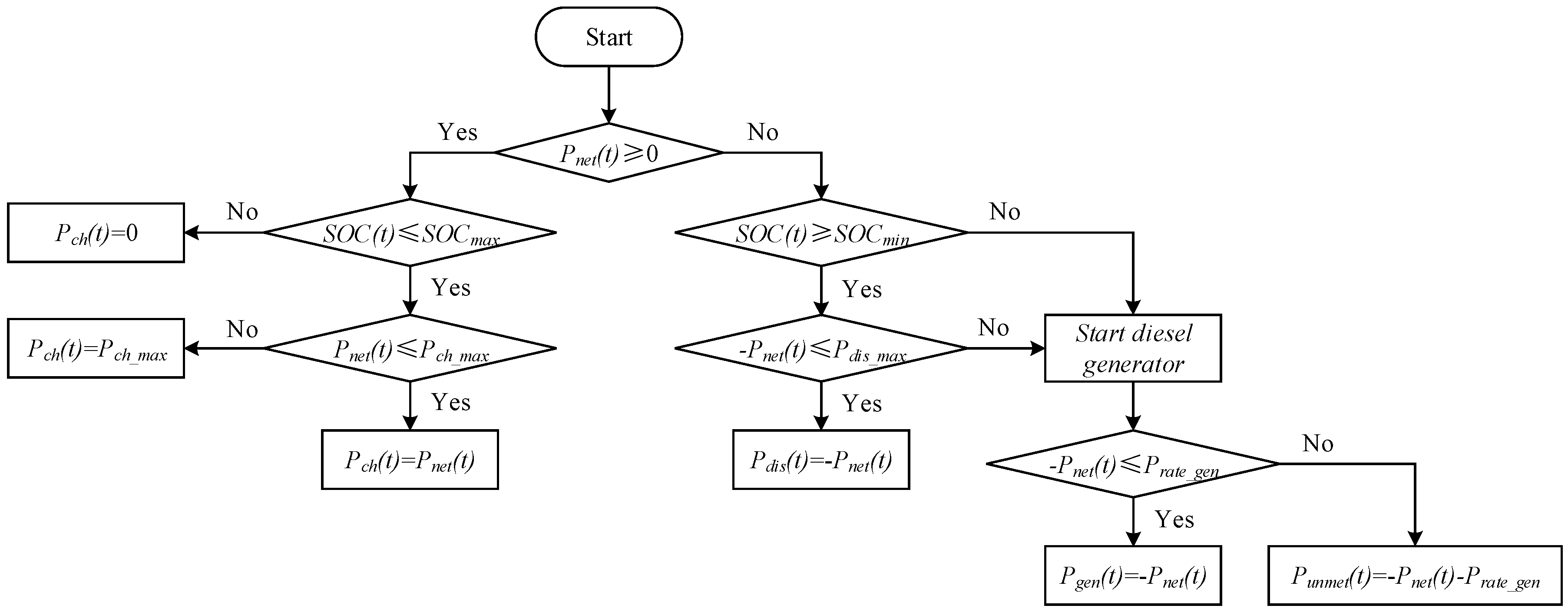
2.2. Control Strategy
3. Problem Formulation
3.1. Evaluation Indices
3.1.1. Reliability Index
3.1.2. Economic Index
3.1.3. Practical Index
3.1.4. Environmental Sustainability Index
3.2. Objective Function
4. Methodology
4.1. Entropy Weight Method
- Step 1: Initialization of the decision matrix. Assuming that there are alternatives need to be evaluated in terms of indices, the initial decision matrix can be established as follows:
- Step 2: Normalization of the decision matrix. In order to solve the uniformity of indices’ units, the normalization of all indices is performed. For benefit type, the higher value the better performance, the normalization can be conducted by the listed expression [41]:For cost type, the lower value the better property, the normalization can be conducted by the listed expression:Then, the normalized decision matrix can be obtained.
- Step 3: Calculation of weighting factors. The information entropy of each index is calculated by:where is the information entropy of each index, can be calculated by:Based on the value of the information entropy, the weighting factors of each index can be calculated by:where and .
4.2. Description of the Proposed Method
- Step 1: System simulation with HOMER. Several types of data including load profile, component specifications, meteorological data, system control, search space, and constraints are fed into HOMER. After that, every feasible combination in search space will be simulated in each time step of the year, and the desired output such as LPSP, LCOE, OA and RF will be calculated for further use.
- Step 2: Evaluation system establishment. Multi-objective function is carried out by adopting the weight sum method. Then, weighting factors of each index is calculated according to the output data obtained from previous step.
- Step 3: Decision making process. The rating values of each feasible configuration is calculated by multiplying the index value and corresponding weighting factors. Finally, the configuration with maximum rating value will be recommended as the optimal one.
5. Results and Discussions
5.1. Case Study
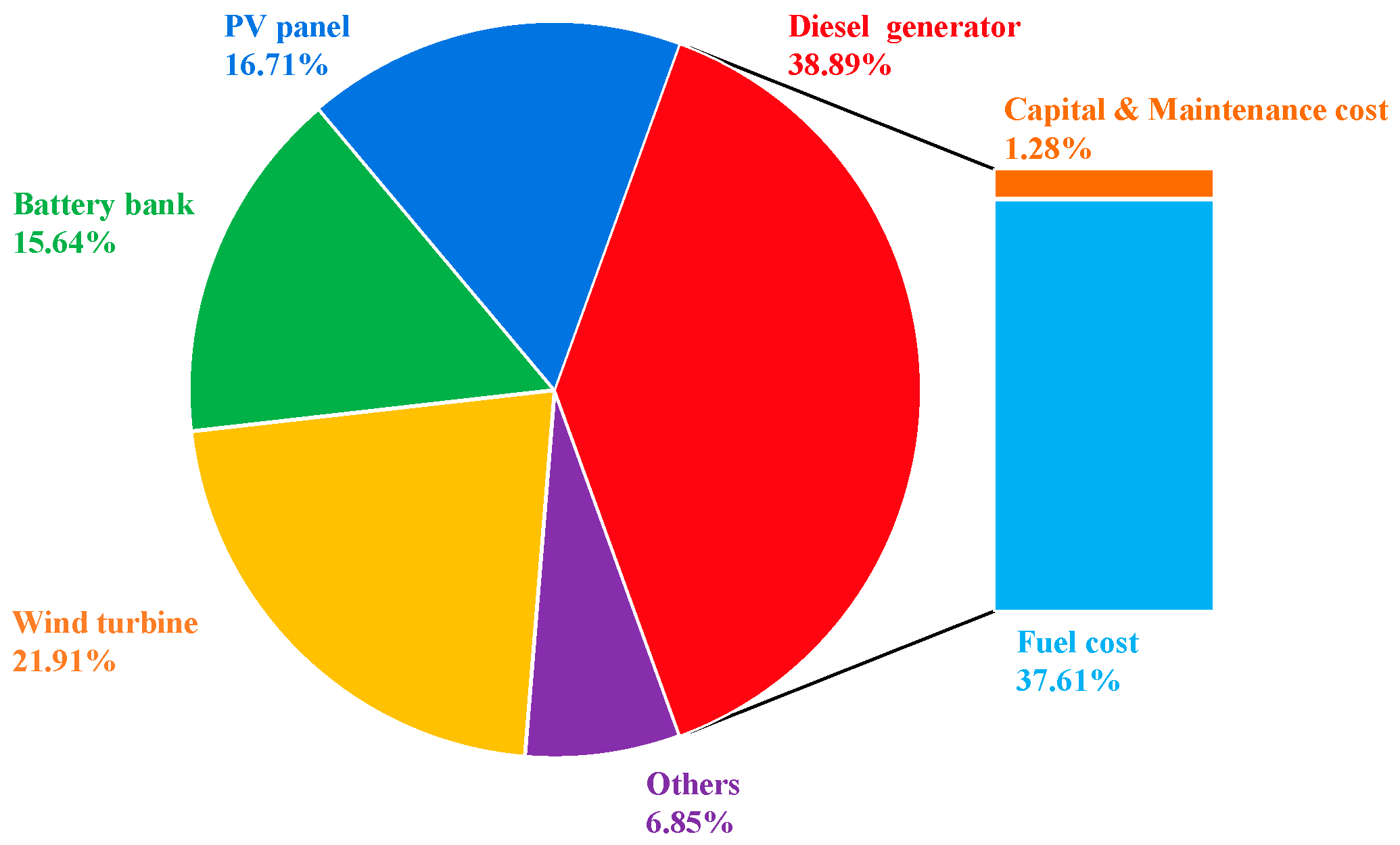
5.2. Economic Analysis
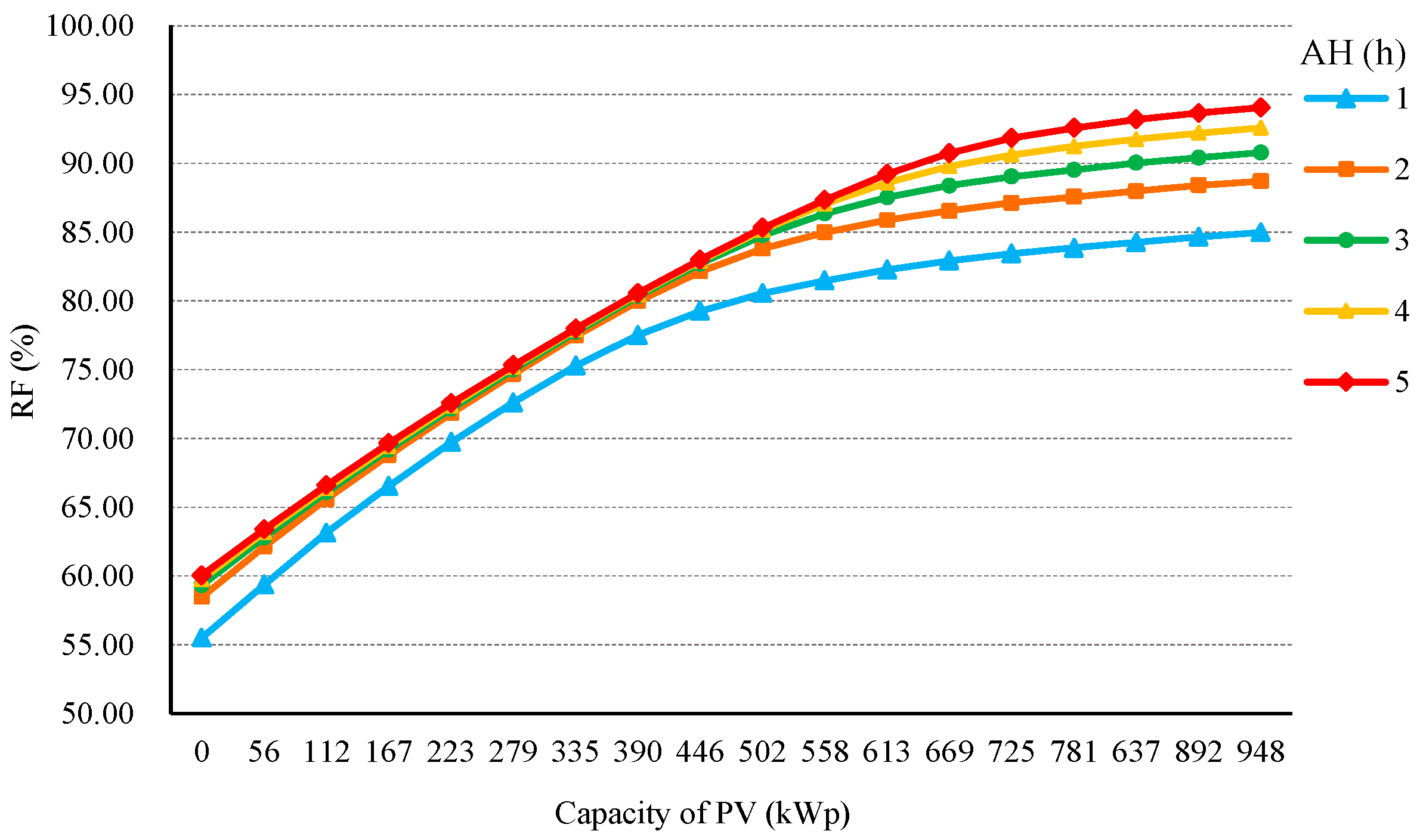
5.3. Environmental Analysis
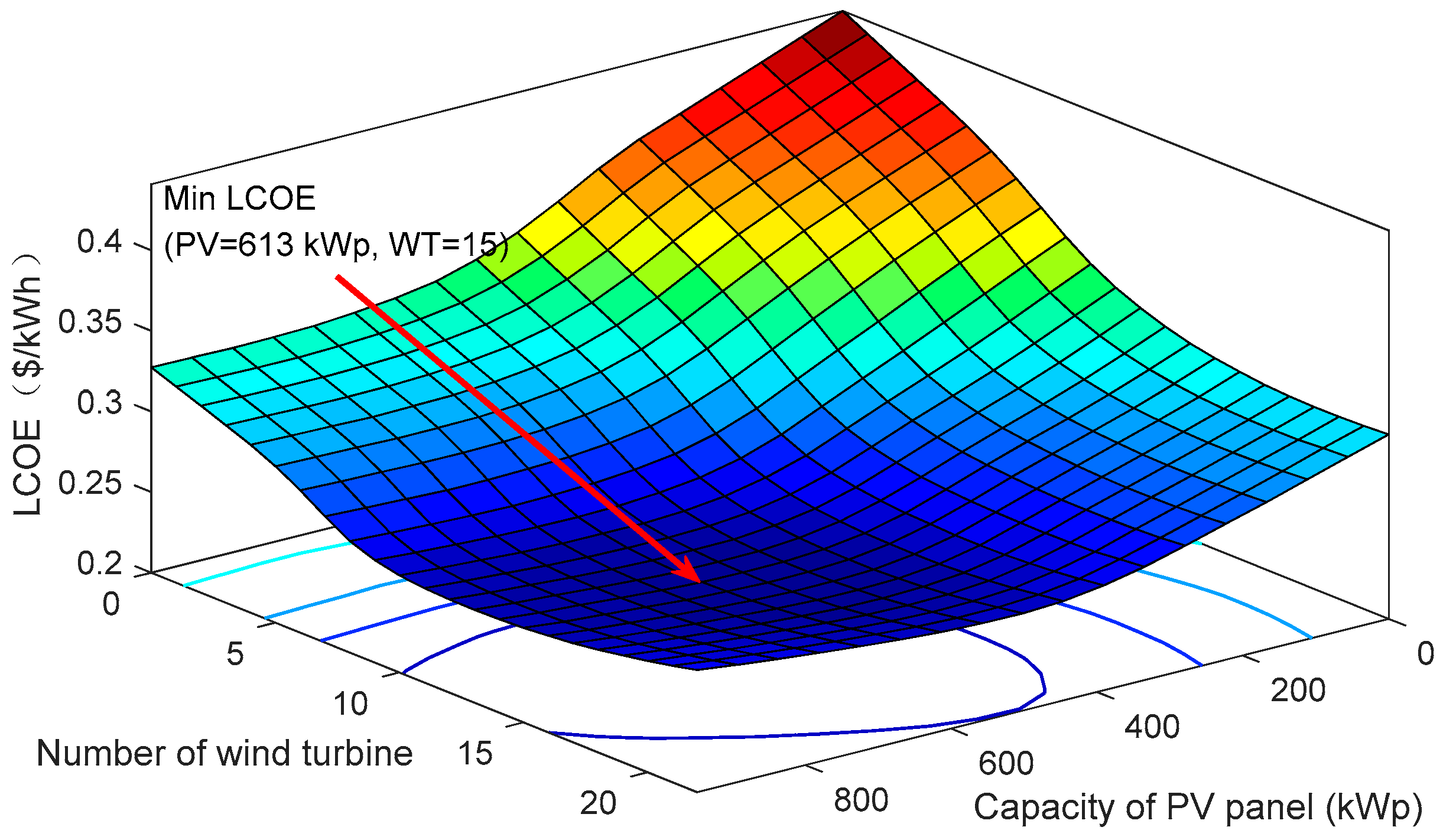
5.4. Optimal Design of HES
- Scenario 1: The most economical scenario. Only LCOE is taken into consideration, and the rest of the indices in Equation (18) are neglected. Configuration with least LCOE would be recognized as the most economical scenario.
- Scenario 2: The most practical scenario. According to simulation results from HOMER, there are only 1941 feasible configurations compliant with the regulations presented by the State Grid Corporation of China (LOLE ≤ 8). Among them, the configuration with least OA would be recognized as the most practical scenario.
- Scenario 3: The environmental best scenario. This scenario is similar to the most economical one, except the index is composed of RF only, and the configuration with maximum RF would be recognized as the environmental best scenario.
5.5. Analysis of the Best Configuration
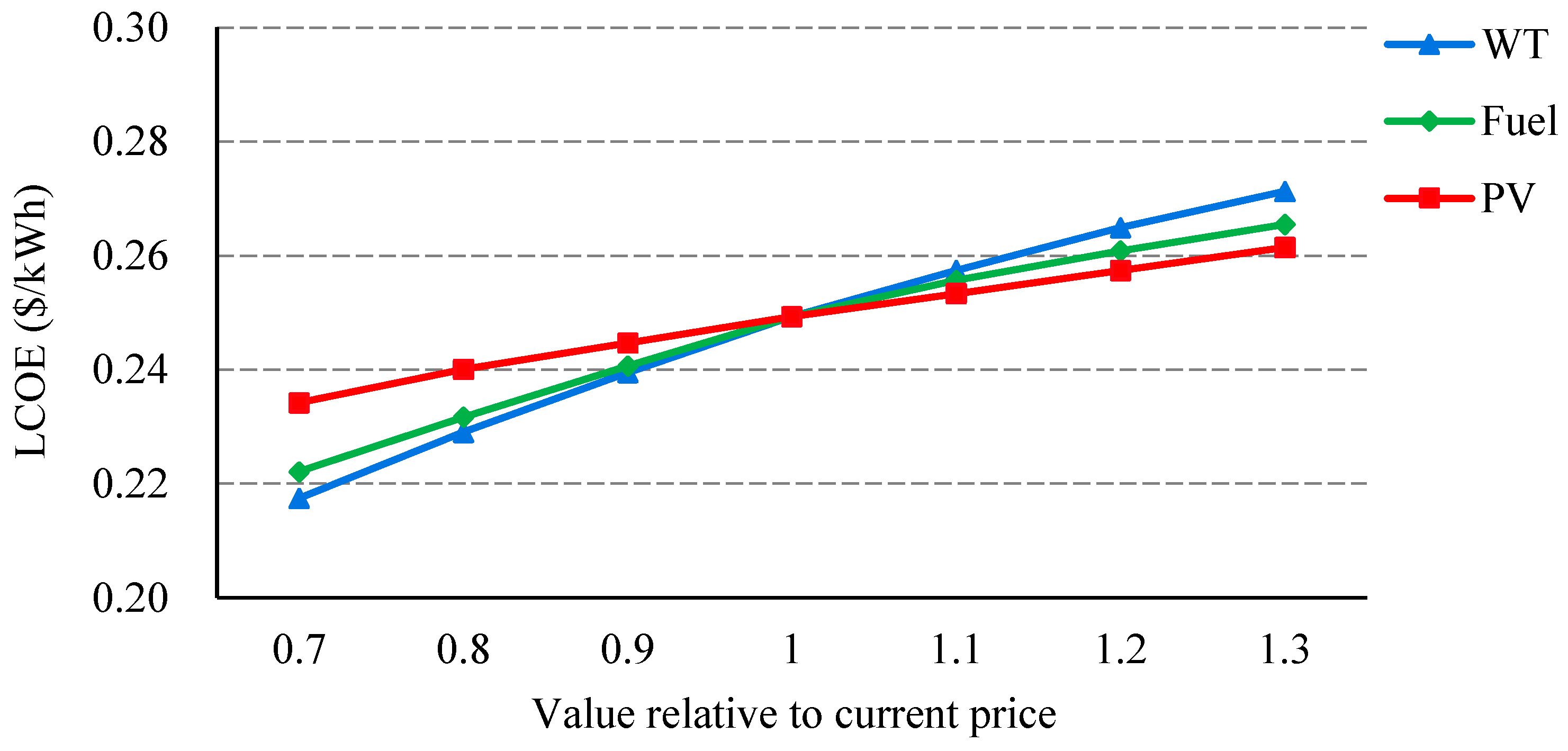
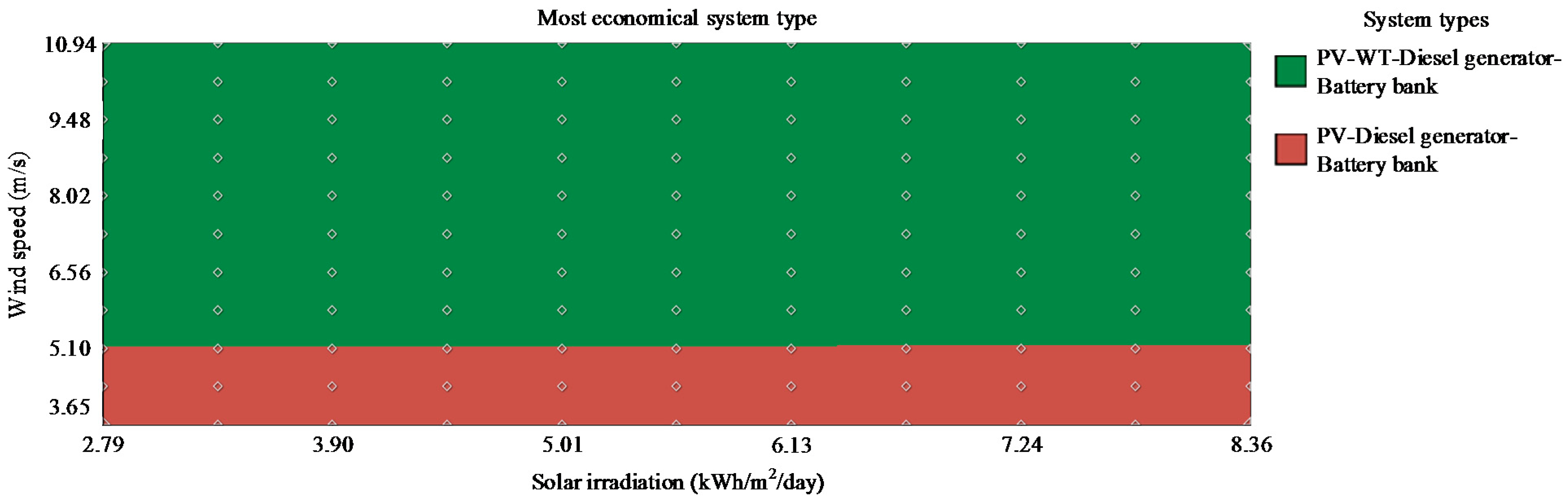
5.6. Sensitivity Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- World Bank. Sustainable Energy for All (SE4ALL) Database from World Bank Global Electrification Database. Available online: http://data.worldbank.org/indicator/EG.ELC.ACCS.ZS (accessed on 20 March 2017).
- Goodarzi, H.M.; Kazemi, M. A novel optimal control method for islanded microgrids based on droop control using the ICA-GA algorithm. Energies 2017, 10, 485. [Google Scholar] [CrossRef]
- Borhanazad, H.; Mekhilef, A.; Ganapathy, V.G. Optimization of micro-grid system using MOPSO. Renew. Energy 2014, 71, 295–306. [Google Scholar] [CrossRef]
- Yan, B.; Wang, B.; Zhu, L.; Liu, H.; Liu, Y.; Ji, X. A novel, stable, and economic power sharing scheme for an autonomous microgrid in the energy internet. Energies 2015, 8, 12741–12764. [Google Scholar] [CrossRef]
- Dufo-López, R.; Bernal-Agustín, J.L. Multi-objective design of PV-wind-diesel-hydrogen-battery systems. Renew. Energy 2008, 33, 2559–2572. [Google Scholar] [CrossRef]
- Jing, L.; Wei, W.; Ji, X. A simple sizing algorithm for stand-alone PV/Wind/Battery hybrid microgrids. Energies 2012, 5, 5307–5323. [Google Scholar]
- Ahmad, M.A.E.M.; Bekdache, S.K.; Barrios, L.A. Optimal sizing for a hybrid power system with wind/energy storage based in stochastic environment. Renew. Sustain. Energy Rev. 2016, 59, 1149–1158. [Google Scholar]
- Zhou, N.; Liu, N.; Zhang, J.; Lei, J. Multi-objective optimal sizing for battery storage of PV-based microgrid with demand response. Energies 2016, 9, 591. [Google Scholar] [CrossRef]
- Kamjoo, A.; Maheri, A.; Dizqah, A.M. Multi-objective design under uncertainties of hybrid renewable energy system using NSGA-II and chance constrained programming. Int. J. Electr. Power Energy Syst. 2016, 74, 187–194. [Google Scholar] [CrossRef]
- Kaabeche, A.; Belhamel, M.; Ibtiouen, R. Sizing optimization of grid-independent hybrid photovoltaic wind power generation system. Energy 2011, 36, 1214–1222. [Google Scholar] [CrossRef]
- Ren, H.; Zhou, W.; Nakagami, K. Multi-objective optimization for the operation of distributed energy systems considering economic and environmental aspects. Appl. Energy 2010, 87, 3642–3651. [Google Scholar] [CrossRef]
- Arun, P.; Banerjee, R.; Bandyopadhyay, S. Optimum sizing of battery-integrated diesel generator for remote electrification through design-space approach. Energy 2008, 33, 1155–1168. [Google Scholar] [CrossRef]
- Jakhrani, A.Q.; Othman, A.K.; Rigit, A.R.H. A novel analytical model for optimal sizing of standalone photovoltaic systems. Energy 2012, 46, 675–682. [Google Scholar] [CrossRef]
- Tezer, T.; Yaman, R.; Yaman, G. Evaluation of approaches used for optimization of stand-alone hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2017, 73, 840–853. [Google Scholar] [CrossRef]
- Wu, Y.K.; Lee, C.Y.; Liu, L.C. Study of reconfiguration for the distribution system with distributed generators. IEEE Trans. Power Deliv. 2010, 25, 1678–1685. [Google Scholar] [CrossRef]
- Shayeghi, H.; Hashemi, Y. Application of fuzzy decision-making based on INSGA-II to designing PV-wind hybrid system. Eng. Appl. Artif. Intell. 2015, 45, 1–17. [Google Scholar] [CrossRef]
- Raji, A.; Noboru, Y. Distributed renewable generation and storage system sizing based on smart dispatch of microgrids. Energies 2016, 9, 176. [Google Scholar]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B. Reliability/cost-based multi-objective Pareto optimal design of stand-alone wind/PV/FC generation microgrid system. Energy 2016, 115, 1022–1041. [Google Scholar] [CrossRef]
- Katsigiannis, Y.A.; Georgilakis, P.S.; Karapidakis, E.S. Hybrid simulated annealing-tabu search method for optimal sizing of autonomous power systems with renewables. IEEE Trans. Sustain. Energy 2012, 3, 330–338. [Google Scholar] [CrossRef]
- Dufo-López, R.; Bernal-Agustín, J.L.; Yusta-Loyo, J.M. Multi-objective optimization minimizing cost and life cycle emissions of stand-alone PV-wind-diesel systems with batteries storage. Appl. Energy 2011, 88, 4033–4041. [Google Scholar] [CrossRef]
- Mendes, G.; Ioakimidis, C.; Ferrão, P. On the planning and analysis of integrated community energy systems: A review and survey of available tools. Renew. Sustain. Energy Rev. 2011, 15, 4836–4854. [Google Scholar] [CrossRef]
- Sigarchian, S.G.; Paleta, R.; Malmquist, A. Feasibility study of using a biogas engine as backup in a decentralized hybrid (PV/wind/battery) power generation system—Case study Kenya. Energy 2015, 90, 1830–1841. [Google Scholar] [CrossRef]
- Chauhan, A.; Saini, R.P. Techno-economic feasibility study on integrated renewable energy system for an isolated community of India. Renew. Sustain. Energy Rev. 2016, 59, 388–405. [Google Scholar] [CrossRef]
- Kusakana, K. Techno-economic analysis of off-grid hydrokinetic-based hybrid energy systems for onshore/remote area in South Africa. Energy 2014, 68, 947–957. [Google Scholar] [CrossRef]
- Bahramara, S.; Moghaddam, M.P.; Haghifam, M.R. Optimal planning of hybrid renewable energy systems using HOMER: A review. Renew. Sustain. Energy Rev. 2016, 62, 609–620. [Google Scholar] [CrossRef]
- Ding, M.; Wang, B.; Zhao, B.; Chen, Z.N. Configuration optimization of capacity of standalone PV-wind-diesel-battery hybrid microgrid. Power Syst. Technol. 2013, 37, 575–581. [Google Scholar]
- Li, G.; Liu, W.; Jiao, B.; Wang, C. Multi-objective optimal planning design method for stand-alone microgrid system. Proc. CSEE 2014, 34, 524–536. [Google Scholar]
- Manwell, J.F.; Mcgowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Azaza, M.; Wallin, F. Multi objective particle swarm optimization of hybrid micro-grid system: A case study in Sweden. Energy 2017, 123, 108–118. [Google Scholar] [CrossRef]
- Mamaghani, A.H.; Escandon, S.A.A.; Najafi, B. Techno-economic feasibility of photovoltaic, wind, diesel and hybrid electrification systems for off-grid rural electrification in Colombia. Renew. Energy 2016, 97, 293–305. [Google Scholar] [CrossRef]
- Tazvinga, H.; Zhu, B.; Xia, X. Energy dispatch strategy for a photovoltaic-wind-diesel-battery hybrid power system. Sol. Energy 2014, 108, 412–420. [Google Scholar] [CrossRef]
- Khan, M.R.B.; Jidin, R.; Pasupuleti, J. Optimal combination of solar, wind, micro-hydro and diesel systems based on actual seasonal load profiles for a resort island in the South China Sea. Energy 2015, 82, 80–97. [Google Scholar] [CrossRef]
- Acuña, L.G.; Padilla, R.V.; Mercado, A.S. Measuring reliability of hybrid photovoltaic-wind energy systems: A new indicator. Renew. Energy 2017, 106, 68–77. [Google Scholar] [CrossRef]
- Bakelli, Y.; Arab, A.H.; Azoui, B. Optimal sizing of photovoltaic pumping system with water tank storage using LPSP concept. Sol. Energy 2011, 852, 288–294. [Google Scholar] [CrossRef]
- Maheri, A. Multi-objective design optimisation of standalone hybrid wind-PV-diesel systems under uncertainties. Renew. Energy 2014, 66, 650–661. [Google Scholar] [CrossRef]
- State Grid Corporation of China. Power Grid Standards. Available online: http://www.sgcc.com.cn/fgbz/dwbzgf/default.shtml (accessed on 3 October 2017).
- Bortolini, M.; Gamberi, M.; Graziani, A. Economic and environmental bi-objective design of an off-grid photovoltaic-battery-diesel generator hybrid energy system. Energy Convers. Manag. 2015, 106, 1024–1038. [Google Scholar] [CrossRef]
- Wang, S.; Li, Z.; Wu, L. New metrics for assessing the reliability and economics of microgrids in distribution system. IEEE Trans. Power Syst. 2013, 28, 2852–2861. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; The University of Illinois Press: Urbana, IL, USA, 1947. [Google Scholar]
- Jian, L.; Zhiman, H.; Youyuan, W.; Jinzhuang, L.; Linjie, Z. A two-dimensional cloud model for condition assessment of HVDC converter transformers. Energies 2012, 5, 157–167. [Google Scholar]
- Ji, Y.; Huang, G.H.; Sun, W. Risk assessment of hydropower stations through an integrated fuzzy entropy-weight multiple criteria decision making method: A case study of the Xiangxi River. Expert Syst. Appl. 2015, 42, 5380–5389. [Google Scholar] [CrossRef]
- Atmospheric Science Data Center. Available online: https://eosweb.larc.nasa.gov/ (accessed on 13 March 2017).



| Parameter | Value |
|---|---|
| Capital cost ($/kW) | 2250 |
| Operation and maintenance cost ($/year) | 0 |
| Replacement cost ($/kW) | 2250 |
| Derating factor (%) | 93.5 |
| Efficiency at standard test condition (%) | 19.5 |
| Nominal operating cell temperature (°C) | 46 |
| Temperature coefficient of power (%/°C) | −0.38 |
| Parameter | Value |
|---|---|
| Capital cost ($) | 96,500 |
| Operation and maintenance cost ($/year) | 8100 |
| Replacement cost ($) | 81,000 |
| Cut-in wind speed (m/s) | 3 |
| Cut-out wind speed (m/s) | 25 |
| Rated wind speed (m/s) | 13 |
| Hub height (m) | 16 |
| Parameter | Value |
|---|---|
| Capital cost ($/battery) | 314 |
| Operation and maintenance cost ($/battery/year) | 31 |
| Replacement cost ($) | 314 |
| Nominal capacity (kWh) | 1.92 |
| Roundtrip efficiency (%) | 86 |
| Parameter | Value |
|---|---|
| Capital cost ($) | 56,000 |
| Operation and maintenance cost ($/h) | 0.277 |
| Replacement cost ($) | 40,000 |
| Minimum load ratio (%) | 30 |
| Life time (h) | 90,000 |
| Indices | LPSP | LCOE | OA | RF |
|---|---|---|---|---|
| Information entropy | 0.99392 | 0.991628 | 0.986248 | 0.9959 |
| Weighting factors (%) | 12.7 | 18.8 | 42.6 | 25.9 |
| Scenarios | Most Economical | Most Practical | Environmental Best | Best Configuration |
|---|---|---|---|---|
| PV panel (kW) | 613.47 | 111.54 | 948.09 | 613.47 |
| Wind turbine | 15 | 1 | 22 | 9 |
| Battery bank (kWh) | 898 | 449 | 2245 | 1796 |
| LOLE (h/year) | 0 | 8 | 0 | 0 |
| LCOE ($/kWh) | 0.2488 | 0.405 | 0.2836 | 0.2592 |
| OA (m2) | 4505 | 506 | 6728 | 3361 |
| RF (%) | 86 | 13 | 97 | 81 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Wang, W.; Zhang, Y.; Cheng, S. Multi-Objective Optimal Design of Stand-Alone Hybrid Energy System Using Entropy Weight Method Based on HOMER. Energies 2017, 10, 1664. https://doi.org/10.3390/en10101664
Lu J, Wang W, Zhang Y, Cheng S. Multi-Objective Optimal Design of Stand-Alone Hybrid Energy System Using Entropy Weight Method Based on HOMER. Energies. 2017; 10(10):1664. https://doi.org/10.3390/en10101664
Chicago/Turabian StyleLu, Jiaxin, Weijun Wang, Yingchao Zhang, and Song Cheng. 2017. "Multi-Objective Optimal Design of Stand-Alone Hybrid Energy System Using Entropy Weight Method Based on HOMER" Energies 10, no. 10: 1664. https://doi.org/10.3390/en10101664
APA StyleLu, J., Wang, W., Zhang, Y., & Cheng, S. (2017). Multi-Objective Optimal Design of Stand-Alone Hybrid Energy System Using Entropy Weight Method Based on HOMER. Energies, 10(10), 1664. https://doi.org/10.3390/en10101664





