1. Introduction
An Energy Storage System (ESS) is a significant tool for a more energy efficient ecosystem and help to decrease environmental concerns [
1,
2]. In general, the objective of an ESS is to reduce the cost of electricity and avoid the need to upgrade the distribution network by shifting energy consumption from peak to valley periods [
2]. ESS’s are expected to be more frequently applied to a wide range of demand side applications. Recently, sea ports are moving towards replacing diesel RTG cranes [
3,
4], which move containers on a port platform and organise container storage in the yard area, with electric RTG cranes to reduce green gas emissions and improve energy efficiency [
1,
2,
3]. In RTG crane system, most of electricity energy or fuel consumption comes from hoisting containers with different weights to several heights. Furthermore, the peak demand increases when the RTG crane moves heavier containers [
5]. The details of RTG crane energy topology are discussed in
Section 2. The shift to the use of electrified RTG cranes can reduce the costs for equipment repairs and maintenance by around 30% compared to diesel RTG cranes. However, as electricity demand on the ports’ electrical distribution networks augments due to the electrification of RTG cranes, port operators will be forced to reinforce the network to meet this increased demand [
3,
4]. The traditional reinforcement solutions focus on upgrading or replacing existing electrical infrastructure such as cables and substations. This solution is effective but commercially expensive, which motivates the consideration of different ESSs technologies and control methods for supporting the power grid. In ports, ESS could play a vital role in reducing peak demand, the carbon gas emissions and Rubber Tyre Gantry (RTG) crane operation costs [
4]. RTG crane load profiles have a highly volatile and stochastic behavior compared to other low and medium voltage loads including domestic customers. The nature of the electrified RTG crane load as well as the vague physically explanatory relationships between the crane load and exogenous variables such as temperature, wind speed and seasonality trends increase the challenges and difficulties in forecasting RTG crane load demand compared to low and medium voltage loads [
5]. Difficulty in generating accurate crane load forecasts and the unpredictable load behaviour make it substantially more challenging to control and improve storage performance using forecast data. Most peak demand reduction strategies in the RTG crane and port applications equipped with ESS mainly focus on using a set-point control strategy to charge and discharge the storage based on the voltage, power or State of Charge (SoC) level. Furthermore, to the best of the author’s knowledge, there are no studies which specifically consider the electrified RTG crane load forecast as an input to a control strategy.
In RTG crane systems, the majority of the energy consumption is produced by lifting containers to different heights. In order to increase the energy savings in electrified or diesel RTG crane systems, ESSs have been used for peak shaving during the lifting period by using recovered potential energy that has accrued during the lowering period and avoid dissipating energy through the dump resistors as heat [
1,
6,
7,
8,
9,
10,
11]. In the literature, ESS control algorithms on an RTG crane system, which can be either a diesel or electrified crane, mainly focus on using conventional control strategies that use a reference value (set-point control) of power [
1,
9], SoC [
7] or voltage [
3,
11] to store recovered potential energy and regenerate it during the lifting phase which helps to increase energy savings and reduce gas emissions.
Table 1 summarises the peak reduction algorithms used in an RTG crane model produced by different authors along with their achievements and limitations.
Table 1 shows that the majority of studies used set-point controller to increase energy saving of RTG crane systems and no research models use an MPC controller. Also, this table shows that there is limited literature on using different optimal control algorithms for increasing the energy efficiency of RTG cranes. To the best of the authors’ knowledge, there are no studies on using the electricity bill cost in the objective function and load forecast profile to optimise the energy flow in RTG cranes network system by using optimal power management strategies or an MPC controller.
Pietrosanti et al. [
1] present an optimal management strategy for RTG cranes with flywheel energy storage located at the DC side of the crane. The control strategy aims to find the optimal operation conditions for ESSs by charging the storage during the lowering mode and discharging it during the lifting mode, under uncertainties of the duration of RTG crane stochastic power loads [
1]. Baalbergen et al. [
12] developed diesel RTG crane systems equipped with battery storage. The authors in [
12] presented a power management system which aims to increase the energy savings and minimise costs by regenerating the recovery energy. In this paper, we introduce an optimal peak shaving control strategy, which minimises the energy costs of an RTG crane system equipped with an ESS using real-time data. Unlike previous works that used the recovery energy from the lowering phase to minimise the cost and increase energy savings [
1,
12], the proposed optimal control in this paper aims to maintain an optimal charging and discharging schedule by using real-time electricity prices and RTG crane load data.
Furthermore, the focus of this paper is to minimise the peak demand and the energy costs for electrified RTG cranes by developing a model predictive control (MPC) strategy, to take into consideration the high level of uncertainty in the forecasts of RTG crane demand. This paper presents control algorithms using real-time data collected from electrified RTG cranes at the Port of Felixstowe, UK, to control the energy storage system located at the substation side of RTG crane network systems.
MPC controller has been used effectively within microgrids and low voltage network applications which involve high uncertainties in demand applications [
2,
13,
14] to decrease the operation costs and increase the system efficiency. For example, Rowe et al. [
2] presented a MPC controller that allows distribution network operators to control the energy storage systems on the low voltage network, which feeds domestic customers. The MPC controller integrates a deterministic forecast with the objective of maximising the peak reduction of the distribution network [
2]. As in the study of Rowe et al., Oh et al. [
13] developed an optimisation scheme for an islanded microgrid, using an MPC strategy [
13]. The use of a multi-step MPC controller performed well for controlling diesel power sources and renewable energy sources with an ESS to minimise the energy cost operation [
13]. Stochastic forecast loads with scenario-based MPC models of a microgrid system with Electric Vehicle (EV) integration have been presented in [
14], where Ji et al. [
14] developed a forecast model based on knowing of EVs charging schedules in advance, so they assume that they know when the electric vehicle needs charging. In case there are unknown charging requests, the MPC controller will apply the worst-case scenario and set the boundary at the greatest possible charging loads. In order to meet the demand scheduling of the grid, Xiong et al. [
15] presented real-time MPC to optimise the power flow for a wind farm system equipped with an ESS. The objective function of the MPC controller contained three sub-objectives: firstly, it aimed to reduce the impact of a wind curtailment factor; secondly, to increase the ratio of generated wind power fed to the power grid; thirdly, to maintain the generation of power to the grid plan. The MPC controller successfully followed the power plan of the electrical power grid system [
15]. In addition, other authors have used MPC controllers for large scale ESS located at wind power plants to improve the energy dispatchability [
16]. The simulation results have shown that an ESS with model predictive control (MPC) can reduce the generation plan errors to meet the power grid needs by approximately 80% [
16]. The work successfully shows the impact of the scheduling horizon on the generation plan error, where shorter scheduling horizons reduce the error in the generation plan by approximately 15% [
16]. These sets of studies show the usefulness and capabilities of using MPC as an ESS control technique.
The literature has shown that an ESS can be beneficial for decreasing the energy costs and peak demand; accordingly, it is important to develop an optimal control strategy that maximises the advantages of the ESS and minimises the costs. An adequate power control strategy for electrified RTG cranes system equipped with ESS could be of great interest worldwide, as it will help ports around the world to decrease the electricity bill and gas emission. This is particularly important since RTG cranes are vital ingredients in the export and import goods processes. Aiming to fill the gap in the literature, this paper attempts to present and compare optimal energy management and MPC controllers for the control of ESS on the low voltage networks that feed electrified RTG cranes. The main objective of both controllers is presented to minimise electricity bills and peak demand. The optimisation algorithms in this paper will be tested to establish their appropriateness for electrified RTG cranes with ESS control by testing the control algorithms on data sets that have been collected over different RTG crane operation days. Therefore, the paper has three key new contributions that are listed as follows:
- (1)
We present an optimal energy management controller with the aim of minimising the energy costs and achieving the greatest peak demand reduction. This is contrast to the limited literature focused on using the regenerative power to increase energy savings in RTG crane systems.
- (2)
We predict half hourly electrified RTG crane power demand for one day-ahead and the forecast model is updated at each time step by including the real-time readings and the forecast error.
- (3)
Unlike previous studies, which often use the set-point controls to increase energy saving in an RTG crane system and neglect the forecast algorithm as inputs to improve the ESS efficiency, we present an MPC controller that helps to decrease the energy costs and achieve maximum possible peak reduction by using the RTG crane load forecast data as the main input parameter.
The remaining sections of this paper are organised as follows:
Section 2 describes the topology of the ESS and RTG crane demand model.
Section 3 introduces the RTG crane load demand and cost problem and the optimal controller. In
Section 4, the model predictive controller is presented and discussed. The simulation results and analysis are discussed in
Section 5. Finally, a summary of the work and conclusions are presented in
Section 6.
2. ESS and RTG Crane Demand model Topology
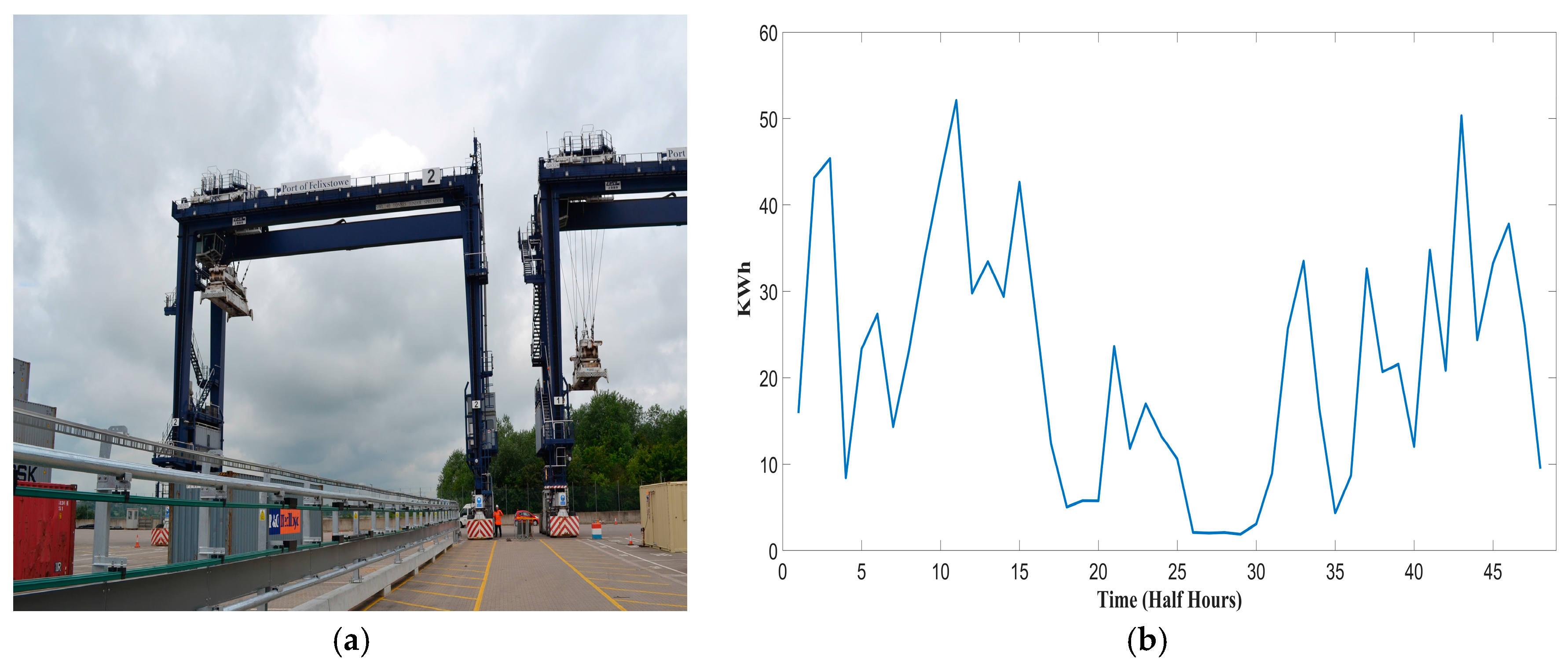
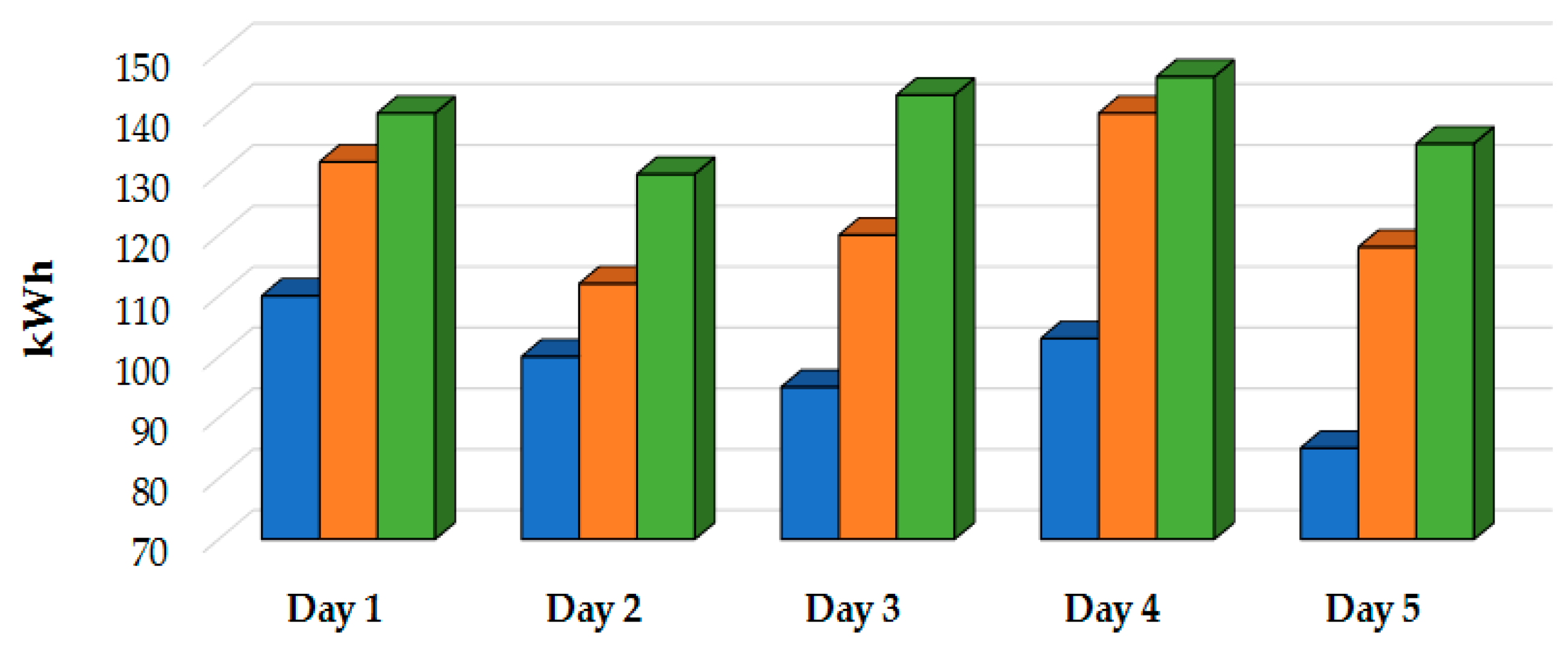
This section introduces the ESS and RTG crane model topology and addresses the RTG crane demand characteristics. The electrified RTG used in this work is shown in
Figure 1a and it has been retrofitted to be powered by the distribution power network at the port via a conductor bar of length 217 m. This crane is manufactured by Shanghai Zhenhua Heavy Industries (ZPMC, Shanghai, China) and is currently used at the Port of Felixstowe [
1], the numerical specifications of the RTG crane model is presented in
Section 5.1. In addition, the half hourly RTG crane power demand
in
Figure 1b shows a highly volatile and stochastic nature. The schematic diagram, shown in
Figure 2, displays the power flow
from the energy sources (the power grid
) and ESS
to the RTG crane load
The power flow diagram shows that the power grid
supplies all the required power consumption to operate both the RTG crane
and charge the ESS
. In case the ESS starts discharging, the power grid
will only supply power of the RTG crane load
minus the discharged ESS power
. The power flow can be described in the following equation [
1,
17]:
2.1. The Energy Storage System
The primary energy source in the electrified RTG crane model is a substation (11 kV/415 V). The secondary side of the substation is connected to the DC bus in the crane system through a diode rectifier. In this paper, the Energy Storage System (ESS) is located at the low voltage side (415 V) in order to minimise the peak power and cost, as shown in
Figure 3, at the substation side based on the real-time electricity price cost through the proposed optimal and Model Predictive Control (MPC) controller. As in [
2,
15,
18], the ESS used in this paper is described by Equations (2)–(8):
The stored energy in the ESS is calculated as in Equation (2), with the storage system operating under the following constraints:
The ESS operation efficiency
In this work, the control of the ESS aims to determine an optimal value of
in kW and the stored energy. The stored energy
is given as
, during a period of time ∆t. In this work, the energy stored in the ESS is increased and decreased, based on the RTG crane demand
and the real-time electricity price, and is described as
. The stored energy in every time step
, can be taken as a positive/negative change to present the increase/decrease of energy in the ESS. The negative value of ∆
means that the energy in the ESS has decreased (storage system in discharging mode) and when it is positive it means the energy in the ESS has increased (storage system in charging mode). Furthermore, the storage system is operated by constraints to maintain an upper limit on the stored energy
and a lower limit on the stored energy
. Similarly, we define a maximum and minimum stored power,
and
These limitation rules are described in Equations (3)–(5), respectively. Also, the power limitation of the ESS are defined in Equations (6) and (7). The storage system algorithm considers the ESS efficiency [
2,
18] by combining the stored energy in each time step
into a variable describing the storage efficiency
. When the stored energy is
< 0, the efficiency of the ESS is equal to
and when
is ≥0, the storage efficiency is
. Typically, the
quantity is defined as a value between
and
as in [
1,
2,
18], the
can also be described as the State of Charge (SoC). The SoC at the end of each time step is updated based on the previous state of charge
and the value of ESS charging or discharging energy
.
2.2 The Electrified RTG Crane Load Demand
As described in
Section 2, and shown in
Figure 1 and
Figure 3, electrified RTG crane load profiles show a highly volatile and stochastic nature. Equation (1) describes the power flow in an RTG crane system equipped with an ESS located on the low voltage network. The objectives in this research is to minimise the peak demand
in the power distribution network by using the ESS, which is defined in
Section 2.1. The volatile crane demand,
, is equal to the summation of storage
and substation power
, where this summation is used to generate a charge and discharge control decision for the ESS. In this paper, we present two optimisation controllers to control the ESS as follow:
- (1)
Optimal energy management controller: the real-time RTG crane demand and electricity price data are used to feed the optimal management control system. As indicated previously, the RTG crane load profile is highly stochastic; therefore, developing an optimal management control is difficult and challenging. This control will be described in
Section 3.
- (2)
Model Predictive Control (MPC) controller: the MPC in this research is designed to use forecasted RTG crane load profile and electricity price data to find the optimal ESS output that minimise the peak load and cost. The MPC controller model will be described in
Section 4. In this research, we extend the Artificial Neural Network (ANN) forecast model in [
5] to create a rolling RTG crane power forecast as follows:
As mentioned previously, the electrified RTG crane demand is challenging to predict due to the highly volatile nature of the load and there is no clear relation with physical exogenous variables such as temperature or seasonality [
5]. However, the electrified RTG crane demand increases and decreases based on variables such as container gross weight, number of crane moves and the behaviour of the crane driver (human factor) [
5]. These variables caused a wide range of forecast errors increasing the challenge of controlling the ESS.
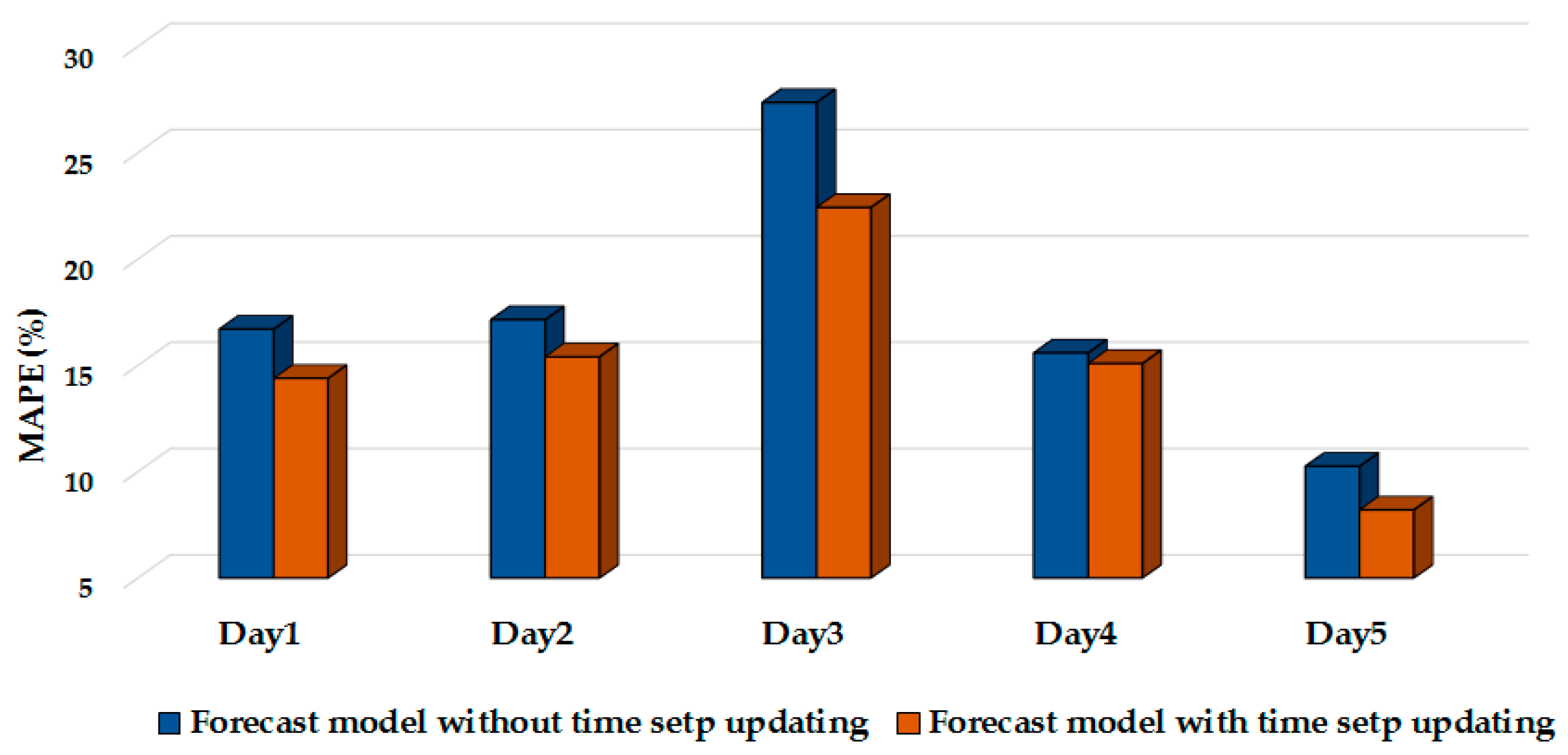
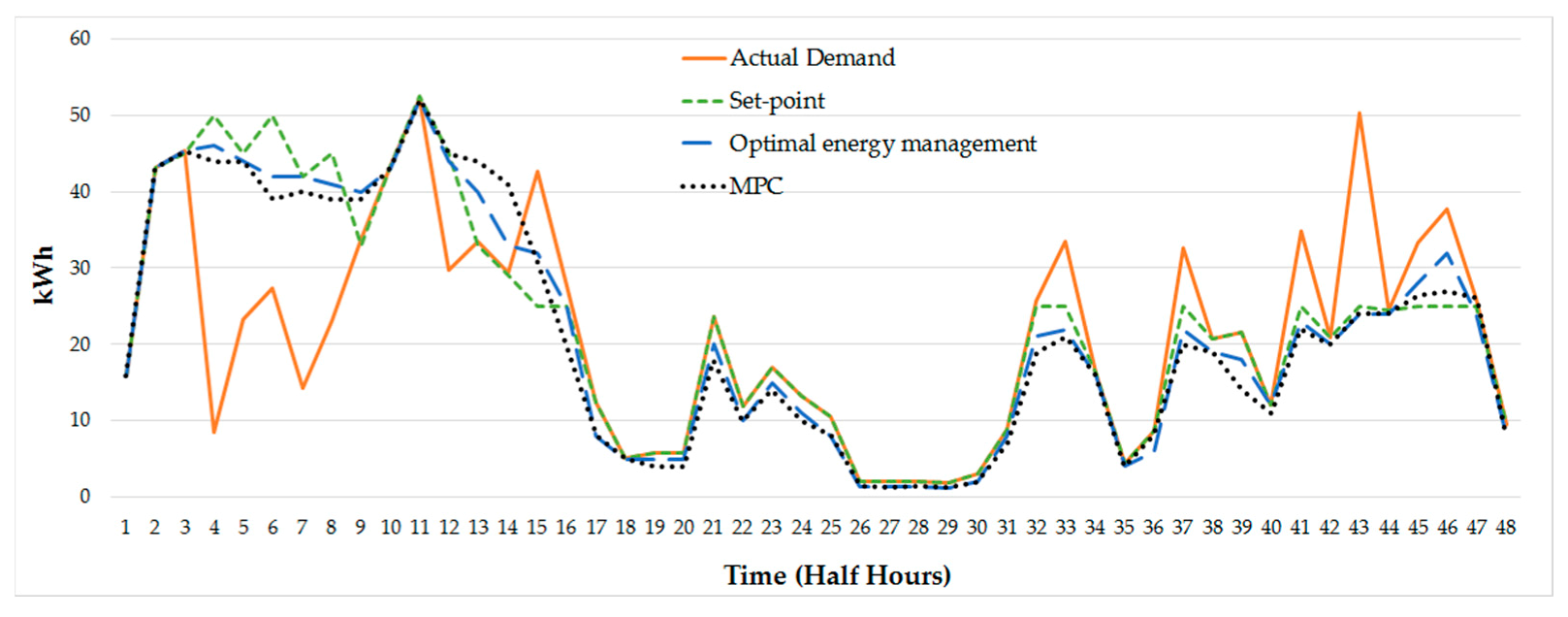
Figure 4 presents the daily mean absolute percentage error (MAPE) between the actual electrified RTG crane load and the load forecast [
5], as described in Equation (9).
where
is the actual load value at time t,
is the forecast load value at time t and t is the hourly time. In addition, the MAPE calculation is undefined when actual load is zero.
Figure 4 presents the daily MAPE error over 30 days of electrified RTG crane demand, the high number of occurrences is concentrated between 6% and 9%. Furthermore, the largest MAPE values (above 15%) are only repeated twice for MAPE errors equal to 24% and 27%. As seen in
Figure 4, around 30% of the MAPE errors over one month are equal to 12% and around 80% of the MAPE values are under 12%. However, the MAPE results in
Figure 4 show a wide range of values up to 30% which increase the challenging to develop a controller based on a load forecast profile. The electrified RTG crane demand has a highly volatile and stationary nature, without a clear relation with physical exogenous variables such as temperature or seasonality [
5]. However, the correlation analysis in [
5] showed that the container gross weight and number of crane moves are required to generate more accurate forecast model. The effect of human unpredictability on the demand shown comparing different crane electric demands for the same container gross weight [
5]. In general, the crane operator decides the path for the crane move during the hoisting operation, where based on the site condition and container location they may choose to hoist the container through arc or oscillatory paths. The different move path means variations in the energy consumption for the same container weight which leads to less predictable demand.
3. Optimal Energy Management Controller
The optimal energy management controller can be designed for multiple objectives compared to the set-point algorithm [
19,
20] and find optimal solutions to control the designed model [
21]. In this section, the objective of the optimal controller is to minimise the total cost
of using the electrified RTG crane (electricity bill), as described by Equation (10):
where
represent the real-time electricity cost at the Port of Felixstowe,
is the store energy and
is the original electrified RTG crane demand at the current time step t.
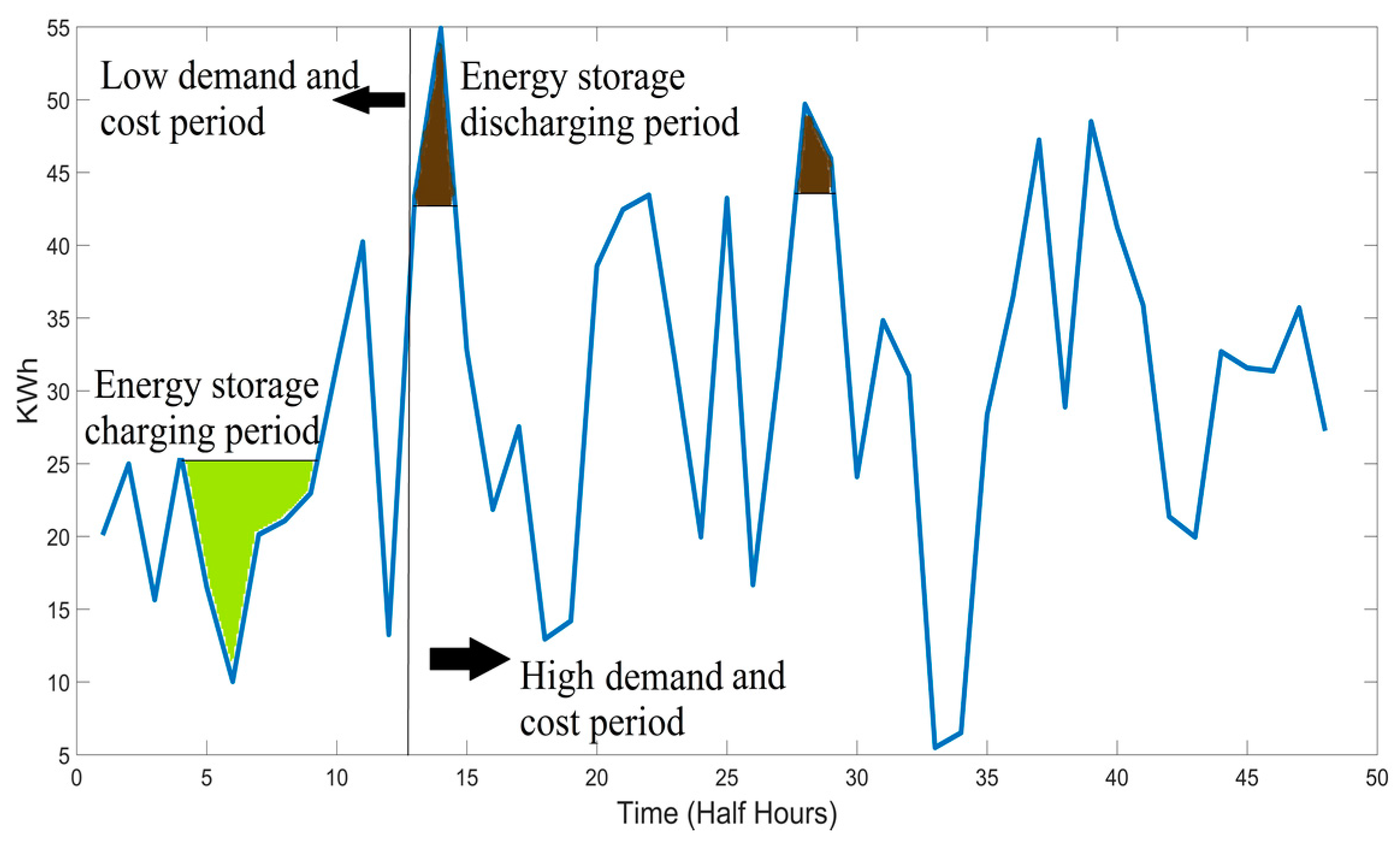
Figure 5 presents the proposed optimal management control loop for the electrified RTG crane system. The actual load profile of the crane, the real-time electricity price and the ESS measurement are fed to the controller in order to generate a control signal by minimising a cost function.
In order to minimise the energy cost and peak demand of RTG crane load for the daily time step, we minimize the cost function, defined by Equation (11), to find the optimal energy storage power:
where t is the current time step, N is the daily time steps (N = 48, half-hours) and the controller is designed to compute the optimal control decision and apply it to the network system. The optimal energy management controller in Equation (11) takes into account the Equations (2)–(8) and will be subject to the constraint which are given by Equations (12)–(14):
Equation (12) describes the electricity energy price at the Port of Felixstowe, where
. The electricity price during the day-time (
between
and midnight, will be higher than the price during the rest of the day-time (
. This electricity tariff helps to shift the peak to a lower price period in order to minimise the cost and demand. In order to avoid superfluous charging periods and generation of new peak points, we define new constraints given by Equations (13) and (14):
Equation (13) is used to maintain the power at the grid side under a set-point value during the ESS charging period, where the
value is negative and
. The set-point value
is found from a priori load data [
1,
22]. The limitation in Equation (14) is to make sure that the stored energy amount is more than or equal to the discharge amount of energy in the energy storage system.
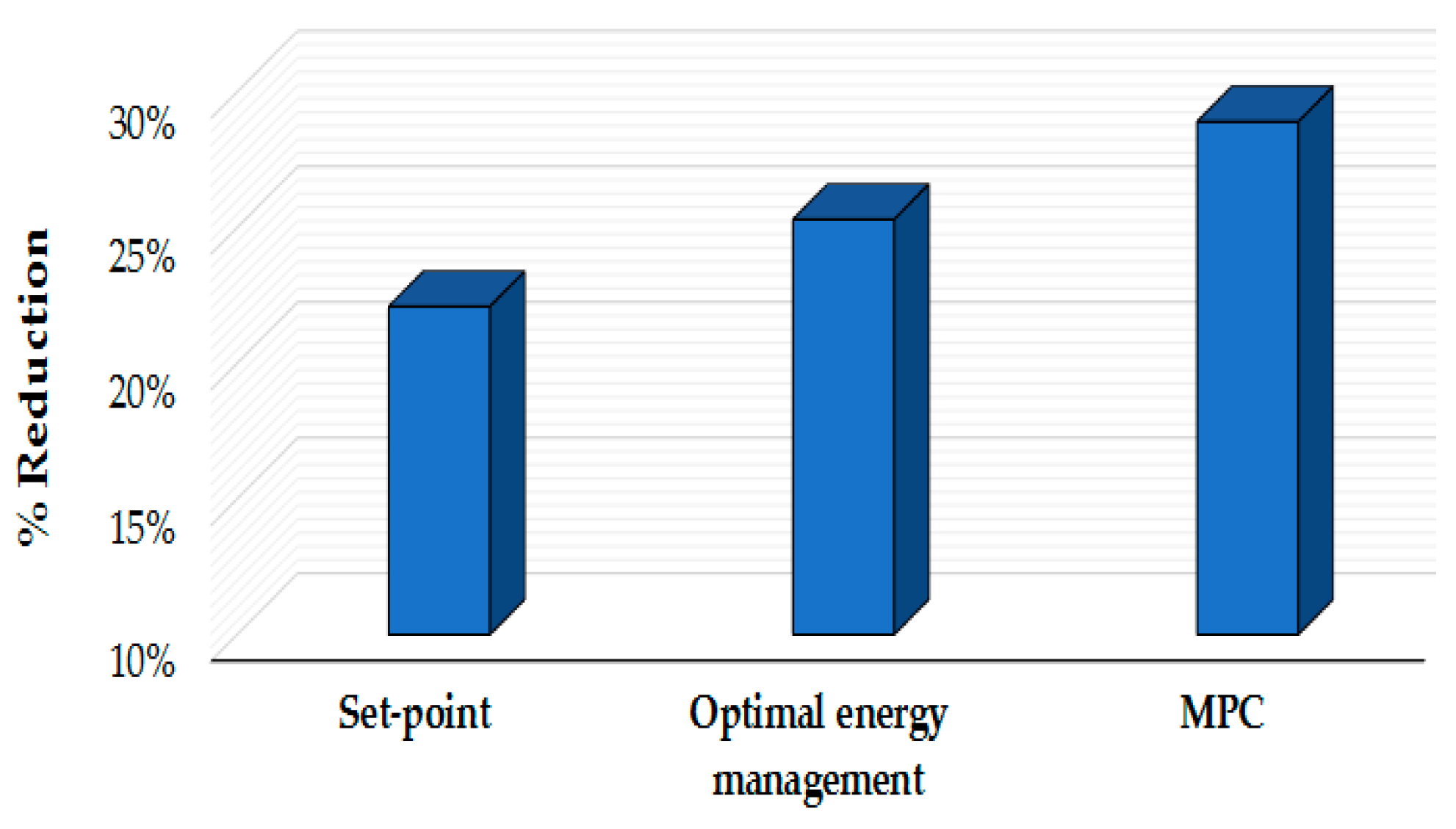
In the optimal energy control model, the weighted sum of the electricity energy cost is calculated by the objective function, as in Equation (11). The optimal controller uses the peak shaving techniques to achieve the minimum cost and reduce peak demand by shifting demand from a high electricity price half hour to a low price half hour, as described in Equation (12). The peak shifting achieves the optimal solution by finding the optimal ESS output values which minimises a Cost function (electricity bill), as described in Equation (11). The ESS output calculates under constraint Equations (13) and (14) to avoid creating new peak points whilst charging the ESS especially since the optimal management control does not include the forecast load element. In
Section 5, we will highlight and discuss the optimal management controller performance compared to a standard set-point controller. The set-point controller has been widely used in RTG cranes and different industrial applications and the set value is mainly developed using a priori load data [
1,
9,
11]. Current energy storage control research studies have been initiated to inspect the benefits of load forecasting and planning control methods such as Model Predictive Control (MPC). As discussed previously, the highly volatile and stochastic nature of electrified RTG crane demand, and the difficulty in predicting the crane demand, make it more challenging to control the ESS using an MPC controller. The following section will present the MPC strategy and RTG crane load forecast problem.
4. Model Predictive Control (MPC) Controller
The MPC controller, sometimes known as the generalised predictive control and receding horizon control, is a time horizon optimisation model that determines a series of optimal control decisions over a specific future time period [
23,
24]. In the first control action, the MPC controller computes the decision for the first-time period based on the demand forecast and updates of other variables. In the subsequent time intervals the predictive control updates the forecast data and other operation variables in order to adjust the optimal control signal in every time step. This is repeated for all time steps [
25,
26].
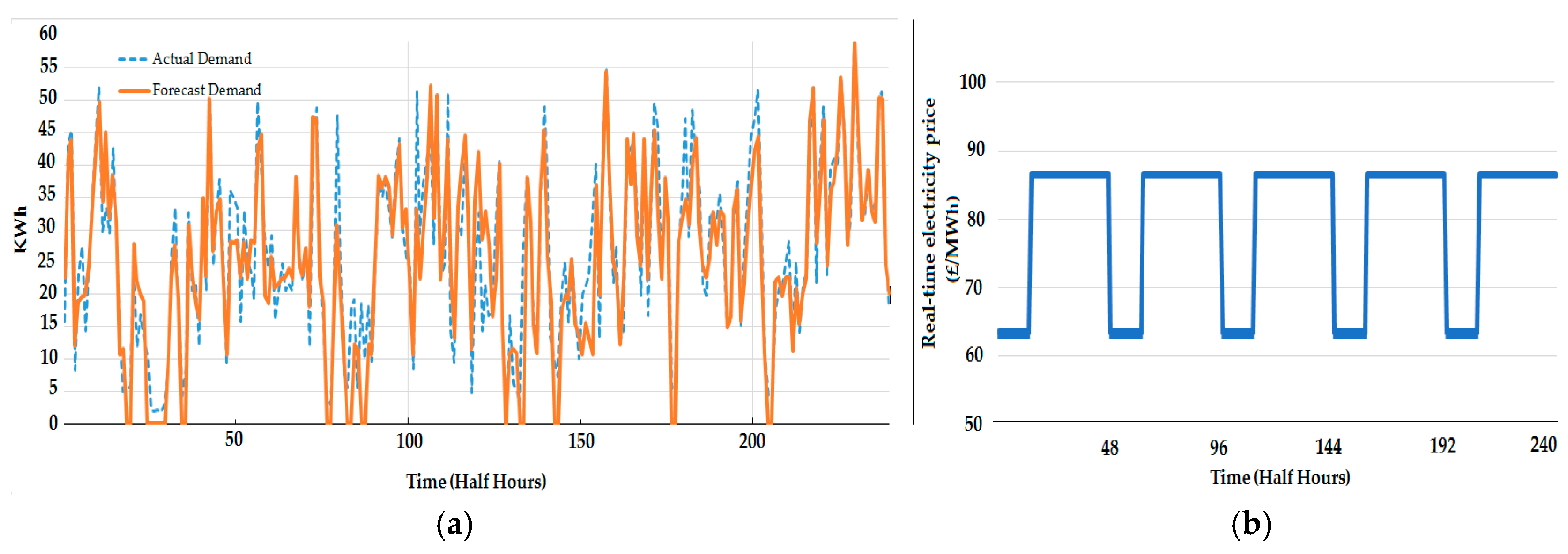
Figure 6 presents the exemplified control scheme of the MPC system for an electrified RTG crane system with ESS. The crane measurement, updated demand forecast data, real-time electricity price and storage measurements are fed to the MPC controller in order to generate a control signal. The control decision uses the cost function in Equation (11) to minimise the electricity energy cost and peak demand.
Figure 6 shows how the forecast model uses the real-time data (forecast error) to update the demand prediction at each time step. In this paper, the forecast model is designed to:
Firstly, forecast the half hourly electrified RTG crane demand for 24 h ahead and generate a forecast load profile over t + 48.
Secondly, calculate the forecast error at time t.
Thirdly, regenerate the forecast load profile at each time step t for day ahead t + 48 by using the forecast error and actual measurements at time t, where the ANN forecast is rerun with the new observation.
As with the optimal energy management formulation, Equation (11) finds the optimal ESS energy that minimise the electricity bill (cost function). This cost formulation is subject to the constraints presented in Equations (2)–(8) and Equations (12)–(14) that aim to reduce peak demand and avoid creating a new demand peak. The MPC controller algorithm is described in Algorithm 1, where at the current time interval (t), the controller model gets the updated demand prediction data between t and t + i, where i is the forecast time step and
and N is the one-day ahead forecast time (N = 48). Then the MPC controller calculates the optimal control decision by calculating the ESS energy in Equation (11) to minimize the cost function and implements the control signal to the network system. These steps are repeated at every time step t + 1 by updating the forecast data and other system variables and using the updated forecast data t + 1 + i to compute the control signal. The forecast model is designed to predict the load for one day ahead and then help the MPC to plan the control decision. After each time step the forecast model will use the actual data for this step and the forecast error to recalculate and update the forecast model. The MPC algorithm shows that the controller performance mainly depends on the accuracy of the prediction model [
27,
28]. As previously mentioned, the forecast data has been generated in this research by extending a prediction model developed in [
5]. In addition, the forecast and the proposed control model in this work have been developed and solved using Matlab/Mathworks (R2016b, The MathWorks, Inc., Natick, Massachusetts, United States). The highly stochastic behavior of RTG crane demand and forecast error makes it more difficult and challenging to use an MPC control in an electrified RTG crane system. The literature has presented the MPC controller as vital for ESSs with volatile demands. The following section, discusses the performance of an MPC controller compared to set-point control and the optimal power management control.
| Algorithm 1: Basic concept for MPC for electrified RTG crane system model with ESS. |
Selecting the time horizon step and prediction horizon. Determine the control objective and constraints. Initialize: the crane, forecast data and ESS data. For t = 1 to N (daily demand operation), do Solve optimal Equation (10), subject to:
Find the optimal signal for (t + 1) and apply it to the system. Update the forecast model for (t + 1) by regenerating the forecast load profile with the new observation and update the other system variables. Set t = t + 1,
Exit For loop. An optimal solution is achieved for the electrified RTG crane system model with ESS for the specific day. Repeat all steps for the next day.
|