Design of a Fractional Order Frequency PID Controller for an Islanded Microgrid: A Multi-Objective Extremal Optimization Method
Abstract
:1. Introduction
2. Preliminaries
2.1. FOPID Controller
2.2. Multi-Objective Optimization
3. Microgrid Models Based on Small-Signal Analysis
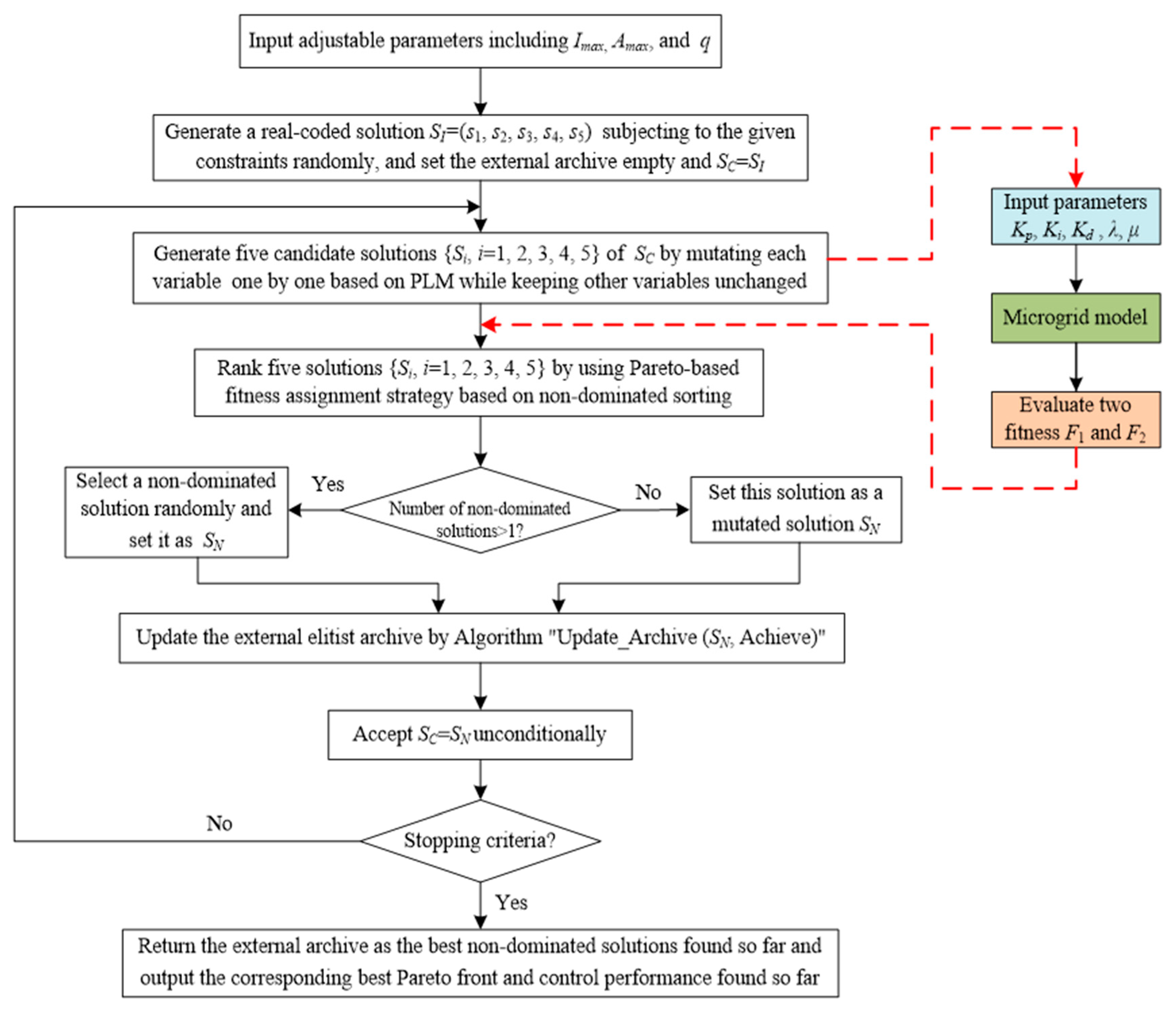
4. Multi-Objective Extremal Optimization Based FOPID Method for the Frequency Control of Islanded Microgrids
MOEO-FOPID-Based Frequency Controller Optimal Design Algorithm for an Islanded Microgrid
- Step 1:
- Generate a real-coded solution S = (s1,s2, s3, s4, s5) representing the control parameters of a FOPID-based frequency controller (Kp, Ki, Kd, λ, μ) in an islanded microgrid subject to the given constraints (10) randomly, and set the external archive A as empty and SC = S.
- Step 2:
- By mutating each variable si (i = 1, 2, 3, 4, 5) of the current solution SC one-by-one based on multi-non-uniform mutation (MNUM)while keeping other variables unchanged, generate five candidate solutions{Si, i = 1, 2, 3, 4, 5}. The detailed process is formulated as follows:where IC is the number of current iterations in the optimization process, both r and r1 are uniform random numbers between 0 and 1, and q is the shape parameter used in MNUM.
- Step 3:
- Rank five solutions {Si, i = 1, 2, 3, 4, 5} based on the non-dominated sorting strategy, where the two objective functions F1 and F2 are evaluated by Definition 2.
- Step 4:
- If the number of non-dominated solutions is just one, then select the only non-dominated solution Snd as the new solution SN; otherwise, select one from several non-dominated solutions randomly, and set this one as the new solution SN.
- Step 5:
- Update A by algorithm “Update_Archive (SN, Achieve)” [37] shown in Algorithm 1.
- Step 6:
- Accept SC = SN unconditionally.
- Step 7:
- If the predefined stopping criteria, e.g., maximum number of iterations Imax is met, then return to Step 2; otherwise, go to Step 8.
- Step 8:
- Return external archive A as the best non-dominated solutions for the FOPID controller for the frequency control of an islanded microgrid, and output the best Pareto front found so far and the corresponding control performance.
| Algorithm 1 The Pseudo-Code of Algorithm “Update_Archive (SN, Archive)” [37] |
| 1: Begin |
| 2: If the solution SN is dominated by at least one member of the archive, then |
| 3: The archive keeps unchanged |
| 4: Else if some members of archive are dominated by SN, then |
| 5: Remove all the dominated members from the archive and add SN to the archive |
| 6: End if |
| 7: Else |
| 8: If the number of archive is smaller than Amax, i.e., the predefined maximum number of the archive, then |
| 9: Add SN to the archive |
| 10: Else |
| 11: If SN resides in the most crowded region of the archive, then |
| 12: The archive keeps unchanged |
| 13: Else |
| 14: Replace the member in the most crowded region of the archive by SN |
| 15: End if |
| 16: End if |
| 17: End if |
| 18: End |
5. Simulation Results
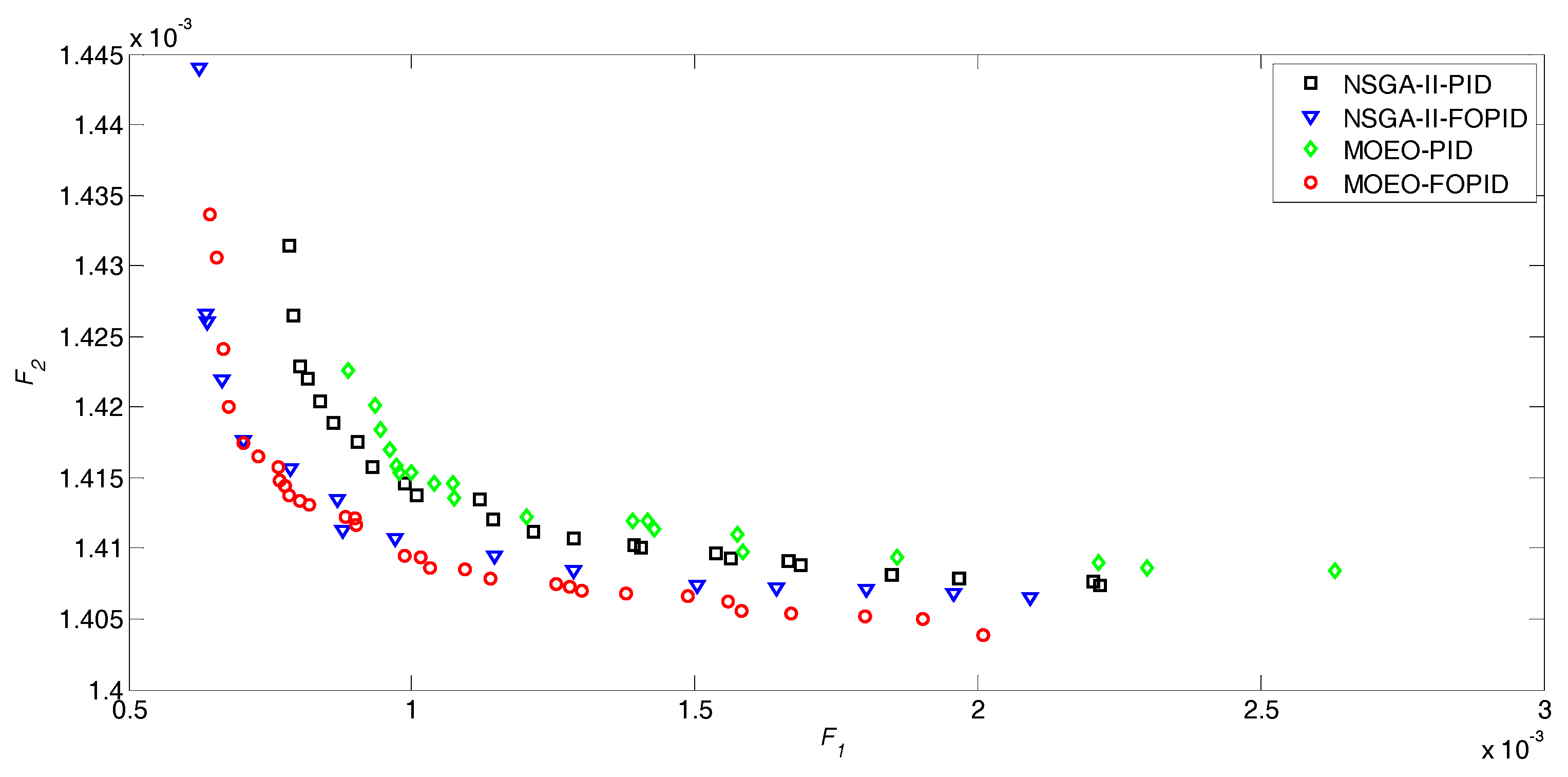
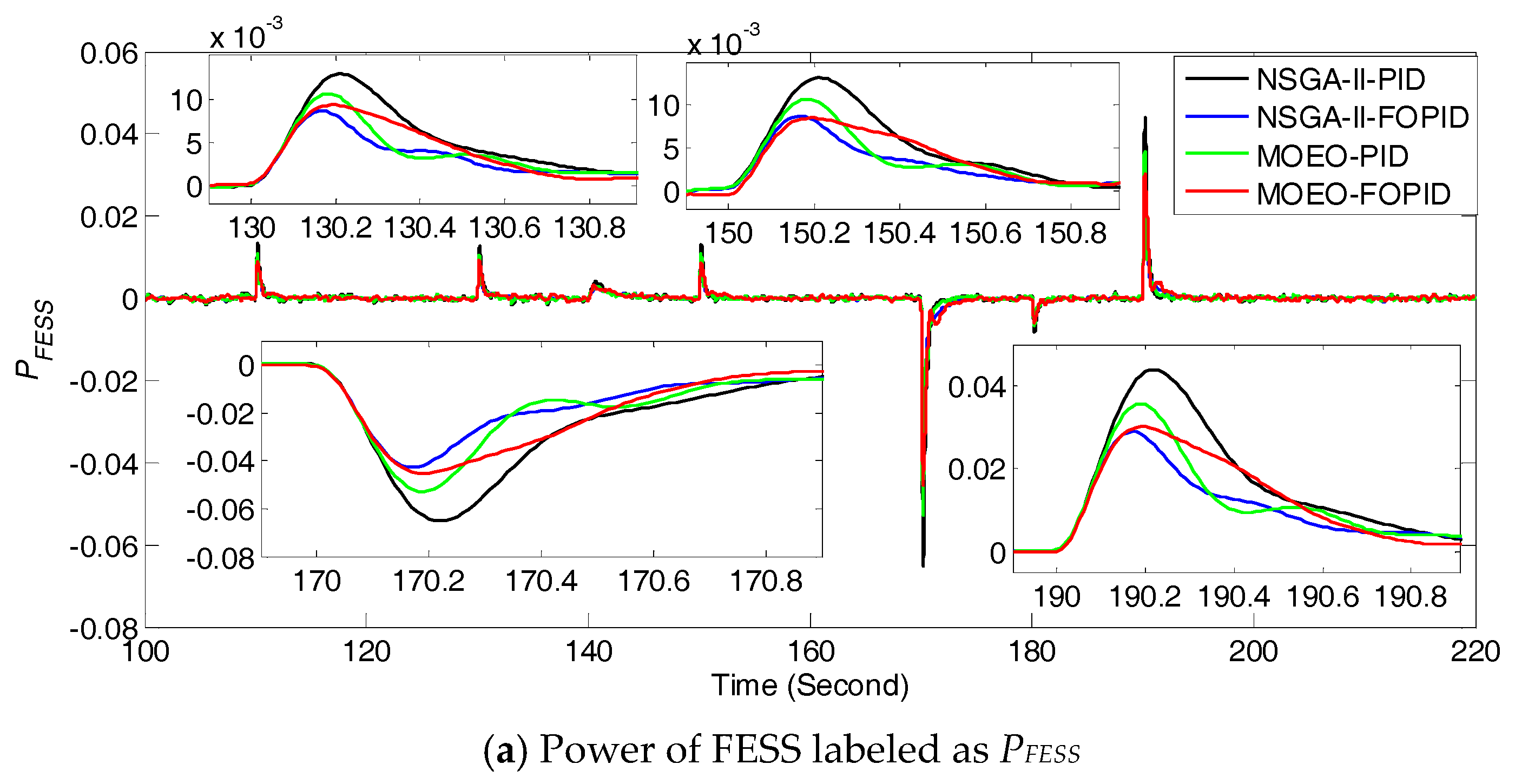
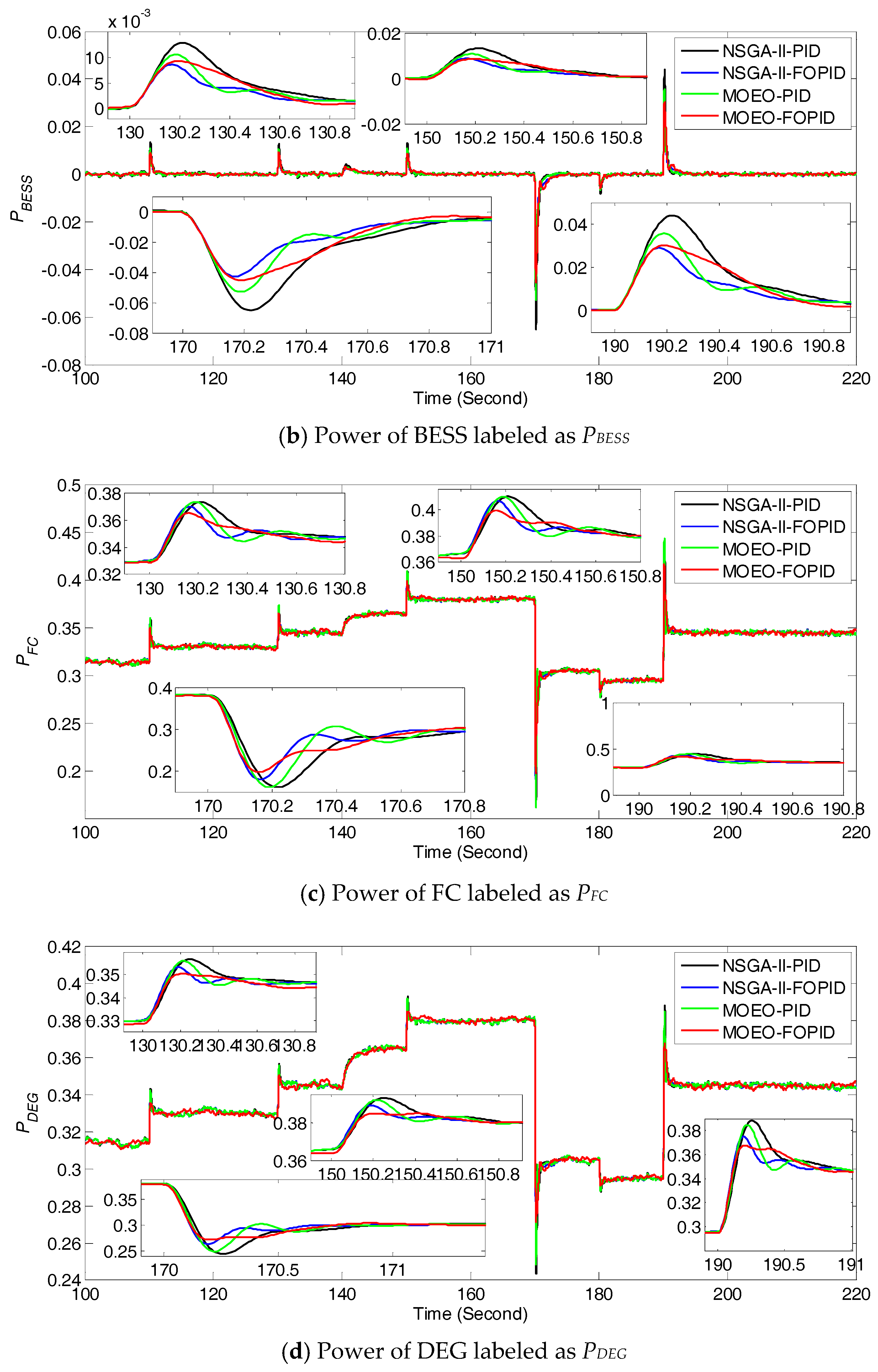
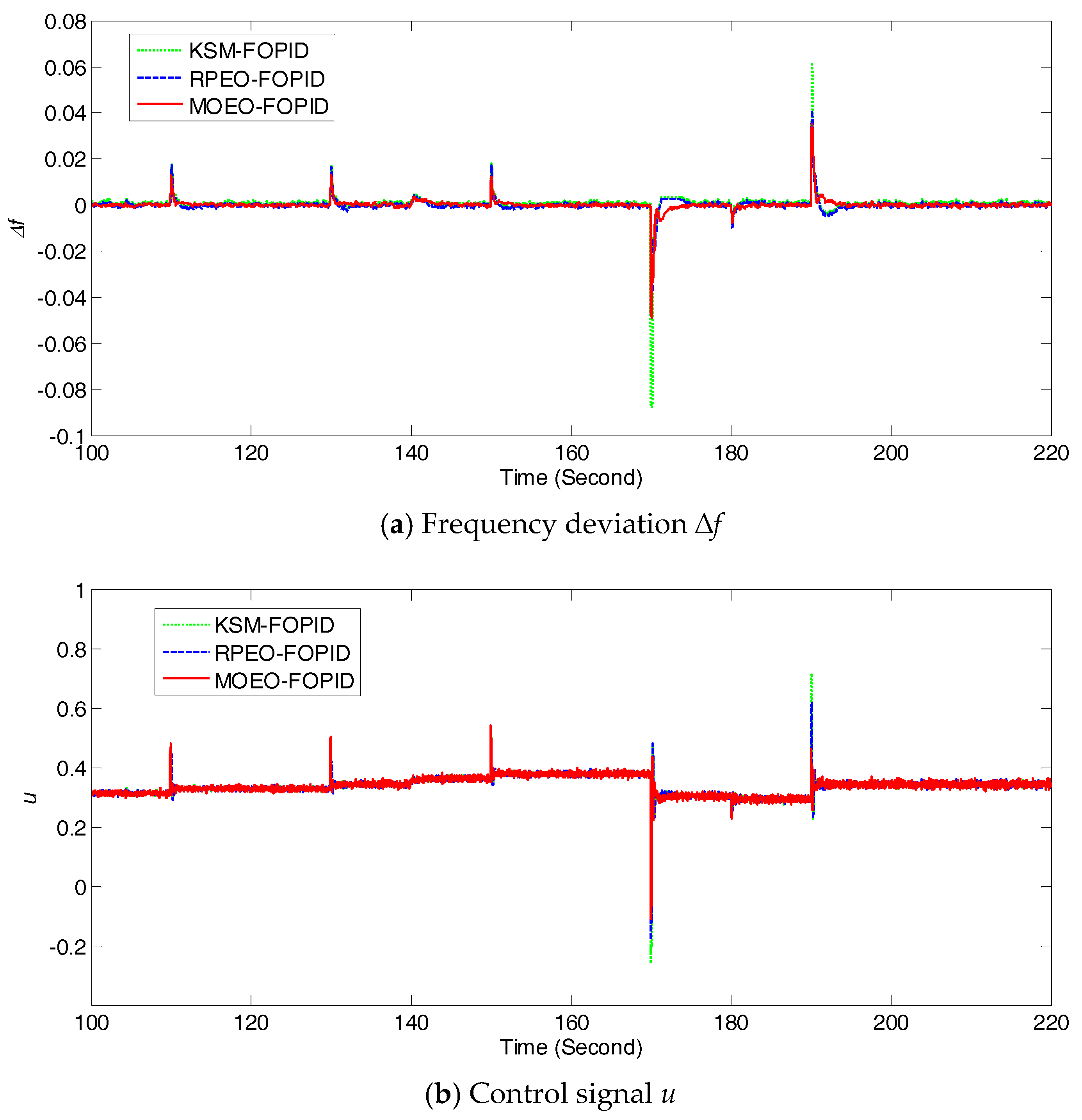
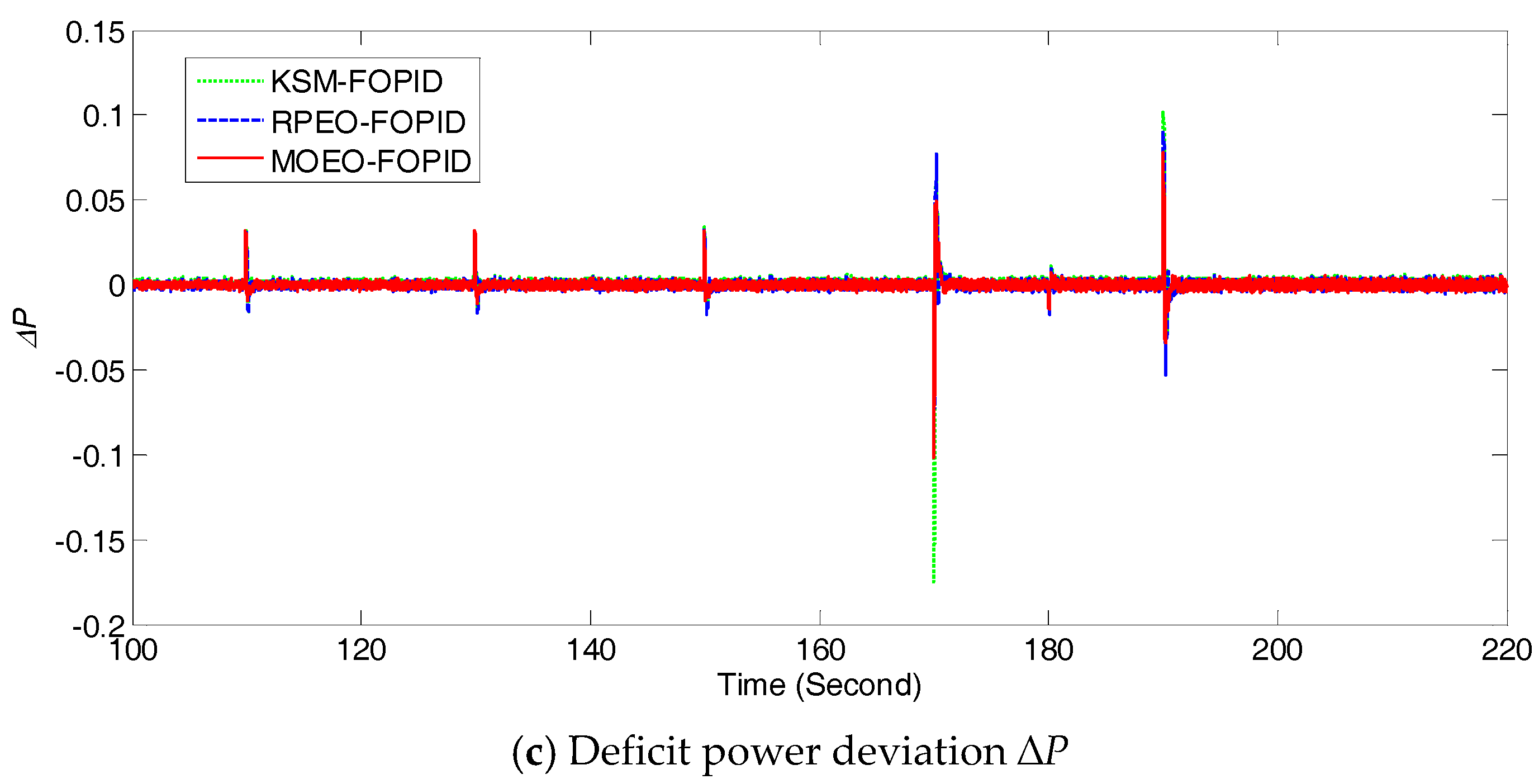
5.1. Performance Comparison in Nominal Microgrid Conditions
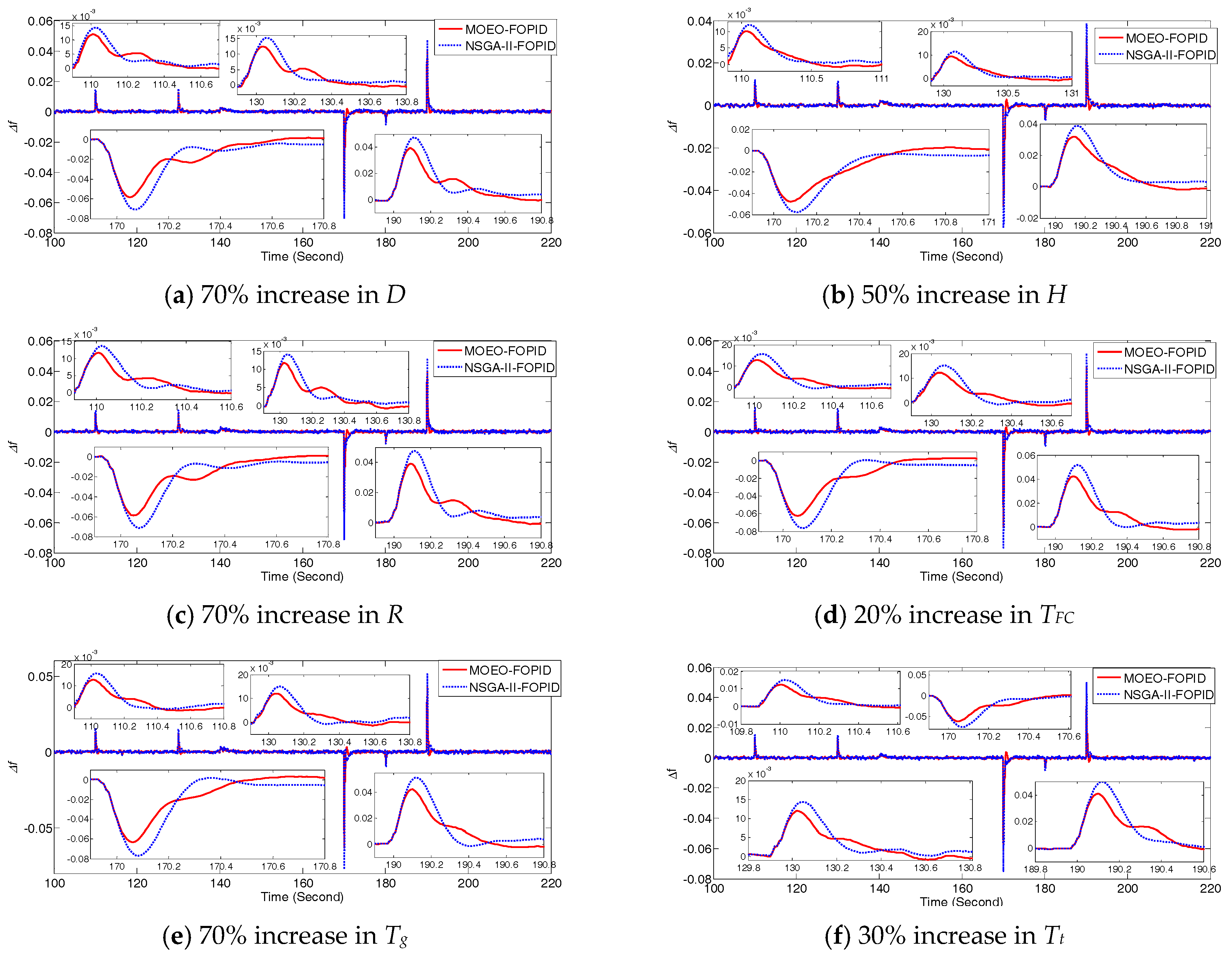
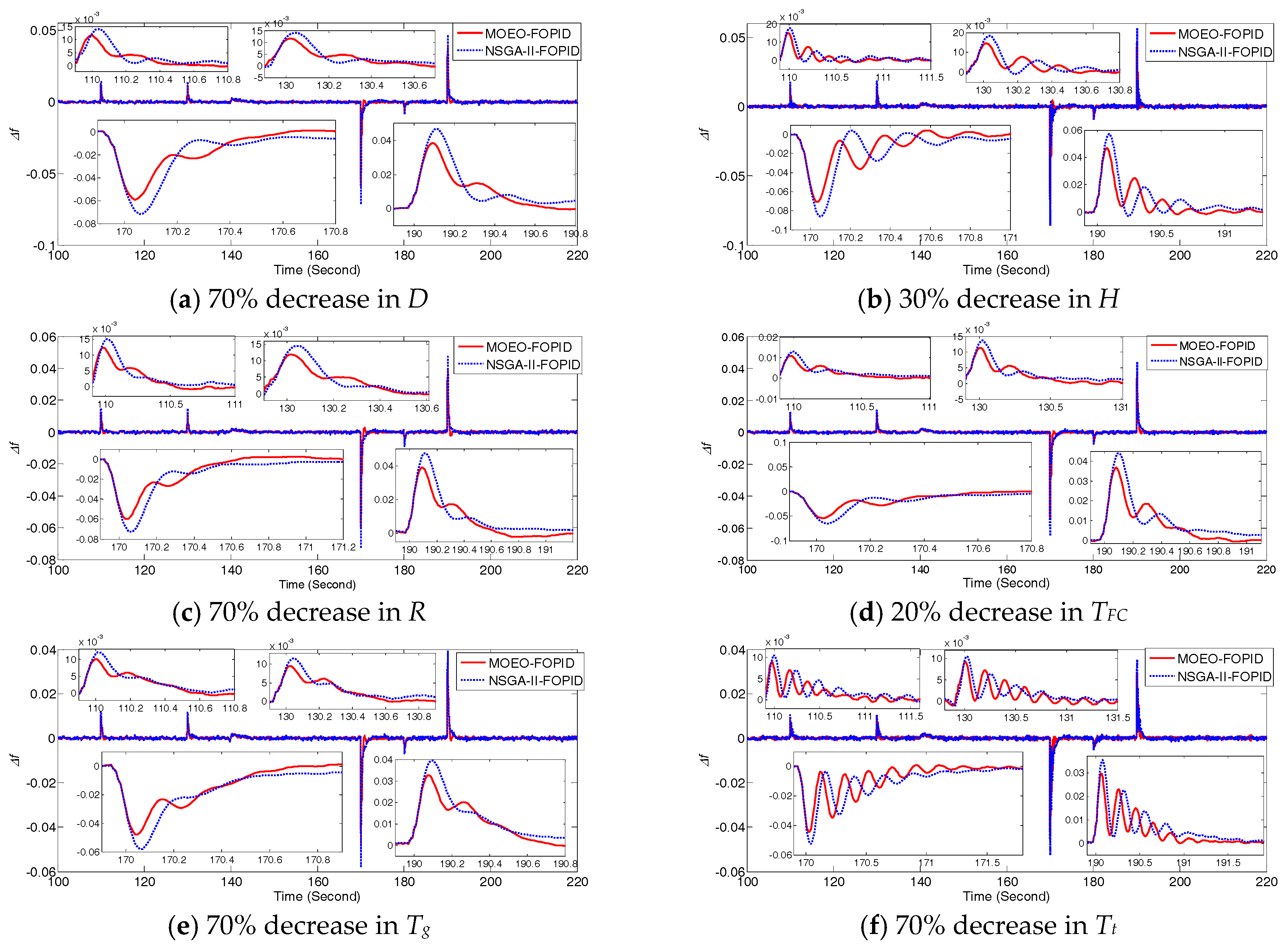
5.2. Robustness Tests under Perturbed System Parameters
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mahmoud, M.S.; Hussain, S.A.; Abido, M.A. Modeling and control of microgrid: An overview. J. Frankl. Inst. 2014, 351, 2822–2859. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Canizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in microgrid control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Lidula, N.W.A.; Rajapakse, A.D. Microgrids research: A review of experimental microgrids and test systems. Renew. Sustain. Energy Rev. 2011, 15, 186–202. [Google Scholar] [CrossRef]
- Kamel, R.M. New inverter control for balancing standalone micro-grid phase voltages: A review on MG power quality improvement. Renew. Sustain. Energy Rev. 2016, 63, 520–532. [Google Scholar] [CrossRef]
- Mariam, L.; Basu, M.; Conlon, M.F. Microgrid: Architecture, policy and future trends. Renew. Sustain. Energy Rev. 2016, 64, 477–489. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, P.; Guerrero, J.M.; Xu, Z.; Green, T.C. Multiple-time-scales hierarchical frequency stability control strategy of medium-voltage isolated microgrid. IEEE Trans. Power Electron. 2016, 31, 5974–5991. [Google Scholar] [CrossRef]
- Pandey, S.K.; Mohanty, S.R.; Kishor, N. A literature survey on load-frequency control for conventional and distribution generation power systems. Renew. Sustain. Energy Rev. 2013, 25, 318–334. [Google Scholar] [CrossRef]
- Lee, D.J.; Wang, L. Small-signal stability analysis of an autonomous hybrid renewable energy power generation/energy storage system part I: Time-domain simulations. IEEE Trans. Energy Convers. 2008, 23, 311–320. [Google Scholar] [CrossRef]
- Ray, P.K.; Mohanty, S.R.; Kishor, N. Proportional–integral controller based small-signal analysis of hybrid distributed generation systems. Energy Convers. Manag. 2011, 52, 1943–1954. [Google Scholar] [CrossRef]
- Dahal, S.; Mithulananthan, N.; Saha, T.K. Assessment and enhancement of small signal stability of a renewable-energy-based electricity distribution system. IEEE Trans. Sustain. Energy 2012, 3, 407–415. [Google Scholar] [CrossRef]
- Bevrani, H.; Habibi, F.; Babahajyani, P.; Watanabe, M.; Mitani, Y. Intelligent frequency control in an AC microgrid: Online PSO-based fuzzy tuning approach. IEEE Trans. Smart Grid 2012, 3, 1935–1944. [Google Scholar] [CrossRef]
- Divshali, P.H.; Alimardani, A.; Hosseinian, S.H.; Abedi, M. Decentralized cooperative control strategy of microsources for stabilizing autonomous vsc-based microgrids. IEEE Trans. Power Syst. 2012, 27, 1949–1959. [Google Scholar] [CrossRef]
- Das, D.C.; Roy, A.K.; Sinha, N. GA based frequency controller for solar thermal-diesel-wind hybrid energy generation/energy storage system. Int. J. Electr. Power Energy Syst. 2012, 43, 262–279. [Google Scholar] [CrossRef]
- Singh, V.P.; Mohanty, S.R.; Kishor, N.; Ray, P.K. Robust H-infinity load frequency control in hybrid distributed generation system. Int. J. Electr. Power Energy Syst. 2013, 46, 294–305. [Google Scholar] [CrossRef]
- Bevrani, H.; Feizi, M.R.; Ataee, S. Robust frequency control in an islanded microgrid: H∞ and μ-Synthesis Approaches. IEEE Trans. Smart Grid 2016, 7, 706–717. [Google Scholar]
- Bendato, I.; Bonfiglio, A.; Brignone, M.; Delfino, F.; Pampararo, F.; Procopio, R. A real-time energy management system for the integration of economical aspects and system operator requirements: Definition and validation. Renew. Energy 2017, 102, 406–416. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PIλDμ controllers. IEEE Trans. Autom. Control 1999, 44, 208–213. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Petráš, I.; Xue, D.Y. Fractional order control—A tutorial. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 1397–1411. [Google Scholar]
- Monje, C.A.; Chen, Y.Q.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Meng, L.; Xue, D. Design of an optimal fractional-order PID controller using multi-objective GA optimization. In Proceedings of the Control and Decision Conference CCDC, Guilin, China, 17–19 June 2009; pp. 3849–3853. [Google Scholar]
- Pan, I.; Das, S. Chaotic multi-objective optimization based design of fractional order PIλDμ controller in AVR system. Int. J. Electr. Power Energy Syst. 2012, 43, 393–407. [Google Scholar] [CrossRef]
- Zeng, G.Q.; Liu, H.Y.; Wu, D.; Li, L.M.; Wu, L.; Dai, Y.X.; Lu, K.D. A real-coded extremal optimization method with multi-non-uniform mutation for the design of fractional order PID controllers. Inf. Technol. Control 2016, 45, 358–375. [Google Scholar] [CrossRef]
- Ahmed, B.S.; Sahib, M.A.; Gambardella, L.M.; Afzal, W.; Zamli, K.Z. Optimum design of PI λ D μ controller for an automatic voltage regulator system using combinatorial test design. PLoS ONE 2016, 11, e0166150. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Wang, H.; Zeng, G.Q.; Lu, K.D. Design of fractional-order PID controllers for fractional-order systems: A binary-coded individual-based extremal optimization method. ICIC Express Lett. 2016, 10, 2191–2196. [Google Scholar]
- Pan, I.; Das, S. Kriging based surrogate modeling for fractional order control of microgrids. IEEE Trans. Smart Grid 2015, 6, 36–44. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Fractional order fuzzy control of hybrid power system with renewable generation using chaotic PSO. ISA Trans. 2016, 62, 19–29. [Google Scholar] [CrossRef] [PubMed]
- Pan, I.; Das, S. Fractional-order load-frequency control of interconnected power systems using chaotic multi-objective optimization. Appl. Soft Comput. 2015, 29, 328–344. [Google Scholar] [CrossRef]
- Boettcher, S.; Percus, A. Nature’s way of optimizing. Artif. Intell. 2000, 119, 275–286. [Google Scholar] [CrossRef]
- Boettcher, S.; Percus, A.G. Optimization with extremal dynamics. Phys. Rev. Lett. 2001, 86, 5211. [Google Scholar] [CrossRef] [PubMed]
- Bak, P.; Sneppen, K. Punctuated equilibrium and criticality in a simple model of evolution. Phys. Rev. Lett. 1993, 71, 4083. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.Z.; Chen, Y.W.; Chen, M.R.; Chen, P.; Zeng, G.Q. Extremal Optimization: Fundamentals, Algorithms, and Applications; CRC Press & Chemical Industry Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Dai, Y.X.; Wang, H.; Zeng, G.Q. Double closed-loop PI control of three-phase inverters by binary-coded extremal optimization. IEEE Access 2016, 4, 7621–7632. [Google Scholar] [CrossRef]
- Chen, M.R.; Lu, Y.Z. A novel elitist multiobjective optimization algorithm: Multiobjectiveextremal optimization. Eur. J. Oper. Res. 2008, 188, 637–651. [Google Scholar] [CrossRef]
- Chen, M.R.; Lu, Y.Z.; Yang, G. Multiobjective optimization using population-based extremal optimization. Neural Comput. Appl. 2008, 17, 101–109. [Google Scholar] [CrossRef]
- Randall, M.; Lewis, A. Population extremal optimization for discrete multi-objective optimization problems. Inf. Sci. 2016, 367, 390–402. [Google Scholar] [CrossRef]
- Zeng, G.Q.; Chen, J.; Li, L.M.; Chen, M.R.; Wu, L.; Dai, Y.X.; Zheng, C.W. An improved multi-objective population-based extremal optimization algorithm with polynomial mutation. Inf. Sci. 2016, 330, 49–73. [Google Scholar] [CrossRef]
- Zeng, G.Q.; Chen, J.; Dai, Y.X.; Li, L.M.; Zheng, C.W.; Chen, M.R. Design of fractional order PID controller for automatic regulator voltage system based on multi-objective extremal optimization. Neurocomputing 2015, 160, 173–184. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Collette, Y.; Siarry, P. Multiobjective Optimization: Principles and Case Studies; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Li, L.M.; Lu, K.D.; Zeng, G.Q.; Wu, L.; Chen, M.R. A novel real-coded population-based extremal optimization algorithm with polynomial mutation: A non-parametric statistical study on continuous optimization problems. Neurocomputing 2016, 174, 577–587. [Google Scholar] [CrossRef]

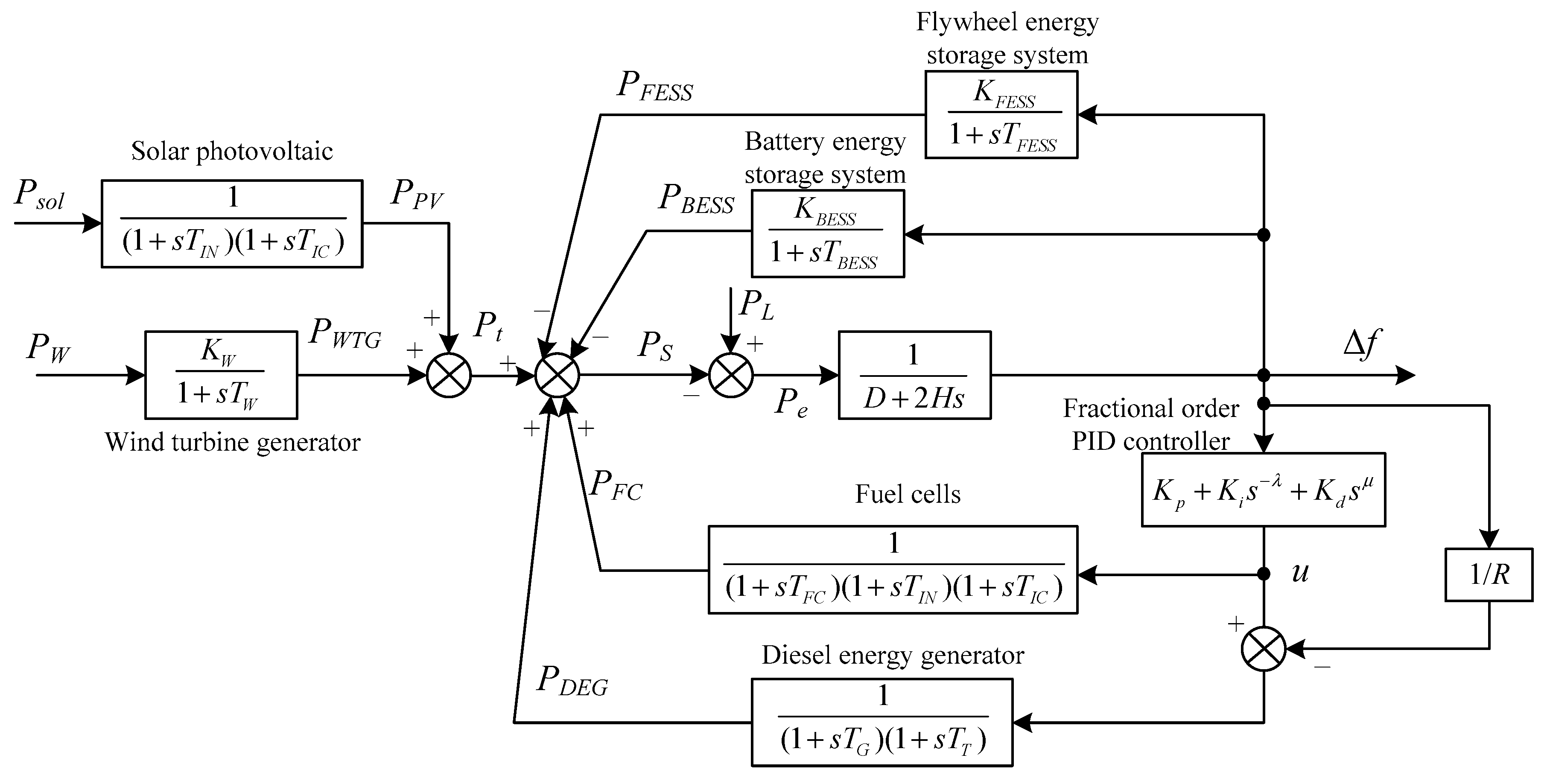




| Component | Transfer Function | Parameters |
|---|---|---|
| Wind turbine generator (WTG) | KW = 1, TW = 1.5 s | |
| Solar photovoltaic (PV) | TIN = 0.04 s, TIC = 0.004 s | |
| Fuel cell (FC) | KFC = 1, TFC = 0.26 s | |
| Diesel energy generator (DEG) | TG = 0.08 s, TT = 0.4 s | |
| Microgrid system | D = 0.015 pu/Hz, H = 1/12 pu.sec, R = 3 Hz/pu | |
| Flywheel energy storage system (FESS) | KFESS = 1, TFESS = 0.1 s | |
| Battery energy storage system (BESS) | KBESS = 1, TBESS = 0.1 s |
| Stochastic Models | Model Parameters |
|---|---|
| Wind power generation | ϕ~U(−1, 1), η = 0.8, β = 10, G(s) = 1/(104s + 1), Γ = 0.24H(t) − 0.04H(t − 140) |
| Solar power generation | ϕ~U(−1, 1), η = 0.1, β = 10, δ = 0.1, G(s) = 1/(104s + 1), Γ = 0.05H(t) + 0.02H(t − 180) |
| Demand loads | ϕ~U(−1, 1), η = 0.9, β = 10, G(s) = (300/(300s + 1)) + (1/(1800s + 1)), Γ = (1/χ)[0.9H(t) + 0.03H(t − 110) + 0.03H(t − 130) + 0.03H(t − 150) − 0.15H(t − 170)+ 0.1H(t − 190)] + 0.02H(t) |
| Algorithm | Parameters |
|---|---|
| NSGA-II-FOPID/PID [20,38] | Imax = 500, population size NP = 30, crossover probability pc = 0.9, mutation probability pm = 1/n, distribution indexes ηc = 20and ηm = 20 for simulated binary crossover (SBX) and PLM |
| MOEO-FOPID/PID | Imax = 500, Amax = 30, q = 6 |
| Performance Metrics | Algorithm | Minimum | Median | Maxmum | Mean | Standard Deviation |
|---|---|---|---|---|---|---|
| Hypervolume indicator (HI, min) | NSGA-II-PID | 1.83 × 10−4 | 2.07 × 10−4 | 2.26 × 10−4 | 2.06 × 10−4 | 1.15 × 10−5 |
| MOEO-PID | 1.26 × 10−4 | 2.16 × 10−4 | 3.92 × 10−4 | 2.24 × 10−4 | 7.78 × 10−5 | |
| NSGA-II-FOPID | 1.56 × 10−4 | 2.03 × 10−4 | 3.35 × 10−4 | 2.13 × 10−4 | 5.08 × 10−5 | |
| MOEO-FOPID | 1.04 × 10−4 | 1.63 × 10−4 | 2.20 × 10−4 | 1.63 × 10−4 | 2.95 × 10−5 | |
| Spacing metric (SP, max) | NSGA-II-PID | 5.41 × 10−3 | 9.93 × 10−3 | 1.50 × 10−2 | 1.00 × 10−2 | 2.69 × 10−3 |
| MOEO-PID | 4.28 × 10−3 | 1.20 × 10−2 | 2.32 × 10−2 | 1.26 × 10−2 | 5.43 × 10−3 | |
| NSGA-II-FOPID | 6.93 × 10−3 | 1.59 × 10−2 | 2.84 × 10−2 | 1.52 × 10−2 | 4.56 × 10−3 | |
| MOEO-FOPID | 1.91 × 10−3 | 4.24 × 10−3 | 7.97 × 10−3 | 4.61 × 10−3 | 1.22 × 10−3 | |
| Inertia-based diversity metric (I, max) | NSGA-II-PID | 7.07 × 10−2 | 0.107 | 0.120 | 0.103 | 1.30 × 10−2 |
| MOEO-PID | 6.50 × 10−2 | 6.15 × 10−2 | 4.35 × 10−2 | 6.01 × 10−2 | 4.28 × 10−3 | |
| NSGA-II-FOPID | 0.131 | 0.103 | 5.78 × 10−2 | 0.103 | 2.14 × 10−2 | |
| MOEO-FOPID | 0.135 | 0.117 | 8.10 × 10−2 | 0.113 | 1.69 × 10−2 | |
| Inverted generational distance (IGD, min) | NSGA-II-PID | 7.00 × 10−3 | 8.08 × 10−3 | 9.58 × 10−3 | 8.09 × 10−3 | 6.16 × 10−4 |
| MOEO-PID | 9.52 × 10−3 | 1.07 × 10−2 | 1.38 × 10−2 | 1.08 × 10−2 | 9.43 × 10−4 | |
| NSGA-II-FOPID | 3.43 × 10−3 | 5.52 × 10−3 | 9.22 × 10−3 | 5.66 × 10−3 | 1.17 × 10−3 | |
| MOEO-FOPID | 3.16 × 10−3 | 4.39 × 10−3 | 1.20 × 10−2 | 4.68 × 10−3 | 1.59 × 10−3 |
| Algorithm | F1 | F2 | Kp | Ki | Kd | λ | μ |
|---|---|---|---|---|---|---|---|
| NSGA-II-PID | 8.3877 × 10−4 | 1.4204 × 10−3 | 4.78192 | 4.76904 | 0.95045 | 1 | 1 |
| MOEO-PID | 8.1589 × 10−4 | 1.4250 × 10−3 | 4.53357 | 4.85426 | 1.05329 | 1 | 1 |
| NSGA-II-FOPID | 7.8307 × 10−4 | 1.4198 × 10−3 | 5 | 4.99475 | 0.54391 | 1.00950 | 1.20039 |
| MOEO-FOPID | 7.2219 × 10−4 | 1.4174 × 10−3 | 4.90695 | 4.16141 | 0.78012 | 1.00730 | 1.13911 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zeng, G.; Dai, Y.; Bi, D.; Sun, J.; Xie, X. Design of a Fractional Order Frequency PID Controller for an Islanded Microgrid: A Multi-Objective Extremal Optimization Method. Energies 2017, 10, 1502. https://doi.org/10.3390/en10101502
Wang H, Zeng G, Dai Y, Bi D, Sun J, Xie X. Design of a Fractional Order Frequency PID Controller for an Islanded Microgrid: A Multi-Objective Extremal Optimization Method. Energies. 2017; 10(10):1502. https://doi.org/10.3390/en10101502
Chicago/Turabian StyleWang, Huan, Guoqiang Zeng, Yuxing Dai, Daqiang Bi, Jingliao Sun, and Xiaoqing Xie. 2017. "Design of a Fractional Order Frequency PID Controller for an Islanded Microgrid: A Multi-Objective Extremal Optimization Method" Energies 10, no. 10: 1502. https://doi.org/10.3390/en10101502
APA StyleWang, H., Zeng, G., Dai, Y., Bi, D., Sun, J., & Xie, X. (2017). Design of a Fractional Order Frequency PID Controller for an Islanded Microgrid: A Multi-Objective Extremal Optimization Method. Energies, 10(10), 1502. https://doi.org/10.3390/en10101502




