Performance Analysis of Thermoelectric Based Automotive Waste Heat Recovery System with Nanofluid Coolant
Abstract
:1. Introduction
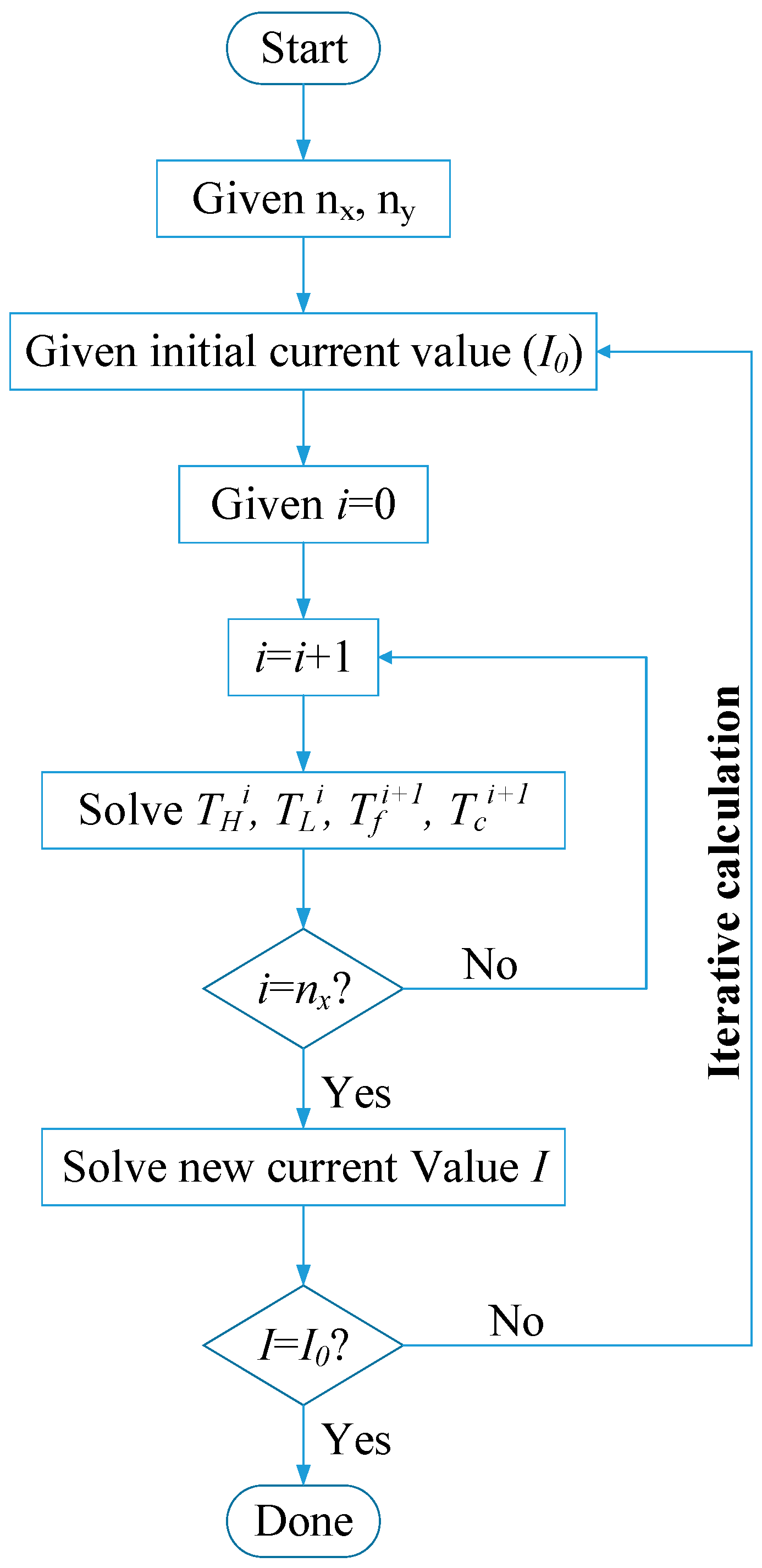
2. Mathematical Model
- (1)
- The heat transfer process is steady;
- (2)
- All the TEMs in the system are in series. Geometric configurations properties of P-type and N-type materials are identical, and physical properties of each P-type legs are identical, as well as the N-type legs;
- (3)
- Air between TEMs and heat exchangers are omitted because it is quite small. Thermal radiation is not taken into consideration. Contact resistance between TEMs and heat exchangers, thermal resistance perpendicular to flow direction of fluid, and Thomson effect are also omitted;
- (4)
- The external load resistance is equal to the internal resistance;
- (5)
- Thermoelectric material used in this study is Bi2Te3, its thermoelectric parameters are constants, and Table 1 presents the basic calculation parameters.
3. Results and Discussion
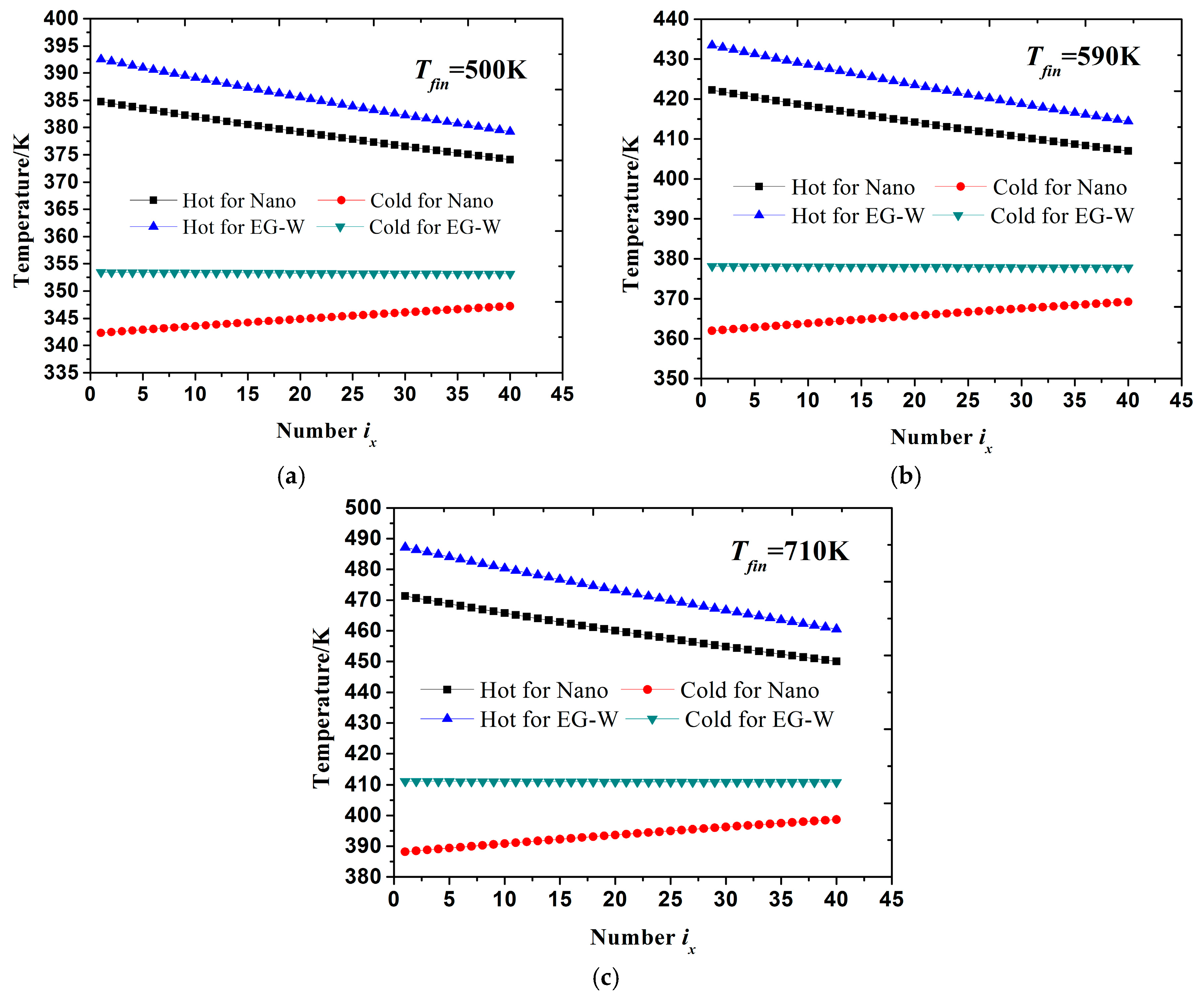
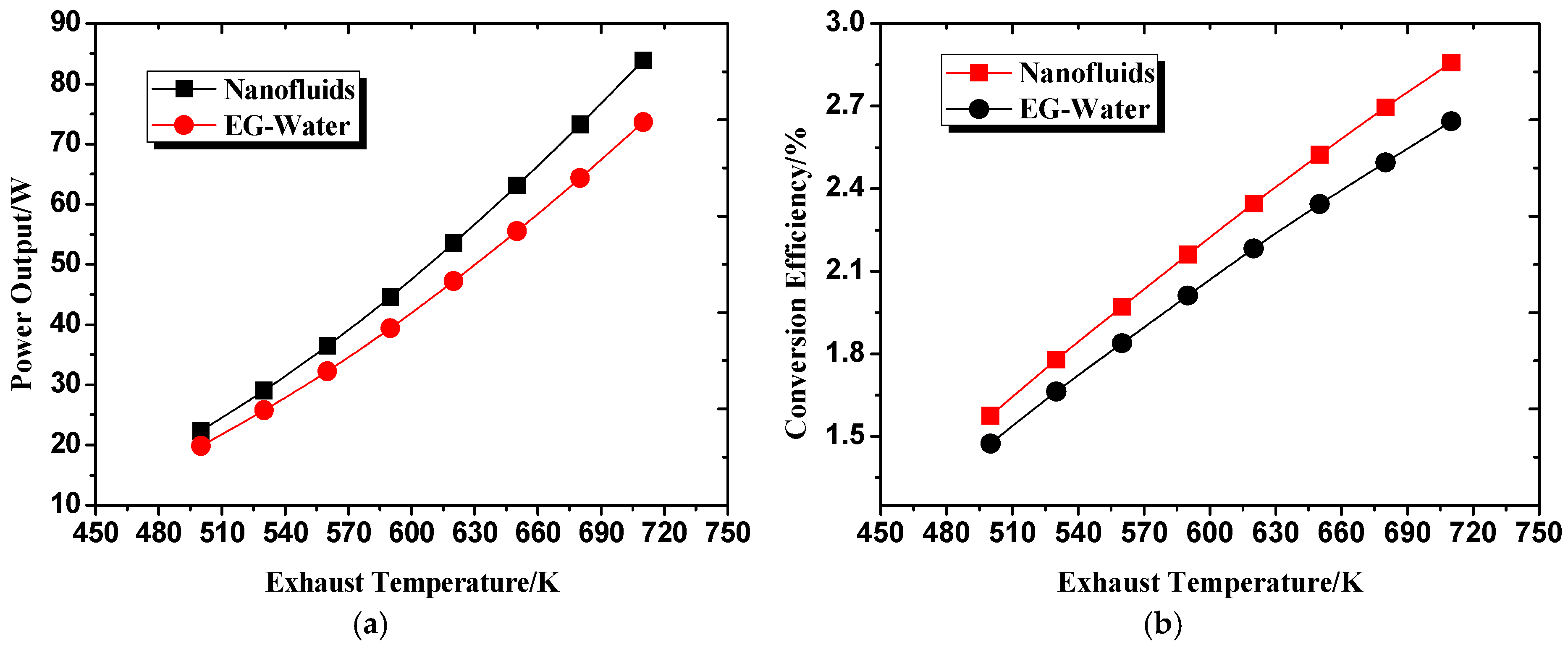
3.1. Comparison between Cu-EG Nanofluid and EG-W
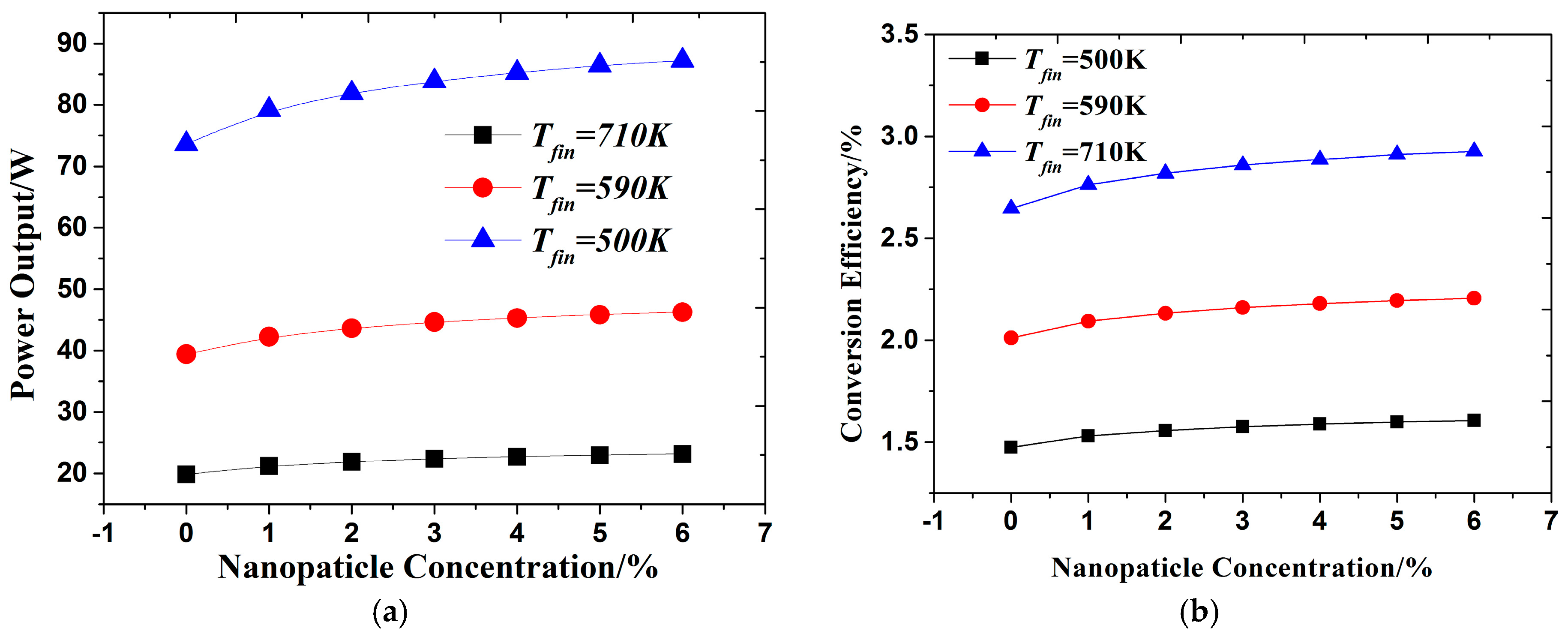
3.2. Comparison between Different Cu-EG Nanofluid Concentrations
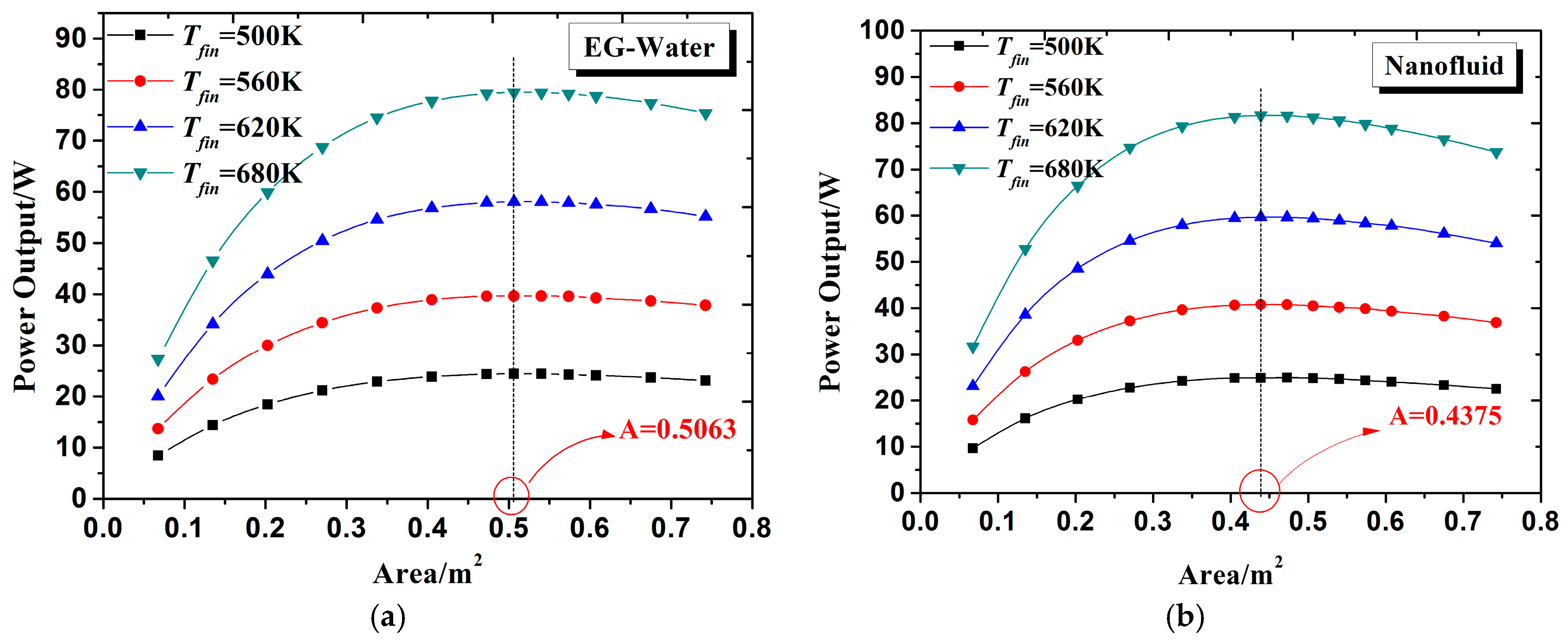
3.3. Analysis of Total Area of TEMs
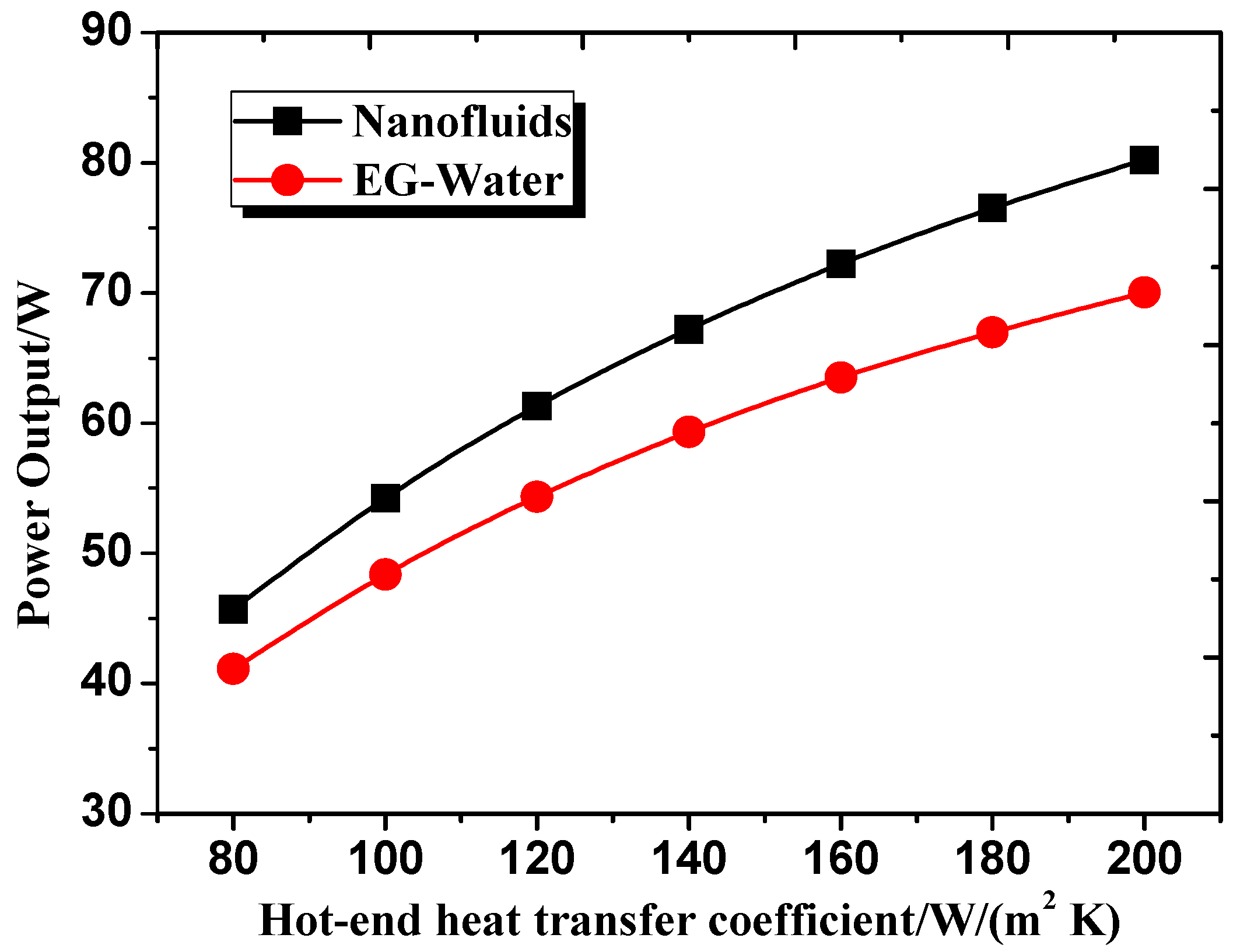
3.4. Effect of Hot Side Heat Transfer Coefficient of TEMs
4. Conclusions
- (1)
- Compared to conventional EG-W coolant, Cu-EG nanofluid can attain a lower cold side temperature of TEMs and a larger temperature difference between hot and cold end of TEMs under equal mass flow rate, which will effectively improve power output and thermoelectric conversion efficiency for the TEG system;
- (2)
- Cu-EG nanofluid as coolant can decrease the optimal total area of TEMs and increase the power output compared with EG-W coolant under equal mass flow rate. This finding will bring significant advantages for the optimization and arrangement of TEMs in the system. When the arrangement space of TEMs for the system is sufficient, less TEMs are required when using Cu-EG nanofluid as coolant, which will save thermoelectric materials and the cost. When the arrangement space of TEMs is limited, Cu-EG nanofluid as coolant can make system output more power compared to EG-W coolant under the same amount of TEMs;
- (3)
- Power output enhancement under Cu-EG nanofluid coolant is larger than that of EG-W coolant as the increase of hot side heat transfer coefficient of TEMs. From the perspective of synergy effect on heat transfer enhancement for the hot side of the TEMs, Cu-EG nanofluid as coolant for the cold side of the TEMs is also superior to EG-W coolant.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Nomenclature | |
| Specific heat of exhaust (kJ kg−1 K−1) | |
| Specific heat of coolant (kJ kg−1 K−1) | |
| Diameter of tube (m) | |
| dp | Diameter of nanoparticle (mm) |
| h | Height of TEM leg (mm) |
| Heat transfer coefficient of hot side (W m−2 K−1) | |
| Heat transfer coefficient of cold side (W m−2 K−1) | |
| i | Direction of x coordinate |
| j | Direction of y coordinate |
| Thermal conductivity of basic fluid (W m−1 K−1) | |
| Thermal conductivity of nanoparticle (W m−1 K−1) | |
| Thermal conductivity of nanofluid (kJ m−3 K−1) | |
| l | Length of TEM leg (mm) |
| Mass flow rate of exhaust (kg/s) | |
| Mass flow rate of coolant (kg/s) | |
| Number of TE modules in x direction | |
| Number of TE modules in y direction | |
| Heat flow density for hot side (W/m2) | |
| Heat flow density for cold side (W/m2) | |
| Resistance for a P-N junction (Ω) | |
| Electrical load resistance (Ω) | |
| Temperature of cold fluid (K) | |
| Temperature of exhaust (K) | |
| Hot side temperature of TEM (K) | |
| Cold side temperature of TEM (K) | |
| Average speed of nanofluid (m/s) | |
| w | Width of TEM leg (mm) |
| Greek Symbols | |
| Seebeck coefficient of N-type material (V/K) | |
| Thermal diffusivity coefficient of nanofluid (m2/s) | |
| Seebeck coefficient of P-type material (V/K) | |
| Thermal conductivity of P-type material (W m−1 K−1) | |
| Thermal conductivity of N-type material (W m−1 K−1) | |
| Density of nanoparticle (kg/m3) | |
| Density of nanofluid (kg/m3) | |
| Density of base fluid (kg/m3) | |
| Resistivity of P-type material (Ω·m) | |
| Product of density and specific heat capacity for base fluid (kJ m−3 K−1) | |
| Product of density and specific heat capacity for nanoparticle (kJ m−3 K−1) | |
| Product of density and specific heat capacity for nanofluid (kJ m−3 K−1) | |
| Kinematic viscosity of nanofluid (m2/s) | |
| Dynamic viscosity of basic fluid (Pa s) | |
| φ | Concentration of nanofluid |
References
- Liang, X.; Sun, X.; Tian, H.; Shu, G.; Wang, Y.; Wang, X. Comparison and parameter optimization of a two-stage thermoelectric generator using high temperature exhaust of internal combustion engine. Appl. Energy 2014, 130, 190–199. [Google Scholar] [CrossRef]
- Talbi, M.; Agnew, B. Energy recovery from diesel engine exhaust gases for performance and air conditioning. Appl. Therm. Eng. 2002, 22, 693–702. [Google Scholar] [CrossRef]
- Zhang, H.G.; Wang, E.H.; Fan, B.Y. A performance analysis of a novel system of a dual loop bottoming organic Rankine cycle (ORC) with a light-duty diesel engine. Appl. Energy 2013, 102, 1504–1513. [Google Scholar] [CrossRef]
- Vazquez, J.; Sanz-Bobi, M.; Palacios, R.; Arenas, A. State of the art of thermoelectric generators based on heat recovered from the exhaust of automobiles. In Proceedings of the Seventh European Workshop on Thermoelectric, Pamplona, Spain, 3–4 October 2002. [Google Scholar]
- Liang, X.; Sun, X.; Shu, G.; Sun, K.; Wang, X.; Wang, X. Using the analytic network process (ANP) to determine method of waste energy recovery from engine. Energy Convers. Manag. 2013, 66, 304–311. [Google Scholar] [CrossRef]
- Gewald, D.; Karellas, S.; Schuster, A.; Spliethoff, H. Integrated system approach for increase of engine combined cycle efficiency. Energy Convers Manag. 2012, 60, 32–44. [Google Scholar] [CrossRef]
- Stevens, R.J.; Weinstein, S.J.; Koppula, K.S. Theoretical limits of thermoelectric power generation from exhaust gases. Appl. Energy 2014, 133, 80–88. [Google Scholar] [CrossRef]
- Liu, X.; Deng, Y.D.; Li, Z.; Su, C.Q. Performance analysis of a waste heat recovery thermoelectric generation system for automotive application. Energy Convers. Manag. 2015, 90, 121–127. [Google Scholar] [CrossRef]
- Haidar, J.G.; Ghogel, J.I. Waste heat recovery from the exhaust of low-power diesel engine using thermal electric generators. In Proceedings of the 20th International Conference on Thermoelectrics (ICT2001), Beijing, China, 8–11 June 2001. [Google Scholar]
- Biswas, K.; He, J.Q.; Blum, I.D.; Wu, C.I.; Hogan, T.P.; Seidman, D.N.; Nan, C.-W. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature 2012, 489, 414–418. [Google Scholar] [CrossRef] [PubMed]
- Butt, S.; Ren, Y.Y.; Farooq, M.Y.; Zhan, B.; Sagar, R.U.R.; Lin, Y.H.; Nan, C.W. Enhanced thermoelectric performance of heavy-metals (M: Ba, Pb) doped misfit-layered ceramics: (Ca2−xMxCoO3)0.62(CoO2). Energy Convers. Manag. 2014, 83, 35–41. [Google Scholar] [CrossRef]
- Zhao, L.D.; Lo, S.H.; Zhang, Y.S.; Sun, H.; Tan, G.J.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 2014, 508, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.I.; Lee, K.H.; Mun, H.A.; Kim, H.S.; Hwang, S.W.; Roh, J.W.; Yang, D.J.; Shin, W.H.; Li, X.S.; Lee, Y.H.; et al. Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science 2015, 348, 109–114. [Google Scholar] [CrossRef] [PubMed]
- Sahin, A.; Yilbas, B.S. The thermoelement as thermoelectric power generator: Effect of leg geometry on the efficiency and power generation. Energy Convers. Manag. 2013, 65, 26–32. [Google Scholar] [CrossRef]
- Niu, Z.; Diao, H.; Yu, S.; Jiao, K.; Du, Q.; Shu, G. Investigation and design optimization of exhaust-based thermoelectric generator system for internal combustion engine. Energy Convers. Manag. 2014, 85, 85–101. [Google Scholar] [CrossRef]
- Belanger, S.; Gosselin, L. Thermoelectric generator sandwiched in a crossflow heat exchanger with optimal connectivity between modules. Energy Convers. Manag. 2011, 552, 2911–2918. [Google Scholar] [CrossRef]
- Wang, T.; Luan, W.; Wang, W.; Tu, S.-T. Waste heat recovery through plate heat exchanger based thermoelectric generator system. Appl. Energy 2014, 136, 860–865. [Google Scholar] [CrossRef]
- Wang, Y.; Dai, C.; Wang, S. Theoretical analysis of a thermoelectric generator using exhaust gas of vehicles as heat source. Appl. Energy 2013, 112, 1171–1180. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Developments and Applications of Non-Newtonian Flow, Proceedings of the ASME International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995; Siginer, D.A., Wang, H.P., Eds.; American Society of Mechanical Engineers: New York, NY, USA, 1995. [Google Scholar]
- Tzeng, S.C.; Lin, C.W.; Huang, K.D. Heat transfer enhancement of nanofluids in rotary blade coupling of four-wheel-drive vehicles. Acta Mech. 2005, 179, 11–23. [Google Scholar] [CrossRef]
- Kulkarni, D.P.; Vajjha, R.S.; Das, D.K.; Oliva, D. Application of aluminum oxide nanofluids in diesel electric generator as jacket water coolant. Appl. Therm. Eng. 2008, 28, 1774–1781. [Google Scholar] [CrossRef]
- Peyghambarzadeh, S.M.; Hashemabadi, S.H.; Hoseini, S.M.; Jamnani, M.S. Experimental study of heat transfer enhancement using water/ethylene glycol based nanofluids as a new coolant for car radiators. Int. Commun. Heat Mass Transf. 2011, 38, 1283–1290. [Google Scholar] [CrossRef]
- He, W.; Wang, S.X.; Zhang, X.; Li, Y.Z.; Lu, C. Optimization design method of thermoelectric generator based on exhaust gas parameters for recovery of engine waste heat. Energy 2015, 91, 1–9. [Google Scholar] [CrossRef]
- He, W.; Wang, S.X.; Lu, C.; Zhang, X.; Li, Y.Z. Influence of different cooling methods on thermoelectric performance of an engine exhaust gas waste heat recovery system. Appl. Energy 2016, 162, 1251–1258. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q. Investigation on convective heat transfer and flow features of nanofluids. J. Heat Transf. Trans. ASME 2003, 125, 151–155. [Google Scholar] [CrossRef]
- Xuan, Y.; Roetzel, W. Conceptions of heat transfer correlation of nanofluids. Int. J. Heat Mass Transf. 2000, 43, 3701–3707. [Google Scholar] [CrossRef]
- Pak, B.C.; Cho, Y.I. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Exp. Heat Transf. 1998, 11, 151–170. [Google Scholar] [CrossRef]
- Mancin, S.; Zilio, C.; Diani, A.; Rossetto, L. Air forced convection through metal foams: Experimental results and modeling. Int. J. Heat Mass Transf. 2013, 62, 112–123. [Google Scholar] [CrossRef]
- Mancin, S.; Zilio, C.; Diani, A.; Rossetto, L. Experimental air heat transfer and pressure drop through copper foams. Exp. Therm. Fluid Sci. 2012, 36, 224–232. [Google Scholar] [CrossRef]

| Semiconductor Parameters | Value |
|---|---|
| Seebeck coefficient of P-type leg | 2.037 × 10−4 V K−1 |
| Seebeck coefficient of N-type leg | −1.721 × 10−4 V K−1 |
| Resistivity of P-type leg | 1.314 × 10−5 Ω m |
| Resistivity of N-type leg | 1.119 × 10−5 Ω m |
| Thermal conductivity of P-type leg | 1.265 W m−1 K−1 |
| Thermal conductivity of N-type leg | 1.011 W m−1 K−1 |
| Length of P- and N-type leg | 5 mm |
| Width of P- and N-type leg | 5 mm |
| Height of P- and N-type leg | 5 mm |
| Parameters | Value |
|---|---|
| Inlet temperature of cold fluid | 298 K |
| Specific heat capacity of Cu-EG nanofluid | 2775 J kg−1 K−1 |
| Specific heat capacity of EG-W | 3400 J kg−1 K−1 |
| Specific heat capacity of exhaust gas | 1020 J kg−1 K−1 |
| Heat transfer coefficient of Cu-EG nanofluid | 204 W m−2 K−1 |
| Heat transfer coefficient of EG-W | 152 W m−2 K−1 |
| Heat transfer coefficient of exhaust gas | 80 W m−2 K−1 |
| Mass flow rate of exhaust gas | 0.03 kg s−1 |
| Mass flow rate of cold fluid | 0.03 kg s−1 |
| Concentration φ | Heat Transfer Coefficient (W·m−2·K−1) | Specific Heat Capacity (J·kg−1·K−1) | Density (kg·m−3) | Thermal Diffusivity (m2·s−1) | Dynamic Viscosity (Pa·s) |
|---|---|---|---|---|---|
| 1% | 176 | 3160 | 1136 | 1.15 × 10−7 | 0.00183 |
| 2% | 191 | 2955 | 1215 | 1.19 × 10−7 | 0.00187 |
| 3% | 204 | 2775 | 1293 | 1.22 × 10−7 | 0.00192 |
| 4% | 215 | 2615 | 1371 | 1.26 × 10−7 | 0.00197 |
| 5% | 225 | 2473 | 1450 | 1.30 × 10−7 | 0.00202 |
| 6% | 234 | 2346 | 1528 | 1.34 × 10−7 | 0.00208 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Li, W.; Chen, Z. Performance Analysis of Thermoelectric Based Automotive Waste Heat Recovery System with Nanofluid Coolant. Energies 2017, 10, 1489. https://doi.org/10.3390/en10101489
Li Z, Li W, Chen Z. Performance Analysis of Thermoelectric Based Automotive Waste Heat Recovery System with Nanofluid Coolant. Energies. 2017; 10(10):1489. https://doi.org/10.3390/en10101489
Chicago/Turabian StyleLi, Zhi, Wenhao Li, and Zhen Chen. 2017. "Performance Analysis of Thermoelectric Based Automotive Waste Heat Recovery System with Nanofluid Coolant" Energies 10, no. 10: 1489. https://doi.org/10.3390/en10101489
APA StyleLi, Z., Li, W., & Chen, Z. (2017). Performance Analysis of Thermoelectric Based Automotive Waste Heat Recovery System with Nanofluid Coolant. Energies, 10(10), 1489. https://doi.org/10.3390/en10101489






