Optimal Allocation of Photovoltaic Systems and Energy Storage Systems based on Vulnerability Analysis
Abstract
:1. Introduction
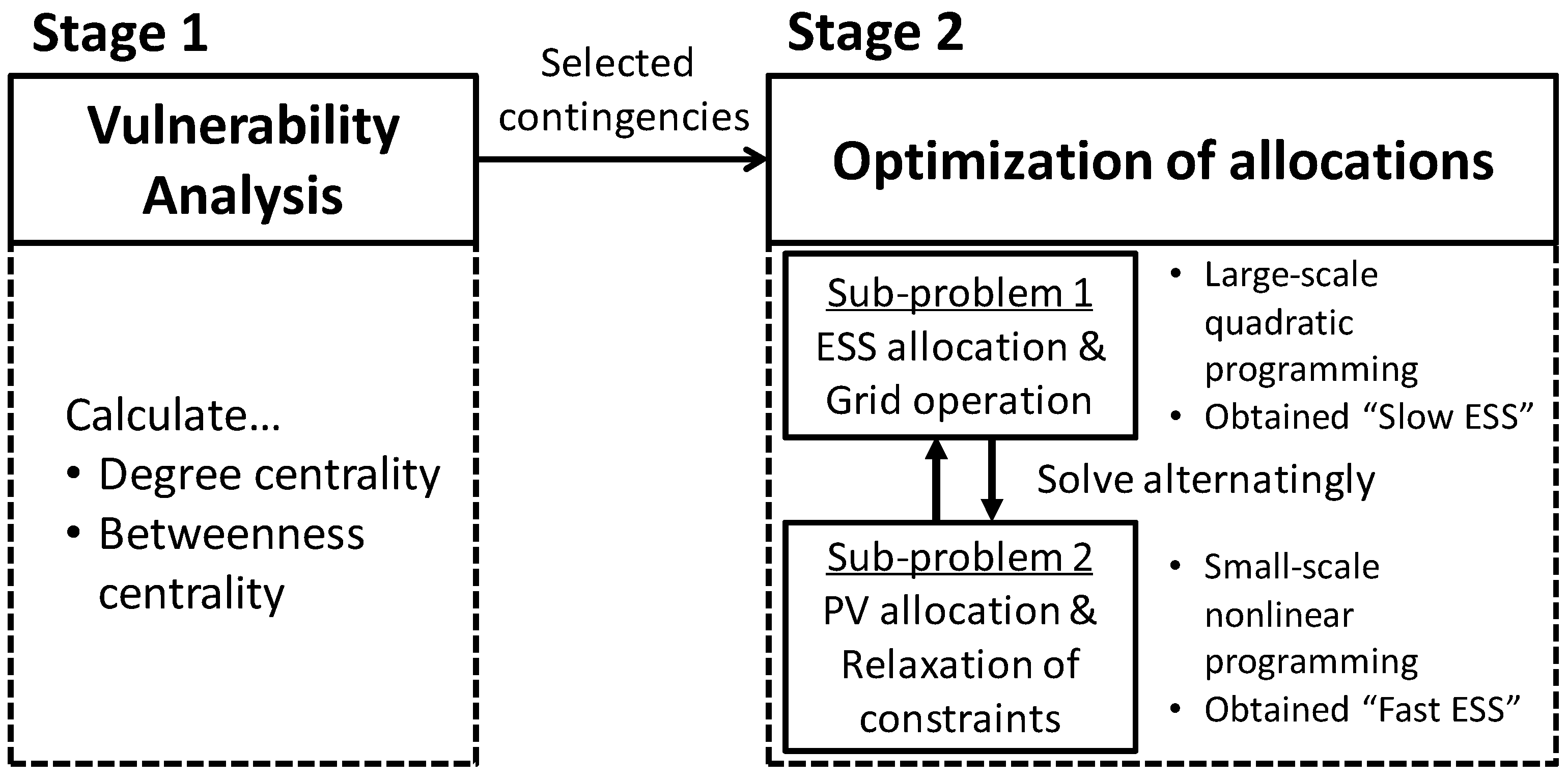
2. Optimal Allocation of PVs and ESSs based on Vulnerability Analysis
2.1. Vulnerability Analysis
2.1.1. Assumptions
2.1.2. Centrality Measures
2.2. Optimal Allocation of PV and ESS Considering Uncertainties
2.2.1. Optimization Problem without Uncertainties
- -
- Installation target of PVs in the grid:where is installation target of PVs.
- -
- Supply-demand balance that considers the PV outputs:indicates mismatch of power demand and supply in bus i at t, and the negative and positive values of denote power shortage and surplus, respectively. consists of the following terms: the total output of conventional generators in each bus (), an output of PV per unit () , a scheduling of slow ESSs (), inflow/outflow power (), and an electricity demand ().
- -
- Limitation of shortages and surpluses:where and are upper limits of power shortages and surpluses for 1 h in bus i at t, respectively.
- -
- Output of conventional power plants in each bus:is converted from by using a generator connection matrix and its element, and .
- -
- Limitation of output of conventional power plants:
- -
- Relationship between the phase angle in a bus and the transmission power:denotes a phase angle in bus i at t, and is susceptance between buses i and j, using a DC approximation.
- -
- Limitation of transmission capacity:where is a capacity of transmission line between buses i and j.
- -
- Relational expression for charging/discharging and state of charge:where is a state of charge of slow ESSs in bus i at t.
- -
- Limitation of state of charge:where is a capacity of slow ESSs.
2.2.2. Probabilistic Indices of Power Shortage and Surplus
2.2.3. Optimization Problem with Uncertainties
- -
- Investment costs of PVs and ESSs:
- -
- Fuel costs of conventional power plants:
- -
- Penalty costs of violated EENS and EENU:where is a penalty term for the violation of constraints of EENS and EENU.
- -
- Supply-demand balance that considers the expectation of PV outputs:
- -
- Limistations of EENS and EENU:
- -
2.2.4. Solving Procedure
3. Modeling
3.1. Power Systems
3.2. Conditions of Grid Operation
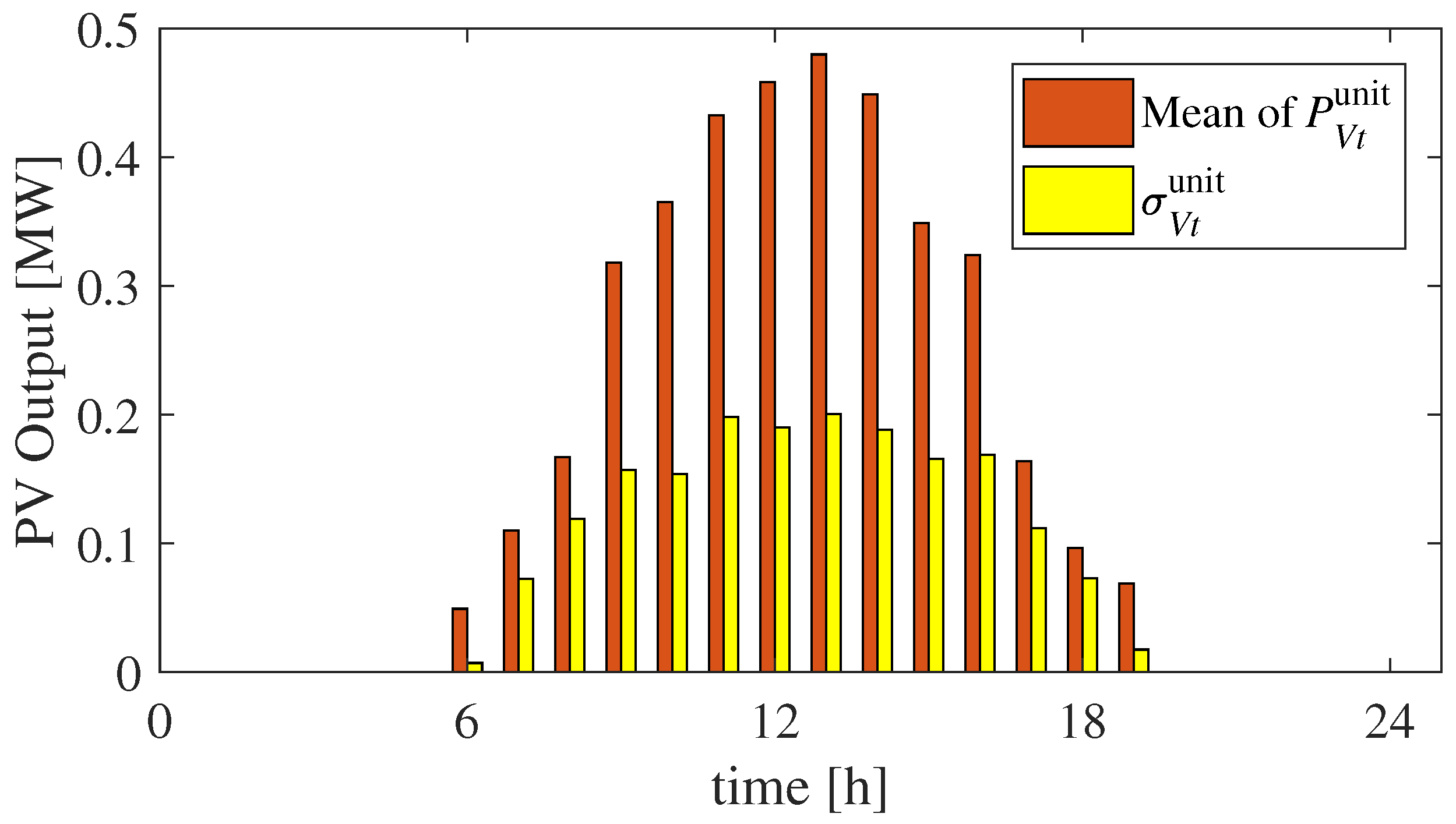
3.3. Parameter Settings and Data
4. Simulation Results
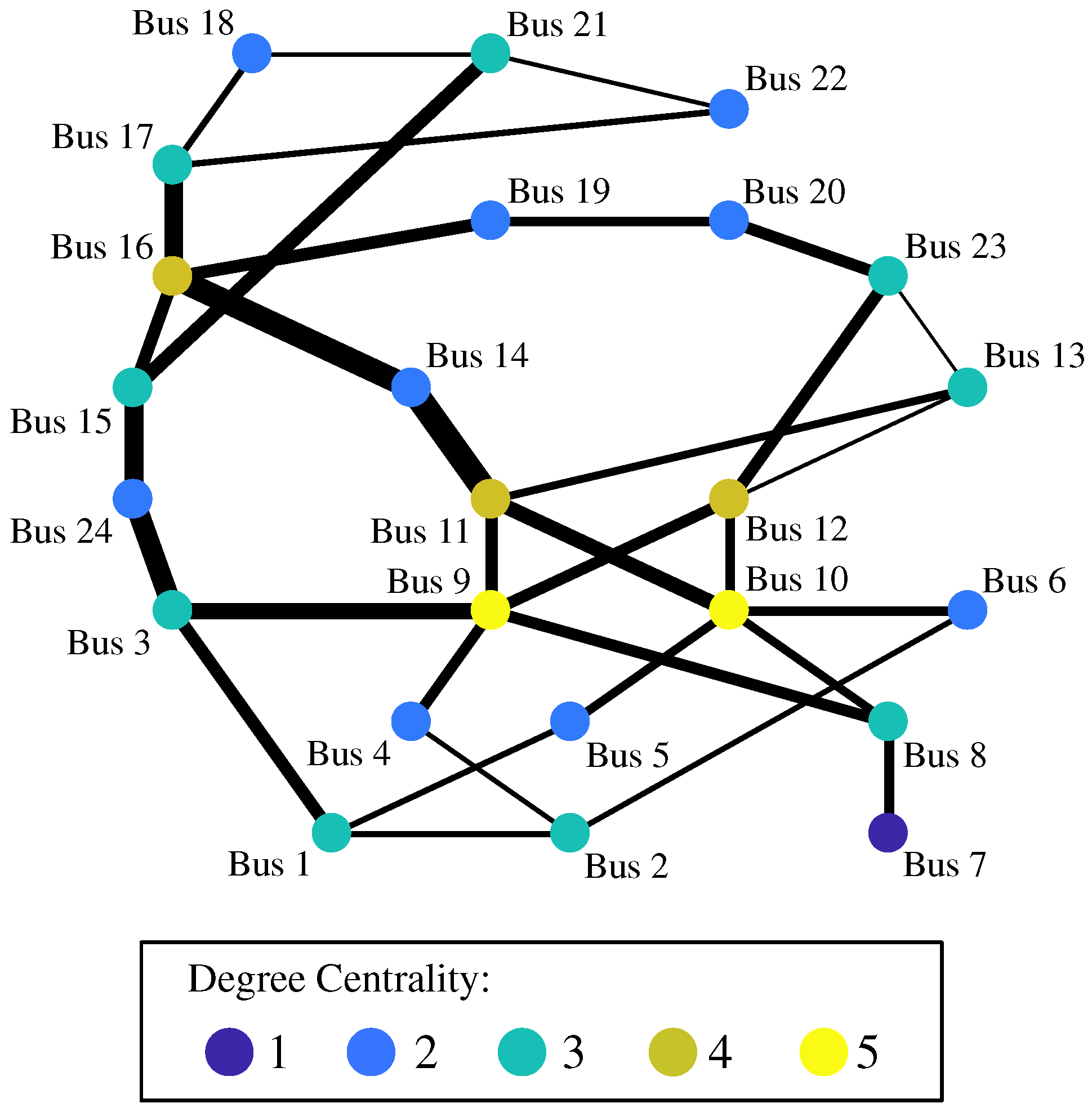
4.1. Results of Vulnerability Analysis
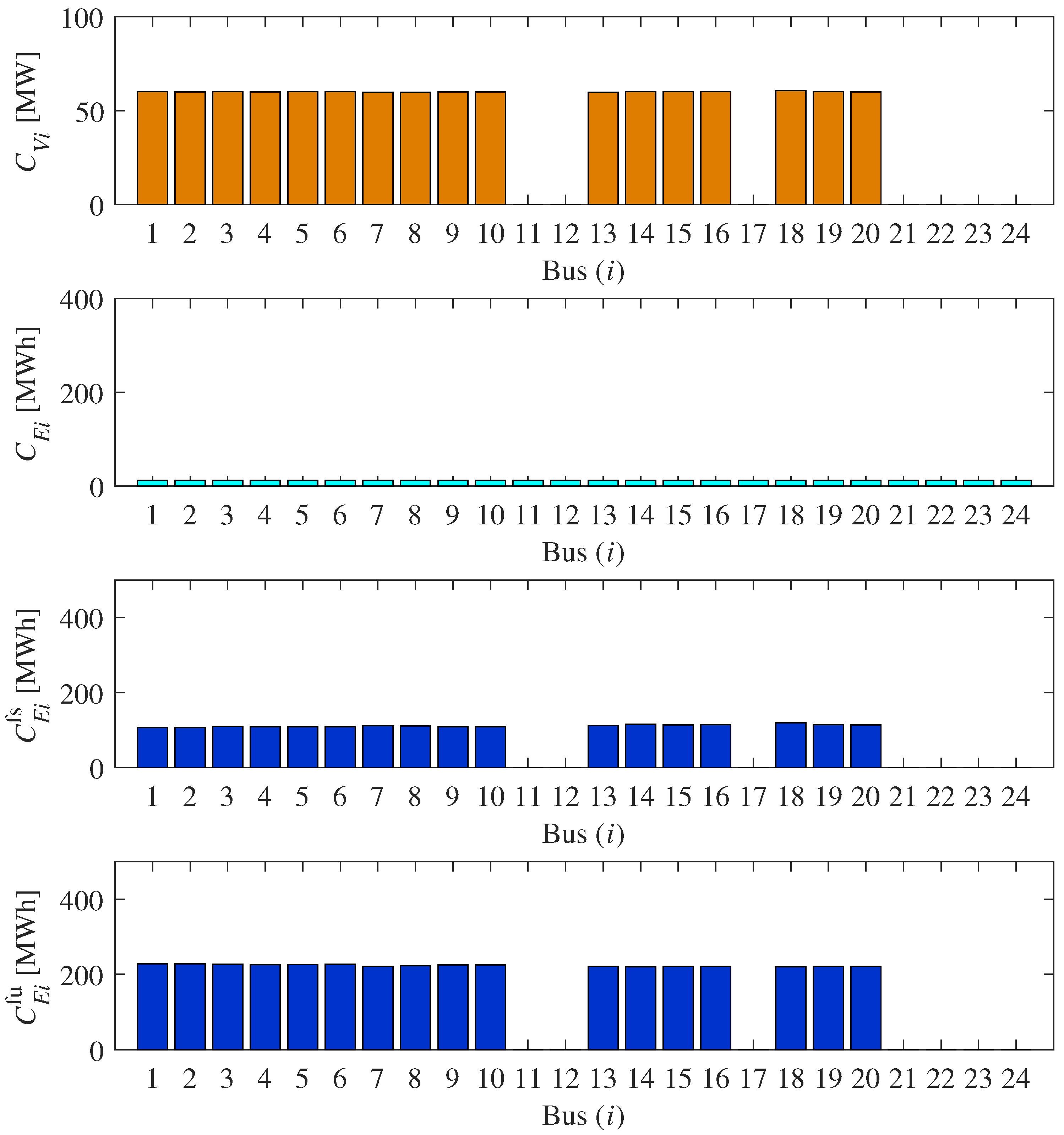
4.2. Results of PV and ESS Allocation
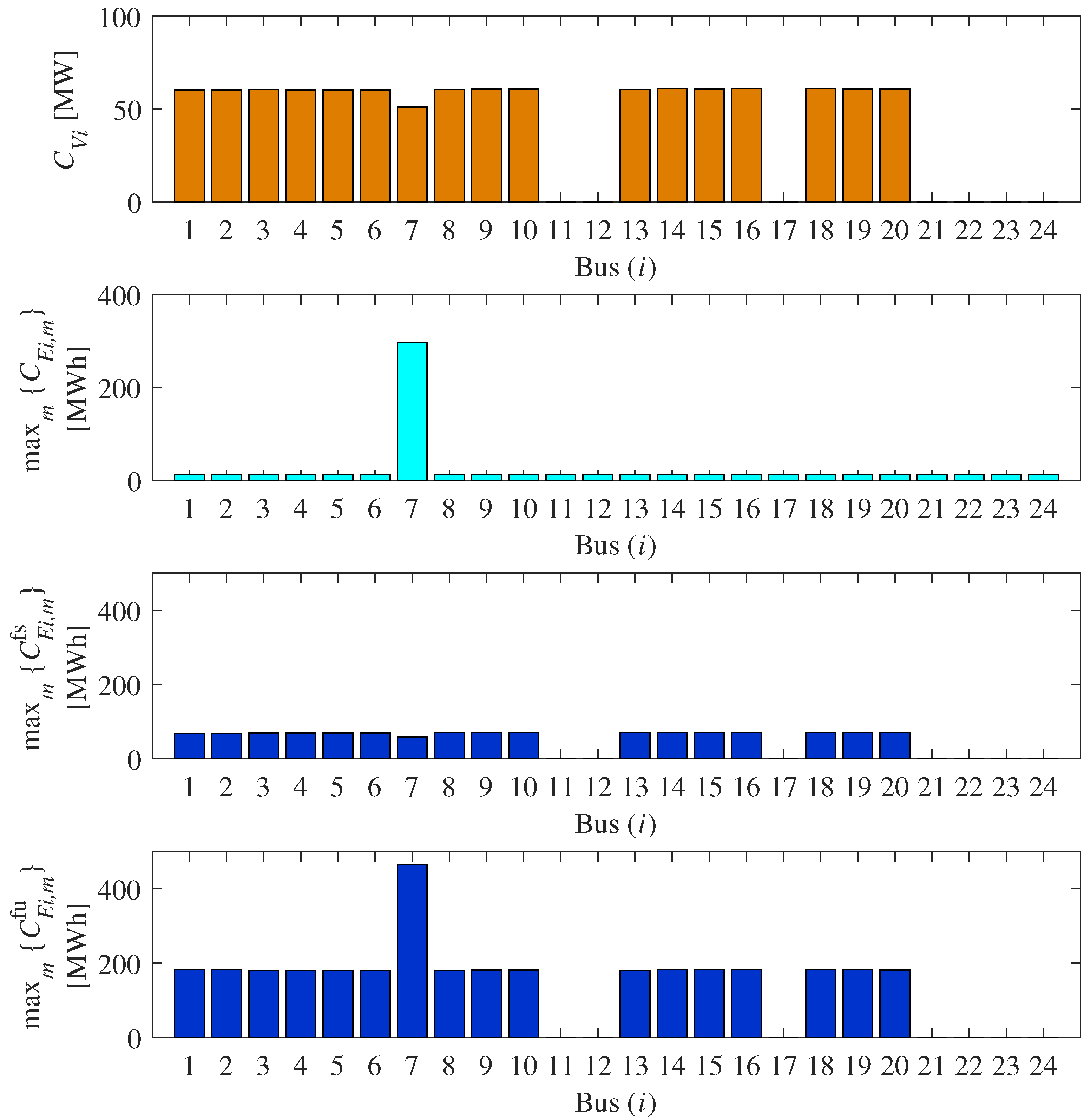
4.2.1. Case 1: Without Failures
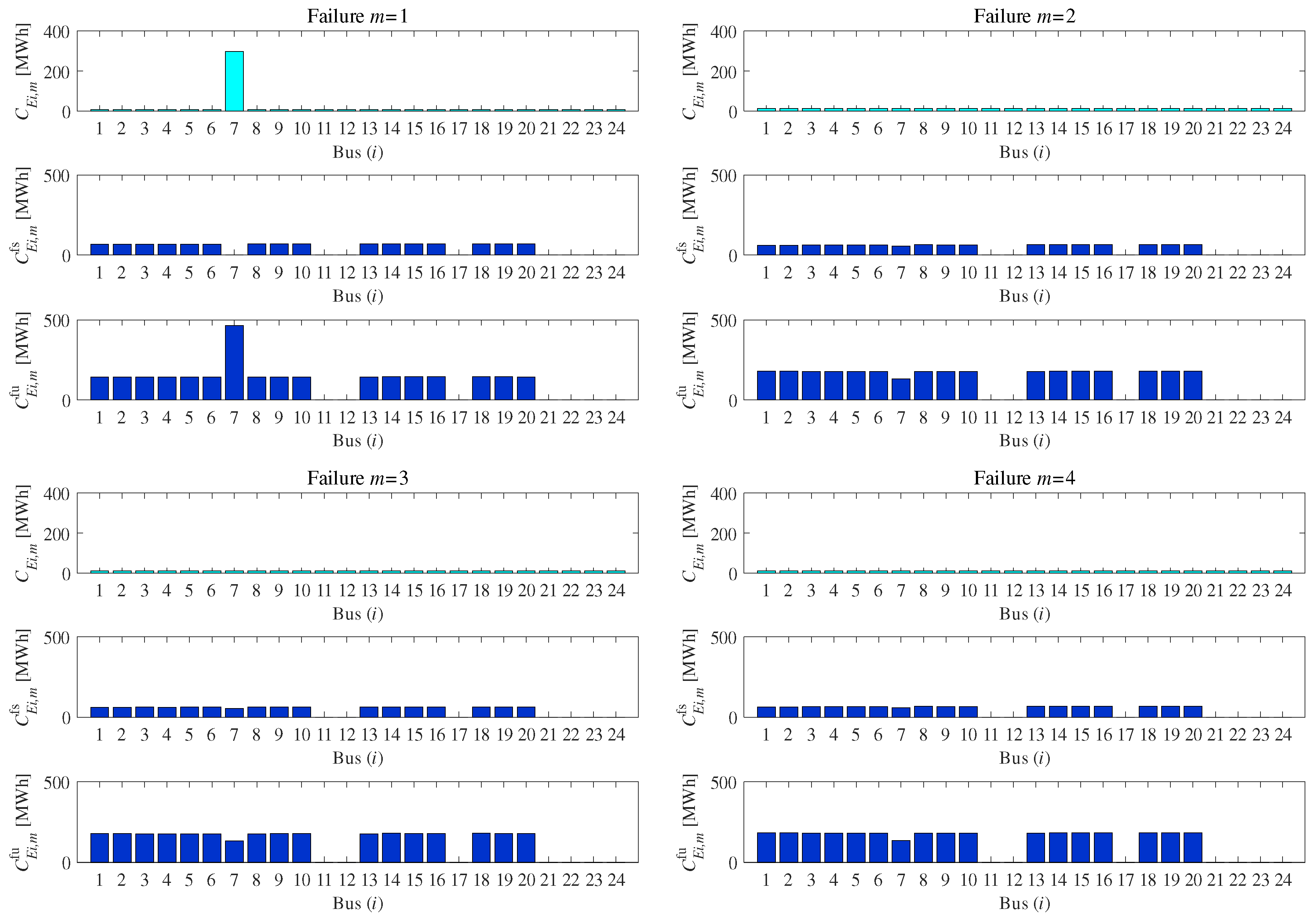
4.2.2. Case 2: With Selected Failures
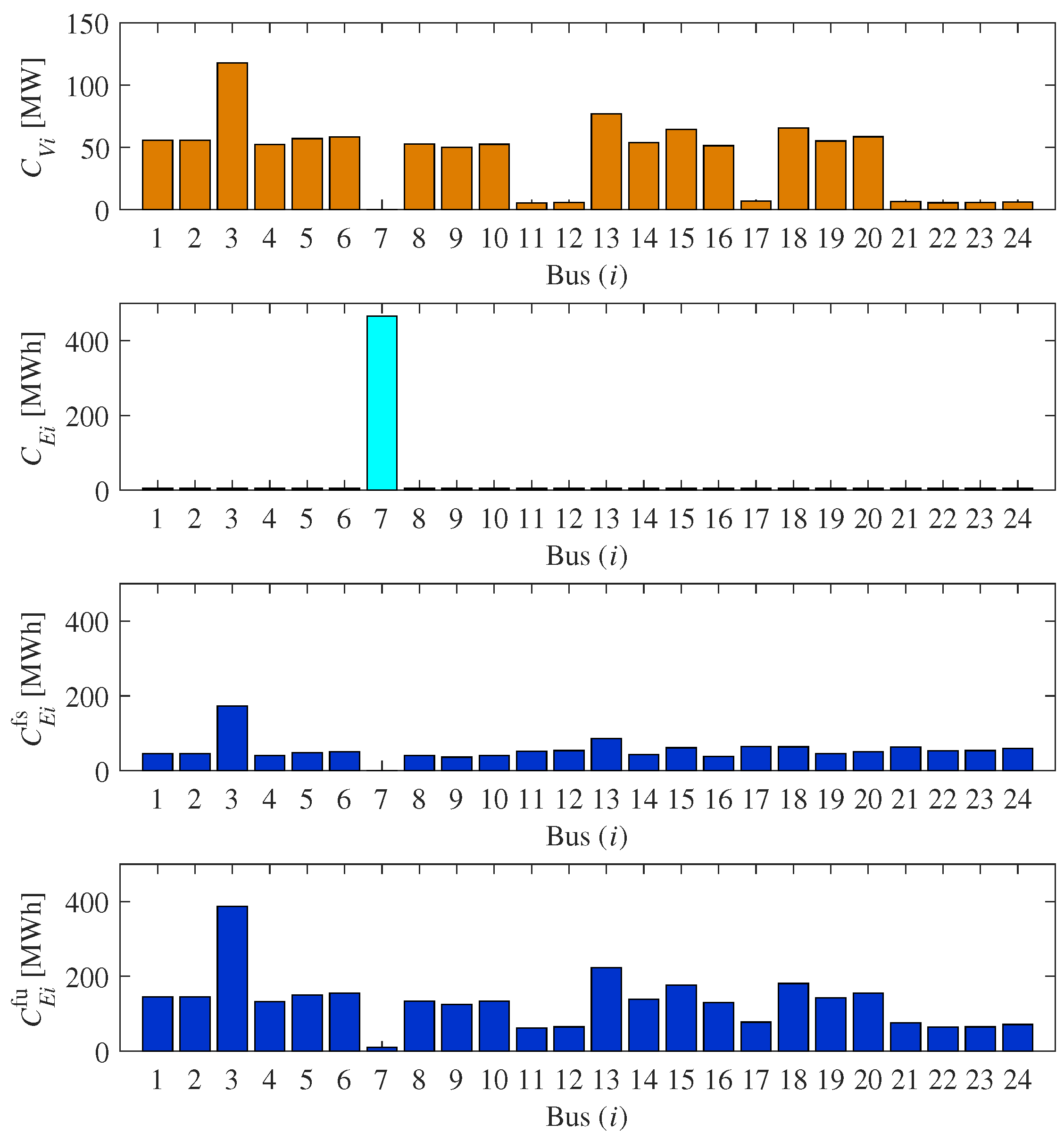
4.2.3. Case 3: By Comparison Method
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| i | Index of buses, running from 1 to |
| l | Index of transmission lines, running from 1 to |
| k | Index of conventional generators, running from 1 to |
| m | Index of grid failures, running from 1 to |
| t | Index of time, running from 1 to |
| Set of buses in power systems | |
| Set of conventional generators () | |
| Set of buses with demands () |
| Output of the k th conventional generator at t | |
| Total output of conventional generators in bus i at t | |
| Capacity of PVs in bus i | |
| Capacity of slow ESSs in bus i at t | |
| Capacity of fast ESSs for shortages and surpluses in bus i at t, respectively | |
| Mismatch of power demand and supply in bus i at t | |
| Scheduling of slow ESSs in bus i at t | |
| Scheduling of fast ESSs for shortages and surpluses in bus i at t, respectively | |
| Inflow/outflow power in bus i at t | |
| Phase angle in bus i at t | |
| State of charge of slow ESSs in bus i at t | |
| Relaxation of power shortages and surpluses for 1 h in bus i at t, respectively | |
| Vector of decision variables related to allocation of PV and ESS | |
| Vector of decision variables related to grid operation |
| Degree centrality of bus i | |
| Adjacency matrix of a power system and its element, respectively | |
| Betweenness centrality for the l th transmission line | |
| Number of shortest paths between buses i and j including the l th transmission line | |
| Total number of shortest paths between buses i and j | |
| Polynomial coefficient of the n th term in a fuel cost function of the k th generator | |
| r | Discount rate |
| Useful lifetime of ESSs and PVs in years, respectively | |
| Price of ESSs and PVs, respectively | |
| Installation target of PVs | |
| Output of PV per unit in bus i at t | |
| Electricity demand in bus i at t | |
| Susceptance between buses i and j | |
| Capacity of transmission line between buses i and j | |
| Upper limits of power shortages and surpluses for 1 h in bus i at t | |
| Generator connection matrix and its element, respectively | |
| Minimum and maximum output of the k th generator, respectively | |
| Maximum difference of the k th generator for 1 h | |
| Standard deviation of PV output in bus i at t for 1 h | |
| Penalty term for the violation of constraints of EENS and EENU |
| Probability density function of Gaussian distribution | |
| Error function | |
| Function of EENS and EENU for 1 h in bus i at t, respectively | |
| Probability of the m th grid failure | |
| Estimated value of stochastic variable x | |
| Mean value of stochastic variable x | |
| Optimal value in the previous step in BCD Method |
References
- Zheng, L.; Hu, W.; Lu, Q.; Min, Y. Optimal energy storage system allocation and operation for improving wind power penetration. IET Gener. Transm. Distrib. 2015, 9, 2672–2678. [Google Scholar] [CrossRef]
- Ghofrani, M.; Arabali, A.; Etezadi-Amoli, M.; Fadali, M.S. Energy storage application for performance enhancement of wind integration. IEEE Trans. Power Syst. 2013, 28, 4803–4811. [Google Scholar] [CrossRef]
- Wogrin, S.; Gayme, D.F. Optimizing storage siting, sizing, and technology portfolios in transmission-constrained networks. IEEE Trans. Power Syst. 2015, 30, 3304–3313. [Google Scholar] [CrossRef]
- Vovos, P.N.; Harrison, G.P.; Wallace, A.R.; Bialek, J.W. Optimal power flow as a tool for fault level-constrained network capacity analysis. IEEE Trans. Power Syst. 2005, 20, 734–741. [Google Scholar] [CrossRef]
- Masaud, T.M.; Mistry, R.D.; Sen, P.K. Placement of large-scale utility-owned wind distributed generation based on probabilistic forecasting of line congestion. IET Renew. Power Gener. 2017, 11, 979–986. [Google Scholar] [CrossRef]
- Zhang, B.; Dehghanian, P.; Kezunovic, M. Optimal allocation of pv generation and battery storage for enhanced resilience. IEEE Trans. Smart Grid. [CrossRef]
- Konishi, R.; Takahashi, M. Optimal allocation of photovoltaic systems and energy storages in power systems considering power shortage and surplus. In Proceedings of the 9th International: 2014 Electric Power Quality and Supply Reliability Conference (PQ), Rakvere, Estonia, 11–13 June 2014; pp. 127–132. [Google Scholar]
- Billinton, R.; Allan, R. Reliability Evaluation of Power Systems, 1 ed.; Springer: New York, NY, USA, 1996. [Google Scholar]
- Dent, C.J.; Ochoa, L.F.; Harrison, G.P.; Bialek, J.W. Efficient secure AC OPF for network generation capacity assessment. IEEE Trans. Power Syst. 2010, 25, 575–583. [Google Scholar] [CrossRef] [Green Version]
- Konishi, R.; Takahashi, M. Optimal facility allocation and determination of demand response participation rate considering uncertainties in power systems. Trans. Inst. Syst. Control Inf. Eng. 2017, 30, 10–19. [Google Scholar] [CrossRef]
- Subcommittee, P.M. IEEE reliability test system. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 2047–2054. [Google Scholar] [CrossRef]
- Baldick, R.; Chowdhury, B.; Dobson, I.; Dong, Z.; Gou, B.; Hawkins, D.; Huang, Z.; Joung, M.; Kim, J.; Kirschen, D.; et al. Vulnerability assessment for cascading failures in electric power systems. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–9. [Google Scholar]
- Bompard, E.; Pons, E.; Wu, D. Extended topological metrics for the analysis of power grid vulnerability. IEEE Syst. J. 2012, 6, 481–487. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35. [Google Scholar] [CrossRef]
- Snyder, L. Multi-period optimal power flow problems. Optima 2013, 93, 8–9. [Google Scholar]
- Stott, B.; Jardim, J.; Alsac, O. DC power flow revisited. IEEE Trans. Power Syst. 2009, 24, 1290–1300. [Google Scholar] [CrossRef]
- Wang, P.; Gao, Z.; Tjernberg, L.B. Operational adequacy studies of power systems with wind farms and energy storages. In Proceedings of the 2013 IEEE Power Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]
- Grippo, L.; Sciandrone, M. On the convergence of the block nonlinear Gauss-Seidel method under convex constraints. Oper. Res. Lett. 2000, 26, 127–136. [Google Scholar] [CrossRef]
- AMATERASS. Specified Nonprofit Corporation Solar Radiation Consortium. Available online: http://www.amaterass.org/ (accessed on 1 August 2017). (In Japanese).
- Chung, D.; Davidson, C.; Fu, R.; Ardani, K.; Margolis, R. U.S. Photovoltaic Prices and Cost Breakdowns: Q1 2015 Benchmarks for Residential, Commercial, and Utility-Scale Systems; Technical Report September; National Renewable Energy Laboratory: Golden, CO, USA, 2015.
- Deloitte. Energy Storage: Tracking the Technologies That Will Transform the Power Sector. Available online: https://www2.deloitte.com/content/dam/Deloitte/us/Documents/energy-resources/us-er-energy-storage-tracking-technologies-transform-power-sector.pdf (accessed on 15 August 2017).
- Zimmerman, R.; Murillo Sánchez, C.; Thomas, R. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- Zio, E.; Golea, L.R. Analyzing the topological, electrical and reliability characteristics of a power transmission system for identifying its critical elements. Reliab. Eng. Syst. Saf. 2012, 101, 67–74. [Google Scholar] [CrossRef] [Green Version]

| l | From Bus | To Bus | l | From Bus | To Bus | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 7.4 | 0.24 | 18 | 11 | 13 | 9.0 | 0.40 |
| 2 | 1 | 3 | 14.8 | 0.51 | 19 | 11 | 14 | 30.8 | 0.39 |
| 3 | 1 | 5 | 6.9 | 0.33 | 20 | 12 | 13 | 4.0 | 0.40 |
| 4 | 2 | 4 | 5.3 | 0.39 | 21 | 12 | 23 | 14.4 | 0.52 |
| 5 | 2 | 6 | 6.3 | 0.48 | 22 | 13 | 23 | 3.0 | 0.49 |
| 6 | 3 | 9 | 19.2 | 0.38 | 23 | 14 | 16 | 28.3 | 0.38 |
| 7 | 3 | 24 | 25.3 | 0.02 | 24 | 15 | 16 | 14.9 | 0.33 |
| 8 | 4 | 9 | 12.5 | 0.36 | 25 | 15 | 21 | 17.4 | 0.41 |
| 9 | 5 | 10 | 10.1 | 0.34 | 26 | 15 | 24 | 22.8 | 0.41 |
| 10 | 6 | 10 | 11.5 | 0.33 | 27 | 16 | 17 | 22.6 | 0.35 |
| 11 | 7 | 8 | 11.5 | 0.30 | 28 | 16 | 19 | 15.0 | 0.34 |
| 12 | 8 | 9 | 13.6 | 0.44 | 29 | 17 | 18 | 7.3 | 0.32 |
| 13 | 8 | 10 | 10.0 | 0.44 | 30 | 17 | 22 | 7.3 | 0.54 |
| 14 | 9 | 11 | 14.4 | 0.02 | 31 | 18 | 21 | 4.7 | 0.35 |
| 15 | 9 | 12 | 13.6 | 0.02 | 32 | 19 | 20 | 11.4 | 0.38 |
| 16 | 10 | 11 | 17.9 | 0.02 | 33 | 20 | 23 | 13.9 | 0.34 |
| 17 | 10 | 12 | 11.4 | 0.02 | 34 | 21 | 22 | 4.7 | 0.45 |
| Type of ESS | Allocated | Derived under the mth Failure | |||
|---|---|---|---|---|---|
| Capacity | |||||
| Slow | 587 | 469 | 302 | 302 | 302 |
| Fast for Shortage | 1168 | 1110 | 1082 | 1058 | 1128 |
| Fast for Surplus | 3370 | 2994 | 2970 | 2970 | 3040 |
| Total | 5126 | 4573 | 4354 | 4330 | 4470 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konishi, R.; Takahashi, M. Optimal Allocation of Photovoltaic Systems and Energy Storage Systems based on Vulnerability Analysis. Energies 2017, 10, 1477. https://doi.org/10.3390/en10101477
Konishi R, Takahashi M. Optimal Allocation of Photovoltaic Systems and Energy Storage Systems based on Vulnerability Analysis. Energies. 2017; 10(10):1477. https://doi.org/10.3390/en10101477
Chicago/Turabian StyleKonishi, Ryusuke, and Masaki Takahashi. 2017. "Optimal Allocation of Photovoltaic Systems and Energy Storage Systems based on Vulnerability Analysis" Energies 10, no. 10: 1477. https://doi.org/10.3390/en10101477
APA StyleKonishi, R., & Takahashi, M. (2017). Optimal Allocation of Photovoltaic Systems and Energy Storage Systems based on Vulnerability Analysis. Energies, 10(10), 1477. https://doi.org/10.3390/en10101477





