Characterization of Extremal Unicyclic Graphs with Fixed Leaves Using the Lanzhou Index

Abstract

A topological index being a graph theoretic parameter plays a role of function for the assignment of a numerical value to a molecular graph which predicts the several physical and chemical properties of the underlying molecular graph such as heat of evaporation, critical temperature, surface tension, boiling point, octanol-water partition coefficient, density and flash points. For a (molecular) graph $\mathsf{\Gamma }$, the Lanzhou index (Lz index) is obtained by the sum of $deg{\left(v\right)}^2$$d\overline{e}g\left(v\right)$ over all the vertices, where $deg\left(v\right)$ and $d\overline{e}g\left(v\right)$ are degrees of the vertex v in $\mathsf{\Gamma }$ and its complement $\overline{\mathsf{\Gamma }}$ respectively. Let ${\mathcal{V}}_{\alpha }^{\beta }$ be a class of unicyclic graphs (same order and size) such that each graph of this class has order $\alpha$ and $\beta$ leaves (vertices of degree one). In this note, we compute the lower and upper bounds of Lz index for each unicyclic graph in the class of graphs ${\mathcal{V}}_{\alpha }^{\beta }.$ Moreover, we characterize the extremal graphs with respect to Lz index in the same class of graphs.

1. Introduction

A topological index ($TI$) is a function that associates a numerical value with a (molecular) graph that predicts its various chemical and structural properties, such as boiling point, stability, melting point, volatility, chirality, solubility, and connectivity. $TI$s are also used in cheminformatics to study the quantitative structure activities and property relationships (QSAR and QSPR) [1], which connect a molecular structure with some biological properties with the help of a mathematical formula

$$P=F\left(M\right),$$

where P represents the property, M shows a molecular structure, and F plays the role of the function, which depends on the molecular structure. In general, $TI$s are divided into four classes (distance, degree, spectral, and polynomial based) but our focus is on degree-based $TI$s, which are mathematically defined as

$$TI\left(\mathsf{\Gamma }\right)=\sum _{uv\in E\left(\mathsf{\Gamma }\right)}F(deg\left(u\right),deg\left(v\right)),$$

where F is a function.

If $F\left(deg\right(u),$$deg\left(v\right))=deg(u)+deg(v)$, then we first have the Zagreb index, and for $F\left(deg\right(u),deg(v\left)\right)=deg\left(u\right)deg\left(v\right)$, we obtain the second Zagreb index. These $TI$s are defined by Gutman and Trinajsti$\acute{c}$ in 1972 [2] to measure the total $\pi -electron$ energy of molecules in the molecular structures. In the literature, there exists a large number of results related to these Zagreb indices for different graphs, such as nanotubes [3], dendrimer structures [4], silicate & oxide networks [5], and carbon structures [6]. In [2], another $TI$ is defined by the sum of the cube of the degrees of all vertices. Furtula and Gutman in 2015 [7] re-investigated this index by studying its basic properties. After years of the obliviousness to this $TI$, they gave this index a new name: the forgotten topological index (F-index). For more details on various $TI$s, see [8,9,10,11].

Vukicevic et al. (2018) [12] defined the Lanzhou index (Lzindex) as the sum of the product between $d\overline{e}g\left(v\right)$ and the square of $deg\left(v\right)$ over all vertices v of $\mathsf{\Gamma }$ where $deg\left(v\right)$ represents the degree of v in $\mathsf{\Gamma }$ and $d\overline{e}g\left(v\right)$ represents the degree of v in the complement graph of $\mathsf{\Gamma }$. It is important to note that this index can be formed by the relation between the forgotten index and the first Zagreb index as

$$Lz\left(\mathsf{\Gamma }\right)=(n-1)M_1\left(\mathsf{\Gamma }\right)-F\left(\mathsf{\Gamma }\right),$$

where $M_1\left(\mathsf{\Gamma }\right)$ and $F\left(\mathsf{\Gamma }\right)$ present the first Zagreb and forgotten indices of the (molecular) graph, respectively. Furthermore, they found the bounds of the Lz index for acyclic graphs. Dehgardi and Liu in 2021 extended these results of the Lz index for acyclic graphs under the condition of maximum degree [13]. Zeng and Wu (2021) determined the sharp upper bound of the Lz index for a special class of graphs that was obtained by some transformations on acyclic graphs [14]. Recently, Liu et al. (2022) determined the lower and upper bounds of unicyclic graphs [15]. Javaid et al. (2018) [16] found the upper and lower bounds of the forgotten index for a family of graphs known as unicyclic graphs with certain pendent vertices (leaves). In this note, we compute the bounds (lower and upper) for the Lz index on the class of unicyclic graphs under the condition of fixed leaves. Moreover, we characterized the extremal graphs with respect to the Lz index in the same class of graphs.

2. Preliminaries

Let $\mathsf{\Gamma }\left(V\right(\mathsf{\Gamma }),E(\mathsf{\Gamma }\left)\right)$ be a graph with edge-set $E\left(\mathsf{\Gamma }\right)$ and vertex-set $V\left(\mathsf{\Gamma }\right)$, such that $e=\left|E\right(\mathsf{\Gamma }\left)\right|$ and $u=\left|V\right(\mathsf{\Gamma }\left)\right|$ are the size and order of the graph $\mathsf{\Gamma }$, respectively. The adjacent vertices r and s were treated by an edge $e=rs$. The edges that have the same starting vertex and end vertex are known as loops. A connected graph $\mathsf{\Gamma }$ with $\left|V\right(\mathsf{\Gamma }\left)\right|=\left|E\right(\mathsf{\Gamma }\left)\right|-1$ is called a tree (acyclic graph). Moreover, for a graph $\mathsf{\Gamma }$, if $\left|V\right(\mathsf{\Gamma }\left)\right|=\left|E\right(\mathsf{\Gamma }\left)\right|$, then $\mathsf{\Gamma }$ is called a unicyclic graph. This paper deals with simple (no loops and multiple edges) and undirected graphs. For a detailed study of graph-related notions, please refer to [17]. We define some TIs that are used in the present study for the development of our main results.

Definition 1 

([2,7]). The

first Zagreb index and forgotten index (F-index) for a molecular graph Γ are $M_1\left(\mathsf{\Gamma }\right)={\displaystyle \sum _{pq\in E\left(\mathsf{\Gamma }\right)}}[deg\left(p\right)+deg\left(q\right)]\phantom{a}$ and $F\left(\mathsf{\Gamma }\right)={\displaystyle \sum _{p\in V\left(\mathsf{\Gamma }\right)}}{\left[deg\left(p\right)\right]}^3.$

Definition 2 

([12]). The Lanzhou index (Lz index) for a molecular graph Γ is

$$Lz\left(\mathsf{\Gamma }\right)=\sum _{p\in V\left(\mathsf{\Gamma }\right)}{\left(deg\left(p\right)\right)}^2\left(de\overline{g}\left(p\right)\right).$$

For more details on TIs, see [18,19,20].

If a graph is connected and $\phi$-cyclic, then $s=\alpha -1+\phi$, where s is the total number of edges (size) and $\alpha$ is the total number of vertices (order) of the graph. If $\phi =0$, then the graph is a tree, if $\phi =1$ then the graph is unicyclic, and if $\phi =2$, then the graph is bicyclic.

Now, by using base graphs, we can use more unicyclic graphs. For $u=\alpha -lx$, assume that $C_u$ is a cycle of order u, then the unicyclic graphs $\mathcal{V}$$(\alpha ,l,x)$ are obtained from $C_u$ by joining l leaves to the $x\ge 2$ vertices of $C_u$, where $\alpha =\left|V\right(\alpha ,l,x\left)\right|$. Moreover, suppose that $P_y,C_v,$ and $S_{1,l^{\prime }}$ present the path, cycle, and star graph of order y, v, and $l^{\prime }+1$. Then the graph ${\mathcal{V}}^{\prime }$$(\alpha ,l^{\prime },y)$ is obtained by emerging one vertex of degree one of the path with $C_v$ and the other vertex of degree one with the central vertex of $S_{1,l^{\prime }}$, where $v=\alpha -l^{\prime }-y+1$ and $2\le y\le \alpha -l^{\prime }-2$. If $\mathbf{V}=\mathcal{V}$$(\alpha ,l,x)$ and ${\mathbf{V}}^{\prime }={\mathcal{V}}^{\prime }$$(\alpha ,l^{\prime },y)$ then

Table 1. Degree-vertex partition of $\mathbf{V}$.

$deg\left(v\right),forv\in \mathbf{V}$	$1$	$2$	$l+2$
$\left|deg\right(v\left)\right|$	$xl$	$u-x$	$x$

and

Table 2. Degree-vertex partition ${\mathbf{V}}^{\prime }$.

$deg\left(v\right),forv\in {\mathbf{V}}^{\prime }$	1	2	$l^{\prime }+1$	3
$\left|deg\right(v\left)\right|$	$l^{\prime }$	$v+y-3$	1	1

present the vertex partition with respect to their degrees respectively as follows:

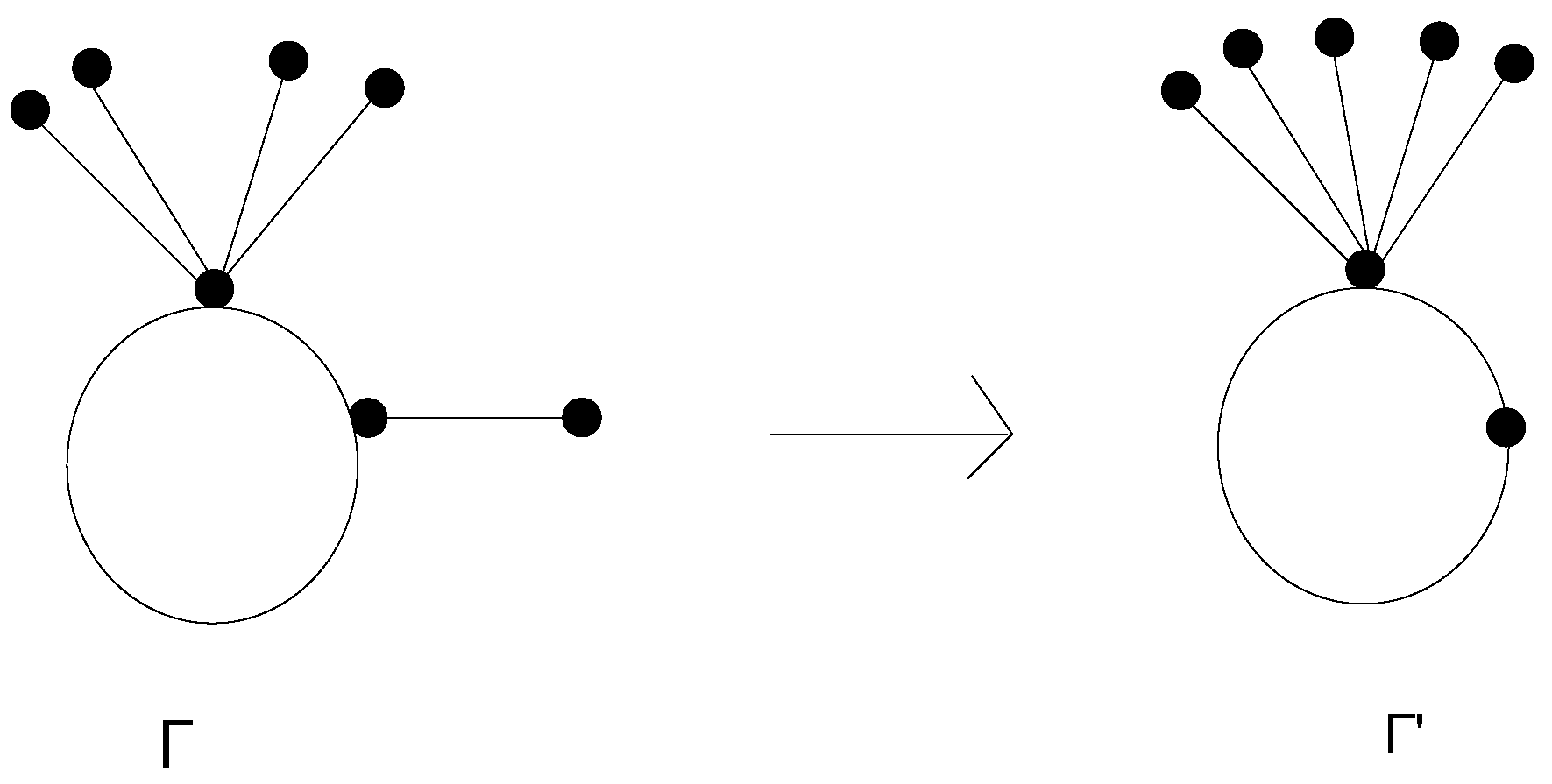
For $2\le x\le u$, then ${\mathbf{V}}_{\mathbf{x}-\mathbf{l}}$ is obtained from the graph ${\mathbf{V}}_{\mathbf{x}-\mathbf{2}}$ by removing $(x-1)l$ leaves from the vertex whose degree is $(x-1)l+2$ and connect these vertices to the end vertex whose degree is $l+2$; for more details of this transformation, see Figure 1.

Now, we define ${\mathcal{V}}_{\alpha }^{\beta }=\{\mathsf{\Gamma }:|V\left(\mathsf{\Gamma }\right)|=\alpha$ and $\mathsf{\Gamma }$ have $\beta$ leaves}; suppose three subclasses—${\mathcal{V}}_{\mathbf{1}}$, ${\mathcal{V}}_{\mathbf{2}}$, and ${\mathcal{V}}_{\mathbf{3}}$ of ${\mathcal{V}}_{\alpha }^{\beta }$, such that leaves are connected with the tree vertices, cycle vertices, and both (and vice versa).

3. Main Results

In this section, we present our main findings related to the Lz index on the unicyclic graphs.

Lemma 1. 

For two connected graphs, ${\mathsf{\Gamma }}_1$ and ${\mathsf{\Gamma }}_2$, of the same size and order with degree sequences $<de{g}_1^1,de{g}_2^1,de{g}_3^1,\dots ,de{g}_{\alpha }^1>$ and $<de{g}_1^2,de{g}_2^2,de{g}_3^2,\dots ,de{g}_{\alpha }^2>$ if $de{g}_j^1=de{g}_j^2$ for $1\le j\le \alpha$, then $Lz\left({\mathsf{\Gamma }}_1\right)=Lz\left({\mathsf{\Gamma }}_2\right)$, where $de{g}_j^i$ is the degree of vertices $v_j^i$ in ${\mathsf{\Gamma }}_j^i$ for $1\le i\le 2$ and $\alpha =|V\left({\mathsf{\Gamma }}_1\right)|=|V\left({\mathsf{\Gamma }}_2\right)|$.

Proof. 

If graphs are isomorphic, then we are done. Suppose that the graphs are non-isomorphic. As $de{g}_j^1=de{g}_j^2$ for $1\le j\le \alpha$, consequently,

$$<de{g}_1^1,de{g}_2^1,de{g}_3^1,\dots ,de{g}_{\alpha }^1>=<de{g}_1^2,de{g}_2^2,de{g}_3^2,\dots ,de{g}_{\alpha }^2>.$$

Thus, for $1\le j\le \alpha$

$$de{g}_j^1=de{g}_j^2$$

, then

$$\alpha -1-de{g}_j^1=\alpha -1-de{g}_j^2$$

, which implies that

$$d\overline{e}{g}_j^1=d\overline{e}{g}_j^2$$

for $1\le j\le \alpha .$ Therefore, ${\displaystyle \sum _{j=1}^{\alpha }}{\left(de{g}_j^1\right)}^2\times d\overline{e}{g}_j^1={\displaystyle \sum _{j=1}^{\alpha }}{\left(de{g}_j^2\right)}^2\times d\overline{e}{g}_j^2$, which implies that

$$Lz\left({\mathsf{\Gamma }}_1\right)=Lz\left({\mathsf{\Gamma }}_2\right).$$

□

Lemma 2. 

For a graph $\mathsf{\Gamma }\left(V\right(\mathsf{\Gamma }),E(\mathsf{\Gamma }\left)\right)$ and $xy\in E\left(\mathsf{\Gamma }\right)$, if ${\mathsf{\Gamma }}^{\prime }$ is obtained from Γ by the deletion of $xy$ and joining x to z, i.e., ${\mathsf{\Gamma }}^{\prime }=\mathsf{\Gamma }-xy+xz$. Then,

(1) $Lz\left({\mathsf{\Gamma }}^{\prime }\right)=Lz\left(\mathsf{\Gamma }\right)$ if $deg\left(z\right)=deg\left(y\right)-1$, or $3\left(deg\right(x)+deg(w\left)\right)=2(\alpha -1)$

(2) $deg\left(z\right)>deg\left(y\right)-1$

(i) If $3\left(deg\right(z)+deg(y\left)\right)>2(\alpha -1)$ then $Lz\left(\mathsf{\Gamma }\right)>lz\left({\mathsf{\Gamma }}^{\prime }\right)$

(ii) If $3\left(deg\right(z)+deg(y\left)\right)<2(\alpha -1)$ then $Lz\left({\mathsf{\Gamma }}^{\prime }\right)>Lz\left(\mathsf{\Gamma }\right)$

(3) $deg\left(z\right)<deg\left(y\right)-1$

(i) If $3\left(deg\right(z)+deg(y\left)\right)<2(\alpha -1)$ then $Lz\left(\mathsf{\Gamma }\right)>Lz\left({\mathsf{\Gamma }}^{\prime }\right)$

(ii) If $3\left(deg\right(z)+deg(v\left)\right)>2(\alpha -1)$ then $Lz\left({\mathsf{\Gamma }}^{\prime }\right)>Lz\left(\mathsf{\Gamma }\right)$where $deg\left(y\right)$ and $deg\left(z\right)$ are degrees of y and z in Γ, and vice versa.

Proof. 

As $deg\left(y\right)$ and $deg\left(z\right)$ denote the degrees of y and z in $\mathsf{\Gamma }$, and vice versa, we have

$$\begin{array}{c}Lz\left(\mathsf{\Gamma }\right)-Lz\left({\mathsf{\Gamma }}^{\prime }\right)=\left(deg{\left(y\right)}^2\right)(\alpha -1-deg\left(y\right))+\left(deg{\left(z\right)}^3\right)(\alpha -1-deg\left(z\right))\hfill \\ \hfill -\left({(deg\left(y\right)-1)}^2\right)(\alpha -1-(deg\left(y\right)-1))-\left({(deg\left(z\right)+1)}^2\right)(\alpha -1-(deg\left(z\right)+1)\end{array}$$

$$\phantom{aa}=\left(3deg\right(z)+3deg(y)-2\alpha +2)\left(deg\right(z)-(deg\left(y\right)-1\left)\right).$$

Now, we face three cases for $deg\left(z\right)=deg\left(y\right)-1$, $deg\left(z\right)>deg\left(y\right)-1$, and $deg\left(z\right)<deg\left(y\right)-1$. So, we obtain the required results. Thus, we are done. □

Lemma 3. 

For $l\ge 2$, $u,v\ge 3$, $2\le x\le u$, $2\le y\le v-3$ and $0\le i\le x-1$, $Lz$-index of ${\mathbf{V}}_{\mathbf{i}}$ and ${\mathbf{V}}^{\prime }$ are

$$\left(i\right)Lz\left({\mathbf{V}}_{\mathbf{i}}\right)=lx(\alpha -2)+4(u-x+i)(\alpha -3)+{(l+2)}^2(x-i-1)(\alpha -l-3)+{((i+1)l+2)}^2(\alpha -3-(i+1)l)\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$$

$$\left(ii\right)Lz\left({\mathbf{V}}^{\prime }\right)=l^{\prime }(\alpha -2)+4(y+v-3)(\alpha -3)+9(\alpha -4)+{(l^{\prime }+1)}^2(\alpha -2-l^{\prime }).\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$$

Proof. 

By Definition 2, and Table 1 and Table 2, the results are done. □

Putting $i=0$ in Lemma 3, we obtain the following results:

Corollary 1. 

For unicyclic graphs V, the Lz index is

$$Lz\left(\mathbf{V}\right)=lx(\alpha -2)+4(u-x)(\alpha -3)+x{(l+2)}^2(\alpha -3-l).$$

where $l\ge 2$, $u\ge 3$, and $2\le x\le u$.

Theorem 1. 

Let $l\ge 2$, $u,v\ge 3$, $2\le x\le u$, $2\le y\le v-3$ and $0\le i\le x-1$. Then,

$$\left(i\right)\phantom{a}Lz\left({\mathcal{V}}^{\prime }(\alpha ,l,2)\right)>Lz\left(\mathcal{V}(\alpha ,l,1)\right),\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$$

$$\left(ii\right)\phantom{a}Lz\left({\mathcal{V}}^{\prime }(\alpha ,l,y)\right)=Lz\left({\mathcal{V}}^{\prime }(\alpha ,l,y+1)\right),\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$$

$$\left(iii\right)\phantom{a}Lz\left(\mathcal{V}(\alpha ,l,x)\right)>Lz\left({\mathcal{V}}^{\prime }(\alpha ,l,2)\right),\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$$

$$\left(iv\right)\phantom{a}Lz\left({\mathbf{V}}_{\mathbf{0}}\right)>Lz\left({\mathbf{V}}_{\mathbf{1}}\right)>\dots >Lz\left({\mathbf{V}}_{\mathbf{x}-\mathbf{1}}\right),\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$$

$$\left(v\right)\phantom{a}Lz\left({\mathcal{V}}^{\prime }(\alpha ,l,y)\right)>Lz\left(\mathcal{V}(\alpha ,l,1)\right).\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$$

Proof. 

(i) By placing $x=1$ in Corollary 1, we have,

$$Lz\left(\mathcal{V}(\alpha ,l,1)\right)=l(\alpha -2)+4(u-1)(\alpha -3)+{(l+2)}^2(\alpha -3-l).$$

For $y=2$, Lemma 3 (ii) gives

$$Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },2)\right)=l^{\prime }(\alpha -2)+4(v-1)(\alpha -3)+9(\alpha -4)+{(l^{\prime }+1)}^2(\alpha -2-l^{\prime }).$$

Since $u=\alpha -lx$, $v=\alpha -l^{\prime }-y+1$, $l^{\prime }=lx$ and $u-v=l^{\prime }-l+1$, for $x=1$ and $y=2$ we have

$$Lz({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },2)-Lz\left(\mathcal{V}(\alpha ,l,1)\right))=11l+3l^2+2\alpha -14-2l\alpha >0$$

Therefore, $Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },2)\right)>Lz\left(\mathcal{V}(\alpha ,l,1)\right)$ for $l\ge 2$.

(ii) By using Lemma 3 (ii),

$$Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },y)\right)=l^{\prime }(\alpha -2)+4(v+y-3)(\alpha -3)+9(\alpha -4)+{(l^{\prime }+1)}^2(\alpha -2-l^{\prime }).$$

Since for $y=y+1$, we have $v=v-1$. Hence,

$$Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },y+1)\right)=l^{\prime }(\alpha -2)+4(v+y-3)(\alpha -3)+9(\alpha -4)+{(l^{\prime }+1)}^2(\alpha -2-l^{\prime }).$$

Thus, $Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },y)\right)=Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },y+1)\right).$

(iii) With the help of Corollary 1 and Lemma 3, we have

$$Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },2)\right)=l^{\prime }(\alpha -2)+4(v-1)(\alpha -3)+9(\alpha -4)+{(l^{\prime }+1)}^2(\alpha -2-l^{\prime })\mathrm{and}$$

$$Lz\left(\mathcal{V}(\alpha ,l,x)\right)=lx(\alpha -2)+4(u-x)(\alpha -3)+x{(l+2)}^2(\alpha -3-l).$$

Since $u-v=l^{\prime }-lx+1$, $l^{\prime }=lx$ and $y=2$; hence,

$$Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },2)\right)-Lz\left(\mathcal{V}(\alpha ,l,x)\right)=2\alpha +l^2{x}^2(\alpha -4-lx)+lx(13+7l-l\alpha +l^2-4\alpha )-14<0.$$

Therefore $Lz\left(\mathcal{V}(\alpha ,l,x)\right)>Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },2)\right).$

(iv) With the help of Lemma 3 (i), we have

$$Lz\left({\mathbf{V}}_{\mathbf{i}+\mathbf{1}}\right)-Lz\left({\mathbf{V}}_{\mathbf{i}}\right)=17i{l}^3-8l\alpha -14l^2-6l^3+4i{l}^2-4l\alpha -2l^2\alpha -6i{l}^2-2i{l}^3-4il\alpha +4i^2{l}^2.$$

By Lemma 2 (iii), $Lz\left({\mathbf{V}}_{\mathbf{i}}\right)>Lz\left({\mathbf{V}}_{\mathbf{i}+\mathbf{1}}\right).$ Using $i=0,1,2,3,\dots ,x-2$, we have $Lz\left({\mathbf{V}}_{\mathbf{0}}\right)$$>Lz\left({\mathbf{V}}_{\mathbf{1}}\right)$$>\dots >Lz\left({\mathbf{V}}_{\mathbf{x}-\mathbf{1}}\right).$

(v) With the help of (i) and (ii), we have

$$Lz\left({\mathcal{V}}^{\prime }(\alpha ,l,2)\right)>Lz\left(\mathcal{V}(\alpha ,l,1)\right)\phantom{a}and\phantom{a}Lz\left({\mathcal{V}}^{\prime }(\alpha ,l,y)\right)=Lz\left({\mathcal{V}}^{\prime }(\alpha ,l,y+1)\right).$$

Therefore,

$$Lz\left({\mathcal{V}}^{\prime }(\alpha ,l,2)\right)=Lz\left({\mathcal{V}}^{\prime }(\alpha ,l,3)\right)=\dots =Lz\left({\mathcal{V}}^{\prime }(\alpha ,l,v-3)\right)$$

Thus, $Lz\left({\mathcal{V}}^{\prime }(\alpha ,l,y)\right)>Lz\left(\mathcal{V}(\alpha ,l,1)\right)$ where $2\le y\le v-3$. □

Theorem 2. 

If $l\ge 2$, $u\ge 3$, $2\le x\le u$, $\beta =lx$ and $\alpha \ge 5$ then, for every $\mathsf{\Gamma }\in {\mathcal{V}}_{\alpha }^{\beta }$

$$\left(a\right)\phantom{a}Lz\left(\mathcal{V}\right(\alpha ,l,x\left)\right)\ge Lz\left(\mathsf{\Gamma }\right),\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$$

$$\left(b\right)\phantom{a}Lz\left(\mathsf{\Gamma }\right)\ge Lz\left(\mathcal{V}\right(\alpha ,l,1\left)\right),\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$$

Furthermore, equality holds if $\mathsf{\Gamma }\cong {\mathcal{V}}^{\prime }(\alpha ,l,x)$ and $\mathsf{\Gamma }\cong \mathcal{V}(\alpha ,l,x)$ respectively.

Proof. 

(a) The proof is computed with the help of the following cases.

Case 1: Suppose that $\mathsf{\Gamma }\in {\mathcal{V}}_{\mathbf{1}}$ and $\mathsf{\Gamma }\cong {\mathbf{V}}_{\mathbf{i}}$ where $1\le i\le x-1.$ Since, $\mathcal{V}(\alpha ,l,x)={\mathbf{V}}_{\mathbf{0}}$; therefore, by using Theorem 1 (iv) $\mathcal{V}(\alpha ,l,x))\ge \mathsf{\Gamma }\cong {\mathbf{V}}_{\mathbf{i}}$ where $1\le i\le x-1$.

Case 2: If $\mathsf{\Gamma }\in {\mathcal{V}}_{\mathbf{2}}$, such that $\mathsf{\Gamma }\cong {\mathcal{V}}^{\prime }(\alpha ,l^{\prime },y)$. By using Theorems 1 (ii) and (iii), we have

$$Lz\left(\mathcal{V}(\alpha ,l,x)\right)>Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },2)\right)\phantom{a}\mathrm{and}\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$$

$$Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },2)\right)=Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },3)\right)=\dots =Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },y)\right).\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$$

Hence, $Lz\left(\mathcal{V}(\alpha ,l,x)\right)>Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },y)\right)$ for each $y\ge 2$. If $\mathsf{\Gamma }\in {\mathcal{V}}_{\mathbf{2}}$ is other than ${\mathcal{V}}^{\prime }(\alpha ,l^{\prime },y)$, then by applying the transformation of the addition and deletion of an edge, we have $\mathsf{\Gamma }\cong {\mathcal{V}}^{\prime }(\alpha ,l^{\prime },y).$ Then by Theorem 1 (ii) and Lemma 2, we have $Lz\left(\mathcal{V}(\alpha ,l,x)\right)>Lz\left({\mathcal{V}}^{\prime }(\alpha ,l^{\prime },y)\right)$. Therefore, $Lz\left(\mathcal{V}\right(\alpha ,l,x\left)\right)>\mathsf{\Gamma }$ for each $\mathsf{\Gamma }\in {\mathcal{V}}_{\mathbf{2}}.$

Case 3: If $\mathsf{\Gamma }\in {\mathcal{V}}_{\mathbf{3}}$, then we have the following possibilities. (i) By applying the transformations of the addition and deletion of the edges, we have ${\mathsf{\Gamma }}^{*}\in {\mathcal{V}}_{\mathbf{1}}$ or ${\mathsf{\Gamma }}^{*}\in {\mathcal{V}}_{\mathbf{2}}$, such that $Lz\left({\mathsf{\Gamma }}^{*}\right)\ge Lz\left(\mathsf{\Gamma }\right)$ by using Lemma 2. (ii) There exists ${\mathsf{\Gamma }}^{*}\in {\mathsf{\Gamma }}_1\cup {\mathsf{\Gamma }}_2$, $\mathsf{\Gamma }$, and ${\mathsf{\Gamma }}^{*}$, which have the same degree sequence. Then, with the help of Lemma 2(i), $Lz\left(\mathsf{\Gamma }\right)=Lz\left({\mathsf{\Gamma }}^{*}\right)$; eventually, we proved the above result with the help of case (i) and case (ii).

From the above cases, $Lz\left(\mathcal{V}\right(\alpha ,l,x\left)\right)\ge Lz\left(\mathsf{\Gamma }\right)$ for every $\mathsf{\Gamma }\in {\mathcal{V}}_{\alpha }^{\beta }.$

(b) The proof was done on the same pattern as in the above part (a) using Theorem 1 and Lemmas 2. □

Theorem 3. 

Let ${\mathcal{V}}_{\alpha }^{\beta }$ be a class of unicyclic graphs in such a way that every graph has α order and β leaves. Then,

$$4\alpha (\alpha -3)-{\beta }^2(\beta +7)-\beta (6-\alpha \beta )+\alpha \beta \le Lz\left(\mathsf{\Gamma }\right)\le 2(\alpha \beta +2{\alpha }^2-7\beta -6\alpha )$$

for each $\mathsf{\Gamma }\in {\mathcal{V}}_{\alpha }^{\beta }$, where the upper bound is obtained if and only if $\mathsf{\Gamma }\cong \mathcal{V}(\alpha ,1,x)$ and the lower bound is obtained if and only if $\mathsf{\Gamma }\cong \mathcal{V}(\alpha ,l,1).$

Proof. 

With the help of Corollary 1, we have $Lz\left(\mathcal{V}(\alpha ,l,1)\right)=4\alpha (\alpha -3)-{\beta }^2(\beta +7)-\beta (6-\alpha \beta )+\alpha \beta$ and $Lz\left(\mathcal{V}\right(\alpha ,1,x\left)\right)$$=2(\alpha \beta +2{\alpha }^2-7\beta -6\alpha )$ for $\beta =lx$ leaves. Furthermore, with the help of Theorem 2, (a) $Lz\left(\mathcal{V}\right(\alpha ,l,x\left)\right)\ge Lz\left(\mathsf{\Gamma }\right)$ implies that $Lz\left(\mathcal{V}\right(\alpha ,1,x\left)\right)\ge Lz\left(\mathcal{V}\right(\alpha ,l,x\left)\right)\ge Lz\left(\mathsf{\Gamma }\right)$ and $Lz\left(\mathsf{\Gamma }\right)\ge Lz\left(\mathcal{V}\right(\alpha ,l,1\left)\right)$ for each ${\mathcal{V}}_{\alpha }^{\beta }$ Therefore, we obtain

$$4\alpha (\alpha -3)-{\beta }^2(\beta +7)-\beta (6-\alpha \beta )+\alpha \beta \le Lz\left(\mathsf{\Gamma }\right)\le 2(\alpha \beta +2{\alpha }^2-7\beta -6\alpha )$$

for each $\mathsf{\Gamma }\in {\mathcal{V}}_{\alpha }^{\beta }$. Furthermore, the upper bound is obtained if and only if $\mathsf{\Gamma }\cong \mathcal{V}(\alpha ,1,x)$ and the lower bound is obtained if and only if $\mathsf{\Gamma }\cong \mathcal{V}(\alpha ,l,1).$ □

4. Conclusions

In this article, we computed the Lz index for each graph that belonged to the class of unicyclic graphs with fixed pendent vertices. Moreover, we characterized the extremal graphs with respect to the Lz index in the same class of graphs. For the illustration of the obtained results, we presented the exact values of the Lz index (obtained by the definition) and bounded values of the Lz index (using Theorem 3) for some unicyclic graphs in

Table 3. The values of the Lz index for unicyclic graphs.

$\mathcal{V}(\alpha ,l,x)$	Exact value of Lz index	Lower Bound of Lz index	Upper Bound of Lz index
$\mathcal{V}(8,2,2)$	$152$	$120$	$168$
$\mathcal{V}(6,1,3)$	$66$	$36$	$66$
$\mathcal{V}(10,2,1)$	$220$	$216$	$292$
$\mathcal{V}(11,3,2)$	$400$	$310$	$400$

. This table shows that the exact values fall within our established bounds.

Open Problem: Investigate the lower and upper bounds of the Lz index for the classes of bicyclic and tricyclic graphs with fixed pendent vertices.