A Biomechanical Comparison of Three 1.5-mm Plate and Screw Configurations and a Single 2.0-mm Plate for Internal Fixation of a Mandibular Condylar Fracture
Abstract
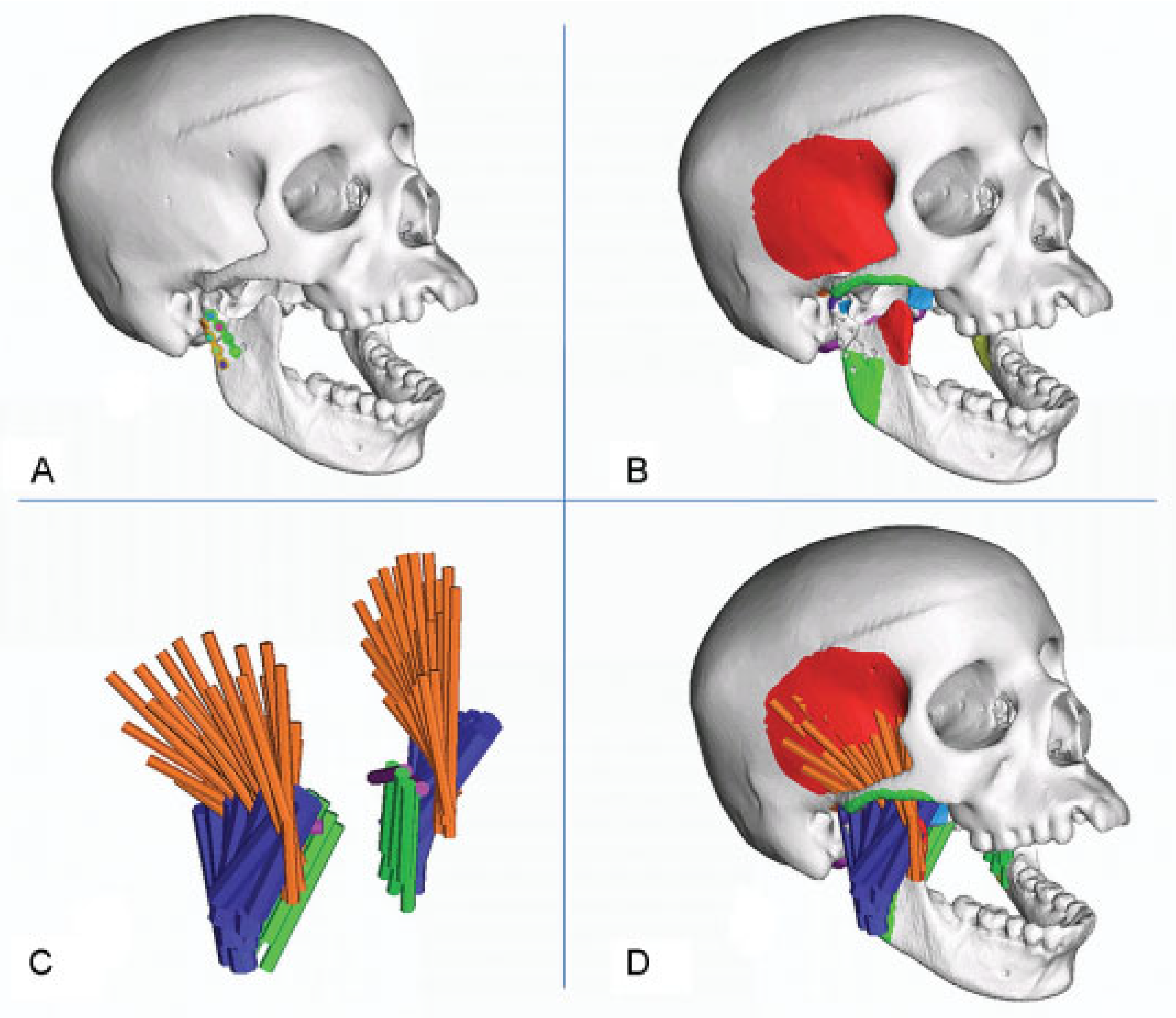
:Materials and Methods
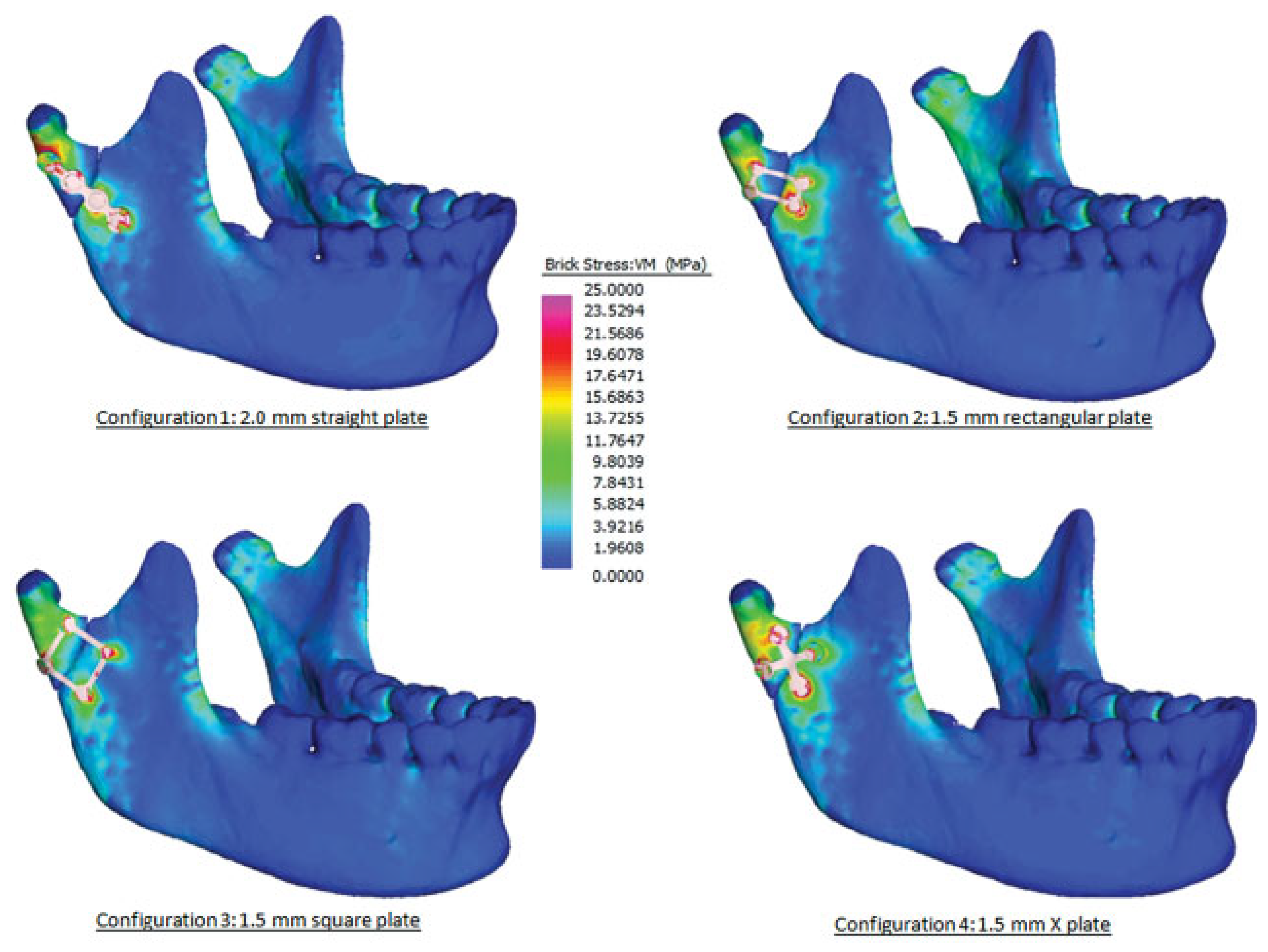
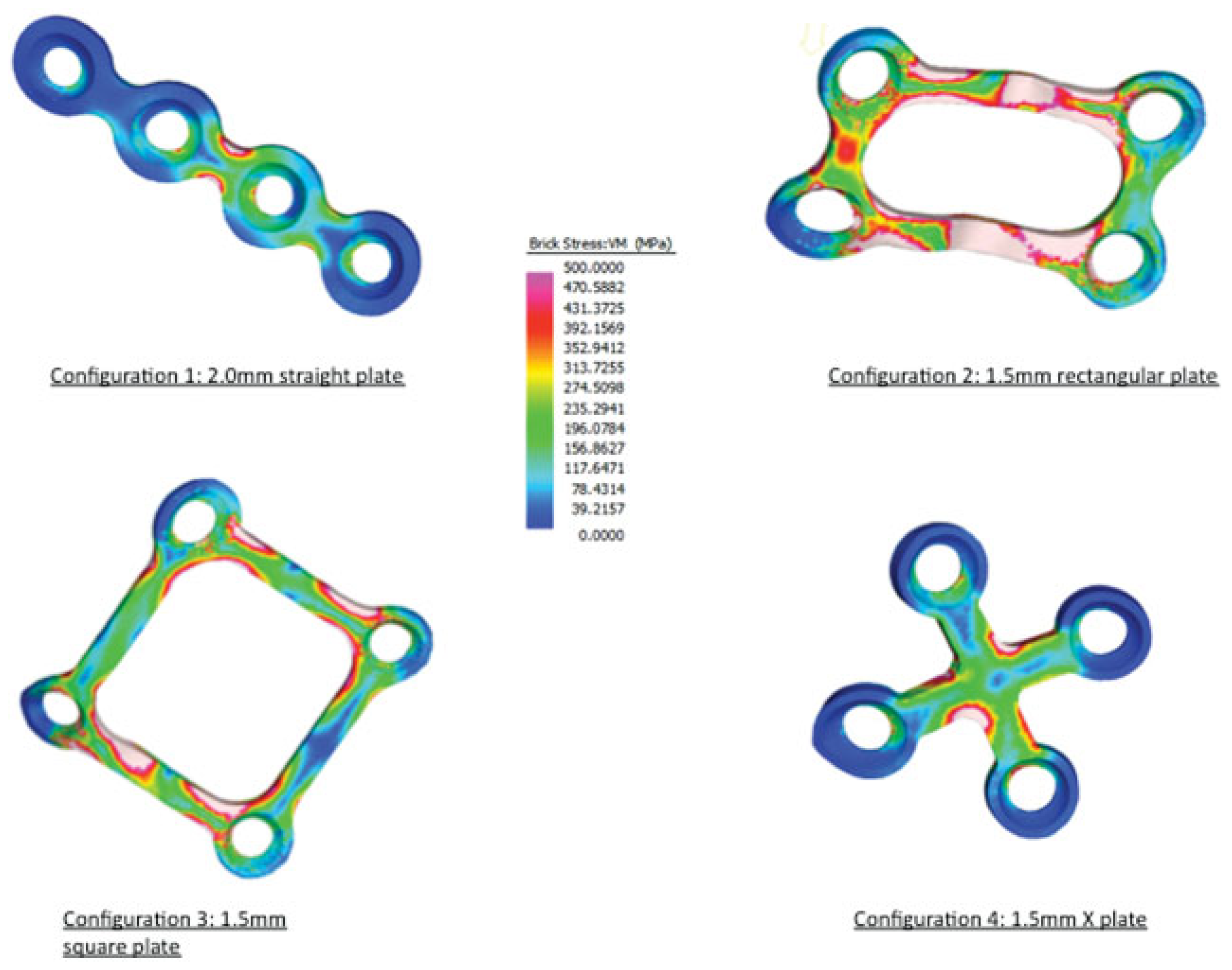
Results
Discussion
Acknowledgments
References
- Bochlogyros, P.N. A retrospective study of 1,521 mandibular fractures. J Oral Maxillofac Surg 1985, 43, 597–599. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Galil, K.; Loukota, R. Fractures of the mandibular condyle: evidence base and current concepts of management. Br J Oral Maxillofac Surg 2010, 48, 520–526. [Google Scholar] [CrossRef]
- Park, J.M.; Jang, Y.W.; Kim, S.G.; et al. Comparative study of the prognosis of an extracorporeal reduction and a closed treatment in mandibular condyle head and/or neck fractures. J Oral Maxillofac Surg 2010, 68, 2986–2993. [Google Scholar] [CrossRef] [PubMed]
- Danda, A.K.; Muthusekhar, M.R.; Narayanan, V.; Baig, M.F.; Siddareddi, A. Open versus closed treatment of unilateral subcondylar and condylar neck fractures: a prospective, randomized clinical study. J Oral Maxillofac Surg 2010, 68, 1238–1241. [Google Scholar] [CrossRef]
- Schneider, M.; Erasmus, F.; Gerlach, K.L.; et al. Open reduction and internal fixation versus closed treatment and mandibulomaxillary fixation of fractures of the mandibular condylar process: a randomized, prospective, multicenter study with special evaluation of fracture level. J Oral Maxillofac Surg 2008, 66, 2537–2544. [Google Scholar] [CrossRef] [PubMed]
- Alkan, A.; Metin, M.; Muğlali, M.; Ozden, B.; Celebi, N. Biomechanical comparison of plating techniques for fractures of the mandibular condyle. Br J Oral Maxillofac Surg 2007, 45, 145–149. [Google Scholar] [CrossRef]
- Choi, B.; Kim, K.; Kim, H.; Kim, M. An In vitro evaluation of condylar neck fracture plating techniques. Int J Oral Maxillofac Surg 1999, 28 (Suppl. S1), 78–78. [Google Scholar] [CrossRef]
- Choi, B.-H.; Kim, K.-N.; Kim, H.-J.; Kim, M.-K. Evaluation of condylar neck fracture plating techniques. J Craniomaxillofac Surg 1999, 27, 109–112. [Google Scholar] [CrossRef]
- Hammer, B.; Schier, P.; Prein, J. Osteosynthesis of condylar neck fractures: a review of 30 patients. Br J Oral Maxillofac Surg 1997, 35, 288–291. [Google Scholar] [CrossRef]
- Pilling, E.; Eckelt, U.; Loukota, R.; Schneider, K.; Stadlinger, B. Comparative evaluation of ten different condylar base fracture osteosynthesis techniques. Br J Oral Maxillofac Surg 2010, 48, 527–531. [Google Scholar] [CrossRef]
- Haug, R.H.; Peterson, G.P.; Goltz, M. A biomechanical evaluation of mandibular condyle fracture plating techniques. J Oral Maxillofac Surg 2002, 60, 73–80, discussion 80–81. [Google Scholar] [CrossRef]
- Aquilina, P.; Chamoli, U.; Parr, W.C.H.; Clausen, P.D.; Wroe, S. Finite element analysis of three patterns of internal fixation of fractures of the mandibular condyle. Br J Oral Maxillofac Surg 2013, 51, 326–331. [Google Scholar] [CrossRef] [PubMed]
- Rayfield, E.J. Finite element analysis and understanding the biomechanics and evolution of living and fossil organisms. Annu Rev Earth Planet Sci 2007, 35, 541–576. [Google Scholar] [CrossRef]
- Korioth, T.W.P.; Versluis, A. Modeling the mechanical behavior of the jaws and their related structures by finite element (FE) analysis. Crit Rev Oral Biol Med 1997, 8, 90–104. [Google Scholar] [CrossRef] [PubMed]
- Korioth, T.W.P.; Romilly, D.P.; Hannam, A.G. Three-dimensional finite element stress analysis of the dentate human mandible. Am J Phys Anthropol 1992, 88, 69–96. [Google Scholar] [CrossRef] [PubMed]
- Ross, C.F. Finite element analysis in vertebrate biomechanics. Anat Rec A Discov Mol Cell Evol Biol 2005, 283, 253–258. [Google Scholar] [CrossRef]
- van Eijden, T.M.G.J. Biomechanics of the mandible. Crit Rev Oral Biol Med 2000, 11, 123–136. [Google Scholar] [CrossRef]
- Fernández, J.R.; Gallas, M.; Burguera, M.; Viaño, J.M. A three-dimensional numerical simulation of mandible fracture reduction with screwed miniplates. J Biomech 2003, 36, 329–337. [Google Scholar] [CrossRef]
- Wagner, A.; Krach, W.; Schicho, K.; Undt, G.; Ploder, O.; Ewers, R. A 3-dimensional finite-element analysis investigating the biomechanical behavior of the mandible and plate osteosynthesis in cases of fractures of the condylar process. Oral Surg Oral Med Oral Pathol Oral Radiol Endod 2002, 94, 678–686. [Google Scholar] [CrossRef]
- Kimsal, J.; Baack, B.; Candelaria, L.; Khraishi, T.; Lovald, S. Biomechanical analysis of mandibular angle fractures. J Oral Maxillofac Surg 2011, 69, 3010–3014. [Google Scholar] [CrossRef]
- Lovald, S.T.; Khraishi, T.; Wagner, J.; Baack, B.; Kelly, J.; Wood, J. Comparison of plate-screw systems used in mandibular fracture reduction: finite element analysis. J Biomech Eng 2006, 128, 654–662. [Google Scholar] [CrossRef] [PubMed]
- Lovald, S.T.; Wagner, J.D.; Baack, B. Biomechanical optimization of bone plates used in rigid fixation of mandibular fractures. J Oral Maxillofac Surg 2009, 67, 973–985. [Google Scholar] [CrossRef] [PubMed]
- Arbag, H.; Korkmaz, H.H.; Ozturk, K.; Uyar, Y. Comparative evaluation of different miniplates for internal fixation of mandible fractures using finite element analysis. J Oral Maxillofac Surg 2008, 66, 1225–1232. [Google Scholar] [CrossRef]
- Cox, T.; Kohn, M.W.; Impelluso, T. Computerized analysis of resorbable polymer plates and screws for the rigid fixation of mandibular angle fractures. J Oral Maxillofac Surg 2003, 61, 481–487, discussion 487–488. [Google Scholar] [CrossRef]
- Tams, J.; Van Loon, J.-P.; Otten, B.; Bos, R.R.M. A computer study of biodegradable plates for internal fixation of mandibular angle fractures. J Oral Maxillofac Surg 2001, 59, 404–407, discussion 407–408. [Google Scholar] [CrossRef]
- Trabelsi, N.; Yosibash, Z.; Wutte, C.; Augat, P.; Eberle, S. Patient-specific finite element analysis of the human femur—a double-blinded biomechanical validation. J Biomech 2011, 44, 1666–1672. [Google Scholar] [CrossRef]
- Wroe, S.; Moreno, K.; Clausen, P.; McHenry, C.; Curnoe, D. High-resolution three-dimensional computer simulation of hominid cranial mechanics. Anat Rec (Hoboken) 2007, 290, 1248–1255. [Google Scholar] [CrossRef] [PubMed]
- Thomason, J.J. Cranial strength in relation to estimated biting forces in some mammals. Can J Zool 1991, 69, 2326–2333. [Google Scholar] [CrossRef]
- Parr, W.C.H.; Wroe, S.; Chamoli, U.; et al. Toward integration of geometric morphometrics and computational biomechanics: new methods for 3D virtual reconstruction and quantitative analysis of finite element models. J Theor Biol 2012, 301, 1–14. [Google Scholar] [CrossRef]
- McHenry, C.R.; Wroe, S.; Clausen, P.D.; Moreno, K.; Cunningham, E. Supermodeled sabercat, predatory behavior in Smilodon fatalis revealed by high-resolution 3D computer simulation. Proc Natl Acad Sci U S A 2007, 104, 16010–16015. [Google Scholar] [CrossRef]
- Søballe, K. Hydroxyapatite ceramic coating for bone implant fixation. Mechanical and histological studies in dogs. Acta Orthop Scand Suppl 1993, 255, 1–58. [Google Scholar] [CrossRef]
- Seemann, R.; Frerich, B.; Müller, S.; et al. Comparison of locking and nonlocking plates in the treatment of mandibular condyle fractures. Oral Surg Oral Med Oral Pathol Oral Radiol Endod 2009, 108, 328–334. [Google Scholar] [CrossRef] [PubMed]
- Lauer, G.; Haim, D.; Proff, P.; et al. Plate osteosynthesis of the mandibular condyle. Ann Anat 2007, 189, 412–417. [Google Scholar] [CrossRef] [PubMed]
- Shinohara, E.H.; Martini, M.Z. ’Double barrel’ 2.0mm mini-plates to fix fractures of the neck of the mandibular condyle. Br J Oral Maxillofac Surg 2006, 44, 166–166. [Google Scholar] [CrossRef] [PubMed]
- Choi, B.H.; Yi, C.K.; Yoo, J.H. Clinical evaluation of 3 types of plate osteosynthesis for fixation of condylar neck fractures. J Oral Maxillofac Surg 2001, 59, 734–737, discussion 738. [Google Scholar] [CrossRef]
- Parascandolo, S.; Spinzia, A.; Parascandolo, S.; Piombino, P.; Califano, L. Two load sharing plates fixation in mandibular condylar fractures: biomechanical basis. J Craniomaxillofac Surg 2010, 38, 385–390. [Google Scholar] [CrossRef]
- Ichim, I.; Kieser, J.A.; Swain, M.V. Functional significance of strain distribution in the human mandible under masticatory load: numerical predictions. Arch Oral Biol 2007, 52, 465–473. [Google Scholar] [CrossRef]
- Vollmer, D.; Meyer, U.; Joos, U.; Vègh, A.; Piffko, J. Experimental and finite element study of a human mandible. J Craniomaxillofac Surg 2000, 28, 91–96. [Google Scholar] [CrossRef]
- Haug, R.H.; Brandt, M.T. Closed reduction, open reduction, and endoscopic assistance: current thoughts on the management of mandibular condyle fractures. Plast Reconstr Surg 2007, 120 (Suppl. S2), 90S–102S. [Google Scholar] [CrossRef]
- Asprino, L.; Consani, S.; de Moraes, M. A comparative biomechanical evaluation of mandibular condyle fracture plating techniques. J Oral Maxillofac Surg 2006, 64, 452–456. [Google Scholar] [CrossRef]
| Number of truss elements on one side | Force/truss (N) | Truss diameter (mm) | Young modulus (MPa) | Density (T/mm3) | |
|---|---|---|---|---|---|
| Medial pterygoid | 6 | 3 | 5 | 0.1 | 1 × 10−09 |
| Lateral pterygoid | 2 | 3 | 5 | 0.1 | 1 × 10−09 |
| Masseter | 11 | 17.91 | 8.72 | 0.1 | 1 × 10−09 |
| Temporalis | 31 | 3.58 | 3.90 | 0.1 | 1 × 10−09 |
| Brick material properties | Young modulus (MPa) | Density (T/mm3) |
|---|---|---|
| Material 1 | 1,527 | 2.508 × 10−10 |
| Material 2 | 1,868.6 | 2.916 × 10−10 |
| Material 3 | 2,223.4 | 3.325 × 10−10 |
| Material 4 | 10,786.8 | 1.094 × 10−09 |
| Material 5 | 21,734.2 | 1.855 × 10−09 |
| Material 6 | 27,082.2 | 2.190 × 10−09 |
| Material 7 | 32,704.3 | 2.525 × 10−09 |
| Material 8 | 38,575.4 | 2.860 × 10−09 |
| Relative movement, μm (SD) | Volume-weighted mean VM stress | Plate volume (mm3) | |
|---|---|---|---|
| Straight plate | 113.9 (54.3) | 78.7 | 64.4 |
| Rectangular plate | 330.9 (42.4) | 312.6 | 21.0 |
| Square plate | 269.0 (6.86) | 198.8 | 28.6 |
| X plate | 115.8 (65.6) | 119.0 | 44.8 |
© 2014 by the author. The Author(s) 2014.
Share and Cite
Aquilina, P.; Parr, W.C.H.; Chamoli, U.; Wroe, S.; Clausen, P. A Biomechanical Comparison of Three 1.5-mm Plate and Screw Configurations and a Single 2.0-mm Plate for Internal Fixation of a Mandibular Condylar Fracture. Craniomaxillofac. Trauma Reconstr. 2014, 7, 218-223. https://doi.org/10.1055/s-0034-1375172
Aquilina P, Parr WCH, Chamoli U, Wroe S, Clausen P. A Biomechanical Comparison of Three 1.5-mm Plate and Screw Configurations and a Single 2.0-mm Plate for Internal Fixation of a Mandibular Condylar Fracture. Craniomaxillofacial Trauma & Reconstruction. 2014; 7(3):218-223. https://doi.org/10.1055/s-0034-1375172
Chicago/Turabian StyleAquilina, Peter, William C.H. Parr, Uphar Chamoli, Stephen Wroe, and Philip Clausen. 2014. "A Biomechanical Comparison of Three 1.5-mm Plate and Screw Configurations and a Single 2.0-mm Plate for Internal Fixation of a Mandibular Condylar Fracture" Craniomaxillofacial Trauma & Reconstruction 7, no. 3: 218-223. https://doi.org/10.1055/s-0034-1375172
APA StyleAquilina, P., Parr, W. C. H., Chamoli, U., Wroe, S., & Clausen, P. (2014). A Biomechanical Comparison of Three 1.5-mm Plate and Screw Configurations and a Single 2.0-mm Plate for Internal Fixation of a Mandibular Condylar Fracture. Craniomaxillofacial Trauma & Reconstruction, 7(3), 218-223. https://doi.org/10.1055/s-0034-1375172



