Mathematical Modeling of Vessel Geometry and Circumference in Microvascular Surgery
Abstract
:Introduction
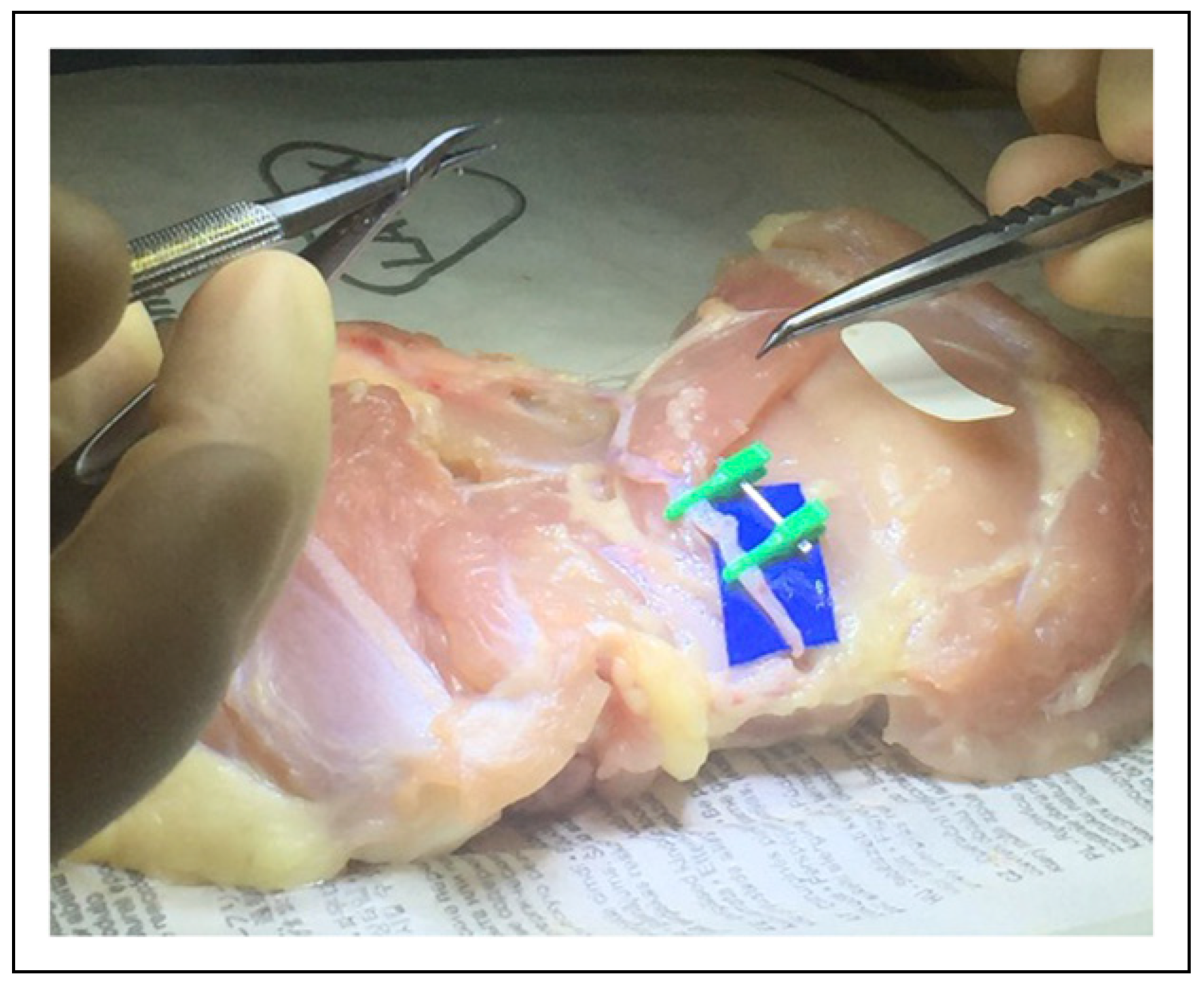
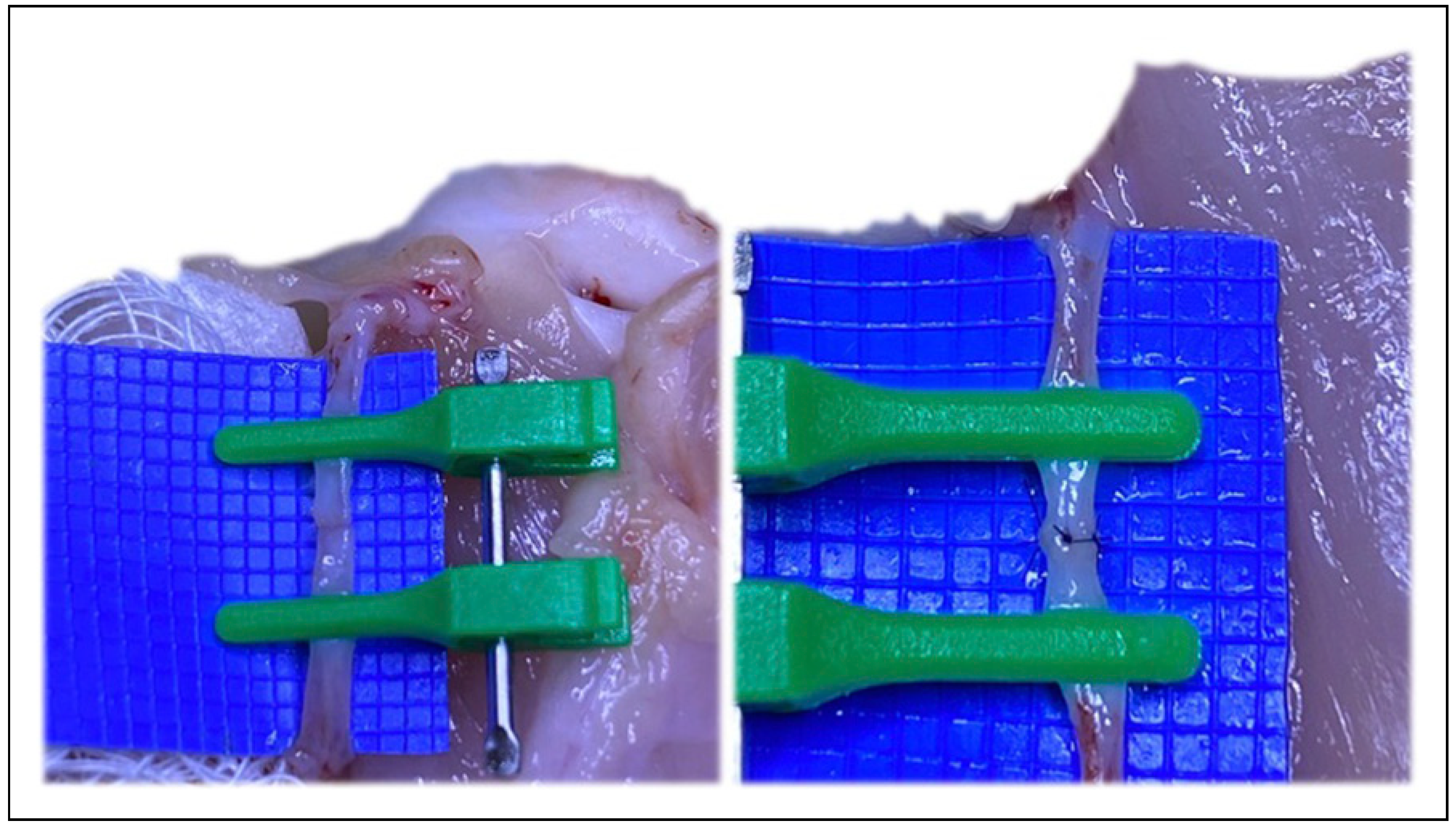
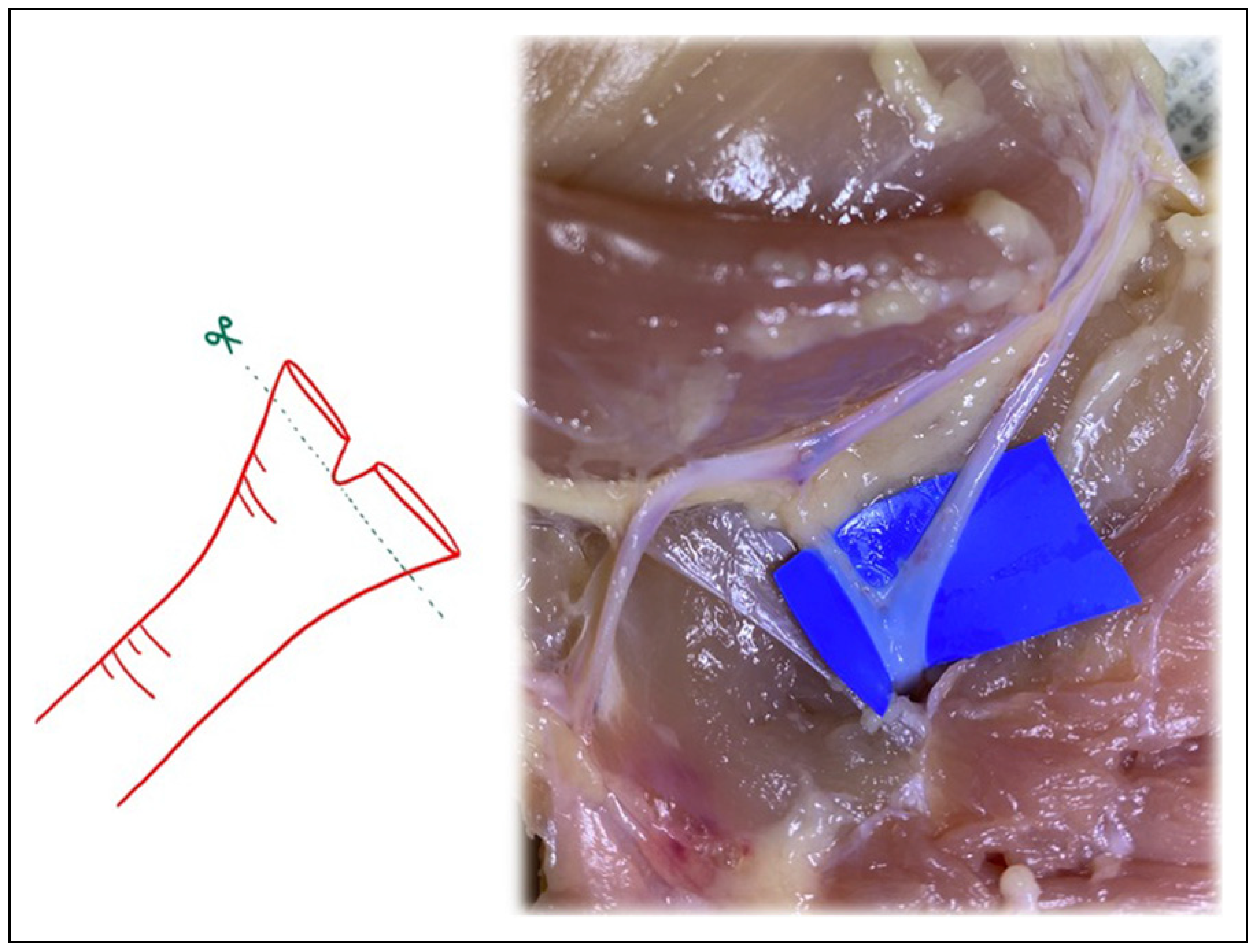
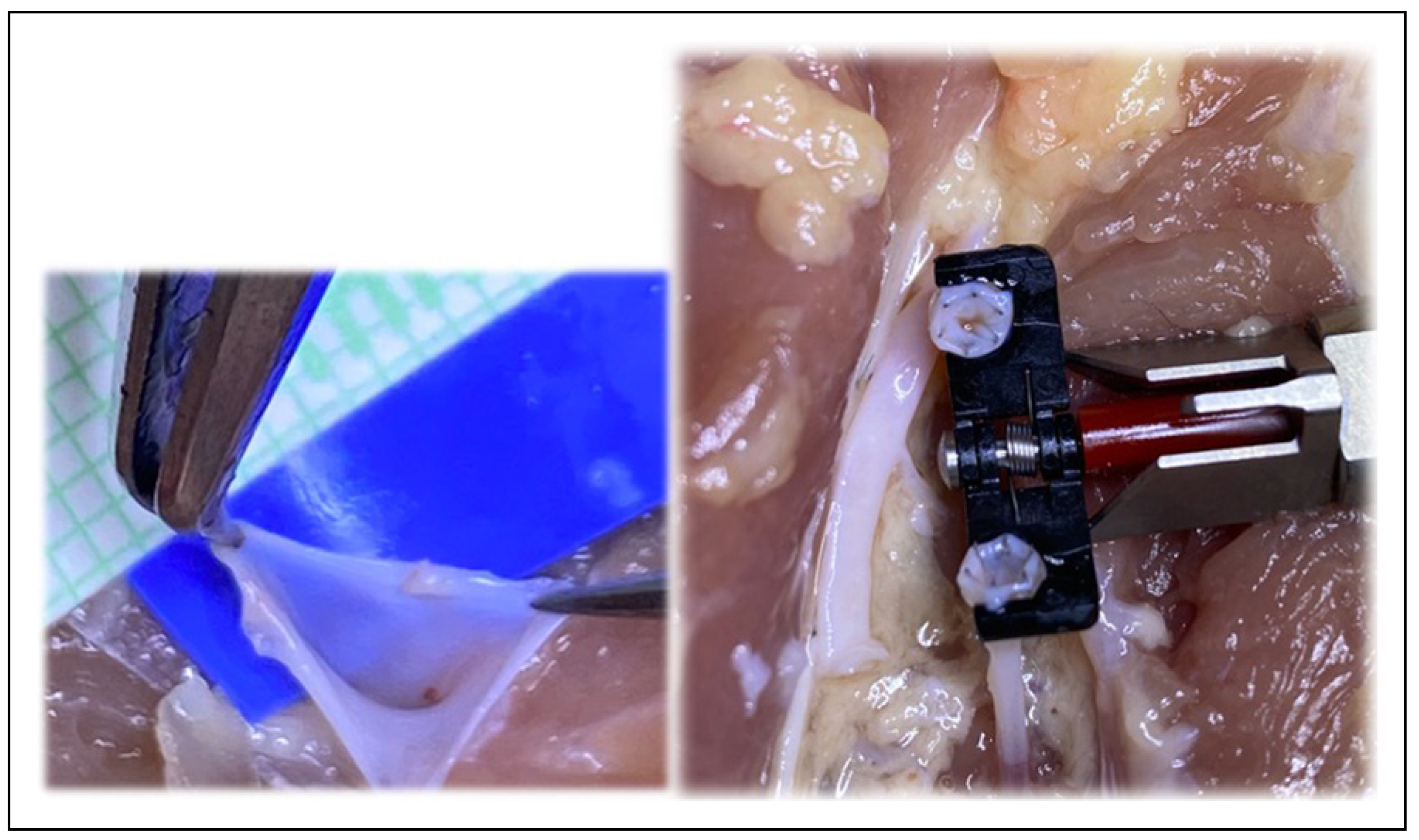
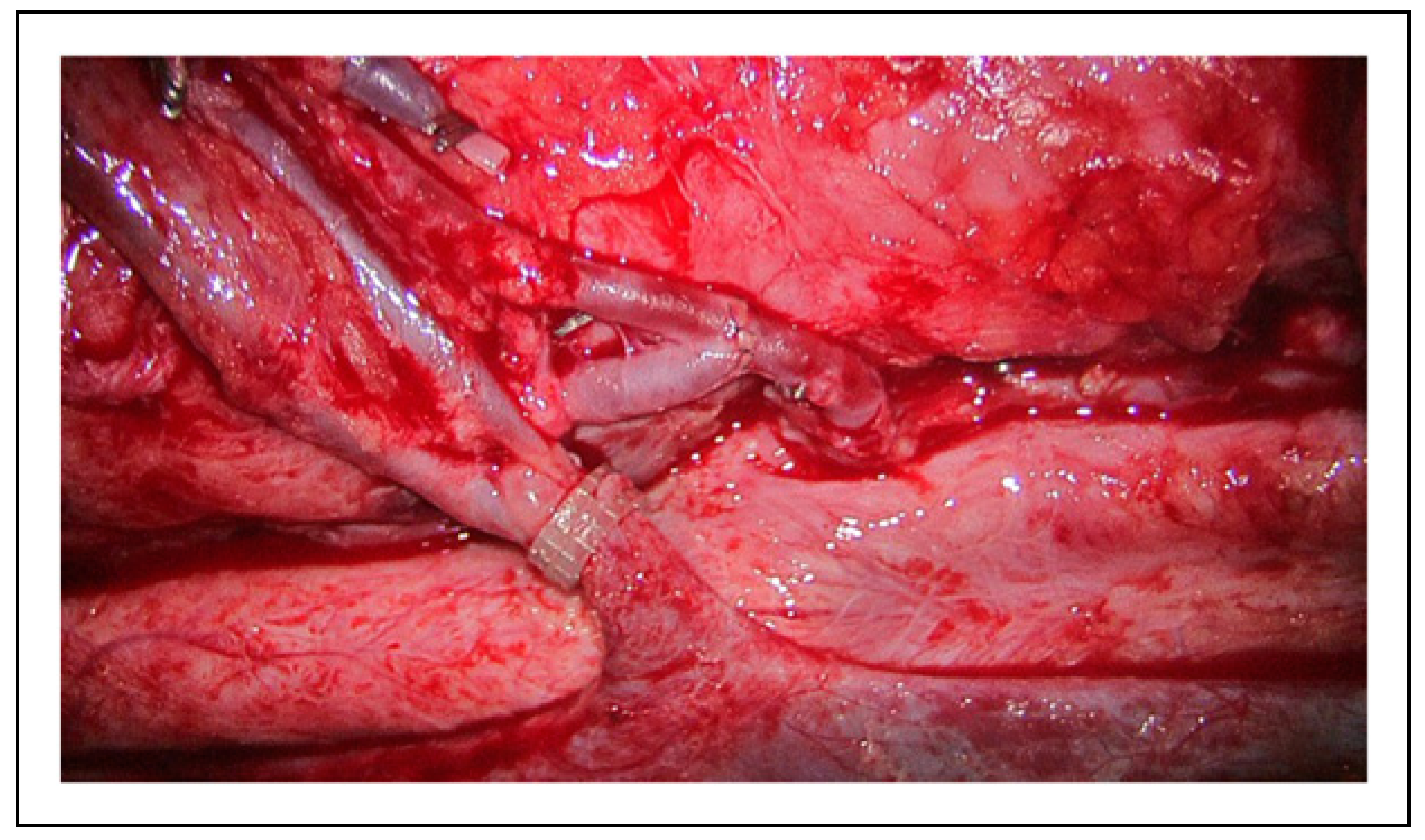
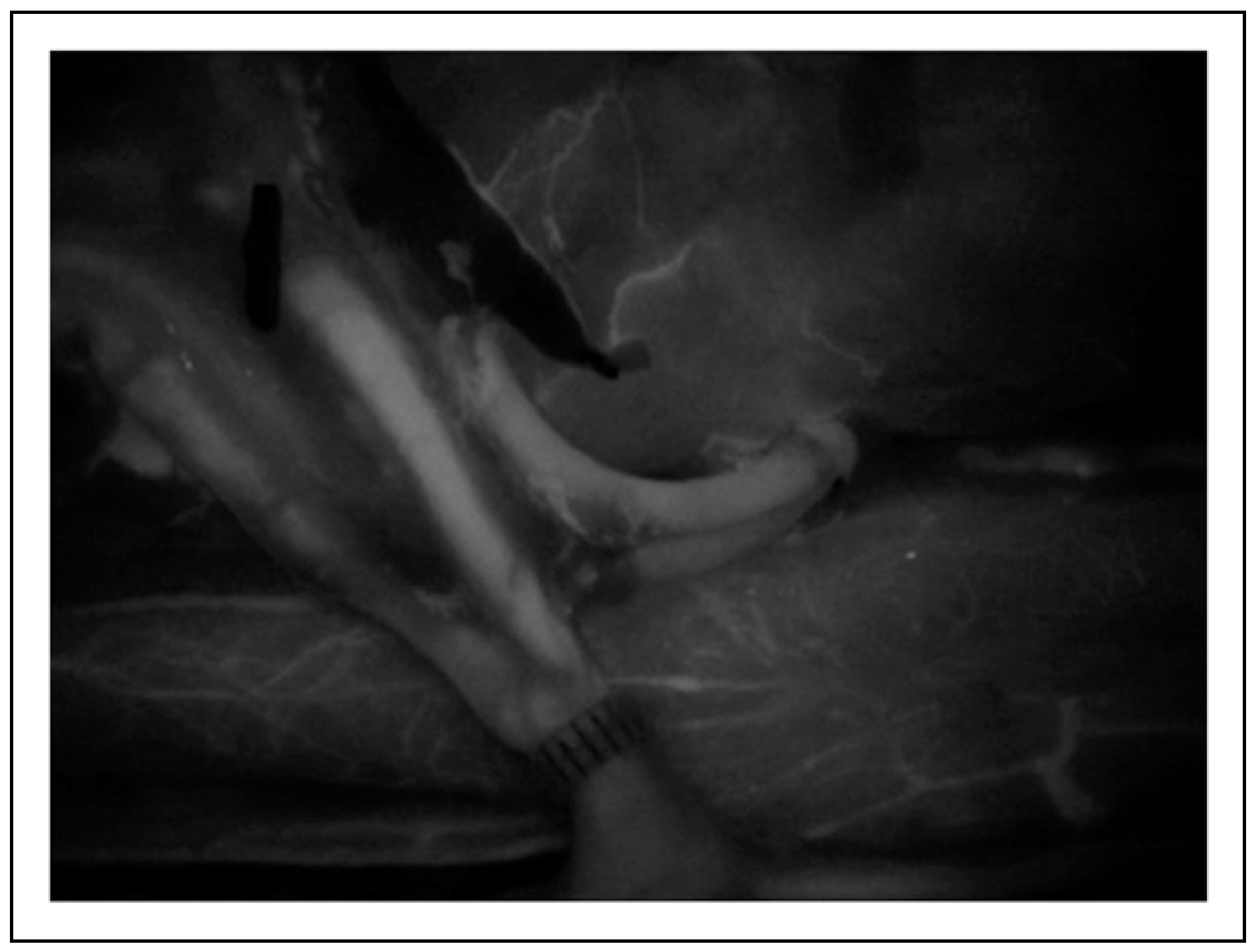
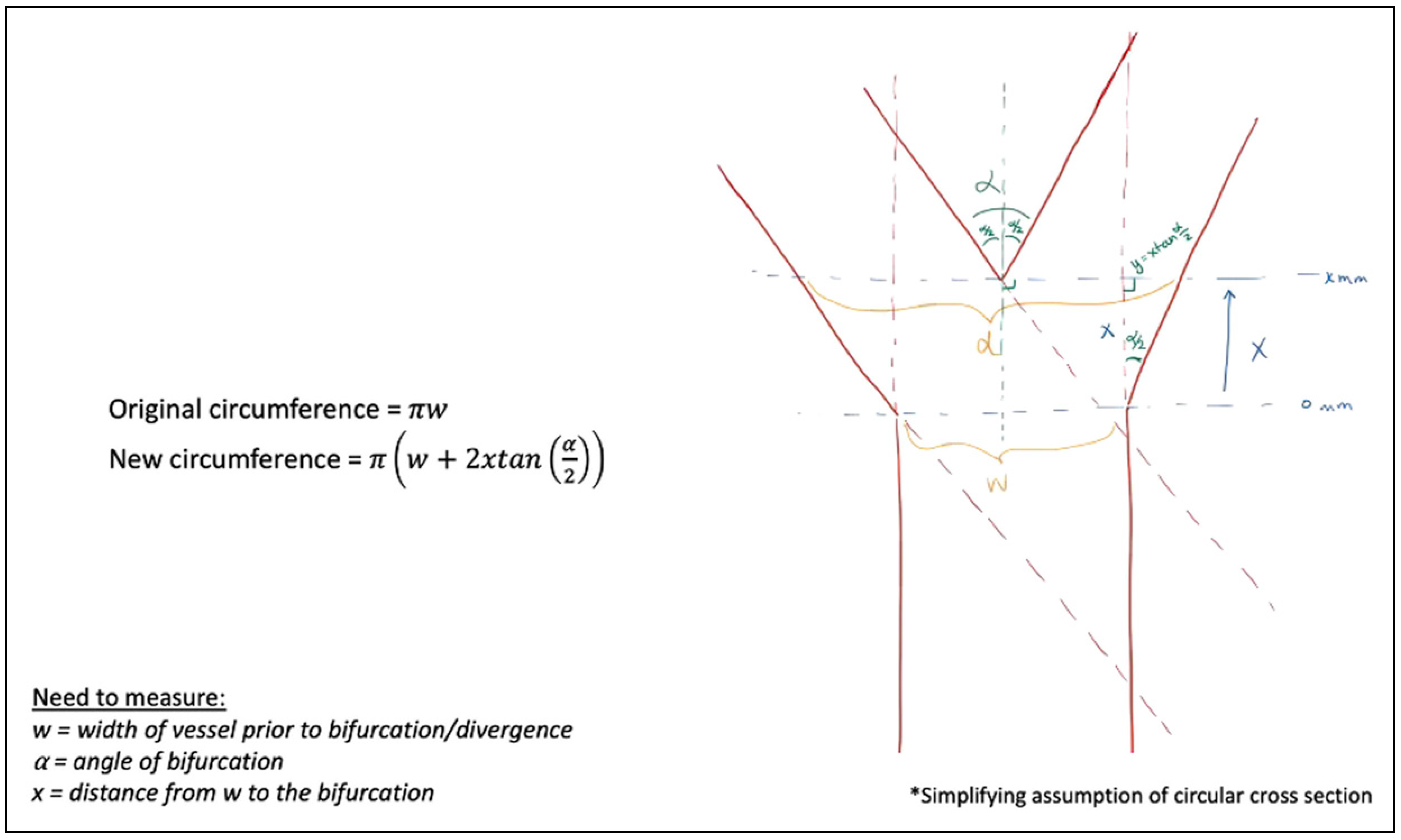
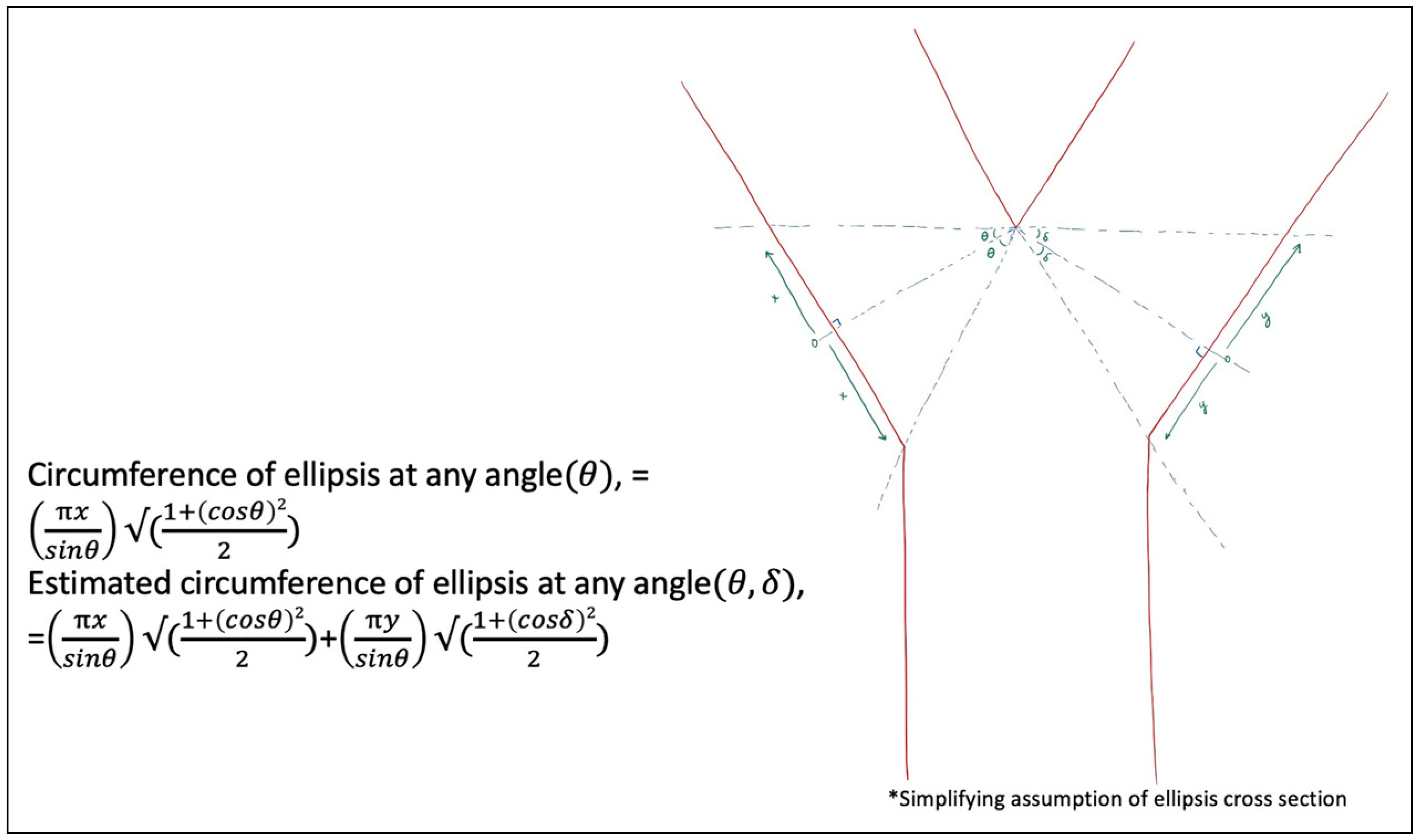
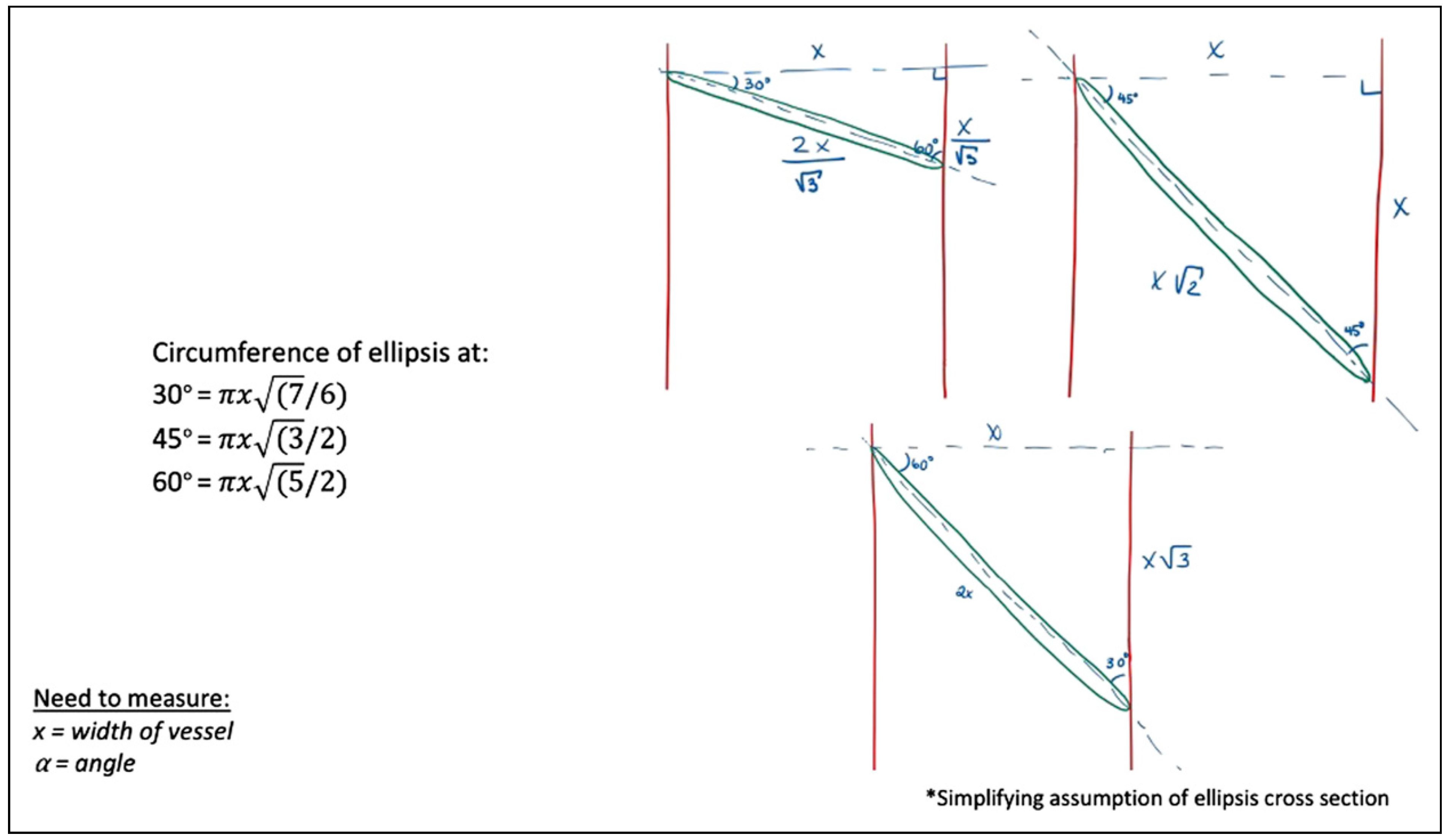
Materials and Methods
Results
Discussion
Conclusion
Author’s Note
Author Contributions
Funding
Consent
Conflicts of Interest
References
- Akan, M.; Cakir, B.; Aköz, T. “Open Y” technique in vessel diameter discrepancy. Microsurgery 2006, 26, 506–514. [Google Scholar] [CrossRef] [PubMed]
- Akan, M.; Cakir, B.; Aköz, T. Increasing vessel diameter with the open Y technique for diameter discrepancy. J. Reconstr. Microsurg. 2004, 20, 651–657. [Google Scholar] [CrossRef] [PubMed]
- Akan, M.; Cakir, B.; Gideroglu, K.; Aköz, T.; Kavurmacioglu, L. End-to-side anastomosis with “Open-Y” technique on small vessels to increase patency and facilitate anastomosis. J. Craniofac Surg. 2009, 20, 2226–2229. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-C.; Scaglioni, M.F.; Huang, E.-Y.; Kuo, Y.-R. Utility of “open-Y” anastomosis technique in the use of superior thyroid artery as recipient vessel for head and neck reconstruction with free flap. Microsurgery 2016, 36, 391–396. [Google Scholar] [CrossRef]
- Sabapathy, S.R. Vessels. In Flaps and Reconstructive Surgery, 2nd ed.; Wei, F.-C., Mardini, S., Eds.; Elsevier: London, NY, 2017; pp. 310–322. [Google Scholar]
- Chia, H.-L.; Wong, C.-H.; Tan, B.-K.; Tan, K.-C.; Ong, Y.-S. An algorithm for recipient vessel selection in microsurgical head and neck reconstruction. J. Reconstr. Microsurg. 2011, 27, 047–056. [Google Scholar] [CrossRef]
- López-Monjardin, H.; de la Peña-Salcedo, J.A. Techniques for management of size discrepancies in microvascular anastomosis. Microsurgery 2000, 20, 162–166. [Google Scholar] [CrossRef] [PubMed]
- Scaglioni, M.F.; Meroni, M.; Fritsche, E. Application of the “Open-Y” technique in recipient perforator vessels: A comparison study between“ Open-Y” and conventional end-to-end anastomosis in terms of postoperative complications. Microsurgery 2021, 41, 527–532. [Google Scholar] [CrossRef]
- Wain, R.A.J.; Whitty, J.P.M.; Dalal, M.D.; Holmes, M.C.; Ahmed, W. Blood flow through sutured and coupled microvascular anastomoses: A comparative computational study. J. Plast. Reconstr. Aesthetic Surg. 2014, 67, 951–959. [Google Scholar] [CrossRef]
- Monsivais, J.J. Microvascular grafts: Effect of diameter discrepancy on patency rates. Microsurgery 1990, 11, 285–287. [Google Scholar] [CrossRef]
- Xiu, Z.F.; Song, Y.G. A new technique to anastomose vessels with great discrepancy in diameter. Br. J. Plast. Surg. 1993, 46, 619–620. [Google Scholar] [CrossRef]
- de la Peña-Salcedo, J.A.; Cuesy, C.; López-Monjardin, H. Experimental microvascular sleeve anastomosis in size discrepancy vessels. Microsurgery 2000, 20, 173–175. [Google Scholar] [CrossRef] [PubMed]
- Rickard, R.F.; Engelbrecht, G.H.C.; Hudson, D.A. Experimental investigation of two techniques of arterial microanastomosis used to manage a small-to-large diameter discrepancy. J. Plast. Reconstr. Aesthetic Surg. 2011, 64, 1088–1095. [Google Scholar] [CrossRef] [PubMed]
- Iida, T.; Yoshimatsu, H.; Yamamoto, T.; Koshima, I. A pilot study demonstrating the feasibility of supermicrosurgical end-to-side anastomosis onto large recipient vessels in head and neck reconstruction. J. Plast. Reconstr. Aesthetic Surg. 2016, 69, 1662–1668. [Google Scholar] [CrossRef]
- de la Peña-Salcedo, J.A.; López-Monjardin, H. Sleeve anastomosis in head and neck reconstruction. Microsurgery 2000, 20, 193–194. [Google Scholar] [CrossRef]
- Dibo, S.; Zgheib, E.; Papazian, N.; Bakhach, J. The V-Plasty: A novel microsurgical technique for anastomosis of vessels with marked size discrepancy. J. Reconstr. Microsurg. 2015, 32, 128–136. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.-H.; Wu, H.-J.; Ji, T.; Wang, K.; Gokavarapu, S.; Zhang, C.-P. Clinical application of an original vascular anastomosis: A clinical multicenter study. J. Oral Maxillofac. Surg. 2016, 74, 2288–2294. [Google Scholar] [CrossRef]
- Harashina, T.; Irigaray, A. Expansion of smaller vessel diameter by fish-mouth incision in microvascular anastomosis with marked size discrepancy. Plast. Reconstr. Surg. 1980, 65, 502–503. [Google Scholar] [CrossRef]
- Mohammad, M.; Adjei, B.; George, S.; et al. Microsurgery and vessel caliber mismatch: A review of microsurgery anastomosis techniques to over- come vessel diameter discrepancy. J. Orthoplastic Surg. 2020, 3, 87–95. [Google Scholar]
- Boeckx, W.; de Lorenzi, F.; van der Hulst, R. Increasing the flow output by Y-Shaped microvascular anastomosis. J. Reconstr. Microsurg. 2002, 18, 381–386. [Google Scholar] [CrossRef]
- Albertiengo, J.B.; Rodriguez, A.; Buncke, H.J.; Hall, E.J. A comparative study of flap survival rates in end-to-end and end-to-side microvascular anastomosis. Plast. Reconstr. Surg. 1981, 67, 194–199. [Google Scholar]
- Samaha, F.J.; Oliva, A.; Buncke, G.M.; Buncke, H.J.; Siko, P.P. A clinical study of end-to-end versus end-to-side techniques for microvascular anastomosis. Plast. Reconstr. Surg. 1997, 99, 1109–1111. [Google Scholar] [CrossRef] [PubMed]
- Godina, M. Preferential use of end-to-side arterial anastomoses in free flap transfers. Plast. Reconstr. Surg. 1979, 64, 673–682. [Google Scholar] [CrossRef]
- Karanasiou, G.S.; Gatsios, D.A.; Lykissas, M.G.; Stefanou, K.A.; Rigas, G.A.; Lagaris, I.E.; et al. Modeling of blood flow through sutured micro-vascular anastomoses. In Proceedings of the 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015. [Google Scholar] [CrossRef]
- Wain, R.A.; Gaskell, N.J.; Fsadni, A.M.; Francis, J.; Whitty, J.P. Finite element predictions of sutured and coupled microarterial anastomoses. Adv. Biomed. Eng. 2019, 8, 63–77. [Google Scholar] [CrossRef]
- Zakaria, H.; Robertson, A.M.; Kerber, C.W. A parametric model for studies of flow in Arterial Bifurcations. Ann. Biomed. Eng. 2008, 36, 1515–1530. [Google Scholar] [CrossRef] [PubMed]





© 2022 by the authors. Multimed Inc.
Share and Cite
Nedrud, S.; Fleissig, Y.; Sanjuan-Sanjuan, A.; Bunnell, A.; Fernandes, R. Mathematical Modeling of Vessel Geometry and Circumference in Microvascular Surgery. Craniomaxillofac. Trauma Reconstr. 2023, 16, 195-204. https://doi.org/10.1177/19433875221097252
Nedrud S, Fleissig Y, Sanjuan-Sanjuan A, Bunnell A, Fernandes R. Mathematical Modeling of Vessel Geometry and Circumference in Microvascular Surgery. Craniomaxillofacial Trauma & Reconstruction. 2023; 16(3):195-204. https://doi.org/10.1177/19433875221097252
Chicago/Turabian StyleNedrud, Stacey, Yoram Fleissig, Alba Sanjuan-Sanjuan, Anthony Bunnell, and Rui Fernandes. 2023. "Mathematical Modeling of Vessel Geometry and Circumference in Microvascular Surgery" Craniomaxillofacial Trauma & Reconstruction 16, no. 3: 195-204. https://doi.org/10.1177/19433875221097252
APA StyleNedrud, S., Fleissig, Y., Sanjuan-Sanjuan, A., Bunnell, A., & Fernandes, R. (2023). Mathematical Modeling of Vessel Geometry and Circumference in Microvascular Surgery. Craniomaxillofacial Trauma & Reconstruction, 16(3), 195-204. https://doi.org/10.1177/19433875221097252



