Computer-Aided Fracture Size Measurement in Orbital Fractures—An Alternative to Manual Evaluation
Abstract
Introduction
Materials and Methods
Study Design
Study Variables
Manual Measurements
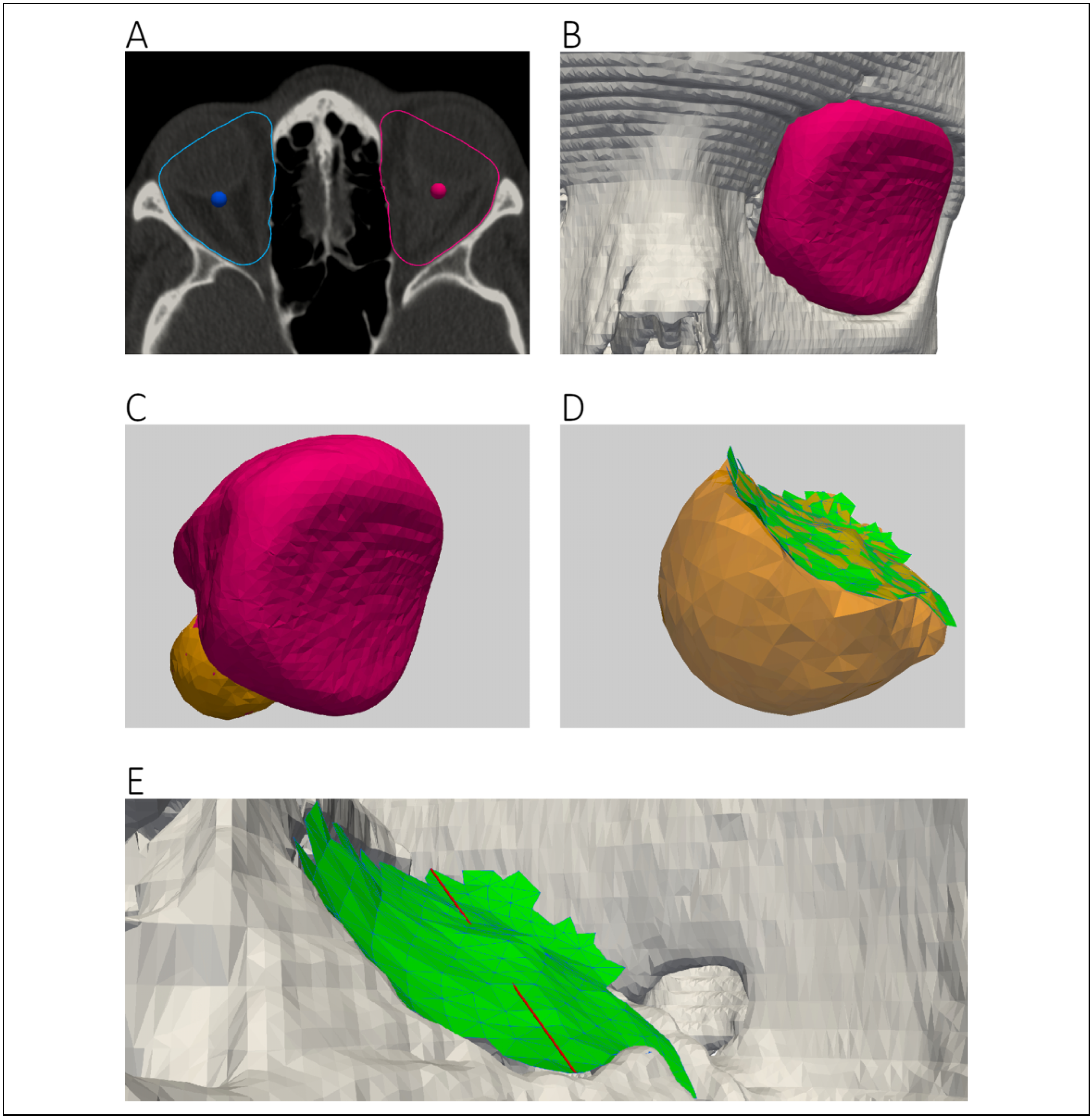
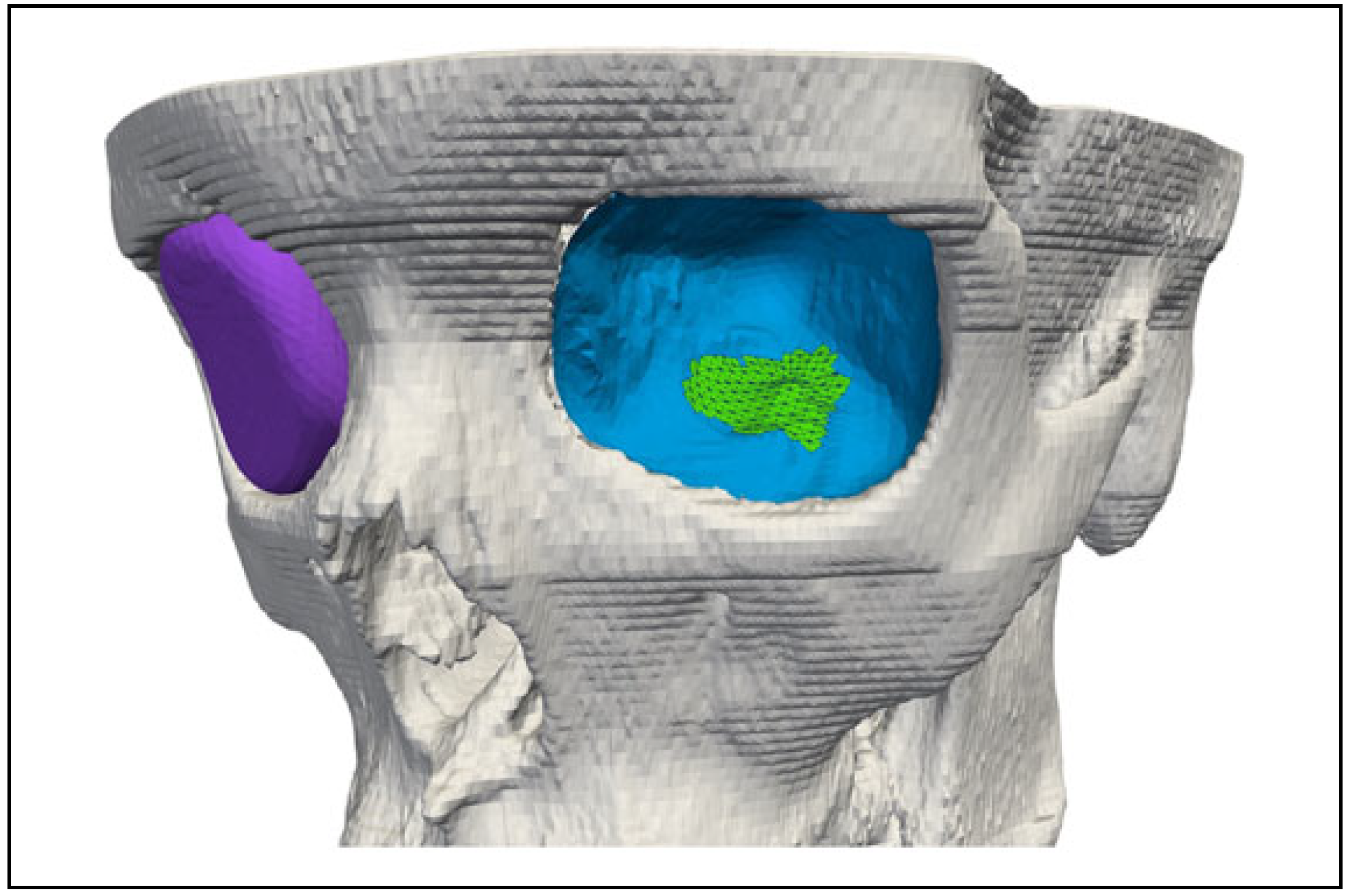
Semiautomatic Fracture Dimension Measurement and Workflow
Statistical Analysis
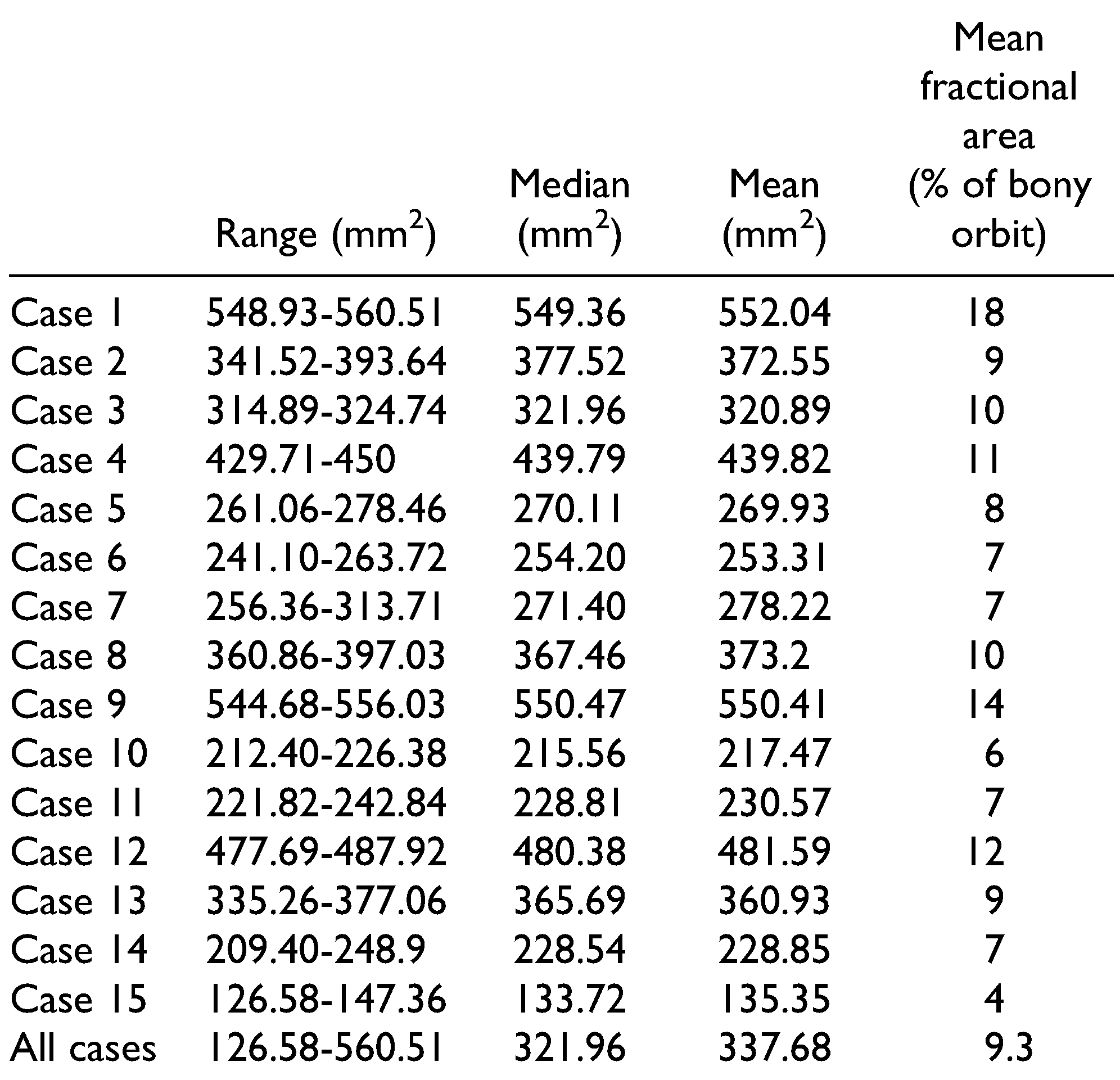
Results
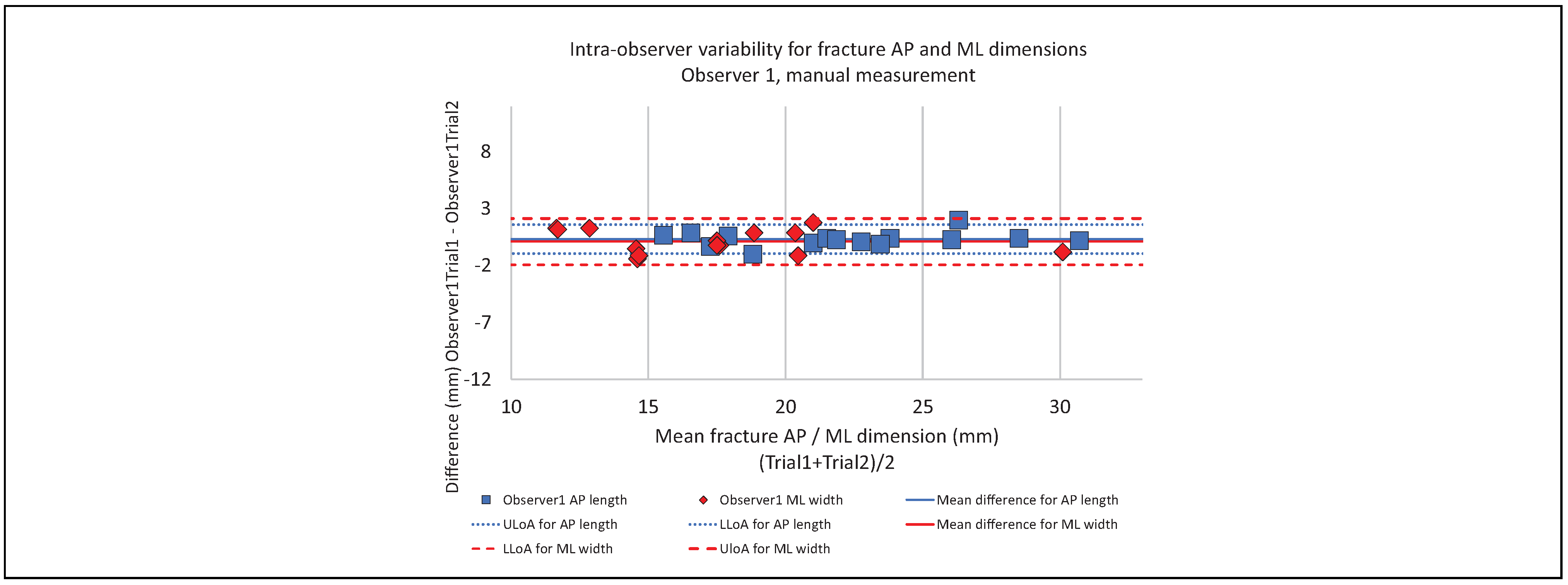
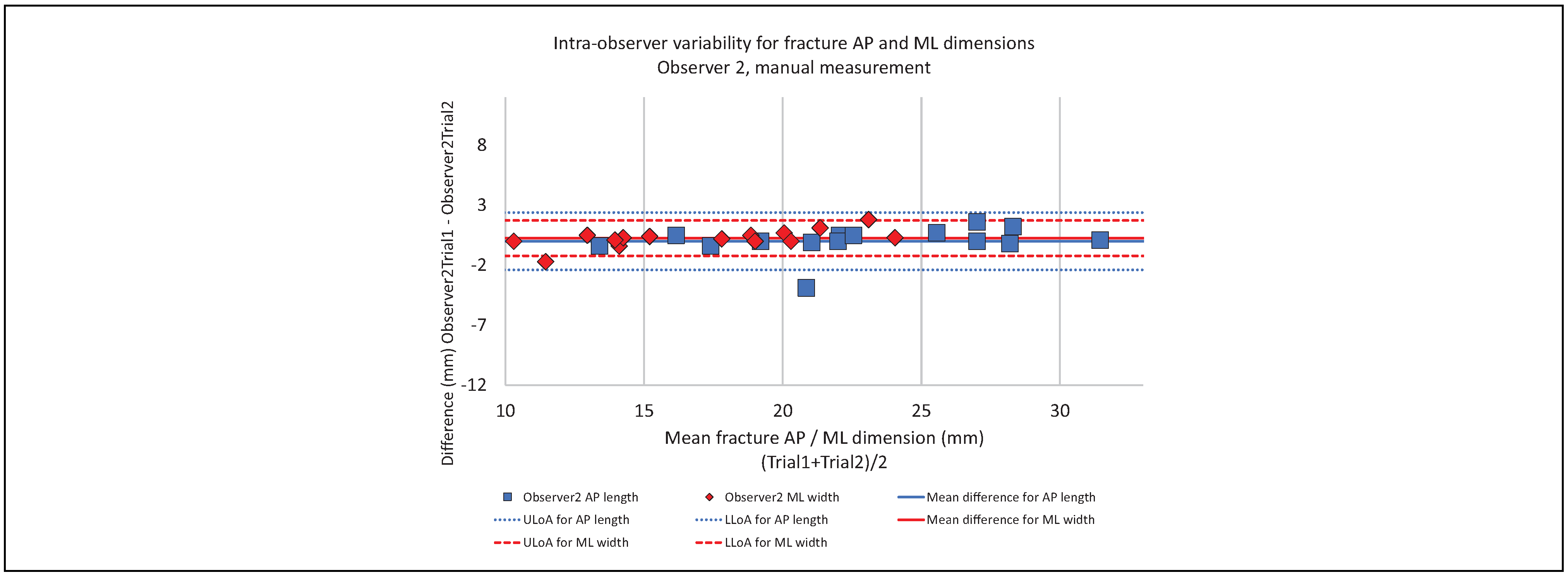
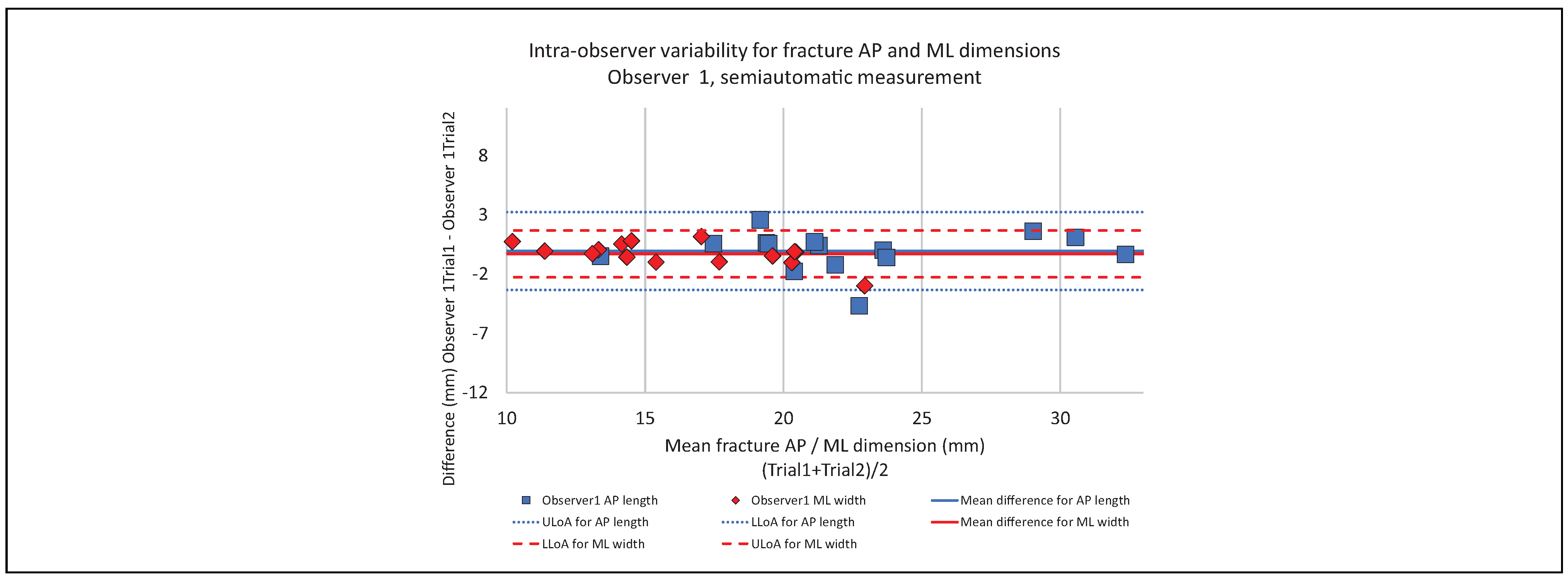
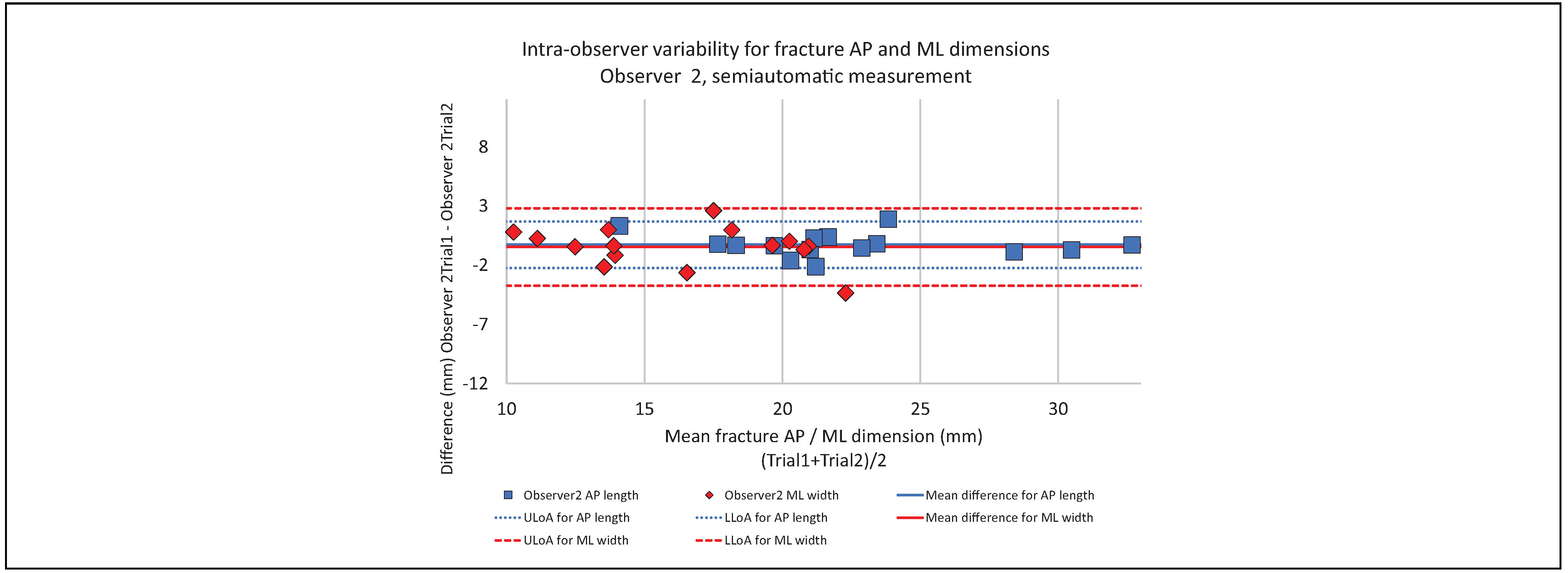
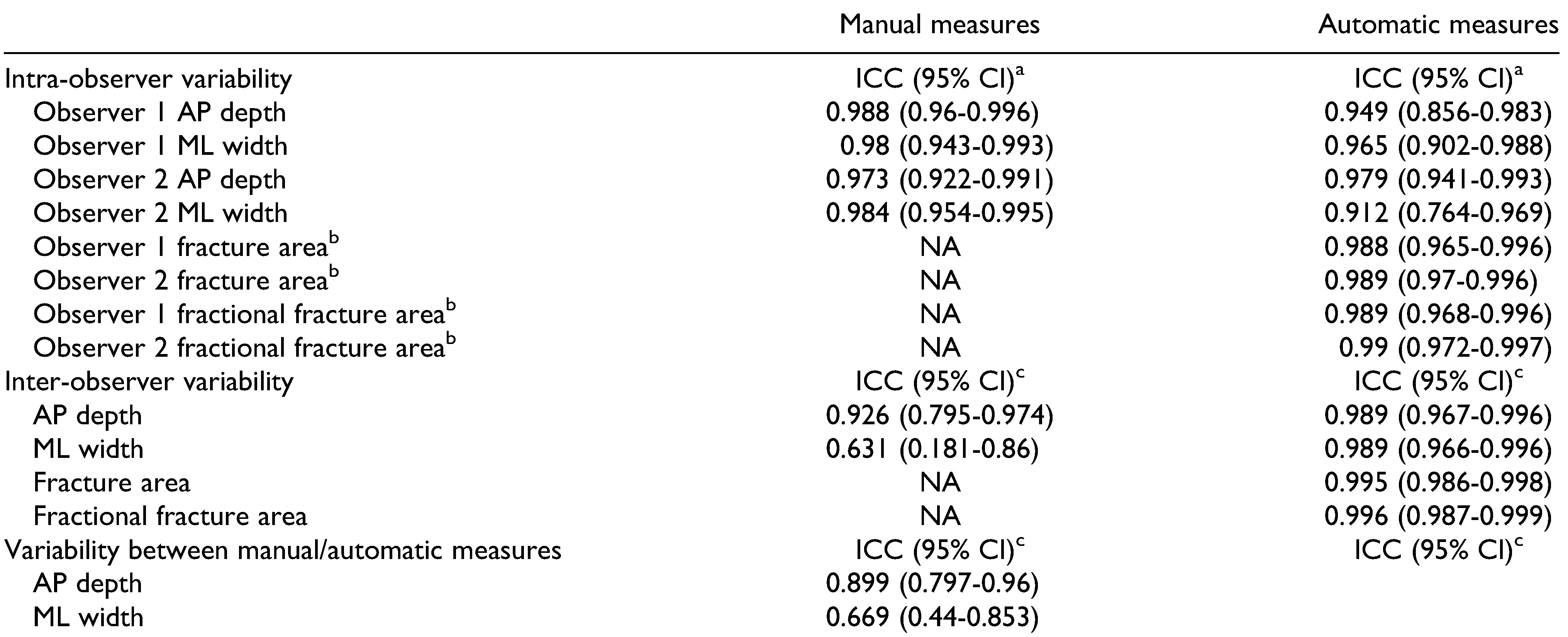
Intra-Observer Variability
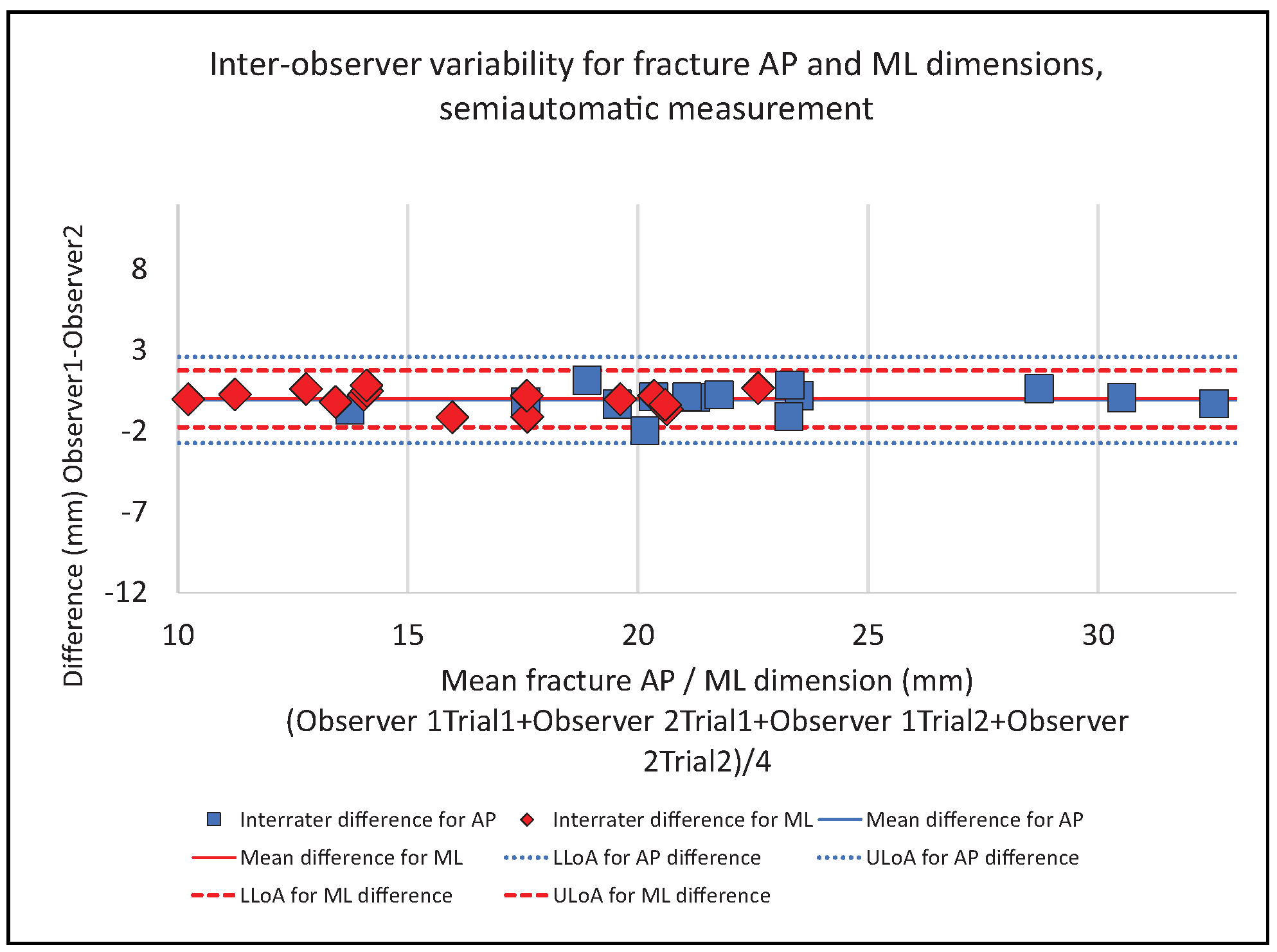
Inter-Observer Variability
Agreement Between Manual and Automatic Measurements
Discussion
Conclusions
Authors’ Note
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Dubois, L.; Steenen, S.A.; Gooris, P.J.; Mourits, M.P.; Becking, A.G. Controversies in orbital reconstruction—I. Defect-driven orbital reconstruction: a systematic review. Int J Oral Maxillofac Surg. 2015, 44, 308–315. [Google Scholar] [PubMed]
- Schouman, T.; Scolozzi, P. Simple CT-based calculations of orbital floor fracture defect size are not sufficiently accurate for clinical use. J Oral Maxillofac Surg. 2015, 73, 577. [Google Scholar] [CrossRef] [PubMed]
- Garcia, B.G.; Ferrer, A.D. Indicaciones quirúrgicas de las fracturas orbitarias atendiendo al taman˜o del defecto de fractura determinado por tomografía computarizada: una revisión sistemática. Rev Esp Cir Oral Maxilofac. 2016, 38, 42–48. [Google Scholar] [CrossRef][Green Version]
- Choi, J.; Park, S.W.; Kim, J.; Park, J.; Kim, J.S. Predicting late enophthalmos: differences between medial and inferior orbital wall fractures. J Plast Reconstr Aesthet Surg. 2016, 69, 238–244. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.H.; Kang, D.H. Prediction of late enophthalmos using preoperative orbital volume and fracture area measurements in blowout fracture. J Craniofac Surg. 2017, 28, 1717–1720. [Google Scholar] [CrossRef] [PubMed]
- Kunz, C.; Sigron, G.R.; Jaquiéry, C. Functional outcome after nonsurgical management of orbital fractures—the bias of decisionmaking according to size of defect: critical review of 48 patients. Br J Oral Maxillofac Surg. 2013, 51, 486–492. [Google Scholar] [CrossRef] [PubMed]
- Schouman, T.; Courvoisier, D.S.; Imholz, B.; Van Issum, C.; Terzic, A.; Scolozzi, P. Can systematic computed tomographic scan assessment predict treatment decision in pure orbital floor blowout fractures? J Oral Maxillofac Surg. 2012, 70, 1627–1632. [Google Scholar] [CrossRef] [PubMed]
- Raskin, E.M.; Millman, A.L.; Lubkin, V.; Della Rocca, R.C.; Lisman, R.D.; Maher, E.A. Prediction of late enophthalmos by volumetric analysis of orbital fractures. Ophthalmic Plast Reconstr Surg. 1998, 14, 19–26. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhang, Y.; He, Y.; An, J.; Zwahlen, R.A. Correlation between volume of herniated orbital contents and the amount of enophthalmos in orbital floor and wall fractures. J Oral Maxillofac Surg. 2012, 70, 68–73. [Google Scholar] [CrossRef] [PubMed]
- Jansen, J.; Schreurs, R.; Dubois, L.; Maal, T.J.; Gooris, P.J.; Becking, A.G. Orbital volume analysis: validation of a semi-automatic software segmentation method. Int J Comput Assist Radiol Surg. 2016, 11, 11–18. [Google Scholar] [CrossRef] [PubMed]
- Ahn, H.B.; Ryu, W.Y.; Yoo, K.W.; et al. Prediction of enophthalmos by computer-based volume measurement of orbital fractures in a Korean population. Ophthalmic Plast Reconstr Surg. 2008, 24, 36–39. [Google Scholar] [CrossRef] [PubMed]
- Kärkkäinen, M.; Wilkman, T.; Mesimäki, K.; Snäll, J. Primary reconstruction of orbital fractures using patient-specific titanium milled implants: the Helsinki protocol. Br J Oral Maxillofac Surg. 2018, 56, 791–796. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat Methods Med Res. 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]
- Dubois, L.; Jansen, J.; Schreurs, R.; et al. How reliable is the visual appraisal of a surgeon for diagnosing orbital fractures? J Craniomaxillofac Surg. 2016, 44, 1015–1024. [Google Scholar] [CrossRef] [PubMed]
- Vicinanzo, M.G.; McGwin GJr Allamneni, C.; Long, J.A. Interreader variability of computed tomography for orbital floor fracture. JAMA Ophthalmol. 2015, 133, 1393–1397. [Google Scholar] [CrossRef] [PubMed]
- Bruneau, S.; De Haller, R.; Courvoisier, D.S.; Scolozzi, P. Can a specific computed tomography-based assessment predict the ophthalmological outcome in pure orbital floor blowout fractures? J Craniofac Surg. 2016, 27, 2092–2097. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.T.; Kim, H.K.; Chung, S.M. Relationship between smallsize medial orbital wall fracture and late enophthalmos. J Craniofac Surg. 2009, 20, 75–80. [Google Scholar] [CrossRef] [PubMed]
- Goggin, J.; Jupiter, D.C.; Czerwinski, M. Simple computed tomography-based calculations of orbital floor fracture defect size are not sufficiently accurate for clinical use. J Oral Maxillofac Surg. 2015, 73, 112–116. [Google Scholar] [CrossRef] [PubMed]
- Schouman, T.; Courvoisier, D.S.; Imholz, B.; Van Issum, C.; Scolozzi, P. Computational area measurement of orbital floor fractures: reliability, accuracy and rapidity. Eur J Radiol. 2012, 81, 2251–2254. [Google Scholar] [CrossRef] [PubMed]
- Ang, C.H.; Low, J.R.; Shen, J.Y.; et al. A protocol to reduce interobserver variability in the computed tomography measurement of orbital floor fractures. Craniomaxillofac Trauma Reconstr. 2015, 8, 289–298. [Google Scholar] [CrossRef] [PubMed]
- Doerfler, H.M.; Huempfner-Hierl, H.; Kruber, D.; Schulze, P.; Hierl, T. Template-based orbital wall fracture treatment using statistical shape analysis. J Oral Maxillofac Surg. 2017, 75, 1475. [Google Scholar] [CrossRef]



 |
 |
© 2020 by the author. The Author(s) 2020.
Share and Cite
Saloniemi, M.; Lehtinen, V.; Snäll, J. Computer-Aided Fracture Size Measurement in Orbital Fractures—An Alternative to Manual Evaluation. Craniomaxillofac. Trauma Reconstr. 2021, 14, 209-217. https://doi.org/10.1177/1943387520962691
Saloniemi M, Lehtinen V, Snäll J. Computer-Aided Fracture Size Measurement in Orbital Fractures—An Alternative to Manual Evaluation. Craniomaxillofacial Trauma & Reconstruction. 2021; 14(3):209-217. https://doi.org/10.1177/1943387520962691
Chicago/Turabian StyleSaloniemi, Mikko, Valtteri Lehtinen, and Johanna Snäll. 2021. "Computer-Aided Fracture Size Measurement in Orbital Fractures—An Alternative to Manual Evaluation" Craniomaxillofacial Trauma & Reconstruction 14, no. 3: 209-217. https://doi.org/10.1177/1943387520962691
APA StyleSaloniemi, M., Lehtinen, V., & Snäll, J. (2021). Computer-Aided Fracture Size Measurement in Orbital Fractures—An Alternative to Manual Evaluation. Craniomaxillofacial Trauma & Reconstruction, 14(3), 209-217. https://doi.org/10.1177/1943387520962691



