Global Market Shocks and Tail Risk Spillovers: Evidence from a Copula-Based Contagion Framework

Abstract

This study investigates the dynamics of financial contagion using a flexible mixture copula framework, specifically a combination of the Survival Clayton and Survival Gumbel copulas, to estimate the lower tail dependence coefficient, interpreted as a measure of extreme downside co-movement or contagion. The model captures nonlinear and asymmetric dependencies between the global stock market and nine national markets: Australia, China, Hungary, India, New Zealand, Spain, Thailand, the United Kingdom, and the United States. The analysis spans the period from 2018 to 2024 and focuses on three major global crises: the China–U.S. trade war, the COVID-19 pandemic, and the Russia–Ukraine conflict. The results reveal substantial heterogeneity in contagion intensity across countries and crises. The COVID-19 pandemic generated the highest and most synchronized levels of contagion, with tail dependence exceeding 0.8 in the United States and above 0.6 in several developed and emerging markets. The China–U.S. trade war resulted in moderate contagion, particularly in countries with close trade links to the U.S. and China. The Russia–Ukraine conflict produced elevated contagion in European and energy-sensitive markets such as the UK and Spain. Conversely, China and New Zealand exhibited relatively lower levels of contagion across all periods

1. Introduction

The phenomenon of financial contagion has become a central concern in global finance, particularly in light of recent episodes of market turbulence (Maneejuk & Yamaka, 2021). Contagion refers to the transmission of shocks from one market to others, beyond what would be explained by economic fundamentals alone (Forbes & Rigobon, 2002). In times of financial distress, such as the Global Financial Crisis of 2008 or the COVID-19 pandemic, stock markets often exhibit heightened co-movements, indicating that local markets are increasingly susceptible to global shocks (Bekaert et al., 2005; Longstaff et al., 2011). Studying the contagion effect is therefore of critical importance for policymakers, investors, and researchers, as it influences decisions on risk management, diversification, and financial regulation (Dungey et al., 2005). However, identifying and quantifying contagion is methodologically challenging, as it requires disentangling true crisis-induced spillovers from normal market interdependence (Forbes & Rigobon, 2002). Traditional correlation-based approaches often fail to capture the nonlinear, time-varying, and regime-switching nature of contagion (Dungey et al., 2005; Rigobon, 2003). To address these limitations, this study proposes a time-varying contagion modeling framework based on a mixture copula model, which allows for flexible and dynamic dependence structures that vary over time. Traditional copula models often assume a static relationship, which may not adequately capture shifts in market behavior during periods of stress or calm.

Financial contagion describes the rapid and disproportionate spread of financial shocks from one market or economy to others, often triggered during periods of crisis. This phenomenon gained global attention following the 1997 Asian financial crisis, which revealed how localized financial instability can cascade through interconnected markets, amplifying systemic risk (Forbes & Rigobon, 2002; Yamaka et al., 2023). Thus, researchers have developed various methods to detect and quantify contagion, including static correlation measures, time-varying correlation models, and more recently, copula-based frameworks.

While correlation-based approaches offer a straightforward way to measure financial contagion, they often fall short in capturing the complex, nonlinear relationships and extreme co-movements that typically emerge during financial crises. These limitations are particularly evident when traditional models underestimate the joint probability of extreme losses across markets. To address this gap, researchers have increasingly turned to the concept of tail dependence, which quantifies the likelihood of extreme events occurring simultaneously across different markets (Nelson, 2006). This measure is especially valuable for identifying systemic risk during turbulent periods, such as global stock market crashes. A significant advancement in this area was proposed by Patton (2006), who introduced a copula-based approach for estimating tail dependence. Copulas are mathematical functions that allow the construction of a joint distribution by linking individual marginal distributions, thereby offering a flexible framework for modeling both linear and nonlinear dependence structures (Sklar, 1959). One of the most powerful features of copula models is their ability to isolate and model dependence in the tails of the distribution, precisely where traditional methods are weakest. Tail dependence coefficients, derived from the copula of two continuous random variables, provide a direct measure of the strength of association between extreme outcomes (McNeil et al., 2005). These coefficients are crucial for understanding extremal dependence, which is the defining characteristic of contagion during financial turmoil (Rodriguez, 2007).

Recently, to enhance model flexibility and better capture the complexities of financial dependence, mixture copula models have gained increasing prominence. These models combine multiple copula functions, often from different copula families, to account for the heterogeneous and dynamic dependence structures observed in financial data (Joe, 2001). Mixture copulas are particularly effective in capturing regime-switching behavior and various forms of tail dependence, as different copula components can dominate under different market conditions (Oh & Patton, 2018). As a result, they have emerged as powerful tools for analyzing time-varying contagion and assessing systemic risk in global financial markets. However, a critical challenge in applying mixture copulas lies in the accurate estimation of the mixing weights that determine the relative contribution of each copula component. If these weights are poorly estimated, the resulting copula model may provide a misleading representation of the dependence structure, particularly in the tails, where precision is essential for capturing contagion effects.

While traditional methods such as maximum likelihood estimation (MLE) are widely used for optimizing copula parameters (Genest et al., 1995), estimating the weights in a mixture copula setting is substantially more complex. This difficulty arises because the likelihood surface can become highly nonlinear and multimodal, especially when multiple copula families with different characteristics are combined. In practice, weights are often estimated jointly with copula parameters via MLE, or selected using model selection criteria such as the Bayesian Information Criterion (BIC) or Bayesian Information Criterion (BIC) to identify the best-fitting model structure (Burnham, 2002). Neverthelss, these methods can be sensitive to initialization, model specification, and data characteristics, leading to suboptimal or unstable solutions.

To address the challenge of selecting optimal weights in mixture copula models, Saekow et al. (2024) proposed two Bayesian approaches: Bayesian Model Averaging (BMA) and log-transformed Bayesian Model Averaging (BMAlog), aimed at improving the estimation of tail dependence coefficients. Their study compared these methods with conventional maximum likelihood estimation (MLE) and found that, on average, MLE outperformed both BMA and BMAlog in general scenarios, particularly when the weight distribution was not heavily skewed. However, they also identified important exceptions. Specifically, when the copula weight is located at the extremes of the parameter space, i.e., below 0.1 or above 0.9, the BMAlog method demonstrated superior performance. This improvement is attributed to the log-transformed weighting mechanism, which provides a more effective adjustment under highly unbalanced conditions.

Building on this foundation, the primary objective of this study is to evaluate the dynamic contagion effect between the MSCI World Index and nine national stock markets using Bayesian Model Averaging with log-transformed weights (BMAlog) to estimate time-varying tail dependence coefficients. A rolling-window approach is employed over the period from January 2018 to December 2024, capturing the evolving nature of extreme market co-movements across both tranquil and turbulent periods. This timeframe spans three major global crises that have reshaped international financial dynamics: the China–U.S. trade war (July 2019–January 2020) (Beckmann et al., 2024), the COVID-19 pandemic (March 2020–July 2020) (Lim & Choi, 2024), and the Russia–Ukraine war (February 2022–June 2022) (Zhang et al., 2024). These events offer a critical opportunity to examine how global shocks translate into localized financial stress, highlighting the significance of contagion risk. The nine markets selected for this study—Australia, China, Hungary, India, Spain, Thailand, the United Kingdom, and the United States—represent a geographically and economically diverse set of countries. This includes both advanced economies (e.g., the United States, United Kingdom, Spain, Australia) and emerging markets (e.g., China, India, Thailand, Hungary), thereby allowing for a comparative analysis of contagion dynamics across different stages of market development and financial integration. The inclusion of countries from Asia, Europe, and North America ensures a global perspective on contagion pathways and systemic risk exposure.

By integrating mixture copula modeling with the BMAlog estimation technique, this study contributes in several important ways. First, it advances the methodological literature by addressing a long-standing limitation of mixture copula models: the difficulty of estimating mixing weights when distributions are unbalanced or when component copulas exhibit similar structures. The BMAlog procedure offers a novel solution to this problem by stabilizing weight estimation and improving inference on systemic risk. Second, it contributes to the theoretical understanding of contagion by focusing explicitly on lower-tail dependence, which captures extreme downside risk spillovers that are often underestimated by correlation-based measures. This provides a more accurate representation of contagion during crisis episodes. Third, it delivers practical contributions by examining how contagion evolves under different types of global shocks—policy-driven (China–U.S. trade war), real-economy (COVID-19), and geopolitical/energy-related (Russia–Ukraine)—and by identifying cross-country heterogeneity in contagion intensity across advanced and emerging markets. These insights are directly relevant for global investors seeking to diversify risk, as well as for regulators and policymakers concerned with safeguarding financial stability.

Accordingly, the central research question guiding this study is: How do extreme downside co-movements between the MSCI World Index and national equity markets evolve across three distinct global shocks—the China–U.S. trade war, the COVID-19 pandemic, and the Russia–Ukraine conflict—and what does the cross-country heterogeneity in lower-tail dependence coefficients reveal about the role of crisis type in shaping contagion? We address this question by estimating time-varying lower tail dependence coefficients (LTDCs) through a mixture of survival Clayton and survival Gumbel copulas with BMAlog weights over 2018–2024, and by comparing patterns across countries to uncover how crisis type and market characteristics jointly determine contagion dynamics.

The remainder of the paper is organized as follows. Section 2 reviews the relevant literature. Section 3 outlines the methodology, while Section 4 presents the empirical results. Section 5 provides a discussion of the findings, and Section 6 concludes the paper with final remarks and policy implications.

2. Literature Review

2.1. Theoretical Foundation

The concept of economic contagion has been interpreted in various ways in the literature. Dornbusch et al. (2000) distinguished three perspectives: (i) contagion as the transmission of a shock from one economy or market to others, (ii) contagion as the co-movement of shocks or volatilities across markets, and (iii) contagion as a significant increase in such co-movements during periods of turbulence. Forbes and Rigobon (2002) further argued that much of what is often labeled contagion may in fact reflect normal interdependence, and proposed that contagion should be understood as a significant rise in cross-market linkages following a shock. Similarly, Bai et al. (2019) described contagion as the propagation of financial or economic crises across countries or regions. Taken together, these perspectives emphasize both the transmission of shocks and the amplification of interconnections under stress, underscoring the need to distinguish between normal interdependence and crisis-driven contagion.

In terms of measurement, early empirical research relied on correlation-based statistics. While intuitive, such measures fail to capture nonlinear and asymmetric dependence, and they systematically underestimate the joint probability of extreme losses. This limitation often leads to a distorted picture of systemic risk during crises. To overcome these shortcomings, researchers have developed a variety of econometric approaches. Initial contributions include multivariate GARCH (MGARCH) and Dynamic Conditional Correlation (DCC) models (R. Engle, 2002), which provide time-varying measures of dependence but remain correlation-driven. Quantile regression methods (Koenker, 2005) have also been used to assess downside risk, while network-based models such as the Diebold–Yilmaz connectedness framework (Diebold & Yilmaz, 2014) and time-varying parameter VAR (TVP-VAR) models (Primiceri, 2005) allow for evolving interdependence across markets, though they do not explicitly capture tail-specific dynamics.

A major methodological advance came with the introduction of copula models. Patton (2006) pioneered the use of copulas to estimate time-varying dependence structures. Copulas allow the construction of joint distributions from marginal distributions and, crucially, enable the modeling of nonlinear and asymmetric dependencies in the tails where contagion is most pronounced. Tail dependence coefficients derived from copulas (McNeil et al., 2005) have since become standard tools for evaluating extremal co-movements during crises (Rodriguez, 2007). The copula literature has expanded to include dynamic conditional copulas (Christoffersen et al., 2012; Jondeau et al., 2006), vine copulas for high-dimensional dependence (Aas et al., 2009; Czado, 2019), and Markov-switching copulas (Chollete et al., 2009; Hafner & Manner, 2012), all of which capture nonlinear and regime-dependent changes in dependence structures.

Beyond the copula framework, other nonlinear and tail-focused methods have also been proposed. Extreme Value Theory and Peaks-over-Threshold methods has been widely applied to capture extreme dependence in equity markets (Longin, 2001). Quantile VAR (QVAR) frameworks (White et al., 2015) and Conditional Autoregressive Value-at-Risk (CAViaR) models (R. F. Engle & Manganelli, 2004) explicitly target distributional tails, while bootstrap-based probabilistic contagion analysis (Pesaran et al., 2016) provides robust inference for joint extreme events. More recently, network-oriented approaches such as the Tail-Event-Driven Network (TENET) method (Billio et al., 2012) have been employed to trace contagion pathways across complex financial systems.

Despite these advances, existing approaches still face important limitations. Correlation-based and GARCH-type models underestimate joint tail risk. Markov-switching copulas capture regime shifts but typically rely on a limited number of latent states, which may oversimplify heterogeneous crisis dynamics. Vine copulas offer flexibility but are computationally intensive and sometimes difficult to interpret. EVT-based and quantile regression approaches focus narrowly on tail distributions but may neglect broader dependence structures, while network models emphasize spillover propagation without fully modeling nonlinear tail dependence.

To address these gaps, this study develops a mixture copula framework estimated with the BMAlog technique to model financial contagion. Mixture copulas, which combine several copula families, are well suited to capture the heterogeneous, asymmetric, and tail-dependent dependence structures commonly observed in financial data (Aas et al., 2009; Czado, 2019; Patton, 2006; Saekow et al., 2024). However, a well-known limitation of mixture copulas is the estimation of mixing weights: MLE often struggles to identify these parameters reliably, especially when component copulas exhibit similar dependence structures. The BMAlog approach provides a solution by estimating weights through a Bayesian model averaging procedure with a log-sum formulation, which stabilizes the optimization and yields more consistent parameter estimates. This integration enhances the reliability of tail-dependence measurement and improves inference on systemic risk during crisis periods.

2.2. Empirical Reviews

The empirical evidence on financial contagion is extensive but often mixed, reflecting differences in definitions, methodologies, time horizons, and regional focus. Early studies such as King and Wadhwani (1990) and Calvo and Reinhart (1996) documented strong cross-market linkages, suggesting that shocks in one market can rapidly transmit to others. Dornbusch et al. (2000) emphasized that contagion is most visible during crises, when correlations and volatility spillovers rise sharply. In contrast, Forbes and Rigobon (2002) argued that much of what is often labeled contagion may simply reflect interdependence, showing that, after correcting for heteroskedasticity, many apparent increases in cross-country linkages during the Asian crisis disappeared. Rigobon (2003) further reinforced the importance of identification, warning that failure to address heteroskedasticity and endogeneity leads to spurious contagion findings.

Subsequent empirical work produced more nuanced insights. Bekaert et al. (2005) found that contagion is not universal but tends to be stronger in less financially integrated or emerging markets. Dungey et al. (2005) provided a comprehensive review showing that detection depends heavily on methodology: while correlation and integration tests often suggest stability, crisis-window approaches typically detect contagion surges. Longstaff (2010) and Longstaff et al. (2011) extended the analysis to sovereign and credit markets, documenting systemic spillovers during the subprime and Eurozone debt crises when risk premia rose simultaneously across countries. Similarly, Longin (2001) observed extreme correlation spikes during global equity downturns, suggesting that diversification benefits collapse precisely when they are most needed.

Since the Global Financial Crisis (GFC), studies have increasingly employed nonlinear and tail-focused models. Rodriguez (2007) showed that during the Mexican peso crisis and the Asian financial crisis, tail dependence rose sharply, confirming contagion beyond linear correlation. Maneejuk et al. (2018) demonstrated that copula-based methods capture nonlinear and regime-dependent co-movements missed by traditional models. Similarly, quantile-based approaches (e.g., Quantile VAR and CAViaR) (R. F. Engle & Manganelli, 2004; White et al., 2015) highlight how shocks disproportionately affect the distributional tails, reinforcing the importance of tail-sensitive measures. Extreme Value Theory techniques (Longin, 2001) also provide evidence of heightened dependence in extreme events.

Recent advances emphasize network and high-dimensional approaches. Diebold and Yilmaz (2014) proposed connectedness measures capturing variance spillovers across financial systems, while Billio et al. (2012) developed econometric connectedness indices for systemic risk. Vine copula methods (Aas et al., 2009; Czado, 2019) and Markov-switching copulas (Chollete et al., 2009; Hafner & Manner, 2012) have further enriched the literature, enabling researchers to capture regime shifts, asymmetric dependence, and heterogeneous channels of contagion.

Empirical studies focusing on recent crises provide additional evidence. During the China–U.S. trade war, Beckmann et al. (2024) showed that trade policy uncertainty generated significant spillovers to European markets. The COVID-19 pandemic triggered unprecedented contagion: Lim and Choi (2024) reported strong credit risk transmissions across industries, while Zhang et al. (2024) found that both equity and commodity markets exhibited persistent and synchronized contagion. Maneejuk et al. (2024) linked contagion to the resumption of global tourism, illustrating how real-economy channels amplify financial spillovers. More recently, the Russia–Ukraine conflict has been shown to intensify contagion in European and energy-sensitive markets, with Zhang et al. (2024) highlighting prolonged spillovers to oil markets and exchange rates.

Another stream of research stresses heterogeneity across advanced and emerging markets. Longstaff et al. (2011) and Bekaert et al. (2005) observed that advanced economies act as key transmitters of shocks, while emerging markets experience more selective but sometimes sharper contagion episodes. Endri et al. (2024) found that the Indonesian stock market exhibited strong co-movements with its major trading partners, while Bai et al. (2019) showed that economic policy uncertainty spillovers were particularly strong among large emerging economies. These findings underscore that financial integration, institutional quality, and structural characteristics shape the intensity and persistence of contagion.

3. Materials and Methods

We measure extreme downside co-movement using the LTDC between the MSCI World Index and each national market. LTDC is estimated from a mixture of survival Clayton and survival Gumbel copula (SCSG) whose time-varying log-weights are fit in rolling windows using a BMA-log scheme, allowing dependence to switch across regimes while preserving interpretable tail-risk metrics. To study how crisis type shapes contagion, we evaluate LTDC in three pre-specified time period (Trade war: Jul-2019–Jan-2020; COVID-19: Mar–Jul 2020; Russia–Ukraine: Feb–Jun 2022).

3.1. Marginal Modeling

Before estimating the copula, the marginal distributions of the return series must be transformed into uniform variables on $[0,1]$, as required by Sklar’s theorem. In this study, we adopt a nonparametric approach by using standardized returns and their empirical cumulative distribution functions (CDFs). Specifically, for each market i and time t, the return $r_{i,t}$ is standardized as

$$r_{i,t}^{*}={\displaystyle \frac{r_{i,t}}{\widehat{\sigma }\left(r_i\right)}},$$

(1)

where $\widehat{\sigma }\left(r_i\right)$ denotes the sample standard deviation of returns for market i. The standardized returns are then transformed into cumulative probabilities using the empirical CDF,

$$u_{i,t}={\widehat{F}}_i\left(r_{i,t}^{*}\right)={\displaystyle \frac{1}{T}}\sum _{s=1}^T\mathbf{1}(r_{i,s}^{*}\le r_{i,t}^{*}),$$

(2)

where $\mathbf{1}(·)$ is the indicator function and T is the sample size. This transformation produces probability integral transforms that are approximately uniform on $[0,1]$, which serve as inputs to the copula model.

The choice of empirical CDFs is motivated by the desire to avoid potential misspecification associated with parametric marginal models (e.g., ARMA–GARCH). Since our main focus is on the dependence structure rather than marginal dynamics, the nonparametric approach provides a robust and distribution-free method for handling marginals.

To evaluate the adequacy of this transformation, we conducted uniformity diagnostics on the transformed variables. Kolmogorov–Smirnov and Anderson–Darling tests did not reject the null hypothesis of uniformity at the 5% level for all series, indicating that the marginals are well-specified. Furthermore, we verified that the probability integral transforms (PITs) exhibited no significant autocorrelation, ensuring that the inputs to the copula model are both i.i.d. and uniform, as required for reliable copula estimation.

3.2. Copula

Copula functions are essential tools for modeling the dependence structure between random variables. A copula is defined as a joint distribution function whose marginals are uniform on the interval $[0,1]$. It allows researchers to separate the marginal behavior of each variable from their joint dependence, offering a flexible and powerful framework for constructing multivariate models.

A two-dimensional copula is a function $C:{[0,1]}^2\to [0,1]$ that satisfies two key properties. First, for all $v,z\in [0,1]$, the boundary conditions hold: $C(v,0)=0=C(0,z)$, and $C(v,1)=v$, $C(1,z)=z$. These conditions ensure that the function behaves consistently at the edges of the unit square. Second, for any $v_1\le v_2$ and $z_1\le z_2$ in $[0,1]$, the function satisfies the inequality

$$C(v_2,z_2)-C(v_2,z_1)-C(v_1,z_2)+C(v_1,z_1)\ge 0.$$

These properties enable copulas to capture a wide range of dependency structures beyond what linear correlation can describe, making them particularly valuable in fields like finance, insurance, and risk management (Nelson, 2006).

A foundational result in copula theory is Sklar’s Theorem (Sklar, 1959), which provides a formal mechanism to decompose any multivariate joint distribution into its marginal distributions and a copula that captures the dependence structure. Let $F\left(x\right)$ and $G\left(y\right)$ denote the marginal distribution functions of random variables X and Y, respectively. Then, for all $(x,y)\in {\mathbb{R}}^2$, Sklar’s Theorem states:

(i)

If $\mathcal{C}$ is a subcopula defined on $\mathrm{Range}\left(F\right)\times \mathrm{Range}\left(G\right)$, then the function

$$H(x,y)=\mathcal{C}\left(F\right(x),G(y\left)\right)$$

(3)

is a valid joint distribution with marginals F and G.

(ii)

Conversely, for any joint distribution $H(x,y)$ with marginals $F\left(x\right)$ and $G\left(y\right)$, there exists a unique subcopula $\mathcal{C}$ satisfying Equation (3). If F and G are continuous, $\mathcal{C}$ extends to a copula C on ${[0,1]}^2$ such that:

$$H(x,y)=C\left(F\right(x),G(y\left)\right)$$

(4)

This decomposition is especially useful in finance and risk management, where separating marginal behavior from joint dependence allows for flexible and realistic multivariate modeling.

A key family of copulas used in modeling dependence is the Archimedean copula. These copulas are generated using a continuous, strictly decreasing function $\varphi :[0,1]\to [0,\infty ]$, known as the generator, with $\varphi \left(1\right)=0$. Let ${\varphi }^{[-1]}$ denote the pseudo-inverse of $\varphi$, defined as:

$${\varphi }^{[-1]}\left(t\right)=\left\{\begin{array}{cc}{\varphi }^{-1}\left(t\right),\hfill & t\in [0,\varphi (0\left)\right]\hfill \\ 0,\hfill & t>\varphi \left(0\right)\hfill \end{array}\right.$$

Using this, the Archimedean copula is constructed as:

$$C(v,z)={\varphi }^{[-1]}(\varphi \left(v\right)+\varphi \left(z\right))$$

(5)

These copulas are widely used due to their simplicity and ability to capture a variety of dependence structures (Nelson, 2006).

Two well-known examples of Archimedean copulas are the Clayton and Gumbel-Hougaard copulas:

• Clayton copula: Generated by $\varphi \left(t\right)={\displaystyle \frac{t^{-\theta }-1}{\theta }}$, for $\theta \in [-1,\infty )$, the copula function is:

  $$C_{\theta }(v,z)=max\left[{(v^{-\theta }+z^{-\theta }-1)}^{-1/\theta },0\right]$$

  (6)
• Gumbel-Hougaard copula: Generated by $\varphi \left(t\right)={(-lnt)}^{\theta }$, for $\theta \in [1,\infty )$, the copula function is:

  $$C_{\theta }(v,z)=exp\left(-{\left[{(-lnv)}^{\theta }+{(-lnz)}^{\theta }\right]}^{1/\theta }\right)$$

  (7)

In addition to standard copulas, the concept of a survival copula is useful when modeling joint tail behavior. Given a copula function C, the corresponding survival copula $\widehat{C}$ is defined as:

$$\widehat{C}(v,z)=v+z-1+C(1-v,1-z)$$

(8)

This transformation reflects the original copula across both axes and emphasizes the co-movement of extreme lower tail events, which is particularly important in applications such as stress testing and systemic risk modeling (Nelson, 2006).

An important concept in dependence modeling, particularly in risk management and extreme value analysis, is the lower tail dependence coefficient (TDCL) (McNeil et al., 2005), denoted by ${\lambda }_L$. This coefficient measures the extent to which two random variables jointly experience extreme low outcomes. Formally, let X and Y be random variables with cumulative distribution functions F and G, respectively. The coefficient of lower tail dependence is defined as

$${\lambda }_L=\underset{v\to 0^{+}}{lim}\mathbb{P}(Y\le G^{-1}\left(v\right)\mid X\le F^{-1}\left(v\right)),$$

provided that the limit exists and lies in the interval $[0,1]$. If ${\lambda }_L$ lies strictly between 0 and 1, the variables X and Y exhibit lower tail dependence, indicating that extreme low values of one variable are likely to coincide with those of the other. If ${\lambda }_L=0$, the variables are said to be asymptotically independent in the lower tail.

This definition can be conveniently expressed in terms of the copula function C that links the marginals F and G via Sklar’s Theorem. Specifically, the lower tail dependence coefficient can be rewritten as

$${\lambda }_L=\underset{v\to 0^{+}}{lim}{\displaystyle \frac{C(v,v)}{v}}.$$

Given a copula function, this formulation enables a direct analytical calculation of the lower tail dependence. For example, several well-known copulas have the following TDCL values:

For the Clayton copula, the coefficient is ${\lambda }_L=2^{-1/\theta },$ which indicates positive lower tail dependence for all $\theta >0$. In contrast, the survival Clayton copula, which reflects upper tail behavior, yields ${\lambda }_L=0,$ indicating asymptotic independence in the lower tail. Similarly, the Gumbel copula, which primarily models upper tail dependence, also has ${\lambda }_L=0.$ However, its survival counterpart, thesurvival Gumbel copula, captures lower tail dependence with ${\lambda }_L=2-2^{1/\theta }.$

These examples illustrate how the choice of copula significantly influences the modeling of joint extreme events, and highlight the value of tail dependence coefficients in evaluating co-movement in risk-prone regions of the distribution.

In practical applications, it is often the case that multiple copula models provide similarly good fits to empirical data. However, standard practice typically involves selecting a single best copula model, often the one with the lowest information criterion or best statistical fit, and treating it as the true underlying copula. This approach, while convenient, ignores model uncertainty and may lead to inaccurate conclusions, particularly through underestimation or overestimation of dependence in the tails of the distribution.

An alternative and more robust approach involves combining multiple candidate copulas into a mixture. If $C_1(v,z)$ and $C_2(v,z)$ are two bivariate copula functions, and if $w_1,w_2\in [0,1]$ are weights such that $w_1+w_2=1$, then the convex combination

$$C_{\mathrm{mix}}(v,z)=w_1{C}_1(v,z)+w_2{C}_2(v,z)$$

also defines a valid copula function (Nelson, 2006). This result provides a theoretical foundation for mixture copula models, which allow for more flexible modeling of complex dependence structures.

When analyzing the tail dependence of such a mixture, the lower tail dependence coefficient of the mixture copula, ${\lambda }_{L_{C_{\mathrm{mix}}}}$, can be derived as a weighted average of the lower tail dependence coefficients of the individual components:

$${\lambda }_{L_{C_{\mathrm{mix}}}}=w_1{\lambda }_{L_{C_1}}+w_2{\lambda }_{L_{C_2}}.$$

In this study, we focus on a specific mixture copula formed by combining the survival Clayton copula and the survival Gumbel copula, referred to as the SCSG copula. Given that the survival Clayton copula has zero lower tail dependence (${\lambda }_L=0$), and the survival Gumbel copula has lower tail dependence coefficient ${\lambda }_L=2-2^{1/\theta }$, the mixture’s lower tail dependence simplifies to:

$${\lambda }_L=w_2(2-2^{1/\theta }),$$

which highlights how the choice of weights and parameter $\theta$ directly influences the joint behavior in the lower tail.

There are several techniques available for estimating copula functions, with varying degrees of complexity and accuracy. Among these, the Maximum Likelihood Estimation (MLE) method is one of the most widely used approaches (Joe, 2001). In the context of this study, MLE is employed to estimate the parameters of the copula by fitting it to observed data within a specified parametric family. This method offers a structured and statistically efficient framework for capturing the dependence structure between variables. By maximizing the likelihood function associated with the joint distribution defined by the copula and its marginals, MLE ensures precise estimation and reliable inference. Given its ability to effectively model complex interdependencies, this research adopts the MLE technique for copula estimation under the chosen parametric framework.

Saekow et al. (2024) proposed selecting the optimal weight parameter in a mixed copula model using a Bayesian Information Criterion (BIC)-based Bayesian Model Averaging (BMA) approach. They defined a grid of candidate weight parameters $\left\{w_i\right\}$ across the interval $[0,1]$. For each candidate weight $w_i$, the copula parameters ${\theta }_1$ and ${\theta }_2$ are estimated using Maximum Likelihood Estimation (MLE), and the corresponding BIC is calculated as:

$$\mathrm{BIC}\left(w_i\right)=-2·L(w_i,\theta |\mathrm{data})+d_i·log\left(n\right),$$

(9)

where $L(w_i,\theta |\mathrm{data})$ denotes the log-likelihood of the mixed copula model with weight $w_i$, $d_i$ is the number of estimated parameters, and n is the number of observations.

To estimate the lower tail dependence coefficient, two approaches are considered:

• Original BIC-Based BMA:

  $${\widehat{\lambda }}_{\mathrm{BMA}}=\sum _{i=1}^K{W}_{C_i}{\widehat{\lambda }}_{C_i},$$

  (10)

  where the posterior weight $W_{C_i}$ is given by:

  $$W_{C_i}={\displaystyle \frac{exp\left(-\frac{1}{2}{\mathrm{BIC}}_i\right)}{{\sum }_{k=1}^{K}exp\left(-\frac{1}{2}{\mathrm{BIC}}_k\right)}}.$$

  (11)
• Log-Transformed BIC-Based BMA (BMA_log):

  $${\widehat{\lambda }}_{\mathrm{BMAlog}}=\sum _{i=1}^K{W}_{C_i}^{log}{\widehat{\lambda }}_{C_i},$$

  (12)

  with the adjusted weight defined as:

  $$W_{C_i}^{log}={\displaystyle \frac{exp\left(-\frac{1}{2}\frac{{\mathrm{BIC}}_i}{log\left(n\right)}\right)}{{\sum }_{k=1}^{K}exp\left(-\frac{1}{2}\frac{{\mathrm{BIC}}_k}{log\left(n\right)}\right)}}.$$

  (13)

In the specific case of a mixture between the Survival Clayton and Survival Gumbel copulas, the lower tail dependence coefficient simplifies as follows:

• BMA Estimate:

  $${\widehat{\lambda }}_{\mathrm{BMA}}={\displaystyle \frac{exp\left(-\frac{1}{2}{\mathrm{BIC}}_2\right)}{{\sum }_{i=1}^{2}exp\left(-\frac{1}{2}{\mathrm{BIC}}_i\right)}}·(2-2^{1/\theta }),$$

  (14)
• BMA_log Estimate:

  $${\widehat{\lambda }}_{\mathrm{BMAlog}}={\displaystyle \frac{exp\left(-\frac{1}{2}\frac{{\mathrm{BIC}}_2}{log\left(n\right)}\right)}{{\sum }_{i=1}^{2}exp\left(-\frac{1}{2}\frac{{\mathrm{BIC}}_i}{log\left(n\right)}\right)}}·(2-2^{1/\theta }).$$

  (15)

These BMA-based estimators provide a flexible and robust mechanism for selecting the optimal copula weight by incorporating model uncertainty and accounting for sample size effects. The use of BMA_log, in particular, offers an improved adjustment under highly skewed weight distributions, making it a valuable complement to conventional estimation techniques.

For the BMAlog implementation, the procedure is as follows. A discrete weight grid $\left\{w_i\right\}$ is constructed across the interval $[0,1]$ at regular increments (e.g., 0.01 or 0.05), ensuring sufficient resolution to capture variations in the likelihood surface. For each candidate weight $w_i$, the copula parameters ${\theta }_1$ (for the Survival Clayton) and ${\theta }_2$ (for the Survival Gumbel) are estimated by maximizing the log-likelihood function via Maximum Likelihood Estimation (MLE). This optimization is performed using a quasi-Newton routine with robust convergence criteria to ensure stability across different starting values. The Bayesian Information Criterion (BIC) is then calculated for each specification, and posterior weights are assigned according to either the standard BMA rule or the log-adjusted BMAlog formulation. Finally, the lower-tail dependence coefficient is computed as a weighted average across the candidate models, with the log-transformation in BMAlog serving to smooth extreme differences in BIC values and to provide more stable weight estimates under small-sample or highly unbalanced conditions.

4. Empirical Study

We examine nine stock markets from a diverse set of countries across different regions, specifically: Australia, China, Hungary, India, Spain, Thailand, the United Kingdom, and the United States. The dataset comprises the daily log returns of these national stock indices, along with the MSCI World Index, spanning the period from 1 January 2018, to 31 December 2024. To evaluate the most appropriate copula structure for modeling tail dependence, we begin by comparing the BIC values of four alternative specifications: Student-t copula, Clayton copula, the survival Gumbel copula, and a mixture copula composed of the survival Clayton and survival Gumbel copulas. This comparison allows us to determine whether a single copula or a mixture model provides a better fit to the dependence structure observed in the data, especially during periods of financial stress when tail behavior is most pronounced.

Prior to presenting the estimation results, we evaluate the stationarity of the return series using the Augmented Dickey–Fuller (ADF) unit root test at the 5% significance level. Stationarity is a fundamental assumption for valid copula-based dependence modeling, as it ensures the statistical properties of the series remain consistent over time. The test results, summarized in

Table 1. ADF Unit Root Test.

Market	ADF Statistic	p-Value	Result
MSCI	−5.3458	0.0000	Stationary
Australia	−4.4675	0.0000	Stationary
China	−3.9867	0.0000	Stationary
Hungary	−3.87187	0.0000	Stationary
India	−5.0526	0.0000	Stationary
New Zealand	−4.7987	0.0000	Stationary
Spain	−4.7011	0.0000	Stationary
Thailand	−5.1507	0.0000	Stationary
UK	−5.1738	0.0000	Stationary
US	−5.09028	0.0000	Stationary

, confirm that all return series are stationary, thereby validating their suitability for use in tail dependence and copula estimation.

The results of

Table 2. BIC of Copulas.

Country	Clayton	Survival Gumbel	Survival Clayton–Survival Gumbel	Student-t
Australia	−257.33	−386.84	−425.70	−244.17
China	−90.49	−120.08	−136.46	−79.60
Hungary	−265.99	−341.14	−369.08	−205.62
India	−285.02	−413.91	−440.40	−215.21
New Zealand	−155.24	−198.77	−232.11	−140.45
Spain	−593.97	−766.23	−837.06	−434.27
Thailand	−196.11	−295.14	−325.23	−182.57
UK	−601.05	−778.84	−832.87	−433.15
US	−1993.28	−2442.44	−2572.88	−1309.30

indicate that the BIC for the mixture of the survival Clayton and survival Gumbel copulas is the lowest among the three models considered. This finding suggests that the mixture copula provides a better fit to the data than either the single Clayton or survival Gumbel copula alone, thereby confirming the advantage of capturing multiple tail dependence structures through a flexible mixture framework.

Table 3. BMAlog Estimation of Mixture of Survival Clayton and Survival Gumbel Copula.

	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{w}}_1$	${\mathit{w}}_2$	${\mathit{\lambda }}_{{\mathit{L}}_{{\mathit{C}}_{\mathbf{mix}}}}$
Australia	0.5907	1.6925	0.1001	0.8999	0.4939
China	0.5263	1.3462	0.0708	0.9292	0.3034
Hungary	0.6423	1.6388	0.0212	0.9788	0.4734
India	0.6700	1.7503	0.1106	0.8894	0.5141
New Zealand	0.7237	1.4470	0.0205	0.9795	0.3776
Spain	1.2220	2.1373	0.0301	0.9699	0.6169
Thailand	0.9063	1.6065	0.1007	0.8993	0.4602
UK	1.2424	2.1353	0.0214	0.9786	0.6203
US	5.0865	4.4238	0.0382	0.9618	0.8304

presents the BMAlog estimation results of a mixture copula model composed of Survival Clayton and Survival Gumbel copulas, capturing the dependence structure between the global market and individual country stock markets. The parameters ${\theta }_1$ and ${\theta }_2$ represent the strength of dependence for the Clayton and Gumbel copulas, respectively, while $w_1$ and $w_2$ denote their corresponding mixture weights. The most critical insight is conveyed by the lower tail dependence coefficient ${\lambda }_{L_{C_{\mathrm{mix}}}}$, which quantifies the extent of extreme downside co-movement, interpreted here as a static measure of contagion. Notably, the United States exhibits the highest degree of tail dependence with the global market ($\lambda =0.8304$), indicating strong systemic vulnerability to global shocks. European markets such as the United Kingdom and Spain also demonstrate substantial contagion effects, with $\lambda$ values of 0.6203 and 0.6169, respectively, reflecting their high financial integration. In contrast, China reports the lowest tail dependence ($\lambda =0.3034$), suggesting relative insulation from global market downturns, potentially due to capital flow controls and a more segmented financial system. Emerging markets like India and Thailand show moderate levels of contagion, while Australia and New Zealand lie between integrated and decoupled states. These findings underscore the heterogeneous nature of global financial linkages and highlight the importance of accounting for asymmetric and non-linear dependence structures when assessing contagion risk.

Then, the selected mixture copula model is re-estimated using the rolling window technique to capture the evolution of tail dependence over time. The rolling window method is widely applied in time series analysis to model dynamic relationships by performing repeated estimations over a fixed-length moving window.

In this study, we set the window size to 100 observations, which approximately corresponds to five months of daily trading data. Given a total of n observations, the data are partitioned into overlapping blocks as follows: from observations 1 to 100, 2 to 101, 3 to 102, and so on, until the final window from $n-99$ to n. The choice of a 100-day rolling window was motivated by the need to balance two considerations: (i) capturing the time-varying dynamics of contagion with sufficient resolution, and (ii) ensuring enough observations within each window to obtain stable tail-dependence estimates. For each window, the tail dependence coefficient is estimated using the previously selected mixture of survival Clayton and survival Gumbel copulas, with the copula weights determined by the BMA_log method. This approach allows us to generate a sequence of time-varying tail dependence estimates, which reveal how contagion effects between each national stock market and the MSCI World Index evolve over time. In particular, it enables the identification of periods of heightened dependence, especially during episodes of global financial stress such as the China–US trade war, the COVID-19 pandemic, and the Russia–Ukraine conflict.

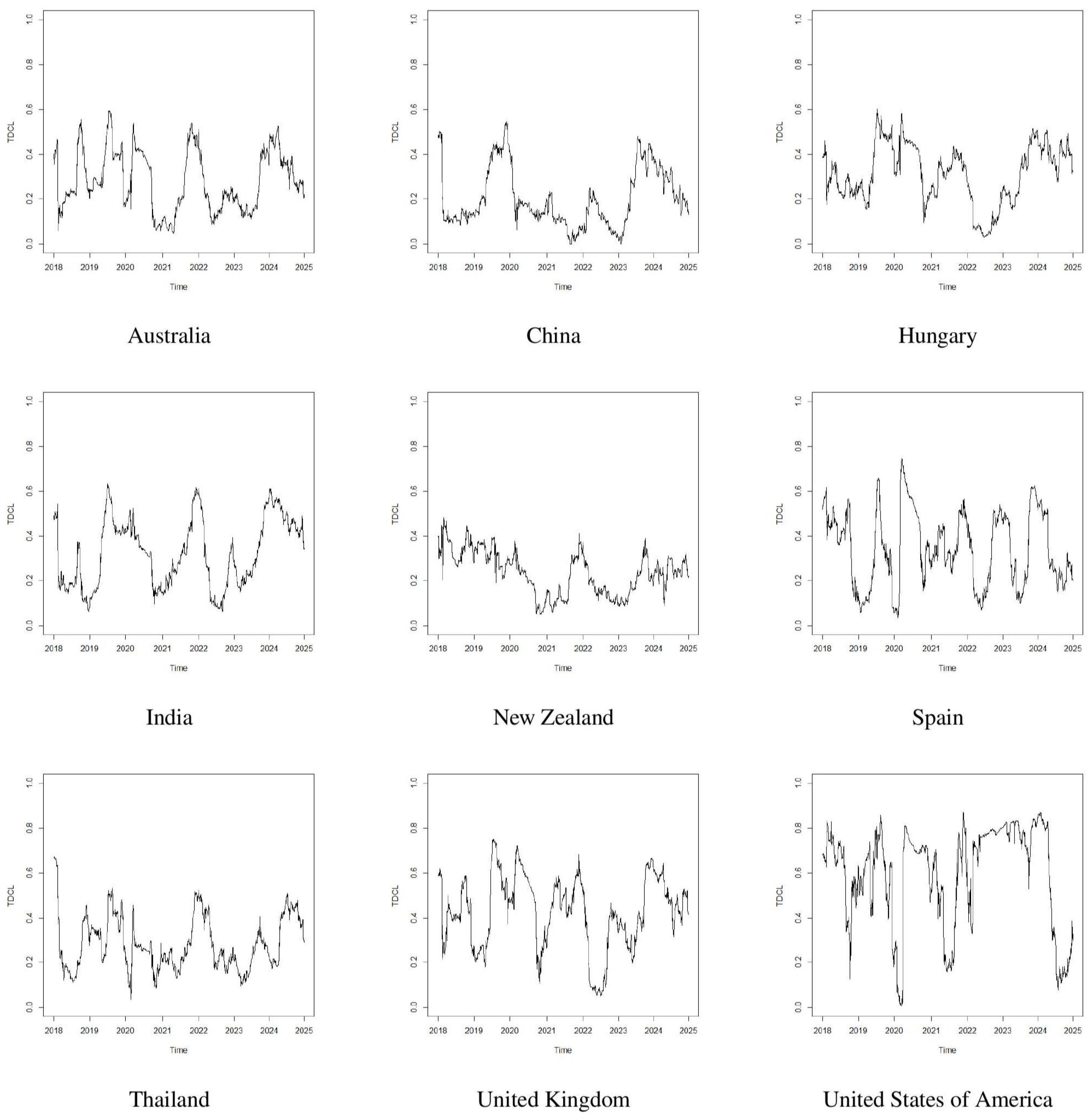
Figure 1 illustrates the evolution of LTDCs between the MSCI World Index and the stock markets of nine countries: Australia, China, Hungary, India, New Zealand, Spain, Thailand, the United Kingdom, and the United States. The plots reveal that contagion levels fluctuate significantly over time and vary across countries, suggesting that global shocks affect markets differently depending on economic structure, market openness, and regional exposure.

Notably, several periods show distinct spikes in tail dependence, indicating heightened co-movement during financial stress. To further analyze these dynamics, we focus on three major crises during the sample period: The China–US trade war (July 2019–January 2020), The COVID-19 pandemic (March 2020–July 2020), and The Russia–Ukraine war (February 2022–June 2022). These events provide clear benchmarks for evaluating how systemic shocks influence the strength and persistence of contagion across markets. By examining the trajectory of tail dependence around these periods, we aim to assess whether financial contagion intensified globally and to what extent it was asymmetric across countries.

4.1. Contagion of Australia

To gain a clearer understanding of contagion behavior over time, we summarize the tail dependence statistics for each country during the three major crisis periods. The summary results are presented in

Table 4. Contagion During Each Time Period.

Country	Period	Mean	Min	Max
Australia	China-US Trade War	0.3861	0.1655	0.5957
	COVID Outbreak	0.5429	0.4743	0.5817
	Russia-Ukraine War	0.4178	0.2951	0.5380
	Full Period	0.2329	0.0466	0.5957
China	China-US Trade War	0.4358	0.2412	0.5463
	COVID Outbreak	0.3407	0.2851	0.3656
	Russia-Ukraine War	0.1708	0.0623	0.2135
	Full Period	0.1851	0.0000	0.5463
Hungary	China-US Trade War	0.4701	0.3017	0.6014
	COVID Outbreak	0.5529	0.5439	0.5790
	Russia-Ukraine War	0.4669	0.3901	0.5824
	Full Period	0.2989	0.0280	0.6014
India	China-US Trade War	0.4662	0.4024	0.6335
	COVID Outbreak	0.5411	0.5218	0.5894
	Russia-Ukraine War	0.3772	0.3175	0.5231
	Full Period	0.2438	0.0622	0.6335
New Zealand	China-US Trade War	0.2920	0.1911	0.3945
	COVID Outbreak	0.4484	0.4127	0.5259
	Russia-Ukraine War	0.2366	0.1863	0.3479
	Full Period	0.3490	0.0501	0.4831
Spain	China-US Trade War	0.3214	0.0458	0.6580
	COVID Outbreak	0.6785	0.4512	0.7075
	Russia-Ukraine War	0.6099	0.4354	0.7468
	Full Period	0.4621	0.0359	0.7468
Thailand	China-US Trade War	0.3879	0.1029	0.5335
	COVID Outbreak	0.5002	0.2989	0.5680
	Russia-Ukraine War	0.2780	0.1474	0.4580
	Full Period	0.2787	0.0351	0.6720
UK	China-US Trade War	0.5882	0.3745	0.7492
	COVID Outbreak	0.6713	0.6540	0.6927
	Russia-Ukraine War	0.6164	0.5264	0.7221
	Full Period	0.4169	0.0499	0.7492
US	China-US Trade War	0.5616	0.0664	0.8583
	COVID Outbreak	0.8141	0.5269	0.8503
	Russia-Ukraine War	0.6146	0.0057	0.8129
	Full Period	0.7105	0.0057	0.8697

, which report descriptive statistics for each country’s dynamic tail dependence with the MSCI World Index during the China–US trade war, the COVID-19 pandemic, and the Russia–Ukraine war. During the China–US trade war (July 2019 to January 2020), Australia experienced a notable increase in contagion levels. This can be attributed to Australia’s strong economic linkages with both China, its largest export partner, and the United States, a dominant global economic force. The elevated co-movements during this period highlight the sensitivity of the Australian stock market to geopolitical tensions and disruptions in global trade dynamics.

The COVID-19 pandemic (March 2020 to July 2020) marked the peak of average contagion for Australia across the three events. The sharp rise in tail dependence reflects the unprecedented global scope of the pandemic, which triggered widespread market panic, synchronized economic downturns, and elevated uncertainty. These conditions led to a dramatic increase in cross-border financial co-movements, even among relatively stable markets like Australia.

During the Russia–Ukraine conflict (February 2022 to June 2022), Australia’s contagion level rose again, though not as sharply as during the pandemic. The observed increase is likely driven by global commodity price shocks, disruptions to international supply chains, and heightened investor risk aversion. Despite Australia’s geographical distance from the conflict, its integration into global financial markets and its exposure to energy and resource trade amplified its susceptibility to the resulting financial volatility.

4.2. Contagion of China

According to Table 4, the average contagion for China is relatively low, suggesting that under normal circumstances, China maintains a comparatively insulated financial position with limited susceptibility to external shocks. Its capital controls, large domestic market, and unique economic structure likely help reduce overall exposure to global contagion.

Unsurprisingly, the contagion level peaked during the trade war with the United States. As a key participant and central figure in the conflict, China faced elevated financial volatility, investor uncertainty, and disruptions to trade flows. The rise to 0.4358 indicates heightened sensitivity to policy risks, which spread across regional and global markets.

During the initial outbreak of the COVID pandemic, China also experienced a surge in contagion, though less severe than during the trade war. As the virus originated in China, the country faced early economic lockdowns, supply chain disruptions, and investor flight. The increase in contagion here reflects China’s central role in global trade and how shocks within its borders reverberated through the world economy, amplifying feedback effects.

In contrast, contagion during the Russia-Ukraine conflict was relatively muted. This reflects China’s more indirect involvement in the geopolitical event. While global markets were affected, particularly energy and commodity sectors, China’s internal financial mechanisms and political positioning likely shielded it from broader spillovers. The contagion value falling below the long-term average highlights China’s relative resilience during this period.

4.3. Contagion of Hungary

Hungary’s contagion level in Table 4 surged during the China-US trade tensions. Although Hungary was not a direct participant, the global nature of the conflict, especially its impact on European exports and investor sentiment, significantly affected Hungary’s financial system. As a member of the EU and a participant in global supply chains, Hungary faced indirect repercussions, illustrating how even geographically distant conflicts can ripple through interconnected economies.

The highest average contagion value for Hungary occurred during the early months of the COVID-19 pandemic. The widespread economic lockdowns, healthcare crises, and market panic triggered intense cross-market correlations and capital flight, severely impacting emerging European economies like Hungary. This figure highlights the extent to which global systemic crises, particularly those involving economic shutdowns, can overwhelm domestic markets, regardless of their origin.

The Russia-Ukraine conflict resulted in another spike in contagion for Hungary, which shares both geographical proximity and strong economic interdependence with the region. As a neighboring country, Hungary was particularly vulnerable to energy price shocks, refugee inflows, and regional security concerns. This elevated contagion level reflects direct exposure to geopolitical instability in Eastern Europe, compounded by Hungary’s reliance on Russian energy.

4.4. Contagion of India

During the trade war, India experienced a marked increase in contagion as shown in Table 4. While not a direct party to the conflict, India was exposed to the global trade uncertainty and supply chain shifts caused by tensions between the world’s two largest economies. The elevated contagion suggests that investor risk aversion and capital reallocation from emerging markets affected India significantly during this period.

Contagion reached its highest level during the COVID-19 pandemic, reflecting the global nature of the shock. Lockdowns, collapsing demand, capital flight, and heightened volatility hit India hard. This spike underscores how systemic crises with broad economic disruption can sharply increase cross-market linkages, especially in emerging markets that are integrated but not fully shielded.

Contagion also rose during the early stages of the Russia-Ukraine war. While India was geographically removed from the conflict, the war triggered global energy and commodity price volatility, with inflationary pressures and financial market instability spilling over into emerging markets. India’s relatively high average contagion value during this period points to its vulnerability to global inflationary shocks and geopolitical risk perceptions.

4.5. Contagion of New Zealand

New Zealand’s average contagion level is relatively high compared to larger economies like China (0.1851) or Australia (0.2329) as shown in Table 4. This suggests that even outside of major crisis periods, New Zealand’s financial system is fairly responsive to global shocks.

Interestingly, contagion during the trade war period was lower than the long-term average. This could be attributed to New Zealand’s more peripheral role in the trade conflict. While the country does maintain substantial trade relationships with both China and the U.S., it was not a central player in the geopolitical tension. This relative insulation may have helped limit the transmission of financial stress during this episode.

Contagion surged significantly during the COVID-19 crisis. The sharp rise reflects widespread investor panic, synchronized global downturns, and capital outflows that heavily affected open economies like New Zealand. Despite effective domestic public health responses, the globalized nature of the economy and dependence on tourism, trade, and commodity exports amplified financial vulnerabilities during this period.

Contagion dropped below both the baseline and previous crisis levels during the Russia-Ukraine conflict. This relatively muted response suggests that New Zealand was largely insulated from the direct economic and geopolitical fallout of the war. While global markets reacted to energy shocks and risk aversion, New Zealand’s geographic and trade distance from the conflict zone likely helped buffer its financial system.

4.6. Contagion of Spain

From Table 4, this high long-term average indicates that Spain’s financial system is persistently influenced by international market dynamics, even in periods without active global crises. As a member of the Eurozone with open capital markets and substantial international trade and investment flows.

During the China-US trade conflict, contagion in Spain was moderate and below its baseline level. This reflects Spain’s limited direct trade exposure to either China or the United States and relative insulation from the epicenter of the conflict. While investor sentiment globally was affected, Spain’s financial system was not significantly impacted. The Eurozone’s stability mechanisms may have helped buffer the country from sharper spillovers. The contagion value during this period shows Spain was not a primary transmission channel for this geopolitical-economic shock.

This was the highest contagion level for Spain during the observed period. Spain was one of the earliest and most severely impacted countries in Europe during the COVID-19 pandemic, facing prolonged lockdowns, a sharp decline in economic activity, and a strained healthcare system. The financial market responded accordingly, with heightened co-movement with global shocks, sharp equity declines, and capital outflows. The systemic nature of the crisis made contagion especially pronounced for Eurozone countries like Spain, which share financial infrastructure and monetary policy with the rest of Europe.

Contagion remained high during the Russia-Ukraine conflict, reflecting Europe’s direct economic and geopolitical exposure to the war. Although Spain is geographically further west, the broader European Union faced energy supply shocks, inflationary pressures, and market volatility. The financial interlinkages within the EU amplified the spillover effects, resulting in significant contagion to Spain’s markets as part of the broader European financial reaction.

4.7. Contagion of Thailand

Thailand’s long-term average contagion level is moderate according to Table 4. It suggests a steady but not extreme vulnerability to global financial disturbances. This baseline reflects the country’s export-driven economy, its role as a regional manufacturing and tourism hub and its involvement in global investment flows, especially from China and the U.S. While not as exposed as highly integrated financial centers, Thailand’s economy remains sensitive to changes in global demand and investor sentiment.

During the trade war, Thailand’s contagion rose sharply above its baseline. This is expected, given that Thailand is heavily linked to both China and the U.S. through trade, especially in electronics and intermediate goods. Global supply chain disruptions during the trade war created downstream effects for economies like Thailand, which serve as manufacturing hubs and re-exporters. The elevated contagion value reflects both direct trade exposure and indirect financial market co-movement driven by investor uncertainty.

Thailand experienced its highest contagion level during the COVID-19 pandemic, consistent with most countries. The pandemic caused a collapse in global tourism, severely impacting Thailand’s service sector, sharp declines in exports, and capital flight from emerging markets, including Southeast Asia. Financial panic and synchronized global downturns contributed to high contagion, revealing Thailand’s dual exposure to both global economic conditions and external investor behavior.

Contagion during the Russia-Ukraine conflict was low and nearly identical to Thailand’s baseline. This indicates that the war’s financial spillover to Thailand was relatively limited. Key reasons include Thailand’s geographic distance and minimal direct trade with Russia or Ukraine, limited financial market linkages with the region and a relatively low dependence on energy imports from conflict-affected areas. While global commodity price volatility may have had some indirect effects, the overall impact on Thailand’s financial markets remained contained.

4.8. Contagion of the United Kingdom

The UK’s average contagion level is relatively high in Table 4, underscoring its role as a globally interconnected economy. This reflects London’s position as a global financial hub, high exposure to cross-border capital flows, and deep ties to both developed and emerging markets through trade, investment, and banking. This level of contagion suggests that the UK is regularly influenced by shifts in global investor sentiment and economic conditions, even outside of crisis periods.

During the China-US trade conflict, the UK saw a substantial rise in contagion above its baseline. While not directly involved, the UK was affected by global trade uncertainty, which impacted business confidence and investment, volatility in global equity and currency markets, and its strong financial links to both Chinese and U.S. capital markets. The elevated contagion reflects the UK’s sensitivity to systemic risks, particularly when they originate from major economies that drive global financial dynamics.

The COVID-19 pandemic produced the highest contagion level for the UK during this period. This spike was driven by severe economic contraction and lockdowns, panic-driven global selloffs in equity and bond markets and sharp declines in consumer and investor confidence. As a country with a large, services-driven economy, and heavy reliance on international trade and finance, the UK experienced strong co-movement with global financial markets. The contagion level reflects both the global nature of the crisis and the UK’s exposure to systemic risk.

Contagion remained high during the Russia-Ukraine conflict, reflecting the UK’s proximity to the crisis in geopolitical and economic terms, despite not being in the Eurozone. This high contagion value illustrates the UK’s exposure to regional shocks and their global reverberations, particularly through energy markets and investor behavior.

4.9. Contagion of the United States of America

The U.S. has the highest baseline contagion among all countries analyzed in Table 4, indicating that its financial markets are continuously co-moving with global trends, even in the absence of acute shocks. This persistent high contagion reflects the U.S.’s position as the core of the global financial system, the global dominance of U.S. capital markets and the widespread use of the U.S. dollar as the world’s reserve currency. Due to these structural factors, the U.S. is both a source and recipient of contagion, amplifying its role in transmitting and absorbing global financial volatility.

Contagion during the trade war was substantial, though lower than the long-term average. As one of the two principal actors in the conflict, the U.S. experienced market volatility driven by trade policy uncertainty, fluctuations in tariff announcements and negotiations, and a shift in global investor sentiment. The contagion level reflects both domestic reactions to policy changes and international spillovers, with U.S. markets closely synchronized to global risk movements during this period.

The COVID-19 pandemic resulted in the highest contagion level for the U.S., reaching a peak of 0.8141. This figure captures the extraordinary scale of the crisis sharp equity market declines and record-breaking volatility, mass unemployment, disrupted supply chains, and emergency policy interventions, rapid capital outflows and synchronized downturns in global markets. As the epicenter of global finance, the U.S. experienced deep internal shocks and intense financial co-movement with the rest of the world. The high contagion reflects both outgoing and incoming financial transmissions, demonstrating the U.S.’s systemic centrality during a global crisis.

Contagion during the Russia-Ukraine conflict was also elevated even if it’s lower than the baseline for the U.S bur is well above the contagion baseline for most countries, though not as extreme as during the pandemic. The high contagion value reflects the global market repercussions of geopolitical tensions, with U.S. financial markets acting as a barometer and transmitter of global sentiment.

5. Discussion

The results of this study provide valuable insights into the dynamics of financial contagion and its dependence on the type and timing of global crises. First, the evidence clearly supports the view that contagion is not a static phenomenon, but rather highly time-varying. Figure 1 and Table 4 show that tail dependence coefficients surge sharply during episodes of market stress, such as the China–US trade war, the COVID-19 pandemic, and the Russia–Ukraine conflict. This is consistent with theoretical perspectives that contagion becomes most visible in turbulent periods (Dornbusch et al., 2000) and empirical evidence from earlier crises, such as Longin (2001), who observed extreme correlation increases during global equity downturns.

Second, the findings highlight that the *nature of the crisis* matters for the intensity and distribution of contagion. The China–US trade war produced moderate contagion concentrated in countries with strong trade ties to the U.S. and China, such as Australia, India, and Thailand. This aligns with the view of Bekaert et al. (2005), who argued that emerging markets and trade-dependent economies are more vulnerable to policy-driven shocks. By contrast, the COVID-19 pandemic triggered the highest and most synchronized levels of contagion across all markets, with LTDCs exceeding 0.8 in the U.S. and above 0.6 in several advanced and emerging markets. This finding confirms the hypothesis of Forbes and Rigobon (2002), who emphasized that contagion represents a significant rise in cross-market linkages during crises, and aligns with recent evidence that systemic real-economy shocks erode diversification benefits globally (Longstaff et al., 2011). The Russia–Ukraine conflict generated more regionally concentrated contagion, particularly in European countries such as Spain, the UK, and Hungary, reflecting their dependence on Russian energy supplies and geographic proximity to the conflict. This supports network-based theories of risk propagation (Billio et al., 2012; Diebold & Yilmaz, 2014), where shocks transmit more strongly through closely linked regional markets.

Third, the methodology applied in this study contributes to the empirical contagion literature by focusing on nonlinear and asymmetric dependence. Correlation-based and GARCH-type models are known to underestimate tail co-movements, especially during crises (R. Engle, 2002; R. F. Engle & Manganelli, 2004). The mixture copula framework with BMAlog estimation used here provides a more flexible structure, capturing heterogeneous dependence patterns across markets and over time. Compared to the Student-t copula benchmark, the mixture copula consistently achieved lower BIC values across all countries (Table 2), confirming its superior fit. This result is consistent with recent advances in contagion modeling that stress the importance of flexible copula structures (Christoffersen et al., 2012; Maneejuk et al., 2018; Rodriguez, 2007; Yamaka et al., 2023). By explicitly modeling lower-tail dependence, our results also align with McNeil et al. (2005), who emphasize that tail risk is the defining feature of systemic contagion.

Fourth, the empirical results provide theoretical confirmation of the systemic risk transmission mechanism. Portfolio theory suggests that diversification benefits decline when assets become highly correlated in downturns (Bekaert et al., 2005; King & Wadhwani, 1990). Our results confirm this, as contagion peaked during global crises when diversification opportunities were most needed but least available. The evidence also supports the interpretation of Rigobon (2003), who showed that failure to properly account for heteroskedasticity may lead to spurious contagion findings. By relying on copula-based tail dependence, we address this limitation and provide a more reliable measure of crisis-driven co-movements. In addition, the findings resonate with Dungey et al. (2005), who argued that methodological choice critically determines whether contagion is detected; our results show that tail-focused approaches provide clear evidence of contagion that may be overlooked by linear models.

Finally, the heterogeneity across countries illustrates that contagion is not uniform but shaped by market structure, openness, and regional exposure. Advanced economies such as the U.S. and UK display persistently high contagion due to their central role in global finance, consistent with Longstaff (2010) who documented the U.S. as a primary transmitter of financial shocks. Emerging markets such as China and Thailand exhibit more selective contagion episodes, reflecting structural differences such as capital controls (China) or heavy dependence on trade and tourism (Thailand). This heterogeneity confirms that contagion risk is context-specific and crisis-dependent, reinforcing the importance of adopting flexible, country-specific modeling frameworks.

In sum, the discussion highlights three key contributions of this study: (i) it confirms that contagion intensifies during systemic crises, with crisis type shaping both the intensity and geography of spillovers; (ii) it provides theoretical validation of contagion as extreme downside co-movement, consistent with portfolio theory and modern systemic risk definitions; and (iii) it demonstrates the value of mixture copula models with BMAlog estimation in capturing nonlinear, time-varying dependencies more accurately than conventional methods. These insights strengthen the theoretical and empirical foundations of financial contagion research and carry important implications for investors, regulators, and policymakers tasked with monitoring global systemic risk.

6. Conclusions

This study examines the static financial contagion between the global market and selected national stock markets, Australia, China, Hungary, India, New Zealand, Spain, Thailand, the United Kingdom, and the United States, over the period 2018 to 2024. Employing a flexible mixture copula approach that combines Survival Clayton and Survival Gumbel structures, the analysis captures nonlinear and asymmetric dependencies, especially in the lower tail of joint return distributions. The time frame encompasses three major global crises: the China–U.S. trade war, the COVID-19 pandemic, and the Russia–Ukraine conflict, enabling a comprehensive assessment of crisis-specific contagion dynamics.

The empirical findings reveal considerable heterogeneity in contagion intensity across countries and crises. The COVID-19 pandemic produced the most severe and widespread contagion, with tail dependence values frequently exceeding 0.5 and reaching peaks above 0.8 in the United States, highlighting the systemic and synchronized nature of the shock. In contrast, the China–U.S. trade war generated more moderate contagion, concentrated in trade-linked economies such as India, Hungary, and Thailand. The Russia–Ukraine conflict triggered elevated contagion in Europe-adjacent markets such as Spain and the UK due to energy supply disruptions and geopolitical uncertainty, while effects on emerging markets were more muted.

The results yield several clear policy recommendations. Countries with high levels of financial integration and exposure to external shocks should strengthen their macroprudential toolkits by implementing countercyclical capital buffers, conducting stress tests that explicitly incorporate tail-risk scenarios, and ensuring access to targeted liquidity facilities during crises. Equally important is the promotion of regional and global cooperation frameworks, such as ASEAN, the European Union, or IMF-led initiatives, that facilitate joint monitoring, cross-border liquidity support, and coordinated policy responses. Regulatory coordination across jurisdictions and transparent, timely dissemination of market-relevant information are essential to limit panic-driven contagion.

For emerging and developing economies, building greater institutional robustness, particularly in financial supervision, crisis management, and capital market deepening, is critical to reduce vulnerability to volatility spillovers from global markets. At the same time, fostering financial inclusion and more inclusive financial systems can enhance resilience by broadening participation in financial markets, reducing concentration of risks among a few large players, and improving access to credit for households and small firms during downturns. By expanding the reach of financial safety nets and deepening domestic capital markets, inclusive systems can help dampen the amplification of global shocks.

From the perspective of global investors, the findings highlight three key lessons. First, contagion intensifies during crises and substantially weakens diversification benefits, underscoring the importance of monitoring downside tail dependence rather than relying on average correlations. Second, contagion is heterogeneous: advanced economies such as the U.S. and UK exhibit persistently high co-movement with global markets, while emerging markets such as China and Thailand experience contagion more selectively. This implies that diversification strategies must be tailored not only to the structural characteristics of each market but also to the degree of financial development and inclusion. Third, different crisis types—policy-driven (China–U.S. trade war), real-economy (COVID-19), or geopolitical (Russia–Ukraine)—generate distinct contagion patterns. Investors should therefore adapt hedging and portfolio allocation strategies to the nature of the shock rather than assuming uniform responses across crises.

Despite these contributions, several limitations remain. First, although our rolling–window mixture–copula with BMAlog captures time variation in lower–tail dependence, it relies on a local–stationarity approximation, the choice of window length, and the fixed rolling scheme. While this approach is effective for highlighting broad contagion dynamics, future work could complement it by endogenizing dynamics through state–space or score–driven (GAS) dynamic copulas, or by employing regime–switching mixture copulas with time–varying BMAlog weights. Second, the reliance on aggregate market indices may conceal sectoral and firm–level heterogeneity; extending the analysis to industry portfolios or high–dimensional frameworks (e.g., vine copulas) would uncover richer contagion channels. Third, our nonparametric marginal specification based on empirical CDFs is robust but abstracts from volatility dynamics; comparing results with ARMA–GARCH or skew-t marginals, and allowing time-varying margins, would test the sensitivity of tail-dependence estimates. Fourth, although we use rolling windows to evaluate contagion around pre-defined crisis periods, we pre-specify these crisis windows and rely on the MSCI World as a single global factor; future work could explore data-driven break detection and multi-factor global/regional benchmarks to sharpen the identification of shock types. Finally, model risk remains: we restrict the mixture to Survival Clayton and Survival Gumbel; incorporating additional copula families and reporting bootstrap or Bayesian interval estimates would further strengthen robustness and the practical usefulness of the results. In addition, an important avenue for future research is to explore the extent to which financial inclusion policies and regional cooperation mechanisms mitigate contagion risk in developing economies. For example, empirical models could test whether countries with deeper and more inclusive financial systems, or with stronger participation in regional safety-net arrangements, are less exposed to tail-risk spillovers. Such analyses would enrich the understanding of how institutional and policy frameworks interact with market dynamics to shape resilience against global shocks.