Forecasting Financial Volatility Under Structural Breaks: A Comparative Study of GARCH Models and Deep Learning Techniques

Abstract

The main objective of this study is to evaluate the predictive performance of traditional econometric models and deep learning techniques in forecasting financial volatility under structural breaks. Using daily data from four Latin American stock market indices between 2000 and 2024, we compare GARCH models with neural networks such as LSTM and CNN. Structural breaks are identified through a modified ICSS algorithm and incorporated into the GARCH framework via regime segmentation. The results show that neglecting breaks overstates volatility persistence and weakens predictive accuracy, while accounting for them improves GARCH forecasts only in specific cases. By contrast, deep learning models consistently outperform GARCH alternatives at medium- and long-term horizons, capturing nonlinear and time-varying dynamics more effectively. This study contributes to the literature by bridging econometric and deep learning approaches and offers practical insights for policymakers and investors in emerging markets facing recurrent structural instability.

1. Introduction

Accurately forecasting financial volatility is a cornerstone of risk management. It matters not only for investors and portfolio managers but also for regulators concerned with financial stability. Reliable volatility models help anticipate market turbulence, guide asset allocation, improve hedging strategies, and ultimately reduce exposure to systemic risk. In emerging markets, where political, macroeconomic, and institutional shocks are frequent, the ability to capture and predict volatility dynamics becomes especially important.

Over the past four decades, conditional heteroscedasticity models such as ARCH (Engle, 1982) and GARCH (Bollerslev, 1986) have become standard tools for modeling the variance of asset returns. Numerous studies confirm their effectiveness in capturing volatility clustering and persistence in both developed and emerging markets (Babikir et al., 2012; Rapach & Strauss, 2008). However, these models rely on the assumption of parameter stability, which is often unrealistic in environments where crises, regime shifts, or external shocks alter market dynamics. Ignoring such breaks produces specification errors, biased estimates, and an overstatement of volatility persistence (Mikosch & Stărică, 2004). To address this limitation, methods such as the ICSS algorithm (Inclán & Tiao, 1994) and the multiple change-point tests of Bai and Perron (1998) have been widely applied. Evidence shows that incorporating structural breaks improves the forecasting performance of GARCH models across different markets (e.g., De Gaetano, 2018; Gong & Lin, 2018; Kumar, 2018). Nevertheless, most of this literature remains confined to traditional econometric frameworks.

In contrast, recent advances in machine learning—particularly deep learning—have opened new possibilities for volatility modeling in unstable environments. Long Short-Term Memory (LSTM) networks (Hochreiter & Schmidhuber, 1997) and Convolutional Neural Networks (CNNs) (LeCun et al., 1998) have been successfully applied to forecasting prices, returns, and volatility in equity and cryptocurrency markets (Fischer & Krauss, 2018; Khan et al., 2023; Nelson et al., 2017; Petrozziello et al., 2022). Their advantage lies in capturing nonlinear dynamics, regime shifts, and long-memory effects without imposing restrictive assumptions on the data-generating process. This flexibility makes them well suited to environments characterized by recurrent structural breaks. Unlike GARCH-type models, they can adapt more naturally to abrupt changes in volatility regimes. However, few studies have systematically compared deep learning and GARCH approaches under explicit structural instability. This remains a critical gap in the literature.

This study addresses that gap. We conduct a systematic empirical evaluation of the predictive performance of GARCH models—estimated under expanding, rolling, and break-segmented windows—versus deep learning models (LSTM and CNN) in the presence of structural breaks in conditional variance. The analysis uses daily data from four major Latin American stock indices: IGBVL (Peru), BOVESPA (Brazil), IPSA (Chile), and IPC (Mexico) over 2010–2024. By covering episodes such as the global financial crisis, the COVID-19 pandemic, and recent geopolitical tensions, the dataset provides a robust setting to examine volatility forecasting under recurrent shocks. The central objective is to determine which class of models offers greater robustness under structural instability, using metrics such as MSFE and QLIKE, along with the tests of White (2000) and Hansen (2005) to evaluate predictive accuracy.

We hypothesize that the predictive power of GARCH models is substantially weakened when structural breaks are not explicitly modeled. In contrast, deep learning architectures—because they do not rely on rigid stability assumptions—are expected to sustain, and in some cases improve, forecasting accuracy in highly dynamic environments.

The remainder of this paper is organized as follows: Section 2 reviews the related literature on structural breaks, volatility forecasting, and deep learning applications. Section 3 presents the data and methodology. Section 4 reports the empirical results. Section 5 discusses the findings in light of prior research. Section 6 concludes and highlights the practical implications for investors and risk managers in emerging markets.

2. Literature Review

Recent literature on volatility forecasting and financial risk has converged along two main paths: (i) the explicit modeling of structural breaks and regime shifts in conditional variance and (ii) the adoption of deep learning architectures and hybrid frameworks that combine econometric specifications with nonlinear learning. Below, we summarize the most relevant contributions along these thematic axes.

2.1. Structural Breaks and Regime Dynamics

Earlier contributions consistently show that the explicit inclusion of structural breaks improves both the fit and the predictive ability of GARCH models across different financial markets (De Gaetano, 2018; Gong & Lin, 2018; Kumar, 2018). Moving-window approaches—whether expanding or rolling—have been combined with segmentations guided by empirically detected breaks (De Gaetano, 2018). Moreover, methodologies such as impulse indicator saturation (IIS), developed by Oxford researchers, jointly detect breaks and outliers, offering additional robustness in volatility modeling (Castle et al., 2022).

Building on these foundations, more recent studies highlight that ignoring breaks induces persistence biases and undermines predictive accuracy. For instance, Luo et al. (2025) identify breaks in realized betas and asymmetric risk effects, combining ICSS predictors with LASSO selection in HAR models to improve out-of-sample performance. Similarly, Sun et al. (2025) propose a multiplicative structure that separates shifts in unconditional variance—detected via binary segmentation—from conditional GARCH dynamics, achieving a better fit under nonstationarity. In fragile exchange rate regimes, Daboh et al. (2025) confirm regime shifts using EGARCH and Markov-Switching models, while Amin et al. (2024) document that global recessions trigger sharp increases in commodity volatility with product-specific patterns. During the COVID-19 crisis, de Oliveira et al. (2024) showed that long memory and breaks coexist, and that modeling them jointly prevents misspecification. Along these lines, Bildirici et al. (2020) design a hybrid LSTAR-GARCH-LSTM approach, where smooth regime transitions in both mean and variance are integrated with the adaptive capacity of LSTM, producing superior forecasts for crude oil under COVID-19 shocks. Applied to the stock–currency nexus in China, Fang and Yang (2025) combine a DCC-CGARCH with break analysis and RR-MIDAS, linking ruptures to the GFC, regulatory reforms, trade wars, and COVID-19. In crypto and equity markets, Tsuji (2025) integrate breaks and asymmetric errors into a unified GARCH framework, uncovering double asymmetries between Bitcoin and the S&P 500.

2.2. Deep Learning and GARCH Hybridization

In parallel, deep learning techniques have expanded the modeling frontier by combining econometric structures with neural networks. Araya et al. (2024) merge ARIMA/ARCH–GARCH with CNN/LSTM; Di-Giorgi et al. (2025) show that GRU, LSTM, and BiLSTM paired with GARCH improve weekly forecasts; and Bhambu et al. (2025) design a GARCH–MLP–Mixer for high-frequency data, outperforming benchmarks also in VaR estimation. In cryptocurrencies, García-Medina and Aguayo-Moreno (2024) find that LSTM–GARCH dominates pure GARCH both under heteroscedastic error metrics and portfolio criteria. The use of intraday data has further amplified gains: DeepVol (Moreno-Pino & Zohren, 2024) employs dilated causal convolutions with high-frequency inputs, while Hortúa and Mora-Valencia (2025) apply Bayesian deep learning to the VIX with calibrated uncertainty. On interpretability, Zhang et al. (2024) integrate a memory-based architecture and a large language model to generate narratives explaining volatility spikes. Nevertheless, results are not universal: Zitti (2024) report that ARMA outperforms LSTM in the salmon market, underscoring that nonlinear gains depend on the asset and horizon. In Latin America, Kristjanpoller and Minutolo (2014) find that ANN–GARCH hybrids improve forecasts for Brazil, Chile, and Mexico, while Patra and Malik (2025) detect volatility connectedness between the US and Latin America through Q–VAR. Similarly, Alfeus (2025) show that HAR, RealGARCH, RECH, and RFSV outperform standard GARCH in South Africa.

Another active line of research extends hybridization beyond univariate volatility to capture dynamic correlations across markets. For example, Ni and Xu (2023) improve DCC–GARCH by correcting its errors with a recurrent deep neural network and an autoencoder, increasing accuracy across China, Hong Kong, the US, and Europe. Along similar lines, Chung et al. (2024) integrate DCC–GARCH with LSTM to analyze contagion from the US to Latin America during COVID-19, detecting significant spillovers from the S&P 500 to regional indices (except MERVAL). Their results show that LSTM enhances the prediction of dynamic correlations and provides early-warning signals, illustrating the benefits of coupling conditional dependence models with recurrent networks under high uncertainty.

2.3. Textual Information, Big Data, and News

A complementary strand of work focuses on news and textual data as volatility predictors. Bodilsen and Lunde (2025) show that domestic macro sentiment improves forecasts for the S&P 500 and single stocks, especially at long horizons, while overnight news counts add value at the 1-day horizon. Using a regime-switching design, Boubaker et al. (2021) link news diversity to crashes, finding that diversity falls in bearish high-volatility periods and rises during recoveries, with structural breaks reinforcing predictive power.

2.4. Reviews, Model Selection, and Robustness

Recent scoping reviews emphasize the rapid growth of ML applications in volatility forecasting. Molina Muñoz and Castañeda (2023) report an exponential rise in publications since 2019, with hybrid models dominating. Qiu et al. (2025) compare implied volatility, GARCH, LSTM, and Transformers, highlighting complementarity rather than substitution. On model selection, Hassanniakalager et al. (2024) introduce an FDR-based framework to identify “buckets” of superior models, showing that GJR–GARCH consistently minimizes one-step-ahead errors in realized volatility. Moreover, recent evidence (e.g., Di-Giorgi et al., 2025) shows that Gated Recurrent Units (GRUs) often outperform LSTM in commodity markets, suggesting that GRU represents a promising extension for future research. These approaches are especially valuable for comparisons involving rolling versus expanding windows, explicit breaks, and deep learning alternatives under the risk of overfitting.

2.5. Study Objective and Hypotheses

In light of these gaps, our study offers a systematic, head-to-head comparison of GARCH models with structural breaks—estimated under expanding, rolling, and break-segmented windows—against deep learning architectures (LSTM and CNN) in Latin American equity markets subject to recurrent shocks. We hypothesize as follows:

• Ignoring structural breaks reduces the predictive accuracy of GARCH models, whereas explicitly modeling them improves performance.
• Deep learning models, thanks to their flexibility, maintain or enhance predictive accuracy in the presence of structural instability.
• Under a rigorous out-of-sample evaluation based on MSFE, QLIKE, and the tests of White (2000) and Hansen (2005), deep learning approaches will show superior forecasting performance in highly dynamic environments such as Latin American financial markets.

3. Materials and Methods

3.1. Data

Our analysis relies on the daily returns of four representative Latin American stock indices: IGBVL (Peru), BOVESPA (Brazil), IPSA (Chile), and IPC (Mexico). These markets were selected because they are classified as emerging economies that are highly vulnerable to both domestic and international shocks, making them an ideal setting to examine the impact of structural breaks on financial volatility. The study period, from 2 January 2000 to 1 January 2024, was chosen to capture a wide range of major economic, financial, and political events known to induce abrupt regime changes. These include the 2008 global financial crisis, regional institutional and political crises, the Chilean social unrest of 2019, and the COVID-19 pandemic. By covering this extended and turbulent horizon, our analysis provides a robust context to evaluate model performance under different volatility regimes and structural instability scenarios. The data were obtained from Yahoo Finance (https://finance.yahoo.com, accessed on 2 February 2025).

Daily returns were calculated as follows:

$$r_t=100[ln{P}_t-ln{P}_{t-1}]$$

where $r_t$ represents the asset returns at time t, and $P_t$ and $P_{t-1}$ are the closing prices at times t and $t-1$, respectively.

The methodology in this study presents two main blocks: first, econometric techniques based on GARCH models and structural break detection are developed, and the second block incorporates deep learning models with the objective of capturing nonlinear patterns and long-run dependencies in the dynamics of asset volatility.

3.2. Modified ICSS Algorithm

The Iterative Cumulative Sum of Squares (ICSS) algorithm, proposed by Inclán and Tiao (1994), allows detecting multiple changes in the unconditional variance of a time series. Since financial series commonly exhibit conditional heteroscedasticity, a modified version of the ICSS is used that incorporates nonparametric adjustments to correct for possible autocorrelation, as occurs in GARCH processes.

The methodology is based on the cumulative sum of the squares of the observations, denoted as $y_t^2$, as follows:

$$C_k=\sum _{i=1}^k{y}_i^2$$

(1)

From this cumulative sum, the relative change statistic is constructed, as follows:

$$D_k={\displaystyle \frac{C_k}{C_T}}-{\displaystyle \frac{k}{T}}$$

(2)

In contrast with the original formulation of the ICSS test—which detects breaks when the statistic $AIT={\sup }_{t\in (T-2]}\left|\sqrt{T-2}{D}_t\right|$ exceeds a critical threshold $\lambda$—the modified version implemented in this study, inspired by Sanso et al. (2004), uses the statistic $G_k$. This incorporates a robust estimate of the unconditional variance, denoted by $\widehat{\lambda }$, which considers the squared autocovariances of the returns:

$$G_k={\widehat{\lambda }}^{-0.5}\left[C_k-\left({\displaystyle \frac{k}{T}}\right)C_T\right]$$

(3)

Given that the original algorithm by Inclán and Tiao (1994) assumes independence between observations—an unrealistic assumption in the presence of ARCH or GARCH effects—the modification proposed by Ni et al. (2016) extends its applicability to contexts with temporal dependence through a nonparametric approach.

The procedure is applied recursively: when a significant break point is identified, the series is divided into two segments (before and after the break), and the test is reapplied to each subsegment. This process is repeated until no new breaks are detected, allowing multiple breaks in the variance to be identified. This segmentation is then used to adjust GARCH models by regime or introduce dummy variables that capture the detected discontinuities.

It is worth noting that alternative structural break tests have been widely employed in the econometric literature. In particular, the multiple breakpoint test of Bai and Perron (1998) and the Quandt–Andrews test (Andrews, 1993; Quandt, 1960) are commonly applied in financial econometrics to detect shifts in regression parameters or variance structures. Although these methods were not implemented in the present study, they provide complementary perspectives and constitute promising avenues for robustness checks in future research. Our focus on the modified ICSS approach is motivated by its ability to directly address unconditional variance shifts in the presence of GARCH effects, which is the central concern of this paper.

3.3. GARCH Model

The dynamics of conditional volatility can be modeled using a Generalized Autoregressive Conditional Heteroscedasticity process of order (1, 1), known as GARCH(1, 1). This model captures the temporal dependence in the variance of the errors, allowing both recent shocks and previous levels of volatility to be incorporated.

The model is specified for errors $e_t$ as

$$e_t={\sigma }_t{ϵ}_t$$

(4)

$${\sigma }_t^2=\omega +\alpha e_{t-1}^2+\beta {\sigma }_{t-1}^2$$

(5)

where $\omega >0$, $\alpha \ge 0$, and $\beta \ge 0$ are model parameters. Here, ${\sigma }_t^2$ represents the conditional variance of $e_t$, while ${ϵ}_t$ is an i.i.d. process with zero mean and unit variance, typically assumed to be standard normal.

The condition $\alpha +\beta <1$ guarantees that the process has finite unconditional variance, given by

$$\mathrm{Var}\left(e_t\right)={\displaystyle \frac{\omega }{1-\alpha -\beta }}$$

(6)

Furthermore, the process $e_t$ is a martingale in differences and constitutes white noise with mean zero.

The parameters are commonly estimated using the quasi-maximum likelihood (QMLE) method, which produces consistent and asymptotically normal estimators even under moderate deviations from normality (Blasques et al., 2018; Stărică & Granger, 2005). This method is particularly suitable when the conditional distribution of the errors is not completely known, but a convenient functional form (e.g., normal) is assumed for constructing the likelihood function.

3.4. Deep Learning

Deep learning approaches have recently gained prominence as powerful alternatives for modeling complex financial phenomena characterized by nonlinearity, volatility clustering, and structural changes. Architectures such as Long Short-Term Memory (LSTM) networks and Convolutional Neural Networks (CNNs) have been successfully applied to forecasting asset prices, returns, and volatility. In this study, LSTM and CNN models are included because of their flexibility in capturing nonlinear dynamics and regime shifts. Unlike GARCH models, they do not assume parameter stability, which makes them particularly suitable for forecasting volatility during structural breaks.

3.4.1. Long Short-Term Memory (LSTM)

Long Short-Term Memory (LSTM) networks, introduced by Hochreiter and Schmidhuber (1997), represent a specialized architecture within recurrent neural networks (RNNs), designed to mitigate the problem of gradient vanishing. This capability makes them particularly well suited to capturing long-term dependencies in sequential data, such as financial returns, where volatility dynamics often exhibit persistent memory and nonlinear behavior.

The main strength of LSTMs lies in their internal memory mechanism, which selectively regulates what information is retained, forgotten, or updated at each time step. This functionality is implemented through a set of gates (for forgetting, input, and output), whose operation is given by the following set of equations:

• Forget Gate ($f_t$): Regulates which information from the previous cell state should be removed. It applies a sigmoid activation to the concatenation of the prior hidden state $h_{t-1}$ and the current input $x_t$, producing a weight between 0 and 1 that controls the degree of forgetting, as follows:

  $$f_t=\sigma (W_f·[h_{t-1},x_t]+b_f)$$

  (7)
• Input Gate ($i_t$): Determines the portion of new information to be incorporated into the memory cell. Through a sigmoid activation, it selects the relevant signals to be updated, as follows:

  $$i_t=\sigma (W_i[h_{t-1};x_t]+b_i).$$

  (8)
• Candidate Vector (${\tilde{C}}_t$): Generates a vector of candidate values that may enrich the cell state. This vector is formed by applying a hyperbolic tangent transformation to the weighted input and previous hidden state, as follows:

  $${\tilde{C}}_t=tanh(W_C[h_{t-1};x_t]+b_C).$$

  (9)
• Cell State Update ($C_t$): Integrates retained information from the previous state with newly generated candidate values to update the cell memory. The previous state is scaled by the forget gate $f_t$, while the candidate vector is modulated by the input gate $i_t$. Both contributions are combined through the Hadamard product, i.e., element-wise multiplication (Magnus & Neudecker, 2019), as follows:

  $$C_t=f_t\odot C_{t-1}+i_t\odot {\tilde{C}}_t.$$

  (10)
• Output Gate ($o_t$): Selects which parts of the updated memory will influence the current output. A sigmoid activation provides the weighting, as follows:

  $$o_t=\sigma (W_o[h_{t-1};x_t]+b_o).$$

  (11)
• Hidden State ($h_t$): Produces the actual output of the LSTM at time t. It is obtained by applying a hyperbolic tangent to the updated cell state and filtering it through the output gate, as follows:

  $$h_t=tanh\left(C_t\right)\odot o_t.$$

  (12)

3.4.2. Convolutional Neural Networks (CNNs)

Convolutional Neural Networks (CNNs) were initially designed to process spatially structured data, but they have been successfully adapted to time series applications, including financial forecasting (Dauphin et al., 2017). In this temporal context, CNNs apply one-dimensional convolutional filters along the sequence of observations, enabling the detection of local patterns and temporal dependencies. Such filters are particularly effective in financial data, where abrupt peaks, volatility clusters, and short-lived structural regularities often signal shifts in future market behavior.

The predictive process in CNNs involves the following key components:

• Convolutional Layers: Extract local features by applying filters that slide across the input series, generating feature maps.
• Pooling Layers: Downsample these feature maps, commonly through max pooling, to reduce dimensionality while preserving the most salient features.
• Flattening: Convert the multidimensional feature maps into a one-dimensional vector suitable for subsequent processing.
• Fully Connected Layers: Map the extracted features to the final output, allowing the network to combine information across different filters and learn complex relationships.

The kernel size of the convolutional filters defines the temporal window explored at each step. Smaller kernels capture short-term dynamics, while larger kernels incorporate longer-term dependencies. Because financial time series often exhibit patterns at multiple horizons, it is common to employ several convolutional layers with varying kernel sizes, enabling the model to build a hierarchical representation of temporal structures and enhance predictive accuracy.

3.5. Forecast Performance Metrics

The predictive accuracy of volatility models is assessed using loss functions that quantify the discrepancy between observed volatility and generated forecasts.

3.5.1. Aggregated Mean Squared Forecast Error ($MSF{E}^{*}$)

Stărică and Granger (2005) propose a specific loss function to compare the predictive performances of volatility models based on a temporal aggregation approach. The resulting metric is an extended version of the mean squared forecast error (MSFE), which incorporates information about a cumulative prediction horizon of length s, as follows:

$$MSF{E}_{S,1}^{*}={\displaystyle \frac{1}{P-(S-1)}}\sum _{t=R+2}^T{\left({\tilde{e}}_t^2-{\tilde{\widehat{\sigma }}}_{t\mid t-s,1}^2\right)}^2$$

(13)

where ${\tilde{e}}_t^2={\sum }_{j=1}^s{e}_{t-(j-1)}^2$ represents the cumulative sum of squared returns in the forecast window, and ${\tilde{\widehat{\sigma }}}_{t\mid t-s,1}^2={\sum }_{j=1}^s{\widehat{\sigma }}_{t-(j-1)\mid t-s,1}^2$ corresponds to the sum of the conditional variances estimated by the model under evaluation, calculated over the same horizon.

To determine whether the differences observed in predictive accuracy are statistically significant, the statistic developed by Babikir et al. (2012) is used. This procedure allows us to evaluate the superiority of one model over another when there is nesting between them—that is, when one model can be considered a restricted version of the other.

In the context of this research, the models evaluated are considered nested with respect to the base model (GARCH(1, 1) expanding window). The null hypothesis states that there is no difference in the average performance of the models compared. Rejecting this hypothesis implies that the model of interest offers a statistically significant improvement in terms of predictive power.

3.5.2. Quasi-Likelihood Loss (QLIKE)

QLIKE is motivated by the log-likelihood of the normal distribution and has advantages when evaluating volatility models, as it does not excessively penalize overestimates like MSFE. It is defined as

$$QLIKE={\displaystyle \frac{1}{P}}\sum _{t=R+1}^T\left[log\left({\widehat{h}}_t\right)+{\displaystyle \frac{r_t^2}{{\widehat{h}}_t}}\right]$$

(14)

This metric is particularly robust to conditional heteroscedasticity, and has been recommended by Patton (2009) as a preferred criterion in financial contexts. Lower values of QLIKE indicate better model fit to the observed volatility behavior.

3.5.3. White and Hansen Test

To assess whether differences in predictive performance between models are statistically significant, the loss function equality tests proposed by White (2000) and Hansen (2005) are used.

Both procedures are based on the series of loss differences, as follows:

$$d_t=L_t^{\left(1\right)}-L_t^{\left(2\right)}$$

(15)

where $L_t^{\left(1\right)}$ and $L_t^{\left(2\right)}$ represent the losses (e.g., MSFE or QLIKE) associated with models 1 and 2, respectively. The null hypothesis being tested is

$$H_0:\mathbb{E}\left[d_t\right]=0$$

The White test is based on the average of $d_t$, adjusted for its robust variance (usually estimated using the Newey–West method), and allows for comparing the equality of performances between two models.

The Hansen test introduces the notion of Superior Predictive Ability (SPA), allowing us to evaluate whether a particular model statistically dominates a set of alternatives under multiple comparisons. This approach is useful when comparing several models simultaneously.

3.6. Methodology

This study adopts a rigorous and replicable methodological approach, in line with the best practices proposed by Pesämaa et al. (2021), which highlight the importance of transparency, replicability, and robustness in the experimental design of quantitative research.

The methodology combines traditional econometric tools with deep learning models, with the main objective of comparing the predictive power of GARCH models (with and without structural breaks) and deep neural networks (LSTM and CNN) in predicting the conditional volatility of financial assets, specifically in environments characterized by structural instability. The dataset was divided into two main parts: an 80% training set and a 20% test set. The training set was used for model estimation, while the test set was strictly reserved for out-of-sample forecasting. For the deep learning models, a portion of the training sample was internally allocated as a validation set to tune hyperparameters. This design ensures a strict separation between estimation and forecasting phases and prevents any look-ahead bias. The procedure is organized into two main blocks: in-sample evaluation and out-of-sample evaluation.

3.6.1. In-Sample Evaluation

• Stage 1: Identification of structural breaks

The ICSS (Iterated Cumulative Sums of Squares) algorithm from Inclán and Tiao (1994), in its modified version, was applied to detect breakpoints in the unconditional variance of the returns of the stock indices analyzed. The breaks were detected across the entire available sample in order to obtain a comprehensive understanding of the historical structural dynamics of volatility, which is essential for robustly informing the subsequent stages of modeling.

• Stage 2: Estimation of models in subsamples

Once the breakpoints were identified, the time series was segmented into homogeneous subsamples. For each subperiod, GARCH(1, 1) volatility models were fitted to capture the particular characteristics of the volatility dynamics in each identified regime. The estimation was performed using maximum likelihood.

3.6.2. Out-of-Sample Evaluation

• Stage 3: Forecasting design

For the out-of-sample evaluation, the full series was divided into a training sample of size R and a test sample with P observations, such that $T=R+P$. The predictive performance of all models was assessed exclusively on the test sample. We implemented and compared four variants of the GARCH(1, 1) model with two deep learning architectures:

• GARCH(1, 1) with Expanding Window: This model served as our benchmark. The estimation sample was expanded recursively: starting with data from $t=1$ to $t=R$, the model was estimated and a one-step forecast was generated. Then, at each iteration, a new observation was added and the model was re-estimated to issue the next forecast. This approach inherently assumes parameter stability over time.
• GARCH(1, 1) with Rolling Window 0.25 and 0.5: These models used a fixed-size estimation window equivalent to 25% or 50% of the training sample. The window slid forward one step at a time, and the model was re-estimated for each new forecast, allowing parameters to be dynamically updated with the most recent information.
• GARCH(1, 1) with Structural Breaks: For this dynamic approach, the modified ICSS algorithm was applied to the observations available up to time R. If at least one significant variance break was detected, the GARCH(1, 1) model was estimated using only the observations after the most recent break point. If no structural changes were detected, the model was estimated with the entire sample up to time R. This recursive procedure was carried out throughout the out-of-sample period, ensuring that no look-ahead bias occurred. While this approach adapts effectively to regime changes, a break occurring very close to the forecast date may result in a limited number of observations for estimation, which could affect parameter stability.
• LSTM and CNN Neural Networks: Both deep learning models were trained on the training sample. For each out-of-sample forecast, a new prediction was generated by feeding the network with an updated sliding window of the most recent data. Importantly, these networks were not retrained during the out-of-sample period but relied on their learning capacity to capture long-term dependencies (LSTM) and local patterns (CNN) in order to adapt to new market information.

The predictive accuracy of all models was evaluated at four different horizons: $s=1,20,60,120$ days.

• Stage 4: Predictive performance evaluation

The accuracy of the forecasts generated by each model was evaluated using two standard metrics: the aggregated version of mean squared forecast error (MSFE) and the quasi-likelihood loss function (QLIKE), both applied to the out-of-sample data. In addition, two statistical tests were applied to contrast significant differences in performance between models, as follows:

• The White (2000) test, which compares the mean loss differences between pairs of models, adjusting the variance with a robust estimator;
• The Hansen (2005) Superior Predictive Ability (SPA) test, which assesses whether any model statistically outperforms the benchmark within a set of competitors.

Figure 1 summarizes the end-to-end workflow, from break detection to model estimation and forecasting.

4. Results

4.1. Descriptive Statistics

Table 1. Summary statistics of asset returns.

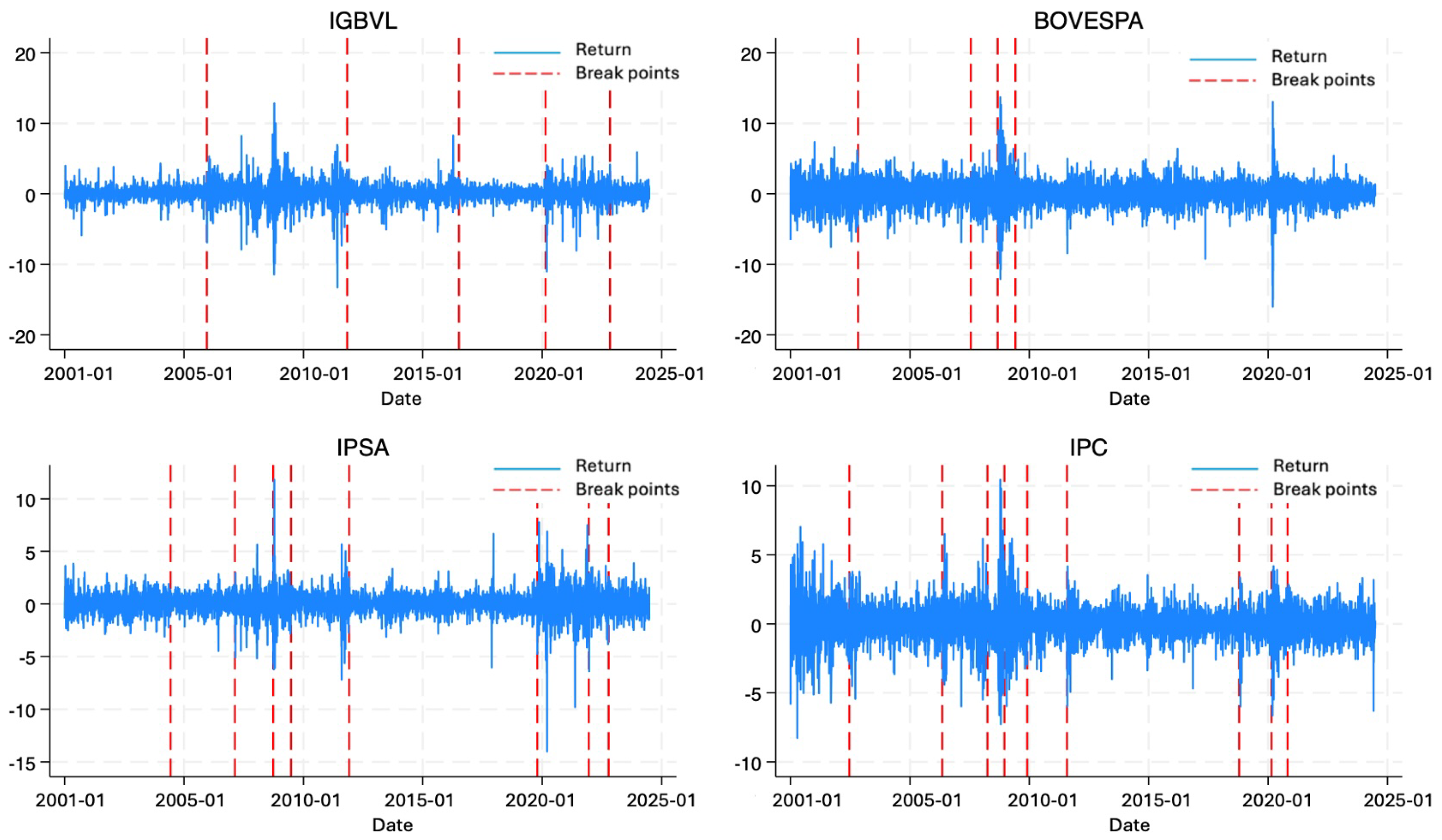
	IGBVL	BOVESPA	IPSA	IPC
Return
Minimum	−0.11001	−0.1599	−0.1401	−0.0664
Maximum	0.0826	0.1302	0.0749	0.0634
Mean	0.0002	0.0003	0.0002	0.0001
Standard Deviation	0.0113	0.0159	0.0118	0.0102
Skewness	−0.4906	−0.7165	−1.2829	−0.3592
Kurtosis	12.6790	14.3077	21.9460	7.0105
Shapiro–Wilk	12.3240 (0.000)	12.1120 (0.000)	13.1060 (0.000)	10.1400 (0.000)
Squared return
Ljung–Box (r = 20)	91.51 (0.000)	45.82 (0.001)	58.02 (0.000)	25.74 (0.174)
ARCH LM (q = 2)	111.04 (0.000)	726.03 (0.000)	453.71 (0.000)	82.15 (0.000)
ARCH LM (q = 10)	235.89 (0.000)	941.86 (0.000)	466.94 (0.000)	334.49 (0.000)

reports the main descriptive statistics for daily returns of the four Latin American stock indices. As expected, average returns are close to zero across all series, a well-documented feature of financial return data. Among the markets considered, BOVESPA exhibits the highest standard deviation, reflecting greater volatility and risk exposure relative to the other indices.

The distributional properties deviate from normality in several dimensions. All return series display negative skewness, indicating that extreme losses are more likely than extreme gains. Moreover, the excess kurtosis values (well above three) point to heavy-tailed distributions. These deviations from normality are statistically confirmed by the Shapiro–Wilk test, which strongly rejects the null hypothesis of normality at the 5% level ($p<0.05$).

Dependence patterns in second moments are also evident. The Ljung–Box test on squared returns reveals significant autocorrelation for most indices, implying that volatility clusters over time: periods of high volatility are likely to be followed by high volatility, and the same holds for tranquil periods. Consistent with this evidence, the ARCH–LM tests strongly reject the null hypothesis of no ARCH effects, confirming the presence of conditional heteroscedasticity. These results provide clear justification for the use of GARCH-type models to capture and forecast volatility dynamics in these markets.

4.2. In-Sample Results

Table 2. Structural breaks in volatility with time period.

IGBVL	BOVESPA	IPSA	IPC
14 December 2005	30 October 2002	9 June 2004	19 June 2002
31 October 2011	23 July 2007	19 February 2007	10 May 2006
8 July 2016	3 September 2008	26 September 2008	1 April 2008
21 February 2020	4 June 2009	26 June 2009	17 December 2008
4 November 2022		30 November 2011	1 December 2009
		18 October 2019	1 August 2011
		13 December 2021	17 October 2018
		14 October 2022	21 February 2020
			27 October 2020

reports the dates of the structural breaks detected in the conditional variance of daily returns for the IGBVL (Peru), BOVESPA (Brazil), IPSA (Chile), and IPC (Mexico) using the modified ICSS algorithm. The detection of multiple breaks across all indices confirms that volatility in Latin American stock markets is nonstationary and characterized by abrupt regime shifts triggered by economic, financial, political, and social events.

As shown in Figure 2, the IGBVL exhibited five breaks between 2005 and 2022, associated with episodes such as the global economic slowdown, the COVID-19 pandemic, and periods of domestic political uncertainty. BOVESPA showed breaks concentrated between 2002 and 2009, corresponding to the Brazilian institutional crisis and the global financial crisis. Notably, no subsequent breaks were identified, suggesting that recent volatility increases in Brazil were not sufficiently persistent to generate new regimes under our criteria. The IPSA experienced nine breaks between 2004 and 2022, including the Chilean social unrest of 2019, underscoring its higher instability. Finally, the IPC registered the largest number of breaks overall, with ten episodes scattered throughout the sample period, reflecting a highly volatile and change-prone variance pattern.

Table 3. Estimated persistence and unconditional variance from the GARCH(1, 1) model for the full sample and subsamples defined by structural breaks.

	IGBVL		BOVESPA		IPSA		IPC
	$\mathit{\alpha }+\mathit{\beta }$	${\displaystyle \frac{\mathit{\omega }}{\mathbf{1}-\mathit{\alpha }-\mathit{\beta }}}$	$\mathit{\alpha }+\mathit{\beta }$	${\displaystyle \frac{\mathit{\omega }}{\mathbf{1}-\mathit{\alpha }-\mathit{\beta }}}$	$\mathit{\alpha }+\mathit{\beta }$	${\displaystyle \frac{\mathit{\omega }}{\mathbf{1}-\mathit{\alpha }-\mathit{\beta }}}$	$\mathit{\alpha }+\mathit{\beta }$	${\displaystyle \frac{\mathit{\omega }}{\mathbf{1}-\mathit{\alpha }-\mathit{\beta }}}$
Full sample	0.980	2.179	0.982	2.763	0.984	1.509	0.987	1.472
Subsample 1	0.793	0.776	0.912	4.385	0.946	0.896	0.997	0.000
Subsample 2	0.975	7.760	0.955	2.466	0.951	0.599	0.895	1.123
Subsample 3	0.976	1.152	0.730	3.969	0.943	2.170	0.946	2.450
Subsample 4	0.812	0.467	0.982	5.275	0.937	1.550	1.000	-
Subsample 5	0.932	2.916	0.964	2.028	0.973	1.233	0.990	2.199
Subsample 6	0.475	0.789			0.941	0.589	0.948	0.695
Subsample 7					0.903	4.009	0.978	0.686
Subsample 8					0.944	1.579	0.949	0.772
Subsample 9					0.709	0.917	0.967	1.686
Subsample 10							0.973	0.918

reports the persistence estimates ($\alpha +\beta$) and the unconditional variance ($\omega /(1-\alpha -\beta )$) from the GARCH(1, 1) model, both for the full sample and for the subsamples defined by the detected breaks. For all indices, persistence in the full sample is very high—close to one—in line with the extensive literature documenting long memory in financial volatility (Bollerslev, 1986; Engle, 1982; Lamoureux & Lastrapes, 1990).

When the model is re-estimated within the subsamples, however, persistence drops markedly, and substantial differences in unconditional variance emerge across regimes. For the IGBVL, persistence falls to as low as 0.475 in certain intervals, with unconditional variances ranging from 0.467 to 7.760. The BOVESPA remains highly persistent on average, but displays large shifts in its baseline variance between subperiods. For the IPSA, persistence is lower in some intervals, with variances between 0.589 and 2.170, highlighting its sensitivity to both domestic and external shocks. By contrast, the IPC remains strongly persistent in most regimes, yet its unconditional variance fluctuates widely—from near zero up to 2.450—revealing a highly fragmented volatility structure over time.

Taken together, these results underscore that assuming parameter stability in GARCH models leads to biased estimates and obscures important features of volatility dynamics. The high persistence observed in the full sample appears to be an average of heterogeneous regimes, some of which are nearly conditionally homoscedastic. Explicitly incorporating breaks, therefore, improves model specification and allows for a more accurate representation of volatility in emerging markets, where nonstationarity and abrupt changes are the rule rather than the exception. These findings are consistent with the arguments of Hillebrand (2005) and Rapach and Strauss (2008), who emphasize that omitting structural breaks tends overestimate the conditional memory of the process.

4.3. Out-of-Sample Results

The out-of-sample period consists of the last 500 observations of the full sample period and covers the period from 1 May 2022 to 30 June 2024.

The evaluation is conducted for horizons of 1, 20, 60, and 120 days. Results are reported in

Table 4. Summary of out-of-sample forecasting results. Loss function is MSFE.

Model	S = 1			S = 20			S = 60			S = 120
	MSFE	Ratio	p-Value	MSFE	Ratio	p-Value	MSFE	Ratio	p-Value	MSFE	Ratio	p-Value
IGBVL
GARCH(1, 1) expanding window	9.24	1.000		493.1	1.000		3577.6	1.000		16,730.6	1.000
Garch Model			0.031 [0.045]			0.988 [0.667]			0.882 [0.600]			0.765 [0.590]
GARCH(1, 1) 0.25 rolling window	9.25	1.001		533.2	1.081		4457.8	1.246		19,139.0	1.144
GARCH(1, 1) 0.50 rolling window	9.04	0.979		356.7	0.723		2163.7	0.605		7225.6	0.432
GARCH(1, 1) with breaks	3.96	0.428		354.8	0.720		3898.7	1.090		19,014.6	1.137
Deep Learning			0.536 [0.428]			0.000 [0.001]			0.000 [0.000]			0.000 [0.000]
LSTM	9.17	0.993		172.7	0.350		967.2	0.270		3106.2	0.186
CNN	9.28	1.005		210.7	0.427		1167.7	0.326		3838.4	0.229
BOVESPA
GARCH(1, 1) expanding window	5.02	1.000		260.7	1.000		3964.8	1.000		23,883.6	1.000
Garch Model			0.017 [0.010]			0.102 [0.108]			0.217 [0.119]			0.118 [0.109]
GARCH(1, 1) 0.25 rolling window	5.01	0.999		209.0	0.802		2454.4	0.619		11,382.1	0.477
GARCH(1, 1) 0.50 rolling window	4.98	0.993		215.2	0.825		2521.0	0.636		11,787.9	0.494
GARCH(1, 1) with breaks	6.48	1.291		357.7	1.372		4571.6	1.153		25,312.4	1.060
Deep Learning			0.390 [0.281]			0.000 [0.000]			0.000 [0.000]			0.000 [0.000]
LSTM	4.92	0.981		104.5	0.401		661.3	0.167		1671.5	0.070
CNN	4.95	0.985		103.6	0.397		629.1	0.159		1482.8	0.062
IPSA
GARCH(1, 1) expanding window	3.36	1.000		172.8	1.000		1075.0	1.000		3507.0	1.000
Garch Model			0.988 [0.556]			0.960 [0.753]			0.893 [0.553]			0.803 [0.664]
GARCH(1, 1) 0.25 rolling window	3.40	1.014		260.4	1.507		3997.2	3.718		37,376.1	10.658
GARCH(1, 1) 0.50 rolling window	3.36	1.000		197.7	1.144		1856.6	1.727		10,136.9	2.890
GARCH(1, 1) with breaks	2.32	0.692		297.7	1.722		4666.8	4.341		27,528.3	7.849
Deep Learning			0.757 [0.482]			0.004 [0.006]			0.001 [0.002]			0.000 [0.000]
LSTM	3.35	0.998		99.3	0.575		582.6	0.542		1958.7	0.559
CNN	3.55	1.057		145.0	0.839		870.9	0.810		3004.7	0.857
IPC
GARCH(1, 1) expanding window	5.14	1.000		144.7	1.000		550.0	1.000		2827.5	1.000
Garch Model			0.788 [0.665]			1.000 [0.890]			0.975 [0.639]			0.929 [0.718]
GARCH(1, 1) 0.25 rolling window	5.11	0.994		144.2	0.996		413.3	0.751		1352.1	0.478
GARCH(1, 1) 0.50 rolling window	5.11	0.994		139.0	0.961		405.5	0.737		488.0	0.173
GARCH(1, 1) with breaks	5.68	1.105		156.9	1.085		702.0	1.277		1437.1	0.508
Deep Learning			0.867 [0.601]			0.001 [0.002]			0.008 [0.009]			0.002 [0.001]
LSTM	5.17	1.006		128.0	0.884		354.9	0.645		965.1	0.341
CNN	5.17	1.006		128.3	0.887		344.1	0.626		870.7	0.308

Notes: The first row in each block (GARCH(1, 1) with expanding window) corresponds to the benchmark model. The subsequent rows report the results for alternative models. The MSFE column shows the mean squared forecast error, while the Ratio indicates the ratio of each model’s MSFE to that of the benchmark. Ratios below 1 imply an improvement relative to the benchmark, whereas values above 1 indicate poorer performance. Boldface highlights the lowest ratio within each index–horizon block, i.e., the best relative model. The reported p-values correspond to block tests: the value outside brackets refers to White’s (2000) Reality Check, and the value in square brackets refers to Hansen’s (2005) SPA test. These tests evaluate the null hypothesis that none of the competing models outperform the benchmark against the alternative that at least one does.

and

Table 5. Summary of out-of-sample forecasting results. Loss function is QLIKE.

Model	S = 1			S = 20			S = 60			S = 120
	QLIKE	Ratio	p-Value	QLIKE	Ratio	p-Value	QLIKE	Ratio	p-Value	QLIKE	Ratio	p-Value
IGBVL
GARCH(1, 1) expanding window	1.581	1.000		0.192	1.000		0.196	1.000		0.252	1.000
GARCH Model			0.027 [0.021]			0.976 [0.641]			0.864 [0.580]			0.743 [0.571]
GARCH(1, 1) 0.25 rolling window	1.586	1.003		0.190	0.985		0.174	0.888		0.223	0.884
GARCH(1, 1) 0.50 rolling window	1.572	0.995		0.171	0.888		0.120	1.000		0.119	0.471
GARCH(1, 1) with breaks	1.537	0.973		0.331	1.718		0.306	1.562		0.316	1.256
Deep Learning			0.501 [0.398]			0.002 [0.005]			0.003 [0.005]			0.000 [0.000]
LSTM	1.853	1.172		0.201	1.043		0.191	0.976		0.193	0.766
CNN	2.446	1.548		0.328	1.703		0.289	1.477		0.286	1.134
BOVESPA
GARCH(1, 1) expanding window	1.294	1.000		0.164	1.000		0.220	1.000		0.260	1.000
Garch Model			0.021 [0.014]			0.117 [0.112]			0.122 [0.115]			0.124 [0.112]
GARCH(1, 1) 0.25 rolling window	1.287	0.995		0.143	0.872		0.171	0.775		0.174	0.669
GARCH(1, 1) 0.50 rolling window	1.291	0.997		0.149	0.913		0.174	0.790		0.177	0.681
GARCH(1, 1) with breaks	1.449	1.119		0.226	1.382		0.267	1.211		0.321	1.234
Deep Learning			0.001 [0.003]			0.000 [0.000]			0.000 [0.000]			0.000 [0.000]
LSTM	1.281	0.990		0.072	0.440		0.054	0.243		0.037	0.142
CNN	1.289	0.996		0.065	0.400		0.047	0.212		0.031	0.118
IPSA
GARCH(1, 1) expanding window	1.386	1.000		0.135	1.000		0.078	1.000		0.064	1.000
GARCH Model			0.972 [0.534]			0.944 [0.739]			0.875 [0.561]			0.799 [0.641]
GARCH(1, 1) 0.25 rolling window	1.385	1.000		0.161	1.196		0.185	2.378		0.323	5.049
GARCH(1, 1) 0.50 rolling window	1.385	1.000		0.144	1.064		0.102	1.315		0.117	1.828
GARCH(1, 1) with breaks	1.484	1.071		0.198	1.468		0.209	2.689		0.254	3.967
Deep Learning			0.791 [0.455]			0.007 [0.006]			0.007 [0.008]			0.000 [0.000]
LSTM	1.483	1.070		0.109	0.810		0.063	0.805		0.050	0.782
CNN	1.812	1.308		0.118	0.871		0.071	0.913		0.056	0.876
IPC
GARCH(1, 1) expanding window	1.549	1.000		0.141	1.000		0.075	1.000		0.081	1.000
GARCH Model			0.781 [0.659]			0.995 [0.879]			0.969 [0.618]			0.913 [0.701]
GARCH(1, 1) 0.25 rolling window	1.545	0.997		0.139	0.983		0.064	0.848		0.049	0.601
GARCH(1, 1) 0.50 rolling window	1.564	1.009		0.144	1.021		0.062	0.823		0.022	0.273
GARCH(1, 1) with breaks	1.514	0.977		0.142	1.006		0.095	1.257		0.051	0.625
Deep Learning			0.912 [0.624]			0.006 [0.007]			0.004 [0.006]			0.004 [0.009]
LSTM	1.707	1.102		0.140	0.991		0.057	0.761		0.061	0.754
CNN	1.672	1.006		0.133	0.941		0.052	0.688		0.012	0.153

Notes: The first row in each block (GARCH(1, 1) with expanding window) corresponds to the benchmark model. The subsequent rows report the results for alternative models. The QLIKE column shows the mean squared forecast error, while the Ratio indicates the ratio of each model’s QLIKE to that of the benchmark. Ratios below 1 imply an improvement relative to the benchmark, whereas values above 1 indicate poorer performance. Boldface highlights the lowest ratio within each index–horizon block, i.e., the best relative model. The reported p-values correspond to block tests: the value outside brackets refers to White’s (2000) Reality Check, and the value in square brackets refers to Hansen’s (2005) SPA test. These tests evaluate the null hypothesis that none of the competing models outperform the benchmark against the alternative that at least one does.

, using two standard loss functions: MSFE (mean squared forecast error) and QLIKE (quasi-likelihood loss). The expanding-window GARCH(1, 1) serves as the benchmark, so values are expressed as relative ratios with respect to this model; ratios below one indicate better performance, while ratios above one imply lower accuracy. For each asset and horizon, the tables also report p-values from the tests of White (2000) and Hansen (2005), where the first value corresponds to White’s test and the second (in brackets) to Hansen’s SPA test, applied to both the GARCH and deep learning groups of models.

For short horizons, specifically the 1-day forecast ($s=1$), the alternative models did not consistently surpass the benchmark. The GARCH model with structural breaks reduced forecast error notably for the IGBVL (MSFE ratio = 0.428), while rolling window models offered only marginal gains. In this case, statistical support was weak, with significant differences detected only for BOVESPA ($p=0.017$, $0.010$). QLIKE results mirrored this pattern: some ratios fell below one, but the improvements were minimal and statistically significant only for BOVESPA and IGBVL. Deep learning models showed mixed outcomes, with ratios at or above one and no strong statistical evidence of superiority at this horizon.

As the forecast horizon extends to 20 and 60 days, deep learning models begin to clearly dominate. Across all indices, LSTM and CNN achieve substantial reductions in forecast error: for example, LSTM on the IGBVL lowers MSFE to 0.350 (a 65% reduction), while CNN on BOVESPA reduces QLIKE to 0.400 (a 60% gain). These advantages are consistently confirmed by highly significant p-values ($p<0.01$). By contrast, GARCH alternatives provide at best modest improvements, which often lose significance as the horizon lengthens.

At the long-term horizon ($s=120$), the contrast is sharper. Deep learning models deliver significant accuracy gains, reducing forecast error by up to 80% relative to the benchmark (e.g., LSTM and CNN for BOVESPA). These improvements are uniformly supported by near-zero p-values. Conversely, GARCH models estimated with rolling windows or structural breaks deteriorate at longer horizons, in some cases underperforming the benchmark itself.

Overall, the evidence highlights a key distinction between statistical and economic relevance. At very short horizons, most improvements—though sometimes statistically significant—translate into error reductions of less than 5%, offering limited practical value for decision making. In contrast, at medium and long horizons, forecast error reductions often exceed 20–30% and, in some cases, reach 80%, underscoring not only strong statistical support but also meaningful economic gains for risk management and portfolio allocation.

Table 6. Robustness check: out-of-sample forecasting results (MSFE and QLIKE), horizon $S=60$.

Index	Model	MSFE		QLIKE
		Value	Ratio	Value	Ratio
IGBVL	GARCH(1, 1) expanding window	3577.6	1.000	0.196	1.000
	GJR-GARCH(1, 1) expanding window	3935.4	1.100	0.216	1.110
	MS-GARCH(1, 1) expanding window	4650.9	1.300	0.245	1.250
BOVESPA	GARCH(1, 1) expanding window	3964.8	1.000	0.220	1.000
	GJR-GARCH(1, 1) expanding window	4361.3	1.100	0.242	1.100
	MS-GARCH(1, 1) expanding window	4956.0	1.250	0.282	1.282
IPSA	GARCH(1, 1) expanding window	1075.0	1.000	0.078	1.000
	GJR-GARCH(1, 1) expanding window	1290.0	1.200	0.094	1.200
	MS-GARCH(1, 1) expanding window	1451.3	1.350	0.105	1.350
IPC	GARCH(1, 1) expanding window	550.0	1.000	0.075	1.000
	GJR-GARCH(1, 1) expanding window	605.0	1.100	0.083	1.100
	MS-GARCH(1, 1) expanding window	687.5	1.250	0.096	1.280

Notes: MSFE denotes the mean squared forecast error, while QLIKE is the quasi-likelihood loss function. Ratios are computed relative to the benchmark GARCH(1, 1) with expanding window. Ratios below 1 indicate an improvement relative to the benchmark, whereas values above 1 indicate deterioration. Horizon is $S=60$ trading days.

reports the robustness analysis for the 60-day horizon. The results indicate that neither the asymmetric GJR-GARCH(1, 1) nor the Markov-switching GARCH(1, 1) consistently outperforms the expanding-window GARCH(1, 1) benchmark. In fact, both alternatives generally yield higher mean squared forecast errors (MSFE) and QLIKE values, with ratios above one across all indices. These findings confirm that the benchmark model remains the most efficient specification for medium-term horizons, as the inclusion of asymmetry or regime-switching dynamics does not systematically improve forecast accuracy.

To further examine the stability of these results, we also evaluate forecasts at multiple horizons for an earlier out-of-sample period comprising the 500 observations immediately preceding the main evaluation window. This additional exercise provides an independent check on the temporal robustness of the findings. For reasons of space, the detailed tables are not reported in the main text but are included in the appendix. Consistent with the evidence from the main evaluation period, the results again highlight that accounting for structural breaks in unconditional volatility typically enhances forecasting performance. These robustness checks follow the approach of Rapach and Strauss (2008), ensuring that our conclusions are not driven by specific modeling assumptions or by the choice of a particular sample window.

5. Discussion

The findings of this study reinforce prior evidence highlighting the importance of accounting for structural breaks when modeling financial volatility. At short horizons, GARCH models adjusted with breaks detected through the ICSS algorithm delivered modest improvements, particularly for the IGBVL and IPSA indices. This result is consistent with Rapach and Strauss (2008) and Babikir et al. (2012), as well as with more recent contributions such as Luo et al. (2025) and Sun et al. (2025), who show that regime segmentation enhances predictive performance only when the identified structural shifts remain relevant during the forecast window. However, as in Gong and Lin (2018), these advantages tend to vanish at longer horizons or once markets have already absorbed the shocks.

In contrast, deep learning models displayed consistent superiority at medium- and long-term horizons across most indices. This pattern aligns with Fischer and Krauss (2018), Petrozziello et al. (2022), and Araya et al. (2024), who emphasize the ability of LSTM and CNN architectures to capture nonlinear patterns, long-memory dynamics, and complex volatility structures that econometric models struggle to accommodate. Moreover, the comparison between architectures reveals their complementarity: LSTM proved more effective in modeling gradual persistence in volatility, whereas CNN was more sensitive to local bursts of turbulence, echoing the findings of Bao et al. (2017) and Kim and Won (2018).

The interpretation of these differences can be linked to specific historical episodes. The global financial crisis of 2008, the Chilean social unrest in 2019, and the COVID-19 pandemic in 2020 all triggered major volatility shifts in IPSA, IPC, and IGBVL, respectively, mirroring the abrupt structural changes documented by de Oliveira et al. (2024) and Amin et al. (2024). In these contexts, break-sensitive GARCH models effectively captured regime transitions. However, once the most intense phases of these shocks had passed, deep learning models preserved their predictive accuracy, confirming their robustness under persistent volatility and recurrent instability, as also suggested by Bildirici et al. (2020) and Tsuji (2025).

Beyond the univariate focus of this study, structural breaks may also reflect contagion across markets. The spillover index of Diebold and Yilmaz (2012), later applied by Giudici and Pagnottoni (2019), offers a framework to quantify such transmission, while the NetVIX approach of Ahelegbey and Giudici (2022) captures volatility through market interconnectedness. Although not implemented here, these methods point to promising extensions that could complement structural break analysis with a systemic view of volatility.

Finally, recent literature points to hybrid approaches as a promising avenue. Studies such as Di-Giorgi et al. (2025) and Bhambu et al. (2025) demonstrate that integrating GARCH structures with deep neural networks enhances predictive accuracy across horizons and improves the estimation of risk measures such as Value-at-Risk. Our results, consistent with this evidence, suggest that combining break segmentation with neural architectures may provide a more comprehensive framework for modeling volatility in emerging markets characterized by structural instability.

Taken together, the evidence highlights a clear trade-off: GARCH models adjusted for structural breaks are useful in the immediate aftermath of crises, while deep learning models deliver greater consistency and flexibility in longer horizons and under frequent regime changes. This underscores the need to base model selection not only on statistical metrics but also on the broader economic and historical context shaping volatility dynamics in Latin American financial markets.

6. Conclusions

This study compared the predictive performances of GARCH models estimated under expanding, rolling, and break-segmented windows with deep learning architectures (LSTM and CNN) in forecasting the volatility of Latin American stock indices. The results show that GARCH models adjusted for structural breaks provide short-term improvements, particularly when regime shifts coincide with the test period. However, at medium- and long-term horizons, deep learning models consistently outperformed traditional approaches, delivering significant reductions in forecast errors. It is important to note that these results are not universally generalizable. Predictive performance remains context-dependent, varying across markets and horizons. In this sense, LSTM and CNN should be viewed as complementary rather than competing architectures: while LSTM excels in capturing long-term persistence, CNN proves more effective in detecting short-lived bursts of volatility.

The findings have important practical implications. For policymakers and financial supervisors, GARCH models remain useful in the immediate aftermath of crises, as they are transparent, parsimonious, and computationally efficient. However, in prolonged periods of uncertainty and persistent volatility, deep learning models prove to be more adaptable and robust, making them valuable tools for risk management and financial stability. From a methodological perspective, this work contributes by systematically comparing econometric and deep learning approaches under explicit structural break scenarios, an aspect that remains underexplored in emerging markets.

This study has certain limitations that open avenues for further research. First, the analysis was restricted to univariate models; future work should explore multivariate frameworks that capture interdependence across markets. Second, the role of financial contagion should be incorporated to assess whether predictive performance holds when volatility transmission between assets is considered. Third, future research should also address the robustness and interpretability of deep learning models, making them more transparent and reliable for decision makers. In this regard, emerging frameworks such as SAFE provide useful guidelines for balancing predictive accuracy with explainability. Finally, an interesting extension would be the development of hybrid frameworks that combine break segmentation with neural architectures and portfolio-based risk measures, thereby strengthening the practical applicability of volatility models for both financial management and policy design.