Determinants of Financial Stability and Development in South Africa: Insights from a Quantile ARDL Model of the South African Financial Cycle

Abstract

This study investigates the short-run and long-run dynamics of the financial cycle in South Africa, focusing on its macroeconomic drivers and their asymmetric effects across different phases. It addresses the persistent challenge in emerging market economies of balancing financial development and stability amidst volatile conditions. Using monthly data from 2000 to 2024, the research employs a quantile autoregressive distributed lag (QARDL) model to capture the heterogeneity and persistence of macro-financial linkages across the financial cycle’s distribution. The use of the QARDL model in this study allows for capturing asymmetric and quantile-specific relationships that traditional linear models might overlook. Findings reveal that monetary policy, and the housing sector are key drivers of long-term financial development in South Africa, showing positive effects. Conversely, exchange rate movements, inflation, money supply, and macroprudential policy dampen financial development. Short-term financial booms are associated with GDP growth, credit, share, and housing prices. Money supply and inflation are more closely linked to burst phases. These results underscore the importance of policy coordination, particularly between monetary and macroprudential authorities, to balance promoting financial development and ensuring stability in emerging markets. This study contributes to the empirical literature and offers practical insights for policymakers.

1. Introduction

Since the global financial crisis (GFC) of 2007–2009, it has become increasingly clear that developments within the financial sector carry significant systemic consequences for the broader economy (Coimbra & Rey, 2024; Adarov, 2022; Miranda-Agrippino & Rey, 2022; Qin et al., 2021; Beirne, 2020; Aldasoro et al., 2020; C. Borio et al., 2020; Ha et al., 2020). When properly developed, the financial sector contributes meaningfully to economic development. However, the collapse of even a narrow segment of financial markets can induce deep recessions, with effects that reverberate nationally and globally (Kohler & Stockhammer, 2022; C. E. Borio et al., 2018; Kindleberger, 2016). Financial synchronization across countries can amplify the transmission of economic shocks, undermining domestic regulatory frameworks and importing risks from abroad (Magubane et al., 2024; Gammadigbe, 2022; Prabheesh et al., 2021). Nonetheless, a well-functioning financial system remains vital in supporting investment and spending, which, in turn, stimulate economic activity. Consequently, macroprudential policymakers have intensified efforts to promote soundness and stability in the financial system to support both financial and economic development (Epure et al., 2024; Vollmer, 2022).

This paper explores the persistent challenge faced by emerging market economies, i.e., the dual objective of achieving financial development, which refers to the improvement in the financial system’s ability to allocate resources efficiently, foster access to financial services, and promote economic growth, and maintaining financial stability amid volatile macroeconomic conditions. In South Africa, this dual mandate is particularly complex due to enduring structural problems, such as high unemployment, limited financial inclusion, and pronounced income inequality. The country’s financial system is highly susceptible to external shocks, such as capital flow reversals and commodity price volatility, which interact with internal vulnerabilities. Financial cycles often magnify macroeconomic fragilities in this context, particularly when policies prioritize short-term stability over long-term development. Addressing these challenges requires a coherent policy strategy grounded in a robust understanding of the drivers of financial fluctuations and development dynamics.

Financial cycles offer a systemic lens through which to assess the state of the financial sector. A widely cited definition describes them as self-reinforcing interactions between risk perceptions, asset valuations, and financing constraints, frequently resulting in boom-and-bust dynamics (C. Borio, 2014). Adarov (2022) recently defined financial cycles as cyclical deviations in financial market activity from long-run equilibrium, characterized by the build-up and subsequent correction of financial imbalances. This definition highlights two interrelated dimensions, namely the long-term trend of financial development and the shorter-term cyclical component. The trend reflects deeper financial intermediation that supports efficient capital allocation and sustained economic growth, while the cyclical component captures the fluctuations associated with financial booms and busts. This distinction is crucial for macroprudential surveillance and policy intervention (Skare et al., 2025; Yang, 2019; C. E. Borio et al., 2019; Ibrahim & Alagidede, 2018; Durusu-Ciftci et al., 2017). In this study, this duality is adopted in the identification of the financial cycle, where the cyclical component is interpreted in terms of financial stability—referring to episodes of excessive expansion and contraction—while the long-term component reflects the level of financial development.

Despite the rising recognition of financial cycle developments in the aftermath of the GFC, the underlying drivers of financial cycle fluctuations and their relationship with financial development remain poorly understood. Theoretically, this relationship is contested. The finance–growth literature suggests a bidirectional causality, where financial development is both a precondition and a consequence of economic growth (Beck et al., 2000; Levine, 2018). Meanwhile, Keynesian and debt-deflation perspectives argue that financial conditions amplify business cycles through procyclical links between the financial and real sectors (Bakar & Sulong, 2018; Chiarella & Di Guilmi, 2017; Hudson, 2012; Fink et al., 2004; Blum et al., 2002; Young, 1993; Robinson, 1979). In contrast, neoclassical business cycle models from the 1980s and 1990s largely downplayed the role of finance, treating financial cycles as nominal frictions with limited macroeconomic importance (Foroni et al., 2022; Giri et al., 2019; Christensen et al., 2018; Gilchrist et al., 1998; Bernanke et al., 1994). The Modigliani–Miller theorem, for instance, rests on the assumption of perfect markets and a complete separation between financial and real sectors (Villamil, 2008; Stiglitz, 1969; Modigliani & Miller, 1958). The efficient market hypothesis similarly treats financial fluctuations as minor and fundamentally rational deviations (Timmermann & Granger, 2004; Malkiel, 1989), while Minsky’s financial instability hypothesis emphasizes the endogenous and destabilizing nature of credit booms (Knell, 2015; Vercelli, 2011; Minsky, 1992).

The key limitation shared across many of these theories is their failure to incorporate the dynamics of financial cycles and the evolving role of macroprudential policy frameworks. These omissions render their predictions increasingly inadequate for explaining the complex, nonlinear interactions between financial fluctuations, development, and regulatory responses in modern economies. They do not account for how macroprudential tools—such as countercyclical capital buffers, loan-to-value ratios, and sectoral risk weights—designed to lean against financial excesses, can influence long-term financial development. As a result, these theoretical models lack the structural mechanisms to capture the endogeneity and feedback effects between financial development, financial fluctuations, and macroprudential regulatory interventions. This theoretical gap underscores the need for updated empirical frameworks that reflect the realities of post-GFC macro-financial interactions—an issue this study seeks to address directly.

Meanwhile, empirical research at the system-wide level of the financial sector has also shown limitations. Most studies focus on documenting stylized facts about financial cycles—such as duration, amplitude, and synchronization—using statistical tools, like bandpass filters, turning point algorithms, and wavelet methods (C. Borio, 2014; C. Borio et al., 2020; Adarov, 2022; Beirne, 2020; Qin et al., 2021; Ha et al., 2020; De Wet & Botha, 2022; Oman, 2019; Skare et al., 2025; Yang, 2019; Adrian & Shin, 2010; Claessens et al., 2012; Drehmann et al., 2012; Jordà et al., 2013; Alessi & Detken, 2011; Rünstler & Vlekke, 2018; Krznar & Matheson, 2017). For instance, Claessens et al. (2012) find that financial recessions, particularly those led by credit and housing busts, tend to be deeper and longer than normal recessions. Similarly, Jordà et al. (2013) show that credit booms often precede more severe economic downturns. However, few of these studies explore these fluctuations’ structural or policy-related causes.

The financial development literature tends to emphasize the positive long-run effects of financial development on growth and capital accumulation, often through such channels as improved allocation of resources and enhanced access to finance (King & Levine, 1993; Levine, 1997; Rajan & Zingales, 1998; Beck et al., 2000; Hassan et al., 2011; Swamy & Dharani, 2019; Demetriades & Rewilak, 2020). For example, Beck et al. (2000) provide evidence that financial development is strongly associated with higher GDP per capita and productivity growth. Levine (1997) find that stock market liquidity and banking development are robust predictors of economic growth. However, this strand of the literature rarely accounts for financial instability or cyclical reversals that may arise from rapid credit growth or excessive financial innovation. Furthermore, these studies tend to rely on linear estimation techniques, which limit their ability to capture the nonlinearities and threshold effects commonly observed in financial cycle turning points.

First, there is an apparent disconnect between these two strands of literature. Studies on financial cycles rarely engage with theories of financial development and vice versa, resulting in fragmented insights that fail to capture the dynamic interactions between structural financial deepening and cyclical changes. This gap calls for an integrated empirical framework that considers both long-run development trends and short-run financial instabilities (Claessens & Kose, 2018; Drehmann et al., 2012). Without such synthesis, policies designed to promote financial development may inadvertently amplify systemic risks.

Second, many empirical investigations in both strands rely heavily on linear econometric models, including autoregressive distributed lag (ARDL), vector error-correction mechanism (VECM), vector autoregression (VAR), and static panel regressions (Demetriades & Rewilak, 2020; Odhiambo, 2010; Ang, 2008). These linear specifications are often ill-suited to capture the asymmetric, nonlinear, and threshold-based behavior of financial cycles, particularly under conditions of financial exuberance or distress (Alessi & Detken, 2011; C. Borio, 2014; Skare et al., 2025). As a result, the models may underestimate tail risks and regime shifts critical for understanding the macro-financial linkages.

Third, a significant limitation in much of the existing literature is the exclusion of macroprudential policy variables. Despite the growing adoption of macroprudential tools globally after the GFC, their role in shaping or moderating financial cycles remains underexplored. This omission is particularly problematic in studies of financial development and stability, as macroprudential instruments directly influence credit growth, asset prices, and systemic risk (Claessens et al., 2013; Galati & Moessner, 2013). Furthermore, interactions between macroprudential and monetary policy—both complementary and conflicting—are rarely examined, even though they are crucial in determining the overall effectiveness of financial regulation and macroeconomic stabilization (Smets, 2018; Agénor et al., 2018; Lambert & Ueda, 2014). By overlooking how these policies interact, existing empirical work fails to account for financial stability and development dynamics.

These limitations in the literature leave us with the challenge of investigating the short-term triggers of financial fluctuations and the drivers of long-term financial stability within a unified framework. This framework must account for macroprudential policy, its interactions with monetary policy, and the dynamics of financial cycles. This present study develops a quantile autoregressive distributed lag (QARDL) model of South Africa’s financial cycle. It empirically investigates the short-term triggers of financial cycle deviations and the long-run drivers of financial development within a single framework that accommodates asymmetries across different phases of the financial cycle. The QARDL approach is well-suited for capturing these nonlinearities. It offers granular insights into the structural dynamics of the financial sector, as it accommodates both short- and long-run asymmetries, accounts for distributional heterogeneity across different quantiles, and remains robust in the presence of non-normal error terms and outliers.

Several key questions must be addressed in light of this study’s main objective. First, what are the primary triggers of financial cycle fluctuations in South Africa, and what are the fundamental drivers of financial development within the South African context? Second, how does macroprudential policy in South Africa impact financial stability and financial development? Finally, how do monetary and macroprudential policies interact in South Africa, and how does this interplay influence financial stability and development outcomes? Together, these questions aim to deepen empirical and theoretical insights into the complex relationships between financial cycles, policy interventions, and economic development in South Africa.

Focusing on South Africa is both timely and analytically relevant for several reasons. First, scholarly interest has markedly increased in the country’s financial cycle dynamics. Recent studies—including Nyati et al. (2021), Pahla (2019), Magubane (2024), Farrell and Kemp (2020), De Wet and Botha (2022), and Bosch and Koch (2020)—have made important contributions by identifying the presence and characteristics of financial cycles in South Africa. However, these studies have largely focused on detecting cyclical patterns, with limited attention given to the underlying drivers of long-term financial development or the determinants of short-term financial fluctuations. This limitation leaves a critical gap in understanding how different forces shape the evolution and volatility of the financial system over time.

Second, the South African financial sector is pivotal in the country’s economic architecture. The equity market, dominated by the Johannesburg Stock Exchange (JSE), is one of emerging economies’ most sophisticated and liquid markets. It is home to many of Africa’s largest listed companies and serves as a major conduit for capital formation, portfolio investment, and wealth generation. The JSE alone accounts for a market capitalization that exceeds 300% of GDP, reflecting the depth and scale of the financial intermediation that it facilitates. Similarly, the credit sector, comprising commercial banks, insurers, and other financial intermediaries, is a key consumer and business spending engine. Household credit, in particular, has been a major driver of domestic demand, with household debt reaching approximately 62% of disposable income in recent years. These unique features make South Africa a compelling case for exploring the interplay between financial cycle volatility and financial development in a way that can inform both national and broader emerging market policy debates.

The present study provides important empirical insights into the complex dynamics of financial cycles. Concerning the first research question—i.e., the triggers of financial cycle fluctuations and drivers of financial development—the findings reveal that stronger economic fundamentals, captured by variables, such as GDP, inflation, exchange rates, credit, and money supply, generally exert a dampening effect on the financial cycle. This finding suggests that sound macroeconomic conditions are critical in moderating cyclical financial excesses. Conversely, the positive associations found with house prices and the repo rate underscore the amplifying role of asset price booms and monetary policy stance on financial development, corroborating the prior literature that links credit and asset price cycles as key drivers of financial instability (De Wet & Botha, 2022; Bosch & Koch, 2020). The negative long-run relationship between GDP and the financial cycle further implies that robust real-sector growth can stabilize against disruptive financial fluctuations, highlighting the importance of integrating real economic performance within financial cycle analysis.

Turning to the second and third research questions regarding the impact of macroprudential policy and its interaction with monetary policy, the study’s findings offer compelling evidence of their differentiated and state-dependent effects. Notably, macroprudential policy measures have a stronger and statistically significant restraining effect on financial cycle fluctuations during higher quantiles—periods characterized by more intense financial booms. This important finding reinforces the emerging consensus in the literature that macroprudential tools are effective countercyclical instruments designed to mitigate systemic risks by tempering credit expansions and asset price bubbles (Magubane & Mncayi-Makhanya, 2025). The quantile-based approach reveals that the effectiveness of such policies is conditional on the phase of the cycle, suggesting that a one-size-fits-all policy approach may be suboptimal.

Furthermore, the observed positive association between the repo rate and financial cycle intensity highlights monetary policy’s complex role. Rather than always dampening financial imbalances, an accommodative monetary stance may inadvertently amplify asset price booms and credit growth, especially in environments with loosened macroprudential constraints. This finding raises important questions about the nature of monetary and macroprudential policy interactions: are these policies complementary factors that jointly promote financial stability, or do they sometimes conflict, creating policy trade-offs? The evidence from South Africa suggests a nuanced interaction where the macroprudential framework can potentially offset some of the destabilizing side effects of monetary easing, thus acting as a critical stabilizing complement.

Overall, the study advances the understanding that financial cycles are not monolithic but rather complex, state-dependent phenomena shaped by the interplay of domestic macroeconomic fundamentals, asset prices, and policy interventions. By integrating a comprehensive set of variables and employing an advanced econometric framework, the research fills significant gaps in emerging market financial cycle analysis, particularly by highlighting the heterogeneous impacts of macroprudential policies. These findings underscore the policy implication that macroprudential measures should be carefully calibrated to the financial cycle’s phase to maximize their stabilizing effect. Simultaneously, coordinated policy action between monetary and macroprudential authorities is vital to effectively balancing growth and stability objectives.

The remainder of the study is structured as follows: Section 2 discusses the relevant literature; Section 3 discusses the data and methodology used; Section 4 presents the results and their discussion; and Section 5 concludes the study.

2. Related Literature

This study connects to two strands of literature concerning the financial sector. The first strand focuses on documenting stylized facts of financial cycles—such as duration, amplitude, and synchronization—using various tools like, bandpass filters, turning point algorithms, and wavelet methods. However, fewer studies in this strand explore the structural causes of financial cycle fluctuations. The second strand examines financial development, often without addressing short-run instability or financial fragility. This study bridges these strands by examining the short-term triggers of financial fluctuations and the drivers of financial development within a unified framework. It provides a more comprehensive perspective by incorporating macroprudential policy and monetary variables, which are often neglected in both strands. Additionally, the study employs a nonlinear framework, the QARDL model, to analyze these dynamics and their interactions with policy tools.

Concerning the first strand, Adrian and Shin (2010) emphasized the procyclical nature of leverage in the financial system, showing how financial intermediaries amplify cycles through risk-taking behavior. Alessi and Detken (2011) developed early warning indicators for asset price booms and financial imbalances, demonstrating their ability to signal systemic financial crises ahead of time. Claessens et al. (2012) documented that recessions associated with financial busts are more severe and protracted than those linked to normal business cycles, highlighting the macroeconomic significance of financial fluctuations. Drehmann et al. (2012) proposed the credit-to-GDP gap as a useful early warning signal, arguing that financial cycles are longer and larger than business cycles and tend to build up gradually before leading to crises. Jordà et al. (2013) empirically confirmed that credit booms—especially those involving real estate—are powerful predictors of financial crises, with financial upswings typically lasting longer than normal output expansions.

C. Borio (2014) synthesized findings from multiple countries and showed that financial cycles—primarily measured through credit and property prices—have a typical duration of 16 to 20 years, compared to 8 to 10 years for business cycles, and are characterized by much greater amplitude. He argued that their persistence poses distinct challenges for macroeconomic management. Krznar and Matheson (2017) supported this view in the Canadian context, finding that financial cycles last significantly longer than business cycles and are closely tied to real estate lending dynamics. Rünstler and Vlekke (2018) developed a multivariate financial cycle index for euro area countries and confirmed that financial cycles are more persistent and display longer duration—about 15 to 20 years—compared to standard output cycles.

There is a significant scarcity of research into financial cycle-stylized facts in South Africa. Farrell and Kemp (2020) found evidence of a financial cycle in South Africa, identified by the co-movement of credit and asset prices. Their analysis revealed a strong synchronization between credit growth, house prices, and equity prices, suggesting a distinct financial cycle that is decoupled from short-term economic fluctuations. This finding was further echoed by Magubane (2024), who confirmed the strong coherence among these variables and noted that their correlation with the business cycle was relatively weak—indicating that financial cycles in South Africa evolve more slowly and independently from standard output cycles.

Bosch and Koch (2020), using a similar approach that focused on credit and asset prices, estimated the duration of South Africa’s financial cycle to be approximately 17 years, in contrast to the business cycle, which they found to span around 5 years. This supports broader international findings that financial cycles tend to be longer and more persistent than business cycles, often due to structural factors in credit markets and asset price behavior.

Other studies have expanded the scope of analysis beyond credit and asset prices to capture broader macro-financial dynamics. De Wet and Botha (2022) incorporated variables, such as interest rates, economic confidence indices, capital flows, the monetary conditions index, and balance sheet indicators. Their results diverged from earlier studies: they estimated the average duration of South Africa’s financial cycle to be approximately 7 years—shorter than international estimates, and notably close to typical business cycle durations found in the literature (which generally range from 6 to 8 years in emerging markets). This raises important questions about whether these shorter cycles truly reflect underlying financial dynamics or instead capture hybrid macroeconomic patterns that blend financial and real activity. It also highlights the sensitivity of cycle measurement to the choice of indicators, methodology, and filtering techniques used.

Similarly, Nyati et al. (2021) used additional financial variables—including treasury bill rates, government bond yields, and the nominal exchange rate—and also estimated a financial cycle of around 7 years and 2 months. These shorter durations suggest that there may be multiple overlapping financial cycles in South Africa—some driven by domestic credit and housing market conditions, and others influenced by external financial flows and macroeconomic policy shifts.

In a more recent contribution, Magubane and Mncayi-Makhanya (2025) investigated the role of global versus domestic drivers of the South African financial cycle. Their findings suggest that the financial cycle in South Africa responds more strongly to external factors, such as capital flows, international oil prices, the VIX (Volatility Index), and the U.S. Federal Reserve rate, than to domestic variables, like inflation and macroprudential regulation. This implies that while the cycle may appear domestically driven in terms of timing and structure, global financial conditions significantly influence its amplitude and turning points. However, further empirical verification is needed to confirm the robustness of these results, particularly given the complexity of financial transmission mechanisms in open emerging market economies, like South Africa.

Regarding the second strand of the literature, seminal works, such as McKinnon (1973) and Fry (1980), laid the foundation for the “finance-led growth” hypothesis by arguing that liberalized and well-functioning financial systems facilitate investment, savings mobilization, and efficient resource allocation—key ingredients for sustained economic growth. Greenwood and Jovanovic (1990) formalized this view in a dynamic model, suggesting that financial development and economic growth evolve together, with finance improving capital allocation as economies mature.

King and Levine (1993) and Levine and Zervos (1998) provided empirical support for this relationship, and found strong cross-country evidence that financial depth—measured by indicators, like private credit and stock market liquidity—predicts future growth, capital accumulation, and productivity improvements. Beck et al. (2000) further reinforced these findings, demonstrating that financial development disproportionately benefits low-income people by improving access to financial services and reducing income inequality. Similarly, Rajan and Zingales (1998) showed that industries that are more dependent on external finance grow faster in countries with more developed financial markets, linking finance to comparative advantage.

Hassan et al. (2011) extended this analysis to low-income and developing countries, finding that the finance–growth nexus holds across income levels. However, institutional quality mediates the strength of the relationship. Demirgüç-Kunt and Maksimovic (1998) contributed firm-level evidence, showing that access to long-term finance enables firms to grow beyond their internally generated funds. Aghion et al. (2005) explored the interaction between volatility and finance, showing that financial development reduces growth volatility by easing liquidity constraints, particularly in innovative sectors.

In the African context, Odhiambo (2010) found that the direction of causality between finance and growth is country-specific, often bidirectional, and closely tied to structural characteristics, such as savings behavior, financial openness, and inflation dynamics. Similarly, Ang (2008) and Rioja and Valev (2004) showed that financial development has threshold effects—it promotes growth more effectively once a certain level of institutional development is achieved. Swamy and Dharani (2019) added nuance by showing that the finance–growth relationship is contingent on macroeconomic stability and governance quality.

Focusing specifically on South Africa, several empirical studies provide additional insights into the finance–growth dynamic. Aron and Muellbauer (2013) highlighted the importance of financial liberalization and monetary policy reforms in South Africa during the 1990s, noting that improvements in financial sector efficiency contributed positively to economic growth. However, the impact was moderated by persistent structural challenges, such as inequality and labor market rigidities. Assefa and Mollick (2017) examined the role of financial development on promoting economic growth. They found a positive but nonlinear relationship with economic growth, echoing the threshold effect of broader African and emerging market studies.

More recently, tests to show that financial deepening—particularly measured by credit to the private sec-tor—significantly positively influences South African economic growth. However, their analysis also suggested that this relationship is sensitive to macroeconomic shocks and policy shifts, reinforcing the importance of macroeconomic stability, as found by Swamy and Dharani (2019). Ghartey (2015) found evidence of bidirectional causality between financial development and growth in South Africa, consistent with the broader African context identified by Odhiambo (2010). They stressed that institutional quality plays a crucial role in shaping this dynamic.

In addition, Odhiambo (2009) investigated the impact of financial development on economic growth in South Africa and concluded that financial depth positively affects growth, but that the effects are more pronounced when combined with sound governance and inflation control. This aligns with Bassier and Woolard (2021) findings, who emphasized the role of inclusive financial policies in promoting sustainable growth and reducing inequality in South Africa.

Theoretical critiques have emerged in parallel. Arestis and Demetriades (1997) challenged the overly optimistic assumption that all financial deepening is beneficial, cautioning that rapid liberalization without robust regulation can lead to credit booms and misallocation. Acemoglu et al. (2005) argued that financial development alone cannot explain cross-country growth differentials without accounting for political institutions and state capacity.

Recent contributions have pushed this critical perspective further. Cecchetti and Kharroubi (2012) and Arcand et al. (2015) provided compelling evidence that “too much finance” can be detrimental to growth, especially when financial sector expansion comes at the cost of real sector productivity. These studies find an inverted U-shaped relationship between finance and growth: while early financial development spurs growth, beyond a certain point, additional credit and financialization may hinder it by diverting talent and capital away from productive use.

Demetriades and Rewilak (2020) revisit the literature’s early optimism and argue that the positive finance–growth link has been overstated due to methodological weaknesses, including endogeneity and measurement issues. They advocate for more context-sensitive and institutionally grounded analyses that distinguish between beneficial and harmful forms of financial development.

Haber et al. (2003) and Rousseau and Wachtel (2000) caution that the finance–growth relationship is not automatic or linear; it depends on historical contingencies, legal systems, and policy frameworks. Countries with weak institutions or captured regulatory environments may experience financial development that fuels instability, asset bubbles, and inequality, rather than growth.

3. Materials and Methods

3.1. Theoretical Framework

The theoretical framework for this study is built upon multiple complementary economic theories that provide a comprehensive understanding of financial cycle dynamics and their relationship with financial development. Given the complexity and contested nature of financial cycles, relying on a single theory would inadequately capture the multifaceted interactions between the financial sector, macroeconomic variables, and policy interventions.

This framework integrates finance–growth theory, which posits a bidirectional causal link between financial development and economic growth, highlighting the essential role of a deepening financial sector in supporting sustainable growth and vice versa. It also draws from Keynesian and debt-deflation theories, emphasizing how financial conditions and credit expansions can amplify economic fluctuations through procyclical effects between the real and financial sectors. These perspectives are especially relevant for South Africa, where credit booms and asset price dynamics have historically influenced economic cycles.

To balance this, the framework considers neoclassical business cycle models that traditionally minimize the role of finance in macroeconomic fluctuations, offering a critical viewpoint on the limits of financial sector influence. Additionally, insights from the Modigliani–Miller theorem and efficient market hypothesis provide foundational assumptions about market efficiency and the separation between financial and real sectors. These serve as a benchmark against which financial cycle anomalies are measured.

Lastly, the framework incorporates Minsky’s financial instability hypothesis, which underscores the endogenous build-up of financial vulnerabilities through credit booms, a phenomenon observed in emerging markets, like South Africa. Together, these theories guide empirical investigation by informing the selection of variables, the expected relationships, and the interpretation of policy impacts, particularly the roles of monetary and macroprudential policies in stabilizing financial cycles.

3.2. Data and Variables

To represent the South African financial cycle, the following variables are used: total domestic credit as a percentage of GDP (CR), real house price index (HP), and real all share price index (SP). These variables are widely employed in both the global and South African financial cycle literature as core indicators of cyclical financial activity (Claessens et al., 2012; Drehmann et al., 2012; C. Borio, 2014; Nyati et al., 2021; Pahla, 2019; Magubane, 2024; Nkusu, 2011). The theoretical justification for including these variables lies in their function as channels through which financial shocks and expansions propagate throughout the economy. Credit, housing, and equity markets are not only core components of financial development but are also inherently procyclical, meaning that they tend to amplify both upturns and downturns in financial conditions (C. E. Borio & Drehmann, 2009; Schularick & Taylor, 2012). These components interact through self-reinforcing mechanisms—where rising credit fuels asset price increases and vice versa—thus forming the foundation of boom–bust cycles.

Empirically, these variables have been shown to exhibit strong co-movement and synchronization around major turning points in financial conditions, with their peaks and troughs often aligning with broader systemic fluctuations (C. E. Borio et al., 2019; Jordà et al., 2018). In the South African context, the practical rationale for their selection is twofold: first, they correspond to the country’s three most developed and systemically important financial sectors, namely the credit sector (dominated by commercial banks and insurers), the real estate market, and the Johannesburg Stock Exchange. Second, these sectors serve as transmission belts between global financial shocks and domestic macro-financial conditions, thus providing an effective composite signal of the domestic financial cycle.

Furthermore, previous studies on South Africa’s financial dynamics confirm that excessive credit growth, real estate booms, and equity price surges have preceded periods of financial stress or slowdown, underscoring their diagnostic value in identifying systemic risk and cyclical shifts (Culp et al., 2018; Magubane, 2024). Therefore, the inclusion of CR, HP, and SP offers a theoretically grounded, empirically validated, and contextually appropriate approach to capturing the evolution and turning points of South Africa’s financial cycle.

There are two important caveats regarding the use of these variables in the study. First, they are used to construct the financial cycle. They are aggregated into a single index, in the study; principal component analysis (PCA) is used to achieve this task. For the purpose of this exercise, the variables are standardized using their mean and standard deviation. To confirm the suitability of CR, HP, and SP as optimal variables for the construction of the financial cycle, the KMO measure and Bartlett’s test were conducted.

Table 1. KMO, eigenvalues, and Bartlett’s test summary.

Measure	CR	HP	Share	Notes/Interpretation
KMO (MSA)	0.5	0.5	0.43	Overall KMO = 0.50 (marginal adequacy)
Bartlett’s test (LR test)	—	—	—	χ2(3) = 40.07, p = 0.0000 (significant)
Eigenvalues (factor analysis)	—	—	—	Factor 1 = 1.36 (45.2%); Factor 2 = 1.00 (33.3%); Factor 3 = 0.64
Factor loadings (Factor 1)	0.49	−0.49	0.03	Indicates CR and HP drive systemic variation
Factor score coefficient (F1)	0.36	−0.36	0.02	Used to construct composite financial cycle index
PCA loading (Component 1)	0.704	−0.7072	0.0655	CR and HP dominate PC1, retained as the final index

presents the findings. Multiple diagnostic tests were conducted to assess the suitability of CR, HP, and SP as variables for constructing the South African financial cycle. Table 1 presents a summary of these results. The Kaiser–Meyer–Olkin (KMO) measure of sampling adequacy shows an overall value of 0.50, with individual scores of 0.50 for CR and HP, and 0.43 for SP. These results indicate marginal adequacy, suggesting the data are sufficient for factor analysis, although improvements in variable selection could yield stronger results (Kaiser, 1974). Bartlett’s test of sphericity is statistically significant (χ²(3) = 40.07, p < 0.001), confirming that the correlation matrix is not an identity matrix and that the variables are suitably interrelated for factor extraction (Bartlett, 1950).

The factor analysis retained two factors with eigenvalues above 1. The first factor had an eigenvalue of 1.36, explaining 45.2% of the total variance, while the second explained 33.3%, bringing the cumulative variance to 78.5%. Given that Factor 1 accounts for the highest variance, it was retained as the composite index for the financial cycle, in line with standard practice in the literature (C. Borio, 2014; Drehmann et al., 2012; Nyati et al., 2021). The factor loadings show that both CR (0.49) and HP (−0.49) load strongly and inversely on the first factor, reflecting their countercyclical dynamics, while SP (0.03) contributes minimally. Similarly, the factor score coefficients for CR and HP are 0.36 and −0.36, respectively, confirming their dominant role in shaping the extracted financial cycle.

PCA results further validate these findings. The first principal component (Comp1) is again dominated by CR (0.7040) and HP (−0.7072), with negligible contribution from SP (0.0655), reinforcing that the credit and housing sectors are the primary drivers of cyclical financial behavior in South Africa. As such, Component 1 from the PCA and Factor 1 from the factor analysis converge, providing robust justification for using the resulting index as a valid proxy for the South African financial cycle. Accordingly, CR, HP, and SP were retained in this study as the composite indicators for capturing financial cycle fluctuations. In turn, the component that explains the most variations in these variables was retained to represent the financial cycle.

Secondly, the CR, HP and SP variables are used as explanatory variables in the QARDL of the estimated cycle. For this purpose, these variables are not standardized. However, to address the multicollinearity issue, the lags of the variables and other explanatory variables were used. Accordingly, the Akaike information criterion is used to determine the optimal lag to be included in the QARDL. After determining the number of lags to be included, each variable is transformed to its optimal lag using the transformation (y = x[_- N-l], where y is the new transformed variable, x is the original variable, N is the current observation, and l is the optimal lag. The main motivation for including the credit, house prices, and share prices in the QARDL is to uncover the magnitude and direction of their impact on the cycle, which cannot be robustly performed in the PCA.

Other explanatory variables include the real effective exchange rate (EXCH), GDP, inflation rate (INF), broad money supply (M3), the repo rate (REPO), and the macroprudential policy index (MPI). Their significant roles justify the inclusion of these variables in the model to shape the dynamics of the financial cycle and economic conditions in South Africa. Exchange rates are included because they capture the effects of the foreign exchange market, which are particularly relevant in South Africa due to its free-floating exchange rate system. This system makes the South African financial system more vulnerable to external shocks, such as fluctuations in global commodity prices and changes in international investor sentiment (Mlachila et al., 2013). Exchange rate volatility can directly impact inflation, external debt, and trade balances, which influence the broader economy and financial stability (C. E. Borio et al., 2019). GDP is incorporated as a key indicator, because substantial evidence suggests that the business and financial cycles are closely related, typically moving in tandem in a procyclical manner. In other words, periods of strong economic growth are often associated with financial booms, while economic downturns tend to coincide with financial contractions. Therefore, GDP serves as an essential driver in understanding both the short-term fluctuations and long-term trends within the financial cycle.

The inflation rate is included due to the significant threats that an unstable price environment poses to the financial system. High inflation can erode purchasing power, destabilize currency values, and increase uncertainty, which may prompt financial market volatility and disrupt investment decisions. On the other hand, deflation can lead to reduced consumer demand, rising debt burdens, and greater risks of financial crises. Thus, inflation is critical in analyzing financial cycles and their impact on economic stability. Monetary policy variables, such as interest rates, are essential in understanding the cost of borrowing, which directly affects financial activities, such as lending, investment, and consumption (Bernanke & Gertler, 1995). Changes in the policy rate influence the level of credit in the economy and can exacerbate or dampen financial cycle fluctuations. As such, the repo rate, a key policy tool in South Africa, is included to reflect the central bank’s stance on liquidity and borrowing costs. Finally, macroprudential policy is included because it specifically targets the stabilization of the financial cycle. The goal of macroprudential measures is to mitigate systemic risks and enhance the financial system’s resilience, especially during periods of financial instability (C. Borio, 2011). By addressing imbalances and vulnerabilities within the financial sector, macroprudential policies aim to prevent the amplification of financial cycles and their detrimental effects on the broader economy. This makes the inclusion of the MPI crucial to understanding how regulatory actions influence the financial cycle. The MPI collected from the IMF is selected because it effectively captures both the frequency and direction—tightening or easing—of macroprudential policy actions within a given timeframe.

Originally, the MPI was constructed as a dummy variable; however, this study adopted the rolling window approach to convert the MPI into a continuous time series. Under this method, each macroprudential tightening increases the index by one unit, irrespective of the specific tool or its intensity, while each easing decreases the index by one unit similarly. The index retains its updated value until the next policy change occurs. For example, if two tightening measures are implemented within the same quarter without easing, the index rises by two units during that period. This cumulative approach to indexing aligns with methodologies used by Bruno (2023) and Zdzienicka et al. (2015). It contrasts with an alternative MPI formulation that takes into account the introducing or removing policy measures but do not capture changes in the intensity or level of individual tools over time. In addition to these key variables, the real effective exchange rate, broad money supply, and other monetary variables help provide a comprehensive picture of the financial cycle’s drivers and the interactions between domestic and external economic conditions.

The data used in this study span from 2000 to 2024, monthly. However, not all variables are available monthly; EXCH, GDP, CR, HP, and SP are reported quarterly. To align these with the monthly frequency of other variables, interpolation was applied to convert the quarterly data into monthly observations. Interpolation is a statistical method that estimates intermediate values between known data points, allowing for a smooth distribution of quarterly values across the corresponding months (Denton, 1971; Fernandez, 1981). This approach preserves the overall trend and seasonal patterns of the data, ensuring consistency for high-frequency analysis. The use of interpolation for frequency conversion is well established in macro-financial studies (Charemza & Deadman, 1997) and is appropriate when higher-frequency data are unavailable. The chosen sample period—spanning from January 2000 to December 2024 monthly—is methodologically and contextually justified, given the focus of the study on South Africa’s inflation targeting (IT) regime and the evolution of its financial stability architecture. South Africa officially adopted the inflation targeting framework in February 2000, marking a significant shift in the conduct of monetary policy. This period serves as a natural starting point, as it represents the establishment of a coherent, rules-based monetary policy regime with price stability as the primary objective (Aron & Muellbauer, 2013).

Importantly, within the inflation targeting period, two major institutional developments directly relate to this study’s scope. First, in the early 2000s, the SARB began integrating financial developments into its macroeconomic assessments, although inflation remained the primary concern. Prudential tools, such as minimum capital requirements and liquidity ratios, were applied, but largely as auxiliary mechanisms to support the inflation-targeting framework. Financial indicators were monitored to the extent that they influenced price dynamics.

Second, a more substantial institutional shift occurred in 2017, when the SARB was granted an explicit financial stability mandate through the Financial Sector Regulation Act (Act No. 9 of 2017), leading to the establishment of the Prudential Authority. This reform formalized macroprudential oversight in South Africa and represented a decisive move toward a dual-mandate framework—maintaining both price and financial stability. Consequently, this latter period enables a more rigorous analysis of the interaction between monetary and macroprudential policies, as well as their respective impacts on financial cycles.

Using monthly data over this 25-year period provides sufficient degrees of freedom for robust time series analysis, particularly for models, such as QARDL, which estimate parameters across multiple quantiles. Monthly frequency also allows the model to detect short-term dynamics and regime shifts more accurately, especially in response to cyclical financial developments and evolving policy interventions.

Table 2. Data definition and sources.

VAR	Definition	Source
Cycle	The South African financial cycle index was constructed in the study using PCA.	Own construction
EXCH	Real effective exchange rate	Bank of International Settlements
CR	Credit-to-GDP ratio	Bank of International Settlements
HP	All house price index	Bank of International Settlements
INF	Consumer price inflation rate	Bank of International Settlements
REPO	Policy rate	Bank of International Settlements
GDP	Real gross domestic product	South African Reserve Bank
SP	Share prices	South African Reserve Bank
M3	Broad money supply as a % of GDP	South African Reserve Bank
MPI	Macroprudential Policy Index	International Monetary Fund

below provides a summary of the data. This period was specifically chosen for several reasons. First, it coincides with South Africa’s adoption of a flexible inflation targeting framework, which has shaped monetary policy decisions since its implementation. Second, the focus on macroprudential policy and financial stability concerns began around 2002, following the banking crisis in the country, marking a critical point in the evolution of financial regulation. The chosen period is also sufficiently long to capture both short-run and long-run effects of the financial cycle. The CR, HP, REPO, EXCH, and INF data were obtained from the Bank for International Settlements statistics. The M3, GDP and share prices (SP) variables were collected from the SARB statistical time series database. The MPI was sourced from the International Monetary Fund Integrated Macroprudential Policy database. These data sources provide reliable and consistent indicators crucial for understanding the South African financial cycle dynamics during this period.

3.3. Quantile ARDL

The study applies the quantile ARDL model to examine the short-run and long-term impact of the exchange rate, gross domestic product, inflation rate, total domestic credit, house prices, share prices, money supply, repo rate, and macroprudential policy index on the South African financial cycle. The first reason for selecting the QARDL model is based on practical considerations related to the nature of the South African financial cycle. The financial cycle is inherently nonlinear and characterized by multiple distinct phases—expansions, contractions, peaks, and troughs—often asymmetric in duration and intensity (Claessens et al., 2012; Drehmann et al., 2012). Traditional linear models, such as the standard ARDL (Pesaran et al., 2001) or vector autoregression (Sims, 1980), assume homogeneous relationships across the conditional distribution of the dependent variable, thereby masking critical phase-specific dynamics. In contrast, the QARDL model, as introduced by Lee and Cho (2017), estimates the relationships at different quantiles of the conditional distribution, making it particularly well-suited to capturing the heterogeneous behavior of macro-financial variables across different stages of the financial cycle.

For instance, during the upswing of the financial cycle (i.e., upper quantiles), credit growth and asset prices may exhibit stronger responses to policy and macroeconomic shocks compared to the downturn phase (i.e., lower quantiles), where the effects are often weaker or delayed due to credit constraints or risk aversion (Adrian et al., 2019). The QARDL framework captures these variations by allowing short-run and long-run coefficients to vary across quantiles, thereby offering a more granular and nuanced understanding of the underlying dynamics.

While alternative nonlinear models, such as smooth transition regression (STR) (Granger & Teräsvirta, 1993), threshold VAR (TVAR) (Balke, 2000), and Markov-switching models (Hamilton, 1989) also attempt to capture regime changes or nonlinear adjustments, they typically require a priori specification of thresholds or rely on latent state processes. These assumptions can be restrictive and prone to misclassification, especially in emerging market contexts where structural breaks and financial frictions are more prevalent (Akinci & Queralto, 2014). Moreover, such models often fail to account for the gradual variation in relationships across the conditional distribution of the dependent variable, a key advantage of the QARDL approach.

Therefore, the QARDL model is preferred in this study for its robustness in capturing asymmetric, phase-dependent dynamics and its flexibility in addressing the complexities of South Africa’s financial cycle between 2002 and 2022.

The second reason for employing the QARDL model is its econometric strength and versatility. Specifically, the model demonstrates robustness to non-normal error distributions, a common feature in macroeconomic and financial data, especially in emerging markets, like South Africa. Financial time series often exhibit heavy tails, excess kurtosis, and skewness due to shocks, volatility clustering, and structural changes—features that violate the classical assumptions underpinning ordinary least squares (OLS) and standard time series models. The QARDL model, by focusing on conditional quantiles rather than the conditional mean, remains robust in the presence of such non-normality (Hashmi et al., 2022).

Moreover, QARDL is particularly effective in dealing with outliers and heterogeneity in the response variable. Outliers, which could result from financial crises, policy shocks, or abrupt changes in investor behavior, tend to distort estimates in mean-based models. In contrast, quantile regression techniques—including QARDL—are less sensitive to outliers since they do not rely on minimizing squared residuals. This feature makes the model highly suitable for financial and macroeconomic applications, where outliers carry substantive information rather than mere statistical noise (Sharif et al., 2020).

Additionally, QARDL allows for slope heterogeneity across different quantiles, meaning the relationship between the explanatory and dependent variables can change depending on the level or state of the dependent variable. This flexibility enables the model to capture asymmetric adjustments and nonlinear dynamics that are often present in financial development and financial cycle studies (Anwar et al., 2021). Such heterogeneity is especially important in analyzing economies with pronounced structural divides and segmented financial markets, where the same policy shock may have vastly different effects depending on prevailing economic conditions.

Additionally, the model facilitates the examination of both short-run and long-run effects of independent variables on the dependent variable across different quantiles (Hashmi et al., 2022). It provides more reliable results when the sample size is small and, like the ARDL model, is particularly useful when the variables are integrated of either order zero I(0) or one I(1) (Mensi et al., 2019).

We use the following OLS specification as a benchmark for estimating the impact of the aforementioned explanatory variables:

$$\begin{gathered} \ln CYCL{E}_t={\beta }_0+{\beta }_{1}lnEXC{H}_t+{\beta }_{2}lnGD{P}_t+{\beta }_{3}lnIN{F}_t+{\beta }_{4}lnC{R}_t+{\beta }_{5}lnH{P}_t+{\beta }_{6}lnSP+{\beta }_{7}lnM{3}_{\mathrm{t}} \\ +{\beta }_{8}lnREP{O}_t+{\beta }_{9}lnMP{I}_t+{ϵ}_t \end{gathered}$$

(1)

where ln denotes the natural logarithm of the variables. The cycle represents the financial cycle index, which is the dependent variable. EXCH is the real effective exchange rate, GDP is real gross domestic product, INF is the inflation rate, CR is the credit-to-GDP ratio, HP is the all-house price index, SHARE is the all share price index, M3 is the broad money supply, REPO is the repo rate, and MPI is the macroprudential policy index. The QARDL model is not particularly robust when integrating order two (I2) variables. Therefore, the augmented Dickey–Fuller (ADF) unit root test is conducted to examine the order of integration of variables. After the order of integration is determined, we will proceed and use the QARDL. The model estimated in the study is similar to that of Hashmi et al. (2022). An extension of the ARDL model into the QARDL model leads to the following Equation (2), which is the standardized version of the OLS model in Equation (1):

$$\begin{gathered} Q_{CYCL{E}_t}\left(\mathsf{\tau }\right)=\alpha {\left(\tau \right)}_0+{\sum }_{i=1}^{n1}{b}_i∆LnCYCL{E}_{t-i}+{\sum }_{i=0}^{n2}+c_i\left(\tau \right)∆{LnY6}_{t-i}^{\top }+{\sum }_{i=0}^{n3}{d}_i\left(\tau \right)∆Ln{X}_{t-i}^{\top }+{\sum }_{i=0}^{n4}{e}_i\left(\tau \right)∆Ln{Z}_{t-i}^{\top }+ \\ {\beta }_1\left(\tau \right)Ln{Y}_{t-i}^{\top }+{\beta }_2\left(\tau \right)Ln{X}_{t-i}^{\top }+{\beta }_3\left(\tau \right)Ln{Z}_{t-i}^{\top }+{ϵ}_t \end{gathered}$$

(2)

where $Y$ is the vector of financial explanatory variables, i.e., CR, HP, and SP, which maintain the lag of the dependent variable. $X$ is a vector of real variables containing EXCH, GDP, and INF. $Z$ is a vector of policy variables which contains M3, REPO, and MPI. The parameter $\tau$ is the quantile measurement. In order to empirically investigate the impact of the above variables on the financial cycle, the study utilizes the following quantiles: $\tau \in \{0.05,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,0.95\}$. A Wald test is used to assess parameters’ short-run and long-run symmetry. For the short run, the symmetry is tested using the following null hypothesis:

$$H_0^s:\cdot {\mathrm{c}}_{\mathrm{i}}\left(0.05\right)={\mathrm{b}}_{\mathrm{i}}\left(0.1\right)=\cdots ={\mathrm{b}}_{\mathrm{i}}\left(0.95\right)$$

$$H_0^s:\cdot {\mathrm{d}}_{\mathrm{i}}\left(0.05\right)={\mathrm{c}}_{\mathrm{i}}\left(0.1\right)=\cdots ={\mathrm{c}}_{\mathrm{i}}\left(0.95\right)$$

$$H_0^s:\cdot {\mathrm{e}}_{\mathrm{i}}\left(0.05\right)={\mathrm{d}}_{\mathrm{i}}\left(0.1\right)=\cdots ={\mathrm{d}}_{\mathrm{i}}\left(0.95\right)$$

Similarly, the long-run symmetry is tested using the following null hypothesis:

$$\begin{gathered} H_0^l:\cdot {\mathsf{\beta }}_1\left(0.05\right)={\mathsf{\beta }}_1\left(0.1\right)=\cdots ={\mathsf{\beta }}_1\left(0.95\right) \\ {H}_0^l:\cdot {\mathsf{\beta }}_2\left(0.05\right)={\mathsf{\beta }}_2\left(0.1\right)=\cdots ={\mathsf{\beta }}_3\left(0.95\right) \\ {H}_0^l:\cdot {\mathsf{\beta }}_3\left(0.05\right)={\mathsf{\beta }}_3\left(0.1\right)=\cdots ={\mathsf{\beta }}_4\left(0.95\right) \end{gathered}$$

At the end of estimation, several stability and diagnostic tests are conducted to assess the model’s goodness of fit in Equation (2). The Breusch–Pagan–Godfrey heteroscedasticity test is employed to assess whether the residuals are homoscedastic. The Breusch–Pagan LM test is employed to assess whether there is serial correlation in the lags of residuals. A Wald test is used to assess whether there should be variables that should be omitted. The Ramsey reset test is employed to assess the robustness of the model specification. The CUSUM and the recursive coefficient tests are employed to assess the stability of the model and the estimated parameters.

4. Results and Discussion

4.1. Preliminary Results

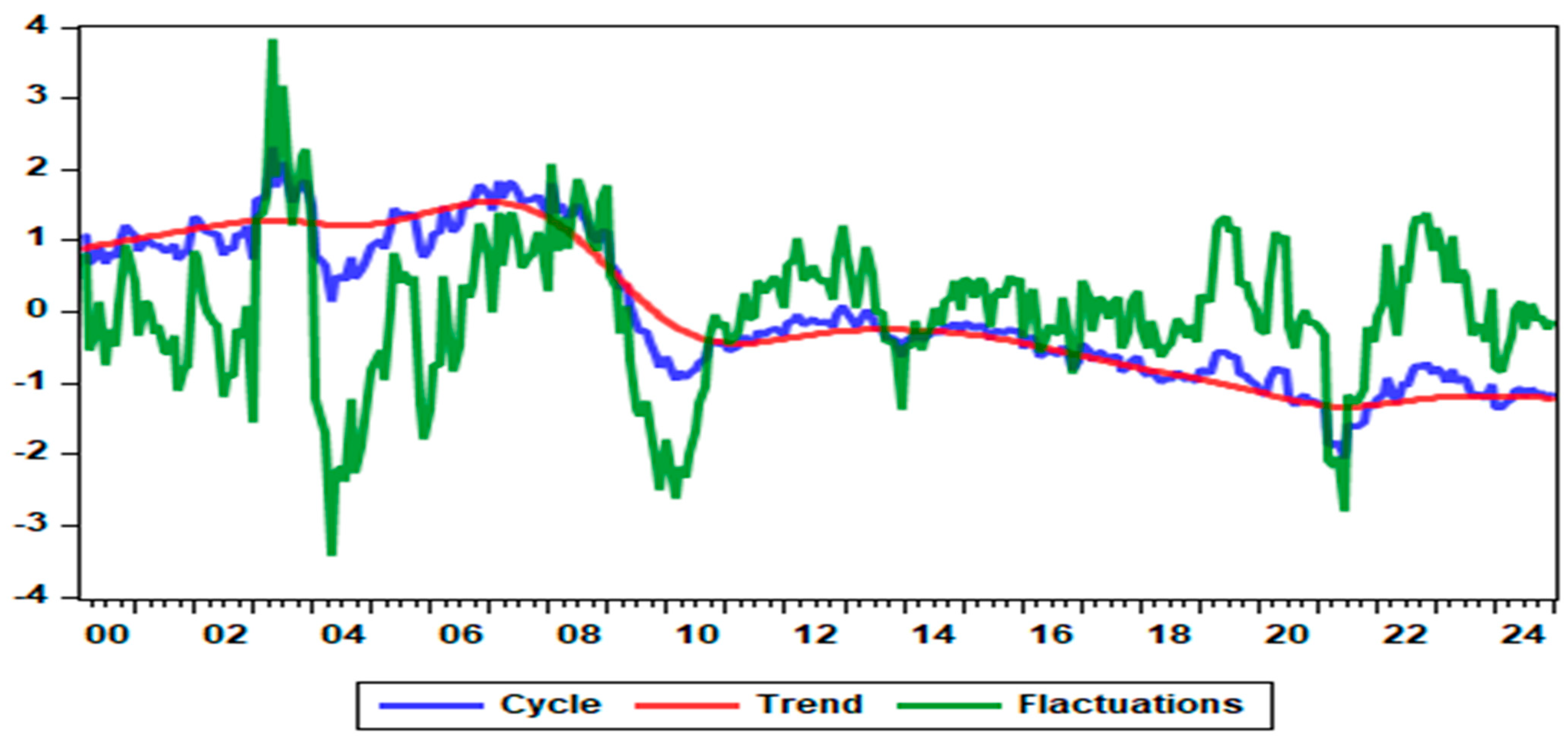
This section presents the study’s key findings. Figure 1 illustrates the South African financial cycle, decomposed into its long-term trend and short-term fluctuations using the Hodrick–Prescott Filter (HP filter). As shown in the figure, the long-term trend has been on a persistent downward trajectory since the early 2000s, indicating a gradual weakening in the underlying dynamics of financial development over time. A downward trend in financial development reflects a deterioration in the ability of the financial system to effectively support economic growth, allocate capital efficiently, mobilize savings, and extend credit to households and businesses. This trend has serious implications in developing economies, like South Africa—it may result in reduced access to financial services, lower investor confidence, and weaker economic performance. Financial development is critical in enabling productivity gains and supporting entrepreneurship and long-term investment. Therefore, when financial systems begin to contract or lose efficiency, the broader macroeconomic implications can be substantial. Beck and Levine (2004) argue that well-functioning financial systems are vital in fostering economic development by reducing transaction costs and improving risk-sharing. Thus, a downward trend signals the reversal of these gains.

Recent developments in South Africa mirror this concern. The South African rand (ZAR) has experienced significant depreciation and volatility over the past decade, driven by domestic political uncertainty, tightening of global monetary policy, and episodes of capital flight. The “Nenegate” incident in 2015 in which a finance minister was unexpectedly replaced, led to a sharp fall in the rand and signaled weakening institutional credibility. Similar pressures resurfaced during the COVID-19 pandemic and the 2021 unrest, leading to further currency instability and capital outflows. These events discouraged long-term investment and undermined investor confidence, consistent with the findings of Aye and Odhiambo (2021), who note that currency volatility in South Africa is strongly associated with lower financial market efficiency and reduced private investment.

Stagnation in private sector credit extension also indicates a weakening financial system. According to the South African Reserve Bank, real growth in private sector credit extension has been below historical averages since 2020. Lending to households and corporates remains cautious amid high debt levels, weak consumer confidence, and rising interest rates. This stagnation restricts investment and consumption, ultimately constraining economic recovery. Mlachila et al. (2013) similarly observe that in low- and middle-income economies, a reduction in credit growth often reflects deeper structural issues in financial intermediation, including risk aversion among lenders and a lack of innovative financial products.

South Africa’s housing market shows further evidence of a downward trend. House price growth has remained below inflation in many parts of the country, pointing to weak demand and affordability constraints. Real house prices have declined in several metropolitan areas, particularly where unemployment and credit access are limited (Mwanyepedza & Mishi, 2024). The housing sector is typically a driver of wealth accumulation and collateral formation, especially for middle-income households. Weakness in this sector constrains both consumer wealth and borrowing capacity, thereby limiting financial system depth and development. This observation is supported by Aron and Muellbauer (2016), who find that real house price stagnation negatively affects consumption and loan demand.

Financial inclusivity, a key component of financial development, has also seen setbacks despite improvements in digital financial services. Many low-income households remain unbanked or underbanked, particularly in rural areas. The FinScope Consumer Survey in 2022 revealed that significant population segments still lack access to formal savings instruments, credit facilities, and insurance products (Nanziri & Gbahabo, 2025). These patterns highlight barriers, such as limited financial literacy, high transaction costs, and weak infrastructure. Sahay et al. (2015) argue that financial inclusion is critical to achieving broader financial development and that exclusion undermines economic equality and limits the effectiveness of monetary policy transmission.

In summary, South Africa’s financial development trajectory has shown signs of decline, with multiple indicators reflecting the financial sector’s reduced efficiency, inclusivity, and resilience. These findings align with the empirical literature pointing to a growing disconnect between financial sector performance and real economic outcomes in emerging markets (De la Torre et al., 2017). Reversing this trend will require strengthening institutional frameworks, promoting financial literacy, improving credit infrastructure, and restoring macroeconomic stability.

The cyclical component of the South African financial cycle reveals several noteworthy dynamics with important implications for academic inquiry and macroprudential policy design. Notably, the peaks of the financial cycle coincide with key periods of financial stress, underscoring the cycle’s procyclical nature and its role in amplifying systemic risk. Three distinct episodes are aligned with these peaks. The first occurred in 2002–2003 during a domestic banking crisis that saw the collapse of institutions, such as Saambou Bank and BOE Bank, precipitated by liquidity shortages, poor asset quality, and a loss of depositor confidence. Although the crisis was relatively contained, it led to significant consolidation in the sector and prompted enhanced supervisory frameworks (Van der Merwe, 2004).

The second major peak occurred during the global financial crisis from 2007 to 2009. While South Africa’s banking system remained solvent, the economy experienced sharp declines in credit growth, portfolio investment, and consumer confidence. Asset prices fell markedly, and the rand depreciated significantly as global risk aversion surged. These events were mirrored in the financial cycle, which peaked before the crisis, providing early signals of the impending slowdown. This evidence supports the broader literature that views the financial cycle as a leading indicator of macro-financial vulnerabilities (Aikman et al., 2015; Drehmann et al., 2012).

The third peak of the financial cycle aligns with the 2019–2020 COVID-19 pandemic, which triggered a global economic shock. South Africa, already facing fiscal constraints and sluggish growth, experienced a sharp contraction in GDP, deterioration in household and corporate balance sheets, and a spike in financial market volatility. The South African Reserve Bank intervened through rate cuts and liquidity support, but financial conditions remained fragile. The turning point in the financial cycle accurately captured this phase of financial distress, further validating its use as a real-time monitoring tool.

In addition to signaling crises, the cyclical component captures episodes of rapid financial expansion. Between 2004 and 2007, the South African economy experienced a credit and housing boom supported by accommodative monetary policy, strong global demand for commodities, and positive domestic sentiment. Household debt as a share of disposable income rose sharply, and residential property prices surged, developments that were reflected in the steep upward trajectory of the financial cycle during this period. Similar, albeit more moderate, recoveries were observed in the post-GFC and post-COVID-19 periods, as indicated by the rebound in the cyclical component driven by policy stimulus and renewed credit demand.

These findings highlight the analytical value of the financial cycle as a medium-term macro-financial indicator. While traditional indicators, such as GDP or inflation, provide snapshots of economic conditions, they often fail to capture latent financial risks. By aggregating information on credit volumes, asset prices, and leverage, the financial cycle offers a richer understanding of systemic dynamics (C. Borio, 2014; Claessens et al., 2011). Its historical alignment with crises in South Africa strengthens the case for its incorporation into early-warning frameworks and financial stability assessments.

From a policy perspective, these insights suggest that macroprudential authorities should closely monitor the financial cycle and calibrate their tools accordingly. Time-varying instruments—such as countercyclical capital buffers (CCyB), dynamic loan-to-value (LTV) ratios, and debt-to-income (DTI) caps—should be tightened during the upswing to contain excess credit growth and loosened during downturns to avoid credit crunches. This approach is consistent with international recommendations from the Basel Committee on Banking Supervision and empirical studies showing that pre-emptive tightening of macroprudential policy can reduce the probability and severity of financial crises (Cerutti et al., 2017).

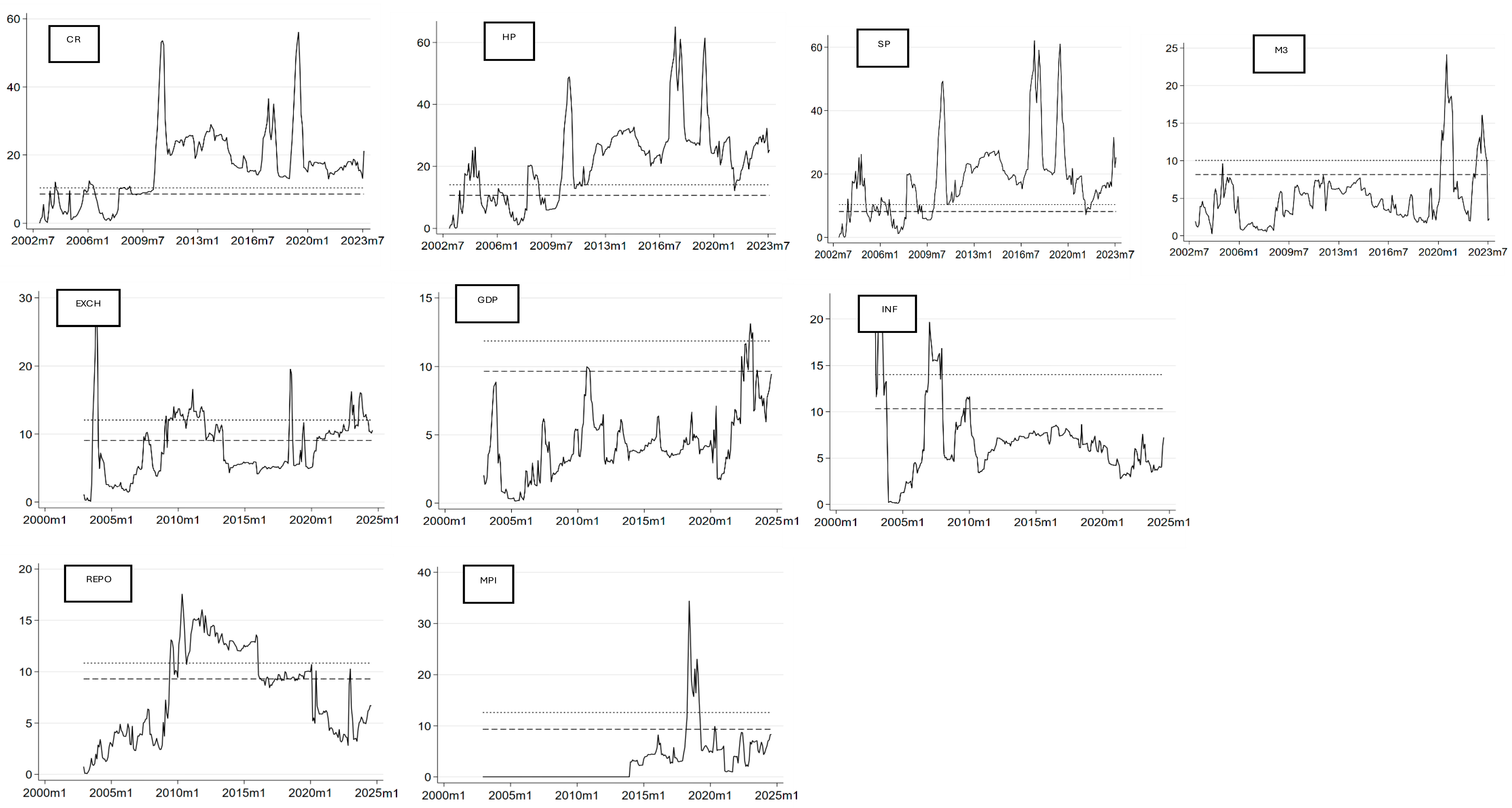
Unit root tests using the Augmented Dickey–Fuller (ADF) method were employed to determine the stationarity properties of all variables. The results in

Table 3. Augmented Dickey–Fuller stationarity test.

	Level		First Difference
	${\mathit{T}}_{\mathit{a}}$	p-Value	${\mathit{T}}_{\mathit{a}}$	p-Value
CYCLE	−3.753	0.004	−8.291	0.000
EXCH	−2.541	0.107	−14.025	0.000
GDP	−2.831	0.055	−5.841	0.000
INF	−2.664	0.082	−6.575	0.000
CR	−1.847	0.357	−6.679	0.000
HP	−1.927	0.320	−2.818	0.057
SP	−13.707	0.000	−12.163	0.000
M3	3.148	1.000	−7.039	0.000
Repo	−2.876	0.049	−5.166	0.000
MPI	−1.109	0.711	−9.476	0.000

Notes: $T_a$ refers to the t-statistics.

reveal that the variables exhibit a mixed order of integration. Specifically, the financial cycle, share price index, and the policy interest rate are stationary at level—indicating they are integrated of order zero, I(0). The remaining variables, namely the real effective exchange rate, real GDP, inflation, credit-to-GDP ratio, house prices, broad money supply, and the macroprudential policy index, became stationary only after first differencing and are, therefore, classified as integrated of order one, I(1). None of the variables were found to be integrated of order two, I(2), thus satisfying a key prerequisite for applying the autoregressive distributed lag (ARDL) modelling framework.

Econometric theory, as established by Pesaran et al. (1999) and Pesaran et al. (2001), demonstrates that the ARDL bounds testing approach to cointegration is robust in the presence of a combination of I(0) and I(1) variables. Unlike traditional methods, such as Johansen or Engle–Granger, which require all variables to be integrated of the same order, the ARDL method can accommodate regressors with differing levels of integration without compromising the validity of long-run relationships. Accordingly, this study estimates the model using I(0) and I(1) variables without transforming them to the same order of integration.

Based on the unit root test results presented above, it is evident that some variables are stationary at level I(0), such as SP and Repo, while others become stationary only after first differencing I(1), such as EXCH, GDP, and INF. In line with standard econometric practice, the I(1) variables were differenced before estimation to achieve stationarity. However, the I(0) variables were not transformed, as differencing them would unnecessarily strip the data of valuable long-run information.

This approach is consistent with the ARDL bounds testing methodology, which, according to Pesaran et al. (1999) and Pesaran et al. (2001), remains valid when applied to a mix of I(0) and I(1) variables. Unlike traditional cointegration techniques, such as Johansen or Engle–Granger, which require all series to be integrated of the same order, the ARDL framework allows for the inclusion of variables with differing orders of integration without compromising the validity of the long-run estimations. Consequently, this study estimates the model using both I(0) and I(1) variables in their respective forms—levels for stationary series and first differences for non-stationary series—reflecting both empirical evidence and methodological soundness.

The Zivot–Andrews (ZA) unit root test was employed alongside the ADF test to address the possibility of structural breaks within the time series data. The ZA test accounts for a single endogenous structural break in either the intercept or trend of a series, offering a more robust stationarity assessment in contexts where economic variables may be subject to sudden shifts due to policy changes, crises, or structural transformations (Zivot & Andrews, 2002). This methodological refinement is particularly relevant given the historical volatility observed in emerging market economies.

Table 4. Zivot–Andrews unit root test.

Variable	${\mathit{T}}_{\mathit{a}}$	Date of Break	Results
CYCLE	−5.049 *	2007M5	Stationary
EXCH	−3.882 *	2006M5	Stationary
GDP	−4.867	2011M7	Not stationary
INF	−4.474	2006M5	Not stationary
CR	−4.275 ***	2008M8	Stationary
HP	−4.760 ***	2007M7	Stationary
SP	−14.032 **	2007M5	Stationary
M3	−2.778	2017M2	Not stationary
Repo	−4.354 ***	2009M2	Stationary
MPI	−3.743 ***	2016M1	Stationary

Notes: $T_a$ refers to the t-statistics, whereas *, **, and *** refer to the probability values calculated from a standard t-distribution to the 10% 5%, and 1% critical values, respectively.

presents the findings. The ZA results confirm that several variables become stationary once structural breaks are accounted for, even though they appeared non-stationary under the ADF test. Notably, CYCLE, which was already stationary at level in the ADF test, remains stationary under ZA, with a structural break identified in 2007M5. This date coincides with the initial phase of the global financial crisis, which began unfolding in mid-2007, triggering widespread financial stress globally (C. Borio, 2011). Similarly, EXCH, which was non-stationary in the ADF test, is found to be stationary under ZA with a break in 2006M5—likely linked to the commodity price boom and the surge in capital flows to emerging markets that characterized this period (Akinboade & Makina, 2009). By contrast, GDP and INF remain non-stationary under ZA, with break dates in 2011M7 and 2006M5, respectively. The persistence of unit roots in these series even after allowing for breaks suggests a strong underlying trend component. For GDP, the 2011M7 break may correspond with the lagged effects of the GFC on real economic activity and the onset of fiscal consolidation measures. For INF, the break coincides with a transitional period in the SARB’s inflation-targeting regime, which may have altered the dynamic path of inflation without achieving mean reversion (Aron & Muellbauer, 2013).

The ZA test also affirms the stationarity of CR, HP, SP, Repo, and MPI, all of which exhibit statistically significant breaks between 2007 and 2016. For instance, the structural break in Repo in 2009M2 aligns with SARB’s response to the domestic recession through aggressive interest rate cuts. Similarly, the 2016M1 break in MPI corresponds with a period of intensified global emphasis on macroprudential policy frameworks following the GFC (Claessens et al., 2013). In contrast, M3 remains non-stationary under both ADF and ZA tests, with a structural break identified in 2017M2. This likely reflects continued shifts in monetary aggregates during a period marked by investor uncertainty, political volatility, and credit rating downgrades in South Africa (Meyer et al., 2018). Taken together, the ZA results corroborate the findings from the ADF test while providing additional insight into the timing and nature of structural breaks affecting the data. They confirm that the dataset consists of a combination of I(0) and I(1) variables, validating the use of the ARDL bounds testing approach.

The ZA test results reveal that many of the variables exhibit structural breaks around the global financial crisis (GFC) period, notably between 2006 and 2009. However, it is important to note that this study did not directly incorporate structural breaks into the QARDL model specification. This decision was motivated by several important considerations. First, the available sample size is relatively small, and the QARDL framework already includes a sizable number of variables and quantile partitions. Introducing multiple break dummies or interaction terms would significantly reduce degrees of freedom, heighten the risk of overparameterization, and potentially lead to overfitting, thereby undermining the reliability and interpretability of the model (Pesaran et al., 1999; Narayan & Popp, 2010).

Moreover, the ZA test results show that structural breaks do not occur uniformly across all variables or at a common point; instead, they are heterogeneous and span different dates, reflecting the uneven transmission of external shocks and internal dynamics across variables and economies. This lack of synchronicity makes it difficult to apply a single dummy variable or breakpoint uniformly across the model without introducing identification problems or misrepresenting the nature of regime shifts. Recognizing these limitations, the study also estimates the time-varying Granger causality test to corroborate the findings of the QARDL.

To assess the existence of a long-run relationship between the financial cycle and the macroeconomic and financial variables, the ARDL bounds test for cointegration was conducted.

Table 5. Diagnostic tests.

Test	Statistic
Bounds test F-Stats	68.432 ***
Breusch–Pagan–Godfrey heteroscedasticity F-Stats	3.127
Breusch–Godfrey LM F-Stats	41.562
Jarque–Bera test	47.893
T Wald Test F-Stats	8.956 ***
T Waldlr Test F-Stats	125.47 ***
T Waldsr Test F-Stats	198.34 ***
Ramsey Test F-Stats	9.784

Note: *** refer to the probability values calculated from a standard t-distribution to the 1% critical value.

presents the findings. The results returned a highly significant F-statistic of 68.432 (***), which exceeds the critical upper bounds at the 1% level, confirming the presence of a long-run cointegrating relationship between the financial cycle (the dependent variable) and its regressors, including GDP, inflation, credit, house prices, monetary policy, and macroprudential policy. This result is consistent with the theoretical expectation that these variables share stable long-term relationships, despite short-term fluctuations (Pesaran et al., 2001; Narayan, 2005). The finding aligns with previous studies that emphasize the financial cycle as an important indicator of economic stability and financial health (C. Borio, 2011; Drehmann et al., 2012).

Several diagnostic tests were performed to ensure the robustness and validity of the ARDL model estimates (see Table 5). First, the Breusch–Pagan–Godfrey test for heteroscedasticity yielded an F-statistic of 3.127 (***), which is statistically significant. This finding suggests that the model suffers from heteroscedasticity and that the residuals have constant variance across observations. This result is crucial for ensuring that standard errors are consistent and reliable, which is essential for valid hypothesis testing and inference (Breusch & Pagan, 1979). The Jarque–Bera test was conducted to assess the normality of residuals. Its main advantage lies in its ability to jointly test for both skewness and kurtosis. The test statistic, i.e., 47.893 (see Table 5), is statistically insignificant, indicating that the study fails to reject the null hypothesis of normally distributed residuals. Hence, the study concludes that the estimated residuals are normally distributed.

The Breusch–Godfrey LM test for serial correlation returned an F-statistic of 41.562 (***), indicating the presence of autocorrelation in the residuals. Autocorrelation is common in macroeconomic time series data and may arise due to omitted dynamics or lagged effects not captured in the model. To ensure that the model returns robust standard errors in our model in the presence of heteroscedasticity and autocorrelation, the heteroskedasticity and autocorrelation consistent (HAC) estimator was employed when estimating the QARDL. This approach corrects for potential heteroskedasticity and autocorrelation in the error terms, ensuring more reliable inference. The HAC estimator was applied by first estimating the model at each quantile to obtain residuals, then computing a kernel-weighted covariance matrix of these residuals that adjusts for heteroskedasticity and autocorrelation. These robust covariance matrices were used to calculate standard errors for each quantile’s coefficients, ensuring valid inference despite serial correlation and changing error variance in the time series data. This adjustment helped to improve the estimated coefficients’ reliability and the results’ consistency.

The T Wald test for joint significance yielded an F-statistic of 9.784, indicating that the combined short-run and long-run coefficients are jointly significant in explaining variations in the financial cycle. This confirms that the selected macroeconomic and financial variables collectively influence financial cycle dynamics across the entire conditional distribution, supporting the robustness of the QARDL model. The long-run Wald test (T Waldlr) produced a highly significant F-statistic of 125.47, affirming the presence of strong long-run equilibrium relationships between the financial cycle and its determinants. Similarly, the short-run Wald test (T Waldsr) with an F-statistic of 198.34 confirms that short-term fluctuations significantly affect the financial cycle.

Lastly, the Ramsey RESET test for model specification returned an insignificant F-statistic of 10.011, indicating no evidence of functional form misspecification. Together, these results validate the model’s reliability and appropriateness in capturing both the short- and long-run dynamics of South Africa’s financial cycle. Despite autocorrelation, the model remains robust regarding long-run relationships, absence of heteroscedasticity, and overall explanatory power. These findings support using the ARDL methodology to model the dynamics of the financial cycle and its interaction with macroeconomic and financial variables, such as monetary policy, credit, and house prices, in the South African context. This approach is particularly suitable for assessing the role of financial cycles in policy formulation, as it allows for the simultaneous estimation of both short-run and long-run effects, which is crucial for understanding the effectiveness of monetary and macroprudential policies in maintaining economic stability (C. E. Borio & Drehmann, 2009).

4.2. Main Results

Table 6. Quantile ARDL results.

T	Exch	GDP	INF	CR	HP	SP	M3	REPO	MPI
Long-run quantile ARDL results; CYCLE dependent variable
0.1	−0.023 **	−0.023	−0.003 ***	−0.002 ***	0.001 ***	−0.023 *	−0.059 ***	0.021 ***	−0.030
0.2	−0.025 ***	−0.052 **	−0.003 ***	−0.003 ***	0.001 ***	−0.029 ***	−0.060 ***	0.023 ***	−0.025
0.3	−0.023 ***	−0.046 **	−0.002 ***	−0.002 ***	0.001 ***	−0.031 ***	−0.055 ***	0.027 ***	−0.023
0.4	−0.024 ***	−0.045 **	−0.002 ***	−0.002 ***	0.001 ***	−0.031 **	−0.055 ***	0.027 ***	−0.021
0.5	−0.025 ***	−0.045 **	−0.002 ***	−0.002 ***	0.001 ***	−0.032 **	−0.056 ***	0.026 ***	−0.022
0.6	−0.024 ***	−0.034 *	−0.002 ***	−0.003 ***	0.002 ***	−0.002 ***	−0.061 ***	0.040 ***	−0.086 ***
0.7	−0.027 ***	−0.037 *	−0.001 ***	−0.003 ***	0.002 ***	−0.002 ***	−0.059 ***	0.038 ***	−0.076 ***
0.8	−0.022 ***	−0.042 *	−0.001 **	−0.003 ***	0.001	−0.001 ***	−0.050 ***	0.038 ***	−0.055 **
0.9	−0.019	−0.081	−0.001 **	−0.003 ***	0.001	−0.001 ***	−0.058 **	0.037 ***	−0.057 ***
Short-run quantile ARDL results; CYCLE dependent variable
0.1	−0.00009	0.021	−0.015 *	0.061 ***	−0.033 ***	0.005 ***	−0.006	0.007	−0.053
0.2	−0.012 ***	0.048	−0.018 ***	0.061 ***	−0.031 ***	0.005 ***	−0.004	0.014	−0.058 **
0.3	−0.009	0.048	−0.018 ***	0.060 ***	−0.027 ***	0.005 ***	−0.005	0.018	−0.064 **
0.4	−0.011 **	0.047	−0.017 ***	0.061 ***	−0.027 ***	0.005 ***	−0.005	0.017	−0.065 **
0.5	−0.010 **	0.047	−0.018 ***	0.060 ***	−0.027 ***	0.005 ***	−0.004	0.017	−0.064 **
0.6	−0.014 *	−0.070	−0.009 **	0.061 ***	−0.019 ***	0.005 ***	−0.005 *	0.007	−0.065 ***
0.7	−0.013 *	0.025	−0.009 *	0.060 ***	−0.018 ***	0.005 ***	−0.055 *	0.005	−0.002 ***
0.8	−0.0001	−0.011	−0.005	0.060 ***	−0.016 **	0.005 ***	−0.037	0.002	−0.009
0.9	−0.00006	−0.034	−0.002	0.060 ***	−0.023 ***	0.005 ***	−0.025	0.002	0.004
EC	−0.257 ***

Notes: *, **, *** refers to the significance of the p-values at 10 percent, 5 percent, and 1 percent, respectively; EC refers to the error correction term, and $T$ or Tau refers to quantiles.

presents the results of the QARDL model. The observed error correction term of −0.257, particularly its statistical significance, provides a critical insight into the dynamics of the financial cycle index, which serves as the dependent variable in this analysis. The negative sign of the coefficient is paramount, as it unequivocally confirms the existence of a long-run cointegrating relationship between the financial cycle index and its identified macroeconomic drivers. This implies that any short-term deviation from the established long-run equilibrium will naturally trigger a corrective mechanism, steering the financial cycle back towards its sustainable path. Conversely, a positive coefficient would suggest a divergent system where imbalances are amplified rather than resolved.

The magnitude of this coefficient, −0.257, quantifies the speed at which this adjustment occurs. Specifically, it indicates that roughly 25.7% of any disequilibrium in the financial cycle index observed in the previous period is corrected within the current period. This rate suggests a moderate speed of adjustment. For instance, a coefficient closer to −1 would signify a rapid, almost immediate, correction, whereas a value near zero (though still significant) would point to a sluggish return to equilibrium. The statistical significance of this EC further validates the reliability of this adjustment mechanism, confirming that the observed reversion to equilibrium is not merely a product of random fluctuations.

In practical terms, this finding suggests that if the financial cycle index were to deviate above its long-run equilibrium—perhaps indicating a period of unsustainable financial expansion or a “boom”—approximately 25.7% of that excess would be naturally unwound in the subsequent period, guiding the cycle back towards balance. Conversely, during a financial downturn or “bust,” where the index falls below its equilibrium, a similar proportion of the deficit would be recovered in the next period. For policymakers in South Africa, this implies that the financial system possesses an inherent self-correcting tendency. While this automatic adjustment is beneficial, its moderate speed suggests that significant or prolonged deviations might still necessitate timely and well-calibrated policy interventions, such as macroprudential measures, to prevent an extended overheating or deep contraction of the financial cycle.

Turning to specific variables, the results reveal that GDP growth exhibits a negative relationship with the financial cycle in the long run, despite its generally accepted positive role in financial development according to standard economic theory (Levine, 2005). This counterintuitive finding may be interpreted within the South African context, where prolonged sluggish growth and high levels of public and household debt have arguably limited productive investment and constrained financial intermediation (Adusei, 2013). However, GDP demonstrates a positive short-run effect on the financial cycle, particularly at higher quantiles, suggesting that economic expansions may fuel financial booms in the late stages of the cycle, in line with the procyclical financial behavior documented in the boom–bust literature (Claessens et al., 2011).

The exchange rate negatively impacts the financial cycle in both the long and short run, especially at lower quantiles. However, the short-run effect is not statistically significant at higher quantiles. This finding implies that currency depreciations are generally associated with financial instability and hinder long-term financial development. This finding is theoretically consistent with the view that exchange rate volatility undermines investor confidence, raises borrowing costs, and deters foreign capital inflows (Ranciere et al., 2008). For instance, during the Asian Financial Crisis 1997, severe currency devaluations in certain countries, like Thailand and Indonesia, led to banking collapses and reversed years of financial sector gains. In South Africa, the “Nenegate” incident of December 2015, when then-Finance Minister Nhlanhla Nene was abruptly fired, led to a sharp depreciation of the rand and a subsequent loss of market confidence, reflecting the vulnerability of financial development to currency shocks.

Similarly, inflation negatively affects the financial cycle throughout, reinforcing its destabilizing role. High inflation erodes the real value of financial assets and discourages long-term saving and lending, corroborating the classical view of inflation as a tax on financial intermediation (Boyd et al., 2001). This finding aligns with studies showing that inflation thresholds exist beyond which financial development deteriorates, particularly in emerging markets (Khan et al., 2006).

Contrary to the positive role of credit expansion in many development models, the results show that credit has a negative long-run effect on the cycle. This finding may reflect excessive household indebtedness and unproductive lending practices that fuel consumption rather than investment (Beck et al., 2000). However, credit contributes positively to short-term financial booms across all quantiles, suggesting a cyclical pattern where credit expansions precede financial upswings. This finding is consistent with Schularick and Taylor (2012), who emphasize the role of credit booms in generating financial instability. A similar duality is observed with share prices and housing prices. While the long-run effect of share prices is negative—possibly due to speculative and volatile equity markets—their short-run impact is positive, consistent with the wealth effect and increased liquidity during market rallies (Mishkin, 2007).

In contrast, the housing sector appears to promote financial development in the long term, reflecting its role in asset-backed lending and capital formation (Green & Malpezzi, 2003). However, in the short-term, rising housing prices can contribute to burst phases, consistent with the experiences of housing-led financial crises. For instance, the 2007–2008 global financial crisis, which began in the U.S. subprime mortgage market, illustrates how housing bubbles can amplify credit booms and ultimately trigger systemic collapses. The empirical results affirm this view by showing the negative short-run effect of housing prices, despite their long-run contribution to financial development.

Turning to policy variables, the repo rate positively affects the financial cycle in both the short and long term. However, the short-run effect is not statistically significant. This suggests that tighter monetary policy—often aimed at controlling inflation and stabilizing macroeconomic conditions—supports financial development by fostering credibility and reducing volatility (Bernanke & Gertler, 1995). However, the insignificant short-term effect underscores the limitation of monetary policy alone in managing financial cycle fluctuations. In contrast, the macroprudential policy index consistently exerts an adverse effect across all periods. While this supports the notion that strict macroprudential regulations may restrict credit and financial activity, they appear to play a stabilizing role by mitigating short-term fluctuations. This result aligns with Claessens (2015), who argues that macroprudential tools are designed more for financial stability than for promoting financial development per se.

The combined interpretations and results show that the drivers of financial development in South Africa appear to be monetary policy and the housing sector, which have shown positive long-term effects. On the other hand, other variables, such as exchange rate movements, inflation, money supply, and macroprudential policy, constrain financial development. Regarding triggers of short-term financial booms and bursts, the evidence points to GDP growth, credit, share prices, and, to some extent, housing prices, as sources of temporary upswings in financial activity. Conversely, money supply and inflation are more closely associated with burst phases and financial volatility. These findings stress the importance of policy coordination—particularly between monetary and macroprudential authorities—to balance promoting financial development and ensuring financial stability in emerging markets.

Figure 2 presents the results of the cumulative sum (CUSUM) and cumulative sum of squares (CUSUMSQ) tests, which assess the stability of model parameters over time. The left panel displays the CUSUM test, which plots the cumulative sum of recursive residuals against the 5% significance bounds. The CUSUM line remains within these bounds throughout the sample period, indicating parameter stability. Similarly, the right panel shows the results of the CUSUMSQ test, which evaluates the constancy of residual variance. The CUSUMSQ line also stays well within the 5% critical bounds, suggesting no evidence of heteroskedasticity or variance instability. Taken together, these diagnostics indicate that the model maintains stable parameters and a consistent error variance over time.

The stability in Figure 2 and Figure 3 adds robustness to the study’s findings. It confirms that the relationships identified—namely the variables that drive long-term financial development and those that trigger short-run cyclical deviations—are significant and stable across time. This stability enhances the model’s utility for policy analysis and forecasting, assuring macroprudential authorities that the estimated relationships can be relied upon when designing interventions to manage financial cycles and promote financial stability in South Africa.

Table 7. Variance inflation factor.

Variable	Coefficient	Uncentered	Centered
	Variance	VIF	VIF
EXCH	7.56 × 10−7	6.370	2.162
GDP	0.378887	4.311	2.174
INF	5.79 × 10−5	4.111	3.411
CR	6.51 × 10−6	10.180	2.740
HP	4.70 × 10−7	6.453	5.110
SP	6.16 × 10−6	1.175	1.123
M3	2.93 × 10−6	2.804	7.873
REPO	0.000144	3.831	1.097
MPI	5.38 × 10−5	10.478	7.049

presents the results of the variance inflation factor (VIF) analysis to assess the degree of multicollinearity among explanatory variables. The uncentered VIFs are moderately high for some variables, notably MPI (10.48), CR (10.18), HP (6.45), and EXCH (6.37), indicating potential collinearity concerns when the model is not mean-centered or lacks an intercept.

After centering the variables, the VIF values decline across the board. Importantly, all centered VIFs fall at or below the conventional threshold of 10, which indicates no severe multicollinearity. The highest centered VIFs are observed for M3 (7.87), MPI (7.05), HP (5.11), and INF (3.41), while variables, such as EXCH (2.16), GDP (2.17), CR (2.74), SP (1.12), and REPO (1.10), exhibit minimal collinearity concerns. Multicollinearity is a typical feature of macroeconomic datasets, as certain variables, like M3, INF, HP, and MPI, often co-move due to shared structural and cyclical dynamics (Wooldridge, 2016; Gujarati & Porter, 2009). Although such correlations can inflate standard errors and affect coefficient precision in OLS models (Kennedy, 2008), the centered VIF results—none of which exceed the threshold of 10—indicate that multicollinearity is not a concern in this study.

The time-varying Granger causality (TVGC) test was used to corroborate the findings of the QARDL. The TVGC test offers a distinct advantage over fixed-parameter and Fourier causality approaches, particularly in contexts characterized by structural breaks, regime shifts, and episodic causal relationships. Unlike Fourier causality, which is designed to capture gradual and smooth structural changes by approximating nonlinearities with trigonometric terms (Jones & Enders, 2016), TVGC is more adept at identifying abrupt, temporary, and nonrepetitive changes in causal dynamics that often arise in emerging market economies exposed to frequent shocks. This flexibility is achieved by estimating causality in a rolling or recursive window framework, allowing for the detection of both the emergence and disappearance of causal linkages over time (Balcilar et al., 2010). Empirical applications—such as Lu et al. (2017) on oil price–growth dynamics, Iyke and Ho (2021) on monetary policy–inflation interactions, and Baum et al. (2025) on industrial production—have consistently demonstrated that TVGC uncovers nuanced, time-varying causality patterns that are otherwise obscured in models assuming constant parameters.

Turning to the empirical results for the South African financial cycle in Figure 3, the plots show the time-varying Wald test statistics (solid black line) relative to the bootstrapped 10% (short dash) and 5% (long dash) critical values. The null hypothesis of no Granger causality is rejected whenever the test statistic exceeds either critical value. For Exch, there is strong and persistent causality from around 2010 onwards, with particularly elevated influence during the 2020–2022 period, coinciding with pandemic-driven exchange rate volatility and capital flow reversals. GDP exhibits intermittent causality, with clear episodes of influence in the early 2010s and again around the mid-2010s, but the effect largely disappears after 2020, suggesting weakened macroeconomic transmission to the financial cycle. Inflation weak sustained causality around 2012, after which the relationship disappears, possibly reflecting a decoupling due to unconventional policy measures and external shocks.

Broad money supply exerts episodic but notable causality, particularly around 2010–2012 and in short bursts post-2018, consistent with liquidity expansions feeding asset price cycles. The repo rate’s influence is strongest in the immediate post-2008 period and resurfaces briefly around 2015–2017 before fading, indicating time-specific effectiveness of monetary tightening or easing on the financial cycle. The macroprudential policy index shows sharp spikes of causality—especially a pronounced peak around 2016—highlighting targeted regulatory interventions affecting systemic risk. Credit displays persistent causality from 2012 to 2020, aligning with credit cycle dynamics driving leverage and asset market fluctuations. House prices show multiple causality episodes, peaking around 2020, consistent with property market sensitivity to macro-financial conditions. Share prices reveal a clear and sustained causal link from 2014 onward, reflecting the increasing integration of equity markets into the broader financial cycle.

The TVGC results corroborate the QARDL findings by confirming that the relationships between the financial cycle and its drivers are time-dependent and shaped by economic shocks. The QARDL model’s negative long-run and positive short-run effect of GDP is mirrored in the TVGC, where GDP causality appears only in specific periods, especially in the early and mid-2010s. Persistent post-2010 causality from the exchange rate in the TVGC reinforces the QARDL model’s long-run negative link, capturing such events as “Nenegate” in 2015 and pandemic-induced volatility in 2020. Sustained inflation causality from 2010–2019 in the TVGC supports the QARDL model’s finding of its destabilizing effect. Credit and asset prices show episodic but strong causality in the TVGC, consistent with the QARDL model’s negative long-run and positive short-run effects linked to boom–bust cycles. Housing price causality peaks in 2020 in the TVGC align with the QARDL model’s view of its long-run support for financial development but short-run instability. Intermittent policy rate causality in the TVGC mirrors its long-run positive but short-run insignificant role in the QARDL, while brief macroprudential policy causality episodes support the QARDL model’s stabilization view. Overall, the TVGC validates the QARDL model’s equilibrium-based insights, showing that key macro-financial drivers exert influence episodically, warranting state-dependent policy responses.

5. Conclusions

This study sought to investigate the drivers and triggers of South Africa’s financial cycle, motivated by notable gaps in the empirical literature. As highlighted in the Introduction, existing research treats financial cycle development and fluctuations as distinct areas of inquiry, often using disjointed empirical approaches. Furthermore, the theoretical literature provides conflicting perspectives on the relationship between the macroeconomy and financial cycles—ranging from procyclical to independent or destabilizing interactions. In response, this study constructed a quantile autoregressive distributed lag (QARDL) model to empirically examine both the long-run determinants of financial development and the short-run triggers of cyclical fluctuations within a unified framework. Given its relatively large financial cycle and macroprudential policy relevance, the South African case provided an important and under-researched context for this analysis. The study achieved its aims by using a quantile ARDL framework that accommodated both I(0) and I(1) variables without transforming them, consistent with the bounds testing procedure developed by Pesaran et al. (2001).

The findings reveal that financial development in South Africa is primarily shaped by long-run fundamentals, such as inflation, credit growth, real house prices, money supply, and the repo rate, with varying significance across the distribution of the financial cycle. In contrast, short-run cyclical deviations were most strongly triggered by shocks to inflation, credit, house prices, and the macroprudential policy index—particularly during lower and middle quantiles of the financial cycle. Notably, the asymmetric effects captured through the quantile approach revealed that certain variables, such as the macroprudential index and money supply, exert a stronger influence during financial cycle contraction than expansion. These findings align partially with the Minsky hypothesis, which suggests that credit booms and asset price dynamics are key drivers of instability, while also supporting more recent empirical work emphasizing the dual role of inflation and interest rates in financial cycles (Claessens et al., 2011; Adarov, 2022).

The findings indicate that the drivers of financial development in South Africa appear to be monetary policy and the housing sector, both of which exhibit positive long-term effects. Conversely, certain variables, such as exchange rate movements, inflation, money supply, and macroprudential policy, constrain financial development. Regarding short-term financial booms and bursts, GDP growth, credit, share prices, and, to some extent, housing prices are triggers for temporary upswings in financial activity. On the other hand, money supply and inflation are more closely associated with burst phases and financial volatility. These results underscore the critical importance of policy coordination—particularly between monetary and macroprudential authorities—in balancing promoting financial development and maintaining financial stability, especially in emerging market economies, such as South Africa. In this context, these policies should be considered complementary rather than substitutive. Macroprudential policy should be employed to mitigate short-term excessive fluctuations in the financial system, while monetary policy should focus on anchoring long-term financial development and ensuring price stability.

The TVGC confirms the QARDL model’s key insights, showing that drivers, like GDP, exchange rate, inflation, credit, asset and housing prices, policy rates, and macroprudential measures influence the financial cycle episodically, reinforcing the need for timely, state-dependent policy actions. However, the research is not without limitations. The use of monthly data, while appropriate for macro-financial analysis, may obscure high-frequency fluctuations and rapid policy reactions. Additionally, the macroprudential policy index used in the model—while novel and empirically tractable—may not capture all dimensions of regulatory tightening or loosening, particularly those related to institutional quality or regulatory enforcement. Future research could address these limitations by employing higher-frequency data, incorporating international spillover effects through global financial variables, or using machine learning methods to construct more granular macroprudential indices. Moreover, extending the QARDL approach to a panel of emerging markets could shed light on the extent to which these findings hold across different institutional and economic environments.

In sum, this study provides robust empirical evidence on the dual dynamics of financial cycles in South Africa. By identifying the key long-run drivers of financial development and the short-run triggers of cyclical disruptions, the findings offer important insights for policymakers aiming to foster financial stability while promoting sustainable economic growth. Future studies should build on this framework to further our understanding of financial cycle dynamics in an increasingly complex and interconnected global economy.