5.1. Forecast Results in 4 Week Rolling
We adopt a rolling window strategy with a 4-week window to forecast WTI returns, training the model on the most recent 4 weeks of data at each step. Input features are constructed by lagging daily variables by 1 week and monthly variables by 4 weeks, so that only information available prior to the forecast period is used. To further ensure temporal alignment and data consistency, monthly variables are interpolated to a weekly frequency before being lagged, so that each week is assigned a unique, smoothly evolving value for these features. This interpolation avoids abrupt step-wise changes, better reflects the gradual evolution of economic indicators, and allows the model to capture macroeconomic trends more realistically. This rolling window design allows the model to systematically update with the latest available data, ensuring that each prediction reflects prevailing market conditions and relies solely on historical information, thus mitigating information leakage or forecast bias and contributing to the robustness of the results. In addition, by incorporating lagged features, the model is able to capture temporal dependencies and evolving patterns commonly observed in financial time series. This approach not only aligns forecasts with current market dynamics but also simulates an out-of-sample setting at every step, further reducing the risk of information leakage. From an economic perspective, this methodology reflects the adaptive nature of financial markets, where agents continually update their beliefs and strategies based on new information, and past behaviors can influence future prices through mechanisms such as momentum, mean reversion, and delayed information diffusion. As a result, our approach helps mitigate look-ahead bias, reduces the risk of overfitting, and naturally provides an out-of-sample evaluation with each forecast.
Given the sensitivity of OLS to multicollinearity, we addressed this issue by applying principal component analysis (PCA) to the predictor variables prior to model fitting. PCA transforms the original potentially correlated features into a set of orthogonal principal components, thereby reducing multicollinearity and improving the reliability of OLS estimates. In addition, for all models, including OLS and more complex models, all input features were standardized to have zero mean and unit variance. This standardization ensures comparability between models and enhances convergence and stability during training, especially for algorithms that are sensitive to the scale of input variables.
To assess the contribution of sustainability and external risk variables, we first conducted model training and prediction without these variables, and subsequently repeated the process with their inclusion. As presented in
Table 4 and
Table 5, the addition of these variables resulted in consistent performance improvements across all models. For instance, the accuracy of XGBoost increased from 0.7468 to 0.7643, with parallel enhancements observed in other metrics such as MSE and MAE. These findings suggest that sustainability and external risk variables offer substantial informational value, enabling models to deliver more accurate and robust predictions. This improvement can be attributed to the fact that sustainability and external risk factors encapsulate underlying economic, environmental, and market dynamics that exert direct or indirect influence on financial outcomes. By integrating these variables, the models are able to capture a broader spectrum of risks and opportunities, thereby enhancing their capacity to discern complex patterns and adapt to evolving conditions within financial markets.
After incorporating all variables associated with the mechanism, the predictive performance of the models was further evaluated. As shown in
Table 5, we compared the linear model (OLS) with five nonlinear models (XGBoost, RF, CNN, BP, MLP, and LSTM). The OLS model presented MSE, MAE, RMSE, and ACC values of 0.0047, 0.3442, 0.0331, 0.0682, and 0.5650, respectively. In contrast, the non-linear XGBoost model showed MSE, MAE, RMSE, and ACC values of 0.0048, 0.3242, 0.0113, 0.0693, and 0.7643, respectively. XGBoost exhibited superior performance across all metrics, particularly in accuracy, where it was approximately 20% higher than that of OLS. Furthermore, XGBoost’s MAE of 0.0113, significantly lower than that of OLS at 0.0331, indicates more precise error control. Among all models compared, XGBoost performed the best, not only achieving the highest accuracy rate of 76.43% and demonstrating strong predictive performance across other key metrics. These results underscore XGBoost’s efficiency and reliability in capturing complex nonlinear patterns and handling large datasets, making it a robust choice for financial prediction tasks.
5.2. Model Interpretation
In this section, we employ the Shapley Additive exPlanations (SHAP) method to interpret the model. Developed from the principles of game theory, SHAP values are a powerful tool to measure the contribution of each variable towards the prediction outcome (
Lundberg & Lee, 2017). High precision models, such as ensemble models and deep learning models, feature complex and variable internal structures that are not intuitively understandable. However, SHAP, a classical post hoc explanation framework, can calculate the importance value of each feature variable in every sample, thereby achieving an explanatory effect. The advantage of this method lies in its ability to provide insights into both the local and global behaviors of the model, which is crucial for confirming the reliability and performance of dynamic models within the volatile environments of financial markets.
Using the best performing XGBoost model as an example, we utilized SHAP to assess and output the top 10 variables important for predicting WTI return rates, as illustrated in
Figure 3. The right side displays the SHAP values for each feature within the model, where each dot represents a variable’s contribution to the model output in a given instance. Positive SHAP values (pink dots) indicate that higher variable values tend to increase the predicted returns, whereas negative values (blue dots) suggest a decrease in returns. On the left, the average of the absolute values of SHAP for each variable is shown; the more significant the value, the greater the average influence of the variable within the model. Among these variables, rate of change (ROC) stands out as the most important predictor, exhibiting the highest mean absolute SHAP value. Notably, ROC demonstrates large SHAP values in both positive and negative directions, with substantial color variability, indicating a broad range of impacts on the model predictions. This suggests that ROC plays a pivotal role in shaping the model’s output under different market conditions. The strong influence of ROC aligns with economic theory, as it reflects momentum shifts in asset prices, which are widely used by traders and analysts to gauge market sentiment and potential trend reversals.
In financial market analysis, ROC is a key momentum indicator that helps identify potential buy or sell signals. It is particularly valuable in volatile markets like crude oil, where price fluctuations occur rapidly. The high SHAP value of ROC underscores its ability to capture short-term market dynamics, allowing the model to adapt swiftly to changing conditions. Moreover, the bidirectional impact of ROC, as seen in the SHAP analysis, highlights its role in both upward and downward price movements, reinforcing its significance in technical analysis and trading strategies.
As shown in
Table 6, we compare the rankings of feature importance across seven different machine learning models in predicting WTI returns. Since the ordinary OLS model cannot utilize SHAP values, we assess the significance of each coefficient in the model using statistical measures (T-values). Significant differences exist between linear (OLS) and nonlinear models (including XGBoost, Random Forest, CNN, BP, MLP, and LSTM) in identifying key variables. In addition to differing in evaluation methods, OLS, as a linear model, solely focuses on the direct linear relationships between features and the target variable, ignoring any interactions or nonlinear relationships. Consequently, the features it identifies as necessary may differ from those other models recognize.
In contrast, nonlinear models can capture complex nonlinear relationships and better handle interactions and pattern recognition among variables.
Furthermore, the deep learning models such as CNN, BP, MLP, and LSTM share the same top ten important features, likely due to their strong capabilities in data representation and abstraction, which results in a higher dependency on similar features. Random forest and the deep learning models display identical feature rankings, and the top ten essential variables in the XGBoost model are also highly similar to those in the deep learning models. This indicates that these variables exhibit strong predictive signals or significant statistical correlations, contributing substantial explanatory power to the models.
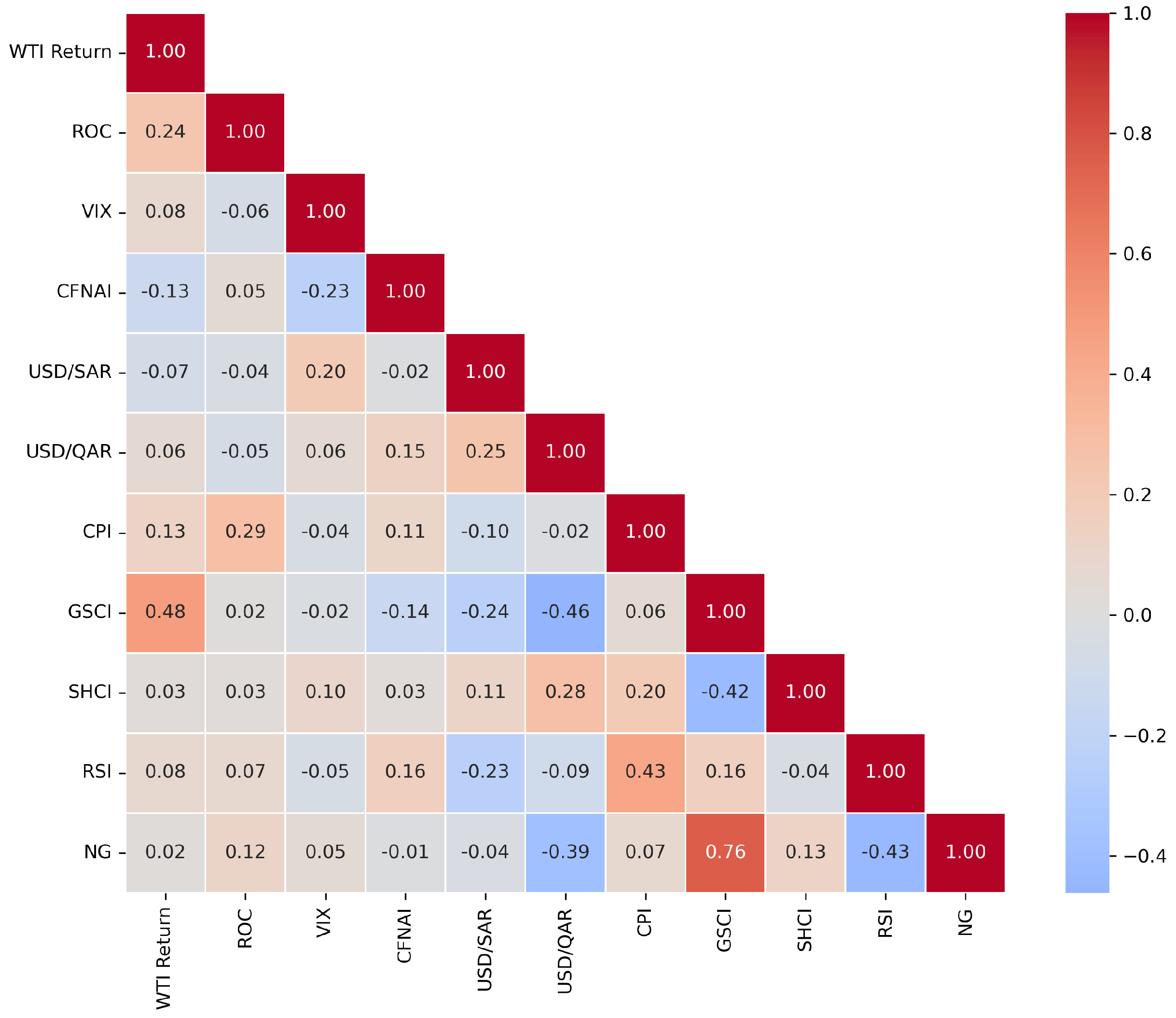
The results show that various nonlinear models significantly emphasize variables such as ROC, VIX, CFNAI, USD/SAR, USD/QAR, and CPI. Notably, ROC is the most crucial feature in all models, highlighting its key role in predicting WTI returns due to price momentum. VIX, CFNAI, and CPI also receive high ranks, emphasizing their strong influence on oil investment returns through market volatility and macroeconomic activities. The significance of USD/SAR and USD/QAR in predicting WTI returns is primarily linked to the roles of Saudi Arabia and Qatar in the global energy market. As major oil-exporters, these nations experience exchange rate fluctuations that may influence their oil production and export decisions, thereby impacting WTI investment returns.
In addition to the aggregated importance rankings, it is also instructive to examine how the importance of these variables evolves over time.
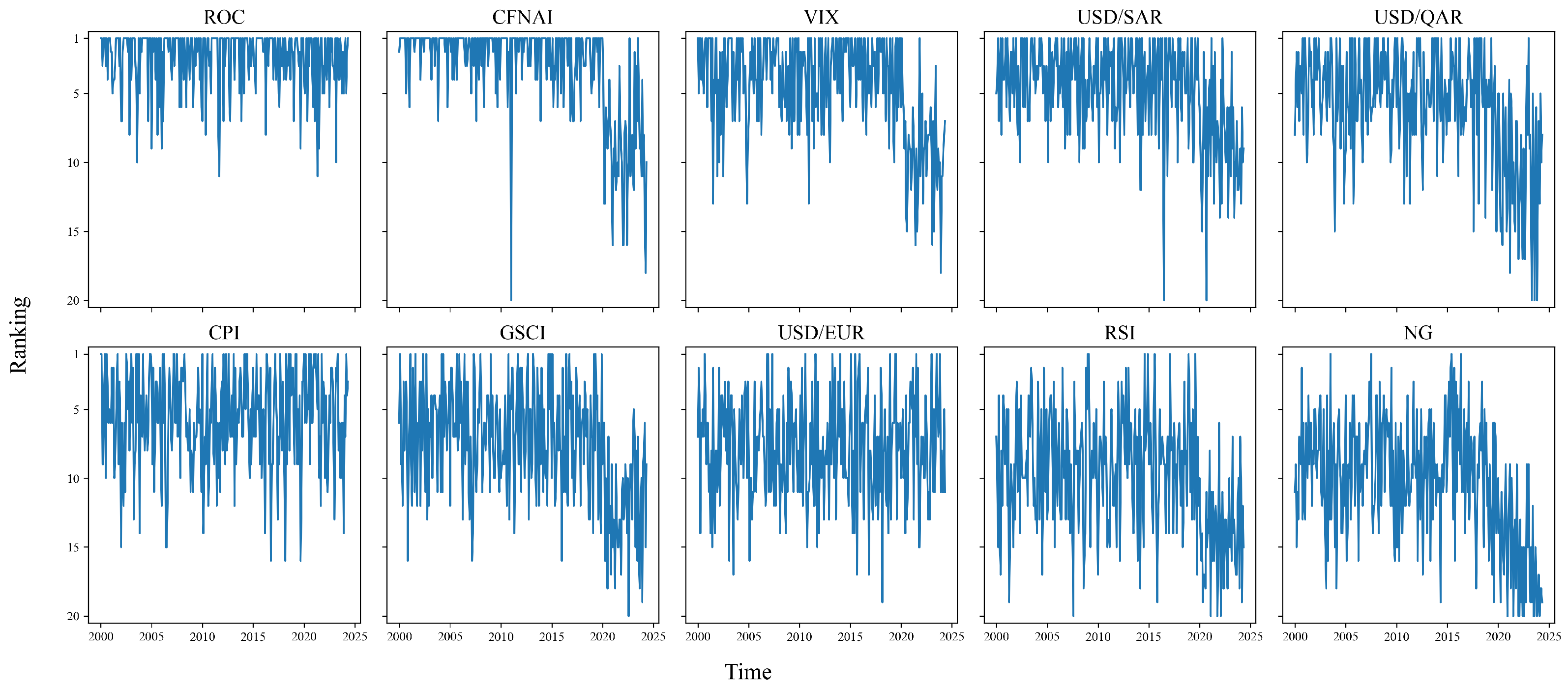
Figure 4 displays the dynamic ranking trajectories of the top 10 features identified by XGBoost, where lower values on the vertical axis correspond to higher importance. Each subplot traces the ranking of a specific variable across the full sample period.
The plots reveal several important patterns. First, ROC consistently maintains the highest importance, with its ranking rarely dropping below the top few positions, which further corroborates its central role in the predictive modeling of WTI returns. Other macroeconomic and financial indicators, such as CFNAI, VIX, USD/SAR, and USD/QAR, also maintain relatively high rankings throughout most of the sample but show notable declines in importance during and after the COVID-19 period—reflecting structural changes in market dynamics and the relative informativeness of different features in turbulent times. In contrast, variables like CPI and USD/EUR display more stable ranking trajectories, indicating that their predictive contributions remain relatively constant over time.
This dynamic perspective on feature importance is particularly valuable in the context of financial time series forecasting, where market regimes and the relationships among variables can change rapidly over time. By tracking the ranking trajectories of each variable across rolling forecast windows, we provide clear evidence that the predictive roles of even the most important features are not fixed, but can shift significantly with evolving economic conditions or major events such as the COVID-19 pandemic. This approach enables us to identify periods when certain variables become especially influential or, conversely, lose their predictive power, which may signal underlying changes in market structure or investor behavior. As a result, practitioners can use such insights to adjust their trading and risk management strategies proactively, ensuring that models remain relevant and robust in the face of ongoing market changes.
5.3. Strategy Validation
- (1)
Validity
To evaluate the practical application of machine learning models, this study develops a trading strategy based on model predictions and calculates its capital curve under scenarios with and without transaction fees. When transaction fees are not considered, positions are determined based on the model’s weekly returns prediction: long positions are taken when the predicted return is above zero, short positions are taken when it is below zero, and no positions are held when the prediction is zero. Profits or losses are calculated weekly based on these positions. The total cumulative return since the strategy’s inception is ultimately determined by aggregating these weekly net profits or losses. The strategy’s effectiveness is demonstrated using a simulated capital curve, starting with an initial capital of 1. The equity curve is calculated with the following formula:
This equity curve reflects the trajectory of capital changes when an investor starts with an initial capital of 1 and invests according to the machine learning model strategy.
When transaction fees are considered and the initial capital is set at 1, a fee of 5% of the initial capital, or 0.05, is deducted for calculating net profits or losses. This fee adjustment is then applied to calculate the cumulative return and capital curve. As shown in
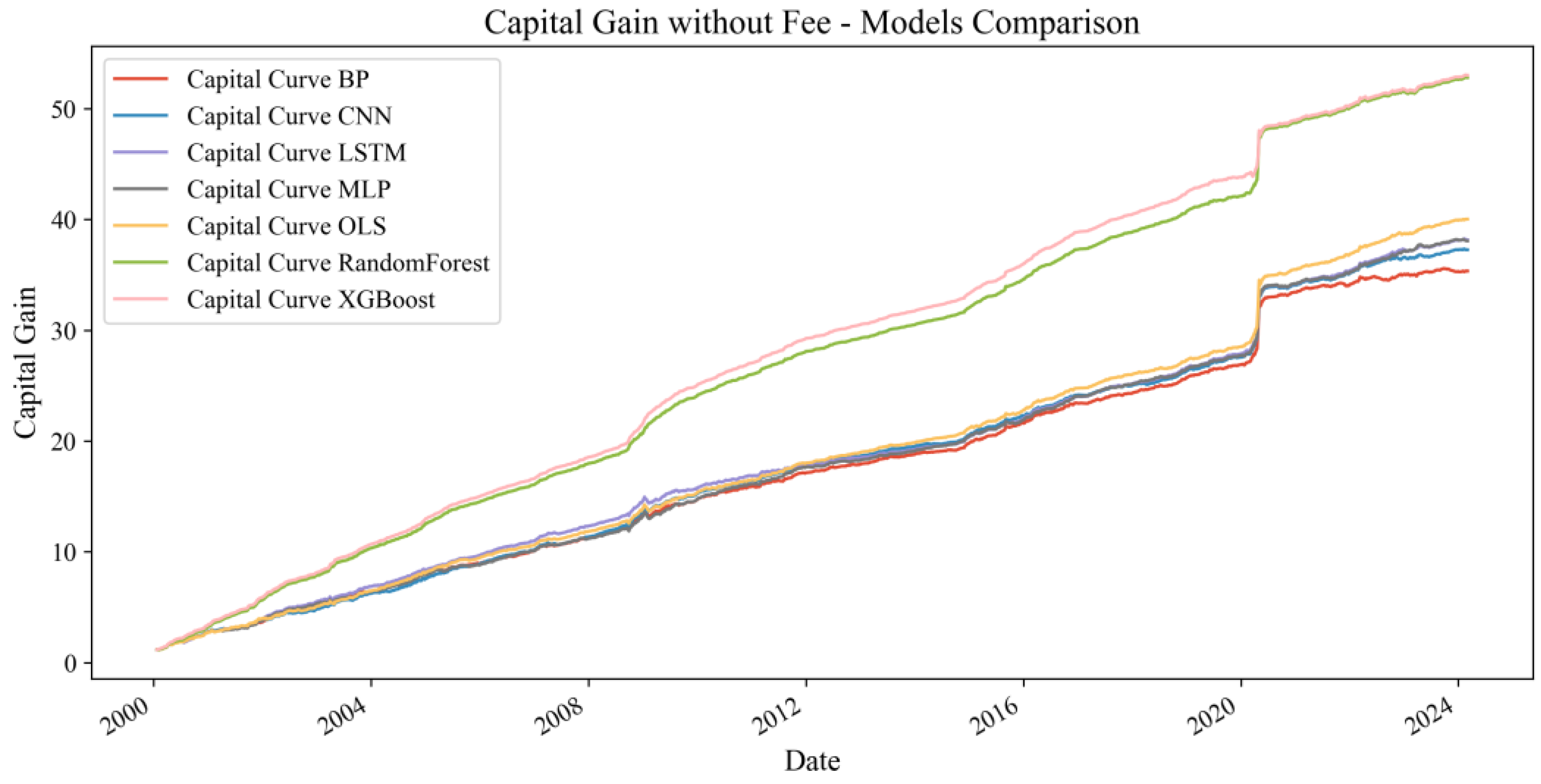
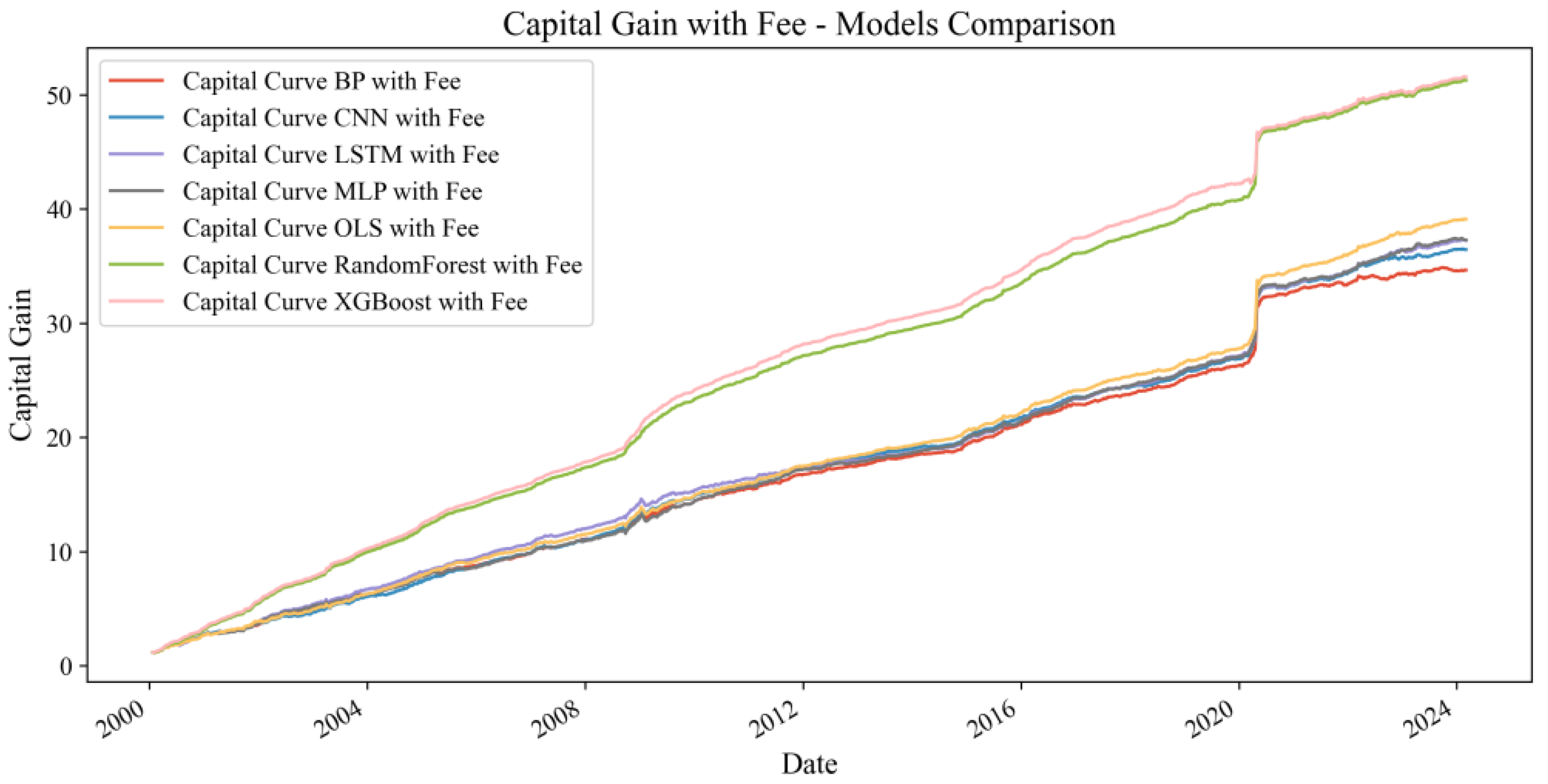
Figure 5, accounting for transaction costs, all model capital growth curves demonstrate annual increases from 2000 to 2024, emphasizing the strategic advantage of machine learning models in predicting crude oil investment returns. Notably, the XGBoost model maintains a higher level of capital growth, significantly outperforming others and indicating robust strategy effectiveness even with trading costs. As illustrated in
Figure 6, excluding transaction costs improves all model returns, yet the XGBoost model maintains a clear advantage. This underscores the efficiency and practicality of the XGBoost model in forecasting WTI crude oil returns.
Table 7 presents the comprehensive performance metrics for all evaluated models. The results show that all machine learning models, including traditional OLS, achieve relatively high annualized returns and Sharpe ratios, which demonstrates their effectiveness in predicting crude oil returns. Among all models, the XGBoost model exhibits the strongest overall performance. It achieves the highest annualized return, reaching 17.10% without transaction fees and 17.05% with transaction fees. In addition, XGBoost records the highest Sharpe ratio at 2.10 without fees and 2.08 with fees. Its maximum drawdown is also the lowest among all models, at −7.4% without fees and −8.0% with fees, indicating better risk control and more stable performance. Furthermore, the annualized volatility of XGBoost remains at a relatively low level (37.9% without fees and 37.8% with fees), which further supports its risk-adjusted advantage.
Other models, such as OLS, random forest, BP, MLP, and CNN, also deliver solid results. They all generate annualized returns and Sharpe ratios that are only slightly lower than those of XGBoost. However, these models tend to experience higher maximum drawdowns and volatility, which suggests that their risk management capability is not as strong as that of XGBoost. In contrast, the LSTM model, although it achieves a reasonable annualized return of 15.20% (15.15% with transaction fees), suffers from a much larger maximum drawdown of −38.6% (−39.0% with transaction fees) and the highest annualized volatility at 47.5% (47.4% with transaction fees). This indicates that the LSTM-based strategy is exposed to significant risks and shows considerable instability during the backtesting period.
In conclusion, these results confirm that machine learning models can effectively improve crude oil return prediction and strategy performance. The XGBoost model, in particular, demonstrates a strong balance between profitability and risk control. Its superior results under both scenarios, with and without transaction costs, highlight its practicality and robustness for quantitative investment in the crude oil market.
- (2)
Dynamics
The return curves confirm the effectiveness of our strategy, indicating that the model consistently achieves stable predictive performance across most scenarios. However, as depicted in
Figure 5 and
Figure 6, all models display a significant spike around the year 2020, pointing to considerable market changes during that time. This observation necessitates an acknowledgment of the inherent market volatility. Such volatility underscores that although our strategy performs well under normal conditions, the model’s performance could be adversely affected during periods of significant market shifts or unusual events.
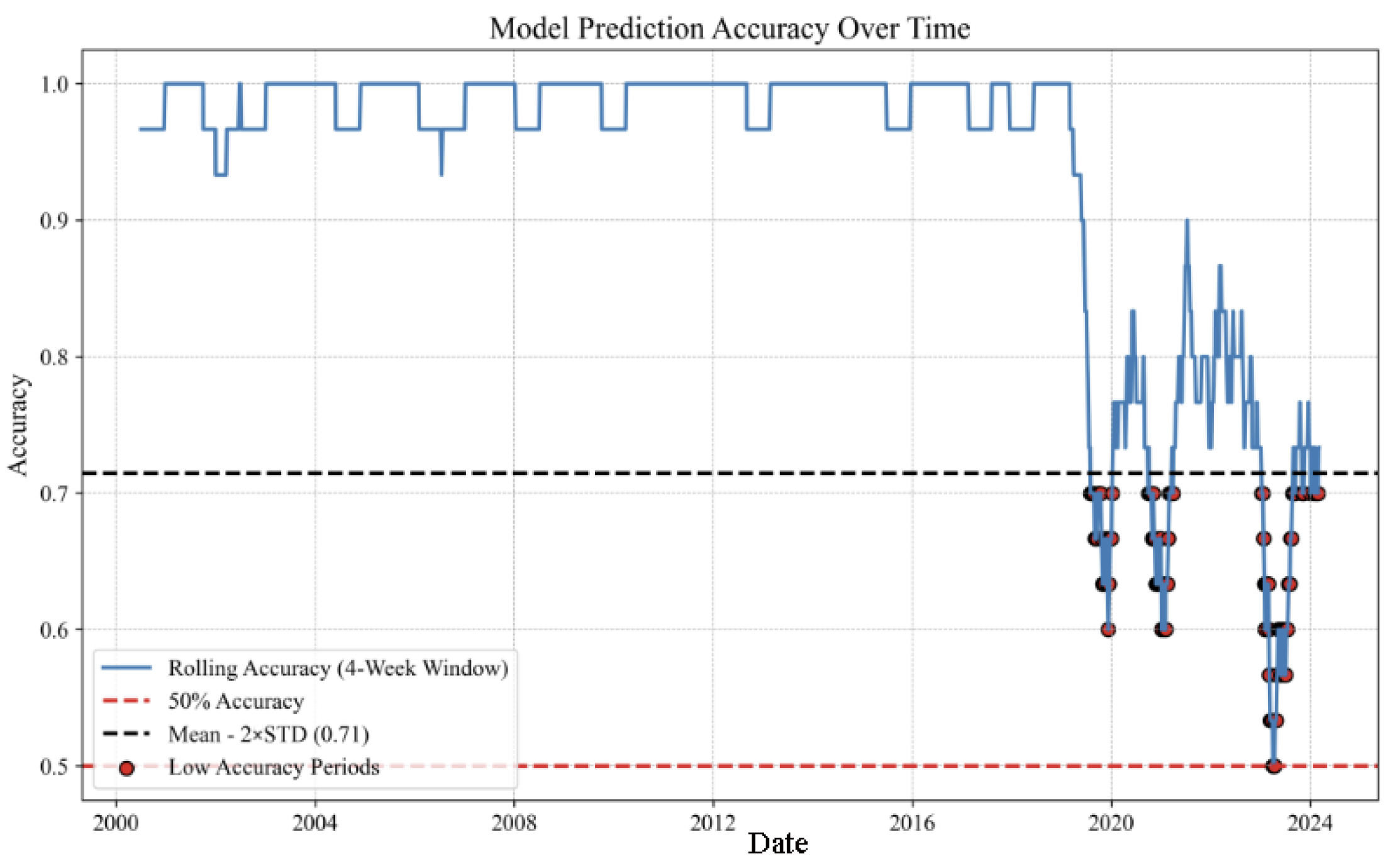
We analyze these fluctuations by examining model accuracy, taking the high-performing and high-accuracy XGBoost model as an example, as illustrated in
Figure 7. The blue line represents the model accuracy calculated on a rolling 4-week basis, while the red dashed line indicates a 50% accuracy level, serving as the threshold for assessing model effectiveness. Accuracy above this line suggests that the model’s predictive performance surpasses random guessing, which is a critical minimum standard in practical applications. The black dashed line, representing the mean minus twice the standard deviation, marks the boundary for performance evaluation, identifying periods of significantly low performance. The model maintained an accuracy rate above 90% for most of the time. However, near 2020, there was a significant drop in predictive accuracy, with subsequent fluctuations and no stable periods. This period coincided with the outbreak of COVID-19, which had a profound impact on global economic activities and caused unprecedented volatility in the crude oil market. The pandemic led to a slowdown in global economic activities, mainly stalling the aviation and transportation industries, resulting in a sharp decline in oil demand. Simultaneously, OPEC+ initially disagree on production cuts, leading to an oversupply in the market. In April 2020, WTI crude oil futures prices historically fell below zero, causing market panic. From 2020 to 2024, in addition to pandemic-induced market volatility, various extreme events such as the Russo–Ukrainian War and changes in OPEC’s production decisions caused energy market fluctuations, leading to low and unstable model accuracy. This indicates a significant decline in the model’s predictive ability under extreme market conditions and economic uncertainty, reflecting inadequacies in adapting to new market dynamics caused by the pandemic and other special events.
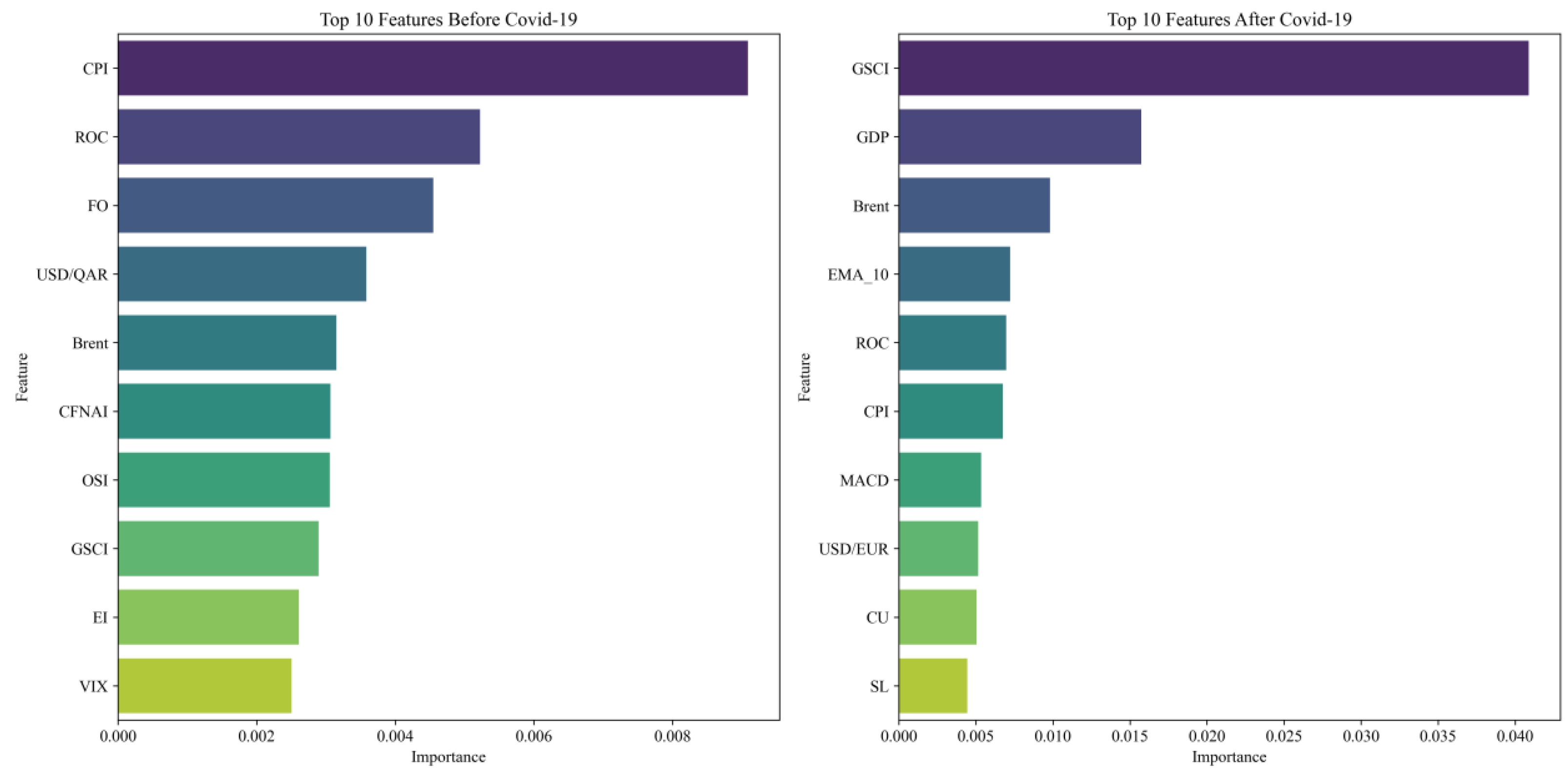
We further validated the model dynamics by examining the changes in the ranking of variable importance for predictions made by the XGBoost model before and after the pandemic, as illustrated in
Figure 8. Before the pandemic, the top ten variables were dominated by the consumer price index (CPI) and other macro-economic and energy market variables, reflecting a WTI market driven by broad economic activities and energy market dynamics. After the pandemic, there was a significant shift in the landscape of feature importance. The Goldman Sachs Commodity Index (GSCI) became the most critical predictive factor, ranking several momentum indicators highly. This shift suggests that during periods of global economic turbulence, the relevance of direct commodity prices in predicting crude oil investment returns increased, and technical indicators, capable of rapidly tracking market dynamics, played a more significant role. The changes in the importance of these model variables, both before and after the pandemic, highlight the market volatility triggered by COVID-19 and underscore the dynamic shifts in key variables and fluctuations in model effectiveness during different phases of the crisis in predicting WTI returns. This demonstrates the dynamism that significant market changes may bring to machine learning models when predicting financial time series.
This shift in variable importance reflects deeper changes in market drivers under the impact of the COVID-19 pandemic. The increased prominence of GSCI and GDP after the pandemic suggests that broader commodity market trends and macroeconomic growth expectations became more significant in forecasting WTI returns, likely due to heightened global economic uncertainty and synchronized shocks across markets. The elevated importance of technical indicators, such as EMA and MACD, indicates that market participants may have relied more on short term trading signals and price momentum to guide investment decisions amid volatility and rapidly changing market conditions.
These findings underscore the dynamic and adaptive nature of financial markets in response to major global events. The observed patterns suggest that during stable periods, fundamental macroeconomic and energy-specific variables are primary drivers of crude oil returns. However, during and after periods of crisis, the market’s attention may shift more towards broad commodity indices, macroeconomic growth measures, and technical trading signals. This highlights the necessity for flexible modeling frameworks that can swiftly adapt to changing market regimes.
From a practical perspective, these results have important implications for both investors and policymakers. For investors, dynamically adjusting model features or portfolio strategies in response to shifting market drivers can enhance prediction accuracy and risk management. For policymakers, understanding which variables gain prominence during crises can help in monitoring market stability and the effectiveness of intervention policies.
5.4. Robustness Analysis
- (1)
Rolling window
We tested the robustness of our models by extending the forecasting period from a 4-week rolling window to an 8-week rolling window. This approach assessed the sustainability of different models in terms of performance metrics and evaluated their adaptability over a slightly extended forecasting horizon.
As shown in
Table 8, after extending the rolling window, the error metrics (MSE, MAE, RMSE) slightly increased, and accuracy decreased slightly, yet the models still maintained a good performance level comparable to the 4-week rolling performance. The ranking of model performances remained unchanged, with XGBoost continuing to show the best results. Although all models displayed some sensitivity to the extended forecasting window, they still performed excellently on evaluation metrics, indicating that our machine learning models are a very robust choice for predicting WTI returns. Additionally, it was found that models with shorter rolling forecasting periods demonstrated superior effectiveness and adaptability.
- (2)
Variable selection
After passing the robustness test with an adjusted rolling window, we further tested the robustness of our model predictions by modifying the variables. As shown in
Table 9, we selected the top 10 important variables from a combination of seven nonlinear models for prediction input and then reviewed the model’s evaluation metrics. All models demonstrated significant improvements: error metrics decreased, and accuracy levels increased. Compared to deep learning models, the OLS, XGBoost, and random forest models exhibited slight performance enhancements, underscoring their stability in scenarios with reduced features. Conversely, CNN, BP, MLP, and LSTM models, due to the characteristics of neural networks, benefited from using highly correlated input variables, which allowed for faster convergence and improved more prediction performance. However, when using all variables as inputs, the performance might decrease due to increased model complexity. Therefore, these deep learning models, being more sensitive to data disturbances, showed less robustness when adjusting input variables than OLS, XGBoost, and random forest models.
5.5. Mechanism
In forecasting WTI returns, the impact of different variable mechanisms on prediction accuracy is crucial. This section analyzes five major variable mechanisms: macroeconomic, financial and futures markets, energy markets, momentum, and natural disaster counts, evaluating their importance in the best performing XGBoost model. As shown in
Figure 9, momentum variables have the most minor error indicators and the highest accuracy, demonstrating the best prediction performance among all mechanisms. This result aligns with the existing empirical evidence on momentum effects in financial markets, where recent price trends tend to persist over short horizons. In the context of oil markets, such persistence may reflect gradual information diffusion, investor herding, or technical trading, all of which can reinforce short-term price movements, given that they reflect market trends and dynamics in real time and provide immediate market sentiment and trend changes, unmatched by other financial or macroeconomic variables.
The second best-performing mechanism is the financial and futures markets, while exogenous shocks and uncertainty rank lowest. The strong predictive power of financial and futures market variables is economically intuitive, as these markets quickly aggregate and reflect participants’ heterogeneous expectations and risk assessments. Futures prices and trading volumes serve as forward looking indicators that promptly react to new information, providing timely signals for spot returns. The liquidity and transparency of these markets further enhance the quality and informativeness of the data. Financial and futures markets are closely linked to WTI prices; feature prices and trading volumes directly reflect market participants’ expectations and behavior. These variables offer timely and forward-looking information, aiding in more accurate predictions of WTI returns. Additionally, financial market data are typically more comprehensive, systematic, higher quality, and more readily available, which may also contribute to their superior predictive performance.
In the case of sustainability and external risk variables, their low importance ranking may be attributed to the fact that their effects on the crude oil market are often gradual, long-term, and diffuse, rather than immediate or directly observable. Many sustainability-related factors, such as environmental policies or shifts in global energy demand, unfold over extended periods and are slowly incorporated into market expectations and prices. As a result, their incremental predictive value for short term return forecasting tends to be limited, which reduces their relative importance within the model.