The Feedback Effects of Sovereign Debt in a Country’s Economic System: A Model and Application
Abstract
1. Introduction
2. Theoretical Model
2.1. Feedback Effect of Sovereign Debt Risk on a Country’s GDP
2.2. Subproblems
2.2.1. Boundary Conditions
2.2.2. Zero-Order Subproblem
3. Comparative Statics and Implications
Empirical Implications
4. Generalizing the Model
- a = 0, b = 0 GDP denominated by domestic currency and costs of debt ignored;
- a = 1, b = 0 GDP denominated by a foreign currency and costs of debt ignored;
- a = 0, b = 1 GDP denominated by domestic currency and costs of debt included;
- a = 1, b = 1 GDP denominated by a foreign currency and costs of debt included.
5. Empirical Evidence on Feedback Effects
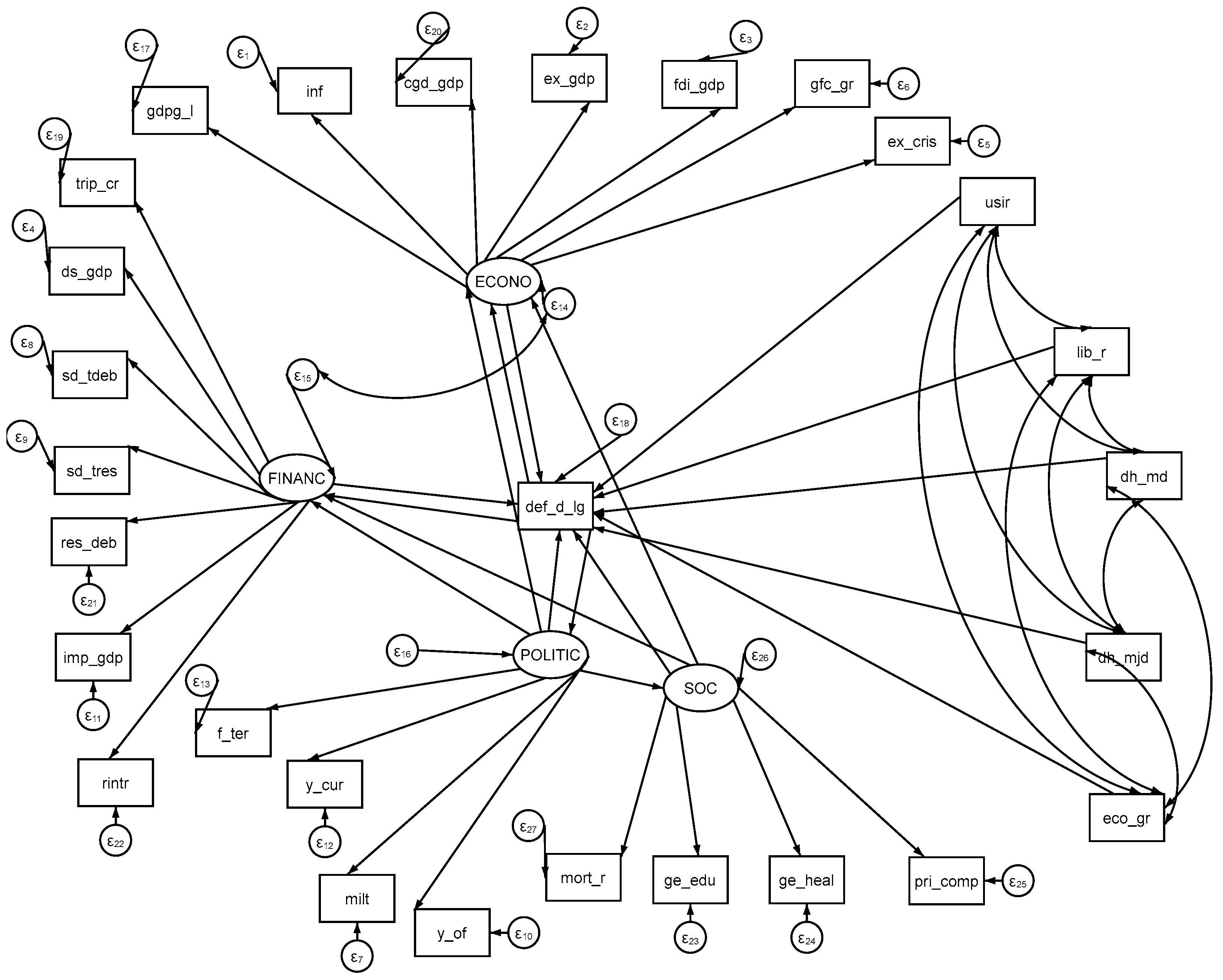
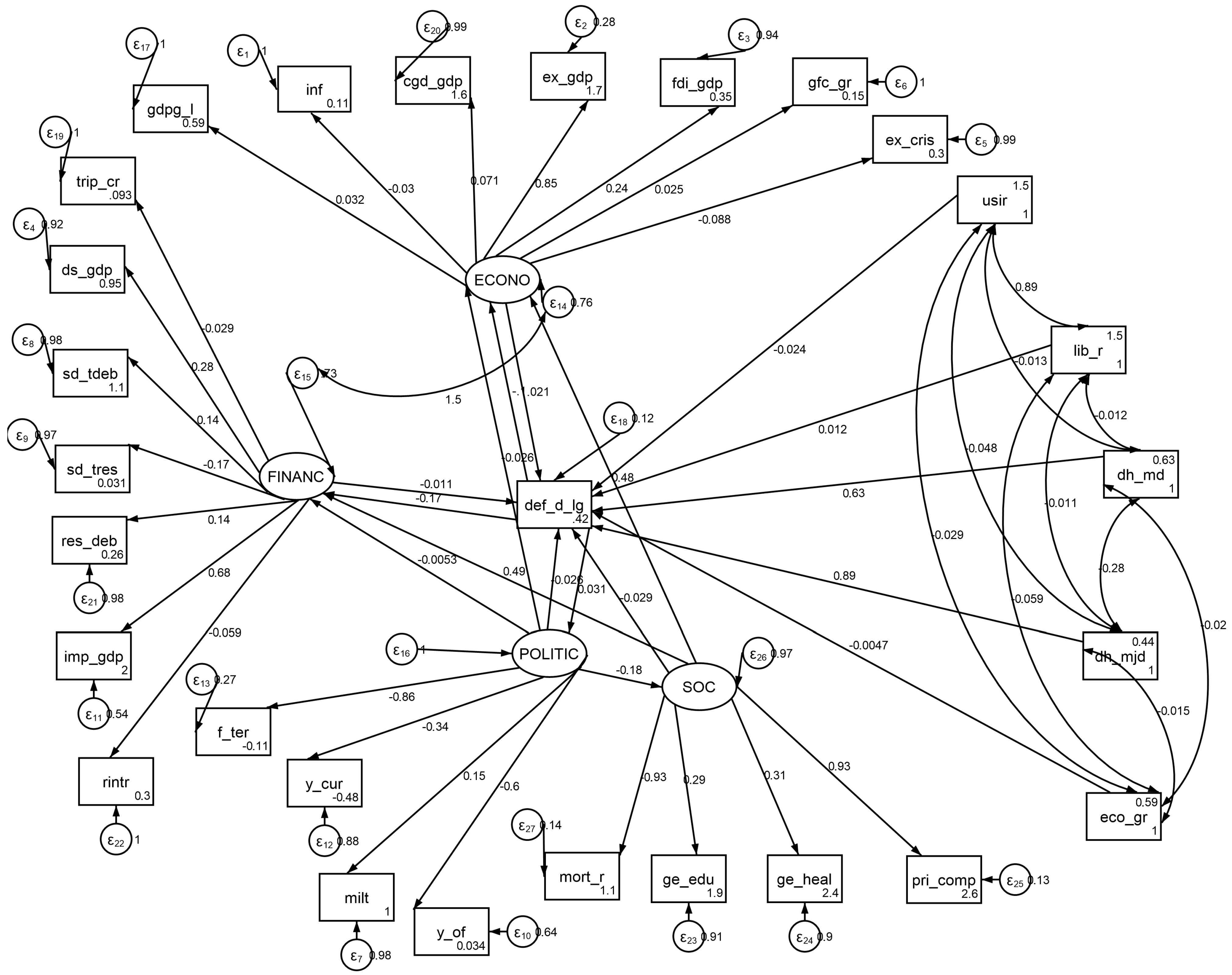
5.1. Methodological Framework (Structural Equation Model of Feedback Effects)
5.2. Data Sources and Detailed Description of Variables
5.3. Main Empirical Findings and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. A Domestic Debt
| 1 | A government may not default its debt based on a fixed default boundary but makes a default decision optimally. The default boundary can be endogenously determined as an optimization problem (Leland, 1994; Leland & Toft, 1996). As a first step, we enforced this boundary condition for simplicity. |
| 2 | Fk(V) is the outer solution in the perturbation method. |
| 3 | The reason for this is that we do not want to double count the common parts in the composite solution. |
| 4 | This solution is the composite solution in the perturbation method. |
| 5 | Including higher order solutions can increase the accuracy further. |
| 6 | More specifically, assume the GDP is 50 (say billion), while the default boundary is 15 (billion) which is 30% of the GDP, a relatively less leveraged economy. With a USD 1 billion increase in the default boundary, −0.01 represents a USD 10 million reduction in the debt value. Thus, from −0.07 to −0.09 represents a USD 20 million loss in the debt value. Furthermore, the feedback is compounding on itself. In a simple discounting, it takes about 10 years for an initial value to be cut in half at −7% but takes about 8 years to cut in half at −9%. |
| 7 | This is true assuming the real interest rates are the same for domestic debt and foreign debt. If the real interest rates are different in the short run, then the international Fisher effect does not apply. |
References
- Acemoglu, D., Ozdaglar, A., & Tahbaz-Salehi, A. (2015). Systemic risk and stability in financial networks. American Economic Review, 105(2), 564–608. [Google Scholar] [CrossRef]
- Acharya, V., Engle, R., & Richardson, M. (2012). Capital shortfall: A new approach to ranking and regulating systemic risks. American Economic Review, 102(3), 59–64. [Google Scholar] [CrossRef]
- Allen, F., & Gale, D. (2000). Financial contagion. Journal of Political Economy, 108(1), 1–33. [Google Scholar] [CrossRef]
- Ang, A., & Longstaff, F. A. (2013). Systemic sovereign credit risk: Lessons from the US and Europe. Journal of Monetary Economics, 60(5), 493–510. [Google Scholar] [CrossRef]
- Baker, D. (2018). The housing bubble and the great recession: Ten years later. Center for Economic and Policy Research. [Google Scholar]
- Benbouzid, N., Mallick, S. K., & Sousa, R. M. (2017). Do country-level financial structures explain bank-level CDS spreads? Journal of International Financial Markets, Institutions and Money, 48, 135–145. [Google Scholar] [CrossRef]
- Bernanke, B. S. (2018). The real effects of disrupted credit: Evidence from the global financial crisis. Brookings Papers on Economic Activity, 2018(2), 251–342. [Google Scholar] [CrossRef]
- Bernstein, S. (2017). The United Nations and the governance of sustainable development goals. In Governing through goals: Sustainable Development Goals as governance innovation (pp. 213–239). MIT Press. [Google Scholar]
- Brennan, M. J., & Schwartz, E. S. (1978). Corporate income taxes, valuation, and the problem of optimal capital structure. Journal of Business, 51, 103–114. [Google Scholar] [CrossRef]
- Brunnermeier, M. K., & Pedersen, L. H. (2009). Market liquidity and funding liquidity. The Review of Financial Studies, 22(6), 2201–2238. [Google Scholar] [CrossRef]
- Campbell, J. Y., & Cochrane, J. H. (1999). By force of habit: A consumption-based explanation of aggregate stock market behavior. Journal of Political Economy, 107(2), 205–251. [Google Scholar] [CrossRef]
- Cencini, A. (2017). The sovereign debt crisis: The case of Spain. Cuadernos de Economía, 40(112), 1–13. [Google Scholar] [CrossRef][Green Version]
- Chen, H. (2013). Comment on “Systemic sovereign credit risk: Lessons from the US and Europe” by Ang and Longstaff. Journal of Monetary Economics, 60(5), 511–516. [Google Scholar] [CrossRef]
- Cuadra, G., & Sapriza, H. (2008). Sovereign default, interest rates and political uncertainty in emerging markets. Journal of International Economics, 76(1), 78–88. [Google Scholar] [CrossRef]
- Dana, R. A. (2007). Financial markets in continuous time. Springer. [Google Scholar]
- D’Erasmo, P., & Mendoza, E. G. (2021). History remembered: Optimal sovereign default on domestic and external debt. Journal of Monetary Economics, 117, 969–989. [Google Scholar] [CrossRef]
- Erdem, H. F., & Yamak, R. (2014). The dynamic relationship economics and financial instability. International Reviews Business Research Papers, 10(1), 39–48. [Google Scholar] [CrossRef]
- Fama, E. F., & French, K. R. (1989). Business conditions and expected returns on stocks and bonds. Journal of Financial Economics, 25(1), 23–49. [Google Scholar] [CrossRef]
- Gennaioli, N., Shleifer, A., & Vishny, R. (2015). Neglected risks: The psychology of financial crises. American Economic Review, 105(5), 310–314. [Google Scholar] [CrossRef]
- Ghulam, Y. (2025). A further examination of sovereign domestic and external debt defaults. The North American Journal of Economics and Finance, 76, 102322. [Google Scholar] [CrossRef]
- Giglio, S., Kelly, B., & Pruitt, S. (2016). Systemic risk and the macroeconomy: An empirical evaluation. Journal of Financial Economics, 119(3), 457–471. [Google Scholar] [CrossRef]
- Glover, B., & Richards-Shubik, S. (2014). Contagion in the European sovereign debt crisis (No. w20567). National Bureau of Economic Research. [Google Scholar]
- Hilscher, J., & Nosbusch, Y. (2010). Determinants of sovereign risk: Macroeconomic fundamentals and the pricing of sovereign debt. Review of Finance, 14(2), 235–262. [Google Scholar] [CrossRef]
- Keen, S. (1995). Finance and economic breakdown: Modeling Minsky’s “financial instability hypothesis”. Journal of Post Keynesian Economics, 17(4), 607–635. [Google Scholar] [CrossRef]
- Leland, H. E. (1994). Corporate debt value, bond covenants, and optimal capital structure. The Journal of Finance, 49(4), 1213–1252. [Google Scholar] [CrossRef]
- Leland, H. E., & Toft, K. B. (1996). Optimal capital structure, endogenous bankruptcy, and the term structure of credit spreads. The Journal of Finance, 51(3), 987–1019. [Google Scholar] [CrossRef]
- Manasse, P., & Roubini, N. (2009). “Rules of thumb” for sovereign debt crises. Journal of International Economics, 78(2), 192–205. [Google Scholar] [CrossRef]
- Merton, R. C. (1974). On the pricing of corporate debt: The risk structure of interest rates. The Journal of Finance, 29(2), 449–470. [Google Scholar]
- Minsky, H. P. (1992). The financial instability hypothesis (No. 74). Working paper. Levy Economics Institute of Bard College. [Google Scholar]
- Mpapalika, J., & Malikane, C. (2019). The determinants of sovereign risk premium in African countries. Journal of Risk and Financial Management, 12(1), 29. [Google Scholar] [CrossRef]
- Musiela, M., & Rutkowski, M. (2006). Martingale methods in financial modelling (Vol. 36). Springer Science & Business Media. [Google Scholar]
- Nakatani, R. (2023). Sovereign debt crisis and fiscal devolution. Journal of Risk and Financial Management, 17(1), 9. [Google Scholar] [CrossRef]
- Palley, T. I. (2009). The limits of Minsky’s financial instability hypothesis as an explanation of the crisis (No. 11/2009). IMK Working Paper. Hans-Böckler-Stiftung, Institut für Makroökonomie und Konjunkturforschung (IMK). [Google Scholar]
- Panizza, U., Sturzenegger, F., & Zettelmeyer, J. (2009). The economics and law of sovereign debt and default. Journal of Economic Literature, 47(3), 651–698. [Google Scholar] [CrossRef]
- Rahman, H. U., Arian, A., & Sands, J. (2023). Does fiscal consolidation affect non-performing loans? Global evidence from heavily indebted countries (HICs). Journal of Risk and Financial Management, 16(9), 417. [Google Scholar] [CrossRef]
- Reinhart, C. M., & Rogoff, K. S. (2009). This time is different: Eight centuries of financial folly. Princeton University Press. [Google Scholar]
- Reinhart, C. M., & Rogoff, K. S. (2011a). The forgotten history of domestic debt. The Economic Journal, 121(552), 319–350. [Google Scholar] [CrossRef]
- Reinhart, C. M., & Rogoff, K. S. (2011b). From financial crash to debt crisis. American Economic Review, 101(5), 1676–1706. [Google Scholar] [CrossRef]
- Schoenmaker, D. (2019). A framework for sustainable finance. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3125351 (accessed on 23 July 2023).
- Sturzenegger, F., & Zettelmeyer, J. (2008). Haircuts: Estimating investor losses in sovereign debt restructurings, 1998–2005. Journal of International Money and Finance, 27(5), 780–805. [Google Scholar] [CrossRef]
- Taylor, J. B. (2009). The financial crisis and the policy responses: An empirical analysis of what went wrong (No. w14631). National Bureau of Economic Research. [Google Scholar]
- Taylor, J. B., & Williams, J. C. (2009). A black swan in the money market. American Economic Journal: Macroeconomics, 1(1), 58–83. [Google Scholar] [CrossRef]
- Trebesch, C. (2019). Resolving sovereign debt crises: The role of political risk. Oxford Economic Papers, 71(2), 421–444. [Google Scholar] [CrossRef]
- Tse, J. (2001). Minsky’s financial instability hypothesis. Oeconomicus, 4, 77–81. [Google Scholar]
- Van Rijckeghem, C., & Weder, B. (2009). Political institutions and debt crises. Public Choice, 138, 387–408. [Google Scholar] [CrossRef]
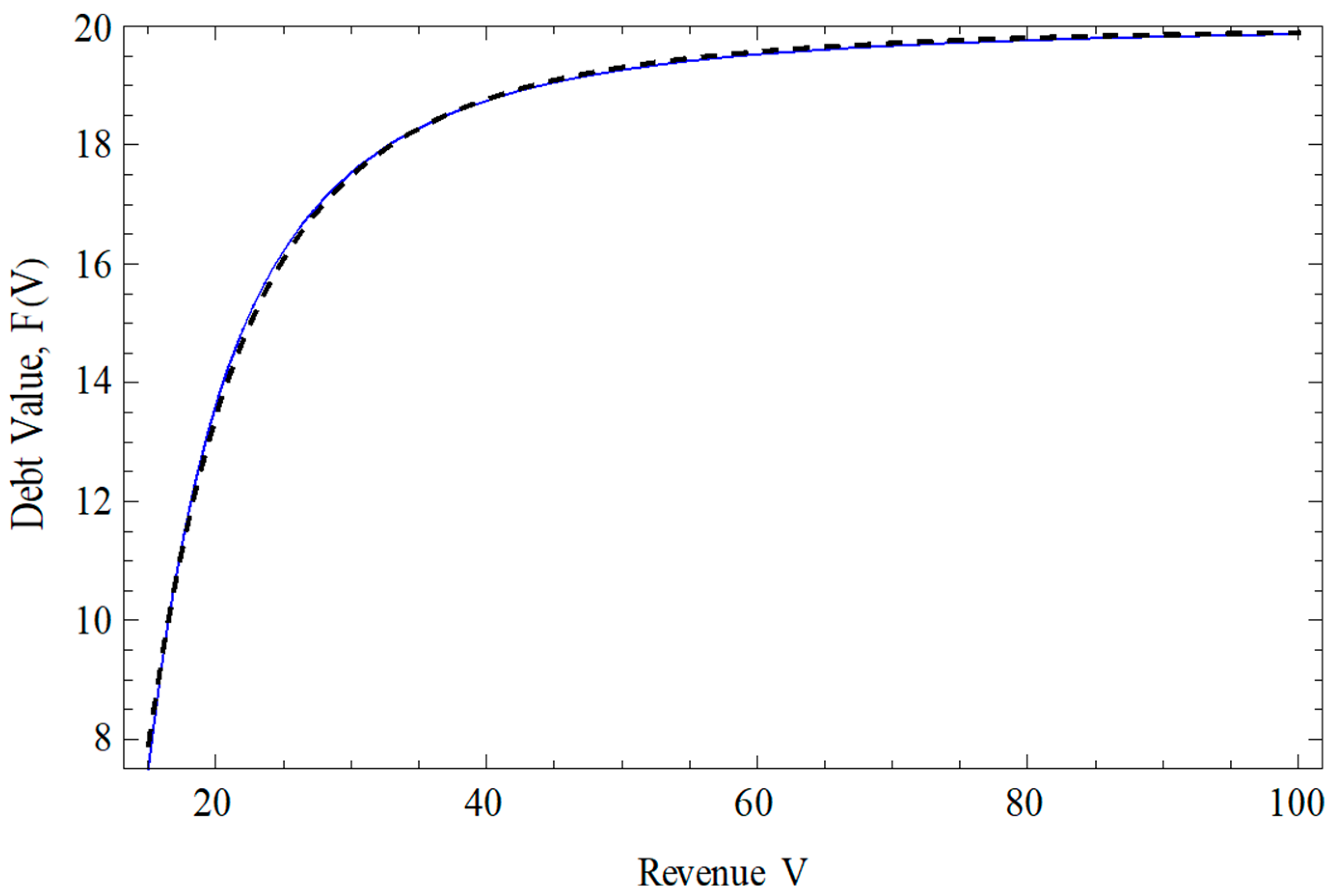
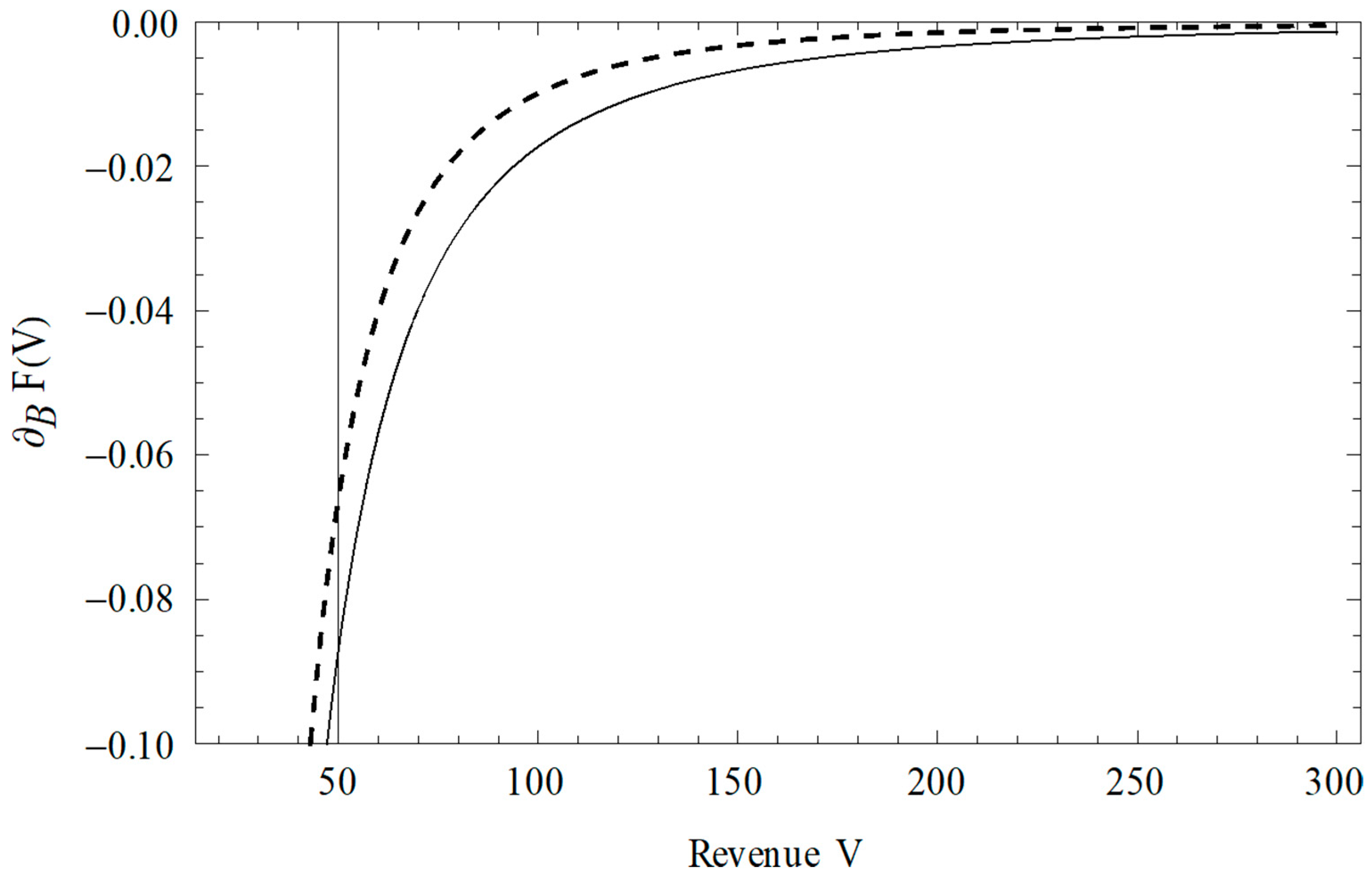
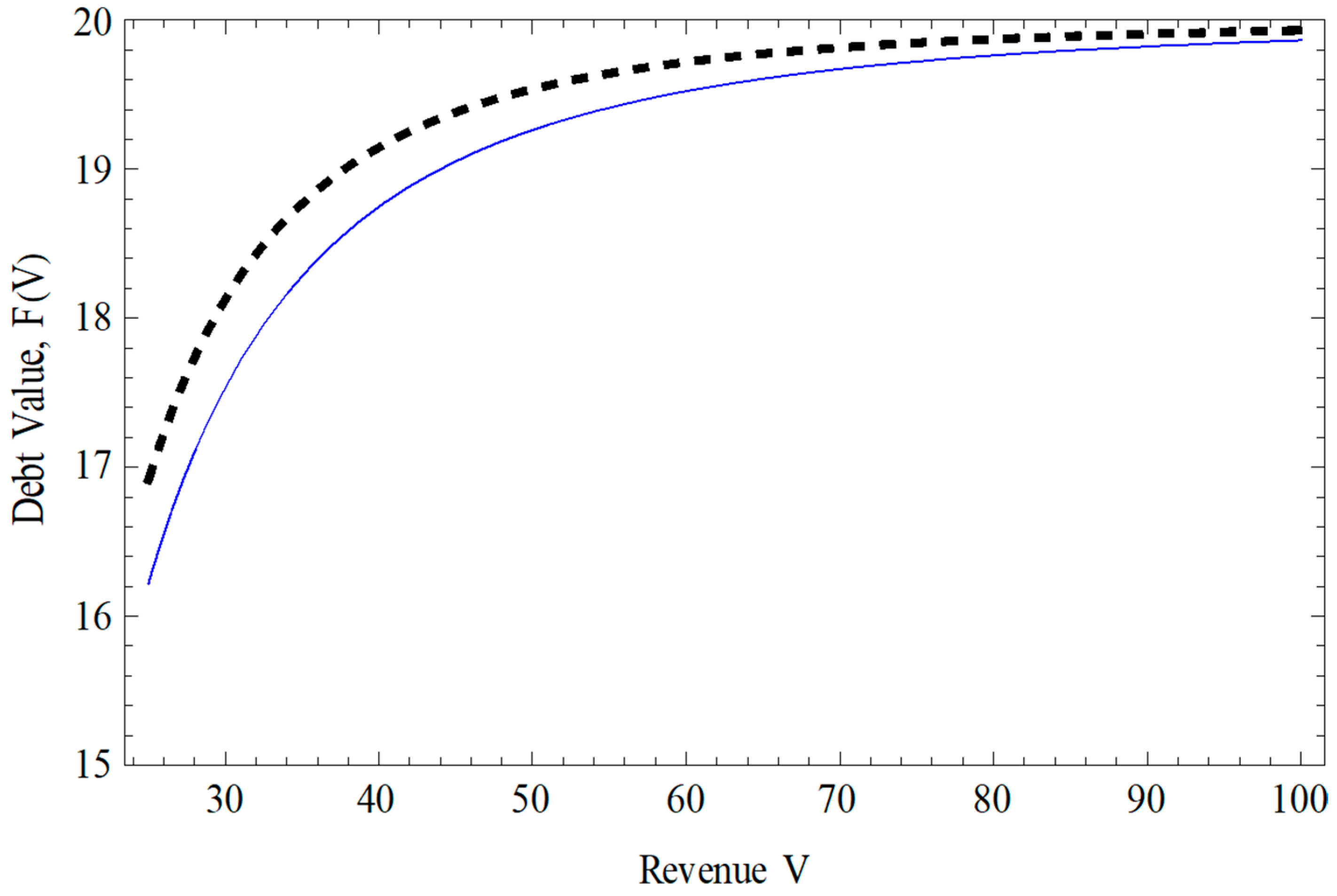
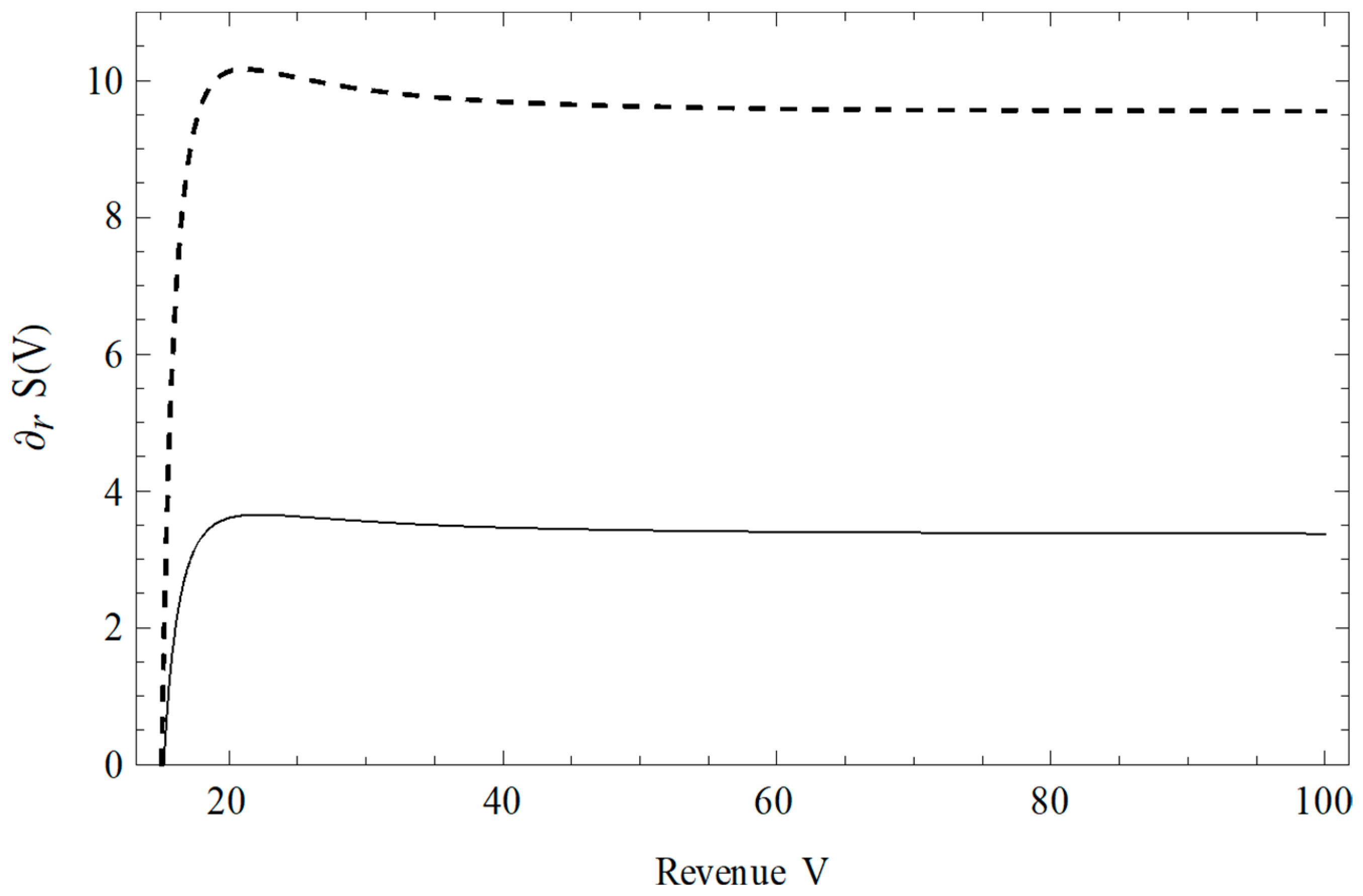

| Panel A. Parameter values used in numerical simulations | Panel B. Definitions of parameters and variables in the search-based model | |
| Parameter | Value | B—default boundary; C—annual coupon payment; q—asset position of agents; r—risk-free interest rate; X—parameter defined in Equation (22); Y—parameter defined in Equation (15); Z—parameter defined in Equation (A4); γ—recovery rate of debt; µ—growth rate of a country’s economy, denominated by the domestic currency; σ—GDP volatility |
| B | 15 | |
| C | 1 | |
| r | 5% | |
| 0.2 | ||
| 0.5 | ||
| 0.15 | ||
| 0.3 | ||
| 0 | |
| Variable | Description |
|---|---|
| def_d_lg | defaulted debt level (logged) |
| ECON | latent variable—economy |
| gdpg_l | lagged GDP growth rate |
| inf | inflation |
| gfc_gr | gross fixed capital formation growth rate |
| ex_gdp | exports/GDP |
| fdi_gdp | FDI/GDP |
| cgd_gdp | central government debt/GDP |
| ex_cris | exchange rate crisis (local currency depreciating more than 15% against the USD) |
| FINANC | latent variable—public finances |
| sd_tdeb | short-term debt as a percentage of total public debt |
| sd_res | short-term debt as a percentage of reserves |
| res_deb | reserves as a percentage of total debt |
| imp_gdp | Imports-to-GDP ratio |
| rintr | real interest rate |
| ds_gdp | debt service as a percentage of GDP |
| trip_cr | triple crisis, comprising banking, currency, and sovereign debt |
| POLITIC | latent variable—domestic political system functioning |
| f_ter | dummy variable representing finite term in office (=1) |
| milt | military expenditure as a % of GDP |
| y_of | years since government in office |
| y_cur | years left in the current term |
| SOC | latent variable—social sector |
| ge_edu | country’s expenditures on education as a percentage of GDP |
| ge_heal | country’s expenditures on health as a percentage of GDP |
| mort_r | mortality rate |
| pri_comp | primary education competition rate |
| Observed variables | |
| usir | US interest rate |
| lib_r | LIBOR rate |
| eco_gr | economic GDP growth rate |
| dh_md | history of medium levels of debt defaults (USD 50 million—<USD 1 billion) |
| dh_mjd | history of high levels of debt defaults (>=1 billion USD) |
| Coeff. | SE | P > |z| | Coeff. | SE | P > |z| | ||
|---|---|---|---|---|---|---|---|
| def_d_lg | ECONO | ||||||
| ECONO | 0.021 | 0.010 | 0.032 | def_d_lg | −0.103 | 0.019 | 0.000 |
| FINANC | −0.011 | 0.008 | 0.145 | POLITIC | −0.026 | 0.051 | 0.606 |
| POLITIC | −0.026 | 0.007 | 0.000 | SOC | 0.476 | 0.021 | 0.000 |
| SOC | −0.029 | 0.007 | 0.000 | FINANC | |||
| usir | −0.024 | 0.011 | 0.032 | def_d_lg | −0.166 | 0.024 | 0.000 |
| lib_r | 0.012 | 0.012 | 0.309 | POLITIC | −0.005 | 0.033 | 0.871 |
| eco_gr | −0.005 | 0.005 | 0.388 | SOC | 0.493 | 0.028 | 0.000 |
| dh_md | 0.629 | 0.009 | 0.000 | SOC | |||
| dh_mjd | 0.893 | 0.009 | 0.000 | POLITIC | −0.185 | 0.019 | 0.000 |
| _cons | 0.416 | 0.014 | 0.000 | POLITIC | |||
| def_d_lg | 0.031 | 0.018 | 0.083 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghulam, Y.; Liu, S. The Feedback Effects of Sovereign Debt in a Country’s Economic System: A Model and Application. J. Risk Financial Manag. 2025, 18, 302. https://doi.org/10.3390/jrfm18060302
Ghulam Y, Liu S. The Feedback Effects of Sovereign Debt in a Country’s Economic System: A Model and Application. Journal of Risk and Financial Management. 2025; 18(6):302. https://doi.org/10.3390/jrfm18060302
Chicago/Turabian StyleGhulam, Yaseen, and Sheen Liu. 2025. "The Feedback Effects of Sovereign Debt in a Country’s Economic System: A Model and Application" Journal of Risk and Financial Management 18, no. 6: 302. https://doi.org/10.3390/jrfm18060302
APA StyleGhulam, Y., & Liu, S. (2025). The Feedback Effects of Sovereign Debt in a Country’s Economic System: A Model and Application. Journal of Risk and Financial Management, 18(6), 302. https://doi.org/10.3390/jrfm18060302








