Application of Adaptive Neuro-Fuzzy Inference System for EPS Prediction in the European Banking Sector

Abstract

Financial forecasting remains essential for supporting strategic decisions and risk oversight in the banking sector. This study examines whether Adaptive Neuro-Fuzzy Inference Systems (ANFISs) can enhance Earnings per Share (EPS) prediction for European banks by integrating four core financial indicators: Return on Assets, Return on Equity, Capital Ratio, and Profit Margin. Using an annual panel of 25 institutions between 2013 and 2023, we benchmark multiple membership function shapes and granularities to identify robust model configurations. The empirical analysis combines chronological holdout testing with Leave-One-Out cross-validation to evaluate accuracy and stability. Findings highlight a sigmoid-based ANFIS specification with four fuzzy sets per input as the most consistent performer, offering interpretable rules that complement conventional forecasting techniques.

1. Introduction

The banking sector is one of the most influential pillars of the global economy, functioning as the primary intermediary between capital providers and capital users. Through credit allocation, investment services, and risk management, banks not only ensure the efficient functioning of financial markets but also directly impact economic stability and growth. Over the past decades, this role has become even more significant due to the rapid pace of globalization, technological transformation, and increasingly complex regulatory frameworks (Buch & Goldberg, 2024; Budnik et al., 2021). Global events such as the 2008 financial crisis and the more recent economic disruptions caused by the COVID-19 pandemic and geopolitical tensions have highlighted the importance of financial stability and the necessity for accurate forecasting tools that can support decision-making in an uncertain environment. Within the European banking system, institutions face the dual challenge of meeting shareholder expectations while also complying with strict regulatory requirements, such as those outlined in the Basel III framework (Basel Committee, 2010). This regulatory environment places greater emphasis on transparency, risk management, and the maintenance of adequate capital and liquidity levels (Giordana & Schumacher, 2017). As a result, banks must not only monitor their performance but also develop forecasting capabilities that enable them to anticipate potential risks and adapt their strategies in a timely manner (Basel Committee, 2010).

One of the most critical aspects of financial performance evaluation is the measurement and prediction of profitability. While various indicators exist for assessing a bank’s efficiency and financial health, Earnings per Share (EPS) stands out as a key metric. EPS directly reflects a company’s ability to generate profit for its shareholders and is widely used by investors, analysts, and regulators when evaluating corporate performance. Accurate EPS forecasting is particularly valuable in guiding investment decisions, maintaining investor confidence, and supporting long-term strategic planning. However, predicting EPS in the banking sector presents several challenges. Financial indicators are often interconnected through complex, nonlinear relationships that are difficult to capture using traditional statistical methods. Regression models and time-series forecasting techniques, while valuable in certain contexts, tend to oversimplify these relationships and struggle to adapt to rapidly changing market conditions. This limitation has driven researchers to explore advanced computational methods capable of handling uncertainty, nonlinearity, and multi-variable interactions more effectively.

Hybrid approaches that combine elements of artificial intelligence and fuzzy logic have gained increasing attention in this regard. Among them, the Adaptive Neuro-Fuzzy Inference System (ANFIS) has emerged as a promising solution, merging the learning capability of neural networks with the transparency and rule-based reasoning of fuzzy logic systems (Ahmed et al., 2023). ANFIS has already demonstrated its potential in various domains, such as credit risk assessment, stock price prediction, and macroeconomic forecasting. Despite this, its application in predicting EPS within the European banking sector remains underexplored (Mehdi et al., 2025; Szabó et al., 2025).

This study addresses those gaps by developing ANFIS models that leverage four core financial indicators: Return on Assets (ROA), Return on Equity (ROE), Capital Ratio (CR), and Profit Margin (PM) to forecast next-period EPS for 25 European banks between 2013 and 2023. We benchmark multiple MF shapes and granularities, assess their out-of-sample performance with Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), and Pearson correlation, and corroborate the findings via Leave-One-Out (LOO) cross-validation. The results indicate that a sigmoid-based ANFIS configuration with four fuzzy sets per input is the most accurate and stable alternative.

The rest of the paper is organized as follows. Section 2 reviews the relevant literature on ANFIS applications in financial forecasting and explains our research questions. Section 3 describes the dataset, variable selection, and modeling framework. Section 4 presents the empirical results and their practical implications. Section 5 concludes and suggests key directions for future research.

2. Literature Review

2.1. Overview of ANFIS in Financial Forecasting

Adaptive Neuro-Fuzzy Inference System (ANFIS) models embed a Takagi–Sugeno fuzzy inference structure within a multilayer neural network, enabling simultaneous learning of membership parameters and transparent if–then rules (Jang, 1993). This hybrid design retains the interpretability of fuzzy logic while adapting the rule base through data-driven optimization, which is particularly attractive for financial problems characterized by nonlinear interactions and noisy observations (Mehdi et al., 2025).

Early financial applications confirmed that ANFIS can rival or outperform traditional benchmarks such as ARIMA processes and feedforward neural networks when forecasting stock indices, exchange rates, or corporate distress (Boyacioglu & Avci, 2010). These studies emphasize that performance hinges on careful input selection and membership calibration, foreshadowing the configuration analysis pursued in the present research.

2.2. ANFIS and Fuzzy Logic Applications in Finance

Subsequent work broadened ANFIS usage across equity, currency, and portfolio management contexts, often in combination with feature engineering or signal-processing techniques to stabilize noisy market data (Sharma et al., 2021; Atsalakis & Valavanis, 2009). The neuro-fuzzy approach has also been applied to volatility estimation, credit scoring, and bankruptcy prediction, signaling its versatility across forecasting and classification tasks (Chen, 2013; Orozco-Castañeda et al., 2024).

Closer to accounting fundamentals, researchers have explored ANFIS-based earnings modeling to capture nonlinear relations between profitability ratios and share performance, reporting notable accuracy gains over linear regressions (Wei et al., 2011; Do & Van Trang, 2019). Nevertheless, evidence remains scarce for European banks, where regulatory features and capital structures differ markedly from manufacturing or technology firms, motivating the present focus on institutional EPS forecasting.

Membership function design plays a central role in shaping ANFIS behavior because fuzzy set boundaries determine how financial indicators are partitioned and aggregated (Liu & Zhang, 2019; Bhattacharya & Konar, 2017). Practitioners typically adopt triangular or trapezoidal functions for simplicity, yet smoother Gaussian and sigmoid profiles may approximate continuous ratio distributions more faithfully when sufficient data are available (Esfahanipour & Mardani, 2011; Talpur et al., 2017).

Comparative investigations show that no single membership family dominates across markets: piecewise-linear sets can be robust under data scarcity, whereas bell-shaped functions improve accuracy when nonlinear thresholds exist (Janková & Rakovská, 2022). Exploring multiple shapes and granularities is therefore essential for understanding how fuzzification choices influence predictive performance, a hypothesis we test explicitly (Chourmouziadis & Chatzoglou, 2016).

2.3. Model Validation and Performance Evaluation Techniques

Robust evaluation frameworks are equally important. Financial studies typically rely on chronological train–test splits to avoid look-ahead bias, complemented by cross-validation when sample sizes are limited or panel structures are present (Boyacioglu & Avci, 2010; Szabó et al., 2025).

Among cross-validation schemes, Leave-One-Out maximizes the use of the training data while providing nearly unbiased error estimates, albeit at a higher computational cost. It is especially valuable in banking applications where the number of institutions is modest, yet each data point carries high informational content (Arlot & Celisse, 2010).

Performance is commonly summarized with root mean squared error, mean absolute error, and correlation-based diagnostics, sometimes augmented by directional accuracy metrics to capture investment relevance (Chen, 2013). Triangulating these indicators guards against overfitting and helps compare neuro-fuzzy models with statistical or machine-learning baselines (Pishnamazi et al., 2020).

2.4. Recent Advances and Related Fuzzy Forecasting Studies

Recent contributions push neuro-fuzzy forecasting toward greater adaptability by incorporating type-2 fuzzy sets, metaheuristic optimization, and hybrid architectures that blend ANFIS with deep learning or ensemble methods (Yao & Poh, 1996; Bai & Wang, 2025). Such enhancements aim to cope with heightened uncertainty and dynamic market regimes, though they often trade interpretability for complexity.

In banking-specific research, neuro-fuzzy systems have assisted in failure prediction and earnings assessment, yet comparative evidence with alternative machine-learning techniques remains limited (Tsai & Wu, 2008; Khashei & Bijari, 2011). This study extends the dialogue by evaluating a rich set of membership specifications within an EPS-focused ANFIS framework tailored to European regulatory conditions.

3. Methodology

3.1. Data Collection and Preprocessing

A panel dataset was assembled from 25 major European banks covering the 2013–2023 period. For each bank, four financial indicators were collected from publicly available sources such as annual and quarterly reports: Return on Assets (ROA), Return on Equity (ROE), Capital Ratio (CR), and Profit Margin (PM). The selection of these indicators was guided not only by their theoretical connection to Earnings per Share (EPS) but also by expert validation through two focus group discussions. Both academic and professional participants emphasized that these four indicators provide the most reliable basis for EPS prediction, as they jointly reflect profitability, stability, and efficiency.

Based on this consensus, the study proceeded with ROA, ROE, CR, and PM as input variables, with EPS serving as the output. Their definitions are as follows:

ROA (Return on Assets): Net income divided by total assets, indicating how efficiently the bank uses its assets to generate profits.

$$\mathrm{R}\mathrm{O}\mathrm{A}\left(\%\right)={\displaystyle \frac{\mathrm{N}\mathrm{e}\mathrm{t} \mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}}{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{a}\mathrm{s}\mathrm{s}\mathrm{e}\mathrm{t}\mathrm{s}}}$$

ROE (Return on Equity): Net income divided by shareholder equity, reflecting return to shareholders and overall profitability.

$$\mathrm{R}\mathrm{O}\mathrm{E}\left(\%\right)={\displaystyle \frac{\mathrm{N}\mathrm{e}\mathrm{t} \mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}}{\mathrm{E}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{t}\mathrm{y}}}$$

CR (Capital Ratio): The ratio of a bank’s capital to its risk-weighted assets (a regulatory measure of solvency); higher CR implies greater financial stability.

$$\mathrm{C}\mathrm{a}\mathrm{p}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}={\displaystyle \frac{\mathrm{T}\mathrm{i}\mathrm{e}\mathrm{r} 1 \mathrm{C}\mathrm{a}\mathrm{p}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{l}}{\mathrm{R}\mathrm{i}\mathrm{s}\mathrm{k}-\mathrm{W}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}\mathrm{e}\mathrm{d} \mathrm{A}\mathrm{s}\mathrm{s}\mathrm{e}\mathrm{t}\mathrm{s}}}\times 100$$

PM (Profit Margin): Net profit divided by total revenues, measuring what proportion of income is converted to profit.

$$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{i}\mathrm{t} \mathrm{M}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{i}\mathrm{n}\left(\%\right)={\displaystyle \frac{\mathrm{N}\mathrm{e}\mathrm{t} \mathrm{p}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{i}\mathrm{t}}{\mathrm{R}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{u}\mathrm{e}}}$$

These four ratios jointly capture profitability, capital adequacy, and cost efficiency—dimensions that prior banking EPS studies isolate as the strongest drivers of earnings dynamics (Flannery & Rangan, 2004). ROA and ROE track internal profit generation, the capital ratio encodes regulatory solvency buffers, while profit margin signals the effectiveness of revenue conversion; together, they underpin most prudential scorecards (Frederic et al., 2023).

Each of these indicators was compiled into a master spreadsheet. The earnings per share (EPS) value for each bank year was designated as the target for prediction. Prior to modeling, all variables (inputs and EPS) were min–max scaled to [0, 1] using parameters computed on the training window (2013–2019) and applied unchanged to the 2020–2023 hold-out, preserving out-of-sample integrity. Each observation, therefore, captures a bank’s financial ratios at year t together with the EPS realized at t + 1, supporting next-period forecasting while preserving temporal causality.

The resulting panel comprises 275 bank-year observations (25 institutions observed annually between 2013 and 2023). All series are aligned to calendar-year reporting to preserve comparability across jurisdictions.

The modelling pipeline respects temporal ordering: 2013–2019 observations (175 bank-years) are used for training, while 2020–2023 observations (100 bank-years) constitute the out-of-sample evaluation window. This chronological partitioning follows best practices for bank forecasting under structural breaks. The complete list of sampled banks appears in Appendix A.

3.2. Focus Group Interviews for Indicator Selection

To qualitatively substantiate the choice of the four key financial indicators as predictors for EPS, two focus group discussions were conducted with domain experts. The first focus group, held in November 2024, involved 10 academic experts (university lecturers and professors in finance and economics). The second focus group, held in January 2025, involved 10 financial industry professionals (experienced banking and finance practitioners). Each session lasted approximately 1–1.5 h and was guided by a moderator using a semi-structured format aimed at eliciting the participants’ insights on important EPS predictors.

The discussions in each focus group were steered by five open-ended questions designed to gather opinions on which metrics most strongly influence EPS. The key questions included:

• Which financial indicators do you find most useful for predicting a bank’s future earnings per share (EPS)?
• If you were creating a model to forecast EPS, which metrics would you prioritize as inputs and why?
• In your experience, are there any commonly used financial metrics that you consider less relevant or misleading for EPS prediction?
• How many key indicators do you believe are sufficient to achieve a reliable EPS forecast without adding unnecessary complexity?
• If you had to select a small set of top indicators (e.g., around four) for predicting EPS, which ones would you choose and what is your rationale for each?

Both focus groups yielded consistent insights that reinforced our variable selection. Across the academic and industry discussions, participants overwhelmingly identified four specific metrics: ROA, ROE, CR, and PM, as the most influential factors for forecasting EPS in banks. In fact, the majority of participants explicitly agreed that these four indicators together provide the best basis for predicting EPS, noting that they collectively capture a bank’s profitability (through ROA, ROE, and PM) and financial stability (through CR). Although other financial measures were mentioned during the sessions, none were as broadly endorsed as these four. This expert feedback validated our initial theoretical rationale and confirmed that focusing on ROA, ROE, CR, and PM would likely yield the most robust EPS predictions. Therefore, the qualitative consensus from the focus groups served to underpin and justify the selection of these four input variables in our ANFIS modeling approach.

3.3. ANFIS Model Configuration

The forecasting models were constructed using an Adaptive Neuro-Fuzzy Inference System (ANFIS), which combines neural network learning with fuzzy logic inference. Each ANFIS model implemented a first-order Takagi–Sugeno fuzzy system with four inputs (ROA, ROE, CR, PM) and one output (EPS). The general ANFIS architecture consists of five layers: input fuzzification, rule firing, normalization, consequent calculation, and output summation. In Layer 1, each input variable is transformed into membership grades across several fuzzy sets; Layer 2 computes the firing strength of each rule by combining these grades; Layer 3 normalizes the strengths; Layer 4 computes a linear output for each rule; and Layer 5 aggregates these to produce the predicted EPS.

To explore the effect of different fuzzy representations, we tested four types of membership function (MF) shapes for the input variables: triangular, trapezoidal, Gaussian, and sigmoidal (S-shaped). For each MF type, two configurations of fuzzy granularity were examined: using three fuzzy sets per input versus four fuzzy sets per input. This results in eight total ANFIS configurations (4 MF shapes × 2 set counts). For example, the “Sigmoid–4 sets” model refers to using sigmoidal membership functions with four fuzzy sets for each of the four inputs. The number of fuzzy rules in a Takagi–Sugeno system is the Cartesian product of the fuzzy sets across inputs, yielding 3⁴ = 81 rules for three sets per input and 4⁴ = 256 rules for four sets per input. These configurations allowed investigation of both the effect of MF smoothness and model complexity on predictive performance.

Each initial FIS (Fuzzy Inference System) structure was generated using MATLAB’s (R2024a) Fuzzy Logic Toolbox. Specifically, we used a grid-partitioning approach (e.g., the genfis function with grid option), which uniformly divides each input’s range into the specified number of fuzzy sets. For example, the trapezoidal MF configuration with four sets per input would place four trapezoidal functions evenly across each input dimension. The parameters of each membership function (centers, widths, etc.) were initially set to evenly cover the data range. Both ‘low’, ‘medium’, ’medium-high’ and ‘high’ regions were automatically captured by these initial partitions. By systematically testing each MF shape and set number, we could compare piecewise-linear membership boundaries (triangular/trapezoidal) versus smooth nonlinear boundaries (Gaussian/sigmoid) and simpler versus finer input partitions.

Once initialized, the ANFIS models were trained on the training subset. The MATLAB anfis function was used for this purpose, employing the standard hybrid learning algorithm. This algorithm alternates between a forward pass (solving linear consequent parameters via least-squares) and a backward pass (updating fuzzy membership parameters via gradient descent). Training was run for a sufficient number of epochs (up to 100) or until the decrease in training error became negligible. During this process, the root mean squared error (RMSE) between predicted and actual EPS on the training set was monitored. The hybrid learning ensures that each ANFIS model tunes both the fuzzy rules and the shape of its membership functions to fit the data. Each of the eight configurations was trained separately on the same training data, resulting in eight distinct ANFIS models.

3.4. Performance Evaluation on Test Set

After training, each ANFIS model was evaluated on the held-out test set. Two error metrics were computed to quantify predictive accuracy: the Root Mean Squared Error (RMSE) and the Mean Absolute Error (MAE). RMSE is defined as

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}$$

and MAE as

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|y_i-\widehat{y_i}\right|$$

where yi is the actual EPS value, ŷi is the predicted EPS value for the i-th test sample, and n is the total number of test samples. Lower RMSE and MAE values indicate higher predictive accuracy. In addition, the Pearson correlation coefficient (r) was calculated to measure the strength and direction of the linear relationship between predicted and actual EPS values, capturing how well the model aligns with the timing and magnitude of EPS movements.

For each of the eight models, RMSE, MAE, and Pearson r were calculated on the test set. As an illustrative result, the model with sigmoidal membership functions and four fuzzy sets per input (Sigmoid–4) yielded the best accuracy: it achieved a test RMSE of approximately 0.186 (in the normalized EPS scale) and an MAE of about 0.195. This model also produced a high Pearson correlation (around 0.82) between predicted and observed EPS values in the test period, indicating strong alignment in the pattern of earnings. In comparison, models with triangular or trapezoidal MFs generally had larger errors. The Gaussian MF models showed mixed results, sometimes overfitting (very low training error but higher test error). Overall, the Sigmoid–4 model consistently outperformed the alternatives by yielding the lowest errors and highest correlation.

3.5. Baseline Models

Alongside the ANFIS configurations, we include two transparent baselines under the same one-step-ahead protocol and chronological split (train: 2013–2019; hold-out: 2020–2023) on the annual bank-year panel. A pooled OLS uses accounting predictors observed at year t (ROA, ROE, PM, CR) to forecast EPS at t + 1, estimated on the training window and applied to the hold-out. A per-bank ARIMA models each bank’s annual EPS history univariately; orders are selected by AIC from a small candidate set, and one-step forecasts are generated for 2020–2023. Accuracy is evaluated by RMSE, MAE, and Pearson’s r on the hold-out, consistent with the ANFIS evaluation.

Rationale for one-step horizon. We restrict horizons to one-step-ahead because the dataset is annual, so iterative multi-year procedures would compound approximation errors, and decision relevance for issuers/investors is strongest around the next reporting period (guidance and budgeting). This preserves a clean, apple-to-apple comparison across ANFIS membership-function designs.

3.6. Leave-One-Out Cross-Validation

To further validate model robustness, a leave-one-out (LOO) cross-validation was performed on the entire dataset. In this procedure, each data point (one bank at one time period) is treated in turn as a held-out test sample, while the model is trained on all remaining points. Specifically, with a total of N observations, the model is trained N times. In each iteration, one observation is left out from the training set and used as the test sample, while the remaining N − 1 observations are used for training. This process is repeated until every observation has been used exactly once as the test sample. This LOO approach provides an almost unbiased estimate of model performance without reducing the training sample size too much, which is valuable for relatively modest datasets. For each trial, we recorded the error (RMSE and MAE) and the correlation between predicted and actual EPS for the single left-out sample.

3.7. Model Selection and Final Performance

Based on the evaluations above, the ANFIS configuration with sigmoidal membership functions and four fuzzy sets per input was selected as the final model. This choice was driven by its superior accuracy in both the holdout test and cross-validation. The final model was re-trained on the full training set (or, equivalently, effectively trained via LOO), and its overall errors were taken as reported above. In summary, the modeling procedure demonstrated that combining key profitability indicators (ROA, ROE, CR, PM) in an ANFIS framework can effectively capture the complex nonlinear mapping to EPS. The quantitative results highlight the high predictive precision achieved. All modeling steps from data preprocessing to fuzzy model training and validation were implemented in MATLAB to ensure reproducibility and consistency of the methodology. This rigorous approach provides confidence that the reported EPS forecasts accurately reflect the underlying financial patterns of the banks studied

4. Results and Discussion

Comparison across the eight ANFIS configurations shows that the sigmoid membership function with four fuzzy sets per input yielded the lowest holdout error (RMSE 0.1956; MAE 0.195), far outperforming the triangular and trapezoidal variants, whose RMSE values exceeded 0.65. The smoother nonlinear partitions capture EPS inflection points more effectively than piecewise-linear alternatives.

Adding a fourth fuzzy set improved performance across all membership families, indicating that additional granularity is required to distinguish profitability regimes among the 25 banks. Maintaining all four financial indicators likewise yielded better forecasts than any three-variable subset, confirming that ROA, ROE, CR, and PM provide complementary signals. Despite the richer rule base, the sigmoid-4 specification remained interpretable by mapping economically intuitive combinations of profitability, capitalization, and efficiency to observed EPS regimes.

Table 1. Summary of ANFIS model performance across different membership functions and number of fuzzy sets. Source: Author’s elaboration.

Model Configuration (Membership Function-Number of Fuzzy Sets)	RMSE (Training)	RMSE (Test)
Triangular-3 sets	0.0080	1.0660
Triangular-4 sets	0.0005	0.8450
Trapezoidal-3 sets	0.0040	1.0150
Trapezoidal-4 sets	0.0012	0.6560
Gauss-3 sets	0.0019	0.5810
Gauss-4 sets	0.0003	0.5280
Sigmoid-3 sets	0.1050	0.2250
Sigmoid-4 sets	0.1100	0.1956

summarizes these holdout comparisons and documents that Gaussian profiles offered intermediate accuracy, whereas simpler triangular or trapezoidal structures struggled to balance bias and variance.

4.1. Leave-One-Out Cross-Validation Results

To further evaluate the robustness of the ANFIS model configurations, Leave-One-Out (LOO) cross-validation was performed. Unlike the initial chronological hold-out (train-, 2013–2019; hold-out 2020–2023) the LOO procedure iteratively leaves one observation. This approach provides a more granular and unbiased estimate of model performance, particularly valuable when working with relatively limited datasets, such as annual banking data.

The LOO validation results were consistent with the original findings. The sigmoid membership function with four fuzzy sets continued to perform the best among all configurations, achieving a mean RMSE of 0.0998, a mean absolute error (MAE) of 0.1331, and a Pearson correlation coefficient of 0.8181 under the LOO scheme. Other membership function types (triangular, trapezoidal, Gaussian) and input dimensionalities (3D, 4D) also followed a similar trend as in the original evaluation, though performance varied slightly due to the stricter validation criterion.

The

Table 2. LOO cross-validation results by membership function type and input dimension. Source: Author’s elaboration.

MF Type	RMSE	MAE	Pearson r
Triangular	0.1757	0.1359	0.6600
Triangular	0.1618	0.1128	0.7633
Trapezoidal	0.1894	0.1355	0.6390
Trapezoidal	0.2174	0.1210	0.6658
Gauss	0.2594	0.1542	0.4855
Gauss	0.3469	0.1290	0.4914
Sigmoid	0.1631	0.1311	0.7081
Sigmoid	0.0998	0.1331	0.8181

below summarizes the key performance indicators for selected configurations under LOO cross-validation:

These results (Table 2) confirm that the selected ANFIS model configuration not only performed well under conventional train/test evaluation but also maintained predictive consistency under a more rigorous cross-validation protocol.

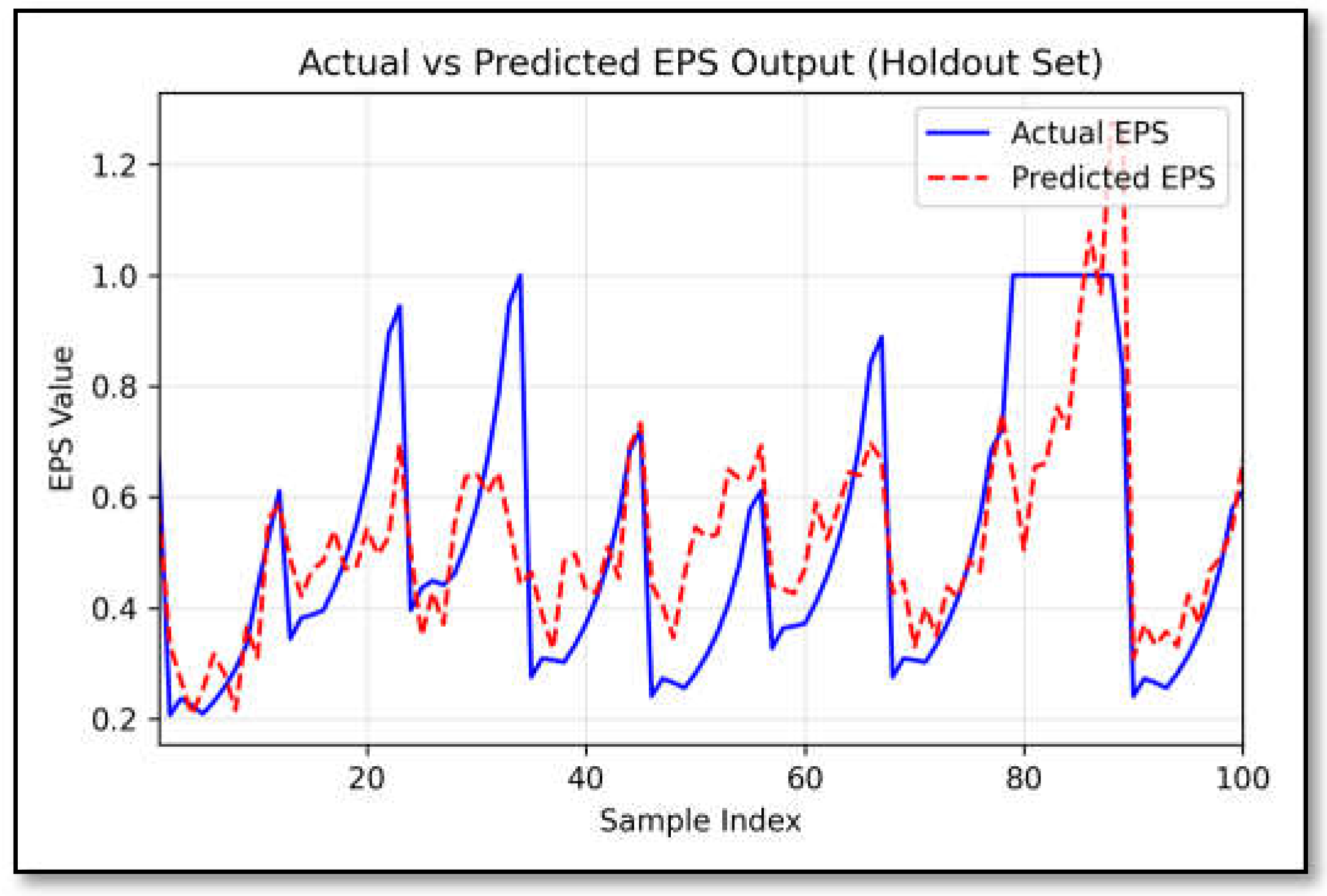
The forecast curve of the best-performing model vividly illustrates how effectively the sigmoid-based ANFIS model with four fuzzy sets tracks the temporal dynamics of EPS time series for European banks. The predicted values closely parallel with the actual EPS data, accurately capturing major trends and turning points. The temporal pattern of forecasting errors indicates that the model successfully filters out short-term noise while preserving the essential long-term patterns. Based on the results (Figure 1), it can be concluded that the presented neuro-fuzzy model is well-suited for forecasting the EPS values of European banks, thereby contributing to enhanced accuracy and reliability in financial analyses.

4.2. Baseline Models: OLS and ARIMA

Baseline performance.

Table 3. Baseline predictive performance on the 2020–2023 hold-out (annual bank-year panel; one-step-ahead).

Model	RMSE	MAE	Pearson r
OLS	0.334	0.309	0.785
ARIMA	0.213	0.278	0.792

reports the out-of-sample (2020–2023) accuracy of the pooled OLS and the per-bank ARIMA under the same one-step and chronological protocol. The ARIMA baseline achieves lower errors and a higher linear association on the hold-out data (RMSE 0.213, MAE 0.278, r 0.792) compared to the pooled OLS (RMSE 0.334, MAE 0.309, r 0.785). These results indicate that simple bank-specific dynamics in annual EPS are captured reasonably well by a univariate time-series approach, providing a meaningful calibration for the ANFIS comparisons.

Interpretation. Because both baselines are intentionally parsimonious and use only information available at year t (and, for ARIMA, only the EPS history), their role is not to compete with ANFIS but to calibrate task difficulty. Improvements of the best ANFIS setup over these references therefore reflect modeling value beyond naive cross-sectional averages or univariate dynamics.

4.3. Practical Implications

The ANFIS framework developed here provides a reliable tool for bank-level EPS forecasting, and the empirical results translate into actionable insights for the European banking sector. A model that can reliably forecast Earnings per Share (EPS) gives investors a stronger basis for decision-making. Since EPS remains one of the most widely followed indicators of bank profitability, accurate predictions reduce uncertainty and help investors adjust their portfolios with greater confidence. When earnings expectations are met more consistently, investment risks decline, and returns can be optimized.

The baselines show that even minimal forecasting rules (pooled OLS; per-bank ARIMA) achieve reasonable accuracy on annual EPS. This strengthens the interpretation of the ANFIS results: gains over these parsimonious references constitute value-added beyond naive cross-sectional and purely univariate dynamics, particularly for near-term guidance around the next reporting period.

For banks themselves, better EPS forecasts translate into more effective planning. Management teams can evaluate whether current business strategies are sustainable and, if necessary, make timely adjustments. Reliable projections also help with budgeting and capital allocation, as executives gain foresight into potential shifts in profitability. This makes the model not only a forecasting tool but also a strategic asset for internal governance.

While supervisory authorities primarily focus on prudential metrics (capital, liquidity and asset quality), improved EPS forecasts can still be indirectly informative: forward-looking signals about profitability pressures may complement risk monitoring and supervisory dialogues. The principal beneficiaries, however, are issuers and investors, for whom one-step-ahead EPS guidance is decision-relevant for budgeting, capital planning and communication.

Taken together, the findings show that hybrid neuro-fuzzy systems can do more than provide marginally better forecasts. They can support the work of investors, bank managers, and regulators alike, making financial decisions more transparent and more robust. If adopted more widely, models of this kind could become part of a broader toolkit for improving resilience in the European banking sector. Given how banks issue guidance and adjust capital plans around the next reporting period, a one-step-ahead horizon most directly serves investor communication and managerial planning

4.4. Limitations

Despite these encouraging results, several professional and mathematical limitations of the research should be acknowledged. First, the model’s input space was constrained to four internal financial variables; while these were carefully selected for their relevance, they do not encompass all factors influencing EPS. Important drivers such as macroeconomic conditions, regulatory changes, or market sentiment were beyond the scope of this study, which may limit the completeness of the predictions. Furthermore, the modeling approach treated each period’s data as independent, without incorporating explicit temporal features (e.g., lagged EPS values), so any time-series patterns in EPS were not directly captured. Second, the dataset itself represents a relatively narrow sample. As a consequence, the findings and the optimized model are most directly applicable to similar European banking contexts. One should be cautious in generalizing these results to other industries, geographic regions, or time periods without additional validation, as structural differences in those contexts could affect model performance. Future research could extend the feature set with explicitly supervisory variables, most notably the gap between actual and required capital ratios and incorporate benchmark interest-rate curves to capture funding-cost dynamics.

From a methodological perspective, the ANFIS modeling approach also has intrinsic limitations. One issue is the sensitivity of the fuzzy model to initial parameter settings. The performance of ANFIS can depend on the starting values of membership function parameters and other training hyperparameters; different initializations could lead to convergence on suboptimal solutions or require more training iterations. Although the hybrid learning algorithm used (combining gradient descent with least squares estimation) helped achieve reliable training in this study, ensuring consistency may require careful tuning or multiple runs to avoid local minimum. Another challenge is the complexity of the final model, which in the best-case configuration employs four fuzzy sets per input. This granularity greatly increases the number of fuzzy if–then rules in the inference system (potentially on the order of a few hundred rules when all combinations are considered). While in theory every rule is interpretable, in practice such a large rule base becomes difficult to interpret and analyze. This highlights a trade-off between accuracy and interpretability: the very feature that gives ANFIS a transparency advantage over black-box models, the explicit rule structure can become a hindrance when the rule set is too extensive for human experts to readily comprehend.

Notwithstanding these limitations, the outcomes of this research have clear practical significance. The demonstrated ability of the ANFIS model to predict EPS with high accuracy makes it a valuable decision-support tool for various stakeholders in the financial domain. Bank management teams could incorporate the model’s forecasts into their strategic planning and risk management processes to anticipate earnings fluctuations and adjust their operations accordingly. Investors and financial analysts might use the EPS predictions to complement their fundamental analysis, identifying early signs of performance improvement or deterioration that could inform investment decisions. Moreover, the partially interpretable nature of the neuro-fuzzy model aligns with the growing demand for explainable AI in finance. Stakeholders, ranging from bank executives to regulators can derive not only predictions from the model but also insights into the reasoning behind those predictions, which is crucial for trust and adoption in a risk-sensitive field like banking.

5. Conclusions

This paper evaluated Adaptive Neuro-Fuzzy Inference Systems for forecasting bank earnings per share using annual data from 25 European institutions covering 2013–2023. The analysis shows that a sigmoid-based configuration with four fuzzy sets balances predictive accuracy and interpretability, providing actionable guidance for analysts and risk managers who rely on EPS trajectories.

Future research should: (1) extend the information set with macro-financial and sentiment indicators, supervisory capital buffers (actual-versus-required CR spreads), and term-structure interest rates to capture external shocks; (2) benchmark ANFIS against sequence-learning and ensemble methods to clarify its comparative strengths; and (3) investigate streamlined rule bases or online learning schemes that preserve transparency while accommodating rapidly evolving market conditions, while also incorporating performance diagnostics such as Theil’s U to compare models against naïve baselines.

Addressing these directions would deepen understanding of how neuro-fuzzy models can support decision-making in regulated banking environments and strengthen their adoption as complementary forecasting tools.