Diffusion-Based Parameters for Stock Clustering: Sector Separation and Out-of-Sample Evidence

Abstract

Clustering techniques are widely applied to equity markets to uncover sectoral structures and regime shifts, yet most studies rely solely on empirical returns. This paper introduces a novel perspective by using diffusion-based parameters from the Black–Scholes model, namely monthly drift and diffusion, as clustering features. Using SET100 stocks in 2020, we applied k-means clustering and evaluated performances with silhouette scores, the Adjusted Rand Index, Wilcoxon tests, and an out-of-sample portfolio exercise. The results showed that diffusion-based features achieved higher silhouette scores in turbulent months, where they revealed sectoral divergence that log-returns failed to capture. The partition for November 2020 provided clearer sector separation and smaller portfolio losses, demonstrating predictive value beyond in-sample fit. Practically, the findings indicate that diffusion-based parameters can signal early signs of market stress, guide sector rotation decisions during volatile regimes, and enhance portfolio risk management by isolating persistent volatility structures across sectors. Theoretically, this model-based framework bridges equity clustering with stochastic diffusion representations used in derivatives valuation, offering a unified and interpretable tool for data-driven market monitoring.

1. Introduction

Applying clustering techniques to stock groups or market indices can uncover underlying structures and interconnections within financial markets. Clustering has been used across diverse datasets, from global indices to individual stock exchanges, and has proven effective at detecting market regimes, sectoral relationships, and crisis dynamics. Methods such as k-means clustering, Gaussian mixture models, spectral clustering, and correlation-based approaches are commonly employed to analyze historical prices, returns, and market microstructure features. The insights obtained not only enhance the understanding of market dynamics but also support practical applications in portfolio diversification, index construction, and risk management (Aslam et al., 2023; Nagy & Ormos, 2018).

Empirical research on stock clustering has developed over several decades. Osborne (1962) was among the first to document clustering in closing prices on the New York Stock Exchange, and Niederhoffer (1965) later showed that such clustering varied by stock type. Subsequent studies provided evidence of persistent clustering across different markets, including the Australian Stock Exchange (Aitken et al., 1996), the London Stock Exchange (Grossman et al., 1997), the Singapore Exchange (Hameed & Terry, 1998), the Kuala Lumpur Stock Exchange (Chung et al., 2005), the Tokyo Stock Exchange (Aşçıoğlu et al., 2007), and the Chinese markets in Shanghai and Shenzhen (Brown & Mitchell, 2008). However, most of these studies focused on price or return data. The diffusion processes underlying stock price dynamics were only addressed in a few works, such as those of Hirukawa (2006) and De Gregorio and Iacus (2010).

A widely adopted feature of investment performance analysis is the log-return (LR), defined as the logarithmic difference of consecutive stock prices. LR clustering has been extensively used to detect patterns, anomalies, and common behaviors among assets, and has been combined with k-means variants, subspaces, and temporal clustering to enhance the analysis (Gan & Chen, 2016; Gramuglia et al., 2021). Despite the popularity of LR clustering as an investment analysis technique, it struggles with irregular temporal structures and often fails to capture deeper market dynamics due to its sensitivity to noise and outliers.

Alternatively, stock price movements can be modeled using Geometric Brownian Motion (GBM), a cornerstone of quantitative financial analysis. GBM assumes that the logarithm of stock prices follows a Brownian motion with drift, producing continuous paths characterized by two parameters: drift (expected return) and volatility (random fluctuations). It ensures positive prices, captures compounded returns, and underlies the Black–Scholes (BS) model. While more sophisticated models such as stochastic volatility or jump-diffusion processes have been proposed, classical GBM remains widely used due to its simplicity and analytical tractability (Chai, 2019).

Therefore, although stock clustering has been extensively examined in the literature, most existing studies continue to rely primarily on returns-based features. Analytical frameworks grounded in stochastic differential equations (SDEs), which have long provided closed-form foundations for modeling asset dynamics and option valuation (Cox et al., 1985; Duffie et al., 2003; Heston, 1993; Merton, 1973) have also been extended in recent research to regime-switching, trending volatility, and generalized diffusion settings (Chumpong et al., 2024, 2022; Duangpan et al., 2022; Rujivan, 2025; Rujivan et al., 2023, 2025; Sutthimat & Mekchay, 2022). This perspective highlights the relevance of parameter estimation beyond realized returns and motivates our use of BS-based features in capturing the underlying risk–return structure of stocks.

In particular, the drift and diffusion parameters from the BS framework offer a theoretically grounded representation of stock dynamics, yet have rarely been employed in clustering analysis. This study makes three key contributions. First, it shifts stock clustering from descriptive statistics (LR means and standard deviation) to structural parameters (drift and diffusion) that govern the stochastic process of prices, embedding clustering in the underlying dynamics rather than surface-level summaries. Second, by showing that diffusion-based features sharpen sector separation during market stress (e.g., COVID-19 shocks), the study demonstrates their value as regime-detection tools. Third, because the structural parameters are directly applied to derivatives pricing, the framework creates a novel bridge between equity clustering and derivatives valuation. Together, these aspects elevate diffusion-based clustering beyond a simple feature replacement to a new paradigm that integrates market structure analysis, stress detection, and the pricing of derivatives.

The remainder of this article is structured as follows. Section 2 details the data and methodology, including lognormality testing, feature extraction, and clustering evaluation. Section 3 reports the empirical findings, while Section 4 provides interpretation and discusses practical implications. Section 5 concludes with a summary of the study and suggestions for future research.

2. Model and Methodology

This section outlines the methodological framework of the study. All analyses were implemented in Python (version 3.13) using standard scientific libraries such as NumPy, pandas, SciPy, and scikit-learn. We begin by testing the lognormality of stock prices to ensure the appropriateness of using diffusion-based parameters. Next, we describe the feature extraction process, including the derivation of LRs and the estimation of drift and diffusion parameters from the BS model. These features are then standardized and used as inputs to k-means clustering. Finally, clustering performance is evaluated using internal validity indices and statistical tests.

2.1. Model

Black and Scholes (1973) proposed their famous and widely used stock price estimation model in 1973. Since the real market is too complex to be fully modelled, the model has been simplified. The dynamics of the stock price i for $i=1,2,\dots ,N$, $S_t^{\left(i\right)}$ is assumed to follow the SDE

$$\begin{array}{c}\hfill d{S}_t^{\left(i\right)}=r_i{S}_t^{\left(i\right)}dt+{\sigma }_i{S}_t^{\left(i\right)}d{W}_t^{\left(i\right)},\end{array}$$

(1)

where $r_i$ is the risk-free interest rate, ${\sigma }_i$ is the volatility of the stock price and $d{W}_t^{\left(i\right)}$ is a Brownian motion in the probability space $(\Omega ,\mathcal{F},\mathbb{P})$ in which $d{W}_t^{\left(i\right)}$ and $d{W}_t^{\left(j\right)}$ are assumed to be independent for $i\ne j$. In the resulting continuous-time model, the GBM of the stock price is given by

$$\begin{array}{c}\hfill S_t^{\left(i\right)}=S_0^{\left(i\right)}exp\left({\mu }_{i}t+{\sigma }_i{W}_t^{\left(i\right)}\right)\mathrm{and}{\mu }_i=r_i-{\displaystyle \frac{1}{2}}{\sigma }_i^2,\end{array}$$

where $S_0^{\left(i\right)}$ is the stock price at time 0. This means that $S_t^{\left(i\right)}$ has a lognormal distribution (Hull & Basu, 2016) and in this research, we consider all stock prices to be lognormally distributed. Then, we estimate the corresponding parameters based on the historical data of the stock market in Thailand for group stocks by k-means clustering.

2.2. Testing of Price Distribution from SET100

We collected secondary data on closing prices of the constituents of the SET100 index from 2 January to 30 December 2020. The data comprises the 100 biggest companies in terms of market capitalisation as calculated by the SET100 index.

In general, two approaches can be taken to examine the lognormal distribution of stock prices: informal graphical methods and formal statistical hypothesis tests. While graphical tools such as histograms can provide intuition, they are insufficient for rigorous analysis. Therefore, this study adopted the Anderson–Darling (AD) test, which has been shown to be particularly effective for testing lognormality (Anderson & Darling, 1952; Aşçıoğlu et al., 2007; Tolikas & Heravi, 2008; Ul-Islam, 2011). To improve accuracy in small samples, we used the correction formulas for p-values proposed by D’Agostino and Stephens (1986). For each SET100 stock and each month of 2020, the null hypothesis of lognormality was tested at the 5% significance level. Stocks that passed the test were retained for subsequent parameter estimation and clustering analysis. The AD tests were performed using the scipy.stats.anderson function from the SciPy library.

This screening step, utilizing the AD test, ensures that the stock prices used for parameter estimation are consistent with the lognormal assumption fundamental to the BS framework. Although this procedure reduces the sample size in certain months, it preserves the theoretical integrity required for subsequent model-based estimation. This unavoidable trade-off between data coverage and theoretical validity was considered acceptable to ensure the reliability of the maximum-likelihood estimation (MLE) of the BS parameters under the GBM assumption.

2.3. Parameter Estimation

For clustering, we extract two sets of features: drift and diffusion from the BS model, and mean and standard deviation from empirical LRs. These complementary selections are detailed below.

2.3.1. Estimated Parameters from the Black–Scholes Model

There are many commonly used methods of estimating probability parameters. One of the most efficient methods is maximum likelihood estimation, which provides a consistent but flexible approach, suitable for a wide variety of applications. Furthermore, under standard regularity conditions, the resulting MLE is consistent, asymptotically normal, and asymptotically efficient, attaining the Cramer–Rao lower bound in large samples.

In the BS model, the dynamics of the stock price S are assumed to follow the parameters of constant drift r and volatility $\sigma$. To force the corresponding parameters to produce model dynamics as close as possible to the empirical stock market data, we use the techniques of Aït-Sahaliat-Sahalia (2002), Egorov et al. (2003), and Rujivan (2010). The transition probability density function of the BS model is denoted by

$$\begin{array}{c}\hfill p(S^{\left(i\right)},t\mid S_0^{\left(i\right)},\tau ;({\sigma }_i,r_i))={\displaystyle \frac{1}{S_t^{\left(i\right)}\sqrt{2\pi {\sigma }_i^2(t-\tau )}}}exp\left(-{\displaystyle \frac{{\left(ln\left(\frac{S_t^{\left(i\right)}}{S_{\tau }^{\left(i\right)}}\right)-(r_i-\frac{1}{2}{\sigma }_i^2)(t-\tau )\right)}^2}{2{\sigma }_i^2(t-\tau )}}\right).\end{array}$$

Let $S_{t_j}^{\left(i\right)}$ be the closing stock price i observed at times $t_j$ such that $t_j=j\Delta t$ with equally spaced discrete observations, $\Delta t=t_j-t_{j-1}>0,j=1,2,\dots ,N$ for some positive integer N. Applying Bayes’s rule to the Markov process, for $S_t^{\left(i\right)}$, we get the following log-likelihood function,

$$\begin{array}{c}\hfill L_N\left(({\sigma }_i,r_i)\right)=\sum _{j=1}^{N}lnp\left(S_{t_j}^{\left(i\right)},t_j\mid S_{t_{j-1}}^{\left(i\right)},t_{j-1};({\sigma }_i,r_i)\right).\end{array}$$

(2)

Maximizing $L_N\left(({\sigma }_i,r_i)\right)$ over a particular parameter space $\Theta =\{({\sigma }_i,r_i)\in {\mathbb{R}}^{+}\times \mathbb{R}\mathrm{for}i=1,2,\dots ,N\}$, one can get an MLE ${\theta }_N^{\mathrm{MLE}}$ which is a solution of the optimization problem,

$$\begin{array}{c}\hfill {\theta }_{N,i}^{\mathrm{MLE}}=arg\underset{({\sigma }_i,r_i)\in \Theta }{max}{L}_N\left(({\sigma }_i,r_i)\right).\end{array}$$

The log-likelihood function is approximated by $L_N^{(K,\Delta t)}\left(({\sigma }_i,r_i)\right)$ for some positive integer K. Replacing $L_N\left(({\sigma }_i,r_i)\right)$ in Equation (2) with $L_N^{(K,\Delta t)}\left(({\sigma }_i,r_i)\right)$ and solving the problem, we obtain an approximate MLE ${\widehat{\theta }}_{N,i}^{\mathrm{MLE}}=({\widehat{\sigma }}_i,{\widehat{r}}_i)$ that converges in probability when K is large and $\Delta$ is small. The estimation steps are summarized in Algorithm 1.

Algorithm 1 Monthly GBM Parameter Estimation with Iterative Simulation and Categorization

Require: Set of months $\mathcal{M}$; for each month M: list of stocks in SET100

1: Daily close prices $\{S_{t_0}^{\left(i\right)},\dots ,S_{t_N}^{\left(i\right)}\}$ for each stock i in month M from the number of trading days N   2: Time step $\Delta t=1/N$; number of simulation rounds $B=50,000$

Ensure: For each stock i in each month M: estimated parameters $({\widehat{\sigma }}_i,{\widehat{\mu }}_i)$

3: for each month M do   4:     for each stock i in SET100 do   5:         Extract daily close prices $\{S_{t_0}^{\left(i\right)},\dots ,S_{t_N}^{\left(i\right)}\}$ in month M   6:         Estimate initial GBM parameters $({\sigma }_{\mathrm{current}},r_{\mathrm{current}})$ from observed prices   7:         Create empty lists to store $\sigma$ and r from simulations   8:         for $k\leftarrow 1$ to B do   9:            Simulate a price path using $({\sigma }_{\mathrm{current}},r_{\mathrm{current}})$ with the GBM model 10:            Estimate new parameters $({\sigma }_{\mathrm{new}},r_{\mathrm{new}})$ from the simulated path 11:            Save ${\sigma }_{\mathrm{new}}$ and $r_{\mathrm{new}}$ into the lists 12:            Update $({\sigma }_{\mathrm{current}},r_{\mathrm{current}})\leftarrow ({\sigma }_{\mathrm{new}},r_{\mathrm{new}})$ 13:         end for 14:         Compute ${\widehat{\sigma }}_i\leftarrow$ average of all ${\sigma }_{\mathrm{new}}$ values 15:         Compute ${\widehat{r}}_i\leftarrow$ average of all $r_{\mathrm{new}}$ values 16:         Set ${\widehat{\mu }}_i\leftarrow {\widehat{r}}_i-\frac{1}{2}{\widehat{\sigma }}_i^2$ 17:     end for 18:     Categorize stocks based on ${\widehat{\sigma }}_i$ and ${\widehat{\mu }}_i$ values 19:     Store month-M results for further analysis 20: end for

Although the BS parameters can be estimated approximately by maximum likelihood estimation, short monthly series may cause small-sample bias and instability. To improve the robustness of the method, we implemented an iterative simulation procedure (Algorithm 1) with B = 50,000 replications, which yields estimates close to those yielded by maximum likelihood estimation but more stable in practice.

The choice of the BS model, grounded in the GBM stochastic process, represents a deliberate methodological decision. As the simplest and most widely recognized continuous-time diffusion model in finance, the BS framework provides a tractable and theoretically consistent benchmark for parameter estimation. By linking drift and volatility to a structural stochastic process, it yields forward-looking measures of expected return and risk that serve as interpretable features for clustering analysis.

2.3.2. Estimated Parameters from Empirical Log Returns

The empirical LR approach provides a simple and model-free way to summarize the distributional characteristics of asset price changes over a given period. Unlike the BS estimation in the previous subsection, which relies on the continuous-time GBM assumption and maximizes a log-likelihood function, this method computes the parameters directly from observed price data without any diffusion model assumptions. It serves as a baseline for comparison with the BS parameter estimates.

Let $S_{t_j}^{\left(i\right)}$ be the observed daily closing price of stock i on trading day $t_j$ in month $\mathcal{M}$, where $j=1,2,\dots ,N$ and N is the number of trading days in the month. The continuously compounded (log) return between $t_{j-1}$ and $t_j$ is given by

$$X_j^{\left(i\right)}=ln\left({\displaystyle \frac{S_{t_j}^{\left(i\right)}}{S_{t_{j-1}}^{\left(i\right)}}}\right),j=2,\dots ,N.$$

Since there are N observed prices, the total number of log returns is $N-1$.

The empirical mean and standard deviation of the log returns are computed as

$${\overline{\mu }}_i={\displaystyle \frac{1}{N-1}}\sum _{j=2}^N{X}_j^{\left(i\right)},{\overline{\sigma }}_i=\sqrt{{\displaystyle \frac{1}{N-2}}\sum _{j=2}^N{\left(X_j^{\left(i\right)}-{\overline{\mu }}_i\right)}^2}.$$

These two quantities provide a straightforward measure of the average return and volatility of stock i in month $\mathcal{M}$. They are directly interpretable and can be calculated for any asset with sufficient historical data. Algorithm 2 provides the empirical LR baseline for comparison with the model-based BS estimation in Algorithm 1. Although the computation of $\overline{\mu }$ and $\overline{\sigma }$ from historical LRs is a standard procedure, its explicit inclusion clarifies the methodological contrast between data-driven and diffusion-based parameter estimation and ensures reproducibility within the monthly clustering framework.

Algorithm 2 Monthly Empirical LR Parameters Calculation

Require: Set of months $\mathcal{M}$; for each month M: list of stocks in SET100

1: Daily close prices $\{S_{t_1}^{\left(i\right)},\dots ,S_{t_N}^{\left(i\right)}\}$ for each stock i from the number of trading days N

Ensure: For each stock i in each month M: estimated parameters $({\overline{\sigma }}_i,{\overline{\mu }}_i)$

2: for each month M do  3:     for each stock i in SET100 do  4:         Extract daily close prices for stock i in month M  5:         Compute log returns $X_j^{\left(i\right)}=ln(S_{t_j}^{\left(i\right)}/S_{t_{j-1}}^{\left(i\right)})$ for $j=2$ to N  6:         Calculate ${\overline{\mu }}_i$ and ${\overline{\sigma }}_i$  7:     end for  8:     Categorize stocks based on ${\overline{\sigma }}_i$ and ${\overline{\mu }}_i$ values  9:     Store month-M results for further analysis 10: end for

In the clustering process, the empirical values $({\overline{\sigma }}_i,{\overline{\mu }}_i)$ are compared with the corresponding parameters $({\widehat{\sigma }}_i,{\widehat{\mu }}_i)$ estimated from the BS model. Prior to clustering, features are z-score standardized within each month M across the n available stocks. Standardization is applied separately to the BS features $({\widehat{\sigma }}_i,{\widehat{\mu }}_i)$ and to the empirical LR features $({\overline{\sigma }}_i,{\overline{\mu }}_i)$, using the same intersection of tickers in month M.

2.4. K-Means Clustering for Parameters

For each month, the estimated parameters of the n stocks can be expressed as a set of vectors $\{({\widehat{a}}_1,{\widehat{b}}_1),({\widehat{a}}_2,{\widehat{b}}_2),\dots ,({\widehat{a}}_n,{\widehat{b}}_n)\}$. The K-means algorithm partitions these n vectors into K disjoint clusters $S=\{S_1,S_2,\dots ,S_K\}$, each represented by a centroid $C=\{(a_1,b_1),(a_2,b_2),\dots ,(a_K,b_K)\}$. The objective is to minimize the total distance between parameter vectors and their assigned centroids:

$$\begin{array}{c}\hfill \underset{S,C}{min}\sum _{k=1}^K\sum _{i\in S_k}\sqrt{{({\widehat{a}}_i-a_k)}^2+{({\widehat{b}}_i-b_k)}^2}.\end{array}$$

Cluster centroids are initialized randomly and updated iteratively until convergence (Ball & Hall, 1967; MacQueen, 1962). The final result is a partition of the parameter space into K clusters with corresponding centroids.

To evaluate the quality of clustering, we use the silhouette coefficient, which compares the average intra-cluster distance of each point with the nearest-cluster distance. For a given point $({\widehat{a}}_i,{\widehat{b}}_i)$, the silhouette value is defined as

$$\begin{array}{c}\hfill s_K({\widehat{a}}_i,{\widehat{b}}_i)={\displaystyle \frac{b_K({\widehat{a}}_i,{\widehat{b}}_i)-a_K({\widehat{a}}_i,{\widehat{b}}_i)}{max\{a_K({\widehat{a}}_i,{\widehat{b}}_i),b_K({\widehat{a}}_i,{\widehat{b}}_i)\}}},\end{array}$$

where $a_K(·)$ is the mean distance to other samples in the same cluster and $b_K(·)$ is the minimum mean distance to samples in any other cluster. The silhouette coefficient for the partition with K clusters is then

$$\begin{array}{c}\hfill \mathrm{Sil}\left(K\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{s}_K({\widehat{a}}_i,{\widehat{b}}_i),\end{array}$$

which lies between $-1$ and 1. The value of K that maximizes $\mathrm{Sil}\left(K\right)$ is typically chosen as the most appropriate number of clusters (Rousseeuw, 1987).

2.5. Adjusted Rand Index

To quantify the agreement between clusterings derived from different parameterizations of the same stocks (e.g., k-means on BS parameters $({\widehat{\sigma }}_i,{\widehat{\mu }}_i)$ versus k-means on empirical LR statistics $({\overline{\sigma }}_i,{\overline{\mu }}_i)$), we employ the Adjusted Rand Index (ARI) (Hubert & Arabie, 1985; Rand, 1971). For each month M, let n denote the number of stocks under comparison (we use the intersection of tickers available in both representations). Consider two partitions of $\{1,\dots ,n\}$, $\mathcal{S}=\{S_1,\dots ,S_K\}$ and $\mathcal{T}=\{T_1,\dots ,T_L\}$, with nonempty, disjoint clusters. The contingency counts $N_{k\ell }=|S_k\cap T_{\ell }|$, the row sums $a_k={\sum }_{\ell =1}^L{N}_{k\ell }$, and the column sums $b_{\ell }={\sum }_{k=1}^K{N}_{k\ell }$. The ARI is given in closed form by

$$\mathrm{ARI}(K,L)={\displaystyle \frac{{\displaystyle \sum _{k=1}^K\sum _{\ell =1}^L\left(\genfrac{}{}{0pt}{}{N_{k\ell }}{2}\right)-\frac{1}{\left(\genfrac{}{}{0pt}{}{n}{2}\right)}\left({\displaystyle \sum _{k=1}^K\left(\genfrac{}{}{0pt}{}{a_k}{2}\right)}\right)\left({\displaystyle \sum _{\ell =1}^L\left(\genfrac{}{}{0pt}{}{b_{\ell }}{2}\right)}\right)}}{{\displaystyle {\displaystyle \frac{1}{2}}\left({\displaystyle \sum _{k=1}^K\left(\genfrac{}{}{0pt}{}{a_k}{2}\right)+\sum _{\ell =1}^L\left(\genfrac{}{}{0pt}{}{b_{\ell }}{2}\right)}\right)-\frac{1}{\left(\genfrac{}{}{0pt}{}{n}{2}\right)}\left(\sum _{k=1}^K\left(\genfrac{}{}{0pt}{}{a_k}{2}\right)\right)\left(\sum _{\ell =1}^L\left(\genfrac{}{}{0pt}{}{b_{\ell }}{2}\right)\right)}}}.$$

In $\mathrm{ARI}\in [-1,1]$, $\mathrm{ARI}=1$ indicates that partitions are identical (perfect agreement), values near 0 indicate the chance-level agreement of partitions, and negative values indicate less agreement than expected by chance. The ARI is permutation–invariant and defines arbitrary cluster cardinalities $(K,L)$ well. In our empirical analyses, we set $K=L$ and report $\mathrm{ARI}(M,K)$ for $K\in \{2,\dots ,10\}$ in month M.

2.6. Wilcoxon Signed-Rank Test

The Wilcoxon signed-rank test is a nonparametric method for paired comparisons that does not require normality and is well suited to small samples. It is therefore appropriate for assessing the differences in clustering quality between the two feature sets (Woolson, 2007).

In our analysis, the null assumption is that the median difference in silhouette scores between BS and Empirical LR features is zero, meaning that both approaches perform equally well. We first applied a two-sided test at the 5% level to check for any difference. When this was significant, we followed with a one-sided test to evaluate whether clustering based on BS features provided higher quality than clustering based on LRs. To assess the robustness of the directional hypothesis, the Bonferroni correction (${\alpha }_{\mathrm{adj}}=0.05/12\approx 0.0042$) was applied to the one-sided tests, controlling the Family-Wise Error Rate (FWER) across the 12 monthly comparisons.

2.7. Overall Monthly Clustering Pipeline

The entire procedure is organized as a monthly pipeline. First, daily closing prices are screened for log-normality using the AD test, and only stocks that pass are retained. For these stocks, two feature sets are obtained: BS parameters estimated by iterative simulation and maximum likelihood, and empirical parameters computed directly from LRs. Both feature sets are standardized within each month and clustered separately by k-means over candidate values of K. Clustering quality is evaluated by the silhouette coefficient, and agreement between the two representations is quantified by the ARI. Cluster quality is compared within each month using paired Wilcoxon tests on silhouette values. If the two-sided test is significant, a one-sided test assesses whether BS parameters outperform LRs. Algorithm 3 summarizes the full workflow in pseudocode form.

Algorithm 3 Monthly Clustering Pipeline with ARI and Wilcoxon Tests

Require: Set of months $\mathcal{M}$; for each month M: list of SET100 stocks; significance level $\alpha =0.05$ for all statistical tests; candidate cluster sizes $K\in \{2,\dots ,10\}$

Ensure: For each M: standardized features on the screened set ${\mathcal{I}}_M$; k-means labels; $\mathrm{ARI}(M,K)$; and Wilcoxon p-values

1: for each month $M\in \mathcal{M}$ do   2:     Screening: compute daily LRs for each stock; test log-normality at level $\alpha$; let ${\mathcal{I}}_M$ be the set that passes   3:     BS parameters: for each $i\in {\mathcal{I}}_M$, run Algorithm 1 to obtain $({\widehat{\sigma }}_i,{\widehat{\mu }}_i)$   4:     Empirical LR parameters: for each $i\in {\mathcal{I}}_M$, run Algorithm 2 to obtain $({\overline{\sigma }}_i,{\overline{\mu }}_i)$   5:     Standardize: z-score both feature sets within month M over the same index ${\mathcal{I}}_M$   6:     initialize empty list $\mathcal{D}$   7:     for each $K=2,\dots ,10$ do   8:         Fit K-means on standardized BS features → labels $z^{\mathrm{BS}}(M,K)$   9:         Fit K-means on standardized LR features → labels $z^{\mathrm{LR}}(M,K)$ 10:         Compute $\mathrm{ARI}(M,K)$ from $z^{\mathrm{BS}}(M,K)$ and $z^{\mathrm{LR}}(M,K)$ 11:         Compute ${\mathrm{Sil}}^{\mathrm{BS}}(M,K)$ from Silhouette of $z^{\mathrm{BS}}(M,K)$ 12:         Compute ${\mathrm{Sil}}^{\mathrm{LR}}(M,K)$ from Silhouette of $z^{\mathrm{LR}}(M,K)$ 13:         $D_K\leftarrow {\mathrm{Sil}}^{\mathrm{BS}}(M,K)-{\mathrm{Sil}}^{\mathrm{LR}}(M,K)$; append $D_K$ to $\mathcal{D}$ 14:     end for 15:     Wilcoxon signed-rank test (within month M): 16:     Compute two-sided Wilcoxon on $\mathcal{D}$$\to p_{\text{two-sided}}\left(M\right)$ 17:     if $p_{\text{two-sided}}\left(M\right)<\alpha$ then 18:         Compute one-sided Wilcoxon on $\mathcal{D}$$\to p_{\mathrm{greater}}\left(M\right)$ 19:     end if 20:     Store all outputs for month M 21: end for

3. Results

This section presents the empirical findings of the study. We begin with data screening and summary statistics of the estimated parameters derived from the SET100 constituents, followed by an evaluation of clustering performances using both BS parameters and empirical LRs. The degree of agreement between the two approaches is then assessed through the ARI, and statistical comparisons of cluster quality are carried out using the Wilcoxon signed-rank test. Finally, we provide out-of-sample evidence based on cumulative returns to evaluate the practical implications of the clustering outcomes.

3.1. Data Screening and Parameter Summary Statistics

Daily closing prices of SET100 stocks in 2020 were tested for lognormality using the AD test at the 5% level. Only stocks that passed were retained for parameter estimation and clustering, resulting in varying sample sizes across months. In addition, a few outliers were excluded: CRC and BAM in February, STA and PRM in March, STA in May, THANI in August, and DELTA in December. The final counts of retained stocks (the number of stocks that passed the lognormality test, denoted by N) are reported in

Table 1. Monthly descriptive statistics across all stocks for estimated parameters.

Month	Feature	Mean	Std. Dev.	Min	Max	Skewness	Kurtosis	N
January	$\widehat{\mu }$	−0.0781	0.1169	−0.3157	0.2337	−0.0193	−0.0128	55
	$\widehat{\sigma }$	0.1118	0.0372	0.0424	0.2275	0.5600	0.4916
	$\overline{\mu }$	−0.0040	0.0053	−0.0150	0.0056	−0.3325	−0.6091
	$\overline{\sigma }$	0.0250	0.0084	0.0094	0.0502	0.4777	0.1568
February	$\widehat{\mu }$	−0.0870	0.0867	−0.3223	0.0388	−1.0516	1.1981	38
	$\widehat{\sigma }$	0.1300	0.0358	0.0617	0.1997	−0.0977	−0.6185
	$\overline{\mu }$	−0.0049	0.0048	−0.0179	0.0021	−1.0199	1.0613
	$\overline{\sigma }$	0.0311	0.0086	0.0148	0.0477	−0.0964	−0.6420
March	$\widehat{\mu }$	−0.0796	0.1100	−0.3018	0.1313	−0.0537	0.5292	22
	$\widehat{\sigma }$	0.2854	0.0537	0.1833	0.3701	−0.3246	−0.3458
	$\overline{\mu }$	−0.0038	0.0053	−0.0144	0.0063	−0.0352	0.5008
	$\overline{\sigma }$	0.0631	0.0119	0.0405	0.0818	−0.3264	−0.3494
April	$\widehat{\mu }$	0.1882	0.1194	−0.0230	0.5336	0.3385	0.2981	49
	$\widehat{\sigma }$	0.1460	0.0413	0.0696	0.2284	0.0847	−0.9619
	$\overline{\mu }$	0.0094	0.0060	−0.0011	0.0267	0.3440	0.3186
	$\overline{\sigma }$	0.0331	0.0094	0.0158	0.0518	0.0849	−0.9602
May	$\widehat{\mu }$	0.0540	0.0693	−0.0949	0.2235	0.0638	0.0397	56
	$\widehat{\sigma }$	0.1007	0.0317	0.0458	0.1855	0.5062	0.0825
	$\overline{\mu }$	0.0032	0.0041	−0.0056	0.0131	0.0617	0.0400
	$\overline{\sigma }$	0.0248	0.0078	0.0113	0.0457	0.5082	0.0854
June	$\widehat{\mu }$	−0.0019	0.0869	−0.1428	0.3234	1.3057	2.2533	77
	$\widehat{\sigma }$	0.1147	0.0406	0.0419	0.2458	0.6734	0.8391
	$\overline{\mu }$	−0.0001	0.0043	−0.0071	0.0162	1.3102	2.2638
	$\overline{\sigma }$	0.0260	0.0092	0.0095	0.0557	0.6748	0.8417
July	$\widehat{\mu }$	−0.0192	0.0809	−0.1629	0.2407	0.8466	1.1012	70
	$\widehat{\sigma }$	0.0970	0.0369	0.0419	0.2666	1.6862	5.5707
	$\overline{\mu }$	−0.0005	0.0061	−0.0086	0.0353	3.2149	16.9343
	$\overline{\sigma }$	0.0230	0.0095	0.0097	0.0619	1.8333	5.1185
August	$\widehat{\mu }$	0.0079	0.0609	−0.1333	0.2241	0.7572	1.6808	73
	$\widehat{\sigma }$	0.1030	0.0506	0.0376	0.3916	2.9465	13.8249
	$\overline{\mu }$	0.0004	0.0032	−0.0070	0.0118	0.7644	1.7130
	$\overline{\sigma }$	0.0240	0.0118	0.0088	0.0910	2.9438	13.8004
September	$\widehat{\mu }$	−0.0535	0.0651	−0.1806	0.1076	0.2876	−0.3085	70
	$\widehat{\sigma }$	0.0895	0.0325	0.0380	0.1923	0.6713	0.5433
	$\overline{\mu }$	−0.0028	0.0034	−0.0095	0.0057	0.2830	−0.3094
	$\overline{\sigma }$	0.0208	0.0076	0.0088	0.0448	0.6735	0.5515
October	$\widehat{\mu }$	−0.0282	0.1056	−0.3071	0.2992	0.3022	1.5921	57
	$\widehat{\sigma }$	0.0933	0.0305	0.0231	0.1695	0.2402	−0.4345
	$\overline{\mu }$	−0.0015	0.0055	−0.0162	0.0158	0.3024	1.6904
	$\overline{\sigma }$	0.0222	0.0070	0.0054	0.0395	0.1223	−0.4024
November	$\widehat{\mu }$	0.1423	0.1312	−0.0551	0.4415	0.2312	−0.9068	52
	$\widehat{\sigma }$	0.1157	0.0412	0.0593	0.2601	1.2853	2.0257
	$\overline{\mu }$	0.0072	0.0065	−0.0027	0.0221	0.2086	−0.8640
	$\overline{\sigma }$	0.0263	0.0093	0.0134	0.0590	1.2951	2.1146
December	$\widehat{\mu }$	0.0033	0.0623	−0.1246	0.1498	0.3255	−0.0538	63
	$\widehat{\sigma }$	0.1133	0.0283	0.0595	0.1857	0.3543	0.1271
	$\overline{\mu }$	0.0002	0.0034	−0.0069	0.0083	0.3186	−0.0494
	$\overline{\sigma }$	0.0273	0.0066	0.0142	0.0444	0.3598	0.2017

.

Table 1 reports monthly summary statistics of the estimated parameters. For each month, both model-based parameters $(\widehat{\mu },\widehat{\sigma })$ from the Black–Scholes framework and empirical statistics $(\overline{\mu },\overline{\sigma })$ from log returns are summarized in terms of their mean, standard deviation, minimum, maximum, skewness, and kurtosis across all retained stocks.

Overall, the estimated drifts $\widehat{\mu }$ were mostly negative during the first quarter, consistent with the COVID-19 shock, and became positive in April and November, reflecting brief market recoveries. Volatility parameters $\widehat{\sigma }$ peaked in March, July, and December, indicating turbulent periods with heavy-tailed behavior, as confirmed by elevated skewness and kurtosis values in those months. The empirical moments $(\overline{\mu },\overline{\sigma })$ displayed similar but less pronounced patterns, suggesting that the model-based estimation captured stronger dispersion dynamics than the raw return measures. These descriptive patterns reveal alternating episodes of contraction and rebound throughout 2020, providing a contextual backdrop for the clustering analysis in the following section. These features collectively capture market heterogeneity over time and motivate the use of clustering techniques to identify distinct parameter-based stock groupings.

3.2. Clustering Performance

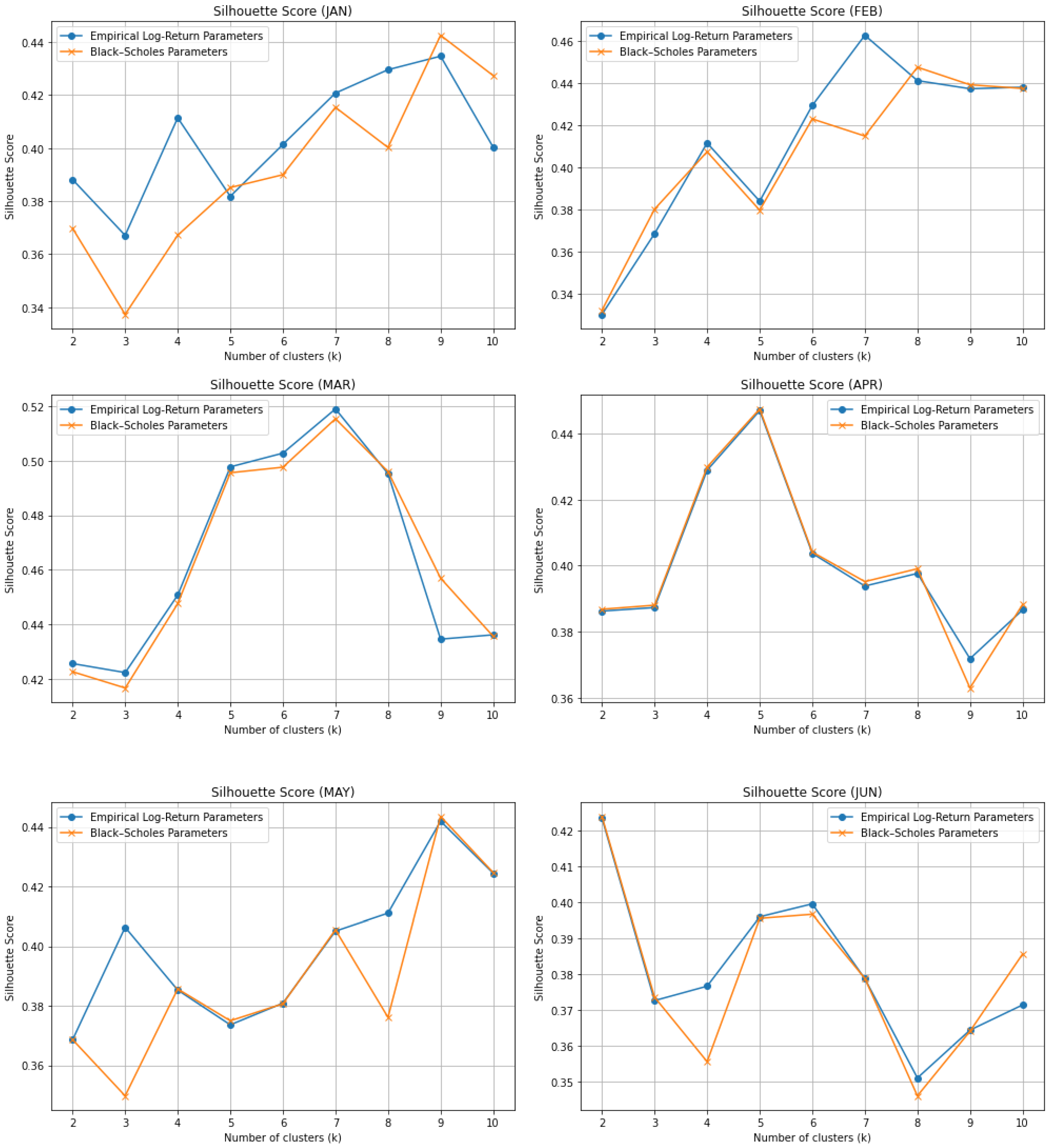
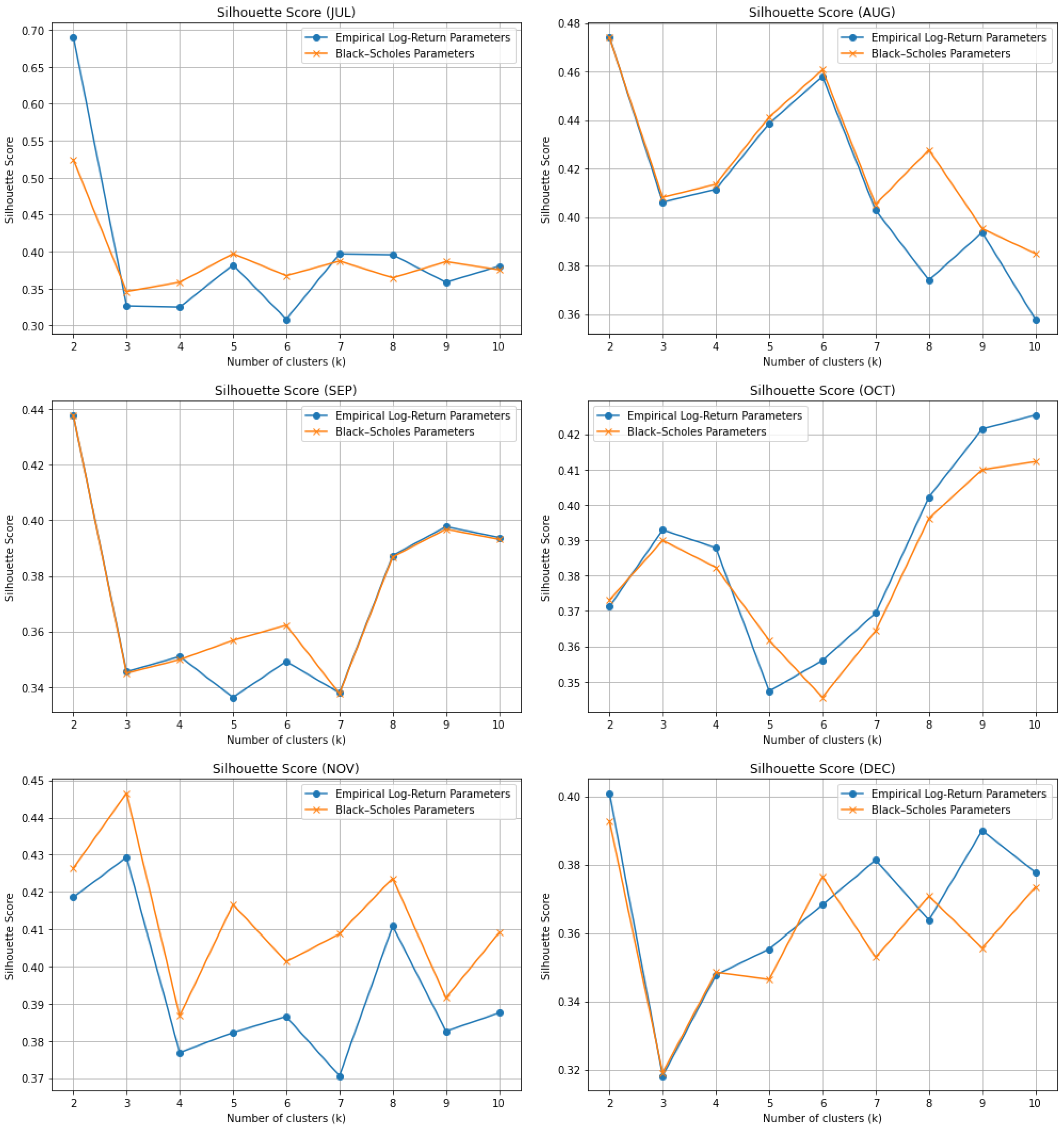
Figure 1 and Figure 2 display the silhouette scores of k-means clustering across different numbers of clusters ($k=2,\dots ,10$), separated into the first and second halves of the year, respectively. The results show that silhouette values varied considerably across months and cluster sizes. In some months, clustering based on the BS parameters produced higher scores, indicating more cohesive and well-separated groups. In other months, the results were similar, highlighting the inconsistency of the relative performances of the two approaches throughout the year.

To complement Figure 1 and Figure 2 and to enhance the visual interpretation of month-by-month variations, an additional Difference Heatmap (Figure 3) is presented. This figure directly displays the differences in silhouette scores (BS-LR) across all months and cluster numbers ($k=2,\dots ,10$), allowing a clearer high-level comparison between the two feature sets. The heatmap highlights the specific months and cluster sizes where BS-based clustering achieves stronger cohesion, while confirming that neither approach consistently dominates throughout the year.

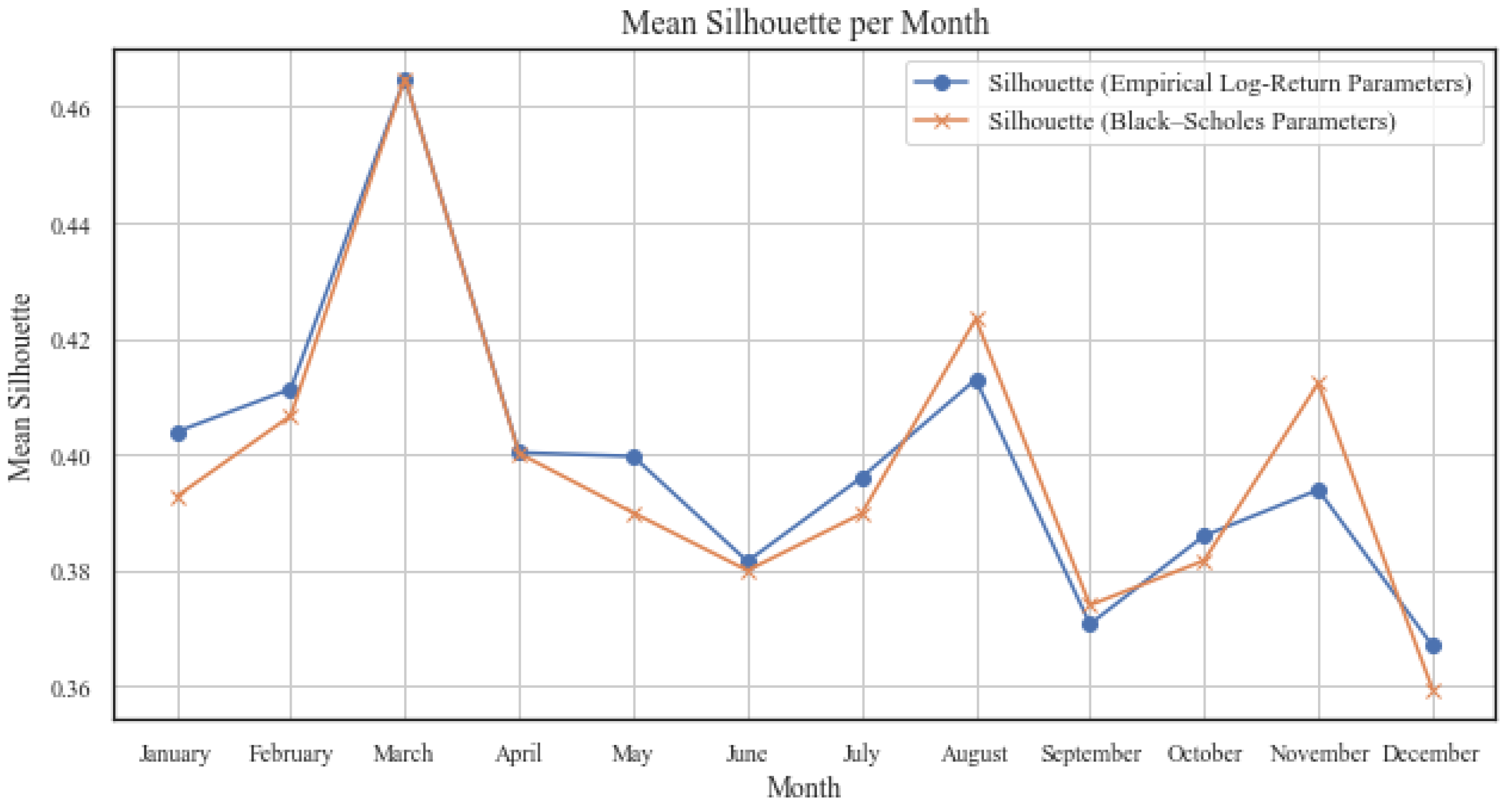
Figure 4 provides an overall summary by presenting the monthly average silhouette scores, which allow a clearer comparison between the two approaches. On average, the BS parameterization tended to yield slightly higher silhouette scores, although the advantage was not consistent across months.

It should be noted that the number of stocks included in each month was not identical, as only those passing the lognormality screening and not identified as outliers were retained (see Table 1). Since higher silhouette values reflect more compact and well-separated clusters, the results suggest that BS parameterization captured additional structure in stock behavior beyond that conveyed by simple LR statistics, although the advantage was not uniform across all months.

3.3. Clustering Agreement

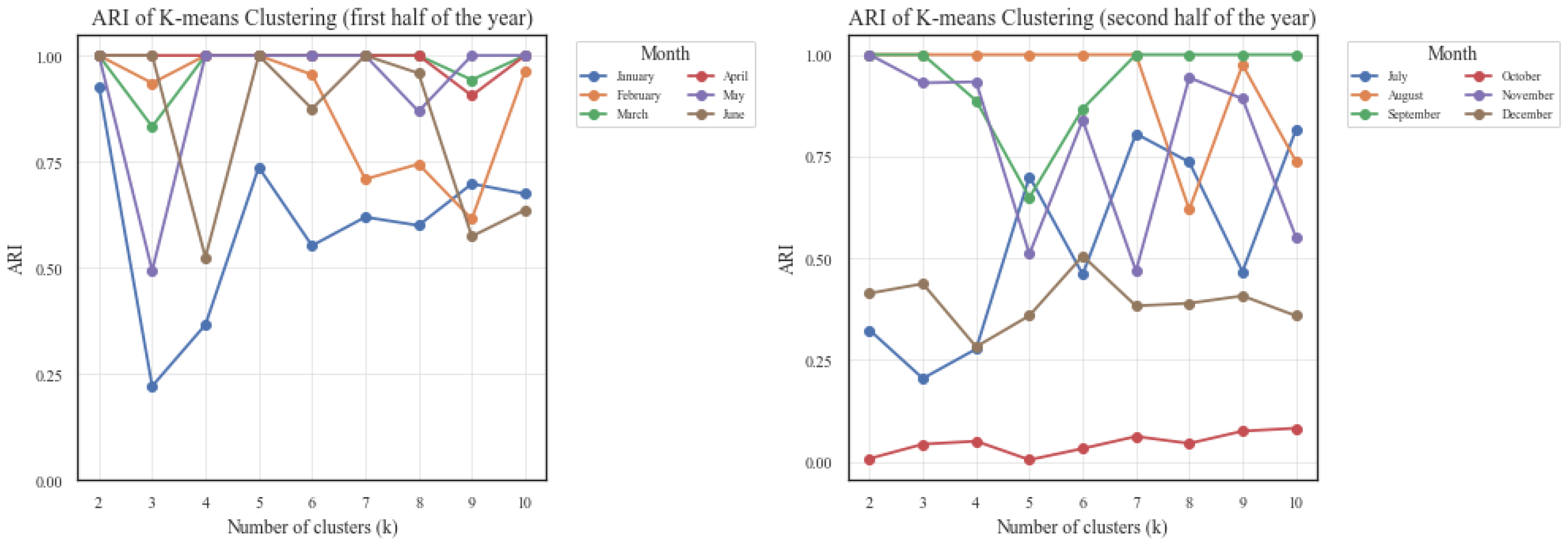
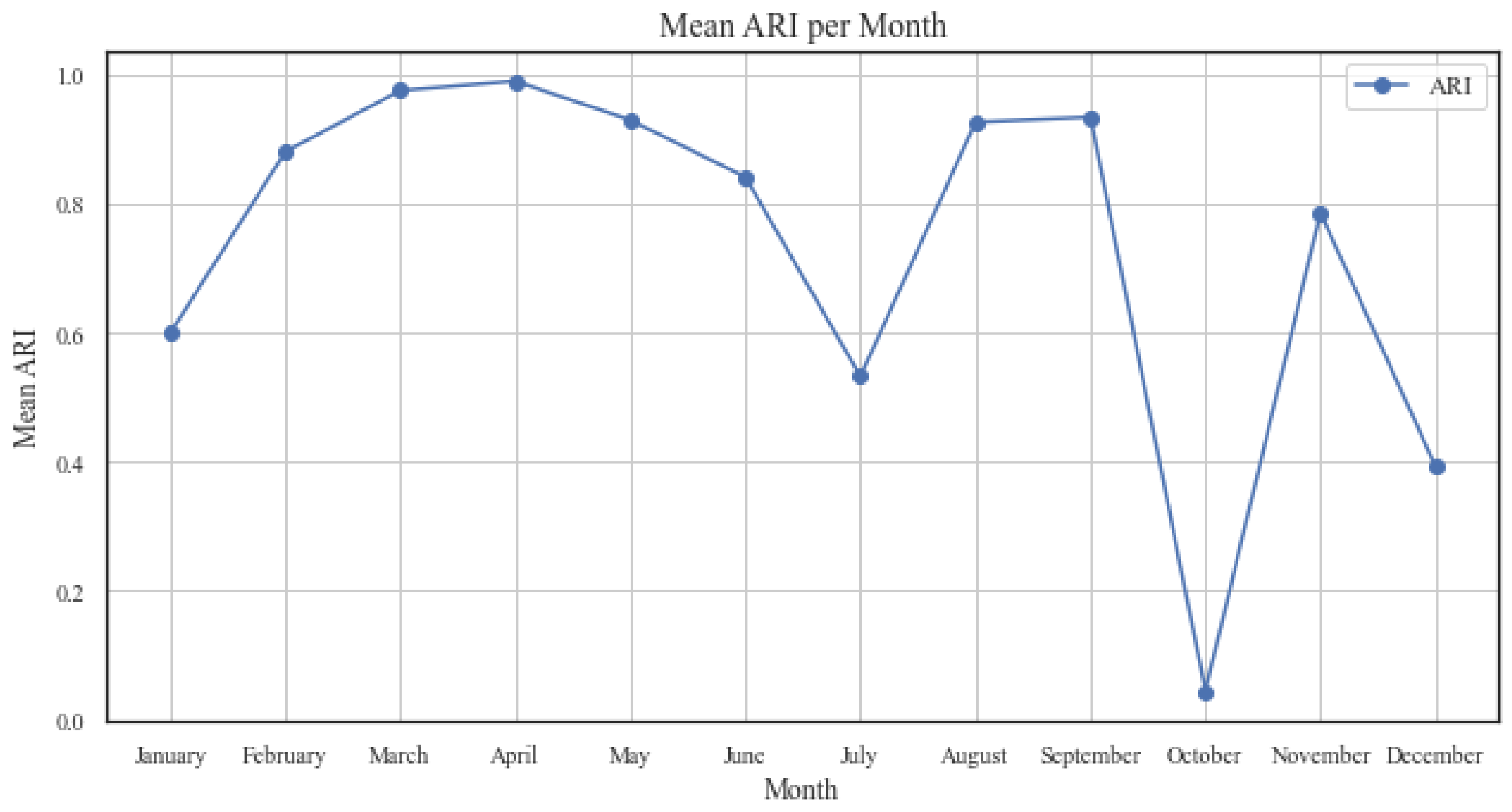
Figure 5 displays ARI values across cluster sizes ($K=2,\dots ,10$) for each month. The results indicate that the level of agreement was most often moderate to high. In several months, ARI values reached relatively high levels, showing that BS parameters and empirical LRs produced broadly consistent partitions. In other months, the ARI values were moderate, reflecting partial but meaningful consistency. Truly low values were observed only occasionally, indicating that the two approaches rarely produced completely divergent cluster structures.

Figure 6 presents the monthly average ARI values, providing a clearer overall comparison. Most months show average agreement in the moderate-to-high range, with a few months falling lower. Taken together, Figure 5 and Figure 6 indicate that the clustering results from BS parameters and empirical LRs were broadly consistent, although the degree of correspondence varied across months and cluster sizes. Although the moderate-to-high ARI values indicate broad agreement in overall cluster boundaries, the additional structure captured by the BS-based features, which yields higher silhouette scores, appears primarily as tighter within-cluster cohesion rather than fundamentally different stock groupings. This suggests that the diffusion parameters effectively filtered noise and enhanced the definition of existing clusters.

3.4. Statistical Comparison of Cluster Quality

Wilcoxon signed-rank tests were applied to the silhouette values across cluster sizes ($K=2,\dots ,10$) for each month. The results are shown in

Table 2. Wilcoxon signed-rank test p-values comparing silhouette scores.

Month	Two-Sided p-Value	One-Sided p-Value (BS > LR)
January	0.1641	–
February	0.7344	–
March	0.2031	–
April	0.1289	–
May	0.7344	–
June	0.6523	–
July	0.6523	–
August	0.0078	0.0039 *
September	0.6523	–
October	0.1641	–
November	0.0039	0.0020 *
December	0.3008	–

Notes: p-values marked with * are statistically significant after Bonferroni correction.

. The two-sided tests indicated no significant differences in most months ($p>0.05$), except for August ($p=0.0078$) and November ($p=0.0039$). For these two months, one-sided tests confirmed that clustering based on BS parameters achieved significantly higher silhouette scores (August $p=0.0039$, November $p=0.0020$). Furthermore, after applying the Bonferroni correction for multiple comparisons on the one-sided tests (${\alpha }_{\mathrm{adj}}\approx 0.0042$), the significant outperformance of BS features was confirmed in both August and November, confirming the robustness of the advantage. Overall, clustering quality was generally comparable between the two approaches, with the diffusion-based representation showing a clear advantage in these specific months.

3.5. Out-of-Sample Cumulative Return Analysis

To evaluate whether the clustering outcomes contained predictive information, we examined the subsequent cumulative returns of selected clusters. We began with August 2020, where BS-based clustering achieved a significantly higher silhouette score than LR-based clustering. In this month, the highest silhouette value occurred at $K=2$, but such a coarse partition provided limited insight, as nearly all stocks were grouped into only two broad clusters. The second-best value was obtained at $K=6$, which maintained a competitive silhouette score while offering a more granular structure that facilitated interpretation. In practice, however, both BS and LR produced identical cluster assignments at $K=6$, so the subsequent cumulative returns in September were indistinguishable. This underscores that higher silhouette values do not always translate into practical differences when the resulting partitions coincide.

In contrast, November 2020 revealed a stronger divergence. In this case, the highest silhouette values were found at $K=2$ and $K=3$, but such coarse partitions provided limited insight as they fail to capture meaningful sectoral structure for investment practice. The third-highest value was at $K=8$, which was selected as a representative case study that offered a reasonable balance between statistical cohesion and economic granularity. More importantly, at $K=8$, BS and LR produced visibly different memberships, providing a natural candidate for out-of-sample testing. Specifically, we focused on the two clusters in November 2020 ($K=8$) where BS and LR memberships diverged. Each cluster was represented by its five nearest-to-centroid stocks. 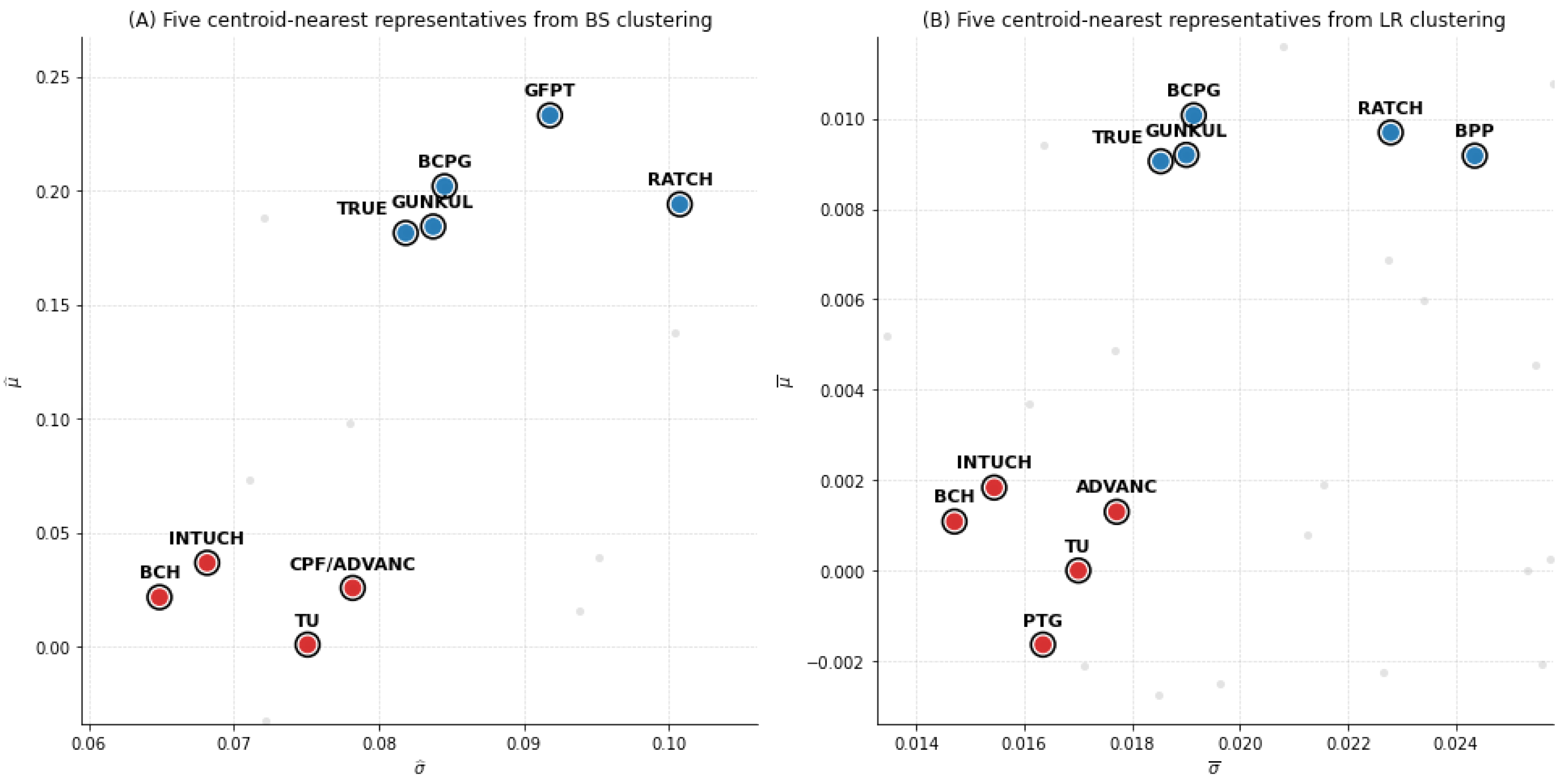Figure 7 compares clustering results based on BS (left) and LR (right) at $K=8$ for November 2020. Within the zoomed region, only the ten centroid-nearest representatives (five per cluster) are highlighted (red = Group A, blue = Group B), while all other stocks are plotted faintly. Under BS parameterization, CPF appears in Group A and GFPT in Group B, whereas under LR parameterization, PTG replaces CPF in Group A and BPP replaces GFPT in Group B.

We then evaluated whether these membership differences carried predictive value by computing cumulative returns in the subsequent month (December 2020). For each method, we tracked the five representative stocks (those closest to the cluster centroid) identified in Figure 7 and calculated their portfolio-level growth. Cumulative returns were computed from simple daily returns according to

$$R=\prod _{t=1}^N(1+r_t)-1,$$

where $r_t$ denotes the daily return and N the number of trading days in December. To complement this analysis, we also evaluated the risk-adjusted performance of the representative portfolios by computing their Sharpe ratios. The Sharpe ratio was defined as the mean daily portfolio return divided by its standard deviation, assuming a zero risk-free rate, thereby quantifying the average excess return earned per unit of risk.

Table 3. Average cumulative returns and Sharpe ratios in December 2020 for two selected clusters from November.

Method/Cluster	Representative Stocks	R (%)	Sharpe Ratio
BS—Cluster A	CPF, ADVANC, TU, INTUCH, BCH	−3.44	−0.12
LR—Cluster A	ADVANC, TU, INTUCH, BCH, PTG	−4.38	−0.16
BS—Cluster B	GUNKUL, BCPG, TRUE, RATCH, GFPT	−1.01	−0.01
LR—Cluster B	GUNKUL, BCPG, TRUE, RATCH, BPP	−2.33	−0.04

thus reports both the cumulative returns and the corresponding Sharpe ratios for each cluster and method.

Portfolios were constructed as equal-weighted baskets of the five centroid-nearest representatives, rebalanced at the beginning of the subsequent month and held for the full duration of the month. Transaction costs, taxes, and dividends were ignored to focus on the comparative effect of clustering assignments. All selected stocks are highly liquid constituents of the SET100 index; therefore, any transaction cost differences are negligible and would not materially alter the relative performance between BS- and LR-based portfolios.

The contrast is clear. In the first case, BS included CPF (a defensive food stock) instead of PTG (an energy stock with higher volatility), cutting the average loss from $-4.38\%$ to $-3.44\%$. In the second, BS selected GFPT (a food sector stock) rather than BPP (a power producer), reducing the loss from $-2.33\%$ to $-1.01\%$. Beyond raw returns, the Sharpe ratios also improved from $-0.16$ to $-0.12$ in Cluster A and from $-0.04$ to $-0.01$ in Cluster B, confirming that BS-based clusters achieved superior risk-adjusted performance. These results indicate that the diffusion-based parameterization yields not only structurally coherent clusters but also portfolios that remain more resilient to market turbulence.

Thus, while August with $K=6$ showed no predictive differences because BS and LR partitions were identical, November with $K=8$ clearly showed that diffusion-based features can form clusters with more resilient out-of-sample performances, strengthening the practical value of the BS parameterization.

4. Discussion

4.1. Summary of Findings

The analysis yielded five main results. First, stock returns in 2020 varied substantially, with volatility spikes and heavy tails in February, March, July, and December. Second, clustering with BS parameters generally produced higher silhouette scores than LRs, though not in every month. Third, ARI values showed moderate to high agreement, indicating broadly similar partitions from both feature sets. Fourth, Wilcoxon tests identified significant BS gains only in August and November. Finally, the out-of-sample test confirmed that the November BS partition achieved clearer sector separation and smaller portfolio losses, while predictive differences were limited in other months.

4.2. Interpretation of Results

To further interpret the clustering results, we conducted a supplementary analysis of cross-sector divergence. For each month, we computed market volatility as the cross-sectional mean of all stock volatilities, and compared this with the average volatility within each sector. The absolute difference between these two values was taken as a measure of how much each sector diverged from the overall market. This provided a simple way to capture heterogeneity in sectoral behavior.

The analysis revealed that August and November stood out, as the BS parameterization consistently produced larger sector-to-market divergences across almost all sectors than the empirical LR parameterization. In other words, BS features highlighted sectoral differences more strongly—an outcome that was consistent with the significantly higher silhouette scores observed in these months. Both months also coincided with major COVID-19 developments—the domestic second wave in August and the announcement of effective vaccines in November—which triggered heterogeneous sector responses. These conditions likely contributed to the superior clustering performance of the BS features during these months. These findings suggest that the advantages of the BS parameterization emerge particularly under market conditions characterized by heightened sectoral divergence.

Specifically, the BS diffusion volatility was estimated via maximum likelihood under the assumption of a continuous diffusion process. This estimation acted as a statistical filter that smoothed transitory noise and outliers in daily returns, providing a more stable and structural representation of the underlying volatility dynamics. Such stability allowed the clustering algorithm to capture persistent cross-sectional differences among stocks rather than reacting to short-lived fluctuations, which explained the superior cohesion and sectoral interpretability observed in BS-based clusters.

Although the empirical LR statistics also represent a form of risk–return trade-off, they are inherently backward-looking, capturing realized outcomes within each month. In contrast, the BS-based parameters are estimated under a continuous diffusion framework that provides a theoretically consistent and forward-looking representation of price dynamics. Rather than summarizing past data, these parameters reflect the market’s expected risk–return structure and filter out transitory noise, allowing the clustering to capture persistent differences in underlying diffusion regimes.

4.3. Statistical and Econometric Perspectives on Robustness

From a statistical standpoint, conducting multiple hypothesis tests across twelve monthly directional evaluations increased the likelihood of Type I errors. To control the FWER appropriately, a Bonferroni correction was applied to the one-sided Wilcoxon signed-rank results, setting the adjusted significance level at ${\alpha }_{\mathrm{adj}}=0.0042$. After this adjustment, the significant outperformance of BS features was confirmed in both August and November. This result refines the inference while fully confirming the robustness of the study’s original finding of two significant months.

From an econometric perspective, however, these monthly tests are not fully independent because the same stock universe contributes to multiple cross-sections. Hence, the Bonferroni adjustment represents a conservative upper bound on the true FWER. Even under this stringent criterion, the persistence of the confirmed significance in both months strongly supports the economic interpretation that BS-based clustering remains more resilient and structurally informative in high-volatility market regimes.

Although the original analysis utilized the unadjusted 5% level for primary inference, this correction serves as a necessary robustness confirmation that validates the study’s empirical conclusions against a rigorous statistical standard.

4.4. Predictive Value of Clustering

The out-of-sample evidence provided an important complement to the statistical evaluation of clustering quality. In August ($K=6$), BS and LR produced identical partitions, indicating that a higher silhouette score alone does not guarantee predictive relevance when group memberships coincide. By contrast, in November ($K=8$), BS and LR generated distinct partitions, and the BS-based clusters aligned with more resilient performance in the subsequent month. This contrast suggests that diffusion-based features are particularly valuable under conditions of sectoral divergence and market stress, where volatility structures play a critical role in separating stock behaviors. More broadly, the findings underscore that internal validity metrics such as silhouette scores, while useful, are not sufficient on their own; economic interpretation and out-of-sample confirmation are essential to establish practical value. These insights set the stage for a discussion of how clustering outcomes can inform market analysis and portfolio strategies, which follows in the next section.

4.5. Practical Implications for Market Analysis

Building on the evidence that BS-based clustering can reveal predictive value during periods of sectoral divergence, several practical implications emerge for market practitioners. First, the use of diffusion-based parameters provides an alternative feature space for clustering stocks, which can uncover sectoral structures that may not be visible when relying solely on LRs. This is particularly valuable during periods of market stress or structural change, when volatility heterogeneity across sectors becomes more pronounced.

Second, identifying months in which BS parameterization yields clearer clusters can help analysts recognize when volatility-driven factors dominate market behavior. Such insights may support sector rotation strategies, risk management practices, and the design of diversified portfolios that adapt to changing market regimes. To make this insight operational, we propose a Market-Regime Decision Framework to guide when the BS-based or LR-based clustering should be applied. The framework uses the outcome of the Wilcoxon signed-rank test as a market-state indicator:

• Market-Stress Regime (BS Superior): When the Wilcoxon test comparing BS- and LR-based silhouette scores is statistically significant (e.g., $p<{\alpha }_{adj}$), it signals that the market’s volatility structure is undergoing sectoral divergence. In this regime, the BS-based clustering should be adopted, as it better captures the underlying structural heterogeneity.
• Normal-Market Regime (Comparable): When the test is not significant ($p\ge {\alpha }_{adj}$), the market is deemed stable or less divergent. In this case, the simpler LR-based clustering may be preferred to maximize operational stability and computational efficiency, as the LR results are less prone to implementation error and avoid unnecessary reliance on simulation-based parameter estimation when its incremental value is minimal.

This rule-based procedure provides a data-driven guideline for practitioners to determine when diffusion-based clustering should be prioritized, offering an executable bridge between empirical results and real-world decision-making.

From a practical standpoint, Algorithm 1 requires 50,000 Monte Carlo simulations per stock per month, which entails a higher computational burden than directly computing historical means and standard deviations. Nevertheless, this additional cost was moderate and justified by the methodological benefits. The simulation-based estimation produced stochastically robust parameters that more effectively captured the underlying return distribution, yielding clearer and more stable clusters during volatile market periods. Ultimately, the incremental computational effort represents a necessary and reasonable trade-off between efficiency and methodological robustness.

Finally, the methodological framework developed here—combining model-based parameter estimation, clustering evaluation, and statistical comparison—can be extended beyond equity markets. For example, diffusion-based features could decipher the clustering of derivative instruments or credit products, offering a richer perspective for both academic research and applied financial analysis.

4.6. Comparison with Previous Studies

Previous research has commonly compared clustering methods based on empirical returns or alternative statistical transformations, but few studies have explicitly contrasted diffusion-based parameterizations with raw LRs. Most applications of the BS framework have focused on derivatives pricing and risk management rather than unsupervised learning of equity structures. In this sense, our work contributes a novel perspective by showing that parameters estimated from a diffusion model can also serve as effective clustering features. While earlier studies generally reported limited differences between returns-based representations, our findings highlight that BS features may offer advantages under specific market conditions characterized by sectoral divergence. This approach complements rather than contradicts the existing literature, suggesting that diffusion-based features provide additional explanatory power in settings where volatility heterogeneity is central. These insights not only extend the clustering literature but also reinforce the practical implications discussed above, where volatility-sensitive features can play a decisive role in portfolio analysis.

4.7. Broader Applications: Derivatives Pricing

Beyond clustering analysis, the estimation of BS parameters has direct relevance for derivatives pricing. The drift and diffusion terms obtained from our procedure are precisely those required in the valuation of European-style options under the BS framework. This alignment suggests that the parameter estimation approach developed here can serve a dual purpose: not only as an input for unsupervised learning, but also as a foundation for pricing and hedging derivative securities.

Moreover, the ability of the BS features to capture sectoral heterogeneity suggests that option-implied valuations based on these parameters may more accurately reflect differences in risk between sectors. This can be valuable for practitioners who need to price derivatives or manage positions under conditions of market stress, where volatility dynamics play a central role. Crucially, the clustering outcomes themselves carry practical implications for derivative pricing and portfolio risk control. By grouping stocks into diffusion-based clusters that share similar drift–volatility dynamics, market participants can identify coherent volatility regimes that may guide the calibration of implied volatility surfaces or correlation structures in multi-asset options. Tracking transitions in cluster composition over time can also serve as an early signal of regime shifts in volatility, enabling more responsive adjustments to hedging ratios or option portfolio exposures. Taken together, the clustering results provide a bridge between statistical segmentation and actionable decisions in derivative pricing and risk management.

In this way, the methodological framework proposed in this study contributes both to market structure analysis and to traditional applications of stochastic diffusion models in finance. While the immediate application is option valuation, the same diffusion parameters can also underpin other derivatives such as volatility swaps or moment swaps, where accurate volatility modeling is critical.

4.8. Study Limitations and Future Work

This study has several limitations that should be acknowledged. First, the analysis was restricted to the SET100 constituents within a single year (2020), which may reflect COVID-specific market behavior and limit generalizability. Future research could extend the framework to longer time horizons or to different markets in order to assess robustness across economic regimes. Second, the BS parameters were estimated using the classical BS diffusion as a simplified baseline for parameter estimation. While this model ensured analytical tractability, it did not fully capture stylized facts of financial time series such as volatility clustering, heavy tails, or price jumps. Future extensions could therefore incorporate richer stochastic processes such as stochastic volatility, jump-diffusion, or mean-reverting models to provide more realistic feature representations for clustering. In particular, parameters such as the volatility-of-volatility in stochastic-volatility models or the jump-intensity in jump-diffusion settings could be evaluated to determine whether the observed improvements arose from model specification itself or from the broader use of structural diffusion parameters as clustering features. Third, months with severely reduced samples (e.g., March 2020) should be interpreted with caution due to limited statistical power, as smaller cross-sectional sets inherently reduce the reliability of cluster-level statistical comparisons. Future research may relax the lognormality screening threshold (e.g., $\alpha =0.10$) to examine the robustness of the proposed clustering framework under less restrictive distributional assumptions. Fourth, the clustering analysis was based solely on k-means and a limited set of evaluation metrics. While this choice provided interpretability and comparability, alternative clustering methods, such as hierarchical or density-based approaches, and complementary validity indices could yield additional insights. Finally, although we discussed potential applications for market analysis and derivatives pricing, this study did not directly evaluate the out-of-sample predictive utility of the clusters. Future work could therefore investigate how diffusion-based features influence portfolio performance, risk forecasting, or option market dynamics in practice.

5. Conclusions

This study investigated whether parameters estimated from the Black–Scholes diffusion model can serve as informative features for stock clustering, using SET100 constituents in 2020 as a case study. Compared with empirical log-returns, Black–Scholes parameters often produced higher silhouette scores, although the advantage was mainly concentrated in periods of market stress such as August and November 2020. Clustering agreement, as measured by the Adjusted Rand Index, was moderate to high, suggesting that the two approaches captured broadly similar structures in most months. Statistical testing confirmed significant gains for Black–Scholes features only in selected months, yet the out-of-sample analysis demonstrated that the November 2020 Black–Scholes partition achieved clearer sector separation and smaller portfolio losses than its log-returns counterpart.

The novelty of this work lies in extending stock clustering beyond traditional returns-based features to diffusion-based parameters that capture the underlying price-generating process. This model-based perspective revealed sectoral divergences that are often obscured in empirical returns, particularly during turbulent market regimes. The inclusion of risk-adjusted portfolio evaluation through Sharpe ratios and a simple Market-Regime Decision Framework further strengthens its practical relevance. Beyond its methodological contribution, the study carries broader implications for financial practice—diffusion-based features can provide early warning signals of market stress, inform sector rotation strategies, and strengthen risk management frameworks. More generally, the findings demonstrate how incorporating model-based representations of stock prices can enrich our understanding of market structure and sectoral behavior across different economic conditions.