Ranking Investment Opportunities Across Risk-Aversion Levels: Application to Islamic and Conventional Indices

Abstract

We introduce the Reward–VaR curve, a novel framework for evaluating risk-adjusted investment performance across a range of investor risk preferences. When returns are normally distributed, the Reward–VaR curve yields the same asset ranking as the Sharpe ratio. However, when the third-order modified VaR is used, a new paradigm emerges beyond the simplistic “better/worse” ranking: if no asset dominates at all confidence levels, one becomes preferable for risk-averse investors, while the other is favored by the risk-tolerant. For empirical implementation, we incorporate bootstrapping to separate robust performance patterns from sampling noise. We apply the methodology to compare conventional equity indices and their Islamic counterparts from the S&P Dow Jones Global Index family across nine markets from 2000 to 2024: Asia-Pacific, Canada, Developed, Emerging, Europe, Japan, UK, US, and World. Our empirical results reveal market-condition dependent dominance patterns. During bull markets, conventional indices dominate in most regions, except the European and World markets, where no dominance is observed, and Japan, where the Islamic index outperforms. In bear markets, Islamic indices dominate in most regions, with the exception of Emerging Markets, where dominance is partial, and Japan, where no clear difference is observed. Over the full sample, most markets show no significant long-run dominance, except Canada and Emerging Markets, where conventional indices outperform.

1. Introduction

Individuals choose investments based on their unique risk preferences, shaped by a combination of investment goals, market conditions, diversification needs, regulatory and tax considerations, ethical values and personal preferences. However, the risk profile is significant enough that, in most modern countries, regulations mandate that investment firms assess the risk profile of their clients. These regulations aim to protect investors from unsuitable investments. Their goal is to ensure that portfolios are managed in accordance with individual risk preferences. This underlines the importance of selecting a risk level when assessing the relative performance of investment opportunities.

Despite the central role of risk preferences in investment decision-making, the metrics commonly used to assess investment performance rarely account for such heterogeneity. Traditional risk-adjusted performance measures typically rely on crude, uniform proxies for risk. Even when more refined metrics such as Value-at-Risk (VaR) are employed, assessments are usually confined to a fixed confidence level (e.g., 95% VaR). Alexander and Baptista (2003) observed that VaR-based rankings may vary with the confidence level. Yet, we are not aware of any performance evaluation approach that establishes a consistent and coherent behavior as the confidence level varies across a range of values, let alone the full range of confidence levels where VaR is positive.

To address these issues, we introduce a new risk–reward metric—the Reward–VaR curve—as an enhancement over traditional measures. Its performance ranking aligns with the Sharpe ratio under normal return distributions, but when a third-order variant of VaR (called mVaR) is used, skewness starts to affect asset rankings. This leads to a ranking of assets that depends on risk preferences. When one asset does not dominate the other at all confidence levels, a phase transition emerges: one asset is preferred by low–risk-aversion investors, and the other by highly risk-averse ones. We also address the problem of ranking sensitivity to noise in empirical studies—an issue particularly salient with VaR at high levels of confidence—by using bootstrapping. This results in an expanded set of dominance patterns for comparing the risk-adjusted performance of two assets. One asset may dominate, or the two may be statistically equivalent. Alternatively, one asset dominates for risk-averse investors, the other for risk-tolerant ones, while both perform equivalently for investors in between. The key advantage of our metric is that it can detect situations where investment A is preferred to B by risk-averse investors and B is preferred to A by risk-tolerant investors. To the best of our knowledge, this possibility has never been considered by traditional performance measures.

The second goal of this paper is to investigate the relative performance of Islamic and conventional equity indices using the Reward–VaR curve framework. Islamic finance represents a rapidly growing segment of global financial markets, with total assets projected to exceed $6.7 trillion by 2027 (ICD-LSEG, 2023). This growth is driven in part by the sustained economic development of countries with large Muslim populations. Many of these economies are projected to rank among the world’s largest by mid-century (PwC, 2017). A natural question is whether Islamic screening affects the performance of Islamic indices relative to their conventional benchmarks.

Empirical studies report widely varying results. Some studies find Islamic indices outperform, others find the reverse, and many report no difference. In short, the literature lacks consensus and exhibits a scattered pattern of findings. One possible explanation is that one index is preferable for risk-averse investors, while the other is better suited for risk-tolerant investors. The advantage of our approach is that it can identify if the preference between indices remains constant across all risk profiles, or if it changes as investor attitudes shift from risk-tolerant to risk-averse. However, our empirical results point to a nuanced variant of that risk-profile-sensitive idea. Conventional indices dominate during bull markets, Islamic indices offer stronger downside protection in bear markets, and both indices perform equally well over the long run. While this pattern is not universal, it recurs with notable consistency across a diverse set of regional markets and is supported by significant statistical evidence.

2. Risk-Adjusted Performance Metrics and Dominance Pattern

An important aspect of any investment is the risk–reward structure. On average, a risky investment should reward investors with a greater return than a conservative investment. Moreover, an investment vehicle should be rejected if other investment instruments can provide similar or better returns with lower risks. This is significant in evaluating the relative performance of investment opportunities, as individuals seeking different risk exposure will select different investments.

One of the main metrics of risk-adjusted performance is the Sharpe ratio (Sharpe, 1994), developed by Nobel laureate William F. Sharpe. Others include Jensen’s alpha (Jensen, 1968), Treynor ratio (Treynor, 1965), and more recent alternatives like the Sortino ratio (Sortino & Price, 1994), Calmar ratio (Young, 1991), Modigliani $M^2$ Performance Measure (Modigliani & Modigliani, 1997), and stochastic dominance analysis stochastic dominance analysis (see Levy (2006)). These performance measures have proven useful in both academic research and practical portfolio evaluation. However, they tend to rely on simplified representations of risk that are insensitive to investor risk preferences. Most treat risk as a uniform penalty and do not accommodate variations in investor risk preferences or sensitivity to tail risk when ranking asset performance.

A more nuanced measure of risk is the Value-at-Risk (VaR), which captures the potential for extreme losses at a given confidence level. For continuous distributions, VaR at level $\alpha$ corresponds to the minimum loss that occurs in the worst $(1-\alpha )$ portion of the distribution. Widely used in both practice and regulation, VaR is particularly prevalent in financial institutions and investment management, where it serves as a critical tool for assessing and managing market risk. VaR and other risk measures gained significant traction and prominence during and after the 2008–2009 financial crisis, as institutions and regulators sought tools to better understand and control risk. The crisis also highlighted the importance of developing complementary methods that offer greater sensitivity to risk preferences and tail behavior, prompting refinements in both practice and theory.

Given the importance of risk considerations when making investments, it is unsurprising that risk-adjusted performance metrics were introduced that factor in VaR and other risk measures such as Conditional Value at Risk (CVaR), Tail Value-at-Risk (TVaR) or modified Value at Risk (mVaR). These risk-adjusted performance metrics, sometimes referred to as generalized Sharpe ratios, are typically expressed as a ratio of excess gain to risk. This ratio is formulated as

$${\displaystyle \frac{{\overline{R}}_S-r_f}{\mathrm{measure}\mathrm{of}\mathrm{risk}\mathrm{at}\mathrm{a}\mathrm{level}\alpha }},$$

where ${\overline{R}}_S$ represents the expected return of the asset S considered, $r_f$ denotes the risk-free rate, and $0\le \alpha \le 1$ is the confidence level. The risk measure can be the VaR (see, for instance, Dowd (2000)), the CVaR (see, for example, Martin et al. (2003) or Stoyanov et al. (2007)), or the mVaR, which is the Cornish–Fisher modified VaR (see, for instance, Favre and Galeano (2002) or Amédée-Manesme and Barthélémy (2022)). It is certainly conceivable to replace the VaR, CVaR, TVaR, or mVaR with any other risk measure. The economic implications of using such risk-adjusted performance metrics are analyzed in Alexander and Baptista (2002).

An interesting modification of the above generalized Sharpe ratios, known as the Reward-to-VaR ratio, is suggested by Alexander and Baptista (2003). It is defined as

$$Rt{V}_S\left(\alpha \right)={\displaystyle \frac{{\overline{R}}_S-r_f}{Va{R}_S\left(\alpha \right)+r_f}}.$$

(1)

It is important that the denominator be $Va{R}_S\left(\alpha \right)+r_f$ rather than $Va{R}_S\left(\alpha \right)$, because this formulation ensures that

$${\displaystyle \frac{\partial {\overline{R}}_{\Lambda }}{\partial Va{R}_{\Lambda }\left(\alpha \right)}}=Rt{V}_S\left(\alpha \right),$$

where $\Lambda$ denotes a portfolio combining the risk-free asset and the risky asset S. In this way, the Reward-to-VaR ratio quantifies the additional expected return that investors can earn by accepting an extra percentage point of VaR, achieved through reallocating wealth from the risk-free asset to the risky portfolio. The Reward-to-VaR ratio possesses several interesting properties. First, under the typical condition that the excess return over the risk-free rate is normally distributed, the ranking given by the Sharpe ratio and the Reward-to-VaR ratio coincide. However, when this normality assumption is dropped, the portfolio performance ranking may differ from that obtained through the Sharpe ratio. Importantly, portfolio performance rankings under the Reward-to-VaR ratio may vary across different VaR risk levels.

When risk-adjusted performance ranking uses risk measures such as VaR, CVaR, mVaR, or others, it is standard practice to evaluate these measures at high confidence levels—typically 99%, 95%, or 90%. See, for instance, Grau-Carles et al. (2019), Uryasev et al. (2010), or Alexander and Baptista (2002). This reflects the standard confidence levels employed by financial institutions in their risk management processes. However, large losses are rarely the sole focus of typical stock traders, even those working for large institutional investors. A less risk-averse investor might prefer to be generously rewarded for typical losses, rather than for large ones. Indeed, over a given horizon, investors typically face many small losses without being subjected to exceptionally large ones. In such a typical scenario, being adequately rewarded for those losses can make the difference between a successful investment and a mediocre one.

Ranking investment opportunities is typically aimed at identifying the most performant asset from a given set. However, it is broadly recognized that investors’ risk profile plays an important role in determining which investments are most suitable for them. An investment may be preferable for a risk-averse individual with a short time horizon, while another may be more suitable for a risk-tolerant investor with a long time horizon.

Our study takes a broader and more nuanced perspective than the simplistic “better/worse” rankings of two investment options. First, we allow for statistical equivalence, where neither asset is clearly superior. Moreover, we allow for a phase transition to occur: the risk-averse investor prefers one asset, the moderate investor sees them as equivalent, and the speculative investor prefers the other. Taken together, these give rise to the concept of dominance patterns which capture the different ways in which the risk–reward relationship between two assets can manifest. In our framework, the expected return is expressed as a function of the VaR. Risk-averse investors seek to be adequately rewarded for potential large losses corresponding to VaR at high confidence levels, while risk-tolerant investors prefer to be rewarded for typical losses corresponding to VaR at lower confidence levels.

Dominance patterns are obtained through the new risk-adjusted performance metric introduced in this article, the Reward–VaR curve. It possesses several noteworthy properties. First, it extends the classical Sharpe ratio: when all assets are normally distributed, the ranking based on Reward–VaR curves coincides exactly with that produced by the Sharpe ratio. Second, when the VaR is replaced by the modified VaR (mVaR) of order three, an interesting structural property emerges when comparing two assets: one dominates, their performance is equivalent, or a phase transition occurs. No incoherent dominance pattern is possible. Third, the incorporation of bootstrapping enables the Reward–VaR curve to distinguish statistically meaningful performance from noise, allowing for assets to be classified as statistically equivalent.

Finally, because the ranking is based on expected returns, the Reward–VaR curve not only identifies which asset dominates but also quantifies the margin of outperformance. This enables a more informed judgment in cases where one asset is found to dominate the other in a statistically significant manner, but the excess return remains marginal. Investors may still prefer the less performant asset when other considerations—such as market views, tax efficiency, or diversification objectives—are sufficiently important to outweigh a modest performance difference.

2.1. Reward-VaR Curves

Throughout this section, we assume that a fixed horizon h is specified. Following Alexander and Baptista (2003), we suppose that a portfolio $\Lambda$, depending on a parameter $0\le \lambda \le 1$, is constructed where $100\lambda \%$ of the value of the portfolio is invested in S, and $100\left(1-\lambda \right)\%$ is invested in the risk-free asset B. If $R_{\Lambda }$ is the return of the portfolio $\Lambda$ over the horizon h, then

$$R_{\Lambda }=r_f+\lambda \left(R_S-r_f\right),$$

where $R_S$ is the return of asset S, and $r_f$ is the return on B. Denoting by ${\overline{R}}_{\Lambda }$ and ${\overline{R}}_S$ the expected returns of $\Lambda$ and S, respectively, we obtain

$${\overline{R}}_{\Lambda }=r_f+\lambda \left({\overline{R}}_S-r_f\right).$$

Let $Q_{\Lambda }\left(\alpha \right)$ and $Q_S\left(\alpha \right)$ be the usual quantile functions of $\Lambda$ and S at a confidence level $\alpha$, and let $Va{R}_S\left(\alpha \right)$ denote the value at risk of S at a level of confidence $0\le \alpha \le 1$. By definition,

$$Va{R}_S\left(\alpha \right)=-Q_S\left(1-\alpha \right).$$

If $\lambda >0$, then

$$\begin{array}{cc}\hfill 1-\alpha & =P\left(R_{\Lambda }\le Q_{\Lambda }\left(1-\alpha \right)\right)\hfill \\ \hfill & =P\left[r_f+\lambda \left(R_S-r_f\right)\le r_f+\lambda \left(Q_S\left(1-\alpha \right)-r_f\right)\right].\hfill \end{array}$$

Let $v\ge 0$ denote the value at risk of portofilio $\Lambda$. Then,

$$-v=r_f+\lambda \left(Q_S\left(1-\alpha \right)-r_f\right).$$

Solving this equation for $\lambda$, we find that its solution ${\lambda }_S\left(v,\alpha \right)$ satisfies the formula

$${\lambda }_S\left(v,\alpha \right)={\displaystyle \frac{r_f+v}{r_f-Q_S\left(1-\alpha \right)}}={\displaystyle \frac{r_f+v}{r_f+Va{R}_S\left(\alpha \right)}}.$$

(2)

Thus, given any Value at Risk $v>0$ and a confidence level $\alpha$, if we choose $\lambda ={\lambda }_S\left(v,\alpha \right)$ to form the portfolio $\Lambda$, then

$$1-\alpha =P\left[R_{\Lambda }\le -v\right].$$

That is, by choosing the appropriate value of $\lambda$ according to (2), the Value at Risk of portfolio $\Lambda$ at the confidence level $\alpha$ is precisely equal to v. Note that while v can be any value, provided that ${\lambda }_S\left(v,\alpha \right)>0$, it is natural to focus on $v\ge 0$.

Clearly, the return, $R_{\Lambda }\left(v,\alpha \right)$, of portfolio $\Lambda$ is

$$R_{\Lambda }\left(v,\alpha \right)=r_f+\lambda \left(v,\alpha \right)\left(R_S-r_f\right).$$

The expectation of $R_{\Lambda }\left(v,\alpha \right)$, denoted by ${\overline{R}}_{\Lambda }\left(v,\alpha \right)$, therefore satisfies

$${\overline{R}}_{\Lambda }\left(v,\alpha \right)=r_f+\lambda \left(v,\alpha \right)\left({\overline{R}}_S-r_f\right)=r_f+{\displaystyle \frac{\left(r_f+v\right)\left({\overline{R}}_S-r_f\right)}{r_f+Va{R}_S\left(\alpha \right)}}.$$

(3)

In other words, once a fraction, $1-\lambda \left(v,\alpha \right)$, of the investment in asset S is shifted to the risk-free asset so that the portfolio’s value at risk equals v, the expected return of that portfolio, ${\overline{R}}_{\Lambda }\left(v,\alpha \right)$, is determined by Equation (3). Note that,

$$\begin{array}{cc}\hfill \lambda \left(v,\alpha \right)& =0⟺v=-r_f,\hfill \\ \hfill \lambda \left(v,\alpha \right)& =1⟺v=Va{R}_S\left(\alpha \right).\hfill \end{array}$$

The previous equalities mean that if asset S is absent from the portfolio, that is, when $\lambda \left(v,\alpha \right)=0$, the value at risk of the resulting portfolio corresponds to that of the risk-free asset. At the other extreme, when the portfolio is fully invested in asset S, that is, when $\lambda \left(v,\alpha \right)=1$, the value at risk of the portfolio coincides with that of asset S. Certainly, it is natural to restrict ourselves to positive Values at Risk, that is, to the levels of confidence $\alpha$ that falls in the positive-VaR interval defined by

$${\alpha }_0\le \alpha \le 1,\mathrm{where}Va{R}_S\left({\alpha }_0\right)=0.$$

When several assets $S_1,\dots ,S_L$ are considered, the positive-VaR interval becomes

$${\alpha }_0\le \alpha \le 1,\mathrm{where}min\left(Va{R}_{S_1}\left({\alpha }_0\right),\dots ,Va{R}_{S_L}\left({\alpha }_0\right)\right)=0.$$

We set

$${\lambda }_i\left(\alpha \right)={\displaystyle \frac{r_f+min\left(Va{R}_{S_1}\left(\alpha \right),\dots ,Va{R}_{S_L}\left(\alpha \right)\right)}{r_f+Va{R}_{S_i}\left(\alpha \right)}},i=1,\dots ,L.$$

Suppose that $Va{R}_{S_{i_0}}\left(\alpha \right)=min\left(Va{R}_{S_1}\left(\alpha \right),\dots ,Va{R}_{S_L}\left(\alpha \right)\right)$, then ${\lambda }_{i_0}\left(\alpha \right)=1$. Otherwise, $0<{\lambda }_{i_0}\left(\alpha \right)\le 1$ for $i=1,\dots ,L$. We denote by ${\Lambda }_i\left(\alpha \right)$ the protfolio where $100{\lambda }_i\left(\alpha \right)\%$ of the value of the portfolio is invested in S, and $100\left(1-{\lambda }_i\left(\alpha \right)\right)\%$ is invested in the risk-free asset B. Then, for asset $S_{i_0}$, $100\%$ of the value of the portfolio ${\Lambda }_{i_0}\left(\alpha \right)$ is invested in $S_{i_0}$. The portfolios ${\Lambda }_1\left(\alpha \right),\dots ,{\Lambda }_L\left(\alpha \right)$ all share the same VaR. Specifically, their common Var is $Va{R}_{S_{i_0}}\left(\alpha \right)$. Since all the portfolios have exactly the same VaR, the most performant portfolio amongst ${\Lambda }_1\left(\alpha \right),\dots ,{\Lambda }_L\left(\alpha \right)$ is the one for which the expected return is greatest. The expected return of portfolio ${\Lambda }_i\left(\alpha \right)$ is denoted by $R{V}_i\left(\alpha \right)$. We call $R{V}_i\left(\alpha \right)$ the Reward-VaR at the level of confidence $\alpha$. The formula for $R{V}_i\left(\alpha \right)$, obtained from (3), is given by

$$R{V}_i\left(\alpha \right)=r_f+{\displaystyle \frac{\left(r_f+min\left(Va{R}_{S_1}\left(\alpha \right),\dots ,Va{R}_{S_L}\left(\alpha \right)\right)\right)}{r_f+Va{R}_{S_i}\left(\alpha \right)}}\left({\overline{R}}_{S_i}-r_f\right),$$

(4)

where ${\overline{R}}_{S_i}$ is the expected rate of return of $S_i$ and $r_f$ is the risk-free rate.

Equation (4) formalizes a minimalist risk equalization scheme. Among all possible combinations of risky and risk-free holdings that yield identical value at risk across assets, it selects the configuration requiring the smallest possible transfer of capital into the risk-free asset. In this setup, at least one asset remains fully invested (i.e., ${\lambda }_i=0$), while the others are proportionally adjusted to match its downside risk level. This construction preserves comparability across assets while avoiding unnecessary reduction of overall portfolio risk and return. The expected return of each resulting portfolio, composed of asset $S_i$ and the risk-free asset, is then given by Equation (4).

This gives a simple and natural way to compare the risk-adjusted performance of assets $S_1,\dots ,S_L$. A portion of the investment in each $S_i$ is reallocated towards the risk-free asset B, so that all resulting portfolios ${\Lambda }_i$ have the same Value-at-Risk $v_0$ at the confidence level $\alpha$, where $v_0$ is the minimum of $Va{R}_{S_1}\left(\alpha \right),\dots ,Va{R}_{S_L}\left(\alpha \right)$. Then, asset $S_{{\mathsf{\ell }}_0}$ has the highest risk-adjusted performance among $S_1,\dots ,S_L$ if the expected return $R{V}_{{\mathsf{\ell }}_0}\left(\alpha \right)$ of the portfolio ${\Lambda }_{{\mathsf{\ell }}_0}$ is greater than or equal to the expected return $R{V}_i\left(\alpha \right)$ of all the other portfolios ${\Lambda }_i$.

As a result,

$$max\left(R{V}_1\left(\alpha \right),\dots ,R{V}_L\left(\alpha \right)\right)$$

represents the optimal expected risk-adjusted return achievable among $S_1,\dots ,S_L$, as a function of the minimum loss within the worst $1-\alpha$ tail of each asset’s loss distribution. The larger the value of $\alpha$, the more focused on extreme losses the investor is, and accordingly, $\alpha$ can be viewed as a risk-aversion parameter.

From (3), we see that the Reward–VaR curve, $R{V}_S\left(\alpha \right)$, of an asset S can be expressed as

$$R{V}_S\left(\alpha \right)=r_f+\left(r_f+min\left(Va{R}_{S_1}\left(\alpha \right),\dots ,Va{R}_{S_L}\left(\alpha \right)\right)\right)Rt{V}_S\left(\alpha \right)$$

where

$$Rt{V}_S\left(\alpha \right)={\displaystyle \frac{{\overline{R}}_S-r_f}{r_f+Va{R}_S\left(\alpha \right)}}$$

denotes the Reward-to-VaR ratio introduced by Alexander and Baptista (2003). Therefore, $R{V}_{{\mathsf{\ell }}_0}\left(\alpha \right)$ is greater than or equal to $R{V}_1\left(\alpha \right)$, …, $R{V}_L\left(\alpha \right)$ if and only if $Rt{V}_{{\mathsf{\ell }}_0}\left(\alpha \right)$ is greater than or equal to $Rt{V}_1\left(\alpha \right)$, …, $Rt{V}_L\left(\alpha \right)$. This implies that ranking assets by their Reward–VaR curves yields the same ordering as the Reward-to-VaR ratio. However, since the Reward–VaR curve equals the expected return, ${\overline{R}}_{\Lambda }$, of portfolio $\Lambda$, whereas the Reward-to-VaR ratio corresponds to its rate of change, $\partial {\overline{R}}_{\Lambda }/\partial Va{R}_{\Lambda }\left(\alpha \right)$, ranking investment opportunities by Reward–VaR curves also quantifies by how much one opportunity outperforms another. This can be important when an asset only marginally outperforms others, and diversification strategies, regulatory and tax considerations, market views, ethical preferences, or other personal considerations play a significant role.

The Reward–VaR curve, as we will see below, possesses several interesting features. It is an extension of the Sharpe ratio: when VaR is replaced by the mVaR of order 2—which occurs when assets are normally distributed—the ranking coincides with that of the Sharpe ratio. When VaR is replaced by the mVaR of order 3, an interesting phenomenon occurs: if one asset does not completely dominate another at all confidence levels within the positive-VaR interval, a dominance phase transition emerges: one asset becomes preferable for risk-averse investors, while the other is favored by risk-tolerant investors. Finally, enhancing Reward–VaR curves with bootstrapping makes it possible to identify cases where the outperformance of an asset is likely due to noise in the empirical data.

2.2. Modified Reward–VaR Curves and Dominance Phase Transition

Since Reward–VaR curves depend on the underlying VaR estimates, we want to examine the properties of VaR itself. VaR is widely used in risk management; however, it is often non-smooth: at high confidence levels, empirical estimates can be noisy and sensitive to sample variability because they rely on only a few extreme observations. The Cornish–Fisher expansion provides a mathematically tractable way to approximate quantiles beyond normal cases. Because it is based on cumulants of the distribution, it leads to a smooth estimate of VaR known as the modified Value-at-Risk (mVaR), a widely adopted approximation of VaR.

Let $Q_S\left(\alpha \right)$ denote the quantile function of a continuous random variable S, that is, $P(S\le Q_S\left(\alpha \right))=\alpha$. Recall that the value at risk of S at confidence level $0\le \alpha \le 1$ is then defined as the negative of the $(1-\alpha )$-quantile of its return distribution,

$$Va{R}_S\left(\alpha \right)=-Q_S(1-\alpha ).$$

If $C{F}_S$ denotes the Cornish–Fisher expansion of $Q_S\left(\alpha \right)$, which approximates the quantile in terms of the distribution’s cumulants, the corresponding modified value at risk is given by

$$mVa{R}_S\left(\alpha \right)=-C{F}_S(1-\alpha ).$$

The Cornish–Fisher expansion, and the corresponding mVaRs derived from it, can be expressed at various orders depending on the level of detail required. At second order, the expansion includes only the mean and variance terms, corresponding to the normal case and yielding the standard normal VaR. At the third order, it incorporates skewness, yielding an mVaR that captures asymmetries in the return distribution. Higher orders (fourth, fifth, etc.) can also be included to account for kurtosis and beyond, if needed. This feature makes the approach particularly appealing in finance, as it links the behavior of VaR directly to familiar statistical properties of asset returns. Economists and practitioners can therefore interpret changes in $mVa{R}_S\left(\alpha \right)$ in terms of intuitive distributional effects: greater variance increases risk symmetrically, positive skewness reduces downside risk, and higher kurtosis amplifies tail risk.

When the VaR is replaced by the mVaR in the calculation of the Reward–VaR curve, the resulting function is called the modified Reward–VaR curve and denoted by $mRV\left(\alpha \right)$. Assume that two investment opportunities are to be compared. We will show in the subsections below that when the modified Reward–VaR curve of order two is used to rank investment opportunities, one asset dominates at all confidence levels, and both the Sharpe ratio and the modified Reward–VaR curve produce the same ranking. However, when the modified Reward–VaR curve of order three is used, risk-adjusted preferences may shift across confidence levels: one asset may appeal more to risk-averse individuals, while the other is preferable to those who are more risk-tolerant.

It is important to note that the Cornish–Fisher expansion is an asymptotic approximation that performs well when higher-order cumulants remain moderate, but it may lose accuracy for highly non-normal or heavy-tailed return distributions, where large fourth- or higher-order cumulants can distort the estimated quantiles. Despite this limitation, it remains widely used because it provides a smooth and analytically tractable approximation of VaR based on easily interpretable distributional moments. Furthermore, the ranking under the modified Reward–VaR curve of order two coincides exactly with that of the Sharpe ratio. Thus, extending the expansion to the third order represents a natural methodological refinement that captures skewness effects while maintaining tractability.

2.2.1. Dominance Phase Transition

Assume that two investment opportunities, $S_1$ and $S_2$ are to be ranked for risk-adjusted performance. For asset $S_i$, the mVaR of order three is given by

$$mVa{R}_i\left(\alpha \right)=-{\overline{R}}_{S_i}+{\sigma }_{S_i}\left[z_{\alpha }-{\displaystyle \frac{{\gamma }_{S_i}}{6}}(z_{\alpha }^2-1)\right],$$

where ${\overline{R}}_{S_i}$ is the expected return of asset i, ${\sigma }_{S_i}$ is its standard deviation, $z_{\alpha }$ is the $\alpha$-quantile of the standard normal distribution, and ${\gamma }_{S_i}$ is the skewness of asset i. Note that returns on financial assets are typically left-skewed, meaning that large losses are more likely than large gains. Consequently, the skewness coefficient ${\gamma }_{S_i}$ is typically negative. Since we focus on potential losses, we consider confidence levels for which the mVaR is positive; in the standard normal case, this occurs only for $\alpha >0.5$. With left-skewed distributions, we expect this pattern to persist. To ensure that both assets’ $mVaR$ values are positive, we restrict our analysis to confidence levels in the interval ${\alpha }_0<\alpha \le 1$, where ${\alpha }_0$ is the smallest level $\alpha \ge 0.5$ for which both $mVa{R}_1\left(\alpha \right)$ and $mVa{R}_2\left(\alpha \right)$ are non-negative for all ${\alpha }_0<\alpha \le 1$.

We now investigate in detail the confidence levels $\alpha$ at which investment opportunity $S_1$ is preferable to $S_2$, and vice versa. With the $mVaR$ approximation, we find that $S_1$ is preferable to $S_2$ if

$$mR{V}_1\left(\alpha \right)-mR{V}_2\left(\alpha \right)\ge 0.$$

(5)

The opposite holds if the difference is negative, while equality means that both investments perform equally well. The modified Reward–VaR curve for investment $S_i$ can be written as

$$mR{V}_i\left(\alpha \right)=r_f+\left(r_f+mVa{R}_{i_0}\left(\alpha \right)\right){\displaystyle \frac{{\overline{R}}_{S_i}-r_f}{r_f-{\overline{R}}_{S_i}+{\sigma }_{S_i}\left[z_{\alpha }-\frac{{\gamma }_{S_i}}{6}(z_{\alpha }^2-1)\right]}},$$

where $i_0$ is either equal to 1 or 2. Dividing both sides of (5) by $r_f+mVa{R}_{i_0}\left(\alpha \right)$ gives

$${\displaystyle \frac{{\overline{R}}_{S_1}-r_f}{D_1\left(\alpha \right)}}-{\displaystyle \frac{{\overline{R}}_{S_2}-r_f}{D_2\left(\alpha \right)}}\ge 0,$$

where

$$D_i\left(\alpha \right)=r_f-{\overline{R}}_{S_i}+{\sigma }_{S_i}\left[z_{\alpha }-{\displaystyle \frac{{\gamma }_{S_i}}{6}}(z_{\alpha }^2-1)\right].$$

Cross-multiplying yields

$$({\overline{R}}_{S_1}-r_f)D_2\left(\alpha \right)-({\overline{R}}_{S_2}-r_f)D_1\left(\alpha \right)\ge 0.$$

(6)

We define

$$A_i=r_f-{\overline{R}}_{S_i},B_i={\sigma }_{S_i},C_i=-{\displaystyle \frac{{\sigma }_{S_i}{\gamma }_{S_i}}{6}},$$

and hence $D_i\left(\alpha \right)$ can be rewritten as

$$D_i\left(\alpha \right)=A_i+B_i{z}_{\alpha }+C_i(z_{\alpha }^2-1).$$

Then the inequality (6) becomes

$$-A_1\left[A_2+B_2{z}_{\alpha }+C_2(z_{\alpha }^2-1)\right]+A_2\left[A_1+B_1{z}_{\alpha }+C_1(z_{\alpha }^2-1)\right]\ge 0.$$

Grouping terms by powers of $z_{\alpha }$, this inequality can be rewritten as

$$\mathcal{A}{z}_{\alpha }^2+\mathcal{B}{z}_{\alpha }-\mathcal{A}\ge 0,$$

(7)

where

$$\mathcal{A}=A_2{C}_1-A_1{C}_2,\mathcal{B}=A_2{B}_1-A_1{B}_2.$$

Equation (7) is equivalent to $mR{V}_1\left(\alpha \right)-mR{V}_2\left(\alpha \right)\ge 0$. When this condition holds, $S_1$ provides a higher risk-adjusted reward than $S_2$ at the corresponding confidence level $\alpha$; when reversed, $S_2$ is preferable. Equality indicates that both assets exhibit the same return–risk trade-off.

Suppose first that $\mathcal{A}=0$. Then (7) reduces to

$$\mathcal{B}{z}_{\alpha }\ge 0.$$

If $\mathcal{B}>0$, then $\mathcal{B}{z}_{\alpha }>0$ for all $z_{\alpha }>0$, and hence $mR{V}_1\left(\alpha \right)-mR{V}_2\left(\alpha \right)>0$. In this case, $S_1$ dominates $S_2$ for all $\alpha \in [{\alpha }_0,1]$. If $\mathcal{B}<0$, the inequality reverses and $S_2$ dominates $S_1$ for all $\alpha \in [{\alpha }_0,1]$. If $\mathcal{B}=0$, then $\mathcal{B}{z}_{\alpha }=0$ for all $z_{\alpha }>0$, and both investments are equivalent in performance for all $\alpha \in [{\alpha }_0,1]$.

Suppose now that $\mathcal{A}\ne 0$. Solving the quadratic equation $\mathcal{A}{z}_{\alpha }^2+\mathcal{B}{z}_{\alpha }-\mathcal{A}=0$ yields

$$z_{\alpha }={\displaystyle \frac{-\mathcal{B}\pm \sqrt{{\mathcal{B}}^2+4{\mathcal{A}}^2}}{2\mathcal{A}}}.$$

Exactly one of these solutions is positive; we denote the corresponding confidence level by ${\alpha }_1$. A phase transition appears, with two possible outcomes: if $\mathcal{A}>0$, then the quadratic function $\mathcal{A}{z}_{\alpha }^2+\mathcal{B}{z}_{\alpha }-\mathcal{A}$ is negative between its roots and positive elsewhere. This implies that $S_2$ dominates for $\alpha \in [{\alpha }_0,{\alpha }_1)$, while $S_1$ is preferable for $\alpha \in ({\alpha }_1,1]$. If $\mathcal{A}<0$, the opposite is true: $S_1$ dominates for $\alpha \in [{\alpha }_0,{\alpha }_1)$, while $S_2$ is preferable for $\alpha \in ({\alpha }_1,1]$. At $\alpha ={\alpha }_1$, both investments yield identical risk-adjusted performance.

This phase transition mirrors a shift in risk-adjusted preference. Investor with lower risk-aversion, who measure their risk-adjusted return as a function of small and typical losses—those corresponding to the mVaR at lower levels of confidence—will find the investment that dominates in the interval ${\alpha }_0\le \alpha <{\alpha }_1$ most rewarding. On the other hand, risk-averse investors, who focus on rare but large losses—those corresponding to the mVaR at higher levels of confidence—will find the investment dominating in the interval ${\alpha }_1<\alpha \le 1$ to offer a better risk-adjusted return. In this context, the confidence level $\alpha$ effectively serves as a proxy for the investor’s level of risk aversion, and we will sometimes refer to it as such in what follows.

2.2.2. Modified Reward-VaR Curves as an Extension of the Sharpe Ratio

For asset $S_i$, the mVaR of order two is given by

$$mVa{R}_i\left(\alpha \right)=-{\overline{R}}_{S_i}+{\sigma }_{S_i}{z}_{\alpha }.$$

This is just a special case of the third-order mVaR where the skewness is zero. Then, inequality (7) simplifies to a linear condition: $\mathcal{B}{z}_{\alpha }\ge 0$. Since $z_{\alpha }>0$ for all $\alpha \in [0.5,1]$, investment $S_1$ is preferable to (or as good as) $S_2$ across this entire range if and only if $\mathcal{B}\ge 0$. Using $\mathcal{B}=A_2{B}_1-A_1{B}_2$, with $B_i={\sigma }_{S_i}$ and $A_i=R_{S_i}-r_f$, the condition $\mathcal{B}\ge 0$ can be rearranged as

$${\displaystyle \frac{R_{S_1}-r_f}{{\sigma }_{S_1}}}\ge {\displaystyle \frac{R_{S_2}-r_f}{{\sigma }_{S_2}}},$$

which is precisely the Sharpe ratio comparison between $S_1$ and $S_2$. Hence, when skewness is absent (or equivalently, when the second-order mVaR is used), the modified Reward–VaR curve ranking aligns exactly with that of the Sharpe ratio.

2.3. Bootstrapped Reward-VaR Curves and Dominance Patterns

To assess the robustness of empirical Reward–VaR curves, we use bootstrapping, generating multiple synthetic return series by randomly selecting observations with replacement from the original empirical returns. This non-parametric approach, a standard tool across applied statistical domains, allows us to assign measures of accuracy to statistics derived from the empirical data, such as the RV curves.

Starting from a collection $\{R_1,R_2,\dots ,R_{\mathcal{L}}\}$ of daily returns for an asset S, the bootstrap procedure generates N samples, $\{R_1^{\left(n\right)},R_2^{\left(n\right)},\dots ,R_{\mathcal{L}}^{\left(n\right)}\}$, for $n=1,\dots ,N$, by resampling with replacement from the original data. This allows us to obtain N Reward–VaR curves, $R{V}_S^{\left(n\right)}\left(\alpha \right)$, for $n=1,\dots ,N$. Then, the average

$$bR{V}_S\left(\alpha \right)={\displaystyle \frac{R{V}_S^{\left(1\right)}\left(\alpha \right)+\dots +R{V}_S^{\left(N\right)}\left(\alpha \right)}{N}}$$

serves as the bootstrap estimation of the Reward–VaR curve. We call $bR{V}_S\left(\alpha \right)$ the bootstrapped Reward–VaR curve. We define the positive-bVaR interval as the set of confidence levels $\alpha \in ({\alpha }_0,1]$ for which the VaR of all bootstrap samples $\{R_1^{\left(n\right)},R_2^{\left(n\right)},\dots ,R_{\mathcal{L}}^{\left(n\right)}\}$ is positive.

Given two assets, CO and IS, to be ranked by their risk-adjusted performance, we obtain two bootstrapped Reward–VaR curves, $bR{V}_{\mathrm{CO}}\left(\alpha \right)$ and $bR{V}_{\mathrm{IS}}\left(\alpha \right)$, together with the standard deviation $\sigma \left(\alpha \right)$ of their difference $R{V}_{\mathrm{CO}}^{\left(n\right)}\left(\alpha \right)-R{V}_{\mathrm{IS}}^{\left(n\right)}\left(\alpha \right)$ at each confidence level $\alpha$. We define a positive-bVaR interval as the intersection between the positive-bVaR interval of CO and the positive-bVaR interval of IS.

The standard deviation $\sigma \left(\alpha \right)$ quantifies the dispersion of the bootstrapped differences $R{V}_{\mathrm{CO}}^{\left(n\right)}\left(\alpha \right)-R{V}_{\mathrm{IS}}^{\left(n\right)}\left(\alpha \right)$ around their mean, and serves as a measure of statistical uncertainty associated with $bR{V}_{\mathrm{CO}}\left(\alpha \right)-bR{V}_{\mathrm{IS}}\left(\alpha \right)$ at each confidence level $\alpha$. In line with common bootstrap practice, we introduce a proximity threshold $\delta >0$ to determine whether this average difference is materially significant relative to its sampling variability. Specifically, we consider the difference statistically insignificant whenever its absolute value remains smaller than $\delta$ times the standard deviation $\sigma \left(\alpha \right)$.

The choice of $\delta$ reflects the degree of statistical stringency applied when assessing the materiality of differences: smaller values of $\delta$ increase sensitivity to minor deviations, while larger values enforce stricter dominance criteria. The parameter $\delta$ plays a role analogous to a critical value in hypothesis testing, defining how many standard deviations away from the mean a difference must be before it is deemed statistically meaningful. Choosing $\delta <1$ does not make much sense because it would yield false dominance (either $CO>IS$ or $IS>CO$) about a third of the time. By contrast, under the rule that declares $CO$ dominance when $bR{V}_{\mathrm{CO}}\left(\alpha \right)-bR{V}_{\mathrm{IS}}\left(\alpha \right)>\delta \sigma \left(\alpha \right)$, the false detection rate of $CO$ dominance is $1-\Phi \left(\delta \right)$. The same false detection rate of $1-\Phi \left(\delta \right)$ occurs if one declares $IS$ dominance when $bR{V}_{\mathrm{IS}}\left(\alpha \right)-bR{V}_{\mathrm{CO}}\left(\alpha \right)>\delta \sigma \left(\alpha \right)$. For practical interpretation, $\delta =1.15$ gives an error rate of about $12.5\%$. This level provides only an indication of dominance. At $\delta =1.28$, the error rate falls to $10\%$, showing significant evidence. With $\delta =1.64$, the error rate is $5\%$, which indicates strong evidence. At $\delta =1.96$, the error rate drops to $2.5\%$, giving very strong evidence of dominance.

In this context, if $\left|bR{V}_{\mathrm{CO}}\left(\alpha \right)-bR{V}_{\mathrm{IS}}\left(\alpha \right)\right|\le \delta \sigma \left(\alpha \right),$ the bootstrapped Reward–VaR curves $bR{V}_{\mathrm{CO}}\left(\alpha \right)$ and $bR{V}_{\mathrm{IS}}\left(\alpha \right)$ are considered statistically indistinguishable at level $\alpha$, and we write

$$bR{V}_{\mathrm{CO}}\left(\alpha \right)\approx bR{V}_{\mathrm{IS}}\left(\alpha \right).$$

Otherwise, if $bR{V}_{\mathrm{CO}}\left(\alpha \right)>bR{V}_{\mathrm{IS}}\left(\alpha \right)+\delta \sigma \left(\alpha \right),$ then $bR{V}_{\mathrm{CO}}\left(\alpha \right)$ is considered to statistically exceed $bR{V}_{\mathrm{IS}}\left(\alpha \right)$, and we write

$$bR{V}_{\mathrm{CO}}\left(\alpha \right)\succ bR{V}_{\mathrm{IS}}\left(\alpha \right).$$

Similarly, when $bR{V}_{\mathrm{IS}}\left(\alpha \right)>bR{V}_{\mathrm{CO}}\left(\alpha \right)+\delta \sigma \left(\alpha \right),$ we write $bR{V}_{\mathrm{IS}}\left(\alpha \right)\succ bR{V}_1\left(\alpha \right)$. Finally,

$$bR{V}_{\mathrm{CO}}\left(\alpha \right)\succsim bR{V}_{\mathrm{IS}}\left(\alpha \right)$$

means that $bR{V}_{\mathrm{CO}}\left(\alpha \right)\succ bR{V}_{\mathrm{IS}}\left(\alpha \right)$ or $bR{V}_{\mathrm{CO}}\left(\alpha \right)\approx bR{V}_{\mathrm{IS}}\left(\alpha \right)$. An analogous definition holds for the relation $bR{V}_{\mathrm{IS}}\left(\alpha \right)\succsim bR{V}_{\mathrm{CO}}\left(\alpha \right)$.

Given an interval $I\subseteq [0,1]$, we define the dominance relationships between CO and IS as follows:

• CO dominates IS on I if $bR{V}_{\mathrm{CO}}\left(\alpha \right)\succsim bR{V}_{\mathrm{IS}}\left(\alpha \right)$ for every $\alpha \in I$.
• IS dominates CO on I if $bR{V}_{\mathrm{IS}}\left(\alpha \right)\succsim bR{V}_{\mathrm{CO}}\left(\alpha \right)$ for every $\alpha \in I$.
• CO is equivalent to IS on I if $bR{V}_{\mathrm{CO}}\left(\alpha \right)\approx bR{V}_{\mathrm{IS}}\left(\alpha \right)$ for every $\alpha \in I$.

This leads to natural dominance patterns between CO and IS, capturing how the preference between the two assets changes as the confidence level varies. It is possible that CO dominates IS throughout the range of confidence levels, IS dominates CO throughout, or the two assets are statistically equivalent throughout. A phase transition may also occur, where one asset dominates at lower confidence levels before being overtaken by the other at higher levels, or vice versa. Finally, it is possible that no clear dominance pattern emerges, with dominance fluctuating in a way that does not conform to any of the above-mentioned basic patterns.

The dominance patterns are listed and defined as follows. Here, [${\alpha }_0$,1] denotes the positive-bVaR interval.

• All_Equal: CO and IS are statistically equivalent on the interval $[{\alpha }_0,1]$.
• All_CO: CO dominates IS throughout the interval $[{\alpha }_0,1]$.
• All_IS: IS dominates CO throughout the interval $[{\alpha }_0,1]$.
• CO_Equal_IS: The interval $[{\alpha }_0,1]$ can be partitioned into three subintervals, $[{\alpha }_0,a]$, $[a,b]$, and $[b,1]$, such that CO dominates IS on $[{\alpha }_0,a]$, CO and IS are equivalent on $[a,b]$, and IS dominates CO on $[b,1]$.
• IS_Equal_CO: Defined analogously, with IS dominating at lower confidence levels, equivalence in the middle, and CO dominating at higher levels.
• No_Phase_Pattern: None of the above patterns apply.

To be specific and precise, in the case of CO_Equal_IS, the interval boundaries are defined as follows. The confidence level a is the supremum of all $\alpha$ such that $bR{V}_{\mathrm{CO}}\left(\alpha \right)\succ bR{V}_{\mathrm{IS}}\left(\alpha \right)$. Conversely, b is the infimum of all $\alpha$ such that $bR{V}_{\mathrm{CO}}\left(\alpha \right)\prec bR{V}_{\mathrm{IS}}\left(\alpha \right)$. The same definitions of a and b apply in the case of IS_Equal_CO, with the roles of CO and IS reversed.

3. An Empirical Study of Dominance Patterns Between Conventional and Islamic Indices

Stock indices are considered to be one of the safest ways to invest in stocks due to their inherent diversification benefits. They are accessible through numerous exchange-traded funds (ETFs). Islamic indices are constructed to ensure that the companies included in them comply with Islamic principles. Such investments represent a significant and growing segment of global financial markets, with a total estimated value exceeding $200 billion worldwide, according to the General Council for Islamic Banks and Financial Institutions (see Selmi et al. (2023)). This value has grown by more than 300% over the last decade. With the continued economic development of emerging economies with large Muslim populations—such as Indonesia, Pakistan, Bangladesh, Nigeria, Egypt, Turkey, and others—many of which are projected to rank among the world’s largest economies by mid-century (see PwC (2017))—the share of global financial markets represented by Islamic financial assets is expected to continue expanding over the coming decades.

The performance of Islamic indices may differ from that of conventional ones. Depending on market conditions, this may result in either outperformance or underperformance. Studies investigating the impact of ethical screening on the performance of Islamic indices relative to their conventional counterparts have yielded mixed results. Several research efforts, including studies by Ahmad and Ibrahim (2002), Albaity and Ahmad (2008), K. Hussein (2004), K. A. Hussein (2007), Girard and Hassan (2008), Hassan and Girard (2010), Dharani and Natarajan (2011), and Abbes (2012), found no significant difference in the risk-adjusted performance of Islamic and conventional indices over their respective study periods. Similarly, a study by Hakim and Rashidian (2002) suggested that the overall risk–return performance of Islamic indices was not adversely affected by the screening process to exclude non-compliant firms. In their literature review, Delle Foglie and Panetta (2020) conclude that the existing body of literature has not conclusively proven differences in the performance of Islamic finance instruments.

In contrast, other studies have found evidence favoring conventional indices. O. Al-Khazali et al. (2014) found that conventional indices stochastically dominate Islamic indices in all markets except the European market. Similarly, O. M. Al-Khazali et al. (2016) and Abadi and Silva (2020) concluded that conventional indices tend to be more efficient or at least as efficient as their Islamic counterparts. Ashraf et al. (2017) cautioned that restrictions imposed by Shariah screening negatively affect portfolio performance, except during economic downturns. Haroon et al. (2019) found that in the markets studied, conventional indices perform better or at least as well as their Islamic counterparts. Abu-Alkheil et al. (2020) obtained mixed results that were generally in favor of conventional indices.

Conversely, other studies have found that Islamic indices often outperform their conventional counterparts. Ashraf and Mohammad (2014) demonstrated that Islamic indices generally outperformed conventional ones from June 2002 to May 2012, especially during crisis periods like the Dotcom crisis (2000–2002) and the Global Financial Crisis (2007–2008). Similarly, Ho et al. (2014) reported that Islamic indices performed better during crisis periods, though results were inconclusive for non-crisis periods. Charles et al. (2015) and Alam and Ansari (2020) concluded that Islamic indices tend to either outperform or perform equally well as their non-Islamic counterpart. Asutay et al. (2021) also observed that over most periods studied, Islamic indices either outperformed or performed equally well as conventional ones, except for the period from 2009 to 2013, where the results were inconclusive. Alamgir and Cheng (2023) found that Islamic indices generally outperformed their conventional counterparts, although the results varied across regions and time periods.

Some studies focused on the relative performance of conventional and Islamic indices during periods of growth and economic downturn. K. Hussein (2004), K. A. Hussein (2007), Hassan and Girard (2010), and Jawadi et al. (2014) observed that Islamic indices outperformed conventional ones, especially during the Global Financial Crisis, while non-Islamic indices were preferred during calm periods. Khan and Azmat (2020) found that Islamic indices exhibit better performance during economic downturns due to the lower debt of Islamic equity. In contrast, Hasan et al. (2021) warn that Islamic stocks do not present a superior investment alternative, especially in economic turmoil. Abbes (2012) noted that Islamic indices yielded statistically significant positive abnormal returns in bull market periods but underperformed their conventional counterparts in bear market periods.

In terms of risk, Al-Zoubi and Maghyereh (2007) reported that Islamic indices exhibited significantly lower volatility than a representative market basket of stocks. In contrast, Charles et al. (2015) found that Islamic indices carry a higher risk compared to non-Islamic indices. Additionally, Chazi et al. (2023) observed that the volatility of Islamic indices is relatively lower than that of conventional peers during periods of turmoil.

As the preceding review shows, the literature offers no clear consensus on the comparative performance of Islamic and conventional indices. Their relative ranking may be risk profile-sensitive—that is, dependent on the investor’s degree of risk aversion. It may also be regime-sensitive, varying across market conditions such as bull and bear periods. In any given scenario—full sample, bear or bull period, or a specific subperiod—the relationship between the indices may exhibit any of the canonical dominance patterns: statistical equivalence, simple dominance, phase transitions, or even an absence of coherent risk-adjusted behavior. All of these possibilities can be systematically identified using the bootstrapped Reward–VaR curve methodology. To the best of our knowledge, this is the first study to examine the relative performance of Islamic and conventional indices through this lens.

3.1. Dominance Patterns Between Conventional and Islamic Indices

We apply the bootstrapped Reward–VaR methodology to determine the dominance patterns emerging from performance comparisons between conventional indices and their Islamic counterparts. To ensure high stability and negligible variation across runs, we use 5000 bootstrap samples. To highlight the most statistically meaningful patterns, we report our key empirical findings for the overall, bull, and bear periods using $\delta =1.28$, the threshold corresponding to statistically significant evidence. For detailed analysis by market and subperiod—including shorter subperiods with smaller sample sizes and wider confidence intervals—we adopt a lower proximity threshold of $\delta =1.15$ to enhance sensitivity to early dominance signals. A full robustness check across $\delta \in [1,2]$ is provided in Appendix A.

We examine nine pairs of indices from the S&P Dow Jones Global Index family, covering nine regional and global markets: Asia-Pacific, Canada, Developed Markets, Emerging Markets, Europe, Japan, the United Kingdom, the United States, and the World. These indices are described in Appendix B.

To capture regime-dependent dynamics, we divide the empirical study period, from 1 January 2000 to 1 July 2024, into multiple subperiods reflecting Bull and Bear market phases identified ex post. These regimes are defined objectively based on the well-established bull and bear cycles of the Dow Jones Industrial Average (DJIA), where turning points correspond to historical peaks and troughs marked by declines or recoveries of at least 20% from the previous extremum. The subperiods are defined as follows:

• Bear1: 1 January 2000 to 9 October 2002;
• Bull1: 9 October 2002 to 9 October 2007;
• Bear2: 9 October 2007 to 9 March 2009;
• Bull2: 9 March 2009 to 12 February 2020;
• Bear3 (COVID crash): 12 February 2020 to 23 March 2020;
• Bull3: 23 March 2020 to 4 January 2022;
• Bear4: 4 January 2022 to 30 September 2023;
• Bull4: 30 September 2023 to 1 July 2024.

In addition to analyzing each subperiod individually, we also define three aggregate periods. The Overall period corresponds to the full sample from 1 January 2000 to 1 July 2024. The Overall Bear period is composed of the union of all four Bear phases, and the Overall Bull period is composed of the union of all four Bull phases. These broader intervals allow us to assess long-term performance patterns during full market cycles, extended downturns, and extended upswings, respectively. This yields a total of 11 distinct periods of study, which, when applied across the nine markets, define 99 market-period scenarios for empirical analysis.

For each of the 99 market-period scenarios, we generate a dominance pattern using the bootstrapped Reward–VaR methodology detailed in Section 2.3, characterizing the dominance relationship between the conventional and Islamic indices for that specific market-period scenario. These dominance patterns are grouped by market and presented in tables, each containing 11 entries corresponding to the periods under study.

Specifically, for each period—Overall, Bull, Bear, and their respective subperiods—the table identifies the dominance pattern, the corresponding dominance interval, and the average Reward–VaR values of both indices over this interval. It also reports the absolute and relative differences in average Reward–VaR between the two indices, providing a concise summary of their risk-adjusted performance relationship across different market regimes.1

As an illustration of how to interpret the dominance-pattern tables provided in this study,

Table 1. Illustrative example of Overall Bull and Bear periods ($\delta =1.15$).

Period	Interval	Index	Avg bRVCO	Avg bRVIS	Diff.	% Diff.
Bull	[0.59, 1.00]	CO	19.32%	17.17%	2.15%	13%
Bear	[0.54, 0.68]	IS	−28.44%	−23.60%	4.84%	17%
	[0.68, 0.99]	Equal	−28.42%	−27.16%	1.26%	4%
	[0.99, 1.00]	CO	−27.02%	−31.55%	4.53%	14%

presents illustrative entries corresponding to an Overall Bull and Overall Bear period. The table indicates that, during the Bull period, the conventional index (CO) dominates the Islamic index (IS) over the entire positive-bVaR interval $[0.59,1.00]$. This corresponds to the All_CO dominance pattern. Over this interval, the average value of $bR{V}_{\mathrm{CO}}\left(\alpha \right)$ is $19.32\%$, while the average of $bR{V}_{\mathrm{IS}}\left(\alpha \right)$ is $17.17\%$. This results in an advantage of $2.15\%$ for CO, meaning that the average value of the bootstrapped Reward–VaR curve for CO is $13\%$ higher than that of IS.

In the illustrative Bear period of Table 1, the dominance relationship between CO and IS varies across subintervals within the positive-bVaR interval $[0.54,1.00]$. This corresponds to a CO_Equal_IS dominance pattern. Over the range $[0.54,0.68]$, the average value of $bR{V}_{\mathrm{IS}}\left(\alpha \right)$ is $-23.60\%$, while the average of $bR{V}_{\mathrm{CO}}\left(\alpha \right)$ is $-28.44\%$. This results in an advantage of $4.84\%$ for IS, meaning that the average value of the bootstrapped Reward–VaR curve for IS is $17\%$ higher (less negative) than that of CO, indicating stronger downside protection by the Islamic index in this subinterval. In this illustrative example, between $[0.68,0.99]$, the indices are statistically equivalent, with a modest average difference of $1.26\%$ between $bR{V}_{\mathrm{CO}}\left(\alpha \right)$ and $bR{V}_{\mathrm{IS}}\left(\alpha \right)$. Over the extreme confidence range $[0.99,1.00]$, the conventional index regains dominance, with $bR{V}_{\mathrm{CO}}\left(\alpha \right)$ averaging $-27.02\%$ versus $-31.55\%$ for IS. This corresponds to an advantage of $4.53\%$ for CO, or a $14\%$ relative improvement compared to IS. This illustrative example is provided solely to clarify how the dominance-pattern tables should be read and interpreted.

3.2. Key Empirical Findings

Our main empirical results show that several consistent dominance patterns emerge across the various markets.

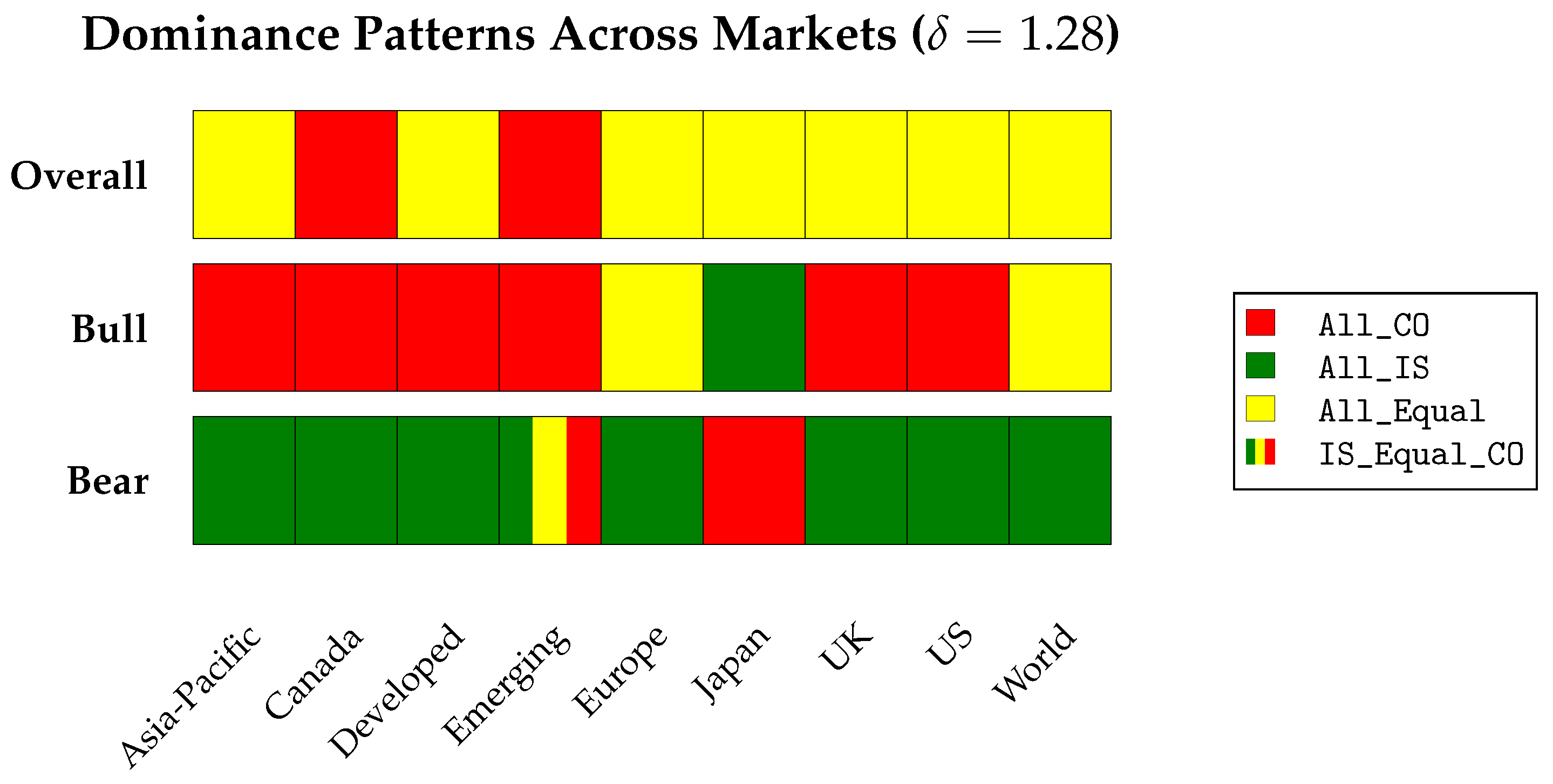
In the overall period, most markets exhibit no clear dominance between the Islamic and conventional indices. The majority of markets display the All_Equal pattern, indicating no statistically significant long-run difference in performance when all periods are considered together. The only exceptions are Canada and Emerging Markets, which show All_CO dominance over the full sample.

Under bull markets, conventional indices tend to dominate across most regions. Specifically, six out of nine markets exhibit the All_CO pattern, indicating that conventional indices consistently outperform their Islamic counterparts during rising market conditions. In the European and World markets, neither the conventional nor the Islamic index establishes dominance. In sharp contrast to the broader trend, the Islamic index dominates with statistical significance in the Japanese market. Taken together, these results indicate that conventional indices tend to exhibit stronger risk-adjusted performance than their Islamic counterparts during bull markets.

Across bear markets, Islamic indices generally exhibit stronger risk-adjusted performance than their conventional counterparts. Seven out of nine markets are classified as All_IS, and one additional market (Emerging) shows partial dominance with the pattern IS_Equal_CO. Only Japan reports All_Equal in the bear regime, suggesting no clear difference in performance during downturns. Overall, this pattern indicates that Islamic indices are more resilient in adverse market conditions.

A broad picture emerges: conventional indices tend to outperform during bull markets, while Islamic indices offer stronger downside protection during bear markets. This phase-sensitive behavior often leads to statistical equivalence over the full sample. This asymmetry suggests that, in general, more risk-averse investors may prefer Islamic indices for their downside protection, whereas more return-seeking investors may favor conventional indices during periods of economic growth. Our findings may also support diversification strategies that adjust exposure based on macroeconomic conditions. Finally, across most markets, the results offer reassurance to ethically motivated investors that Shariah-compliant investing can be pursued without compromising long-run outcomes.

The dominance-pattern bar chart in Figure 1 provides a visual summary of the results across all markets. The chart offers a compact cross-market overview, showing the prevailing dominance pattern (color-coded) for each market under the Overall, Bull, and Bear regimes.

Alternatively, the dominance-pattern results across all markets for the Overall, Bull, and Bear regimes are presented in symbolic form in

Table 2. Key Dominance Patterns by Market ($\delta =1.28$).

Market	Overall	Bull	Bear
Asia-Pacific	All_Equal	All_CO	All_IS
Canada	All_CO	All_CO	All_IS
Developed	All_Equal	All_CO	All_IS
Emerging	All_CO	All_CO	IS_Equal_CO
Europe	All_Equal	All_Equal	All_IS
Japan	All_Equal	All_IS	All_CO
UK	All_Equal	All_CO	All_IS
US	All_Equal	All_CO	All_IS
World	All_Equal	All_Equal	All_IS

, using the canonical codes All_CO, All_IS, All_Equal, IS_Equal_CO, and CO_Equal_IS.

3.3. Detailed Results by Market

3.3.1. Asia-Pacific

The dominance-pattern bar chart in Figure 2 provides a visual summary of the results for the Asia-Pacific market.

The detailed results for the Asia-Pacific market are provided in

Table 3. Dominance Patterns in the Asia-Pacific Market ($\delta =1.15$).

Period	Interval	Index	Avg bRVCO	Avg bRVIS	Diff.	% Diff.
Overall Period
Overall	[0.58, 1.00]	Equal	4.05%	3.53%	0.52%	13%
Bull and Bear Periods
Bull	[0.62, 0.63]	CO	15.18%	11.31%	3.87%	34%
	[0.63, 1.00]	Equal	15.14%	14.98%	0.16%	1%
	[1.00, 1.00]	IS	13.52%	15.89%	2.37%	18%
Bear	[0.52, 1.00]	IS	−30.38%	−28.23%	2.15%	7%
Bull and Bear Subperiods
Bull Subperiods
Bull1	[0.61, 1.00]	CO	19.78%	18.16%	1.62%	9%
Bull2	[0.62, 1.00]	Equal	10.27%	11.08%	0.81%	8%
Bull3	[0.69, 1.00]	Equal	27.92%	25.27%	2.65%	9%
Bull4	[0.70, 1.00]	Equal	19.46%	18.11%	1.35%	7%
Bear Subperiods
Bear1	[0.53, 1.00]	Equal	−24.57%	−24.92%	0.35%	1%
Bear2	[0.58, 1.00]	Equal	−48.14%	−48.02%	0.12%	0%
Bear3	[0.79, 1.00]	Equal	−214.93%	−195.75%	19.18%	9%
Bear4	[0.60, 1.00]	Equal	−7.46%	−10.16%	2.70%	36%

and discussed below.

Table 3 shows that in the Asia-Pacific market, the overall performance of the Islamic and conventional indices is statistically equivalent, with the conventional index displaying a slight numerical advantage that remains within the range of statistical noise. When the data is segmented by regime, a more nuanced pattern emerges. During the aggregate bull period, the dominance structure follows a phase transition: the conventional index dominates at lower levels of risk-aversion, transitions to statistical equivalence at intermediate levels, and eventually the Islamic index dominates for highly risk-averse investors.2. In contrast, the bear period shows a clear and statistically significant advantage for the Islamic index. Although the Islamic index’s edge during bear markets may appear stronger than that of the conventional index in the bull period, the much longer duration of bull periods offsets this difference, resulting in long-term statistical equivalence between the two indices.

Across the bull subperiods, the conventional index dominates during Bull1, while Bull2 shows a slight Islamic advantage that does not reach statistical significance. In Bull3 and Bull4, the conventional index again records higher average returns, though the differences remain within the proximity threshold. Taken together, these outcomes result in a transition from early conventional dominance to statistical equivalence and ultimately to Islamic dominance for highly risk-averse investors.

On the bear side, Bear1 and Bear2 show a mild Islamic edge that is not statistically significant. In Bear3 (the COVID crash), the Islamic index significantly outperforms numerically, though high volatility precludes statistical significance. Annualized losses during that period correspond to daily effective rates of roughly $-0.85\%$ for the conventional index and $-0.78\%$ for the Islamic index, in line with market conditions observed during the COVID crash. In Bear4, the conventional index slightly outperforms, but again not significantly. When aggregated, the Islamic index’s tendency to outperform becomes statistically significant, resulting in dominance during the overall bear period.

3.3.2. Canada

The dominance-pattern bar chart in Figure 3 provides a visual summary of the results for the Canadian market.

The detailed results for the Canadian market are provided in

Table 4. Dominance Patterns in the Canadian Market ($\delta =1.15$).

Period	Interval	Index	Avg bRVCO	Avg bRVIS	Diff.	% Diff.
Overall Period
Overall	[0.56, 1.00]	CO	7.47%	4.56%	2.91%	64%
Bull and Bear Periods
Bull	[0.57, 1.00]	CO	19.33%	13.65%	5.68%	42%
Bear	[0.53, 1.00]	IS	−25.60%	−20.77%	4.83%	19%
Bull and Bear Subperiods
Bull Subperiods
Bull1	[0.61, 1.00]	CO	28.82%	21.75%	7.07%	33%
Bull2	[0.57, 1.00]	CO	10.46%	6.50%	3.96%	61%
Bull3	[0.67, 1.00]	CO	46.42%	26.99%	19.43%	72%
Bull4	[0.69, 1.00]	Equal	20.27%	19.89%	0.38%	2%
Bear Subperiods
Bear1	[0.55, 1.00]	Equal	−14.50%	−17.66%	3.16%	22%
Bear2	[0.58, 1.00]	IS	−49.62%	−32.34%	17.28%	35%
Bear3	[0.73, 1.00]	Equal	−286.84%	−222.23%	64.61%	23%
Bear4	[0.59, 1.00]	Equal	−4.81%	−4.85%	0.04%	1%

and discussed below.

Table 4 shows that in the Canadian market, the conventional index statistically dominates the Islamic index during the overall period. This result reflects a strong conventional outperformance during bull markets, with an average bootstrapped Reward–VaR of 19.33% versus 13.65% for the Islamic index. Although the Islamic index performs strongly during bear markets, with an average bootstrapped Reward–VaR of $-20.77\%$ compared to $-25.60\%$ for the conventional index, the strength and length of the bull periods are sufficient to give the conventional index the overall edge.

Across the bull subperiods, the conventional index exhibits clear dominance in Bull1, Bull2, and Bull3, with differences reaching as high as 19.43 percentage points. Bull4 is the only subperiod showing statistical equivalence, with a negligible gap of 0.38%. This consistent strength across most subperiods underlies the conventional index’s statistical dominance during the aggregate bull period.

In the bear subperiods, Bear2 stands out with a significant Islamic advantage, while Bear1 and Bear4 show moderate numerical differences but statistical equivalence. During the COVID crash (Bear3), the Islamic index again records a large numerical lead, though extreme volatility prevents statistical confirmation. Collectively, these patterns support the Islamic index’s dominance in the aggregate bear period.

3.3.3. Developed Markets

The dominance-pattern bar chart in Figure 4 provides a visual summary of the results for the developed markets.

The detailed results for the developed markets are provided in

Table 5. Dominance Patterns in the Developed Markets ($\delta =1.15$).

Period	Interval	Index	Avg bRVCO	Avg bRVIS	Diff.	% Diff.
Overall Period
Overall	[0.56, 1.00]	Equal	6.06%	6.17%	0.11%	2%
Bull and Bear Periods
Bull	[0.59, 1.00]	CO	18.10%	17.37%	0.73%	4%
Bear	[0.52, 1.00]	IS	−27.94%	−24.36%	3.58%	13%
Bull and Bear Subperiods
Bull Subperiods
Bull1	[0.61, 1.00]	CO	18.11%	15.50%	2.61%	17%
Bull2	[0.59, 1.00]	Equal	13.54%	13.55%	0.01%	0%
Bull3	[0.68, 1.00]	Equal	40.51%	37.25%	3.26%	8%
Bull4	[0.73, 1.00]	Equal	29.02%	29.47%	0.45%	2%
Bear Subperiods
Bear1	[0.53, 1.00]	Equal	−21.16%	−21.14%	−0.02%	0%
Bear2	[0.59, 1.00]	IS	−48.36%	−40.33%	8.03%	17%
Bear3	[0.66, 1.00]	IS	−257.41%	−220.41%	37.00%	14%
Bear4	[0.58, 1.00]	Equal	−4.36%	−4.10%	0.26%	6%

and discussed below.

Table 5 shows that in the developed markets, the Islamic and conventional indices are statistically equivalent during the overall period. The conventional index achieves a slightly higher average bootstrapped Reward–VaR in bull markets, while the Islamic index performs better in bear markets. However, these opposing tendencies largely balance each other out in the long run, resulting in statistical parity between the two indices over the full sample.

Across the bull subperiods, the conventional index dominates in Bull1, while Bull2 shows near-identical performance. In Bull3 and Bull4, numerical differences favor one index or the other but remain within the threshold for statistical equivalence. Taken together, these results yield modest but statistically significant conventional dominance in the aggregate bull period.

In the bear subperiods, the Islamic index shows clear strength in Bear2 and Bear3, both marked by statistically significant outperformance. Bear1 and Bear4 exhibit near equivalence. During the COVID crash (Bear3), the conventional index suffered annualized losses of 257.41% (approximately 1.02% daily), compared to 220.41% (approximately 0.87% daily) for the Islamic index. These results support statistical dominance for the Islamic index during bear markets.

3.3.4. Emerging Markets

The dominance-pattern bar in Figure 5 below provides a visual summary of the results for the emerging markets.

The detailed results for the emerging markets are provided in

Table 6. Dominance Patterns in the Emerging Markets ($\delta =1.15$).

Period	Interval	Index	Avg bRVCO	Avg bRVIS	Diff.	% Diff.
Overall Period
Overall	[0.57, 1.00]	CO	7.23%	5.11%	2.12%	41%
Bull and Bear Periods
Bull	[0.59, 1.00]	CO	19.32%	17.17%	2.15%	13%
Bear	[0.54, 0.68]	IS	−28.44%	−23.60%	4.84%	17%
	[0.68, 0.99]	Equal	−28.42%	−27.16%	1.26%	4%
	[0.99, 1.00]	CO	−27.02%	−31.55%	4.53%	14%
Bull and Bear Subperiods
Bull Subperiods
Bull1	[0.66, 1.00]	CO	32.37%	23.46%	8.91%	38%
Bull2	[0.58, 1.00]	IS	10.93%	11.76%	0.83%	8%
Bull3	[0.66, 1.00]	CO	29.76%	24.76%	5.00%	20%
Bull4	[0.68, 1.00]	Equal	19.55%	17.32%	2.23%	11%
Bear Subperiods
Bear1	[0.57, 1.00]	IS	−19.27%	−18.63%	0.64%	3%
Bear2	[0.57, 1.00]	Equal	−50.85%	−51.93%	1.08%	2%
Bear3	[0.81, 1.00]	IS	−241.02%	−203.97%	37.05%	15%
Bear4	[0.59, 1.00]	CO	−8.56%	−11.16%	2.60%	23%

and discussed below.

Table 6 shows that in the emerging markets, the conventional index dominates during the overall period, with an average bootstrapped Reward–VaR of 7.23% compared to 5.11% for the Islamic index. This statistical dominance stems primarily from strong conventional outperformance during bull periods. The bear regime is more fragmented: for lower confidence levels (i.e., lower risk aversion), the Islamic index shows a significant advantage; for mid-range confidence levels, it continues to outperform but not in a statistically significant way; and for very high confidence levels (i.e., very high risk aversion), the conventional index gains the upper hand. For almost all but the most extreme confidence levels, the Islamic index is preferable or at least as effective as the conventional index in bear markets. Despite this nuanced structure, the strength and consistency of conventional gains in bull markets drive overall dominance.

Across the bull subperiods, the conventional index outperforms in Bull1 and Bull3, with substantial gaps of 8.91% and 5.00%, respectively. Bull4 shows a moderate numerical advantage for the conventional index, though within the bounds of statistical equivalence. In Bull2, the Islamic index performs slightly better, but the difference is not statistically meaningful. Taken together, these results yield clear and statistically significant dominance for the conventional index during bull markets.

The bear subperiods display a more mixed structure. In Bear1 and Bear3, the Islamic index outperforms, with Bear3 showing especially large numerical differences: the conventional index loses an annualized 241.02% (approximately 1.03% daily), compared to 203.97% (approximately 0.94% daily) for the Islamic index. Bear2 reflects statistical equivalence, while Bear4 shows a conventional advantage. A detailed examination of the bootstrapped Reward-Var curve reveals that, in the aggregate bear regime, the conventional index tends to perform best at high levels of confidence (i.e., high risk aversion). Taken together, these results indicate that the Islamic index is preferable—or at least as effective as the conventional index—at all but the most extreme confidence levels.

3.3.5. Europe

The dominance-pattern bar chart in Figure 6 provides a visual summary of the results for the European market.

The detailed results for the European market are provided in

Table 7. Dominance Patterns in the European Market ($\delta =1.15$).

Period	Interval	Index	Avg bRVCO	Avg bRVIS	Diff.	% Diff.
Overall Period
Overall	[0.55, 1.00]	Equal	5.14%	5.48%	0.34%	7%
Bull and Bear Periods
Bull	[0.58, 1.00]	Equal	17.29%	16.83%	0.46%	3%
Bear	[0.53, 1.00]	IS	−30.72%	−26.18%	4.54%	15%
Bull and Bear Subperiods
Bull Subperiods
Bull1	[0.61, 1.00]	CO	22.11%	18.86%	3.25%	17%
Bull2	[0.58, 1.00]	IS	11.28%	12.08%	0.80%	7%
Bull3	[0.68, 1.00]	Equal	36.55%	35.54%	1.01%	3%
Bull4	[0.71, 1.00]	Equal	24.38%	26.25%	1.87%	8%
Bear Subperiods
Bear1	[0.56, 1.00]	Equal	−23.29%	−20.47%	2.82%	12%
Bear2	[0.58, 1.00]	IS	−55.12%	−44.51%	10.61%	19%
Bear3	[0.76, 1.00]	Equal	−251.89%	−236.60%	15.29%	6%
Bear4	[0.58, 1.00]	Equal	−4.47%	−7.68%	3.21%	72%

and discussed below.

Table 7 shows that in the European market, the Islamic and conventional indices are statistically equivalent over the full sample period. This statistical equivalence reflects a balance of contrasting behaviors across different market regimes, with bull periods showing no clear dominance and bear periods favoring the Islamic index. Since the overall bull market spans more than three times the length of the bear market, the Islamic index’s bear-period gains and the conventional index’s modest edge in bull markets effectively offset each other, yielding a slight yet statistically insignificant numerical advantage for the Islamic index.

Across the bull subperiods, the conventional index dominates in Bull1, with a 3.25% advantage. The Islamic index outperforms in Bull2 by 0.80%, a smaller margin but over a substantially longer interval. Bull3 slightly favors the Islamic index (1.01%), while Bull4 slightly favors the conventional index (1.87%), though both are classified as statistically equivalent. Taken together, the combination of offsetting numerical gaps and unequal subperiod durations yields statistical equivalence in the aggregate bull period.

In the bear subperiods, Bear2 exhibits a strong and statistically significant advantage for the Islamic index. The remaining subperiods—Bear1, Bear3, and Bear4—are statistically equivalent, though Bear1 and Bear3 show visible numerical differences favoring the Islamic index. These results support statistical dominance for the Islamic index during the aggregate bear period.

3.3.6. Japan

The dominance-pattern bar chart in Figure 7 provides a visual summary of the results for the Japanese market.

The detailed results for the Japanese market are provided in

Table 8. Dominance Patterns in the Japanese Market ($\delta =1.15$).

Period	Interval	Index	Avg bRVCO	Avg bRVIS	Diff.	% Diff.
Overall Period
Overall	[0.54, 1.00]	Equal	3.57%	3.23%	0.34%	10%
Bull and Bear Periods
Bull	[0.56, 1.00]	IS	13.53%	15.08%	1.55%	11%
Bear	[0.50, 1.00]	CO	−27.36%	−29.77%	2.41%	8%
Bull and Bear Subperiods
Bull Subperiods
Bull1	[0.59, 1.00]	CO	16.99%	13.56%	3.43%	25%
Bull2	[0.57, 1.00]	IS	9.43%	12.94%	3.51%	37%
Bull3	[0.64, 1.00]	Equal	27.34%	30.52%	3.18%	12%
Bull4	[0.73, 1.00]	Equal	19.08%	19.31%	0.23%	1%
Bear Subperiods
Bear1	[0.52, 1.00]	Equal	−26.30%	−28.30%	2.00%	8%
Bear2	[0.56, 1.00]	Equal	−37.89%	−41.64%	3.75%	10%
Bear3	[0.59, 1.00]	Equal	−226.96%	−213.42%	13.54%	6%
Bear4	[0.57, 1.00]	CO	−3.44%	−11.40%	7.96%	70%

and discussed below.

Table 8 shows that in the Japanese market, the Islamic and conventional indices are statistically equivalent over the full sample period. This statistical equivalence results from contrasting dynamics across different regimes: bull markets favor the Islamic index, while bear markets favor the conventional index.

Across the bull subperiods, the Islamic index outperforms in Bull2, with a 3.51% advantage over a relatively long interval. The conventional index leads in Bull1 by a nearly identical 3.43%, but over a shorter time span. Bull3 and Bull4 are both classified as Equal, with minor numerical differences that do not reach statistical significance. Taken together, these outcomes result in statistical dominance for the Islamic index during the aggregate bull period.

In the bear subperiods, Bear1, Bear2, and Bear3 are statistically equivalent, despite notable numerical gaps, while Bear4 shows a clear and statistically significant advantage for the conventional index. This result is sufficient to yield conventional dominance over the aggregate bear period.

3.3.7. UK

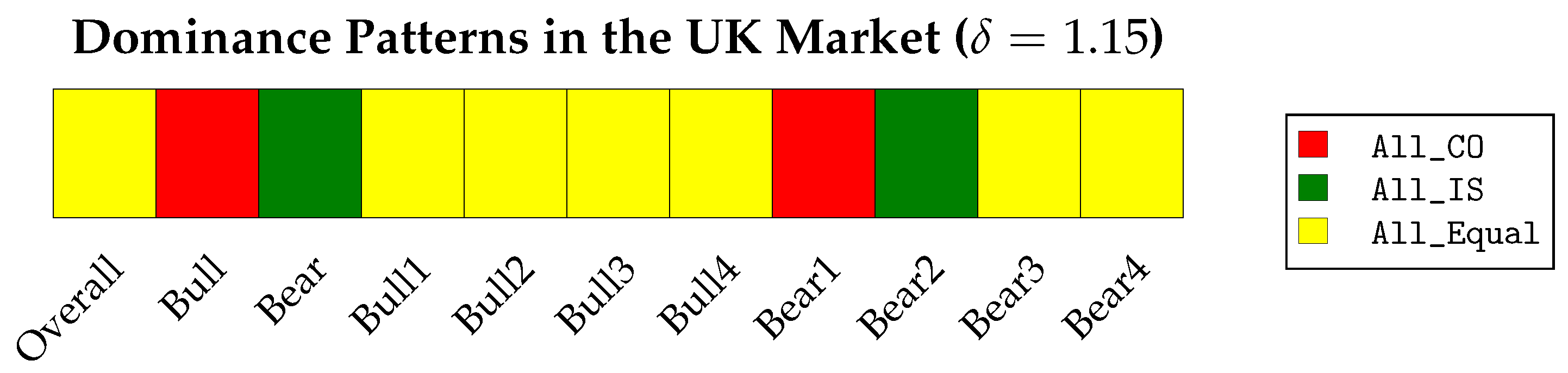
The dominance-pattern bar chart in Figure 8 provides a visual summary of the results for the UK market.

The detailed results for the UK market are provided in

Table 9. Dominance Patterns in the UK Market ($\delta =1.15$).

Period	Interval	Index	Avg bRVCO	Avg bRVIS	Diff.	% Diff.
Overall Period
Overall	[0.55, 1.00]	Equal	3.68%	3.55%	0.13%	4%
Bull and Bear Periods
Bull	[0.57, 1.00]	CO	15.54%	14.36%	1.18%	8%
Bear	[0.54, 1.00]	IS	−29.42%	−25.46%	3.96%	13%
Bull and Bear Subperiods
Bull Subperiods
Bull1	[0.60, 1.00]	Equal	18.36%	17.23%	1.13%	6%
Bull2	[0.57, 1.00]	Equal	10.46%	9.70%	0.76%	7%
Bull3	[0.65, 1.00]	Equal	33.62%	33.99%	0.37%	1%
Bull4	[0.66, 1.00]	Equal	20.70%	20.55%	0.15%	1%
Bear Subperiods
Bear1	[0.56, 1.00]	CO	−19.10%	−19.75%	0.65%	3%
Bear2	[0.59, 1.00]	IS	−55.89%	−40.79%	15.10%	27%
Bear3	[0.79, 1.00]	Equal	−319.42%	−299.82%	19.60%	6%
Bear4	[0.60, 1.00]	Equal	−1.66%	−4.18%	2.52%	152%

and discussed below.

Table 9 shows that in the UK market, the Islamic and conventional indices are statistically equivalent over the full sample period. This statistical equivalence reflects a balance of opposing effects across different market regimes, with the conventional index performing better in bull markets and the Islamic index showing strength in bear markets.

Across the bull subperiods, all four episodes are classified as Equal. The conventional index holds numerical advantages in Bull1 and Bull2, while the Islamic index displays a numerical edge in Bull3 and Bull4. However, all differences fall well within the statistical threshold. Since Bull1 and Bull2 together account for over 70% of the total bull period, their cumulative influence is confirmed by a statistical advantage for the conventional index during the aggregate bull period.

In the bear subperiods, Bear2 stands out with a strong and statistically significant advantage for the Islamic index. Bear1 favors the conventional index, but the difference, while statistically meaningful, is modest. Bear3 and Bear4 are statistically equivalent, with opposing numerical tendencies that largely offset each other. Because Bear2 is both long and strongly favorable to the Islamic index, it dominates the aggregate outcome, resulting in statistical dominance over the full bear period.

3.3.8. United States

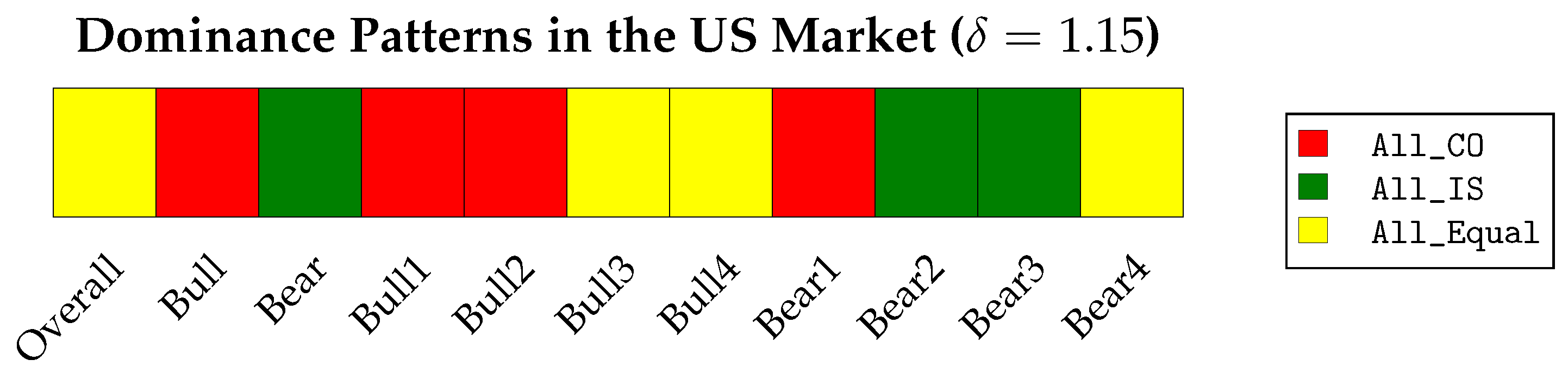
The dominance-pattern bar chart in Figure 9 provides a visual summary of the results for the US market.

The detailed results for the US market are provided in

Table 10. Dominance Patterns in the US Market ($\delta =1.15$).

Period	Interval	Index	Avg bRVCO	Avg bRVIS	Diff.	% Diff.
Overall Period
Overall	[0.57, 1.00]	Equal	9.20%	8.51%	0.69%	7%
Bull and Bear Periods
Bull	[0.59, 1.00]	CO	21.12%	19.27%	1.85%	10%
Bear	[0.54, 1.00]	IS	−23.83%	−21.20%	2.63%	11%
Bull and Bear Subperiods
Bull Subperiods
Bull1	[0.64, 1.00]	CO	17.00%	15.16%	1.84%	12%
Bull2	[0.59, 1.00]	CO	17.92%	16.22%	1.70%	10%
Bull3	[0.69, 1.00]	Equal	45.43%	43.55%	1.88%	4%
Bull4	[0.73, 1.00]	Equal	33.95%	32.28%	1.67%	5%
Bear Subperiods
Bear1	[0.57, 1.00]	CO	−16.85%	−17.97%	1.12%	6%
Bear2	[0.60, 1.00]	IS	−40.51%	−33.85%	6.66%	16%
Bear3	[0.69, 1.00]	IS	−257.04%	−232.90%	24.14%	9%
Bear4	[0.58, 1.00]	Equal	−3.55%	−2.57%	0.98%	28%

and discussed below.

Table 10 shows that in the US market, there is a balanced dynamic between the two indices, with the conventional index holding an advantage during bull markets and the Islamic index prevailing in bear markets. These opposing effects offset each other, resulting in overall statistical equivalence.

The reason for the overall dominance of the conventional index during bull markets is clear: it achieves a higher average bootstrapped Reward–VaR value across all subperiods and, in particular, does so in a statistically significant manner during Bull1 and Bull2, which together account for a large portion of the full bull period.

In contrast, bear markets favor the Islamic index, which achieves a statistically significant advantage overall. Bear1 shows a modest but statistically significant edge for the conventional index. However, this is outweighed by the Islamic index’s strong and statistically significant outperformance in Bear2 and Bear3. Bear4 is statistically equivalent, despite a numerical edge for the Islamic index. The strength and duration of Bear2 and Bear3 jointly explain the Islamic index’s aggregate dominance in bear markets.

3.3.9. World

The dominance-pattern bar chart in Figure 10 provides a visual summary of the results for the World market.

The detailed results for the World market are provided in

Table 11. Dominance Patterns in the World Market ($\delta =1.15$).

Period	Interval	Index	Avg bRVCO	Avg bRVIS	Diff.	% Diff.
Overall Period
Overall	[0.56, 1.00]	Equal	4.68%	5.19%	0.51%	11%
Bull and Bear Periods
Bull	[0.59, 1.00]	Equal	16.63%	16.55%	0.08%	0%
Bear	[0.52, 1.00]	IS	−28.96%	−25.40%	3.56%	12%
Bull and Bear Subperiods
Bull Subperiods
Bull1	[0.61, 1.00]	CO	18.74%	15.91%	2.83%	18%
Bull2	[0.59, 1.00]	IS	11.41%	12.43%	1.02%	9%
Bull3	[0.69, 1.00]	Equal	36.50%	35.38%	1.12%	3%
Bull4	[0.75, 1.00]	Equal	25.88%	27.46%	1.58%	6%
Bear Subperiods
Bear1	[0.54, 1.00]	Equal	−21.00%	−20.83%	0.17%	1%
Bear2	[0.58, 1.00]	IS	−48.59%	−41.91%	6.68%	14%
Bear3	[0.66, 1.00]	IS	−267.85%	−232.03%	35.82%	13%
Bear4	[0.58, 1.00]	Equal	−7.08%	−6.13%	0.95%	13%

and discussed below.

Table 11 shows that in the World market, there is no clear dominance between the two indices, resulting in overall statistical equivalence. While bull markets exhibit no statistically significant difference between the indices, bear markets favor the Islamic index.

During bull markets, there is no statistically significant difference between the two indices. Bull1 favors the conventional index with an 18% edge, while Bull2 shows a 9% advantage for the Islamic index. Bull3 and Bull4 are classified as statistically equivalent, with small numerical differences of 3% and 6%, respectively. These mixed results, combined with the modest overall gap of only 0.08%, lead to statistical equivalence in the aggregate.

In bear markets, the Islamic index shows strong and statistically significant dominance in Bear2 and Bear3, with large gaps of 6.68% and 35.82%, respectively. Bear1 and Bear4 also favor the Islamic index, though the differences are smaller and not statistically significant. Taken together, all four bear subperiods align in favor of the Islamic index, and the strength and duration of Bear2 and Bear3 drive a clear statistical advantage over the full bear period.

4. Conclusions

Over more than two decades of research, the comparative performance of Islamic and conventional equity indices has remained an open question, with studies reaching divergent conclusions. One way to reconcile these inconsistencies is to recognize that neither index may be universally superior: each could outperform the other for investors with different risk preferences. This new analytical perspective was examined in this paper using the Reward–VaR curve—a novel risk–reward metric that evaluates asset performance across the full spectrum of risk preferences. Within our framework, the level of risk aversion is measured by the confidence level $\alpha$ of VaR, allowing performance to be evaluated continuously as investor preferences range from risk-tolerant to risk-averse.

Our study examines whether one index consistently outperforms the other across all risk levels, or whether each index is preferred by investors with different risk profiles. A third possibility is the absence of a coherent pattern—or the presence of a complicated one—which would have suggested that asset preferences do not follow a simple relationship with the confidence level.

Our empirical analysis reveals a coherent pattern. Conventional indices tend to dominate during bull markets, whereas Islamic indices provide stronger downside protection in bear markets. Over the long run, both indices exhibit comparable performance. While this pattern is not universal, it recurs with remarkable regularity across a broad range of regional markets and is supported by significant statistical evidence.

An explanation for this behavior may lie in the Islamic screening process, which prohibits excessive leverage—a rule rooted in the broader principles of avoiding gharar (excessive uncertainty) and riba (interest-based financing). By systematically excluding firms whose debt-to-market-capitalization ratios exceed prescribed thresholds (Derigs & Marzban, 2008), Islamic equity indices limit exposure to highly leveraged companies. Because leverage amplifies both gains and losses, the lower leverage of Islamic indices limits their upside potential in bull markets but cushions their performance during downturns. The opposing effects of lower leverage in bull and bear markets largely offset one another, leading to comparable outcomes over the long run.

For faith-based investors, the results are reassuring, as they indicate that adherence to Islamic principles does not entail a performance penalty in the long run. For other investors and portfolio managers, a regime-based strategy—shifting exposure between Islamic and conventional indices across market cycles—could potentially enhance portfolio performance.

It is clear that ranking investment opportunities across risk-aversion levels is of primary importance. No one would recommend the same investments to a recently retired individual on a tight budget as to a bullish twenty-year-old with a forty-year horizon. This is why regulations in most developed countries require investment firms to assess the risk profile of their clients.

Future research could extend the scope of this paper in several directions. Ranking investment opportunities across risk-aversion levels using the Reward-VaR curve could be extended to a broad range of asset classes, such as value versus growth stock indices or small-cap versus blue-chip portfolios. Its study should include not only empirical return distributions, but also theoretical ones such as the Student-t and skewed-t families, which capture the heavy tails and asymmetries commonly observed in financial data through their respective kurtosis and skewness parameters.

New approaches to approximating and smoothing the VaR, beyond the mVaR framework, could also be explored. Polynomial regression methods or modern machine-learning algorithms could be used to obtain smooth, analytically simple, and computationally efficient approximations of VaR.

In the modified Reward–VaR curve of order 3, a phase transition in asset ranking is demonstrated. Given that the ranking generated by the curve of order 2 coincides with that of the Sharpe ratio, the order-3 version represents a natural extension that incorporates skewness. It would therefore be interesting to investigate the practical and economic implications of moving from the Sharpe ratio to the Reward–VaR curve of order 3. More fundamentally, this raises a broader question for future research: what are the economic consequences when the ranking of assets is no longer absolute but depends on the level of risk aversion?